Introduction

In recent years, a plethora of researches has been focused on micro- and nanoscale transport marvels. The systems designed based on these phenomena are usually known as micro- and nanoelectromechanical systems (MEMS/NEMS). Such small-scale systems have opened new applications in different fields such as electronic industry, medical applications, fundamental science, microsensors, micropumps, accelerometers, and vitality collecting [1]. The widespread use of microchannels has now challenged researchers with methods and solutions to control the fluid flow, friction, and heat transfer [2, 3] for improved transport and cooling purposes in order to maintain the desired performance [4]. The researches have been conducted toward different aspects [5], in particular the design of geometry, adjustments to fluidic medium and material properties, liquid elements of the system, and applying outer irritations such as electric or attractive fields.

Microchannels are classified by several parameters. The size is the most important characteristic in which the applicability of microchannels is defined. Large microchannels with length scale more than 25 μm are designed for compact heat exchangers and arteries, and smaller ones are used to manipulate and separate live cells and viruses and other biomedical application. Another parameter is the material of microchannels which is specified based on the working fluid properties such as thermal conductivity and the level of erosion. The last well-known parameter is the shape of microchannels which is dictated by the system design. There may be different shapes of microchannel cross sections in heat sink application [6].

Microchannels in thermal management systems are flumes that dissipate a great deal of heat with respect to other methods due to their high ratio of heat transfer surface to fluid volume [7]. Besides, great cooling performance observed in microchannels contributes to the increased heat transfer coefficient as a result of hydraulic diameter reduction. Therefore, they have been regarded as a prevalent choice in fine-scale and precise cooling processes.

Recently, much attention has been paid to numerical investigations to model and optimize the working conditions in these applications. These investigations have been performed on accurate analysis of flow conditions, and the inclusive results are mostly used to reduce pumping power and improve cooling efficiency [8]. In a comprehensive research, Tullius et al. [9] investigated various designs and methods used to enhance the cooling performance of microchannels.

Common fluids such as water, ethylene glycol, and heat transfer oil play an important role in many industrial processes such as power generation, heating or cooling processes, chemical processes, and microelectronics. However, these fluids have relatively low thermal conductivity and thus cannot reach high heat exchange rates in thermal engineering devices. A way to overcome this barrier is using ultra-fine solid particles suspended in common fluids to improve their thermal conductivity. The suspension of nanosized particles (1–100 nm) in a conventional base fluid is called a nanofluid [10]. Nanofluids, compared to suspensions with particles of millimeter or micrometer size, show better stability, rheological properties, and considerably higher thermal conductivities.

Nowadays, nanofluids are widely used as an effective method to improve the heat transfer characteristics in different applications, e.g., heat exchangers [11], coolants, and especially the microchannels [12]. In this method, the conductive nanoparticles such as Au and Ag are added to the base fluid, e.g., water and oil. The magnetic field which produces a force in the opposite direction of flow in electrically conductive fluids can be used as another method to enhance the heat transfer [5] in microchannels. A review in the field [13] has thoroughly analyzed the studies on the effect of magnetic field on heat transfer enhancement within confined geometries.

The flow field in microchannels for both Newtonian [14] and non-Newtonian [15] fluids can be affected by a transverse magnetic field which can be performed by changing the Lorentz force [13]. It is experimentally proved [16] that the flow resistance coefficient in microchannel varies with the length and strength of the applied magnetic field.

A numerical study of the magnetic field effect on the flow characteristics in a magnetohydrodynamic micropump has been performed by Duwairi and Abdullah [17]. They showed that the magnetic flux, the potential difference, and the electrical conductivity play an important role in heat transfer controlling in a microchannel. Moreover, in another numerical study, Aminossadati et al. [18] examined the effect of magnetic field on water–Al2O3 nanofluid flowing in a microchannel. They revealed that the magnetic field could boost the average Nusselt number for different nanofluid concentrations, especially at high Reynolds and Hartmann numbers.

Although the transverse magnetic field enhances the heat transfer, it has a negative effect on increasing the higher shear stress, which makes the higher demand for pumping power. In this regard, using hydrophobic material on the microchannel walls and making a super-hydrophobic surface could be an effective solution. Velocity slip was observed experimentally by Tretheway and Meinhart [19], when they used a nanometer coating layer to make a rectangular microchannel with super-hydrophobic walls. It should be noted that liquids (nanofluids) flowing in microchannels are in continuous flow regime where Knudsen number is less than 0.001 [20]. Nonetheless, due to using super-hydrophobic surface in the microchannel, liquids (nanofluids) flow is in slip flow regime [21].

Afrand et al. [22] numerically implied the transverse magnetic field on a microchannel and monitored the effects of velocity slip and magnetic force on the flow characteristics of functionalized multiwalled carbon nanotubes (FMWCNTs)–water nanofluid. The microchannel was modeled by two parallel plates, when the plates’ temperatures were kept constant. Likewise, Karimipour et al. [23] applied the constant heat flux instead of the constant temperature on the walls. Their results reveal that using the transverse magnetic field can be promising in thermally developing region and it is insignificant in the thermally fully developed region.

Karimipour and Afrand [24] simulated the Cu–water nanofluid in a microchannel and examined the effect of Hartmann number and volume fraction of nanofluid on heat transfer. The results showed that the magnetic field effect was more conspicuous than the Reynolds number in increasing heat transfer performance. In another study, Karimipour et al. [25] used Al2O3 and Ag nanoparticles as MHD nanofluid in a microchannel. They considered the velocity slip and temperature jump, and the walls were of constant temperature boundary condition. They observed that, in higher Hartmann numbers, the Nusselt number decreased with the increase in slip coefficient.

In recent years, various nanoparticles have been produced by using synthetic methods. In Table 1, only some recent investigations, which studied the effect of different nanoparticles in the microchannel flow, have been listed. Moreover, the fluid flow regime and characteristic are presented.

Table 1 List of selected recent studies focusing on the effect of nanofluid types in fluid flow and heat transfer in microchannels
Full size table

Lattice Boltzmann method (LBM) [35] is a numerical method which is based on mesoscale method similar to dissipative particle dynamics (DPD) [36]. It has been proved that this method is of great importance in analyzing problems such as particle-laden flows [37], mixed and natural convection heat transfer [38], and multiphase flow [39]. The other point that makes LBM more interesting than traditional computational fluid dynamic (CFD) methods is that the programming is much easier and can be easily parallelized computationally [40].

The modeling and simulation of fluid flow and heat transfer in cavities and enclosures using MHD fluid have been extensively investigated using LBM [41]. Lattice Boltzmann simulation of magnetic field effect on a conductive gas has been performed by Agarwal [42], when the gas was in slip flow regime. The results signified good agreement with the analytical solution. Kalteh and Abedinzadeh [43] studied the effect of magnetic field on fluid flow and heat transfer characteristics in a microchannel with forced convection flow. The temperature of the microchannel walls was constant as a boundary condition. The results represented that the effect of the magnetic field could be ignored on heat transfer coefficient, while its effect was considerable on the friction factor coefficient (up to 86% increase).

As LBM is widely used in analyzing nanofluids with magnetohydrodynamics (MHD) flows [44], many studies have been carried out on applying velocity slip and temperature jump at the liquid–solid interface. There have been numerous works considering not any of these two conditions [18], some researches just implemented velocity slip [45], while other works implemented temperature jump as well [46].

It is stated here that if the temperature jump at the boundaries is not regarded, the temperature profile will be inaccurate and the Nusselt number will be over-estimated. To the best knowledge of the authors, no previous studies have been carried out so far on heat transfer of nanofluids (with variable thermal conductivity) in microchannels with considering both velocity slip and temperature jump boundary conditions on the application of transverse magnetic field and constant heat flux boundary condition. As a result, we use the incompressible preconditioned lattice Boltzmann method (IPLBM) of a super-hydrophobic microchannel with slip flow regime. Furthermore, in the present study, we studied the effects of magnetic field intensity, wall hydrophobicity level, and different nanofluids on flow hydrodynamics and heat transfer.

This work is purpose-specific numerical methods on top of which subsequent research works either numerical or experimental can be built in the future.

Problem statement

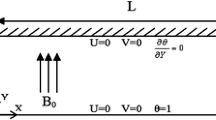
Figure 1 represents schematic of a 2D microchannel in which 70% trailing segment of the upper wall is under the influence of a magnetic field (0.3 L < x < L ( in addition to the uniform heat flux boundary condition. The height and length of the microchannel are 40 and 25 μm, respectively. When the hydrophobic coating is applied on the walls, there is a slip flow regime where the velocity slip and temperature jump should be considered. The Reynolds number of 50 has been studied for all the cases at hand. The lower wall of the microchannel is all insulated, while the insulation of the upper wall has been applied just on the 30% leading segment (x < 0.3 L).

Fig. 1
figure 1

Geometry of the 2D microchannel with partially insulated walls along with applying a magnetic field and heat flux

Full size image

The thermo-physical properties of water as the base fluid and different nanoparticles which were used in the present study are presented in Table 2.

Table 2 Properties of water, Al2O3, CuO, and Ag and Fe solid particles [47]
Full size table

Mathematical formulations

Lattice Boltzmann method

For the first time, Guo et al. [48] introduced the preconditioned LBM (PLBM) to increase convergence in the customary LBM. Moreover, He and Luo [49] used the incompressible version of the LBM (ILBM) in order to reduce the errors in LBM simulations. In the present study, we have used a combination (IPLBM) with a source term. The discretized form of hydrodynamic Boltzmann equation is to be solved which consists of two collision and streaming processes [50] that is as follows [37]:

$$f_{\text{k}} \left( {\vec{r} + \Delta \vec{r},t + \Delta t} \right) - f_{\text{k}} \left( {\vec{r},t} \right) = - \frac{{\Delta t}}{{\tau_{\text{f}} }}\left[ {f_{\text{k}} \left( {\vec{r},t} \right) - f_{\text{k}}^{\text{eq}} \left( {\vec{r},t} \right)} \right] + \Delta t F_{\text{k}} .$$
(1)

In Eq. (1), f represents the density distribution function at the mesoscopic scale. Also, k subscript is the direction for lattice links, \(\vec{r} = x \vec{i} + y\overrightarrow { j}\) is the position vector, \(\Delta \vec{r}\) is the product that is related to discrete lattice velocity \((c_{\text{k}} )\) and time step ∆t. τf represents the relaxation time that is used for density distribution function and is related to kinematic viscosity \((\upsilon )\) as the following relation [48]:

$$\upsilon = \gamma C_{\text{s}}^{2} \left( {\frac{{\tau_{\text{f}} }}{\Delta t} - 0.5} \right)\Delta t,$$
(2)

where γ is a parameter (0 < γ ≤ 1) that is used to increase the convergence rate [44]. Also, \(c_{\text{s}}\) is the speed of sound and it is a combination of displacement and time \(\left( {c_{\text{s}} = \Delta x/\left( {\sqrt 3 \Delta t} \right)} \right)\). Moreover, feq is the equilibrium distribution function and is defined as follows [51]:

$$f_{\text{k}}^{\text{eq}} = w_{\text{k}} \left[ {\rho + \rho_{0} \left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{2} }} + \frac{1}{2\gamma }\left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{2} }}} \right)^{2} - \frac{{\vec{V} \cdot \vec{V}}}{{2\gamma c_{\text{s}}^{2} }}} \right)} \right].$$
(3)

In this equation, \(\rho\) and \(\rho_{0}\) are the fluid density and the constant initial density, respectively. Also, \(\vec{V}\) is the macroscopic velocity and \(\overrightarrow {{c_{\text{k}} }}\) is the microscopic lattice velocity vector defined as follows [35]:

$$\overrightarrow {{c_{\text{k}} }} = \left\{ {\begin{array}{*{20}l} {\left( {0,0} \right)} \hfill & {k = 0} \hfill \\ {\left( {\cos \frac{{\pi \left( {k - 1} \right)}}{2},\sin \frac{{\pi \left( {k - 1} \right)}}{2}} \right)\frac{\Delta x}{\Delta t}} \hfill & {k = 1 - 4} \hfill \\ {\sqrt 2 \left( {\cos \frac{{\pi \left( {2k - 1} \right)}}{4},\sin \frac{{\pi \left( {2k - 1} \right)}}{4}} \right)\frac{\Delta x}{\Delta t}} \hfill & {k = 5 - 8} \hfill \\ \end{array} } \right..$$
(4)

Moreover, \(w_{\text{k}}\) is the weight function along with various directions of lattice links (k) that is demonstrated as [52]:

$${\text{w}}_{\text{k}} = \left\{ {\begin{array}{*{20}l} {\frac{1}{4}} \hfill & {k = 0 } \hfill \\ {\frac{1}{9}} \hfill & {k = 1 - 4} \hfill \\ {\frac{1}{36}} \hfill & {k = 5 - 8} \hfill \\ \end{array} } \right\}.$$
(5)

In Eq. (1), Fk is the source term and is defined in the direction of lattice links. It is represented as follows [50]:

$$F_{\text{k}} = \frac{1}{{\gamma^{2} }}w_{\text{k}} \left( {1 - \frac{\Delta t}{{2\tau_{\text{f}} }}} \right)\left[ {\frac{{\overrightarrow {{c_{\text{k}} }} - \vec{V}}}{{c_{\text{s}}^{2} }} + \left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{4} }}} \right)\overrightarrow {{c_{\text{k}} }} } \right] \cdot \rho_{0} \vec{a}.$$
(6)

Here, \(\vec{a}\) is the acceleration vector for the transverse magnetic field [53]:

$$\vec{a} = a_{\text{x}} \vec{i} + a_{\text{y}} \overrightarrow { j} = - \frac{{B_{0}^{2} \sigma_{\text{nf}} }}{{\rho_{0} }}u \vec{i} + 0 \overrightarrow { j} = \frac{{Ha^{2} \mu_{\text{nf}} }}{{\rho_{0} H_{\text{c}}^{2} }} \vec{i}.$$
(7)

In the above relations, \(\sigma_{\text{nf}}\) is the electrical conductivity and \(\mu_{\text{nf}}\) is the dynamic viscosity of the nanofluid. Also, Ha represents the Hartmann number which is a dimensionless number.

In the following relations, macroscopic nanofluid density and velocity in the D2Q9 lattice (Fig. 2) method have been brought as follows [50]:

$$\rho = \mathop \sum \limits_{{{\text{k}} = 0}}^{8} f_{\text{k}}$$
(8)
$$\rho_{0} \vec{V} = \mathop \sum \limits_{{{\text{k}} = 0}}^{8} \overrightarrow {{C_{\text{k}} }} \cdot f_{\text{k}} + \frac{\Delta t}{2}\rho_{0} \vec{a}.$$
(9)

The temperature field is solved using standard LBM based on passive scalar approach with D2Q9 lattice via the discretized Boltzmann equation in the following form [54]:

$$g_{\text{k}} \left( {\vec{r} + \overrightarrow {\Delta r} ,t + \Delta t} \right) - g_{\text{k}} \left( {\vec{r},t} \right) = - \frac{\Delta t}{{\tau_{\text{g}} }}\left[ {g_{\text{k}} \left( {\vec{r},t} \right) - g_{\text{k}}^{\text{eq}} \left( {\vec{r},t} \right)} \right].$$
(10)

In this equation, g and geq are distribution function and equilibrium distribution function of dimensionless temperature field, respectively. Also, τg is the relaxation time for dimensionless temperature distribution function and is based on the following relation [54]:

$$\alpha = C_{\text{s}}^{2} \left( {\frac{{\tau_{\text{g}} }}{\Delta t} - 0.5} \right)\Delta t.$$
(11)

Moreover, geq along the various directions of lattice links (k) is as follows [54]:

$$g_{\text{k}}^{\text{eq}} = w_{\text{k}} \theta \left[ {1 + \left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{2} }} + \frac{1}{2}\left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{2} }}} \right)^{2} - \frac{{\vec{V} \cdot \vec{V}}}{{2c_{\text{s}}^{2} }}} \right)} \right].$$
(12)

Also, the dimensionless temperature is calculated via:

$$\theta = \mathop \sum \limits_{{{\text{k}} = 0}}^{8} g_{\text{k}}$$
(13)

Dimensionless parameters in this study are defined as follows:

$$X^{*} = \frac{x}{Hc},\quad Y^{*} = \frac{y}{Hc},\quad u^{*} = \frac{u}{{u_{\text{in}} }},\quad v^{*} = \frac{v}{{u_{\text{in}} }},\quad \theta = \frac{{T - T_{\text{in}} }}{{\frac{{q^{\prime \prime } Hc}}{{k_{\text{f}} }}}},$$
(14)

where \(k_{\text{f}}\) is the thermal conductivity coefficient of the base fluid.

Fig. 2
figure 2

Lattice unit structure in D2Q9 lattice model

Full size image

Boundary conditions

In the inlet section, a counter-slip approach with second-order accuracy [55] is implemented. On the other hand, the second-order extrapolation scheme is used for the outlet [56]. Moreover, the Navier formula is used [19] in the lower wall to consider no-slip and slip boundary conditions:

$$u = B\frac{\partial u}{{\partial Y^{*} }}|_{{{\text{Y}}^{*} = 0}} ,$$
(15)

where \(B = \frac{\beta }{Hc}\) is the dimensionless slip coefficient and β is the slip coefficient. By second-order forward derivative discretization, Eq. (15) will be as follows:

$$u_{0} = \frac{B}{{2\Delta Y^{*} + 3B}}\left( {4u_{1} - u_{2} } \right).$$
(16)

In this equation, \(u_{0}\), \(u_{1}\), and \(u_{2}\) are the horizontal velocity, respectively, on the wall boundary, the first and second nodes above the lower wall.

Moreover, the counter-slip boundary condition is used at the inlet and second-order extrapolation is used to calculate unknown distribution functions at the outlet. The lower wall is fully insulated, and the upper one is only partially insulated x = 0.3 L [56]. Energy balance on the walls in dimensionless form is as follows:

$$\left. {\frac{\partial \theta }{{\partial Y^{*} }}} \right|_{{{\text{Y}}^{*} = 1}} = - 1.$$
(17)

Upon performing discretization method on this equation with second-order backward derivative, the dimensionless temperature of fluid on the wall (θn) has been developed. Temperature jump occurs on the upper wall of the non-insulated section and is applied as the following relation [25]:

$$T_{\text{nf}} = T_{\text{w}} + \zeta^{*} \frac{\partial T}{{\partial y^{*} }}_{{\left| {{\text{y}}^{*} = 1} \right.}} .$$
(18)

In this equation, \(\zeta^{*} = \frac{\zeta }{Hc} = \frac{B 2\varGamma }{{Pr\left( {\varGamma + 1} \right)}}\) is the dimensionless temperature jump coefficient. Also, \(T_{\text{nf}}\) is the nanofluid temperature adjacent to the upper wall \((T_{\text{w}} )\). Dimensionless temperature jump is then defined by:

$$\theta_{\text{jump}} = \frac{{T_{\text{nf}} - T_{\text{w}} }}{{\frac{{q^{\prime \prime } Hc}}{{k_{\text{f}} }}}}.$$
(19)

Moreover, the average wall shear stress, friction factor coefficient, and local and average Nusselt numbers [57] are defined as follows:

$$\overline{{\tau_{\text{w}} }} = \frac{{\mathop \int \nolimits_{0}^{L} \mu_{\text{nf}} \frac{\partial u}{\partial y}|_{{{\text{y}} = 0}} {\text{d}}x}}{L},\quad \overline{{c_{\text{f}} }} = \frac{{2\overline{{\tau_{\text{w}} }} }}{{\rho u_{\text{in}}^{2} }},\quad Nu = \frac{{\left. { - k_{\text{nf}} \frac{\partial T}{\partial y}} \right|_{{{\text{y}} = {\text{Hc}}}} }}{{T_{\text{w}} - T_{\text{in}} }} \frac{Hc}{{k_{\text{f}} }},\quad \overline{Nu} = \frac{{\mathop \int \nolimits_{{0.3\,{\text{L}}}}^{L} Nu {\text{d}}x}}{{0.7\,{\text{L}}}}.$$
(20)

Also, the dimensionless average velocity is defined as:

$$V_{\text{avg}}^{*} = \frac{{{\iint }\rho \vec{V} \cdot \vec{n}{\text{d}}A}}{{\rho A U_{\text{in}} }} = \frac{{\mathop \int \nolimits_{0}^{\text{Hc}} \vec{V} \cdot \vec{n} {\text{d}}y}}{{Hc U_{\text{in}} }} = \frac{{\mathop \int \nolimits_{0}^{\text{Hc}} \left( {u \vec{i} + v \vec{j}} \right) \cdot \vec{i} {\text{d}}y}}{{Hc U_{\text{in}} }} = \frac{{\mathop \int \nolimits_{0}^{\text{Hc}} u\,{\text{d}}y}}{{Hc U_{\text{in}} }} = \frac{{u_{\text{avg}} }}{{U_{\text{in}} }} = u_{\text{avg}}^{*} ,$$
(21)

where \(k_{\text{nf}}\) is the thermal conductivity coefficient of nanofluid.

Nanofluid modeling

The following relations are used for modeling density and specific heat capacity of nanofluid as a two-phase mixture model [54]:

$$\rho_{\text{nf}} = \left( {1 - \varphi_{\text{p}} } \right)\rho_{\text{f}} + \varphi_{\text{p}} \rho_{\text{P}}$$
(22)
$$\left( {\rho c_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \varphi_{\text{p}} } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \varphi_{\text{p}} \left( {\rho c_{\text{p}} } \right)_{\text{p}} .$$
(23)

The Roscoe model [58] is also used for modeling nanofluid viscosity:

$$\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} = \frac{1}{{\left( {1 - 1.35\varphi_{\text{p}} } \right)^{2.5} }}.$$
(24)

In order to calculate the thermal conductivity of nanofluid, Patel model has been implemented [59]:

$$\frac{{k_{\text{nf}} - k_{\text{f}} }}{{k_{\text{f}} }} = \frac{{k_{\text{p}} }}{{k_{\text{f}} }}\left( {1 + Cte Pe_{\text{p}} } \right)\frac{{d_{\text{f}} }}{{d_{\text{p}} }}\frac{{\varphi_{\text{p}} }}{{1 - \varphi_{\text{p}} }},$$
(25)

where k is the thermal conductivity coefficient and Cte is a constant equal to 25,000. Moreover, \(Pe_{\text{p}}\) is the Peclet number of the nanoparticles and is defined as follows:

$$Pe_{\text{p}} = \frac{{u_{\text{p}} d_{\text{p}} }}{{\alpha_{\text{f}} }}$$
(26)

where \(u_{\text{p}}\) is the Brownian motion velocity:

$$u_{\text{p}} = \frac{{2k_{{{\text{B}} }} T}}{{\mu_{\text{f}} \pi d_{\text{p}}^{2} }}$$
(27)

where T is the nanofluid temperature and kB is the Boltzmann constant. Also, \(\alpha_{\text{f}}\) stands for the thermal diffusion coefficient of the base fluid.

Convergence, validation, and grid study

In this section, the incompressible preconditioned LBM with \(\gamma = 0.7\) has been compared with the standard LBM in the case of implementing a partial magnetic field. In Fig. 3, the dimensionless average velocity along the microchannel has been shown for the results regarding standard LBM and incompressible LBM, at Ha= 0 and 40, B= 0.03, grids resolution of (80 × 2400), and zero initial velocity \(u^{*} = V^{*} = 0\).

Fig. 3
figure 3

Standard LBM and IPLBM comparison (along the microchannel for Ha= 0 and Ha= 40 at B = 0.03)

Full size image

As shown in Fig. 3, the non-dimensional velocity regarding the standard LBM cannot remain constant along the channel length. It is due to the compressibility effect which yields non-physical predictions of flow and heat transfer characteristics. However, the issue is solved in incompressible preconditioned lattice Boltzmann method. The convergence of the flow field is reached by the following criteria:

$$\left\{ {\begin{array}{*{20}l} {\sqrt[2]{{\frac{{\mathop \sum \nolimits_{\text{x,y}} \{ [u\left( {x,y,t + \Delta t} \right) - u\left( {x,y,t} \right)]^{2} + \left[ {v\left( {x,y,t + \Delta t} \right) - v\left( {x,y,t} \right)} \right]^{2} \} }}{{\mathop \sum \nolimits_{\text{x,y}} \left[ {u\left( {x,y,t} \right)^{2} + v\left( {x,y,t} \right)^{2} } \right]}}}} < 10^{ - 6} } \hfill \\ {{\text{Error}} = \hbox{max} \left( {\frac{{u_{\text{avg}}^{*} \left( x \right) - u_{\text{inlet}}^{*} }}{{u_{\text{inlet}}^{*} }}} \right) < 0.01} \hfill \\ \end{array} } \right..$$
(28)

For further accuracy, the second criterion is defined as the non-dimensional velocity along the channel length. It should reach a value between 0.99 and 1.01 in all cross sections.

Concerning the temperature field, the following criterion is defined:

$$\sqrt[2]{{\frac{{\mathop \sum \nolimits_{\text{x,y}} \{ [\theta \left( {x,y,t + \Delta t} \right) - \theta \left( {x,y,t} \right)]^{2} \} }}{{\mathop \sum \nolimits_{\text{x,y}} \left[ {\theta \left( {x,y,t} \right)^{2} } \right]}}}} < 10^{ - 6} .$$
(29)

While there is a uniform magnetic field in Hartmann numbers of 0 and 20, heat transfer rate quantified by local Nusselt number is verified by Aminossadati et al. [18] that a reasonable agreement has been observed (Fig. 4).

Fig. 4
figure 4

Local Nusselt number comparison at Ha= 0 and 20 for nanofluid (φ = 2%) with the numerical results of Aminossadati et al. [18]

Full size image

To do further validation, the Nusselt number at different horizontal cross sections has been calculated numerically and compared with experimental results of Manay and Sahin [60]. The results are related to three different cross sections along the microchannel. The microchannel has a height of 200 μm and length of 50 mm. The nanofluid consists of titanium nanoparticles in water with a volume concentration of 2 percent and the mass flow rate of 37.7 kg h−1. The results show an acceptable agreement between the experimental and numerical simulations (Table 3).

Table 3 Comparison of the Nusselt number between the present work and experimental study [60] in different horizontal sections for pure water and TiO2–water nanofluid with the volume fraction of 2% and mass flow rate of 37.7 kg h−1
Full size table

The governing equations are developed in a FORTRAN code. In order to show the accuracy of the results, Table 4 represents the average wall friction factor and Nusselt number at Ha= 40 and B= 0.03, for nanofluid with the volume fraction of 1%. Based on the grid independence study, it can be seen that (80 * 2400) grid resolution is a good choice for our further calculations.

Table 4 Grid independence study—averaged Nu and Cf for Ag–water nanofluid Ha = 40 and B = 0.03
Full size table

Results and discussion

The results of this study are presented for water-based nanofluid with different nanoparticles: Al2O3, CuO, Ag, and Fe. The considered volume fraction of these nanoparticles is 1%, and their diameter is 20 nm which is constant in all cases. The thermal load is 500 kW m−2. The properties of water and above-mentioned nanoparticles are available in Table 1. Also, the Hartmann number effect is studied in the range of 0–40. Moreover, slip conditions (with the temperature jump on the wall) in dimensionless slip coefficients of 0, 0.005, 0.01, 0.02, and 0.03 are considered to analysis.

Figure 5 shows the local shear stress in the microchannel wall in terms of microchannel length under non-dimensional slip coefficient of B= 0.03 for all investigated nanofluids at Hartman number of 0 and 40.

Fig. 5
figure 5

Local shear stress on microchannel wall at B = 0.03 \((\varphi = 0)\)

Full size image

While there is no external magnetic field, the local shear stress shows a falling behavior along the microchannel to a point where the shear stress reaches a fixed value. This behavior is seen for all nanofluids. Also, local shear stress reduces for the particles in this order: Al2O3, CuO, Fe, and Ag nanoparticles. In other words, the microchannels using the water–alumina and water–silver nanofluids, respectively, experience the highest and the lowest local shear stress. Another point about shear stress is a significant increase in shear stress by applying a magnetic field (Ha= 40). A considerable issue is the local shear stress reduction process for Ha= 40 along the microchannel, which indicates that the hydrodynamic development is delayed. In this case, the local shear stress plots are arranged such as cases without a magnetic field. Moreover, a sudden decrease in the local shear stress behavior after the magnetic field start point indicates a collision in the hydrodynamic boundary layer at this point. In Fig. 6, the local shear stress is shown for two dimensionless slip coefficients of B= 0 and B= 0.03 and the Hartmann number of Ha= 40 along the channel.

Fig. 6
figure 6

Local shear stress on microchannels wall at Ha= 40

Full size image

As shown in Fig. 6, increasing the slip coefficient from 0 to 0.03 leads to a significant reduction in the local shear stress variation. The reason for this is the direct relationship between shear stress and velocity gradient in the microchannel wall. Figures 5 and 6 indicate that by using the coating on the microchannel surface and providing a hydrophobic coating, the shear stress is significantly reduced. It can also be seen that hydrophobic coating is effective for all nanofluids examined in this text. In Table 5, the average values of shear stress on the microchannel wall for different nanofluids are presented for the Hartmann number of 40 and different slip coefficients.

Table 5 Variations of average shear stress on the microchannel wall in the Hartmann number of 40 versus dimensionless slip coefficient and the percentage difference with average shear stress in slip coefficient of zero
Full size table

By calculating the average relative shear stress for all slip coefficients compared to the alumina–water nanofluid, the mean values of this difference for silver nanoparticles, iron, and copper oxide are 5.95, 3.62, and 2.36, respectively. Also, by increasing the slip coefficient for all nanofluids, the average shear stress is reduced approximately by 15%, 26%, 41%, and 51% relative to the slip coefficient of zero.

In general, it can be concluded that increasing the slip coefficient has a significant effect on the shear stress applied to the wall of the microchannels. Considering the development of technology in the construction of advanced surfaces with desirable properties, this can lead micro-designers to improve the mechanisms for pumping fluids in micro- and nanoscales.

In heat transfer analysis in a microchannel equipped with hydrophobic surfaces, various factors must be taken into account. Some of these factors are: the growth of the properties of the nanoparticles and the base fluid, the existence of jump in the distribution of temperature near the hydrophobic surface, and the effect of the magnetic field caused by the formation of shear stress gradient that results in the decrease in temperature gradient near the wall. The set of these factors is characterized by the thermal boundary layer, and hence it determines the heat transfer rate.

In Fig. 7, the dimensionless temperature at the midpoint of the microchannel in the zero slip coefficient is given for two Hartmann numbers of 0 and 40 for different nanofluids.

Fig. 7
figure 7

Dimensionless temperature in the middle section for different nanofluids and Hartmann numbers of 0 and 40, when the slip coefficient is 0

Full size image

As expected, with the increase in the Hartmann number, the maximum temperature of the dimensionless temperature has been decreased. This is due to the effect of the opposite force exerting on the magnetic field. There is also a remarkable difference between the water–silver nanofluids and other nanofluids in Fig. 7, which shows the reinforcement of the properties of this nanoparticle compared to the other ones. Moreover, the maximum dimensionless temperature values belong to the water–oxide copper, water–alumina, iron–water, and silver–water nanofluid, respectively.

Figure 8 represents the temperature contour, when the \(X^{ *}\) changes between 3 and 6 for two types of nanofluids (CuO and Ag). These two types of nanoparticles are selected, because there is a big difference in their thermal conductivity. Furthermore, the effect of the Hartmann number is investigated on the temperature contour. The results show that, by adding the magnetic field, the velocity gradient increases and it makes the temperature gradient near the wall. As a result, the temperature contours are denser near the contact line for the case of Ha= 40 rather than Ha= 0.

Fig. 8
figure 8

Temperature contours in the region of \(3 \le X^{*} \le 6\) at constant value of B = 0 and Re= 50 for two types of nanofluids for two Ha numbers of 0 and 40

Full size image

Besides, the Ag nanofluid temperature contours are different from those of CuO nanofluid that is due to the difference in their thermal conductivity.

In Fig. 9, the values of the dimensionless temperature in the Hartmann number of 40 are shown for two zero-dimensional slip coefficients of 0 and 0.03 at the end of the channel X* = 0.8.

Fig. 9
figure 9

Dimensionless temperature for two slip coefficients of 0 and 0.03 in the Hartmann number of 40 for silver, alumina, and iron nanofluids

Full size image

The effect of the slip coefficient (hydrophobic surfaces) is perfectly observed on the dimensionless temperature behavior, where the dimensionless temperature decreases with the increase in the dimensionless slip coefficient. In this case, it is necessary to change the behavior of the water–silver nanofluid, which is less in slip coefficient than the other nanofluids. On the other hand, in the slip coefficient of 0.03, the dimensionless temperature of this nanofluid is closer to the other nanofluids. It can be concluded that the effect of the high slip coefficient compared to the nanofluid properties is the dominant mechanism on the dimensionless temperature.

Figure 10 shows the variation of local Nusselt number for different nanofluids in the slip coefficient of 0.03 and Hartmann numbers of 0 and 40.

Fig. 10
figure 10

Local Nusselt number on the microchannel wall in two dimensionless slip coefficients of 0 (higher) and 0.03 (lower)

Full size image

Increasing Hartmann number leads to an increase in the velocity gradient and temperature near the wall, resulting in an increase in the local Nusselt number. (Note that the vertical axis is displayed in the logarithmic scale.)

By analyzing Fig. 10, it can be seen that magnetic fields and nanofluids are two important options that have been used for increasing heat transfer in microchannels. In this figure, it is seen that the effect of the Hartmann numbers variation from 0 to 40 is approximately equal to the change in Nusselt number due to the exchange of the nanoparticle material from copper oxide to silver.

Figure 11 shows the variation of the local Nusselt number on the microchannel wall by changing the slip coefficient in the constant Hartman number of 40.

Fig. 11
figure 11

Local Nusselt number for different slip coefficients and different nanofluids

Full size image

Upon increasing the slip coefficient, the local Nusselt number increases to a certain extent. But what makes the use of these surfaces interesting is that they highly decrease the shear stress. In fact, using hydrophobic surfaces allows the designer to reduce the shear stress in addition to increasing the Nusselt number.

Variations of the average Nusselt number on the microchannel wall for different nanofluids for the Hartmann numbers of 0 and 40 with increasing slip coefficient are presented in Fig. 12.

Fig. 12
figure 12

Average Nusselt number versus non-dimensional slip coefficient for Ha= 0 (top) and Ha= 40 (bottom) and nanofluid volume fraction of 1%

Full size image

In the Hartmann number of 40, the average Nusselt number is generally higher than that of the Hartman number of 0. The effect of Hartmann number increase on different nanofluids is approximately the same, so that the displacement in the upper and lower graphs is not seen in terms of a large degree of nanofluid. Finally, the interesting result of the current study is changing the behavior of the average Nusselt number versus the slip coefficient by using the magnetic field, so that in the Hartman number of 0, the Nusselt number increases almost linearly with increasing slip coefficient. While in the Hartmann number of 40, an increase in the average Nusselt number with a slip coefficient is approximately parabolic. Thus, by increasing the slip coefficient, the effect of this coefficient on the Nusselt number is reduced (Ha= 40), where the Nusselt number undergoes no change by increasing the slip coefficient from 0.02 to 0.03.

This suggests that when a magnetic field is applied to the microchannel, heat transfer cannot be increased by increasing the slip coefficient, and the amount of slip coefficient appropriate for each microchannel in the design should be considered. Table 6 shows the average Nusselt number for different nanofluids in two Hartmann numbers of 0 and 40 and two slip coefficients of 0 and 0.03. Table 7 represents the average Nusselt number difference by changing the dimensionless slip coefficient.

Table 6 Averaged Nusselt numbers and changes from Hartmann numbers from 0 to 40 and non-dimensional slip coefficient from 0 to 0.03
Full size table
Table 7 Average Nusselt number difference with non-dimensional slip coefficient at Ha= 0 and Ha= 40
Full size table

By examining the mean values of the Nusselt number, it is determined that the effect of increasing the Hartmann number from 0 to 40 is almost equal for both slip coefficients 0 and 0.03, ranges from 27 to 33% (Table 6). While the effect of the slip coefficient on the average Nusselt number is different and it becomes zero upon increasing the slip coefficient to values close to 4%, further increase does not affect the heat transfer (Table 7).

Conclusions

The IPLBM was implemented to study the effect of the partial uniform magnetic field on the flow and heat transfer characteristics in microchannels with surface hydrophobicity. The flow is assumed to be laminar, 2D, and incompressible. Different parameters such as non-dimensional slip coefficient, Hartmann number, and type of nanofluid are investigated, and the following results are obtained from the performed simulations.

  • As Hartmann numbers increases, the shear stress and Nusselt number rise simultaneously.

  • In heat transfer point of view, it is shown that Ag nanoparticles have a more positive effect on Nusselt number compared to the other nanoparticles where Fe, Al2O3, and CuO, respectively, increase the Nusselt number.

  • The Al2O3, CuO, Fe, and Ag, respectively, increase the shear stress of base fluid in the studied range.

  • Ag is the best choice due to the largest effect on heat transfer increment and less on shear stress.

  • The present modeling strategy can be progressed to more advanced phases in the future, such as conjugate heat transfer incorporation in the future, especially for heat sink microchannel.