Introduction

Convective heat transfer characteristics in cavities are important in many engineering applications such as in solar power, electronic cooling and many others. In many cases, the configurations are simplified to two-dimensional square cavity. Many active and passive techniques were offered to control the heat transfer and fluid flow characteristics within cavities. In one of these methods, nanofluids are used instead of convectional heat transfer fluids such as water, refrigerant and ethylene glycol. The use of nanofluids is encountered in many thermal engineering applications such as heat exchangers, air conditioning systems, solar power, thermal management and thermal storage. More compact heat exchangers can be designed, and refrigeration systems with less environmental side effects can be obtained. A small amount of nanoparticle addition to the base fluid may result in very higher heat transfer coefficient enhancements with little cost for pressure drop [25, 36, 46, 49,50,51]. There are various factors that affect the thermal conductivity enhancement of the nanofluid such as type, size and shape of the particle [11, 37]. Tremendous amount of numerical and experimental research for the application of the nanofluids in thermal engineering problems for 2D cavities can be found in the literature [2,3,4, 6, 10, 22, 26,27,28,29, 34, 40, 42, 55, 56, 66, 70].

Magnetic field effects are encountered in a variety of engineering applications such as coolers of nuclear reactors, microelectronic devices and purification of molten metals. In cavity flow applications, it was shown that the magnetic field can be used to control the convective heat transfer characteristics [1, 7, 18, 32, 39, 43, 48, 52, 60,61,62]. An externally imposed magnetic field affects the fluid motion and thus heat transfer characteristics. In cavity flow, magnetic field effect was found to dampen the fluid motion and to reduce the convective heat transfer rate. However, in configurations with separated flows, magnetic field can augment the heat transfer rate due to the suppression of the recirculation regions. Use of magnetic field with nanofluids is a good possibility to control the convective heat transfer in cavities [5, 15, 16, 30, 31, 44, 45, 47, 54, 57, 58, 60, 63]. When nanofluids are used with magnetic field effects, not only the thermal conductivity enhances but the electrical conductivity as well.

Thermal management and thermal energy storage are important issues in solar power, electronic cooling, solidification and many others applications. Energy costs and environmental effects become important factors that should be considered before design of thermal engineering systems. Therefore, thermal energy storage and their related technologies capture great attention by the researchers, recently. Phase change materials (PCMs) provide effective solutions for thermal storage and thermal management purposes. Phase change materials can be considered as latent heat storage systems due to their energy storing and releasing properties. Chemical stability, higher thermal conductivity, proper melting temperature for the desired application, higher specific heat, higher latent heat of fusion, low corrosiveness and low cost can be mentioned as some of the desirable properties of PCMs. A vast amount of literature for use of PCM in thermal engineering applications can be found in references [8, 9, 12,13,14, 17, 19,20,21, 24, 35, 38, 64, 65, 67, 69]. A numerical study for the melting behavior of PCM in a heat exchanger system was performed by [38]. Increasing the eccentricity was found to enhance the heat transfer process for the last stages of melting. Optimal thickness and melting temperature of the PCM for a PV/PCM module were experimentally determined by [35]. A numerical model for PCM application in thermal storage coaxial tubes with fins for an air conditioning system was developed by [21]. The thermal performance of a PCM integrated into a building wall was performed by [20]. The optimal location of the PCM was found when the melting temperature and thickness of the PCM were changed.

The aim of the present study is to investigate the role of magnetic field with nanofluids on natural convection in a square cavity which has a phase change material (PCM) and a conductive partition attached to its vertical wall. PCM parameters, nanofluids and magnetic field effects on the fluid flow, and heat transfer characteristics in a square cavity are numerically examined. The results of the current investigation could be used for the design, optimization and flow control for natural convection in 2D cavities which involves magnetic field.

Mathematical formulation of the physical problem

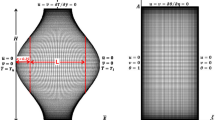
Figure 1 shows a schematic view of computational domain of a square cavity with a conductive partition and phase change material (PCM). The length of the cavity, conductive partition and PCM are H, \({L}_\mathrm{cp}\) and \({L}_\mathrm{FDM}\), while the height of PCM is \({H}_\mathrm{FDM}\). The left vertical wall is kept at constant hot temperature of \(T_\mathrm{h}\), while the right vertical wall of the PCM and conductive partition and top wall of the PCM are maintained at constant cold temperature of \(T_\mathrm{c}\). A uniform magnetic field of strength \(B_0\) which makes an inclination angle of \(\gamma\) with the horizontal axis is imposed. Natural convection, conduction and phase change heat transfer are considered in the square cavity, conductive partition and phase change material. Water–CuO nanofluid was used in the square cavity, and incompressible, Newtonian fluid model was employed even at the highest solid nanoparticle volume fraction. Two-dimensional, laminar and unsteady flow configuration was assumed. Various effects such as Joule heating, induced magnetic and electric field, viscous dissipation and radiation were considered to be negligible. Heat generation due to the magnetic field in the solid wall was also neglected. Thermophysical properties of water and CuO are demonstrated in Table 1 [60].

Table 1 Thermophysical properties of base fluid and nanoparticle [60]
Full size table

Governing equations and boundary conditions

Mass, momentum and energy equations for a two-dimensional, incompressible, laminar and unsteady flow configuration can be expressed as follows [43]:

$$\begin{aligned}&\frac{\partial {u}}{\partial {x}}+\frac{\partial {v}}{\partial {y}}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial {u}}{\partial {x}}+v \frac{\partial {u}}{\partial {y}}=-{\frac{1}{\rho _{\mathrm{nf}}}} \frac{\partial {p}}{\partial {x}}+\nu _{\mathrm{nf}}\left( \frac{\partial ^2{u}}{\partial {x^2}} +\frac{\partial ^2{u}}{\partial {y^2}} \right) \\&+\frac{\sigma _\mathrm{nf}B_{0}^2}{\rho _\mathrm{nf}}\left( v \sin (\gamma ) \cos (\gamma )-u \sin ^{2} (\gamma ) \right) , \end{aligned} \end{aligned}$$
(2)
$$\begin{aligned}&\begin{aligned}&\frac{\partial v}{\partial t}+u\frac{\partial {v}}{\partial {x}}+v\frac{\partial {v}}{\partial {y}}=-{\frac{1}{\rho _{\mathrm{nf}}}} \frac{\partial {p}}{\partial {y}}+\nu _{\mathrm{nf}}\left( \frac{\partial ^2{v}}{\partial {x^2}} +\frac{\partial ^2{v}}{\partial {y^2}} \right) \\&+\beta _{\mathrm{nf}} g (T-T_\mathrm{c})+\frac{\sigma _\mathrm{nf}B_{0}^2}{\rho _\mathrm{nf}}\left( u \sin (\gamma ) \cos (\gamma )-v \cos ^{2} (\gamma ) \right) , \end{aligned} \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial {T}}{\partial {x}}+v\frac{\partial {T}}{\partial {y}}= \alpha _{\mathrm{nf}}\left( \frac{\partial ^2{T}}{\partial {x^2}} +\frac{\partial ^2{T}}{\partial {y^2}} \right) . \end{aligned}$$
(4)

The last two terms of Eqs. (2) and (3) are due to the Lorentz forces.

For the conductive solid medium,

$$\begin{aligned} \rho C_\mathrm{p} \frac{\partial {T}}{\partial {t}}=k \left( \frac{\partial ^2{T}}{\partial {x^2}} +\frac{\partial ^2{T}}{\partial {y^2}} \right) \end{aligned}$$
(5)

Phase change material (PCM) was added to the right vertical part of the cavity. The phase change heat transfer was considered in this domain. Energy equation for the PCM is expressed as [23, 53]:

$$\begin{aligned} \rho C_\mathrm{p} \frac{\partial {T}}{\partial {t}}+\rho C_\mathrm{p} \mathbf {u}\cdot \nabla T=\nabla \cdot \left( k \nabla T \right) \end{aligned}$$
(6)

For the PCM medium, a temperature-dependent function can be defined which has the following form [23, 53]:

$$F = \left\{ {\begin{array}{*{20}l} 0 \hfill & {T < T_{{\text{m}}} - \Delta T} \hfill \\ {(T - T_{{\text{m}}} + \Delta T)/2\Delta TT_{{\text{m}}} } \hfill & { - \Delta T \le T \le T_{{\text{m}}} + \Delta T} \hfill \\ 1 \hfill & {T > T_{{\text{m}}} + \Delta T} \hfill \\ \end{array} } \right.$$
(7)

In the above equation, \(T_\mathrm{m}\) and \(\Delta T\) denote the melting temperature and transition temperature, respectively. In the solid and liquid phase of PCM, values of F are 0 and 1 and it linearly varies from 0 to 1 within the transitional zone. Density and thermal conductivity of the PCM are defined as [23, 53]:

$$\begin{aligned} \rho (T)_\mathrm{FDM}&= \rho _\mathrm{s}+(\rho _\mathrm{l}-\rho _\mathrm{s})F \end{aligned}$$
(8)
$$\begin{aligned} k (T)_\mathrm{FDM}&= k_\mathrm{s}+(k_\mathrm{l}-k_\mathrm{s})F \end{aligned}$$
(9)

The specific heat of the PCM is defined as:

$$C_{{\text{p}}} (T)_{{{\text{FDM}}}} = C_{{{\text{p}}_{{\text{s}}} }} + (C_{{{\text{p}}_{{\text{l}}} }} - C_{{{\text{p}}_{{\text{s}}} }} )F + \lambda D$$
(10)

where \(\lambda\) is the PCM heat of fusion and D is the delta Dirac function which has the following form [23]:

$$\begin{aligned} D=e^{\frac{-(T-T_\mathrm{m})^2}{\Delta T ^2}}/ \sqrt{\pi \Delta T ^2} \end{aligned}$$
(11)

which takes 0 except for the transition region.

The momentum equation within the PCM along with the buoyancy force \(\vec {F}_\mathrm{b}\) and additional force \(\vec {F}_\mathrm{a}\) appeared, and they are defined as [23, 53]:

$$\begin{aligned} \vec{F}_\mathrm{b}=-\rho _\mathrm{l} \left( 1-\beta (T-T_\mathrm{m}) \right) \vec {g},\quad \vec {F}_\mathrm{a}=-A(T) \vec {u} \end{aligned}$$
(12)

with A(T) from the Carman–Kozeny relation in a porous medium and is defined as [23, 53]:

$$\begin{aligned} A(T)=\frac{C (1-F(T))^2}{F(T)^3+q} \end{aligned}$$
(13)

In the above expression, C and q are constants which are taken as \(10^5\) and \(10^{-3}\).

Boundary conditions that are in dimensional form can be stated as follows:

  • For the left vertical wall (cavity), \(u=v=0,\ T=T_\mathrm{h}\).

  • For the right vertical walls (PCM and conductive partition), \(u=v=0, T=T_\mathrm{c}\).

  • For the top wall (PCM ), \(u=v=0,\ T=T_\mathrm{c}\).

  • For the other walls, \(u=v=0,\ \frac{\partial {T}}{\partial {n}}=0\).

  • Along the interface of the domains (continuity condition): \(T_\mathrm{i}=T_\mathrm{j}, \ (kA)_\mathrm{i}\left( \frac{\partial {T}}{\partial {n}}\right) _\mathrm{i}=(kA)_\mathrm{j}\left( \frac{\partial {T}}{\partial {n}}\right) _\mathrm{j}\)

Following parameters can be used to obtain the non-dimensional form of the governing equations:

$$\begin{aligned} X&= \frac{x}{H},\quad Y=\frac{y}{H},\quad U=\frac{uH}{\alpha },\quad V=\frac{vH}{\alpha },\quad {\text{Kr}}=\frac{k_\mathrm{s}}{k_\mathrm{f}},\\ \theta&= \frac{T-T_\mathrm{c}}{T_\mathrm{h}-T_\mathrm{c}},\quad P=\frac{pH^{2}}{\rho _\mathrm{f}{\alpha^2_{\mathrm{f}}}},\quad Fo=\frac{t \alpha _\mathrm{f}}{H^{2}},\quad Ste=\frac{c_\mathrm{l}(T_\mathrm{h}-T_\mathrm{f})}{\lambda },\\ Ha&= B_{0}H {\sqrt{\frac{\sigma }{\rho \nu }}},\quad Gr=\frac{g \beta (T_\mathrm{h}-T_\mathrm{c})H^{3}}{\nu ^{2}},\quad Pr=\frac{\nu }{\alpha },\quad Ra=GrPr \end{aligned}$$
(14)

In the above expressions, Ste denotes the Stefan number which is the ratio of the sensible heat to the latent heat of the PCM. Fo is the Fourier number which denotes the non-dimensional time. Ha is the Hartmann number which shows the significance of the imposed magnetic field strength. Kr is the conductivity ratio of the solid to the fluid. A uniform magnetic field was imposed only in the nanofluid domain. A solid partition was added between the PCM domain and nanofluid domain.

Correlations for the effective thermophysical properties of nanofluid

Density, specific heat and thermal expansion coefficient of the nanofluid are defined by using the following relations:

$$\begin{aligned} (\rho S)_\mathrm{nf}=(1-\phi )(\rho S)_\mathrm{f}+\phi (\rho S)_\mathrm{p} \end{aligned}$$
(15)

where the subscripts f, nf and p denote the base fluid, nanofluid and solid particle, respectively. S takes values of 1, \(c_\mathrm{p}\) and \(\beta\) for density, specific heat and thermal expansion coefficient, respectively.

In the definition of thermal conductivity of nanofluid, Brownian motion effect was included. The effective thermal conductivity of the nanofluid takes into account the particle size, particle volume fraction and temperature, and it is defined by using the following relation [25]:

$$\begin{aligned} \begin{aligned}&k_\mathrm{nf}=k_\mathrm{f}\left[ \frac{(k_\mathrm{p}+2k_\mathrm{f})-2 \phi (k_\mathrm{f}-k_\mathrm{p}) }{(k_\mathrm{p}+2k_\mathrm{f})+ \phi (k_\mathrm{f}-k_\mathrm{p})} \right] \\&+5 \times 10^{4} \times 1.9526 \times (100 \phi )^{-1.4594}\phi \rho _\mathrm{f} c_\mathrm{p,f}\sqrt{\frac{\kappa _\mathrm{b}T}{\rho _\mathrm{p} d_\mathrm{p}}}f'(T, \phi ) \end{aligned} \end{aligned}$$
(16)

where the first term for the right-hand side equation is the thermal conductivity defined in [33], and the function \(f'\) for CuO–water nanofluid is defined in [25].

Nanofluid viscosity model is defined as [25]

$$\begin{aligned} \mu _\mathrm{nf}=\mu _\mathrm{f} \frac{1}{\left( 1- 34.87 \left( \frac{d_\mathrm{p}}{d_\mathrm{f}}\right) ^{-0.3} \phi ^{1.03}\right) }. \end{aligned}$$
(17)

For electrical conductivity of the nanofluid, Maxwell’s model [33] was utilized which was developed for calculating the electrical conductivity for random suspension of spherical particles [33]. The electrical conductivity of nanofluid is given as:

$$\begin{aligned} \sigma _\mathrm{nf}=\sigma _\mathrm{f} \left( 1+\frac{3 (f-1) \phi }{(f+2)-(f-1) \phi }\right) \end{aligned}$$
(18)

where \(f=\frac{\sigma _\mathrm{p}}{\sigma _\mathrm{f}}\) is the conductivity ratio of the two phases.

Numerical solution method

Governing equations with appropriate boundary and initial conditions were solved with finite element method. Initial velocities are assumed to be zero, while initial temperature was \(T=T_\mathrm{c}\) for the whole computational domain. Galerkin weighted residual formulation was utilized to obtain the weak form of governing equations. Lagrange finite elements of different orders were used to approximate the flow variables within the non-overlapping regions of the computational domain. Residual R is obtained when the approximated field variables are inserted into the governing equations. In this method, weighted average of residual will forced to be zero over the computational domain as:

$$\begin{aligned} \int _{\Omega } W R {\text{d}}v=0 \end{aligned}$$
(19)

where W is the weight function, and in the Galerkin method, it is chosen from the same set of functions as of the trial functions. At the nodes of internal element domain, nonlinear residual equations are achieved.

Mesh independent of the solution was assured by using various number of elements (mixed type—triangular and quadrilateral). Grid independence tests were preformed by various grids and two values of Hartmann numbers. Table 2 shows the average Nusselt number values for the hot wall (\(\gamma =45^{\circ}\), \(\phi =0.04\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\)) for different number of elements. G4 with 18,090 elements was chosen for the subsequent computations.

Table 2 Grid independence study (\(\gamma =45^{\circ}\), \(\phi =0.04\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))
Full size table

Local and average Nusselt number for the hot vertical wall are calculated as:

$$\begin{aligned} {Nu}_\mathrm{y}=- \frac{k_\mathrm{nf}}{k_{\mathrm{f}}}\left( \frac{\partial {\theta }}{\partial{n}} \right) _\mathrm{wall}, \ \ {Nu}_{\mathrm{m}}=\frac{1}{H} \int _{0}^{H} {Nu}_\mathrm{y} {\text{d}}y. \end{aligned}$$
(20)

In the above expressions, the time dependence of the local and average Nusselt number is considered. For the time-dependent part, fourth-order Runge–Kutta time-marching with variable time step was used.

Different existing numerical results are used to validate the present solver. In the numerical study by [41], free convection effects under the influence of magnetic field were investigated. Table 3 shows the average Nusselt numbers obtained with present solver and calculated in [41] for two values of Grashof number for different values of Hartmann number. A comparison with the numerical results of [59] was also added where results were obtained with lattice Boltzmann method. Another comparison study is made with the numerical results of [68] for a partitioned cavity filled with air and water. Table 4 presents the comparison of the average Nusselt numbers for various Grashof numbers. The results shown in Tables 3 and 4 provide sufficient confidence for the accuracy of the current solver.

Table 3 Code validation study: comparison of average Nusselt number for MHD free convection
Full size table
Table 4 Code validation: comparison of averaged Nusselt numbers along the hot wall for various Grashof numbers
Full size table

Results and discussion

In this study, MHD natural convection of CuO–water nanofluid in a cavity with a conductive partition and phase change material (PCM) attached to its vertical wall was numerically investigated. Effects of various parameters such as Hartmann number (between 0 and 100), magnetic inclination angle (between 0\(^{\circ}\) and 90\(^{\circ}\)), solid nanoparticle volume fraction (between 0 and 0.04), height (between 0.2H and 0.8H) and length (between 0.2H and 0.6H) of the phase change material and thermal conductivity ratio of the fluid to the PCM (between 0.1 and 100) on the fluid flow and heat transfer characteristics were numerically analyzed. Results are illustrated with streamlines, isotherms and Nusselt number distribution plots for various values of parameter combinations.

Effects of Rayleigh number

Figures 2 and 3 show the variation of streamlines and isotherms within the square cavity for various time instances (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\)). At Rayleigh number of \(10^5\), two recirculation zones and a small corner vortex are established within the cavity for \(t=50\) s. As the time evolves, the whole cavity is occupied with a single vortex. As the value of Rayleigh number increases, natural convection effects become important, but one vortex is established within the cavity for all time instances. The main vortex alignment is toward the diagonal direction for lower Rayleigh number value. Isotherms within the cavity become parallel to the horizontal walls with higher Ra values due to the increased effect of natural convection. Temperature gradients become steeper in the lower part of the hot wall when value of Rayleigh number augments. Since we consider a conductive partition and phase change material for the right vertical wall of the cavity, thermal gradients within the cavity are affected in the vicinity of those location for different Rayleigh numbers.

Variations of local and average Nusselt number for the hot wall are shown in Fig. 4 for various values of Rayleigh numbers. Local heat transfer is higher for the lower part of the cavity and enhances with higher values of Rayleigh number. Water and nanofluid at various solid particle volume fractions show heat transfer augmentation with Rayleigh number. At \(Ra=10^6\), \(7\%\) higher average heat transfer is obtained with nanofluid at the highest solid particle volume fraction. This value is 5\(\%\) higher for lower value of Rayleigh number at \(Ra=10^5\) but the average Nusselt number value is lower.

Fig. 1
figure 1

Schematic description of the physical model

Full size image
Fig. 2
figure 2

Influence of Rayleigh number on the distribution of streamlines for different time instances (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Fig. 3
figure 3

Effects of Rayleigh number on the isotherm distributions for different time instances (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Fig. 4
figure 4

Variation of local (a) and average (b) Nusselt number for various Rayleigh numbers (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\), t = 500)

Full size image
Fig. 5
figure 5

Influence of Hartmann number on the distribution of streamlines for different time instances (\(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image

Magnetic field parameter effects

Figures 5 and 6 demonstrate the effects of Hartmann number on the distribution of streamlines and isotherms within the square cavity for different time instances for fixed values of (\(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\)). In the absence of magnetic field, a recirculation vortex is established in the cavity and its center is closer to the left vertical wall. As the time evolves, this vortex breaks up into two recirculation regions and the extent of the vortex in the right half of the cavity increases. When the magnetic field is imposed, the single vortex elongates in the diagonal direction and the value of maximum stream function decreases. At the highest value of Hartmann number, more orientation of the streamline in the diagonal direction is observed which is due to the fluid motion dampening with magnetic field. For all time instances, one single recirculation zone is established within the cavity when magnetic field is imposed.

Isotherm distributions show typical patterns within the cavity for a differential heated cavity, but due to conduction heat transfer in the partition and phase change heat transfer in the PCM, thermal patterns show a layered distribution in the vicinity of partitions and PCM. As the time evolves, isotherms within the PCM show a progress with a front due to the energy transfer in melting within the PCM. When magnetic field is imposed and its strength is increased with higher values of Hartmann number, the parallel alignment of the isotherms to the horizontal walls within the cavity becomes distorted and they tend to become parallel to the vertical walls which indicates the reduction in natural convection heat transfer mechanism. In the PCM, isotherm distributions become different for different time instances with the applied magnetic field.

Local Nusselt number distribution along the hot vertical wall of the cavity is shown in Fig. 7a for various values of Hartmann numbers. Along the vertical wall, local heat transfer is higher in the lower part and decreases toward the upper part of the hot wall. The local Nusselt number is reduced in the location for \(0.25H \le y \le 0.9H\) when Hartmann number augments. In the lower part of the hot wall, magnetic field acts in a way to increase the local heat transfer. The average Nusselt number reduces with Hartmann number due to the dampening of the fluid motion within the cavity for higher values of magnetic field strength. In Fig. 7b, effects of various nanoparticle volume fractions are also shown. A higher value of solid particle volume fraction results in heat transfer enhancement due to the thermal conductivity enhancement but the electrical conductivity changes as well which was given by the Maxwell correlation in Eq. (5). When Hartmann number is increased from 0 to 100, reduction in the average Nusselt numbers is \(31.81\%\) and \(26.19\%\) for the water and for the nanofluid with the highest particle solid volume fraction. Imposing a magnetic field results in more reduction in average heat transfer for water as compared to nanofluid. The electrical conductivity enhances, and more suppression of the convection is achieved but heat transfer enhancement due to the thermal conductivity enhancement is higher which results in more augmentation of average Nusselt number. A polynomial fit for the average Nusselt number of the hot wall which depends on the Hartmann number and solid particle volume fraction is obtained for magnetic inclination angle of \(\gamma =45^{\circ}\). The polynomial relation has the following form:

$$\begin{aligned} Nu_\mathrm{m}=p00+p10*Ha_\mathrm{n}+p01*\phi _\mathrm{n}+p20*Ha_\mathrm{n}^2+p11*Ha_\mathrm{n}*\phi _\mathrm{n} \end{aligned}$$
(21)

where \(Ha_\mathrm{n}\) and \(\phi _\mathrm{n}\) are the normalized Hartmann number (\(Ha_\mathrm{n}=\frac{Ha-37}{36.46}\)) and solid particle volume fraction (\(\phi _\mathrm{n}=\frac{\phi -0.02}{0.0144}\)). Coefficients of the polynomial fit with their \(95\%\) confidence bounds are demonstrated in Table 5. The root mean square (RMSE) and R2 values of the polynomial fit are 0.01615 and 0.9967, respectively. Figure 8 shows the surface map and residuals of average Nusselt number versus Ha and \(\phi\). Interaction of the magnetic field with the nanoparticle solid volume fraction is given with p11 coefficient.

Influence of magnetic inclination angle on the variation of streamlines and isotherms within the cavity is shown in Figs. 9 and 10 for different time instances (\(Ha=30\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\)). For \(45^{\circ}\) inclination, more elongation of the single recirculation zone is seen when time evolves and at the highest value of inclination, two recirculation cells are established within the square cavity which is due to the Lorentz forces for this flow configuration. Isotherm distributions show some slight changes for the cavity, conductive partition and PCM for various magnetic inclination angles for the same time instance. Local Nusselt number enhances in the lower part of the hot wall for higher \(\gamma\) values (Fig. 11a). The average Nusselt number increases with \(\gamma\) for fluid and nanofluid at various solid particle volume fractions (Fig. 11b). For water and nanofluid at the highest particle volume fraction, only \(4\%\) and \(3.36\%\) of average heat transfer enhancements are achieved when magnetic inclination angles increase from \(0^{\circ}\) to \(90^{\circ}\).

Fig. 6
figure 6

Effects of Hartmann number on the isotherm distributions for different time instances (\(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Fig. 7
figure 7

Variation of local (a) and average (b) Nusselt number for various Hartmann numbers (\(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Fig. 8
figure 8

Surface fit of average Nusselt number for the hot wall and residuals with polynomial fit (\(\gamma =45^{\circ}\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Fig. 9
figure 9

Influence of magnetic inclination angle on the distribution of streamlines for different time instances (\(Ha=30\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Fig. 10
figure 10

Effects of magnetic inclination angle on the isotherm distributions for different time instances (\(Ha=30\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Table 5 Polynomial constant coefficients (within their \(95\%\) confidence interval)
Full size table

Phase change material parameter effects

In this study, a phase change material (PCM) and a conductive partition are attached to the right vertical wall of the square enclosure. Thermophysical properties of PCM are shown in Table 6. Effects of height, length and thermal conductivity of the PCM on the convective heat transfer characteristics for the square cavity are analyzed. Figure 12 shows the isotherm distributions for three different height parameters of the PCM for several time instances (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\)). In the vicinity of the conductive partition and PCM, isotherms are highly affected by the variation of the height of PCM. Melting of the PCM gives different melting front characteristics within the PCM, and they show different behaviors for different heights considering various time instances. In the interior of the cavity, some slight variations are obtained especially near the bottom wall, and this will effect the temperature gradient for the lower part of the heater. Local Nusselt number reduces with higher values of height of the PCM. Reduction in the average Nusselt number is \(42.14\%\) when the height of the PCM is increased from 0.2H to 0.8H (Fig. 13). The length of the PCM is not significant on the local and average Nusselt number distributions for the hot wall as shown in Fig. 14. Only \(3.3\%\) reduction in the average heat transfer is achieved when the length is increased from 0.1H to 0.4H.

Table 6 Thermophysical properties of PCM
Full size table

Thermal conductivity of the PCM is low in common applications; therefore, there are some attempts to increase its conductivity. In this numerical study, a parameter called the conductivity ratio (Kr) which denotes the ratio of the thermal conductivity of PCM to the water was defined. Figure 15 shows the variations of local and average Nusselt number distributions for the hot wall with various Kr values. Local and average heat transfer augments with higher Kr values, and there is very little increase in the average Nu when Kr is increased from 10 to 100. Average heat transfer enhancement is \(29.5\%\) for water when Kr changes from 0.1 to 10. This value is only \(2\%\) higher when nanofluid with the highest particle volume fraction is used. The saturation type curve for the average Nusselt number versus conductivity ratio shows similar trends for all nanofluids containing various particle volume fractions.

Fig. 11
figure 11

Variation of local (a) and average (b) Nusselt number for various magnetic inclination angles (\(Ha=30\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Fig. 12
figure 12

Effects of PCM height on the distribution of isotherms for various time instances (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\))

Full size image
Fig. 13
figure 13

Local (a) and average Nusselt number (b) variations for the hot wall various PCM heights (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\))

Full size image
Fig. 14
figure 14

Local (a) and average Nusselt number (b) variations for the hot wall for various PCM lengths (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({H}_\mathrm{FDM}=0.5H\))

Full size image
Fig. 15
figure 15

Influence of thermal conductivity ratio of the fluid to the PCM on the variation of local (a) and average (b) Nusselt number variations for the hot wall (\(Ha=30\), \(\gamma =45^{\circ}\), \(\phi =0.02\), \({L}_\mathrm{FDM}=0.3H\), \({H}_\mathrm{FDM}=0.5H\))

Full size image

Conclusions

Numerical simulation of natural convection of MHD flow in a 2D cavity filled with CuO–water nanofluid with a phase change material attached to its vertical wall is performed. It was observed that magnetic field parameters (strength and inclination angle) with nanofluid properties (thermal and electrical conductivity enhancement) have significant effects on the fluid flow and heat transfer characteristics. Among various properties of the side wall-attached PCM properties, height and thermal conductivity have influence on heat transfer enhancement whereas the length has little influence. The average Nusselt number is found to rise with magnetic field inclination angle, but the values are less than 5%. The average Nusselt number reduces with magnetic field strength, and more reduction is obtained for water as compared to nanofluid which is \(31.81\%\) at the highest value of Hartmann number. Lower value of the height of PCM and higher value of thermal conductivity ratio (PCM to base fluid) result in local and average heat transfer enhancement. The average Nusselt number augments \(29.5\%\) when the conductivity ratio is increased from 0.1 to 10.