MHD Natural Convection Flow of CuO/Water Nanofluid in a Differentially Heated Hexagonal Enclosure with a Tilted Square Block

Abstract

A numerical investigation has been performed to analyze the effect of magnetohydrodynamic natural convection flow in a differentially heated hexagonal enclosure having a tilted square block filled with CuO/water nanofluid. The horizontal walls of the cavity and tilted walls of the obstacle are uniformly heated of temperature $\hbox {T}_\mathrm{h}$ while the inclined walls are kept at constant temperature $\hbox {T}_\mathrm{c}$. The governing conservation equations of the physical problem have been solved using finite element method based on Galerkin weighted residual technique and obtained numerical results are presented graphically in terms of streamlines, isotherms, average Nusselt numbers, mid height horizontal and vertical velocities, average temperature and average velocity of nanofluid for a range of Rayleigh number ($10^{3} \le { Ra} \le 10^{6}$), Hartmann number ($0 \le { Ha} \le 70$) and solid volume fraction ($0.1\% \le \phi \le 5\%$) to show the flow structures and temperature characteristics. It is found that the flow fields and temperature distributions are influenced significantly for the effect of pertinent parameters. In addition, overall heat transfer rate enhanced due to higher values of Ra and $\phi$ along with lower value of Ha. Comparisons of the present results with the previously published results on the basis of special cases are performed and found to be in good agreement.

Introduction

Heat transfer analysis due to natural convection within closed enclosures is an important research area in science and engineering because of its widespread applications in diverse fields such as geophysics, energy storage and conservation, solar energy, electronic cooling, heat exchangers, nuclear reactor systems, thermal systems, food and metallurgical industries etc. In recent years, researchers found limitations of enhancing heat transfer rate in conventional fluids like water, oil and ethylene glycol or propylene etc. To break down these limitations, a new class of fluids was developed named as nanofluids which are stable and highly conductive suspensions of nano-meter sized particles (1–100 nm) in conventional liquids. Nanofluids having relatively high thermal conductivity, reduced pumping power, particle clogging and adjustable concentrations play significant roles in electronics, high speed automotives, gas recovery, refrigeration, energy generation, nuclear systems, biomedical applications, solar systems and space technologies etc, where improved heat transfer is required. Considering the importance of natural convection heat transfer in nanofluids within closed enclosures a number of experimental and theoretical investigations have been reported extensively by many researchers.

Khanafer et al. [1] firstly investigated the heat transfer performance for nanofluids in a two-dimensional enclosure. In this analysis, they found that the suspended nanoparticles increase the heat transfer rate substantially and also alter the structure of the fluid flow. Jou and Tzeng [2] utilized the Khanafer model to investigate heat transfer enhancement of nanofluid in a rectangular enclosure and observed that the heat transfer coefficient increases significantly for increasing buoyancy parameter and dispersion of nanoparticles in the base fluid. Daungthongsuk and Wongwises [3] summarized the experimental and numerical studies of forced convective heat transfer of nanofluids and concluded that nanofluids have great potential to enhance the overall heat transfer mechanisms and suitable for practical heat transfer processes. Heat transfer behaviors in a two-sided lid-driven differentially heated cavity were analyzed by Tiwari and Das [4] and they observed that heat transfer characteristics of nanofluids within the enclosure were affected by the governing parameters.

Abu-Nada [5] carried out a numerical study on heat transfer and flow structure in nanofluids due to natural convection in a partially heated rectangular enclosure with different ultrafine particles and indicated that heat transfer enhancement occurred for the presence of nanoparicles and accentuated due to the low aspect ratio than higher. Later on, Abu-Nada et al. [6] examined the sensitivity of average Nusselt number depending on Rayleigh numbers using variable thermal conductivity and variable viscosity of nanofluids in a differentially heated square enclosure. Ghasemi and Aminossadati [7] reported thermal performance of nanofluids in a lid-driven triangular enclosure and found that nanoparticles increase the heat transfer rate for all values of Richardson number. Yu et al. [8] employed finite volume method together with Brownian motion of nanoparticles to analyze transient natural convection flow of aqueous nanofluids in a heated square cavity. Their results indicated that the time-averaged Nusselt number is lower with higher volume fraction of nanoparticles. Finite element method was applied by Basak and Chamkha [9] to analyze the heat lines for natural convection flow of nanofluids in square cavities with various thermal boundary conditions and they ensured that the considered nanofluids have larger enhancement of heat transfer rate. Nasrin et al. [10] investigated the influence of governing parameters on natural convection flow in a differentially heated closed chamber filled with water-$\hbox {Al}_{2}\hbox {O}_{3}$ nanofluid and indicated that the flow and temperature characteristics within the cavity strongly depend on the governing parameters. Qi et al. [11] carried out a numerical solution for natural convection heat transfer in a square cavity filled with nanofluids to predict the influence of volume fraction of nanoparticles and Rayleigh numbers on average Nusselt number. Their results showed that the average Nusselt numbers increases with lower volume fraction and higher Rayleigh number. Later on, Ahmed and Eslamian [12] extended this analysis by incorporating thermophoresis and Brownian forces inside an inclined square enclosure. In this investigation they found that inclination angle, Rayleigh number and thermophoresis have considerable effects on heat transfer enhancement. Sheikholeslami et al. [13] employed control volume-based finite element method (CVFEM) to analyze the natural convection heat transfer in water based nanofluids between the circular enclosure and elliptic cylinder. They found that Nusselt number increases with the increase of physical parameters of the problem and the minimum heat transfer enhancement occurred at right angle. Sheremet et al. [14] considered the Buongiorno’s mathematical model to investigate the flow and heat transfer behaviors of nanofluids inside a right-angled porous trapezoidal cavity and observed that the flow strength, Nusselt number and Sherwood number are affected by the variation of the pertinent parameters. Later on, Esfe et al. [15] accomplished a numerical study on the flow field, temperature distribution and rate of heat transfer due to natural convection flow in carbon nanotube-EG-water nanofluid within a trapezoidal enclosure. Their results highlighted that heat transfer rate is dominated by higher Rayleigh number.

In addition, magnetic field is an interesting research area due to its technical importance in realistic engineering such as electronic devices, chemical processing equipments, high-energy equipments, nuclear reactors, solar collectors, crystal growth in liquids, geothermal reservoirs, thermal insulations and petroleum reservoirs and drying technologies etc. Moreover, external magnetic field effects have been receiving a considerable attention due to its numerous applications in industries and engineering. M’hamed et al. [16] reviewed the effects of external magnetic field on nanofluids properties and fluid flow and they summarized that the applied magnetic field has a positive effect to control the overall fluid flow characteristics as well as the thermal conductivity of nanofluids. However, natural convection heat transfer under the influence of external magnetic field is of great importance in many industrial applications. In this context, a number of theoretical and experimental studies have been conducted by many researchers to find out the flow and heat transfer behaviors inside cavities. Ece and Buyuk [17] considered steady laminar natural convection flow in a heated inclined rectangular cavity in presence of magnetic field and they employed differential quadrature method to obtain numerical solution for the stream function and temperature. They found that flow and temperature fields strongly depend on orientation, aspect ratio, strength and direction of imposed magnetic field. Kahveci and Oztuna [18] applied the polynomial differential quadrature (PDQ) method to analyze the effect of MHD natural convection flow in a heated partitioned enclosure and their results indicated that the flow and heat transfer are suppressed significantly due to the influence of magnetic field and the locations of partitioned. Pirmohammadi et al. [19] utilized the finite volume code based on PATANKAR’s SIMPLER method to analyze the effect of natural convection flow in a heated square cavity in presence of a magnetic field. They focused that convective heat transfer is decreased for the effect of magnetic field. Penalty finite element method with bi-quadratic rectangular elements used by Sathiyamoorthy and Chamkha [20] to investigate the effect of natural convection flow of electrically conducting liquid gallium in a square cavity. Later on, they [21] extended this analysis by considering magnetic field effect on natural convection heat transfer in an enclosure with uniformly or linearly heated adjacent walls and found that magnetic field causes significant effects on the local and average Nusselt numbers. A numerical study has been conducted by Nasrin and Parvin [22] to analyze flow and heat transfer characteristics for hydrodynamic mixed convection flow in a lid-driven cavity with sinusoidal surface. They observed that average Nusselt number increases for increasing number of waves and Reynolds number and decrease for the effect of magnetic field. Saha [23] modeled thermo-magnetic convection and heat transfer of paramagnetic fluid with micro-gravity condition in an open square cavity and concluded that heat transfer rate is suppressed for the influence of magnetic field and increased paramagnetic fluid parameter. Bondareva and Sheremet [24] studied numerically the effect of natural convection melting in a square cavity with a local heat source on the bottom wall and indicated that the flow and temperature patterns are influenced noticeably by the presence of inclined magnetic field and temperature difference inside the cavity. Thus, natural convection heat transfer in a heated enclosure in presence of magnetic field is a prototype of many engineering applications. In the present literature review, a number of theoretical and numerical investigations have been reported on natural convection flow and heat transfer in different geometries like square, rectangular, triangular, cylindrical and spherical enclosures. It is important to note that the basic differences in fluid flow structure are observed due to the presence of cornered edges of hexagonal enclosure. Thus, the presence of inclined edges of hexagonal enclosure can significantly affect momentum and heat transfer characteristics as compared to other geometrical shapes. Accordingly, natural convection flow of nanofluids inside a hexagonal enclosure in presence of magnetic effect is of special technical significance because of its frequent occurrence in many industrial applications such as heat exchangers, electronic devices, nano-electronics, Boron nitride nanosheets, fuel cells, design of solar collectors, thermal insulations, nuclear technologies, aerodynamics and space technologies etc. But there is a lack of information on the topic of MHD natural convection heat transfer in a hexagonal enclosure filled with CuO/water nanofluid.

However, to the best of authors’ knowledge, no work has been conducted on magnetohydrodynamic natural convection heat transfer in a hexagonal enclosure filled with nanofluids. So, the major objective of this study is to explore the flow fields, temperature distributions and heat transfer behaviors for MHD natural convection flow using CuO/water nanofluid inside a hexagonal enclosure. The numerical outcomes of this study hope to be a useful guide for advanced research on natural convection heat transfer in nanofluids inside hexagonal enclosure in presence of magnetic field.

Physical Model

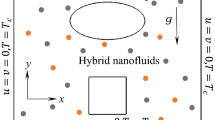
We consider a steady two-dimensional, laminar and incompressible natural convection flow in a regular hexagonal enclosure of side length L filled with CuO/water nanofluid. A tilted hot square block is placed at the centre of the cavity whose side walls are heated at temperature $\hbox {T}_\mathrm{h}$. The temperature of the top and bottom horizontal walls of the cavity is supposed to be at temperature $\hbox {T}_\mathrm{h}$ while the inclined walls are fixed at constant temperature $\hbox {T}_\mathrm{c}$, maintaining $\hbox {T}_{\mathrm{h}} > \hbox {T}_\mathrm{c}$ for all situations. The fluid properties are assumed to be constant except the density variation with temperature in the body force term of the momentum equation and the radiation effect is ignored. It is assumed that the shape and size of the nanoparticles are to be uniform and thermal equilibrium exists between the base fluid and nanoparticles. The thermo-physical properties of the base fluid and copper-oxide nanoparticles are given in the Table 1. Dimensional coordinate systems are considered as such that the x-axis is along the horizontal detection and y-axis is normal to it along the vertically upward direction and the gravitational force, g, is acted along the negative y- axis, indicated downward direction. A uniform magnetic field of strength $\hbox {B}_{0}$ is applied along the horizontal direction. All the solid boundaries of the enclosure are assumed to be rigid no-slip walls. The geometry and coordinate systems are schematically presented in Fig. 1.

Table 1 Thermo physical properties of base fluid and copper-oxide

Fig. 1

Schematic diagram of the hexagonal enclosure

Mathematical Formulation

Using the balance laws of mass, momentum, and energy and also Boussinesq approximation for natural convection flow, the governing conservation equations for this model can be written as follows:

$$\begin{aligned} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y }= & {} 0 \end{aligned}$$

(1)

$$\begin{aligned} u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}= & {} - \frac{1}{\rho _{nf} }\frac{\partial p}{\partial x} + \frac{\mu _{nf} }{\rho _{nf} } \left( {\frac{\partial ^{2}u}{\partial x^{2}} + \frac{\partial ^{2}u}{\partial y^{2}}} \right) \end{aligned}$$

(2)

$$\begin{aligned} u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}= & {} - \frac{1}{\rho _{nf} }\frac{\partial p}{\partial y} + \frac{\mu _{nf} }{\rho _{nf} } \left( {\frac{\partial ^{2}v}{\partial x^{2}} + \frac{\partial ^{2}v}{\partial y^{2}}} \right) + \frac{1}{\rho _{nf} } [g \beta _{nf} \rho _{nf} \left( {T-T_c } \right) ]\nonumber \\&-\frac{1}{\rho _{nf} } [\sigma _{nf} B_0^2 v] \end{aligned}$$

(3)

$$\begin{aligned} u\frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y}= & {} \alpha _{nf } \left( {\frac{\partial ^{2}T}{\partial x^{2}} + \frac{\partial ^{2}T}{\partial y^{2}}} \right) \end{aligned}$$

(4)

where $\rho _{nf} = \left( {1-\phi } \right) \rho _f +\phi \rho _s$ is the density, $\left( {\rho C_p } \right) _{nf} = \left( {1-\phi } \right) \left( {\rho C_p} \right) _f +\phi \left( {\rho C_p} \right) _s$ is the heat capacitance, $\beta _{nf} = \left( {1-\phi } \right) \beta _f +\phi \beta _s$ is the thermal expansion coefficient, $\alpha _{nf} = {k_{nf}}/{\left( {\rho C_p } \right) _{nf}}$is the thermal diffusivity, $\sigma _{nf} = \sigma _f (1+((3(({\sigma _s }/{\sigma _f})-1)\phi )/((({\sigma _s }/{\sigma _f })+2)-(({\sigma _s }/{\sigma _f})-1)\phi ))$ is the electrical conductivity, $k_{nf} = k_f ((k_{s } + 2k_f - 2 \phi (k_f -k_s ))/(k_{s } + 2k_f + \phi (k_f -k_s )))$ [25] is the thermal conductivity and $\mu _{nf} = \mu _f (1+39.11\phi +533.9\phi ^{2})$ [26] is the dynamic viscosity of nanofluid.

The appropriate boundary conditions for the governing equations are as follows:

$$\begin{aligned}&\hbox {at the inclined walls of the enclosure: } u = v = 0 \hbox { and } T = T_c \end{aligned}$$

(5)

$$\begin{aligned}&\hbox {at the horizontal walls of the enclosure: } u = v = 0 \hbox { and } T = T_h \end{aligned}$$

(6)

$$\begin{aligned}&\hbox {at the side walls of the block: } u = v = 0 \hbox { and } T = T_h \end{aligned}$$

(7)

To obtain non-dimensional governing equations, we incorporate the following dimensionless dependent and independent variables:

$$\begin{aligned} X= \frac{x}{L}, \,\, Y= \frac{y}{L}, \,\, U= \frac{u L}{\alpha _f }, \,\, V= \frac{vL}{\alpha _f }, \,\, P= \frac{p L^{2}}{\rho _{nf} \alpha _f^2 } \hbox { and } \theta = \frac{T-T_c }{T_h -T_c } \end{aligned}$$

(8)

Introducing the above relations into the Eqs. (1)–(4), the non-dimensional governing equations can be written as follows:

$$\begin{aligned} \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y}= & {} 0 \end{aligned}$$

(9)

$$\begin{aligned} U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y}= & {} - \frac{\partial P}{\partial X} + \frac{\mu _{nf} }{\rho _{nf} \alpha _f }\left( {\frac{\partial ^{2}U}{\partial X^{2}} + \frac{\partial ^{2}U}{\partial Y^{2}}} \right) \end{aligned}$$

(10)

$$\begin{aligned} U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y}= & {} - \frac{\partial P}{\partial Y} + \frac{\mu _{nf} }{\rho _{nf} \alpha _f }\left( {\frac{\partial ^{2}V}{\partial X^{2}} + \frac{\partial ^{2}V}{\partial Y^{2}}} \right) + \left( {\frac{\rho _{nf} }{\rho _{nf} }} \right) \left( {\frac{\beta _{nf} }{\beta _f }} \right) { Ra} \textit{Pr} \theta \nonumber \\&- \left( {\frac{\rho _f }{\rho _{nf} }} \right) \left( {\frac{\sigma _{nf} }{\sigma _f }} \right) { Ha}^{2}{} \textit{Pr} V \end{aligned}$$

(11)

$$\begin{aligned} U\frac{\partial \theta }{\partial X} + V \frac{\partial \theta }{\partial Y}= & {} \frac{\alpha _{nf} }{\alpha _f }\left( {\frac{\partial ^{2}\theta }{\partial X^{2}} + \frac{\partial ^{2}\theta }{\partial Y^{2}}} \right) \end{aligned}$$

(12)

where $\textit{Pr} = \frac{\nu _f }{\alpha _f}$ is the Prandtl number, ${ Ha}^{2} = \frac{\sigma _{f} B_0^2 L^{2}}{\rho _{f} \nu _f}$ is the Hartmann number and ${ Ra} = \frac{g\beta _f (T_h - T_c ) L^{3}}{\nu _f \alpha _f}$ is the Rayleigh number.

According to the Eq. (8), the boundary conditions (Eqs. (5)–(7)) are rewritten into dimensionless form as:

$$\begin{aligned}&\hbox {at the inclined walls of the enclosure: } U = V = 0 \hbox { and } \theta = 0 \end{aligned}$$

(13)

$$\begin{aligned}&\hbox {at the horizontal walls of the enclosure: } U = V = 0 \hbox { and } \theta = 1 \end{aligned}$$

(14)

$$\begin{aligned}&\hbox {at the side walls of the centered block: } U = V = 0 \hbox { and } \theta = 1 \end{aligned}$$

(15)

From the physical point of view, it is important to calculate the heat transfer rate in terms of local Nusselt number and average Nusselt number at the bottom heated wall of the enclosure. The local Nusselt number in dimensional form is defined as:

$$\begin{aligned} \bar{{Nu}} = - \frac{k_{nf} }{k_f } \frac{\partial T}{\partial x} \end{aligned}$$

(16)

and the average Nusselt number along the bottom heated wall can be calculated by the following expression:

$$\begin{aligned} \textit{Nu}= \frac{1}{L}\int _{0}^{ L} { \bar{{Nu}}\, dY} \end{aligned}$$

(17)

Also, the average temperature of the fluid domain inside the cavity can be calculated using the following relation:

$$\begin{aligned} \theta _\textit{av} = \int {(\theta /{\bar{{V}}}) d\bar{{V}}} \end{aligned}$$

(18)

where $\bar{{V}}$ is the volume of the enclosure.

Numerical Method

In this analysis, nanofluid can be assumed to be single-phase fluid and the classical theory for single phase nanofluids can be applied. The governing Eqs. (9)–(12) along with the boundary conditions (13)–(15) have been solved numerically by using Galerkin weighted residual finite-element technique. To obtain the finite element equations of the present problem, the weighted residual method as described by Zienkiewicz and Taylor [27] is applied to the governing Eqs. (9)–(12) and the finite element equations are:

$$\begin{aligned}&\int _{ A} { N_\alpha \left( {\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y}} \right) } dA = 0 \end{aligned}$$

(19)

$$\begin{aligned}&\int _{ A} { N_\alpha \left( {U \frac{\partial U}{\partial X} + V \frac{\partial U}{\partial Y}} \right) } dA = - \int _{ A} { H_\lambda \frac{\partial P}{\partial X} } dA+ \frac{\nu _{nf} }{\alpha _f } \int _{ A} { N_\alpha \left( {\frac{\partial ^{2} U}{\partial X^{2}} + \frac{\partial ^{2} U}{\partial Y^{2}}} \right) dA} \end{aligned}$$

(20)

$$\begin{aligned}&\int _{ A} { N_\alpha \left( {U \frac{\partial V}{\partial X} + V \frac{\partial V}{\partial Y}} \right) } dA = - \int _{ A} { H_\lambda \frac{\partial P}{\partial Y} } dA+ \frac{\nu _{nf} }{\alpha _f } \int _{ A} { N_\alpha \left( {\frac{\partial ^{2} V}{\partial X^{2}} + \frac{\partial ^{2} V}{\partial Y^{2}}} \right) dA} \nonumber \\&\quad + \left( {\frac{\beta _{nf} }{\beta _f }} \right) Ra \,\textit{Pr} \int _{ A} { N_\alpha \theta dA- } \left( {\frac{\rho _f }{\rho _{nf} }} \right) \left( {\frac{\sigma _{nf} }{\sigma _f }} \right) Ha^{2} \textit{Pr} \int _{ A} { N_\alpha V dA} \end{aligned}$$

(21)

$$\begin{aligned}&\int _{ A} { N_\alpha \left( {U \frac{\partial \theta }{\partial X} + V \frac{\partial \theta }{\partial Y}} \right) } dA = \frac{\alpha _{nf} }{\alpha _f } \int _{ A} { N_\alpha \left( {\frac{\partial ^{2} \theta }{\partial X^{2}} + \frac{\partial ^{2} \theta }{\partial Y^{2}}} \right) dA} \end{aligned}$$

(22)

where A is the element area, $N_\alpha ( \alpha = 1,2,... ... ,6 )$ are the element shape functions or interpolation functions for the velocity components and temperature and $H_\lambda ( \lambda = 1, 2, 3.)$ are the element shape function for the pressure.

In order to generate the boundary integral terms associated with the surface tractions and heat flux in the momentum and the energy equations the Gaussian divergence theorem has been introduced and we obtained the following equations:

$$\begin{aligned}&\int _{ A} { N_\alpha \left( {U \frac{\partial U}{\partial X} + V \frac{\partial U}{\partial Y}} \right) } dA + \int _{ A} { H_\lambda \frac{\partial P}{\partial X} } dA+ \frac{\nu _{nf} }{\alpha _f } \int _{ A} { \left( {\frac{\partial N_\alpha }{\partial X}\frac{\partial U}{\partial X} + \frac{\partial N_\alpha }{\partial Y}\frac{\partial U}{\partial Y}} \right) dA}\nonumber \\&\quad =\int _{ A_0 } {N_\alpha A_x dA_0 }\end{aligned}$$

(23)

$$\begin{aligned}&\int _{ A} { N_\alpha \left( {U \frac{\partial V}{\partial X} + V \frac{\partial V}{\partial Y}} \right) } dA + \int _{ A} { H_\lambda \frac{\partial P}{\partial Y} } dA+ \frac{\nu _{nf} }{\alpha _f } \int _{ A} { \left( {\frac{\partial N_\alpha }{\partial X}\frac{\partial V}{\partial X} + \frac{\partial N_\alpha }{\partial Y}\frac{\partial V}{\partial Y}} \right) dA} \nonumber \\&\quad -\left( {\frac{\beta _{nf} }{\beta _f }} \right) Ra \,\textit{Pr} \int _{ A} { N_\alpha \theta \,dA+ } \left( {\frac{\rho _f }{\rho _{nf} }} \right) \left( {\frac{\sigma _{nf} }{\sigma _f }} \right) Ha^{2}\, \textit{Pr} \int _{ A} { N_\alpha V dA} =\int _{ A_0 } {N_\alpha A_y \,dA_0 } \end{aligned}$$

(24)

$$\begin{aligned}&\int _{ A} { N_\alpha \left( {U \frac{\partial \theta }{\partial X} + V \frac{\partial \theta }{\partial Y}} \right) } dA + \frac{\alpha _{nf} }{\alpha _f } \int _{ A} { \left( {\frac{\partial N_\alpha }{\partial X}\frac{\partial \theta }{\partial X} + \frac{\partial N_\alpha }{\partial Y}\frac{\partial \theta }{\partial Y}} \right) dA} = \int _{ A_w } {N_\alpha q_w dA_w }\nonumber \\ \end{aligned}$$

(25)

where the surface tractions ($A_x, A_y$) along the outflow boundary $A_0$ and velocity components and fluid temperature or heat flux ($q_w$) that flows into or out from the domain along wall boundary $A_w$. The basic unknown for the above differential equations are the velocity components (U, V), temperature $\theta$ and the pressure P. For the development of the finite element equations, the six node triangular element is used in this analysis. All six nodes are associated with velocities as well as temperature, only the three corner nodes are linked with pressure. This means that a lower order polynomial is chosen for pressure and which is satisfied through continuity equation. The velocity components, temperature profiles and linear interpolation for the pressure distribution according to their highest derivative orders for the differential Eqs. (9)–(12) are as:

$$\begin{aligned} U (X, Y)= & {} N_\beta U_{\beta } \end{aligned}$$

(26)

$$\begin{aligned} V (X, Y)= & {} N_\beta V_{\beta }\end{aligned}$$

(27)

$$\begin{aligned} \theta (X, Y)= & {} N_\beta \theta _{\beta }\end{aligned}$$

(28)

$$\begin{aligned} P (X, Y)= & {} H_\lambda P_{\lambda } \end{aligned}$$

(29)

where $\beta = 1, 2, {\ldots } {\ldots }, 6$ and $\lambda = 1, 2, 3$.

Substituting the element velocity component distributions, the temperature distributions and the pressure distribution from Eqs. (26)–(29), into the Eqs. (23)–(25), the finite element equations can be written in the following form:

$$\begin{aligned}&U_\beta \int _{ A} {N_\alpha N_{\beta , x} } dA+V_\beta \int _{ A} {N_\alpha N_{\beta , y} } dA = 0 \end{aligned}$$

(30)

$$\begin{aligned}&U_{\beta } U_{\gamma } \int _{ A} { N_\alpha N_\beta N_{\gamma , x } } \,dA + V_{\beta } U_{\gamma } \int _{ A} { N_\alpha N_\beta N_{\gamma , y } } \,dA+ P_\mu \int _{ A} { H_\lambda H_{\mu , x} } \,dA \nonumber \\&\qquad + \frac{\nu _{nf} }{\alpha _f } U_\beta \int _{ A} { \left( {N_{\alpha , x} N_{\beta , x} + N_{\alpha , y} N_{\beta , y} } \right) dA} =\int _{ A_0 } {N_\alpha A_x \,dA_0 } \end{aligned}$$

(31)

$$\begin{aligned}&U_{\beta } V_{\gamma } \int _{ A} { N_\alpha N_\beta N_{\gamma , x } } \,dA + V_{\beta } V_{\gamma } \int _{ A} { N_\alpha N_\beta N_{\gamma , y } } \,dA+ P_\mu \int _{ A} {H_\lambda H_{\mu , y} } \,dA\nonumber \\&\qquad +\frac{\nu _{nf} }{\alpha _f } V_\beta \int _{ A} { \left( {N_{\alpha , x} N_{\beta , x} + N_{\alpha , y} N_{\beta , y} } \right) \,dA} \nonumber \\&\qquad -\left( {\frac{\beta _{nf} }{\beta _f }} \right) Ra \,\textit{Pr}\, \theta _\beta \int _{ A } {N_\alpha N_{\beta } \,dA+ \left( {\frac{\rho _f }{\rho _{nf} }} \right) \left( {\frac{\sigma _{nf} }{\sigma _f }} \right) Ha^{2} \textit{Pr} V_\beta \int _{ A} { N_\alpha N_\beta \,dA} } \nonumber \\&\quad =\int _{ A_0 } {N_\alpha A_y \,dA_0 } \end{aligned}$$

(32)

$$\begin{aligned}&U_\beta \theta _\gamma \int _{ A} { N_\alpha N_\beta N_{\gamma ,x} \,dA + V_\beta \theta _\gamma \int _{ A} { N_\alpha N_\beta N_{\gamma ,y} \,dA } } \nonumber \\&\qquad + \frac{\alpha _{nf} }{\alpha _f } \theta _\beta \int _{ A} { \left( {N_{\alpha , x} N_{\beta , x} + N_{\alpha , y} N_{\beta , y} } \right) \,dA} = \int _{ A_w } {N_\alpha q_w \,dA_w } \end{aligned}$$

(33)

Now we consider the coefficients in the above governing equations are as follows:

$$\begin{aligned} K_{\alpha \beta ^{x}}= & {} \int _{ A} {N_\alpha N_{\beta , x} } \,dA, \,\, K_{\alpha \beta ^{y}} = \int _{ A} {N_\alpha N_{\beta , y} } \,dA, K_{\alpha \beta \gamma ^{x}} = \int _{ A} { N_\alpha N_\beta N_{\gamma , x } } \,dA\\ K_{\alpha \beta \gamma ^{y}}= & {} \int _{ A} { N_\alpha N_\beta N_{\gamma , y } } \,dA, \,\, K_{\alpha \beta } = \int _{ A} {N_\alpha N_\beta } \,dA, \,\, S_{\alpha \beta ^{xx}} = \int _{ A} {N_{\alpha ,x} N_{\beta ,x} } \,dA\\ S_{\alpha \beta ^{yy}}= & {} \int _{ A} {N_{\alpha ,y} N_{\beta ,y} } \,dA, \,\, M_{\lambda \mu ^{x} } = \int _{ A} { H_\lambda H_{\mu , x} } \,dA, \,\, M_{\lambda \mu ^{y} } = \int _{ A} { H_\lambda H_{\mu , y} } \,dA\\ Q_{\alpha ^{u}}= & {} \int _{ A_0 } {N_\alpha A_x \,dA_0 } , \,\, Q_{\alpha ^{v}} = \int _{ A_0 } {N_\alpha A_y \,dA_0 } , \,\, Q_{\alpha ^{\theta }} = \int _{ A_w } {N_\alpha q_w \,dA_w } \end{aligned}$$

These element matrices are evaluated in closed form for numerical simulation. Details of the derivation for these element matrices are omitted for brevity.

With the help of the above coefficients the finite element equations can be written in the following type

$$\begin{aligned}&K_{\alpha \beta ^{x}} U_\beta + K_{\alpha \beta ^{y}} V_\beta = 0 \end{aligned}$$

(34)

$$\begin{aligned}&K_{\alpha \beta \gamma ^{x}} U_\beta U_\gamma +K_{\alpha \beta \gamma ^{y}} V_\beta U_\gamma + M_{\lambda \mu ^{x} } P_\mu +\frac{\nu _{nf} }{\alpha _f } U_\beta \left( {S_{\alpha \beta ^{xx}} +S_{\alpha \beta ^{yy}} } \right) = Q_{\alpha ^{u}} \end{aligned}$$

(35)

$$\begin{aligned}&K_{\alpha \beta \gamma ^{x}} U_\beta V_\gamma +K_{\alpha \beta \gamma ^{y}} V_\beta V_\gamma + M_{\lambda \mu ^{Y} } P_\mu +\frac{\nu _{nf} }{\alpha _f } V_\beta \left( {S_{\alpha \beta ^{xx}} +S_{\alpha \beta ^{yy}} } \right) \nonumber \\&\quad -\left( {\frac{\beta _{nf} }{\beta _f }} \right) Ra \,\textit{Pr}\, K_{\alpha \beta } \,\theta _\beta +\left( {\frac{\rho _f }{\rho _{nf} }} \right) \left( {\frac{\sigma _{nf} }{\sigma _f }} \right) Ha^{2} \textit{Pr} \,K_{\alpha \beta } V_\beta = Q_{\alpha ^{V}} \end{aligned}$$

(36)

$$\begin{aligned}&K_{\alpha \beta \gamma ^{x}} U_\beta \theta _\gamma + K_{\alpha \beta \gamma ^{y}} V_\beta \theta _\gamma + \frac{\alpha _{nf} }{\alpha _f } \theta _\beta \left( {S_{\alpha \beta ^{xx}} +S_{\alpha \beta ^{yy}} } \right) = Q_{\alpha ^{\theta }} \end{aligned}$$

(37)

Using Newton–Raphson method explained by Reddy [28], the obtained nonlinear Eqs. (34)–(37) are converted into linear algebraic equations. Finally, these linear equations are solved by employing Triangular Factorization method and reduced integration method expressed by Zeinkiewicz et al. [29]. The convergence criterion of the numerical solution along with error estimation has been set to $\left| {\varphi ^{m+1} - \varphi ^{m}} \right| \le 10^{-5}$, where m is the number of iteration and $\varphi$ is a function of U, V and $\uptheta$. The application of this simulation is well described by Taylor and Hood [30] and Dechaumphai [31].

Grid Sensitivity Test

An extensive mesh testing procedure has been conducted using five types of different meshes to obtain the appropriate grid size for the solution of the present problem considering ${ Pr} = 6.2, { Ra} = 10^{3}$, ${ Ha} = 20$ and $\phi = 1\%$. The numerical technique is carried out for highly precise key in the average Nusselt number (${ Nu}_{{ av}}$) for the different meshes to develop an understanding of the grid fineness as shown in Table 2 and Fig. 2. Comparing the obtained numerical results and graphical presentation of average Nusselt number, it is found that the value of ${ Nu}_\textit{av}$ for 12132 elements indicates little difference with the results calculated for other elements. Therefore, the grid size of 6218 nodes and 12132 elements is found to meet the requirements of accurate solution for the present problem.

Fig. 2

Grid sensitivity test

Table 2 Grid sensitivity test at ${ Pr} = 0.6.2, { Ra} = 1000$ and $\phi = 1\%$ and ${ Ha} = 20$

Mesh Generation

In finite element method, the mesh generation is a procedure to subdivide a domain into a set of sub-domains, called finite elements, control volumes, etc. The numerical grids have been defined at discrete locations of the geometric domain, where the variables of the current problem are calculated. Thus, it is basically a discrete presentation of geometric domain where the present problem is to be solved. Mesh generation is an essential configuration of geometric domain for finite elements method which is very useful technique to solve the boundary value problems occurring in various fields of engineering. The finite element mesh of the present physical problem is displayed in Fig. 3.

Fig. 3

Mesh generation of the hexagonal enclosure

Validation of the Code

The computational model is validated by comparing the present numerical results for the base fluid solutions with the previously published results by Tiwari and Das [4], Pirmohammadi et al. [19], De Vahl Davis [32] and Hadjisophocleous et al. [33]. Due to the lack of experimental and theoretical results for natural convection heat transfer in a hexagonal enclosure, the present simulation has been performed for similar enclosure with similar boundary conditions of mentioned researchers [4, 19, 32, 33]. Moreover, comparison also made for different values of Rayleigh number and Hartman number. It is found that the computed results are in excellent agreement (Tables 3, 4).

Table 3 Comparison of the present results for base fluid solutions with the previous works for $\textit{Pr} = 0.70$

Table 4 Comparison of average Nusselt number for various Rayleigh number and Hartmann number

Results and Discussion

In this section, the obtained numerical results for magnetohydrodynamic natural convection heat transfer in CuO/water nanofluid inside a regular hexagonal enclosure are discussed. In performing the numerical simulation, the non-dimensional parameters are considered as : Rayleigh number, from ${ Ra} =10^{3}$ to ${ Ra} = 10^{6}$; solid volume fraction of nanoparticles, from $\phi = 0.1\%$ to $\phi = 5\%$; magnetic field parameter, from ${ Ha} = 0$ to ${ Ha} = 70$; Prandtl number ${ Pr} = 6.2$ and then presented graphically in terms of streamlines, isotherms, mid height horizontal and vertical velocities, average velocity, average Nusselt number and average temperature. For more information regarding the effects of physical parameters of this study, a comprehensive discussion has been presented.

Figure 4a, b display the effects of Rayleigh number (Ra) on the streamlines and isotherms respectively while the value of other parameters are considered as ${ Pr} = 6.2$, ${ Ha} = 20$ and $\phi = 1\%$. From Fig. 4a, it can be observed that for different values of Ra, two oppositely rotating circulations are formed beside the obstacle within the enclosure where one is in clockwise direction and another is in counter clockwise direction. The fluid near to the heated walls of the enclosure is much hotter than the fluid near to the cold inclined walls. Accordingly, fluids near to the heated walls have lower density than fluids near to the cold walls. As a result, fluid is moving up from bottom to top near to the middle of the bottom wall and down from top to bottom along the inclined cold walls. Consequently, streamlines rise up and then down in similar directions besides the block that is shown in Fig. 4a. Moreover, the numerical values of stream function indicate that the strength of flow circulation increases with increasing of natural convection parameter Ra. It is also seen that the shape of interior cells are changed with greater buoyancy parameter and the streamlines are intensified near to the hot and cold walls for increasing Ra. From Fig. 4b, it is observed that the variation of isotherms is closely related to the variation of Ra. It is important to note that, the isotherms are more compressed near to the corners of the top and bottom horizontal walls and the heat lines are almost similar to each other within the flow region beside the block. These patterns tell us that the dominance of conduction mode of heat transfer at low value of Ra. Moreover, the isotherms are more dispersed from middle to the boundary walls of the enclosure and the denseness of the heat lines near to the hot and cold walls increases due to the greater effect of Ra which indicates that the dominance of convection mode of heat transfer for higher values of Ra. This pattern reflects that more convective heat energy flow occurred into the fluid flow region for increasing of Ra. In addition, a thick thermal boundary layer exists near to the hot walls of the cavity which become thinner due to greater Ra, indicating a higher heat transfer rate. Furthermore, the numerical values on temperature reveal that overall temperature distributions changed for higher Ra. In addition, Fig. 5 demonstrated the temperature contours at different locations within the cavity. Accordingly, the temperature distribution and flow circulation within the enclosure are modified noticeably for rising value of Rayleigh number.

Fig. 4

Effect of Ra on streamlines (left) and isotherms (right) while ${ Pr} = 6.2$, ${ Ha} = 20$ and $\phi = 1\%$

Fig. 5

Effect of Ra on temperature distribution while ${ Pr} = 6.2$, ${ Ha }= 20$ and $\phi = 1\%$

Figure 6a, b illustrate the effect of solid volume fraction on the streamlines and isotherms while the value of controlling parameters are kept as ${ Pr} = 6.2$, ${ Ra} = 10^{3}$ and ${ Ha} = 20$. From Fig. 6a, it is observed that the streamlines are characterized by symmetric rotations with clockwise and anticlockwise direction beside the centered square obstacle, which occupies the entire enclosure. The shape of rotating cells near to the centre of the eddy is affected noticeably with increasing of $\phi$ but no remarkable changes were found near to the boundary cells. Observing the numerical values of velocity magnitude, it is clear that the flow strength reduces with increasing concentration of nanopartcles in base fluid. The physical scenario behind it’s that increasing solid concentration in base fluid, increase the density of the fluid which leads to reduce the motion of nanofluid. On the other hand, from Fig. 6b, it can be seen that volume fraction plays an insignificant role on the variation of the shape of isotherms. In addition, the presence of nanoparticles in base fluid enhances the thermal conductivity of the developed liquid and modifies the temperature distribution within the flow domain. Moreover, the curvature of isotherms decreases with increase in percentage of nanoparticles and the heat lines are more compressed near the corners of the heated walls, indicating conduction heat transfer dominated. It is also observed that the isotherms are almost symetrical within the enclosure. Furthermore, Fig. 7 represents the topologies of temperature fields for various solid volume fraction. Consequently, the isotherm contours are influenced noticeably for the variation of $\phi$.

Fig. 6

Effect of $\phi$ on streamlines (left) and isotherms (right) while ${ Pr} = 6.2$, ${ Ra} = 10^{3 }$and ${ Ha} = 20$

Fig. 7

Effect of $\phi$ on temperature distribution while ${ Pr} = 6.2$, ${ Ra} = 10^{3}$ and ${ Ha} = 20$

Figure 8a depicts the influence of magnetic field (Ha) on the streamlines. From Fig. 8a, it is seen that in absence of magnetic field ($\hbox {Ha} = 0$), there produced two symmetrical vortices in opposite direction beside the centered obstacle that occupy almost the entire region of the enclosure. Among them one is rotating in clockwise direction and other one in counter clock wise direction with different strength. Comparing the obtained numerical results of stream function, it is clear that the strength of flow circulation decreases for increasing of Ha that is shown in Fig. 8a and the movements of fluid become slower with higher Ha. This is because; applied magnetic field creates Lorentz’s force which reduces the fluid motion. Moreover, for the greater effect of magnetic field the central cells are affected noticeably and changed to reniform-shaped with two small eyes due to higher Ha but no significant changes were found in clockwise and counter clockwise calls near to the boundary surfaces. On the other hand, Fig. 8b displays the effects of Ha on the isotherm contours within the enclosure. From these figures, it is seen that the isotherms plots are symmetrical about the central block and show that high temperature regions exist near to the hot walls. The physical fact behind is that, the existing thermal boundary layer is less influenced due to the strength of applied magnetic field. Moreover, the isotherms are almost parallel to each other for greater Ha and uniformly distributed inside the enclosure which indicates that the weaker convection as well as the dominance of conduction mode of heat transfer. These are expected, because, the external magnetic field effect tends to reduce the convection mode of heat transfer. Furthermore, the influence of magnetic field on the temperature contours is shown in Fig. 9.

Fig. 8

Effect of Ha on streamlines (left) and isotherms (right) while ${ Pr} = 6.2$, ${ Ra} = 10^{3}$ and $\phi = 1\%$

Fig. 9

Effect of Ha on temperature distribution while ${ Pr} = 6.2$, ${ Ra} = 10^{3}$ and $\phi = 1\%$

Figure 10 plots the numerical results of average Nusselt number at the bottom wall for different values of Rayleigh number, Hartmann number and solid volume fraction. From these figures, it is observed that the average Nusselt number, a measure of heat transfer rate, increases monotonically with increasing of Ra and $\phi$ and decreases for increasing Ha. It is important to note that the addition of nanparticles into the host fluid accelerates the increasing rate of heat transfer inside the enclosure that is shown in Fig. 10b, c respectively, but the strength of magnetic field suppressed the enhancing rate of heat transfer that is presented in Fig. 10a, d, respectively. These are expected phenomenon, because, increasing $\phi$, increases the concentration level of nanoparticles (CuO) in the base fluid that improves the capability of carrying more heat energy into fluid due to the higher thermal conductivity of nanoparticles. Besides this, greater Ha causes lower temperature differences within the temperature field. Moreover, from numerical computations, it is also observed that heat transfer increases by 246.90, 234.70, 207.46 and 176.15% at the selected values of Ha (0, 20, 45, 70) for the variation of convective force, Ra, from $10^{3}$ to $10^{6}$ whereas heat transfer rate increases by 219.72, 234.70, 246.33 and 266.16% for the specified values of solid volume fraction with the same variation of Ra.

Fig. 10

Variation of average Nusselt number

Figure 11a, b illustrate the horizontal velocity profiles U (Y) and vertical velocity profiles V(X) at the mid-section of the hexagonal enclosure for the specified values of Ra, Ha and $\phi$. From these figures, it is clear that the velocity profiles are changed significantly due to rising of governing parameters which are good concordances to the effects of pertinent parameters. Because, relatively higher value of Ra increases the movement of the fluid and the presence of external magnetic field as well as nanoparticles tends to slow down the motion of the fluid inside the enclosure. Accordingly, the magnitude of velocity increases for increasing of Ra whereas decreases for higher Ha and $\phi$. Moreover, the maximum and minimum values of velocity varied along with increasing in distances as well as of Ra, Ha and $\phi$. Furthermore, serpentine shaped profiles are formed in U velocities for the effect of Ra, Ha and $\phi$.

Fig. 11

Effect of Ra, Ha and $\phi$ on U-velocity (left) and V-velocity (right)

The variations of average temperature in nanofluid and base fluid for the different values of Ra, Ha and $\phi$ within the enclosure are displayed in Fig. 12a–c, respectively. From Fig. 12, it is seen that mean temperature increases smoothly for increasing Ha and $\phi$ but decreases for increasing Ra. These are consistent to the effects of governing parameters. Moreover, average temperature is prominent for nanofluid than base fluid. In addition, the presence of magnetic field causes greater effect on the influence of Ra and $\phi$ to modify the nature of average temperature. It is well known that rising effect of magnetic field enhance fluid temperature.

Fig. 12

Variation of average temperature

Figure 13a–d illustrate the variation of mean velocity of nanofluid inside the enclosure for the various values of Ra, Ha and $\phi$. Observing these figures (Fig. 13), it is found that average velocities influenced remarkably for varying of Rayleigh number, magnetic field parameter and solid volume fraction. In addition, the enhancing profiles of $\omega _\textit{av}$ are found for different values of Ra, which are suppressed for greater effect of Ha and $\phi$. On the other hand, decreasing profiles are also observed for increasing $\phi$ and Ha. These are expected phenomenon for the effects of aforesaid parameters because relatively higher value of Ra accelerates the flow strength while the greater Ha and $\phi$ slow down the fluid motion.

Fig. 13

Variation of average velocity

Conclusion

The influence of magnetic field on the flow and heat transfer characteristics due to natural convection heat transfer in a differentially heated hexagonal enclosure filled with CuO/water nanofluid has been examined in this study. The finite element method has been employed to carry out numerical solutions of velocity and temperature fields in terms of streamlines, isotherms, average Nusselt number, mid height horizontal and vertical velocity components, average temperature and mean velocity for a range of pertinent parameters. Based on obtained numerical results and discussions, the following conclusions can be summarized:

• The structure of flow field within the hexagonal enclosure is affected remarkably due to higher Rayleigh number but the flow pattern does not change noticeably for the greater Ha and $\upphi$. In addition, the strength of flow circulations is strongly depended on the effect of natural convection parameter, magnetic field and solid volume fraction of nanoparticles.

• The isotherms contours are influenced significantly due to the variation of Ra, Ha and $\phi$.

• Average temperature of the nanofluid increased with increasing of Ha and $\phi$ but decreased of greater Ra.

• The effects of Ra, Ha and $\phi$ on the mid height horizontal and vertical velocities and also average velocities are remarkable.

• Increasing buoyancy parameter and solid volume fraction of nanoparticles as well as lowest Ha have positive effects to accelerate the heat transfer enhancement.