Introduction

Phosphates of the type M3(PO4)2 have various potential applications. They are used as selective catalysts [1], pigments [2], active substances of corrosion-protecting materials [3], magnetic materials [4], and bioceramic materials [5]. Especially, cobalt and nickel phosphate are of considerable interest in a number of technological fields. They are the catalysts for organic synthesis reactions [1, 6]. For example, mesoporous nickel and cobalt phosphates are used as catalysts for styrene oxidation [1] and a number of cobalt and nickel phosphates are used as pigments based on their colors, insolubility in water, and chemical and thermal stability [2, 6, 7]. Additionally, Ni3(PO4)2 exhibits magnetic property [4]. Many researchers have synthesized metal phosphates via hydrate precursors [1, 6, 8].

Recently, Viter and Nagornyi [7] reported the synthesis of M3(PO4)2·8H2O (M = Ni and Co) by reacting a mixture of CoSO4 and NiSO4 solution with a Na2HPO4 solution at 90 °C and a reaction duration of 1–5 days. The synthesis of Ni3(PO4)2 was extensively studied and reported in the literature [4, 9] due to its magnetic property. Unfortunately, the reported synthetic routes were mostly time and energy consuming. Therefore, the development of a new synthetic route is essential. The crystal structure of Ni3(PO4)2·8H2O consists of octahedral edge-sharing dimers, Ni2O6(H2O)4, and insular octahedral NiO2(H2O)4, linked by PO 3−4 tetrahedra in complex sheets parallel to the (101) plane [10, 11]. The calcined product at 800 °C is Ni3(PO4)2 belonging to a monoclinic structure. This work focuses on the development of the synthetic route of Ni3(PO4)2·8H2O and the study of the kinetic triplet of the dehydration process of this compound which can be used as the precursor for the production of Ni3(PO4)2 used in industry.

The non-isothermal method [12] is based on multiple heating rates’ data by setting the assumption that the parameters of the model are identical for all heating rates. However, the isothermal kinetic [8, 13] investigation would be of assistance in selecting a proper mechanism reaction. The Ozawa–Flynn–Wall (OFW) [14, 15] and Kissigner–Akahira–Sunose (KAS) [16, 17] methods are selected for the estimation of kinetic parameters, while the iterative method [18–22] is used to determine the exact values of E.

In this work, Ni3(PO4)2·8H2O was synthesized by a wet chemical reaction between Na3PO4·12H2O and NiSO4·6H2O at 70 °C, which is lower than the reported condition [7]. The synthesized hydrate and its calcined product were characterized by X-ray diffraction (XRD), Fourier transform infrared spectroscopy (FTIR), thermogravimetry/differential thermogravimetric analysis/differential thermal analysis (TG/DTG/DTA), and atomic absorption spectrophotometry (AAS). The morphology of the synthesized hydrate and its calcined product were studied using scanning electron microscopy (SEM). The non-isothermal decomposition kinetics of Ni3(PO4)2·8H2O was carried out according to the OFW, KAS, and Coats–Redfern methods, and the iterative method was used to determine the exact value of E. The kinetic triplet (E, A, and g(α)) and thermodynamic functions of the transition state complexes (ΔS ≠, ΔH ≠, and ΔG ≠) for the dehydration step of Ni3(PO4)2·8H2O were determined and are reported for the first time. Besides, the isokinetic temperature (T i) was determined and reported.

Experimental

Preparations

The nickel phosphate octahydrate was synthesized by the simple wet chemical reaction between 0.5 M Na3PO4·12H2O (Carlo Erba) and 0.5 M NiSO4·6H2O (Univar) at a Ni/P ratio of 3:2 without a surfactant or template. The mixture suspension was heated for 24 h at 70 °C. A pale green precipitate was obtained and isolated by filtration, washed with DI water several times, and dried in a desiccator. The synthesized sample was calcined in a furnace at 800 °C in air atmosphere for 4 h and the thermal transformation product was further characterized.

Characterizations

The nickel content of Ni3(PO4)2·8H2O dissolved in 3 % v/v HNO3 (Carlo Erba) was determined by the AAS method (Perkin-Elmer Analyst 100). The thermal decomposition of the synthesized sample was investigated on a TG/DTG/DTA instrument (Perkin-Elmer Pyris Diamond) at the heating rate of 5, 10, 15, and 20 °C min−1 over the temperature range from 50 to 1,000 °C in N2 atmosphere with the flow rate of 100 mL min−1. The sample mass of about 5.9 mg (accurate) was filled into an alumina pan. The TG/DTG/DTA curves of the sample were recorded in an alumina pan using α-Al2O3 as the reference material. The structures of the prepared sample and its calcined product were characterized by XRD (Phillips 3710) using the scan rate of 1° min−1 in the 2θ range of 5–70° with Cu Kα radiation (λ = 0.15406 Å). The crystallite size was calculated using the Scherrer equation (i.e., D = Kλ/β cosθ, where λ is the wavelength of X-ray radiation, K is a constant taken as 0.89, θ is the diffraction angle, and β is the full width at half maximum (FWHM)) [23, 24]. The FTIR spectra of the synthesized sample and the calcined product were recorded on a Perkin-Elmer spectrum GX FTIR/FT Raman spectrophotometer using the KBr pellet technique in the wavenumber range of 4,000–370 cm−1 with 32 scans and the resolution of 4 cm−1. The morphologies of the synthesized hydrate and the calcined product were investigated by SEM (LEO SEM VP1450) after gold coating.

Kinetics study

The non-isothermal decomposition kinetic study of the solid-state reaction in the type of A(solid) → B(solid) + C(gas) is assumed to be based on the following isothermal rate equation [25]:

$$ \frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = A{\text{e}}^{\text{-E/RT}} f(\alpha),$$
(1)

where α is the extent of conversion and is equal to (m i − m T)/(m i − m f); m i, m T, and m f are the initial mass, current mass at temperature T, and final mass at a temperature at which the mass loss is approximately unchanged, respectively. A, E, and R are the pre-exponential factor, the activation energy (kJ mol−1), and the gas constant (8.314 J K−1 mol−1), respectively.

Alternatively, Eq. (1) can be transformed into a non-isothermal rate expression, where dα/dT is the non-isothermal rate and dT/dt is the heating rate (β) and the following equation is obtained [25]:

$$ \frac{{{\text{d}}\alpha }}{{{\text{d}}T}} = \frac{A}{\beta } \cdot {\text{e}}^{{{{\text{ -E}} \mathord{\left/ {\vphantom {{\text{ -E}}{\text{RT}}}} \right. \kern-0pt}{\text{RT}}}}} \cdot f\left( \alpha \right) $$
(2)

The integral of Eq. (2), after rearranging, leads to Eq. (3):

$$ g\left( \alpha \right) = \int\limits_{0}^{\alpha } {\frac{{{\text{d}}\left( \alpha \right)}}{f\left( \alpha \right)} = \frac{A}{\beta }\int\limits_{{{{T}}_{0} }}^{\text{T}} {{\text{e}}^{{{{ \text{-E}} \mathord{\left/ {\vphantom {{ \text{-E}} {\text{RT}}}} \right. \kern-0pt} {\text{RT}}}}} } {\text{d}}T} $$
(3)

This temperature integral (Eq. 3) has not been widely implemented. To transform the above integral in Eq. (3) to the more general form found in mathematical handbooks, the integration variable can be redefined as \( x = \frac{E}{RT} \) and the temperature integral then becomes

$$ g(\alpha ) = \frac{AE}{\beta R}\int\limits_{x}^{\infty } {\frac{{{\text{e}}^{ \text{- x}} }}{{x^{2} }}{\text{d}}x} $$
(4)

If \( p\left( x \right) = \int\limits_{x}^{\infty } {\frac{{e^{ - x} }}{{x^{2} }}{\text{d}}x} \), then Eq. (4) can be written as

$$ g(\alpha ) = \frac{AE}{\beta R}p\left( x \right), $$
(5)

where p(x) is the Arrhenius temperature integral and g(α) is the integral form of the conversion function. The right-hand side of Eq. (5) does not have a simple analytical solution as a number of approximate solutions were offered in the past. In the present study, the kinetic parameters (E and A) were calculated from TG data through the OFW (Eq. 6), KAS (Eq. (7)), and Coats–Redfern (Eq. 8) equations.

OFW [14, 15]:

$$ \ln \beta = \ln \left( {\frac{0.0048AE}{Rg(\alpha )}} \right) - 1.0516\left( \frac{E}{RT} \right) $$
(6)

KAS [16, 17]:

$$ \ln \left( {\frac{\beta }{{T^{2} }}} \right) = \ln \left( {\frac{AE}{Rg(\alpha )}} \right) - \left( \frac{E}{RT} \right) $$
(7)

Coats–Redfern [26]:

$$ \ln \left( {\frac{g(\alpha )}{{T^{2} }}} \right) = \ln \left( {\frac{AR}{\beta E}} \right) - \left( \frac{E}{RT} \right) $$
(8)

The TG/DTG/DTA curves were recorded at four heating rates of 5, 10, 15, and 20 °C min−1. The conversion factor α and T from TG curves at four heating rates was recorded. The activation energy E values were calculated from the slopes of the plots of lnβ versus 1,000/T (OFW equation) and the plots of ln(β/T 2) versus 1,000/T (KAS equation) at the α values between 0.2 and 0.8 with 0.1 increment. Additionally, the iterative methods [18–22] for OFW and KAS equations were used to calculate E approximating the exact value, according to the equations

$$ \ln \frac{\beta }{H(x)} = \ln \left( {\frac{0.0048AE}{g\left( \alpha \right)R}} \right) - 1.0516\left( \frac{E}{RT} \right) $$
(9)
$$ \ln \left( {\frac{\beta }{{h(x)T^{2} }}} \right) = \ln \frac{AR}{g\left( \alpha \right)E} - \frac{E}{RT}, $$
(10)

where h(x) is expressed by the fourth Senum and Yang [27] approximation formula

$$ h(x) = \frac{{x^{4} + 18x^{3} + 88x^{2} + 96x}}{{x^{4} + 20x^{3} + 120x^{2} + 240x + 120}}, $$

where x = E/RT and H(x) is express as

$$ H(x) = \frac{{\exp ( - x)h(x)/x^{2} }}{0.0048\exp ( - 1.0516x)} $$

The iterative procedure can be performed according to the following steps [18–22]:

  1. (i)

    Assume h(x) or H(x) = 1 to estimate the initial value of E 1. The isoconversional methods stop the calculation at this step.

  2. (ii)

    Using E 1, calculate a new value of E 2 from the plot of ln [β/H(x)] versus 1,000/T (OFW equation) or ln [β/h(x)T 2] versus 1,000/T (KAS equation).

  3. (iii)

    Repeat step (ii), replacing E 1 with E 2. When E i − E i−1 < 0.1 kJ mol−1, the last value of E i was considered to be the exact value of activation energy of the reaction.

Therefore, the activation energy values obtained by this method are usually regarded as reliable.

The following equation was used to estimate the probable mechanism function, g(α) [28]:

$$ \ln g\left( \alpha \right) = \left[ {\ln \frac{{AE}}{R} + \ln \frac{{{\text{e}}^{ \text{- x}} }}{{x^{2} }} + \ln h(x)} \right] - \ln \beta $$
(11)

However, Eq. (11) is suitable only for the single-step process reaction.

In this work, the most probable mechanism function for the dehydration process of the synthesized hydrate was determined from the plot of ln β versus ln g(α) using a linear regression of the least-square method. The degrees of conversion α corresponding to four heating rates taken from two selected temperatures (180 and 185 °C) were substituted into 35 types of mechanism functions [29] as illustrated in Table S1 (supporting information). The most probable mechanism function exhibits the slope and the linear correlation coefficient r 2 closest to −1.0000 and unity, respectively [28, 30, 31]. Consequently, the pre-exponential factor A can be determined from the slopes of OFW and KAS plots by substitution of g(α) into the equations.

Recently, the ICTAC Kinetics Committee [32] reported that the kinetic computations based on a single heating rate must be avoided such as Coats–Redfern. Moreover, the most probable mechanism function was insured using the Coats–Redfern method which is expressed as Eq. (8) [26] because the most probable mechanism function from Eq. (11) was used to confirm the probable mechanism function obtained from the Coats–Redfern method.

Based on the Coats–Redfern equation, the plot between ln (g(α)/T 2) and 1,000/T for different α values (0.2–0.8) at the single β must give rise to a single master straight line. The activation energy and pre-exponential factor were calculated via Eq. (8) combined with 35 types of conversion functions (Table S1). The model with the highest correlation coefficient (closest to 1.0000) is the best-fit kinetic model; meanwhile, the calculated activation energy values from four heating rates must be close to the values calculated from the iterative method [31]. The five probable mechanism functions for the dehydration process of Ni3(PO4)2·8H2O are shown in Table 1.

Table 1 Slopes, correlation coefficient (r 2) values from the plots of lng(α) versus lnβ at 180 and 185 °C of the five probable mechanism functions (g(α)), and average kinetic parameters obtained from Coats–Redfern method during the dehydration process of Ni3(PO4)2·8H2O
Full size table

Moreover, the isothermal kinetic method as one acceptable method is used to confirm the solid-state kinetic model. The shape of the plot of α versus time can be classified into acceleratory, deceleratory, and sigmoidal models [25, 32]. The acceleratory models are those that indicate the increasing of the reaction rate with the reaction progress. In contrast, the deceleratory models exhibit the decreasing of the reaction rate with the reaction progress. The sigmoidal (autocatalytic) models show an s shape of α-time plot. The confirmation of the kinetic model using the isothermal kinetic method was carried out at four isothermal programs with a fast heating rate (150 °C min−1) starting from 50 °C and holding at 180, 200, 220, and 240 °C for 60 min. The degree of conversion α and the time from TG curves at four isothermal programs were recorded. The plot of α versus t (min) for each isothermal program was used to assist the selection of a suitable model.

The isokinetic temperature (T i) is the actual temperature at which rates of all members of a series of related reactions are equal [33], which is often close to, or within, the temperature interval of the measured kinetic data [34]. The kinetic compensation effects (KCE) will be considered by which a linear relationship between the E and lnA was described according to following equation [35]:

$$ \ln A = aE + b, $$
(12)

where a and b are the kinetic compensation constant values. From the Arrhenius equation, we obtain

$$ \ln A = \frac{1}{RT}E + \ln k $$
(13)

The corresponding Arrhenius line has a common point intersection, which is the isokinetic point (k = k i and T = T i) [33, 34, 36]. The Eq. (13) can be written as

$$ \ln A = \frac{1}{{RT_{\text{i}} }}E + \ln k_{\text{i}} , $$
(14)

where

$$ \ln k_{\text{i}} = b \quad {\text{and}}\quad T_{\text{i}} = \frac{1}{aR} $$
(15)

Moreover, the authors demonstrated [37–39] based on the equation suggested by Vlase et al. [40] that the specificity of non-isothermal decomposition is due to the vibrational energy on a certain bond, upon anharmonic oscillation. Consequently, T i can be calculated from observed vibrational bands corresponding to the specific group undergoing decomposition (here is water) by using Eqs. (16) and (17):

$$ \omega_{\text{calc}} = \frac{{k_{\text{B}} }}{hc}T_{\text{i}} = 0.695T_{\text{i}} $$
(16)

and

$$ \omega_{\text{sp}} = q\omega_{\text{calc}} , $$
(17)

where k B and h are the Boltzmann and Planck constants, respectively, c is the light velocity, q is the number of quanta (\( q \in N \)), and ω sp is the assigned spectroscopic wavenumber for the bond supposed to be broken. T i relates to the activation energy and pre-exponential factor [41–43]. The calculation of this value from kinetic compensation effect is complicated; therefore, the isokinetic temperature T i can be calculated from the spectroscopic data as an alternative way. In this work, five vibrational band positions of water of crystallization were observed on FTIR spectra of the hydrate, and then we determined the calculated wavenumber (ω calc) values from Eq. (17). Then, T i was estimated from spectroscopic data according to Eq. (16).

The thermodynamic functions of activated complex can be estimated from the activated complex (transition state) theory of Eyring [44]. The corresponding Eyring equation is

$$ k_{\exp } = \chi K^{ \ne } \frac{{k_{\text{B}} T}}{h}, $$
(18)

where K ≠ is the equilibrium constant between the activated complex (having four translational degree of freedom) and the reactants. χ is the transmission coefficient as the ratio of systems reacting. For many simple reactions, this parameter is approximately unity. k B and h are the same as mentioned before. The entropy and enthalpy change of activated complex (ΔS ≠ and ΔH ≠) can be expressed by the equation

$$ K^{ \ne } = \exp \left( {\frac{{\Updelta S^{ \ne } }}{R}} \right)\exp \left( { - \frac{{\Updelta H^{ \ne } }}{RT}} \right) $$
(19)

By substituted Eq. (19) into Eq. (18), Eq. (20) is obtained:

$$ k_{\exp } = \chi \frac{{k_{\text{B}} T}}{h}\exp \left( {\frac{{\Updelta S^{ \ne } }}{R}} \right)\exp \left( { - \frac{{\Updelta H^{ \ne } }}{RT}} \right), $$
(20)

where \( \Updelta H^{ \ne } = E^{ \ne } - RT_{{}} \); Eq. (20) will then be written as

$$ k_{\exp } = \chi {\text{e}}\frac{{k_{\text{B}} T}}{h}\exp \left( {\frac{{\Updelta S^{ \ne } }}{R}} \right)\exp \left( { - \frac{E}{RT}} \right), $$
(21)

where e is the Neper number (e = 2.7183).

The isokinetic point (k exp = k i and T = T i) is the point of intersection of any particular family of Arrhenius plots such that there is one value of k exp at on unique ΔS, as well as ΔG, as rotational and translational modes tend to remain constant [45]. Eq. (21) can be written as

$$ k_{\text{i}} = \chi {\text{e}}\frac{{k_{\text{B}} T_{\text{i}} }}{h}\exp \left( {\frac{{\Updelta S^{ \ne } }}{R}} \right)\exp \left( { - \frac{E}{{RT_{\text{i}} }}} \right), $$
(22)

where \( A = \frac{{k_{\text{i}} }}{{\exp \left( {{{ - E} \mathord{\left/ {\vphantom {{ - E} {RT_{\text{i}} }}} \right. \kern-0pt} {RT_{\text{i}} }}} \right)}} \) and then

$$ A = \left( {\frac{{\chi ek_{\text{B}} T_{\text{i}} }}{h}} \right)\exp \left( {\frac{{\Updelta S^{ \ne } }}{R}} \right) $$
(23)

The entropy change of the activated complex (ΔS ≠) for the dehydration step ∆S ≠ can be calculated using Eq. (24).

$$ \Updelta S^{ \ne } = R\ln \left( {\frac{Ah}{{\chi {\text{e}}k_{\text{B}} T_{\text{i}} }}} \right) $$
(24)

The enthalpy (∆H ≠) and Gibbs free energy (∆G ≠) changes of the activated complex of the dehydration step can be calculated using Eqs. (25) and (26), respectively.

$$ \Updelta H^{ \ne } = E^{ \ne } - RT_{\text{i}} $$
(25)
$$ \Updelta G^{ \ne } = \Updelta H^{ \ne } - T_{\text{i}} \Updelta S^{ \ne } $$
(26)

In this work, we suggest the usage of the average T i calculated from spectroscopic data and the KCE method for the calculation of ∆S ≠, ∆H ≠, and ∆G ≠ values.

Results and discussion

Chemical analysis

The nickel content of the Ni3(PO4)2·8H2O was determined using the AAS technique, and it was found to be 3.25 mol, which agrees well with the theoretical value of 3 mol. The water content in this hydrate was determined using the TG/DTG/DTA technique in N2 atmosphere at the heating rate of 10 °C min−1. The TG/DTG/DTA curves are shown in Fig. 1, where one decomposition step over the temperature range of 150–250 °C is illustrated. The observed total mass loss in this temperature range is 28.53 % (8.1 mol of water of crystallization), which agrees well with the theoretical mass loss of 28.22 % and confirmed 8 mol of water of crystallization in the formula. The thermal decomposition reaction is suggested as follows:

$$ {\text{Ni}}_{ 3} ( {\text{PO}}_{ 4} )_{ 2} \cdot 8 {\text{H}}_{ 2} {\text{O}}\mathop{\longrightarrow}\limits^{{ 1 5 0 { - 250}\,^{\text{o}} {\text{C}}}}{\text{ Ni}}_{ 3} ( {\text{PO}}_{ 4} )_{ 2} + {\text{ 8H}}_{ 2} {\text{O}} $$
(27)

The DTA curve of the Ni3(PO4)2·8H2O at the heating rate of 10 °C min−1 shows one maximum peak at 199.9 °C, which agrees well with the DTG peak at 201.7 °C. One additional peak at 776.1 °C of the DTA curve was observed, which is suggested to be due to the phase transition from low crystallinity of Ni3(PO4)2 to higher crystallinity. The thermal decomposition product is Ni3(PO4)2.

Fig. 1
figure 1

TG/DTG/DTA curves of Ni3(PO4)2·8H2O at four heating rates (5, 10, 15, and 20 °C min−1) in N2 atmosphere over the temperature range of 50–1,000 °C

Full size image

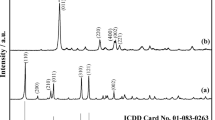
X-ray powder diffraction

The XRD patterns of the synthesized Ni3(PO4)2·8H2O and its calcined product at 800 °C in air are shown in Fig. 2a, b, respectively. All detectable peaks of the synthesized hydrate and the calcined product are indexed as Ni3(PO4)2·8H2O and Ni3(PO4)2 according to the standard data of PDF # 33–0951 and PDF # 38–1473, respectively. These results indicated that all crystal structures are in the monoclinic system with space group I2/m or \( C_{2{\text{h}}}^{3} \) (12) and P21/a or \( C_{2{\text{h}}}^{5} \) (14). The average crystallite sizes and the lattice parameters of these compounds were calculated from XRD data [23]. The crystallite sizes of Ni3(PO4)2·8H2O and its calcined product are 63.2 ± 8 and 59.2 ± 13 nm, respectively. The lattice parameters of Ni3(PO4)2·8H2O are a = 9.845 Å, b = 13.16 Å, c = 4.634 Å, and β = 102.31°, while those of Ni3(PO4)2 are a = 10.11 Å, b = 4.699 Å, c = 5.828 Å, and β = 90.87°; these results agree with the reported standard data.

Fig. 2
figure 2

The XRD patterns of the synthesized Ni3(PO4)2·8H2O (a) and its calcined product at 800 °C (b) in air atmosphere

Full size image

FTIR spectroscopy

The FTIR spectra of the synthesized Ni3(PO4)2·8H2O and its calcined product at 800 °C are shown in Fig. 3a, b, respectively. The vibrational bands in the region of 3,200–3,000 cm−1 (Fig. 3a) are assigned to ν1(A1)H2O, whereas the bands at about 3,400 cm−1 are attributed to ν3(B2)H2O. The bending mode of water, ν2(A1)H2O was observed in the region of 1,700–1,600 cm−1. The vibrational bands of PO 3−4 anion can be observed around 1,076–990 cm−1, 965–880 cm−1, 600–540 cm−1, and 473 cm−1 for the ν3(F2)PO 3−4 , ν1(A1)PO 3−4 , ν4(F2)PO 3−4 , and ν2(E) PO 3−4 , respectively. The librational modes of water can be observed at around 736 cm−1 (rocking, ρ r) [46], which disappear in the spectra of the calcined product (Fig. 3b). The bands in the region of 1,140–1,068 cm−1 and 976–887 cm−1 of the calcined product are assigned to ν3(F2) and ν1(A1) of PO 3−4 , respectively. The asymmetric bending ν4(F2)PO 3−4 and the symmetric bending ν2(E)\( {{\text{PO}}_{4}}^{3 - } \) are observed in the region of 640–530 cm−1 and around 450 cm−1, respectively. The splitting of the ν4(F2)PO 3−4 and ν2(E)PO 3−4 bands indicates that the phosphate group is located at a site of lower symmetry than T d.

Fig. 3
figure 3

The FTIR spectra of Ni3(PO4)2·8H2O (a) and its calcined product at 800 °C in air atmosphere (b)

Full size image

Study of morphology

The SEM micrographs of Ni3(PO4)2·8H2O and its calcined product at 800 °C are illustrated in Fig. 4a, b, respectively. Figure 4a exhibits thin plates of a width × length between (800 × 1,000) and (1,000 × 2,000) nm, whereas the particle shape of the calcined product Ni3(PO4)2 (Fig. 4b) shows the agglomeration of a thin plate of smaller size than the synthetic hydrate and agrees well with the XRD data.

Fig. 4
figure 4

The SEM micrographs of Ni3(PO4)2·8H2O (a) and its calcined product at 800 °C in air atmosphere (b)

Full size image

Kinetics study

Determination of kinetic triplet

The kinetic triplet (E, A, and g(α)) of the dehydration process of Ni3(PO4)2·8H2O is reported for the first time. The plots of log(β) versus 1,000/T (OFW method) and log(β/T 2) versus 1,000/T (KAS method) are shown in Figs. 5 and 6, respectively. The calculated E values of the dehydration of Ni3(PO4)2·8H2O from OFW and KAS equations are tabulated in Table 2. Additionally, the E values were calculated from the iterative methods of OFW and KAS equations. The difference between the E values from the iterative and OFW or KAS equations including the relative error (%) is summarized in Table 3. According to Tables 2 and 3, the calculated E values from the OFW method are more different from the iterative methods than the KAS method, due to the temperature integral approximation [22]. The OFW equation is approximated using Doyle’s approximation [14, 15, 32], but the KAS equation is approximated using Murray and White’s approximation as the more accurate one [16, 17, 32]. It is considered that the OFW method should not be used without performing an iterative correction procedure [32]. In the other hand, the KAS method gives a more reliable E value, which is close to that from the iterative method as an accepted method for the determination of the exact value of E [18–22, 32]. The calculated E values from all methods change little with α. Moreover, the relative errors (%) of the E values from OFW, KAS, and iterative methods (Table 3) are <10 %, which indicate that the dehydration process of Ni3(PO4)2·8H2O could be a single-step mechanism [19, 22, 47].

Fig. 5
figure 5

OFW plots (lnβ vs 1,000/T) of Ni3(PO4)2·8H2O from TG data in N2 atmosphere

Full size image
Fig. 6
figure 6

KAS plots (ln(β/T 2) vs 1,000/T) of Ni3(PO4)2·8H2O from TG data in N2 atmosphere

Full size image
Table 2 Activation energy E, pre-exponential factor A values, and correlation coefficient r 2 calculated by OFW and KAS methods for the dehydration step of Ni3(PO4)2·8H2O
Full size table
Table 3 Activation energy E and the relative error of slopes calculated by iterative of OFW and KAS equations for the dehydration step of Ni3(PO4)2·8H2O
Full size table

The most probable mechanism function for the dehydration process of Ni3(PO4)2·8H2O was determined and the selected five probable mechanism models are tabulated in Table 1. The results from both temperatures (180 and 185 °C) show that the R1 model with the g(α) = α (zero-order) has slope and r 2 values close to −1.0000 and 1.0000, respectively. Additional, the calculated E values from the Coats–Redfern method for g(α) = α are close to the values from the iterative methods. The geometrical contraction R models [25, 48] are the mechanisms of rapid nucleation occurrence on the surface of the crystal and the rate of reaction is controlled by the reaction interface progress toward the center of the crystal depending on the crystal shape. The induction period may be too short to permit defection and the maximum reaction rate is attained at low α. Thereafter, the α-time curve is a deceleratory type [25, 32, 48]. The progressing interface reaction can be generally expressed as f(α) = 1 − (1 − α)1/n, where n is the number of dimensions in which the interface progresses. In the contracting volume equation, n = 3 (R3), for the contracting area equation, n = 2 (R2); and when there is a linear progress of the interface in a single direction, n = 1 (R1). The zero-order kinetic behavior in an unusual dehydration reaction has been shown to be due to the constant area of the reaction interface, and this interface has been identified as the original surface of the reaction crystallite which does not advance. Water molecules are mobile within the reactant structure and the desorption step at the immobile interface is rate limiting [48]. The pre-exponential factor values were calculated from Ozawa and KAS equations with g(α) = α and are tabulated in Table 2.

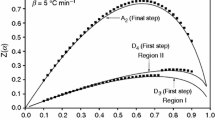
The isothermal kinetic shapes (α-time relation) of four isothermal programs (hold at 180, 200, 220, and 240 °C programs) of Ni3(PO4)2·8H2O are illustrated in Fig. 7. The shape of kinetic curves represents the processes whose reaction rate is at a maximum at the beginning and decreases continuously as the extent of conversion increases, which is the character of the deceleratory model [25]; the system in this study corresponds to the R1 model type [32]. Hence, the results from the isothermal kinetic study agree well with those from the non-isothermal kinetic study.

Fig. 7
figure 7

The kinetic α-time curves using isothermal programs of Ni3(PO4)2·8H2O hold at 180, 200, 220, and 240 °C for 60 min in N2 atmosphere

Full size image

Determination of the isokinetic temperature

The isokinetic temperature (T i) was calculated using the kinetic compensation effects’ (KCEs) equation (Eqs. 14, 15) and the spectroscopic data (Eqs. 16, 17). Based on Eq. (14), T i was calculated from the slope of the plot between lnA and E via Eq. (15) and found to be 187.58 °C. On the other side, T i was determined from spectroscopic data using Eqs. (16) and (17). The calculated wavenumber (ω calc) values were obtained using Eq. (11) for each number of quanta (q), and the observed ω sp values are presented in Table 4. Five vibrational band positions were selected to get the nearest values to ω calc for the case of water of crystallization of the hydrate. The calculated average ω calc from Eq. (16) was tabulated in Table 4. Consequently, the T i can be calculated to be 214.80 °C, which is close to the calculated T i from KCE equation.

Table 4 Calculation of isokinetic temperature (T i) from spectroscopic data compared with that from kinetic compensation effect (KCE) methods
Full size table

Estimation of thermodynamic functions of activated complex

In the non-isothermal decomposition kinetic study, the calculated A (both from OFW and KAS methods) and the isokinetic temperature (T i) were used to estimate the thermodynamic functions of activated complex, namely, entropy ΔS ≠, enthalpy ΔH ≠, and Gibbs free energy ΔG ≠ changes of the activated complex. The calculated ΔS ≠, ΔH ≠, and ΔG ≠ from Ozawa are −40.40 J K−1 mol−1, 83.99 kJ mol−1, and 92.12 kJ mol−1, while those from KAS are −49.61 J K−1 mol−1, 80.50 kJ mol−1, and 90.48 kJ mol−1, respectively. The negative ΔS ≠ values for the dehydration process of Ni3(PO4)2·8H2O indicate the higher orderness of the activated state than the initial state. These results may be interpreted as a slow stage [35, 42, 43]. The positive values of ΔH ≠ agree with the endothermic peak in the DTA upon the dehydration reaction step. The positive values of ΔG ≠ can be interpreted such that the dehydration process of the hydrate is a non-spontaneous process for the transition from the reactant to the activated complex.

Conclusions

The Ni3(PO4)2·8H2O was successfully synthesized by a simple and energy-saving method compared with those reported in the literature. The results from AAS, TG/DTG/DTA, FTIR, and XRD confirm the formula of the synthesized compound to be Ni3(PO4)2·8H2O and its calcined product at 800 °C to be Ni3(PO4)2, which is important for industrial applications. The thermal transformation from Ni3(PO4)2·8H2O into Ni3(PO4)2 via the dehydration process occurred in one step at around 200–250 °C, according to the TG/DTG/DTA and kinetic data. The kinetics of the dehydration process of the title compound was studied using non-isothermal TG as a model-fitting method. The activation energy E and pre-exponential factor A were determined by the OFW and KAS methods. The deceleratory R1 model (g(α) = α) is found to be the most probable mechanism for the dehydration step of Ni3(PO4)2·8H2O. The Coats–Redfern and isothermal run methods were additionally used to confirm the most probable mechanism function. The calculated E values from the Coats–Redfern method agree well with the OFW and KAS methods. The exact values of E from the iterative method were determined and compared. The isokinetic temperatures (T i) calculated using the KCE equation and the spectroscopic data are close to each other, which suggests that the vibrational spectroscopic data can be the alternative method to calculate T i. The values of ΔS ≠, ΔH ≠, and ΔG ≠ for the activated complex of the dehydration process were calculated using kinetic parameters based on the Eyring method. The obtained values of ΔS ≠, ΔH ≠, and ΔG ≠ indicate the lesser disorderness of the activated complex than the reactant and the process is endothermic and non-spontaneous.