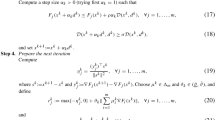A Quasi-Newton Method with Wolfe Line Searches for Multiobjective Optimization

Abstract

We propose a BFGS method with Wolfe line searches for unconstrained multiobjective optimization problems. The algorithm is well defined even for general nonconvex problems. Global convergence and R-linear convergence to a Pareto optimal point are established for strongly convex problems. In the local convergence analysis, if the objective functions are locally strongly convex with Lipschitz continuous Hessians, the rate of convergence is Q-superlinear. In this respect, our method exactly mimics the classical BFGS method for single-criterion optimization.

1 Introduction

In multiobjective optimization, we seek to minimize two or more objective functions simultaneously. Usually, in a problem of this class, there is no single point that minimizes all the functions at once. In that case, the objectives are said to be conflicting and we use the concept of Pareto optimality to characterize a solution of the problem. A point is called Pareto optimal if none of the objective functions can be improved without degrading another. Multiobjective optimization problems appear in many fields of science. We refer the reader to [3, 56] and references therein for some interesting practical applications.

Over the past two decades, several iterative methods for scalar-value optimization have been extended and analyzed for multiobjective optimization. This line of research was opened in [25] with the extension of the steepest descent method; see also [24]. Other algorithms include Newton [10, 24, 30, 59], quasi-Newton [1, 36, 42, 47, 49, 52, 53], conjugate gradient [28, 40], projected gradient [2, 22, 26, 27, 29], and proximal methods [5, 7,8,9, 11]. As a common feature, these methods enjoy convergence properties and do not transform the problem at hand into a parameterized scalar problem and then solve it, being attractive alternatives for scalarization [21] and heuristic approaches [37].

Quasi-Newton algorithms are one of the most popular classes of methods for solving an unconstrained single-objective optimization problem. Its long history began in 1959 with the work of Davidon [16] and was popularized four years later by Fletcher and Powell [23]. Since then, quasi-Newton algorithms have attracted the attention of the scientific community primarily because they avoid computations of second derivatives and perform well in practice. Papers on the subject are too many to list, including contributions from the most prominent names in the optimization community. In a quasi-Newton method, the search direction is computed based on a quadratic model of the objective function, where the true Hessian is replaced by some approximation which is updated after each iteration. The most effective quasi-Newton update scheme is the BFGS formula, which was independently discovered by Broyden, Fletcher, Goldfarb, and Shanno in 1970. Under some proper assumptions, the BFGS algorithm with an adequate line search is globally and superlinearly convergent on strongly convex problems [6, 50]. On the other hand, it may not converge for general nonconvex functions [13, 14, 43].

The BFGS method for multiobjective optimization was first proposed in [49] and later also studied in [36, 42, 47, 52, 53]. Similarly to the single-criterion case, the search direction is defined as the solution of a problem involving quadratic models of the objective functions, where BFGS updates are used in place of the true Hessians. Despite the aforementioned papers, the convergence theory of the BFGS method for multiobjective optimization problems can still be considered incomplete. In the following, we highlight some shortcomings of the existing references: (i) the algorithms are usually designed for strongly convex problems; (ii) the BFGS updates and their inverses are often assumed to be uniformly bounded (which seems unrealistic, see [48, Section 6.4]); (iii) some key intermediate steps in convergence analysis are often stated without proof. The aim of the present paper is to overcome all these drawbacks.

We propose a BFGS algorithm for unconstrained multiobjective optimization problems, where the step sizes satisfy the standard (vector) Wolfe conditions recently introduced in [40]. The Wolfe conditions are a key tool to preserve the positive definiteness of the Hessian approximations. As a consequence, our algorithm is well defined even for general nonconvex problems. Global convergence and R-linear convergence to a Pareto optimal point are established for strongly convex problems. In the local convergence analysis, assuming that the objective functions are locally strongly convex with Lipschitz continuous Hessians, we prove that the rate of convergence is Q-superlinear. As an intermediate result, we show that the unit step size eventually satisfies the Wolfe conditions. Furthermore, a Dennis–Moré-type condition for multiobjective optimization problems will appear very clearly. We emphasize that all assumptions considered are natural extensions of those made for the scalar optimization case. Numerical experiments on convex and nonconvex multiobjective problems illustrating the potential practical advantages of our approach are presented.

The outline of this paper is as follows. Section 2 presents some basic concepts and results of multiobjective optimization. In Sect. 3, we describe our algorithm and show that it is well defined even on general nonconvex problems. Global and local convergence results are discussed in Sects. 4 and 5, respectively. Numerical experiments are presented in Sect. 6, and final remarks are made in Sect. 7.

2 Preliminaries

Notation $\mathbb {R}$ and $\mathbb {R}_{++}$ denote the set of real numbers and the set of positive real numbers, respectively. As usual, $\mathbb {R}^n$ and $\mathbb {R}^{n\times p}$ denote the set of n-dimensional real column vectors and the set of ${n\times p}$ real matrices, respectively. The identity matrix of size n is denoted by $I_n$. If $u,v\in \mathbb {R}^n$, then $u\le v$ is to be understood in a componentwise sense, i.e., $u_i\le v_i$ for all $i=1,\ldots ,n$. For $A\in \mathbb {R}^{n\times n}$, $A \succ 0$ (resp. $A \prec 0$) means that A is positive (resp. negative) definite. $\Vert \cdot \Vert$ is the Euclidean norm. The cardinality of a set C is denoted by |C|. The ceiling and floor functions are denoted by $\lceil \cdot \rceil$ and $\lfloor \cdot \rfloor$, respectively, i.e., if $x\in \mathbb {R}$, then $\lceil x \rceil$ is the least integer greater than or equal to x and $\lfloor x \rfloor$ is the greatest integer less than or equal to x. Given two real sequences $\{a_k\}$ and $\{b_k\}$ (with $b_k>0$ for all k), we write $a_k=o(b_k)$ if $\lim _{k\rightarrow \infty }a_k/b_k=0$. If $K = \{k_1, k_2, \ldots \} \subseteq \mathbb {N}$, with $k_j < k_{j+1}$ for all $j\in \mathbb {N}$, then we denote $K \displaystyle \mathop {\subset }_{\infty }\mathbb {N}$.

Given $F:\mathbb {R}^n \rightarrow \mathbb {R}^m$ a continuously differentiable function, we are interested in finding a Pareto optimal point of F. We denote this problem as

$$\begin{aligned} \min _{x \in \mathbb {R}^n} F(x). \end{aligned}$$

(1)

A point $x^{*}\in \mathbb {R}^n$ is Pareto optimal (resp. weak Pareto optimal) if there exists no other $x\in \mathbb {R}^n$ with $F(x)\le F(x^{*})$ and $F(x)\ne F(x^{*})$ (resp. $F(x)< F(x^{*})$). These concepts are also defined locally: We say that $x^{*}\in \mathbb {R}^n$ is a local Pareto optimal (resp. local weak Pareto optimal) if there exists a neighborhood $U\subset \mathbb {R}^n$ of $x^{*}$ such that $x^{*}$ is Pareto optimal (resp. weak Pareto optimal) for F restricted to U. A necessary (but in general not sufficient) condition for local weak Pareto-optimality of $x^{*}$ is

$$\begin{aligned} -(\mathbb {R}^m_{++})\cap {\text {Image}}(JF(x^{*}))=\emptyset , \end{aligned}$$

(2)

where $JF(x^{*})$ denotes the image set of the Jacobian of F at $x^{*}$. A point $x^{*}$ that satisfies (2) is called a Pareto critical point. Note that if $x\in \mathbb {R}^n$ is not Pareto critical, then there exists a direction $d\in \mathbb {R}^n$ such that $\nabla F_j(x)^Td<0$ for all $j=1,\ldots ,m$. This implies that d is a descent direction for F at x, i.e., there exists $\varepsilon >0$ such that $F(x+\alpha d)<F(x)$ for all $\alpha \in ]0,\varepsilon ]$. We say that $F:\mathbb {R}^n\rightarrow \mathbb {R}^m$ is convex (resp. strongly convex) if its components $F_j:\mathbb {R}^n\rightarrow \mathbb {R}$ are convex (resp. strongly convex), for all $j=1,\ldots ,m$. The next result relates the concepts of criticality, optimality, and convexity.

Lemma 2.1

[24, Theorem 3.1] The following statements hold:

• (i) if $x^{*}$ is local weak Pareto optimal, then $x^{*}$ is a critical point for F;

• (ii) if F is convex and $x^{*}$ is critical for F, then $x^{*}$ is weak Pareto optimal;

• (iii) if F is twice continuously differentiable, $\nabla ^2F_j(x) > 0$ for all $j \in \{1, \ldots ,m\}$ and all $x \in \mathbb {R}^n$, and if $x^{*}$ is critical for F, then $x^{*}$ is Pareto optimal.

Define $\mathcal {D}:\mathbb {R}^n\times \mathbb {R}^n\rightarrow \mathbb {R}$ by

$$\begin{aligned} \mathcal {D}(x,d):=\max _{j = 1,\dots ,m }\nabla F_j(x)^Td. \end{aligned}$$

The function $\mathcal {D}$ characterizes the descent direction for F at x. Indeed, it is easy to see that if $\mathcal {D}(x,d)<0$, then d is a descent direction for F at x. Moreover, x is a Pareto critical point if and only if $\mathcal {D}(x,d)\ge 0$ for all $d\in \mathbb {R}^n$. Next we present other useful properties of function $\mathcal {D}$ that can be trivially obtained from its definition.

Lemma 2.2

The following statements hold:

• (i) for any $x\in \mathbb {R}^n$ and $\alpha \ge 0$, we have $\mathcal {D}(x, \alpha d ) = \alpha \mathcal {D}(x, d)$;

• (ii) the mapping $(x,d)\mapsto \mathcal {D}(x,d)$ is continuous.

The quasi-Newton methods for solving (1) belong to a class of algorithms in which the search direction d(x) from a given $x\in \mathbb {R}^n$ is defined as the solution of

$$\begin{aligned} \min _{d\in \mathbb {R}^n} \max _{j=1,\ldots ,m} \nabla F_j (x)^Td + \frac{1}{2}d^TB_j d, \end{aligned}$$

(3)

where $B_j\in \mathbb {R}^{n\times n}$ is some approximation of $\nabla ^2 F_j(x)$ for all $j=1,\ldots ,m$, see [49]. If $B_j\succ 0$ for all $j=1,\ldots ,m$, then the objective function is strongly convex and hence (3) has a unique solution. We will denote the optimal value of problem (3) by $\theta (x)$, i.e.,

$$\begin{aligned} {} d(x):=\mathrm{arg}\!\min _{d \in \mathbb {R}^n}\; \max _{j = 1,\dots ,m }\nabla F_j (x)^Td + \frac{1}{2}d^TB_j d, \end{aligned}$$

(4)

and

$$\begin{aligned} {} \theta (x) : = \max _{j = 1,\dots ,m } \nabla F_j (x)^Td(x) + \frac{1}{2}d(x)^TB_j d(x). \end{aligned}$$

(5)

In the particular case where $B_j=I_n$ for all $j=1,\ldots ,m$, d(x) corresponds to the steepest descent direction, see [25]. In turn, if $B_j=\nabla ^2 F_j(x)$ for all $j=1,\ldots ,m$, d(x) turns out to be the Newton direction, see [24].

In what follows, we assume that $B_j\succ 0$ for all $j=1,\ldots ,m$. In this case, (3) is equivalent to the following convex quadratic optimization problem:

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{(t,d)\in \mathbb {R}\times \mathbb {R}^n} &{} \; t \\ \text{ s. } \text{ t. } &{} \nabla F_j (x)^Td + \frac{1}{2}d^TB_j d \le t, \quad \forall j = 1,\dots ,m. \end{array} \end{aligned}$$

(6)

The unique solution of (6) is given by $(t,d):=(\theta (x), d(x))$. Since (6) is convex and has a Slater point (e.g., $(1, 0)\in \mathbb {R}\times \mathbb {R}^n$), there exists a multiplier $\lambda (x) \in \mathbb {R}^m$ such that the triple $(t,d,\lambda ):=(\theta (x), d(x),\lambda (x)) \in \mathbb {R}\times \mathbb {R}^n\times \mathbb {R}^m$ satisfies the Karush–Kuhn–Tucker system:

$$\begin{aligned} \sum _{j=1}^{m} \lambda _j=1, \quad \sum _{j=1}^{m} \lambda _j\left[ \nabla F_j (x) + B_jd\right] =0, \end{aligned}$$

and

$$\begin{aligned} \lambda _j\ge 0, \quad \nabla F_j (x)^Td + \frac{1}{2}d^TB_j d \le t, \quad \lambda _j\left[ \nabla F_j (x)^Td + \frac{1}{2}d^TB_j d-t\right] =0, \end{aligned}$$

for all $j=1,\ldots ,m$. Therefore, some manipulations yield

$$\begin{aligned} d(x)= & {} - \left[ \sum _{j=1}^{m} \lambda _j(x)B_j \right] ^{-1} \sum _{j=1}^{m}\lambda _j(x)\nabla F_j (x), \end{aligned}$$

(7)

$$\begin{aligned} \qquad \sum _{j=1}^{m} \lambda _j(x)= & {} 1,\quad \lambda _j(x) \ge 0, \quad \forall j=1,\ldots ,m, \end{aligned}$$

(8)

and

$$\begin{aligned} \theta (x) = -\frac{1}{2} d(x)^T\left[ \sum _{j=1}^{m} \lambda _j(x)B_j \right] d(x). \end{aligned}$$

(9)

The following lemma shows that direction d(x) and the optimum value $\theta (x)$ can be used to characterize Pareto critical points of problem (1).

Lemma 2.3

Let $d:\mathbb {R}^n\rightarrow \mathbb {R}^n$ and $\theta :\mathbb {R}^n\rightarrow \mathbb {R}$ given by (4) and (5), respectively. Assume that $B_j\succ 0$ for all $j=1,\ldots ,m$. Then, we have:

• (i) x is Pareto critical if and only if $d(x)=0$ and $\theta (x)=0$;

• (ii) if x is not Pareto critical, then $d(x)\ne 0$ and $\mathcal {D}(x,d(x))< \theta (x)<0$ (in particular, d(x) is a descent direction for F at x).

Proof

See [24, Lemma 3.2] and [49, Lemma 2]. $\square$

As mentioned, if $B_j=I_n$ for all $j=1,\ldots ,m$, the solution of (3) corresponds to the steepest descent direction, which will be denoted by $d_{SD}(x)$, i.e.,

$$\begin{aligned} {} d_{SD}(x):=\mathrm{arg}\!\min _{d \in \mathbb {R}^n}\; \max _{j = 1,\dots ,m }\nabla F_j (x)^Td + \frac{1}{2}\Vert d\Vert ^2. \end{aligned}$$

(10)

Taking into account the previous discussion, it follows that there exists $\lambda ^{SD}(x)\in \mathbb {R}^m$ such that

$$\begin{aligned} {} \sum _{j=1}^{m} \lambda _j^{SD}(x) =1, \quad \lambda ^{SD}_j(x)\ge 0, \quad \forall j=1,\ldots ,m, \end{aligned}$$

(11)

and

$$\begin{aligned} {} d_{SD}(x) =- \displaystyle \sum _{j=1}^{m} \lambda ^{SD}_j(x)\nabla F_j (x). \end{aligned}$$

(12)

In the following, we revise some useful properties related to $d_{SD}(\cdot )$.

Lemma 2.4

Let $d_{SD}:\mathbb {R}^n\rightarrow \mathbb {R}^n$ be given by (10). Then,

• (i) x is Pareto critical if and only if $d_{SD}(x)=0$;

• (ii) if x is not Pareto critical, then we have $d_{SD}(x)\ne 0$ and $\mathcal {D}(x,d_{SD}(x))<-(1/2)\Vert d_{SD}(x)\Vert ^2<0$ (in particular, $d_{SD}(x)$ is a descent direction for F at x);

• (iii) the mapping $d_{SD}(\cdot )$ is continuous;

• (iv) for any $x\in \mathbb {R}^n$, $-d_{SD}(x)$ is the minimal norm element of the set

  $$\begin{aligned} \left\{ u\in \mathbb {R}^n \mid u = \displaystyle \sum _{j=1}^{m} \lambda _j\nabla F_j (x), \sum _{j=1}^{m} \lambda _j =1, \lambda _j\ge 0 \text{ for } \text{ all } j=1,\ldots ,m \right\} , \end{aligned}$$

  i.e., in the convex hull of $\{\nabla F_1(x),\ldots ,\nabla F_m(x)\}$.

Proof

For items (i), (ii), and (iii), see [31, Lemma 3.3]. For item (iv), see [57, Corollary 2.3]. $\square$

3 Algorithm

This section provides a detailed description of the main algorithm. At each iteration k and for each $j=1,\ldots ,m$, the true Hessian $\nabla ^2 F_j(x^k)$ is approximated by a matrix $B_j^k$ using a BFGS-type updating, see (15). The algorithm uses a line search procedure satisfying the (vector) Wolfe conditions. As we will see, this will be essential to obtain positive definite updates $B_j^k$’s for nonconvex problems.

Algorithm 1

A BFGS algorithm with Wolfe line searches

Let $c_1\in ]0,1/2[$, $c_2\in ]c_1,1[$, $x^0\in \mathbb {R}^n$, and $B_j^0\succ 0$ for all $j=1,\ldots ,m$ be given. Initialize $k \leftarrow 0$.

Step 1.:

Compute the search direction

Compute $d^k :=d(x^k)$ and $\theta (x^k)$ as in (4) and (5), respectively.

Step 2.:

Stopping criterion

If $\theta (x^k)=0$, then STOP.

Step 3.:

Line search procedure

Compute a step size $\alpha _{k}>0$ (trying first $\alpha _{k}=1$) such that

$$\begin{aligned} F_j(x^k+\alpha _k d^k)&\le F_j(x^k)+c_1 \alpha _k \mathcal {D}(x^k,d^k), \quad \forall j = 1,\ldots ,m, \end{aligned}$$

(13)

$$\begin{aligned} \mathcal {D}(x^k+\alpha _kd^k,d^k)&\ge c_2 \mathcal {D}(x^k,d^k), \end{aligned}$$

(14)

and set $x^{k+1} :=x^k + \alpha _k d^k$.

Step 4.:

Prepare the next iteration

For each $j=1,\ldots ,m$, define

$$\begin{aligned} \begin{aligned} B_j^{k+1} :=&B_j^{k} - \dfrac{(\rho _j^k)^{-1}B_j^{k}s_ks_k^{T}B_j^{k}}{\left( (\rho _j^k)^{-1}-s_k^{T}y_j^{k}\right) ^2 + (\rho _j^k)^{-1}s_k^{T}B_j^ks_k} \\&+\dfrac{(s_k^{T}B_j^{k}s_k) y_j^{k} (y_j^{k})^{T}}{\left( (\rho _j^k)^{-1}-s_k^{T}y_j^{k}\right) ^2 + (\rho _j^k)^{-1}s_k^{T}B_j^ks_k} \\&+ \left( (\rho _j^k)^{-1} - s_k^{T}y_j^{k}\right) \dfrac{y_j^{k}s_k^{T}B_j^{k} + B_j^{k}s_k(y_j^{k})^{T}}{\left( (\rho _j^k)^{-1}-s_k^{T}y_j^{k}\right) ^2 + (\rho _j^k)^{-1}s_k^{T}B_j^ks_k}, \end{aligned} \end{aligned}$$

(15)

where $y_j^k :=\nabla F_{j}(x^{k+1})-\nabla F_j(x^k)$, $s_k :=x^{k+1}-x^{k}$, and

$$\begin{aligned} \rho _j^k :=\left\{ \begin{array}{ll} 1/s_k^Ty_j^{k}, &{} \text{ if } s_k^Ty_j^{k} > 0\\ 1/\left( \mathcal {D}(x^{k+1},s_k)-\nabla F_j(x^k)^Ts_k\right) , &{} \text{ otherwise }.\\ \end{array}\right. \end{aligned}$$

(16)

Set $k\leftarrow k+1$ and go to Step 1.

Remark 3.1

(i) In practice, at Step 1, $d^k$ and $\theta (x^k)$ are calculated by solving the scalar convex quadratic optimization problem (6). Thus, there are many algorithms capable of effectively dealing with this subproblem. (ii) At Step 2, from Lemma 2.3(i), Algorithm 1 stops at iteration k if and only if $x^k$ is Pareto critical. (iii) At Step 3, we always try the step size $\alpha _{k}=1$ first. This detail turns out to be crucial in obtaining a fast convergence rate. Conditions (13)–(14) correspond to the (vector) standard Wolfe conditions recently introduced in [40]. It is possible to show that if $d^k$ is a descent direction of F at $x^k$ and F is bounded below along $d^k$, then there exist intervals of positive step sizes satisfying these conditions, see [40, Proposition 3.2]. The m inequalities in (13) stipulate that $\alpha _{k}$ must give a sufficient decrease, proportional to both $\alpha _{k}$ and $\mathcal {D}(x^k,d^k)$, in each objective function. In turn, the curvature condition (14) consists of a single inequality involving information from all objective functions. Let $\alpha _{t}>0$ be a trial step size that satisfies (13). If $\alpha _{t}>0$ is such that $\nabla F_j(x^k+\alpha _{t} d^k)^Td^k$ is strongly negative for all $j=1,\ldots ,m$ (and hence also $\mathcal {D}(x^k+\alpha _td^k,d^k)$), it is a sign that we can simultaneously reduce all objectives by moving further along $d^k$ and then $\alpha _{t}$ is ruled out by condition (14). On the other hand, if there exists $j\in \{1,\ldots ,m\}$ for which $\nabla F_j(x^k+\alpha _{t} d^k)^Td^k$ is only slightly negative or even positive (more precisely, greater than or equal to the right hand side of (14)), we suspect that we cannot expect much more decrease in the objective $F_j$ along direction $d^k$, so it makes sense to end the line search by accepting $\alpha _{t}$ as the step size, i.e., $\alpha _k:=\alpha _{t}$. Note that, in the latter case, we have $\mathcal {D}(x^k+\alpha _td^k,d^k) \ge \nabla F_j(x^k+\alpha _{t} d^k)^Td^k \ge c_2 \mathcal {D}(x^k,d^k)$ and therefore condition (14) is satisfied for $\alpha _{t}$. In particular, we observe that (14) rules out unacceptably short step sizes that satisfy (13). We refer the reader to [48, Section 3.1] for a careful discussion about this issue in the scalar optimization approach. (iv) At Step 4, if $\rho _j^k = 1/s_k^Ty_j^{k}$, then (15) reduces to the classical BFGS update for function $F_j$. This is certainly the case when $F_j$ is strictly convex. Furthermore, in the scalar optimization case ($m=1$), the curvature condition (14) implies $s_k^Ty_1^{k}>0$ and hence we have $\rho _1^k = 1/s_k^Ty_1^{k}$ and Algorithm 1 becomes the classical scalar BFGS algorithm with standard Wolfe line searches.

Let us provide a motivation for our choice of $B_j^{k+1}$ in (15). The classical BFGS updating formula is commonly derived by working with the inverse Hessian approximation. For each $j=1,\ldots ,m$, denote by $H_j^k$ the approximation for $[\nabla ^2 F_j(x^k)]^{-1}$. The updated BFGS approximation $H_j^{k+1}$ is then naturally defined as

$$\begin{aligned} H_j^{k+1} :=\left( I - \rho _j^ks_k(y_j^{k})^T\right) H_j^{k} \left( I - \rho _j^ky_j^{k}s_k^{T}\right) + \rho _j^ks_ks_k^T, \end{aligned}$$

(17)

with $\rho _j^k$ given by (16); see, for example, [48]. Now, by taking the inverse of $H_j^{k+1}$ in (17) (which can be easily done using the Sherman–Morrison formula), we obtain the update formula for $B_j^{k+1}$ in (15).

The next theorem shows that Algorithm 1 is well defined without imposing any convexity assumptions on the objectives. Its proof basically consists in showing that $B_j^{k+1}$ will be positive definite whenever $B_j^k$ is positive definite, for each $j=1,\ldots ,m$. From now on, we denote by ${{\mathcal {L}}}(x^0)$ the level set $\{x\in \mathbb {R}^n\mid F(x)\le F(x^0)\}$.

Theorem 3.2

Suppose that F is bounded below in ${{\mathcal {L}}}(x^0)$. Then, Algorithm 1 is well-defined.

Proof

The proof is by induction. Assume that $B_j^k$ is positive definite for all $j=1,\ldots ,m$ (which trivially holds for $k=0$). Therefore, the subproblem in Step 1 is solvable. If $x^k$ is Pareto critical, then by Lemma 2.3(i), Algorithm 1 stops at Step 2. Thus, let us assume that $x^k$ is not Pareto critical. In this case, Lemma 2.3(ii) implies that $d^k$ is a descent direction of F at $x^k$. Since F is bounded below in ${{\mathcal {L}}}(x^0)$, by [40, Proposition 3.2], there exist intervals of positive step sizes satisfying conditions (13)–(14) in Step 3 and hence $x^{k+1}$ can be properly defined. We now show that $B_j^{k+1}$ in (15) remain definite positive for all $j=1,\ldots ,m$. This will be done by showing that $H_j^{k+1}$ in (17) is definite positive for all $j=1,\ldots ,m$. Since $s_k=\alpha _kd^k$, by the definition of $\mathcal {D}$, Lemma 2.2(i), and (14), we have

$$\begin{aligned} \mathcal {D}(x^{k+1},s_k)-\nabla F_j(x^k)^Ts_k&\ge \alpha _k [\mathcal {D}(x^{k+1},d^k)-\mathcal {D}(x^k,d^k)] \\&\ge -\alpha _k (1-c_2)\mathcal {D}(x^k,d^k)>0, \end{aligned}$$

and hence $\rho _j^k$ defined in (16) is positive for all $j=1,\ldots ,m$. Let $j\in \{1,\ldots ,m\}$ and $0\ne z\in \mathbb {R}^n$. Then, by (17),

$$\begin{aligned} z^TH_j^{k+1}z = \left( z - \rho _j^kz^Ts_ky_j^{k}\right) ^T H_j^{k} \left( z- \rho _j^kz^Ts_ky_j^{k}\right) + \rho _j^k(z^Ts_k)^2\ge 0, \end{aligned}$$

where the inequality follows from the fact that $H_j^{k} \succ 0$ and $\rho _j^k>0$. If $z^TH_j^{k+1}z=0$, then $z- \rho _j^kz^Ts_ky_j^{k}=0$ and $z^Ts_k=0$, which imply that $z=0$, giving a contradiction with the definition of z. Therefore, $z^TH_j^{k+1}z>0$ and hence $H_j^{k+1}$ is definite positive for each $j=1,\ldots ,m$. $\square$

The following example illustrates that, in multicriteria optimization, in contrast to the scalar case, $s_k^Ty_j^{k}$ can be nonpositive for some $j\in \{1,\ldots ,m\}$ even when a Wolfe line search is used. This justifies our choice for $\rho _j^k$ in (16), since a key condition for the well-definedness of Algorithm 1 is that $\rho _j^k>0$ for all $j=1,\ldots ,m$ (see Theorem 3.2).

Example 3.3

Let $\beta \ge 1$, $c_1=10^{-4}$, $c_2=0.9$, $x^0=0$, and $B_1^0=B_2^0=1$ be given and consider the application of Algorithm 1 to the problem (1) with $F:\mathbb {R}\rightarrow \mathbb {R}^2$ defined by

$$\begin{aligned} F_1(x):=\dfrac{x^2}{3}-x \quad \text{ and } \quad F_2(x):=\left\{ \begin{array}{ll} -x, &{}\quad \text{ if } \quad x<0\\ (1-\beta )x^3+(\beta -1)x^2-x, &{}\quad \text{ if } \quad 0\le x<1, \\ -\beta x+\beta -1, &{}\quad \text{ if } \quad 1\le x<2, \\ \beta x^2-5\beta x+5 \beta -1, &{}\quad \text{ if } \quad x\ge 2.\\ \end{array}\right. \end{aligned}$$

We note that F is continuously differentiable and bounded below in $\mathbb {R}$. Direct calculation show that $d^0=1$ and $\alpha _0=1$ satisfies the Wolfe conditions (13)–(14), implying that $x^1=1$. Then, we have $s_0^Ty_1^0=2/3$ and $s_0^Ty_2^0=1-\beta \le 0$. If we take $\rho _j^k=1/s_k^Ty_j^{k}$ in (15), the algorithm breaks down by trying to divide by zero, in the case where $\beta = 1$. For $\beta > 1$, we would have $B_2^1=1-\beta \prec 0$.

We end this section by establishing that Algorithm 1 satisfies the Zoutendijk-type condition introduced in [40]. This will be an important result for the convergence analysis.

Proposition 3.4

Suppose that F is bounded below in ${{\mathcal {L}}}(x^0)$ and the Jacobian JF is Lipschitz continuous in an open set ${\mathcal {N}}$ containing the level set ${{\mathcal {L}}}(x^0)$, i.e., there exists $L>0$ such that $\Vert JF(x)-JF(y)\Vert \le L\Vert x-y\Vert$ for all $x,y\in {\mathcal {N}}$. Assume that Algorithm 1 generates an infinite sequence $\{x^k,d^k\}$. Then,

$$\begin{aligned} \sum _{k\ge 0} \dfrac{\mathcal {D}(x^k,d^k)^2}{\Vert d^k\Vert ^2} < \infty . \end{aligned}$$

Proof

See [40, Proposition 3.3]. $\square$

4 Global Convergence

In this section, we present global convergence results for Algorithm 1. As is usual in the scalar case, we assume that the objective functions are strongly convex, as formally stated below.

Assumption 4.1

(i) F is twice continuously differentiable. (ii) The level set ${{\mathcal {L}}}(x^0)$ is convex and there exist constants $a,b>0$ such that

$$\begin{aligned} a\Vert z\Vert ^2 \le z^T\nabla ^2 F_j(x)z\le b\Vert z\Vert ^2, \quad \forall j=1,\ldots ,m, \end{aligned}$$

(18)

for all $z \in \mathbb {R}^n$ and $x \in {{\mathcal {L}}}(x^0)$.

Note that, under Assumption 4.1, $s_k^Ty_j^{k} > 0$ and hence $\rho _j^k=1/s_k^Ty_j^{k}$ for all $j=1,\ldots ,m$ and $k\ge 0$. In this case, (15) always reduces to the classical BFGS update for $F_j$. Furthermore, the assumptions of Theorem 3.2 and Proposition 3.4 are trivially satisfied.

Hereafter, for all $k\ge 1$ and $j=1,\ldots ,m$, we denote by $\beta _j^{k}$ the angle between $s_k$ and $B_j^ks_k$, i.e.,

$$\begin{aligned} \cos \beta _j^{k} :=\dfrac{s_k^TB_j^ks_k}{\Vert s_k\Vert \Vert B_j^ks_k\Vert }, \quad \forall k\ge 1, \quad \forall j=1,\ldots ,m. \end{aligned}$$

The following lemma presents a key result: we prove that $\cos \beta _j^{k}$ stays away from 0, simultaneously for all objectives, for an arbitrary fraction p of the iterates. As far as we know, in the single-criterion optimization, this result was first shown in [6, Theorem 2.1]; see also [50, Lemma 4].

Lemma 4.2

Suppose that Assumption 4.1 holds and that $\{x^k\}$ is a sequence generated by Algorithm 1. Then, for any $p \in ]0,1[$, there exists a constant $\delta > 0$ such that, for any $k \ge 1$, the relation

$$\begin{aligned} \cos \beta _j^{\ell } \ge \delta , \quad \forall j = 1,\ldots ,m, \end{aligned}$$

holds for at least $\lceil p(k+1) \rceil$ values of $\ell \in \{0,1,\ldots ,k\}$.

Proof

Let $k\ge 1$ and $p \in ]0,1[$ be given and set $\varepsilon :=1-p$ and $\bar{p}:=1-\varepsilon /m$. For each $j=1,\ldots ,m$, we can proceed as in [6, Theorem 2.1] with $\bar{p}\in ]0,1[$ to show that there exists $\delta _j>0$ such that $\cos \beta _j^{\ell } \ge \delta _j$ for at least $\lceil \bar{p}(k+1) \rceil$ values of $\ell \in \{0,1,\ldots ,k\}$. Define $\delta :=\min _{j=1,\ldots ,m}\delta _j$, ${{\mathcal {G}}}_j^k:=\{\ell \in \{0,1,\ldots ,k\}\mid \cos \beta _j^{\ell } \ge \delta \}$, and ${{\mathcal {B}}}_j^k:=\{\ell \in \{0,1,\ldots ,k\}\mid \cos \beta _j^{\ell } < \delta \}$ for all $j=1,\ldots ,m$. Note that ${{\mathcal {G}}}_j^k\cap {{\mathcal {B}}}_j^k=\emptyset$ and $k+1=|{{\mathcal {G}}}_j^k|+|{{\mathcal {B}}}_j^k|$ for all $j=1,\ldots ,m$. Therefore, by the definition of $\bar{p}$ and using some properties of the ceiling and floor functions, we have

$$\begin{aligned} |{{\mathcal {G}}}_j^k| \ge \lceil \bar{p}(k+1) \rceil = (k+1) + \lceil - \frac{\varepsilon }{m}(k+1)\rceil = (k+1) - \lfloor \frac{\varepsilon }{m}(k+1)\rfloor , \end{aligned}$$

and

$$\begin{aligned} |{{\mathcal {B}}}_j^k|\le \lfloor \frac{\varepsilon }{m}(k+1)\rfloor , \end{aligned}$$

for all $j=1,\ldots ,m$. Thus, $|\mathop \cup _{j=1}^m {{\mathcal {B}}}_j^k|\le m \lfloor \frac{\varepsilon }{m}(k+1)\rfloor \le \varepsilon (k+1)$. As consequence, since we also have $k+1=|\mathop \cap _{j=1}^m {{\mathcal {G}}}_j^k|\ + |\mathop \cup _{j=1}^m {{\mathcal {B}}}_j^k|$, by the definition of $\varepsilon$, it follows that

$$\begin{aligned} |\mathop \cap _{j=1}^m {{\mathcal {G}}}_j^k| \ge (k+1) - \varepsilon (k+1) = (1-\varepsilon )(k+1)=p(k+1), \end{aligned}$$

completing the proof. $\square$

The next lemma presents a useful technical result.

Lemma 4.3

Suppose that Assumption 4.1 holds and that $\{x^k\}$ is a sequence generated by Algorithm 1. Then, for all $k\ge 0$,

$$\begin{aligned} \mathcal {D}(x^k,d^k) \le -\dfrac{\delta _k}{2}\Vert d^k\Vert \Vert d_{SD}(x^k)\Vert , \end{aligned}$$

where $\delta _k :=\min _{j =1,\dots ,m } \cos \beta _j^k$.

Proof

Let $k\ge 0$ be given. By the definitions of $\delta _k$, $\cos \beta _j^k$, and $s_k$, we have

$$\begin{aligned} \delta _k\le \cos \beta _j^k = \frac{s_k^TB_j^ks_k}{\Vert s_k\Vert \Vert B_j^ks_k\Vert }=\frac{(d^k)^TB_j^kd^k}{\Vert d^k\Vert \Vert B_j^kd^k\Vert }, \quad \forall j=1,\ldots ,m. \end{aligned}$$

Therefore,

$$\begin{aligned} (d^k)^TB_j^kd^k \ge \delta _k \Vert d^k\Vert \Vert B_j^kd^k\Vert , \quad \forall j=1,\ldots ,m. \end{aligned}$$

Hence, from Lemma 2.3(ii) and (9), we obtain

$$\begin{aligned} -\mathcal {D}(x^k,d^k)>-\theta (x^k) = \frac{1}{2} \sum _{j=1}^{m} \lambda _j^k (d^k)^TB_j^k d^k \ge \frac{\delta _k}{2} \Vert d^k\Vert \sum _{j=1}^{m} \lambda _j^k \Vert B_j^kd^k\Vert . \end{aligned}$$

Thus, the triangle inequality, together with (7), (8), and Lemma 2.4(iv), implies

$$\begin{aligned} -\mathcal {D}(x^k,d^k)\ge & {} \frac{ \delta _k}{2} \Vert d^k\Vert \Vert \sum _{j=1}^{m} \lambda _j^k B_j^kd^k\Vert = \frac{\delta _k}{2} \Vert d^k\Vert \Vert \sum _{j=1}^{m} \lambda _j^k \nabla F_j(x^k)\Vert \\ {}\ge & {} \frac{ \delta _k}{2} \Vert d^k\Vert \Vert d_{SD}(x^k)\Vert , \end{aligned}$$

obtaining the desired result. $\square$

We are now ready to present the main convergence result of this section.

Theorem 4.4

Suppose that Assumption 4.1 holds and that $\{x^k\}$ is a sequence generated by Algorithm 1. Then, $\{x^k\}$ converges to a Pareto optimal point $x^{*}$ of F.

Proof

By Lemma 4.2, there exist a constant $\delta >0$ and $K\displaystyle \mathop {\subset }_{\infty }\mathbb {N}$ such that

$$\begin{aligned} \cos \beta _j^{k} \ge \delta , \quad \forall k\in K \quad \text{ and } \quad \forall j = 1,\ldots ,m. \end{aligned}$$

Therefore, Lemma 4.3 implies that

$$\begin{aligned} \mathcal {D}(x^k,d^k) \le -\dfrac{\delta }{2}\Vert d^k\Vert \Vert d_{SD}(x^k)\Vert , \quad \forall k\in K. \end{aligned}$$

Thus, from Proposition 3.4, we have

$$\begin{aligned} \infty > \sum _{k\ge 0} \dfrac{\mathcal {D}(x^k,d^k)^2}{\Vert d^k\Vert ^2}\ge \sum _{k\in K} \dfrac{\mathcal {D}(x^k,d^k)^2}{\Vert d^k\Vert ^2}\ge \sum _{k\in K} \dfrac{\delta ^4}{4} \Vert d_{SD}(x^k)\Vert ^2, \end{aligned}$$

and hence

$$\begin{aligned} \lim _{k\in K}d_{SD}(x^k)=0. \end{aligned}$$

(19)

Now, since ${\mathcal {L}}$ is compact and $x^k\in {\mathcal {L}}$ for all $k\in K$, there exist $K_1\displaystyle \mathop {\subset }_{\infty }K$ and $x^{*}\in {\mathcal {L}}$ such that $\lim _{k\in K_1}x^k=x^{*}$. Thus, by (19) and Lemma 2.4(iii), we obtain $d_{SD}(x^{*})=0$. Hence, by Lemma 2.1(iii), we conclude that $x^{*}$ is Pareto optimal.

Let us show that $\lim _{k\rightarrow \infty }x^k=x^{*}$. Suppose for contradiction that there exist $\bar{x}\in {\mathcal {L}}$ with $\bar{x}\ne x^{*}$ and $K_2\displaystyle \mathop {\subset }_{\infty }\mathbb {N}$ such that $\lim _{k\in K_2}x^k=\bar{x}$. We first claim that $F(\bar{x})\ne F(x^{*})$. Indeed, if $F(\bar{x})= F(x^{*})$, by Assumption 4.1, for all $t\in [0,1]$, we have

$$\begin{aligned} F_j(t\bar{x} + (1-t)x^{*}) < tF_j(\bar{x}) + (1-t)F_j(x^{*}) = F_j(x^{*}), \quad \forall j = 1,\ldots ,m, \end{aligned}$$

contradicting the fact that $x^{*}$ is a Pareto optimal point. Hence, $F(\bar{x})\ne F(x^{*})$ holds, as claimed. Now, since $x^{*}$ is Pareto optimal, there exists $j_0\in \{1,\ldots ,m\}$ such that $F_{j_0}(x^{*})<F_{j_0}(\bar{x})$. Therefore, remembering that $\lim _{k\in K_1}x^k=x^{*}$ and $\lim _{k\in K_2}x^k=\bar{x}$, we can choose $k_1\in K_1$ and $k_2\in K_2$ with $k_1<k_2$ so that $F_{j_0}(x^{k_1})<F_{j_0}(x^{k_2})$. This contradicts the sufficient decrease condition (13) which, in particular, implies that $\{F_j(x^k)\}$ is a decreasing sequence for all $j = 1,\ldots ,m$. Thus, $\lim _{k\rightarrow \infty }x^k=x^{*}$ and the proof is complete. $\square$

In the remainder of this section, our aim is to show that $\{x^k\}$ converges to $x^{*}$ rapidly enough that

$$\begin{aligned} \sum _{k\ge 0}\Vert x^k-x^{*}\Vert < \infty . \end{aligned}$$

(20)

To the best of our knowledge, this is the first work to establish this result for multiobjective optimization. As we will see, (20) plays an important role in the superlinear convergence. We start with some technical results.

Lemma 4.5

Suppose that Assumption 4.1 holds and that $\{x^k\}$ is a sequence generated by Algorithm 1. Let $x^{*}$ be as in Theorem 4.4. Then, for all $k\ge 0$, we have

• (i) $\Vert x^k-x^{*}\Vert \le \dfrac{2}{a}\Vert d_{SD}(x^k)\Vert$;

• (ii) $\Vert s_k\Vert \ge \dfrac{(1-c_2)}{2b}\delta _k\Vert d_{SD}(x^k)\Vert$, where $\delta _k$ is given as in Lemma 4.3.

Proof

Let $k\ge 0$ be given and consider $\lambda ^{SD}(x^k)\in \mathbb {R}^m$ as in (11)–(12), i.e., $\lambda ^{SD}(x^k)$ is such that $d_{SD}(x^k)=- \sum _{j=1}^{m} \lambda _j^{SD}(x^k)\nabla F_j (x^k)$. Define the scalar-valued function $F_{SD}:\mathbb {R}^n\rightarrow \mathbb {R}$ by

$$\begin{aligned} F_{SD}(x):=\sum _{j=1}^m \lambda ^{SD}_j(x^k) F_j(x). \end{aligned}$$

Therefore, by (11) and (18), it is easy to see that

$$\begin{aligned} \int _{0}^{1} (1 - \tau )z^T \nabla ^2 F_{SD}(x^k + \tau z)z\hbox {d}\tau \ge \dfrac{a}{2}\Vert z\Vert ^2, \quad \forall z\in \mathbb {R}^n. \end{aligned}$$

Thus, by evaluating the above integral (which can be done by integration by parts), taking $z:=x^{*}-x^k$, and considering that $d_{SD}(x^k)=-\nabla F_{SD}(x^k)$, we obtain

$$\begin{aligned} F_{SD}(x^{*})-F_{SD}(x^k)+d_{SD}(x^k)^T(x^{*}-x^k)\ge \dfrac{a}{2}\Vert x^{*}-x^k\Vert ^2. \end{aligned}$$

Since $F_j(x^{*})\le F_j(x^k)$ for all $j=1,\ldots ,m$, we have $F_{SD}(x^{*})-F_{SD}(x^k)\le 0$ and hence

$$\begin{aligned} \dfrac{a}{2}\Vert x^{*}-x^k\Vert ^2\le d_{SD}(x^k)^T(x^{*}-x^k)\le \Vert d_{SD}(x^k)\Vert \Vert x^{*}-x^k\Vert , \end{aligned}$$

proving part (i).

Let us consider part (ii). Let $k\ge 0$ be given and define

$$\begin{aligned} \bar{G}_j^k :=\int _{0}^{1} \nabla ^2 F_j(x^k + \tau s_k)\hbox {d}\tau , \quad \forall j = 1,\dots ,m. \end{aligned}$$

Then,

$$\begin{aligned} \bar{G}_j^ks_k = y_j^k, \quad \forall j = 1,\dots ,m. \end{aligned}$$

(21)

Now, by (14) and the definition of ${\mathcal {D}}$, it follows that

$$\begin{aligned} (c_2-1)\mathcal {D}(x^k,d^k)\le & {} \mathcal {D}(x^{k+1},d^k) - \mathcal {D}(x^k,d^k)\\\le & {} \max _{j = 1,\dots ,m }(\nabla F_j(x^{k+1}) - \nabla F_j(x^k))^Td^k = \max _{j = 1,\dots ,m }(y_j^k)^Td^k, \end{aligned}$$

where the second inequality follows from the fact that, for any $u,v\in \mathbb {R}^m$, we have $\max _j(u_j - v_j) \ge \max _ju_j - \max _jv_j$. Therefore, by (21), we obtain

$$\begin{aligned} (c_2-1)\mathcal {D}(x^k,d^k)\le & {} \max _{j = 1,\dots ,m }s_k^T \bar{G}_j^k d^k =\alpha _k \max _{j = 1,\dots ,m }(d^k)^T \bar{G}_j^k d^k \\\le & {} b \alpha _k \Vert d^k\Vert ^2=b\Vert s_k\Vert \Vert d^k\Vert , \end{aligned}$$

where the second inequality comes from (18). Hence, using Lemma 4.3 and taking into account that $c_2<1$, we have

$$\begin{aligned} -(c_2-1)\dfrac{\delta _k}{2}\Vert d^k\Vert \Vert d_{SD}(x^k)\Vert \le b\Vert s_k\Vert \Vert d^k\Vert , \end{aligned}$$

concluding the proof. $\square$

Theorem 4.6

Suppose that Assumption 4.1 holds and that $\{x^k\}$ is a sequence generated by Algorithm 1. Let $x^{*}$ be as in Theorem 4.4. Then, $\{x^k\}$ converges R-linearly to $x^{*}$. As a consequence, (20) holds.

Proof

Let $\lambda ^{SD}(x^{*})\in \mathbb {R}^m$ be a steepest descent multiplier associated with $x^{*}$ as in (11)–(12), i.e., $d_{SD}(x^{*}) =- \sum _{j=1}^{m} \lambda ^{SD}_j(x^{*})\nabla F_j (x^{*})$. Let us define the scalar-valued function $F_{*}:\mathbb {R}^n\rightarrow \mathbb {R}$ given by

$$\begin{aligned} F_{*}(x):=\sum _{j=1}^m \lambda ^{SD}_j(x^{*}) F_j(x). \end{aligned}$$

Note that

$$\begin{aligned} \nabla F_{*}(x^{*})= \sum _{j=1}^m \lambda ^{SD}_j(x^{*}) \nabla F_j(x^{*}) = -d_{SD}(x^{*}) = 0, \end{aligned}$$

(22)

where the last equality comes from Lemma 2.4(i). Now, by doing a second-order Taylor series expansion of $F_j$ around $x^{*}$ and using (18), we obtain

$$\begin{aligned} \nabla F_j(x^{*})^T(x^k - x^{*}) + \dfrac{a}{2}\Vert x^k - x^{*}\Vert ^2\le & {} F_j(x^k) - F_j(x^{*}) \\\le & {} \nabla F_j(x^{*})^T(x^k - x^{*}) + \dfrac{b}{2}\Vert x^k - x^{*}\Vert ^2, \end{aligned}$$

for all $j=1,\ldots ,m$ and for all $k\ge 0$. By multiplying this expression by $\lambda _j^{SD}(x^{*})$, summing over all indices $j=1,\ldots ,m$, and taking into account (11) and (22), we obtain

$$\begin{aligned} \dfrac{a}{2}\Vert x^k - x^{*}\Vert ^2 \le F_{*}(x^k) - F_{*}(x^{*}) \le \dfrac{b}{2}\Vert x^k - x^{*}\Vert ^2, \quad \forall k\ge 0. \end{aligned}$$

(23)

From the right hand side of (23) and Lemma 4.5(i), we obtain

$$\begin{aligned} F_{*}(x^k) - F_{*}(x^{*}) \le \dfrac{2b}{a^2}\Vert d_{SD}(x^k)\Vert ^2, \quad \forall k\ge 0. \end{aligned}$$

(24)

On the other hand, similarly to (23), the sufficient descent condition (13) implies

$$\begin{aligned} F_{*}(x^{k+1}) \le F_{*}(x^k)+c_1 \alpha _k \mathcal {D}(x^k,d^k), \quad \forall k\ge 0. \end{aligned}$$

By subtracting the term $F_{*}(x^{*})$ in both sides of this inequality and using Lemma 4.3, we have

$$\begin{aligned} F_{*}(x^{k+1}) - F_{*}(x^{*}) \le F_{*}(x^k)-F_{*}(x^{*}) - \dfrac{c_1}{2}\delta _k\Vert s_k\Vert \Vert d_{SD}(x^k)\Vert , \end{aligned}$$

for all $k\ge 0$, where $\delta _k = \min _{j =1,\dots ,m } \cos \beta _j^k$. Therefore, by Lemma 4.5(ii), it follows that

$$\begin{aligned} F_{*}(x^{k+1}) - F_{*}(x^{*}) \le F_{*}(x^k)-F_{*}(x^{*}) - \dfrac{c_1(1-c_2)}{4b}\delta _k^2 \Vert d_{SD}(x^k)\Vert ^2, \quad \forall k\ge 0. \end{aligned}$$

Hence, by (24), we have

$$\begin{aligned} F_{*}(x^{k+1}) - F_{*}(x^{*}) \le \left( 1 - \dfrac{c_1(1-c_2)a^2}{8b^2}\delta _k^2 \right) \left( F_{*}(x^k)-F_{*}(x^{*})\right) , \quad \forall k\ge 0.\qquad \end{aligned}$$

(25)

For each $k\ge 0$, define ${\bar{r}}_k:=1-c_1(1-c_2)a^2\delta _k^2/(8b^2)$. It is easy to see that ${\bar{r}}_k\in ]0,1]$, for all $k\ge 0$.

Now, let $p\in ]0,1[$ be given. Then, by Lemma 4.2, there exists a constant $\delta > 0$ such that, for any $k\ge 1$, the number of elements $\ell \in \{0,1,\ldots ,k\}$ for which $\delta _{\ell } \ge \delta$ is at least $\lceil p(k+1) \rceil$. Hence, by defining ${{\mathcal {G}}}_k:=\{\ell \in \{0,1,\ldots ,k\}\mid \delta _{\ell } \ge \delta \}$, we have $|{{\mathcal {G}}}_k|\ge \lceil p(k+1) \rceil$ and

$$\begin{aligned} {\bar{r}}_{\ell }\le 1 - \dfrac{c_1(1-c_2)a^2\delta ^2}{8b^2} :={\bar{r}}<1, \quad \forall \ell \in {{\mathcal {G}}}_k. \end{aligned}$$

Therefore, by (25) and taking into account that $F_{*}(x^0) - F_{*}(x^{*}) >0$, we obtain, for all $k\ge 1$,

$$\begin{aligned} F_{*}(x^{k+1}) - F_{*}(x^{*})\le & {} \left[ \prod _{\ell = 0}^{k} {{\bar{r}}}_{\ell }\right] \left( F_{*}(x^0) - F_{*}(x^{*}) \right) \\\le & {} \left[ \prod _{\ell \in {{\mathcal {G}}}_k}{{\bar{r}}}_{\ell } \right] \left( F_{*}(x^0) - F_{*}(x^{*}) \right) \\\le & {} \left[ \prod _{\ell \in {{\mathcal {G}}}_k}{{\bar{r}}} \right] \left( F_{*}(x^0) - F_{*}(x^{*}) \right) \\\le & {} {{\bar{r}}}^{ \lceil p(k+1) \rceil } \left( F_{*}(x^0) - F_{*}(x^{*}) \right) , \end{aligned}$$

where the second inequality follows from the fact that ${{\bar{r}}}_{\ell }\le 1$ for all $\ell \notin {{\mathcal {G}}}_k$. Thus, by defining $r^{1/p}:={\bar{r}}$, we have

$$\begin{aligned} F_{*}(x^{k+1}) - F_{*}(x^{*})\le r^{k+1}\left( F_{*}(x^0) - F_{*}(x^{*}) \right) , \quad \forall k\ge 1. \end{aligned}$$

(26)

By combining the left hand side of (23) with the above inequality, we find that

$$\begin{aligned} \Vert x^{k+1} - x^{*}\Vert \le \left[ \dfrac{2}{a}\left( F_{*}(x^0) - F_{*}(x^{*}) \right) \right] ^{1/2} (r^{1/2})^{k+1}, \end{aligned}$$

and hence $\{x^k\}$ converges R-linearly to $x^{*}$. Finally, by summing this expression and taking into account that $r<1$, we conclude that (20) holds. $\square$

Remark 4.7

Note that (26) implies that $\{F_{*}(x^k)\}$ is R-linearly convergent to $F_{*}(x^{*})$. It is worth mentioning that Theorem 4.6 can be seen as the extension of [6, Theorem 3.1] for multiobjective optimization; see also [50, Lemma 5].

5 Superlinear Local Convergence

Now we study the local convergence properties of Algorithm 1. The results of this section also apply to nonconvex problems, although it is not possible to establish global convergence in this general case. We will assume that $\{x^k\}$ converges to a Pareto optimal point $x^{*}$ and prove, under suitable assumptions, that the rate of convergence is Q-superlinear.

Assumption 5.1

(i) F is twice continuously differentiable. (ii) The sequence $\{x^k\}$ generated by Algorithm 1 converges to a Pareto optimal point $x^{*}$. (iii) For each $j=1,\ldots ,m$, $\nabla ^2 F_j(x^{*})$ is positive definite and L-Lipschitz continuous at $x^{*}$. Thus, there exist a neighborhood U of $x^{*}$ and positive constants a, b, and L such that

$$\begin{aligned} a\Vert z\Vert ^2 \le z^T\nabla ^2 F_j(x)z\le b\Vert z\Vert ^2, \quad \forall j=1,\ldots ,m, \end{aligned}$$

(27)

and

$$\begin{aligned} \Vert \nabla ^2 F_j(x)-\nabla ^2 F_j(x^{*})\Vert \le L \Vert x-x^{*}\Vert , \quad \forall j=1,\ldots ,m, \end{aligned}$$

(28)

for all $z \in \mathbb {R}^n$ and $x \in U$.

Essentially, Assumption 5.1 says that, in a neighborhood U of $x^{*}$, F is strongly convex and the Hessians $\nabla ^2 F_j$ ($j=1,\ldots ,m$) are Lipschitz continuous at $x^{*}$. Throughout this section, we assume, without loss of generality, that $\{x^k\}\subset U$, i.e., (27) and (28) hold at $x^k$ for all $k\ge 0$. Since Assumption 5.1 is more restrictive than Assumption 4.1, the results of the previous section remain true and will be used here without further explanation.

The next theorem establishes that the Dennis–Moré condition [18] holds individually for each objective function $F_j$ (see (30) below). The proof of this result is quite straightforward from the scalar case, and its details will therefore be omitted. We emphasize, however, that (20) plays an essential role in this task. We also include in the statement of the theorem an intermediate step (see (29) below) that will be evoked in forthcoming results.

Theorem 5.2

Suppose that Assumption 5.1 holds. Then,

$$\begin{aligned} \lim _{k\rightarrow \infty } \dfrac{s_k^TB_j^ks_k}{s_k^T\nabla ^2 F_j(x^{*})s_k} \quad \forall j=1,\ldots ,m. \end{aligned}$$

(29)

and

$$\begin{aligned} \lim _{k \rightarrow \infty }\dfrac{\Vert (B_j^k - \nabla ^2F_j(x^{*}))d^k\Vert }{\Vert d^k\Vert } = 0, \quad \forall j=1,\ldots ,m, \end{aligned}$$

(30)

or, equivalently,

$$\begin{aligned} \lim _{k \rightarrow \infty }\dfrac{\Vert (B_j^k - \nabla ^2F_j(x^k))d^k\Vert }{\Vert d^k\Vert } = 0, \quad \forall j=1,\ldots ,m. \end{aligned}$$

(31)

Proof

Using (20), the proof follows similarly to [48, Theorem 6.6] (see also [6, Theorem 3.2]). $\square$

Let $\lambda ^k:=\lambda (x^k)\in \mathbb {R}^m$ be the Lagrange multiplier associated with $x^k$ of problem (6) fulfilling (7)–(9). From now on, we define, for all $k\ge 0$,

$$\begin{aligned} F_{\lambda }^k(x) :=\sum _{j = 1}^{m} \lambda _j^k F_j(x) \quad \text{ and } \quad B_{\lambda }^k :=\sum _{j = 1}^{m}\lambda _j^kB_j^{k}. \end{aligned}$$

(32)

In the following, we show that the family of functions $\{F_{\lambda }^k(x)\}_{k\ge 0}$ satisfies a Dennis–Moré-type condition.

Theorem 5.3

Suppose that Assumption 5.1 holds. For each $k\ge 0$, consider $F_{\lambda }^k:\mathbb {R}^n\rightarrow \mathbb {R}$ and $B_{\lambda }^k$ as in (32). Then,

$$\begin{aligned} \lim _{k \rightarrow \infty } \dfrac{\Vert (B_{\lambda }^k - \nabla ^2 F_{\lambda }^k(x^{*}))d^k\Vert }{\Vert d^k\Vert }=0 \end{aligned}$$

(33)

or, equivalently,

$$\begin{aligned} \lim _{k \rightarrow \infty } \dfrac{\Vert \nabla F_{\lambda }^k(x^k) + \nabla ^2 F_{\lambda }^k(x^k)d^k\Vert }{\Vert d^k\Vert }=0. \end{aligned}$$

(34)

Proof

From the definitions of $B_{\lambda }^k$ and $F_{\lambda }^k$, using the triangle inequality, and taking into account (8), we have

$$\begin{aligned} \lim _{k \rightarrow \infty } \dfrac{\Vert (B_{\lambda }^k - \nabla ^2 F_{\lambda }^k(x^{*}))d^k\Vert }{\Vert d^k\Vert }&= \lim _{k \rightarrow \infty } \dfrac{\Vert \sum _{j=1}^m \lambda _j^k (B_j^k - \nabla ^2 F_j(x^{*}))d^k\Vert }{\Vert d^k\Vert } \\&\le \lim _{k \rightarrow \infty } \sum _{j=1}^m \lambda _j^k\dfrac{ \Vert (B_j^k - \nabla ^2 F_j(x^{*}))d^k\Vert }{\Vert d^k\Vert } \\&\le \lim _{k \rightarrow \infty } \max _{j=1,\ldots ,m} \dfrac{ \Vert (B_j^k - \nabla ^2 F_j(x^{*}))d^k\Vert }{\Vert d^k\Vert }. \end{aligned}$$

This inequality, together with (30), yields (33). Let us prove that (33) implies (34). First, note that, by (7), we have $B_{\lambda }^kd^k=-\nabla F_{\lambda }^k(x^k)$ and hence (34) is equivalent to

$$\begin{aligned} \lim _{k \rightarrow \infty } \dfrac{\Vert (B_{\lambda }^k - \nabla ^2 F_{\lambda }^k(x^k))d^k\Vert }{\Vert d^k\Vert }=0. \end{aligned}$$

(35)

Now, it is easy to see that

$$\begin{aligned} \begin{aligned} \lim _{k \rightarrow \infty } \dfrac{\Vert (B_{\lambda }^k - \nabla ^2 F_{\lambda }^k(x^k))d^k\Vert }{\Vert d^k\Vert } \le&\lim _{k \rightarrow \infty } \dfrac{\Vert (B_{\lambda }^k - \nabla ^2 F_{\lambda }^k(x^{*}))d^k\Vert }{\Vert d^k\Vert }\\&+ \lim _{k \rightarrow \infty } \Vert \nabla ^2 F_{\lambda }^k(x^{*}) - \nabla ^2 F_{\lambda }^k(x^k)\Vert \end{aligned} \end{aligned}$$

(36)

and

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert \nabla ^2 F_{\lambda }^k(x^{*}) - \nabla ^2 F_{\lambda }^k(x^k)\Vert&= \lim _{k \rightarrow \infty } \Vert \sum _{j=1}^m \lambda _j^k( \nabla ^2 F_j(x^{*})- \nabla ^2 F_j(x^k))\Vert \\&\le \lim _{k \rightarrow \infty } \sum _{j=1}^m \lambda _j^k \Vert \nabla ^2 F_j(x^{*})- \nabla ^2 F_j(x^k)\Vert \\&\le \lim _{k \rightarrow \infty } \max _{j=1,\ldots ,m} \Vert \nabla ^2 F_j(x^{*})- \nabla ^2 F_j(x^k)\Vert =0, \end{aligned}$$

because $\nabla ^2 F_j(\cdot )$ is continuous for every $j=1,\ldots ,m$. Therefore, (35) follows from (36) and (33). The proof that (34) implies (33) can be obtained similarly. $\square$

The following auxiliary result provides some properties related to the length of direction $d^k$ and the optimal value $\theta (x^k)$.

Lemma 5.4

Suppose that Assumption 5.1 holds. Then, there exist positive constants $\bar{a}$ and $\bar{b}$ such that, for all k sufficiently large, we have:

$$\begin{aligned} \bar{a}\Vert d^k\Vert ^2 \le |\theta (x^k)|\le \bar{b}\Vert d^k\Vert ^2. \end{aligned}$$

(37)

Moreover,

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert d^k\Vert =0. \end{aligned}$$

(38)

Proof

By (29), taking $\gamma \in ]0,1[$, we obtain

$$\begin{aligned} 1-\gamma \le \dfrac{s_k^T B_j^{k}s_k}{s_k^T \nabla ^2 F_j(x^{*}) s_k} \le 1+ \gamma , \quad \forall j=1,\ldots ,m, \end{aligned}$$

(39)

for all k sufficiently large. On the other hand, by (27), it follows that

$$\begin{aligned} \dfrac{1}{b}\dfrac{s_k^TB_j^ks_k}{\Vert s_k\Vert ^2}\le \dfrac{s_k^TB_j^ks_k}{s_k^T\nabla ^2F_j(x^{*})s_k} \le \dfrac{1}{a} \dfrac{s_k^TB_j^ks_k}{\Vert s_k\Vert ^2},\quad \forall k\ge 0,\quad \forall j=1,\ldots ,m. \end{aligned}$$

Therefore, by using (39) and recalling that $s_k=\alpha _k d^k$, we have

$$\begin{aligned} a(1- \gamma )\le \dfrac{s_k^TB_j^ks_k}{\Vert s_k\Vert ^2}= \dfrac{(d^k)^TB_j^kd^k}{\Vert d^k\Vert ^2} \le b(1+ \gamma ), \quad \forall j=1,\ldots ,m, \end{aligned}$$

for all k sufficiently large. Hence, by (8) and (9), we obtain

$$\begin{aligned} \dfrac{a(1- \gamma )}{2}\Vert d^k\Vert ^2 \le |\theta (x)| = \frac{1}{2} \sum _{j=1}^{m} \lambda _j^k (d^k)^T B_j^kd^k \le \dfrac{b(1+ \gamma )}{2}\Vert d^k\Vert ^2, \end{aligned}$$

for all k sufficiently large. By defining $\bar{a}:=a(1- \gamma )/2$ and $\bar{b}:=b(1+ \gamma )/2$, we prove (37).

Finally, by (37), we have

$$\begin{aligned} 0\le \lim _{k\rightarrow \infty }\bar{a}\Vert d^k\Vert \le \lim _{k\rightarrow \infty } \dfrac{|\theta (x)|}{\Vert d^k\Vert }\le \lim _{k\rightarrow \infty } \dfrac{|\mathcal {D}(x^k,d^k)|}{\Vert d^k\Vert }=0, \end{aligned}$$

where the second inequality follows from the fact that $\mathcal {D}(x^k,d^k)<\theta (x)<0$ (see Lemma 2.3(ii)) and the final equality is a consequence of Proposition 3.4. This concludes the proof. $\square$

The following result shows that the unit step size satisfies the Wolfe conditions (13)–(14) as the iterates converge to $x^{*}$.

Theorem 5.5

Suppose that Assumption 5.1 holds. Then, the step size $\alpha _k =1$ is admissible for all k sufficiently large.

Proof

Let $j\in \{1,\ldots ,m\}$ be an arbitrary index. By Taylor’s formula, we have

$$\begin{aligned} F_j(x^k + d^k) =&F_j(x^k) + \nabla F_j(x^k)^Td^k + \dfrac{1}{2}(d^k)^T \nabla ^2 F_j(x^k)d^k + o(\Vert d^k\Vert ^2)\\ =&F_j(x^k) + \nabla F_j(x^k)^Td^k + \dfrac{1}{2}(d^k)^TB_j^kd^k \\&+ \dfrac{1}{2}(d^k)^T\left( \nabla ^2 F_j(x^k) - B_j^k\right) d^k + o(\Vert d^k\Vert ^2)\\ =&F_j(x^k) + \nabla F_j(x^k)^Td^k + \dfrac{1}{2}(d^k)^TB_j^kd^k + o(\Vert d^k\Vert ^2), \end{aligned}$$

where the last equality is a consequence of (31). Therefore, by (5),

$$\begin{aligned} F_j(x^k + d^k) \le F_j(x^k) + t\theta (x^k) +(1-t)\theta (x^k) + o(\Vert d^k\Vert ^2), \end{aligned}$$

where $t:=2c_1<1$. Thus, by (37), we have, for all k sufficiently large,

$$\begin{aligned} F_j(x^k + d^k)\le & {} F_j(x^k) + t\theta (x^k) -\bar{a}(1-t)\Vert d^k\Vert ^2+ o(\Vert d^k\Vert ^2),\\= & {} F_j(x^k) + t\theta (x^k) +\left[ -\bar{a}(1-t)+ \dfrac{o(\Vert d^k\Vert ^2)}{\Vert d^k\Vert ^2}\right] \Vert d^k\Vert ^2. \end{aligned}$$

For k large enough, the term in square brackets is negative and then

$$\begin{aligned} F_j(x^k + d^k) \le F_j(x^k) + t\theta (x^k). \end{aligned}$$

On the other hand, combining (7)–(9), we obtain

$$\begin{aligned} \theta (x^k)=\dfrac{1}{2}\sum _{j=1}^m\lambda _j^k\nabla F_j(x^k)^Td^k \le \dfrac{1}{2}\mathcal {D}(x^k,d^k). \end{aligned}$$

It follows that from the last two inequalities and the definition of t that

$$\begin{aligned} F_j(x^k + d^k) \le F_j(x^k) + c_1\mathcal {D}(x^k,d^k), \end{aligned}$$

for all k sufficiently large. Since $j\in \{1,\ldots ,m\}$ was arbitrary, we conclude that the step size $\alpha _k =1$ satisfies (13) for all k sufficiently large.

Consider now the curvature condition (14). From the definition of $F_{\lambda }^k$ in (32), we have

$$\begin{aligned} -\sum _{j = 1}^{m}\lambda _j^k\nabla F_j(x^k)^Td^k&= (d^k)^T\sum _{j = 1}^{m}\lambda _j^k\nabla ^2F_j(x^k)d^k\\&\quad - \sum _{j = 1}^{m}\lambda _j^k\left[ \nabla ^2F_j(x^k)d^k +\nabla F_j(x^k)\right] ^Td^k \\&=(d^k)^T\sum _{j = 1}^{m}\lambda _j^k\nabla ^2F_j(x^k)d^k\\ {}&\quad - \left[ \nabla F_{\lambda }^k(x^k) + \nabla ^2 F_{\lambda }^k(x^k)d^k\right] ^Td^k. \end{aligned}$$

Therefore, by (27), (8), and (34), we obtain

$$\begin{aligned} -\sum _{j = 1}^{m}\lambda _j^k\nabla F_j(x^k)^Td^k \ge a\Vert d^k\Vert ^2 + o(\Vert d^k\Vert ^2) = \Vert d^k\Vert ^2\left[ a + \dfrac{o(\Vert d^k\Vert ^2)}{\Vert d^k\Vert ^2}\right] . \end{aligned}$$

Hence, by (38), for k sufficiently large, it follows that

$$\begin{aligned} -\sum _{j = 1}^{m}\lambda _j^k\nabla F_j(x^k)^Td^k \ge \dfrac{a}{2}\Vert d^k\Vert ^2. \end{aligned}$$

(40)

On the other hand, by the mean value theorem, there exists $v^k:=x^k+t_kd^k$ for some $t_k\in ]0,1[$ such that

$$\begin{aligned} \nabla F_{\lambda }^k(x^k + d^k) =\nabla F_{\lambda }^k(x^k) + \nabla ^2F_{\lambda }^k(v^k)d^k. \end{aligned}$$

Therefore,

$$\begin{aligned} \dfrac{|\nabla F_{\lambda }^k(x^k + d^k)^T d^k|}{\Vert d^k\Vert ^2}\le & {} \dfrac{\Vert \nabla F_{\lambda }^k(x^k)+ \nabla ^2F_{\lambda }^k(x^k)d^k\Vert }{\Vert d^k\Vert }+\Vert \nabla ^2F_{\lambda }^k(v^k)-\nabla ^2F_{\lambda }^k(x^k)\Vert .\nonumber \\ \end{aligned}$$

(41)

Now, by the definitions of $F_{\lambda }^k$ and $v^k$, and taking into account (8) and (38), we obtain

$$\begin{aligned}&\lim _{k \rightarrow \infty } \Vert \nabla ^2F_{\lambda }^k(v^k)-\nabla ^2F_{\lambda }^k(x^k)\Vert = \lim _{k \rightarrow \infty } \Vert \sum _{j=1}^m\lambda _j^k ( \nabla ^2F_j(x^k+t_kd^k)-\nabla ^2F_j(x^k))\Vert \\&\quad \le \lim _{k \rightarrow \infty } \sum _{j=1}^m\lambda _j^k \Vert \nabla ^2F_j(x^k+t_kd^k)-\nabla ^2F_j(x^k)\Vert \\&\quad \le \lim _{k \rightarrow \infty } \max _{j=1,\ldots ,m} \Vert \nabla ^2F_j(x^k+t_kd^k)-\nabla ^2F_j(x^k)\Vert =0. \end{aligned}$$

Hence, it follows from (34) and (41) that

$$\begin{aligned} \lim _{k \rightarrow \infty } \dfrac{|\nabla F_{\lambda }^k(x^k + d^k)^T d^k|}{\Vert d^k\Vert ^2}=0. \end{aligned}$$

Thus, for k large enough, we have

$$\begin{aligned} |\nabla F_{\lambda }^k(x^k + d^k)^T d^k| \le c_2\dfrac{a}{4}\Vert d^k\Vert ^2, \end{aligned}$$

which, together with (40), yields

$$\begin{aligned} \sum _{j=1}^m\lambda _j^k \nabla F_j(x^k + d^k)^T d^k= & {} \nabla F_{\lambda }^k(x^k + d^k)^T d^k \ge - c_2\dfrac{a}{4}\Vert d^k\Vert ^2 \\\ge & {} \dfrac{c_2}{2} \sum _{j = 1}^{m}\lambda _j^k\nabla F_j(x^k)^Td^k. \end{aligned}$$

Finally, remembering that $\theta (x^k)=(1/2)\sum _{j=1}^m\lambda _j^k\nabla F_j(x^k)^Td^k$, if follows from the last inequality and Lemma 2.3(ii) that

$$\begin{aligned} \mathcal {D}(x^k+d^k,d^k)\ge \sum _{j=1}^m\lambda _j^k \nabla F_j(x^k + d^k)^T d^k \ge c_2 \theta (x^k) \ge c_2 \mathcal {D}(x^k,d^k), \end{aligned}$$

for all k sufficiently large, concluding the proof. $\square$

The next lemma presents a useful inequality that will be used in our main result. Its proof can be found in [19, Lemma 4.1.15] and will therefore be omitted here.

Lemma 5.6

Suppose that Assumption 5.1 holds. Then, for all $j= 1,\ldots ,m$, there holds:

$$\begin{aligned} \Vert \nabla F_j(x^{k+1}) - \nabla F_j(x^k) - \nabla ^2F_j(x^{*})(x^{k+1}-x^k)\Vert \\ \le L \dfrac{\Vert x^{k+1} - x^{*}\Vert + \Vert x^k - x^{*}\Vert }{2}\Vert x^{k+1} - x^k\Vert , \end{aligned}$$

where L is given in (28).

We are now able to prove the superlinear convergence of Algorithm 1. This result is based on [18, Theorem 2.2].

Theorem 5.7

Suppose that Assumption 5.1 holds. Then, $\{x^k\}$ converges to $x^{*}$ Q-superlinearly.

Proof

By Theorem 5.5, we may assume, without loss of generality, that $\alpha _k=1$ and hence $d^k=x^{k+1}-x^k$, for all k. Thus, by (7), we have $B_{\lambda }^k (x^{k+1} - x^k) = - \nabla F_{\lambda }^k(x^k)$ and then

$$\begin{aligned} (B_{\lambda }^k-\nabla ^2F_{\lambda }^k(x^{*}))(x^{k+1} - x^k)=&\nabla F_{\lambda }^k(x^{k+1}) -\nabla F_{\lambda }^k(x^k)\\&-\nabla ^2F_{\lambda }^k(x^{*})(x^{k+1} - x^k)-\nabla F_{\lambda }^k(x^{k+1}). \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} \dfrac{\Vert \nabla F_{\lambda }^k(x^{k+1})\Vert }{\Vert x^{k+1}-x^k\Vert } \le&\dfrac{\Vert (B_{\lambda }^k-\nabla ^2F_{\lambda }^k(x^{*}))(x^{k+1} - x^k)\Vert }{\Vert x^{k+1}-x^k\Vert } \\&+\dfrac{\Vert \nabla F_{\lambda }^k(x^{k+1})-\nabla F_{\lambda }^k(x^k)-\nabla ^2F_{\lambda }^k(x^{*})(x^{k+1} - x^k)\Vert }{\Vert x^{k+1}-x^k\Vert }. \end{aligned} \end{aligned}$$

(42)

Note that the second term on the right hand side of this inequality is less than or equal to

$$\begin{aligned} \max _{j=1,\ldots ,m}\dfrac{\Vert \nabla F_j(x^{k+1})-\nabla F_j(x^k)-\nabla ^2F_j(x^{*})(x^{k+1} - x^k)\Vert }{\Vert x^{k+1}-x^k\Vert } \end{aligned}$$

and, by Lemma 5.6, this last expression is less than or equal to

$$\begin{aligned} L\dfrac{\Vert x^{k+1} - x^{*}\Vert + \Vert x^k - x^{*}\Vert }{2}. \end{aligned}$$

Hence, taking limits on both sides of (42) and using (33), we get

$$\begin{aligned} \lim _{k \rightarrow \infty } \dfrac{\Vert \nabla F_{\lambda }^k(x^{k+1})\Vert }{\Vert x^{k+1}-x^k\Vert }=0. \end{aligned}$$

(43)

On the other hand, by the definition of $F_{\lambda }^k$, Lemma 2.4(iv), and Lemma 4.5(i), we find that

$$\begin{aligned} \dfrac{\Vert \nabla F_{\lambda }^k(x^{k+1})\Vert }{\Vert x^{k+1}-x^k\Vert }&\ge \dfrac{\Vert \sum _{j = 1}^{m}\lambda _j^k \nabla F_{j}(x^{k+1})\Vert }{\Vert x^{k+1} -x^{*}\Vert + \Vert x^k-x^{*}\Vert } \ge \dfrac{\Vert d_{SD}(x^{k+1})\Vert }{\Vert x^{k+1} -x^{*}\Vert + \Vert x^k-x^{*}\Vert } \\&\ge \dfrac{a}{2}\dfrac{\Vert x^{k+1} -x^{*}\Vert }{\Vert x^{k+1} -x^{*}\Vert + \Vert x^k-x^{*}\Vert }= \dfrac{a}{2}\dfrac{1}{1+ \frac{\Vert x^k-x^{*}\Vert }{\Vert x^{k+1} -x^{*}\Vert }}. \end{aligned}$$

Therefore, by using (43), we obtain

$$\begin{aligned} \lim _{k \rightarrow \infty } \dfrac{\Vert x^{k+1}-x^{*}\Vert }{\Vert x^k -x^{*}\Vert }=0, \end{aligned}$$

and hence that the rate of convergence is Q-superlinear. $\square$

6 Numerical Experiments

This section presents some numerical results in order to illustrate the potential practical advantages of Algorithm 1. We are mainly interested in verifying the effectiveness of using a Wolfe line search procedure and updating the Hessian approximations at each iteration in a BFGS scheme. For this purpose, we considered the following methods in the reported tests:

• Algorithm 1 (BFGS-Wolfe): our proposed scheme in which the Hessian approximations are updated at each iteration by (15) and the step sizes are calculated satisfying the Wolfe conditions (13)–(14).

• Standard BFGS-Armijo: a BFGS algorithm in which the Hessian approximations are updated, for each $j=1,\ldots ,m$, by

  $$\begin{aligned} B_j^{k+1}\!:=\!\left\{ \begin{array}{ll} B_j^{k}\! -\! \dfrac{B_j^{k}s_ks_k^{T}B_j^{k}}{s_k^{T}B_j^ks_k}\! +\!\dfrac{y_j^{k}(y_j^{k})^{T}}{s_k^{T}y_j^{k}}, &{}{}\quad \hbox {if} \; s_k^{T}y_j^{k}\ge \varepsilon \min \{1,|\theta (x^k)|\},\\ B_j^{k}, &{}{}\quad \text{ otherwise }, \end{array}\right. \end{aligned}$$

  (44)

  where $\varepsilon >0$ is an algorithmic parameter and the step sizes are calculated satisfying the Armijo-type condition (13). In our experiments, we used $\varepsilon =10^{-6}$.

• Standard BFGS-Wolfe: a BFGS algorithm in which the Hessian approximations are updated by (44) and the step sizes are calculated satisfying the Wolfe conditions (13)–(14).

To the best of our knowledge, until the present work, cautious updates as in (44) were the only alternatives to BFGS methods when applied to nonconvex multiobjective problems. The update scheme (44) was proposed in [52] and is similar to the one used in [38] for scalar optimization.

We implemented the algorithms in Fortran 90. The search directions $d(x^k)$ and the optimal values $\theta (x^k)$ were calculated by solving subproblem (6) using Algencan [4], an augmented Lagrangian code for general nonlinear programming. For computing a step size satisfying the Wolfe conditions (13)–(14), we used the algorithm proposed in [41]. This algorithm involves several quadratic/cubic polynomial interpolations of the objective functions, combines backtracking and extrapolation strategies, and is capable of calculating the step size in a finite number of (inner) iterations. Interpolations techniques were also used to compute step sizes that satisfy only the Armijo-type condition (13). We used $c_1=10^{-4}$, $c_2=0.1$, and set $B_j^0 = I_n$ for all $j=1,\ldots ,m$. We stopped the algorithms at $x^k$ reporting convergence when $\left| {\theta (x^k)}\right| \le 5 \times \texttt {eps}^{1/2},$ where $\texttt {eps}=2^{-52}\approx 2.22 \times 10^{-16}$ is the machine precision. The maximum number of allowed iterations was set to 2000. Our codes are freely available at https://github.com/lfprudente/bfgsMOP.

Although the BFGS method enjoys global convergence only under convexity assumptions, favorable numerical experiences are also commonly observed for nonconvex problems. Thus, the set of test problems chosen includes convex and nonconvex problems commonly found in the multiobjective optimization literature. Table 1 shows their main characteristics. The first two columns contain the problem name and the corresponding reference. Columns “n" and “m" give the number of variables and the number of objectives, respectively. “Conv." indicates whether the problem is convex or not. Many problems have box constraints in their original definitions. In some of them, the objectives are unbounded outside the box. In these cases, we added a term that penalizes the lack of fulfillment of the constraints to each objective. If we denote the box by $\{x\in \mathbb {R}^n \mid l\le x \le u\}$ where $l,u\in \mathbb {R}^n$, the penalty term is defined by $\frac{\mu }{3} \left[ \Vert \max \{0,x-u\}\Vert ^3_3+ \Vert \max \{0,-x+l\}\Vert ^3_3 \right]$, where $\mu = 10^{10}$ and the maximum is taken componentwise. This forces the iterates to remain inside the box. Column “Penal.” reports whether a given problem was penalized or not. The starting points were taken belonging to the corresponding boxes. We point out that the boxes are not considered by the algorithms themselves.

Table 1 List of test problems

Given a multiobjective optimization problem, we are especially interested in estimating its Pareto frontier. Toward this goal, a strategy often used is to run the algorithm at hand from several different starting points. In view of this application, we considered 300 random starting points for each problem in Table 1. Each instance was seen as an independent problem and was solved by all algorithms. Figure 1 shows the results using performance profiles [20]. We compared the algorithms with respect to: (a) number of iterations; (b) CPU time; (c) number of objective function evaluations; (d) number of derivative evaluations.

We start our analysis by noting that all algorithms proved to be robust on the chosen set of test problems, which illustrates the practical capability of the BFGS method even for nonconvex problems. Algorithm 1, Standard BFGS-Armijo and Standard BFGS-Wolfe algorithms successfully solved $99.8\%$, $99.7\%$, and $98.6\%$ of the problem instances. Regarding efficiency, taking into account the number of iterations, Algorithm 1 ($86.2\%$) had the best performance followed by Standard BFGS-Wolfe ($76.5\%$) and Standard BFGS-Armijo ($27.3\%$) algorithms, see Fig. 1a. This was directly reflected in CPU time (efficiency of $68.7\%$, $61.6\%$, and $22.6\%$ for Algorithm 1, Standard BFGS-Wolfe algorithm, and Standard BFGS-Armijo algorithm, respectively), as seen in Fig. 1b. Concerning the number of function and derivative evaluations, the Standard BFGS-Armijo algorithm was the most efficient, see Fig. 1c, d. This was somewhat expected as the Wolfe line search uses more information from the objectives than the Armijo line search. Even so, the Standard BFGS-Armijo algorithm was quickly outperformed by the other algorithms in terms of the number of function evaluations. The strong correlation between the number of iterations and CPU time can be explained by the fact that, in our experiments, the computational cost is largely dominated by the solutions of the subproblems to calculate the search directions. In fact, Algorithm 1 and the Standard BFGS-Armijo algorithm spent, on average, 93.2% and 94.5% of the total CPU time on solving the subproblems, and only 2.0% and 0.7% on calculating the step sizes, respectively. Therefore, at least in our tests, the computational effort in the line searches can be neglected and the use of Wolfe step sizes is justified due to its impact on decreasing the number of iterations and, consequently, the CPU time. Another issue of interest concerns the length of step sizes calculated by the Wolfe and Armijo line search procedures. Figure 2 shows the histograms (normalized by relative probability) containing the frequency distribution of all step sizes calculated by Algorithm 1 and the Standard BFGS-Armijo algorithm. As can be seen, in 83.61% of the iterations, the Wolfe step size was greater than or equal to one. We point out that, due to the use of extrapolation strategies, even step sizes larger than one can be considered in the Wolfe line search procedure. A similar frequency (78.18%) for the unit step was observed for the Armijo step sizes. In contrast, step sizes smaller than 0.1 were observed in 8.66% and 18.28% for the Wolfe and Armijo line searches, respectively. This corroborates the discussion in Remark 3.1 about the Wolfe conditions preventing the method from taking excessively small step sizes when larger step sizes are possible.

Fig. 1

Performance profiles considering 300 starting points for each test problem using as the performance measurement: a number of iterations; b CPU time; c number of functions evaluations; d number of derivative evaluations

Fig. 2

Histograms (normalized by relative probability) containing the frequency distribution of all step sizes calculated by: a Algorithm 1 (Wolfe step sizes); b standard BFGS-Armijo algorithm (Armijo step sizes)

We now compare the ability of the solvers to properly generate Pareto frontiers. For that, we use the well-known Purity and ($\Gamma$ and $\Delta$) Spread metrics. Roughly speaking, given a solver and a problem, the Purity metric measures the ability of the solver to find points on the Pareto frontier of the problem, while a Spread metric seeks to measure the ability of the solver to obtain well-distributed points along the Pareto frontier. We refer the reader to [12] for a detailed explanation of these metrics and their uses along with performance profiles. The results in Fig. 3 show that Algorithm 1 and the Standard BFGS-Wolfe algorithm outperformed the Standard BFGS-Armijo algorithm in relation to the Purity metric, while no significant difference was observed for the Spread metrics.

Fig. 3

Metric performance profiles

Figure 4 shows the outline of the Image sets and Pareto frontiers obtained by Algorithm 1 for problems Hil1, KW2, MMR3, and MOP6. In the graphics, a full point represents a final iterate while the beginning of a straight segment represents the corresponding starting point. Pareto optimal points also have a square marker. As expected, since these problems are nonconvex, Algorithm 1 converges to some nonoptimal Pareto critical points.

Fig. 4

Image sets and Pareto frontiers obtained by Algorithm 1 for the nonconvex problems Hil1, KW2, MMR3, and MOP6

Finally, we check the behavior of the methods as the number of objective functions increases. For this, we compare the performance of Algorithm 1 and the Standard BFGS-Armijo algorithm in larger instances of problems DTLZ1, DTLZ2, DTLZ3, DTLZ4, MGH26, Toi9, and Toi10. These are the customizable problems in dimension m of Table 1. MGH26, Toi9, and Toi10 are extensions of scalar optimization problems also known as Trigonometric, Shifted TRIDIA, and Rosenbrock, respectively. The first three columns of Table 2 identify the problem and the considered dimensions. For each instance, we ran both algorithms from 10 different random starting points. We emphasize that the algorithms reported convergence in all cases. The table gives the averages of: number of iterations (it), CPU time in seconds (time), number of function (nfev) and derivative (ngev) evaluations. The smallest reported data for each instance is highlighted in bold. We point out that we considered each evaluation of an objective (resp. objective gradient) in the calculation of nfev (resp. ngev). As can be seen, for MGH26 and DTLZ problems, Algorithm 1 strongly outperformed the Standard BFGS-Armijo algorithm with respect to the number of iterations and CPU time. Typically, taking into account these performance measures, Algorithm 1 uses less than half of the computational resources required by the Standard BFGS-Armijo algorithm in this group of problems. Even with respect to the number of function and derivative evaluations, an advantage for Algorithm 1 was, in general, observed. Regarding Toi9 and Toi10 problems, the algorithms presented more homogeneous performances. While the Standard BFGS-Armijo algorithm was the most efficient in terms of function and derivative evaluations, Algorithm 1 always required fewer iterations, resulting in CPU time savings in four of the six instances.

Table 2 Performance of Algorithm 1 (BFGS-Wolfe) and Standard BFGS-Armijo algorithm on larger instances of problems DTLZ1, DTLZ2, DTLZ3, DTLZ4, MGH26, Toi9, and Toi10

7 Conclusions

In this work, we proposed a new BFGS update scheme for multiobjective optimization problems. This scheme generates positive definite Hessian approximations whenever the initial approximations are positive definite and the step sizes satisfy the Wolfe conditions. As a result, Algorithm 1 is well defined even for general nonconvex problems. As far as we know, this is the first BFGS-type algorithm designed to nonconvex multiobjective problems that updates the Hessian approximations at each iteration. We provided a comprehensive study of the main global and local convergence properties of the method, using assumptions that are natural extensions of those made for the scalar minimization case. Our numerical experiments suggest that the techniques used here potentially provide a nonnegligible acceleration of the BFGS method. We hope that these techniques can also be useful for other variants of quasi-Newton methods for multiobjective optimization.