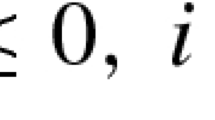1 Introduction

The problem of minimizing a maximum of finitely many functions subject to inequality constraints, known as discrete minimax program, arises in many areas of applications in engineering and commerce, as resource allocation and planning problems (see [1, 2] and other references therein). More recently, discrete minimax programs have appeared in robust optimization [3, 4], which is becoming increasingly important in optimization due to the reality of uncertainty in many real-world optimization problems and the importance of finding solutions that are immunized against data uncertainty [3, 5].

On the other hand, the standard convex polynomial program, where we minimize a single convex polynomial subject to convex polynomial inequality constraints, appears, often in the form of a convex quadratic program, in decision-making problems of finance and engineering. Remarkably, there is no duality gap between a primal convex polynomial program and its Lagrangian dual [6]. However, the Lagrangian dual, in general, may not easily be solvable. Recent research has shown that, whenever the functions involved in the primal convex program are sum-of-squares convex polynomials (in short, SOS-convex polynomials (see Definition 2.1), the convex program enjoys special properties such as exact sum of squares relaxation and zero duality gap between the primal and its dual [7, 8]. The key feature of these results is that the sum of squares relaxation problem or the dual problem is representable as a semidefinite programming problem (SDP). Such a result is of great interest in optimization because semidefinite programs can efficiently be solved by interior-point methods [9], and so the optimal value of the original problem can be found by solving its relaxation or dual problem.

The new class of SOS-convex polynomials from algebraic geometry [7, 10] is an important subclass of convex polynomials and it includes convex quadratic functions and separable convex polynomials. The SOS-convexity of polynomials can numerically be checked by solving semidefinite programming problems, whereas deciding convexity of polynomials is generally very hard [11, 12].

In this paper, we study discrete minimax programs with SOS-convex polynomials and examine the very basic issue of which discrete minimax programs can be presented with zero duality gap, where the duals can be represented as semidefinite linear programming problems. We make the following contributions to minimax optimization.

  1. I.

    Without any qualifications, we establish dual characterizations of non-negativity of max functions of convex polynomials over a system of convex polynomial inequalities and then derive sum-of-squares polynomial representations of non-negativity of max functions of SOS-convex polynomials over a system of SOS-convex polynomial inequalities.

  2. II.

    Using the sum-of-squares polynomial representations, we introduce a dual program, which is representable as a semidefinite linear programming problem, and show that there is no duality gap between the primal and its dual, whenever the functions involved in the primal program are SOS-convex polynomials. Under a constraint qualification, we prove that strong duality holds between the primal minimax problem and its dual problem. As an application, we prove that the value of a robust convex programming problem under polytopic data uncertainty is equal to its dual semidefinite program. The significance of our duality theorems is that the value of our primal minimax program can easily be found by solving its dual semidefinite program.

  3. III.

    Under a constraint qualification, we establish that strong duality continues to hold for SOS-convex minimax fractional programming problems with their corresponding dual semidefinite programs, including minimax linear fractional programming problems, for which the dual semidefinite programs reduce to linear programming problems.

The outline of the paper is as follows. Section 2 provides dual characterizations and representations of non-negativity of max functions of convex polynomials as well as SOS-convex polynomials over a system of inequalities. Section 3 presents zero duality gaps and strong duality results. Section 4 gives applications of our duality results to classes of robust convex optimization problems and minimax fractional programming problems. Appendix provides basic re-formulation of our dual problem as a semidefinite linear programming problem.

2 Dual Characterizations and Representations of Non-negativity

In this section, we present dual characterizations of solvability of inequality systems involving convex as well as SOS-convex polynomials. Firstly, we shall recall a few basic definitions and results which will be needed later in the sequel. We say that a real polynomial f is sum-of-squares [13] iff there exist real polynomials f j , j=1,…,s, such that \(f=\sum_{j=1}^{s}{f_{j}^{2}}\). The set of all sum-of-squares real polynomials is denoted by Σ 2, whereas the set consisting of all sum of squares real polynomials with degree at most d is denoted by \(\varSigma^{2}_{d}\). Similarly, we say a matrix polynomial \(F \in\mathbb{R}[x]^{n \times n}\) is a SOS-matrix polynomial provided that F(x)=H(x)H(x)T, where \(H(x) \in \mathbb{R}[x]^{n \times s}\) is a matrix polynomial for some \(s \in \mathbb{N}\). We now introduce the definition of SOS-convex polynomial.

Definition 2.1

[10, 11]

A real polynomial f on \(\mathbb{R}^{n}\) is called SOS-convex iff the Hessian matrix function x↦∇2 f(x) is a SOS-matrix polynomial.

Clearly, a SOS-convex polynomial is convex. However, the converse is not true. Thus, there exists a convex polynomial, which is not SOS-convex [11]. It is known that any convex quadratic function and any convex separable polynomial is a SOS-convex polynomial. Moreover, a SOS-convex polynomial can be non-quadratic and non-separable. For instance, \(f(x)=x_{1}^{8}+x_{1}^{2}+x_{1}x_{2}+x_{2}^{2}\) is a SOS-convex polynomial (see [14]), which is non-quadratic and non-separable.

The following basic known results on convex polynomials will play key roles throughout the paper.

Lemma 2.1

[10, Lemma 8]

Let f be a SOS-convex polynomial. If f(u)=0 and ∇f(u)=0 for some \(u\in\mathbb{R}^{n}\), then f is a sum-of-squares polynomial.

Lemma 2.2

([15, Theorem 3])

Let f 0,f 1,…,f m be convex polynomials on \(\mathbb{R}^{n}\). Suppose that inf x∈C f 0(x)>−∞, where \(C:=\{x \in\mathbb {R}^{n} : f_{i}(x) \leq0, i\in\mathbb{N}_{m} \} \neq\emptyset\). Then, \(\operatorname*{argmin}_{x\in C} f_{0}(x) \neq\emptyset\).

Corollary 2.1

Let f be a non-negative SOS-convex polynomial on \(\mathbb{R}^{n}\). Then, f is a sum-of-squares polynomial.

Proof

Assume that f is a non-negative SOS-convex polynomial on \(\mathbb {R}^{n}\). In virtue of Lemma 2.2, we know that \(\min_{x\in \mathbb{R}^{n}} f(x) = f(x^{*})\) for some \(x^{*}\in\mathbb{R}^{n}\). Therefore, h:=f−f(x ∗) is a non-negative SOS-convex polynomial such that h(x ∗)=0 and ∇h(x ∗)=0. By applying Lemma 2.1, we find that h is a sum-of-squares polynomial, so f−f(x ∗)=σ for some σ∈Σ 2. Therefore, f=σ+f(x ∗) is a sum-of-squares polynomial since f(x ∗)≥0. □

Let Δ be the simplex in \(\mathbb{R}^{r}\), that is, \(\Delta:= \{ \delta\in\mathbb{R}^{r}_{+} : \sum_{j=1}^{r} \delta_{j} = 1 \}\). Note that for \(l\in \mathbb{N}\), \(\mathbb{N}_{l}\) is defined by \(\mathbb{N}_{l}=\{1,2,\ldots,l\}\)

Theorem 2.1

(Dual characterization of non-negativity)

Let p j and g i be convex polynomials for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\), with \(\mathcal{F}:= \{ x\in\mathbb{R}^{n} : g_{i}(x) \leq0, i\in\mathbb{N}_{m}\} \) a nonempty set. Then, the following statements are equivalent:

  1. (i)

    \(g_{i}(x) \leq0, \, i\in\mathbb{N}_{m} \Rightarrow\max _{j\in\mathbb{N}_{r}} p_{j}(x) \geq0 \).

  2. (ii)

    (∀ε>0) \((\exists\,\bar{\delta}\in\Delta , \bar{\lambda}\in\mathbb{R}^{m}_{+})\) \(\sum_{j=1}^{r}{\bar{\delta }_{j} p_{j}} + \sum_{i=1}^{m}{\bar{\lambda}_{i} g_{i}} + \varepsilon> 0 \).

Proof

(ii) ⇒ (i) Suppose that, for each ε>0, there exist \(\bar{\delta}\in\Delta\) and \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) such that \(\sum_{j=1}^{r}{\bar{\delta}_{j} p_{j}} + \sum_{i=1}^{m}{\bar{\lambda }_{i} g_{i}} + \varepsilon> 0 \). Then, for any \(x\in\mathcal{F}\) we have

$$\max_{\delta\in\Delta} \sum_{j=1}^{r}{\delta_j p_j(x)} + \varepsilon\geq\sum_{j=1}^{r}{\bar{\delta}_j p_j(x)} + \varepsilon\geq\sum_{j=1}^{r}{\bar{\delta}_j p_j(x)} + \sum _{i=1}^{m}{\bar{\lambda}_i g_i(x)} + \varepsilon> 0. $$

Letting ε→0, we see that

$$\max_{j\in \mathbb{N}_r} p_j(x) = \max_{\delta\in\Delta} \sum _{j=1}^{r}{\delta_j p_j(x)} \geq0$$

for all \(x\in\mathcal{F}\).

(i) ⇒ (ii) Assume that (i) holds. Let ε>0 be arbitrary and let f j :=p j +ε for all \(j\in\mathbb{N}_{r}\). Then, one has

$$ \max _{j\in\mathbb{N}_r} f_j(x) = \max _{j\in\mathbb{N}_r} \bigl\{ p_j(x)\bigr\} + \varepsilon> 0 \quad\forall x\in\mathcal{F}. $$

Now, we will show that the set

$$ G:= \bigl\{ z= (\underline{z},\overline{z} )\in\mathbb{R}^{r+m} : \exists\,x \in\mathbb{R}^n \text{ s.t. } f_j(x) \leq \underline{z}_j, j\in\mathbb{N}_r, g_i(x) \leq\overline{z}_i, i\in\mathbb{N}_m \bigr\} $$

is a closed and convex set. As f j and g i are all convex polynomials, then G is clearly a convex set. To see that it is closed, let \(\{z^{k}\}_{k\in\mathbb{N}} \subset G\) be such that {z k}→z ∗ as k→∞. Then, for each \(k\in\mathbb {N}\), there exists \(x^{k} \in\mathbb{R}^{n}\) such that \(f_{j}(x^{k}) \leq \underline{z}^{k}_{j}\) and \(g_{i}(x^{k}) \leq\overline{z}^{k}_{i}\), for all \(j\in \mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\). Now, consider the convex optimization problem

$$\begin{aligned} &(\bar{{P}})\quad \min_{x\in\mathbb{R}^n,u\in\mathbb{R}^{r+m}} \Vert u-z^*\Vert ^2 \\ &\phantom{(\bar{\mathrm{P}})\quad} \text{s.t.} \quad f_j(x)-\underline{u}_j \leq0,\quad j\in\mathbb{N}_r, \\ &\phantom{(\bar{\mathrm{P}})\quad\text{s.t.} \quad} g_i(x)-\overline{u}_i \leq0,\quad i\in\mathbb{N}_m. \end{aligned}$$

Obviously, \(0 \leq\inf(\bar{P}) \leq \Vert z^{k}-z^{*}\Vert ^{2} \) for all \(k\in\mathbb{N}\), where \(\inf(\bar{P})\) denotes the optimal value of the problem \(\inf(\bar{P})\). Since ∥z k−z ∗∥2→0 as k→∞, we get \(\inf(\bar{P}) = 0\). Moreover, Lemma 2.2 implies that \(\inf(\bar{P})\) is attained, and so, there exists \(x^{*} \in\mathbb{R}^{n}\) such that \(f_{j}(x^{*}) \leq\underline{z}^{*}_{j}\), \(j\in\mathbb{N}_{r}\), and \(g_{i}(x^{*}) \leq\overline{z}^{*}_{i}\), \(i\in\mathbb{N}_{m}\). So z ∗∈G, and consequently, G is closed.

Since \(\max_{j\in\mathbb{N}_{r}} f_{j}(x) > 0\) for all \(x\in\mathcal{F}\), 0∉G. Hence, by the strict separation theorem [16, Theorem 1.1.5], there exist \(v = (\underline{v},\overline{v} )\in\mathbb {R}^{r+m} \backslash\{0\}\), \(\alpha\in\mathbb{R}\) and ξ>0 such that

$$ 0 = v^T 0 \leq\alpha< \alpha+ \xi\leq\underline{v}^T \underline{z} + \overline{v}^T \overline{z} $$

for all z∈G. Since \(G + (\mathbb{R}^{r}_{+} \times\mathbb{R}^{m}_{+} ) \subset G\), \(\underline{v}_{j} \geq0\) and \(\overline{v}_{i} \geq0\), for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\). Observe that, for each \(x \in\mathbb{R}^{n}\), (f 1(x),…,f r (x),g 1(x),…,g m (x))∈G. So, for each \(x \in\mathbb{R}^{n}\),

$$ \sum_{j=1}^{r} \underline{v}_j f_j(x) + \sum _{i=1}^m \overline{v}_i g_i(x) \geq\alpha+\xi\geq\xi> 0 . $$
(1)

Now, we claim that \(\underline{v}\in\mathbb{R}^{r}_{+} \backslash\{0\}\). Otherwise, if \(\underline{v} = 0\), then from (1) we get \(\sum _{i=1}^{m} \overline{v}_{i} g_{i}(\bar{x}) > 0\) for any \(\bar{x}\in\mathcal{F}\) (recall that \(\mathcal{F}\) is nonempty). Since \(g_{i}(\bar{x}) \leq0\) and \(\overline{v}_{i} \geq0\) for all \(i\in\mathbb{N}_{m}\), \(\sum_{i=1}^{m} \overline{v}_{i} g_{i}(\bar{x}) \leq0\), which is a contradiction. So, one has \(\kappa:=\sum_{j=1}^{r} \underline{v}_{j} > 0\). Therefore, (1) implies that

$$ \sum _{j=1}^{r}{\bar{\delta}_j f_j(x)} + \sum _{i=1}^{m}{\bar{ \lambda}_i g_i(x)} \geq\bar{\xi} > 0 $$

for all \(x \in\mathbb{R}^{n}\), where \(\bar{\delta}_{j}:= \kappa ^{-1}\underline{v}_{j} \geq0\) for all \(j\in\mathbb{N}_{r}\), \(\bar{\lambda }_{i}:=\kappa^{-1}\overline{v}_{i} \geq0 \) for all \(i\in\mathbb{N}_{m}\), and \(\bar{\xi}:= \kappa^{-1} \xi> 0\). Since \(\sum_{j=1}^{r}\bar{\delta}_{j} = 1\), we can write

$$ \sum _{j=1}^{r}{\bar{\delta}_j p_j} + \sum _{i=1}^{m}{\bar{ \lambda}_i g_i} + \varepsilon> 0. $$

Thus, the conclusion follows. □

Let d be the smallest even number such that

$$d\geq\max\Bigl\{ \max _{j\in\mathbb{N}_r}\deg p_j, \max_{i\in\mathbb{N}_m}\deg g_i \Bigr\} .$$

Theorem 2.2

(SOS-Convexity and representation of non-negativity)

Let p j and g i be SOS-convex polynomials for all \(j\in\mathbb {N}_{r}\) and \(i\in\mathbb{N}_{m}\). Assume that the set \(\mathcal{F}:= \{ x\in\mathbb{R}^{n} : g_{i}(x) \leq0, i\in\mathbb{N}_{m}\} \) is nonempty. Then, the following statements are equivalent:

  1. (i)

    \(g_{i}(x) \leq0, \, i\in\mathbb{N}_{m} \Rightarrow\max _{j\in\mathbb{N}_{r}} p_{j}(x) \geq0 \).

  2. (ii)

    (∀ε>0) \((\exists\,\bar{\delta}\in\Delta , \bar{\lambda}\in\mathbb{R}^{m}_{+},\bar{\sigma}\in\varSigma^{2}_{d})\) \(\sum _{j=1}^{r}{\bar{\delta}_{j} p_{j}} + \sum_{i=1}^{m}{\bar {\lambda}_{i} g_{i}} + \varepsilon= \bar{\sigma} \).

Proof

(ii) ⇒ (i) Suppose that for each ε>0, there exist \(\bar{\delta}\in\Delta\), \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) and \(\bar{\sigma}\in\varSigma^{2}_{d}\) such that \(\sum_{j=1}^{r}{\bar{\delta}_{j} p_{j}} + \sum_{i=1}^{m}{\bar{\lambda}_{i} g_{i}} + \varepsilon= \bar{\sigma }\). Then, for any \(x\in\mathcal{F}\) we have

$$\max_{\delta\in\Delta} \sum_{j=1}^{r}{\delta_j p_j(x)} + \varepsilon\geq\sum_{j=1}^{r}{\bar{\delta}_j p_j(x)} + \varepsilon= \bar{\sigma}(x) - \sum_{i=1}^{m}{\bar{\lambda}_i g_i(x)} \geq0. $$

Letting ε→0, we see that \(\max_{j\in \mathbb{N}_{r}} p_{j}(x) \geq0\) for all \(x\in\mathcal{F}\).

(i) ⇒ (ii) Assume that (i) holds and let ε>0 arbitrary. Then, by Theorem 2.1, there exist \(\bar {\delta}\in\Delta\) and \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) such that

$$L:=\sum_{j=1}^{r}{\bar{\delta}_j p_j} + \sum _{i=1}^{m}{\bar{\lambda}_i g_i} + \varepsilon> 0. $$

Since p j and g i are all SOS-convex polynomials, then L is a (non-negative) SOS-convex polynomial too. Hence, Corollary 2.1 ensures that L is a sum-of-squares polynomial (of degree at most d), that is, there exist \(\bar{\sigma}\in\varSigma^{2}_{d}\) such that

$$\sum_{j=1}^{r}{\bar{\delta}_j p_j} + \sum_{i=1}^{m}{\bar {\lambda}_i g_i} + \varepsilon = \bar{\sigma}. $$

Thus, the conclusion follows. □

3 Duality for Minimax Programs with SOS-Convex Polynomials

In this section, we introduce the dual problem for our minimax model problem and establish duality theorems whenever the functions involved are SOS-convex polynomials.

Consider the minimax programming problem

$$\begin{aligned} \begin{aligned} &(P) \quad \inf_{x\in\mathbb{R}^n} \max_{j\in \mathbb{N}_r}\,p_j(x) \\ &\phantom{(P) \quad\ } \text{s.t.} \quad g_i(x) \leq0, \quad i\in\mathbb{N}_m, \end{aligned} \end{aligned}$$
(2)

and its associated dual problem

$$ \begin{aligned} &(D)\quad \sup \mu\\ &\phantom{(D)\quad\ } \text{s.t.} \quad \sum_{j=1}^{r}{\delta_j p_j} + \sum _{i=1}^{m}{\lambda_i g_i} -\mu \in\varSigma^2_d \\ &\phantom{\ (D)\quad\text{s.t.} \quad } \delta\in\Delta,\quad \lambda\in\mathbb{R}^m_+, \quad\mu\in\mathbb{R}, \end{aligned} $$
(3)

where p j and g i are real polynomials on \(\mathbb{R}^{n}\) for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\) and d is the smallest even number such that \(d\geq\max\{ \max_{j\in\mathbb{N}_{r}}\deg p_{j}, \max_{i\in\mathbb{N}_{m}}\deg g_{i} \}\).

Throughout the paper, the set \(\mathcal{F}:= \{ x\in\mathbb{R}^{n} : g_{i}(x) \leq0, i\in\mathbb{N}_{m}\}\) is assumed to be nonempty.

It is well known that optimization problems of the form (D) can equivalently be re-formulated as semidefinite programming problem [7]. See the appendix for details. For instance, consider the quadratic optimization problem (P cq) where p j and g i are all quadratic functions, that is, for all \(x\in\mathbb{R}^{n}\), \(p_{j}(x) = x^{T} A_{j} x + a_{j}^{T} x + \alpha_{j}\) and \(g_{i}(x) = x^{T} C_{i} x + c_{i}^{T} x + \gamma_{i}\), with \(A_{j}, C_{i} \in\mathbb{S}^{n}\), the space of all symmetric (n×n) matrices, \(a_{j}, c_{i} \in\mathbb{R}^{n}\) and \(\alpha_{j},\gamma_{i} \in\mathbb{R}\) for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\), that is,

$$ \begin{aligned} &(P^{cq}) \quad \inf_{x\in\mathbb{R}^n} \max_{j\in\mathbb{N}_r}\,x^T A_j x + a_j^T x + \alpha_j \\ & \phantom{(P^{cq}) \quad}\text{s.t.}\quad x^T C_i x + c_i^T x + \gamma_i \leq0,\quad \forall i\in \mathbb{N}_m. \end{aligned} $$
(4)

In this particular case, the sum-of-squares constraint in its associated dual problem \(\sum_{j=1}^{r}{\delta_{j} p_{j}} + \sum _{i=1}^{m}{\lambda_{i} g_{i}} -\mu \in\varSigma^{2}_{2}\) is equivalent to \(\sum_{j=1}^{r}{\delta_{j} p_{j}} + \sum_{i=1}^{m}{\lambda_{i} g_{i}} -\mu \geq0\). This, in turn (see [17, p. 163]), is equivalent to

$$ \left(\begin{array}{c@{\quad}c} \sum_{j=1}^r\delta_j \alpha_j + \sum_{i=1}^m\lambda _i\gamma_i -\mu & \frac{1}{2} (\sum_{j=1}^r \delta_j a_j^T + \sum_{i=1}^m\lambda_i c_i^T ) \\ \frac{1}{2} (\sum_{j=1}^r \delta_j a_j + \sum _{i=1}^m\lambda_i c_i ) & \sum_{j=1}^r \delta_j A_j + \sum _{i=1}^m\lambda_i C_i \end{array} \right) \succeq0. $$

Therefore, the dual problem of (P cq) becomes

$$ \begin{aligned} &(D^{cq})\quad\sup \mu \\ & \phantom{(D^{cq})\quad\ }\text{s.t.}\quad \sum_{j=1}^r\delta_j \left( \begin{array}{c@{\quad}c} 2\alpha_j & a_j^T \\ a_j & 2A_j \end{array} \right) + \sum_{i=1}^m \lambda_i \left( \begin{array}{c@{\quad}c} 2\gamma_i & c_i^T \\ c_i & 2C_i \end{array} \right) - \mu \left( \begin{array}{c@{\quad}c} 2 & 0 \\ 0 & 0 \end{array} \right) \succeq0, \\ &\phantom{(D^{cq})\quad\text{s.t.}\quad\ } \delta\in\Delta,\quad \lambda\in\mathbb{R}^m_+,\quad \mu\in\mathbb{R}, \end{aligned} $$
(5)

which is clearly a semidefinite programming problem.

Lemma 3.1

Let p j and g i be convex polynomials for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\). Then,

$$ \inf(P) = \sup_{\delta\in\Delta, \lambda\in\mathbb{R}^m_+} \inf_{x\in\mathbb{R}^{n}} \Biggl\{ \sum_{j=1}^{r}{\delta_j p_j(x)} + \sum_{i=1}^{m}{\lambda_i g_i(x)} \Biggr\} . $$

Proof

Note that, for any \(\bar{x}\in\mathcal{F}\), \(\bar{\delta}\in \Delta\) and \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\), one has

$$\max_{j\in\mathbb{N}_r} p_j(\bar{x}) \geq\sum_{j=1}^r \bar{\delta}_j p_j(\bar{x}) + \sum_{i=1}^m \bar{\lambda}_i g_i(\bar{x}) \geq\inf_{x\in\mathbb{R}^{n}} \Biggl\{ \sum _{j=1}^r \bar{\delta}_j p_j(x) + \sum_{i=1}^m \bar{\lambda}_i g_i(x) \Biggr\} . $$

Therefore, \(\inf(P) \geq\sup_{\delta\in\Delta, \lambda\in\mathbb {R}^{m}_{+}} \inf_{x\in\mathbb{R}^{n}} \{ \sum_{j=1}^{r}{\delta_{j} p_{j}(x)} + \sum_{i=1}^{m}{\lambda_{i} g_{i}(x)} \} \).

To see the reverse inequality, we may assume without any loss of generality that inf(P)>−∞, otherwise the conclusion follows immediately. Since \(\mathcal{F}\neq\emptyset\), we have \(\mu^{*}:=\inf(P) \in\mathbb{R}\). Then, for ε>0 arbitrary, as \(\max_{j\in \mathbb{N}_{r}} \{ p_{j}(x) -\mu^{*} \} \geq0\) for all \(x\in\mathcal{F}\), by Theorem 2.1 we see that there exist \(\bar{\delta}\in \Delta\) and \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) such that \(\sum _{j=1}^{r}{\bar{\delta}_{j} p_{j}} + \sum_{i=1}^{m}{\bar{\lambda}_{i} g_{i}} > \mu^{*} - \varepsilon\). Consequently,

$$\sup_{\delta\in\Delta, \lambda\in\mathbb{R}^m_+} \inf _{x\in\mathbb{R}^{n}} \Biggl\{ \sum_{j=1}^{r}{\delta_j p_j(x)} + \sum _{i=1}^{m}{\lambda_i g_i(x)} \Biggr\} \geq \mu^* - \varepsilon. $$

Since the above inequality holds for any ε>0, passing to the limit we obtain the desired inequality, which concludes the proof. □

As a consequence of Lemma 3.1, we derive the following zero duality gap result for (P).

Theorem 3.1

(Zero duality gap)

Let p j and g i be SOS-convex polynomials for all \(j\in\mathbb {N}_{r}\) and \(i\in\mathbb{N}_{m}\). Then, inf(P)=sup(D).

Proof

For any feasible points \(\bar{x}\in\mathcal{F}\) and \(\bar {\delta}\in\Delta\), \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) and \(\bar{\mu}\in \mathbb{R}\) such that \(\sum_{j=1}^{r}{\bar{\delta}_{j} p_{j}} + \sum _{i=1}^{m}{\bar{\lambda}_{i} g_{i}} -\bar{\mu} = \bar{\sigma} \in\varSigma^{2}_{d}\),

$$\sum_{j=1}^r \bar{\delta}_j (p_j(\bar{x}) - \bar{\mu} ) = \sum _{j=1}^r \bar{\delta}_j p_j(\bar{x}) - \bar{\mu} = \bar{\sigma }(\bar{x}) - \sum_{i=1}^m \bar{\lambda}_i g_i(\bar{x}) \geq 0. $$

Then, there exists \(j_{0}\in\mathbb{N}_{r}\) such that \(p_{j_{0}}(\bar {x})-\bar{\mu} \geq0\), and so, \(\bar{\mu} \leq\max_{j\in \mathbb{N}_{r}} p_{j}(\bar{x}) \). Thus, sup(D)≤inf(P).

To see the reverse inequality, we may assume without any loss of generality that inf(P)>−∞, otherwise the conclusion follows immediately. Since \(\mathcal{F}\neq\emptyset\), we have \(\mu^{*}:=\inf(P) \in\mathbb{R}\). Then, as a consequence of Lemma 3.1, for ε>0 arbitrary we have

$$\sup_{\delta\in\Delta, \lambda\in\mathbb{R}^m_+, \mu\in\mathbb {R}} \Biggl\{ \mu: \sum_{j=1}^{r}{\delta_j p_j} + \sum _{i=1}^{m}{\lambda_i g_i} -\mu\geq0 \Biggr\} \geq \mu^* - \varepsilon. $$

As p j and g i are all SOS-convex polynomials, then \(L:=\sum _{j=1}^{r}{\delta_{j} p_{j}} + \sum_{i=1}^{m}{\lambda_{i} g_{i}} -\mu\) is a SOS-convex polynomial too. So, by Corollary 2.1, L is non-negative if and only if \(L\in\varSigma^{2}_{d}\). Hence, μ ∗−ε≤sup(D). Since the previous inequality holds for any ε>0, passing to the limit we get μ ∗≤sup(D), which concludes the proof. □

Corollary 3.1

Let f and g i be SOS-convex polynomials for all \(i\in\mathbb {N}_{m}\). Then,

$$\inf_{x\in\mathbb{R}^{n}} \bigl\{ f(x) : g_i(x)\leq0, i\in\mathbb {N}_{m} \bigr\} = \sup_{\lambda\in\mathbb{R}^m_+, \mu\in\mathbb{R}} \Biggl\{ \mu: f+\sum_{i=1}^{m}{\lambda_i g_i}-\mu\in\varSigma^2_d, \Biggr\} $$

where d is the smallest even number such that \(d\geq\max\{ \deg f, \max_{i\in\mathbb{N}_{m}}\deg g_{i} \}\).

Proof

It is a straightforward consequence of Theorem 3.1 by taking r=1. □

Remark 3.1

It is worth observing that the conclusion of Theorem 3.1 can be also obtained from Corollary 3.1. To see this, let us consider the following SOS-convex polynomial optimization problem associated with (P):

$$ \begin{aligned} &(P_{e}) \quad\inf_{(x,z)\in\mathbb{R}^{n}\times\mathbb{R}} \, z\\ &\phantom{(P_{e}) \quad}\text{s.t.}\quad p_j(x) -z \leq0,\quad \forall j\in\mathbb{N}_r, \\ &\phantom{(P_{e}) \quad \text{s.t.}\quad} g_i(x) \leq0, \quad \forall i\in\mathbb{N}_m. \end{aligned} $$
(6)

Then, inf(P)=inf(P e ). Corollary 3.1 gives us that inf(P e )=sup(D e ), where the dual problem (D e ) is given by

$$ \sup _{\substack{\mu\in\mathbb{R}, \sigma\in\varSigma^2 \\ \lambda\in\mathbb {R}^m_+, \delta\in\mathbb{R}^r_+}}\Biggl\{ \mu: z + \sum _{i=1}^{m}{ \lambda_i g_i(x)} + \sum _{j=1}^{r}{ \delta_j \bigl(p_j(x)-z\bigr)} -\mu= \sigma(x,z), \forall(x,z)\in\mathbb{R}^{n+1} \Biggr\} $$

The constraint in the above dual problem can be written as follows:

$$ z\Biggl(1 - \sum_{j=1}^{r}{ \delta_j}\Biggr) + \sum_{j=1}^{r}{ \delta_j p_j(x)} + \sum_{i=1}^{m}{ \lambda_i g_i(x)} - \mu= \sigma(x,z) $$
(7)

for all \((x,z)\in\mathbb{R}^{n+1}\). Let \(\gamma:=1 - \sum _{j=1}^{r}{\delta_{j}}\) and fix \(x=x_{0}\in\mathbb{R}^{n}\). Following the arguments employed in [18], we claim that γ=0. If γ>0, letting \(z\in\mathbb{R}\) small enough we find that the right-hand side of (7) becomes negative, which contradicts the fact that σ(x 0,z)≥0 for all \(z\in\mathbb{R}\). On the other hand, if γ<0, letting \(z\in\mathbb{R}\) large enough, we see that the right-hand side of (7) becomes negative, which implies again a contradiction. Consequently, γ=0 and σ does not depend on z. So, the problem (D e ) collapses to problem (D) introduced in (3).

We now see that whenever the Slater condition,

$$\bigl\{ x\in\mathbb{R}^n : g_i(x) < 0, i\in\mathbb{N}_m \bigr\} \neq\emptyset, $$

is satisfied, strong duality between (P) and (D) holds.

Theorem 3.2

(Strong duality)

Let p j and g i be SOS-convex polynomials for all \(j\in\mathbb {N}_{r}\) and \(i\in\mathbb{N}_{m}\). If the Slater condition holds, then inf(P)=max(D).

Proof

Let \(f:=\max_{j\in\mathbb{N}_{r}} p_{j}\) and \(\mu^{*} := \inf(P) \in\mathbb {R}\). Thus, since the Slater condition is fulfilled, by the usual convex programming duality and the convex-concave minimax theorem, we get

$$\begin{aligned} \mu^* \leq\inf(P) =& \inf _{x\in\mathbb{R}^n} \bigl\{ f(x) : g_i(x)\leq0, i\in \mathbb{N}_m \bigr\} \\ =& \max _{\lambda\in\mathbb{R}^m_+} \, \inf _{x\in\mathbb{R}^n} \Biggl\{ f(x) + \sum _{i=1}^m \lambda_i g_i(x) \Biggr\} \\ =& \max _{\lambda\in\mathbb{R}^m_+} \, \inf _{x\in\mathbb{R}^n} \, \max_{\delta\in\Delta} \Biggl\{ \sum_{i=1}^{r}{\delta_j p_j(x)} + \sum_{i=1}^m \lambda_i g_i(x) \Biggr\} \\ =& \max _{\lambda\in\mathbb{R}^m_+, \delta\in\Delta} \, \inf _{x\in\mathbb{R}^n} \Biggl\{ \sum _{i=1}^{r}{\delta_j p_j(x)} + \sum_{i=1}^m \lambda_i g_i(x) \Biggr\} . \end{aligned}$$

Hence, there exist \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) and \(\bar{\delta }\in\Delta\) such that

$$ L:=\sum _{j=1}^{r}{\bar{\delta}_j p_j} + \sum_{i=1}^{m}{\bar{ \lambda}_i g_i} -\mu^* \geq0. $$

As p j and g i are all SOS-convex polynomials, L is a (non-negative) SOS-convex polynomial too, and consequently, in virtue of Corollary 2.1, L is a sum-of-squares polynomial (of degree at most d). Hence, \((\bar{\delta},\bar{\lambda},\mu^{*})\) is a feasible point of (D), so μ ∗≤sup(D). Since weak duality always holds, we conclude inf(P)=max(D). □

Recall the minimax quadratic programming problem (P cq) introduced in (4) and its dual problem (D cq) given in (5). Note that the set of all (n×n) positive semidefinite matrices is denoted by \(\mathbb{S}^{n}_{+}\).

Corollary 3.2

Let \(A_{j}, C_{i} \in\mathbb{S}^{n}_{+}\), \(a_{j}, c_{i} \in\mathbb{R}^{n}\), and \(\alpha_{j},\gamma_{i} \in\mathbb{R}\) for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\). If there exists \(\bar{x}\in\mathbb{R}^{n}\) such that \(\bar{x}^{T} C_{i} \bar{x} + c_{i}^{T} \bar{x} + \gamma_{i} < 0\) for all \(i\in \mathbb{N}_{m}\), then inf(P cq)=max(D cq).

Proof

As \(A_{j}, C_{i} \in\mathbb{S}^{n}_{+}\) for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\), all the quadratic functions involved in (P cq) are convex. Hence, since the Slater condition holds and any convex quadratic function is a SOS-convex polynomial, by applying Theorem 3.2 we get inf(P cq)=max(D cq). □

Remark 3.2

(Attainment of the optimal value)

For the problem (P) introduced in (2), note that, if \(f:=\max_{j\in\mathbb{N}_{r}}\,p_{j}\) (which is not a polynomial, in general) is bounded from below on the nonempty set \(\mathcal{F}\), then f attains its minimum on \(\mathcal{F}\). In other words, if \(\inf(P) \in\mathbb{R}\), then there exists \(x^{*}\in\mathcal{F}\) such that f(x ∗)=min(P). To see this, let consider again the convex polynomial optimization problem (P e ) introduced in (6). Let \(\mathcal{F}_{e}\) be the (nonempty) feasible set of (P e ). Observe that \(x_{0}\in\mathcal{F}\) implies \((x_{0},z_{0}) \in\mathcal{F}_{e}\) for all z 0≥f(x 0), and conversely, \((x_{0},z_{0}) \in\mathcal{F}_{e}\) implies \(x_{0}\in\mathcal{F}\). Moreover, one has inf(P)=inf(P e ). Thus, Lemma 2.2 can be applied to problem (P e ) and then, there exists \((x^{*},z^{*})\in\mathcal{F}_{e}\) such that z ∗=min(P e ). Since z ∗≤z for all \((x,z)\in\mathcal{F}_{e}\) and \((x,f(x))\in\mathcal{F}_{e}\) for all \(x\in\mathcal{F}\), then we get

$$ z^* \leq f(x) \quad\forall x\in\mathcal{F}. $$
(8)

On the other hand, as \((x^{*},z^{*})\in\mathcal{F}_{e}\) we get \(x^{*}\in \mathcal{F}\) and

$$ f\bigl(x^*\bigr) \leq z^*. $$
(9)

Combining (8) and (9), we conclude f(x ∗)≤f(x) for all \(x\in\mathcal{F}\), and so, x ∗ is a minimizer of (P).

Recall that the subdifferential of the (convex) function f at \(x\in \mathbb{R}^{n}\) is defined to be the set

$$\partial f(x):= \bigl\{ v\in\mathbb{R}^n : f(y) \geq f(x) + v^T(y-x),\ \forall y\in \operatorname{dom}f \bigr\} . $$

For a convex set \(C\subset\mathbb{R}^{n}\), the normal cone of C of at x∈C is given by

$$N_C(x):= \bigl\{ v\in\mathbb{R}^n : v^T(y-x)\leq0,\ \forall y\in C \bigr\} . $$

We will say that the normal cone condition holds for \(\mathcal{F}\) at \(x\in\mathcal{F}\), provided that

$$N_\mathcal{F}(x) = \Biggl\{ \sum_{i=1}^m \lambda_i \nabla g_i(x) : \lambda\in \mathbb{R}^{m}_{+}, \sum_{i=1}^{m}{\lambda_i g_i(x)} = 0 \Biggr\} . $$

It is known that the Slater condition guarantees the normal cone condition (see [19, Sect. 2.2]). However, the converse statement is not true in general. The following exampleFootnote 1 shows this fact.

Example 3.1

Let \(g_{1}(x_{1},x_{2}):=x_{1}+x_{2}^{2}\), \(g_{2}(x_{1},x_{2}):=-x_{1}+x_{2}^{2}\), \(g_{3}(x_{1},x_{2}):=x_{1}^{2}+x_{2}\) and \(g_{4}(x_{1},x_{2}):=x_{1}^{2}-x_{2}\), for all \(x\in \mathbb{R}^{2}\). Then, it is easy to check that each g i is a SOS-convex polynomial and \(\mathcal{F}:= \{ x\in\mathbb{R}^{2} : g_{i}(x) \leq0, i\in\mathbb{N}_{4}\} = \{ (0,0) \}\). So, \(N_{\mathcal{F}}(x)=\mathbb{R}^{2}\) for all \(x\in\mathcal{F}\). Since, for all \(x\in \mathcal{F}\),

$$\Biggl\{ \sum_{i=1}^4 \lambda_i \nabla g_i(x) : \lambda\in\mathbb {R}^{4}_{+}, \sum_{i=1}^{4}{\lambda_i g_i(x)} = 0 \Biggr\} = \bigcup_{\lambda \in\mathbb{R}^{4}_{+}}(\lambda_1-\lambda_2,\lambda_3-\lambda_4) = \mathbb{R}^{2}, $$

then the normal condition holds. On the other hand, it is easy to see that the Slater condition fails.

Theorem 3.3

(Min-max duality)

Let p j and g i be SOS-convex polynomials for all \(j\in\mathbb {N}_{r}\) and \(i\in\mathbb{N}_{m}\). Let \(x^{*}\in\mathcal{F}\) be an optimal solution of (P) and assume that the normal cone condition for \(\mathcal{F}\) at x ∗ holds. Then, min(P)=max(D).

Proof

Let \(f:=\max_{j\in\mathbb{N}_{r}} p_{j}\) and \(\mu^{*} := \min(P) \in\mathbb {R}\). If \(x^{*}\in\mathcal{F}\) is an optimal solution of (P), that is, f(x ∗)=μ ∗, then by optimality conditions we have \(0\in\partial f(x^{*}) + N_{\mathcal{F}}(x^{*})\). As a consequence of the normal cone condition for \(\mathcal{F}\) at x ∗ and [20, Proposition 2.3.12], we get

$$0 = \sum_{j=1}^{r}{\bar{\delta}_j \nabla p_j(x^*)} + \sum _{i=1}^m \bar{\lambda}_i \nabla g_i(x^*) $$

for some \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) with \(\bar{\lambda}_{i} g_{i}(x^{*}) = 0\) for all \(i\in\mathbb{N}_{m}\), and \(\bar{\delta}\in\Delta\) with \(\bar{\delta}_{j}=0\) for those \(j\in\mathbb{N}_{r}\) such that p j (x ∗)≠μ ∗. Note that the polynomial

$$ L :=\sum _{j=1}^{r}{\bar{\delta}_j p_j} + \sum _{i=1}^m \bar{ \lambda}_i g_i - \mu^* $$

satisfies L(x ∗)=0 and ∇L(x ∗)=0. Moreover, L is a SOS-convex polynomial since p j and g i are all SOS-convex polynomials. Then, as a consequence of Lemma 2.1, L is a sum-of-squares polynomial (of degree at most d). Then, \((\bar{\delta },\bar{\lambda},\mu^{*})\) is a feasible point of (D), so μ ∗≤sup(D). Since weak duality always holds, we conclude min(P)=max(D). □

The following simple example illustrates the above min-max duality theorem.

Example 3.2

Consider the optimization problem

$$ (P_1)\quad\min _{x\in\mathbb{R}} \bigl\{ \max\bigl\{ 2x^4-x, 5x^2+x \bigr\} : x\geq-2 \bigr\} . $$

It is easy to check that x ∗=0 is a minimizer of (P 1) and min(P 1)=0. The corresponding dual problem of (P 1) is

$$ (D_1) \quad\max _{\delta\geq0,\lambda\geq0, \mu\in\mathbb{R}} \bigl\{ \mu: \delta \bigl(2x^4-x\bigr) + (1-\delta) \bigl(5x^2+x\bigr) - \lambda(x+2) - \mu\in\varSigma^2_4 \bigr\} . $$

As \(x^{4} + \frac{5}{2}x^{2} \in\varSigma^{2}_{4} \), \(\delta= \frac{1}{2}\), λ=0 and μ=0 is a feasible point of (D 1). So, sup(D 1)≥0. On the other hand, the sum-of-squares constraint in (D 1) gives us −2λ−μ≥0. Consequently, μ≤−2λ≤0, which implies max(D)=0.

4 Applications to Robust Optimization and Rational Programs

In this section, we provide applications of our duality theorems to robust SOS-convex programming problems under data uncertainty and to rational programming problems.

Let us consider the following optimization program with the data uncertainty in the constraints and in the objective function:

$$(\mathit{UP}) \quad\inf _{x\in\mathbb{R}^n} \bigl\{ f_0(x,v_0) : f_i(x,v_i) \leq0,\ \forall i=1,\ldots,k\bigr\} , $$

where, for each \(i\in\{0\}\cup\mathbb{N}_{k}\), v i is an uncertain parameter and \(v_{i} \in\mathcal{V}_{i}\) for some \(\mathcal{V}_{i} \subset \mathbb{R}^{n_{i}}\). The robust counterpart of (UP) is given by

$$(\mathit{RP}) \quad \inf_{x\in\mathbb{R}^n} \sup _{v_0\in\mathcal{V}_0} \bigl\{ f_0(x,v_0) \ : \ f_i(x,v_i) \leq0,\ \forall v_i\in\mathcal{V}_i, \forall i=1, \ldots,k \bigr\} . $$

Theorem 4.1

(Finite data uncertainty)

Let f i (⋅,v i ) be a SOS-convex polynomial for each \(v_{i}\in \mathcal{V}_{i} :=\{v_{i}^{1},\ldots,v_{i}^{s_{i}} \}\) and each \(i\in\{0\}\cup \mathbb{N}_{k}\) and let r:=s 0. Assume that there exists \(\bar{x}\in \mathbb{R}^{n}\) such that \(f_{i}(\bar{x},v_{i}^{j}) < 0\) for all \(j\in\mathbb {N}_{s_{i}}\) and \(i\in\mathbb{N}_{k}\). Then, one has inf(RP)=max(RD) where

$$ \begin{aligned} &(\mathit{RD})\quad \sup \mu \\ &\phantom{(\mathit{RD})\quad} \textit{s.t.} \quad \sum_{l=1}^{r}{\delta_l f_0\bigl(\cdot,v_0^l\bigr)} + \sum _{i=1}^{k}{\sum_{j=1}^{s_i}{ \lambda_i^j f_i\bigl(\cdot,v_i^j\bigr) }} - \mu\in\varSigma^2_t \\ &\phantom{(\mathit{RD})\quad \textit{s.t.} \quad} \delta\in\Delta,\quad \lambda_i\in\mathbb{R}^{s_i}_{+}\ (\forall i\in \mathbb{N}_k),\quad \mu\in\mathbb{R}, \end{aligned} $$
(10)

and t is the smallest even number such that

$$t\geq \max\Bigl\{ \max_{l\in\mathbb{N}_{r}}\deg f_0\bigl(\cdot,v_0^l\bigr), \max_{i\in\mathbb{N}_k}\max_{j\in\mathbb{N}_{s_i}}\deg f_i(\cdot,v_i^j) \Bigr\} . $$

Proof

It is easy to see that problem (RP) is equivalent to

$$(\mathit{RP}_e)\quad\inf\max _{j\in\mathbb{N}_{r}} \bigl\{ f_0\bigl(x,v_0^j\bigr) \ : \ f_i\bigl(x,v_i^j\bigr) \leq0,\ \forall j \in\mathbb{N}_{s_i}, \forall i=1,\ldots,k\bigr\} . $$

Since the Slater condition holds, we conclude inf(RP e )=max(RD) by applying Theorem 3.2. □

Theorem 4.2

(Polytopic data uncertainty)

Suppose that, for each \(i\in\{0\}\cup\mathbb{N}_{k}\), x↦f i (x,v i ) is a SOS-convex polynomial for each \(v_{i} \in\mathcal{V}_{i}:=\operatorname{conv}\{v_{i}^{1},\ldots,v_{i}^{s_{i}} \}\) with r:=s 0, and v i ↦f i (x,v i ) is affine for each \(x\in\mathbb{R}^{n}\). Assume that there exists \(\bar{x}\in\mathbb{R}^{n}\) such that \(f_{i}(\bar{x},v_{i}^{j}) < 0\) for all \(j\in\mathbb{N}_{s_{i}}\) and \(i\in\mathbb{N}_{k}\). Then, one has inf(RP)=max(RD), where the problem (RD) is defined in (10).

Proof

Let \(i\in\mathbb{N}_{k}\). As f i (x,⋅) is affine for each \(x\in \mathbb{R}^{n}\), then f i (x,v i )≤0 for all \(v_{i}\in\mathcal{V}_{i}:=\operatorname{conv}\{v_{i}^{1},\ldots,v_{i}^{s_{i}}\}\) if and only if \(f_{i}(x,v_{i}^{j}) \leq 0\) for all \(j\in\mathbb{N}_{s_{i}}\). Moreover, we see that

$$\sup_{v_0\in\mathcal{V}_0} f_0(x,v_0) = \max_{j\in\mathbb {N}_{r}} f_0(x,v_0^j). $$

Hence, problem (RP) is equivalent to (RP e ). Reasoning as in the proof of the above theorem, we conclude inf(RP)=max(RD). □

Now, consider the following minimax rational programming problem,

$$(\mathcal{P})\quad\inf _{x\in\mathbb{R}^n} \biggl\{ \max _{j\in\mathbb{N}_r}\,\frac{p_j(x)}{q(x)} : g_i(x) \leq0, i \in\mathbb{N}_m\biggr\} , $$

where p j , for \(j\in\mathbb{N}_{r}\), q, and g i , for \(i\in\mathbb {N}_{m}\), are real polynomials on \(\mathbb{R}^{n}\), and for each \(j\in \mathbb{N}_{r}\), p j (x)≥0 and q(x)>0 over the feasible set \(\mathcal{F}\), which is assumed to be nonempty. This is a generalization of problem (P) introduced in (2). For related minimax fractional programs, see [21, 22]. Minimax fractional programs often appear in resource allocation and planning problems of management science where the objective function in their optimization problems involve ratios such as cost or profit in time, return on capital and earnings per share (see [23]).

We associate with \((\mathcal{P})\) the following SDP dual problem

$$ \begin{aligned} &(\mathcal{D})\quad \sup \mu\\ &\phantom{(\mathcal{D})\quad} \text{s.t.} \quad \sum_{j=1}^{r}{\delta_j p_j} + \sum _{i=1}^{m}{\lambda_i g_i} -\mu q \in\varSigma^2_d \\ & \phantom{(\mathcal{D})\quad \text{s.t.} \quad} \delta\in\Delta,\quad \lambda\in\mathbb{R}^m_+, \quad\mu\in\mathbb{R}, \end{aligned} $$
(11)

where d is the smallest even number such that

$$d\geq\max\Bigl\{ \deg q, \max_{j\in\mathbb{N}_r}\deg p_j, \max _{i\in\mathbb{N}_m}\deg g_i \Bigr\} . $$

It is worth noting that, in general, problem \((\mathcal{P})\) may not attain its optimal value when it is finite, even when r=1. To see this, consider the rational programming problem \((\mathcal{P}_{1})\) \(\inf _{x\in\mathbb{R}} \{ \frac{1}{x} : 1-x \leq0 \}\). Obviously, \(\inf (\mathcal{P}_{1}) = 0\), however, for any feasible point x, one has \(\frac {1}{x}>0\). Thus, the optimal value of \((\mathcal{P}_{1})\) is not attained.

Theorem 4.3

(Strong duality for minimax rational programs)

Let p j , g i and −q be SOS-convex polynomials for all \(j\in \mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\), such that p j (x)≥0 and q(x)>0 for all \(x\in\mathcal{F}\). If the Slater condition holds, then

$$\inf(\mathcal{P}) = \max(\mathcal{D}). $$

Proof

Note that, for any \(\mu\in\mathbb{R}_{+}\), one has \(\inf(\mathcal{P})\geq \mu\) if and only if inf(P μ )≥0, where

$$ (P_{\mu}) \quad\inf _{x\in\mathcal{F}}\,\max _{j\in\mathbb{N}_r}\,\bigl\{ p_j(x)-\mu q(x)\bigr\} . $$
(12)

By the assumption, \(\inf(\mathcal{P})\) is finite. So, it follows easily that \(\mu^{*} := \inf(\mathcal{P}) \in\mathbb{R}_{+} \) and then \(\inf(P_{\mu ^{*}}) \geq0\). Since, for each \(j\in\mathbb{N}_{r}\), p j −μ ∗ q is a SOS-convex polynomial and the Slater condition holds, by Theorem 3.2, we have \(\inf(P_{\mu^{*}}) = \max(D_{\mu^{*}})\), where

$$ \begin{aligned} &(D_{\mu^*})\quad \sup \theta\\ &\phantom{(D_{\mu^*})\quad} \text{s.t.} \quad \sum_{j=1}^{r}{\delta_j p_j} + \sum _{i=1}^{m}{\lambda_i g_i} -\mu^* q -\theta\in\varSigma^2_d \\ & \phantom{(D_{\mu^*})\quad \text{s.t.} \quad} \delta\in\Delta,\quad \lambda\in\mathbb{R}^m_+, \quad\theta\in\mathbb{R}. \end{aligned} $$
(13)

As \(\max(D_{\mu^{*}})=\inf(P_{\mu^{*}}) \geq0\), there exist \(\bar{\delta }\in\Delta\), \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) and \(\bar{\theta}\in \mathbb{R}_{+}\) such that

$$\sum_{j=1}^{r}{\bar{\delta}_j p_j} + \sum_{i=1}^{m}{\bar{\lambda }_i g_i} -\mu^*q \in(\bar{\theta} + \varSigma^2_d) \subset\varSigma^2_d. $$

Therefore, \((\bar{\delta},\bar{\lambda},\mu^{*})\) is a feasible point of \((\mathcal{D})\), so \(\mu^{*} \leq\sup(\mathcal{D}) \). Since weak duality always holds, we conclude \(\inf(\mathcal{P}) = \max(\mathcal{D})\). □

Let us consider the particular problem \((\mathcal{P}^{cq})\) where p j , q and g i are all quadratic functions; that is, \(p_{j}(x) = x^{T} A_{j} x + a_{j}^{T} x + \alpha_{j}\), q(x)=x T Bx+b T x+β and \(g_{i}(x) = x^{T} C_{i} x + c_{i}^{T} x + \gamma_{i}\) for all \(x\in\mathbb{R}^{n}\), with \(A_{j}, B, C_{i} \in\mathbb{S}^{n}\), \(a_{j}, b, c_{i} \in\mathbb{R}^{n}\) and \(\alpha _{j},\beta,\gamma_{i} \in\mathbb{R}\) for all \(j\in\mathbb{N}_{r}\) and \(i\in \mathbb{N}_{m}\); that is,

$$ \begin{aligned} &(\mathcal{P}^{cq}) \quad \inf_{x\in\mathbb{R}^n} \max_{j\in\mathbb{N}_r}\, \frac{x^T A_j x + a_j^T x + \alpha_j}{x^T B x + b^T x + \beta}\\ &\phantom{(\mathcal{P}^{cq}) \quad} \text{s.t.} \quad x^T C_i x + c_i^T x + \gamma_i \leq0,\quad i\in\mathbb{N}_m. \end{aligned} $$

Assume that p j (x)≥0 and q(x)>0 over the feasible set. The dual problem of \((\mathcal{P}^{cq})\) is given by

$$ \begin{aligned} &(\mathcal{D}^{cq})\quad \sup \mu \\ &\phantom{(\mathcal{D}^{cq})\quad} \text{s.t.} \quad \sum_{j=1}^r\delta_j \left( \begin{array}{c@{\quad}c} 2\alpha_j & a_j^T \\ a_j & 2A_j \end{array} \right) + \sum_{i=1}^m \lambda_i \left( \begin{array}{c@{\quad}c} 2\gamma_i & c_i^T \\ c_i & 2C_i \end{array} \right) - \mu \left( \begin{array}{c@{\quad}c} 2\beta& b^T \\ b & 2B \end{array} \right) \succeq0, \\ &\phantom{(\mathcal{D}^{cq})\quad \text{s.t.} \quad} \delta\in\Delta, \quad\lambda\in\mathbb{R}^m_+, \quad\mu\in\mathbb{R}, \end{aligned} $$

which is clearly a semidefinite programming problem.

Corollary 4.1

Let consider the problem \((\mathcal{P}^{cq})\) such that \(A_{j}, -B, C_{i} \in\mathbb{S}^{n}_{+}\) for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb {N}_{m}\). If there exists \(\bar{x}\in\mathbb{R}^{n}\) such that \(\bar{x}^{T} C_{i} \bar{x} + c_{i}^{T} \bar{x} + \gamma_{i} < 0\) for all \(i\in\mathbb {N}_{m}\), then

$$\inf(\mathcal{P}^{cq}) = \max(\mathcal{D}^{cq}). $$

Proof

Note that the sum-of-squares constraint in its associated dual problem \(\sum_{j=1}^{r}{\delta_{j} p_{j}} + \sum_{i=1}^{m}{\lambda_{i} g_{i}} -\mu q \in\varSigma^{2}_{2}\) is equivalent to \(\sum_{j=1}^{r}{\delta _{j} p_{j}} + \sum_{i=1}^{m}{\lambda_{i} g_{i}} -\mu q \geq0\). This is further equivalent to

$$ \left( \begin{array}{c@{\quad}c} \sum_{j=1}^r\delta_j \alpha_j + \sum_{i=1}^m\lambda _i\gamma_i -\mu\beta & \frac{1}{2} (\sum_{j=1}^r \delta_j a_j^T + \sum_{i=1}^m\lambda_i c_i^T -\mu b^T) \\ \frac{1}{2} (\sum_{j=1}^r \delta_j a_j + \sum _{i=1}^m\lambda_i c_i -\mu b) & \sum_{j=1}^r \delta_j A_j + \sum _{i=1}^m\lambda_i C_i -\mu B \end{array} \right) \succeq0. $$

So, our dual problem \((\mathcal{D})\) collapses to \((\mathcal{D}^{cq})\). Since the Slater condition holds and any convex quadratic function is a SOS-convex polynomial, by applying Theorem 4.3 we get \(\inf(\mathcal{P}^{cq}) = \max(\mathcal{D}^{cq})\). □

Corollary 4.2

Let p, g i and −q be SOS-convex polynomials for all \(i\in\mathbb {N}_{m}\), such that p(x)≥0 and q(x)>0 for all \(x\in\mathcal{F}\). If the Slater condition holds, then

$$\inf_{x\in\mathcal{F}} \frac{p(x)}{q(x)} = \max_{\mu\in \mathbb{R},\lambda\in\mathbb{R}^m_+} \Biggl\{ \mu: p + \sum_{i=1}^{m}{\lambda _i g_i} -\mu q \in\varSigma^2_k \Biggr\} $$

where k is the smallest even number such that \(k\geq\max\{ \deg p, \deg q, \max_{i\in\mathbb{N}_{m}}\deg g_{i} \}\).

Proof

It is a straightforward consequence of Theorem 4.3 when r=1. □

Next we show that the non-negativity of the polynomials p j can be dropped whenever q is an affine function.

Corollary 4.3

Let p j and g i be SOS-convex polynomials for each \(j\in\mathbb {N}_{r}\) and each \(i\in\mathbb{N}_{m}\), \(b\in\mathbb{R}^{n}\) and \(\beta\in \mathbb{R}\) such that b T x+β>0 for all \(x\in\mathcal{F}\). If the Slater condition holds, then

$$ \inf _{x\in\mathcal{F}} \, \max _{j\in\mathbb{N}_r} \, \frac{p_j(x)}{b^Tx+\beta} = \max _{\substack{\mu\in\mathbb{R} \\ \delta\in\Delta, \lambda\in\mathbb {R}^m_+}} \Biggl\{ \mu: \sum _{j=1}^{r}{\delta_j p_j} + \sum _{i=1}^{m}{ \lambda_i g_i} -\mu\bigl(b^{T}(\cdot) + \beta\bigr) \in\varSigma^2_d \Biggr\} . $$

Proof

The proof follows the same line of arguments as the proof of Theorem 4.3, except that, in the case q(x):=b T x+β for all \(x\in\mathbb{R}^{n}\), all polynomials p j −μ ∗ q are SOS-convex without the non-negativity of all p j ’s, and therefore, of μ ∗. □

For the particular problem

$$\bigl(\mathcal{P}^{l}\bigr)\quad\inf _{x\in\mathbb{R}^n}\biggl\{ \max _{j\in\mathbb{N}_r}\, \frac{a_j^T x + \alpha_j}{b^T x + \beta} \ : \ c_i^T x + \gamma_i \leq0, \ i\in\mathbb{N}_m \biggr\} , $$

the corresponding dual problem can be stated as the following linear programming problem:

$$\begin{aligned} &\bigl(\mathcal{D}^{l}\bigr) \quad\max \mu \\ &\phantom{\bigl(\mathcal{D}^{l}\bigr) \quad} \text{s.t.} \quad \sum _{j=1}^r \delta_j a_j + \sum _{i=1}^m \lambda_i c_i -\mu b = 0, \end{aligned}$$
(14)
$$\begin{aligned} &\phantom{\bigl(\mathcal{D}^{l}\bigr) \quad \text{s.t.} \quad} \sum _{j=1}^r \delta_j \alpha_j + \sum _{i=1}^m \lambda_i\gamma_i - \mu\beta\geq0, \\ &\phantom{\bigl(\mathcal{D}^{l}\bigr) \quad \text{s.t.} \quad} \delta\in\Delta, \quad\lambda\in\mathbb{R}^m_+, \quad\mu\in\mathbb{R}. \end{aligned}$$
(15)

Corollary 4.4

Let \(\alpha_{j},\beta,\gamma_{i} \in\mathbb{R}\) and \(a_{j},b,c_{i} \in\mathbb {R}^{n}\) for all \(j\in\mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\). Assume that b T x+β>0 for all feasible point x of \(\mathcal{P}^{l}\). Then,

$$\inf(\mathcal{P}^{l}) = \max(\mathcal{D}^{l}). $$

Proof

By applying Corollary 4.3, we find that \(\inf(\mathcal{P}^{l})\) equals

$$ \max _{\substack{\mu\in\mathbb{R} \\ \delta\in\Delta, \lambda\in\mathbb {R}^m_+}} \Biggl\{ \mu: \sum _{j=1}^r \delta_j \bigl( a_j^T x + \alpha_j \bigr) + \sum _{i=1}^m \lambda_i \bigl(c_i^T x + \gamma_i \bigr) - \mu\bigl( b^T x + \beta\bigr) \in \varSigma^2_2 \Biggr\} . $$

Since the sum-of-squares constraint in the above dual problem is equivalent to (14) and (15), we conclude \(\inf(\mathcal{P}^{l}) = \max(\mathcal{D}^{l})\). □

If a minimizer x ∗ of \((\mathcal{P})\) is known, then the Slater condition in Theorem 4.3 can be replaced by a weaker condition in order to derive strong duality between \((\mathcal{P})\) and \((\mathcal{D})\).

Theorem 4.4

Let p j , g i and −q be SOS-convex polynomials for all \(j\in \mathbb{N}_{r}\) and \(i\in\mathbb{N}_{m}\), such that p j (x)≥0 and q(x)>0 for all \(x\in\mathcal{F}\). Let \(x^{*}\in\mathcal{F}\) be an optimal solution of \((\mathcal{P})\) and assume that the normal cone condition for \(\mathcal{F}\) at x ∗ holds. Then, \(\min(\mathcal{P}) = \max(\mathcal{D})\).

Proof

Let \(\mu^{*} := \min(\mathcal{P}) \in\mathbb{R}_{+}\). Note that \((\mathcal{P})\) has optimal solution x ∗ with optimal value μ ∗ if and only if x ∗ is an optimal solution of \((P_{\mu^{*}})\) with optimal value 0 (cf. [22, Lemma 2.3]), where \((P_{\mu^{*}})\) is stated in (12). Since, for each \(j\in\mathbb{N}_{r}\), p j −μ ∗ q is a SOS-convex polynomial and the normal cone condition for \(\mathcal{F}\) at x ∗ holds, by Theorem 3.3 we have \(\min (P_{\mu^{*}}) = \max(D_{\mu^{*}})\), where \((D_{\mu^{*}})\) has been stated in (13). As \(\max(D_{\mu^{*}}) = 0\), there exist \(\bar{\delta}\in \Delta\) and \(\bar{\lambda}\in\mathbb{R}^{m}_{+}\) such that

$$\sum_{j=1}^{r}{\bar{\delta}_j p_j} + \sum_{i=1}^{m}{\bar{\lambda }_i g_i} -\mu^*q \in\varSigma^2_d. $$

Therefore, \((\bar{\delta},\bar{\lambda},\mu^{*})\) is a feasible point of \((\mathcal{D})\), so \(\mu^{*} \leq\sup(\mathcal{D}) \). Since weak duality always holds, we conclude \(\min(\mathcal{P}) = \max(\mathcal{D})\). □

5 Conclusions

In this paper, we have shown that various classes of minimax programs involving sum-of-squares convex (SOS-convex) polynomials exhibit zero duality gaps with their corresponding dual programs without any qualifications. The significance of the results is that the dual programs are representable as semidefinite programs which can efficiently be solved by interior-point methods. So, the optimal values of the original minimax problems can be found by solving their dual programs. Under constraint qualifications, we further derived strong duality results where the dual programs attain their optimal values. We applied our results to obtain corresponding results for robust SOS-convex programs under polytopic data uncertainty and to minimax fractional programs including minimax fractional programs involving quadratic functions.