Tutte Polynomials of Two Self-similar Network Models

Abstract

The Tutte polynomial T(G; x, y) of a graph G, or equivalently the q-state Potts model partition function, is a two-variable polynomial graph invariant of considerable importance in combinatorics and statistical physics. Graph operations have been extensively applied to model complex networks recently. In this paper, we study the Tutte polynomials of the diamond hierarchical lattices and a class of self-similar fractal models which can be constructed through graph operations. Firstly, we find out the behavior of the Tutte polynomial under k-inflation and k-subdivision which are two graph operations. Secondly, we compute and gain the Tutte polynomials of this two self-similar fractal models by using their structure characteristic. Moreover, as an application of the obtained results, some evaluations of their Tutte polynomials are derived, such as the number of spanning trees and the number of spanning forests.

1 Introduction

The Tutte polynomial of a graph, also known as the partition function of the Potts model, is a polynomial in two variables which plays an important role in several areas of sciences. Though originally studied in algebraic graph theory as a generalization of counting problems related to graph coloring [1], it has many interesting connections with statistical mechanical models as the Potts model [2, 3], the Abelian Sandple Model [4, 5], as well as the Jones polynomial [6] from knot theory. In a strong sense it contains every graphical invariant that can be computed by deleting and contraction operations which are natural reductions for many network models. The Tutte polynomial for a particular point at (x, y)-plane is related to much combinatorial information and algebraic properties of a graph, including the number of spanning trees, the number of spanning connected subgraphs and many more. Moreover, the Tutte polynomial contains several other polynomial invariants, such as the chromatic polynomial, the flow polynomial and the all terminal reliability polynomial as partial evaluations [7, 8]. However, there are no widely available effective computational tools to compute the Tutte polynomial of a graph of reasonable size.

In general, it is much easier to compute the Tutte polynomial of a small graph than a large one. Since a large graph can be obtained from some small graphs by using some kinds of graph operations, we can reduce the difficulty of computing the Tutte polynomial of a large graph if we find out the recurrence relations of the Tutte polynomials under these graph operations. It is well known that the diamond hierarchical lattices [9,10,11,12,13] can be constructed recursively by replacing each edge at one step by a set of edges in a diamond shape. The beauty of these lattices is that the Migdal–Kadanoff real-space renormalization is exact. Using this fact, Muzy and Salinas [14] analyzed the critical behavior of a q-state Potts model with correlated disordered ferromagnetic exchange interactions along the layers of the first type of the diamond hierarchical lattice. Bleher and Lyubich [15] studied the analytical continuation in the complex plane of free energy of the Ising model on the second type of the diamond hierarchical lattice and proved that for almost all (with respect to the harmonic measure) geodesics the complex critical exponent is common. Qiao [16] studied the phase transition of the Potts model on the second type of the diamond hierarchical lattice and gave a complete description about the connectivity of the set of the complex singularities. However, not much work has been done on the computing the Potts model partition functions of these hierarchical lattices. Recently, Ma and Yao [17] introduced a class of self-similar fractal models $\{L_t\}$ through subdivision [18] which is a kind of graph operation. By using both induction and iterative computational method, they got an exact analytical solution for the number of spanning trees of this model.

In this paper, we follow a combinatorial approach and use the recursive structure to investigate the Tutte polynomials of the diamond hierarchical lattices and the fractal models. Firstly, based on the construction methods, we study the relations between the spanning subgraphs of graph G and the spanning subgraphs of its operation graphs. Secondly, using these relations, we divide the sets of spanning subgraphs of its operation graphs into disjoint subsets and compute the contribution of each subset. Thirdly, we find recursive expressions of the Tutte polynomials of its operation graphs. Finally, as an application of the obtained recurrence relations, we compute and gain the Tutte polynomials of two types of the diamond hierarchical lattices and a class of self-similar fractal models. Moreover, we obtain some evaluations of these Tutte polynomials, such as the number of spanning trees and the number of totally cyclic orientations. It is worth mentioning that the Tutte polynomials of some special graphs (or lattices) have been computed by several different methods in both fields of combinatorics and statistical physics recently [19,20,21,22,23,24,25,26]. The method used in this work is different with others. Our technique could be extended to compute the Tutte polynomials of other classes of recursive graphs which could be obtained through edge replacement graph operations.

2 Preliminaries

In this section we briefly discuss some necessary background that will be used for our calculations. We use standard graph terminology and the words “network”, “lattice”, and “graph” indistinctly.

2.1 Tutte Polynomial

For a graph G we denote by V(G) its set of vertices and by E(G) its set of edges. Let |V(G)| and |E(G)| denote the cardinality of V(G) and E(G), respectively. Let k(G) be the number of connected components of the graph G. There is a useful relation that expresses the Tutte polynomial T(G; x, y) as a sum of contributions from spanning subgraphs of G. Here, a spanning subgraph$A=(V(A),E(A))$ has the same vertex set as G and a subset of E(G), $E(A)\subseteq E(G)$. If G is connected, this relation is

$$\begin{aligned} T(G;x,y)= \sum _{A\subseteq G}(x-1)^{k(A)-1}(y-1)^{n(A)}, \end{aligned}$$

where $n(A)=|E(A)|+k(A)-|V(A)|$ is the nullity of A. Note that throughout this paper n(G) only denote the nullity of a graph G, it does not denote the number of vertices of G. Recall that a one-point join $G*H$ of two graphs G and H is formed by identifying a vertex of G and a vertex of H into a single vertex of $G*H$. It is well known that the Tutte polynomial fulfills the following property:

$$\begin{aligned} T(G*H;x,y)=T(G;x,y)T(H;x,y). \end{aligned}$$

We will refer to this equality as one-point join property hereafter. In the sequel of the paper, we will be interested in special evaluations of the Tutte polynomial at some particular points (x, y), that allow us to deduce many combinatorial and algebraic properties of the considered graphs. The special evaluations of interest are (i) $T(G;1,1)=\tau (G)$, the number of spanning trees of G; (ii) $T(G;2,1)=\sigma (G)$, the number of spanning forests of G [7].

2.2 The Diamond Hierarchical Lattices

As we know, the hierarchical lattices are generated in an iterative manner, starting from an edge. One then repeatedly uses an operation of replacing each edge by a diamond shape simple graph. Different diamond shape simple graphs lead to different diamond hierarchical lattices. We only study two famous types of the diamond hierarchical lattices in this paper.

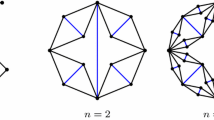
The first type of the diamond hierarchical lattice $F_t$ (see Fig. 1), also known as the (2, 2)-flower in [27], is a particular case of the (x, y)-flower [28]. Clearly, the network is self-similar. It is easy to see that the number of edges in $F_t$ is $|E(F_t)|=4^t$. According to the generating algorithm for the first type of the diamond hierarchical lattice, the number of vertices $|V(F_t)|$ in $F_t$ satisfies the recursive relation $|V(F_t)|=|V(F_{t-1})|+2|E(F_{t-1})|$, which together with the initial condition $|V(F_0)|=2$ yields $|V(F_t)|=\frac{2}{3}(4^t+2)$.

Fig. 1

The first three generations of $F_t$

The second type of the diamond hierarchical lattice $Q_t$ (see Fig. 2) is also self-similar. The number of edges in $Q_t$ is $|E(Q_t)|=6^t$. The number of vertices $|V(Q_t)|$ in $Q_t$ satisfies the recursive relation $|V(Q_t)|=|V(Q_{t-1})|+3|E(Q_{t-1})|$, which together with the initial condition $|V(Q_0)|=2$ yields $|V(Q_t)|=\frac{3}{5}\left( 6^t+\frac{7}{3}\right)$.

Fig. 2

The first three generations of $Q_t$

2.3 The Network Model $L_t$

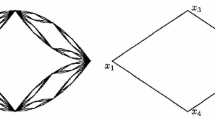
This class of self-similar fractal models $\{L_t\}$ can be created in the following recursive way. For $t=0$, $L_0$ is the complete graph $K_3$. For $t\ge 1$, $L_t$ is obtained from $L_{t-1}$: every existing edge in $L_{t-1}$ is replaced with a path of length 2; every existing vertex in $L_{t-1}$ is replaced with a copy of the complete graph $K_3$. Figure 3 illustrates the construction process for the first three generations.

Fig. 3

The first three generations of $L_t$

According to the network construction method, one can see that at each step t$(t\ge 1)$,

$$\begin{aligned} \left\{ \begin{array}{ll} |V(L_t)|=3|V(L_{t-1})|+|E(L_{t-1})|; \\ |E(L_t)|=3|V(L_{t-1})|+2|E(L_{t-1})|. \end{array} \right. \end{aligned}$$

Under the initial conditions $|E(L_0)|=3$ and $|V(L_0)|=3$, we can know

$$\begin{aligned} |E(L_t)|= & {} \frac{3}{\lambda -\mu } \left( 5(\lambda ^t-\mu ^t)-\lambda \mu (\lambda ^{t-1}-\mu ^{t-1})\right) ,\\ |V(L_t)|= & {} \frac{3}{\lambda -\mu } \left( 5(\lambda ^t-\mu ^t)-(\lambda \mu +5)(\lambda ^{t-1}- \mu ^{t-1})+\lambda \mu (\lambda ^{t-2}-\mu ^{t-2})\right) , \end{aligned}$$

where $\lambda =\frac{5+\sqrt{13}}{2}$, $\mu =\frac{5-\sqrt{13}}{2}$. Note that this result is consistent with previous work [17].

3 Tutte Polynomial of Two Operation Graphs

Let G be a simple and connected graph with n vertices and m edges. Let D(G) denote the set of spanning subgraphs of G.

3.1 The Tutte Polynomial of the Inflation Graph

The k-inflation graph of graph G, denoted by $I_k(G)$, is the graph obtained from G by replacing each edge in G by k new edges connecting the same vertices. An example of $I_2(G)$ is given in Fig. 4. It is not difficult to see that $I_k(G)$ has km edges. Then $|D(I_k(G))|=2^{km}$.

Fig. 4

Graph G and its 2-inflation graph $I_2(G)$

Let R be the k-inflation graph of an edge. Let H be a spanning subgraph of G with $i\in \{0,1,\cdots ,m\}$ edges. If a graph A can be obtained from H by replacing each edge $e \in E(H)$ with at least one edge of R, A is an expanded graph of H. Figure 5 shows an example of expanded graph. According to the construction process of $I_k(G)$ we know that every expanded graph of H is a spanning subgraph of $I_k(G)$.

Fig. 5

A is an expanded graph of H

Lemma 3.1

Let H be a spanning subgraph of G with $i\in \{0,1,\cdots ,m\}$ edges, and let $[H]_1$ denote the set of expanded graphs of H. Then $|[H]_1|=(2^k-1)^i$.

Proof

Each edge $e\in H$ could be replaced by at least one edge of R. There are $\left( {\begin{array}{c}k\\ 1\end{array}}\right) +\cdots +\left( {\begin{array}{c}k\\ i\end{array}}\right) +\left( {\begin{array}{c}k\\ k\end{array}}\right) =2^{k}-1$ different ways to replace the edge e. Since H has i edges and the replacement is independent with each other, we have $(2^k-1)^{i}$ different ways to replace the edges in H. It is clear that each way of replacing determines an expanded graph and different ways of replacing determine different expanded graphs. Therefore, $|[H]_1|=(2^k-1)^{i}$. $\square$

Lemma 3.2

Let ${\widehat{H}}=\bigcup _{H\in D(G)}[H]_1$. Then ${\widehat{H}}=D(I_k(G))$.

Proof

For every $H \in D(G)$, $[H]_1\subseteq D(I_k(G))$. So ${\widehat{H}}\subseteq D(I_k(G))$. Suppose that $H_1,H_2$ are two different spanning subgraphs of G. It is easy to see that $[H_1]_1\cap [H_2]_1=\emptyset$. For each $i\in \{0,1,\ldots ,m\}$, graph G has $\left( {\begin{array}{c}m\\ i\end{array}}\right)$ spanning subgraphs which have i edges. From Lemma 3.1 we have that $\left( {\begin{array}{c}m\\ 0\end{array}}\right) (2^k-1)^0+\left( {\begin{array}{c}m\\ 1\end{array}}\right) (2^k-1)+\cdots +\left( {\begin{array}{c}m\\ m\end{array}}\right) (2^k-1)^m=(2^k-1+1)^m=2^{km}$. Since $|D(I_k(G))|=2^{km}$,  ${\widehat{H}}=D(I_k(G))$. $\square$

Lemma 3.2 implies that $D(I_k(G))$ could be divided into $2^{km}$ disjoint subsets. Next we will compute the contribution to $T(I_k(G);x,y)$ of each subset.

Lemma 3.3

Let H be a spanning subgraph of G with i edges. Then

$$\begin{aligned} \sum _{A\in [H]_1}(x-1)^{k(A)-1}(y-1)^{n(A)}=(1+y+\cdots +y^{k-1})^i(x-1)^{k(H)-1}(y-1)^{n(H)}. \end{aligned}$$

Proof

For every $A\in [H]_1$, we have $k(A)=k(H)$ and

$$\begin{aligned} n(A)-n(H)= & {} (|E(A)|+k(A)-|V(A)|)-(|E(H)|+k(H)-|V(H)|)\\= & {} |E(A)|-|E(H)|. \end{aligned}$$

Therefore, the contribution of A is given by

$$\begin{aligned} (x-1)^{k(A)-1}(y-1)^{n(A)}=(x-1)^{k(H)-1}(y-1)^{n(H)}(y-1)^{|E(A)|-|E(H)|}. \end{aligned}$$

Let $\Delta E^A_e$ be the number of edges increased by replacing the edge $e\in H$ in the construction process of A. So $|E(A)|-|E(H)|=\sum _{e\in H}\Delta E^A_e$. Thus,

$$\begin{aligned} (y-1)^{|E(A)|-|E(H)|}=\prod _{e\in H}(y-1)^{\Delta E^A_e}. \end{aligned}$$

Hence, we have

$$\begin{aligned} \sum _{A\in [H]_1}(x-1)^{k(A)-1}(y-1)^{n(A)}= & {} (x-1)^{k(H)-1}(y-1)^{n(H)}\sum _{A\in [H]_1}(y-1)^{|E(A)|-|E(H)|}\\= & {} (x-1)^{k(H)-1}(y-1)^{n(H)}\sum _{A\in [H]_1}\prod _{e\in H}(y-1)^{\Delta E^A_e}. \end{aligned}$$

Let $\eta =\sum _{A\in [H]_1}\prod _{e\in H}(y-1)^{\Delta E^A_e}$. It is not easy to evaluate $\eta$ directly. Thus, we will compute it in an alternative way. For every edge $e \in H$, if the edge e is replaced by $t\in \{1,2,\cdots ,k\}$ edges of R, the number of edges increased by $t-1$. Since R has k edges, the contribution to $\eta$ given by replacing the edge e is $\left( {\begin{array}{c}k\\ 1\end{array}}\right) (y-1)^0+\cdots +\left( {\begin{array}{c}k\\ t\end{array}}\right) (y-1)^{t-1}+\cdots +\left( {\begin{array}{c}k\\ k\end{array}}\right) (y-1)^{k-1}=\frac{y^k-1}{y-1}=1+y+\cdots +y^{k-1}$. Since $|E(H)|=i$ and the replacement is independent with each other, the contribution given by replacing all edges of H is $(1+y+\cdots +y^{k-1})^{i}$. It is important to note that all expanded graphs $A \in [H]_1$ can be obtained from H by replacing edges. So we have $\eta =\sum _{A\in [H]_1}\prod _{e\in H}(y-1)^{\Delta E^A_e}=(1+y+\cdots +y^{k-1})^i$. $\square$

Theorem 3.4

Let G be a simple and connected graph with n vertices and m edges. Then

$$\begin{aligned} T(I_k(G);x,y)=(1+y+\cdots +y^{k-1})^{n-1}T\left( G;\frac{x+y+ \cdots +y^{k-1}}{1+y+\cdots +y^{k-1}},y^k\right) . \end{aligned}$$

Proof

According to Lemmas 3.2 and 3.3, it follows that

$$\begin{aligned} T(I_k(G);x,y)= & {} \sum _{H\in D(G)}\sum _{A\in [H]_1}(x-1)^{k(A)-1}(y-1)^{n(A)}\\= & {} \sum _{H\in D(G)}\left( 1+y+\cdots +y^{k-1}\right) ^{|E(H)|}(x-1)^{k(H)-1}(y-1)^{n(H)}\\= & {} \left( 1+y+\cdots +y^{k-1}\right) ^{n-1}\sum _{H\in D(G)}\left( \frac{x-1}{1+y+\cdots +y^{k-1}}\right) ^{k(H)-1}(y^k-1)^{n(H)}\\= & {} \left( 1+y+\cdots +y^{k-1}\right) ^{n-1}\sum _{H\in D(G)}\left( \frac{x+y+\cdots +y^{k-1}}{1+y+\cdots +y^{k-1}}-1\right) ^{k(H)-1}(y^k-1)^{n(H)}\\= & {} \left( 1+y+\cdots +y^{k-1}\right) ^{n-1}T\left( G;\frac{x+y+\cdots +y^{k-1}}{1+y+\cdots +y^{k-1}},y^k\right) . \end{aligned}$$

$\square$

Let $x=y=1$, we can compute the number of spanning trees of $I_k(G)$.

$$\begin{aligned} \tau (I_k(G))=k^{n-1}\tau (G). \end{aligned}$$

3.2 The Tutte Polynomial of the Subdivision Graph

The k-subdivision graph of graph G, denoted by $S_k(G)$, is the graph obtained from G by inserting k new vertices into each edge in G. Figure 6 illustrates an example of $S_2(G)$. In fact, the k-subdivision graph $S_k(G)$ is a path-replacement of G. It could be obtained from G by replacing each edge of G with a path of length k. It is not difficult to see that $S_k(G)$ has km edges. Then $|D(S_k(G))|=2^{km}$.

Fig. 6

Graph G and its 2-subdivision graph $S_2(G)$

If a graph B is a spanning subgraph of G and $B\ne G$, then B is called a proper spanning subgraph of G. Let P be the k-subdivision graph of an edge. Let H be a spanning subgraph of G with $i\in \{0,1,\ldots ,m\}$ edges, and let $C(H)=E(G)-E(H)$. Then $|C(H)|=m-i$. A graph A is said to be an extended graph of H if it can be obtained from G by replacing each edge $e \in E(H)$ with P and replacing each edge $e \in C(H)$ with a proper spanning subgraph of P. From the construction method of $S_k(G)$ we know that every extended graph A is a spanning subgraph of $S_k(G)$. Figure 7 displays an example of extended graph.

Fig. 7

A is an extended graph of H

Lemma 3.5

Let H be a spanning subgraph of G with i edges, and let $[H]_2$ denote the set of extended graphs of H. Then  $|[H]_2|=(2^k-1)^{m-i}$.

Proof

Since P has k edges, it has $2^k-1$ proper spanning subgraphs. For each edge $e\in C(H)$, it should be replaced by a proper spanning subgraph of P. So there are $2^k-1$ different ways to replace e. Since C(H) has $m-i$ edges, there are $(2^k-1)^{m-i}$ different ways to replace all edges in C(H). It is not difficult to see that each way of replacing edges of C(H) determines an extended graph and different ways determine different extended graphs. Therefore, $|[H]_2|=(2^k-1)^{m-i}$. $\square$

Lemma 3.6

Let ${\tilde{H}}=\bigcup _{H\in D(G)}[H]_2$. Then ${\tilde{H}}=D(S_k(G))$.

Proof

For each $H\in D(G)$, $[H]_2\subseteq D(S_k(G))$, then ${\tilde{H}}\subseteq D(S_k(G))$. Suppose that $H_1,H_2$ are two different spanning subgraphs of G. It is not difficult to see that $[H_1]_2\cap [H_2]_2=\emptyset$. Graph G has $\left( {\begin{array}{c}m\\ i\end{array}}\right)$ spanning subgraphs for each $i\in \{0,\ldots , m\}$. From Lemma 3.5 we have that $|{\tilde{H}}|=\left( {\begin{array}{c}m\\ 0\end{array}}\right) (2^k-1)^m+\cdots +\left( {\begin{array}{c}m\\ i\end{array}}\right) (2^k-1)^{m-i}+\cdots +\left( {\begin{array}{c}m\\ m\end{array}}\right) =(2^k-1+1)^m=2^{km}$. Since $|D(S_k(G))|=2^{km}$,  ${\tilde{H}}=D(S_k(G))$. $\square$

Lemma 3.6 says that $D(S_k(G))$ could be divided into $2^{km}$ disjoint subsets. Next we will compute the contribution to $T(S_k(G);x,y)$ of each subset.

Lemma 3.7

Let H be a simple graph. Then $n(S_k(H))=n(H)$.

Proof

Suppose that H has n vertices and i edges. Hence $S_k(H)$ has $n+(k-1)i$ vertices and ki edges. Clearly, $k(H)=k(S_k(H))$. Therefore,

$$\begin{aligned} n(S_k(H))= & {} ki+k(S_k(G))-(n+(k-1)i)\\= & {} i+k(S_k(G))-n\\= & {} n(H). \end{aligned}$$

$\square$

A pendant vertex is a vertex of degree 1 and a pendant edge is an edge incident with a pendant vertex. Let $p=v_0v_1\ldots v_s$$(s\ge 1)$ be a path with $d(v_1)=d(v_2)=\cdots =d(v_{s-1})=2$ where d(v) is the degree of the vertex v. We call p a pendant path if the $d(v_s)=1$ and $d(v_0)\ge 3$. The following three lemmas can be easily got by applying the definition of nullity.

Lemma 3.8

Let u be an isolated vertex of a graph H. Then $n(H-u)=n(H)$.

Lemma 3.9

Let e be a pendant edge of a graph H. Then $n(H-e)=n(H).$

Lemma 3.10

Let p be a pendant path of a graph H. Then $n(H-p)=n(H).$

Lemma 3.11

Let H be a spanning subgraph of graph G and graph $A\in [H]_2$. Then $n(A)=n(H)$.

Proof

Every proper spanning subgraph of P is constituted by isolated vertices, pendant edges and pendant paths. An extended graph $A\in [H]_2$ is obtained from G by replacing edges in C(H) with proper spanning subgraphs of P and replacing edges in H with P. Let $A'$ be the graph obtained from A by deleting all the proper spanning subgraphs of P which replace the edges belonging to C(H) in the construction process of A. Lemmas 3.8, 3.9 and 3.10 tell us that $n(A)=n(A')$. In fact, $A'$ is the k-subdivision graph of H. By Lemma 3.7, $n(A')=n(H)$. Therefore, $n(A)=n(H)$. $\square$

Lemma 3.12

Let H be a spanning subgraph of G with $i\in \{0,1,\cdots ,m\}$ edges. Then

$$\begin{aligned} \sum _{A\in [H]_2}(x-1)^{k(A)-1}(y-1)^{n(A)}=(1+x+\cdots +x^{k-1})^{m-i}(x-1)^{k(H)-1}(y-1)^{n(H)}. \end{aligned}$$

Proof

For every $A\in [H]_2$, $n(A)=n(H)$. Then the contribution given by A can be computed as follows.

$$\begin{aligned} (x-1)^{k(A)-1}(y-1)^{n(A)}=(x-1)^{k(H)-1}(y-1)^{n(H)}(x-1)^{k(A)-k(H)}. \end{aligned}$$

Let $\Delta k^A_e$ be the number of connected components increased by replacing the edge $e\in C(H)$ in the construction process of A. Then, $k(A)-k(H)=\sum _{e\in C(H) }\Delta k^A_e$. Hence,

$$\begin{aligned} (x-1)^{k(A)-k(H)}=\prod _{e\in C(H) }(x-1)^{\Delta k^A_e}. \end{aligned}$$

So, we have

$$\begin{aligned} \sum _{A\in [H]_2}(x-1)^{k(A)-1}(y-1)^{n(A)}= & {} (x-1)^{k(H)-1}(y-1)^{n(H)}\sum _{A\in [H]_2}(x-1)^{k(A)-k(H)}\\= & {} (x-1)^{k(H)-1}(y-1)^{n(H)}\sum _{A\in [H]_2}\prod _{e\in C(H)}(x-1)^{\Delta k^A_e}. \end{aligned}$$

Let $\theta =\sum _{A\in [H]_2}\prod _{e\in C(H)}(x-1)^{\Delta k^A_e}$. It is not easy to evaluate $\theta$ directly. Thus, we will compute it in an alternative way. Let $P'$ be a proper spanning subgraph of P with $t\in \{0,1,\ldots ,k-1\}$ edges. Since P is a path with k edges, then $P'$ has $k-t+1$ connected components and P has $\left( {\begin{array}{c}k\\ t\end{array}}\right)$ such proper spanning subgraphs. Let e be an edge in C(H). If it is replaced by $P'$, the number of connected components increased by $k-t-1$ since $e\notin H$. Therefore, the contribution to $\theta$ given by replacing the edge e is $\left( {\begin{array}{c}k\\ 0\end{array}}\right) (x-1)^{k-1}+\cdots +\left( {\begin{array}{c}k\\ t\end{array}}\right) (x-1)^{k-t-1}+\cdots +\left( {\begin{array}{c}k\\ k-1\end{array}}\right) (x-1)^{0}=\frac{x^k-1}{x-1}=1+x+\cdots +x^{k-1}$. Since $|C(H)|=m-i$ and the replacement is independent with each other, the contribution given by replacing edges is $(1+x+\cdots +x^{k-1})^{m-i}$. It is important to note that all extended graphs $A \in [H]_2$ can be obtained by this way. So we have $\theta =\sum _{A\in [H]_2}\prod _{e\in C(H)}(x-1)^{\Delta k^A_e}=(1+x+\cdots +x^{k-1})^{m-i}$. $\square$

Theorem 3.13

Let G be a simple and connected graph with n vertices and m edges. Then

$$\begin{aligned} T(S_k(G);x,y)=\left( 1+x+\cdots +x^{k-1}\right) ^{m-n+1}T\left( G;x^k,\frac{y+x+ \cdots +x^{k-1}}{1+x+\cdots +x^{k-1}}\right) . \end{aligned}$$

Proof

From Lemmas 3.6 and 3.12 we have

$$\begin{aligned} T(S_k(G);x,y)= & {} \sum _{H\in D(G)}\sum _{A\in [H]_2}(x-1)^{k(A)-1}(y-1)^{n(A)}\\= & {} \sum _{H\in D(G)}\left( 1+x+\cdots +x^{k-1}\right) ^{m-|E(H)|}(x-1)^{k(H)-1}(y-1)^{n(H)}\\= & {} (1+x+\cdots +x^{k-1})^{m-n+1}\sum _{H\in D(G)}(x^k-1)^{k(H)-1}\left( \frac{y-1}{1+x+\cdots +x^{k-1}}\right) ^{n(H)}\\= & {} \left( 1+x+\cdots +x^{k-1}\right) ^{m-n+1}T\left( G;x^k,\frac{y+x+ \cdots +x^{k-1}}{1+x+\cdots +x^{k-1}}\right) . \end{aligned}$$

$\square$

Let $x=y=1$, we can compute the number of spanning trees of $S_k(G)$.

$$\begin{aligned} \tau (S_k(G))=k^{m-n+1}\tau (G). \end{aligned}$$

When $k=2$, we have

$$\begin{aligned} \tau (S_2(G))=2^{m-n+1}\tau (G). \end{aligned}$$

Huang and Li [29] have proved that this equation holds for regular graphs. We prove that this equation also holds for a general simple graph.

4 Applications

We will study the Tutte polynomials of a class of self-similar fractal models and two types of diamond hierarchical lattices in this section. For convenience, we denote $I_2(G)$ by I(G) and denote $S_2(G)$ by S(G).

4.1 The Tutte Polynomial of $L_t$

As shown in Fig. 8, $L_t$ may be obtained from $S(L_{t-1})$ by joining a copy of the complete graph $K_3$ at every vertex existing in $L_{t-1}$. It is well known that $T(K_3;x,y)=y+x+x^2$.

Fig. 8

Illustration of the construction of $L_1$ by using the subdivision graph $S(L_0)$

Theorem 4.1

For each $t\ge 1$, The Tutte polynomial of $L_t$ is given by

$$\begin{aligned} T(L_t;x,y)= & {} (y+x+x^2)^{|V(L_{t-1})|}(1+x)^{|E(L_{t-1})|-|V(L_{t-1})|+1}T\left( L_{t-1};x^2,\frac{y+x}{1+x}\right) , \end{aligned}$$

with the initial condition $T(L_0;x,y)=y+x+x^2$.

Proof

This theorem follows from Theorem 3.13 and the one-point join property of Tutte polynomial immediately. $\square$

By setting $x=y=1$, we can obtain the number of spanning trees of $L_t$.

$$\begin{aligned} \tau (L_t)=T(L_t;1,1)=2^{t+\sum _{i=0}^{t-2}|E(L_{i})|}3^{1+\sum _{i=0}^{t-1}|V(L_{i})|}. \end{aligned}$$

Let $x=0,y=2$, we can obtain the number of totally cyclic orientations [7] of $L_t$.

$$\begin{aligned} o(L_t)=T(L_t;0,2)=2^{1+\sum _{i=0}^{t-1}|V(L_{i})|}. \end{aligned}$$

4.2 The Tutte Polynomials of the Diamond Hierarchical Lattices

As shown in Fig. 1, The first type of the diamond hierarchical lattice $F_t$ can be obtained from $F_{t-1}$ by 2-inflation and subdivision. Actually, $F_t=S(I(F_{t-1}))$. According to Theorems 3.4 and 3.13, we have the following theorem.

Theorem 4.2

For each $t\ge 1$, The Tutte polynomial of $F_t$ is given by

$$\begin{aligned} T(F_t;x,y)= & {} (1+x)^{2(|E(L_{t-1})|-|V(L_{t-1})|+1)}(1+2x+y)^{|V(L_{t-1})|-1}\\&\cdot T\left( F_{t-1};\frac{y+x+x^2+x^3}{1+2x+y},(\frac{x+y}{1+x})^2\right) . \end{aligned}$$

with the initial condition $T(F_0;x,y)=x$.

Proof

Graph $I(F_{t-1})$ has $|V(F_{t-1})|$ vertices and $2|E(F_{t-1})|$ edges.

$$\begin{aligned} T(F_t;x,y)= & {} T(S(I(F_{t-1}));x,y)\\= & {} (1+x)^{2|E(F_{t-1})|-|V(F_{t-1})|+1}T\left( I(F_{t-1});x^2,\frac{x+y}{1+x}\right) \\= & {} (1+x)^{2|E(F_{t-1})|-|V(F_{t-1})|+1}\left( 1+\frac{x+y}{1+x}\right) ^{|V(F_{t-1})|-1}\\&\cdot T\left( F_{t-1};\frac{x^2+\frac{x+y}{1+x}}{1+\frac{x+y}{1+x}},\left( \frac{x+y}{1+x}\right) ^2\right) \\= & {} (1+x)^{2(|E(F_{t-1})|-|V(F_{t-1})|+1)}(1+2x+y)^{|V(F_{t-1})|-1}\\&\cdot \,\, T\left( F_{t-1};\frac{y+x+x^2+x^3}{1+2x+y},\left( \frac{x+y}{1+x}\right) ^2\right) . \end{aligned}$$

$\square$

Let $x=y=1$, we can compute the number of spanning trees of $F_t$.

$$\begin{aligned} \tau (F_t)=4^{\sum _{i=0}^{t-1}|E_i|}=4^{\frac{1}{3}(4^t-1)}. \end{aligned}$$

Similarly, we can compute the Tutte polynomial of the second type of the diamond hierarchical lattice $Q_t$.

Theorem 4.3

For each $t\ge 1$, The Tutte polynomial of $Q_t$ is given by

$$\begin{aligned} T(Q_t;x,y)= & {} (1+x)^{3(|E(Q_{t-1})|-|V(Q_{t-1})|+1)}( 1+3x+y+3x^2+3xy+y^2)^{|V(Q_{t-1})|-1}\\&\cdot T\left( Q_{t-1};\frac{x+y+3x^2+3xy+y^2+2x^3+x^4}{ 1+3x+y+3x^2+3xy+y^2},\left( \frac{x+y}{1+x}\right) ^3\right) \end{aligned}$$

with the initial condition $T(Q_0;x,y)=x$.

Proof

Note that $Q_t=S(I_3(Q_{t-1}))$. $I_3(Q_{t-1})$ has $|V(Q_{t-1})|$ vertices and $3|E(Q_{t-1})|$ edges.

$$\begin{aligned} T(Q_t;x,y)= & {} (1+x)^{3|E(Q_{t-1})|-|V(Q_{t-1})|+1}T\left( I_3(G);x^2, \frac{y+x}{1+x}\right) \\= & {} (1+x)^{3|E(Q_{t-1})|-|V(Q_{t-1})|+1}\left( 1+\frac{x+y}{1+x}+\left( \frac{x+y}{1+x}\right) ^2\right) ^{|V(Q_{t-1})|-1}\\&\cdot T\left( Q_{t-1};\frac{x^2+\frac{x+y}{1+x}+\left( \frac{x+y}{1+x}\right) ^ 2}{1+\frac{x+y}{1+x}+\left( \frac{x+y}{1+x}\right) ^2},\left( \frac{x+y}{1+x}\right) ^3\right) \\= & {} (1+x)^{3(|E(Q_{t-1})|-|V(Q_{t-1})|+1)}(1+3x+y+3x^2+3xy+y^2)^{| V(Q_{t-1})|-1}\\&\cdot T\left( Q_{t-1};\frac{x+y+3x^2+3xy+y^2+2x^3+x^4}{1+3x+y+3x^2+3xy+y^ 2},\left( \frac{x+y}{1+x}\right) ^3\right) . \end{aligned}$$

$\square$

Let $x=y=1$, we can obtain the number of spanning trees of $Q_t$.

$$\begin{aligned} \tau (Q_t)=2^{\frac{12}{25}(6^t-1)-\frac{2}{5}t}3^{\frac{3}{25}(6^t-1)+\frac{2}{5}t}. \end{aligned}$$

Let $x=2,y=1$, we can obtain the number of spanning forests of $Q_t$.

$$\begin{aligned} \sigma (Q_t)=2\times 3^{\frac{3}{5}(6^t-1)}. \end{aligned}$$