Tutte Polynomial of Scale-Free Networks

Abstract

The Tutte polynomial of a graph, or equivalently the q-state Potts model partition function, is a two-variable polynomial graph invariant of considerable importance in both statistical physics and combinatorics. The computation of this invariant for a graph is NP-hard in general. In this paper, we focus on two iteratively growing scale-free networks, which are ubiquitous in real-life systems. Based on their self-similar structures, we mainly obtain recursive formulas for the Tutte polynomials of two scale-free networks (lattices), one is fractal and “large world”, while the other is non-fractal but possess the small-world property. Furthermore, we give some exact analytical expressions of the Tutte polynomial for several special points at (x, y)-plane, such as, the number of spanning trees, the number of acyclic orientations, etc.

1 Introduction

The Tutte polynomial T(G; x, y) of a graph G, due to Tutte [1], is a polynomial in two variables which plays an important role in several areas of sciences. Though originally studied in algebraic graph theory as a generalization of counting problems related to graph coloring and nowhere-zero flow, it has many interesting connections with statistical mechanical model as the Potts model [2, 3], the Abelian Sandple Model, as well as the Jones polynomial from knot theory. It is also the source of several central computational problems in theoretical computer science. For a thorough survey on the Tutte polynomial, we would like refer the reader to Refs. [4–9]. In a strong sense it contains every graphical invariant that can be computed by deleting and contraction operations which are natural reductions for many networks model. The Tutte polynomial for a particular point at (x, y)-plane is related to much combinatorial information and algebraic properties of a graph, including the number of spanning trees, the number of acyclic orientations, the dimension of the bicycle space and many more. Moreover, the Tutte polynomial contains several other polynomial invariants, such as the chromatic polynomial, the flow polynomial and the all terminal reliability polynomial as partial evaluations.

Generally, the Tutte polynomial or the partition function of Potts models is computationally intractable. In both fields of combinatorics and statistical physics, the Tutte polynomials of some graphs (or lattices) have been studied by many different methods (see Refs. [10–16]). It is worth mentioning that, about twenty years ago, a q-state Potts model of the diamond hierarchical lattice had been considered by Derrida et al. [17, 18]. After that a lot of work have been done on hierarchical model (see Refs. [19–22]). Recently, on the basis of the subgraph expansion definition of the Tutte polynomial, a very useful method for computing the Tutte polynomial, called the subgraph-decomposition method, was used to study the Tutte polynomial of the Sierpiński and Hanoi graphs in [23]. This technique is highly suited for computing the Tutte polynomial of self-similar graphs, and some applications of it can be found in [24–26].

The two classes of scale-free networks (lattices) under consideration, are two different novel network structures based on the diamond hierarchical lattice augmented by adding a new edge in each iteration (see Ref. [27–29]), both of which display the striking scale-free behavior, with their degree distribution P(k) obeying a power law form $P(k)\sim k^{-\gamma }$. By locating the new adding edge in two different ways, one is “large world”, while the other possesses the small-world property. This two scale-free networks have attracted a wide spread attention from the viewpoint of complex networks (see Refs. [30–34]).

In this paper, we focus our attention on computation of the Tutte polynomial of this two classes of scale-free networks, by using a subgraph-decomposition method. We determine the recursive formula for computing the Tutte polynomial. Furthermore, the chromatic polynomial of the small-word self-similar networks can be solved efficiently by applying a useful technique. In particular, as special cases of the general Tutte polynomial, we mainly obtain:

• the number of spanning trees (see Eqs. 33 and 53);

• the number of acyclic orientations (see Eq. 61);

• the number of acyclic root-connected orientations (see Eqs. 42 and 63);

• the number of indegree sequences of strongly connected orientations (see Eq. 46).

2 Preliminaries

In this section, we briefly discuss some necessary background that will be used for our calculations. We use standard graph terminology and the words “network” and “graph” synonymously. Let G be a graph with its vertex set V(G) and edge set E(G). A spanning subgraph $H=(V(H),E(H))$ is a subgraph of G such that H has the same vertex set as G and $E(H)\subseteq E(G)$. In particular, a spanning tree of G is a spanning subgraph of G which is a tree. The number of spanning trees of a graph G is also called complexity of G. An orientation of graph G is the digraph defined by the choice of a direction for every edge of E(G). A directed cycle of a digraph is a set of edges forming a cycle of the graph such that they are all directed accordingly with a direction for the cycle. A digraph is acyclic if it has no directed cycle, and it is strongly connected if for every pair of vertices there is a directed cycle containing them. A sink for a digraph is a vertex with no outgoing edge. The indegree sequence of an orientation is a mapping defined on V associating with $v\in V$ the indegree of v.

A network is said to be scale-free [35] if its degree obeys, at least asymptotically, the following distribution: $P(x)=\mathcal {C}x^{-\gamma }$ ($x\ge x_{\text {min}}$), where $\mathcal {C}$ and $\gamma >1$ are positive constants. The requirement of $\gamma >1$ ensures that P(x) can be normalized. In a real network, $\gamma$ is typically in the range $2<\gamma \le 3$ [36], although occasionally it may lie beyond these bounds. By the definition, in a scale-free network, most vertices have a low degree, while these exist a small number of vertices with large degree, which is in contrast to other networks with an exponential or a Poisson degree distribution, where large-degree vertices are absent.

A network is said to possess the small-world [37] property if the leading scaling of its average distance grows proportionally to, or slower than, the logarithm of the number of vertices in the network. In general, a small-world network is a type of mathematical graph in which most vertices are not be reached neighbors of one another, but most vertices can be reached from every other by a small number of steps.

A network is said to be fractal if it has a finite fractal dimension, otherwise it is non-fractal. Generally, the fractal dimension of a network can be obtained by applying a box-covering method defined as follows [38]. One uses boxes, each having a linear size $l_{B}$, to cover all vertices in the network, such that for any pair of verities in each box, their distance in their original network is less than $l_{B}$. Let $N_{B}$ denoted the minimum possible number of boxes required to cover all vertices in the whole network. Then the fractal dimension or box dimension, denoted by $d_{B}$ ($0<d_{B}<\infty$), of the network is given by $N_{B}\approx l_{B}^{-d_{B}}$ [39]. For a fractal network, the number of vertices is a power function of its average distance. In contrast, for a non-fractal network, its size is an exponential function of its average distance. Self-similarity refers to the scale invariance of the degree distribution under coarse-graining with different box size $l_{B}$ as well as under the iterative operations of coarse-graining with fixed $l_{B}$. Intuitively, a self-similar network is exactly or approximately similar to a part of itself. Note that fractality and self-similarity do not always imply each other. A fractal is always self-similar, but a self-similar network may be not fractal [40].

There are several very different, but nevertheless equivalent, definitions of the Tutte polynomial. Here, we will present the subgraph expansion definition which is often the easiest way to prove the properties of the Tutte polynomial. The Tutte polynomial T(G; x, y) of the graph G is defined as

$$\begin{aligned} T(G;x,y)=\sum \limits _{H\subseteq G}(x-1)^{r(G)-r(H)}(y-1)^{n(H)}, \end{aligned}$$

(1)

where the sum runs over all the spanning subgraphs H of G, $r(G)=|V(G)|-k(G)$ is the rank of H and $n(G)=|E(G)|-|V(G)|+k(G)$ is the nullity of H and k(G) is the number of components of G.

The connection between the partition function of Potts model and the Tutte polynomial is given in [6]

$$\begin{aligned} Z_{G}(q,v)=q^{k(G)}v^{n-k(G)}T(G;(q+v)/v,v+1). \end{aligned}$$

(2)

Moreover, it is worth mentioning that the chromatic polynomial P(G, q) occurs as a special limiting case, namely the zero-temperature limit of the anti-ferromagnetic Potts model

$$\begin{aligned} Z_{G}(q,-1)=P(G,q)=(-q)^{k(G)}(-1)^{n(G)}T(G;1-q,0). \end{aligned}$$

(3)

It is well-known in [5, 6] that the evaluation of the Tutte polynomial for a particular point at (x, y)-plane is related to some combinatorial information and algebraic properties of the graph considered.

• (1) $T(G;1,1)=N_{ST}(G)$, i.e., the number of spanning trees of G;

• (2) $T(G;1,0)=$ the number of acyclic root-connected orientations of G;

• (3) $T(G;1,2)=$ the number of spanning connected subgraphs of G;

• (4) $T(G;2,1)=$ the number of spanning forests of G;

• (5) $T(G;2,2)=2^{|E(G)|}$, i.e., the number of spanning subgraphs of G;

• (6) $T(G;2,0)=N_{AO}(G)$, the number of acyclic orientations of G;

• (7) $T(G;-1,-1)=(-1)^{|E(G)|}(-2)^{dim(\mathcal {B})}$, where $\mathcal {B}$ is the bicyclic space of G;

• (8) $T(G;0,1)=$ the number of indegree sequences of strongly connected orientations of G.

Fig. 1

First three iterations of the scale-free fractal network

3 Tutte Polynomial of a Fractal Scale-Free Network

In this section, we give the computational formulas of the Tutte polynomial of a fractal scale-free network $G_n$ in detail.

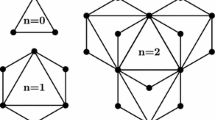
We begin by giving the definition and relevant structural properties of the network under consideration, as shown in Fig. 1. The fractal scale-free network $G_{n}=(V_{n},E_{n})$, $n\ge 0$, with the vertex set $V_{n}$ and edge set $E_{n}$, can be constructed as follows:

Fig. 2

Illustration for the construction of $G_{n+1}$

For $n=0$, $G_0$ is the complete graph $K_2$.

For $n\ge 1$, $G_{n}$ can be constructed from four copies of $G_{n-1}$ by merging four groups of vertices and adding a new edge. Specifically, let $X_n$ and $Y_n$, hereafter called special vertices of $G_n$, be the leftmost and the rightmost vertex of $G_n$. $X_{n}$ and $X_{n}$ are combined into the special vertex $X_{n+1}$ of $G_{n+1}$, $Y_{n}$ and $Y_{n}$ are combined into the special vertex $Y_{n+1}$ of $G_{n+1}$, and a new edge $e_n$ is added between two vertices combined by $Y_{n}$ and $X_{n}$. The construction of $G_{n+1}$ is illustrated in Fig. 2.

We can see that the network $G_n$ is self-similar from Fig. 2, which is another typical features of real systems and suggests an alternative network construction method. And it is easy to obtain that the order and the size of the network $G_n$ are $|V_n|=(2\times 4^n+4)/3$ and $|E_n|=(4^{n+1}-1)/{3}$, respectively. Then the average degree after n iterations is $\langle k \rangle _{n}=\frac{2|E_n|}{|V_n|}$, which approaches 4 in the infinite n limit. The graph is fractal with a fractal dimension equal to 2 [31]. It has a power-law degree distribution $P(k)\propto k^{-3}$, for large n. Therefore, it is scale-free, a common property shared by many real-life networks. For very large n, the average distance $\overline{d}_{n}$ of $G_{n}$, scale as $\overline{d}_{n}\sim |V_{n}|^{1/2}$ [31], shows that the graph is not small-world but “large-world”. Notice that real-life networks, e.g., global network of avian influenza outbreaks, display a similar “large-world” phenomenon. To investigate the Tutte polynomial $T(G_n;x,y)$, first of all, we partition the set of the spanning subgraph of $G_n$ into two disjoint subsets:

• $\mathcal {G}_{1,n}$ denotes the set of spanning subgraphs of $G_n$, where two special vertices $X_n$ and $Y_n$ of $G_n$ belong to the same component;

• $\mathcal {G}_{2,n}$ denotes the set of spanning subgraphs of $G_n$, where two special vertices $X_n$ and $Y_n$ of $G_n$ do not belong to the same component.

For $n\ge 0$, $\mathcal {G}_{1,n}\cup \mathcal {G}_{2,n}$ is a partition of spanning subgraphs of $G_n$. Next, let $T_n(x,y)=T(G_n;x,y)$ be the Tutte polynomial of $G_n$, and for $n\ge 1$, $T_{1,n}(x,y)$ and $T_{2,n}(x,y)$ denote the following polynomials:

• $T_{1,n}(x,y)= \sum _{H \in \mathcal {G}_{1,n}}(x-1)^{r(G_n)-r(H)}(y-1)^{n(H)}$;

• $T_{2,n}(x,y)=\sum _{H \in \mathcal {G}_{2,n}}(x-1)^{r(G_n)-r(H)}(y-1)^{n(H)}$.

Then we have

$$\begin{aligned} T_n(x,y)=T_{1,n}(x,y)+T_{2,n}(x,y). \end{aligned}$$

(4)

In order to obtain $T_n(x,y)$, we need to find the recursive formulas on $T_{1,n}(x,y)$ and $T_{2,n}(x,y)$. For this purpose, we analyze the relation between the spanning subgraphs of $G_{n+1}$ and the spanning subgraphs of $G_{n}$. Note that $G_{n+1}$ is obtained from four copies of $G_{n}$ by merging some special vertices and adding a new edge $e_n$, any spanning subgraph of $G_{n+1}$ consists of S and four spanning subgraphs from the four copies $G_{n}^{i}$ ($i=1,2,3,4$) of $G_{n}$, respectively, where S may be $\{e_{n}\}$ or $\emptyset$ (the empty set). Indeed, a spanning subgraph H of $G_{n+1}$ is uniquely determined by the restriction of H to the four copies $G_{n}^{i}$ (denoted by $H_i$ ($i=1,2,3,4$), respectively) and S, and vice versa. Therefore, the Tutte polynomial of $G_{n+1}$ can be written as

$$\begin{aligned} T_{n+1}(x,y)=\sum _{H=(\bigcup \limits _{i=1}^4 H_i) \bigcup S; H_i \subseteq G_{n}^{i}}(x-1)^{r(G_{n+1})-r(H)}(y-1)^{n(H)}, \end{aligned}$$

(5)

where the sum runs over all spanning subgraphs $H_i$ of $G_{n}^{i}$ ($i=1,2,3,4$) and S. Now, we need to know how r(H) and n(H) depend on $r(H_i)$ and $n(H_i)$ ($i=1,2,3,4$). Note that $|V(G_{n+1})|=4|V(G_n)|-4$, $|E(H)|=\sum _{i=1}^{4} |E(H_i)|+1$ for $S=\{e_n\}$ and $|E(H)|=\sum _{i=1}^{4} |E(H_i)|$ for $S=\emptyset$, there are two cases to be considered.

Case 1 $S=\{e_n\}$.

In this case, the spanning subgraph H of $G_{n+1}$ contains the new adding edge $\{e_n\}$, and $|E(H)|=\sum _{i=1}^{4}|E(H_i)|+1$.

Subcase 1 If $k(H)=\sum \limits _{i=1}^{4}k(H_{i})-3$, then

$$\begin{aligned} r(H)=|V(H)|-k(H)=(4|V(G_{n})|-4)-\left( \sum _{i=1}^{4}k(H_{i})-3\right) =\sum _{i=1}^{4}r(H_{i})-1. \end{aligned}$$

(6)

Moreover, we have

$$\begin{aligned} n(H)=|E(H)|-r(H)=\left( \sum _{i=1}^{4}|E(H_i)|+1\right) -\left( \sum _{i=1}^{4}r(H_{i})-1\right) =\sum _{i=1}^{4}n(H_i)+2 \end{aligned}$$

(7)

and

$$\begin{aligned} r(G_{n+1})-r(H)=(|V(G_{n+1})|-1)-\left( \sum _{i=1}^{4}r(H_i)-1\right) =\sum _{i=1}^{4}(r(G_{n})-r(H_i)). \end{aligned}$$

(8)

Thus,

$$\begin{aligned} (x-1)^{r(G_{n+1})-r(H)}(y-1)^{n(H)}=(y-1)^{2}\prod _{i=1}^{4}(x-1)^{r(G_{n})-r(H_{i})}(y-1)^{n(H_i)}. \end{aligned}$$

(9)

Subcase 2 If $k(H)=\sum \limits _{i=1}^{4}k(H_{i})-4$, then

$$\begin{aligned} r(H)=|V(H)|-k(H) =(4|V(G_{n})|-4)-\left( \sum _{i=1}^{4}k(H_{i})-4\right) =\sum _{i=1}^{4}r(H_{i}). \end{aligned}$$

(10)

Moreover, we have

$$\begin{aligned} n(H)=|E(H)|-r(H)=\left( \sum _{i=1}^{4}|E(H_i)|+1\right) -\left( \sum _{i=1}^{4}r(H_{i})\right) =\sum _{i=1}^{4}n(H_i)+1 \end{aligned}$$

(11)

and

$$\begin{aligned} r(G_{n+1})-r(H)=(|V(G_{n+1})|-1)-\left( \sum _{i=1}^{4}r(H_i)\right) =\sum _{i=1}^{4}(r(G_{n})-r(H_i))-1. \end{aligned}$$

(12)

Hence,

$$\begin{aligned} (x-1)^{r(G_{n+1})-r(H)}(y-1)^{n(H)}=\frac{y-1}{x-1}\prod _{i=1}^{4}(x-1)^{r(G_{n})-r(H_{i})}(y-1)^{n(H_i)}. \end{aligned}$$

(13)

Subcase 3 If $k(H)=\sum \limits _{i=1}^{4}k(H_{i})-5$, then we can obtain, similarly, that

$$\begin{aligned} (x-1)^{r(G_{n+1})-r(H)}(y-1)^{n(H)}=\frac{1}{(x-1)^2}\prod _{i=1}^{4}(x-1)^{r(G_{n})-r(H_{i})}(y-1)^{n(H_i)}. \end{aligned}$$

(14)

Case 2 $S=\emptyset$.

In this case, the spanning subgraph H of $G_{n+1}$ does not contain the new adding edge $e_n$, and $|E(H)|=\sum _{i=1}^{4}|E(H_i)|$.

Subcase 1 If $k(H)=\sum \limits _{i=1}^{4}k(H_{i})-3$, then

$$\begin{aligned} r(H) =|V(H)|-k(H)=(4|V(G_{n})|-4)-\left( \sum _{i=1}^{4}k(H_{i})-3\right) = \sum _{i=1}^{4}r(H_{i})-1. \end{aligned}$$

(15)

Moreover, we have

$$\begin{aligned} n(H)=|E(H)|-r(H) =\left( \sum _{i=1}^{4}|E(H_i)|\right) -\left( \sum _{i=1}^{4}r(H_{i})-1\right) =\sum _{i=1}^{4}n(H_i)+1 \end{aligned}$$

(16)

and

$$\begin{aligned} r(G_{n+1})-r(H)=(|V(G_{n+1})|-1)-\left( \sum _{i=1}^{4}r(H_i)-1\right) =\sum _{i=1}^{4}(r(G_{n})-r(H_i)). \end{aligned}$$

(17)

Thus,

$$\begin{aligned} (x-1)^{r(G_{n+1})-r(H)}(y-1)^{n(H)}=(y-1)\prod _{i=1}^{4}(x-1)^{r(G_{n})-r(H_{i})}(y-1)^{n(H_i)}. \end{aligned}$$

(18)

Subcase 2 If $k(H)=\sum \limits _{i=1}^{4}k(H_{i})-4$, then

$$\begin{aligned} r(H)=|V(H)|-k(H)=(4|V(G_{n})|-4)-\left( \sum _{i=1}^{4}k(H_{i})-4\right) =\sum _{i=1}^{4}r(H_{i}). \end{aligned}$$

(19)

Moreover, we have

$$\begin{aligned} n(H)=|E(H)|-r(H)=\left( \sum _{i=1}^{4}|E(H_i)|\right) -\left( \sum _{i=1}^{4}r(H_{i})\right) =\sum _{i=1}^{4}n(H_i) \end{aligned}$$

(20)

and

$$\begin{aligned} r(G_{n+1})-r(H)=(|V(G_{n+1})|-1)-\left( \sum _{i=1}^{4}r(H_i)\right) =\sum _{i=1}^{4}(r(G_{n})-r(H_i))-1. \end{aligned}$$

(21)

Thus, we have

$$\begin{aligned} (x-1)^{r(G_{n+1})-r(H)}(y-1)^{n(H)}=\frac{1}{x-1}\prod _{i=1}^{4}(x-1)^{r(G_{n})-r(H_{i})}(y-1)^{n(H_i)}. \end{aligned}$$

(22)

For convenience, we use solid lines to join the two special vertices when the corresponding spanning subgraph of $G_n$ belongs to $\mathcal {G}_{1,n}$; Otherwise, we use dotted lines instead of solid lines. Two different types of spanning subgraphs are shown in Fig. 3.

Fig. 3

Two types of spanning subgraphs in $G_{n}$: Type I (left), Type II (right)

Theorem 1

The Tutte polynomial $T_{n+1}(x,y)$ of $G_{n+1}$ is given by

$$\begin{aligned} T_{n+1}(x,y)=T_{1,n+1}(x,y)+T_{2,n+1}(x,y) \end{aligned}$$

(23)

where the polynomials $T_{1,n+1}(x,y)$ and $T_{2,n+1}(x,y)$ satisfy the following recursive relations:

$$\begin{aligned} T_{1,n+1}(x,y)\,=\,y(y-1)T_{1,n}^4 +\frac{4y}{x-1}T_{1,n}^{3}T_{2,n}+\frac{2x+2}{(x-1)^{2}}T_{1,n}^{2}T_{2,n}^2, \end{aligned}$$

(24)

$$\begin{aligned} T_{2,n+1}(x,y)=\frac{2y+2}{{x-1}}T_{1,n}^{2}T_{2,n}^2 +\frac{4x}{(x-1)^{2}}T_{1,n}T_{2,n}^{3}+\frac{x}{(x-1)^{2}}T_{2,n}^4 \end{aligned}$$

(25)

with the initial conditions $T_{1,0}(x,y)=1$, $T_{2,0}(x,y)=x-1$.

Table 1 All combinations and corresponding contributions

Proof

The initial conditions are easily verified. The strategy of the proof is to study all possible configurations of the spanning subgraph $H_i$ in $G_n^i$ ($i=1,2,3,4$), and analyze the contributions of the configurations to $T_{1,n}(x,y)$ or $T_{2,n}(x,y)$. As shown in Table 1, a configuration produces a basic term of form $T_{1,n}^{i}T_{2,n}^{j}$ ($i+j=4$), and by the previous analysis, each basic term has to be multiplied by a factor $(y-1)^2$, $\frac{y-1}{x-1}$, $\frac{1}{(y-1)^2}$ or $y-1$, $\frac{1}{x-1}$ according to Case 1 and Case 2, respectively. From Table 1, we can establish Eqs. (24–25), and the proof is completed. $\square$

According to Eq. (25), it is easy to prove by induction on n that $x-1$ divides $T_{2,n}(x,y)$ in Z[x, y]. Thus, we can rewrite $T_{2,n}(x,y)$ as $(x-1)N_{n}(x,y)$ in Z[x, y], and Theorem 1 can be reduced to the following:

Theorem 2

The Tutte polynomial $T_{n+1}(x,y)$ of $G_{n+1}$ is given by

$$\begin{aligned} T_{n+1}(x,y)=T_{1,n+1}(x,y)+(x-1)N_{n+1}(x,y) \end{aligned}$$

(26)

where the polynomial $T_{1,n+1}(x,y)$, $N_{n+1}(x,y)$ satisfy the following recursive relations:

$$\begin{aligned} T_{1,n+1}(x,y) = y(y-1)T_{1,n}^{4}+4yT_{1,n}^{3}N_{n}+(2x+2)T_{1,n}^{2}N_{n}^{2}, \end{aligned}$$

(27)

$$\begin{aligned} N_{n+1}(x,y) =(2y+2)T_{1,n}^{2}N_{n}^{2}+4xT_{1,n}N_{n}^{3}+x(x-1)N_{n}^{4} \end{aligned}$$

(28)

with the initial conditions $T_{1,0}(x,y)=1$, $N_{0}(x,y)=1$.

Corollary 1

For a positive integer n, the Tutte polynomial $T_n(x,y)$ of $G_n$ along the line $y=x$ is given by

$$\begin{aligned} T_n(x,x)=x(x^2+5x+2)^{\frac{4^n-1}{3}}. \end{aligned}$$

(29)

Proof

By taking $y=x$ in Theorem 2, we have

$$\begin{aligned} T_{1,n}(x,x)=x(x-1)T_{1,n-1}^4 +4xT_{1,n-1}^{3}N_{n-1}+(2x+2)T_{1,n-1}^{2}N_{n-1}^{2}, \end{aligned}$$

(30)

$$\begin{aligned} N_{n}(x,x)=(2x+2)T_{1,n-1}^{2}N_{n-1}^{2}+4xT_{1,n-1}N_{n-1}^{3}+x(x-1)N_{n-1}^{4}, \end{aligned}$$

(31)

and $T_{1,0}(x,x)=N_{0}(x,x)=1$. It can be obtained easily that $T_{1,n}(x,x)=N_{n}(x,x)$ by induction on n (In fact, the functions satisfy $N_n(x,y)=T_{1,n}(y,x)$, they are symmetric alone the line $y=x$). Substituting it into Eq. (31) and using the initial condition $N_{0}(x,x)=1$, we have

$$\begin{aligned} N_{n}(x,x)=(x^2+5x+2)N_{n-1}^{4}=(x^2+5x+2)^{\frac{4^n-1}{3}}. \end{aligned}$$

(32)

By Eq. (26), $T_{n}(x,x)=T_{1,n}(x,x)+(x-1)N_{n}(x,x)=xN_{n}(x,x)=x(x^2+5x+2)^{\frac{4^n-1}{3}}$. $\square$

Since the number of spanning trees is $N_{ST}(G)=T(G;1,1)$, from Corollary 1, we can obtain immediately that

• the number of spanning trees of $G_n$ is

  $$\begin{aligned} N_{ST}(G_{n})=T_{n}(1,1)=8^{\frac{4^n-1}{3}}=2^{4^n-1} \end{aligned}$$

  (33)

which was also obtained in [31] by employing the decimation technique;

• the asymptotic growth constant of the spanning trees of $G_n$ is

  $$\begin{aligned} \lim _{n\rightarrow \infty }\frac{\ln N_{ST}(G_n)}{|V(G_n)|}=\frac{3}{2}\ln {2}\approx 1.0397. \end{aligned}$$

  (34)

Similarly,

$$\begin{aligned} T_n(-1,-1)=(-1)\times (-2)^{\frac{4^n-1}{3}}= (-1)^{\frac{4^{n+1}-1}{3}}(-2)^{\frac{4^n-1}{3}} =(-1)^{|E(G_n)|}(-2)^{dim(\mathcal {B})} \end{aligned}$$

(35)

by taking $x=-1$ in Corollary 1. So, we exactly obtain that

• the dimension of the bicycle space of $G_n$ is

  $$\begin{aligned} dim(\mathcal {B})=\frac{4^{n}-1}{3}. \end{aligned}$$

  (36)

Now, we consider the number of acyclic root-connected orientations of $G_{n}$. Let $x=1$ and $y=0$ in Theorem 2, we have $T_{n}(1,0)=T_{1,n}(1,0)$, and

$$\begin{aligned} T_{1,n}(1,0)=4T_{1,n-1}^{2}(1,0)N_{n-1}^{2}(1,0), \end{aligned}$$

(37)

$$\begin{aligned} N_{n}(1,0)=2T_{1,n-1}^{2}(1,0)N_{n-1}^{2}(1,0)+4T_{1,n-1}(1,0)N_{n-1}^{3}(1,0). \end{aligned}$$

(38)

A useful relation yields from Eqs. (37) and (38)

$$\begin{aligned} \frac{N_{n}(1,0)}{T_{1,n}(1,0)}=\frac{1}{2}+\frac{N_{n-1}(1,0)}{T_{1,n-1}(1,0)}. \end{aligned}$$

(39)

It implies that

$$\begin{aligned} \frac{N_{n}(1,0)}{T_{1,n}(1,0)}=\frac{n}{2}+\frac{N_{0}(1,0)}{T_{1,0}(1,0)}, \end{aligned}$$

(40)

and

$$\begin{aligned} N_{n}(1,0)=\frac{n+2}{2}T_{1,n}(1,0) \end{aligned}$$

(41)

since $T_{0}(1,0)=1$, $N_{0}(1,0)=1$.

Substituting Eqs. (41) into (37) and using the initial condition $T_{1,0}(1,0)=1$, we obtain that

• the number of acyclic root-connected orientations of $G_{n}$ is

  $$\begin{aligned} T_{1,n}(1,0)=(n+1)^{2}T_{1,n-1}^{4}(1,0)=\prod _{i=1}^{n}(i+1)^{2\times 4^{n-i}}. \end{aligned}$$

  (42)

Similarly, we can obtain the indegree sequences of strongly connected orientations of $G_n$. By taking $x=0$ and $y=1$ in Theorem 2, we have $T_{n}(0,1)=T_{1,n}(0,1)-N_{n}(0,1)$, and

$$\begin{aligned} T_{1,n}(0,1) = 4T_{1,n-1}^{3}(0,1)N_{n}(0,1)+2T_{1,n-1}^{2}(0,1)N_{n-1}^{2}(0,1), \end{aligned}$$

(43)

$$\begin{aligned} N_{n}(0,1) = 4T_{1,n-1}^{2}(0,1)N_{n-1}^{2}(0,1). \end{aligned}$$

(44)

Using the same techniques, we can obtained

$$\begin{aligned} T_{1,n}(0,1)=\frac{n+2}{2}N_{n}(0,1) \text { and } N_{n}(0,1)=\prod _{i=1}^{n}(i+1)^{2\times 4^{n-i}}. \end{aligned}$$

(45)

And

• the number of indegree sequences of strongly connected orientations of $G_{n}$ is

  $$\begin{aligned} T_{n}(0,1)=\frac{n+2}{2}N_{n}(0,1)-N_{n}(0,1)=\frac{n}{2}N_{n}(0,1)=\frac{n}{2}\prod _{i=1}^{n}(i+1)^{2\times 4^{n-i}}. \end{aligned}$$

  (46)

4 Tutte Polynomial of a Non-fractal Scale-Free Network

In the previous section, we have studied the Tutte polynomial of a fractal scale-free network, which is “large-world”. In fact, except some fractal “large-world” scale-free networks, many other real-life networks are non-fractal and small-world [36].

If the newly added edge connects the two special merging vertices in each iteration, we can obtain another scale-free network $G'_{n}$ which presents some typical properties of real-world networks, see Fig. 4. Obviously, the graph $G'_{n}$ has the same number of vertices and edges as in the previous network $G_{n}$. It is scale-free, and has an obvious small-world characteristic, and its geometrical properties are similar to pseudofractal graphs studied in [41]. Its average length of paths increases logarithmically with its number of vertices and its clustering coefficient is very high. In deed, this small-world network constitutes the extreme case $q=1$ of the random construction in [28], where an edge is chosen with probability q at each step.

Fig. 4

First three iterations of the small-world and scale-free network

In this section, we devote to studying the Tutte polynomial for the non-fractal and small-world network $G'_{n}$. The analysis of this small-world network is completely analogous to that of the previous fractal scale-free network $G_{n}$, we only provide the results and skip the details. In the absence of confusion, we use the same notations as the last section.

Theorem 3

For $n\ge 1$, the Tutte polynomial $T_{n}(x,y)$ of the network $G'_{n}$ is given by

$$\begin{aligned} T_{n}(x,y)=T_{1,n}(x,y)+(x-1)N_{n}(x,y), \end{aligned}$$

(47)

where the polynomials $T_{1,n}(x,y)$ and $N_{n}(x,y)$ satisfy the following recursive relations:

$$\begin{aligned} T_{1,n}(x,y)\,=&\,y(y-1)T_{1,n-1}^4+4yT_{1,n-1}^3N_{n-1}+2y(x-1)T_{1,n-1}^2N_{n-1}^2 \nonumber \\&+4T_{1,n-1}^2N_{n-1}^2+4(x-1)T_{1,n-1}N_{n-1}^3+(x-1)^2N_{n-1}^4, \end{aligned}$$

(48)

$$\begin{aligned} N_n(x,y)=4T_{1,n-1}^2N_{n-1}^2+4(x-1)T_{1,n-1}N_{n-1}^3+(x-1)^2N_{n-1}^4 \end{aligned}$$

(49)

with the initial conditions $T_{1,0}(x,y)=1$ and $N_{0}(x,y)=1$.

We can determine the number of spanning trees of $G'_n$ and its asymptotic constants. By Theorem 3, we obtain that $T_{n}(1,1)=T_{1,n}(1,1)$ and

$$\begin{aligned} T_{n}(1,1)=4T_{n-1}^3(1,1)N_{n-1}(1,1)+4T_{n-1}^2(1,1)N_{n-1}^{2}(1,1), \end{aligned}$$

(50)

$$\begin{aligned} N_{n}(1,1)=4T_{n-1}^2(1,1)N_{n-1}^{2}(1,1). \end{aligned}$$

(51)

Eqs. (50) and (51) together yield a useful relation given by $\frac{T_n(1,1)}{N_n(1,1)}=\frac{T_{n-1}(1,1)}{N_{n-1}(1,1)}+1$ with the initial conditions $T_{1}(1,1)=N_{0}(1,1)=1$. Thus, $T_n(1,1)=(n+1)N_n(1,1)$. By Eq. (51), we can obtain that

$$\begin{aligned} N_n(1,1)=2^{(2^{2n+1}-2)/3}\prod _{i=1}^{n}i^{2^{2n-2i+1}}. \end{aligned}$$

(52)

So, we have

• the number of spanning trees of $G'_n$ is

  $$\begin{aligned} N_{ST}(G'_n)=T_n(1,1)=(n+1)N_n(1,1)=(n+1)\cdot 2^{(2^{2n+1}-2)/3}\prod _{i=1}^{n}i^{2^{2n-2i+1}}, \end{aligned}$$

  (53)

• the asymptotic growth constant of the spanning trees is

  $$\begin{aligned} \lim _{n\rightarrow \infty }\frac{\ln N_{ST}(G'_n)}{|V(G'_n)|}\approx 0.8974. \end{aligned}$$

  (54)

It is less than the asymptotic growth constant of the previously “large world” scale-free network.

Since the chromatic polynomial $P(G;\lambda )$ can be specialized by the Tutte polynomial, i.e.,

$$\begin{aligned} P(G;\lambda )=(-1)^{r(G)}\lambda ^{k(G)}T(G;1-\lambda ,0), \end{aligned}$$

(55)

we can use the chromatic polynomial to compute the Tutte polynomial at $y=0$.

A useful technique for computing of the chromatic polynomial is given in [4]. If the intersection of G and H is the complete graph $K_t$ (i.e. $G\cap H=K_t$), then

$$\begin{aligned} P(G\cup H; \lambda )=\frac{P(G; \lambda )\cdot P(H; \lambda )}{P(G\cap H; \lambda )} \end{aligned}$$

(56)

and the chromatic polynomial for the complete graph $K_t$ is given by

$$\begin{aligned} P(K_t; \lambda )=\lambda (\lambda -1)(\lambda -2)\cdots (\lambda -t+1). \end{aligned}$$

(57)

Note that the small-world network $G'_n$ can be also obtained from four replicas of $G'_{n-1}$ by merging with four edges of the unique 4-cycle in the graph $G'_1$, i.e., $G_{n}=G^4_{n-1}\cup (G^3_{n-1}\cup (G^2_{n-1}\cup (G^1_{n-1}\cup G'_1)))$, where $G^1_{n-1}\cap G'_1=K_2$, $G^2_{n-1}\cap (G^1_{n-1}\cup G'_1)=K_2$, $G^3_{n-1}\cap (G^2_{n-1}\cup (G^1_{n-1}\cup G'_1))=K_2$, $G^4_{n-1}\cap (G^3_{n-1}\cup (G^2_{n-1}\cup (G^1_{n-1}\cup G'_1)))=K_2$ and $G^i_{n-1}$ ($i=1,2,3,4$) are replicas of $G'_{n-1}$. By using Eq. (56) four times, we can establish the following relation

$$\begin{aligned} P(G'_n;\lambda )=\frac{P^{4}(G'_{n-1};\lambda )\cdot P(G'_1;\lambda )}{P^{4}(K_{2};\lambda )}, \end{aligned}$$

(58)

where $P(G'_1,\lambda )=\lambda (\lambda -1)(\lambda -2)^2$ and $P(K_2,\lambda )=\lambda (\lambda -1)$, Eq. (58) is solved to yield

$$\begin{aligned} P(G'_n;\lambda )=\lambda (\lambda -1)(\lambda -2)^{\frac{2\times (4^n-1)}{3}}. \end{aligned}$$

(59)

And, it is easy to see that the network $G_n$ is 3-colorable.

Using the relationship of the Tutte polynomial and the chromatic polynomial in Eq. (55), we have

$$\begin{aligned} T(G'_{n};x,0)=x(1+x)^{\frac{2\times (4^n-1)}{3}}. \end{aligned}$$

(60)

From Eq. (60), we can obtain that

• the number of acyclic orientations of $G'_n$ is

  $$\begin{aligned} N_{AO}(G'_{n})=T(G'_{n};2,0)=2\times 3^{\frac{2\times (4^n-1)}{3}}, \end{aligned}$$

  (61)

• the asymptotic growth constant on the number of acyclic orientations of $G'_n$ is

  $$\begin{aligned} \lim \limits _{n\rightarrow \infty }\frac{\ln N_{AO}(G'_n)}{|V(G'_n)|}=\ln 3 \approx 1.0986, \end{aligned}$$

  (62)

• the number of acyclic root-connected orientations of $G'_n$ is

  $$\begin{aligned} T_{n}(1,0)=T(G'_{n}; 1,0)=2^{\frac{2\times (4^n-1)}{3}}. \end{aligned}$$

  (63)

5 Conclusion

The scale-free behavior is ubiquitous in the real-life natural and social network systems. In this paper, we have studied the Tutte polynomials of two classes of scale-free networks: one is fractal and “large world”, the other is non-fractal and small-world. Based on the subgraph-decomposition technique, we obtain the recursive formulas for computing their Tutte polynomials. In particular, the chromatic polynomial for the small-world and self-similar networks can be determined exactly. As a application of these formulas, we obtained some invariants on these two classes of scale-free networks, which including the number of spanning trees, the number of acyclic root-connected orientations and the number of acyclic orientations, etc.

Appendix: Other Scale-Free Networks

In this section, we consider the Tutte polynomial of other typical scale-free networks, which include the diamond hierarchical lattice [27, 29], the (1,3)-flower [42, 43], the Apollonian network [44] and the pseudo-fractal scale-free web [41].

Diamond Hierarchical Lattice If the newly added edge is ignored at each iterative generation, then the scale-free network $G_n$(or $G'_{n}$) considered above becomes the famous diamond hierarchical lattice $L_n$ (see Fig. 5), also known as (2,2)-flower in [42], a particular case of (x, y)-flower $(x\ge 1,y\ge 2)$ presents in [45]. And the contributions to $T_{1,n}(x,y)$ and $T_{2,n}(x,y)$ are degraded into the case of $S=\emptyset$, and listed on the right of Table 1. So, the Tutte polynomial $T_n(x,y)$ of $L_n$ is given by

$$\begin{aligned} T_{n}(x,y)=T_{1,n}(x,y)+(x-1)N_{n}(x,y), \end{aligned}$$

(64)

where the polynomials $T_{1,n}(x,y)$ and $N_n(x,y)$ satisfy the following recursive relations:

$$\begin{aligned} T_{1,n}(x,y) = (y-1)T_{1,n-1}^4 +4T_{1,n-1}^{3}N_{n-1}+2(x-1)T_{1,n-1}^{2}N_{n-1}^{2}, \end{aligned}$$

(65)

$$\begin{aligned} N_{n}(x,y) = 4T_{1,n-1}^{2}N_{n-1}^{2}+4(x-1)T_{1,n-1}N_{n-1}^{3}+(x-1)^{2}N_{n-1}^{4}. \end{aligned}$$

(66)

If $x=y=1$, then $T_n(1,1)=T_{1,n}(1,1)$ and $T_{1,n}(1,1)=N_{n}(1,1)$. Thus, $T_n(1,1)=4T_{n-1}^{4}(1,1)$. Since the initial value $T_{0}(1,1)=1$, we can obtain that the number of spanning trees of $L_n$ is

$$\begin{aligned} N_{ST}(L_{n})=T_{n}(1,1)=2^{\frac{2}{3}(4^n-1)} \end{aligned}$$

(67)

and the asymptotic growth constant of the spanning trees of $L_n$ is

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{\ln N_{ST}(L_n)}{|V(L_n)|}=\ln {2}\approx 0.6931. \end{aligned}$$

(68)

Fig. 5

First three iterations of the Diamond hierarchical lattice

Fig. 6

First three iterations of the (1,3)-flower

(1,3)-Flower Having the same degree sequence with the (2,2)-flower, the (1,3)-flower $F_n$ [42, 43] (see Fig. 6) is scale-free, its degree distribution obeys $P(k)\propto k^{-3}$, and it is small-word but non-fractal. Choosing two adjacent vertices with the highest degree as the special vertices in each iteration, we partition similarly the spanning subgraph of $F_n$ into two disjoin subsets and obtain the following recursive relation:

$$\begin{aligned} T_{n}(x,y)=T_{1,n}(x,y)+(x-1)N_{n}(x,y), \end{aligned}$$

(69)

where the polynomials $T_{1,n}(x,y)$ and $N_n(x,y)$ satisfy the following recursive relations:

$$\begin{aligned} T_{1,n}(x,y)\,=&\,(y-1)T_{1,n-1}^4 +4T_{1,n-1}^{3}N_{n-1}+3(x-1)T_{1,n-1}^{2}N_{n-1}^{2}\end{aligned}$$

(70)

$$\begin{aligned}&+(x-1)^{2}T_{1,n-1}N_{n-1}^{3}, \end{aligned}$$

(71)

$$\begin{aligned} N_{n}(x,y)= 3T_{1,n-1}^{2}N_{n-1}^{2}+3(x-1)T_{1,n-1}N_{n-1}^{3}+(x-1)^{2}N_{n-1}^{4} \end{aligned}$$

(72)

with the initial conditions $T_{1,0}(x,y)=1$ and $N_0(x,y)=1$.

Similarly, if $x=y=1$, then $T_n(1,1)=T_{1,n}(1,1)$ and

$$\begin{aligned} T_{1,n}(1,1)=4T_{1,n-1}^{3}(1,1)N_{n-1}(1,1), \end{aligned}$$

(73)

$$\begin{aligned} N_{n}(1,1)=3T_{1,n-1}^{2}(1,1)N_{n-1}^{2}(1,1). \end{aligned}$$

(74)

From Eqs. (73) and (74), we have

$$\begin{aligned} T_{1,n}(1,1)=\left( \frac{4}{3}\right) ^{n}N_{n}(1,1). \end{aligned}$$

(75)

Since the initial value $N_{0}(1,1)=1$, we can obtain

$$\begin{aligned} N_{ST}(F_{n})=T_{n}(1,1)=3^{\frac{4^n-3n-1}{9}}4^{\frac{2\times 4^n+3n-2}{9}} \end{aligned}$$

(76)

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{\ln N_{ST}(F_n)}{|V(F_n)|}=\frac{1}{6}(4\ln {2}+\ln {3})\approx 0.6452. \end{aligned}$$

(77)

which are coincides with the results in [42] based on the relationship between the determinants of submatrices in the Laplacian matrix.

On the other hand, the (1,3)-flower $F_{n}$ can be constructed by merging four replicas of $F_{n-1}$ with four edges of $C_{4}=F_1$. By applying Eq. (56) four times, the chromatic polynomial of the (1,3)-flower is given by

$$\begin{aligned} P(F_n;\lambda )=\frac{P^{4}(F_{n-1};\lambda )\cdot P(C_4;\lambda )}{P^{4}(K_{2};\lambda )}. \end{aligned}$$

(78)

where the chromatic polynomial of the cycle graph $C_n$ is given in [7]

$$\begin{aligned} P(C_n;\lambda )=(\lambda -1)^{n}+(-1)^{n}(\lambda -1) \end{aligned}$$

(79)

and $P(C_4;\lambda )=(\lambda -1)\lambda (\lambda ^2-3\lambda +3)$. Then, from Eq. (78), we have

$$\begin{aligned} P(F_n;\lambda )=(\lambda -1)\lambda (\lambda ^2-3\lambda +3)^{\frac{4^n-1}{3}} \end{aligned}$$

(80)

and by Eq. (55), we have

$$\begin{aligned} T(F_n;x,0)=x(x^2+x+1)^{\frac{4^n-1}{3}}. \end{aligned}$$

(81)

Thus, the number of acyclic orientations of the (1,3)-flower and its asymptotic constant are given by

$$\begin{aligned} N_{AO}(F_{n})=T(2,0)=2\times 7^{\frac{4^n-1}{3}} \end{aligned}$$

(82)

and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\frac{\ln N_{AO}(F_n)}{|V(F_n)|}=\frac{1}{2}\ln 7 \approx 0.9730. \end{aligned}$$

(83)

In addition, the number of acyclic root-connected orientations of the (1,3)-flower is given by $T(1,0)=3^{({4^n-1})/{3}}$.

Apollonian Network We apply our technique to determine the chromatic polynomial (or the Tutte polynomial along $y=0$) of the Apollonian network $A_n$, which is scale-free and small-world [44], and its number of vertices is $|V(A_n)|=({3^n+5})/{2}$. The Apollonian network is derived from the classic Apollonian packing (see Fig. 7), and can also be constructed iteratively [46]. The Apollonian network $A_{n+1}$ can be constructed by using three copies of $A_{n}$ to cover a assured graph $G^{*}=K_{4}$ such that the intersection of each copy $A_{n}$ and $G^{*}$ is the complete graph $K_{3}$. Using Eq. (56) three times, we have

$$\begin{aligned} P(A_n;\lambda )=\frac{P^{3}(A_{n-1};\lambda )\cdot P(K_4;\lambda )}{P^{3}(K_{3};\lambda )}. \end{aligned}$$

(84)

The chromatic polynomial of the Apollonian network $A_n$ is

$$\begin{aligned} P(A_n;\lambda )=\lambda (\lambda -1)(\lambda -2)(\lambda -3)^{\frac{3^n-1}{2}}, \end{aligned}$$

(85)

and from Eq. (55)

$$\begin{aligned} T(A_n; x, 0)=x(x+1)(x+2)^{\frac{3^n-1}{2}}. \end{aligned}$$

(86)

Thus, the number of acyclic orientations of $A_n$ is given by

$$\begin{aligned} N_{AO}(A_n)=T(A_{n};2,0)=3\times 2^{3^n}. \end{aligned}$$

(87)

Consequently, the asymptotic growth constant is

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\frac{\ln N_{AO}(A_n)}{|V(A_n)|}=\frac{1}{2}\ln 2 \approx 0.3466. \end{aligned}$$

(88)

Also, the number of acyclic root-connected orientations of the Apollonian network $A_n$ is given by $T(1,0)=2\times 3^{\frac{3^n-1}{2}}$.

Fig. 7

Apollonian networks $A_0$, $A_1$, $A_2$ and $A_3$

Fig. 8

Pseudofractal scale-free Web $\Gamma _0$, $\Gamma _1$, $\Gamma _2$

Pseudo-fractal Scale-Free Web The studied pseudo-fractal scale-free network $\Gamma _n$ (see Fig. 8) is a deterministic network and has attracted an amount of attention (see [41, 47, 48]). The network $\Gamma _n$ exhibits some typical properties of real networks. Its degree distribution $P(k )$ obeys a power law $P({k})\propto {k} ^{1+\ln 3/{\ln 2}}$, and its clustering coefficient is 4 / 5. We can easily compute the order and size of the network $\Gamma _n$ are $|V_n|=({3^{n+1}+3})/{2}$ and $|E_n|=3^n$, respectively. They are the same with the Sierpiński gasket [49], which is a typical example of fractal networks. Choosing two adjacent hubs (the most connected vertices) as the special vertices in each iteration, and by the subgraph-decomposition technique, we can obtain the following recursive relations of the Tutte polynomial $T_n(x,y)$ of $\Gamma _n$:

$$\begin{aligned} T_{n}(x,y)=T_{1,n}(x,y)+(x-1)N_{n}(x,y), \end{aligned}$$

(89)

where the polynomials $T_{1,n}(x,y)$ and $N_n(x,y)$ satisfy the following recursive relations:

$$\begin{aligned} T_{1,n}(x,y)=(y-1)T_{1,n-1}^{3}+3T_{1,n-1}^{2}N_{n-1}+(x-1)T_{1,n-1}N_{n-1}^{2}, \end{aligned}$$

(90)

$$\begin{aligned} N_{n}(x,y)=2T_{1,n-1}N_{n-1}^{2}+(x-1)N_{n-1}^3 \end{aligned}$$

(91)

with the initial polynomials $T_{1,0}(x,y)=x+y+1$ and $N_{0}(x,y)=x+1$.

Similarly, if $x=y=1$, then $T_{n}(1,1)=T_{1,n}(1,1)$ and

$$\begin{aligned} T_{1,n}(1,1)=3T_{1,n-1}^2N_{n-1}, \end{aligned}$$

(92)

$$\begin{aligned} N_{n}(1,1)=2T_{1,n-1}N_{n-1}^{2}. \end{aligned}$$

(93)

Now, we denote $T_{1,n}(1,1)$ by $t_n$ temporarily. By Eqs. (92) and (93), we have

$$\begin{aligned} \frac{t_{n}}{t_{n-1}^3}=\frac{2}{3}\cdot \frac{t_{n-1}}{t_{n-2}^3}=\cdots =\Big (\frac{2}{3}\Big )^{n-1}\cdot \frac{t_1}{t_0^3}=2\Big (\frac{2}{3}\Big )^{n-1}. \end{aligned}$$

(94)

Since $T_{1,1}(x,y)=3(x+y+1)^2(x+1)$ and $T_{1,0}(x,y)=(x+y+1)$, the number of spanning trees in $\Gamma _n$ is

$$\begin{aligned} N_{ST}(\Gamma _n)=t_n=2\Big (\frac{2}{3}\Big )^{n-1}t_{n-1}^3=2^{\frac{3^{n+1}-2n-3}{4}}3^{\frac{3^{n+1}+2n+1}{4}}, \end{aligned}$$

(95)

which coincides with the known result in [42] obtained by a re-normalization group method.

Moveover, the asymptotic growth of spanning trees of the network is

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\frac{\ln N_{ST}(\Gamma _n)}{|V(\Gamma _n)|}=\frac{1}{2}(\ln 2+\ln 3)\approx 0.89588. \end{aligned}$$

(96)

The pseudo-fractal graph $\Gamma _n$ can be constructed by merging three replicas of $\Gamma _{n-1}$ with three edges of $K_3$. By applying Eq. (56) three times, the chromatic polynomial of the pseudo-fractal scale-free graph is given by

$$\begin{aligned} P (\Gamma _n;\lambda )=\frac{P^{3}(\Gamma _{n-1};\lambda )\cdot P(K_3;\lambda )}{P^{3}(K_{2};\lambda )}. \end{aligned}$$

(97)

Since $P(K_3;\lambda )=\lambda (\lambda -1)(\lambda -2)$, $P(K_{2};\lambda )=\lambda (\lambda -1)$ and $P(\Gamma _0;\lambda )=P(K_3;\lambda )$, we have

$$\begin{aligned} P(\Gamma _n;\lambda )=\lambda (\lambda -1)(\lambda -2)^{\frac{3^{n+1}-1}{2}}, \end{aligned}$$

(98)

and by Eq. (55)

$$\begin{aligned} T(\Gamma _{n};x,0)=x(1+x)^{\frac{3^{n+1}-1}{2}}. \end{aligned}$$

(99)

Thus, the number of acyclic root-connected orientations of the pseudo-fractal graph $\Gamma _n$ can be obtained by $T_n(1,0)=2^{({3^{n+1}-1})/{2}}$. And the number of acyclic orientations of the pseudo-fractal scale-free graph and its asymptotic growth constant are given by

$$\begin{aligned} N_{AO}(\Gamma _n)=T(\Gamma _n;2,0)=2\times 3^{\frac{3^{n+1}-1}{2}} \end{aligned}$$

(100)

and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\frac{\ln N_{AO}(\Gamma _n)}{|V(\Gamma _n)|}=\ln 3 \approx 1.0986. \end{aligned}$$

(101)

It is less than the asymptotic growth constant for the number of acyclic orientations on the two-dimension Sierpiński gasket, which is 1.27299 in [50].