The Polyanalytic Ginibre Ensembles

Abstract

For integers n,q=1,2,3,… , let Pol _n,q denote the ${\mathbb{C}}$-linear space of polynomials in z and $\bar{z}$, of degree ≤n−1 in z and of degree ≤q−1 in $\bar{z}$. We supply Pol _n,q with the inner product structure of

$$\begin{aligned} L^2 \bigl({\mathbb{C}},\mathrm{e}^{-m|z|^2} {\mathrm{d}}A \bigr),\quad \mbox {where } {\mathrm{d}}A(z)=\pi^{-1}{\mathrm{d}}x {\mathrm{d}}y,\ z= x+ {\mathrm{i}}y; \end{aligned}$$

the resulting Hilbert space is denoted by Pol _m,n,q . Here, it is assumed that m is a positive real. We let K _m,n,q denote the reproducing kernel of Pol _m,n,q , and study the associated determinantal process, in the limit as m,n→+∞ while n=m+O(1); the number q, the degree of polyanalyticity, is kept fixed. We call these processes polyanalytic Ginibre ensembles, because they generalize the Ginibre ensemble—the eigenvalue process of random (normal) matrices with Gaussian weight. There is a physical interpretation in terms of a system of free fermions in a uniform magnetic field so that a fixed number of the first Landau levels have been filled. We consider local blow-ups of the polyanalytic Ginibre ensembles around points in the spectral droplet, which is here the closed unit disk $\bar{\mathbb{D}}:=\{z\in{\mathbb{C}}:|z|\le1\}$. We obtain asymptotics for the blow-up process, using a blow-up to characteristic distance m ^−1/2; the typical distance is the same both for interior and for boundary points of $\bar{\mathbb{D}}$. This amounts to obtaining the asymptotical behavior of the generating kernel K _m,n,q . Following (Ameur et al. in Commun. Pure Appl. Math. 63(12):1533–1584, 2010), the asymptotics of the K _m,n,q are rather conveniently expressed in terms of the Berezin measure (and density)

For interior points |z|<1, we obtain that ${\mathrm{d}}B^{\langle z\rangle}_{m,n,q}(w)\to{\mathrm{d}}\delta_{z}$ in the weak-star sense, where δ _z denotes the unit point mass at z. Moreover, if we blow up to the scale of m ^−1/2 around z, we get convergence to a measure which is Gaussian for q=1, but exhibits more complicated Fresnel zone behavior for q>1. In contrast, for exterior points |z|>1, we have instead that ${\mathrm{d}}B^{\langle z\rangle}_{m,n,q}(w) \to{\mathrm{d}}\omega(w,z, {\mathbb{D}}^{e})$, where ${\mathrm{d}}\omega(w,z,{\mathbb{D}}^{e})$ is the harmonic measure at z with respect to the exterior disk ${\mathbb{D}}^{e}:= \{w\in{\mathbb{C}}:\, |w|>1\}$. For boundary points, |z|=1, the Berezin measure ${\mathrm{d}}B^{\langle z\rangle}_{m,n,q}$ converges to the unit point mass at z, as with interior points, but the blow-up to the scale m ^−1/2 exhibits quite different behavior at boundary points compared with interior points. We also obtain the asymptotic boundary behavior of the 1-point function at the coarser local scale q ^1/2 m ^−1/2.

1 Introduction

1.1 Notation

We will write use standard notation, such as ∂X and int(X) for the boundary and the interior of a subset X of the complex plane ${\mathbb{C}}$. The complex conjugate of a complex number z is usually written as $\bar{z}$. We write ${\mathbb{R}}$ for the real line, ${\mathbb{D}}:=\{z\in{\mathbb{C}}:|z|<1\}$ for the open unit disk, and ${\mathbb{D}}^{e}:=\{z\in{\mathbb{C}}:|z|>1\}$ for the open exterior (punctured) disk. The characteristic function of a set E is written 1 _E . We write

$$\begin{aligned} {\mathrm{d}}A(z)=\pi^{-1}{\mathrm{d}}x {\mathrm{d}}y,\quad\mbox{where}\ z=x+{\mathrm{i}}y \in{\mathbb{C}}, \end{aligned}$$

for the normalized area measure in ${\mathbb{C}}$, and use the standard Wirtinger derivatives

$$\begin{aligned} \partial_z:=\frac{1}{2}(\partial_x-{\mathrm{i}} \partial_y),\qquad \bar{\partial}_z:=\frac{1}{2}( \partial_x+{\mathrm{i}}\partial_y), \quad\mbox{where}\ z=x+{\mathrm{i}}y. \end{aligned}$$

We also write Δ for the (quarter) Laplacian

$$\begin{aligned} \Delta_z:=\partial_z\bar{\partial}_z= \frac{1}{4}\bigl(\partial_x^2+\partial_y^2 \bigr). \end{aligned}$$

1.2 Determinantal Projection Processes

Given a locally compact topological space X with a positive Radon measure μ, a finite determinantal projection process is a random configuration of n points defined by the following probability measure on Xⁿ:

$$\begin{aligned} {\mathrm{d}}P(z_1,\ldots,z_n) = \frac{1}{n!} \det \bigl[K_n(z_i, z_j)\bigr]_{i,j=1}^n {\mathrm{d}}\mu(z_1)\cdots{\mathrm{d}}\mu(z_n). \end{aligned}$$

(1.1)

Here, K _n is the integral kernel of a projection operator to an n-dimensional subspace of L ²(X,μ). It is customary to identify all the permutations of the points and think the process as a random measure $\sum_{j=1}^{n} \delta_{z_{j}}$ on X. It should be mentioned that finite determinantal projection processes presented here are a subclass of more general determinantal point processes which, for instance, can contain infinitely many points. We omit the general definition, as the processes we will consider in this paper are only of the special form (1.1).

Determinantal processes were originally introduced by Macchi [28] to model fermions in quantum mechanics. Indeed, the probability density (1.1) vanishes whenever any two points in the n-tuple (z ₁,…,z _n ) coincide (fermions are forbidden to be in the same state). We interpret this as saying that the points in the n-tuple repel each other. Point processes of this kind appear in several contexts, e.g., in random matrix theory and combinatorics (for general surveys, see [10, 24]; we should also mention the books [6, 11, 12, 15, 29]).

1.3 Eigenvalues of Random Normal Matrix Ensembles

Our main motivating example comes from the theory of random normal matrices. This topic has in recent years been subject to rather active investigation by physicists as well as by mathematicians. For an introduction, see, e.g., [38]. So, we shall use $\mathrm{X}={\mathbb{C}}$ and dμ(z)=e^−mQ(z)dA(z), for a positive weight function Q satisfying some mild regularity and growth conditions; m is a positive real parameter, and dA(z)=π ⁻¹dxdy is the normalized area measure. Let us write $L^{2}({\mathbb{C}}, \mathrm{e}^{-mQ}):=L^{2}(\mathrm {X},\mu )$ in this situation. The determinantal projection process is associated with an n-dimensional subspace of $L^{2}({\mathbb{C}}, \mathrm{e}^{-mQ})$, and we will use the space Pol _n of all polynomials in z of degree ≤n−1; we write Pol _m,n to indicate that we have supplied Pol _n with the Hilbert space structure of $L^{2}({\mathbb{C}}, \mathrm{e}^{-mQ})$. The density of the process is then given by the reproducing kernel K _m,n of the space Pol _m,n . So, we are talking about the probability measure

$$\begin{aligned} {\mathrm{d}}P(z_1,\ldots,z_n) = \frac{1}{n!} \det \bigl[K_{m,n}(z_i, z_j)\bigr]_{i,j=1}^n \mathrm{e}^{-m\{Q(z_1)+\cdots+Q(z_n)\}}{\mathrm{d}}A(z_1)\cdots {\mathrm{d}}A(z_n). \end{aligned}$$

(1.2)

In terms of the correlation kernel

(1.3)

which is the integral kernel of an orthogonal projection on $L^{2}({\mathbb{C}})$, the expression (1.2) simplifies to

(1.4)

The process described by (1.2) and (1.4) represents the eigenvalues of a random normal matrix picked from the distribution

(1.5)

where dvol _nm(n)(M) is the natural Riemannian volume form on the n×n normal matrices inherited from the metric of ${\mathbb{C}}^{n^{2}}$ (see [38]); Z _m,n is the normalization constant needed to make the total mass equal to 1. We are interested in the limiting behavior of the process as m,n→+∞ while n=mτ+O(1) for some positive real number τ. Without loss of generality, we will consider only τ=1.

1.4 Local Blow-Up Processes

Let $\mathcal{N}_{+}$ and $\mathcal{N}_{+,0}$ be the set of points defined by

$$\begin{aligned} \mathcal{N}_+:= \bigl\{w\in{\mathbb{C}}:\,\Delta Q(w)>0 \bigr\} ,\qquad \mathcal{N}_{+,0}:= \bigl\{w\in{\mathbb{C}}:\,\Delta Q(w)\ge0 \bigr \}. \end{aligned}$$

In the arXiv preprint [20], which appeared later in the expanded form [21], the function $\widehat{Q}$ was defined as a certain envelope of Q, namely the largest subharmonic function in ${\mathbb{C}}$ which is ≤Q everywhere and has the growth bound

$$\begin{aligned} \widehat{Q}(z)=\log|z|^2+\mathrm{O}(1),\quad\mbox{as}\ |z|\to +\infty. \end{aligned}$$

It is known that $\Delta\widehat{Q}=1_{\mathcal{S}}\Delta Q$ for some compact set $\mathcal{S}$ (see, e.g., [21]). We assume that $\mathcal{S}$ is the minimal compact with this property, and call $\mathcal{S}$ a spectral droplet. We then have $\mathcal{S}\subset\mathcal{N}_{+,0}$. The point process (1.2) has the following property: as m,n→+∞ while n=m+O(1), the points will tend to accumulate on the set $\mathcal{S}$ with density ΔQ there. Moreover, the set $\mathcal{S}\cap\mathcal{N}_{+}$ is rather regular for real-analytic Q, as the Sakai theory applies (cf. [23]; see also the related papers [19] and [22]). Typically we then expect a real-analytic boundary, with the exception of cusps and contact (or kissing) points. Let us refer to the set $\mathrm{int}(\mathcal{S}\cap\mathcal{N}_{+})$ as the bulk. The results of [3, 4] show that for bulk points z, the local blow-up process at z, with coordinates (ξ ₁,…ξ _n ),

$$\begin{aligned} \xi_j:=m^{1/2}\bigl[\Delta Q(z)\bigr]^{1/2}(z_j-z), \end{aligned}$$

where (z ₁,…,z _n ) are from the process (1.2), converges weakly to the translation invariant Ginibre(∞) process, as m,n→+∞ while n=m+o(1). The associated generating kernel is the reproducing kernel $(\xi,\eta)\mapsto\mathrm{e}^{\xi\bar{\eta}}$ of the Bargmann-Fock space. This has the flavor of a universality result. The corresponding statement in the Hermitian random matrix theory is the universality of the sine kernel for bulk (the points z _j would in this context be eigenvalues of the random matrix). We observe here that the sine kernel is the reproducing kernel for the Paley-Wiener space (a subspace of $L^{2}({\mathbb{R}})$ consisting of entire functions). As for the two boundary points in the GUE model, the Tracy-Widom distribution appears, which is generated by the Airy kernel. The Airy kernel is reproducing for another Hilbert space of entire functions (see [27]). This suggests that for real-analytic Q and $z\in\partial\mathcal {S}\cap \mathcal{N}_{+}$, there should exist a local blow-up

$$\begin{aligned} \xi_j:=m^\theta(z_j-z), \end{aligned}$$

where θ=θ(z) is a suitable positive real, such that as m,n→+∞ while n=m+o(1), the process (ξ ₁,…,ξ _n ) would converge to a determinantal process whose generating kernel is the reproducing kernel of a Hilbert space of entire functions. We verify this in the context of the Ginibre ensemble (i.e., with Q(z)=|z|²), and identify the associated Hilbert space as the closed subspace of the Bargmann-Fock space characterized by slow growth in a half-plane (see also Sect. 5 where a characterization via the Bargmann transform is presented). In that case we have $\theta=\frac{1}{2}$ as in the case of interior points. This is in contrast with Hermitian random matrix theory, where a different scaling is required for boundary and for bulk points.

1.5 The Berezin Measure and the Berezin Density

In [3–5], Ameur, Hedenmalm, and Makarov study the Berezin measure ${\mathrm{d}}B_{m,n}^{\langle z\rangle}$ and Berezin density :

which arise in the study of the Berezin transform. The Berezin measure is a probability measure, which makes it more stable than the reproducing kernel K _m,n of Pol _m,n itself as we let m,n→+∞. In terms of the point process (1.2), measures the amount of repulsion from z caused by placing one of the points at z. For bulk points z, we have the convergence ${\mathrm{d}}B^{\langle z\rangle}_{m,n}\to{\mathrm{d}}\delta_{z}$ in the weak-star sense of measures, as m,n→+∞ while n=m+o(1). Here, dδ _z is the Dirac point mass at z. In fact, there is a better result: the blow-up Berezin density

converges to the standard Gaussian $\mathrm{e}^{-|\xi|^{2}}$. This corresponds to the convergence of the local blow-up of the point process to the Ginibre(∞) process (cf. [3, 4]). On the other hand, for points z outside the spectral droplet, i.e., for $z\in{\mathbb{C}}\setminus\mathcal{S}$, the Berezin measure ${\mathrm{d}}B^{\langle z\rangle}_{m,n}$ converges in the weak-star sense of measures to harmonic measure at z with respect to the exterior domain ${\mathbb{C}}\setminus\mathcal{S}$ as m,n→+∞ while n=m+o(1) (see [3] for Q=|z|², and [4] for the general result).

1.6 The Local Blow-Up of the Point Process and the Berezin Density

It is convenient to think of the point process (1.2) in terms of the k-point intensities

We notice quickly that the intensities are unchanged if the kernel changed to

$$\begin{aligned} K^\chi_{m,n}(z,w):=\chi(z)\bar{\chi}(w)K_{m,n}(z,w), \end{aligned}$$

provided that χ is measurable with |χ(z)|≡1 (we can call this a “gauge transformation”). This can help in the asymptotical analysis of local blow-ups. For k=2, we get the 2-point intensity

$$\begin{aligned} &\bigl\{ K_{m,n}(z_1,z_1)K_{m,n}(z_2,z_2)-\bigl|K_{m,n}(z_1,z_2)\bigr|^2 \bigr\} \mathrm{e}^{-mQ(z_1)-mQ(z_2)} \\ &\quad{}=K_{m,n}(z_1,z_1)\mathrm{e}^{-mQ(z_1)} \biggl \{K_{m,n}(z_2,z_2)\mathrm{e}^{-mQ(z_2)} - \frac{|K_{m,n}(z_1,z_2)|^2}{K_{m,n}(z_1,z_1)}\mathrm{e}^{-mQ(z_2)} \biggr\}, \end{aligned}$$

(1.6)

where we recognize the Berezin density as a correction to the product of the two 1-point densities; the 1-point intensity is

$$\begin{aligned} z\mapsto K_{m,n}(z,z)\,\mathrm{e}^{-mQ(z)}. \end{aligned}$$

So, as far as the 2-point intensity goes, we just need the 1-point intensity and the Berezin density. Since the 1-point intensity is just the restriction to z ₁=z ₂ of the Berezin density, the Berezin density is all we need to describe the 2-point intensity. We will be a little lazy and just work with the Berezin density in the context of local blow-ups, although the asymptotics of the k-point intensity would strictly speaking require a little more work. So, although we state many of our assertions regarding local blow-ups in terms of the Berezin density, we maintain that they generalize to statements about the point processes (cf. [4]).

1.7 The Ginibre Ensemble and Its Polyanalytic Generalization

The case Q(z)=|z|² of (1.5) (or (1.2)) is known as the Ginibre ensemble. The (probability generating or reproducing) kernel is now particularly simple:

$$\begin{aligned} K_{m,n}(z,w)= m\sum_{j=0}^{n-1} \frac{(mz \bar{w})^j}{j!}. \end{aligned}$$

Here, $\mathcal{S}=\bar{\mathbb{D}}$, the closed unit disk. We will consider a family of generalizations of the Ginibre ensemble, the polyanalytic Ginibre ensembles, which are defined by the reproducing kernels K _m,n,q of the subspaces

$$\begin{aligned} \mathrm{Pol}_{m,n,q} := \mathrm{span}\, \bigl\{ z^j \overline{z}^k:\, 0\le j\le n-1,\ 0\leq k \leq q-1 \bigr\} \end{aligned}$$

supplied with the Hilbert space structure of $L^{2}({\mathbb{C}},\mathrm {e}^{-m|z|^{2}})$. The correlation kernels for the polyanalytic Ginibre ensembles are given by the formula analogous to (1.3):

(1.7)

The parameter value q=1 corresponds to the standard Ginibre process. In general, we now project to the nq-dimensional subspace of the polyanalytic polynomials, where the degree in $\bar{z}$ is ≤q−1, and the degree in z is ≤n−1. Note that the dimension of the subspace is now nq and not n.

The polyanalytic Ginibre ensembles can be interpreted physically in the following way. In quantum mechanics, the wavefunction of an n-body system consisting of non-interacting fermions with wavefunctions ψ _j ,j=1,…,n, is given by the Slater determinant

$$\begin{aligned} \det\bigl[\psi_j(z_k)\bigr]_{j,k=1}^n. \end{aligned}$$

The important property of this expression is that it satisfies the Pauli exclusion principle, i.e., it is antisymmetric with respect to interchanging two wavefunctions.

In this paper, the wavefunctions of the form $\psi=u\mathrm{e}^{-\frac{1}{2}m|z|^{2}}$, where u is an eigenfunction of the differential operator (densely defined on $L^{2}({\mathbb{C}},\mathrm {e}^{-m|z|^{2}})$)

$$\begin{aligned} \tilde{\Delta}= - \partial_z \bar{\partial}_z + m \bar{z} \bar{\partial}_z, \end{aligned}$$

play a special role. This operator represents (after suitable normalizations) a single particle in the complex plane within a uniform magnetic field of which is strength m and perpendicular to the plane. The eigenspaces for this operator are of the form (see, e.g., [30])

$$\begin{aligned} \delta A^2_{m,r+1}({\mathbb{C}}):=A^2_{m,r+1}({\mathbb{C}}) \ominus A^2_{m,r}({\mathbb{C}}), \end{aligned}$$

where $A^{2}_{m,r}({\mathbb{C}})$ is the Bargmann-Fock space of polyanalytic functions f satisfying ${\bar{\partial}}^{r} f(z)= 0$ (cf. Sect. 2). These eigenspaces are often referred to as Landau levels (in the literature, the term “Landau level” can also refer to the eigenvalue). The symbol “⊖” means taking the orthogonal difference of the two subspaces of $A^{2}_{m,r+1}$. We will denote by u _r+1,j ,j=1,…,n, some orthonormal basis of the space

$$\begin{aligned} {\delta\mathrm{Pol}}_{m,n,r+1}:=\mathrm{Pol}_{m,n,r+1}\ominus \mathrm{Pol}_{m,n,r} \subset\delta A^2_{m,r+1}({\mathbb{C}}). \end{aligned}$$

and write $\psi_{r+1,j}:=u_{r+1,j}\mathrm{e}^{-\frac{1}{2}m|z|^{2}}$ for the corresponding wavefunctions. We now form the wavefunction for a system where there are n fermions at each of the q first Landau levels:

$$\begin{aligned} \varPsi_{q,n}(z) := \det\bigl[\psi_{r,i}(z_{s,j}) \bigr]_{nq\times nq}, \quad1 \leq i, j \leq n,\ 1 \leq r, s \leq q. \end{aligned}$$

Here, we write z=(z _1,1,…,z _r,i ,…,z _q,n ) for an nq-tuple of complex numbers. The corresponding probability amplitude is $\frac{1}{Z_{q,n}}|\varPsi_{q,n}|^{2}$, where Z _q,n is a normalization constant. By a standard argument in random matrix theory (see [25] p. 47), this expression can be rewritten as (the correlation kernel is given by (1.7))

which is exactly the probability density of the polyanalytic Ginibre ensembles. As a result, the polyanalytic Ginibre ensembles model systems of free fermions where all Landau levels below a given level contain the same number of particles. We will focus on the case where m and n large and kept relatively close to each other: physically, this corresponds to each Landau level being completely filled. We should point out that in our treatment, there is no special significance in the choice of having exactly the same number of particles in each Landau level below the cut-off level—other configurations can be analyzed in a similar manner.

For more background on the free fermion interpretation in the normal matrix (ground state) model, see [37]; more information about the connection between polyanalytic functions and Landau levels is contained in [1, 7, 30, 31, 36].

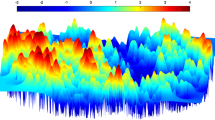
As for the point process, the points generally repel each other, but for q>1, they also tend to avoid certain geometric configurations, such as circles and lines. We have run a simulation in Fig. 1.

Fig. 1

The polyanalytic Ginibre process with the kernel K _m,n,q with m=n=61 and q=3. The simulation is based on the algorithm by Hough, Krishnapur, Peres, and Virág [24]

1.8 Results

Macroscopically, we find that the behavior of the polyanalytic Ginibre ensemble is similar to that of the Ginibre ensemble. If we measure this in terms of the Berezin measure, we have that as m,n→+∞ while n=m+O(1),

$$\begin{aligned} {\mathrm{d}}B_{m,n,q}^{\langle z\rangle}\to{\mathrm{d}}\delta_z\quad \mbox{for}\ z\in\bar{\mathbb{D}},\qquad{\mathrm{d}}B_{m,n,q}^{\langle z\rangle}\to{\mathrm{d}} \omega_z\quad \mbox{for}\ z\in{\mathbb{D}}^e, \end{aligned}$$

where ω _z is the harmonic measure of z with respect to the exterior disk ${\mathbb{D}}^{e}$. Here, K _m,n,q is the reproducing kernel for Pol _m,n,q , and we use the notation

for the corresponding Berezin measure and Berezin density. Interestingly, the microscopic behavior of the Berezin measure ${\mathrm{d}}B^{\langle z\rangle}_{m,n,q}$ is quite different for q>1 compared with the Ginibre case q=1. In terms of the blow-up Berezin density (ΔQ(z)=Δ|z|²≡1 here)

we have the following asymptotics as m,n→+∞ while n=m+O(1):

(1.8)

where $L^{1}_{q-1}$ denotes the generalized Laguerre polynomial of degree q−1 with parameter 1 (see (2.1) for the explicit expression). It is well-known that the Laguerre polynomial $L^{1}_{q-1}$ has exactly q−1 strictly positive roots, which implies that the Berezin density will exhibit a typical Fresnel-type ring pattern (see Fig. 2). Taking (1.6) into account, we see that the zero rings of the Berezin kernel correspond to circles centered at z where in the limit as m,n→+∞ no repulsion occurs between the center z and points on those circles.

Fig. 2

The limiting Berezin density for polyanalytic Ginibre process with q=3 exhibiting Fresnel ring pattern. Here, white is high and black is low Berezin density

This resembles what happens in the one-dimensional GUE case, where the zero density points for the Berezin density come from the zeros of the sine kernel. Actually, the analogy is more than a superficial similarity. If we consider rather big values of q, and scale down to local distance (mq)^−1/2, with

then by the above we have, for $z\in{\mathbb{D}}$,

as m,n→+∞ with n=m+O(1). Next, if we let q→+∞, we get that (see [26] 18.11.5)

$$\begin{aligned} q^{-2} L^{1}_{q-1}\bigl(q^{-1}| \xi'|^2\bigr)^2\mathrm{e}^{-q^{-1}|\xi'|^2} \longrightarrow\Biggl\{\sum_{i=0}^{+\infty} \frac{(-1)^i|\xi'|^{2i}}{i!(i+1)!} \Biggr\}^2 =\frac{J_1(2|\xi '|)^2}{|\xi'|^2}, \end{aligned}$$

where J ₁ is the standard Bessel function. The identity

$$\begin{aligned} \frac{J_1(2|\xi'|)}{|\xi'|}=\int_{\mathbb{D}}\mathrm{e}^{2{\mathrm{i}}\operatorname{Re}[\xi'\bar{\zeta}]}{\mathrm{d}}A(\zeta) \end{aligned}$$

shows that we are dealing with a planar analogue of the sine kernel (the sine kernel is the Fourier transform of the characteristic function of the interval [−1,1], the one-dimensional unit ball). We remark here that the asymptotics (1.8) which is obtained here in the model case Q(z)≡|z|² can be shown to hold at bulk points for rather general weights Q, see [18].

We also investigate the local behaviour of the Berezin transform when |z|=1, i.e., when z is on the boundary of the bulk. Using the same blow-up scale as with an interior point, we show that the blow-up Berezin density tends to a limit which can be expressed in terms of Hermite polynomials (see Theorem 5.10). Here, too, there is a ring-like pattern in the interior direction, but it is not so pronounced as it is for interior points (the bulk). We express the 1-point intensity near a boundary point in terms of a sum of squares of Hermite polynomials. The Wigner semi-circle law then gives the asymptotic behavior of the 1-point function, which tells us the intensity of the process. We find that for big q, but much bigger m,n with m=n+O(1), the 1-point function is nontrivial in the annulus

$$\begin{aligned} 1-q^{1/2}m^{-1/2}\le|z|\le1+q^{1/2}m^{-1/2}; \end{aligned}$$

inside it is essentially constant, and outside it more or less vanishes. Near the outward boundary of the annulus at the scale (mq)^−1/2, we expect the statistics of the point process to be related with the well-known Airy point process (in the sense of Tracy and Widom).

We should mention that the model of the present paper has been studied previously in physics literature, see Dunne [13]. However, as far as we know, the exact scaling limits of the blow-up correlation kernels were not obtained earlier.

1.9 Lifting to Two Complex Variables

Analogous results to [3] are obtained on complex manifolds by Berman [8]. We note that the polyanalytic Ginibre processes can also be viewed as processes in ${\mathbb{C}}^{2}$ with the rather singular weight $\mathrm{e}^{-|z_{1}|^{2}}\delta_{0}(z_{1}-\bar{z}_{2})$, where δ ₀ is unit point mass at 0. Berman considers reproducing kernels of polynomial subspaces as the total degree of the polynomials tends to infinity. In contrast, here we discuss the case where one variable has bounded degree and the degree of the other variable goes to infinity.

1.10 The Polyanalytic Ginibre Ensemble and Weighted Interpolation

It is well known in the theory of random matrices that for complex numbers z ₁,…,z _n , we have

$$\begin{aligned} \frac{1}{n!} \det\bigl[K_{m,n,1}(z_i, z_j) \bigr]_{i,j=1}^n = \frac{1}{Z_{m,n,1}} |\Delta(z_1,\ldots,z_n)|^2, \end{aligned}$$

where Δ(z ₁,…,z _n )=Π _i,j:i<j (z _j −z _i ) is the van der Monde determinant. A point configuration in a compact set which maximizes the van der Monde determinant is known to be a good choice of nodes for Lagrange interpolation [34]. Instead of considering points confined to a compact set, one can add a weight to prevent the points from going off to infinity. This leads to the same expression which arises in the context of random eigenvalues.

We turn to the polyanalytic case. One shows that

$$\begin{aligned} \frac{1}{(nq)!} \det\bigl[K_{m,n,q}(z_i,z_j) \bigr]_{i,j=1}^{nq} = \frac{1}{Z_{m,n,q}}| \Delta_q (z_1,\ldots,z_{nq})|^2, \end{aligned}$$

where Z _m,n,q is a normalization constant

$$\begin{aligned} Z_{m,n,q}:= \int_{{\mathbb{C}}^{nq}}|\Delta_q(z_1,\ldots,z_{nq})|^2 \mathrm{e}^{-m \sum_{j=1}^{nq}Q(z_j)} {\mathrm{d}}A(z_1) \dots {\mathrm{d}} A(z_{nq}) \end{aligned}$$

and

$$\begin{aligned} \Delta_q(z_1,\ldots,z_{nq}) = \mathrm{det} \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & \dots& 1 \\ z_1 & \dots& z_{nq} \\ \vdots& \dots& \vdots \\ z_1^{n-1} & \dots& z_{nq}^{n-1} \\ \bar{z}_1&\dots& \bar{z}_{nq} \\ \bar{z}_1z_1&\dots& \bar{z}_{nq}z_{nq} \\ \vdots& \ddots& \vdots \\ \bar{z}_1^{q-1}&\dots& \bar{z}_{nq}^{q-1} \\ \vdots& \ddots& \vdots \\ \bar{z}_1^{q-1}z_1^{n-1}&\dots& \bar{z}_{nq}^{q-1} z_{nq}^{n-1} \\ \end{array} \right). \end{aligned}$$

So, Δ _q (z ₁,…,z _nq ) is the polyanalytic analogue of the van der Monde determinant. As in the case q=1 (which gives the usual van der Monde determinant), the expression |Δ _q (z ₁,…,z _nq )|² measures how good the configuration is for Lagrange interpolation by polyanalytic polynomials. So, the polyanalytic Ginibre ensemble is a way to produce random Lagrange interpolation sets, using the Gaussian weight for confinement.

1.11 Further Results and Open Problems

In [33] and [4], the authors showed that the fluctuations of eigenvalues of random normal matrices tend to Gaussian free field. The fluctuations of the polyanalytic Ginibre process will be discussed in a separate paper—the limit is again the Gaussian free field, but the variance depends on the degree of polyanalyticity.

One could naturally address all the questions discussed in this article with a more general weight Q. We conjecture that the spectral droplet will be the same as in the analytic case, i.e. that the points from the process will accumulate on the set $\mathcal{S}$, with density given by the equilibrium measure $1_{\mathcal{S}}\Delta Q{\mathrm{d}}A$. It is also likely that the blow-up of the Berezin density at a bulk point z will have a universal limit, which we here computed to be $q^{-1}L^{\langle1\rangle}_{q-1}(|\xi|^{2})^{2}\mathrm{e}^{-|\xi|^{2}}$.

2 Polyanalytic Bargmann-Fock Spaces

2.1 An Orthogonal Basis

We will consider the Bargmann-Fock space $A^{2}_{m,q}({\mathbb{C}})$ of poly-analytic functions of degree ≤q−1, i.e., functions of the form

$$\begin{aligned} f(z) = \sum_{r=0}^{q-1} \bar{z}^r f_r(z), \end{aligned}$$

where all the components f _r are entire, subject to the norm integrability condition

$$\begin{aligned} \|f\|^2_{A^2_{m,q}({\mathbb{C}})}:= \|f\|^2_{L^2({\mathbb{C}},\mathrm{e} ^{-m|z|^2})} =\int _{{\mathbb{C}}} |f(z)|^2 \mathrm{e}^{-m|z|^2} {\mathrm{d}}A(z)<+ \infty. \end{aligned}$$

Here, as always, m>0. We note that $A^{2}_{1,1}({\mathbb{C}})$ is the standard Bargmann-Fock space. As before, let Pol _m,n,q be the closed subspace of $A^{2}_{m,q}({\mathbb{C}})$, defined by the condition that all the components f _r are polynomials of degree less or equal to n−1. Moreover, let K _m,q and K _m,n,q denote the reproducing kernels for $A^{2}_{m,q}({\mathbb{C}})$ and Pol _m,n,q , respectively. We will be concerned with the asymptotic behaviour of the kernel K _m,n,q , as m,n→+∞ while n=m+O(1).

Bargmann-Fock-spaces of polyanalytic functions have been considered in, e.g., [36], where the reproducing kernels and orthonormal bases were identified. We will attempt to supply a self-contained account of these basic matters.

To begin with, we identify an orthonormal basis for the space Pol _m,n,q . Here, and later as well, we will need some standard properties of the classical orthogonal polynomials. For details, we refer the reader to [26]. We need the generalized Laguerre polynomials ((x) _j :=x(x+1)⋯(x+j−1) is the Pochhammer symbol)

$$\begin{aligned} L^\alpha_k(x):=\sum _{i=0}^{k}(-1)^i\binom{k+\alpha}{k-i} \frac{x^i}{i!} =\sum_{i=0}^{k}(-1)^i \frac{(\alpha+i+1)_{k-i}}{i!(k-i)!}x^i. \end{aligned}$$

(2.1)

Proposition 2.1

For q≤n, the following functions form an orthonormal basis for Pol _m,n,q (i,r,j,k are all integer parameters):

$$\begin{aligned} e_{i,r}^{1}(z) :=\sqrt{\frac{r!}{(r+i)!}} \,m^{(i+1)/2}z^i\, L_r^{i} \bigl(m|z|^2\bigr), \quad0\leq i\leq n-r-1,\ 0\leq r\leq q-1, \\ e_{j,k}^{2}(z) :=\sqrt{\frac{j!}{(j+k)!}} \,m^{(k+1)/2}\bar{z}^k\, L^{k}_{j} \bigl(m|z|^2\bigr), \quad0\leq j\leq q-k-1,\ 1\leq k\leq q-1. \end{aligned}$$

Proof

Clearly, all the above functions belong to the space Pol _m,n,q . Also, all the functions $e^{1}_{i,r}$ are orthogonal to each of the functions $e^{2}_{j,k}$, for the indicated ranges of the indices, as can be seen by integrating along circles using polar coordinates. Next, we show that the functions $e^{1}_{i,r}$ form an orthonormal set. Any two functions there having different parameter i are orthogonal, again by integrating along circles using polar coordinates. So, we fix i, and pick two indices r ₁,r ₂. We compute the inner product of two such functions:

$$\begin{aligned} &\int_{\mathbb{C}}e^1_{i,r_1}(z) \overline{e^1_{i,r_2}(z)}\mathrm{e}^{-m|z|^2} {\mathrm{d}}A(z) \\ &\quad{}=\sqrt{\frac{r_1!}{(r_1+i)!}} \sqrt{\frac{r_2!}{(r_2+i)!}}m^{i+1} \int _{{\mathbb{C}}} |z|^{2i}L_{r_1}^{i} \bigl(m|z|^2\bigr)L_{r_2}^{i} \bigl(m|z|^2\bigr) \mathrm{e}^{-m|z|^2} {\mathrm{d}}A(z) \\ &\quad{}=\sqrt{\frac{r_1!r_2!}{(r_1+i)!(r_2+i)!}} \int_{0}^{\infty} L_{r_1}^{i}(t) L_{r_2}^{i}(t) \,t^i\mathrm{e}^{-t} {\mathrm{d}}t = \delta_{r_1,r_2}, \end{aligned}$$

where the delta is in Kronecker’s sense. In a similar fashion, the functions $e^{2}_{j,k}$ form an orthonormal set. So, the functions $e^{1}_{i,r},e^{2}_{j,k}$ together form an orthonormal set. Next, the dimension of the span equals the total number of vectors, which we calculate to nq, which equals the known dimension of the space Pol _m,n,q . The proof is complete. □

2.2 The Reproducing Kernel

For q≤n, we conclude that the reproducing kernel of Pol _m,n,q equals

$$\begin{aligned} K_{m,n,q} (z,w) =& m\sum_{r=0}^{q-1} \sum_{i=0}^{n-r-1} \frac{r!}{(r+i)!} (mz \bar{w})^i L_r^{i}\bigl(m|z|^2 \bigr)L_r^{i}\bigl(m|w|^2\bigr) \\ &{}+ m\sum_{j=0}^{q-2}\sum _{k=1}^{q-j-1} \frac{j!}{(k+j)!} (m \overline{z}w)^k L^{k}_{j}\bigl(m|z|^2 \bigr)L^{k}_{j}\bigl(m|w|^2\bigr). \end{aligned}$$

(2.2)

Remark 2.2

In [2], it is pointed out that Perelomov in his book [32], p. 35, mentions that the formula (2.2)—viewed as the explicit expression for the matrix elements of the displacement operator—had been used by Feynman and Schwinger in a somewhat different form. For this reason, Abreu and Feichtinger [2] suggest naming the orthogonal basis of Proposition 2.1 the Feynman-Schwinger basis for the polyanalytic Bargmann-Fock space.

We note that by plugging in n=+∞ in Proposition 2.1 we get an orthonormal basis for the space $A^{2}_{m,q}({\mathbb{C}})$. It follows that the same procedure of plugging in n=+∞ in the above expression for K _m,n,q gives us K _m,q , the reproducing kernel for $A^{2}_{m,q}({\mathbb{C}})$. What is probably less obvious is that K _m,q may be written in a much simpler form (this representation is, however, known; compare with [7, 31]).

Proposition 2.3

We have that

$$\begin{aligned} K_{m,q} (z,w) =& m\sum_{r=0}^{q-1} \sum_{i=0}^{\infty} \frac{r!}{(r+i)!}(mz \bar{w})^i L_r^{i}\bigl(m|z|^2 \bigr)L_r^{i}\bigl(m|w|^2\bigr) \\ &{}+m\sum_{j=0}^{q-2} \sum _{k=1}^{q-j-1} \frac{j!}{(j+k)!} (m \bar{z}w)^k L^{k}_{j}\bigl(m|z|^2 \bigr)L^{k}_{j}\bigl(m|w|^2\bigr) \\ =&m \,L^{1}_{q-1}\bigl(m|z-w|^2\bigr) \mathrm{e}^{m z \bar{w}}. \end{aligned}$$

Proof

It is clear from Proposition 2.1 that the double sum expression equals K _m,q (z,w), so the only thing that needs attention is the last equality. We first do the case w=0. Many of the terms in the double sum vanish, so that we are left with

$$\begin{aligned} K_{m,q} (z,0)=m\sum_{r=0}^{q-1}L_r^{0} \bigl(m|z|^2\bigr)L_r^{0}(0), \end{aligned}$$

It is well-known that $L_{r}^{0}(0)=1$ and that $\sum_{r=0}^{q-1} L^{\alpha}_{r}=L^{\alpha+1}_{q-1}$, so that the above reduces to

$$\begin{aligned} K_{m,q} (z,0) = m\, L^{1}_{q-1} \bigl(m|z|^2\bigr). \end{aligned}$$

We turn to general $w \in{\mathbb{C}}$. It is well-known that the transformation

$$\begin{aligned} {\mathbf{T}}_w[f](z):=\mathrm{e}^{-\frac{1}{2} m|w|^2-mz\bar{w}}f(z+w) \end{aligned}$$

acts unitarily on $A^{2}_{m,q}({\mathbb{C}})$; its adjoint is ${\mathbf{T}} _{w}^{*}={\mathbf{T}}_{-w}$. By the reproducing property of K _m,q (z,0), we have, for $f\in A^{2}_{m,q}({\mathbb{C}})$,

$$\begin{aligned} \mathrm{e}^{-\frac{1}{2}m|w|^2}f(w)={\mathbf{T}}_w[f](0) =& \int_{\mathbb{C}} {\mathbf{T}}_w f(z)\overline{K_{m,q}(z,0)}\mathrm{e}^{-m|z|^2}{\mathrm{d}} A(z) \\ =&\int_{\mathbb{C}}f(z)\overline{{\mathbf{T}}_w^* \bigl[K_{m,q}(\cdot,0)\bigr](z)}\, \mathrm{e}^{-m|z|^2}{\mathrm{d}}A(z) \\ =&m\mathrm{e}^{-\frac{1}{2}m|w|^2} \int_{\mathbb{C}}f(z)\,L^{1}_q \bigl(m|z-w|^2\bigr)\mathrm{e}^{m\bar{z} w}\mathrm {e}^{-m|z|^2}{\mathrm{d}}A(z). \end{aligned}$$

The claim that $K_{m,q}(z,w)= m\,L^{1}_{q-1}(m|z-w|^{2}) \mathrm{e}^{mz\bar{w}}$ now follows immediately. □

2.3 Szegö Asymptotics

We shall show that the kernel K _m,n,q (z,w) is approximated well by K _m,q (z,w), provided that $z,w\in{\mathbb{D}}$ are rather close to one another. It will be instrumental to study the asymptotic behavior of the partial sums

$$\begin{aligned} E_{k}(\zeta)=\sum_{j=0}^{k} \frac{1}{j!} \zeta^j \end{aligned}$$

of the Taylor expansion of the exponential function. In [35], Szegö showed that

$$\begin{aligned} \frac{E_k(k\zeta)}{\mathrm{e}^{k\zeta}}= 1-\frac {1}{\sqrt {2 \pi k}} \bigl(\zeta \mathrm{e}^{1-\zeta}\bigr)^k \frac{\zeta}{1-\zeta} \bigl(1+ \epsilon^{1}_k(\zeta)\bigr), \end{aligned}$$

(2.3)

provided that |ζe^1−ζ|<1 and |ζ|<1, whereas

$$\begin{aligned} \frac{E_k(k\zeta)}{\mathrm{e}^{k\zeta}}= \frac {1}{\sqrt{2 \pi k}}\bigl(\zeta \mathrm{e}^{1-\zeta}\bigr)^k \frac{\zeta}{\zeta-1} \bigl(1+ \epsilon^{2}_k(\zeta)\bigr), \end{aligned}$$

(2.4)

provided that |ζe^1−ζ|<1 and |ζ|>1. Here, we have the convergence

$$\begin{aligned} \lim_{k\to+\infty}\epsilon^{1}_k(z)=\lim _{k\to+\infty} \epsilon^{2}_k(z)=0 \end{aligned}$$

uniformly on compact subsets of the respective domains. As for (2.4), the uniform convergence $\epsilon^{2}_{k}(\zeta)\to0$ as k→+∞ holds also in certain unbounded subdomains; in particular, along the real line, we have uniform convergence on all intervals [a,+∞[ with a>1.

2.4 An Elementary Estimate of Laguerre Polynomials

The following elementary estimate of generalized Laguerre polynomials will prove useful.

Lemma 2.4

Suppose α is a positive real. Then, for k=0,1,2,…, we have that

$$\begin{aligned} \bigl|L^\alpha_k(x)\bigr|\le\frac{1}{k!}(x+ \alpha+k)^k,\quad x\in[0,+\infty\mathclose{[}. \end{aligned}$$

Moreover, with $\beta:=\alpha+2k-2+2\sqrt{\frac{1}{4}+(k-1)(k+\alpha-1)}$, we have that

$$\begin{aligned} \frac{1}{k!}(x-\beta)^k\le(-1)^k L_k^{\alpha}(x)\le\frac{1}{k!}x^k,\quad x \in[\beta,+\infty\mathclose{[}. \end{aligned}$$

Actually, the related inequality $|L_{k}^{\alpha}(x)|\le\frac {1}{k!}x^{k}$ holds for all $x\in[\frac{1}{2}\beta,+\infty\mathclose{[}$.

Proof

We begin with the estimate (0≤i≤k is assumed)

$$\begin{aligned} (\alpha+i+1)_{k-i}\le(\alpha+k)^{k-i}. \end{aligned}$$

Next, we note that for x≥0 and k=0,1,2,…, we have

$$\begin{aligned} L^\alpha_k(x)=\sum_{i=0}^k(-1)^k \frac{(\alpha+i+1)_{k-i}}{i!(k-i)!} x^i=\sum_{i\ \mathrm{even}} \frac{(\alpha+i+1)_{k-i}}{i!(k-i)!} x^i-\sum_{i\ \mathrm{odd}} \frac{(\alpha+i+1)_{k-i}}{i!(k-i)!} x^i, \end{aligned}$$

and in view of the above estimate,

$$\begin{aligned} \sum_{i\ \mathrm{even}} \frac{(\alpha+i+1)_{k-i}}{i!(k-i)!} \le\sum_{i\ \mathrm {even}}\frac{(\alpha+k)^{k-i}}{i!(k-i)!} = \frac{1}{2\,k!} \bigl((\alpha+k+x)^k+(\alpha+k-x)^k \bigr), \end{aligned}$$

and, analogously,

$$\begin{aligned} \sum_{i\ \mathrm{odd}} \frac{(\alpha+i+1)_{k-i}}{i!(k-i)!} \le\sum_{i\ \mathrm {odd}}\frac{(\alpha+k)^{k-i}}{i!(k-i)!} = \frac{1}{2\,k!} \bigl((\alpha+k+x)^k-(\alpha+k-x)^k \bigr). \end{aligned}$$

By discarding alternatively the even or odd contribution, we arrive at

$$\begin{aligned} \bigl|L^\alpha_k(x)\bigr|\le\frac{1}{2\,k!} \bigl((x+ \alpha+k)^k+|\alpha+k-x|^k \bigr), \end{aligned}$$

which is slightly stronger than the first estimate.

It is well-known that $L_{k}^{\alpha}$ is a polynomial of degree k all of whose zeros are distinct and real, and they all fall in the interval ]0,β[ (see 18.16.13 of [26]). Therefore, we can write

$$\begin{aligned} L^\alpha_k(x)=\frac{(-1)^k}{k!} (x- \beta_1)\cdots(x-\beta_k), \end{aligned}$$

(2.5)

where β ₁<⋯<β _k are the zeros of $L^{\alpha}_{k}$. Now, all the zeros satisfy x−β _j ≥x−β≥0 for x≥β and |x−β _j |≤x for x≥β/2. The remaining estimates of the proposition follow immediately from combining these observations with the representation (2.5). □

2.5 Approximation of the Polynomial Polyanalytic Reproducing Kernel

We estimate the difference K _m,n,q −K _m,q .

Proposition 2.5

Let $z,w\in{\mathbb{C}}$ be such that |zw|≤θ ₁<1 and |zw|e^1−|zw|≤θ ₂<1. Let M be a positive real number. Then, as m,n→+∞ while |m−n|≤M,

$$\begin{aligned} \bigl|K_{m,n,q}(z,w)-K_{m,q}(z,w)\bigr| \,\mathrm{e}^{-m|zw|} \le C m^{q}\theta_2^m(1-\theta_1)^{-2} \bigl[1+|z|^{2q}+|w|^{2q}\bigr], \end{aligned}$$

where the constant C depends on q and M.

Proof

In view of (2.2) and Proposition 2.3, we have that for q≤n,

$$\begin{aligned} K_{m,q}(z,w)-K_{m,n,q}(z,w)=m\sum _{r=0}^{q-1}\sum_{i=n-r}^{+\infty} \frac{r!}{(r+i)!}(mz \bar{w})^i L_r^{i} \bigl(m|z|^2\bigr)L_r^{i}\bigl(m|w|^2 \bigr). \end{aligned}$$

By Lemma 2.4, we get that

$$ \begin{aligned}[b] &\Biggl| \sum^{+\infty}_{i=n-r} \frac{r!}{(r+i)!}(mz \bar{w})^i L_r^{i} \bigl(m|z|^2\bigr)L_r^{i}\bigl(m|w|^2 \bigr) \Biggr| \\ &\quad{}\le\sum^{+\infty}_{i=n-r}\frac{1}{r!(r+i)!}\bigl(m|zw|\bigr)^i \bigl(m|z|^2+i+r\bigr)^r \bigl(m|w|^2+i+r \bigr)^r \\ &\quad{}=\frac{1}{r!}\sum^{+\infty}_{j=0} \frac{1}{(n+j)!}\bigl(m|zw|\bigr)^{n-r+j} \bigl(m|z|^2+n+j \bigr)^r\bigl(m|w|^2+n+j\bigr)^r \\ &\quad{}\le\frac{4^{r-1}}{r!}\sum^{+\infty}_{j=0} \frac{1}{(n+j)!}\bigl(m|zw|\bigr)^{n-r+j} \bigl[\bigl(m|z|^2 \bigr)^r+(n+j)^r\bigr] \bigl[\bigl(m|w|^2 \bigr)^r+(n+j)^r\bigr]. \end{aligned} $$

(2.6)

For r confined to 0≤r≤q−1 and for big n, say n≥n ₀(q), we have

$$\begin{aligned} \frac{(n+j)^{2r}}{(n+j)!}\le\frac{2}{(n+j-2r)!}\quad\mbox{and}\quad\frac{(n+j)^{r}}{(n+j)!} \le\frac{2}{(n+j-r)!}, \end{aligned}$$

so that if we use the notation

$$\begin{aligned} R_k(z)=\sum_{j=k+1}^{+\infty} \frac{1}{j!}z^j=\mathrm{e}^z-E_k(z), \end{aligned}$$

we obtain from (2.6) that for 0≤r≤q−1 and n≥n ₀(q),

$$ \begin{aligned}[b] &\Biggl| \sum^{+\infty}_{i=n-r} \frac{r!}{(r+i)!}(mz \bar{w})^i L_r^{i} \bigl(m|z|^2\bigr)L_r^{i}\bigl(m|w|^2 \bigr) \Biggr| \\ &\quad{}\le\frac{4^{r-1}m^r}{r!} \bigl[ |zw|^r R_{n-1}\bigl(m|zw|\bigr)+ 2 \bigl(|z|^{2r}+|w|^{2r}\bigr) R_{n-r-1}\bigl(m|zw|\bigr) \\ &\qquad+2|zw|^r R_{n-2r-1}\bigl(m|zw|\bigr) \bigr]. \end{aligned} $$

(2.7)

Next, we see from Szegö’s asymptotical expansion (2.3) that for large k,l with l=k+O(1), we have

$$\begin{aligned} \frac{R_k(l\zeta)}{\mathrm{e}^{l\zeta}}= (2 \pi k)^{-1/2}(l/k)^{k} \frac{\zeta}{k/l-\zeta}\bigl(z\mathrm{e}^{1-l\zeta/k}\bigr )^k\bigl(1+ \epsilon^{1}_k(l\zeta/k)\bigr), \end{aligned}$$

(2.8)

as k,l→+∞ and l=k+O(1). By a careful application of (2.8) to (2.7), and summing over 0≤r≤q−1, the assertion of the proposition follows. □

Corollary 2.6

For $z,w\in{\mathbb{D}}$, let 1−|zw|≥τ>0. Then, as m,n→+∞, while |m−n|≤M,

$$\begin{aligned} K_{m,n,q}(z,w)=K_{m,q}(z,w)+\mathrm{O}\bigl(\mathrm{e}^{-\frac{1}{2}m\tau^2} \mathrm{e}^{m|zw|}\bigr), \end{aligned}$$

where the “O” constant depends on τ, q, and M.

Proof

A Taylor series expansion of the logarithm gives that

$$\begin{aligned} t\,\mathrm{e}^{1-t}<\mathrm{e}^{-\frac{1}{2}(1-t)^2},\quad0\le t<1, \end{aligned}$$

and, together with the fact that the exponential function grows faster than any given power, the assertion follows from Proposition 2.5. □

As we shall see, Proposition 2.5 implies that the Berezin density

behaves locally near z like the Berezin density

(2.9)

To make this precise, we recall the definition of the blow-up Berezin density:

Proposition 2.7

Fix $z\in{\mathbb{D}}$. Then

as m,n→+∞ while n=m+O(1).

Proof

By (2.9), we have

so the comparison is with the blow-up Berezin density for K _m,q . We write w:=z+m ^−1/2 ξ; since $z\in{\mathbb{D}}$ is fixed, we have 1−|z|²≥τ>0 for some small τ, and we suppose that w is close to z so that 1−|zw|≥τ>0 as well. Then, by Proposition 2.3 and Corollary 2.6,

so that if we expand the square using that

$$\begin{aligned} \bigl|L^1_{q-1}\bigl(m|z-w|^2\bigr)\bigr|=\mathrm{O} \bigl(m^{q-1}\bigr), \end{aligned}$$

where the “O” depends only on q (this follows from Lemma 2.4), and simplify the expression, we arrive at

which immediate gives that

The corresponding blow-up Berezin density then has

(2.10)

As exponentials grow faster than polynomials, the error terms is negligible for big m. For fixed $z\in{\mathbb{D}}$, the requirement on ξ so that 1−|zw|≥τ for some fixed τ>0 is fulfilled for big m if, say, |ξ|≤logm is required. So, (2.10) has the immediate consequence that

(2.11)

where more generally ${\mathbb{D}}(z_{0},\rho)$ denotes the open disk of radius ρ about z ₀. Since the associated blow-up Berezin measures

are both probability measures, the assertion of the proposition follows from (2.11) once it is noted that the right-hand side of (2.11) tends to 0 as m→+∞. □

We note that the claimed convergence ${\mathrm{d}}B^{\langle z\rangle }_{m,n,q}\to {\mathrm{d}}\delta_{z}$ for $z\in{\mathbb{D}}$ is an immediate consequence of Proposition 2.7.

3 Berezin Density Asymptotics for an Exterior Point

3.1 Convergence to Harmonic Measure

We show that the Berezin measures have the convergence ${\mathrm{d}}B^{\langle z\rangle}_{m,n,q}\to{\mathrm{d}}\omega_{z}$ for $z\in {\mathbb{D}}^{e}$ as m,n→+∞ while n=m+O(1). Here, ω _z is harmonic measure with respect to the point z and the exterior disk ${\mathbb{D}}^{e}$.

3.2 Concentration of the Berezin Mass

We first study the concentration of the Berezin measure to neighborhoods of the closed unit disk $\bar{\mathbb{D}}$. We recall the standard notation ${\mathbb{D}} (z_{0},\rho)$ for the open disk of radius ρ centered at z ₀.

Lemma 3.1

Suppose $z\in{\mathbb{D}}^{e}$ and that ρ>1. Then

(3.1)

as m,n→+∞ while n≤m+O(1).

Proof

Let $w\in{\mathbb{C}}\setminus{\mathbb{D}}(0,\rho)$. We note that

$$\begin{aligned} n-1\le m+\mathrm{O}(1)\le2m \end{aligned}$$

(3.2)

for sufficiently big m, and so, by Lemma 2.4,

$$ \begin{aligned}[b] &\sum_{i=0}^{n-r-1} \frac{r!}{(r+i)!} \bigl|(mz\bar{w})^iL_r^{i} \bigl(m|z|^2\bigr)L_r^{i}\bigl(m|w|^2 \bigr) \bigr| \\ &\quad{}\le\sum_{i=0}^{n-r-1} \frac{1}{r!(r+i)!} \bigl(m|zw|\bigr)^i\bigl(m|z|^2+i+r\bigr)^r \bigl(m|w|^2+i+r\bigr)^r \\ &\quad{}\leq\frac{9^{r}}{r!}\sum _{i=0}^{n-r-1} \frac{1}{(r+i)!}\bigl(m|zw|\bigr)^{i+2r} \le\frac{9^{r}}{r!}\bigl(m|zw|\bigr)^{r}\,E_{n-1}\bigl(m|zw|\bigr). \end{aligned} $$

(3.3)

If we replace (n,r) by (q,j) in (3.3), we obtain

$$\begin{aligned} \sum_{k=1}^{q-j-1} \frac{j!}{(j+k)!} \bigl|(m\bar{z}w)^k L^{k}_{j} \bigl(m|z|^2\bigr)L^{k}_{j} \bigl(m|w|^2\bigr) \bigr| \leq\frac{9^j}{j!}\bigl(m|zw|\bigr)^j E_{q-1}\bigl(m|zw|\bigr). \end{aligned}$$

(3.4)

We may restrict to q≤n; after, we are considering the limit as n→+∞. As E _q−1≤E _n−1 on the positive half-axis for q≤n, an application of (3.3) and (3.4) to (2.2) gives

$$\begin{aligned} \bigl|K_{m,n,q}(z,w)\bigr| \leq2m \mathrm{e}^9\bigl(m|zw|\bigr)^{q-1}E_{n-1}\bigl(m|zw|\bigr). \end{aligned}$$

(3.5)

Next, we observe that Pol _m,n,1⊂Pol _m,n,q (since q≥1), which implies that

$$\begin{aligned} K_{m,n,q}(z,z) \geq K_{m,n,1}(z,z)=mE_{n-1} \bigl(m|z|^2\bigr). \end{aligned}$$

We conclude that the Berezin density may be estimated as follows:

(3.6)

Finally, we see from Szegö’s asymptotical expansion (2.4) that

$$\begin{aligned} \frac{E_k(l\zeta)}{\mathrm{e}^{l\zeta}}= (2 \pi k)^{-1/2}(l/k)^{k} \frac{\zeta}{\zeta-k/l}\bigl(\zeta\mathrm{e}^{1-l\zeta/k}\bigr )^k\bigl(1+ \epsilon^{2}_k(l\zeta/k)\bigr). \end{aligned}$$

(3.7)

Here, k≤l+O(1), where the convergence $\epsilon^{2}_{k}(l\zeta/k)\to0$ is uniform if ζ is real with ζ≥a for some fixed a>1. This leads to

$$\begin{aligned} \frac{E_{n-1}(m|zw|)^2}{E_{n-1}(m|z|^2)}=\bigl[2\pi(n-1)\bigr ]^{-1/2}\bigl[m/(n-1) \bigr]^{n-1} \mathrm{e}^{n-1}|w|^{2n-2}\bigl(1+\mathrm{o}(1)\bigr), \end{aligned}$$

where the “o” term is uniform in the convergence. As we implement this estimate in (3.6), and integrate over ${\mathbb{C}} \setminus {\mathbb{D}}(0,\rho)$, the claim follows. □

3.3 A Principal Value Calculation

We follow the approach of [3], and calculate a certain principal value integral. As on the real line, principal value integrals in the complex plane are defined by first removing a disk of radius ϵ around the singularity and then letting ϵ→0.

Lemma 3.2

Fix $z\in{\mathbb{D}}^{e}$. For any l=0,1,2,…, we have

as m,n→+∞ with n=m+O(1).

Proof

The case q=1 was treated in [3], so we may from now on assume that q≥2. We write

$$\begin{aligned} K_{m,n,q}=K_{m,n,q}^I+K_{m,n,q}^{II}, \end{aligned}$$

where

$$\begin{aligned} K_{m,n,q}^I(z,w):=m\sum_{r=0}^{q-1} \sum_{i=0}^{n-r-1} \frac{r!}{(r+i)!}(mz \bar{w})^i L_r^{i}\bigl(m|z|^2 \bigr)L_r^{i}\bigl(m|w|^2\bigr) \end{aligned}$$

and

$$\begin{aligned} K_{m,n,q}^{II}(z,w):= m\sum_{j=0}^{q-2} \sum_{k=0}^{q-j-1} \frac{j!}{(j+k)!} (m \bar{z}w)^k L^{k}_{j}\bigl(m|z|^2 \bigr)L^{k}_{j}\bigl(m|w|^2\bigr). \end{aligned}$$

It follows that the expression |K _m,n,q |² decomposes accordingly:

$$ \bigl|K_{m,n,q}(z,w)\bigr|^2 =\bigl|K_{m,n,q}^I(z,w)\bigr|^2+\bigl|K_{m,n,q}^{II}(z,w)\bigr|^2 +2\operatorname{Re}\bigl[ K_{m,n,q}^I(z,w)\overline{K_{m,n,q}^{II}(z,w)} \bigr]. $$

(3.8)

We first consider the following integral involving $|K_{m,n,q}^{I}|^{2}$:

$$\begin{aligned} &\operatorname{\mathrm{pv}}\int_{{\mathbb{C}}} w^{-l} \bigl|K^I_{m,n,q}(z,w)\bigr|^2 \mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{}=m^2 \sum_{r_1,r_2=0}^{q-1}\sum _{i_1=0}^{n-r_1-1} \sum _{i_2=0}^{n-r_2-1} \operatorname{\mathrm{pv}}\int_{{\mathbb{C}}} w^{-l} \frac{r_1!r_2!}{(r_1+i_1)!(r_2+i_2)!}(mz\bar{w})^{i_1}(m \bar{z}w)^{i_2} \\ &\qquad{}\times L_{r_1}^{i_1}\bigl(m|z|^2 \bigr)L^{i_1}_{r_1}\bigl(m|w|^2 \bigr)L^{i_2}_{r_2}\bigl(m|z|^2\bigr) L^{i_2}_{r_2}\bigl(m|w|^2\bigr) \mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{}=m^2 z^{-l} \sum_{r_1,r_2=0}^{q-1} \sum_{i_1=0}^{n-r_1-1}\sum _{i_2=0}^{n-r_2-1} \frac {m^{i_1+i_2}r_1!r_2!}{(r_1+i_1)!(r_2+i_2)!}\delta_{i_2,i_1+l} \,|z|^{2i_2} L_{r_1}^{i_1}\bigl(m|z|^2 \bigr)L^{i_2}_{r_2}\bigl(m|z|^2\bigr) \\ &\qquad{}\times\int_{{\mathbb{C}}} |w|^{2i_1} L^{i_1}_{r_1} \bigl(m|w|^2\bigr) L^{i_2}_{r_2} \bigl(m|w|^2\bigr) \mathrm{e}^{-m|w|^2}{\mathrm{d}}A(w), \end{aligned}$$

(3.9)

where the delta is understood in Kronecker’s sense. The identity (for p=1,2,3,…)

$$\begin{aligned} L^{\alpha+p}_r(x)= \sum _{s=0}^r \binom{r-s+p-1}{p-1}\, L_{s}^{\alpha}(x) \end{aligned}$$

(3.10)

plus the standard orthogonality properties of the Laguerre polynomials gives that

$$\begin{aligned} \int_0^{+\infty}t^{i_1}L_{r_1}^{i_1}(t)L_{r_2}^{i_1+l}(t) \mathrm{e}^{-t}{\mathrm{d}}t= \frac {(r_1+i_1)!(r_2-r_1+l-1)!}{r_1!(r_2-r_1)!(l-1)!}, \end{aligned}$$

where the right-hand side should be interpreted as 0 for r ₂<r ₁. By polar coordinates, then, we have

$$\begin{aligned} \int_{\mathbb{C}}|w|^{2i_1}L_{r_1}^{i_1} \bigl(m|w|^2\bigr)L_{r_2}^{i_1+l} \bigl(m|w|^2\bigr)\mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w)= m^{-i_1-1} \frac{(r_1+i_1)!(r_2-r_1+l-1)!}{r_1!(r_2-r_1)!(l-1)!}, \end{aligned}$$

and (3.9) simplifies to

$$\begin{aligned} &\operatorname{\mathrm{pv}}\int_{{\mathbb{C}}} w^{-l} |K^I_{m,n,q}(z,w)|^2\mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{}=m\,z^{-l} \sum_{r_1=0}^{q-1}\sum _{r_2=r_1}^{q-1}\sum _{i_1=0}^{n-l-r_2-1} \frac {r_2!(r_2-r_1+l-1)!}{(r_2-r_1)!(l-1)!(r_2+i_1+l)!} \\ &\qquad{}\times\bigl(m|z|^{2}\bigr)^{i_1+l}L_{r_1}^{i_1} \bigl(m|z|^2\bigr)L^{i_1+l}_{r_2} \bigl(m|z|^2\bigr), \end{aligned}$$

(3.11)

provided n is so big that q+l≤n. Next, we apply Lemma 2.4 and (3.2) (using that $z\in {\mathbb{D}}^{e}$) to arrive at

$$ \begin{aligned}[b] &\sum_{i_1=0}^{n-l-r_2-1} \frac{r_1!r_2!}{(r_2+i_1+l)!} \,\bigl(m|z|^{2}\bigr)^{i_1+l} \bigl|L_{r_1}^{i_1}\bigl(m|z|^2\bigr)L^{i_1+l}_{r_2} \bigl(m|z|^2\bigr) \bigr| \\ &\quad{}\le\sum_{i_1=0}^{n-l-r_2-1}\frac{1}{(r_2+i_1+l)!} \, \bigl(m|z|^{2}\bigr)^{i_1+l}\bigl(m|z|^2+i_1+r_1 \bigr)^{r_1}\bigl(m|z|^2+i_1+l+r_2 \bigr)^{r_2} \\ &\quad{}\le3^{r_1+r_2}\sum_{i_1=0}^{n-l-r_2-1} \frac{1}{(r_2+i_1+l)!} \,\bigl(m|z|^{2}\bigr)^{r_1+r_2+i_1+l}\le 3^{r_1+r_2}\bigl(m|z|^2\bigr)^{r_1}E_{n-1} \bigl(m|z|^2\bigr). \end{aligned} $$

(3.12)

On the other hand, by the estimate from below in Lemma 2.4,

$$\begin{aligned} K_{m,n,q}(z,z) \geq K^{I}_{m,n,q}(z,z) =& m\sum_{r=0}^{q-1} \sum_{i=0}^{n-r-1} \frac{r!}{(r+i)!} \bigl(m|z|^2\bigr)^i L^{i}_{r} \bigl(m|z|^2\bigr)^2 \\ \ge& m\sum_{r=0}^{q-1} \sum _{i=0}^{n-r-1} \frac{1}{r!(r+i)!} \bigl(m|z|^2 \bigr)^i \bigl[m|z|^2-\beta(n)\bigr]^{2r} \end{aligned}$$

(3.13)

provided that m|z|²≥β(n), where

$$\begin{aligned} \beta(n):=n+q-4+2\sqrt{\frac{1}{4}+(q-2) (n-1)}=n+\mathrm{O}(\sqrt{n}). \end{aligned}$$

As we assume $z\in{\mathbb{D}}^{e}$ and n=m+O(1), we must have

$$\begin{aligned} m|z|^2-\beta(n)=m\bigl(|z|^2-1\bigr)+m-\beta(n)\ge \frac{1}{2} m\bigl(|z|^2-1\bigr) \end{aligned}$$

for big enough m,n, and so, by (3.13),

$$\begin{aligned} K_{m,n,q}(z,z) \geq K^{I}_{m,n,q}(z,z) \ge& m\sum_{r=0}^{q-1} \sum_{i=0}^{n-r-1} \frac{4^{-r}}{r!(r+i)!} \bigl(m|z|^2\bigr)^{i+2r} \\ \ge&\frac{4^{1-q}m}{(q-1)!}(m|z|)^{q-1}\bigl[E_{n-1} \bigl(m|z|^2\bigr)- E_{q-2}\bigl(m|z|^2\bigr) \bigr] \\ \ge&\frac{4^{-q}m}{(q-1)!}(m|z|)^{q-1}E_{n-1} \bigl(m|z|^2\bigr). \end{aligned}$$

(3.14)

Here, we used that the E _n−1(m|z|²) is much bigger than E _q−2(m|z|²) as m,n both grow. Let us look at the contribution from 0≤r ₁≤q−2 in the right-hand side of (3.11) using the estimate (3.12):

$$ \begin{aligned} &m\,|z|^{-l} \sum_{r_1=0}^{q-2}\sum _{r_2=r_1}^{q-1}\sum _{i_1=0}^{n-l-r_2-1} \frac {r_2!(r_2-r_1+l-1)!}{(r_2-r_1)!(l-1)!(r_2+i_1+l)!} \, \bigl(m|z|^{2}\bigr)^{i_1+l} \bigl|L_{r_1}^{i_1} \bigl(m|z|^2\bigr)L^{i_1+l}_{r_2} \bigl(m|z|^2\bigr) \bigr| \\ &\quad{}\le m\,\frac{|z|^{-l}}{(l-1)!}\sum_{r_1=0}^{q-2} \sum_{r_2=r_1}^{q-1} \frac{(r_2-r_1+l-1)!}{r_1!(r_2-r_1)!}3^{r_1+r_2} \bigl(m|z|^2\bigr)^{r_1}E_{n-1} \bigl(m|z|^2\bigr) \\ &\quad{}\le m C_1(q,l) \bigl(m|z|^2\bigr)^{q-2}E_{n-1} \bigl(m|z|^2\bigr), \end{aligned} $$

for an appropriate positive constant C ₁(q,l). As we combine this estimate with (3.14), we obtain

$$\begin{aligned} &m\,\frac{|z|^{-l}}{K_{m,n,q}(z,z)} \sum_{r_1=0}^{q-2}\sum _{r_2=r_1}^{q-1}\sum _{i_1=0}^{n-l-r_2-1} \frac{r_2!(r_2-r_1+l-1)!}{(r_2-r_1)!(l-1)!(r_2+i_1+l)!} \\ &\quad{}\times\bigl(m|z|^{2}\bigr)^{i_1+l} \bigl|L_{r_1}^{i_1} \bigl(m|z|^2\bigr)L^{i_1+l}_{r_2} \bigl(m|z|^2\bigr) \bigr| \le C_2(q,l)m^{-1}=\mathrm{O} \bigl(m^{-1}\bigr)\longrightarrow0, \end{aligned}$$

as m,n→+∞ in the prescribed fashion. So the contribution to (3.11) which comes from 0≤r ₁≤q−2 is negligible from the point of view of the Berezin density. It remains to consider the contribution from r ₁=q−1. The corresponding part of the sum in the right-hand side of (3.11) equals

$$\begin{aligned} m\,z^{-l} \sum_{i_1=0}^{n-l-q} \frac{(q-1)!}{(q+i_1+l-1)!} \,\bigl(m|z|^{2}\bigr)^{i_1+l}L_{q-1}^{i_1} \bigl(m|z|^2\bigr)L^{i_1+l}_{q-1} \bigl(m|z|^2\bigr), \end{aligned}$$

and we now claim that

$$ m\,\frac{z^{-l}}{K_{m,n,q}(z,z)} \sum _{i_1=0}^{n-l-q} \frac{(q-1)!}{(q+i_1+l-1)!} \, \bigl(m|z|^{2}\bigr)^{i_1+l}L_{q-1}^{i_1} \bigl(m|z|^2\bigr)L^{i_1+l}_{q-1} \bigl(m|z|^2\bigr) \longrightarrow z^{-l}, $$

(3.15)

as m,n→+∞ in the given fashion. We use the recurrence relation (3.10) to write

$$\begin{aligned} L^{i_1}_{q-1}(x) = L^{i_1+l}_{q-1}(x)- \sum_{s=0}^{q-2} \binom{q+l-s-2}{l-1}\, L^{i_1}_s(x). \end{aligned}$$

(3.16)

A straightforward argument allows us to show that as insert this into (3.15), the sum that is subtracted on the right-hand side of (3.16) makes asymptotically no contribution to the sum in (3.15). Consequently, (3.15) is equivalent to having

$$\begin{aligned} m\,\frac{z^{-l}}{K_{m,n,q}(z,z)}\sum_{i_1=0}^{n-l-q} \frac{(q-1)!}{ (q+i_1+l-1)!} \bigl(m|z|^2\bigr)^{i_1+l} L^{i_1+l}_{q-1}\bigl(m|z|^2\bigr)^2 \longrightarrow z^{-l} \end{aligned}$$

(3.17)

as m,n→+∞ in the given fashion. If we insert the expression (2.2) defining K _m,n,q (z,z), we see that (there is some cancellation of terms)

$$\begin{aligned} &z^{-l}-m\,\frac{z^{-l}}{K_{m,n,q}(z,z)}\sum_{i_1=0}^{n-l-q} \frac{(q-1)!}{ (q+i_1+l-1)!} \bigl(m|z|^2\bigr)^{i_1+l} L^{i_1+l}_{q-1}\bigl(m|z|^2\bigr) L^{i_1+l}_{q-1}\bigl(m|z|^2\bigr) \\ &\quad{}=\frac{z^{-l}}{K_{m,n,q}(z,z)} \Biggl\{ m\sum_{r=0}^{q-2} \sum_{i=0}^{n-r-1} \frac{r!}{(r+i)!} \bigl(m|z|^2\bigr)^i L_r^{i} \bigl(m|z|^2\bigr)^2 \\ &\qquad{}+m \sum_{j=1}^{q-2}\sum _{k=1}^{q-j-1} \frac{j!}{(j+k)!} \bigl(m|z|^2 \bigr)^k L^{k}_{j}\bigl(m|z|^2 \bigr)^2 \\ &\qquad{} +m\sum_{i_1=0}^{l-1} \frac{(q-1)!}{ (q+i-1)!} \bigl(m|z|^2\bigr)^{i} L^{i}_{q-1}\bigl(m|z|^2\bigr)^2 \Biggr\}. \end{aligned}$$

(3.18)

By careful application of Lemma 2.4 to all the Laguerre polynomials in this expression, while inserting (3.13) to control the denominator, we indeed get (3.17). So, after a lot of effort, we have obtained that

$$\begin{aligned} \operatorname{\mathrm{pv}}\int_{{\mathbb{C}}} w^{-l} \frac{|K^I_{m,n,q}(z,w)|^2}{K_{m,n,q}(z,z)}\mathrm{e}^{-m|w|^2} {\mathrm{d}} A(w) \longrightarrow z^{-l} \end{aligned}$$

(3.19)

as m,n→+∞ with n=m+O(1). Analogous but slightly easier arguments (left to the interested reader) show that

$$\begin{aligned} \operatorname{\mathrm{pv}}\int_{{\mathbb{C}}}w^{-j}\frac {|K^{II}_{m,n,q}(z,w)|^2}{K_{m,n,q}(z,z)} \mathrm{e}^{-m|w|^2}{\mathrm{d}}A(w) \longrightarrow0 \end{aligned}$$

and

$$\begin{aligned} \int_{{\mathbb{C}}}w^{-j}\operatorname{Re}\biggl\{\frac{K^{I}_{m,n,q}(z,w) \overline{K^{II}_{m,n,q}(z,w)}}{K_{m,n,q}(z,z)} \biggr\} \,\mathrm{e}^{-m|w|^2}{\mathrm{d}}A(w) \longrightarrow0, \end{aligned}$$

again as m,n→+∞ with n=m+O(1). Finally, we put everything together based on the decomposition (3.8):

as m,n→+∞ with n=m+O(1). This ends the proof. □

3.4 Convergence to Harmonic Measure

We now show that even in the principal value sense, the Berezin density tends to avoid the interior of the unit disk.

Lemma 3.3

Fix a real parameter ρ with 0<ρ<1 and a point $z\in {\mathbb{D}}^{e}$. Then, for l=0,1,2,…, we have the convergence

as m,n→+∞ with n=m+O(1).

Proof

In terms of the decomposition (3.8), we will focus on the term $|K^{I}_{m,n,q}|^{2}$ and leave the other two to the reader (the necessary arguments are similar but slightly easier). The analogue of (3.9) reads

$$\begin{aligned} &\operatorname{\mathrm{pv}}\int_{{\mathbb{D}}(0,\rho )} w^{-l} \bigl|K^I_{m,n,q}(z,w)\bigr|^2\mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{}= m^{2} z^{-l} \sum_{r_1,r_2=0}^{q-1} \sum_{i_1=0}^{\min\{n-r_1-1,n-l-r_2-1\}} \frac {r_1!r_2!}{(r_1+i_1)!(r_2+i_1+l)!} \\ &\qquad{} \times m \bigl(|z|^2\bigr)^{i_1+l}L^{i_1}_{r_1} \bigl(m|z|^2\bigr)L^{i_1+l}_{r_2} \bigl(m|z|^2\bigr) \\ &\qquad{} \times \int_{{\mathbb{D}}(0,\rho)} \bigl(m|w|^2 \bigr)^{i_1}L^{i_1}_{r_1}\bigl(m|w|^2 \bigr) L^{i_1+l}_{r_2}\bigl(m|w|^2\bigr) \mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w). \end{aligned}$$

(3.20)

By Lemma 2.4, we have

$$\begin{aligned} &\int_{{\mathbb{D}}(0,\rho)} \bigl(m|w|^2\bigr)^{i_1} |L^{i_1}_{r_1}\bigl(m|w|^2\bigr) L^{i_1+l}_{r_2}\bigl(m|w|^2\bigr) | \mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{} \le\frac{1}{r_1!r_2!}\int_{{\mathbb{D}}(0,\rho)} \bigl(m|w|^2 \bigr)^{i_1}\bigl(m|w|^2+i_1+r_1 \bigr)^{r_1} \bigl(m|w|^2+i_1+l+r_2 \bigr)^{r_2}\mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{} \le\frac{2^{r_1+r_2-2}}{r_1!r_2!}\int_{{\mathbb{D}}(0,\rho)} \bigl(m|w|^2 \bigr)^{i_1} \bigl[\bigl(m|w|^2\bigr)^{r_1}+(i_1+r_1)^{r_1} \bigr] \\ &\qquad{} \times \bigl[ \bigl(m|w|^2\bigr)^{r_2}+(i_1+l+r_2)^{r_2} \bigr]\mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{} =\frac{2^{r_1+r_2-2}}{r_1!r_2!m} \biggl\{ \int_0^{m\rho^2}t^{i_1+r_1+r_2} \mathrm{e}^{-t}{\mathrm{d}}t+ (i_1+r_1)^{r_1}\int _0^{m\rho^2}t^{i_1+r_2}\mathrm{e}^{-t}{\mathrm{d}} t \\ &\qquad{} +(i_1+l+r_2)^{r_2}\int_0^{m\rho^2}t^{i_1+r_1} \mathrm{e}^{-t}{\mathrm{d}}t +(i_1+r_1)^{r_1}(i_1+l+r_2)^{r_2} \int_0^{m\rho^2}t^{i_1}\mathrm{e}^{-t} {\mathrm{d}}t \biggr\}. \end{aligned}$$

In terms of the function

$$\begin{aligned} \chi(a,b):=\frac{1}{\varGamma(a+1)}\int_0^b t^a \mathrm{e}^{-t}{\mathrm{d}}t, \quad a,b\in[0,+\infty\mathclose{[}, \end{aligned}$$

which takes values in the interval [0,1[, the estimate becomes

$$\begin{aligned} &\int_{{\mathbb{D}}(0,\rho)} \bigl(m|w|^2 \bigr)^{i_1} |L^{i_1}_{r_1}\bigl(m|w|^2 \bigr) L^{i_1+l}_{r_2}\bigl(m|w|^2\bigr) | \mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{} \le\frac{2^{r_1+r_2-2}}{r_1!r_2!m} \bigl\{ (i_1+r_1+r_2)! \chi\bigl(i_1+r_1+r_2,m\rho^2 \bigr)+ (i_1+r_1)^{r_1}(i_1+r_2)! \chi\bigl(i_1+r_2,m\rho^2\bigr) \\ &\qquad{} +(i_1+l+r_2)^{r_2}(i_1+r_1)! \chi\bigl(i_1+r_1,m\rho^2\bigr) +(i_1+r_1)^{r_1}(i_1+l+r_2)^{r_2}i_1! \chi\bigl(i_1,m\rho^2\bigr) \bigr\}. \end{aligned}$$

and if we use that a↦χ(a,b) is decreasing for fixed b (a direct calculation involving derivatives suffices to verify this), we get

$$\begin{aligned} &\int_{{\mathbb{D}}(0,\rho)} \bigl(m|w|^2 \bigr)^{i_1} |L^{i_1}_{r_1}\bigl(m|w|^2 \bigr) L^{i_1+l}_{r_2}\bigl(m|w|^2\bigr) | \mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \\ &\quad{} \le\frac{2^{r_1+r_2-2}}{r_1!r_2!m} \bigl\{ (i_1+r_1+r_2)!+ (i_1+r_1)^{r_1}(i_1+r_2)!+(i_1+l+r_2)^{r_2}(i_1+r_1)! \\ &\qquad{} +(i_1+r_1)^{r_1}(i_1+l+r_2)^{r_2}i_1! \bigr\}\chi\bigl(i_1,m\rho^2\bigr). \end{aligned}$$

(3.21)

Next, since $z\in{\mathbb{D}}^{e}$, n=m+O(1), and i ₁+l≤n−1, we may use another aspect of Lemma 2.4 to see that

$$\begin{aligned} |L^{i_1}_{r_1}\bigl(m|z|^2 \bigr)L^{i_1+l}_{r_2}\bigl(m|z|^2\bigr) |\le \frac{1}{r_1!r_2!} \bigl(m|z|^2\bigr)^{r_1+r_2}, \end{aligned}$$

(3.22)

provided m,n are big enough. As we combine the equality (3.20) with the estimates (3.21) and (3.22), and use some well-understood comparisons of factorials and powers, we arrive at

$$\begin{aligned} &\biggl|\operatorname{\mathrm{pv}}\int_{{\mathbb{D}}(0,\rho)} w^{-l} \bigl|K^I_{m,n,q}(z,w)\bigr|^2\mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \biggr| \\ &\quad{}\le m\,C_3(q,l)|z|^{-l+2q-2}\sum _{i_1=0}^{n-l-1} \frac{(m|z|^2)^{i_1+l}}{(i_1+l)!}\chi \bigl(i_1,m\rho^2\bigr), \end{aligned}$$

(3.23)

for some appropriate positive constant C ₃(q,l). The function χ(i ₁,mρ ²) drops off exponentially quickly to 0 as i ₁ exceeds mρ ² by a margin greater than O(m ^1/2), as can be seen, e.g., by an application of the Central Limit Theorem (compare with the next section). This means that effectively we are summing up to m|ρ|²+O(m ^1/2) in the right-hand side expression of (3.23), which does not permit the sum to compare with the size of K _m,n,q (z,z); cf. (3.14). This results in the convergence

$$\begin{aligned} \operatorname{\mathrm{pv}}\int_{{\mathbb{D}}(0,\rho)} w^{-l} \frac{|K^I_{m,n,q}(z,w)|^2}{K_{m,n,q}(z,z)}\,\mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \longrightarrow0 \end{aligned}$$

as m,n→+∞ with n=m+O(1). Together with the estimates which were left as an exercise to the reader, we get

$$\begin{aligned} \operatorname{\mathrm{pv}}\int_{{\mathbb{D}}(0,\rho)} w^{-l} \frac{|K_{m,n,q}(z,w)|^2}{K_{m,n,q}(z,z)}\,\mathrm{e}^{-m|w|^2} {\mathrm{d}}A(w) \longrightarrow0 \end{aligned}$$

as m,n→+∞ with n=m+O(1), which amounts to the assertion of the lemma. □

As in the proof of the Theorem 2.10 in [3], we may now conclude the following.

Theorem 3.4

Fix $z\in{\mathbb{D}}^{e}$ and a bounded continuous function g on ${\mathbb{C}}$. Then

as m,n→+∞ with n=m+O(1). Here, ${\mathrm{d}}\omega(w,z,{\mathbb{D}} ^{e})$ is harmonic measure with respect to the point z and the domain ${\mathbb{D}}^{e}$.

Naturally, the harmonic measure in question can be written explicitly with the Poisson kernel:

$$\begin{aligned} {\mathrm{d}}\omega\bigl(w,z,{\mathbb{D}}^e\bigr) = \frac{1}{2\pi} \frac{|z|^2-1}{|1-\bar{z} w|^2} {\mathrm{d}}s(w). \end{aligned}$$

Here, ds(w) denotes the arc-length measure on the unit circle.

4 Poly-Bargmann Transforms

4.1 Purpose of the Section

In this section, we discuss the poly-Bargmann transforms, a generalization of the classical Bargmann transform, which are needed later when we analyze the Berezin density at a boundary point. The poly-Bargmann transforms appeared in Vasilevski’s paper [36], where the basic properties were presented.

4.2 The Hermite Polynomials and the Bargmann Transform

We denote by H _j the j-th Hermite polynomial with respect to the Gaussian weight $\mathrm{e}^{-\frac{1}{2}t^{2}}$ (“probabilistic (monic) Hermite polynomials”). The generating function identity

$$\begin{aligned} \mathrm{e}^{tz-\frac{1}{2}z^2} = \sum_{j=0}^{+\infty} H_j(t)\frac{z^j}{j!} \end{aligned}$$

allows us to write

$$\begin{aligned} \frac{1}{(2\pi)^{1/4}}\mathrm{e}^{zt-\frac{1}{2}z^2-\frac{1}{4}t^2}= \sum _{j=0}^{+\infty} \frac{H_j(t)\mathrm{e}^{-t^2/4}}{(2\pi)^{1/4}\sqrt{j!}} \times \frac {z^j}{\sqrt{j!}}. \end{aligned}$$

We recall the standard definition of the Bargmann transform:

$$\begin{aligned} {\mathbf{B}}[f](z)= \frac{1}{(2 \pi)^{1/4}} \int_{{\mathbb{R}}} \mathrm{e}^{zt-\frac{1}{2}z^2-\frac{1}{4}t^2}f(t)\,{\mathrm{d}}t, \quad f \in L^2({\mathbb{R}}). \end{aligned}$$

As the function systems

$$\begin{aligned} \biggl\{\frac{1}{(2\pi)^{1/4}\sqrt{j!}}H_j(t)\mathrm{e}^{-\frac{1}{4}t^2} \biggr \}_{j=0}^{+\infty}\quad\mbox{and}\quad\biggl\{\frac{z^j}{\sqrt{j!}} \biggr\}_{j=0}^{+\infty} \end{aligned}$$

form orthonormal bases for $L^{2}({\mathbb{R}})$ and the Bargmann-Fock space $A^{2}_{1,1}({\mathbb{C}})$ (this is $A^{2}_{m,q}({\mathbb{C}})$ with m=q=1), respectively, we obtain the following well-known fact.

Proposition 4.1

The Bargmann transform ${\mathbf{B}}:L^{2}({\mathbb{R}})\to A_{1,1}^{2}({\mathbb{C}})$ acts isometrically and bijectively, and for each j=0,1,2,…, the basis function $(2\pi)^{-1/4}(j!)^{-1/2}H_{j}(t)\mathrm{e}^{-\frac{1}{4}t^{2}}$ is mapped to the basis function (j!)^−1/2 z ^j.

4.3 A Class of Auxiliary Operators

Let $\partial_{z},\bar{\partial}_{z}$ denote the standard Wirtinger differential operators

$$\begin{aligned} \partial_z:=\frac{1}{2}(\partial_x-{\mathrm{i}} \partial_y),\qquad \bar{\partial}_z:=\frac{1}{2}( \partial_x+{\mathrm{i}}\partial_y), \quad\mbox{where}\ z=x+{\mathrm{i}}y. \end{aligned}$$

For r=0,1,2,…, we introduce the operator

$$\begin{aligned} {\mathbf{T}}_{r}[f](z):=\frac{1}{\sqrt{r!}} \mathrm{e}^{|z|^2}\, \partial_z^r \bigl\{f(z)\mathrm{e}^{-|z|^2} \bigr\}, \end{aligned}$$

with the semi-group property T ₁∘T _r−1=r ^1/2 T _r . We also consider the dilated variant

$$\begin{aligned} {\mathbf{T}}_{m,r}[f](z) = {\mathbf{T}}_r[f_{m^{-1/2}}] \bigl(m^{1/2}z\bigr), \end{aligned}$$

where $f_{m^{-1/2}}(z)=f(m^{-1/2}z)$. It has the semi-group property T _m,1∘T _m,r−1=r ^1/2 T _m,r , and may be expressed in more concrete terms:

$$\begin{aligned} {\mathbf{T}}_{m,r}[f](z) = \frac{m^{-r/2}}{\sqrt{r!}} \mathrm {e}^{m|z|^2}\, \partial_z^r \bigl\{f(z)\mathrm{e}^{-m|z|^2} \bigr\}. \end{aligned}$$

We now study the effect of T _r on the basis elements (j!)^−1/2 z ^j.

Proposition 4.2

For j≥r, we have

$$\begin{aligned} {\mathbf{T}}_r \biggl[\frac{z^j}{\sqrt{j!}} \biggr]= \frac{1}{\sqrt{r!}} \mathrm{e}^{|z|^2} \partial^r_z \biggl\{ \mathrm{e}^{-|z|^2}\frac{z^j}{\sqrt{j!}} \biggr\}= \sqrt{\frac {r!}{j!}}z^{j-r}L^{j-r}_r \bigl(|z|^2\bigr) \end{aligned}$$

while for j≤r,

$$\begin{aligned} {\mathbf{T}}_r \biggl[\frac{z^j}{\sqrt{j!}} \biggr]= \frac{1}{\sqrt{r!}} \mathrm{e}^{|z|^2}\partial^r_z \biggl\{\mathrm{e}^{-|z|^2} \frac{z^j}{\sqrt{j!}} \biggr\}= (-1)^{r-j}\sqrt{\frac{n!}{r!}}\, \bar{z}^{r-j}L^{r-j}_j\bigl(|z|^2 \bigr). \end{aligned}$$

Proof

The proof is based on an induction argument. The statement is obviously true for r=0 and all j. So, by induction, we assume that the statement holds for some r−1≥0 and all j. In case j≥r, we then have

$$\begin{aligned} \partial^r_z\bigl\{\mathrm{e}^{-|z|^2}z^j \bigr\} =& \partial_z \bigl\{(r-1)!\,z^{j-r+1}L^{j-r+1}_{r-1} \bigl(|z|^2\bigr)\mathrm{e}^{-|z|^2} \bigr\} \\ =&(r-1)! z^{j-r} \bigl\{(j-r+1)L^{j-r+1}_{r-1} \bigl(|z|^2\bigr)-L^{j-r+2}_{r-2} \bigl(|z|^2\bigr)|z|^2\\ &{} -|z|^2L^{j-r+1}_{r-1} \bigl(|z|^2\bigr) \bigr\}\mathrm{e}^{-|z|^2} \\ =& r! L^{j-r}_r\bigl(|z|^2\bigr)z^{j-r} \mathrm{e}^{-|z|^2}, \end{aligned}$$

if we use the standard identity $rL^{\alpha}_{r}(x) = (\alpha+ 1 -x) L^{\alpha+1}_{r-1}(x) - xL^{\alpha+2}_{r-2}(x)$. Next, in case j≤r−1, we have instead (see [17], 8.971(5))

$$\begin{aligned} \partial^r_z\bigl\{\mathrm{e}^{-|z|^2}z^j \bigr\} =& (-1)^{r-1-j} \partial\bigl\{ j!\,\bar{z}^{r-1-j}L^{r-1-j}_j \bigl(|z|^2\bigr)\mathrm{e}^{-|z|^2} \bigr\} \\ =&(-1)^{r-j} j! \bar{z}^{r-j} \bigl\{L^{r-j}_{j-1} \bigl(|z|^2\bigr)+ L^{r-j-1}_{j} \bigl(|z|^2\bigr) \bigr\}\mathrm{e}^{-|z|^2}\\ =&(-1)^{r-j} j!\, \bar{z}^{r-j}L^{r-j}_j \bigl(|z|^2 \bigr)\mathrm{e}^{-|z|^2}, \end{aligned}$$

which completes the proof. □

4.4 Pure Poly-analytic Fock Spaces

Write e _j (z):=(j!)^−1/2 z ^j for j=0,1,2,…, which functions form the standard orthonormal basis for the space $A^{2}_{1,1}({\mathbb{C}})$. The function ${\mathbf{T}}_{r}[e_{j}]\in A^{2}_{1,r+1}({\mathbb{C}})$ is then a polynomial in $z,\bar{z}$, where the degree in z remains equal to j, and the degree in $\bar{z}$ equals r. For general positive m, the functions $e_{j,m}(z):= (j!)^{-1/2}m^{\frac{1}{2}(j+1)}z^{j}$, with j=0,1,2,…, form an orthonormal basis for the space $A^{2}_{m,1}({\mathbb{C}})$. The functions T _m,r [e _j,m ] are computed using Proposition 4.2 above, and we then recognize that we can identify them with the basis elements which appear in Proposition 2.1. We clearly have that

$$\begin{aligned} \mathrm{span} \bigl\{{\mathbf{T}}_{m,r}[e_{j,m}]:\ 0\le j\le n-1,\ 0\le r\le q-1 \bigr\}=\mathrm{Pol}_{m,n,q}, \end{aligned}$$

and in view of the orthogonality properties in Proposition 2.1, we also must have

$$\begin{aligned} \mathrm{span}\bigl\{{\mathbf{T}}_{m,r}[e_{j,m}]:\ 0\le j\le n-1 \bigr\} =\mathrm{Pol}_{m,n,r+1}\ominus\mathrm{Pol}_{m,n,r}, \end{aligned}$$

(4.1)

where the “⊖” is with respect to the inner product in $L^{2}({\mathbb{C}},\mathrm{e}^{-m|z|^{2}})$. Following Vasilevski [36], then, we define the pure (true) polyanalytic Fock space of level r+1:

$$ {\delta\mathrm{Pol}}_{m,n,r+1}:=\mathrm{Pol}_{m,n,r+1}\ominus \mathrm{Pol}_{m,n,r},\qquad\delta A^2_{m,n,r+1}( {\mathbb{C}}):=A^2_{m,r+1}({\mathbb{C}})\ominus A^2_{m,r}( {\mathbb{C}}), $$

(4.2)

with the understanding that Pol _m,n,0:={0} and $A^{2}_{m,0}({\mathbb{C}}):=\{0\}$. The operator T _m,r now becomes an isometric isomorphism

$$\begin{aligned} {\mathbf{T}}_{m,r}:A^2_{m,1}({\mathbb{C}})\to\delta A^2_{m,n,r+1}({\mathbb{C}}),\qquad{\mathbf{T}}_{m,r}: \mathrm{Pol}_{m,n,1}\to{\delta\mathrm{Pol}}_{m,n,r+1}. \end{aligned}$$

We obtain the orthogonal decompositions

$$\begin{aligned} \mathrm{Pol}_{m,n,q} = \bigoplus_{r=0}^{q-1} {\delta\mathrm{Pol}}_{m,n,r+1}, \qquad A^2_{m,q}({\mathbb{C}})=\bigoplus _{r=0}^{q-1} \delta A^2_{m,r+1}( {\mathbb{C}}). \end{aligned}$$

As a consequence, if K _δ:m,n,r+1 and K _δ:m,r+1 denote the reproducing kernels for the spaces δPol _m,n,r+1 and $\delta A^{2}_{m,r+1}({\mathbb{C}})$, respectively, we must have that

$$\begin{aligned} K_{m,n,q} = \sum _{r=0}^{q-1} K_{\delta:{m,n,r+1}}, \qquad K_{m,q} = \sum_{r=0}^{q-1} K_{\delta:{m,r}}. \end{aligned}$$

(4.3)

4.5 The Poly-Bargmann Transforms

For m=1, the poly-Bargmann transform of level r is defined by

$$\begin{aligned} {\mathbf{B}}_r[f]:= {\mathbf{T}}_r\circ{\mathbf{B}}[f]. \end{aligned}$$

Proposition 4.3

We have

$$\begin{aligned} {\mathbf{B}}_r[f](z)= \frac{1}{(2\pi)^{1/4}\sqrt{r!}} \int_{{\mathbb{R}}}f(t)H_r(t-z- \bar{z}) \,\mathrm{e}^{tz-\frac{1}{2}z^2-\frac{1}{4}t^2} {\mathrm{d}}t,\quad r=0,1,2,\ldots. \end{aligned}$$

Proof

We proceed by induction. For r=0, the formula reduces to the usual Bargmann transform (if we recall that H ₀=1). By the induction hypothesis, we suppose therefore that the formula is valid for all integers up to r−1. From the semi-group property T ₁∘T _r−1=r ^1/2 T _r , we see that

$$\begin{aligned} {\mathbf{B}}_r[f]={\mathbf{T}}_r\circ{\mathbf{B}}[f]= r^{-1/2} {\mathbf{T}}_1\circ{\mathbf{T}}_{r-1}\circ{\mathbf{B}}[f](z)= r^{-1/2} {\mathbf{T}}_1\circ{\mathbf{B}}_{r-1}[f]. \end{aligned}$$

Since the formula holds for r−1, the following calculation shows that it holds for r as well:

$$\begin{aligned} &r^{-1/2}\mathrm{e}^{|z|^2} \partial_z \bigl(\bigl[(r-1)! \bigr]^{-1/2}H_{r-1}(t-z- \bar{z}) \,\mathrm{e}^{tz-\frac{1}{2}z^2-\frac{1}{4}t^2} \mathrm{e}^{-|z|^2} \bigr) \\ &\quad{}= (r!)^{-1/2} \bigl(-H'_{r-1}(t-z-\bar{z})+ (t-z- \overline{z})H_{r-1}(t-z-\bar{z}) \bigr) \,\mathrm{e}^{tz-\frac{1}{2}z^2-\frac{1}{4}t^2} \\ &\quad{}= (r!)^{-1/2} H_r(t-z-\bar{z})\mathrm{e}^{tz-\frac{1}{2}z^2-\frac{1}{4}t^2}; \end{aligned}$$

here, we used the standard identity $H_{r}(x)=xH_{r-1}(x)-H'_{r-1}(x)$. The proof is complete. □

5 Reproducing Kernel and Berezin Density Asymptotics for a Boundary Point

5.1 Purpose of the Section

In this section, we will calculate the limit of the blow-up Berezin transform at a boundary point z, that is, |z|=1. There is no loss of generality to take z=1. Our strategy is to investigate the blow-up of the reproducing kernel of the space of analytic polynomials Pol _m,n,1 (with q=1) first, and then use this information together with poly-Bargmann transform to lift the asymptotics to the context of the general polyanalytic spaces Pol _m,n,q .

5.2 The Central Limit Theorem Revisited

The following improvement of the central limit theorem will be needed. Let cdf _X denote the cumulative distribution function of a real-valued random variable X and let

$$\begin{aligned} \mathrm{erf}(z) = \frac{1}{\sqrt{2 \pi}} \int_{- \infty}^z \mathrm{e}^{-\frac{1}{2}t^2} {\mathrm{d}}t \end{aligned}$$

be the error function. Here, for complex z, we may think of the contour of integration as following the real line from −∞ to 0, and then from going from 0 to z along any smooth curve.

We shall write i.i.d. as shorthand for independent identically distributed in the context of random variables. The following result is from [9, 14].

Theorem 5.1

(Berry-Esséen)

Let X ₁,X ₂,… be i.i.d. real-valued random variables with E(X _j )=0, $E(X_{j}^{2})=1$ and E(|X _j |³)=ρ<+∞ for all j. Also, let $Y_{n} = n^{-1/2}\sum_{j=1}^{n} X_{j}$. Then there exists an absolute constant C such that

$$\begin{aligned} \bigl\vert\mathrm{cdf}_{Y_n}(x) - \mathrm{erf}(x) \bigr\vert \leq \frac{C \rho}{\sqrt{n}}, \quad x\in{\mathbb{R}}. \end{aligned}$$

The Berry-Esséen theorem gives the following asymptotics for the partial Taylor sums of the exponential function.

Lemma 5.2

We have

$$\begin{aligned} \frac{E_{n-1}(x)}{\mathrm{e}^x} = \mathrm{erf} \biggl(\frac {n-x}{\sqrt {n}} \biggr) + \mathrm{O} \bigl(n^{-1/2}\bigr), \end{aligned}$$

as n→+∞, uniformly in x∈[0,+∞[.

Proof

Let X ₁,…,X _n be independent exponentially distributed random variables on [0,+∞[ with density e^−x. It is well known that the sum $\sum_{j=1}^{n}X_{j}$ obeys a gamma distribution with the cumulative distribution function 1−e^−x E _n−1(x). The random variables X ₁−1,…,X _n −1 all have zero mean and variance 1, and the third moment is finite, so by the Berry-Esséen theorem, we have

$$\begin{aligned} 1-\mathrm{e}^{-x}E_{n-1}(x)=\mbox{cdf}_{\sum_{j=1}^n X_j}(x) = \mathrm{cdf}_{\frac{\sum_{j=1}^n X_j -n }{\sqrt{n}}} \biggl(\frac {x-n}{\sqrt{n}} \biggr) =\mathrm{erf} \biggl(\frac{x-n}{\sqrt{n}} \biggr)+\mathrm{O}\bigl(n^{-1/2}\bigr), \end{aligned}$$

(5.1)

where the “O” term is uniform in x as n→+∞. □

Results of this nature are well known. A reader who prefers a more direct approach might use Taylor’s formula with remainder term to obtain

$$\begin{aligned} E_{n-1}(x)\mathrm{e}^{-x} = 1-\frac{1}{(n-1)!}\int _0^x t^{n-1}\mathrm{e}^{-t} {\mathrm{d}} t, \end{aligned}$$

and then analyze the integral by Laplace’s method.

This allows us to blow up the function $E_{n-1}(mz\bar{w})$ when z and w are close to the point 1 and m,n→+∞ with n=m+O(1).

Lemma 5.3

Fix a positive real ε. For complex $\xi,\eta\in{\mathbb{C}}$, we then have

$$\begin{aligned} \frac{E_{n-1} (m(1+m^{-1/2}\xi)(1+ m^{-1/2}\bar{\eta}) )}{ \mathrm{e}^{m+ \sqrt{m}(\xi+\bar{\eta})}} = \mathrm{e}^{\xi\bar {\eta}} \,\mathrm {erf}(-\xi- \bar{\eta})+ \mathrm{O}\bigl(m^{-\frac{1}{2}+\varepsilon}\bigr), \end{aligned}$$

as m,n→+∞ while n=m+O(1). Here, the “O” expression on the right-hand side is uniform on compact subsets of ${\mathbb{C}}$.

Proof

If we put

$$\begin{aligned} \zeta:=m\bigl(1+m^{-1/2}\xi\bigr) \bigl(1+m^{-1/2}\bar{\eta}\bigr)=m+m^{1/2} (\xi+\bar{\eta})+\xi\bar{\eta}, \end{aligned}$$

then

$$\begin{aligned} \frac{n-\zeta}{\sqrt{n}}=\frac{n-m-m^{1/2}(\xi+\bar{\eta})-\xi \bar{\eta}}{\sqrt{n}} =-\xi-\bar{\eta}+\mathrm{O} \bigl(m^{-1/2}\bigr), \end{aligned}$$

where the “O” term is uniform on compact subsets. If we use that E _n−1 has only nonnegative Taylor coefficients, we get from Lemma 5.2 that

$$\begin{aligned} \frac{|E_{n-1}(\zeta)|}{\mathrm{e}^{|\zeta|}}\le \frac {E_{n-1}(|\zeta|)}{\mathrm{e}^{|\zeta|}} =\mathrm{erf} \biggl( \frac{n-|\zeta|}{\sqrt{n}} \biggr) +\mathrm{O}\bigl(n^{-1/2}\bigr), \end{aligned}$$

(5.2)

with a uniform “O” term. So, for real ξ,η, we may deduce from (5.2) the assertion of the lemma with ε=0. For general complex ξ,η, we note that

$$\begin{aligned} |\zeta| =&m\,|\bigl(1+m^{-1/2}\xi\bigr) \bigl(1+m^{-1/2}\bar{\eta}\bigr)| \\ =&m+m^{1/2}\operatorname{Re}[\xi+\eta]+ \operatorname{Re}\xi \operatorname{Re}\eta+\frac{1}{2}(\operatorname{Im}\xi)^2+ \frac{1}{2}(\operatorname{Im}\eta)^2+\mathrm{O}\bigl(m^{-1/8}\bigr) \end{aligned}$$

uniformly in the domain where max{|ξ|,|η|}≤m ^1/8. As the right-hand side of (5.2) is $\le\frac{3}{2}$ for big n, we see that

$$\begin{aligned} \biggl|\frac{E_{n-1} (m(1+m^{-1/2}\xi)(1+ m^{-1/2}{\eta}) )}{ \mathrm{e}^{m+ \sqrt{m}(\xi+\eta)+\xi\bar{\eta}}} \biggr| \le&\frac{3}{2}\mathrm{e} ^{-(\operatorname{Im} \xi)(\operatorname{Im}\eta)+\frac{1}{2}(\operatorname{Im}\xi )^2+\frac{1}{2}(\operatorname{Im}\eta)^2+ \mathrm{O}(m^{-1/8})}\\ \le&2\mathrm{e}^{\frac{1}{2}[\operatorname{Im}\xi-\operatorname {Im}\eta]^2} \end{aligned}$$

holds in the domain where max{|ξ|,|η|}≤m ^1/8, provided m is big enough. We need to show that the difference

$$\begin{aligned} F_{m,n}(\xi,\eta):=\frac{E_{n-1} (m(1+m^{-1/2}{\xi}) (1+m^{-1/2}\bar{\eta}) )}{\mathrm{e}^{m+ \sqrt{m}(\xi+\bar{\eta})+\xi\bar{\eta}}} - \mathrm{erf}(-\xi-\bar{\eta}) \end{aligned}$$

is of order O(m ^−1/2+ε) uniformly as ξ,η remain confined to some compact subset of ${\mathbb{C}}$. We know that F _m,n (ξ,η)=O(m ^−1/2) uniformly when $\xi,\eta \in{\mathbb{R}}$ with confined to max{|ξ|,|η|}≤m ^1/8. In view of the calculation we just made, we also have a good uniform estimate of F _m,n (ξ,η) when $\xi,\eta\in{\mathbb{C}}$ with max{|ξ|,|η|}≤m ^1/8. With an elementary estimate of harmonic measure (see exercise II.3a in [16]), we can show that F _m,n (ξ,η)=O(m ^ϵ−1/2) holds uniformly when $\xi,\eta\in{\mathbb{C}}$ belong to a compact subset of ${\mathbb{C}}$, and in addition, $\eta\in{\mathbb{R}}$. Here, ϵ is a positive number which we can get as small as we like. A similar argument with η in place ξ worsens the control to F _m,n (ξ,η)=O(m ^2ϵ−1/2), but now the control is uniform when both ξ,η are both complex and confined to some compact subset. The proof is complete with ε=2ϵ. □

5.3 The Reproducing Kernel for a Subspace of the Fock Space

We shall identify both the right-hand and the left-hand side expressions appearing in Lemma 5.3 with reproducing kernels of certain Hilbert spaces of entire functions. This will be the case r=0 of the proposition below.

Let us agree to identify

$$\begin{aligned} L^2({\mathbb{R}}_-) =\bigl\{ f\in L^2({\mathbb{R}}):\ f(x)=0 \ \mbox{ for } x>0\bigr\}. \end{aligned}$$

In the following proposition and later, we encounter integrals ranging from −∞ to some complex number w. We can use any contour that first goes from −∞ to 0 along the real axis and then connects 0 to w. Our integrands are usually holomorphic, so we are allowed us to perturb the contour of integration when needed.

Proposition 5.4

For r=0,1,2,…, the function

$$\begin{aligned} (\xi,\eta)\mapsto\frac{\mathrm{e}^{\xi\bar{\eta}}}{r! \sqrt{2 \pi}} \int_{-\infty}^{-\xi-\bar{\eta}} H_r(t+\xi-\eta) H_r(t+\bar{\eta}-\bar{\xi})\mathrm{e}^{-\frac{1}{2}t^2} {\mathrm{d}}t \end{aligned}$$

is the reproducing kernel for the Hilbert space ${\mathbf{B}}_{r}[L^{2}({\mathbb{R}} _{-})]\subset A^{2}_{1,r+1}({\mathbb{C}})$.

Proof

Let M(ξ,η)=M _η (ξ) be the reproducing kernel for ${\mathbf{B}}_{r}[ L^{2}({\mathbb{R}}_{-})]$. This kernel has $M_{\eta}\in {\mathbf{B}}_{r}[L^{2}({\mathbb{R}} _{-})]$ and

$$\begin{aligned} \frac{1}{\sqrt{r!}(2\pi)^{1/4}} \int_{{\mathbb{R}}}f(t)H_r(t-\eta- \bar{\eta}) \mathrm{e}^{t\eta-\frac{1}{2}\eta^2-\frac{1}{4}t^2}{\mathrm{d}}t = {\mathbf{B}} _r[f](\eta) =& \bigl\langle{\mathbf{B}}_r[f], M_{\eta} \bigr\rangle_{A^2_{1,r+1}({\mathbb{C}})}\\ =& \bigl\langle f, {\mathbf{B}}_r^{-1}[M_{\eta}] \bigr\rangle_{L^2({\mathbb{R}})} \end{aligned}$$

for all $\eta\in{\mathbb{C}}$ and all $f\in L^{2}({\mathbb{R}}_{-})$, which allows us to conclude that

$$\begin{aligned} {\mathbf{B}}_r^{-1}[M_{\eta}](t) =(r!)^{-1/2}(2 \pi)^{-1/4}1_{]-\infty,0]}(t)\, H_r(t-\eta-\bar{\eta})\, \mathrm{e}^{t\bar{\eta}-\frac{1}{2}\bar{\eta}^2-\frac{1}{4}t^2}. \end{aligned}$$

After applying the operator B _r to both sides, we see that (cf. Proposition 4.3)

$$\begin{aligned} M_{\eta}(\xi) =& \frac{1}{r!\sqrt{2\pi}} \int_{-\infty}^{0} H_r(t-\xi-\bar{\xi}) \mathrm{e}^{t \xi- \frac{1}{2}\xi^2-\frac{1}{4} t^2} H_r(t-\eta-\bar{ \eta}) \mathrm{e}^{t\bar{\eta}-\frac{1}{2}\bar{\eta}^2-\frac{1}{4}t^2} {\mathrm{d}}t \\ =&\frac{\mathrm{e}^{\bar{\eta} \xi}}{r! \sqrt{2\pi}} \int _{-\infty}^{0} H_r(t-\xi-\bar{\xi}) H_r(t-\eta-\bar{\eta}) \mathrm{e}^{-\frac{1}{2}(t - \xi- \bar{\eta})^2} {\mathrm{d}}t \\ =&\frac{\mathrm{e}^{\bar{\eta}\xi}}{r! \sqrt{2\pi}} \int _{-\infty }^{-\bar{\eta}-\xi} H_r(t + \bar{\eta} - \bar{\xi}) H_r(t+\xi-\eta) \mathrm{e}^{-\frac{1}{2}t^2} {\mathrm{d}}t. \end{aligned}$$

 □

Remark 5.5

The special case r=0 of the kernel in Proposition 5.4 is $\mathrm{e}^{\xi\bar{\eta}}\mathrm{erf}(-\xi-\bar{\eta})$, which is what we have on the right-hand side in Lemma 5.3.

5.4 The Blow-Up of the Polynomial Space at the Boundary Point

We turn to the polyanalytic analogue of the left-hand side of Lemma 5.3.

Definition 5.6

We introduce the blow-up space at 1,

$$\begin{aligned} \mathrm{Pol}^{\langle1\rangle}_{m,n,q} := \bigl\{\mathrm {e}^{-{m}^{1/2}\xi}p \bigl(1+m^{-1/2}\xi\bigr): p \in\mathrm{Pol}_{m,n,q} \bigr\}, \end{aligned}$$

which we equip with the norm

$$\begin{aligned} \bigl\|\xi\mapsto\mathrm{e}^{-{m}^{1/2}\xi}p\bigl(1+m^{-1/2}\xi\bigr) \bigr\|_{{\mathrm{Pol}}^{\langle1\rangle}_{m,n,q}}:=m^{1/2}\mathrm {e}^{\frac{1}{2}m} \|p\|_{L^2({\mathbb{C}},\mathrm{e}^{-m|z|^2})}. \end{aligned}$$

For 0≤r≤q−1, we denote by ${\delta\mathrm{Pol}}^{\langle 1\rangle }_{m,n,r+1}$ the subspace

$$\begin{aligned} {\delta\mathrm{Pol}}^{\langle1\rangle}_{m,n,r+1} := \bigl\{\mathrm{e} ^{-{m}^{1/2}\xi}p \bigl(1+m^{-1/2}\xi\bigr): p \in{\delta\mathrm {Pol}}_{m,n,r+1} \bigr\}, \end{aligned}$$

equipped with the same norm.

An elementary change of variables argument allows us to identify the norm on $\mathrm{Pol}^{\langle1\rangle}_{m,n,q}$ with that of $A^{2}_{1,q}({\mathbb{C}})$:

$$\begin{aligned} \bigl\|\xi\mapsto\mathrm{e}^{-{m}^{1/2}\xi}p\bigl (1+m^{-1/2}\xi \bigr) \bigr\|_{\mathrm{Pol}^{\langle1\rangle}_{m,n,q}}= \bigl\|\xi\mapsto \mathrm{e}^{-{m}^{1/2}\xi}p\bigl(1+m^{-1/2} \xi\bigr) \bigr\|_{A^2_{1,q}({\mathbb{C}})}. \end{aligned}$$

(5.3)

As a consequence, we may regard $\mathrm{Pol}^{\langle1\rangle}_{m,n,q}$ and ${{\delta\mathrm{Pol}}}^{\langle1\rangle}_{m,n,r+1}$ as norm closed subspaces of $A^{2}_{1,q}({\mathbb{C}})$. We may read off from the definition of the norm in ${\mathrm{Pol}}^{\langle1\rangle}_{m,n,q}$ that the kernel on the left-hand side in Lemma 5.3 is the reproducing kernel for the space $\mathrm{Pol}^{\langle1\rangle}_{m,n,1}$. So, Lemma 5.3 can be understood as saying that

$$\begin{aligned} K_{\mathrm{Pol}^{\langle1\rangle }_{m,n,1}}(\xi,\eta)= K_{{\mathbf{B}}_0[L^2({\mathbb{R}}_-)]}( \xi,\eta)+\mathrm{O}\bigl(m^{-\frac{1}{2}+\varepsilon}\bigr), \end{aligned}$$

(5.4)

where $K_{\mathrm{Pol}_{m,n,1}}$ and $K_{{\mathbf{B}}_{0}[L^{2}({\mathbb{R}}_{-})]}$ denote the reproducing kernels of the spaces in the subscripts, and the bound is locally uniform on compact subsets. We want to generalize (5.4) beyond q=1. To this end, we make use of the operators T _r .

Proposition 5.7

For r=1,2,3,…, we have that

$$\begin{aligned} r^{-1/2}{\mathbf{T}}_{1}:\,{{\delta\mathrm{Pol}}}^{\langle1\rangle}_{m,n,r} \to{{\delta\mathrm{Pol}}}^{\langle1\rangle}_{m,n,r+1} \end{aligned}$$

is an isometric isomorphism.

Proof

From the isometry properties of T _r−1 and T _r together with the semi-group property r ^−1/2 T ₁∘T _r−1=T _r , we get that

$$\begin{aligned} r^{-1/2}{\mathbf{T}}_{1}:\,\delta A^2_{1,r}( {\mathbb{C}})\to\delta A^2_{1,r+1}({\mathbb{C}}) \end{aligned}$$

is an isometric isomorphism. In view of (5.3), the isometry part of the assertion follows. It remains to show that the operator is onto. This is an algebraic exercise which we leave to the reader. □

By iterating Proposition 5.7, we obtain the following.

Corollary 5.8

For r=1,2,3…, we have that

$$\begin{aligned} {\mathbf{T}}_r:\mathrm{Pol}^{\langle1\rangle}_{m,n,1}\to {\delta\mathrm{Pol}}^{\langle1\rangle}_{m,n,r+1} \end{aligned}$$

is an isometric isomorphism.

5.5 The Blow-Up of the Polynomial Reproducing Kernel at a Boundary Point

From Corollary 5.8 above, we get that

$$\begin{aligned} K_{{\delta\mathrm{Pol}}^{\langle1\rangle }_{m,n,r+1}}(\xi ,\eta)=[{\mathbf{T}}_r]_\xi [\bar{\mathbf{T}}_r]_\eta\bigl(K_{\mathrm{Pol}^{\langle1\rangle }_{m,n,1}}(\xi,\eta) \bigr), \end{aligned}$$

(5.5)

where the subscripts z and w are used to indicate that the operator is acting with respect to that variable, and the bar means complex conjugation of the operator. In the above formula, T _r is as before, and $\bar{\mathbf{T}}_{e}$ is given by

$$\begin{aligned} \bar{\mathbf{T}}_r[f](z):=\frac{1}{\sqrt{r!}} \mathrm{e}^{|z|^2}\, \bar{\partial}_z^r \bigl\{f(z)\mathrm{e}^{-|z|^2} \bigr\}. \end{aligned}$$

We would like to plug in the approximation (5.4) into (5.5). We recall that the operator T _r is given by the analogous formula, which expands as a sum of certain polynomials in $\bar{z}$ of degree ≤r times powers of the differential operator ∂ _z of degree ≤r (a similar assertion can be made about $\bar{\mathbf{T}}_{r}$ as well). The Cauchy integral formula allows us to control the size of the derivatives on a compact subset in terms of the size of the functions on a slightly bigger compact subset. This means that the approximation (5.4) carries over, and we find that

$$\begin{aligned} K_{{\delta\mathrm{Pol}}^{\langle 1\rangle }_{m,n,r+1}}(\xi,\eta)= [ {\mathbf{T}}_r]_\xi[\bar{\mathbf{T}}_r]_\eta \bigl(K_{{\mathbf{B}}_0[L^2({\mathbb{R}}_-)]}(\xi,\eta) \bigr )+\mathrm{O}\bigl (m^{-\frac{1}{2}+\varepsilon}\bigr), \end{aligned}$$

(5.6)

with uniform control on compact subsets. Next, as

$$\begin{aligned} \mathrm{Pol}^{\langle1\rangle}_{m,n,q}=\bigoplus _{r=0}^{q-1} {\delta\mathrm{Pol}}^{\langle1\rangle}_{m,n,r+1}, \end{aligned}$$

we get that

$$ K_{\mathrm{Pol}^{\langle1\rangle }_{m,n,q}}(\xi,\eta)= \sum _{r=0}^{q-1}K_{{\delta\mathrm{Pol}}^{\langle1\rangle }_{m,n,r+1}}(\xi,\eta) =\sum_{r=0}^{q-1}[{\mathbf{T}}_r]_\xi[ \bar{\mathbf{T}}_r]_\eta\bigl(K_{{\mathbf{B}}_0[L^2({\mathbb{R}}_-)]}(\xi,\eta) \bigr)+ \mathrm{O}\bigl(m^{-\frac{1}{2}+\varepsilon}\bigr), $$

(5.7)

again with uniform control on compact subsets. Next, it should be rather clear that

$$\begin{aligned}{} [{\mathbf{T}}_r]_\xi[\bar{\mathbf{T}}_r]_\eta \bigl(K_{{\mathbf{B}}_0[L^2({\mathbb{R}}_-)]}(\xi,\eta) \bigr) \end{aligned}$$

is the reproducing kernel for the space ${\mathbf{T}}_{r}{\mathbf{B}}_{0}[L^{2}({\mathbb{R}} _{-})]={\mathbf{B}}_{r} [L^{2}({\mathbb{R}}_{-})]$, which was identified in terms of Hermite polynomials back in Proposition 5.4. We write this down as a proposition.

Proposition 5.9

Fix a positive real number ε. Then the reproducing kernel for $\mathrm{Pol}^{\langle1\rangle}_{m,n,q}$ has the following form:

$$\begin{aligned} K_{\mathrm{Pol}^{\langle1\rangle}_{m,n,q}}(\xi,\eta)= \sum_{r=0}^{q-1} \frac{\mathrm{e}^{\xi\bar{\eta}}}{r! \sqrt{2 \pi}} \int_{-\infty }^{-\xi -\bar{\eta}} H_r(t+\xi-\eta) H_r(t+\bar{\eta}-\bar{\xi})\mathrm{e}^{-\frac{1}{2}t^2} {\mathrm{d}}t+ \mathrm{O}\bigl(m^{-\frac{1}{2}+\varepsilon}\bigr), \end{aligned}$$

as m,n→+∞ while n=m+O(1), where the control is uniform on compact subsets.

If we like, we may use the classical Christoffel-Darboux identity

$$\begin{aligned} \sum_{r=0}^{q-1} \frac{1}{r!}H_r(x)H_r(y)= \frac {H_q(x)H_{q-1}(y)-H_{q-1}(x)H_{q}(y)}{(q-1)!(x-y)} \end{aligned}$$

(5.8)

to rewrite the above sum. Also, we should note that reproducing kernel for the blow-up space $\mathrm{Pol}^{\langle1\rangle}_{m,n,q}$ is connected with the reproducing kernel K _m,n,q for Pol _m,n,q via the identity

$$\begin{aligned} K_{\mathrm{Pol}^{\langle1\rangle}_{m,n,q}}(\xi ,\eta)= m^{-1} \mathrm{e}^{-m-m^{1/2}(\xi+\bar{\eta})}K_{m,n,q}\bigl(1+m^{-1/2}\xi ,1+m^{-1/2} \eta\bigr). \end{aligned}$$

(5.9)

5.6 The Blow-Up of the 1-Point Intensity Near a Boundary Point

The 1-point intensity function is

$$\begin{aligned} K_{m,n,q}(z,z)\mathrm{e}^{-m|z|^2}, \end{aligned}$$

and the localized version with z=1+m ^−1/2 ξ is

$$\begin{aligned} U_{m,n,q}(\xi):= m^{-1}K_{m,n,q}\bigl(1+m^{-1/2} \xi,1+m^{-1/2}\xi\bigr)\,\mathrm{e}^{-m|1+m^{-1/2}\xi|^2}, \end{aligned}$$

where we throw in a factor of m ⁻¹ to compensate for the expected number of Jacobian. In view of (5.9) together with Proposition 5.9, we obtain

$$\begin{aligned} U_{m,n,q}(\xi)=\sum_{r=0}^{q-1} \frac{1}{r!\sqrt{2\pi}}\int_{-\infty}^{-2\operatorname{Re}\xi} H_r(t)^2\mathrm{e}^{-\frac{1}{2}t^2}{\mathrm{d}}t+\mathrm{O} \bigl(m^{-\frac{1}{2}+\varepsilon}\bigr). \end{aligned}$$

So, essentially, the 1-point intensity function is determined by the density

$$\begin{aligned} t\mapsto\sum_{r=0}^{q-1} \frac{1}{r!\sqrt{2\pi}} H_r(t)^2\mathrm{e}^{-\frac{1}{2}t^2}, \end{aligned}$$

which corresponds to filling the lowest energy eigenstates of the harmonic oscillator. By the Wigner semi-circle law, then, we get the approximation

$$\begin{aligned} U_{m,n,q}(\xi)\approx\frac{2q}{\pi}\int _{-1}^{-q^{-1/2}\operatorname{Re}\xi} \sqrt{1-\tau^2}{\mathrm{d}}\tau, \end{aligned}$$

valid for big m,n with n=m+O(1), and big q (but much smaller than m,n). So, if we rescale to characteristic distance q ^1/2 m ^−1/2 we find an interesting law in the limit. To be more precise, we find that

$$\begin{aligned} q^{-1}U_{m,n,q}\bigl(q^{1/2}\xi'\bigr) \to\frac{2}{\pi}\int_{-1}^{-\operatorname{Re}\xi'}\sqrt{1- \tau^2}{\mathrm{d}}\tau, \end{aligned}$$

(5.10)

for ξ′ confined to a compact set with $-1\le\operatorname{Re}\xi '\le1$. Here, it is assumed that the limit m,n→+∞ while m=n+O(1) is taken first, and the limit q→+∞ is taken afterwards. Asymptotically, then, (5.10) asserts that the one-point function is the definite integral of the semi-circle function.

5.7 The Blow-Up Berezin Density at a Boundary Point

The blow-up Berezin density at 1 is given by

From (5.9), we have that

$$\begin{aligned} K_{\mathrm{Pol}^{\langle1\rangle}_{m,n,q}}(0,0)= m^{-1}\mathrm{e} ^{-m}K_{m,n,q}(1,1), \end{aligned}$$

while Proposition 5.9 gives

$$\begin{aligned} K_{\mathrm{Pol}^{\langle1\rangle}_{m,n,q}}(0,0)= \sum_{r=0}^{q-1} \frac{1}{r! \sqrt{2 \pi}} \int_{-\infty}^{0} H_r(t)^2\mathrm{e}^{-\frac{1}{2}t^2} {\mathrm{d}}t+ \mathrm{O} \bigl(m^{-\frac{1}{2}+\varepsilon}\bigr), \end{aligned}$$

as m,n→+∞ with n=m+O(1). Now, as each Hermite polynomial H _r is either even or odd,

$$\begin{aligned} \int_{-\infty}^{0} H_r(t)^2 \mathrm{e}^{-\frac{1}{2}t^2} {\mathrm{d}}t=\frac{1}{2} \int_{-\infty }^{+\infty} H_r(t)^2\mathrm{e}^{-\frac{1}{2}t^2} {\mathrm{d}}t= \frac{r!\sqrt{2\pi}}{2}, \end{aligned}$$

which leads to

$$\begin{aligned} K_{\mathrm{Pol}^{\langle1\rangle}_{m,n,q}}(0,0)= \frac {q}{2}+\mathrm{O} \bigl(m^{-\frac{1}{2}+\varepsilon}\bigr) \end{aligned}$$

and

$$\begin{aligned} K_{m,n,q}(1,1)=\frac{1}{2}\,mq\mathrm{e}^m\bigl[1+\mathrm{O} \bigl(m^{-\frac{1}{2}+\varepsilon}\bigr)\bigr]. \end{aligned}$$

A similar calculation gives that

$$\begin{aligned} K_{m,n,q}\bigl(1+m^{-1/2}\xi,1\bigr) =&m\mathrm{e}^{m+m^{1/2}\xi} K_{\mathrm{Pol}^{\langle1\rangle}_{m,n,q}}(\xi,0) \\ =&m\mathrm{e}^{m+m^{1/2}\xi} \Biggl\{ \sum_{r=0}^{q-1} \frac{1}{r! \sqrt{2 \pi}} \int_{-\infty}^{-\xi} H_r(t+\xi) H_r(t-\bar{\xi})\mathrm{e}^{-\frac{1}{2}t^2} {\mathrm{d}}t\\ &{}+ \mathrm{O}\bigl(m^{-\frac{1}{2}+\varepsilon}\bigr) \Biggr\}. \end{aligned}$$

Putting things together, we obtain the following asymptotics for the blow-up Berezin density.

Theorem 5.10

Fix a positive real number ε. Then the blow-up Berezin density at 1 has the following form:

as m,n→+∞ while n=m+O(1), where the constant of the error term is uniform on compact subsets.

Remark 5.11

When we make some explicit calculations based on Theorem 5.10, we see that the Fresnel zone pattern is less pronounced for a boundary point z.