Maximum of the Characteristic Polynomial of the Ginibre Ensemble

Abstract

We compute the leading asymptotics for the maximum of the (centered) logarithm of the absolute value of the characteristic polynomial, denoted $\Psi _N$, of the Ginibre ensemble as the dimension of the random matrix N tends to $\infty$. The method relies on the log-correlated structure of the field $\Psi _N$ and we obtain the lower-bound for the maximum by constructing a family of Gaussian multiplicative chaos measures associated with certain regularization of $\Psi _N$ at small mesoscopic scales. We also obtain the leading asymptotics for the dimensions of the sets of thick points and verify that they are consistent with the predictions coming from the Gaussian Free Field. A key technical input is the approach from Ameur et al. (Ann Probab 43(3):1157–1201, 2015) to derive the necessary asymptotics, as well as the results from Webb and Wong (Proc Lond Math Soc (3) 118(5):1017–1056, 2019).

1 Introduction and Main Results

The Ginibre ensemble is the canonical example of a non-normal random matrix. It consists of a $N\times N$ matrix filled with independent complex Gaussian random variables of variance 1/N [31]. It is well-known that the eigenvalues $(\lambda _1, \dots , \lambda _N)$ of a Ginibre matrix are asymptotically uniformly distributed inside the unit disk $\mathbb {D} = \{ z\in \mathbb {C} : |z| < 1\}$ in the complex plane – this is known as the circular law [10, 16]. The Ginibre eigenvalues have the same law as the particles in a one component two-dimensional Coulomb gas confined by the potential $Q(x) = |x|^2/2$ at a specific temperature, see [56]. That is, the joint law of the eigenvalues is given by $\mathrm {d}\mathbb {P}_N \propto e^{- \mathrm {H}_N(x)} {\textstyle \prod _{j=1}^N} \mathrm {d}^2 x_j$ where the energy of a configuration $x\in \mathbb {C}^N$ is

$$\begin{aligned} \mathrm {H}_N(x) : = \sum _{\begin{array}{c} j, k =1 , \dots , N \\ j\ne k \end{array}} \log |x_j-x_k|^{-1} + 2 N \sum _{j=1, \dots ,N} Q(x_j) , \end{aligned}$$

(1.1)

and $\mathrm {d}^2x$ denotes the Lebesgue measure on $\mathbb {C}$. Moreover, these eigenvalues form a determinantal point process on $\mathbb {C}$ with a correlation kernel

$$\begin{aligned} K_N(x,z) = {\textstyle \sum _{j=0}^{N-1}} \frac{x^j \overline{z}^j}{j!} N^{j+1} e^{-N |x|^2/2 - N|z|^2/2}. \end{aligned}$$

(1.2)

This means that all the correlation functions (or marginals $\mathbb {P}_{N,n}$) of this point process are given by

$$\begin{aligned} \mathbb {P}_{N,n}[\mathrm {d}x_1, \cdots , \mathrm {d}x_n] = \frac{1}{(N)_n} \det \big [K_N(x_i,x_j) \big ]_{i,j =1}^n \tfrac{\mathrm {d}^2x_1}{\pi } \cdots \tfrac{\mathrm {d}^2x_n}{\pi } , \quad \text {for } n=1, \dots , N, \end{aligned}$$

(1.3)

where $(N)_n = N(N-1)\cdots (N-n+1)$. We refer to [33, Chapter 4] for an introduction to determinantal processes and to [33, Theorem 4.3.10] for a derivation of the Ginibre correlation kernel.

In this article we are interested in the asymptotics of the modulus of the characteristic polynomial $z \in \mathbb {C}\mapsto \prod _{j=1}^N|z-\lambda _j|$ of the Ginibre ensemble and in particular on the maximum size of its fluctuations. Before stating our main result, we need to review some basic properties of the Ginibre eigenvalues process.

First, it follows from a classical result in potential theory that the equilibrium measure which describes the limit of the empirical measure $\frac{1}{N} \sum _{j=1}^N \delta _{\lambda _j}$ is indeed the circular law: $\sigma (\mathrm {d}x) = \frac{1}{\pi } \mathbb {1}_{\mathbb {D}} \mathrm {d}^2 x$, see [56, Section 3.2]. Let $(x)_+ = x \vee 0$ for $x\in \mathbb {R}$. This can be deduced from the fact that the logarithmic potential of the circular law

$$\begin{aligned} \varphi (z) := \int \log |z-x| \sigma (\mathrm {d}x) = (\log |z|)_+ - \frac{(1- |z|^2)_+}{2} , \end{aligned}$$

(1.4)

satisfies the condition

$$\begin{aligned} \varphi (z) = Q(z) - 1/2 \quad \text {for all }z\in \mathbb {D}. \end{aligned}$$

(1.5)

Then, Rider–Viràg [53] showed that the fluctuations of the empirical measure of the Ginibre eigenvalues around the circular law are described by a Gaussian noise. This result was generalized to other ensembles of random matrices in [3, 4], as well as to two-dimensional Coulomb gases at an arbitrary positive temperature in [9, 46]. Let us define

$$\begin{aligned} \mathrm {X}(\mathrm {d}x) : = {\textstyle \sum _{j=1}^N \delta _{\lambda _j}} - N \sigma (\mathrm {d}x) . \end{aligned}$$

(1.6)

This measure describes the fluctuations of the Ginibre eigenvalues and, by [53, Theorem 1.1], for any function $f\in \mathscr {C}^2(\mathbb {C})$ with at most exponential growth, we have as $N\rightarrow \infty$,

$$\begin{aligned} \mathrm {X}(f) = {\textstyle \sum _{j=1}^N f(\lambda _j)} - N \int f(x)\sigma (\mathrm {d}x) \ \overset{\mathrm{law}}{\longrightarrow }\ \mathscr {N}\left( 0, \Sigma ^2(f) \right) . \end{aligned}$$

(1.7)

If f has compact support inside the support of the equilibrium measure, then the asymptotic variance is given by

$$\begin{aligned} \Sigma ^2(f)= \int \overline{\partial }f (x) \partial f(x) \sigma (\mathrm {d}x) . \end{aligned}$$

(1.8)

The object that we study in this article is the centered logarithm of the Ginibre characteristic polynomial:

$$\begin{aligned} \Psi _N(z) : = \log \left( {\textstyle \prod _{j=1}^N } |z-\lambda _j| \right) - N \varphi (z) . \end{aligned}$$

(1.9)

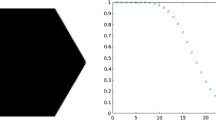
See Fig. 1 below for a sample of the random function $\Psi _N(z)$. Note that it follows from the convergence of the empirical measure to the circular law that for any $z\in \mathbb {C}$, we have in probability as $N\rightarrow \infty$,

$$\begin{aligned} \frac{1}{N} \log \left( {\textstyle \prod _{j=1}^N } |z-\lambda _j| \right) \rightarrow \varphi (z) , \end{aligned}$$

so that the second term on the RHS of (1.9) is necessary to have the field $\Psi _N$ asymptotically centered. In fact, it follows from the result of Webb–Wong [60] that $\mathbb {E}_N[\Psi _N(z)] \rightarrow 1/4$ for all $z\in \mathbb {D}$ as $N\rightarrow \infty$. Moreover, if we interpret $\Psi _N$ as a random generalized function, then the central limit theorem (1.7) implies that $\Psi _N$ converges in distribution to the Gaussian free field (GFF)¹ on $\mathbb {D}$ with free boundary conditions, see [53, Corollary 1.2] and also [4, 58] for further details. Even though the GFF is a random distribution, it can be though of as a random surface which corresponds to the two-dimensional analogue of Brownian motion [57]. The convergence result of Rider–Viràg indicates that we can think of the field $\Psi _N$ as an approximation of the GFF in $\mathbb {D}$. The main feature of the GFF is that it is a log-correlated Gaussian process on $\mathbb {C}$. This log-correlated structure is already visible for the absolute value of the Ginibre characteristic polynomial as it is possible to show that for any $z, x\in \mathbb {D}$,

$$\begin{aligned} \mathbb {E}_N\left[ \Psi _N(z) \Psi _N(x) \right] = \frac{1}{2} \log \left( \sqrt{N} \wedge |x-z|^{-1}\right) + \mathcal {O}(1) , \end{aligned}$$

(1.10)

as $N\rightarrow +\infty$. By analogy with the GFF and other log-correlated fields, we can make the following prediction regarding the maximum of the field $\Psi _N$. We have as $N\rightarrow +\infty$,

$$\begin{aligned} \max _{z\in \mathbb {D}} \Psi _N(z) = \frac{\log N }{\sqrt{2}} - \frac{3 \log \log N}{4\sqrt{2}} +\xi _N , \end{aligned}$$

(1.11)

where the random variable $\xi _N$ is expected to converge in distribution. Analogous predictions have been made for other log-correlated fields associated with normal random matrices. For instance, Fyodorov–Keating [28] first conjectured the asymptotics of the maximum of the logarithm of the absolute value of the characteristic polynomial of the circular unitary ensemble² (CUE), including the distribution of the error term and Fyodorov–Simm [30] made analogous prediction for the Gaussian Unitary Ensemble³ (GUE).

The main goal of this article is to verify the leading order in the asymptotic expansion (1.11). More precisely, we prove the following result:

Theorem 1.1

For any $0<r<1$ and any $\epsilon >0$, it holds

$$\begin{aligned} \lim _{N\rightarrow \infty } \mathbb {P}_N\left[ \frac{1-\epsilon }{\sqrt{2}} \log N \le \max _{|z| \le r} \Psi _N(z) \le \frac{1+\epsilon }{\sqrt{2}} \log N \right] =1 . \end{aligned}$$

It is worth pointing out that like many other asymptotic properties of the eigenvalues of random matrices, we expect the results of Theorem 1.1, as well as the prediction (1.11) modulo the limiting distribution of $\xi _N$, and Theorem 1.3 below to be universal. This means that these results should hold for other random normal matrix ensembles with a different confining potential Q as well as for other non-Hermitian Wigner ensembles under reasonable assumptions on the entries of the random matrix. In the remainder of this section, we review the context and most relevant results related to Theorem 1.1, and we provide several motivations to study the characteristic polynomial of the Ginibre ensemble.

1.1 Comments on Theorem 1.1 and further results

The study of characteristic polynomials for different ensembles of random matrices is an interesting and active topic because of its connections to several problems in diverse areas of mathematics. In particular, there are the analogy between the logarithm of the absolute value of the characteristic polynomial of the CUE and the Riemann $\zeta$-function [38], as well as the connections with Toeplitz or Hankel determinant with Fisher–Hartwig symbols, e.g. [18, 19, 24, 41]. Of essential importance is also the connection between characteristic polynomial of random matrices, log-correlated fields and the theory of Gaussian multiplicative chaos [28, 35]. This connection has been used in several recent works to compute the asymptotics of the maximum of the logarithm of the characteristic polynomial for various ensembles of random matrices. For the CUE, a result analogous to Theorem 1.1 was first obtained by Arguin–Belius–Bourgade [5]. Then, the correction term was computed by Paquette–Zeitouni [49] and the counterpart of the conjecture (1.11) was established for the circular $\beta$-ensembles for general $\beta >0$ by Chhaibi–Madaule–Najnudel⁴ [20]. For the characteristic polynomial of the GUE, as well as other Hermitian unitary invariant ensembles, the law of large numbers for the maximum of the absolute value of the characteristic polynomial was obtained in [43]. Cook and Zeitouni [23] also obtained a law of large numbers for the maximum of the characteristic polynomial of a random permutation matrix, in which case their result does not match with the prediction from Gaussian log-correlated field because of arithmetic effects. These results rely on the log-correlated structure of characteristic polynomials and proceed by analogy with the case of branching random walk using a modified second moment method [39]. This method has also been successful to compute the asymptotics of the Riemann $\zeta$-function in a random interval of the critical line, see [6, 32, 47, 55]. Further recent results on the deep connections between log-correlated fields, Gaussian multiplicative chaos and characteristic polynomials of $\beta$-ensembles can be found in [21, 22, 44] In particular, we prove in  [22] the counterpart of Theorem 1.1 for the imaginary part of the characteristic polynomial of a large class of Hermitian unitary invariant ensembles and show that this implies optimal rigidity bounds for the eigenvalues. Likewise, by adapting the proof of the upper-bound in Theorem 1.1, we can obtain precise rigidity estimates for linear statistics of the Ginibre ensemble in the spirit of [8, Theorem 1.2] and [46, Theorem 2].

Theorem 1.2

For any $0<r<1$ and $\kappa >0$, define

$$\begin{aligned} \mathscr {F}_{r,\kappa } : = \left\{ f\in \mathscr {C}^2(\mathbb {C}) : \Delta f(z) =0\ \text { for all } z\in \mathbb {C}\setminus \mathbb {D}_r \text { and }\max _\mathbb {C}|\Delta f| \le N^\kappa \right\} . \end{aligned}$$

(1.12)

For any $\eta >0$ (possibly depending on N with $\eta \le \frac{N}{\log N}$), there exists a constant $C_{r}>0$ such that

$$\begin{aligned} \mathbb {P}_N\bigg [ \sup \left\{ |\mathrm {X}(f)| : f\in \mathscr {F}_{r,\kappa } \text { and } \int _\mathbb {D}|\Delta f(z)| \frac{\mathrm {d}^2z}{\pi } \le 1 \right\} \ge \eta \log N +1 \bigg ] \le C_r N^{5/4+\kappa -\eta }. \end{aligned}$$

We believe that Theorem 1.2 is of independent interest since it covers any smooth mesoscopic linear statistic at arbitrary small scales in a uniform way. This is to be compared to the local law of [17, Theorem 2.2] which is valid for general Wigner ensembles, but not with the (optimal) logarithmic bound for the fluctuations and without such uniformity in f. The Proof of Theorem 1.2 is given in Sect. 3.2 and it relies on the basic observation that in the sense of distribution, the Laplacian of the field $\Psi _N$ is related to the empirical measure of the Ginibre ensemble suitably centered: $\Delta \Psi _N = 2\pi N \left( \frac{1}{N} \sum _{j=1}^N \delta _{\lambda _j} - \frac{1}{\pi }\mathbb {1}_\mathbb {D}\right)$.

The Proof of Theorem 1.1 consists of an upper-bound⁵ which is based on the subharmonicity of the logarithm of the absolute value of the Ginibre characteristic polynomial and the moments asymptotics from Webb–Wong [60] and of a lower-bound which exploits the log-correlated structure of the field $\Psi _N$. More precisely, by relying on the robust approach from [45], we obtain the lower-bound in Theorem 1.1 by constructing a family of subcritical Gaussian multiplicative chaos measures associated with certain mesoscopic regularization of the field $\Psi _N$ — see Theorem 2.2 below for further details. Gaussian multiplicative chaos (GMC) is a theory which goes back to Kahane [37] and it aims at encoding geometric features of a log-correlated field by means of a family of random measures. These GMC measures are defined by taking the exponential of a log-correlated field through a renormalization procedure. We refer the readers to Sect. 2.1 for a brief overview of the theory and to the review of Rhodes–Vargas [51] or the elegant and short article of Berestycki [11] for more comprehensive presentations. It is well-known that in the subcritical phase, these GMC measures live on the sets of so-called thick points⁶ of the underlying field [51, Section 4]. By exploiting this connection, we obtain from our analysis the leading order of the measure of the sets of thick points of the characteristic polynomial for large N.

Theorem 1.3

Let us define the set of $\beta$-thick points of the Ginibre characteristic polynomial:

$$\begin{aligned} \mathscr {T}_N^\beta (r): = \big \{ x\in \overline{\mathbb {D}_r} : \Psi _N(x) \ge \beta \log N \big \} \end{aligned}$$

(1.13)

and let $|\mathscr {T}_N^\beta (r)|$ be its Lebesgue measure. For any $0<r<1$, any $0 \le \beta < 1/\sqrt{2}$ and any small $\epsilon >0$, we have

$$\begin{aligned} \lim _{N\rightarrow \infty } \mathbb {P}_N\left[ N^{-2\beta ^2-\delta } \le |\mathscr {T}_N^\beta (r)| \le N^{-2\beta ^2+\delta }\right] =1. \end{aligned}$$

(1.14)

The Proof of Theorem 1.3 will be given in Sect. 4 and the result has the following interpretation. By (1.9), the field $-\Psi _N$ corresponds to the (electrostatic) potential energy generated by the random charges $(\lambda _1, \dots , \lambda _N)$ and the negative uniform background $\sigma$. One may view $-\Psi _N$ as a complex energy landscape and the asymptotics (1.14) describe the multi-fractal spectrum of the level sets near the extreme local minima of this landscape. Moreover, as a consequence of Theorems 1.1 and 1.3, we obtain the leading order of the corresponding free energy, i.e. the logarithm of the partition function of the Gibbs measure $e^{\beta \Psi _N}$ for $\beta >0$. Namely, by adapting the Proof of [5, Corollary 1.4], it holds for any $0<r<1$, in probability,

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{1}{\beta \log N} \log \left( \int _{\mathbb {D}_r} e^{\beta \Psi _N(z)} \frac{\mathrm {d}^2z}{\pi } \right) =&{} \max _{\gamma \in [0, 1/\sqrt{2}]}\Big \{ \frac{1}{\beta }+ \gamma -\frac{2}{\beta }\gamma ^2 \Big \}\nonumber \\=&{} {\left\{ \begin{array}{ll} \displaystyle \frac{1}{\beta }+ \frac{\beta }{8} , &{}{} \beta \in [0, \sqrt{8}] \\ \displaystyle 1/\sqrt{2} , &{}{}\beta > \sqrt{8} \end{array}\right. }. \end{aligned}$$

(1.15)

The fact that the free energy is constant and equal to ${\displaystyle \lim _{N\rightarrow +\infty }}\frac{\max _{\mathbb {D}_r} \Psi _N}{\log N}$ in the supercritical regime $\beta >\sqrt{8}$ is called freezing. This property is typical for Gaussian log-correlated fields and our results rigorously establish that the Ginibre characteristic polynomial behave according to the Gaussian predictions which is a well-known heuristic in random matrix theory. Moreover, this freezing scenario is instrumental to predict the full asymptotic behavior (1.11) of the maximum of the field $\Psi _N$, including the law of the error term, see e.g. [27]. For an illustration of level sets of the random function and in particular of the geometry of thick points, see Fig. 2.

Let us return to the connections between our results and the theory of Gaussian multiplicative chaos. The family of GMC measures associated to the GFF are called Liouville measures and they play a fundamental role in recent probabilistic constructions in the context of quantum gravity, imaginary geometries, as well as conformal field theory. We refer to the reviews [7, 52] for further references on these aspects of the theory. Thus, motivated by the result of Rider–Viràg, it is expected that a random measure whose density is given by a small⁷ power of the characteristic polynomial (see Fig. 3) converges when suitably normalized:

$$\begin{aligned} \frac{\prod _{j=1}^N|z-\lambda _j|^\gamma }{\mathbb {E}_N\left[ \prod _{j=1}^N|z-\lambda _j|^\gamma \right] } \frac{\mathrm {d}^2z}{\pi } = \frac{e^{\gamma \Psi _N(z)}}{\mathbb {E}_N\left[ e^{\gamma \Psi _N(z)}\right] } \frac{\mathrm {d}^2z}{\pi } \ \overset{\mathrm{law}}{\longrightarrow } \ \mu _\mathrm {G}^\gamma , \end{aligned}$$

(1.16)

where $\mu _\mathrm {G}^\gamma$ is a Liouville measure with parameter $0<\gamma < \sqrt{8}$. Hence, this provides an interesting connection between the Ginibre ensemble of random matrices and random geometry. As we observed in [22, Section 3], this convergence result in the subcritical phase implies the lower-bound in Theorem 1.1. An important observation that we make in this paper is that it suffices to establish the convergence of $\frac{e^{\gamma \psi _N(z)}}{\mathbb {E}_N\left[ e^{\gamma \psi _N(z)}\right] } \frac{\mathrm {d}^2z}{\pi }$ to a GMC measure for a suitable regularization $\psi _N$ of the field $\Psi _N$ in order to capture the correct leading order asymptotics of its maximum and thick points. The main issues are to work with a regularization at an optimal mesoscopic scale $N^{-1/2+\alpha }$ for arbitrary small $\alpha >0$ and to be able to obtain the convergence in the whole subcritical phase. In particular, our result on GMC, Theorem 2.2, provides strong evidence that the prediction (1.16) holds.

It is an important and challenging problem to obtain (1.16) already in the subcritical phase. In particular, this requires to derive the asymptotics of joint moments of the characteristic polynomials. For a single $z\in \mathbb {D}_r$, such asymptotics are obtained by Webb–Wong in [60] using Riemann–Hilbert techniques. Let us recall their main result which is also a key input in our method.

Theorem 1.4

[60, Theorem 1.1]. For any fixed $0<r<1$, we have

$$\begin{aligned} \mathbb {E}_N[e^{\gamma \Psi _N(z)}] = (1+ o(1)) \frac{(2\pi )^{\gamma /4}}{G(1+\gamma /2)} N^{\gamma ^2/8} , \end{aligned}$$

(1.17)

where the error term is uniform for $\gamma$ in compact sets of $\{ \gamma \in \mathbb {C}: \mathfrak {R}\gamma >-2\}$ and $z\in \mathbb {D}_r$.

Remark 1.5

The asymptotics of the joint exponential moments of $\Psi _N$ remain conjectural, see e.g. [60, Section 1.2], except for even moments for which there are explicit formulae, see [1, 26, 29]. These formulae rely on the determinantal structure of the Ginibre ensemble: for any $n\in \mathbb {N}$, we have for any $z_1, \dots , z_n \in \mathbb {C}$ such that $z_1 \ne \cdots \ne z_n$,

$$\begin{aligned} \mathbb {E}_N\left[ {\textstyle \prod _{i=1}^n \prod _{j=1}^N } |z_i-\lambda _j|^2\right] = \frac{ \pi ^n \prod _{k=N}^{N+n-1} k! }{N^{-Nn - \frac{n(n+1)}{2}} } \frac{\det _{n\times n}[K_{N+n}(z_i,z_j)]}{ \prod _{1\le i< j \le n}| z_i-z_j|^2} e^{N \sum _{i=1}^n |z_i|^2} , \end{aligned}$$

(1.18)

where $K_{N+n}$ is the Ginibre kernel as in (1.2). Using the off-diagonal (Gaussian) decay of the Ginibre kernel, we can show that

$$\begin{aligned} \det _{n\times n}[ K_{N+n}(z_i,z_j)] = {\textstyle \prod _{k=1}^{n} } K_{N+n}(z_i,z_i) \left( 1+ \mathcal {O}(N^{-1}) \right) , \end{aligned}$$

uniformly for all $\inf _{i\ne j} |z_i -z_j| \ge c\sqrt{\frac{\log N}{N}}$ if $c>0$ is a sufficiently large constant. If $|z_i| \le c\sqrt{\frac{\log N}{N}}$, we also have $K_{N+n}(z_i,z_i) = \tfrac{N}{\pi }\left( 1+ \mathcal {O}(N^{-1}) \right)$. Thus, by (1.5) and (1.9) we obtain that for any given $z_1, \dots , z_n \in \mathbb {D}$, such that $z_1 \ne \cdots \ne z_n$,

$$\begin{aligned} \mathbb {E}_N\big [ {\textstyle \prod _{i=1}^n} e^{2 \Psi _N(z_i)}\big ] = \left( \sqrt{2\pi N} \right) ^n |\triangle (z_1,\dots , z_n) |^{-2} \left( 1+ \mathcal {O}(N^{-1}) \right) , \end{aligned}$$

(1.19)

which matches exactly with the Fisher–Hartwig predictions from [60, Section 1.2] with $\gamma _1= \cdots = \gamma _n =2$. $\blacksquare$

Fig. 1

Sample of the logarithm of the absolute value of the Ginibre characteristic polynomial $\Psi _N(z)$ for $z\in \mathbb {D}$ for a random matrix of dimension $N=3000$

Fig. 2

Level sets of the logarithm of the absolute value of the Ginibre characteristic polynomial $\Psi _N(z)$ for a random matrix of dimension $N=5000$

Fig. 3

Sample of the (normalized) Ginibre characteristic polynomial $\frac{\prod _{j=1}^N |z-\lambda _j| }{\mathbb {E}_N[ \prod _{j=1}^N |z-\lambda _j| ] }$ for a random matrix of dimension $N=3000$. This is an approximation of the Liouville measure $\mu _G^\gamma$ with (subcritical) parameter $\gamma =1$

1.2 Outline of the article

The remainder of this article is devoted to the Proof of Theorem 1.1. The result follows directly by combining the upper-bound of Proposition 3.1 and the lower-bound from Proposition 2.1. As we already emphasized the proof of the lower-bound follows from the connection with GMC theory and the details of the argument are reviewed in Sect. 2. In particular, it is important to obtain Gaussian asymptotics for the exponential moments of a mesoscopic regularization of the field $\Psi _N$, see Proposition 2.3. These asymptotics are obtained by using the method developed by Ameur–Hedenmalm–Makarov [4] which relies on Ward identity, also known as loop equation, and the determinantal structure of the Ginibre ensemble. Compared with the proof of the central limit theorem in [4], we face two significant extra technical challenges: we must consider a mesoscopic linear statistic coming from a test function which develops logarithmic singularities as $N\rightarrow \infty$. This implies that we need a more precise approximation for the correlation kernel of the biased determinantal process. For these reasons, we give a detailed Proof of Proposition 2.3 in Sects. 5 and 6. Our proof for the upper-bound is given in Sect. 3 and it relies on the subharmonicity of the logarithm of the absolute value of the Ginibre characteristic polynomial and the asymptotics from Theorem 1.4. In Sect. 3.2, we discuss an application to linear statistics of the Ginibre eigenvalues and give the Proof of Theorem 1.2.

2 Proof of the Lower-Bound

Recall that $\Psi _N$ denotes the centered logarithm of the absolute value of the Ginibre characteristic polynomial, (1.9). The goal of this section is to obtained the following result:

Proposition 2.1

For any $r>0$ and any $\delta >0$, we have

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ \max _{|x| \le r} \Psi _N(x) \ge \frac{1-\delta }{\sqrt{2}} \log N \right] =1 . \end{aligned}$$

Our strategy to prove Proposition 2.1 is to obtain an analogous lower-bound for a mesoscopic regularization of $\Psi _N$ which is also compactly supported inside $\mathbb {D}$. Note that it is also enough to consider the maximum in a disk $\mathbb {D}_{\epsilon _0} = \{x\in \mathbb {C}: |x|\le \epsilon _0 \}$ for a small $\epsilon _0>0$. To construct such a regularization, let us fix $0< \epsilon _0 \le 1/4$ and a mollifier $\phi \in \mathscr {C}^\infty _c(\mathbb {D}_{\epsilon _0})$ which is radial.⁸ For any $0<\epsilon <1$, we denote $\phi _\epsilon (\cdot ) = \phi (\cdot /\epsilon ) \epsilon ^{-2}$ and to approximate the logarithm of the characteristic polynomial, we consider the test function

$$\begin{aligned} \psi _\epsilon (z) : = \int \log |z-x| \phi _\epsilon (x) \mathrm {d}^2x . \end{aligned}$$

(2.1)

We also denote $\psi =\psi _1$. For technical reason, it is simpler to work with test function compactly supported inside $\mathbb {D}$ — which is not the case for $\psi _\epsilon$. However, this can be fixed by making the following modification: for any $z \in \mathbb {D}_{\epsilon _0}$, we define

$$\begin{aligned} g_N^z(x) := \psi _{\epsilon }(x-z) - \psi (x-z) , \quad x\in \mathbb {C}. \end{aligned}$$

(2.2)

It is easy⁹ to see that the function $g_N^z$ is smooth and compactly supported inside $\mathbb {D}(z, \epsilon _0)$. Since we are interested in the regime where $\epsilon (N)\rightarrow 0$ as $N\rightarrow \infty$, we emphasize that $g_N^z$ depends on the dimension $N\in \mathbb {N}$ of the matrix. Then, the random field $z\mapsto \mathrm {X}(g_N^z)$ is related to the logarithm of the Ginibre characteristic polynomial as follows:

$$\begin{aligned} \mathrm {X}(g_N^z) = \int \Psi _N(x) \phi _\epsilon (z+x) \mathrm {d}^2x - \int \Psi _N(x) \phi (z+x) \mathrm {d}^2x . \end{aligned}$$

(2.3)

In particular, $z\mapsto \mathrm {X}(g_N^z)$ is still an approximate log-correlated field. Indeed, according to (1.7), (1.8) and formula (2.8) below, we expect that as $N\rightarrow +\infty$

$$\begin{aligned} \mathbb {E}_N\left[ \mathrm {X}(g_N^z) \mathrm {X}(g_N^x) \right] = \frac{1}{2} \log \left( \epsilon (N)^{-1}\wedge |x-z|^{-1}\right) + \mathcal {O}(1) . \end{aligned}$$

This should be compared with formula (1.10).

2.1 Gaussian multiplicative chaos

Let $\mathrm {G}$ be the Gaussian free field (GFF) on $\mathbb {D}$ with free boundary conditions. That is, $\mathrm {G}$ is a Gaussian process taking values in the space of Schwartz distributions with covariance kernel:

$$\begin{aligned} \mathbb {E}\left[ \mathrm {G}(x) \mathrm {G}(z)\right] = \frac{1}{2} \log |z-x|^{-1} . \end{aligned}$$

(2.4)

Up to a factor of $1/\pi$, the RHS of (2.4) is the Green’s function¹⁰ for the Laplace operator $-\Delta$ on $\mathbb {C}$. Because of the singularity of the kernel (2.4) on the diagonal, $\mathrm {G}$ is called a log-correlated field and it cannot be defined pointwise. In general, $\mathrm {G}$ is interpreted as a random distribution valued in a Sobolev space $H^{-\alpha }(\mathbb {D})$ for any $\alpha >0$ [7]. In particular, for any mollifier $\phi$ as above and any $\epsilon >0$, we view

$$\begin{aligned} \mathrm {G}_\epsilon (z) := \int \mathrm {G}(x) \phi _\epsilon (z+x) \mathrm {d}^2x \end{aligned}$$

(2.5)

as a regularization of $\mathrm {G}$.

The theory of Gaussian multiplicative chaos aims at defining the exponential of a log-correlated field. Since such a field is merely a random distribution, this is a non trivial problem. However, in the so-called subcritical phase, this can be done by a quite simple renormalization procedure. Namely, for $\gamma >0$, we define $\mu ^\gamma _\mathrm {G}= : e^{\gamma \mathrm {G}} :$ as

$$\begin{aligned} \mu ^\gamma _\mathrm {G}(\mathrm {d}x) : = \lim _{\epsilon \rightarrow 0} \frac{e^{\gamma \mathrm {G}_\epsilon (x)}}{\mathbb {E}[e^{\gamma \mathrm {G}_\epsilon (x)}]} \sigma (\mathrm {d}x) . \end{aligned}$$

(2.6)

It turns out that this limit exists almost surely as a random measure on $\mathbb {D}$ and that it does not depend on the mollifier $\phi$ within a reasonable class. Moreover, in the case of the GFF normalized as in (2.4), it is a non trivial measure if and only if the parameter $0<\gamma < \sqrt{8}$ — this is called the subcritical phase [7, 11, 54]. For general log-correlated field, the theory of GMC goes back to the work of Kahane [37] and in the case of the GFF, the construction $\mu ^\gamma _\mathrm {G}$ was re-discovered by Duplantier–Sheffield [25] and Rhodes–Vargas [50] from different perspectives. In a sense, the random measure $\mu ^\gamma _\mathrm {G}$ encodes the geometry of the GFF. For instance, the support of $\mu ^\gamma _\mathrm {G}$ is a fractal set which is closely related to the concept of thick points [34]. We will not discuss these issues here and refer instead to [7, 22] for further details. Let us just point out that the relationship between Theorem 2.2 and Corollary 2.4 below is based on such arguments.

For log-correlated fields which are only asymptotically Gaussian, especially those coming from random matrix theory such as the logarithm of the Ginibre characteristic polynomial $\Psi _N$, the theory of Gaussian multiplicative chaos has been developed in [45, 59]. The construction in [45] is inspired from the approach of Berestycki [11] and it has been recently applied to unitary random matrices in [48], as well as to Hermitian unitary invariant random matrices in [12, 22]. In this paper, we construct subcritical GMC measures coming from the regularization $\mathrm {X}(g_N^z)$, (2.3), of the logarithm of the Ginibre characteristic polynomial at a scale $\epsilon = N^{-1/2+\alpha }$ for any small $\alpha >0$. This mesoscopic regularization makes it simpler to compute the leading asymptotics of the exponential moments of the field $\mathrm {X}(g_N^z)$ — see Proposition 2.3 below. Then, using the main results from [45], it allows us to prove that the limit of the renormalized exponential $\mu ^\gamma _N = : e^{\gamma \mathrm {X}(g_N^z)} :$ exists for all $\gamma >0$ in the subcritical phase and that it is absolutely continuous with respect to the GMC measure $\mu ^\gamma _\mathrm {G}$.

Theorem 2.2

Recall that $0< \epsilon _0 \le 1/4$ is fixed. Let $\gamma >0$ and $g_N^{z}$ be as in (2.2) with $\epsilon =\epsilon (N) = N^{-1/2+\alpha }$ for a fixed $0<\alpha <1/2$. Let us define the random measure $\mu ^\gamma _N$ on $\mathbb {D}_{\epsilon _0}$ by

$$\begin{aligned} \mu ^\gamma _N(\mathrm {d}z) := \frac{\exp \left( \gamma \mathrm {X}(g_N^{z}) \right) }{\mathbb {E}_N[\exp \left( \gamma \mathrm {X}(g_N^{z}) \right) ]} \sigma (\mathrm {d}z) . \end{aligned}$$

For any $0<\gamma < \gamma _* = \sqrt{8}$, the measure $\mu ^\gamma _N$ converges in law as $N\rightarrow +\infty$ with respect to the weak topology toward a random measure $\mu ^\gamma _\infty$ which has the same law, up to a deterministic constant, as $e^{\gamma \mathrm {G}_1(x)}\mu ^\gamma _\mathrm {G}(\mathrm {d}x)$, where $\mathrm {G}_1$ is the smooth Gaussian process obtained from $\mathrm {G}$ as in (2.5) with $\epsilon =1$ and $\mu ^{\gamma }_\mathrm {G}$ is the GMC measure (2.6). In particular, our convergence covers the whole subcritical phase.

The Proof of Theorem 2.2 follows from applying [45, Theorem 2.6]. Let us check that the correct assumptions hold. First, we can deduce [45, Assumption 2.1, Assumption 2.2] from the CLT of Rider–Viràg (1.7). Indeed, for any fixed $\epsilon >0$, as $\psi _\epsilon$ is a smooth function, the process $(z, \epsilon )\mapsto \mathrm {X}\big (\psi _\epsilon (\cdot -z)\big )$ converges in the sense of finite dimensional distributions to a mean-zero Gaussian process whose covariance is given by (1.8).¹¹ Namely, letting $\Sigma (\cdot ;\cdot )$ be the quadratic form associated with $\Sigma (\cdot )$, we have for any $z_1, z_2 \in \mathbb {D}_{\epsilon _0}$ and $0<\epsilon _1, \epsilon _2 \le \epsilon _0$,

$$\begin{aligned}&\lim _{N\rightarrow +\infty } \mathbb {E}_N\left[ \mathrm {X}\left( \psi _{\epsilon _1}(\cdot - z_1 ) \right) \mathrm {X}\left( \psi _{\epsilon _2}(\cdot - z_2) \right) \right] \nonumber \\&\quad =\Sigma \left( \psi _{\epsilon _1}(\cdot - z_1 ) ; \psi _{\epsilon _2}(\cdot - z_2) \right) \nonumber \\&\quad = - \frac{1}{2} \iint \log |x_1-x_2| \phi _{\epsilon _1}(x_1 - z_1) \phi _{\epsilon _2}(x_2-z_2) \mathrm {d}^2 x_1 \mathrm {d}^2 x_2 \nonumber \\&\quad = \mathbb {E}\left[ \mathrm {G}_{\epsilon _1}(z_1) \mathrm {G}_{\epsilon _2}(z_2) \right] \end{aligned}$$

(2.7)

$$\begin{aligned}&\quad = - \frac{1}{2} \iint \log |z_1-z_2 + \epsilon _1 u_1- \epsilon _2u_2| \phi (u_1) \phi (u_2) \mathrm {d}^2 u_1 \mathrm {d}^2 u_2 \nonumber \\&\quad = \frac{1}{2} \log \left( |z_1-z_2 |^{-1} \wedge \epsilon _1^{-1} \wedge \epsilon _2^{-1} \right) + \underset{\epsilon _1, \epsilon _2 \rightarrow 0}{\mathcal {O}(1)} , \end{aligned}$$

(2.8)

where the error term is uniform. In particular, (2.7) shows that the process $(z, \epsilon )\mapsto \mathrm {X}\big (\psi _\epsilon (\cdot -z)\big )$ converges in the sense of finite dimensional distributions to $(z, \epsilon )\mapsto \mathrm {G}_\epsilon (z)$ as in (2.5), which comes from mollifying a GFF. In this case, the [45, Assumption 2.3] follows e.g. from [11, Theorem 1.1]. So, the only important input to deduce Theorem 2.2 is to verify [45, Assumption 2.4] which consists in obtaining Gaussian asymptotics for the joint exponential moments of the field $\mathrm {X}(g_N^z)$. Namely, we need the following asymptotics:

Proposition 2.3

Fix $0<\alpha <1/2$, $R>0$ and let $\epsilon =\epsilon (N) = N^{-1/2+\alpha }$. For any $n\in \mathbb {N}$, $\gamma _1 , \dots \gamma _n \in \mathbb {R}$, $z_1, \dots , z_n \in \mathbb {C}$, we denote

$$\begin{aligned} g_N^{\mathbf {\gamma }, \mathbf {z}} (x) : = {\textstyle \sum _{k=1}^n} \gamma _k \left( \psi _{\epsilon _k}(x-z_k) - \psi (x-z_k) \right) , \quad x\in \mathbb {C}, \end{aligned}$$

(2.9)

with parameters $\epsilon (N)\le \epsilon _1(N) \le \cdots \le \epsilon _n(N) <1$. We have

$$\begin{aligned} \mathbb {E}_N\left[ \exp \left( \mathrm {X}(g_N^{\mathbf {\gamma }, \mathbf {z}} ) \right) \right] = \exp \Big ( \frac{1}{2} \Sigma ^2(g_N^{\mathbf {\gamma }, \mathbf {z}} ) + \underset{N\rightarrow +\infty }{o(1)}\Big ) , \end{aligned}$$

(2.10)

where $\Sigma$ is given by (1.8) and the error term is uniform for all $\mathbf {z} \in \mathbb {D}_{\epsilon _0}^{\times n}$ and $\mathbf {\gamma } \in [-R,R]^n$.

The Proof of Proposition 2.3 is the most technical part of this paper and it is postponed to Sect. 5. It relies on adapting in a non-trivial way the arguments of Ameur–Hedenmalm–Makarov from [4]. In particular, our proofs relies heavily on the determinantal structure of the Ginibre eigenvalues and we need local asymptotics for the correlation kernel of the ensemble obtained after making a small perturbation of the Ginibre potential — see Sect. 5.1. It turns out that these asymptotics are universal and can be derived using techniques inspired from the works of Berman [13, 14] which have also been applied to study the fluctuations of the eigenvalues of normal random matrices in [2,3,4].

As an important consequence of Theorem 2.2, we obtain the following corollary:

Corollary 2.4

Fix $0<\alpha <1/2$, let $\epsilon =\epsilon (N) = N^{-1/2+\alpha }$ and let $\psi _\epsilon$ be as in (2.1). If $\gamma _*=\sqrt{8}$, then for any $\delta >0$ and any $0< \epsilon _0 \le 1/4$, we have

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ \max _{|z| \le \epsilon _0} \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right) \ge (1-\delta )\frac{\gamma ^*}{2} \log \epsilon ^{-1} \right] =1 . \end{aligned}$$

The Proof of Corollary 2.4 follows from [22, Theorem 3.4] with a few non trivial modifications, the details are given in Sect. 2.3.

2.2 Proof of Proposition 2.1

We are now ready to complete the Proof of Proposition 2.1. Observe that by (1.9) and (2.1), we have for $z\in \mathbb {C}$ and $0<\epsilon \le 1$,

$$\begin{aligned} \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right) = \int \Psi _N(z+x) \phi _\epsilon (x) \mathrm {d}^2x . \end{aligned}$$

In particular since ${\text {supp}}(\phi _\epsilon ) \subseteq \mathbb {D}_{\epsilon _0}$ for any $0<\epsilon \le 1$, this implies that we have a deterministic bound for any $z\in \mathbb {C}$,

$$\begin{aligned} \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right) \le \max _{x\in \mathbb {D}(z,\epsilon _0)} \Psi _N(x) . \end{aligned}$$

Then

$$\begin{aligned} \max _{|z| \le \epsilon _0} \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right) \le \max _{|x|\le 2\epsilon _0} \Psi _N(x) \end{aligned}$$

and by Corollary 2.4 with $\alpha =\delta$, we obtain

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ \max _{|x| \le 2\epsilon _0} \Psi _N(x) \ge \frac{1-3\delta }{\sqrt{2}} \log N \right] =1 . \end{aligned}$$

Since $0< \epsilon _0 \le 1/4$ and $0<\delta <1/2$ are arbitrary, this yields the claim.

2.3 Proof of Corollary 2.4

This corollary follows from the results on the behavior of extreme values for general log-correlated fields which are asymptotically Gaussian developed in [22, Section 3]. Let us fix $0<\epsilon _0 \le 1/4$. First of all, we verify that it follows from Proposition 2.3 and formula (2.8) that for any $\gamma \in \mathbb {R}$, as $N\rightarrow +\infty$

$$\begin{aligned} \mathbb {E}_N\left[ \exp \left( \gamma \mathrm {X}(g_N^{z}) \right) \right] = \exp \Big ( \frac{\gamma ^2}{4} \log \epsilon (N)^{-1} + \mathcal {O}(1)\Big ) , \end{aligned}$$

uniformly for all $z\in \mathbb {D}_{\epsilon _0}$. These asymptotics show that the field $z\mapsto \mathrm {X}(g_N^{z})$ satisfies [22, Assumptions 3.1] on the disk $\mathbb {D}_{\epsilon _0}$. Moreover, by Theorem 2.2, $\mu ^\gamma _N(\mathbb {D}_{\epsilon _0}) \rightarrow \mu ^\gamma _\infty (\mathbb {D}_{\epsilon _0})$ in distribution as $N\rightarrow +\infty$ where $0<\mu ^\gamma _\infty (\mathbb {D}_{\epsilon _0}) <+\infty$ almost surely. This follows from the fact that the random measure $\mu ^\gamma _\infty (\mathrm {d}x) \propto e^{\gamma \mathrm {G}_1(x)}\mu ^\gamma _\mathrm {G}(\mathrm {d}x)$, $\mathrm {G}_1$ is a smooth Gaussian process on $\mathbb {D}$, $\mathbb {D}_{\epsilon _0}$ is a continuity set for the GMC measure $\mu ^\gamma _\mathrm {G}$ and $0<\mu ^\gamma _\mathrm {G}(\mathbb {D}_{\epsilon _0}) <+\infty$ almost surely. Thus [22, Assumptions 3.3] holds and we can apply¹² [22, Theorem 3.4] to obtain a lower-bound for the maximum of the field $z\mapsto \mathrm {X}(g_N^{z})$. This shows that for any $0< \epsilon _0 \le 1/4$ and any $\delta >0$,

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ \max _{|z| \le \epsilon _0} \mathrm {X}(g_N^{ z}) \ge \left( 1-\frac{\delta }{2} \right) \frac{\gamma _*}{2} \log \epsilon (N)^{-1} \right] =1 . \end{aligned}$$

(2.11)

Let us point out that heuristically, the lower-bound (2.11) follows from the facts that the random measure $\mu ^\gamma _N$ from Theorem 2.2 has most of its mass in the set $\left\{ z\in \mathbb {D}_{\epsilon _0} : \mathrm {X}(g_N^{z}) \ge \gamma (1-\delta )\Sigma ^2(g_N^{z}) \right\}$ for large N and that $\mu ^\gamma _N$ is a non-trivial measure if and only if $\gamma < \gamma _*$. Moreover, by [22, Proposition 3.8], we also obtain a lower-bound for the measure of the sets where the field $z\mapsto \mathrm {X}(g_N^{ z})$ takes extreme values. Namely, under the assumptions of Proposition 2.2, we have for any $0 \le \gamma < \frac{\gamma _*}{\sqrt{2}}$ and any small $\delta >0$,

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ \bigg | \Big \{ z\in \mathbb {D}_{\epsilon _0} : \mathrm {X}(g_N^{ z}) \ge \tfrac{\gamma }{\sqrt{2}} \log \epsilon (N)^{-1} \Big \}\bigg | \ge \epsilon (N)^{(\gamma ^2-\delta )/2 } \right] =1 . \end{aligned}$$

(2.12)

In Sect. 4, we use these asymptotics to compute the leading order of the measure of the sets of thick points of the Ginibre characteristic polynomial, hence proving Theorem 1.3.

Let us return to the Proof of Corollary 2.4 and recall that $g_N^{z} = \psi _{\epsilon }(\cdot -z) - \psi (\cdot -z)$ with $\epsilon =\epsilon (N)$. So, in order to obtain the lower-bound, we must show that the random variable $\max _{z\in \mathbb {D}_{\epsilon _0}} \left| \mathrm {X}\left( \psi (\cdot -z) \right) \right|$ remains small compared to $\log \epsilon (N)^{-1}$ for large $N\in \mathbb {N}$. To prove this claim, we rely on the following general bound.

Lemma 2.5

Let $\mathscr {F}_{r,0}$ be as in (1.12). For any $0<r<1$, there exists a constant $C_r>0$ such that

$$\begin{aligned} \mathbb {E}_N\Big [ \big ( \max _{f \in \mathscr {F}_{r,0}} \left| \mathrm {X}(f) \right| \big )^2 \Big ] \le C_r \left( 1+\log \sqrt{N} \right) . \end{aligned}$$

(2.13)

Proof

It follows from the estimate (3.1) below that we have uniformly for all $\gamma \in [-1,1]$ and all $z\in \mathbb {D}_r$,

$$\begin{aligned} \mathbb {E}_N\left[ e^{\gamma |\Psi _N(z)|}\right] \le \tfrac{2C_r}{\pi } N^{\gamma ^2/8} . \end{aligned}$$

(2.14)

In particular, by Markov’s inequality, this implies that for any $\lambda >0$,

$$\begin{aligned} \mathbb {P}_N\left[ |\Psi _N(z)| \ge \lambda \right] \le \tfrac{2C_r}{\pi } N^{1/8} e^{- \lambda } . \end{aligned}$$

(2.15)

Observe that according to (1.6), we have for any test function $f\in \mathscr {C}^2(\mathbb {C})$,

$$\begin{aligned} \mathrm {X}(f) = \frac{1}{2\pi } \int _\mathbb {C}\Delta f(x) \Psi _N(x) \mathrm {d}^2x . \end{aligned}$$

(2.16)

In particular, this implies that for all $f\in \mathscr {F}_{r,0}$,

$$\begin{aligned} | \mathrm {X}(f) | \le \frac{1}{2\pi } \int _{|x| \le r} |\Psi _N(x)| \mathrm {d}^2x . \end{aligned}$$

Then, by Jensen’s inequality,

$$\begin{aligned} | \mathrm {X}(f) |^2 \le \frac{1}{4\pi } \int _{|x| \le r} |\Psi _N(x)|^2 \mathrm {d}^2x . \end{aligned}$$

Therefore, it holds that

$$\begin{aligned} \mathbb {E}_N\Big [ \big ( \max _{f \in \mathscr {F}_{r,0}} \left| \mathrm {X}(f) \right| \big )^2 \Big ] \le \frac{1}{4\pi } \int _{|x| \le r} \mathbb {E}_N\left[ |\Psi _N(x)|^2 \right] \mathrm {d}^2x. \end{aligned}$$

Hence, to obtain the bound (2.13), it suffices to show that for all $x\in \mathbb {D}_r$,

$$\begin{aligned} \mathbb {E}_N\left[ |\Psi _N(x)|^2 \right] \le C_r( \log \sqrt{N}+ 1) . \end{aligned}$$

(2.17)

Let us fix $z\in \mathbb {D}_r$ and $\ell _N = \frac{1}{2} \log \sqrt{N}$. Using (2.14) with $\gamma = \lambda /\ell _N$, we obtain for any $0<\lambda < \ell _N$,

$$\begin{aligned} \mathbb {P}_N[|\Psi _N(z)| \ge \lambda ] \le C_re^{ \gamma ^2 \ell _N/2 - \gamma \lambda } = C_r e^{- \lambda ^2/2\ell _N} . \end{aligned}$$

Then, by integrating this estimate, we obtain

$$\begin{aligned} \int _0^{\ell _N} \lambda \mathbb {P}_N\left[ |\Psi _N(z)| \ge \lambda \right] \mathrm {d}\lambda \le C_r \ell _N . \end{aligned}$$

(2.18)

Moreover, using the bound (2.15), we also have

$$\begin{aligned} \begin{aligned} \int _{\ell _N}^{+\infty } \lambda \mathbb {P}_N\left[ |\Psi _N(z)| \ge \lambda \right] d\lambda&\le C_r N^{1/8}\int _{\ell _N}^{+\infty } \lambda e^{-\lambda } d\lambda = C_r N^{1/8} (\ell _N +1) e^{-\ell _N} \\&\le C_r (\ell _N +1) , \end{aligned} \end{aligned}$$

(2.19)

because $N^{1/8} e^{-\ell _N} = N^{-1/8}$. By combining the estimates (2.18) and (2.19), we obtain for any $N\in \mathbb {N}$,

$$\begin{aligned}\begin{aligned} \mathbb {E}_N\left[ |\Psi _N(z)|^2 \right]&= 2\int _0^{+\infty } \lambda \mathbb {P}_N\left[ |\Psi _N(z)| \ge \lambda \right] d\lambda \le 2C_r(2\ell _N +1) . \end{aligned}\end{aligned}$$

This proves the inequality (2.17) and it completes the proof. $\square$

We are now ready to complete the Proof of Corollary 2.4.

Proof of Corollary 2.4

Let us recall that we let $\epsilon =\epsilon (N) = N^{-1/2+\alpha }$ for $0<\alpha <1/2$. Moreover, by (2.1), we have $\Delta \psi = \phi \in \mathscr {C}^\infty _c(\mathbb {D}_{\epsilon _0})$ with $0<\epsilon _0 \le 1/4$. Then, for any $z\in \mathbb {D}_{\epsilon _0}$, the function $x\mapsto \psi (x-z) / \Vert \phi \Vert _\infty$ belongs to $\mathscr {F}_{1/2,0}$. By Lemma 2.5 and Chebyshev’s inequality, this implies that for any $\delta >0$,

$$\begin{aligned} \mathbb {P}_N\left[ \max _{z\in \mathbb {D}_{\epsilon _0}} \left| \mathrm {X}\left( \psi (\cdot -z) \right) \right| \ge \frac{\delta }{2} \log \epsilon ^{-1} \right] \le \frac{2C_{1/2} \Vert \phi \Vert _\infty ^2}{ \delta ^2} \frac{2+\log N }{(\log \epsilon ^{-1})^2} . \end{aligned}$$

(2.20)

In particular, the RHS of (2.20) converges to 0 as $N\rightarrow +\infty$. Moreover, since $\mathrm {X}(\psi _{\epsilon }(\cdot -z)) = \mathrm {X}(g_N^{z}) + \mathrm {X}(\psi (\cdot -z))$ and $\gamma ^*\ge 1$, we have

$$\begin{aligned}\begin{aligned}&\mathbb {P}_N\left[ \max _{|z| \le \epsilon _0} \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right) \ge (1-\delta )\frac{\gamma ^*}{2} \log \epsilon ^{-1} \right] \\&\quad \ge \mathbb {P}_N\left[ \max _{|z| \le \epsilon _0} \mathrm {X}(g_N^{ z}) \ge \left( 1-\frac{\delta }{2} \right) \frac{\gamma _*}{2} \log \epsilon ^{-1} \right] \\&\qquad -\mathbb {P}_N\left[ \max _{z\in \mathbb {D}_{\epsilon _0}} \left| \mathrm {X}\left( \psi (\cdot -z) \right) \right| \ge \frac{\delta }{2} \log \epsilon ^{-1} \right] . \end{aligned}\end{aligned}$$

By (2.11) and (2.20), this implies that

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ \max _{|z| \le \epsilon _0} \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right) \ge (1-\delta )\frac{\gamma ^*}{2} \log \epsilon ^{-1} \right] =1, \end{aligned}$$

which completes the proof. $\square$

3 Proof of the Upper-Bound

The goal of this section is to prove the upper-bound in Theorem 1.1. Then, in Sect. 3.2, we adapt the proof in order to prove Theorem 1.2.

Proposition 3.1

For any fixed $0<r<1$ and $\varepsilon >0$, we have

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N \left[ \max _{\overline{\mathbb {D}_r}} \Psi _N \le \frac{1+\varepsilon }{\sqrt{2}} \log N \right] =1 . \end{aligned}$$

In order to prove Proposition 3.1, we need the following consequence of Theorem 1.4: for any $0<r<1$, there exists a constant $C_r>0$ such that for any $\gamma \in [-1,4]$,

$$\begin{aligned} \mathbb {E}_N[e^{\gamma \Psi _N(z)}] \le \tfrac{C_r}{\pi } N^{\gamma ^2/8} . \end{aligned}$$

(3.1)

In fact, we do not need the precise asymptotics (1.17) and the upper-bound (3.1) for the Laplace transform of the field $\Psi _N$ suffices for our applications. For instance, it is straightforward to deduce the following bounds.

Lemma 3.2

Fix $0<r<1$ and recall the definition (1.13) of the set $\mathscr {T}_N^\beta$ of $\beta$-thick points. We have for any $\beta \in [0,1]$,

$$\begin{aligned} \mathbb {E}_N\big [|\mathscr {T}_N^\beta |\big ] \le C_r N^{-2\beta ^2} . \end{aligned}$$

Proof

By Markov’s inequality, we have for any $\beta \ge 0$,

$$\begin{aligned} \begin{aligned} \mathbb {E}_N\big [|\mathscr {T}_N^\beta |\big ]&= \int _{\mathbb {D}_r} \mathbb {P}[\Psi _N(x) \ge \beta \log N] \mathrm {d}^2x \\&\le N^{-\gamma \beta } \int _{\mathbb {D}_r} \mathbb {E}\left[ e^{\gamma \Psi _N(x)}\right] \mathrm {d}^2x . \end{aligned}\end{aligned}$$

Taking $\gamma =4\beta$ and using the estimate (3.1), this implies the claim. $\square$

For the Proof of Proposition 3.1, we also need the following simple Lemma.

Lemma 3.3

Recall that $(\lambda _1, \dots , \lambda _N)$ denotes the eigenvalues of a Ginibre random matrix. For any $\delta \in [0,1]$ (possibly depending on N), we have for all $N\ge 3$,

$$\begin{aligned} \mathbb {P}_N\left[ \max _{j\in [N]} |\lambda _j| \ge 1+\delta \right] \le \delta ^{-1} \sqrt{N} e^{-N \delta ^2/4} . \end{aligned}$$

Proof

Let us recall that Kostlan’s Theorem [40] states that the random variables $\left\{ N |\lambda _1|^2 , \dots , N |\lambda _N|^2\right\}$ have the same law as $\left\{ \varvec{\gamma }_1, \dots , \varvec{\gamma }_N\right\}$ where $\varvec{\gamma }_k$ are independent random variables with distribution $\mathbb {P}[\varvec{\gamma }_k \ge t] = \frac{1}{\Gamma (k)} \int _t^{+\infty } s^{k-1} e^{-s} ds$ for $k=1, \dots , N$. By a union bound and a change of variable, this implies that

$$\begin{aligned} \begin{aligned} \mathbb {P}_N[ \max _{j\in [N]} |\lambda _j| \ge t ]&\le N \mathbb {P}[ {\varvec{\gamma }_N} \ge N t] \\&\le \frac{N^{N+1}}{\Gamma (N)} \int _{t}^{+\infty } s^{N} e^{-Ns} \frac{ds}{s} \\&\le \frac{N^{N+1}e^{-N}}{\Gamma (N)t} \int _{t}^{+\infty } e^{-N\phi (s)}ds \end{aligned}\end{aligned}$$

where $\phi (s) = s- \log s -1$. Since $\phi$ is strictly convex on $[0,+\infty )$ with $\phi '(t)=1-1/t$, this implies that

$$\begin{aligned} \begin{aligned} \mathbb {P}_N[ \max _{j\in [N]} |\lambda _j| \ge t ]&\le \frac{N^{N+1}e^{-N- N\phi (t)}}{\Gamma (N)t} \int _0^{+\infty } e^{-N(1-\frac{1}{t}) s} ds \\&\le \frac{ \sqrt{N}}{\sqrt{2\pi } (t-1)} e^{-N \phi (t)} . \end{aligned}\end{aligned}$$

Using that $\phi (1+\delta ) \ge t^2/4$ for all $\delta \in [-1,1]$, this completes the proof. $\square$

We are now ready to give the Proof of Proposition 3.1.

3.1 Proof of Proposition 3.1

Fix $0<r<1$ and a small $\varepsilon >0$ such that $r' = r+2\sqrt{\varepsilon } <1$. For $z\in \mathbb {C}$, let $P_N(z) := {\textstyle \prod _{j=1}^N } |z-\lambda _j|$ and recall that the logarithmic potential of the circular law is $\varphi$, (1.4). Conditionally on the event $\left\{ \max _{j\in [N]} |\lambda _j| \le \frac{3}{2} \right\}$, we have the a-priori bound: $\max _{z\in \overline{\mathbb {D}}}|P_N(z)| \le (\frac{5}{2})^N$. Since $\Psi _N = \log P_N - N\varphi$ and $-\varphi \le 1/2$, by Lemma 3.3, this shows that

$$\begin{aligned} \mathbb {P}_N\left[ \max _{\overline{\mathbb {D}}} \Psi _N \ge 3N \right] \le \mathbb {P}_N \left[ \max _{j\in [N]} |\lambda _j| \ge \frac{3}{2} \right] \le 2 \sqrt{N} e^{-N/16} . \end{aligned}$$

(3.2)

The function $\Psi _N$ is upper-semicontinuous on $\mathbb {C}$, so that it attains it maximum on $\overline{\mathbb {D}_r}$. Let $x_* \in \overline{\mathbb {D}_r}$ such that

$$\begin{aligned} \Psi _N(x_*) = {\textstyle \max _{\overline{\mathbb {D}_r}}}\ \Psi _N . \end{aligned}$$

Since the function $z\mapsto \log P_N(z)$ is subharmonic on $\mathbb {C}$, we have for any $\delta >0$,

$$\begin{aligned} \Psi _N(x_*) \le \frac{1}{\pi \delta ^2} \int _{\mathbb {D}(x_*,\delta )} \log P_N(z)\ \mathrm {d}^2z - N \varphi (x_*) . \end{aligned}$$

(3.3)

Observe that as $\varphi (z) = \frac{|z|^2-1}{2}$ for $z\in \mathbb {D}$, if $\mathbb {D}(x_*,\delta ) \subset \mathbb {D}$, then

$$\begin{aligned}\begin{aligned} \frac{1}{\pi \delta ^2} \int _{\mathbb {D}(x_*,\delta )} \varphi (x) \mathrm {d}^2 x&= \varphi (x_*) + \frac{1}{\pi \delta ^2} \int _{\mathbb {D}_\delta } u\cdot \nabla \varphi (x_*)\ \mathrm {d}^2 u + \frac{1}{2\pi \delta ^2} \int _{\mathbb {D}_\delta } u \cdot \nabla ^2 \varphi (x_*) u\ \mathrm {d}^2 u \\&= \varphi (x_*) + \frac{\Delta \varphi (x_*)}{2\pi \delta ^2} \int _{\mathbb {D}_\delta } |u|^2 \mathrm {d}^2 u \\&= \varphi (x_*) + \frac{\delta ^2}{2} . \end{aligned}\end{aligned}$$

By (3.3), this implies that

$$\begin{aligned} \Psi _N(x_*) \le \frac{1}{\pi \delta ^2} \int _{\mathbb {D}(x_*,\delta )} \Psi _N(z) \mathrm {d}^2z + \frac{N \delta ^2}{2} . \end{aligned}$$

(3.4)

Choosing $\delta =\sqrt{ \varepsilon \frac{\log N}{N}}$ in (3.4), we obtain

$$\begin{aligned} \Psi _N(x_*) \le \frac{1}{\pi \delta ^2} \int _{\mathbb {D}(x_*,\delta )} \Psi _N(z) \mathrm {d}^2z + \frac{\varepsilon }{2} \log N . \end{aligned}$$

On the event $\Big \{{\textstyle \max _{\overline{\mathbb {D}_r}}}\ \Psi _N\ge \frac{1+\varepsilon }{\sqrt{2}} \log N \Big \}$, this implies that

$$\begin{aligned} \frac{1}{\pi \delta ^2} \int _{\mathbb {D}(x_*,\delta )} \Psi _N(z) \mathrm {d}^2z \ge \Big ( \tfrac{1}{\sqrt{2}}+ \frac{\varepsilon }{5} \Big ) \log N . \end{aligned}$$

(3.5)

On the other-hand, by (1.13) with $\beta = 1/\sqrt{2}$,

$$\begin{aligned} \frac{1}{\pi \delta ^2} \int _{\mathbb {D}(x_*,\delta )} \Psi _N(z) \mathrm {d}^2z \le \tfrac{\log N}{\sqrt{2}} + \frac{1}{\pi \delta ^2} \int _{\mathscr {T}_N^\beta (r')}\Psi _N(z) \mathrm {d}^2z . \end{aligned}$$

(3.6)

Combining (3.5) and (3.6), this implies

$$\begin{aligned} \int _{\mathscr {T}_N^\beta (r')}\Psi _N(z) \mathrm {d}^2z \ge \frac{\varepsilon \delta ^2}{2} \log N = \frac{(\varepsilon \log N)^2}{2N} . \end{aligned}$$

Hence, we conclude that for any $\eta \in [0,1]$, on the event $\Big \{ \frac{1+\varepsilon }{\sqrt{2}} \log N \le \max _{\overline{\mathbb {D}_r}} \Psi _N \le \max _{\overline{\mathbb {D}_{r'}}} \Psi _N \le \frac{\varepsilon ^2}{2} (\log N)^{1+\eta } \Big \}$,

$$\begin{aligned} |\mathscr {T}_N^\beta (r')| \ge \frac{(\log N)^{1-\eta }}{N} . \end{aligned}$$

By Lemma 3.2 applied with $\beta = 1/\sqrt{2}$, this implies that

$$\begin{aligned}&\mathbb {P}_N\left[ \tfrac{1+\varepsilon }{\sqrt{2}} \log N \le \max _{\overline{\mathbb {D}_r}} \Psi _N \le \max _{\overline{\mathbb {D}_{r'}}} \Psi _N \le \tfrac{\varepsilon ^2}{2} (\log N)^{1+\eta } \right] \nonumber \\&\quad \le \mathbb {P}_N\left[ |\mathscr {T}_N^\beta (r')| \ge \frac{(\log N)^{1-\eta }}{N} \right] \nonumber \\&\quad \le \frac{N }{(\log N)^{1-\eta }} \mathbb {E}_N\left[ |\mathscr {T}_N^\beta (r')| \right] \le \frac{C_{r'}}{(\log N)^{1-\eta }}. \end{aligned}$$

(3.7)

By a similar argument as (3.4), with $\delta = \varepsilon \sqrt{\frac{(\log N)^{1+\eta }}{2N}}$ and choosing $x_*\in \overline{\mathbb {D}_r}$ such that $\Psi _N(x_*) = {\textstyle \max _{\overline{\mathbb {D}_{r'}}}}\ \Psi _N$, it holds conditionally on the event $\big \{\max _{\overline{\mathbb {D}_{r'}}} \Psi _N \ge N \delta ^2\big \}$,

$$\begin{aligned} \frac{N\delta ^2}{2} = \frac{\varepsilon ^2}{4} (\log N)^{1+\eta } \le \frac{1}{\pi \delta ^2} \int _{\mathbb {D}(x_*,\delta )} \Psi _N(z) \mathrm {d}^2z . \end{aligned}$$

Let $\mathscr {A} = \left\{ z\in \overline{\mathbb {D}_{r''}} : \Psi _N(z) \ge \frac{\varepsilon ^2(\log N)^{1+\eta }}{8} \right\}$ with $r'' = r'+\epsilon <1$. Conditionally on the event $\big \{ \tfrac{\varepsilon ^2}{2} (\log N)^{1+\eta } \le \max _{\overline{\mathbb {D}_{r'}}} \Psi _N$$\le \max _{\overline{\mathbb {D}}} \Psi _N \le 3N\big \}$, this gives

$$\begin{aligned} \frac{3N|\mathscr {A}|}{\pi \delta ^2} + \frac{\varepsilon ^2(\log N)^{1+\eta }}{8} \ge \frac{1}{\pi \delta ^2} \int _{\mathbb {D}(x_*,\delta )} \Psi _N(z) \mathrm {d}^2z , \end{aligned}$$

so that with $\eta =1/2$,

$$\begin{aligned} |\mathscr {A}| \ge \frac{\varepsilon ^4(\log N)^{3} }{16 N^2} . \end{aligned}$$

(3.8)

A variation of the Proof of Lemma 3.2 using the estimate (3.1) with $0<r''<1$ and $\gamma =4$ shows that $\mathbb {E}_N\left[ |\mathscr {A}| \right] \le C_{r''} N e^{-\varepsilon ^2(\log N)^{3/2}/2}$. By (3.8), we conclude that

$$\begin{aligned} \mathbb {P}_N \left[ \tfrac{\varepsilon ^2}{2} (\log N)^{1+\epsilon } \le \max _{\overline{\mathbb {D}_{r'}}} \Psi _N \le \max _{\overline{\mathbb {D}}} \Psi _N \le 3N\right]&\le \mathbb {P}_N\left[ |\mathscr {A}| \ge \frac{\varepsilon ^2(\log N)^3 }{8 N^2} \right] \nonumber \\&\le 16 \varepsilon ^{-4} N^2 \mathbb {E}_N\left[ |\mathscr {A}| \right] \nonumber \\&\le 16 \varepsilon ^{-4} C_{r''} N^3 e^{-\varepsilon ^2(\log N)^{3/2}/2} . \end{aligned}$$

(3.9)

In order to complete the proof, it remains to observe that by combining the estimates (3.7), (3.9) and (3.2), we have proved that if $\varepsilon >0$ is sufficiently small, then

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ \tfrac{1+\varepsilon }{\sqrt{2}} \log N \le \max _{\overline{\mathbb {D}_r}} \Psi _N \right] =0 . \end{aligned}$$

3.2 Concentration for linear statistics: Proof of Theorem 1.2

In order to prove Theorem 1.2, we need the following bounds as well as Lemma 3.3.

Lemma 3.4

Fix $\eta >0$ and $0<r<1$. There exists a universal constant $A>0$ such that conditionally on the event $\mathscr {B} = \{ \max _{j=1,\ldots , N} |\lambda _j| \le 2\}$, we have for any function $f\in \mathscr {C}^2(\mathbb {C})$ (possibly depending on $N\in \mathbb {N}$) which is harmonic in $\mathbb {C}\setminus \overline{\mathbb {D}_r}$,

$$\begin{aligned} | \mathrm {X}(f) | \le \eta \log N \int _\mathbb {D}|\Delta f(z)| \frac{\mathrm {d}^2z}{2\pi } + C N \sqrt{ |\mathscr {G}_\eta |} \max _\mathbb {C}|\Delta f| , \end{aligned}$$

(3.10)

where $\mathscr {G}_\eta := \left\{ z\in \mathbb {D}_r : |\Psi _N(z)| > \eta \log N \right\}$ (with $\eta >0$ possibly depending on $N\in \mathbb {N}$) and $C>0$. Moreover, there exists a constant $C_r>0$ such that for any $\kappa >0$,

$$\begin{aligned} \mathbb {P}\left[ |\mathscr {G}_\eta | \ge N^{-\kappa } \right] \le C_r N^{\kappa + 1/8-\eta } . \end{aligned}$$

(3.11)

Proof

Observe that for any $f\in \mathscr {C}^2(\mathbb {C})$ which is harmonic in $\mathbb {C}\setminus \overline{\mathbb {D}_r}$, by definition of $\mathscr {G}_\eta$, we have

$$\begin{aligned} \left| \int _\mathbb {C}\Delta f(z) \Psi _N(z)\ \mathrm {d}^2z \right| \le \eta \log N\int _{\mathbb {D}_r} |\Delta f(z)| \mathrm {d}^2z + \max _{\mathbb {D}_r} |\Delta f| \int _{\mathscr {G}_\eta } |\Psi _N(z)| \mathrm {d}^2z . \end{aligned}$$

(3.12)

Then, by the Cauchy–Schwartz inequality,

$$\begin{aligned} \int _{\mathscr {G}_\eta } |\Psi _N(z)| \mathrm {d}^2z \le \sqrt{|\mathscr {G}_\eta | \int _{\mathbb {D}} |\Psi _N(z)|^2 \mathrm {d}^2z } \end{aligned}$$

and by (1.9), it holds conditionally on the event $\mathscr {B}$,

$$\begin{aligned} \begin{aligned} \int _{\mathbb {D}} |\Psi _N(z)|^2 \mathrm {d}^2z&\le 2\int _{\mathbb {D}} \left( \textstyle {\sum _{j=1}^N \log |z-\lambda _j|} \right) ^2 \mathrm {d}^2z + \frac{N^2}{2} \int _\mathbb {D}(1-|z|^2)^2 \mathrm {d}^2z\\&\le N\left( 2 \int _\mathbb {D}\textstyle {\sum _{j=1}^N \left( \log |z-\lambda _j| \right) ^2} \mathrm {d}^2z + \frac{8\pi }{15} N\right) \\&\le C^2 N^2 , \end{aligned}\end{aligned}$$

where $\displaystyle C= \sqrt{ 2 \sup _{|x| \le 2} \int _\mathbb {D}\left( \log |z-x| \right) ^2 \mathrm {d}^2z + \frac{8\pi }{15}}$ is a numerical constant. This shows that

$$\begin{aligned} \int _{\mathscr {G}_\eta }|\Psi _N(z)| \mathrm {d}^2z \le C N \sqrt{ |\mathscr {G}_\eta |} . \end{aligned}$$

Then, according to formula (2.16) and (3.12), we obtain (3.10). In order to estimate the size of the set $\mathscr {G}_\eta$, let us observe that combining (2.14) with $\gamma =1$ and Markov’s inequality, we obtain

$$\begin{aligned} \begin{aligned} \mathbb {E}_N\left[ |\mathscr {G}_\eta | \right]&= \int _{|x| \le r} \mathbb {P}\left[ |\Psi _N(x)| \ge \eta \log N \right] \mathrm {d}^2x \\&\le N^{-\eta } \int _{|x| \le r} \mathbb {E}[e^{|\Psi _N(x)|}] \mathrm {d}^2x \\&\le C_r N^{1/8-\eta } . \end{aligned}\end{aligned}$$

By Markov’s inequality, this yields the estimate (3.11). $\square$

Proof of Theorem 1.2

By Lemma 3.4, for any test function $f \in \mathscr {F}_{r,\kappa }$, it holds conditionally on the event $\mathscr {B} = \{ \max _{j=1,\dots , N} |\lambda _j| \le 2\}$ that for any small $\eta >0$

$$\begin{aligned} | \mathrm {X}(f) | \le \eta \log N \int _\mathbb {D}|\Delta f(z)| \frac{\mathrm {d}^2z}{2\pi } + C N^{1+\kappa } \sqrt{ |\mathscr {G}_\eta |} . \end{aligned}$$

Hence, this implies that if $N \in \mathbb {N}$ is sufficiently large,

$$\begin{aligned}&\mathbb {P}_N\bigg [ \sup \left\{ |\mathrm {X}(f)| : f\in \mathscr {F}_{r,\kappa } \text { and } \int _\mathbb {D}|\Delta f(z)| \frac{\mathrm {d}^2z}{\pi } \le 1 \right\} \ge \eta \log N +1\bigg ]\\&\quad \le \mathbb {P}_N\left[ |\mathscr {G}_\eta | \ge N^{-9/8-\kappa } \right] + \mathbb {P}_N\left[ \mathscr {B}^c \right] . \end{aligned}$$

By Lemma 3.3 with $\delta =1$ and (3.11), we have shown that $\mathbb {P}_N[\mathscr {B}^c] \le \sqrt{N} e^{-N}$ and $\mathbb {P}_N\left[ |\mathscr {G}_\eta | \ge N^{-9/8-\kappa } \right] \le C_r N^{5/4+\kappa -\eta }$. By combining these estimates, this completes the proof. $\square$

4 Thick Points: Proof of Theorem 1.3

Like the Proof of Theorem 1.1, the Proof of Theorem 1.3 consists of a separate upper-bound (4.1) and lower-bound (Proposition 4.1 below) and it relies on similar techniques. In particular, the upper-bound follows directly from Lemma 3.2. Namely, by Markov’s inequality, we have for any $\beta \in [0,1]$ and $\delta >0$,

$$\begin{aligned} \mathbb {P}_N\left[ |\mathscr {T}_N^\beta (r)| \le N^{-2\beta ^2+\delta }\right] \ge 1- \frac{ C_r}{N^\delta } . \end{aligned}$$

(4.1)

Then, to obtain the lower-bound, we rely the fact that the field $\Psi _N$ can be well approximated by $\mathrm {X}\left( \psi _\epsilon (\cdot -z)\right)$ for $\epsilon = N^{-1/2+\alpha }$ with a small scale $\alpha >0$ and use the estimate (2.12).

Proposition 4.1

For any $0<r<1$, any $0\le \beta <1/\sqrt{2}$ and any $\delta >0$, we have

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ | \mathscr {T}_N^\beta (r) | \ge N^{-2\beta ^2-\delta } \right] =1 . \end{aligned}$$

Proof

We fix parameters $r\in (0,1)$, $\beta \in [0,1/\sqrt{2})$ and we abbreviate $\mathscr {T}_N^\beta = \mathscr {T}_N^\beta (r)$. Recall that $\phi \in \mathscr {C}^\infty _c(\mathbb {D}_{\epsilon _0})$ is a mollifier and that for any $z\in \mathbb {C}$,

$$\begin{aligned} \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right) = \int \Psi _N(x) \phi _\epsilon (z-x) \mathrm {d}^2x , \end{aligned}$$

(4.2)

where $\epsilon =\epsilon (N) = N^{-1/2+\alpha }$ — the scale $0<\alpha <1/2$ will be chosen later in the proof depending on $\beta$ and $\delta$. Throughout the proof, we assume that $\epsilon$ is small compared to $\epsilon _0\le 1/4$, we let $\mathrm {c} = \sup _{x\in \mathbb {C}} \phi (x)$ and for a small $\delta \in (0, 1/2]$,

$$\begin{aligned} \Upsilon _N^\beta : = \Big \{ z\in \mathbb {D}_{\epsilon _0} : \mathrm {X}\big (\psi _\epsilon (\cdot -z)\big ) \ge (\beta + \tfrac{\delta }{8}) \log N \Big \} . \end{aligned}$$

We also define the event (of large probability):

$$\begin{aligned} \mathscr {A}: = \Big \{ \max _{|x| \le r} \Psi _N (x) \le \log N\Big \} . \end{aligned}$$

Since $g_N^{z}= \psi _\epsilon (\cdot -z) -\psi (\cdot -z)$ by (2.2), we have for any $\gamma >0$,

$$\begin{aligned}\begin{aligned}&\mathbb {P}_N\left[ \bigg | \Big \{ z\in \mathbb {D}_{\epsilon _0} : \mathrm {X}(g_N^{ z}) \ge \tfrac{\gamma + \delta }{\sqrt{2}} \log \epsilon ^{-1} \Big \}\bigg | \ge \epsilon ^{\gamma ^2/2- 3\delta /4} \right] \\&\quad \le \mathbb {P}_N\left[ \max _{z\in \mathbb {D}_{\epsilon _0}} \left| \mathrm {X}\left( \psi (\cdot -z) \right) \right| \ge \tfrac{\delta }{2\sqrt{2}} \log \epsilon ^{-1} \right] \ \ \\&\qquad + \mathbb {P}_N\left[ \bigg | \Big \{ z\in \mathbb {D}_{\epsilon _0} : \mathrm {X}\big (\psi _\epsilon (\cdot -z)\big ) \ge \tfrac{\gamma +\delta /2}{\sqrt{2}} \log \epsilon ^{-1} \Big \}\bigg | \ge \epsilon ^{\gamma ^2/2-3\delta /4} \right] . \end{aligned}\end{aligned}$$

Then, using the estimates (2.12) and (2.20), we obtain that for any $0 \le \gamma < \frac{\gamma _*}{\sqrt{2}}$,

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ \bigg | \Big \{ z\in \mathbb {D}_{\epsilon _0} : \mathrm {X}\big (\psi _\epsilon (\cdot -z)\big ) \ge \tfrac{\gamma +\delta /2}{\sqrt{2}} \log \epsilon ^{-1} \Big \}\bigg | \ge \epsilon ^{\gamma ^2/2-3\delta /4} \right] =1 . \end{aligned}$$

Hence, choosing the scale $\alpha = \frac{\delta }{8\sqrt{2}(\gamma +\delta /2)}$ with $\gamma = \sqrt{8}\beta$, this implies that for any $0\le \beta <1/\sqrt{2}$,

$$\begin{aligned} \lim _{N\rightarrow +\infty } \mathbb {P}_N\left[ | \Upsilon _N^\beta | \ge N^{-2\beta ^2-\delta /2} \right] =1 . \end{aligned}$$

(4.3)

By formula (4.2) and the definition of $\beta$-thick points, we have conditionally on $\mathscr {A}$, for any $z\in \mathbb {D}_{\epsilon _0}$,

$$\begin{aligned} \begin{aligned} \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right)&= \int _{\mathbb {D}_r\setminus \mathscr {T}_N^\beta } \Psi _N(x) \phi _\epsilon (x-z) \mathrm {d}^2x + \int _{\mathscr {T}_N^\beta } \Psi _N(x) \phi _\epsilon (x-z) \mathrm {d}^2x \\&\le \beta \log N + \mathrm {c} \big | \mathscr {T}_N^\beta \cap \mathbb {D}(z, \tfrac{\epsilon }{4}) \big | \epsilon ^{-2} \log N , \end{aligned} \end{aligned}$$

(4.4)

where we used that $\phi _\epsilon (x-z) \le \mathrm {c} \epsilon ^{-2} \mathbb {1}_{|x-z| \le \epsilon /4}$ at the last step. Now, let us tile the disk $\mathbb {D}_{\epsilon _0}$ with squares of area $\epsilon ^{2}$. To be specific, let $M = \lceil \epsilon ^{-1} \rceil$ and $\square _{i,j} = [i\epsilon , (i+1)\epsilon ] \times [j\epsilon , (j+1)\epsilon ]$ for all integers $i,j \in [-M,M]$. Note that since $z\mapsto \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right)$ is a continuous process, for any $i,j \in \mathbb {Z} \cap [-M,M]$, we can choose

$$\begin{aligned} z_{i,j} = \arg \max \big \{ \mathrm {X}\left( \psi _\epsilon (\cdot -z)\right) : z\in \square _{i,j} \big \} . \end{aligned}$$

The point of this construction is that we have the deterministic bound

$$\begin{aligned} |\Upsilon _N^\beta | \le \ \epsilon ^2 \sum _{i,j \in \mathbb {Z} \cap [-M,M] } \mathbb {1}_{z_{i,j} \in \Upsilon _N^\beta } . \end{aligned}$$

(4.5)

Moreover if $z_{i,j} \in \Upsilon _N^\beta$, (4.4) shows that conditionally on $\mathscr {A}$,

$$\begin{aligned} \big | \mathscr {T}_N^\beta \cap \mathbb {D}(z_{i,j}, \frac{\epsilon }{4}) \big | \ge \frac{\delta \epsilon ^2}{8\mathrm {c} } . \end{aligned}$$

By (4.5), this implies that

$$\begin{aligned} |\Upsilon _N^\beta | \le \frac{ 8 \mathrm {c}}{\delta } \sum _{i,j \in \mathbb {Z} \cap [-M,M] } \mathbb {1}_{z_{i,j} \in \Upsilon _N^\beta } \big | \mathscr {T}_N^\beta \cap \mathbb {D}(z_{i,j}, \frac{\epsilon }{4}) \big | . \end{aligned}$$

Since the squares $\square _{i,j}$ are disjoint (except for their sides) and $z_{i,j} \in \square _{i,j}$, we further have the deterministic bound

$$\begin{aligned} \sum _{i,j \in \mathbb {Z} \cap [-M,M] } \big | \mathscr {T}_N^\beta \cap \mathbb {D}(z_{i,j}, \frac{\epsilon }{4}) \big | \le 4 |\mathscr {T}_N^\beta | . \end{aligned}$$

Hence, we conclude that conditionally on $\mathscr {A}$, for $0\le \beta <1/\sqrt{2}$ and $\delta >0$ sufficiently small (but independent of N),

$$\begin{aligned} |\mathscr {T}_N^\beta | \ge \frac{\delta }{32\mathrm {c} } |\Upsilon _N^\beta | . \end{aligned}$$

Finally, according to Proposition 3.1, we have $\mathbb {P}_N[\mathscr {A}] \rightarrow 1$ as $N\rightarrow +\infty$, so that by combining the previous estimate with (4.3), this completes the proof. $\square$

5 Gaussian Approximation

In this section, we turn to the proof of our main asymptotic result: Proposition 2.3. Its proof relies on the so-called Ward’s identity or loop equation which have already been used in [4] as well as [8, 9] to study the fluctuations of linear statistics of eigenvalues of random normal matrices and two-dimensional Coulomb gases respectively. For completeness, we provide a detailed proof of the loop equation that we use in Sect. 5.2. Then, to show that the error terms in this equation are small, we rely on the determinantal structure of the ensemble obtained after making a small perturbation of the potential Q and on a local approximation of its correlation kernel (see Proposition 5.3 below). This approximation is justified in Sect. 6 based on the method from [4] and we use it to prove that the error terms are indeed negligible as $N\rightarrow +\infty$ in Sects. 5.4–5.7. Finally, we finish the Proof of Proposition 2.3 in Sect. 5.8 by using a classical argument introduced by Johansson [36] to prove a CLT for linear statistics of $\beta$-ensembles on $\mathbb {R}$. Before starting our analysis, we need to introduce further notations.

5.1 Notation

For any $N\in \mathbb {N}$, we let

$$\begin{aligned} \mathscr {P}_N = \{\text {analytic polynomials of degree}<N \} . \end{aligned}$$

(5.1)

Let us recall that by Cauchy’s formula, if f is smooth and compactly supported inside $\mathbb {D}$, we have

$$\begin{aligned} f(z) = \int \frac{\overline{\partial }f(x) }{z-x}\sigma (\mathrm {d}x) , \end{aligned}$$

(5.2)

where $\sigma (\mathrm {d}x) = \frac{1}{\pi } \mathbb {1}_{\mathbb {D}} \mathrm {d}^2 x$ denotes the circular law. Throughout Sect. 5, we fix $n\in \mathbb {N}$, $\mathbf {\gamma } \in [-R,R]^n$, $\mathbf {z} \in \mathbb {D}_{\epsilon _0}^{\times n}$ and we let $g_N = g_N^{\mathbf {\gamma }, \mathbf {z}}$ be as in formula (2.9). We recall that as $\mathbf {z} \in \mathbb {D}_{\epsilon _0}^{\times n}$ varies, the functions $x\mapsto g_N^{\mathbf {\gamma }, \mathbf {z}}(x)$ remain smooth and compactly supported inside $\mathbb {D}_{2\epsilon _0}$ for all $N\in \mathbb {N}$. Let us define for $t>0$,

$$\begin{aligned} \mathrm {d}\mathbb {P}_N^* : =\frac{e^{t\mathrm {X}(g_N)}}{\mathbb {E}_N [e^{t\mathrm {X}(g_N)}]} \mathrm {d}\mathbb {P}_N . \end{aligned}$$

(5.3)

The biased measure $\mathbb {P}_N^*$ corresponds to an ensemble of the type (1.1) with a perturbed potential $Q^* := Q- \frac{tg_N}{2N}$. Therefore, under $\mathbb {P}_N^*$, $\lambda =(\lambda _1, \dots \lambda _N)$ also forms a determinantal point process on $\mathbb {C}$ with a correlation kernel:

$$\begin{aligned} k^*_N(x,z) := {\textstyle \sum _{k=0}^{N-1}} p_k^*(x) \overline{p_k^*(z)} , \end{aligned}$$

(5.4)

where $(p_0^*, \dots , p_{N-1}^*)$ is an orthonormal basis of $\mathscr {P}_N$ with respect to the inner product inherited from $L^2(e^{-2N Q^*})$ such that ${\text {deg}}(p_k^*) = k$ for $k=0,\dots , N-1$. We denote

$$\begin{aligned} K_N^*(x,z) : = k_N^*(x,z) e^{-N Q^*(x) - N Q^*(z)} \end{aligned}$$

(5.5)

and we define the perturbed one-point function: $u_N^*(x) : = K_N^*(x,x) \ge 0$. By definitions, we record that for any $N\in \mathbb {N}$ and all $x\in \mathbb {C}$,

$$\begin{aligned} \int _{\mathbb {C}} k^*_N(x,z) \mathrm {d}^2z = u_N^*(x) \quad \text {and}\quad \int _{\mathbb {C}} u_N^*(z) \mathrm {d}^2z =N. \end{aligned}$$

(5.6)

Finally, we set $\widetilde{u}_N^* : = u_N^* - \sigma$, so that for any smooth function $f:\mathbb {C}\rightarrow \mathbb {C}$, we have

$$\begin{aligned} \mathbb {E}_N^*[\mathrm {X}(f)] = \int f(x) \widetilde{u}_N^*(x) \mathrm {d}^2x . \end{aligned}$$

(5.7)

Conventions 5.1

As in Proposition 2.3, we fix a scale $0<\alpha <1/2$ and let $\epsilon =\epsilon (N) = N^{-1/2+\alpha }$. We also fix $\beta >1$ and let $\delta = \delta (N) = \sqrt{(\log N)^\beta /N}$ as in Proposition 5.3 below. Throughout Sect. 5, we assume that the dimension $N\in \mathbb {N}$ is sufficiently large so that $\delta /\epsilon \le 1/4$ and $( \delta /\epsilon )^\ell \le N^{-1}$ for a fixed $\ell \in \mathbb {N}$ — e.g. we can pick $\ell = \lfloor 2/\alpha \rfloor$. Moreover, $C, N_0 >0$ are positive constant which may change from line to line and depend only on the mollifier $\phi$, the parameters $R,\alpha ,\beta , \epsilon _0>0$, $n, \ell \in \mathbb {N}$ and $t\in [0,1]$ above. Then, we write $A_N=\mathcal {O}(B_N)$ if there exists such a constant $C>0$ such that $0\le A_N \le C B_N$.

5.2 Ward’s identity

Formula (5.8) below is usually called Ward’s equation or loop equation and the terms $\mathfrak {T}^k_N$ for $k=1,2,3$ should be treated as corrections because of the factor 1/N in front of them.

This equation is the key input of a method pioneered by Johansson [36] to establish that linear statistics of $\beta$-ensembles are asymptotically Gaussian. In the following, we follow the approach of Ameur–Hedenmalm–Makarov [4, Section 2] who applied Johansson’s method to study the fluctuations of the eigenvalues of random normal matrices, including the Ginibre ensemble.

Proposition 5.2

If $g\in \mathscr {C}^2_c(\mathbb {D})$, we have for any $N\in \mathbb {N}$ and $t\in (0,1]$,

$$\begin{aligned} \mathbb {E}_N^*\left[ \mathrm {X}(g) \right] = \Sigma (g;g_N) +\frac{1}{N} \left( \mathfrak {T}^1_N(g) + \mathfrak {T}^2_N(g) - \mathfrak {T}^3_N(g)\right) , \end{aligned}$$

(5.8)

where $\Sigma (\cdot ;\cdot )$ denotes the quadratic form associated with (1.8),

$$\begin{aligned} \begin{aligned}&\mathfrak {T}^1_N(g) := \int \Big ( t \overline{\partial }g (x) \partial g_N(x) +\frac{1}{4} \Delta g(x) \Big ) \widetilde{u}_N^*(x) \mathrm {d}x , \\&\mathfrak {T}^2_N(g) := \iint \frac{\overline{\partial }g(x) }{x-z} \widetilde{u}_N^*(z) \widetilde{u}_N^*(x) \mathrm {d}^2 x\mathrm {d}^2z \end{aligned}\end{aligned}$$

and

$$\begin{aligned} \mathfrak {T}^3_N(g) := \iint \frac{\overline{\partial }g(x) }{x-z} | K_N^*(x,z) |^2 \mathrm {d}^2 x\mathrm {d}^2z . \end{aligned}$$

Proof

An integration by parts gives for any $h\in \mathscr {C}^1(\mathbb {C})$ with compact support:

$$\begin{aligned} \mathbb {E}_N^*\left[ \sum _{j\ne k} \frac{h(x_j)}{x_j-x_k} + \sum _{j} \partial h(x_j) - \sum _{j} h(x_j) \left( 2N \partial Q - t\partial g_N\right) (x_j) \right] =0 . \end{aligned}$$

(5.9)

Observe that with $h = \overline{\partial }g$, by (5.7) and (5.2), it holds

$$\begin{aligned} \mathbb {E}_N^*\left[ \mathrm {X}(g) \right] = \int g(z)\ \widetilde{u}_N^*(z) \mathrm {d}^2 z = \iint \frac{h(x) }{z-x}\sigma (\mathrm {d}x)\ \widetilde{u}_N^*(z) \mathrm {d}^2z . \end{aligned}$$

(5.10)

On the one-hand, using the determinantal formula for the second correlation function of the ensemble $\mathbb {P}_N^*$, we have

$$\begin{aligned}&\mathbb {E}_N^*\left[ \sum _{j\ne k} \frac{h(x_j)}{x_j-x_k} \right] \nonumber \\&\quad = \iint \frac{h(x) }{x-z} u_N^*(x) u_N^*(z) \mathrm {d}^2z\mathrm {d}^2x - \frac{1}{2} \iint \frac{h(x) - h(z)}{x-z} \left| K_N^*(x,z) \right| ^2 \mathrm {d}^2z\mathrm {d}^2x,\nonumber \\ \end{aligned}$$

(5.11)

where the second term is equal to $\mathfrak {T}^3_N(g)$ and the first term on the RHS satisfies

$$\begin{aligned} \begin{aligned} \frac{1}{N} \iint \frac{h(x) }{x-z} u_N^*(x) u_N^*(z) \mathrm {d}^2z\mathrm {d}^2x&= N \iint \frac{h(x) }{x-z} \sigma (\mathrm {d}z)\sigma (\mathrm {d}x) \\&\quad + \iint \frac{h(x) }{x-z} \sigma (\mathrm {d}z) \widetilde{u}_N^*(x) \mathrm {d}^2x \\&\quad + \iint \frac{h(x) }{x-z} \sigma (\mathrm {d}x) \widetilde{u}_N^*(z) \mathrm {d}^2z + \frac{1}{N} \mathfrak {T}^2_N(g) . \end{aligned} \end{aligned}$$

(5.12)

On the other-hand by (1.5), $\partial Q (x) = \partial \varphi (x) = \frac{1}{2} \int \frac{1}{x-z} \sigma (\mathrm {d}z)$ for all $x\in \mathbb {D}$ and as= ${\text {supp}}(h) \subset \mathbb {D}$, we also have

$$\begin{aligned} \mathbb {E}_N^*\left[ \sum _{j} h(x_j) \partial Q (x_j) \right]&= N \int h(x) \partial Q (x) \sigma (\mathrm {d}x) + \int h(x) \partial Q (x)\ \widetilde{u}_N^*(x) \mathrm {d}x \nonumber \\&= \frac{N}{2} \iint \frac{h(x) }{x-z} \sigma (\mathrm {d}z)\sigma (\mathrm {d}x) +\frac{1}{2} \iint \frac{h(x) }{x-z} \sigma (\mathrm {d}z)\ \widetilde{u}_N^*(x) \mathrm {d}x . \end{aligned}$$

(5.13)

Combining formulae (5.11), (5.12) and (5.13), we obtain

$$\begin{aligned} \begin{aligned}&\mathbb {E}_N^*\left[ \frac{1}{N} \sum _{j\ne k} \frac{h(x_j)}{x_j-x_k} - 2 \sum _{j} h(x_j) \partial Q (x_j) \right] \\&\quad = \iint \frac{h(x) }{x-z} \sigma (\mathrm {d}x) \widetilde{u}_N^*(z) \mathrm {d}^2z + \frac{1}{N} \left( \mathfrak {T}^2_N(g) - \mathfrak {T}^3_N(g) \right) . \end{aligned} \end{aligned}$$

By formula (5.10), this implies that

$$\begin{aligned} \mathbb {E}_N^*\left[ \frac{1}{N} \sum _{j\ne k} \frac{h(x_j)}{x_j-x_k} - 2 \sum _{j} h(x_j) \partial Q (x_j) \right] = - \mathbb {E}_N^*\left[ \mathrm {X}(g) \right] + \frac{1}{N} \left( \mathfrak {T}^2_N(g) - \mathfrak {T}^3_N(g) \right) . \end{aligned}$$

(5.14)

Combining formulae (5.9) and (5.14) with $h = \overline{\partial }f$, this shows that

$$\begin{aligned} \mathbb {E}_N^*\left[ \mathrm {X}(g) \right] = \frac{1}{N} \mathbb {E}_N^*\left[ \sum _j \Big (t \overline{\partial }g(x_j) \partial g_N(x_j) +\frac{1}{4} \Delta g(x_j) \Big ) \right] + \frac{1}{N} \left( \mathfrak {T}^2_N(g) - \mathfrak {T}^3_N(g) \right) , \end{aligned}$$

(5.15)

where we used that $\partial \overline{\partial }g = \frac{1}{4} \Delta g$. Finally using that $g\in \mathscr {C}^2_c(\mathbb {D})$, $\displaystyle \int \Delta g(x) \sigma (\mathrm {d}x) =0$ and by (1.8), we conclude that

$$\begin{aligned}&\frac{1}{N} \mathbb {E}_N^*\left[ \sum _j \Big (\overline{\partial }g(x_j) \partial g_N(x_j) +\frac{1}{4} \Delta g(x_j) \Big )\right] \nonumber \\&\quad = t\Sigma (g;g_N) + \frac{1}{N} \int \Big (t\overline{\partial }g(x) \partial g_N(x) +\frac{1}{4} \Delta g(x) \Big ) \widetilde{u}_N^*(x) \mathrm {d}x . \end{aligned}$$

(5.16)

Combining formulae (5.15) and (5.16), this completes the proof. $\square$

5.3 Kernel approximation

Recall that the probability measure $\mathbb {P}_N^*$ induces a determinantal process on $\mathbb {C}^N$ with correlation kernel $K_N^*$, (5.5). In order to control the RHS of (5.8), we need the asymptotics of the this kernel as the dimension $N\rightarrow +\infty$. In general, this is a challenging problem, however it is expected that $K_N^*$ decays quickly off diagonal and its asymptotics near the diagonal are universal in the sense that they are similar to that of the Ginibre correlation kernel $K_N$. In Sect. 6, using the method from Ameur–Hedenmalm–Makarov [2, 4] which relies on Hörmander’s inequality and the properties of reproducing kernels, we compute the asymptotics of $K_N^*$ near the diagonal. Recall that $g_N = g_N^{\mathbf {\gamma }, \mathbf {z}}$ as in (2.9) and our Conventions 5.1. Let us also define the approximate Bergman kernel:

$$\begin{aligned} k^\#_N(x,w) := \frac{N}{\pi } e^{N x \overline{w}} e^{-t \Upsilon _N^w(x-w) } , \qquad x,w\in \mathbb {C}. \end{aligned}$$

(5.17)

where $\Upsilon _N^w(u) : = \sum _{i=0}^{\ell } \frac{u^i}{i!} \partial ^i g_N(w)$. We also let

$$\begin{aligned} K^\#_N(x,w) := k^\#_N(x,w) e^{-NQ^*(z) - N Q^*(w)} , \qquad x,w\in \mathbb {C}. \end{aligned}$$

(5.18)

Let us state our main approximation result for the perturbed kernels which corresponds to [3, Lemma A.1] in the case where the test function $g_N$ depends on $N\in \mathbb {N}$ and develops logarithmic singularities as $N\rightarrow +\infty$. Because of these significant differences, we adapt the proof in Sect. 6.3.

Proposition 5.3

Let $\vartheta _N : = \mathbb {1}_\mathbb {D}+ \sum _{k=1}^n \epsilon _k^{-2} \mathbb {1}_{\mathbb {D}(z_k, \epsilon _k)}$ and $\delta = \delta (N) : = \sqrt{(\log N)^\beta /N}$ for $\beta >1$. There exist constants $L, N_0>0$ such that for all $N\ge N_0$, we have for any $z\in \mathbb {D}_{1-2\delta }$ and all $w\in \mathbb {D}(z,\delta )$,

$$\begin{aligned} \left| K^*_N(w,z) - K^\#_N(w,z) \right| \le L \vartheta _N(z) \end{aligned}$$

Remark 5.4

We emphasize again that the constants $L, N_0>0$ do not depend on $\mathbf {\gamma }\in [-R,R]^n$, $\mathbf {z} \in \mathbb {D}_{\epsilon _0}^{\times n}$, nor $t\in [0,1]$. Consequently, the estimates of Sects. 5.4–5.7 bear the same uniformity even though this will not be emphasized to lighten the presentation. In fact, since the parameter $t\in (0,1]$ is not relevant for our analysis, we will also assume that $t=1$ to simplify notation — this amounts to changing the parameters $\mathbf {\gamma }$ to $t\mathbf {\gamma }$. $\blacksquare$

In the remainder of this section and in Sect. 5.4, we discuss some consequences of the approximation of Proposition 5.3. Then, in Sects. 5.5–5.7, we control the error terms $\mathfrak {T}^k_N(g_N)$ for $k=1,2,3$ in order to complete the Proof of Proposition 2.3 in Sect. 5.8.

By definitions, with $t=1$, we have for any $z\in \mathbb {C}$,

$$\begin{aligned} K^\#_N(z,z) = \frac{N}{\pi } e^{N|z|^2 - g_N(z) - 2N Q^*(z)} = \frac{N}{\pi } . \end{aligned}$$

Then according to (5.7) and by taking $w=z$ in Proposition 5.3, this implies that for any $z\in \mathbb {D}_{1-2\delta }$,

$$\begin{aligned} | \widetilde{u}_N^*(z) | \le L\vartheta _N(z) , \end{aligned}$$

(5.19)

where we used that the circular density $\sigma (z) = 1/\pi$ if $z\in \mathbb {D}$.

Lemma 5.5

It holds as $N\rightarrow +\infty$,

$$\begin{aligned} \int _\mathbb {C}| \widetilde{u}_N^*(x) | \mathrm {d}^2 x = \mathcal {O}(N \delta ) . \end{aligned}$$

Proof

First, let us observe that since $\sigma$ is a probability measure supported on $\overline{\mathbb {D}}$, we have by (5.6),

$$\begin{aligned} \int _{\mathbb {C}\setminus \mathbb {D}} | \widetilde{u}_N^*(x) | \mathrm {d}^2 x = \int _{\mathbb {C}\setminus \mathbb {D}} u_N^*(x) \mathrm {d}^2 x = N - \int _\mathbb {D}u_N^*(x) \mathrm {d}^2 x . \end{aligned}$$

(5.20)

Moreover, by (5.19) and using that $\displaystyle \int _\mathbb {D}\vartheta _N(x) \mathrm {d}^2x = (n+1)\pi$, we also have

$$\begin{aligned} \int _{|x| \le 1-2\delta } | \widetilde{u}_N^*(x) | \mathrm {d}^2 x =\mathcal {O}(1) . \end{aligned}$$

(5.21)

Since $\widetilde{u}_N^* = u_N^* - \sigma$ and $\displaystyle \int _{|x| \le 1-2\delta } \sigma (\mathrm {d}x) = (1-2\delta )^2$, the previous estimate shows that

$$\begin{aligned} \int _\mathbb {D}u_N^*(x) \mathrm {d}^2 x \ge \int _{|x| \le 1-2\delta } u_N^*(x) \mathrm {d}^2 x \ge N - \mathcal {O}(N\delta ) . \end{aligned}$$

(5.22)

Combining (5.22) with formula (5.20), we conclude that as $N\rightarrow +\infty$,

$$\begin{aligned} \int _{\mathbb {C}\setminus \mathbb {D}} | \widetilde{u}_N^*(x) | \mathrm {d}^2 x = \mathcal {O}(N\delta ) . \end{aligned}$$

(5.23)

Moreover, using the uniform bound from Lemma 6.2 below, there exists $C>0$ such that $| \widetilde{u}_N^*(x) | \le C N$ for all $x\in \mathbb {C}$ which implies that

$$\begin{aligned} \int _{ 1-2\delta \le |x| \le 1} | \widetilde{u}_N^*(x) | \mathrm {d}^2 x =\mathcal {O}(N \delta ) . \end{aligned}$$

(5.24)

Combining the estimates (5.21), (5.23) and (5.24), this completes the proof. $\square$

5.4 Technical estimates

We denote the Gaussian density with variance 2/N by $\Phi _N(u) : = \tfrac{N}{\pi } e^{-N|u|^2}$. Since for any $x,z\in \mathbb {C}$,

$$\begin{aligned} NQ^*(z) + NQ^*(x) - N\mathfrak {R}\{z\overline{x}\} + g_N(x) = \frac{N}{2} |z-x|^2 + \frac{ g_N(x) - g_N(z)}{2} , \end{aligned}$$

(5.25)

we deduce from formulae (5.17)–(5.18) with $t=1$ that

$$\begin{aligned} \begin{aligned} | K^\#_N(z,x) |^2&= \tfrac{N}{\pi } \Phi _N(x-z) e^{g_N(z)-g_N(x) -2 \mathfrak {R}\left\{ \sum _{i=1}^\ell \frac{(z-x)^i}{i!} \partial ^i g_N(x) \right\} } . \end{aligned} \end{aligned}$$

(5.26)

We should view the last factor of (5.26) as a correction. Indeed on small scales, i.e. if $|x-z| \le \delta$, then $e^{g_N(z)-g_N(x) -2 \mathfrak {R}\left\{ \sum _{i=1}^\ell \frac{(z-x)^i}{i!} \partial ^i g_N(x) \right\} } = 1+\mathcal {O}(\eta )$ where $\eta = \delta /\epsilon$ goes to 0 as $N\rightarrow +\infty$. In particular, this implies that for N is sufficiently large, it holds for all $x,z\in \mathbb {C}$ such that $|x-z| \le \delta$,

$$\begin{aligned} |K_N^{\#}(x,z)|\le N . \end{aligned}$$

(5.27)

Actually, formula (5.26) shows that on microscopic scales, $| K^\#_N(z,x) |^2$ is well approximated by the Gaussian kernel $\Phi _N(x-z)$. As in [4, Lemma 3.3], we use this fact to prove the following Lemma.¹³

Lemma 5.6

It holds uniformly for all $x\in \mathbb {D}$, as $N\rightarrow +\infty$,

$$\begin{aligned} \int _{|x-z| \le \delta } | K_N^\#(z,x) |^2 \mathrm {d}^2z = N \sigma (x) + \mathcal {O}\big ( \vartheta _N(x) \big ) \end{aligned}$$

where $\vartheta _N$ is as in Proposition 5.3.

Proof

Throughout this proof, let us fix $x\in \mathbb {D}$. Since $g_N$ is a smooth function, by Taylor’s Theorem up to order $2\ell$, there exists a matrix $\mathrm {M} \in \mathbb {R}^{\ell \times \ell }$ (with positive entries) such that for all $u \in \mathbb {D}_{\delta }$,

$$\begin{aligned} g_N(x+u)-g_N(x) = \underset{0<i+j < 2\ell }{\textstyle \sum _{i,j=1}^{2\ell -1} } \mathrm {M}_{i,j} u^i \overline{u}^j \partial ^{i} \overline{\partial }^j g_N(x) + \mathcal {O}\left( \big \{ \Vert \nabla ^{2 \ell } g_N\Vert _\infty \delta ^{2\ell }\big \} \right) . \end{aligned}$$

Let $\mathrm {Y}^1_x (u): = \sum _{i=1}^{\ell -1} \frac{ \mathrm {M}_{i,i} }{4} |u|^{2i} \Delta ^i g_N(x)$ and $\mathrm {A}^1_x (u): = \underset{0<i+j < 2\ell , i\ne j}{\textstyle \sum _{i,j=1}^{2\ell -1} } \mathrm {M}_{i,j} u^i \overline{u}^j \partial ^{i} \overline{\partial }^j g_N(x) -2 \mathfrak {R}\left\{ {\textstyle \sum _{i=1}^\ell } \tfrac{u^i}{i!} \partial ^i g_N(x) \right\}$ for $u\in \mathbb {C}$. Recall that by assumptions, $\Vert \nabla ^k g_N \Vert _{\infty } \le C\epsilon ^{-k}$ for all integer $k\in [1, 2 \ell ]$ and $\eta = \delta /\epsilon$, so that with the previous notation:

$$\begin{aligned} \begin{aligned} g_N(x+u)-g_N(x) -2 \mathfrak {R}\left\{ {\textstyle \sum _{i=1}^\ell } \tfrac{u^i}{i!} \partial ^i g_N(x) \right\} = {\textstyle \sum _{i,j=1}^{\ell } } \mathrm {M}_{i,j} u^i \overline{u}^j \ \partial ^{i} \overline{\partial }^j g_N(x) +\mathcal {O}(\eta ^{2\ell }). \end{aligned}\end{aligned}$$

Using the condition $\eta ^\ell \le N^{-1}$, by (5.26), the previous expansion shows that for all $z\in \mathbb {D}(x,\delta )$,

$$\begin{aligned} | K^\#_N(z,x) |^2 = \tfrac{N}{\pi } \Phi _N(x-z) e^{\mathrm {A}^1_x (z-x)+ \mathrm {Y}^1_x (z-x)+\mathcal {O}(N^{-2})} . \end{aligned}$$

(5.28)

Importantly, note that for $|u|\le \delta$,

$$\begin{aligned} | \mathrm {Y}^1_x(u)| , | \mathrm {A}^1_x(u) | = \mathcal {O}(\eta ^2) , \end{aligned}$$

(5.29)

and that both $\Phi _N$ and $\mathrm {Y}^1_x$ are radial functions, so that it holds for any $k \in \mathbb {N}$,

$$\begin{aligned} \int _{|u| \le \delta } \left( \mathrm {A}^1_x(u) \right) ^k \exp \left( \mathrm {Y}^1_x(u) \right) \Phi _N(\mathrm {d}u) = 0 . \end{aligned}$$

(5.30)

Hence, using (5.28)–(5.30), this implies that for any $x\in \mathbb {D}$,

$$\begin{aligned}\begin{aligned} \int _{|x-z| \le \delta } | K_N^\#(z,x) |^2 \mathrm {d}^2z&= \frac{N}{\pi } \int _{|u| \le \delta } e^{\mathrm {A}^1_x (u)+ \mathrm {Y}^1_x(u)}\Phi _N(\mathrm {d}u) + \mathcal {O}(N^{-1}) \\&= \frac{N}{\pi } \int _{|u| \le \delta } e^{\mathrm {Y}^1_x (u)} \Phi _N(\mathrm {d}u) + \mathcal {O}(N^{-1}) , \end{aligned}\end{aligned}$$

where we used that $\Phi _N$ is a probability measure. Moreover, we verify by (2.9) and (2.1) that $|\Delta ^{k+1} g_N(x)| \le C \epsilon ^{-2k} \vartheta _N(x)$ for all integer $k\in [0, \ell ]$, so we can bound $e^{\mathrm {Y}^1_x (u)} = 1+ \mathcal {O}\big (|u|^2 \vartheta _N(x) \big )$ uniformly for all $|u|\le \delta$, Since for any integer $j\ge 0$,

$$\begin{aligned} \int _{|u| \le \delta } |u|^{2j} \Phi _N(\mathrm {d}u) = N^{-j} \left( j! + \mathcal {O}(e^{- N\delta ^2}) \right) , \end{aligned}$$

(5.31)

we conclude that for all $x\in \mathbb {D}$,

$$\begin{aligned} \int _{|x-z| \le \delta } | K_N^\#(z,x) |^2 \mathrm {d}^2z = \frac{N}{\pi }+ \mathcal {O}\big ( \vartheta _N(x) \big ) \end{aligned}$$

with uniform errors. Since $\sigma (x)= 1/\pi$ for $x\in \mathbb {D}$, this completes the proof. $\square$

We can use Proposition 5.3 and Lemma 5.6 to estimate a similar integral for the correlation kernel $K_N^*$. This corresponds to the counterpart of [4, Corollary 3.4].

Lemma 5.7

It holds for any $x\in \mathbb {D}_{1-2\delta }$, as $N\rightarrow +\infty$

$$\begin{aligned} \int _{|x-w| > \delta } |K^*_N(z,x) |^2 \mathrm {d}^2z = \mathcal {O}\left( N \delta ^2 \vartheta _N(x) \right) . \end{aligned}$$

Proof

First of all, let us bound

$$\begin{aligned} \begin{aligned}&\left| \int _{|x-w| \le \delta } |K^*_N(z,x) |^2 \mathrm {d}^2z - \int _{|x-w| \le \delta } |K^\#_N(z,x) |^2 \mathrm {d}^2z \right| \\&\quad \le 2 \int _{|x-z| \le \delta } |K^\#_N(z,x) | \left| K^*_N(z,x) - K^\#_N(z,x) \right| \mathrm {d}^2z \\&\qquad + \int _{|x-z| \le \delta } \left| K^*_N(z,x) - K^\#_N(z,x) \right| ^2\mathrm {d}^2z . \end{aligned}\end{aligned}$$

According to Proposition 5.3, it holds for any $x\in \mathbb {D}_{1-2\delta }$,

$$\begin{aligned} \int _{|x-z| \le \delta } \left| K^*_N(z,x) - K^\#_N(z,x) \right| ^2\mathrm {d}^2z = \mathcal {O}\left( \delta ^2\vartheta _N(x)^2 \right) . \end{aligned}$$

(5.32)

Similarly, using the estimate (5.27),

$$\begin{aligned} \int _{|x-z| \le \delta } |K^\#_N(z,x) | \left| K^*_N(z,x) - K^\#_N(z,x) \right| \mathrm {d}^2z \le \pi L N \delta ^2 \vartheta _N(x) . \end{aligned}$$

(5.33)

As $\vartheta _N \le (n+1) \epsilon ^{-2} \le N$, this shows that for any $x\in \mathbb {D}_{1-2\delta }$,

$$\begin{aligned} \int _{|x-w| \le \delta } |K^*_N(z,x) |^2 \mathrm {d}^2z = \int _{|x-w| \le \delta } |K^\#_N(z,x) |^2 \mathrm {d}^2z +\mathcal {O}\left( N \delta ^2 \vartheta _N\right) . \end{aligned}$$

Using the reproducing property (5.6) and Lemma 5.6, we conclude that for any $x\in \mathbb {D}_{1-2\delta }$,

$$\begin{aligned} \begin{aligned} \int _{|x-w| > \delta } |K^*_N(z,x) |^2 \mathrm {d}^2z&= u^*_N(x) - \int _{|x-w| \le \delta } |K^\#_N(z,x) |^2 \mathrm {d}^2z + \mathcal {O}\left( N \delta ^2 \vartheta _N\right) \\&= \widetilde{u}^*_N(x) + \mathcal {O}\left( N \delta ^2 \vartheta _N\right) . \end{aligned}\end{aligned}$$

Using the estimate $| \widetilde{u}_N^*(x) | \le L \vartheta _N(x)$, see (5.19), this yields the claim. $\square$

Finally, we need a last Lemma which relies on the anisotropy of the approximate Bergman kernel $K_N^{\#}$ that we can already see from formula (5.26).

Lemma 5.8

It holds as $N\rightarrow +\infty$,

$$\begin{aligned} \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} |K_N^{\#}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x = \mathcal {O}(1) . \end{aligned}$$

Proof

The proof if analogous to that of Lemma 5.6. Since $g_N$ is a smooth function, by Taylor Theorem up to order $2\ell \in \mathbb {N}$, it holds for any $x\in \mathbb {D}_{1/2}$ and $z\in \mathbb {D}(x,\delta )$,

$$\begin{aligned} \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} = \underset{0<i+j\le 2\ell }{\textstyle \sum _{i,j=0}^{2\ell } } \mathrm {M}_{i,j} u^{i-1} \overline{u}^j \partial ^{i} \overline{\partial }^{j+1} g_N(x) \\ + \mathcal {O}\left( \big \{ \Vert \nabla ^{2(\ell +1)} g_N\Vert _\infty \delta ^{2\ell }\big \} \right) , \end{aligned}$$

where $u = (z-x) \ne 0$. Let $\mathrm {Y}^2_x (u): = \sum _{j=0}^{\ell -1} \frac{ \mathrm {M}_{j+1,j} }{4} |u|^{2j} \Delta ^{j+1} g_N(x)$ and $\mathrm {A}^2_x (u): = \underset{0<i+j\le 2\ell , i\ne j+1}{\textstyle \sum _{i,j=0}^{2\ell } } \mathrm {M}_{i,j} u^{i-1} \overline{u}^j \partial ^{i+1} \overline{\partial }^{j+1} g_N(x)$ for $u\in \mathbb {C}$. Since $\Vert \nabla ^{2(\ell +1)} g_N\Vert _\infty \delta ^{2\ell } \le C \eta ^{2\ell } \epsilon ^{-2} \le CN^{-1}$ because we choose $\ell \in \mathbb {N}$ in such a way $\eta ^\ell \le N^{-1}$ with $\eta = \delta /\epsilon$, this shows that uniformly for all $x\in \mathbb {D}_{1/2}$ and $z\in \mathbb {D}(x,\delta )$,

$$\begin{aligned} \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} = \mathrm {Y}^2_x(x-z) + \mathrm {A}^2_x(x-z) + \mathcal {O}(N^{-1}) . \end{aligned}$$

By Lemma 5.6, we immediately see that $\displaystyle \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} |K_N^{\#}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x = \frac{N}{4}+ \mathcal {O}(1)$ and the previous expansion implies that

$$\begin{aligned}&\mathfrak {Z}_N : = \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \frac{\overline{\partial }g(x)- \overline{\partial }g(z)}{x-z} |K_N^{\#}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x\nonumber \\&\quad =\iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \left( \mathrm {Y}^2_x(x-z) + \mathrm {A}^2_x(x-z) \right) |K_N^{\#}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x +\mathcal {O}(1) . \end{aligned}$$

Using formula (5.28), (5.29) and the estimates $|\mathrm {Y}^1_x(u)| , |\mathrm {A}^1_x(u)| = \mathcal {O}(\epsilon ^{-2})$ which are uniform for $x,u\in \mathbb {C}$, we obtain by a change of variable,

$$\begin{aligned} \mathfrak {Z}_N = \frac{N}{\pi } \iint _{\begin{array}{c} |x| \le 1/2 \\ |u| \le \delta \end{array}} \left( \mathrm {Y}^2_x(u) + \mathrm {A}^2_x(u) \right) e^{\mathrm {A}^1_x (u)+ \mathrm {Y}^1_x (u)}\Phi _N(u) \mathrm {d}^2u \mathrm {d}^2x + \mathcal {O}(\epsilon ^{-2}N^{-1}) . \end{aligned}$$

The error term will be negligible. If we proceed exactly as in the Proof of Lemma 5.6, see (5.30), then only the radial parts contributes:

$$\begin{aligned} \begin{aligned} \mathfrak {Z}_N = \frac{N}{\pi } \iint _{\begin{array}{c} |x| \le 1/2 \\ |u| \le \delta \end{array}} \mathrm {Y}^2_x(u) \exp \left( \mathrm {Y}^1_x(u)\right) \Phi _N(\mathrm {d}u) \mathrm {d}^2u \mathrm {d}^2x + \mathcal {O}(\epsilon ^{-2}N^{-1}) . \end{aligned}\end{aligned}$$

Moreover, using that $|\Delta ^{k+1} g_N(x)| \le C \epsilon ^{-2k} \vartheta _N(x)$ for all integer $k\in [0, \ell ]$, we can develop for all $|u| \le \delta$, $\mathrm {Y}^2_x(u) \exp \left( \mathrm {Y}^1_x(u)\right) = \Delta g_N(x)+ \mathcal {O}(\vartheta _N(x)|u|^2 )$ uniformly for all $x\in \mathbb {D}_{1/2}$ — here we used again that the parameter $\eta \le 1/4$ to control the error term. Hence, by (5.31), we conclude that

$$\begin{aligned} \mathfrak {Z}_N = \frac{N}{\pi } \int _{|x| \le 1/2} \Delta g_N(x) \mathrm {d}^2x + \mathcal {O}\bigg ( \int _{|x| \le 1/2} \vartheta _N(x) \mathrm {d}^2x \bigg ) + \mathcal {O}(\epsilon ^{-2}N^{-1}) . \end{aligned}$$

Since the first integral on the RHS vanishes and the second integral is O(1), this completes the proof. $\square$

5.5 Error of type $\mathfrak {T}^1_N$

In Sects. 5.5–5.7, we use the estimates from Sects. 5.3 and 5.4 to bound the error terms when we apply Proposition 5.2 to the function $g_N = g_N^{\mathbf {\gamma }, \mathbf {z}}$ given by (2.9). Let us abbreviate

$$\begin{aligned} \Sigma = \Sigma (g_N) = \sqrt{ \int \overline{\partial }g_N(x) \partial g_N(x) \sigma (\mathrm {d}x)} . \end{aligned}$$

(5.34)

Proposition 5.9

We have $\left| \mathfrak {T}^1_N(g_N) \right| = \mathcal {O}\left( \Sigma ^2 \epsilon ^{-2} \right)$, uniformly for all $t\in (0,1]$, as $N\rightarrow +\infty$.

Proof

A trivial consequence of the estimate (5.19) is that $|\widetilde{u}_N^*(x)| \le C \epsilon ^{-2}$ for all $|x| \le 1/2$. Since ${\text {supp}}(g_N) \subseteq \mathbb {D}_{1/2}$, this implies that

$$\begin{aligned} \left| \int \Delta g_N(x)\ \widetilde{u}_N^*(x)\mathrm {d}^2x \right| \le C \epsilon ^{-2} \int |\Delta g_N(x)| \mathrm {d}^2x = \mathcal {O}( \epsilon ^{-2}) , \end{aligned}$$

where we used that $\Delta g_N(x) = {\textstyle \sum _{k=1}^n} \gamma _k \left( \phi _{\epsilon _k}(x-z_k) - \phi (x-z_k) \right)$ so that $\displaystyle \int |\Delta g_N(x)| \mathrm {d}^2x \le 2 {\textstyle \sum _{k=1}^n} |\gamma _k|$ since $\phi$ is a probability density function on $\mathbb {C}$. Similarly, we have

$$\begin{aligned} \left| \int \overline{\partial }g_N(x) \partial g_N(x) \ \widetilde{u}_N^*(x)\mathrm {d}^2x\right| \le C \epsilon ^{-2} \int \overline{\partial }g_N(x) \partial g_N(x) \mathrm {d}^2x = \mathcal {O}\left( \Sigma ^2 \epsilon ^{-2} \right) , \end{aligned}$$

since $\overline{\partial }g_N= \overline{\partial g_N}$ so that $\overline{\partial }g_N(x) \partial g_N(x) \ge 0$ for all $x\in \mathbb {C}$ and the previous integral is equal to $\pi \Sigma ^2$. By definition of $\mathfrak {T}^1_N$ — see Proposition 5.2 — this proves the claim. $\square$

5.6 Error of type $\mathfrak {T}^2_N$

Proposition 5.10

Recall that $\eta = \delta /\epsilon$. It holds as $N\rightarrow +\infty$, $| \mathfrak {T}^2_N(g_N)| = \mathcal {O}\left( \Sigma N \eta \right)$.

Proof

Fix a small parameter $0< \kappa \le 1/4$ independent of $N\in \mathbb {N}$ and let us split

$$\begin{aligned} \mathfrak {T}^2_N(g_N)= & {} \iint \frac{\overline{\partial }g_N(x) }{x-z} \widetilde{u}_N^*(z) \widetilde{u}_N^*(x) \mathrm {d}^2 x\mathrm {d}^2z\nonumber \\= & {} \mathfrak {Z}_N + \iint _{|z-x| \ge \kappa } \frac{\overline{\partial }g_N(x)}{x-z} \widetilde{u}_N^*(z) \widetilde{u}_N^*(x) \mathrm {d}^2 x\mathrm {d}^2z \end{aligned}$$

(5.35)

where

$$\begin{aligned} \mathfrak {Z}_N : = \iint _{|z-x| \le \kappa } \frac{\overline{\partial }g_N(x) }{x-z} \widetilde{u}_N^*(z) \widetilde{u}_N^*(x)\mathrm {d}^2 x\mathrm {d}^2z . \end{aligned}$$

(5.36)

Since ${\text {supp}}(g_N) \subseteq \mathbb {D}_{1/2}$, by Lemma 5.5, the second term on the RHS of (5.35) satisfies

$$\begin{aligned} \left| \iint _{|z-x| \ge \kappa } \frac{\overline{\partial }g_N(x) }{x-z} \widetilde{u}_N^*(z) \widetilde{u}_N^*(x) \mathrm {d}^2 x\mathrm {d}^2z \right| = \mathcal {O}\left( N \delta \int _{|x|\le 1/2} |\overline{\partial }g_N(x) \widetilde{u}_N^*(x) | \mathrm {d}^2x \right) . \end{aligned}$$

(5.37)

Moreover, using Cauchy–Schwartz inequality and (5.19), this implies that

$$\begin{aligned} \int _{|x|\le 1/2} |\overline{\partial }g_N(x) \widetilde{u}_N^*(x) | \mathrm {d}^2x \le L \sqrt{ \int |\overline{\partial }g_N(x) |^2\mathrm {d}^2x \int _{|x|\le 1/2} \vartheta _N^2(x) \mathrm {d}^2x } . \end{aligned}$$

According to the notation of Proposition 5.3, we verify ${ \displaystyle \int _{|x|\le 1/2} } \vartheta ^2_N(x) \mathrm {d}^2x \le \tfrac{\pi }{2}+ 2\pi \sum _{j,k=1}^n \epsilon _k^{-2} \epsilon _j^{-2}(\epsilon _k^2+\epsilon _j^{2}) \le C\epsilon ^{-2}$, so that by (5.34),

$$\begin{aligned} \int _{|x|\le 1/2} |\overline{\partial }g_N(x) \widetilde{u}_N^*(x) | \mathrm {d}^2x = \mathcal {O}(\Sigma \epsilon ^{-1}). \end{aligned}$$

(5.38)

The estimates (5.37) and (5.38) show that with $\eta = \delta /\epsilon$,

$$\begin{aligned} \left| \iint _{|z-x| \ge \kappa } \frac{\overline{\partial }g_N(x) }{x-z} \widetilde{u}_N^*(z) \widetilde{u}_N^*(x) \mathrm {d}^2 x\mathrm {d}^2z \right| = \mathcal {O}(N \Sigma \eta ) . \end{aligned}$$

(5.39)

Let $\mathscr {S}_N :=\bigcup _{k=1}^n \mathbb {D}(z_k,\epsilon _k)$. In order to control the integral (5.36), we split it into $n+1$ parts and use (5.19) which is valid for all $x\in {\text {supp}}(g_N)$, then we obtain

$$\begin{aligned} \begin{aligned} \left| \mathfrak {Z}_N \right|&\le L \left( \sum _{k=1}^n \epsilon _k^{-2} \int _{|x-z_k| \le \epsilon _k} + \int _{x \notin \mathscr {S}_N} \right) \left( \int _{|w| \le \kappa } |\widetilde{u}_N^*(x+w)| \frac{\mathrm {d}^2 w}{|w|} \right) |\overline{\partial }g_N(x)| \mathrm {d}^2x . \end{aligned} \end{aligned}$$

(5.40)

On the one hand, it follows from (5.19) that for any $x\in \mathbb {D}(z_k,\epsilon _k)$,

$$\begin{aligned} \begin{aligned} \int _{|w| \le \kappa } |\widetilde{u}_N^*(x+w)| \frac{\mathrm {d}^2 w}{|w|} \&\le L \sum _{j=1}^n \epsilon _j^{-2} \int _{w\in \mathbb {D}(z_j-x, \epsilon _j)} \frac{\mathrm {d}^2 w}{|w|} + L \int _{\begin{array}{c} |w| \le \kappa \\ (x+w) \notin \mathscr {S}_N \end{array}} \frac{\mathrm {d}^2 w}{|w|} \\&\le L \sum _{j=1}^n \epsilon _j^{-2} \int _{w\in \mathbb {D}(z_j-z_k, \epsilon _j + \epsilon _k)} \frac{\mathrm {d}^2 w}{|w|} + 2\pi \kappa L \\&\le L \pi \left( 1+ {\textstyle \sum _{j=1}^n} \epsilon _j^{-2} (\epsilon _j + \epsilon _k) \right) . \end{aligned}\end{aligned}$$

On the other hand, as $|\widetilde{u}_N^*(z)| \le nL \epsilon ^{-2}$ for all $|z| \le 3/4$, it also holds for all $x\in \mathbb {D}_{1/2}$,

$$\begin{aligned} \int _{|w| \le \kappa } |\widetilde{u}_N^*(x+w)| \frac{\mathrm {d}^2 w}{|w|} =\mathcal {O}(\epsilon ^{-2}) . \end{aligned}$$

Combining these two bounds with (5.40), we conclude that

$$\begin{aligned} \begin{aligned} \left| \mathfrak {Z}_N \right| \le \pi L^2 \sum _{k, j =1}^n \epsilon _k^{-2} \epsilon _j^{-2} (\epsilon _j + \epsilon _k) \int _{|x-z_k| \le \epsilon _k} |\overline{\partial }g_N(x)| \mathrm {d}^2x +\mathcal {O}\left( \epsilon ^{-2} \int |\overline{\partial }g_N(x)| \mathrm {d}^2x\right) . \end{aligned} \end{aligned}$$

By the Cauchy–Schwartz inequality and (5.34), this implies that

$$\begin{aligned} \left| \mathfrak {Z}_N \right| \le (\pi L)^2 \Sigma \sum _{k, j =1}^n \epsilon _k^{-1} \epsilon _j^{-2} (\epsilon _j + \epsilon _k) + \mathcal {O}(\epsilon ^{-2} \Sigma ) . \end{aligned}$$

Since our parameters $\epsilon _1, \dots , \epsilon _n \ge \epsilon$, we have $\sum _{k, j =1}^n \epsilon _k^{-1} \epsilon _j^{-2} (\epsilon _j + \epsilon _k) \le 2n^2 \epsilon ^{-2}$. Hence, we have proved that

$$\begin{aligned} \left| \mathfrak {Z}_N \right| = \mathcal {O}(\epsilon ^{-2} \Sigma ) . \end{aligned}$$

(5.41)

Since $\epsilon \ge \delta \ge N^{-1/2}$, by combining the estimates (5.39) and (5.41) with (5.35), this completes the proof. $\square$

5.7 Error of type $\mathfrak {T}^3_N$

Proposition 5.11

We have $\left| \mathfrak {T}^3_N(g_N) \right| = \mathcal {O}(N\eta )$ as $N\rightarrow +\infty$.

Proof

First, let us observe that by Lemma 5.7,

$$\begin{aligned} \begin{aligned}&\left| \iint _{|z-x| \ge \delta } \frac{\overline{\partial }g_N(x) }{x-z} | K_N^*(x,z) |^2 \mathrm {d}^2 x\mathrm {d}^2z \right| \\&\quad \le \delta ^{-1} \int |\overline{\partial }g_N(x)| \left( \int _{|z-x| > \delta } | K_N^*(x,z) |^2\mathrm {d}^2z \right) \mathrm {d}^2 x \\&\quad \le C N \delta \int |\overline{\partial }g_N(x)| \vartheta _N(x) \mathrm {d}^2 x . \end{aligned}\end{aligned}$$

Since $\Vert \nabla g_N\Vert _\infty = \mathcal {O}(\epsilon ^{-1})$ and $\displaystyle \int _{|x|\le 1/2} \vartheta _N(x) \mathrm {d}^2 x \le (n+1)\pi$, this shows that

$$\begin{aligned} \left| \iint _{|z-x| \ge \delta } \frac{\overline{\partial }g_N(x) }{x-z} | K_N^*(x,z) |^2 \mathrm {d}^2 x\mathrm {d}^2z \right| = \mathcal {O}(N\eta ) . \end{aligned}$$

(5.42)

Second, since $\displaystyle \left| \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} \right| \le \Vert \nabla ^2 g_N\Vert _\infty = \mathcal {O}(\epsilon ^{-2})$ for all $x,z\in \mathbb {C}$, we have

$$\begin{aligned} \begin{aligned}&\left| \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} |K_N^{*}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x \right. \\&\qquad \left. -\iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} |K_N^{\#}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x \right| \\&\quad \le 2 \epsilon ^{-2} \left( \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} |K^\#_N(z,x) | \left| K^*_N(z,x) - K^\#_N(z,x) \right| \mathrm {d}^2z \mathrm {d}^2x\right. \\&\qquad \left. + \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \left| K^*_N(z,x) - K^\#_N(z,x) \right| ^2\mathrm {d}^2z \mathrm {d}^2x \right) . \end{aligned}\end{aligned}$$

If we integrate the estimate (5.32), respectively (5.33), over the set $|x| \le 1/2$, we obtain

$$\begin{aligned} \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \left| K^*_N(z,x) - K^\#_N(z,x) \right| ^2\mathrm {d}^2z \mathrm {d}^2x = \mathcal {O}(\eta ^2) , \end{aligned}$$

and

$$\begin{aligned} \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} |K^\#_N(z,x) | \left| K^*_N(z,x) - K^\#_N(z,x) \right| \mathrm {d}^2z = \mathcal {O}(N \delta ^2). \end{aligned}$$

Here we used again that $\displaystyle \int _{|x|\le 1/2} \vartheta _N(x) \mathrm {d}^2 x \le (n+1)\pi$. These bounds imply that

$$\begin{aligned}&\left| \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} |K_N^{*}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x \right. \nonumber \\&\quad \left. -\iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} |K_N^{\#}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x \right| = \mathcal {O}(N \eta ^2). \end{aligned}$$

(5.43)

By symmetry, since ${\text {supp}}(g_N) \subseteq \mathbb {D}_{1/2}$,

$$\begin{aligned}&\left| \iint _{|z-x| \le \delta } \frac{\overline{\partial }g_N(x) }{x-z} | K_N^*(x,z) |^2 \mathrm {d}^2 x\mathrm {d}^2z \right| \\&\quad \le \left| \iint _{\begin{array}{c} |x| \le 1/2 \\ |z-x| \le \delta \end{array}} \frac{\overline{\partial }g_N(x)- \overline{\partial }g_N(z)}{x-z} |K_N^{*}(x,z)|^2 \mathrm {d}^2z \mathrm {d}^2x \right| . \end{aligned}$$

Then, using the estimate (5.43) and Lemma 5.8, we obtain

$$\begin{aligned} \left| \iint _{|z-x| \le \delta } \frac{\overline{\partial }g_N(x) }{x-z} | K_N^*(x,z) |^2 \mathrm {d}^2 x\mathrm {d}^2z \right| = \mathcal {O}(N \eta ^2) . \end{aligned}$$

(5.44)

Finally, it remains to combine the estimates (5.42) and (5.44) to complete the proof. $\square$

5.8 Proof of Proposition 2.3

We are now ready to give the Proof of Proposition 2.3. Recall that we use the notation of Sect. 5.1. When we combine Propositions 5.9, 5.10 and 5.11, we obtain that as $N\rightarrow +\infty$,

$$\begin{aligned} \left| \mathfrak {T}^1_N(g_N) + \mathfrak {T}^2_N(g_N) - \mathfrak {T}^3_N(g_N)\right| = \mathcal {O}\left( N \eta \Sigma (g_N) (1+\eta \Sigma (g_N)) \right) , \end{aligned}$$

where, by Remark 5.4, the error term is uniform for all $\mathbf {z} \in \mathbb {D}_{\epsilon _0}^{\times n}$ , all $t\in (0,1]$ and all $\mathbf {\gamma } \in [-R,R]^{n}$ for a fixed $R>0$. Since $\Sigma ^2(g_N) = \mathcal {O}(\log N)$ according to the asymptotics (2.8) and $\eta = \delta /\epsilon = (\log N)^{\beta /2} N^{-\alpha }$, this implies that as $N\rightarrow +\infty$

$$\begin{aligned} \frac{1}{N}\left| \mathfrak {T}^1_N(g_N) + \mathfrak {T}^2_N(g_N) - \mathfrak {T}^3_N(g_N)\right| = \mathcal {O}\left( (\log N)^{\frac{\beta +1}{2}} N^{-\alpha }\right) . \end{aligned}$$

(5.45)

The main idea of the proof, which originates from [36] is to observe that for any $t>0$,

$$\begin{aligned} \frac{d}{dt}\log \mathbb {E}_N\left[ \exp \left( t \mathrm {X}(g_N) \right) \right] = \mathbb {E}_N^*\left[ \mathrm {X}(g_N) \right] . \end{aligned}$$

Hence, by Proposition 5.2 applied to the function $g_N = g_N^{\mathbf {\gamma }, \mathbf {z}}$, using the estimate (5.45), we conclude that

$$\begin{aligned} \frac{d}{dt} \log \mathbb {E}_N\left[ \exp \left( t\mathrm {X}(g_N^{\mathbf {\gamma }, \mathbf {z}}) \right) \right] = t \Sigma ^2(g_N^{\mathbf {\gamma }, \mathbf {z}})+ \mathcal {O}\left( (\log N)^{\frac{\beta +1}{2}} N^{-\alpha }\right) , \end{aligned}$$

(5.46)

where the error term is uniform for all $t\in [0,1]$, all $\mathbf {\gamma }$ in compact subsets of $\mathbb {R}^n$ and all $\mathbf {z} \in \mathbb {D}_{\epsilon _0}^{\times n}$. Then, if we integrate the asymptotics (5.46) for $t\in [0,1]$, we obtain (2.10).

6 Kernel Asymptotics

In this section, we obtain the asymptotics for the correlation kernel induced by the biased measure (5.3) that we need in Sect. 5 in order to control the error term in Ward’s equation. Let us introduce

$$\begin{aligned} \Vert f\Vert _Q^2 = \int _\mathbb {C}|f(x)|^2 e^{-2N Q(x)} \mathrm {d}^2x , \end{aligned}$$

(6.1)

and similarly for the norm $\Vert \cdot \Vert _{Q^*}$. Recall that $Q(x) = |x|^2/2$ is the Ginibre potential and $Q^* = Q- \frac{g_N}{2N}$ is a potential which is perturbed by the function $g_N = g_N^{\mathbf {\gamma }, \mathbf {z}} \in \mathscr {C}_c^\infty (\mathbb {D}_{1/2})$ given by (2.9) with $\mathbf {z} \in \mathbb {D}_{\epsilon _0}^{\times n}$ and $\gamma \in [-R,R]^n$ for some fixed $n\in \mathbb {N}$ and $R>0$. We rely on the Conventions 5.1 and we choose $N_0 \in \mathbb {N}$ sufficiently large so that $\eta \le 1/4$ and $\Vert \Delta g_N\Vert _\infty \le N$ for all $N\ge N_0$.

6.1 Uniform estimates for the 1-point function

In this section, we collect some simple estimates on the 1-point function $u_N^*$ which we need. We skip the details since the argument is the same as in [2, Section 3] only adapted to our situation.

Lemma 6.1

There exists a universal constant $C>0$ such that if $N\ge N_0$, for any function f which is analytic in $\mathbb {D}(z; 2/\sqrt{N})$ for some $z\in \mathbb {C}$,

$$\begin{aligned} |f(z)|^2 e^{-2N Q^*(z)} \le CN \Vert f\Vert ^2_{Q^*} . \end{aligned}$$

Proof

If $N\ge N_0$, we have $\Delta Q^* \le 3$ and by [2, Lemma 3.1], we obtain

$$\begin{aligned} |f(z)|^2 e^{-2N Q^*(z)} \le N \int _{|z-x| \le N^{-1/2}} |f(x)|^2 e^{-2 N Q^*(x)} e^{3N|x-z|^2} \sigma (\mathrm {d}x) . \end{aligned}$$

This immediately yields the claim. $\square$

Lemma 6.2

With the same $C>0$ as in Lemma 6.1, it holds for all $N\ge N_0$ and all $z\in \mathbb {C}$,

$$\begin{aligned} u_N^*(z) \le C N . \end{aligned}$$

Proof

Fix $z\in \mathbb {C}$ and let us apply Lemma 6.1 to the polynomial $k^*_N(\cdot ,z)$, we obtain

$$\begin{aligned} |k^*_N(w,z)|^2 e^{-2 N Q^*(w)} \le C N k^*_N(z,z) , \end{aligned}$$

since $\Vert k^*_N(\cdot ,z)\Vert _{Q^*}^2 = k^*_N(z,z)$ because of the reproducing property of the kernel $k^*_N$. Taking $w=z$ in the previous bound and using that $u_N^*(z) =k^*_N(z,z) e^{-2N Q^*(z)}$, we obtain the claim.

6.2 Preliminary lemmas

Recall that we let $\Upsilon _N^w(u) = \sum _{i=0}^{\ell } \frac{u^i}{i!} \partial ^i g_N(w)$ and that we defined the approximate Bergman kernel $k^\#$ by

$$\begin{aligned} k^\#_N(x,w) = \frac{N}{\pi } e^{N x \overline{w}} e^{- \Upsilon _N^w(x-w) } , \quad x,w\in \mathbb {C}. \end{aligned}$$

We note that this kernel is not Hermitian but it is analytic in $x\in \mathbb {C}$ and we define the corresponding operator:

$$\begin{aligned} K^\#_N[f] (w) = \int _\mathbb {C}\overline{k^\#_N(x,w)} f(x) e^{-2N Q^*(x)} \mathrm {d}^2x , \quad w\in \mathbb {C}, \end{aligned}$$

(6.2)

for any $f\in L^2(e^{-2N Q^*})$. According to (5.4), we make a similar definition for $K^*_N[f]$. Our next Lemma is the counterpart of [4, Lemma A.2] and it relies on the analytic properties of the function $\Upsilon _N^w$. Since the test function $g_N$ develops logarithmic singularities for large N, we need to adapt the proof accordingly.

Assumption 6.3

Let $\chi \in \mathscr {C}^\infty _c\big (\mathbb {D}_{2\delta }\big )$ be a radial function such that $0\le \chi \le 1$, $\chi =1$ on $\mathbb {D}_{\delta }$, and $\Vert \nabla \chi \Vert _\infty \le C \delta ^{-1}$ for a $C>0$ independent of $N\in \mathbb {N}$. In the following for any $z\in \mathbb {C}$, we let $\chi _z = \chi (\cdot -z)$.

Lemma 6.4

There exists a constant $C>0$ (which depends only on $R>0$, the mollifier $\phi$ and $n, \ell \in \mathbb {N}$) such that for any $z\in \mathbb {C}$ and any function $f \in L^2(e^{-2N Q^*})$ which is analytic in $\mathbb {D}(z, 2 \delta )$,

$$\begin{aligned} \left| f(z) -K^\#_N[\chi _z f] (z) \right| \le C \big ( N^{-1/2} \vartheta _N(z) + e^{- N \delta ^2/2} \big ) e^{NQ^*(z)} \Vert f\Vert _{Q^*} , \end{aligned}$$

where $\vartheta _N$ is as in Proposition 5.3.

Proof

We fix $z\in \mathbb {C}$ and by definitions,

$$\begin{aligned} \begin{aligned} K^\#_N[\chi _z f] (z)&= \frac{N}{\pi } \int e^{ g_N(x)- \overline{\Upsilon _N^z(x-z)} } \chi _z(x) f(x) e^{N(z-x) \overline{x} } \mathrm {d}^2x \\&= \int e^{ g_N(x)- \overline{\Upsilon _N^z(x-z)} } \chi _z(x) f(x) \overline{\partial }\left( e^{N(z-x) \overline{x} } \right) \frac{1}{z-x} \frac{\mathrm {d}^2x}{\pi } . \end{aligned}\end{aligned}$$

By formula (5.2), since $\chi _z(z) =1$ and $\Upsilon _N^z(0) =g_N(z) \in \mathbb {R}$, we obtain

$$\begin{aligned} K^\#_N[\chi _z f] (z) = f(z) - \int \overline{\partial }\left( e^{ g_N(x)- \overline{\Upsilon _N^z(x-z)} }\chi _z(x) f(x) \right) e^{N(z-x) \overline{x} } \frac{1}{z-x} \frac{\mathrm {d}^2x}{\pi } . \end{aligned}$$

Since f is analytic in $\mathbb {D}(z,2 \delta ) = {\text {supp}}(\chi _z)$, this implies that

$$\begin{aligned} \begin{aligned} f(z) - K^\#_N[\chi _z f] (z) = \mathfrak {Z}_N + \int e^{ g_N(x)- \overline{\Upsilon _N^z(x-z)}} f(x) \overline{\partial }\chi _z(x) \frac{ e^{Nz\overline{x} } }{z-x} e^{-2NQ(x)} \frac{\mathrm {d}^2x}{\pi } , \end{aligned} \end{aligned}$$

(6.3)

where we let

$$\begin{aligned} \begin{aligned} \mathfrak {Z}_N&: = \int \overline{\partial }\left( e^{ g_N(x)-\overline{\Upsilon _N^z(x-z)}} \right) \chi _z(x) f(x) \frac{e^{N(z-x) \overline{x} } }{z-x} \frac{\mathrm {d}^2x}{\pi } \\&= - \int _{ |x-z| \le 2\delta } \frac{\overline{ \partial g_N(x) - \partial \Upsilon _N^z(x-z)}}{x-z} e^{ g_N(x)- \overline{\Upsilon _N^z(x-z)}} \chi _z(x) f(x) e^{Nz\overline{x} } e^{-2NQ(x)} \frac{\mathrm {d}^2x}{\pi } . \end{aligned} \end{aligned}$$

(6.4)

Using the Assumptions 6.3, the second term on the RHS of (6.3) satisfies

$$\begin{aligned}&\left| \int e^{ g_N(x)- \overline{\Upsilon _N^z(x-z)} } f(x) \overline{\partial }\chi _z(x) \frac{ e^{Nz\overline{x} } }{z-x} e^{-2NQ(x)}\frac{\mathrm {d}^2x}{\pi } \right| \nonumber \\&\quad \le \delta ^{-2} \int _{\delta \le |x-z| \le 2\delta } |f(x)| \ |e^{ g_N(x)-\Upsilon _N^z(x-z) }|\ e^{N\mathfrak {R}\{ z\overline{x} \}} e^{-2NQ(x)} \frac{\mathrm {d}^2x}{\pi } . \end{aligned}$$

(6.5)

Recall $\Vert \nabla ^k g_N\Vert _\infty \le C \epsilon ^{-k}$ for $k=1, \dots , \ell$ and we assume that $\eta = \delta /\epsilon \le 1/4$. Then, by Taylor’s formula, if $|x-z| \le 2\delta$,

$$\begin{aligned} e^{ g_N(x)-\Upsilon _N^z(x-z)} = e^{ g_N(x)/2 - g_N(z)/2} e^{- \mathbf {i}\mathfrak {I}\{ \partial g_N(z) (x-z) \} + \mathcal {O}(\eta ^2) } . \end{aligned}$$

(6.6)

This shows that on the RHS of (6.5), $|e^{ g_N(x)-\Upsilon _N^z(x-z) }| \le C e^{ g_N(x)/2 - g_N(z)/2}$. Moreover, by rearranging (5.25),

$$\begin{aligned} \frac{g_N(x) - g_N(z)}{2} - N \big (2Q(x) - \mathfrak {R}\{z\overline{x}\} \big )= -\frac{N}{2} |z-x|^2 - NQ^*(z) - NQ^*(x), \end{aligned}$$

(6.7)

which shows that

$$\begin{aligned}&\left| \int e^{ g_N(x)-\overline{\Upsilon _N^z(x-z)}} f(x) \overline{\partial }\chi _z(x) \frac{ e^{Nz\overline{x} } }{z-x} e^{-2NQ(x)} \frac{\mathrm {d}^2x}{\pi } \right| \\&\quad \le C \delta ^{-2} e^{NQ^*(z)} \int _{|x-z| \ge \delta } |f(x)| e^{-N |x-z|^2/2} e^{-NQ^*(x)} \frac{\mathrm {d}^2x}{\pi } . \end{aligned}$$

By Cauchy–Schwartz inequality and (6.1), we conclude that the second term on the RHS of (6.3) is bounded by

$$\begin{aligned} \left| \int e^{ g_N(x)- \overline{\Upsilon _N^z(x-z)} } f(x) \overline{\partial }\chi _z(x) \frac{ e^{Nz\overline{x} } }{z-x} e^{-2NQ(x)} \frac{\mathrm {d}^2x}{\pi } \right| \le C e^{NQ^*(z)} \Vert f\Vert _{Q^*} e^{- N \delta ^2/2} . \end{aligned}$$

(6.8)

Here we used that $\delta ^{-2} \le N$ and that for any $r>0$,

$$\begin{aligned} \int _{ |x-z| \ge r} e^{-N |x-z|^2 } \frac{\mathrm {d}^2x}{\pi } = N^{-1} e^{-N r^2} . \end{aligned}$$

(6.9)

The RHS of (6.8) will be negligible and it remains to control $\mathfrak {Z}_N$. Using again formulae (6.6)–(6.7) and taking the $|\cdot |$ inside the integral (6.4), we obtain

$$\begin{aligned} |\mathfrak {Z}_N | \le C e^{NQ^*(z)} \int _{ |x-z| \le 2\delta } \bigg | \frac{ \partial g_N(x) - \partial \Upsilon _N^z(x-z)}{\overline{x-z}} \bigg | | f(x) |e^{- N|z-x|^2/2 } e^{-NQ^*(x)} \frac{\mathrm {d}^2x}{\pi } , \end{aligned}$$

(6.10)

where we used that $\Vert \chi _z\Vert _\infty \le 1$. Since the function $g_N$ is smooth, by Taylor’s Theorem up to order $2\ell$, it holds for any $|u| \le 2\delta$,

$$\begin{aligned} \begin{aligned} \partial g_N(z+u) - \partial \Upsilon _N^z(u)&= {\textstyle \sum _{i=0}^{\ell } } {\textstyle \sum _{j=1}^{\ell } } \mathrm {M}_{i,j} u^i \overline{u}^j \ \partial ^{i+1} \overline{\partial }^j g_N(z)\\&\quad + \mathcal {O}\left( |u| \sup _{\ell \le k \le 2\ell } \big \{ \Vert \nabla ^{k+2} g_N\Vert _\infty \delta ^{k}\big \} \right) , \end{aligned}\end{aligned}$$

where the coefficients $\mathrm {M}_{i,j} >0$. Let us recall that $\Vert \nabla ^{k} g_N\Vert _\infty \le C \epsilon ^{-k}$ for any integer $k\in [1,2\ell ]$, $\eta =\delta /\epsilon$ is small and we fixed $\ell \in \mathbb {N}$ in such a way that the parameter $\eta ^\ell \le N^{-1}$. In particular, we have constructed $\Upsilon _N^z$ in such a way that we deduce from the previous expansion that for any $x\in \mathbb {D}(z,2\delta )$,

$$\begin{aligned} \partial g_N(x) - \partial \Upsilon _N^z(u)= & {} \frac{\overline{u}}{4} {\textstyle \sum _{i=0}^{\ell } } {\textstyle \sum _{j=0}^{\ell -1} } \mathrm {M}_{i,j+1} u^i \overline{u}^{j} \ \partial ^{i} \overline{\partial }^j (\Delta g_N)(z) +\mathcal {O}(|u|N^{-2\alpha }) , \\&\quad \text {where } u = x-z \end{aligned}$$

and we have used that $\partial \overline{\partial }g_N = \frac{1}{4} \Delta g_N$. Using (2.9), (2.1) and the definition of $\vartheta _N$, it is straightforward to verify that for any integer $k\in [0,2\ell ]$ and uniformly for all $z\in \mathbb {C}$, $| \nabla ^k (\Delta g_N)(z)| \le C \epsilon ^{-k} \vartheta _N(z)$. Hence, these estimates imply that uniformly for all $x\in \mathbb {D}(z,2\delta )$,

$$\begin{aligned} \left| \frac{ \partial g_N(x) - \partial \Upsilon _N^z(x-z)}{\overline{x-z}} \right| \le C \vartheta _N(z) + \mathcal {O}\left( N^{-2\alpha }\right) . \end{aligned}$$

(6.11)

Note that the error term is 0 if $z\notin \mathbb {D}$ since $g_N$ has compact support in $\mathbb {D}_{\epsilon _0}$. Therefore, by combining (6.10) and (6.11), we conclude that

$$\begin{aligned} |\mathfrak {Z}_N | \le C N^{-1/2} \vartheta _N(z) e^{NQ^*(z)} \Vert f\Vert _{Q^*} , \end{aligned}$$

(6.12)

where we have used the Cauchy–Schwartz inequality and (6.9) with $r=0$. Finally, by combining the estimates (6.8) and (6.12) with formula (6.3), this completes the proof. $\square$

Our next Lemma is the counterpart of [4, (4.12)]. The proof needs again to be carefully adapted but the general strategy remains the same as in [4] and relies on Hörmander’s inequality and the fact that (5.4) is the reproducing kernel of the Hilbert space $\mathscr {P}_N \cap L^2(e^{-2NQ^*})$.

Lemma 6.5

For any integer $\kappa \ge 0$, there exists $N_\kappa \in \mathbb {N}$ (which depends only on $R>0$, the mollifier $\phi$ and $n, \ell \in \mathbb {N}$) such that if $N \ge N_\kappa$, we have for all $z\in \mathbb {D}_{1-2\delta }$ and all $w\in \mathbb {D}(z,\delta )$,

$$\begin{aligned} \left| k^\#_N(w,z) - K^*_N[\chi _z k^\#_N(\cdot ,z)] (w)\right| \le N^{-\kappa } e^{NQ^*(z) + N Q^*(w)} . \end{aligned}$$

Proof

In this proof, we fix N and $z\in \mathbb {D}_{1-2\delta }$. We let $f := \chi _z k^\#_N(\cdot ,z)$ where $\chi _z$ is as in Assumptions 6.3 and $W(x) := N \big (\varphi (x) +1/2\big ) + \log \sqrt{1+|x|^2}$ where $\varphi$ is as in equations (1.4)–(1.5). Let also V be the minimal solution in $L^2(e^{-2W})$ of the problem $\overline{\partial }V= \overline{\partial }f$ and recall that Hörmander’s inequality, e.g. [2, formula (4.5)], for the $\overline{\partial }$–equation states that

$$\begin{aligned} \Vert V\Vert _{L^2(e^{-2W})}^2 \le 2 \int _\mathbb {D}\left| \overline{\partial }f(x)\right| ^2 \frac{e^{-2W(x)}}{\Delta W(x)} \mathrm {d}^2x . \end{aligned}$$

Here we used that W is strictly subharmonic.¹⁴ By (1.5), since $W(x) \ge N Q(x)$ and $\Delta W(x) \ge N \Delta Q(x) = 2N$ for all $x\in \mathbb {D}$, this implies that

$$\begin{aligned} \Vert V\Vert _{L^2(e^{-2W})}^2 \le N^{-1} \Vert \overline{\partial }f\Vert _{Q}^2 . \end{aligned}$$

Moreover, by (1.4), there exists a universal constant $c>0$ such that $W(x) \le N Q(x) + c$. Therefore, we obtain

$$\begin{aligned} \Vert V\Vert _{Q}^2 \le e^{2c} N^{-1} \Vert \overline{\partial }f\Vert _{Q}^2 . \end{aligned}$$

(6.13)

Recall that $Q^*= Q -\frac{g_N}{2N}$ where the perturbation $g_N$ is given by (2.9) and satisfies $\Vert g_N\Vert _\infty \le C \log \epsilon ^{-1}$. This implies that $L^2(e^{-2NQ^*}) \cong L^2(e^{-2NQ})$ with for any function $h\in L^2(e^{-2NQ})$:

$$\begin{aligned} \epsilon ^{C/2}\Vert h\Vert _{Q^*} \le \Vert h\Vert _{Q} \le \epsilon ^{-C/2} \Vert h\Vert _{Q^*} . \end{aligned}$$

By (6.13), this equivalence of norms shows that if $N\in \mathbb {N}$ is sufficiently large,

$$\begin{aligned} \Vert V\Vert _{Q^*}^2 \le N^{C-1} \Vert \overline{\partial }f\Vert _{Q^*}^2 . \end{aligned}$$

(6.14)

Observe that by (1.4), $W(x) = (N+1) \log |x| +o(1)$ as $|x| \rightarrow +\infty$, hence the Bergman space $A^2(e^{-2W})$ coincide with $\mathscr {P}_N$ and we must have $V- f \in \mathscr {P}_N$, see (5.1).

Now, we let U to be the minimal solution in $L^2(e^{-2NQ^*})$ of the problem $U-f \in \mathscr {P}_N$. Since U has minimal norm, (6.14) implies that

$$\begin{aligned} \Vert U\Vert _{Q^*}^2 \le N^{C-1} \Vert \overline{\partial }f\Vert _{Q^*}^2 . \end{aligned}$$

(6.15)

Since $k^\#_N(\cdot ,z)$ is analytic, see (5.17), $\overline{\partial }f = k^\#_N(\cdot ,z) \overline{\partial }\chi _z$ and according to the Assumptions 6.3,

$$\begin{aligned} \Vert \overline{\partial }f\Vert _{Q^*}^2 \le C \delta ^{-2} \int _{\delta \le |x-z| \le 2\delta } | k^\#_N(x,z) |^2 e^{-2NQ^*(x)} \mathrm {d}^2x . \end{aligned}$$

Recall that $\eta = \delta /\epsilon \le 1/4$ and $\Vert \nabla ^i g_N\Vert \le C \epsilon ^{-i}$ for all $i=1,\dots , \ell$. Then by (5.17) with $t=1$, it holds for all $z \in \mathbb {C}$ and $|x-z| \le 2\delta$, $\Upsilon _N^z(x-z) = g_N(z) + \mathcal {O}(\eta )$ so that

$$\begin{aligned} | k^\#_N(x,z) |^2 \le C e^{-2 g_N(z)+ 2N \mathfrak {R}\{ x \overline{z} \}} . \end{aligned}$$

By (6.7) and using that $|g_N(x)-g_N(z)| =\mathcal {O}(\eta )$, this shows that

$$\begin{aligned} | k^\#_N(x,w) |^2 e^{-2NQ^*(x)} \le C e^{ 2N Q^*(z) - N |x-z|^2} . \end{aligned}$$

Then by (6.9) and using that $\delta ^{-2} \le N$, we obtain

$$\begin{aligned} \begin{aligned} \Vert \overline{\partial }f\Vert _{Q}^2&\le C \delta ^{-2} e^{2NQ^*(z)}\int _{\delta \le |x-z| \le 2\delta } e^{- N |x-z|^2} \frac{\mathrm {d}^2x}{\pi } \\&\le C e^{2NQ^*(z)} e^{-N \delta ^2} . \end{aligned}\end{aligned}$$

Combining the previous estimate with (6.15), we conclude that

$$\begin{aligned} \Vert U\Vert _{Q^*}^2 \le C N^{C-1} e^{2NQ^*(z)} e^{-N \delta ^2}. \end{aligned}$$

(6.16)

We may now turn (6.16) into a pointwise estimate using Lemma 6.1. Note that both f and U are analytic¹⁵ in $\mathbb {D}(z;\delta )$, this implies that for any $w\in \mathbb {D}(z;\delta )$

$$\begin{aligned} |U(w)|^2 e^{-2N Q^*(w)} \le C N^{C} e^{2NQ^*(z)} e^{-N \delta ^2}. \end{aligned}$$

(6.17)

Since $k^*_N$ is the reproducing kernel of the Hilbert space $\mathscr {P}_N \cap L^2(e^{-2NQ^*})$, see (5.4), it is well known that minimal solution U is given by

$$\begin{aligned} U = f - K^*_N[f] . \end{aligned}$$

Conseqently, as $f = \chi _z k^\#_N(\cdot ,z)$ and $\chi _z =1$ on $\mathbb {D}(z;\delta )$, by (6.17), we conclude that for any $w\in \mathbb {D}(z;\delta )$,

$$\begin{aligned} \left| k^\#_N(w,z) - K^*_N[\chi _z k^\#_N(\cdot ,z)] (w) \right| \le C N^{C/4} e^{NQ^*(z) + NQ^*(w)} e^{- N \delta ^2/2} . \end{aligned}$$

Since $e^{N \delta ^2}$ grows faster than any power of $N\in \mathbb {N}$, this completes the proof. $\square$

We are now ready to give the proof of our main approximation for the correlation kernel $K^*_N$, see (5.5).

6.3 Proof of Proposition 5.3

We apply Lemma 6.4 to the function $f(x) = k^*_N(x,w)$ which is analytic for $x\in \mathbb {C}$ with norm

$$\begin{aligned} \Vert f \Vert _{Q^*}^2 = k^*_N(w,w) = u^*_N(w) e^{2N Q^*(w)} , \end{aligned}$$

by the reproducing property. Hence, we obtain for any $z\in \mathbb {D}$ and $w\in \mathbb {C}$,

$$\begin{aligned} \left| k^*_N(z,w) -K^\#_N[\chi _z k^*_N(\cdot ,w)] (z) \right| \le C \vartheta _N(z)\sqrt{\tfrac{u^*_N(w)}{N}} e^{NQ^*(z) + N Q^*(w)} . \end{aligned}$$

By Lemma 6.2, this shows that

$$\begin{aligned} \left| k^*_N(z,w) -K^\#_N[\chi _z k^*_N(\cdot ,z)] (w) \right| \le C\vartheta _N(z) e^{NQ^*(z) + N Q^*(w)} . \end{aligned}$$

(6.18)

Recall that by (6.2), we have

$$\begin{aligned} K^\#_N[\chi _z k^*_N(\cdot ,w)] (z) = \int \overline{k^\#_N(x,z)} \chi _z(x) k^*_N(x,w) e^{-2N Q^*(x)} \mathrm {d}^2x , \end{aligned}$$

so that

$$\begin{aligned} \overline{K^\#_N[\chi _z k^*_N(\cdot ,w)] (z)} = \int k^\#_N(x,z) \chi _z(x) \overline{k^*_N(x,w)} e^{-2N Q^*(x)} \mathrm {d}^2x = K^*_N[\chi _z k^\#_N(\cdot ,z)] (w) . \end{aligned}$$

Then, since the kernel $k^*_N$ is Hermitian, it follows from the bound (6.18) that for any $z, w\in \mathbb {D}$,

$$\begin{aligned} \left| k^*_N(w,z) -K^*_N[\chi _z k^\#_N(\cdot ,z)] (w) \right| \le C\vartheta _N(z) e^{NQ^*(z) + N Q^*(w)} . \end{aligned}$$

(6.19)

Finally, by Lemma 6.5, we conclude that for any $z\in \mathbb {D}_{1-2\delta }$ and all $w\in \mathbb {D}(z,\delta )$,

$$\begin{aligned} \left| k^*_N(w,z) - k^\#_N(w,z) \right| \le C\vartheta _N(z) e^{NQ^*(z) + N Q^*(w)} . \end{aligned}$$