Introduction

Quantitative systems pharmacology (QSP) is an approach that uses mathematical models to describe the dynamic interactions between drugs and (patho)physiologic and biochemical systems. QSP models are increasingly used in drug-development to provide a deeper understanding of the mechanisms of actions of drugs and to identify feasible disease targets for preclinical investigations [1,2,3]. Detailed modelling of complex biological systems often produces models with a large number of parameters and states [4] and often also across multiple time scales [5]. Despite the rapidly developing computational power and hardware, Monte Carlo simulations of such detailed models often require infeasible amounts of time [6]. Additionally, parameter estimation of complex non-linear models is both intrinsically difficult and computationally intensive due to high dimensionality and also may be unreliable if the model is not formally proven to be identifiable.

An alternative approach to using the full QSP model could involve the use of model-order reduction techniques. Model-order reduction (or shortly model reduction) aims to alleviate one or more issues of complexity of QSP models to yield a simplified representation of the desired input–output relationship from the full-order model [7,8,9,10,11]. Recently Hasegawa et al. has shown that a reduced model, produced by lumping a QSP model of bone remodelling [5], was able to be used to extrapolate to new data for two examples (denosumab and alendronate) based on the bone model [12]. In the latter case, the reduced model from the denosumab example was successfully reused for alendronate without reference to the original QSP model and without further development of the reduced model.

The coagulation network is a QSP model that describes the coagulation process as a series of ordinary differential equation (ODEs) representing the interaction of positive and negative feedback and feedforward reactions that result in the formation and subsequent degradation of a fibrin clot [4], which was extended in the work of Gulati et al. [13]. The model contains a number of drug targets that include warfarin, heparins, and other anticoagulants. The network model describes both the in-vivo characteristics of the coagulation system (formation and elimination of various coagulation proteins) and the in-vitro characteristics that arise when a clotting time test is performed (e.g. INR). See Fig. 1 for an illustration of the two components in the system. Importantly, the in-vivo and in-vitro components are discontinuous due to a discrete change in the system that occurs in-between these two components. The in-vitro component is initiated with a snapshot of the in-vivo concentrations of all states at a specific point in time (i.e. the time of the “blood sample” for which a coagulation time test is intended). The in-vitro component is initiated after a dilution of all system states and the addition of an activating agent (e.g. tissue factor). The system is then restarted with all elimination rate constants for factors set to zero (as clotting factor degradation does not take place in the in-vitro setting).

Fig. 1
figure 1

Schematic representation of the coagulation network model related to dose–response relationship of an anticoagulant. Green colour refers to module inputs and the orange colour refers to module outputs. The switch symbol indicates a discrete change in the system that corresponds to taking a blood sample, i.e. switching off elimination rates, addition of an activating agent, etc. ODEs ordinary differential equations, aPTT activated partial thromboplastin time, INR international normalised ratio

Full size image

For unfractionated heparin (UFH), the in -vitro effects on the system are measured by anti-factor Xa activity (aXa) and activated partial thromboplastin time (aPTT). As illustrated in Fig. 1, the two components, in-vivo and in-vitro, are linked through a high-dimensional discontinuous interface (in this case a 62-state vector). Both in-vivo and in-vitro components independently run 62 ODEs using 184 and 188 parameters, respectively.

The dimensionality and discontinuity of the interface creates a difficulty for model reduction techniques. While several techniques have been applied to the coagulation network model, including proper lumping as applied to the in-vivo component [14] and a non-parametric polynomial applied to warfarin [15], these techniques have either been limited to a single component or to provide a specific solutions only. A more general solution remains important. The general technique of lumping involves a search for an optimal lumping scheme among all possible combinations of lumped states that retains the desired characteristics of a reduced (lumped) model when compared with the full-order model [14]. However, the search space grows very fast with the dimension of the model to be reduced leading to potentially long lists of combinations to be tested [7] which is particularly challenging for nonlinear models. In addition, lumping and similar parametric approaches have been optimised for continuously differentiable functions. In this case, due to the high-dimensional discontinuous interface between the in-vivo and in-vitro components, it is possible that a single lumping schema does not exist. For polynomial fitting, the number of polynomial terms grows rapidly with increasing numbers of input variables (n) and orders of interactions. As a result, polynomial fitting becomes problematic for high dimensional inputs especially when higher order interactions between input variables are to be considered due to combinatorial explosion of interaction terms [16].

Artificial neural networks (ANNs) have been widely used in many research fields to model complex non-linear I/O relationships. The universal approximation theorem states that a multi-layer artificial neural network with an arbitrary number of neurons can approximate any continuous function of real variables arbitrarily well [17]. This makes ANNs a potentially useful tool for approximating complex multi-dimensional and non-linear I/O relationships that are typical of QSP models. They have shown to be an efficient tool for order-reduction of various types of models in fields such as systems engineering and control [18].

Different approaches have been proposed for using ANNs in the domain of model reduction. These range from constructing nonparametric surrogate models to emulate a specific input–output behaviour of a complex model based on simulated and experimental data [19] to parametric methods where ANNs are combined with other model reduction methods such as proper orthogonal decompositions to generate reduced-order models that retain meaningful parameters from the full-order model [20]. Despite their apparent utility, we are not aware of the use of ANNs for simplifying QSP models.

Aims

The aim of this article is to explore the use of ANNs as a model reduction technique to approximate a QSP model. Here we use the coagulation network QSP model applied to unfractionated heparin as the motivating example. Specific aims include:

  1. a)

    To find the minimum ANN architecture that can approximate the full-order coagulation QSP model across the in-vivo and in-vitro interface, with an arbitrary accuracy.

  2. b)

    To train an ANN with pseudodata from the full-order model. We use the term pseudodata to indicate that the QSP model is used to simulate I/O data over a range of input variables and no real data is used for training.

  3. c)

    To test the performance of the trained ANNs to predict new I/O data within the range of the training data.

In this work, we chose UFH dose–response in paediatric patients [21] as the target I/O relationship of the coagulation network for the following features that make the problem complex and difficult to perform using other model reduction techniques:

  • The coagulation model contains multiple sources of non-linearity: The coagulation system contains both amplification (positive loop gain) and damping subsystems which means its response to perturbation is non-linear and difficult to predict. In addition, maturation of the system and drug pharmacokinetics add additional layers of non-linearity.

  • The specific I/O relationship to be investigated here spans both in-vivo and in-vitro components (i.e. across the high dimensional interface).

It is important to note that the use of this systems model in this setting does not imply that the model has been validated in this patient group. We are using this as an exploratory example to illustrate the techniques and the utility of these techniques.

Methods

The model reduction technique considered in this work consisted of two steps:

  1. 1.

    Simulation of pseudo I/O data from the full-order model.

  2. 2.

    Training and validation of a minimal ANN architecture that can approximate the I/O relationship up to an arbitrary performance target.

All QSP simulations, data processing, and neural networks construction and training were performed in MATLAB with the Neural Network Toolbox (Release 2018b The MathWorks, Inc., Natick, Massachusetts, United States). The computer used to run this analysis was equipped with 64 GB of RAM and a 36-core processor that supported 72 parallel threads. However, none of the simulation or training processes were parallelised to facilitate runtime comparability across models and platforms. The complete code for the process described in this article is provided in supplemental 3 including the simulated training, evaluation and validation pseudo data. We note that ANN training involves a stochastic component of initialising network weights and biases. This means that re-running the code would be anticipated to produce slightly different results from those reported here.

Simulation of pseudo data

The full-order QSP model was used to simulate training data in the form: \(\{\left({x}_{1},{y}_{1}\right), \left({x}_{2},{y}_{2}\right), \dots , \left({x}_{Q},{y}_{Q}\right)\}\) where \(Q\) is the number of training examples, \({x}_{q}\) is a 4-dimensional input vector, and \({y}_{q}\) is the corresponding 2-dimensional output of the full-order model. The input vector consisted of four variables including patient covariates (weight and age) and dosing information (intravenous infusion dose and duration). Input variables were randomly sampled as follows:

  1. 1.

    Age (in years) was sampled from a log-normal distribution: \(ln(age) \sim N(0.7, 1.1)\). This was to ensure that enough data are available in the highly nonlinear region of the maturation function of the model (0–0.5 year).

  2. 2.

    Infant weight (in kg) was simulated from a published empirical model of paediatric age-matched weights [22]. The model utilised a fifth order polynomial function to describe the trend of weight with age and a constant coefficient of variation to describe the inter-individual variability.

  3. 3.

    Infusion rates of UFH were sampled from a uniform distribution in the range of 10–30 IU/kg/hour. Rates were then converted to total infusion doses before being presented to the full-order QSP model.

  4. 4.

    Infusion durations were sampled from a uniform distribution in the range of 0–12 h.

The output vector was the QSP model predicted aPTT and aXa at the end of infusion for each virtual patient. The simulated dataset consisted of 10,000 input–output pairs of data. The size of training set was selected so that it is likely to be more than adequate for statistically representing the input–output behaviour of the full-order model. It contains more than 3 times the amount of data than the commonly accepted empiric 10 × rule (which states that the amount of training data should generally not be less than tenfold the number of parameters of the proposed ANN model [23]). The simulated data was randomly split into a training set (80%) that was used for ANN parameter estimation and an evaluation set (20%) used to test the performance of the network and determine when training should be stopped (see ANN training section below). The same split was employed for all training experiments throughout this work.

To test the ability of trained neural networks to learn the relationship between each input variable and the output variables, four validation data sets were simulated. In each set, one input variable was varied over the range of the training data while the other variables were fixed to the median value of the training data and the corresponding outputs were simulated from the full-order QSP model. Such data sets are expected to contain combinations of input variable values that are unlikely to be present in the training data set, which challenges the ANN’s ability to interpolate the individual effects of each input variable on outputs. Additionally, full response-time profiles were simulated from the full-order model for two hypothetical patients receiving UFH infusion at a rate of 20 IU/kg/hour. Patient 1 was chosen in the highly nonlinear range of the maturation function (age 0.5 years and weight of 6 kg) while patient 2 was close to the full maturation process (age 12 years and weight of 40 kg). The validation data sets were not incorporated into any part of the training process.

Feedforward ANN

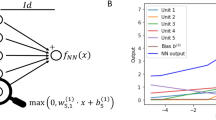
In this section, we present an introductory overview of the computations performed within a neural network for readers who are not familiar with the topic. A more detailed description of the concept of feedforward ANNs is provided elsewhere [24]. Where possible we have used notation that is consistent with the general notation used in statistics and pharmacometrics literature, which is sometimes slightly different from that used in the neural network literature. The ANN used in this work is a feed-forward neural network. A feed-forward neural network consists of artificial neurons (nodes) arranged in three or more layers, an input layer, output layer, and one or more hidden layers in-between as shown in Fig. 2. A neuron is a computation unit that typically receives multiple inputs, calculates a weighted sum of the inputs, adds a bias to the weighted inputs to form the net input, and then passes the net input to an activation function to produce the output as shown in Eq. 1 and Eq. 2 below. This node may be connected to one or more nodes in the next layer with the activation output becoming the input for the next node layer.

$${n}_{m,i}= \sum_{j=1}^{{S}_{m-1}}( {w}_{m,i,j} {a}_{m-1,j})+{b}_{m.i} ,$$
(1)

where \({n}_{m,i}\) is the net input of the \({i}^{th}\) neuron in the \({m}^{th}\) layer, \({S}_{m-1}\) is the number of neurons in the previous (\({m-1}^{th}\)) layer, \({w}_{m,i,j}\) is the connection weight between neuron \(j\) of the \({m-1}^{th}\) layer to the neuron \(i\) in the \({m}^{th}\) layer, \({a}_{m-1,j}\) is the output of the neuron \(j\) in the \({m-1}^{th}\) layer, and \({b}_{m.i}\) is the bias of the neuron \(i\) in the \({m}^{th}\) layer. Note that in this notation style every variable can have up to three indices. The first index represents the layer number, the second represents the number of a node within that layer, and the third represents the node number of a connected previous layer. Note, we omit the node index when we are referring to all nodes within that layer. For example, if \({n}_{m,i}\) refers to node \(i\) in layer \(m\), then \((n_{{m, \cdot }} )\) refers to all nodes in layer \(m\) (e.g. the sum of all inputs) which we write as \(({n}_{m})\). The activation function is described by.

$${a}_{m,i}={f}_{m}\left({n}_{m,i}\right),$$
(2)

where \({f}_{m}\) is the activation function of layer \(m\). Two types of activation functions have been used in this work. The hyperbolic tangent (\(tanh\)) function (given by Eq. 3) was used for all hidden layers while the identity function was used for the output layer.

Fig. 2
figure 2

Schematic presentation of a feedforward neural network. The computations performed by a neuron are shown in the inset box. The input layer is denoted as layer 0 (shown in pink shading), the hidden layers are depicted in blue, and the output layer in green. Nodes are shown as circles. Solid lines represent connectivity in a direction of left to right. The notation a and w represent the activations (either input to a node or output from a node) and weights and b represent the bias (Color figure online)

Full size image
$${f}_{m}\left({n}_{m,i}\right)=\frac{2}{1+{e}^{-2{n}_{m,i}}}-1$$
(3)

Equations 1–3 apply to all neurons of the neural network except for neurons of the input layer. Input neurons contain the input data and perform no computations or transformations. These data then form the activation function for the first hidden layer. Therefore, the output of this layer (\({a}_{0})\) is the same as the values of input variables to the network (\({x}_{q}\)) as shown in Eq. 4:

$${a}_{0} = {x}_{q}$$
(4)

For computational efficiency, outputs of all neurons are computed layer-wise using matrix operations. For example, let \({S}_{m}\) be the number of nodes in layer \(m \in \{ \mathrm{0,1},\dots ,{M}\}\) with \(M\) denoting the last layer. Then, \({S}_{0}\) will be the number of nodes in the first layer which is the same as the number of input variables, and \({S}_{M}\) will be the number of nodes in the output layer which is also the same as the number of output variables. Here \({S}_{0}=4\) and\({S}_{M}=2\). The output of the input layer is the vector of inputs to the network (\({x}_{q} \in {\mathbb{R}}^{{S}_{0}}\)) as in Eq. 4.

In each subsequent layer, i.e. hidden layers, the weights matrix of a layer (\({W}_{m}\)) which has a dimension of \({S}_{m}\times {S}_{m-1}\) is multiplied by outputs from the preceding layer (has a dimension of \({S}_{m-1}\times 1\)). Each row of the weights matrix of a layer \(m\) represents a vector of weights of a neuron within that layer. The product of weights matrix with outputs from previous layer is the weighted input to that layer (and has a dimension of \({S}_{m}\times 1\)). The bias vector (\({b}_{m}\)) which has the same size as the weighted inputs vector are added together to produce the net input (\({n}_{m}\) in Eq. 1). The net input is then passed to the element-wise activation function to produce the layer output (\({a}_{m}\)) as shown in Fig. 3; Eq. 5. The output of a hidden layer represents the input to the next layer, up to the last layer of which the output is the output of the network (\(\widehat{y}\)) as shown in Eq. 6, hence the name output layer.

Fig. 3
figure 3

Layer-wise computation of layer \(m\) outputs for one set of inputs. Black lines represent matrix multiplication while blue lines represent element-wise operations

Full size image
$$a_{m} = f_{m} (W_{m} \cdot a_{{m - 1}} + b_{m} )$$
(5)
$$\widehat{y}= {a}_{M}$$
(6)

The parameter vector \(\theta\) (\(\theta \epsilon {\mathbb{R}}^{{N}_{\theta }}\)) is the concatenation of all learnable parameters of the network, i.e., weight matrices and bias vectors, as shown in Eq. 7.

$$\theta ={[{w}_{\mathrm{1,1},1},{w}_{\mathrm{1,1},2}, \dots , {w}_{1,{S}_{1},{S}_{0}},{b}_{\mathrm{1,1}}, \dots ,{b}_{1,{S}_{1}},\dots ,{w}_{M,{S}_{M},{S}_{M-1}},\dots ,{b}_{M,{S}_{M}}]}^{T}$$
(7)

The number of elements of the parameters vectors (\({N}_{\theta }\)) is given by

$${N}_{\theta }= \sum_{m=1}^{M}{S}_{m}({S}_{m-1}+1)$$
(8)

For a further speed up of neural network computations, all sets of input variables can be passed to the network at once as an input matrix (\(X\)) which has the dimension \({S}_{0}\times Q\) where \(Q\) is the number of sets. Thus, every row represents an input variable and every column is a set of inputs. The outputs of the network will therefore be an \({S}_{M}\times Q\) matrix. We work through a simple example in Supplemental 1.

ANN architecture selection

ANN architecture refers to the number of hidden layers and nodes and the arrangement of nodes within hidden layers. The architecture affects the accuracy with which ANNs can approximate a given continuous function. Ideally, a minimal network that achieves the desired accuracy should be selected. Commonly, optimisation of architecture is usually done through a manual search over a very limited architecture space. This approach has a high potential to select a larger than minimal network architecture and could be time consuming.

In this work, we propose a new approach for selecting the minimal architecture. For our purpose, we assumed that the target network architecture should have fewer parameters than the original full-order QSP model (\({N}_{\theta }\) ≤ 364). This is an arbitrary simplifying assumption to provide a reasonable upper bound to the search space of ANN architectures. This corresponds to 52 neurons if one hidden layer architecture is employed (Eq. 8). An exhaustive list of all possible network architectures that satisfy the following criteria was created [25]:

  1. a)

    Has up to 52 hidden neurons arranged in 1–5 hidden layers.

  2. b)

    Number of nodes in first hidden layer ≥ input layer

  3. c)

    Number of nodes in last hidden layer ≥ output layer

  4. d)

    Number of nodes in any hidden layer ≤ preceding hidden layer.

The list of candidate architectures contained ≈ 104 networks. For our purposes here, of model reduction, candidate architectures were sorted in ascending order of increasing approximation power in order to enable a more efficient search algorithm described below. The approximation power of an architecture was assumed to be directly proportional to:

  1. a)

    The total number of nodes.

  2. b)

    The total number of hidden layers.

  3. c)

    The total number of parameters.

  4. d)

    The mean difference in number of nodes within hidden layers which represents the consistency between network width and depth [26].

A binary search-based algorithm was employed to find the minimal architecture that achieves the desired tolerance of the system predictions (performance goal) [27]. The binary search is an efficient search algorithm for finding elements from a sorted list. It is based on repeatedly dividing in half the portion of the list that contains the element of interest and excluding that half that is known not to contain it until the item of interest is found. The binary search algorithm is efficient for long sorted lists as its implementation time is proportional to the log of the list size. This means that the algorithm can accommodate larger lists without significant increase in implementation time. Steps of the search algorithm employed are illustrated in Fig. 4. To ensure the robustness of the procedure against the influence of random initialisation of parameters, the training of networks was restarted with different initial parameters for up to 5 times if a network fails to achieve a performance goal (our tolerance). Tolerance is defined in Eq. 10.

Fig. 4
figure 4

Block diagram of the binary search algorithm used to find the minimum network architecture that achieves a performance target

Full size image

Data processing

Normalisation of all input and output variables was performed by mapping the minimum and maximum values to the range [− 1, 1] using the following equation:

$${x}_{n}=2 \left(\frac{x- {x}_{min}}{{x}_{max}-{x}_{min}}\right)-1$$
(9)

where \(x\) is a vector of a variable to be normalised (a row from the input matrix \(X\)), \({x}_{n}\) is the normalised variable, \({x}_{max}\) and \({x}_{min}\) are the maximum and minimum values of \(x\), respectively. The same normalisation process was performed with the same maximum and minimum values of each input variable for all training, evaluation and validation datasets. This processing makes the training more efficient as the gradient of the network error becomes independent of the scale of the variables and prevents the activation function from being saturated [28] (see section “ANN training” below). When the trained network is put to use, all new inputs to the network are transformed the same way as training inputs while network outputs are reverse transformed back to the original units of the training data.

ANN performance and training

The ANN training and validation performed here is based on [29] with a recent application provided by [30]. Details are provided, briefly, here.

The performance of ANNs was measured by the mean squared error (MSE) of the normalised outputs as shown in Eq. 10 and Eq. 11.

$$P\left(\theta \right)=\frac{1}{{S}_{M} Q} \sum_{s=1}^{{S}_{M}}\sum_{q=1}^{Q}{{e}_{s,q}}^{2}$$
(10)
$${e}_{s,q}{=\widehat{y}}_{s,q}-{\tilde{y}}_{s,q}$$
(11)

where \({\widehat{y}}_{s,q}\) and \({\tilde{y}}_{s,q}\) are the normalised outputs from the network and pseudodata, respectively.

ANN training is an iterative process that aims to find the values of the parameter vector \(\theta\) that maximises the performance of the network (i.e. minimises the squared prediction error from Eq. 11). Every iteration involves two steps; a forward pass followed by a backward pass. In a forward pass, inputs are presented to the network to produce outputs according to Eqs. 5 and 6 and errors are calculated according to Eq. 11. The backward pass involves back-propagating errors through network layers and updating parameters in the direction that decreases the errors. Different algorithms do exist for error back-propagation and parameter update of which the Levenberg–Marquardt algorithm was used in this work, which is an efficient training algorithm for networks of sizes up to few hundred parameters [29]. Details of this algorithm are provided in Supplemental 2.

Results

Virtual data

A total of 10,000 virtual patients’ ages were randomly generated from a log-normal distribution (\(ln(age) \sim N(0.7, 1.1)\)) to ensure more training data were available at the highly non-linear region of the maturation function. For each virtual patient, random infusion rate and duration were sampled from a uniform distributions in the range of [10, 30] IU/Kg/hour, and [0, 12] hours, respectively. The dose input to the QSP model was the total infusion amount. Therefore, the simulated infusion rate variable was converted to total infusion amount and used for both QSP simulations and ANN training for consistency.

The simulated output vector consisted of QSP model predicted aPTT and aXa at the end of infusion for each patient. The simulated dataset was randomly split into a training set (80%) that was used for parameters estimation and a validation set (20%) used to test the performance of the network on external data. The same split was employed for all training experiments throughout this work. Figure 5 shows histograms of the simulated input and output variables. Four additional validation data sets were simulated where all inputs were fixed to the median value of the training data set except for one input which was varied over the range of the training data. Each additional validation data set consisted of 1000 pairs of I/O data.

Fig. 5
figure 5

Histogram of training and validation data input and output variables. The last column of the aPTT subplot is presented as numbers to reduce scale

Full size image

Training options

The combination factor \(\mu\) was initially set to 0.1 and the adjustment factor \(\beta\) to 10 (see supplemental 2 for explanation of these training parameters). Training with Levenberg–Marquardt algorithm was continued until any of the stopping criteria is satisfied. Table 1 shows stopping criteria and the proportion of experiments a criterion was satisfied.

Table 1 Stopping criteria for network training
Full size table

ANN architecture selection

The total number of the sorted candidate architectures that satisfied the criteria was 9206. The binary search algorithm required a total of 13 training experiments to find the minimum network architecture required to achieve a given performance goal. Figure 6 shows the path of the search process for different performance goals. The minimum network architecture required to approximate the coagulation model was as low as 7 nodes, 2 hidden layers, and 43 parameters which achieved an MSE of 10–3. A performance goal of 10–6 was achievable through a network with 25 nodes, 4 layers and 179 parameters. Table 2 shows the minimum network architectures required to achieve different performance goals.

Fig. 6
figure 6

Binary search process for minimal network architecture at different performance goals. First two experiments are not shown to reduce scale. Red points indicate an architecture that didn’t achieve goal and hence followed by upward search step (red lines) and vice versa for green points. The last architecture to achieves a given performance goal is the selected minimum architecture (different minimum architectures are labelled by letters A, B, C, and D). Experiment number is the number of iteration in the binary search algorithm outlined in Fig. 4 (Color figure online)

Full size image
Table 2 Minimum network architectures that achieved different performance goals
Full size table

Computational cost

The bottle neck for the proposed approach was the simulation of pseudodata for training and validation of neural networks from the original QSP model. Simulation of 10,000 training pseudodata example took 5.8 h of processing time. Training of neural networks on the pseudodata took a median of 17.3 s (range 1.9–59.9 s) per network. Table 3 summarises the training and subsequent simulation cost using the minimal neural networks of different performance levels. Of note, re-simulation of the whole of the pseudodata sets using the trained neural network models with different accuracy levels took a median of 0.02 s (range 0.018–0.027 s). Note that the simulation time is the result of a single run rather than a standard speed benchmarking test. Nonetheless, it gives a rough idea of ANN simulation speed compared to the full-order QSP model.

Table 3 Training epochs and time for neural networks with different performance levels
Full size table

Validation performance

All trained feed forward-ANNs performed on the validation dataset almost as well as on the training set as shown in Table 4. Figure 7 shows the distribution of prediction errors from various networks. It can be seen that the validation and training performance are similar in magnitude (Table 4) and precision (Fig. 7).

Table 4 Validation and training performances of different neural network architectures
Full size table
Fig. 7
figure 7

Distribution of Normalised training and validation errors of different networks architectures

Full size image

The high correlation between validation and training performances of different neural networks, as shown in Table 4, suggests that neural networks were able to be generalised to previously unseen combinations of input variables. This is further confirmed by the performances of the 4 ANNs explored here to describe the additional validation data sets, which was comparable to that of the training and main validation data set as shown in Fig. 8. Smaller networks (e.g. network A), with lower accuracy goals, had relatively more biased distribution of errors around the zero. In comparison, network D, the largest ANN considered, showed approximation errors that were distributed very tightly around zero with minimal bias and an MSE very close to the training goal. This suggests that larger networks may be able to generalise better to input combinations not seen in the training data. This could possibly have an influence on the amount of training data required to achieve a certain validation performance. However, this has not been tested here and further investigations are warranted to determine the optimal training set size for a given network size and validation performance target.

Fig. 8
figure 8

Approximation errors (as per Eq. 14 in supplement 2) of various network architectures on the additional validation data sets. Each panel represents a validation dataset. Numbers on the top right insets are the mean squared errors for the respective network architecture and validation dataset

Full size image

The full response-time profile for the two hypothetical patients as predicted by both the full-order QSP model and different networks are shown in Fig. 9. It is noted that some predictions (e.g. patient 1) were consistently over predicted by some ANNs. However, this was not a systematic bias as shown by Fig. 7 which demonstrates that the distribution of the errors are almost symmetric around zero on both training and evaluation datasets. We note also that the difference of 2–-10 s in aPTT and < 0.05 IU/mL for aXa are of no practical significance. The figure shows that profiles of both patients were predicted reasonably well. However, smaller networks were less able to accurately predict the aPTT profile for patient 1 whose age lied in the highly nonlinear region of the maturation function. Nonetheless, the accuracy improved greatly with increasing the size of the network.

Fig. 9
figure 9

Full response-time profile for two hypothetical patients receiving heparin infusion at a rate of 20 IU/Kg/hour as predicted by full-order (solid lines) and reduced-order models (dashed lines). Patient 1 (top plots) had an age of 0.5 years and a weight of 6 kg. Patient 2 (bottom plots) had and age of 12 years and a weight of 40 kg. QSP: the full-order quantitative systems pharmacology model. Letters A–D indicating different artificial neural networks. aPTT activated partial thromboplastin time

Full size image

Discussion

This work proposes a model reduction approach for a QSP model. In this work, we use the original QSP model to generate pseudodata which we then use to train and validate the ANN. The ANN here represents a non-parametric approach to model reduction [7] as it contains no mechanistic structural elements. It can however be used to simulate future data as well as potentially to be used as a controller for infusion rates of heparin. There exist other non-parametric training-based methods for function approximation, e.g., polynomial or k nearest neighbour (kNN) regression. Such methods have a similar advantage to ANNs of not having any particular requirement about the model structure. However, such methods don’t scale-up appropriately to problems with high dimensional correlated inputs which is not an uncommon scenario in QSP models [16]. Additionally, kNN regression can be prohibitively slow for large datasets and high dimensional inputs [31]. On the other hand, ANNs are better suited to handle high dimensional inputs and large training sets. Although the example used in this work consisted of a 4-dimensional input (which might be amenable to a kNN regression approach), the method proposed here provides a generic solution to any QSP model reduction problem. ANNs have characteristics that make them well-suited for construction of model-based controller systems [32]. In particular they can be trained to describe any given input–output relationship, are computationally very efficient, i.e., can be simulated and re-estimated quickly, and can be easily inverted (at least numerically), i.e., predict outputs from inputs and vice versa. The first two properties have been demonstrated in this work. Although this work did not look at the inversion methods for ANNs, the ease of simulation suggests that numerical inversion could be very efficient. Once an appropriately trained ANN is in hand it can be incorporated in a closed-loop control system as shown in Fig. 10 which outlines a proposed system for the control of the haemostatic system state through heparin infusion.

Fig. 10
figure 10

Schematic presentation of a proposed closed-loop controller to achieve and maintain a desired therapeutic response/effect by adjusting the infusion rate of the drug

Full size image

The choice of network architecture is important for achieving the desired accuracy level. Most current literature do this by a trial and error search through a very limited search space. Such process normally takes an average of 5–15 experiments [33, 34]. In this work, a more systematic search process was followed. The algorithm is based on sorting candidate network architectures first based on their rank order. The accuracy of the sorting criteria depends on many factors such as the random initialisation of weights and biases and the nature of the function being approximated. The binary search process used here was shown to be efficient when applied to a reasonably sized network given a performance target. This approach can search a much wider search space compared to a heuristic approach. We used training performance as a network selection criterion as both training and validation data were simulated under the same model with no noise being introduced into the data. Training and evaluation dataset size (\(Q\)) was selected empirically to exceed the amount of data expected to be needed to represent the input–output behaviour of interest. Further investigation of the effect of dataset size on the performance of trained ANNs is warranted as this may help to achieve further reduction in the computational cost of the approach.

The proposed model reduction technique is applicable to a wide variety of models. It is particularly useful when input to output mapping is a primary goal, which is critical for control problems. This technique can also be useful when the structure of the model is untenable to other reduction techniques as in our case example of non-continuously differentiable input–output relationships. Moreover, this technique can be considered when the structure of the full-order model is not known, such as models provided by third parties. In such cases, only the ability to evaluate the model as a set of inputs and outputs is sufficient for using an ANN. We note that the feedforward neural networks employed here do not handle sequential inputs (a changing infusion rate for example). However, the same approach can be applied to train and validate other types of neural networks that can handle such inputs, e.g. recurrent neural networks [35].

Importantly, the non-parametric nature of the reduced-order model presented in this work means that none of the full-order model parameters, structure, or mechanisms are retained in the reduced model. This is a limitation of the method when tackling problems that require simulation of the model over a range of parameter value, for example to estimate biologically relevant parameters. In such scenarios, parametric methods such as proper lumping would be useful [7]. Alternatively, parameters of interest could be included in the training data as an input variable and hence will be available in the reduced-order model for further analysis. It is also possible to approximate only certain modules of the model through a feed forward ANN leaving the rest of the model structurally intact for further analysis, yielding a hybrid partial black-box approach that is embedded within a full mechanistic model. This then allows speed and numerical efficiency for ANN modules that are not of particular mechanistic interest while retaining mechanistic structure in other areas. As with all model reduction techniques that use the QSP model to generate pseudo-data, the QSP model needs to provide a sufficient description of the system. This differs from parametric model reduction methods which although align mechanistically to the original QSP model are amenable to future parameter estimation which provides some degree of freedom in the application of the model. In theory, therefore, a parametric reduced-order model when used in estimation could outperform the original QSP model. In contrast, a non-parametric reduced-order model can only be, at best, be as good as the full-order model in describing an input–output relationship.

The multi-modular nature of the coagulation network model increases the computational cost of simulations as that involves repeated evaluation of the in-vitro components throughout a single in-vivo simulation. The repeated evaluations of a component or module within the model is computationally expensive and results in long model run times. Such problems are known as the “many-query” problem [36] which can be caused by the structure of the model, as in this example, or the type of the problem under consideration, e.g., stochastic simulation or parameter estimation. This problem becomes more significant as the number of simulations required to perform a certain task increase, e.g. during estimation. Using feed forward ANNs for approximating computationally expensive models (components or modules) can provide a substantial speed boost to these models while maintaining the desired accuracy levels making previously untenable simulation, estimation, or control problems more amenable. In this work we saw a 106 times improvement in speed when the trained ANN was used to generate pseudo-data compared to the original QSP model.

It is important to highlight that all training data-based approximation methods require enough data that is representative of the behaviour of the function to be approximated including any potential emergent properties. However, the training data do not necessarily have to include all possible combinations of input variables. In this work, patients with age-matched weights were randomly simulated and used as training data. In the additional validation data sets, each input variable was varied over the whole range of training data one at a time while other input variables were held constant. These validation data sets will certainly contain combinations of input variables that are different from those in the training data. Our results have shown that, with increasing the approximation power of feed-forward ANNs, their ability to separate the influences of input variables on outputs and hence predict previously unseen combinations of input variables increases (see Fig. 8). This suggests that larger networks (with more nodes and layers) may require less training data and can provide better interpolation power, which may reduce computational cost of simulating training data. In addition, training data used here were pseudo-data simulated from the full-order model which is much easier and cheaper to obtain than real data. This represents a significant advantage of using ANNs for model reduction. It is important to note that the use of a QSP model to simulate pseudo-data is premised on prior validation of the model.

Conclusions

In conclusion, the proposed model reduction technique using ANN enabled the development of efficient approximations to a complex model with the desired level of accuracy. The technique is applicable to any I/O relationship within the coagulation network model and other similar QSP models and provides substantial speed boost for use of such models in simulation and control purposes. Additionally, the proposed technique does not require any experimental data although it could benefit from them if available.