Introduction

Covariate modeling during population analysis is important in identifying patient characteristics that impact pharmacokinetic (PK) or pharmacokinetic/pharmacodynamic (PK/PD) parameters and may subsequently help individualize drug treatment for patient subpopulations. Various methods for covariate selection have been reported in the literature; e.g., stepwise generalized additive modeling procedure (GAM) [1], stepwise covariate modeling (SCM) [2], Wald’s Approximation Method (WAM) [3], the least absolute shrinkage and selection operator (LASSO) [4], full fixed effects model (FFEM) [5], full random effects model (FREM) [6], covariate selection based on genetic algorithm (GA) [7]. There are limited studies in the literature comparing popular selection methods [8, 9]. Wählby et al. [8] compared stepwise GAM followed by backward elimination and SCM together with different versions of these procedures. No major differences in the resulting covariate models were seen, and the predictive performances overlapped.

In general, the SCM algorithm is one of the popular algorithms used within the pharmacometrics community to select potential covariates [10]. Using the likelihood-ratio test (LRT) as selection criteria, the SCM procedure involves testing covariate relationships in a forward inclusion method (e.g., a reduction in the delta objective function value [DOFV] of 3.84150; P < 0.05 for 1 degree of freedom) and backward elimination procedure (e.g., DOFV of 6.63490; P < 0.01 for 1 degree of freedom). Details on the description of the SCM procedure can be found in Jonsson et al. [2] and Lindbom et al. [11] papers. Despite the robustness of the SCM algorithm, it is well known that SCM has several weaknesses, including competition between multiple covariates that increases selection bias (i.e., selecting the incorrect covariates), especially when there is a moderate to high correlation between the respective covariates [9, 12, 13]. These weaknesses may result in an important loss of power to identify the true covariates [12] and in selection of false covariates.

Few analyses exist in the pharmacometrics literature investigating operating characteristics of SCM in a controlled simulated setting. Ribbing et al. [12] investigated the power, selection bias, and predictive performance of population PK covariate model. A univariate covariate selection technique was used to evaluate the operating characteristics of covariate selection. The analysis found that the power (probability of identifying true covariates) increased with covariate effect size and sample size. Reduction of power was reported with increasing correlation among covariates, and selection bias was pronounced with weak covariates. In this paper, we extended the analysis performed by Ribbing et al. [12] by deriving the operating characteristics of SCM in a controlled simulated setting using a more complex structural model (two compartments model with linear absorption) and allowed the model to have up to four different covariates relations (categorical and continuous) simultaneously.

Given the popularity of SCM, findings from this analysis will provide practical value to pharmacometricians who use SCM to evaluate covariates in their routine population analysis. Furthermore, the paper aims to report practical findings when executing SCM within a Perl-speaks-NONMEM (PsN) platform.

Theoretical

Methods

Model

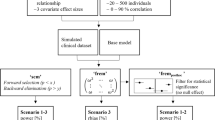
The workflow used to characterize the operating characteristics is presented in Fig. 1. A two-compartment model with first-order absorption was used to simulate the drug concentrations with the following true PK-parameter fixed-effects values: clearance (TVCL) = 0.6 L/h, intercompartmental clearance (Q) = 1.8 L/h, central volume (TVVc) = 20 L, peripheral volume (TVVp) = 80 L, absorption rate (Ka) = 0.7/h and dose = 100 mg. These parameters were coupled with the permutations of four covariates: body weight (BW) and creatinine clearance (CrCL) on apparent clearance, and BW and SEX on volume of distribution using Eqs. 1–3 that created 16 different scenarios (including the no-covariates case) as presented in Table 1. All continuous covariates (e.g., BW) were modeled using power model (see Eq. 1), whereas a linear model was used to model categorical covariates (e.g., SEX) (see Eq. 2).

Fig. 1
figure 1

Simulation workflow

Full size image
Table 1 True covariate coefficients of the 16 scenarios
Full size table
$$CL_{i} = TVCL *\left( {\frac{BW}{\text{Reference BW}}} \right)^{{\theta_{1} }} *\left( {\frac{CrCL}{\text{Reference CRCL}}} \right)^{{\theta_{2} }} *e^{{\eta_{CL,i} }}$$
(1)
$$V_{{c_{i} }} = TVV *\left( {\frac{BW}{Reference BW}} \right)^{{\theta_{3} }} *\left( {1 + sex *\theta_{4} } \right) *e^{{\eta_{Vc,i} }}$$
(2)

where

$$\left[ {\begin{array}{*{20}c} {\eta_{CL,i} } \\ {\eta_{Vc,i} } \\ \end{array} } \right] \sim N\left( {0,\varOmega } \right) \,with\, \varOmega = \left[ {\begin{array}{*{20}l} {\omega_{CL}^{2} } \hfill & {cov(CL,V)} \hfill \\ {cov(CL,V)} \hfill & {\omega_{Vc}^{2} } \hfill \\ \end{array} } \right]$$
(3)

The true model included a correlation coefficient of 0.2 between the two random effects (CL and V) and variances of between-subject variability of ωCL = 0.1 and ωVc = 0.1. A proportional residual error was used to derive the observed concentrations Cobs,ij from the true simulated concentration Cij (see Eq. 4.)

$$C_{obs,ij} = C_{ij} *\left( {1 + \varepsilon_{ij} } \right)$$
(4)

where \(\varepsilon_{ij}\) is normally distributed with mean = 0, and variance σ2 (= 0.01). For this simulation setting, reference BW was assumed to be 70 kg and reference CRCL was assumed to be 95 mL/min which represented median BW and median CRCL respectively.

Simulations

In total, 250 datasets were simulated for each scenario with a sample size of 300 subjects and 6 observations per subject corresponding to 0, 0.05, 0.1, 0.5, 1 and 3 typical half-life (t1/2). This resulted in 16 × 250 × 300 × (6) = 5,400,000 simulated drug concentration records that were used to derive the operating characteristics of SCM. The National Health and Nutrition Examination Survey (NHANES) [14] database was used to sample all covariates. Correlation between covariates observed in the original NHANES dataset was preserved across the 250 bootstrapped datasets by only keeping bootrstapped datasets that had correlation values that range from ± 0.05 of the original observed values. Five covariates (BW, BMI, CrCL, SEX, RACE) for 250 × 300 adults > 17 years of age were bootstrapped from the NHANES database. Note that SEX was coded as 0 for female and 1 for male and RACE was 0 for Asian and 1 for white.

The model without any covariate relation was considered as a reference model during the analysis. Note that the correlation coefficient between the random effects (ωCL and ωVc) in the 250 simulated datasets was controlled to be around 0.2 by selecting only those datasets with correlation values of ≥ 0.15 and ≤ 0.25.

Analysis

To assess the robustness of the models and validate the design of the simulated dataset, all simulated datasets were first re-fitted with the original model applying a stochastic simulation and estimation (SSE) approach [11, 15]. This analysis allowed us to evaluate bias and precision in parameter estimates, as measured by the relative mean root squared error (RMRSE), and model stability. Model stability was assessed by tabulating the percent of runs with successful minimization, the percent of runs with a successful covariance step, and the mean and standard error of the run condition numbers. The RMRSE was defined as:

$$* RMRSE_{{par_{k} }} = \sqrt {\frac{1}{250}\mathop \sum \limits_{i = 1}^{250} \left( {\frac{{par_{k}^{true} - par_{k}^{{est_{i} }} }}{{par_{k}^{true} }}} \right)^{2} }$$

where park is the kth (k = 1,…,Npar) parameter, \({\text{par}}_{\text{k}}^{\text{true}}\) refers to the kth parameter true value (i.e., value used in the simulation) and \({\text{par}}_{\text{k}}^{{{\text{est}}_{\text{i}} }}\) refers to estimated kth parameter based on the ith (i = 1–250) simulated dataset.

Once the robustness of the models and of the design was assessed with the SSE approach, each scenario and its corresponding 250 datasets was then analysed by a full SCM procedure, as implemented in PsN [11, 15], where all the covariates (SEX, RACE, BW, BMI and CrCL) in the dataset were investigated in both CL and Vc parameters. To enable a faster calculation, parallelization of the 250 SCM was performed, which enabled sending up to 20 different SCM processes simultaneously. Due to the high volume of outputs from SCM, a Perl-script was developed to post-process the results and derive the operating characteristics. The script could parse the different final model parameter relations and the relative estimate values from the log file.

Once all the information was retrieved, the power for each scenario to get the correct model was calculated. In addition, the power conditioned on the models that had condition number (CN) < 1000 in the SSE (powerCN) and the power conditioned on the models that had a minimization successful in the SSE (PowerMinSuc) were also calculated. Finally, the relative power to get at least one, two, etc. … out of the number of true covariates (depending on the scenario analysed) was also summarized. Note that the UNCONDITIONAL option was used in the covariance step, which allowed calculating the covariance step in Nonlinear Mixed Effects Modeling (NONMEM), even if the minimization was not successful. It should be noted that the powerCN calculation was a more stringent criterion than simply considering the successful conclusion of the covariance step.

Since the categorical covariate was parametrized by default in SCM according to the category that was the most common in each dataset, the parametrization was made explicit in the SCM configuration file to obtain consistent parametrization of the categorical covariate in all 250 datasets. One of the available options to perform SCM in PsN was to provide boundaries for all covariates estimates. The default bounds were set so that the linear categorical covariate function could not reach negative values (i.e., lower bound = − 1; upper bound = 5), whereas the power continuous covariate had very broad default boundary values (i.e., lower bound = − 1,000,000; upper bound = 1,000,000). However, the user had the opportunity to change the covariate boundaries using the SCM configuration file.

To complete the operating characteristic analysis, the RMRSE of all the population parameters, unconditional as well as conditioned on correct final covariate selection were calculated. The conditional CRMRSE was defined as:

$$* {\text{CRMRSE}}_{{{\text{par}}_{\text{k}} }} = \sqrt {\frac{1}{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{250} \delta_{\text{i}} }}\mathop \sum \limits_{{{\text{i}} = 1}}^{250} \delta_{\text{i}} \left( {\frac{{{\text{par}}_{\text{k}}^{\text{true}} - {\text{par}}_{\text{k}}^{{{\text{est}}_{\text{i}} }} }}{{{\text{par}}_{\text{k}}^{\text{true}} }}} \right)^{2} }$$
$$\delta_{\text{i}} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\, {\text{he}}\,{\text{correct}}\,{\text{covariate}}\,{\text{are}}\,{\text{selected}}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$

Note that the unconditional RMRSE relative to the covariate effects parameters is calculated using all those models that have the covariate selected, independently from the fact that in the model there was the final correct covariate selection. To assess the impact of sample size and the number of samples/subject, the same analysis was repeated in reduced sample size conditions. In particular, the same simulated datasets and scenarios were used, but fewer subjects were considered in each dataset (i.e., two conditions were analysed with 25 and 50 subjects, respectively) or fewer samples per subject (i.e., 300 subjects with one random sample per individual). Note that while reducing the number of subjects, the proportion of the categorical covariate SEX was kept the same as in the original dataset.

Software

The covariate search was performed within a nonlinear mixed effect model framework as implemented in NONMEM 7.2 [16] and SCM as implemented in PsN 4.6.0 [11, 15]. The dataset simulations and the covariate dataset generation were performed using R software [17].

Results

Figure 2 presents a Pearson correlation matrix from bootstrapped covariates of 250 × 300 simulated subjects. The size of the circles in the upper triangle are proportional to the correlation coefficients. The numbers shown in the lower triangle represent the corresponding values of the correlation coefficients. Bodyweight and BMI exhibited the strongest positive correlation of 89% followed by BMI and RACE, with a correlation coefficient of 32%. Correlation between RACE and SEX or BMI and SEX were negligible. Of note, in practice, modellers are unlikely to consider both BW and BMI as potential covariates. In our simulations, we are considering both BW and BMI to represent highly correlated covariates.

Fig. 2
figure 2

Correlation between covariates within simulated master dataset

Full size image

Stability of simulations

Prior to deriving the operating characteristics of SCM, the robustness of model and simulation settings was assessed. Figure 3 shows the robustness in terms of RMRSE of parameters obtained from an SSE approach. Results from 3 scenarios are shown (scenario 2, 9 and 14), similar trends are observed in the rest of the scenarios. In each scenario, the covariance of central volume with clearance has the highest RMRSE (ranging from 35 to 38%), followed by the variance of clearance and central volume (ranging from 20 to 22% for ω2-CL, ranging from 15 to 16% for ω1-Vc). The trend in RMRSE across scenarios was similar: RMRSEs ranged from 1 to 38% considering all scenarios, suggesting that the models could be estimated and were numerically stable. Figure 4 presents information on the model stability in the different scenarios obtained from an SSE approach. Across the various simulation scenarios, the probability of successful minimization was higher (around 90%) than the probability of successful covariance step (around 80%). Note that this result was expected, as the covariance step is computationally more challenging than the minimization step as it requires one more derivation and a matrix inversion.

Fig. 3
figure 3

RMRSE of model parameters

Full size image
Fig. 4
figure 4

Model stability information: percentage of models with successful minimization and covariance steps

Full size image

In all the scenarios, most of the runs had successful minimization and covariance steps which implies that the models can be considered numerically stable (Fig. 4). In particular, it was expected that a certain percentage of models would fail to satisfy the criteria selected (minimization/covariance step successful) and the more stringent the criteria, the higher the percentage of models not satisfying the criteria. Nevertheless, in both scenarios, the percentage was high enough to validate the assumption of numerical stability (approximately 90% and 80%, respectively).

Power to obtain the correct final model after SCM procedure

Power based on all 250 datasets, power conditioned on the condition number < 1000 (PowerCN) and power conditioned on the successful minimization (PowerMinSuc) were calculated. For a stable simulation scenario, these metrics should have been similar, because ideally, the models included in each power calculation should have been the same. Figure 5 presents the power to detect the correct final model after the SCM procedure. The three-metrics behaved similarly and the estimated power of SCM decreased (up to 25% in scenario 16), as the complexity of the true model increased (i.e., the number of covariates introduced). Table S1 presents the relative power of obtaining at least 1,…, N out of the N true covariate relations presented in each scenario. In case of 1 to 2 covariates in the true model, SCM could detect the correct covariates at least 98% of the time (with the exception of scenario 13, where the power was lower—74.4%). Note that, together with the true covariates, SCM could detect additional incorrect covariates, which is attributed to a difference between the power (Fig. 5) and the relative power values (Table S1). In the case of three true covariates in the model, SCM could detect the correct covariates 65% to 93% of the time. Finally, in the most complex scenario, there was a 50% chance that SCM could detect the four true covariates in the final model.

Fig. 5
figure 5

Power to detect the correct final model using the SCM procedure

Full size image

Summary of false relations detected during SCM

The most frequent false relations and their relative frequency for each of the 16 scenarios is reported in (Table S2). The falsely selected covariates are shown in bold. Often, the incorrect/additional covariate selected was a correlated covariate (e.g., BMI instead of BW), which suggested the that likelihood of selecting a false covariate was high for strongly correlated covariates.

Table 2 and Fig. 6 present the unconditional RMRSE for the fixed and random effects parameters, specifically the covariate effect parameter(s). The RMRSEs that were conditional on the models having correct covariate selection in SCM were very similar to the unconditional RMRSEs, with the exception of scenario 16, which had the biggest number of covariates and generally slightly higher RMRSEs in the unconditional case. The RMRSEs ranged from approximately 1% to approximately 62.3% for all fixed effects parameters, increased with the number of covariates included in the model, and were slightly higher than the RMRSE obtained with a simple re-estimation exercise with the true model (i.e., SSE). RMRSE on BSV increased with the number of covariates included in the model, with the correlation term reaching an RMRSE of almost 135% in the most complex scenario. Results from this study confirms the finding of Ribbing et al. [12]: the higher the number of covariate relations in the model, the higher the over-estimation of the covariate effects (Fig. 6).

Table 2 RMRSE (unconditional) of the fixed and random effect parameters
Full size table
Fig. 6
figure 6

RMRSE (unconditional) of the covariate parameters

Full size image

Impact of default boundary condition provided by SCM in power relations

If the default boundary condition option in SCM file input was used, a control stream such as the one presented in Fig. 7 was produced by SCM. Simulations performed in the current analysis showed that a default boundary condition in the continuous power covariate parametrization provided by SCM led to a high initial gradient, which appeared to reduce model stability, and eventually impacted power. Modifying the boundary condition helped to improve the power to detect true covariates. Figure 8 shows the resulting power with more conservative boundary conditions on the continuous covariate (− 10 to 10), which was a benefit in all scenarios.

Fig. 7
figure 7

Example of output file from SCM as produced by PsN

Full size image
Fig. 8
figure 8

Power after reducing the number of subjects in all the 16 scenarios with a new boundary condition on the continuous power covariate relation

Full size image

To understand how much the boundary conditions produced by SCM impacted model stability, an SSE with different boundary conditions was performed. The results of these SSEs were compared to the corresponding outputs from the first SSE analysis that had no boundary implemented in the covariate coefficients. Based on results shown in Table 3, reducing the interval of the boundary condition (e.g., [− 10, 10] for continuous covariates) improved the model stability. In particular, when using the default boundary condition, the number of datasets with successful minimization across the different scenarios was very low compared to no boundary or a narrower boundary proposed. On the contrary, the number of datasets with rounding errors was extremely high when the default boundaries were used. Note that scenario 2 was not influenced by the boundary conditions, as it referred to simulations with one categorical covariate. Moreover, it seemed that in most of the scenarios, the use of a narrower boundary was beneficial for model stability, with respect to no boundary at all. In particular, given that the median CNs in the different scenarios are quite similar between the narrower boundary and the no boundary condition, note that the CN standard deviations for scenarios 2, 3, 5, 6, 8, 9 10, 13, 14 and 16 (i.e. the majority of the cases) obtained with stringent boundaries were smaller than the ones obtained with no boundaries.

Table 3 Summaries of model stability information after an SSE analysis using three different boundary conditions on the continuous covariate power parametrization
Full size table

Impact of sample size on power

One of the key challenges of designing trials is to establish which sample size (e.g., number of subjects, number of samples) is needed to assess covariate effects with a certain power. To address this question, two subsets with a smaller number of subjects (i.e., 25 and 50 subjects) were extracted from the analysis datasets and the power of identifying true covariates was quantified in the 16 different scenarios. A similar reduction exercise on a smaller subset of scenarios was performed with respect to the number of samples: in four randomly selected scenarios, the datasets were reduced to one random sample for each subject. Note that a new narrower boundary condition (− 10 to 10) for the continuous covariate was used in all of these analyses. Figure 8 shows a clear reduction of power with respect to sample size reduction (i.e. number of subjects): in all scenarios the power obtained with less number of subjects is smaller than the power obtained with more subjects. Figure 9 shows more detail of the reduction of power with respect to model complexity. The more complex the model (i.e., the number of covariates included in the final model), the less power there was to identify the correct final model. Table 4 shows a clear reduction of power with reduced sample size. In all the four scenarios, the power obtained in the full dataset was higher than the one obtained with a reduced dataset (one sample per subject). The power was also influenced by model complexity (i.e., the number of covariate relations). The more complex the model, the greater the reduction in the power with reduction of number of samples.

Fig. 9
figure 9

Impact of reduction of sample size on power lumped by model complexity (i.e. number of covariates) with a new boundary condition on the continuous power covariate relation

Full size image
Table 4 Impact of reducing the number of samples per subject on power with a new boundary condition on the continuous power covariate relation
Full size table

Discussion

The SCM procedure has been criticized for selection bias that could result in failure to identify important covariates, while unimportant or incorrect covariate effects could appear to be clinically relevant [3]. Despite these issues, SCM remains one of the most used methods within the pharmacometrics community to select covariates that can potentially impact PK and PK/PD parameters [3, 10].

In this paper, we investigated the operating characteristics (i.e., accuracy, precision, and power) of the SCM procedure in a controlled simulated setting. All covariates within the simulated dataset were sampled from NHANES database, providing a natural way of preserving correlation between covariates being used in the analysis. Sixteen scenarios ranging from no covariates (the simplest case) to a maximum of four covariates (the most complex case) were explored. Note that SCM was run using an initial set with some true and some false covariates, including a highly correlated covariate (i.e., BMI).

As expected, our simulation demonstrated that the power to detect true covariates decreased with model complexity. The inclusion of highly correlated covariates in the final model indicated that the data did not allow discrimination between the competing covariates [4]. Screening highly correlated covariates is a classic challenge for most covariate modelling. LASSO for example, would include more correlated covariates than SCM [4]. FFEM cautions not to include a covariate that has correlation greater than 0.5. The inclusion of highly correlated covariates destabilizes the inversion of gradient matrix, causing instability in parameter estimation. The more complex the model containing highly correlated covariates, the more pronounced the instability of parameter estimation, leading to a decrease of power to detect the true covariates. Our results are consistent with simulation results reported by Bonate [13] showing the impact of collinearity on PK parameter estimates. Bonate reported that for correlation between two covariates greater than 0.5 the population parameters showed an increase in bias and standard error, and that for correlation greater than 0.75, the standard error of parameter estimates was too large to declare statistical significance. As a result, when dealing with correlated covariates, it is advisable to avoid having them both in the search.

Simulations performed in the current analysis showed that a default boundary condition in the continuous power covariate parametrization provided by SCM led to higher initial gradient, which appeared to reduce model stability and eventually reduced power. A stricter boundary condition helped to improve the power to detect true covariates. Note that the new boundary condition [− 10, 10] chosen for the power term did not limit the estimation process, as the relative parameter space was broad enough to cover all plausible values for the parameter. When the maximum likelihood function had a strictly convex shape, there was a unique stationary point, which was the global minimum. In this case, the amplitude of boundary condition did not have much effect on the power to detect the correct covariates. This convexity of the maximum likelihood function seemed to degenerate with the model complexity, which led to several local minima. In this case, the larger the search space (i.e., boundary condition), the easier it is for the algorithm to assign a local minimum as the global maximum. A stricter boundary condition would have reduced the number of local minima of the maximum likelihood function, and hence increased the chance of determining the global minimum. In practice, to evaluate the potential impact of the boundaries in the SCM results, the user should perform sensitivity analyses, where the boundary conditions are varied and the final covariate model results are compared.

Sample size combined with model complexity impacted the power of finding the correct covariates, which increased the selection bias in the estimated covariate coefficients. These results were consistent with Ribbing et al. findings [12].

SCM has been very useful for the pharmacometrician community and is expected to continue to be used despite its challenges. However, pharmacometricians should be cautious when determining correlated covariates and model complexity. In this case, large sample sizes and better-defined boundary conditions were helpful. The results of these simulations also highlighted the importance of having a large enough sample size. However, future studies are needed to be able to draw more general conclusions on the power by investigating the impact of different and more complex model structures.

Conclusions

  • Model complexity and sample size had a notable impact on the power to identify the true covariate model and the accuracy of the parameter estimates.

  • Highly correlated covariates had a high likelihood of being incorrectly selected by SCM.

  • The default boundary condition provided in PsN by SCM for the continuous covariate power model impacted the final SCM selection of covariates.