Lorentz Force Eddy Current Testing: a Prototype Model

Abstract

We report an investigation of the motion of a free-falling permanent magnet in an electrically conducting pipe containing an idealized defect. This problem represents a highly simplified yet enlightening version of a method called Lorentz force eddy current testing which is a modification of the traditional eddy current testing technique. Our investigation is a combination of analytical theory, numerical simulation and experimental validation. The analytical theory allows a rigorous prediction about the relation between the size of the defect and the change in falling time which represents the central result of the present work. The numerical simulation allows to overcome limitations inherent in the analytical theory. We test our predictions by performing a series of experiments. We conclude that our theory properly captures the essence of Lorentz force eddy current testing although a refinement of the experiment is necessary to reduce the discrepancy to the predictions. In spite of its apparent simplicity the present system can serve as a prototype and benchmark for future research on Lorentz force eddy current testing.

1 Introduction and Motivation

The detection and localization of surface and subsurface defects becomes more and more important nowadays. Electromagnetic techniques for nondestructive evaluation such as the well-known eddy current testing technique [1] represent a particularly powerful approach because they are contactless and can be applied to a wide variety of electrically conducting materials. The present work is devoted to an alternative version of eddy current testing whose origin can be traced back to [2, 3] and [4] and for which the authors of [3] and [5] have proposed the term “Lorentz force eddy current testing” (LET). The specific aim of the present paper is to define and solve a conceptually simple model which improves our understanding of the physics underlying LET.

In the traditional version of eddy current testing an alternating (AC) magnetic field is used to induce eddy currents inside the material to be investigated. If the material contains a crack or flaw which make the spatial distribution of the electrical conductivity nonuniform, the path of the eddy currents is perturbed and the impedance of the coil which generates the AC magnetic field is modified. By measuring the impedance of this coil, a crack can hence be detected. Since the eddy currents are generated by an AC magnetic field, their penetration into the subsurface region of the material is limited by the skin effect. The applicability of the traditional version of eddy current testing is therefore limited to the analysis of the immediate vicinity of the surface of a material, usually of the order of one millimeter. Attempts to overcome this fundamental limitation using low frequency coils and superconducting magnetic field sensors have not led to widespread applications.

LET is based on generating eddy currents by setting a direct (DC) magnet system, usually a permanent magnet, into relative motion with respect to the material to be investigated. This approach has the great virtue that the eddy currents penetrate the material to a much greater depth¹ than with traditional eddy current testing [6–8]. A perturbation of the eddy currents is detected through its influence upon the Lorentz force acting both inside the material and inside the permanent magnet. If the permanent magnet is swept across a crack, the Lorentz force acting upon it will experience a short breakdown whose detection is the key to successful implementation of LET. An advantage of the fact that the measurement is reduced to a force measurement is that LET in its wider sense may offer potential benefits for some applications by introducing an alternate method of inducing currents and sensing defects, and is worthy of deeper investigation.

In order to understand the underlying physics of the LET problem it is desirable to formulate and study highly simplified models which can be solved analytically. The definition of such a model is the main aim of the present paper. In addition to its enlightening character, the present model will serve as a benchmark for future LET computations.

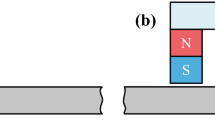
Our model is a slight modification of a popular educational experiment sketched in Fig. 1(a). The experiment is often used to introduce Faraday’s law of induction and consists of dropping a permanent magnet through a vertical electrically conducting nonmagnetic pipe [9–12]. Due to the relative motion eddy currents are induced in the pipe walls. Furthermore, the magnet is exposed to a braking force that is decelerating its free fall to a constant and relatively low velocity. The effect can be recognized by the significantly longer falling time of the magnet compared with its free fall. The braking effect is caused by the Lorentz force. By Newton’s third axiom “actio = reactio” [13] the same braking force acts on the pipe as well, but in opposite direction. This can be used to measure the resulting Lorentz force distribution as a function of time. The same effect occurs when moving an electrically conducting solid state body or liquid metal in the vicinity of a permanent magnet [3, 14]. The resulting force acting on the magnet system can be measured and used to determine the relative velocity, material properties or defects within the material.

Fig. 1

Permanent magnet and pipe with different defect shapes, (a) no defect, (b) idealized axisymmetric defect, (c) non-axisymmetric defect. The present work is devoted to case (b)

We modify the educational experiment in a way that is sketched in Fig. 1(b). We introduce a highly simplified defect which is axisymmetric and consists of replacing a section of the electrically conducting pipe with an electrically insulating part represented by cutting off a piece of the pipe. When the falling magnet passes the region of the defect, the eddy currents will be weakened, the braking Lorentz force will decrease and the magnet will temporarily increase its falling speed. As will be demonstrated below, this problem is amenable to rigorous analytic treatment and efficient numerical simulation and provides a number of unexpected phenomena which are useful for further development of LET. Although the present model has no direct practical application, we believe it is helpful in elucidating the basic laws of LET and in understanding more complex situations such as the one shown in Fig. 1(c).

The structure of the remainder of the paper is as follows. In the following section we formulate the mathematical model and give an outline of its solution. In Sect. 3 we describe the results of analytical and numerical solutions of the ordinary differential equation that we have obtained for the velocity of the falling magnet as a function of time. Section 4 contains results of numerical simulations of the full electromagnetic problem which are intended to check the validity of the one-dimensional model and to highlight one aspect which is absent in the simplified model, namely the deformation of the magnetic field lines at high falling speeds. In Sect. 5 we compare the analytical and numerical models. Section 6 is devoted to the description of a series of experiments which we have performed to validate our theoretical predictions. Section 7 summarizes our conclusions and indicates some problems that would be useful to investigate in future.

2 Definition of the Model

The problem to be investigated here is defined in Figs. 1(b) and 2. We consider an infinitely long electrically conducting nonmagnetic pipe which contains an idealized defect. The defect consists of a gap with prescribed height 2h in which the electrical conductivity is assumed to be zero. This problem can be considered in two different albeit physically similar formulations. The “LET-problem” refers to a magnetic dipole located at a fixed position and a pipe containing the idealized defect, referred to as the defective pipe, which moves with constant velocity relative to the magnetic dipole. When the defect moves across the location of the dipole, the Lorentz force acting upon the dipole is temporarily changed. The goal of the analysis of the LET-problem is to predict the time-dependent longitudinal component of the Lorentz force F(t) acting upon the dipole and to determine the unknown height of the defect from the measurement of F(t). The “creeping-magnet problem” refers to the case when the defective pipe is at rest and the magnetic dipole is released to fall through the pipe. If the pipe contains no defect, the magnetic dipole falls with a constant velocity. In the presence of the defect the falling velocity of the magnetic dipole is temporarily modified. The goal of the analysis for this case is to predict the time-dependent position z(t) of the falling magnetic dipole and to determine the unknown width of the defect from z(t) or from the velocity v(t). In the present work we will focus on the creeping magnet problem, having in mind that the results contain the LET-problem as well.

Fig. 2

Geometrical sketch containing the characteristic parameters, (a) mathematical model, (b) real geometry

2.1 Analytical Model

The analytical model of a magnet falling through an electrically conducting nonmagnetic pipe without defect has been derived in [15] and has been applied in [9]. Nevertheless it is a special case of the creeping-magnet problem containing an idealized defect, which we present here. The solution of this special case can be used for the verification of the creeping-magnet problem.

To describe the movement of the falling magnet we use its instantaneous position z(t) and its velocity $v(t) = dz/dt = \dot{z}$. We use a cylindrical coordinate system (ρ,φ,z) for the computation of the eddy currents that is attached to the dipole and that is shown in Fig. 2(a). The pipe is assumed to be infinitely long and is characterized by its electrical conductivity σ, inner diameter 2R, and by its wall thickness δ. We shall assume that the wall is thin, i.e. δ≪R. To determine the eddy currents induced in the pipe we need the distribution of the magnetic field of the falling magnet. We assume that the magnet is a point dipole which gives a magnetic field of

$$ \mathbf{B}=\frac{\mu_0}{4\pi}\cdot \biggl\{3\cdot\frac{ (\mathbf{m}\cdot \mathbf{r} ) \mathbf{r}}{r^5}- \frac{\mathbf{m}}{r^3} \biggr\} $$

(1)

where r is the field point and μ ₀ the absolute magnetic permeability. The magnetic dipole is characterized by its magnetic moment

$$ \mathbf{m} = - m\cdot\mathbf{e}_z $$

(2)

This represents the so-called impressed or primary magnetic field.

The magnetic flux density of a dipole is decaying in space with r ⁻³ (see Eq. (1)). Since the wall thickness of the used pipe is assumed to be small the variation of the magnetic field across the pipe walls can be neglected. Additionally, the problem at hand is axisymmetric. Thereby, only the radial component of the imposed magnetic field needs to be considered to compute the eddy currents (cf. Fig. 2(b)). Using the dimensionless position coordinate $\xi= \frac{z}{R}$ the B _ρ can be written as

$$ B_\rho= -\frac{3 \mu_0 m}{4 \pi R^3}\cdot\frac{\xi}{ (1+\xi^2 )^{\frac{5}{2}}}. $$

(3)

The relative movement between the dipole and the pipe induces eddy currents that are governed by Ohm’s law for moving electrically conducting materials which has the form

$$ \mathbf{j}=\sigma\cdot (\mathbf{E}+\mathbf{v}\times\mathbf{B} ) $$

(4)

Moreover, if there is no source or sink of electric currents in the pipe, the distribution of the induced eddy currents is purely azimuthal and the electric field is zero. In this case the φ-component of Ohm’s law simplifies to j _φ =σvB _ρ and the eddy currents become

$$ j_{\varphi} = -\frac{3 \mu_0 m \sigma \dot{z}}{4 \pi R^3}\cdot \frac{\xi}{ (1+\xi^2 )^{\frac{5}{2}}}. $$

(5)

These currents give rise to a secondary magnetic field. The resulting magnetic field represents a superposition of both, the primary and the induced secondary field. As will be discussed in Sect. 2.2, the magnetic field associated with the induced eddy currents is much smaller than the applied primary magnetic field. Therefore it can be neglected.

The resulting Lorentz force density can be calculated using f=j×B. Integrating the Lorentz force density over the volume of the pipe leads to the total Lorentz force

$$ \mathbf{F}=\iiint_{(V)} (\mathbf{j}\times\mathbf{B} ) dV $$

(6)

acting both on the pipe and (in opposite direction) on the magnet. Taking all the assumptions into account, the resulting force has only a z-component which is given by

$$ f_{z}=- j_{\varphi} B_\rho = -\frac{9 \mu_0^2 m^2 \sigma \dot {z}}{16 \pi^2 R^6}\cdot \frac{\xi^2}{ (1+\xi^2 )^5}. $$

(7)

Carrying out the integration we obtain finally

$$ F(z)=F_0+\frac{9 \mu_0^2 m^2 \delta \sigma \dot{z}}{8 \pi R^4}\int_{\xi'=\frac{z-h}{R}}^{\xi'=\frac{z+h}{R}}{ \frac{\xi'^2}{ (1+\xi'^2 )^5}} d\xi' $$

(8)

for the total Lorentz force acting upon the pipe where we have introduced the abbreviation

$$F_0 = - \frac{45 \mu_0^2 m^2 \sigma \delta \dot{z}}{1024 R^4}. $$

The Lorentz force consists of two contributions. The term F ₀, corresponding to a force pointing upward, describes the force which acts on a pipe without defect in opposite direction. The second term has a positive sign and hence reduces the magnitude of F ₀. This term represents the reduction of the Lorentz force due to the presence of the defect. Notice that this term vanishes quickly as soon as the distance z between the magnet and the defect becomes larger than the characteristic size h of the defect. When the magnet falls across the defect, its movement will hence be affected only in the immediate vicinity of the defect.

2.1.1 Differential Equation of Motion

The differential equation for the instantaneous position of the dipole z(t) is obtained by taking the z-component of Newton’s equation of motion in the form

$$ M \ddot{z} =F(z)+M g $$

(9)

where F(z) is given by Eq. (8) and where the term Mg represents the gravitational force acting on the magnet with g being the acceleration of gravity. If the magnet is far away from the defect, the main contribution to F(z) comes from the term F ₀ and the dipole moves with a constant velocity v ₀. This velocity can be computed by setting the left-hand side of Eq. (9) equal to zero and using F ₀=−Mg. A straightforward computation leads to the result

$$ v_0 = \frac{1024 M g R^4}{45 \mu_0^2 m^2 \sigma \delta} $$

(10)

To reduce the number of variables we normalize the quantities on the basis of the scales R and v ₀/g for length and time, respectively, which are characteristic for the given problem. As a consequence the time derivatives contain no time t anymore but a dimensionless time parameter τ that can be calculated according to

$$d\tau= \frac{g}{v_0} dt $$

Finally, we obtain the differential equation of motion for the nondimensional coordinate ξ=z/R, the nondimensional velocity $\dot {\xi}=d\xi/d\tau$ and the nondimensional acceleration $\ddot{\xi}=d^{2}\xi /d\tau^{2}$ of the falling magnet

$$ \ddot{\xi}+ \biggl[1-\frac{128}{5\pi} \int_{\xi'=\xi-\beta}^{\xi '=\xi+\beta}{ \frac{\xi'^2}{ (1+\xi'^2 )^5}} d\xi' \biggr]\dot {\xi}=\alpha. $$

(11)

Equation (11) is a nonlinear ordinary differential equation of second order containing two dimensionless parameters, namely the forcing parameter $\alpha=v_{0}^{2}/(g R)$ and the dimensionless defect height β=h/R. The derivation of this equation constitutes a key result of the paper. To highlight the mathematical structure of the obtained equation it can be rewritten as

$$\ddot{\xi} + f (\xi, \beta )\cdot\dot{\xi} = \alpha. $$

The function f(ξ,β) represents a position-dependent electromagnetic friction coefficient which differs from its unperturbed value f=1 only in a small neighborhood of the location ξ=0 of the defect. A peculiarity of the present problem consists of the fact that the value of this coefficient is determined by an integral over the whole pipe. Before passing on the solution of this model it is useful to discuss the physical meaning of the parameters α and β briefly.

All geometrical data and material properties are contained in α. This parameter can be interpreted as a forcing parameter since it appears on the right-hand side of Eq. (11). If there is no defect, this equation reduces to $\ddot{\xi}+\dot{\xi}=\alpha$ whose solution ξ=αt describes steady electromagnetically damped motion of the magnet with constant downward velocity α. Notice that α represents the ratio between the unperturbed velocity v ₀ and the velocity $\sqrt{g R}$ which a freely falling body would attain in the absence of electromagnetic damping after having traversed a height R/2. Hence, small values of α correspond to low velocity and strong electromagnetic damping whereas higher values of α indicate a higher velocity and weak damping. The “geometry” of the defect is described by the parameter β where β=0 represents the pipe without defect. The solution of Eq. (11) will be extensively discussed in Sect. 3.

2.2 Numerical Model

The analytical model developed so far is suitable for the fast determination of the falling time and the characteristic Lorentz force profiles. It was derived using several simplifications which lead to lower accuracy than a full three-dimensional electromagnetic field computation would provide. To take into account the finite shape of both, the pipe and the magnet, and the effect of the secondary magnetic field we have additionally developed a numerical model. This enables us to solve the given problem for thick pipes, arbitrary shapes of the permanent magnet and high falling velocities. The variation of the magnetic field within the pipe walls is properly taken into account as well.

We use the finite element method (FEM) to simulate the real geometry of the given problem. The point dipole is replaced by a spherical permanent magnet. The conducting pipe is modeled as a hollow cylinder with finite wall thickness.

The analysis has been divided into two parts. The first part comprises the consideration of a nondefective pipe. As a result the falling time of the magnet through the pipe is determined. The calculated falling time is used for verification and validation of the numerical simulations. In the second part an ideal defect is introduced into the pipe walls. The main aim of this analysis is to estimate the nondimensional falling time difference Δτ with respect to the nondefective pipe.

2.2.1 Model Parameters

The geometry used for the numerical simulation is presented in Fig. 2(b), comprising the same geometrical parameters presented in Fig. 2(a). The model consists of the falling spherical permanent magnet, the cylindrical pipe and the surrounding air region. The parameters describing the magnet are its radius (R _mag), magnetization (m) and mass density (ρ). The magnetization direction is considered to be coaxial with the z-axis of the used coordinate system. The pipe is represented by its finite length (L), inner radius (R), thickness (δ) and electrical conductivity (σ).

In case of a defective pipe, an ideal defect is modeled as a section of the pipe where conductivity is zero as in the analytical model. It is characterized by its height (2h), (see Fig. 2(b)).

If the magnet moves parallel to the model axis, the induced eddy currents flow in the azimuthal direction (see Fig. 2(b)). Due to the circular distribution of the current density, a 2D axisymmetric model is used instead of a complete three-dimensional setup. This reduces the computational time considerably.

The pipe is assumed to be long enough so that an infinite length can be considered. The entire dynamic behavior of the Lorentz force in time is calculated using two numerical approaches, namely (i) the quasi-static approximation (QS), where the magnetic field reacts instantaneously to the motion of the crack across the magnet and (ii) the transient model (TR), where the magnetic field diffusion time (δ ² μσ) is taken into account. For the transient approach the magnet is considered to be in relative motion to a stationary defective pipe, whereas for the quasi-static approach the magnet is at rest and the pipe is set to move accordingly.

The falling time of the magnet is calculated after reaching the equilibrium state using the following equation

$$ t_0 = t_e + \frac{ (L-L_e )}{v_e} $$

(12)

where t _e is the time needed to reach the equilibrium state, v _e is the calculated equilibrium velocity and L _e is the traveled distance during the time t _e .

2.2.2 Governing Equations

The braking force on the magnet can be calculated using Eq. (6). Therefore, both the magnetic field and the induced eddy currents, have to be determined. The magnetic flux density in the presence of moving conductors can be described by the magnetic field transport equation or the magnetic field induction equation [16]:

$$ \frac{\partial\mathbf{B}}{\partial t} = \nabla\times (\mathbf{v}\times \mathbf{B} ) + \frac{1}{\sigma \mu} \nabla^2 \mathbf{B} $$

(13)

where B=B ₀+b represents the total magnetic field which is the superposition of the primary magnetic field B ₀ and the secondary magnetic field b. Furthermore, μ is the magnetic permeability and v is the velocity of the moving pipe. Note that this is a general equation valid for both, the magnet and the pipe in motion.

So far, in the analytical model, the effect of the secondary magnetic field was neglected. Nevertheless, it is reasonable to expect either explicitly or implicitly, that the pipe slightly perturbs the magnetic field of the magnet. It can be shown that the extent of perturbation depends on several parameters, namely the relative velocity between the magnet and the pipe, the pipe’s conductivity and thickness [16]. In order to reduce the number of dependent variables, the induction equation is normalized based on the scales of length (δ), velocity (v) and time (δ/v). The result is the nondimensional form of the induction equation (see Eq. (14)).

$$ \frac{\partial\mathbf{B}_*}{\partial t_*} = \nabla_* \times (\mathbf {v}_*\times\mathbf{B}_* ) + \frac{1}{R_m} \nabla^2_* \mathbf{B}_* $$

(14)

Subscript ∗ indicates the dimensionless quantities and R _m represents the magnetic Reynolds number defined by

$$ R_m = \mu \sigma v \delta $$

(15)

Using the obtained nondimensional form of the induction equation, the magnetic field perturbation can be analyzed by only one parameter, i.e. R _m . In case of R _m ≪1, the convective term (first term on the right hand side) and the transient term (left hand side) can be neglected with respect to the diffusive term (second term on the right hand side), and the induction equation becomes a diffusion equation. In case of R _m ≫1, convection of the magnetic field dominates over its diffusion and the resulting magnetic field is strongly altered due to the pipe in motion. As a result, the magnetic field is gradually expelled from the pipe walls. This effect is referred to as the skin effect.

Whereas our analytical model is valid for R _m ≪1, we wish to take into account the deformation of the magnetic field lines for high falling speeds in the numerical model and use it for finite values of R _m . We shall therefore assume that the magnetic field reacts instantaneously when the crack is moving across the magnet in which case the time dependent term in Eq. (13) can be neglected. However, we retain the right-hand side of this equation thereby allowing for finite R _m .

Taking all the assumptions into account, the induction equation can be simplified to its final static form:

$$ 0 = \nabla\times (\mathbf{v}\times\mathbf{B} ) + \frac{1}{\sigma \mu} \nabla^2 \mathbf{B} $$

(16)

The derived Eq. (16) together with Eq. (9) forms the final set of equations describing the given problem. This represents the QS approach [5]. The same approach is used in both cases, for the nondefective and for the defective pipe.

The numerical implementation of this approach has been achieved using Matlab and Comsol Multiphysics as FEM solver. Furthermore, magnetostatics module of Comsol has been used to estimate the resulting magnetic field, induced eddy current distribution and the total Lorentz force acting on the magnet (see Eq. (6)).

In the case of a pipe without defect, the model geometry is not changing in time. There are no spatial material changes during the simulation, and thus no remeshing of the computational domain is necessary. The equation of motion (see Eq. (9)) is solved using the finite difference scheme implemented in Matlab. For every time step, the estimated magnet velocity is used for the calculation of the corresponding Lorentz force using the Comsol FEM solver.

For a pipe with an ideal defect the same QS approach is used. To simulate the motion of the pipe the defect is moved with the according velocity

$$ \Delta z (t ) = v (t )\cdot dt. $$

(17)

As a consequence, the model geometry is changing in time which requires additional remeshing of the computational domain in every time step. It results in a longer computing time compared to the nondefective pipe.

The computation is performed iteratively until the values for the Lorentz force and the falling velocity converge. After reaching the convergence criterion the falling time of the magnet and the drop time difference are calculated using Eq. (12).

Strictly speaking, the QS approach is only valid for the investigation of the problems with no spatial material changes in time. It has been shown in [5] that this approach can be successfully applied for the problems involving relatively slow spatial material changes, which is true for the so-called creeping-magnet problem only.

In order to quantitatively evaluate the limits of the QS approach used as a numerical model for high magnetic Reynolds numbers (R _m ≫1) and for a pipe with defects, we consider the so-called transient approach (TR). When R _m ≫1, we can no longer neglect the finite diffusion time and therefore we have to include the time derivative in the magnetic induction equation. For the numerical implementation of the TR approach, we assume the magnet to be in motion relatively to a stationary conducting pipe. With this assumption, the first term on the right hand side of the magnetic induction equation goes to zero and the time derivative of the magnetic field is balanced by its diffusion (see Eq. (18)).

$$ \frac{\partial\mathbf{B}}{\partial t} = \frac{1}{\sigma \mu} \nabla^2 \mathbf{B} $$

(18)

Equation (18) is implemented inside COMSOL Multiphysics using the moving mesh technique [17]. The moving mesh introduces interpolation of the magnetic field between the fixed mesh on the one side and the moving mesh on the other side, providing the coupling of the field between the assembly.

3 Results of the Analytical Model

In this chapter we will discuss the solutions of Eq. (11) for three distinct cases. We start with the general case where the equation has to be solved numerically. This discussion will be followed by an analysis of the narrow defect approximation which is amenable to analytic treatment and is mostly relevant for the comparison with experiments. We will finally discuss the opposite limiting case of a wide defect. In all three cases, the central question is the prediction of the trajectory ξ(t) (or $\dot{\xi }({\xi})$) as well as the falling time difference and the trajectory expansion.

3.1 General Case

We find it illustrative to provide the solutions in Fig. 3 in order to highlight the role of the parameters α and β. Figure 3 shows selected numerical solutions of Eq. (11) in the form $\dot{\xi }=f(\xi)$ representing the velocity of the falling magnet as a function of the position. This representation is more convenient for the present work than the seemingly more natural form ξ=f(τ) because it allows us to compare the falling speeds of magnets at one particular location relative to the defect. Figure 3(a) shows the solution for variable α at a fixed value β=0.01 corresponding to our experiments to be discussed in Sect. 6 whereas in Fig. 3(b) α=0.0592 is kept constant and β is changed. One apparently counterintuitive feature is common to all solutions shown in Fig. 3. Based on qualitative reasoning one may expect that the presence of the defect would lead to a temporary rise in velocity, and that the curve $\dot{\xi }=f(\xi)$ would therefore have a bell-shape with a single maximum velocity close to the location of the defect, i.e. close to ξ=0. By contrast, all curves shown in Fig. 3 have two maxima rather than one. This indicates that the falling magnet experiences two phases of acceleration when passing the defect. The reason for this behavior can be easily understood by invoking Fig. 2(b) in which the qualitative structure of the eddy currents is shown. Figure 2(b) shows that the eddy currents induced by the moving magnet consist of two structures with opposite orientation. This leads to the fact that the Lorentz force has two minima rather than just one and that $\dot{\xi}=f(\xi)$ has two maxima as long as the gap is not too wide.

Fig. 3

Velocity distribution in the defect region as obtained from the solution of Eq. (11) without any further approximations, (a) β=0.01, different α, (b) α=0.0592, different β

Figure 3(a) shows that $\dot{\xi}=f(\xi)$ is symmetric for small values of the forcing parameter. When α increases, the velocity distribution becomes asymmetric due to the increasing influence of inertia for high velocities. Bigger defects cause an asymmetry in the velocity distribution as shown in Fig. 3(b). There, the acceleration phase is dominating when the magnet is experiencing a decrease of the breaking Lorentz force due to the presence of a defect.

The resulting trajectory of the dipole is shown in Fig. 4. When the unperturbed trajectory represented by the full line is compared with the trajectory in the presence of the defect represented by the dotted line, two features become apparent. In a given time the magnetic dipole travels a distance that is Δξ longer than in the unperturbed case. From another point of view, the dipole arrives by Δτ earlier at any position that is sufficiently far “downstream” of the defect. We shall refer to Δτ as the falling time difference whereas Δξ is the trajectory expansion compared to the nondefective pipe.

Fig. 4

Path of the magnetic dipole with and without a defect in the pipe; Δτ—time shift, Δξ—trajectory expansion, where α=0.0592

Since the falling time difference will be measured in our experiments, it is a particularly important quantity. It is used to detect and identify the defect. To get a first idea of the characteristic change of falling time for any size of the defect we investigate the motion in the defect region. Therefore we integrate Eq. (11) for τ=[−τ ^∗,τ ^∗] where τ is the nondimensional time scale and −τ ^∗ the nondimensional time when entering the defect region. Considering the width of the defect region to be $2 \beta= \frac{2\cdot h}{R}$ (Eq. (11)) and the flyby time Δτ=2τ ^∗ we obtain Eq. (19).

(19)

An application of an appropriate Heaviside function and the evaluation of the generated integrals leads consequently to

(20)

(21)

Since 2β is the normalized defect length and Δτ the flyby-time we conclude that the dipole’s trajectory increases by the same length as the size of the defect and the flight time shortens by the unperturbed flyby-time. We have shown analytically that the falling time difference is increasing linearly with the defect height and that Δξ and Δτ obey the rigorous relations

(22)

(23)

This analysis is performed under the assumption that the pipe contains only one idealized defect. Moreover, only the presence and the size of a defect is determined, but not its location.

In order to simplify the equation of motion and gain more information about the behavior of the dipole motion, an analysis dealing with two extreme defect sizes is performed. This is referred to as the so-called narrow and large defect approximation.

3.2 Narrow Defect Approximation

Assuming a very small defect, compared with the radius of the pipe, the equation of motion can be further simplified. Stating that β≪1, the integral appearing in Eq. (11) is approximated as the integrand itself multiplied by the length of the integration domain. This leads to the simplified equation

$$ \ddot{\xi} + \biggl[1-\frac{256 \beta}{5 \pi} \frac{\xi^2}{ (1+\xi^2 )^5} \biggr] \dot{\xi} = \alpha $$

(24)

that can be rewritten as

$$ \ddot{\xi} + C (\xi, \beta ) \dot{\xi} = \alpha $$

(25)

where

$$ C (\xi, \beta )= \biggl[1-\frac{256 \beta}{5 \pi} \frac{\xi^2}{ (1+\xi^2 )^5} \biggr]. $$

(26)

Using the narrow defect approximation (NDA), the dynamics of the falling dipole are equivalent to the motion of a mass with a position-dependent linear friction coefficient. Its value is given by the term C(ξ,β) in Eq. (26). Figure 5 shows the spatial structure of this coefficient which can be considered as an electromagnetic friction coefficient in comparison with the perturbation coefficient f(ξ,β) of the complete solution. Notice that in the framework of the NDA, the width of the defect β only affects the amplitude but not the shape of the position-dependent part of C(ξ,β). It should also be emphasized that C(ξ,β) is symmetric with respect to the location of the defect and C(ξ,β=0)=1 as well as C(ξ=0,β)=1. These properties are consequences of the assumption that the magnetic Reynolds number is small and would disappear if the theory would be extended to finite R _m . By contrast, our numerical simulations to be described in Sect. 4 take into account the finite value of R _m .

Fig. 5

Comparison of the position-dependent perturbation of the dynamics of the motion between the complete solution and the NDA where α=0.0592 and (a) β=0.05, (b) β=1

Using the principle of the perturbation method, according to

$$ \xi (\beta, \tau ) = \xi^{(0)} (\tau ) + \beta \xi^{(1)} (\tau ) + o \bigl(\beta^2, \tau \bigr) $$

(27)

we obtain a differential equation of motion that allows us to characterize the 1^st order perturbation of the motion of the permanent magnet in the narrow defect region

$$ \ddot{\xi}^{(1)}+\dot{\xi}^{(1)}=\frac{256 \alpha}{5\pi} \frac{ (\alpha \tau )^2}{ (1+ (\alpha \tau )^2 )^5} $$

(28)

Equation (28) shows that the magnet is accelerated when entering the defect region, whereas it is decelerated by the Lorentz force again when leaving the defect region. In the phase diagram one can see the typical M-shape that was already obtained in the exact solution (cf. Figs. 6(a) and 6(b)).

Fig. 6

Velocity distribution in the defect region: comparison between approximation and complete solution, (a) NDA, β=0.05, different α, (b) NDA, α=0.0592, different β, (c) LDA, β=2, different α, (d) LDA, α=0.0592, different β

Equation (28) is a linear inhomogeneous differential equation of second order. So a full analytical solution of the NDA equation is gained using Green functions. The full expression is lengthy and can be calculated using mathematical software tools as Maple for example.

Note, that the validity of the NDA is only given for β≪1. In Fig. 5 one finds the comparison of the friction terms. Figure 5(a) shows the case when β≪1. As a consequence the difference to the complete solution f(ξ,β) is very small. In Fig. 5(b) the opposite case is shown where β=1. The shape of the complete solution is changing significantly whereas the NDA is keeping the M-shape constantly and is only changing in magnitude as has been expected from Eq. (26). The resulting error is big and therefore, the NDA not valid anymore.

A changing velocity α does not have much influence on the difference between the full and the NDA solution (see Fig. 6(a)), whereas the comparison in Fig. 6(b) shows the difference in magnitude for higher β. Nevertheless, the NDA is a good approximation of the complete solution for small β that enable us to save computational time since we get rid of the position dependent integration.

3.3 Large Defect Approximation

For large defects (β≫1) there is an approximation possible which we will refer to as the large defect approximation (LDA). We state that the magnet is far enough from the edges of the pipe. Without the edge effects the magnetic dipole reaches equilibrium velocity, i.e. it is falling with a constant velocity v ₀.

We divide the path along the pipe into three parts: first part of the pipe (index U(pper)), free fall (index M(iddle)), second part of the pipe (index L(ower)). The LDA is based on the oversimplification that the magnet is falling with the equilibrium velocity v ₀ in the pipe parts U and L whereas the magnet does not experience any braking Lorentz force in the pipe part M (F=0). The full details of the derivation are not given here in the interests of brevity.

Assuming the large defect, we consequently approximate the solution of the equation by

(29)

The nondimensional times τ _U-M and τ _M-L mark the intersection points of the graphs ξ(τ).

The approximation of the full equation of motion is capturing the general behavior of the magnetic point dipole falling through a pipe with defect. Due to the simplifications and the ansatz using continuity conditions the path of the dipole is slightly different in the transition regions. The characteristic M-shape of the phase curve is not captured (see Figs. 6(c) and 6(d)). But nevertheless, the LDA is an approximation of the complete solution of the ordinary differential equation of motion that is especially useful when the free fall is dominating. Using LDA it is possible to save computational costs since it deals with linear and quadratic equations only and it enables the user to determine defect sizes and to estimate falling times as well.

4 Results of the Numerical Model

In the following section we shall discuss the numerical results for the two cases of the creeping-magnet-problem, namely (i) the nondefective pipe and (ii) the defective pipe. The numerical analysis is divided into three different regimes based on the value of the magnetic Reynolds number as low, intermediate and high. The question of applicability of QS and TR approaches to each regime of the creeping-magnet-problem will be answered.

4.1 Nondefective Pipe

The dynamic behavior of the magnet falling through a nondefective pipe is compared using the QS and TR approaches. For the comparison, the variation of the magnet’s velocity during the acceleration phase is plotted with respect to time for different magnet sizes in Fig. 7(a). We observe that both of the investigated approaches converge to an identical equilibrium velocity. This has been expected because of the isotropy of the material properties in the direction of motion. The comparison of the numerically obtained equilibrium velocity with the analytical solution shows a discrepancy of 59 % owing to the lack of the magnetic field gradients within the pipe wall in the analytical model (material properties according to Table 1, α _num.=0.0938, α _anl.=0.0592). Furthermore, it has to be emphasized that the 1D analytical model is valid only for low values of the magnetic Reynolds numbers unlike the numerical approaches (both QS and TR). In case of intermediate R _m values the results differ significantly. In order to illustrate this effect quantitatively, the total Lorentz force is plotted with respect to the magnetic Reynolds number (Fig. 7(b)). For the analytical solution the Lorentz force increases linearly with R _m , whereas for the numerical models the force initially increases linearly till R _m =0.5 and then begins to saturate to a constant value. It is further expected that the total Lorentz force will decay at high values of R _m [18].

Fig. 7

Comparison between transient (TR) and quasi-static (QS) numerical solutions for the pipe without defect, (a) dynamic behavior of the falling magnet after start, (b) effect of arbitrary magnetic Reynolds number R _m in comparison with the analytical solution (anl.)

Table 1 Geometrical and material properties

4.2 Defective Pipe

The geometrical and material properties for the particular creeping-magnet problem correspond to a low value of magnetic Reynolds number (R _m ≈5×10⁻³, Eq. (15)). The results are shown in Fig. 8.

Fig. 8

Influence of the magnetic Reynolds number R _m on the magnetic field distribution when the magnet is moving down, using α=0.4078 (R _m =0.01)

In case of R _m ≪1 the resulting magnetic field is unperturbed due to the relative motion and it is equal to the imposed primary field B ₀ (Figs. 8(a) and 8(b)). Due to the relatively low velocities all the changes, influenced by the defects, are considered to be slow. Therefore, the reaction of the magnetic field can be considered as instantaneous.

In the extreme case of R _m ≫1 the magnetic field lines are gradually expelled out from the pipe region. Due to the skin effect the induced eddy currents are distributed close to the inner surface of the pipe wall. To enter the regime of high R _m , the permanent magnet falling in the gravitational field has to be accelerated additionally or the experiment has to be build in larger size.

In order to describe the effect of finite values of R _m quantitatively, the numerical analysis is performed for various defect sizes (β) and forcing parameters (α). The analysis helps to compare the QS and TR approaches.

In case of R _m ≪1, the velocity changes due to the present defect is shown for the small and large defects, respectively (Figs. 9(a) and 9(c)). As expected, after passing the defect region the magnet velocity converges to the equilibrium velocity for both numerical models. When having a small defect both models are in good agreement. The discrepancy is increased for larger defects because of the increased falling velocity after passing the defect region. Due to the finite diffusion time in the TR model there is a phase shift between the QS and TR results. Nevertheless, from the obtained results one can conclude that for the creeping-magnet problem the QS approach can be successfully applied even for investigations of relatively large defects.

Fig. 9

Comparison between the transient (TR) and the quasi-static (QS) solution in the defect region for R _m ≪1, α=0.094, R _mag=7.5 mm and F ₀=−0.13145 N: (a) velocity profile, different small β, (b) force profile, different small β, (c) velocity profile, different large β, (d) force profile, different large β

A similar conclusion could be drawn concerning the force profiles (Figs. 9(b) and 9(d)). In the case the defect size is comparable to the size of the magnet itself, the Lorentz force drops to zero unlike in the case of small defects. This results in a higher falling velocity when leaving the defect region.

Figure 10 shows the resulting Lorentz force profiles in the defect region obtained by both QS and TR approaches for finite values of magnetic Reynolds numbers. The defect size β is considered to be small, so that a fair comparison is provided. The obtained results show considerable discrepancy even for small values of R _m (≈1) in Fig. 10(a). Due to the finite diffusion time in the TR approach the amplitude of the force perturbations is different to the one obtained by the QS approach. Nevertheless, the characteristic force profile is still conserved for both models.

Fig. 10

Comparison between the transient (TR) and the quasi-static (QS) solution in the defect region for R _mag=7.5 mm: (a) force profile, different β, where δ=1 mm, R _m ≈1, α=165, (b) force profile, different β, where δ=5 mm, R _m ≈10, α=165⋅10²

If we further increase the values of R _m (≈10) the resulting force profiles differ significantly. There arise phase shifts as shown in Fig. 10(b).

Figure 11 shows the corresponding position of the magnet with respect to the non-dimensional time τ and defect width β. The position of the magnet, after passing the defect region, is used for the calculation of the falling time and the falling time difference Δτ according to Eq. (12).

Fig. 11

Path of the magnet in the defect region for different defect sizes β, TR numerical solution for α=0.094, R _mag=7.5 mm

From the presented results, we want to point out that QS approach is an option to simulate even large defects when the magnetic Reynolds numbers is low (R _m ≪1). In the case of intermediate R _m ≈1, the force profiles obtained by the QS approach and TR approach differ even for relatively small defects as shown in Fig. 10. Therefore, we can no longer neglect the finite time response of the magnetic field, and for accurate calculations of the force perturbation due to defects the TR approach has to be used.

5 Comparison of Analytical and Numerical Models

There are three important differences between the numerical and the analytical model that have to be kept in mind when comparing results. The decay within the pipe walls is neglected in the analytical model, we assume a magnetic dipole instead of a permanent magnet and the effect of arbitrary magnetic Reynolds number R _m is not taken into account.

The verification of both the analytical and the numerical model has been carried out using the common model of a pipe without defect, i.e. β=0. The results of the QS and TR numerical model are the same. There is no change in geometry, therefore both models describe the behavior of the falling model equally taking into account the effect of finite values of R _m . Due to the fact that there is no perturbation of Lorentz force, we forbear from showing well-known figures. In this section we want to emphasize on the comparison between the analytical 1D model and the numerical models described above for the pipe with idealized defect.

As we presented above, the main influence on the velocity is caused by the force perturbation and vice versa since the model equations for force calculation Eq. (8) and differential equation of motion Eq. (11) are fully coupled. Therefore, one can find in Fig. 12 the velocity and the force profiles around the defect region.

Fig. 12

Comparison between the analytical (anl.) and the numerical (num.) solution in the defect region, where R _mag=7.5 mm and F ₀=−0.13145 N: (a) Velocity profile, where δ=1 mm, α _num.=0.094 and α _anl.=0.0592, (b) Force distribution, where δ=1 mm, α _num.=0.094 and α _anl.=0.0592, (c) Velocity profile, where δ=0.25 mm, α _num.=1.064 and α _anl.=0.947, (d) Force distribution, where δ=0.25 mm, α _num.=1.064 and α _anl.=0.947

In Figs. 12(a) and 12(b) we show the influence of the chosen model on the velocity and force profile. Due to the different velocity α the magnitude of the analytical solution differs from the numerical one. Nevertheless, the characteristic shape is conserved for different defect sizes.

In Figs. 12(c) and 12(d) one finds the comparison between analytical and numerical solution for thin pipe walls. The difference between the solutions has become smaller. We conclude that for infinite thin pipe walls we would have the same solution for the analytical and the numerical model.

Finally, the result of the force perturbation that goes along with the velocity perturbation is a change in falling time. In Fig. 13 the nondimensional time shift Δτ with respect to the defect size β is shown. (Please note that we used the QS approach in this calculation to save computational costs.)

Fig. 13

Comparison of the numerical with the analytical model; falling time change versus defect width where ‘ideal Δτ’ is characterized by Eq. (23)

The curve for “ideal Δτ” are calculated according to Eq. (23). As expected the full analytical solution of the differential equation of motion Eq. (11) provides results directly on the graph of the ideal time shift. The numerical obtained falling time changes differ slightly from the ideal ones due to the effect of arbitrary R _m and the full geometry. Nevertheless, the linear dependency between defect size and falling time change Δτ is remarkable in both models and corroborates the result of Eq. (23).

6 Validation

In order to validate the presented analytical and numerical models, an model experiment has been performed. A spherical permanent magnet (NdFeB) has been dropped through a nondefective copper pipe and the falling time has been measured. All necessary geometrical and material properties have been measured according to Table 1. Due to the fact that the measurements have been carried out with a stop watch the reaction time has also been determined (t _react=324±10 ms).

The experiments have been done using two permanent magnets of different diameter. There have been done forty runs for each magnet which allows the investigation of random errors following the guideline [19].

6.1 Nondefective Pipe

The experimental data are shown in Table 2, together with the predicted drop times from the analytical and numerical models.

Table 2 Experimental validation: falling time

The abbreviation STAT means stationary, i.e. the magnet is moving with equilibrium velocity t ₀=L/v ₀. DYN represents the dynamic approach, i.e. the complete solution according to the differential equation of motion (c.f. Eq. (11)).

It is possible to relate the measured falling time to the predicted velocity using Eq. (30). In Table 2 are given the relative errors of the different approaches for the predicted drop velocities $\dot{\xi}$. The numerical approach fits best, naturally. Due to the fact that the real geometry and an arbitrary magnetic Reynolds number is taken into account, it is possible to predict the velocity within of a few percent. The error estimation has been done with respect to the experimentally obtained falling time according to Eq. (31).

(30)

(31)

6.2 Defective Pipe

The validation of the special case of a pipe with a defect of the size β=0 has been performed above. In order to check whether the models fit the more general case of a pipe with an ideal defect we carried out experiments on pipes with different defect sizes.

To record the time changes we build up an pipe with changeable defect size. To minimize the perturbation we mounted a mechanical nonmagnetic and nonconductive guidance. The time was measured as described in Sect. 6.1. The relative errors of the estimation obtained by the described model is shown in Table 3.

Table 3 Experimental validation for a pipe with ideal defect: error estimation between measurements and different mathematical models

In Sect. 3.1 we have shown that the flight time increases linearly with the defect size. This dependency is validated with Figs. 14(a) and (b). The slope differs from the analytical one because of the difference in the forcing parameter α. The numerical solution is much closer to the experimental falling time changes Δτ. Additionally, the errors in time measurement for the experimental data have to be taken into account.

Fig. 14

Comparison of experimental data with analytical and numerical obtained falling time changes Δτ, (a) magnet R _mag=5 mm, subplot: compensated plot, (b) magnet R _mag=7.5 mm, subplot: compensated plot

The difference between the presented solutions of the analytical approach, numerical approach and the experiments with respect to the analytical solution are shown in the subplots of Figs. 14(a) and 14(b). Due to higher speed the error of the measurements with the 5 mm—magnet is larger and the gradient of the graph is bigger than the one of the 7.5 mm—magnet. The same linear behavior has been found in the numerical results (c.f. Fig. 13). We conclude that the presented models represent the physical effect well that has been measured in the experiments.

7 Conclusion

The creeping-magnet problem that has been under investigation refers to the case when the pipe is at rest and the magnet moves. The characteristic behavior we presented is valid for the LET problem as well. The reason for this is that physically the crucial parameter to describe both problems is the relative velocity between pipe and magnet. For mathematical comfort we have chosen the creeping-magnet problem.

Despite of this, it has been shown that the model of the creeping magnet can serve as a good representation in order to understand the basic laws of LET. The presented prototype model that benefits from the simple geometry demonstrates the good agreement between analytical, numerical and experimental results. Obviously the analytical model suffers from the taken assumptions and simplifications from that the neglected field decay within the pipe wall is dominant. The presented model can suit as a demonstrator for educational purposes.

We have shown that there are different possibilities of approaching the gathered differential equation of motion. For different velocity regimes and defect sizes there have been demonstrated the narrow defect approximation, the large defect approximation and the complete solution. All results have been compared with the full numerical solution showing good agreement.

Having the further investigations on LET in mind it is evident that the numerical model can be used to verify the upcoming results. Since the LET problem is crossing different R _m -regimes and we have to take into account geometrical changes when defects are considered, the application of a 3D transient model is necessary. Nevertheless, the presented model serves as a benchmark for the evaluation of software codes due to the relatively simple comparison and low computational costs [20].

We have shown that using time measurement it is possible to distinguish whether there is a defect in the pipe under test or not. Since the cause of the falling time change is a force perturbation we draw conclusions that using force or velocity measurements and appropriate data processing techniques defects can be localized and identified with higher precision [5].

The computed falling time differences due to the velocity perturbation caused by an ideal defect have been validated experimentally. Moreover, the linear dependency between falling time difference and the defect size has been proved. As a result, the time measurement in the creeping-magnet problem represents a straightforward inverse problem that can be solved to detect and localize defects.

Further work will mainly contain research on the LET problem. The Lorentz force profile resulting from the relative movement between a solid state body (e.g. a bar) and a permanent magnet or a magnet system cannot be solved analytically. The presented study can be understood as a verification of the numerical methods to be used in LET problem investigations.