An Efficient Spline Collocation Method for a Nonlinear Fourth-Order Reaction Subdiffusion Equation

Abstract

The nonlinear fourth-order reaction–subdiffusion equation whose solutions display a typical initial weak singularity is considered. A new analytical technique is introduced to analyze orthogonal spline collocation (OSC) method based on L1 scheme on graded mesh. By introducing a discrete convolution kernel and discrete fractional Grönwall inequality, convergence of the scheme is proved rigorously. This novel analytical technique can provide new insights in analyzing other time fractional fourth-order differential equations with weakly singular solutions.

1 Introduction

In the paper, we consider the following nonlinear fourth-order reaction–subdiffusion equation with initial singularity

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \partial ^{\alpha }_tu+\varDelta ^2 u=\varDelta u+f(u)+g({\mathbf {x}},t), &{} { {\mathbf {x}} \in \varOmega ,\ t\in (0,T];} \\ u=u_0({\mathbf {x}}), &{} { {\mathbf {x}} \in \varOmega ,\ t=0;} \\ u=\varDelta u=0, &{} {{\mathbf {x}}\in \partial \varOmega ,\ t\in (0,T].} \end{array} \right. \end{aligned}$$

(1.1)

Here, $\varOmega \subset {\mathbb {R}}^d$ ($d=1,2$). Its closure is denoted by ${\bar{\varOmega }}$. We assume that $\varOmega$ has smooth boundary $\partial \varOmega$ or is convex. $u_0\in C({\bar{\varOmega }})$, g is the given function, the nonlinear function f(u) is smooth, and $\partial ^{\alpha }_tu$ denotes the Caputo fractional derivative

$$\begin{aligned} \partial ^{\alpha }_tu({\mathbf {x}},t) =\int _0^t \omega _{1-\alpha }(t-s)\frac{\partial u({\mathbf {x}},s)}{\partial s}ds, \end{aligned}$$

(1.2)

where $\omega _{1-\alpha }(t-s)=\frac{(t-s)^{-\alpha }}{\varGamma (1-\alpha )}$, $0<\alpha <1$, $t>0$.

The nonlinear equation (1.1) possesses the fractional sub-diffusion and fourth-order derivative terms simultaneously, which makes it distinctive compared to general time-fractional sub-diffusion equations. For sub-diffusion equations with weakly singular solutions, their accurate numerical simulations have been the topic of much recent research, see references [1,2,3,4,5]. Yan et al. [6] established an improved L1 method for time fractional PDEs with nonsmooth data, then Xing and Yan modified this method to get a more higher order scheme in [7]. More recently, there are certain papers concerned with fourth-order fractional differential equations [8,9,10,11,12,13] and nonlinear sub-diffusions [14,15,16,17,18,19]. Ji et al. [20] proposed a high order FDM for fourth-order fractional sub-diffusion equations with the Dirichlet boundary conditions. In particular, Qiao et al. [21,22,23] derived ADI orthogonal spline collocation method for simulating the solution of multi-term time fractional integro-differential equation. However, they ignored a detailed issue and made the theoretical results without initial singularity. This is precisely the starting point of our present work.

We now consider the regularity of the exact solution u of (1.1) by introducing a corresponding linear problem, that is, set $f(u)+g(x,t)=f(x,t)$ in (1.1). According to earlier work of Luchko [24] and Sakamoto and Yamamoto [25], set $\{(\lambda _j, P_j): j=1, 2, \cdots \}$ be the eigenvalues and eigenfunctions for the following problem

$$\begin{aligned} -\varDelta P_j=\lambda _jP_j, \quad \hbox {on }\varOmega \hbox { with the boundary conditions }P_j|_{\partial \varOmega }=0, \end{aligned}$$

with the eigenfunctions normalised by requiring $(P_j, P_j)=1$ for all j, where $(\cdot , \cdot )$ denotes the inner product in $L^2(\varOmega )$. It is well known that the eigenvalues satisfy

$$\begin{aligned} 0<\lambda _1<\lambda _2<\cdots <\lambda _j\rightarrow \infty . \end{aligned}$$

Since $\{P_j: j=1, 2, \ldots \}$ form an orthogonal basis in $L^2(\varOmega )$, then from the earlier work of An and Liu [26, Page 3327], $P_j$, $j=1, 2, \ldots$, is also an eigenfunction for the following problem

$$\begin{aligned} \varDelta ^2 P_j-\varDelta P_j={\hat{\lambda }}_jP_j, \quad \hbox {on} \varOmega \hbox { with the boundary conditions }P_j|_{\partial \varOmega }=\varDelta P_j|_{\partial \varOmega }=0, \end{aligned}$$

where the eigenvalues ${\hat{\lambda }}_j=\lambda _j(\lambda _j+1)$, $j=1, 2,\ldots$.

By using a standard separation of variables scheme (see [24, Eq. (4.29)] or [25, Eq. (2.11)], and imitating the Eq. (2.2) in [27], we can get

$$\begin{aligned} u(x,t)=\sum \limits _{j=1}^{\infty } [(u_0, P_j)E_{\alpha ,1}(-{\hat{\lambda }}_jt^{\alpha })+J_{j,\alpha }(E_{\alpha ,\alpha }; t)]P_j(x),\quad x\in \bar{\varOmega },\quad t\in [0,T].\nonumber \\ \end{aligned}$$

(1.3)

where

$$\begin{aligned} J_{j,\alpha }(E_{\alpha ,\alpha }; t)=\int _0^t s^{\alpha -1}E_{\alpha ,\alpha }(-{\hat{\lambda }}_js^{\alpha })f_j(t-s)ds, \end{aligned}$$

where $f_j(t-s)=(f(\cdot ,t-s),P_j(\cdot ))$, and the generalized two-parameter Mittag–Leffler function $E_{\alpha ,\beta }(z)$ [28], Section 1.2] is defined by

$$\begin{aligned} E_{\upsilon ,\beta }(z)=\sum \limits _{i=0}^{\infty }\frac{z^i}{\varGamma (\upsilon i+\beta )}, \quad \upsilon>0,\beta >0, \quad z\in R. \end{aligned}$$

Set ${\mathfrak {L}} P_j=\varDelta ^2 P_j-\varDelta P_j$, by using the framework of sectorial operators [25], we define following fractional power ${\mathfrak {L}}^{\gamma }$ ($\gamma \in R$) of the operator ${\mathfrak {L}}$ with domain

$$\begin{aligned} D({\mathfrak {L}}^{\gamma })=\left\{ \varphi \in L^2(\varOmega ): \sum \limits _{j=1}^{\infty } {\hat{\lambda }}_j^{2\gamma }|(\varphi ,P_j)|^2<\infty ,\ \gamma \in R \right\} , \end{aligned}$$

and

$$\begin{aligned} \Vert \varphi \Vert _{{\mathfrak {L}}^{\gamma }}=(\sum \limits _{j=1}^{\infty } {\hat{\lambda }}_j^{2\gamma }|(\varphi ,P_j)|^2)^{\frac{1}{2}},\quad \gamma \in R. \end{aligned}$$

Similar to [29, Section 6.1] (cf. [27, Section 2]), one can apply (1.3) and the theory of sectorial operators to get the following regularity of the solution to (1.1).

Let $\ell$ be a non-negative integer. For all $t\in (0, T]$, assume that $u_0\in D({\mathfrak {L}}^{\ell +2})$, $\frac{\partial ^l f(\cdot ,t)}{\partial t^l}\in D({\mathfrak {L}}^{\ell })$ and $\Vert u_0\Vert _{{\mathfrak {L}}^{\ell }+2}+\Vert \frac{\partial ^l f(\cdot ,t)}{\partial t^l}\Vert _{{\mathfrak {L}}^{\ell }+1}\le c_0$ for $l= 1, 2$, where $c_0$ is a constant independent of t. Then we can make the following assumptions about the exact solution u of (1.1).

For $p=1,2, t\in (0,T]$, $\ell \in {\mathbb {N}}_0=\{0,1,\ldots \}$, and a constant $c_0$, we assume

$$\begin{aligned} \Vert u(\cdot ,t)\Vert _{\ell }\le c_0,\ \ \Vert \frac{\partial ^p u(\cdot ,t)}{\partial t^p}\Vert _{\ell }\le c_0(1+t^{\alpha -p}), \end{aligned}$$

(1.4)

where the notation $\Vert \cdot \Vert _{\ell }$ is norm in the standard Sobolev space $H^{\ell }(\varOmega )$.

The paper is organized as follows. In Sect. 2, inspired by L1 formula, L1-OSC scheme is presented. A new theoretical technique for our scheme is presented in Sect. 3. In Sect. 4, some numerical results are given.

2 The Fully Discrete Scheme Based on Orthogonal Spline Collocation

We set $\delta _x: a=x_0<x_1<\cdots <x_{N_x}=b$, $\delta =\delta _x\times \delta _y$ in $\varOmega$ be quasi-uniform, $\delta _y$ is similar to $\delta _x$. Let $h_l^x=x_{l}-x_{l-1}$, $h_k^y=y_{k}-y_{k-1}$, $h=\max (\max \limits _{1\le l\le N_x} h_l^x, \max \nolimits _{1\le k\le N_y} h_k^y)$. For $1\le k\le N_x$, denote

$$\begin{aligned} {\mathcal {M}}_r(\delta _x)=\left\{ v|v\in C^1({\bar{I}}), v|_{[x_{k-1},x_k]}\in P_r, r\ge 3\right\} , \end{aligned}$$

where ${\bar{I}}=[0,1]$, and $P_r$ is the set of polynomials of degree $\le r$. Let

$$\begin{aligned} {\mathcal {M}}^0_r(\delta _x)=\left\{ v|v\in {\mathcal {M}}_r(\delta _x), v(a)=v(b)=0\right\} , \end{aligned}$$

with ${\mathcal {M}}^0_r(\delta _y)$ defined similarly. Set ${\mathcal {M}}_r(\delta )={\mathcal {M}}_r (\delta _x)\otimes {\mathcal {M}}_r( \delta _y)$ and ${\mathcal {M}}^0_r(\delta )={\mathcal {M}}^0_r (\delta _x)\otimes {\mathcal {M}}^0_r( \delta _y).$

We now define collocation points set in $\varOmega$: $\varLambda _r=\{\varsigma =(\varsigma _x, \varsigma _y), \varsigma _x\in \varLambda _x, \varsigma _y\in \varLambda _y\}$, where $\varLambda _x=\{\varsigma ^{i,k}_x\}_{i,k=1}^{N_x,r-1}$, $\varsigma ^{i,k}_x=x_{i-1}+\lambda _kh^x_i,$ $\{\lambda _k\}_{k=1}^{r-1}$ are the nodes of the $(r-1)$-point Legendre quadrature rule. $\varLambda _y$ defined similarly.

Set $\{\omega _i\}_{i=1}^{r-1}$ be weights of the Legendre quadrature rule and $\sum \limits _{i=1}^{r-1}\omega _i=1$, for $\forall \phi ,\varphi$ on ${\mathcal {M}}^0_r(\delta )$, we define the following discrete inner product and norm,

$$\begin{aligned} \left\langle \phi ,\varphi \right\rangle =\sum \limits _{i=1}^{N_x}\sum \limits _{j=1}^{N_y} h_i^xh_j^y\sum \limits _{k=1}^{r-1}\sum \limits _{l=1}^{r-1}\omega _k \omega _l(\phi \varphi )(\varsigma ^{i,k}_x,\varsigma ^{j,l}_y),\qquad \Vert \phi \Vert _{{\mathcal {M}}_r}^2=\langle \phi ,\phi \rangle . \end{aligned}$$

(2.5)

Let $\Vert \cdot \Vert$ be the usual $L^2$ norm, the norms $\Vert \cdot \Vert _{{\mathcal {M}}_r}$ and $\Vert \cdot \Vert$ is equivalent on ${\mathcal {M}}^0_{r}(\delta )$, see [30].

By introducing an auxiliary variable $v=\varDelta u$, we split (1.1) into the following equivalent coupled system:

$$\begin{aligned} \partial ^{\alpha }_tu+\varDelta v= & {} \varDelta u+f(u)+g({\mathbf {x}},t), \quad ({\mathbf {x}},t) \in \varOmega \times (0,T],\nonumber \\&\hbox {and}\quad v({\mathbf {x}},t)-\varDelta u ({\mathbf {x}},t)=0, \quad ({\mathbf {x}},t) \in \varOmega \times (0,T]. \end{aligned}$$

(2.6)

To derive discrete-time L1-OSC schemes, for any $K\in Z^+$, grading constant ${\check{r}}\ge 1$ and $1\le n\le K$, let $\mathrm {T}_{\tau }=\{t_n|t_n=T(n/K)^{{\check{r}}}\}$, $\tau _n=t_n-t_{n-1}$, and $\tau _n\le C_0 TK^{-{\check{r}}}(n-1)^{{\check{r}}-1}$, see [27, Eq. (5.1)]. Denote

$$\begin{aligned} \phi ^n=\phi (\cdot ,t_n),\ \ a_{n-j}^{(n)}=\frac{\tau _j^{-1}}{\varGamma (1-\alpha )}\int ^{t_j}_{t_{j-1}}\frac{ds}{(t_{n}-s)^{\alpha }},\quad j=1,\ldots ,n, \end{aligned}$$

then, $\partial ^{\alpha }_t\phi$ on graded mesh can be approximated by L1 scheme

$$\begin{aligned} D_K^{\alpha }\phi ^n=\sum \limits _{i=1}^{n}a_{n-i}^{(n)}(\triangledown _t\phi ^{i}) =a_{0}^{(n)}\phi ^n-\sum \limits _{i=0}^{n-1}(a_{n-i-1}^{(n)}-a_{n-i}^{(n)})\phi ^{i}, \end{aligned}$$

(2.7)

where $a_{n}^{(n)}=0$,$\triangledown _t\phi ^{i}=(\phi ^i-\phi ^{i-1})$.

By the Lemma 5.1 of [27], we know

$$\begin{aligned} |D_K^{\alpha }\phi ^n-\partial _t^{\alpha }\phi (t_n)|\le C_0 n^{-\min \{{\check{r}}\alpha ,2-\alpha \}}. \end{aligned}$$

(2.8)

We now introduce a sequence of discrete convolution kernels as follow

$$\begin{aligned}&b_{0}^{(n)}=\tau _n^{\alpha }\varGamma (2-\alpha ), \quad 1\le n\le K,\\&b_{n-j}^{(n)}=\tau _j^{\alpha }\varGamma (2-\alpha )\sum \limits _{i=j+1}^{n}(a_{i-j-1}^{(i)}-a_{i-j}^{(i)})b_{n-i}^{(n)},\quad 1\le j\le n-1, \end{aligned}$$

By Lemma 2.1 of [2], we can obtain

$$\begin{aligned}&0<b_{n-j}^{(n)}\le \tau _j^{\alpha }\varGamma (2-\alpha ),\quad \sum \limits _{j=k}^{n}b_{n-j}^{(n)}a_{j-k}^{(j)}=1,\quad 1\le n\le K, \nonumber \\&\hbox {and} \quad \sum \limits _{j=k}^{n}b_{n-j}^{(n)}\omega _{1+m\alpha -\alpha }(t_j)\le \omega _{1+m\alpha }(t_n),\quad m\ge 1,\quad 1\le n\le K. \end{aligned}$$

(2.9)

Thus, using (2.7) and Newton linearization formula, we can construct following fully discrete L1-OSC scheme: seek $\{u^n_h,v^n_h\}\in {\mathcal {M}}^0_r(\delta )\times {\mathcal {M}}^0_r(\delta )$, such that, for $n=1,2,\ldots ,K$

$$\begin{aligned} D_K^{\alpha }u_h^n +\varDelta v^n_h= & {} \varDelta u^n_h+f^{\prime }(u_h^{n-1})(u_h^{n}-u_h^{n-1})+f(u_h^{n-1})+g^n_h\ \hbox {on}\ \ \varLambda _r, \nonumber \\&\hbox {and} \quad v_h^n=\varDelta u_h^n\ \ \hbox {on}\ \ \varLambda _r, \end{aligned}$$

(2.10)

where $g^n_h$ is a fitted approximation to $g(\cdot ,t_n)$. Also, for $\forall \chi ,\psi \in {\mathcal {M}}^0_r(\delta )$, we have

$$\begin{aligned} \left\langle D_K^{\alpha }u_h^n ,\chi \right\rangle= & {} \langle \varDelta u_h^n -\varDelta v_h^n,\chi \rangle +\langle f^{\prime }(u_h^{n-1})(u_h^{n}-u_h^{n-1})+f(u_h^{n-1})+g_h^n,\chi \rangle , \nonumber \\ \hbox {and} \quad \langle v_h^n, \psi \rangle= & {} \langle \varDelta u_h^n,\psi \rangle , \end{aligned}$$

(2.11)

which will be applied to subsequent convergence analysis. (2.10) with the discrete initial and boundary conditions is a linear elliptic problem for every time level, the existence and uniqueness of the solution $\{u_h^j\}_{j=1}^{K-1}$ can be guaranteed by the Lax–Milgram lemma if h is sufficiently small or K sufficiently large.

3 Theoretical Analysis

Lemma 1

[2] If the nonnegative sequences $\{\ \zeta _1^n,\zeta _2^n, |1\le n\le K\}$ are bounded, set ${\tilde{\kappa }}$ be a positive constant independent of n and the nonnegative constants $\kappa _j$ satisfying $0<\sum \limits _{j=0}^{n-1}\kappa _j<{\tilde{\kappa }}$, $1\le n\le K$. If the nonnegative sequence $\{\ \upsilon ^n\}_{n=0}^{K}$ satisfies

$$\begin{aligned} \sum \limits _{i=1}^{n}a_{n-i}^{(n)}\triangledown _t(\upsilon ^{i})^2\le \sum \limits _{j=1}^{n}\kappa _{n-j}(\upsilon ^j)^2+\upsilon ^n\zeta _1^n+(\zeta _2^n)^2,\ 1\le n\le K, \end{aligned}$$

(3.12)

then when the maximum temporal step size satisfies $\tau _K\le (2\varGamma (2-\alpha ){\tilde{\kappa }})^{-1/\alpha }$, for $1\le n\le K$, it holds

$$\begin{aligned} \upsilon ^n \le 2E_{\alpha }(2{\tilde{\kappa }} t_n^{\alpha })\left( \upsilon ^0+\max \limits _{1\le k\le n}\sum \limits _{j=1}^{k}b_{k-j}^{(k)}\zeta _1^j+\sqrt{\varGamma (1-\alpha )}\max \limits _{1\le k\le n} \{t_k^{\alpha /2}\zeta _2^k\} \right) . \end{aligned}$$

To derive convergence, first, define $\{{\widehat{U}},{\widehat{V}}\}$: $[0,T]\rightarrow {\mathcal {M}}^0_r(\delta )\times {\mathcal {M}}^0_r(\delta )$ as

$$\begin{aligned} \langle \varDelta (u-{\widehat{U}}),\chi \rangle =0,\ \langle \varDelta \left( v-{\widehat{V}}\right) ,\psi \rangle =0, \ \ \psi , \chi \in {\mathcal {M}}^0_r(\delta ), \end{aligned}$$

(3.13)

where u and v are the solution of (2.6).

Let $\rho =v-{\widehat{V}}$ and $\eta =u-{\widehat{U}}$, then from [31], we have the following estimates on $\rho$ and $\eta$ and its time derivatives.

Lemma 2

[31] If $\frac{\partial ^i u}{\partial t^i},\frac{\partial ^j v}{\partial t^j}\in L^p( H^{r+3})$, for $t\in \left[ 0,T\right]$, $i,j=0, 1,2$, $p=2, \infty$, then

$$\begin{aligned}&\left\| \frac{\partial ^{\ell +i}\eta }{\partial x^{\ell _1}\partial y^{\ell _2}\partial t^i}\right\| _{{\mathcal {M}}_r}\le C_uh^{r+1-\ell }\left\| \frac{{\partial }^iu}{\partial t^i}\right\| _{H^{r+3}},\nonumber \\&\quad \hbox {and} \quad \left\| \frac{\partial ^{\ell +j}\rho }{\partial x^{\ell _1}\partial y^{\ell _2}\partial t^j}\right\| _{{\mathcal {M}}_r}\le C_vh^{r+1-\ell }\left\| \frac{{\partial }^jv}{\partial t^j}\right\| _{H^{r+3}}, \end{aligned}$$

(3.14)

where the constants $C_u$ and $C_v$ are independent of h and the time step, and $0\le \ell =\ell _1+\ell _2\le 4$.

Set

$$\begin{aligned}&u(t_n) - u^n_h=(u(t_n)-{\widehat{U}}^n)-(u^n_h-{\widehat{U}}^n), \quad 1\le n\le K, \nonumber \\&\eta ^n=u(t_n)-{\widehat{U}}^n,\ \xi ^n=(u^n_h-{\widehat{U}}^n), \quad 1\le n\le K, \end{aligned}$$

(3.15)

and

$$\begin{aligned}&v(t_n) - v^n_h=(v(t_n)-{\widehat{V}}^n)-(v_h^n-{\widehat{V}}^n), \quad 1\le n\le K, \nonumber \\&\rho ^n=(v(t_n)-{\widehat{V}}^n),\ \theta ^n=(v_h^n-{\widehat{V}}^n), \quad 1\le n\le K. \end{aligned}$$

(3.16)

Now we state our main results.

Theorem 1

Suppose $u(\cdot ,t_n)$ are the solutions of (2.6) with the regularity property (1.4), the nonlinear function $f\in C^{2}({\mathbb {R}})$, and $u(\cdot ,t)\in L^{\infty }({\mathbb {R}}^{d})$ for $t\in (0,T]$. Let $u^n_h$ be the discrete solutions of (2.11). If the maximum temporal step size satisfies $\tau _K\le (4\varGamma (2-\alpha ){\hat{\kappa }}_{+})^{-1/\alpha }$, where ${\hat{\kappa }}_{+}$ is defined in (3.27). Then

$$\begin{aligned} \left\| u(t_{n})-u^n_h\right\| \le c_0( K^{-\min \{{\check{r}}\alpha ,2-\alpha \}}+ h^{r+1}), \quad 1\le n\le K, \end{aligned}$$

(3.17)

provided $u_h^0$ is chosen so that $\left\| u^0-{\widehat{U}}^0\right\| \le c_0h^{r+1}$.

Proof

Since the estimates of $\eta ^n$ and $\rho ^n$ are known by Lemma 2, then we need only to estimate $\xi ^n$ and $\theta ^n$. First, for $1\le n\le K$, taking $t=t_n$ in (2.6), and using (2.11), (3.13) and (3.15), we obtain

$$\begin{aligned}&\left\langle D_K^{\alpha }\xi ^n,\chi \right\rangle =\left\langle \varDelta \xi ^n,\chi \right\rangle -\langle \varDelta \theta ^n,\chi \rangle +\left\langle D_K^{\alpha }\eta ^n,\chi \right\rangle +\left\langle \phi ^n+R^n,\chi \right\rangle , \forall \chi \in {\mathcal {M}}^0_r(\delta ), \\&\quad \hbox { and} \quad \langle \theta ^n, \psi \rangle =\langle \varDelta \xi ^n,\psi \rangle +\langle \rho ^n, \psi \rangle ,\ \forall \psi \in {\mathcal {M}}^0_r(\delta ), \end{aligned}$$

where

$$\begin{aligned}&R^n= D_K^{\alpha }u^n-\partial ^{\alpha }_tu(x,t_n) +f(u^n)-(f^{\prime }(u^{n-1})(u^{n}-u^{n-1})+f(u^{n-1})),\\&\phi ^n=f(u^{n-1})+(u^{n}-u^{n-1})f^{\prime }(u^{n-1})-(u_h^{n}-u_h^{n-1})f^{\prime }(u_h^{n-1})-f(u_h^{n-1}). \end{aligned}$$

Taking $\chi =\xi ^n$, $\psi =\theta ^n$ and adding, we attain

$$\begin{aligned}&\left\langle D_K^{\alpha }\xi ^n,\xi ^n\right\rangle +\langle \theta ^n, \theta ^n\rangle - \left\langle \varDelta \xi ^n,\xi ^n \right\rangle \nonumber \\&\quad =-\langle \varDelta \theta ^n,\xi ^n\rangle +\langle \varDelta \xi ^n,\theta ^n\rangle +\left\langle D_K^{\alpha }\eta ^n+ \phi ^n+R^n,\xi ^n\right\rangle +\langle \rho ^n, \theta ^n\rangle , 1\le n\le K.\nonumber \\ \end{aligned}$$

(3.18)

From [32, Eq. (3.4)] or [33, Eq. (2.3) in Lemma 2.1], for $\forall \varpi ,\sigma \in {\mathcal {M}}^0_r(\delta )$, we have

$$\begin{aligned} -\langle \varDelta \varpi ,\sigma \rangle +\langle \varDelta \sigma ,\varpi \rangle =0, \end{aligned}$$

(3.19)

on using (3.19) with $\varpi =\theta ^n$, $\sigma =\xi ^n$, we have

$$\begin{aligned} -\langle \varDelta \theta ^n,\xi ^n\rangle +\langle \varDelta \xi ^n,\theta ^n\rangle =0, \quad 1\le n\le K, \end{aligned}$$

then, (3.18) can be rewritten as

$$\begin{aligned}&\left\langle D_K^{\alpha }\xi ^n,\xi ^n\right\rangle +\langle \theta ^n, \theta ^n\rangle - \left\langle \varDelta \xi ^n,\xi ^n \right\rangle \nonumber \\&\quad =\left\langle D_K^{\alpha }\eta ^n+ \phi ^n+R^n,\xi ^n\right\rangle +\langle \rho ^n, \theta ^n\rangle , 1\le n\le K. \end{aligned}$$

(3.20)

From [32, Eq. (3.5)] or [33, Eq. (2.4) in Lemma 2.1], for $\forall \vartheta \in {\mathcal {M}}^0_r(\delta )$, there exists a positive constant c such that

$$\begin{aligned} -\langle \varDelta \vartheta , \vartheta \rangle \ge c\Vert \nabla \vartheta \Vert ^2\ge 0, \end{aligned}$$

(3.21)

on using (3.21) with $\vartheta =\xi ^n$, then

$$\begin{aligned} -\langle \varDelta \xi ^{n}, \xi ^{n}\rangle \ge \Vert \nabla \xi ^{n}\Vert ^2\ge 0, 1\le n\le K. \end{aligned}$$

(3.22)

By the proof of Lemma 4.1 in [34], we obtain

$$\begin{aligned} 2\left\langle D_K^{\alpha }\xi ^n,\xi ^n\right\rangle \ge \sum \limits _{i=1}^{n}a_{n-i}^{(n)}\triangledown _t(\Vert \xi ^i\Vert ^2_{{\mathcal {M}}_r}) , \quad 1\le n\le K. \end{aligned}$$

(3.23)

Thus, combining (3.20), (3.22) and (3.23), and using Cauchy–Schwarz and Young inequalities, we have

$$\begin{aligned}&\frac{1}{2}\sum \limits _{i=1}^{n}a_{n-i}^{(n)}\triangledown _t(\Vert \xi ^i\Vert ^2_{{\mathcal {M}}_r}) +\Vert \theta ^n\Vert ^2_{{\mathcal {M}}_r}\nonumber \\&\quad \le \left( \Vert D_K^{\alpha }\eta ^n\Vert _{{\mathcal {M}}_r}+\Vert \phi ^n\Vert _{{\mathcal {M}}_r} +\Vert R^n\Vert _{{\mathcal {M}}_r}\right) \Vert \xi ^n \Vert _{{\mathcal {M}}_r} +\frac{1}{4}\Vert \rho ^n \Vert ^2_{{\mathcal {M}}_r}+ \Vert \theta ^n \Vert ^2_{{\mathcal {M}}_r}, 1\le n\le K.\nonumber \\ \end{aligned}$$

(3.24)

By the use of the first condition in (1.4), we obtain

$$\begin{aligned}&\Vert (u^{n-1}-u_h^{n-1}) f^{\prime }(su^{n-1}+(1-s)u_h^{n-1})\Vert _{{\mathcal {M}}_r} \\&\quad \le c_0(\Vert \eta ^{n-1}\Vert _{{\mathcal {M}}_r}+\Vert \xi ^{n-1}\Vert _{{\mathcal {M}}_r}), 1\le n\le K, \\&\Vert f^{\prime }(u_h^{n-1})(u^{n}-u_h^{n}-(u^{n-1}-u_h^{n-1}))\Vert _{{\mathcal {M}}_r} \\&\quad \le c_0(\Vert \eta ^{n}\Vert _{{\mathcal {M}}_r} +\Vert \xi ^{n}\Vert _{{\mathcal {M}}_r}+\Vert \eta ^{n-1}\Vert _{{\mathcal {M}}_r}+\Vert \xi ^{n-1}\Vert _{{\mathcal {M}}_r}), 1\le n\le K, \end{aligned}$$

and

$$\begin{aligned}&\Vert (u^{n}-u^{n-1})(u^{n-1}-u_h^{n-1}) f^{\prime \prime }(su^{n-1}+(1-s)u_h^{n-1})\Vert _{{\mathcal {M}}_r} \\&\quad \le 2K_0c_0(\Vert \eta ^{n-1}\Vert _{{\mathcal {M}}_r}+\Vert \xi ^{n-1}\Vert _{{\mathcal {M}}_r}), 1\le n\le K, \end{aligned}$$

where $K_0=\max \limits _{0\le n\le K}\Vert u^{n}\Vert _{L^{\infty }}+1$.

Since

$$\begin{aligned} \Vert \phi ^n\Vert _{{\mathcal {M}}_r}= & {} \Vert f(u^{n-1})-f(u_h^{n-1})+ (f^{\prime }(u^{n-1})-f^{\prime }(u_h^{n-1}))(u^{n}-u^{n-1}) \\&+f^{\prime }(u_h^{n-1})(u^{n}-u_h^{n}-(u^{n-1}-u_h^{n-1}))\Vert _{{\mathcal {M}}_r} \\\le & {} \Vert (u^{n-1}-u_h^{n-1})\int _{0}^{1} f^{\prime }(su^{n-1}+(1-s)u_h^{n-1})ds\Vert _{{\mathcal {M}}_r} \\&+ \Vert (u^{n}-u^{n-1})(u^{n-1}-u_h^{n-1}) \int _{0}^{1} f^{\prime \prime }(su^{n-1}+(1-s)u_h^{n-1})ds\Vert _{{\mathcal {M}}_r} \\&+\Vert f^{\prime }(u_h^{n-1})(u^{n}-u_h^{n}-(u^{n-1}-u_h^{n-1}))\Vert _{{\mathcal {M}}_r}, 1\le n\le K. \end{aligned}$$

Thus, using Lemma 2, we obtain

$$\begin{aligned} \Vert \phi ^n\Vert _{{\mathcal {M}}_r}\le & {} c_0\Vert \xi ^{n}\Vert _{{\mathcal {M}}_r}+(2c_0+2c_0K_0)\Vert \xi ^{n-1}\Vert _{{\mathcal {M}}_r}\nonumber \\&+(3c_0+2c_0K_0)h^{r+1}\Vert u\Vert _{H^{r+3}}, 1\le n\le K. \end{aligned}$$

(3.25)

By combining (3.24) and (3.25), we obtain

$$\begin{aligned}&\frac{1}{2}\sum \limits _{i=1}^{n}a_{n-i}^{(n)}\triangledown _t(\Vert \xi ^i\Vert ^2_{{\mathcal {M}}_r}) \\\le & {} \left( \Vert D_K^{\alpha }\eta ^n\Vert _{{\mathcal {M}}_r} +\Vert R^n\Vert _{{\mathcal {M}}_r}\right) \Vert \xi ^n \Vert _{{\mathcal {M}}_r} +(c_0\Vert \xi ^{n}\Vert _{{\mathcal {M}}_r}+(2c_0(1+K_0))\Vert \xi ^{n-1}\Vert _{{\mathcal {M}}_r} \\&+(3c_0+2c_0K_0)h^{r+1}\Vert u\Vert _{H^{r+3}})\Vert \xi ^n \Vert _{{\mathcal {M}}_r} +\frac{1}{4}\Vert \rho ^n \Vert ^2_{{\mathcal {M}}_r} \\\le & {} (2c_0+c_0K_0)\Vert \xi ^{n}\Vert ^2_{{\mathcal {M}}_r}+(c_0+c_0K_0)\Vert \xi ^{n-1}\Vert ^2_{{\mathcal {M}}_r} \\&+(c_1(3c_0+2c_0K_0)h^{r+1}+\Vert D_K^{\alpha }\eta ^n\Vert _{{\mathcal {M}}_r} +\Vert R^n\Vert _{{\mathcal {M}}_r})\Vert \xi ^n \Vert _{{\mathcal {M}}_r}+\frac{1}{4}\Vert \rho ^n \Vert ^2_{{\mathcal {M}}_r}, 1\le n\le K, \end{aligned}$$

which has the form of (3.12), then using the discrete fractional Grönwall inequality of Lemma 1, we obtain

$$\begin{aligned}&\Vert \xi ^n\Vert _{{\mathcal {M}}_r}\nonumber \\&\quad \le 4E_{\alpha }(2{\hat{\kappa }}_{+} t_n^{\alpha })\left( \Vert \xi ^0\Vert _{{\mathcal {M}}_r}+\frac{\sqrt{\varGamma (1-\alpha )}}{4}\max \limits _{1\le k\le n} \{t_k^{\alpha /2}\Vert \rho ^k \Vert _{{\mathcal {M}}_r}\} \right. \nonumber \\&\quad \left. +\max \limits _{1\le k\le n}\sum \limits _{j=1}^{k}b_{k-j}^{(k)}(c_1(3c_0+2c_0K_0)h^{r+1}+\Vert D_K^{\alpha }\eta ^n\Vert _{{\mathcal {M}}_r} +\Vert R^n\Vert _{{\mathcal {M}}_r}) \right) , 1\le n\le K,\nonumber \\ \end{aligned}$$

(3.26)

where

$$\begin{aligned} {\hat{\kappa }}_{+}=c_0 (3+2K_0). \end{aligned}$$

(3.27)

We now proceed to estimate the terms on the RHS of (3.26). By using the definition (2.7) and (2.9), we have

$$\begin{aligned} \sum \limits _{j=1}^{n}b_{n-j}^{(n)}\Vert D_K^{\alpha }\eta ^j\Vert _{{\mathcal {M}}_r}\le & {} \sum \limits _{j=1}^{n}b_{n-j}^{(n)} \sum \limits _{k=1}^{j}a_{j-k}^{(j)} \Vert \triangledown _t \eta ^k\Vert _{{\mathcal {M}}_r}\nonumber \\= & {} \sum \limits _{j=1}^{n}\Vert \triangledown _t \eta ^j\Vert _{{\mathcal {M}}_r}, 1\le n\le K. \end{aligned}$$

(3.28)

Moreover, by Lemma 2 and (1.4), we have

$$\begin{aligned} \sum \limits _{j=1}^{n}\left\| \bigtriangledown _t\eta ^{j}\right\| _{{\mathcal {M}}_r}= & {} \sum \limits _{j=1}^{n}\left\| \int _{t_{j}}^{t_{j-1}}\frac{\partial \eta }{\partial s}(s)ds\right\| _{{\mathcal {M}}_r} \\\le & {} \sum \limits _{j=1}^{n}\int _{t_{j}}^{t_{j-1}}\left\| \frac{\partial \eta }{\partial s}(s)\right\| _{{\mathcal {M}}_r} ds \le C_0h^{r+1}(t_{n}+t_n^{\alpha }/\alpha ), 1\le n\le K. \end{aligned}$$

For the term $R^n$, $1\le n\le K$, by using (2.8), we have

$$\begin{aligned}&\sum \limits _{j=1}^{n}b_{n-j}^{(n)}\Vert D_K^{\alpha }u^j-\partial ^{\alpha }_tu(x,t_j)\Vert \nonumber \\&\quad \le \sum \limits _{j=1}^{n}b_{n-j}^{(n)}\omega _{1-\alpha }(t_j)\max \limits _{1\le k\le n}\frac{\Vert D_K^{\alpha }u^k-\partial ^{\alpha }_tu(x,t_k)\Vert }{\omega _{1-\alpha }(t_k)}\nonumber \\&\quad \le \varGamma (1-\alpha )\max \limits _{1\le k\le n}t_k^{\alpha }\Vert D_K^{\alpha }u^k-\partial ^{\alpha }_tu(x,t_k)\Vert \nonumber \\&\quad \le c_0\varGamma (1-\alpha )T^{\alpha } N^{-\min \{{\check{r}}\alpha ,2-\alpha \}}, 1\le n\le K. \end{aligned}$$

(3.29)

Set ${\tilde{R}}^n=f(u^n)-f(u^{n-1})-f^{\prime }(u^{n-1})(u^{n}-u^{n-1})$, $1\le n\le K$, it follows from the Taylor expansion with integral remainder

$$\begin{aligned} {\tilde{R}}^j=(u^{j}-u^{j-1})^2\int _{0}^{1}f^{\prime \prime }(s(u^{j}-u^{j-1})+u^{j-1})(1-s)ds,\ j\ge 1. \end{aligned}$$

By the regularity conditions (1.4), we have

$$\begin{aligned}&|{\tilde{R}}^1|\le c_0(\int _{t_0}^{t_1}|u^{\prime }(t)|dt)^2\le C(\tau _1^2+\tau _1^{2\alpha }/\alpha ^2), \\&\quad {\hbox {and}}\quad |{\tilde{R}}^j|\le c_0(\int _{t_{j-1}}^{t_{j}}|u^{\prime }(t)|dt)^2\le C(\tau _j^2+t_{j-1}^{2\alpha -2}\tau _j^2), \quad 2\le j\le K. \end{aligned}$$

By (2.12) of [14], for $1\le n\le K$, the expression $\sum \limits _{j=1}^{n}b_{n-j}^{(n)}\le \frac{t_n^{\alpha }}{\varGamma (1+\alpha )}$ is true, then,

$$\begin{aligned} \sum \limits _{j=1}^{n}b_{n-j}^{(n)}\Vert {\tilde{R}}^j\Vert\le & {} b_{n-1}^{(n)}\Vert {\tilde{R}}^1\Vert +\sum \limits _{j=2}^{n}b_{n-j}^{(n)}\Vert {\tilde{R}}^j\Vert \\\le & {} c_0\tau _1^{\alpha }\Vert {\tilde{R}}^1\Vert +c_0t_n^{\alpha }\max \limits _{2\le j\le n}\Vert {\tilde{R}}^{j}\Vert \\\le & {} c_0\tau _1^{\alpha }(\tau _1^2+\tau _1^{2\alpha }/\alpha ^2)+c_0t_n^{\alpha }\max \limits _{2\le j\le n}(\tau _j^2+t_{j-1}^{2\alpha -2}\tau _j^2), 1\le n\le K, \end{aligned}$$

thus,

$$\begin{aligned} \sum \limits _{j=1}^{n}b_{n-j}^{(n)}\Vert {\tilde{R}}^j\Vert\le & {} c_0\tau _1^{3\alpha }+c_0t_n^{\alpha } \max \limits _{2\le j\le n}(\tau _j^2+t_{j-1}^{2\alpha -2}\tau _j^2)\nonumber \\\le & {} c_0\tau _1^{3\alpha }+c_0\tau _n^{2} \nonumber \\\le & {} c_0 K^{-\min \{3{\check{r}}\alpha ,2\}}, 1\le n\le K. \end{aligned}$$

(3.30)

Notice that the conditions of theorem about $\xi ^0$, then, with the help of Lemma 2, for $1\le n\le K$, we obtains

$$\begin{aligned} \Vert \xi ^n\Vert _{{\mathcal {M}}_r}\le & {} 4E_{\alpha }(2{\hat{\kappa }}_{+} t_n^{\alpha }) (( c_1\varGamma (1-\alpha )t_n^{\alpha /2}/4+ \varGamma (1-\alpha )T^{\alpha }(3c_0+2c_0K_0))h^{r+1} \\&+(t_n+ t_n^{\alpha }/\alpha )h^{r+1} +c_0\varGamma (1-\alpha )T^{\alpha } K^{-\min \{{\check{r}}\alpha ,2-\alpha \}} +c_0 K^{-\min \{3{\check{r}}\alpha ,2\}}). \end{aligned}$$

Therefore, using triangle inequality, Lemma 2, and the equivalence of norms on ${\mathcal {M}}^0_r(\delta )$ complete the proof. $\square$

Remark 1

The hypothesis $u(\cdot ,t)\in L^{\infty }({\mathbb {R}}^{d})$ for $t\in (0,T]$ means there exists a constant $C_0>0$ such that $\Vert u\Vert _{L^{\infty }}\le C_0$. This hypothesis is proper because the value of u is bounded in the real applications. For example, for the nonlinear term $f(u)=u(1-u)$ in problem (4.32), we have $f'(u)=1-2u$, $f''(u)=-2$, and $\Vert 1-2u\Vert \le 1+2\Vert u\Vert _{L^{\infty }}\le C_0$, $\Vert f''(u)\Vert =2\le C_0$. For the nonlinear term $f(u)=u(1-u)(u-1)$ in problem (3.33), we have $f'(u)=-1+4u-3u^2$, $f''(u)=4-6u$, and $\Vert -1+4u-3u^2\Vert \le (1+3\Vert u\Vert _{L^{\infty }})(1+\Vert u\Vert _{L^{\infty }})\le C_0$, $\Vert 4-6u\Vert \le 4+6\Vert u\Vert _{L^{\infty }}\le C_0$. This indicates the proposed L1-OSC method is able to ensure the unconditionally stable and convergence for problem (4.32) and problem (3.33) according to the proof of Theorem 1.

4 Numerical Experiments

We employ the space of piecewise Hermite cubics, ${\mathcal {M}}^0_{3}(\delta )$, to present our numerical results with graded mesh $t_n=T(n/K)^{{\check{r}}}$.

Example 1

We consider the following fourth-order nonlinear subdiffusion equation with $(x,t)\in (0,1)\times (0,1]$,

$$\begin{aligned} \partial ^{\alpha }_tu+\varDelta ^2 u=\varDelta u+\frac{1}{2+\cos (u)}+g(x,t), \end{aligned}$$

(4.31)

subject to zero-valued boundary, and initial data and the source function g(x, t) are given from the exact solution $u(x,t)=(\omega _{1+\beta }(t)+\omega _{2+\beta }(t))\sin (\pi x)$, $\beta \in (0,1)$ is the regularity parameter.

First, the temporal errors and rate of convergence are shown in Tables 1, 2 and 3 for $1/h=100$ and ${\check{r}}=2-\alpha /\alpha$. Table 1 considers the case of $\beta =\alpha =0.6,0.8$; Table 2 considers the case of $\alpha =0.8$ fixed and $\beta$ changing; Table 3 considers the case of $\beta =0.8$ fixed and $\alpha$ changing. The orders of convergence displayed in Tables 1, 2 and 3 indicate that the rate of convergence is $K^{-(2-\alpha )}$, which match with our theoretical analysis in convergence Theorem.

Taking $K=\lfloor h^{\frac{4}{\alpha -2}}\rfloor$ and ${\check{r}}=2-\alpha /\alpha$, we show the spatial errors and rate of convergence in Table 4. The $O(h^4)$ convergence are observed, again as predicted by convergence Theorem.

Table 1 Convergent results in time with $h=1/100$ for Example 1 in the case $\alpha =\beta$

Table 2 Convergent results in time with $h=1/100$ for Example 1 in the case of $\alpha$ fixed

Table 3 Convergent results in time with $h=1/100$ for Example 1 in the case of $\beta$ fixed

Table 4 Errors and convergence results in spatial direction for Example 1

Example 2

We consider the following fourth-order fractional Fisher-type equation with $(x,t)\in (0,1)\times (0,1]$,

$$\begin{aligned} \partial ^{\alpha }_tu+\varDelta ^2 u=\varDelta u+u(1-u)+g(x,t), \end{aligned}$$

(4.32)

subject to zero-valued boundary, and initial data and the source function g(x, t) are given from the exact solution $u(x,t)=\sin (\pi x)\omega _{1+\beta }(t)$, $\beta \in (0,1)\cup (1,2)$ is the regularity parameter.

The computational parameters are listed as follows.

• Table 5: $K=\lfloor h^{\frac{4}{\alpha -2}}\rfloor$, ${\check{r}}=2-\alpha /\alpha$, $\beta =\alpha =0.4,0.6,0.8$.

• Table 6: $1/h=100$, ${\check{r}}=2-\alpha /\alpha$, $\beta =\alpha =0.4,0.6,0.8$.

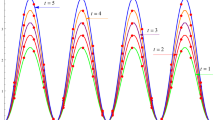
• Figure 1: $1/h=32$, $K=\lfloor h^{\frac{4}{\alpha -2}}\rfloor$, ${\check{r}}=2-\alpha /\alpha$, $\beta =\alpha =0.4$.

• Figure 2: For the fixed $K=8,16,32,64$, $N=16,32,64,128,256$, ${\check{r}}=2-\alpha /\alpha$, $\beta =\alpha =0.4$.

• Figure 3: For the fixed $K=32,64,128,256$, $N=16,32,64,128,256$, ${\check{r}}=2-\alpha /\alpha$, $\beta =\alpha =0.6$.

From Tables 5 and 6, we find that the numerical results match with our theoretical analysis of convergence Theorem. In Fig. 1 we draw the error figure in $\max _{1\le k\le K}\Vert u_h^k-u^k\Vert _{L^{\infty }}$ for $1/h=32$, $K=\lfloor h^{\frac{4}{\alpha -2}}\rfloor$, ${\check{r}}=2-\alpha /\alpha$, $\beta =\alpha =0.4$. We can conclude that our proposed L1-OSC method can approximate well for the solution.

Further, we confirm the unconditional convergence of our proposed method for different $\alpha$. The $L^2$ errors are given in Figs. 2 and 3 for $\alpha =0.4,0.6$. We find that for a fixed K, the $L^2$ errors asymptotically tend to a constant, that is to say that, there is no time-step restrictions for our scheme dependent on the spatial mesh size h.

Table 5 $L^2$ norm convergent results in space with $K=\lfloor h^{\frac{4}{\alpha -2}}\rfloor$ for Example 2

Table 6 Convergent results in time with $h=1/100$ for Example 2

Fig. 1

The global error at $\alpha =0.4$ in time and space for Example 2

Fig. 2

The $L^2$ error at $\alpha =0.4$ for Example 2

Fig. 3

The $L^2$ error at $\alpha =0.6$ for Example 2

Example 3

In the example, we consider the following fourth-order fractional Huxley-type equation (2.6) with $x=(x_1,x_2)\in (0,1)\times (0,1)$, $t\in (0,1]$.

$$\begin{aligned} \partial ^{\alpha }_tu+\varDelta ^2 u=\varDelta u+u(1-u)(u-1)+g(x,t), \end{aligned}$$

(3.33)

subject to zero-valued boundary, and initial data and the function g(x, t) are determined by the exact solution $u(x,t)=\sin (\pi x_1)\sin (\pi x_2)\omega _{1+\beta }(t)$, $\beta \in (0,1)\cup (1,2)$ is the regularity parameter.

The computational parameters are listed as follows.

• Table 7: $K=\lfloor h^{\frac{4}{\alpha -2}}\rfloor$, ${\check{r}}=2-\alpha /\alpha$ for different $\alpha$ and $\beta$.

• Table 8: $1/h=100$, ${\check{r}}=2-\alpha /\alpha$ for different $\alpha$ and $\beta$.

• Figure 4: For the fixed $K=32,64,128,256$, $N=16,32,64,128,256$, ${\check{r}}=2-\alpha /\alpha$, $\beta =\alpha =0.6$.

• Figure 5: For the fixed $K=32,64,128,256$, $N=16,32,64,128,256$, ${\check{r}}=2-\alpha /\alpha$, $\beta =\alpha =0.8$.

The numerical errors and convergence orders are given in Tables 7 and 8, we find that the numerical results match with our theoretical analysis of convergence Theorem. Again, to further confirm the unconditional convergence of our proposed method for different $\alpha$, the $L^2$ errors are shown in Figs. 4 and 5 for $\alpha =0.6,0.8$. The figures results present that for a fixed K, the errors in $L^2$-norm asymptotically tend to a constant, which implies that there is no time-step restrictions for our proposed scheme dependent on the spatial mesh size h. Those results further confirm our theoretical analysis.

Table 7 Errors and convergence results in spatial direction for Example 3

Table 8 Convergent results in time with $h=1/100$ for Example 3

Fig. 4

The $L^2$ error at $\alpha =0.6$ for Example 3

Fig. 5

The $L^2$ error at $\alpha =0.8$ for Example 3

5 Conclusion

In order to effectively solve nonlinear fourth-order reaction–subdiffusion equation whose solutions display a typical initial weak singularity, we introduce the orthogonal spline collocation method to discrete the spatial variable and the L1-scheme on graded meshes to discrete the time-fractional Caputa derivative, the Newton linearized scheme to approximate the nonlinear term. Based on the discrete fractional Grönwall inequality, the discrete fractional convolution kernel and the temporal–spatial OSC error splitting technology, the optimal convergence rate of the Newton linearized L1-OSC method are gained. Moreover the unconditional convergence results of our proposed L1-OSC method are proved with considering the initial singularity. Especially, there is no time step restrictions that depends on the size of the spatial mesh. Our analytical technique can provide new insights in analyzing other fourth-order fractional differential equations with weakly singular solutions.