An Efficient Formulation of Chebyshev Tau Method for Constant Coefficients Systems of Multi-order FDEs

Abstract

The objective of the present work is to introduce a computational approach employing Chebyshev Tau method for approximating the solutions of constant coefficients systems of multi-order fractional differential equations. For this purpose, a series representation for the exact solutions in a neighborhood of the origin is obtained to monitor their smoothness properties. We prove that some derivatives of the exact solutions of the underlying problem often suffer from discontinuity at the origin. To fix this drawback and design a high order approach a regularization procedure is developed. In addition to avoid high computational costs, a suitable strategy is implemented such that approximate solutions are obtained by solving some triangular algebraic systems. Complexity and convergence analysis of the proposed scheme are provided. Various practical test problems are presented to exhibit capability of the given approach.

1 Introduction

For nearly three centuries, the theory of fractional calculus has been considered by mathematicians as a branch of pure mathematics. However, many researchers have recently found that non-integer derivatives and integrals are more useful than integer ones for modeling the phenomena that have inherited and memory properties [3, 17, 31, 43], and in this regard various numerical methods have been introduced to approximate the solutions of the arising fractional order functional equations [22,23,24,25, 34,35,36,37,38,39]. There are many physical issues which correlate a number of separated elements and thereby one may expect that their mathematical modeling leads to systems of differential equations. In this connection, systems of fractional differential equations (FDEs) have recently been used to describe the various properties of the phenomena in physics and engineering such as pollution levels in a lake [7, 29], hepatitis B disease in medicine [9], fractional-order financial system [11], population dynamics [14, 15], fractional order Bloch system [26], electrical circuits [28], fractional-order love triangle system [32], nuclear magnetic resonance (NMR) [33, 50], fractional-order Volta’s system [42], magnetic resonance imaging (MRI) [44], fractional-order Lorenz system [49] and fractional-order Chua’s system [51].

Due to high usage of the systems of FDEs, the researchers have tried to find analytic and numerical methods to solve them. Since it is very difficult or practically impossible to obtain accurate solutions for most systems of FDEs, it is important to provide suitable approximate methods for solving them. Specially due to wide applications for constant coefficients systems of FDEs, researchers have recently adopted various numerical techniques to approximate their solutions such as Homotopy perturbation method [1, 4], Chebyshev Tau method [2], fractional order Laguerre and Jacobi Tau methods [5, 6], Legendre wavelets method [12], Adomian decomposition method [13, 40], differential transform method [19], spectral collocation method [29, 30], variational iteration method (VIM) [40, 46] and Bernoulli wavelets method [47].

However, in some of the aforementioned studies, the effect of the possible discontinuity behavior in the derivatives of the solution has not paid attention, and basis functions are selected from infinitely smooth functions. Most importantly, the available researches often provide numerical methods for systems of single order FDEs and there are a few articles related to a comprehensive numerical analysis of systems of multi-order FDEs. In this regard, the main object of this paper is to fill this gap with providing a reliable and high order numerical technique using Chebyshev Tau method for approximating the solutions of the following constant coefficients system of multi-order FDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\alpha _j}_C y_j(x)=\displaystyle \sum \limits _{i=1}^{n}{a_{ji} y_i(x)}+p_j(x),\quad j=1, 2, \ldots ,n,\\ y_j^{(k)}(0)=y_{j,0}^{(k)},~k=0,1,\ldots , \lceil \alpha _j \rceil -1,~ x \in \Lambda =[0,1],~ \alpha _{j} \in \mathbb {Q}^{+}, \end{array}\right. } \end{aligned}$$

(1)

where $\lceil . \rceil$ is the ceiling function, $a_{ji}$ are given constants, $p_j(x)$ are continuous functions on $\Lambda$ and $y_j(x)$ are unknowns. Here $D^{\alpha _{j}}_{C}$ is the Caputo type fractional derivative of order $\alpha _{j}$ defined by [10, 17, 31, 43]

$$\begin{aligned} D^{\alpha _j}_C y_j(x)=J^{\lceil \alpha _j \rceil -\alpha _{j}}D^{\lceil \alpha _j \rceil }y_{j}(x), \end{aligned}$$

where $J^{\lceil \alpha _j \rceil -\alpha _{j}}$ is the Riemann–Liouville fractional integral operator of order $\lceil \alpha _j \rceil -\alpha _{j}$ and is defined by

$$\begin{aligned} J^{\lceil \alpha _j \rceil -\alpha _{j}}y(x)=\dfrac{1}{\Gamma (\lceil \alpha _j \rceil -\alpha _{j})} \int _0^x{(x-t)^{\lceil \alpha _j \rceil -\alpha _{j}-1}y(t)dt}, \end{aligned}$$

and $\Gamma (.)$ denotes as the Gamma function. It can be seen that for $\alpha , \beta \ge 0$ the following relations hold

$$\begin{aligned} J^{\alpha }D_{C}^{\alpha }y(x)= & {} y(x)-\sum \limits _{k=0}^{\lceil \alpha \rceil -1}\dfrac{D^{k}y(0)}{k!}x^{k},\nonumber \\ J^{\alpha }x^{\beta }= & {} \frac{\Gamma (\beta +1)}{\Gamma (\alpha +\beta +1)}x^{\alpha +\beta }, \end{aligned}$$

(2)

under validity of some requirements for the function y(x) [10, 17, 31, 43].

Although the classical implementation of spectral methods provides a useful tool to produce high order approximations for smooth solutions of functional equations, there are some disadvantages including need for solving complex and ill-conditioned algebraic systems as well as a significant reduction in the accuracy for problems with non-smooth solutions. In this paper, in order to avoid these drawbacks, the numerical approach is designed such that not only the expected higher accuracy is reconstructed regarding the non-smooth problems by proceeding a regularization technique, but also approximate solutions are computed by solving well-conditioned triangular systems.

The remainder of this paper is divided into six sections as follows. In the later section, we first introduce a result on the existence and uniqueness of the solutions of (1). Then, the smoothness theorem is given, which derives a series representation for the solutions of (1) and concludes that some derivatives of the exact solutions often suffer from discontinuity at the origin. To fix this difficulty, a regularization strategy is proceeded. In Sect. 3, to survey the effect of this regularization process on providing high-order approximations, the Chebyshev Tau approach is developed to approximate the solutions of (1) which satisfy the assumptions of the existence, uniqueness and smoothness theorems. The uniquely solvability and complexity analysis of the numerical solution are also justified by solving some triangular algebraic systems. In Sect. 4, we provide a detailed convergence analysis for the proposed scheme in uniform norm. In Sect. 5, efficiency and applicability of the proposed method are examined by different illustrative examples. The final section contains our conclusive remarks.

2 Existence, Uniqueness and Smoothness Results

In this section we investigate existence, uniqueness and smoothness properties of the solutions of (1). First, the existence and uniqueness theorem is given as follows.

Theorem 1

Assume that the functions $\{p_{j}(x)\}_{j=1}^n$ are continuous on $\Lambda$. Then the system of Eq. (1) has a unique continuous solution on $\Lambda$.

Proof

Clearly, it is a straightforward consequence of Theorem 8.11 of [17] and Theorem 2.3 of [16]. $\square$

From the well-known existence and uniqueness theorems of FDEs, we expect some derivatives of the exact solutions of (1) to have a discontinuity at the origin, even for smooth input functions depending on the fractional derivative order [17]. Therefore, to develop high order approximate approaches, recognizing the smoothness properties of the solutions of (1) under certain assumptions on the given functions $p_{j}(x)$ is essential. In this regard, recently in [16] Diethelm et al. investigated the degree of smoothness and asymptotic behavior of the solutions of homogeneous constant coefficients multi-order FDEs when fractional derivatives lie in the interval (0,1). In the following theorem we try to derive the same properties for the constant coefficients systems of multi-order FDEs in the general form (1) by exploring a series representation of the solutions in a neighborhood of the origin.

Theorem 2

Let $\{\alpha _{j}=\eta _{j}/\gamma _{j}\}_{j=1}^n$, such that the integers $\eta _{j}\ge 1$ and $\gamma _{j}\ge 2$ are co-prime and the given continuous functions $p_j(x)$ can be written as $p_j(x)=\bar{p}_j(x^{1/\gamma _1}, x^{1/\gamma _2}, \ldots , x^{1/\gamma _n})$ with analytic functions $\bar{p}_j$ in the neighborhood of $(\underbrace{0,0,\ldots ,0}_{n})$. Then the series representation of the solution $y_j(x)$ of the Eq. (1) in a neighborhood of the origin is given by

$$\begin{aligned} y_j(x)=\phi _j(x)+\sum \limits _{\nu _{j}=\eta _j}^{\infty }{\sum \limits _{\nu _{1},\ldots ,\nu _{j-1},\nu _{j+1}\ldots , \nu _{n}=0}^{\infty }{\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~x^{\frac{\nu _{j}}{\gamma _j}+\sum \nolimits _{k=1,k\ne j}^{n}{\frac{\nu _{k}}{\gamma _k}}}}}, \end{aligned}$$

where $\phi _j(x)=\sum \nolimits _{i=0}^{\lceil \alpha _j \rceil -1}{\frac{y_{j,0}^{(i)}}{i!}x^i}$ and $\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}$ are known coefficients.

Proof

Consider the functions

$$\begin{aligned} y_j(x)=\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~ x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}}}},\quad j=1, 2, \ldots , n, \end{aligned}$$

(3)

satisfying the initial condition of Eq. (1). On the other hand, since the functions $\bar{p}_j$ are analytic, the functions $p_j$ can be written as

$$\begin{aligned} p_j(x)=\bar{p}_j(x^{1/\gamma _1}, x^{1/\gamma _2}, \ldots , x^{1/\gamma _n})=\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{\tilde{p}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}}}}, \end{aligned}$$

(4)

where $\{\tilde{p}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}\}_{j=1}^n$ are known coefficients. In the sequel, we show that the coefficients $\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}$ are calculated in such a way that the representation (3) converges and solves the Eq. (1). Trivially the Eq. (1) is equivalent to the following system of second kind Volterra integral equations

$$\begin{aligned} y_j(x)=\phi _j(x)+\sum \limits _{i=1}^{n}{a_{ji} J^{\alpha _j} y_i(x)}+J^{\alpha _j}p_j(x),\quad j=1, 2, \ldots , n. \end{aligned}$$

(5)

Therefore, assuming uniform convergence and substituting the relations (3) and (4) into (5), the coefficients $\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}$ satisfy in the following equality

$$\begin{aligned}&\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}} }}\\&\quad =\phi _j(x)+\sum \limits _{i=1}^{n}{~\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{a_{ji}~\bar{y}_{i,\nu _{1},\nu _{2},\ldots , \nu _{n}}~J^{\alpha _j}\Bigg (x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _k}{\gamma _k}} }\Bigg )}}\\&\qquad +\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{\tilde{p}_{j,\nu _{1},\nu _{2},\ldots , \nu _{n}}~J^{\alpha _j}\Bigg (x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}}}\Bigg )},~~j=1, 2,\ldots , n. \end{aligned}$$

Using (2) the above equality can be written as

$$\begin{aligned}&\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}} }}\nonumber \\&\quad =\phi _j(x)+\xi _{j}\left( \sum \limits _{i=1}^{n}{~\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{a_{ji}~\bar{y}_{i,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~ ~x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}+\alpha _j} }}}\nonumber \right. \\&\qquad \left. +\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{\tilde{p}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~~ x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}}+\alpha _j}}\right) ,~~j=1, 2,\ldots , n, \end{aligned}$$

(6)

where $\xi _{j}=\frac{\Gamma {(\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}+1})}}{\Gamma {(\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}+\alpha _{j}+1})}}$. Substituting $\nu _j=\nu _j-\eta _j$ in the both series of the right-hand side of (6), we obtain

$$\begin{aligned}&\sum \limits _{\nu _{1},\nu _{2},\ldots , \nu _{n}=0}^{\infty }{\bar{y}_{j,\nu _{1},\nu _{2},\ldots , \nu _{n}}~x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}} }}\nonumber \\&\quad ={\phi _j(x)+\tilde{\xi }_{j}\Bigg (\sum \limits _{i=1}^{n}{~\sum \limits _{\begin{array}{c} \nu _{j}=\eta _{j}\\ \nu _{k}=0,k\ne j \end{array}}^{\infty }{a_{ji}~\bar{y}_{i,\nu _{1},\ldots ,\nu _{j}-\eta _{j},\ldots \nu _{n}}~~x^{\sum \nolimits _{k=1}^{n}\frac{\nu _k}{\gamma _k}} }}}\nonumber \\&\qquad +\sum \limits _{\begin{array}{c} \nu _{j}=\eta _{j}\\ \nu _{k}=0,k\ne j \end{array}}^{\infty }{\tilde{p}_{j,\nu _{1},\ldots ,\nu _{j}-\eta _{j},\ldots \nu _{n}}~ x^{\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}}}}\Bigg ),~~j=1, 2, \ldots , n, \end{aligned}$$

(7)

in which $\tilde{\xi }_{j}=\frac{\Gamma {(\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}-\alpha _{j}+1})}}{\Gamma {(\sum \nolimits _{k=1}^{n}{\frac{\nu _{k}}{\gamma _k}+1})}}$. Now, we try to obtain the unknown coefficients $\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}$ by comparing the coefficients of $x^{\frac{\nu _{1}}{\gamma _1}} x^{\frac{\nu _{2}}{\gamma _2}}...x^{\frac{\nu _{n}}{\gamma _n}}$ on both sides of (7). The results of this comparison depend on $\nu _{j}$. Clearly for $\{\nu _{j}<\eta _j\}_{j=1}^n$, we have

$$\begin{aligned} \bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}=\left\{ \begin{array}{ll} \frac{y_{j,0}^{\left( \frac{\nu _{j}}{\gamma _j}\right) }}{\left( \frac{\nu _{j}}{\gamma _j}\right) !},&{}\quad \nu _{j}=0, \gamma _j,\ldots , (\lceil \alpha _j \rceil -1)\gamma _j,\quad \nu _{k}=0, \quad k\ne j,\\ 0&{}\quad \text {else}. \end{array}\right. \end{aligned}$$

For $\{\nu _{j}\ge \eta _j\}_{j=1}^n$ and $\nu _{k} \ge 0$, $k \ne j$, we obtain

$$\begin{aligned} \bar{y}_{j,\nu _{1}, \nu _{2},\ldots , \nu _{n}}=\tilde{\xi }_{j}\left( \sum \limits _{i=1}^{n} \big (a_{ji}~\bar{y}_{i,\nu _{1},\ldots ,\nu _{j}-\eta _{j},\ldots \nu _{n}}\big )+\tilde{p}_{j,\nu _{1},\ldots ,\nu _{j}-\eta _{j},\ldots \nu _{n}}\right) , \end{aligned}$$

(8)

and thereby the coefficients $\bar{y}_{j,\nu _{1}, \nu _{2},\ldots , \nu _{n}}$ with $\nu _{1}+\nu _{2}+\cdots +\nu _{n}=l$, $l \ge \eta _j$ can be calculated from (8), such that this calculation requires the knowledge of $\bar{y}_{j,\nu _{1}, \nu _{2},\ldots , \nu _{n}}$ with $\nu _{1}+\nu _{2}+\cdots +\nu _{n}\le l-1$. Therefore, we should first evaluate all the coefficients with $\nu _{1}+\nu _{2}+\cdots +\nu _{n}=\eta _j$, then with $\nu _{1}+\nu _{2}+\cdots +\nu _{n}=\eta _{j}+1$, etc. This means that the series representation (3) solves (1).

Now, it should be proved that this series is uniformly and absolutely convergent in a neighborhood of the origin. For this purpose, we apply a suitable modification of the well-known Lindelof’s theorem [17, 27]. Consider the following system of the second kind Volterra integral equations

$$\begin{aligned} Y_j(x)=\tilde{\phi }_j(x)+\sum \limits _{i=1}^{n}{|a_{ji}|J^{\alpha _j}y_i(x)}+J^{\alpha _j}|p_j(x)|,~~j=1, 2,\ldots , n, \end{aligned}$$

where $\tilde{\phi }_j(x)=\sum \nolimits _{k=0}^{\lceil \alpha _j \rceil -1}{\frac{x^k}{k!}|y_{j,0}^{(k)}|}$. Evidently the right-hand side of the above equation is a majorant of the right-hand side of the main Eq. (5) and the formal solution $\{Y_j(x)\}_{j=1}^n$ can be calculated exactly as the previous step such that all of its coefficients are positive. Now we show that the series expansion of $Y_j(x)$ is absolutely convergent for each $x \in [0,\kappa _j]$, with some $\kappa _j>0$ which is defined in the sequel. To this end, it is sufficient to show that the finite partial sum of $Y_j(x)$ is uniformly bounded over $[0,\kappa _j]$. Let

$$\begin{aligned} S_{j,K+1}(x)=\tilde{\phi }_j(x)+\sum \limits _{\nu _{j}=\eta _j}^{K+1}{\sum \limits _{\nu _{1},\ldots ,\nu _{j-1},\nu _{j+1}..., \nu _{n}=0}^{K+1}{\bar{Y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~x^{\frac{\nu _{j}}{\gamma _j}+\sum \nolimits _{k=1,k\ne j}^{n}{\frac{\nu _{k}}{\gamma _k}}}}}, \end{aligned}$$

is the finite partial sum of $Y_j(x)$ for $j=1, 2,\ldots , n$. The following inequality evidently holds

$$\begin{aligned} S_{j,K+1}(x) \le \tilde{\phi }_j(x)+\sum \limits _{i=1}^{n}{|a_{ji}|J^{\alpha _j}S_{i,K}(x)}+J^{\alpha _j}|p_j(x)|,~~j=1, 2,\ldots , n, \end{aligned}$$

in view of the recursive calculation of the coefficients. More precisely, if we expand the right-hand side of the above inequality, all coefficients $\bar{Y}_{j,\nu _{1},\ldots ,\nu _{n}}$ with $\sum \nolimits _{l=1}^{n}{\frac{\nu _{l}}{\gamma _l}}\le (K+1) \left( \sum \nolimits _{l=1}^{n}{\frac{1}{\gamma _l}}\right)$ are eliminated from both sides while there will some additional positive terms remain in the right-hand side with higher order. Considering

$$\begin{aligned}&D_1^{(j)}=\sum \limits _{k=0}^{\lceil \alpha _j \rceil -1}{\frac{1}{k!}|y_{j,0}^{(k)}|},\\&D_2^{(j)}=\max _{(x,z_1,\ldots ,z_n)\in [0,1]\times [0 ,2D_1^{(1)}]\times ...\times [0,2D_1^{(n)}]}{\frac{\left[ \sum _{i=1}^{n}|a_{ji}|z_i+|p_j(x)|\right] }{\Gamma {(\alpha _j+1)}}},\\&\quad j=1, 2,\ldots , n, \end{aligned}$$

we define

$$\begin{aligned} \kappa _j=\min \left\{ 1,\left[ \frac{D_1^{(j)}}{D_2^{(j)}}\right] ^{\frac{1}{\alpha _j}}\right\} ,~~ j=1, 2,\ldots , n. \end{aligned}$$

Now we intend to show that $|S_{j,K}(x)| \le 2 D_1^{(j)}$ for $1 \le j \le n$ and $x \in [0, \kappa _j]$. This issue is done through induction over K. For $K=0$, from definition of $D_1^{(j)}$ we have

$$\begin{aligned} S_{j,0}(x)=|y_{j,0}^{(0)}| \le D_1^{(j)},~~j=1, 2,\ldots , n. \end{aligned}$$

For the induction step from K to $K+1$, we can write

$$\begin{aligned}&|S_{j,K+1}(x)|=S_{j,K+1}(x) \le \tilde{\phi }_j(x)+\sum \limits _{i=1}^{n}{|a_{ji}|J^{\alpha _j}S_{i,K}(x)}+J^{\alpha _j}|p_j(x)|\\&\quad \le \sum \limits _{k=0}^{\lceil \alpha _j \rceil -1}{\frac{\kappa _j^k}{k!}|y_{j,0}^{(k)}|}+\max _{t \in [0,x]} \quad \left[ \sum \limits _{i=1}^{n}{|a_{ji}| S_{i,K}(t)}+|p_j(t)|\right] \frac{x^{\alpha _j}}{\Gamma {(\alpha _j+1)}}\\&\quad \le D_1^{(j)}+\max _{t \in [0,x]} \left[ \sum \limits _{i=1}^{n}{|a_{ji}| S_{i,K}(t)}+|p_j(t)|\right] \frac{x^{\alpha _j}}{\Gamma {(\alpha _j+1)}} \\&\quad \le D_1^{(j)}+\kappa _j^{\alpha _j} D_2^{(j)}\le 2 D_1^{(j)},~~j=1, 2, \ldots , n, \end{aligned}$$

which concludes the uniform boundedness of $S_{j,K+1}(x)$ over $[0, \kappa _j]$. Due to positivity of all its coefficients it is also monotone. Therefore the series expansion of $Y_j$ is absolutely convergent over $[0,\kappa _j]$ and uniformly convergent on the compact subsets of $[0,\kappa _j)$ due to the power series structure of $Y_j(x)$. Finally, Lindelof’s theorem indicates that series expansion of $y_j(x)$ are absolutely and uniformly convergent on the compact subsets of $[0,\kappa _j)$ too. Therefore, the interchange of integration and series was done correctly. $\square$

From Theorem 2, we can conclude that the $\lceil \alpha _j \rceil$th derivative of $y_{j}(x)$ often has a discontinuity at the origin. This difficulty affects accuracy when the classical spectral methods are implemented to approximate the exact solutions. To overcome this weakness, we apply the coordinate transformation

$$\begin{aligned} x=v^\gamma ,\quad t=w^\gamma ,\quad v=x^{\frac{1}{\gamma }},\quad w=t^{\frac{1}{\gamma }}, \end{aligned}$$

(9)

where $\gamma$ is the least common multiple of $\gamma _j$, and convert the Eq. (5) into the following system of equations

$$\begin{aligned} \hat{y}_j(v)=\sum \limits _{i=1}^{n}{a_{ji}\hat{J}^{\alpha _j}\hat{y}_i(v)}+\hat{J}^{\alpha _j}\hat{p}_j(v)+\hat{\phi }_j(v),~~j=1, 2,\ldots , n, \end{aligned}$$

(10)

where $\hat{\phi }_j(v)=\phi _j(v^\gamma )$, $\hat{p}_j(v)=p_j(v^\gamma )$ and

$$\begin{aligned} \hat{J}^{\alpha _j}\hat{y}_i(v)=\frac{\gamma }{\Gamma {(\alpha _j)}}\int \limits _{0}^{v}{(v^\gamma -w^\gamma )^{\alpha _j-1}w^{\gamma -1} \hat{y}_i(w)dw}. \end{aligned}$$

(11)

Here $\hat{y}_j(v)$ is the infinitely smooth exact solution of (10) and given by

$$\begin{aligned}&\hat{y}_j(v)=y_j(v^\gamma )\\&\quad =\hat{\phi }_j(v) +\sum \limits _{\nu _{j}=\eta _j}^{\infty } {\sum \limits _{\nu _{1},\ldots ,\nu _{j-1},\nu _{j+1}..., \nu _{n}=0}^{\infty }{\bar{y}_{j,\nu _{1},\nu _{2},\ldots ,\nu _{n}}~x^{b_j \nu _{j}+\sum \nolimits _{k=1,k \ne j}^{n}{b_k \nu _{k}}}}}, \end{aligned}$$

for $\frac{\gamma }{\gamma _j}=b_j \in \mathbb {N},~j=1, 2,\ldots , n$. Consequently, variable transformation (9) regularizes the solutions and provides the possibility of obtaining the familiar exponential accuracy by implementing the classical spectral methods. To monitor the effect of this regularization process on producing high-order approximations for (1), we assume that the assumptions of Theorem 2 hold in the sequel.

3 Numerical Approach

In this section, we introduce an efficient formulation of Chebyshev Tau approach for approximating the solutions of the transformed Eq. (10). For this purpose, we consider Chebyshev Tau solutions of (10) as follows

$$\begin{aligned} \hat{y}_{j,N}(v)=\sum \limits _{i=0}^{\infty }c_{ji}\mathcal {T}_i(v)=\underline{c}_j\underline{\mathcal {T}}=\underline{c}_j\mathcal {T}\underline{V},\quad \underline{c}_j=[c_{j0},c_{j1},\ldots ,c_{jN},0,\ldots ], \end{aligned}$$

(12)

for $j=1,2,\ldots , n$, where $\underline{\mathcal {T}}=[\mathcal {T}_0(v), \mathcal {T}_1(v),\ldots , \mathcal {T}_N(v),\ldots ]^{T}$ is the vector of shifted Chebyshev polynomial basis with degree $(\mathcal {T}_i(v))\le i$ for $i \ge 0$ on $\Lambda$. Furthermore, $\mathcal {T}$ is a lower triangular invertible matrix and $\underline{V}=[1, v, v^{2},\ldots , v^{N},\ldots ]^T$. Substituting (12) into (10) and assuming

$$\begin{aligned} \hat{\phi }_j(v)= & {} \sum \limits _{i=0}^{\infty }\hat{\phi }_{ji}v^{i}=\underline{\phi }_j\underline{V},\quad \quad \underline{\phi }_j=[ \hat{\phi }_{j0},\hat{\phi }_{j1},\ldots ,\hat{\phi }_{jN},0,\ldots ],\\ \hat{p}_j(v)\simeq & {} \hat{p}_{j,N}(v)=\sum \limits _{i=0}^{\infty }\hat{p}_{ji}\mathcal {T}_i(v)=\underline{p}_j\underline{\mathcal {T}}=\underline{p}_j\mathcal {T}\underline{V},\\ \underline{p}_j= & {} [\hat{p}_{j0},\hat{p}_{j1},\ldots ,\hat{p}_{jN},0,\ldots ], \end{aligned}$$

for $j=1,2,\ldots , n$, we can write

$$\begin{aligned} \underline{c}_j \mathcal {T} \underline{V}=\sum \limits _{i=1}^{n}{a_{ji}\underline{c}_i \mathcal {T} \hat{J}^{\alpha _j}\underline{V}}+\underline{p}_j\mathcal {T} \hat{J}^{\alpha _j}\underline{V}+\underline{\phi }_j\underline{V},~~j=1, 2,\ldots ,n. \end{aligned}$$

(13)

Therefore, it suffices to compute $\{\hat{J}^{\alpha _j}\underline{V}\}_{j=1}^n$. For this purpose using the relation (2) we have

$$\begin{aligned} \hat{J}^{\alpha _j}\underline{V}= & {} [\hat{J}^{\alpha _j}v^{i}]_{i \ge 0}= \Bigg [\frac{\gamma }{\Gamma (\alpha _j)}\int _{0}^{v}(v^{\gamma }-w^{\gamma })^{\alpha _j-1}w^{i+\gamma -1}dw\Bigg ]_{i \ge 0}\nonumber \\= & {} \Bigg [\frac{v^{\gamma \alpha _j+i}}{\Gamma (\alpha _j)}\int _{0}^{1}(1-z)^{\alpha _j-1}z^{i/\gamma }dz\Bigg ]_{i\ge 0}\nonumber \\= & {} \Bigg [\frac{\Gamma {(\frac{i}{\gamma }+1)}}{\Gamma {(\alpha _j+\frac{i}{\gamma }+1)}}v^{\gamma \alpha _j+i}\Bigg ]_{i \ge 0}=\mathcal {B}_j \underline{V},\quad j=1,2,\ldots ,n, \end{aligned}$$

(14)

with

$$\begin{aligned} \mathcal {B}_j= \begin{bmatrix} \overbrace{0 \ldots 0}^{\alpha _{j}\gamma }&{}\quad \frac{1}{\Gamma {(\alpha _j+1)}}&{}\quad 0&{}\quad \ldots &{}\quad \quad \\ \vdots &{}\quad 0&{}\quad \frac{\Gamma {\left( \frac{1}{\gamma }+1\right) }}{\Gamma {\left( \alpha _j+\frac{1}{\gamma }+1\right) }}&{}\quad 0&{}\quad \cdots &{}\quad \quad \\ \vdots &{}\quad \vdots &{}\quad 0&{}\quad \frac{\Gamma {\left( \frac{2}{\gamma }+1\right) }}{\Gamma {\left( \alpha _j+\frac{2}{\gamma }+1\right) }}&{}\quad 0&{}\quad \cdots \\ \cdots &{}\quad \cdots &{}\quad \quad &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots \end{bmatrix}. \end{aligned}$$

Inserting (14) into (13) yields

$$\begin{aligned} \underline{c}_j \mathcal {T}(I-a_{jj} \mathcal {B}_j)\underline{V}=\sum \limits _{i=1,i \ne j}^{n}{a_{ji}\underline{c}_i \mathcal {T} \mathcal {B}_j\underline{V}}+\underline{p}_j\mathcal {T} \mathcal {B}_j\underline{V}+\underline{\phi }_j\underline{V},\quad j=1,2,\ldots ,n, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \sum \limits _{i=1}^{n}{\underline{c}_i \mathcal {A}_{ij}^{\mathcal {T}}}\underline{\mathcal {T}}=\Big (\underline{p}_j\mathcal {B}_j^{\mathcal {T}}+ \underline{\phi }_j\mathcal {T}^{-1}\Big )\underline{\mathcal {T}},\quad j=1,2,\ldots ,n, \end{aligned}$$

(15)

where $\mathcal {A}_{ij}^{\mathcal {T}}=\mathcal {T}\mathcal {A}_{ij}\mathcal {T}^{-1}$, $\mathcal {B}_j^{\mathcal {T}}=\mathcal {T}\mathcal {B}_{j}\mathcal {T}^{-1}$ and

$$\begin{aligned} \mathcal {A}_{ij}=\left\{ \begin{array}{ll} -a_{ji}\mathcal {B}_j,&{}\quad i \ne j,\\ I-a_{jj}\mathcal {B}_j,&{}\quad i=j, \end{array}\right. \end{aligned}$$

(16)

where I is an identity matrix.

Projecting (15) on the space of $\langle \mathcal {T}_0(v), \mathcal {T}_1(v),\ldots , \mathcal {T}_N(v)\rangle$ and using the orthogonality of $\{\mathcal {T}_i(v)\}_{i=0}^N$, the unknown coefficients satisfy in the following block algebraic system of order n

$$\begin{aligned} \sum \limits _{i=1}^{n}{\underline{c}_i^N \Big (\mathcal {A}_{ij}^{\mathcal {T}}\Big )^N}=\underline{p}_j^N\Big (\mathcal {B}_j^{\mathcal {T}}\Big )^N+ \underline{\phi }_j^N \big (\mathcal {T}^N\big )^{-1},\quad j=1,2,\ldots ,n, \end{aligned}$$

(17)

where the corresponding index N on the top of the matrices and vectors represents the principle sub-matrices and sub-vectors of order $N+1$ respectively and $\underline{c}_i^{N}=[ c_{i0},c_{i1},\ldots ,c_{iN}]$ is the unknown vector which can be accessed by solving $n(N+1)\times n(N+1)$ system of algebraic Eq. (17).

3.1 Numerical Solvability and Complexity Analysis

In this subsection the numerical solvability as well as the complexity analysis of the resulting system (17) are studied. In this respect, multiplying both sides of (17) by $\mathcal {T}^{N}$ and assuming

$$\begin{aligned} \underline{c}_i^{\prime ^{N}}=\underline{c}_i^{N}\mathcal {T}^{N}=[ c_{i0}^{\prime },c_{i1}^{\prime },\ldots ,c_{iN}^{\prime }], \quad i=1,2,\ldots ,n, \end{aligned}$$

(18)

the following algebraic system of order $n(N+1)$

$$\begin{aligned} \underline{C}\Phi =\underline{F}, \end{aligned}$$

(19)

with

$$\begin{aligned} \underline{C}=[\underline{c}_1^{\prime ^{N}},\underline{c}_2^{\prime ^{N}},\ldots ,\underline{c}_n^{\prime ^{N}}], \quad \quad \Phi =\big (\mathcal {A}_{ij}^{N}\big )_{i,j=1}^n, \end{aligned}$$

and

$$\begin{aligned} \underline{F}=\left[ \underline{p}_{1}^{N}\mathcal {T}^{N} \mathcal {B}_1^{N}+\underline{\phi }_1^{N}, \underline{p}_{2}^{N}\mathcal {T}^{N} \mathcal {B}_2^{N}+ \underline{\phi }_2^{N},\ldots , \underline{p}_{n}^{N}\mathcal {T}^{N}\mathcal {B}_n^{N}+\underline{\phi }_n^{N}\right] , \end{aligned}$$

can be obtained. Applying block LU-decomposition for the matrix $\Phi$ we derive

$$\begin{aligned} \Phi =LU=\begin{bmatrix} I&{}\quad \quad &{}\quad \quad &{}\quad \quad &{}\quad \quad \\ L_{2,1}&{}\quad \quad I&{}\quad \quad \quad &{}\quad \quad \quad &{}\quad \quad \quad \\ L_{3,1}&{}\quad L_{3,2}&{}\quad I&{}\quad \quad &{}\quad \quad \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \quad \\ L_{n,1}&{}L_{n,2}&{}\cdots &{}L_{n,n-1}&{}I \end{bmatrix}\begin{bmatrix} U_{1,1}&{}U_{1,2}&{}\ldots &{}U_{1,n-1}&{}U_{1,n}\\ \quad &{}U_{2,2}&{}U_{2,3}&{}\ldots &{}U_{2,n}\\ \quad &{}\quad &{}U_{3,3}&{}\ldots &{}U_{3,n}\\ \quad &{}\quad &{}\quad &{}\ddots &{}\vdots \\ \quad &{}\quad &{}\quad &{}\quad &{}U_{n,n} \end{bmatrix}, \end{aligned}$$

(20)

with the following block matrices of order $N+1$

$$\begin{aligned} L_{i,1}= & {} \mathcal {A}_{i1}^{N}(\mathcal {A}_{11}^{N})^{-1},\quad i=2,3,\ldots ,n, \nonumber \\ U_{1,j}= & {} \mathcal {A}_{1j}^{N},\quad j=1,2,\ldots ,n, \nonumber \\ U_{i,j}= & {} \mathcal {A}_{ij}^{N}-\sum \limits _{r=1}^{i-1}{L_{i,r}U_{r,j}},\quad i=2,3,\ldots ,n,~~j=i,i+1,\ldots ,n,\nonumber \\ L_{j+1,i}= & {} \left( \mathcal {A}_{j+1 i}^{N}- \sum \limits _{r=1}^{i-1}{L_{j+1,r}U_{r,i}}\right) (U_{i,i})^{-1},~~ i=2,\ldots ,n-1,~j=i,\ldots ,n-1.\nonumber \\ \end{aligned}$$

(21)

From (16), it is obvious that $\mathcal {A}_{ij}^N$ is an invertible bi-diagonal upper triangular matrix with the diagonal entries one for $i=j$ and is a single diagonal upper triangular matrix with diagonal entries zero for $i \ne j$. Therefore, from (21) it can be concluded that the following matrices

$$\begin{aligned}&L_{i,j},~~i=2, 3,\ldots , n,\quad j=1, 2,\ldots , n-1,\\&U_{i,j},~~i, j=1, 2,\ldots , n,~~ i \ne j, \end{aligned}$$

are upper triangular matrices with diagonal entries zero and the matrices $\{U_{i,i}\}_{i=1}^n$, are upper triangular matrices with diagonal entries one. This property is used in the following remark for justifying the uniquely solvability of the resulting system (19).

Remark 3

From (20) we obtain

$$\begin{aligned} \text {det}(\Phi )=\text {det}(L)\times \text {det}(U)=\prod _{i=1}^{n}\text {det}(U_{i,i})=1, \end{aligned}$$

which concludes the invertibility of the coefficient matrix $\Phi$ and thereby the linear algebraic system (19) is uniquely solvable.

Although the above remark indicates that the system (19) has a unique solution, a direct solution of this system can lead to less accurate approximations, due to high computational costs for large scale systems or high degree of approximations. In order to avoid this difficulty, instead of solving (19) directly, we solve the triangular block systems $\underline{W}U=\underline{F}$ and $\underline{C}L=\underline{W}$ separately with $\underline{W}=[ \underline{w}_1,\underline{w}_2,\ldots ,\underline{w}_n]$. Due to the structure of block matrix U as well as non-singularity of the upper triangular matrix $U_{j,j}$, the unknowns $\{\underline{w}_j\}_{j=1}^n$ are obtained from solving the following n systems of upper triangular algebraic equations of order $N+1$

$$\begin{aligned} \underline{w}_{j}U_{j,j}=\left( \underline{p}_{j}^{N}\mathcal {T}^{N}\mathcal {B}_{j}^{N}+\underline{\phi }_j^{N}\right) - \sum \limits _{r=1}^{j-1}\underline{w}_{r}U_{r,j},\quad j=1,2,\ldots ,n, \end{aligned}$$

and consequently, regarding the structure of block matrix L, the main unknowns $\{\underline{c}_{i}^{\prime ^{N}}\}_{i=1}^n$ are computed by the following recurrence relation:

$$\begin{aligned} \underline{c}_{n}^{\prime ^{N}}= & {} \underline{w}_n,\\ \underline{c}_{n-j}^{\prime ^{N}}= & {} \underline{w}_{n-j}-\sum _{r=(n-j)+1}^{n}\underline{c}_{r}^{\prime ^{N}}L_{r,n-j},\quad j=1,\ldots ,n-1. \end{aligned}$$

In fact, the main advantage of this approach is to avoid solving the $(n(N+1))\times (n(N+1))$ system (19) directly, and calculating the unknowns by solving n non-singular upper triangular systems of order $N+1$ and a recursive relation. Finally, obtaining $\{\underline{c}_{i}^{N}\}_{i=1}^n$, from solving the lower triangular system (18), the Chebyshev Tau solutions (12) for the transformed system of Eq. (10) can be calculated. Since the solutions of the main problem (1) and the transformed problem (10) are equivalent by the relation $\{\hat{y}_j(v)=y_j(v^\gamma )\}_{j=1}^n$, then the approximate solutions $y_{j,N}(x)$ of the main problem (1) are given by

$$\begin{aligned} y_{j,N}(x)=\hat{y}_{j,N}(x^{1/\gamma }),\quad j=1,2,\ldots ,n. \end{aligned}$$

4 Convergence Analysis

The purpose of this section is to analyze convergence properties of the proposed method and provide suitable error bounds for the approximate solutions in uniform norm. For this purpose, some of the required preliminaries are given and then the convergence theorem is proved.

Definition 4

[8, 45]

• The space $C^m(\Lambda )$ for $m \ge 0$ is the set of all m-times continuously differentiable functions on $\Lambda$. For $m=0$, the space $(C(\Lambda ), \Vert .\Vert _\infty )$ is the set of all continuous functions on $\Lambda$ with the uniform norm $\Vert f\Vert _\infty =\max \nolimits _{v \in \Lambda }|f(v)|$.

• The Chebyshev-weighted $L^2$-space with respect to the shifted Chebyshev weight function $\xi (v)=\frac{1}{\sqrt{v (1-v)}}$ is defined by

  $$\begin{aligned}L_{\xi }^{2}(\Lambda )=\lbrace f:\Lambda \rightarrow \mathbb {R}, \Vert f\Vert _{\xi }<\infty \rbrace ,\end{aligned}$$

  equipped with the norm

  $$\begin{aligned} \Vert f \Vert _{\xi }^{2}=(f,f)_{\xi }=\int _{\Lambda }f^{2}(v)\xi (v)dv, \end{aligned}$$

  where $(.,.)_{\xi }$ is the Chebyshev-weighted inner product formula.

• The Chebyshev-weighted Sobolev space of order $m \ge 0$ is defined by

  $$\begin{aligned} H_{\xi }^m(\Lambda )=\{f:\Lambda \rightarrow \mathbb {R},~~\Vert f\Vert _{\xi ,m}<\infty \},\end{aligned}$$

  equipped with the following norm and semi-norm

  $$\begin{aligned} \Vert f\Vert _{\xi ,m}^2=\sum \limits _{k=0}^{m}{\Vert f^{(k)}\Vert _{\xi }^2},\quad |f|_{\xi ,m}=\Vert f^{(m)}\Vert _{\xi }. \end{aligned}$$

• The $L_{\xi }^{2}$-orthogonal Chebyshev projection $\pi _{N}:L_{\xi }^{2}(\Lambda )\rightarrow \mathbb {P}_N$ for the function $f \in L_{\xi }^{2}(\Lambda )$ is defined by

  $$\begin{aligned} (f-\pi _{N}f,\varphi )_{\xi }=0,\quad \forall \varphi \in \mathbb {P}_N, \end{aligned}$$

  where $\mathbb {P}_N$ is the space of all algebraic polynomials with degree at most N.

In the following lemma we present the truncation error $\pi _N f-f$ in the uniform norm.

Lemma 5

[48] For any $f \in H_{\xi }^\mu (\Lambda )$ with $\mu \ge 1$, we have

$$\begin{aligned} \Vert e_{\pi _N}f\Vert _{\infty } \le C N^{\frac{3}{4}-\mu }| f|_{\xi ,\mu }, \end{aligned}$$

where $e_{\pi _N}f=f- \pi _{N} f$ is the truncation errors and C is a positive constant independent of N.

In our analysis we will refer to the following Gronwall’s inequality:

Lemma 6

[18] (Gronwall’s inequality) Suppose that f is a non-negative and locally integrable function satisfying in the following inequality

$$\begin{aligned} f(v) \le b(v)+d\int \limits _{0}^{v}{(v-w)^{-q}f(w)dw}, \quad v \in \Lambda ,~~ 0<q<1,~~ d \ge 0, \end{aligned}$$

where $b(v) \ge 0$. Then, there exists a constant c dependent on q such that

$$\begin{aligned} f(v) \le b(v)+ c\int \limits _{0}^{v}{(v-w)^{-q}b(w)dw},\quad v \in \Lambda . \end{aligned}$$

Now we are ready to present the fundamental result of this section, which provides suitable error bounds of the approximate solutions in the uniform norm.

Theorem 7

Assume that $\{\hat{y}_{j,N}(v)\}_{j=1}^n$, given by (12) are the Chebyshev Tau solutions of the transformed Eq. (10). If $\hat{J}^{\alpha _j}\hat{y}_{i}\in C^{\mu _{ji}+1}(\Lambda ),~~\hat{J}^{\alpha _j}\hat{p}_{j}\in C^{\rho _{j}+1}(\Lambda )$ and $\hat{p}_j \in H_\xi ^{\epsilon _j}(\Lambda )$ for $\mu _{ji}, \rho _{j}, \epsilon _j \ge 1$ and $i,j=1, 2,\ldots , n$, then for sufficiently large values of N we have

$$\begin{aligned} \left\| \hat{e}_{j,N}\right\| _{\infty } \le C\left( \sum \limits _{i=1}^{n} N^{\frac{3}{4}-\mu _{ji}}\left| \hat{J}^{\alpha _j}\hat{y}_{i}\right| _{\xi ,\mu _{ji}}+ N^{\frac{3}{4}-\rho _{j}} \left| \hat{J}^{\alpha _j}\hat{p}_{j}\right| _{\xi ,\rho _{j}}+N^{\frac{3}{4}-\epsilon _{j}}|\hat{p}_j|_{\xi ,\epsilon _j}\right) , \end{aligned}$$

(22)

for $j=1,2,\ldots , n$, where $\hat{e}_{j,N}(v)=\hat{y}_{j}(v)-\hat{y}_{j,N}(v)$ are the error functions and C is a generic positive constant independent of N.

Proof

Implementing the presented approach in the previous section for (10) leads to the following operator equation

$$\begin{aligned} \hat{y}_{j,N}(v)=\sum \limits _{i=1}^{n}a_{ji}~\pi _{N}\left( \hat{J}^{\alpha _j}\hat{y}_{i,N}(v)\right) +\pi _{N} \left( \hat{J}^{\alpha _j}\hat{p}_{j,N}(v)\right) +\pi _N(\hat{\phi }_j(v)), \end{aligned}$$

(23)

for $j=1,2,\ldots , n$. Subtracting (10) from (23) yields

$$\begin{aligned} \hat{e}_{j,N}(v)= & {} \sum \limits _{i=1}^{n}{a_{ji}~\left( \hat{J}^{\alpha _j}\hat{y}_i(v)-\pi _N\left( \hat{J}^{\alpha _j}\hat{y}_{i,N}(v)\right) \right) }\nonumber \\&+\,\hat{J}^{\alpha _j}\hat{p}_j(v)-\pi _{N}\left( \hat{J}^{\alpha _j}\hat{p}_{j,N}(v)\right) , \quad j=1,2,\ldots ,n, \end{aligned}$$

(24)

in view of considering $e_{\pi _N}(\hat{\phi }_j(v))=0$ for sufficiently large values of N. By some simple calculations, the Eq. (24) can be rewritten as follows

$$\begin{aligned} \hat{e}_{j,N}(v)=\sum \limits _{i=1}^{n}{a_{ji} \left( \hat{J}^{\alpha _j}\hat{e}_{i,N}(v)\right) }+\Pi _{j},\quad j=1,2,\ldots ,n, \end{aligned}$$

and equivalently we have

$$\begin{aligned} \hat{e}_{j,N}(v)=\sum \limits _{i=1}^{n}\left( \int _{0}^{v}{k_{ji}(v,w)\hat{e}_{i,N}(w)dw}\right) +\Pi _{j},\quad j=1,2,\ldots ,n, \end{aligned}$$

(25)

where $k_{ji}(v,w)=\dfrac{a_{ji}\gamma }{\Gamma (\alpha _j)}w^{\gamma -1}(v^{\gamma }-w^{\gamma })^{\alpha _{j}-1}$, and

$$\begin{aligned} \Pi _{j}=\sum \limits _{i=1}^{n}{a_{ji} e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{y}_{i,N}(v)\right) }+e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{p}_{j,N}(v)\right) +\hat{J}^{\alpha _j}e_{\pi _N}\left( \hat{p}_j(v)\right) . \end{aligned}$$

(26)

Defining the vectors

$$\begin{aligned} \underline{\widehat{E}}(v)=\big [\hat{e}_{1,N}(v),\hat{e}_{2,N}(v),\ldots ,\hat{e}_{n,N}(v)\big ]^{T},\quad \quad \underline{\Pi }=\big [ \Pi _{1},\Pi _{2},\ldots ,\Pi _{n}\big ]^T, \end{aligned}$$

the Eq. (25) is converted to the following matrix formulation

$$\begin{aligned} \underline{\widehat{E}}(v)=\int _{0}^{v}(v-w)^{\min \limits _{1 \le l \le n}\lbrace \alpha _{l}\rbrace -1}K(v,w)\underline{\widehat{E}}(w)dw+\underline{\Pi }, \end{aligned}$$

(27)

where

$$\begin{aligned} K(v,w)= & {} \bigg [(v-w)^{1-\min \limits _{1 \le l \le n} \lbrace \alpha _{l}\rbrace }k_{ij}(v,w)\bigg ]_{i,j=1}^{n}\\= & {} \bigg [\dfrac{a_{ji}\gamma }{\Gamma (\alpha _j)}w^{\gamma -1}(v-w)^{\alpha _{j}-\min \limits _{1 \le l \le n} \lbrace \alpha _{l}\rbrace }\left( \sum \limits _{r=1}^{\gamma }v^{\gamma -r}w^{r-1}\right) ^{\alpha _{j}-1}\bigg ]_{i,j=1}^{n}, \end{aligned}$$

is a continuous function on $\{(v,w):~ 0 \le w \le v \le 1\}$. From (27) we can write

$$\begin{aligned} \vert \underline{\widehat{E}}\vert \le \Psi \int _{0}^{v}(v-w)^{\min \limits _{1 \le l \le n}\lbrace \alpha _{l}\rbrace -1}\vert \underline{\widehat{E}}(w)\vert dw+\vert \underline{\Pi }\vert , \end{aligned}$$

(28)

where $\Psi =\max \nolimits _{0 \le w \le v \le 1}{\vert K(v,w)\vert }< \infty$. Applying Gronwall’s inequality (i.e., Lemma 6) in (28) indicates

$$\begin{aligned} \Vert \underline{\widehat{E}}\Vert _{\infty } \le C \left\| \underline{\Pi }\right\| _{\infty }, \end{aligned}$$

and thereby the relation (26) concludes

$$\begin{aligned}&\Vert \hat{e}_{j,N}(v)\Vert _{\infty } \le C \Vert \Pi _{j}\Vert _{\infty }\nonumber \\&\quad \le C \left( \sum \limits _{i=1}^{n}{|a_{ji}| \Vert e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{y}_{i,N}(v)\right) \Vert _{\infty }}\right. \nonumber \\&\qquad \left. +\,\Vert e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{p}_{j,N}(v)\right) \Vert _{\infty } +\Vert \hat{J}^{\alpha _j}e_{\pi _N}\left( \hat{p}_j(v)\right) \Vert _{\infty }\right) ,\nonumber \\&\qquad \quad j=1,2,\ldots ,n. \end{aligned}$$

(29)

Using the inequality $\Vert \hat{J}^{\alpha _j}f\Vert _\infty \le C \Vert f\Vert _\infty$ (see [31]), the inequality (29) can be rewritten as

$$\begin{aligned}&\Vert \hat{e}_{j,N}(v)\Vert _{\infty } \le C \left( \sum \limits _{i=1}^{n}{|a_{ji}| \Vert e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{y}_{i,N}(v)\right) \Vert _{\infty }}\right. \nonumber \\&\quad \left. +\,\Vert e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{p}_{j,N}(v)\right) \Vert _{\infty } +\Vert e_{\pi _N}\left( \hat{p}_j(v)\right) \Vert _{\infty }\right) ,\nonumber \\&\quad \quad j=1,2,\ldots ,n. \end{aligned}$$

(30)

Applying Lemma 5, we deduce

$$\begin{aligned} \left\| e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{y}_{i,N}(v)\right) \right\| _{\infty } \le C N^{\frac{3}{4}-\mu _{ji}}|\hat{J}^{\alpha _j}\hat{y}_{i,N}(v)|_{\xi ,\mu _{ji}}. \end{aligned}$$

(31)

Under the assumption $\hat{J}^{\alpha _j}\hat{y}_{i}\in C^{\mu _{ji}+1}(\Lambda )$ and using the first order Taylor formula, the inequality (31) implies

$$\begin{aligned}&\left\| e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{y}_{i,N}(v)\right) \right\| _{\infty } \le C N^{\frac{3}{4}-\mu _{ji}}\left( \left\| \left( \hat{J}^{\alpha _j}\hat{y}_{i}(v)\right) ^{(\mu _{ji})}\right\| _{\xi }\right. \nonumber \\&\qquad \left. +\,\Vert \hat{e}_{i,N}(v)\Vert _{\infty }\left\| \left( \hat{J}^{\alpha _j}\hat{y}_{i}(v)\right) ^{(\mu _{ji}+1)}\right\| _{\xi }\right) \nonumber \\&\quad \le C N^{\frac{3}{4}-\mu _{ji}}\Big (|\hat{J}^{\alpha _j}\hat{y}_{i}(v)|_{\xi ,\mu _{ji}}+\Vert \hat{e}_{i,N}(v)\Vert _{\infty }\Big ),\nonumber \\&\qquad i,j=1,2,\ldots ,n. \end{aligned}$$

(32)

Also, from Lemma 5, we can conclude

$$\begin{aligned} \Vert e_{\pi _N}(\hat{p}_j(v))\Vert _{\infty } \le C N^{\frac{3}{4}-\epsilon _j}|\hat{p}_j(v)|_{\xi ,\epsilon _j},~~j=1,2,\ldots ,n, \end{aligned}$$

(33)

and again by proceeding the same way as (31)–(32), we derive

$$\begin{aligned} \left\| e_{\pi _{N}}\left( \hat{J}^{\alpha _j}\hat{p}_{j,N}(v)\right) \right\| _{\infty }\le & {} C N^{\frac{3}{4}-\rho _{j}}\Big (|\hat{J}^{\alpha _j}\hat{p}_{j}(v)|_{\xi ,\rho _{j}}+\Vert e_{\pi _N}(\hat{p}_j(v))\Vert _{\infty }\Big )\nonumber \\\le & {} C N^{\frac{3}{4}-\rho _{j}}\Big (|\hat{J}^{\alpha _j}\hat{p}_{j}(v)|_{\xi ,\rho _{j}}+N^{\frac{3}{4}-\epsilon _j}|\hat{p}_j(v)|_{\xi ,\epsilon _j}\Big ), \end{aligned}$$

(34)

in view of (33), and the assumption $\hat{J}^{\alpha _j}\hat{p}_{j}\in C^{\rho _{j}+1}(\Lambda )$ for $j=1, 2,\ldots ,n$. Inserting the inequalities (32)–(34) into (30) yields

$$\begin{aligned} \Vert \hat{e}_{j,N}(v)\Vert _{\infty }-C\sum \limits _{i=1}^{n}{N^{\frac{3}{4}-\mu _{ji}}|a_{ji}| \Vert \hat{e}_{i,N}(v)\Vert _{\infty }} \le C G_{j} ,\quad j=1,2,\ldots ,n, \end{aligned}$$

(35)

in which

$$\begin{aligned} G_{j}=\sum \limits _{i=1}^{n} N^{\frac{3}{4}-\mu _{ji}}\left| \hat{J}^{\alpha _j}\hat{y}_{i}\right| _{\xi ,\mu _{ji}}+ N^{\frac{3}{4}-\rho _{j}} \left| \hat{J}^{\alpha _j}\hat{p}_{j}\right| _{\xi ,\rho _{j}}+N^{\frac{3}{4}-\epsilon _{j}}|\hat{p}_j|_{\xi ,\epsilon _j}. \end{aligned}$$

Evidently, the inequality (35) can be written in the following vector-matrix form

$$\begin{aligned} M\underline{\hat{e}} \le C \underline{G}, \end{aligned}$$

(36)

where

$$\begin{aligned} \underline{\hat{e}}= & {} [\Vert \hat{e}_{1,N}\Vert _\infty , \Vert \hat{e}_{2,N}\Vert _\infty ,\ldots ,\Vert \hat{e}_{n,N}\Vert _\infty ]^T,\\ \underline{G}= & {} [G_1, G_2,\ldots , G_n]^T, \end{aligned}$$

and M is a matrix of order n with the following entries

$$\begin{aligned} \big (M\big )_{i,j=1}^n={\left\{ \begin{array}{ll} 1-CN^{\frac{3}{4}-\mu _{jj}}|a_{jj}|,\quad i=j,\\ -CN^{\frac{3}{4}-\mu _{ji}}|a_{ji}|,\quad \quad i \ne j. \end{array}\right. } \end{aligned}$$

Therefore, for large values of N, the matrix M tends to the identity matrix and consequently the inequality (36) gives

$$\begin{aligned} \Vert \hat{e}_{j,N}\Vert _\infty \le C G_j,~~~ j=1,2,\ldots ,n, \end{aligned}$$

which is the desired result. $\square$

5 Illustrative Examples

In this section, some test problems are solved using the proposed method to confirm its efficiency and applicability. All of the calculations were performed using Mathematica software v11.2, running in an Intel (R) Core (TM) i5-4210U CPU@2.40 GHz. If we access the exact solution, the errors are calculated by

$$\begin{aligned} \Vert e_{j,N}\Vert _\infty =\max \limits _{x \in \Lambda }|y_{j}(x)-y_{j,N}(x)|,\quad j=1,2,\ldots ,n, \end{aligned}$$

and if we do not have the exact solution, the errors are estimated by

$$\begin{aligned} \Vert \tilde{e}_{j,N}\Vert _\infty =\max \limits _{x \in \Lambda }|y_{j,2N}(x)-y_{j,N}(x)|,\quad j=1,2,\ldots ,n, \end{aligned}$$

where $y_{j,2N}(x)$ and $y_{j,N}(x)$ are approximations of the exact solution $y_{j}(x)$, and N is the degree of approximation.

Example 1

Consider the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{3/2}_Cy_1(x)=y_1(x)+3y_2(x)-y_3(x)+y_4(x)+p_1(x),\\ D^{5/2}_Cy_2(x)=2y_1(x)-y_2(x)+\frac{3}{2}y_3(x)+\frac{5}{2}y_4(x)+p_2(x),\\ D^{7/2}_Cy_3(x)=-y_1(x)+3y_2(x)+y_3(x)+4y_4(x)+p_3(x),\\ D^{9/2}_Cy_4(x)=y_1(x)+2y_2(x)-y_3(x)-y_4(x)+p_4(x), \end{array}\right. } \end{aligned}$$

with zero initial conditions and the following forcing functions

$$\begin{aligned} p_1(x)= & {} -\sin {x^{\frac{3}{2}}}-x^2\sqrt{x}\left( 3-x+x^2+6x^3-4 x^4+\frac{1}{3}x^5\right) \\&+\,\frac{3\sqrt{\pi }}{4}{_{2}F_{3}}\left( \left\{ \frac{1}{6},\frac{5}{6}\right\} ;\left\{ \frac{1}{3},\frac{2}{3},1\right\} ; -\frac{x^{3}}{4}\right) \\&-\,\frac{45\sqrt{\pi }}{64}x^{3}{_{2}F_{3}}\left( \left\{ \frac{7}{6},\frac{11}{6}\right\} ;\left\{ \frac{4}{3},\frac{5}{3},2\right\} ; -\frac{x^{3}}{4}\right) ,\\ p_2(x)= & {} \frac{15\Gamma \left( \frac{1}{2}\right) }{8}+\frac{231\Gamma \left( \frac{7}{2}\right) }{8}x^{3}-2\sin {x^{\frac{3}{2}}}\\&+\,x^2 \sqrt{x}\left( 1-\frac{3 }{2}x-\frac{5}{2}x^2+2 x^3-6 x^4-\frac{5}{6}x^5\right) ,\\ p_3(x)= & {} \frac{105\Gamma \left( \frac{1}{2}\right) }{16}+\frac{3003\Gamma \left( \frac{7}{2}\right) }{8}x^{3}+\sin {x^{\frac{3}{2}}}\\&-\,x^2\sqrt{x}\left( 3+x+4x^2+6 x^3+4 x^4+\frac{4}{3}x^5\right) ,\\ p_4(x)= & {} \frac{945\Gamma \left( \frac{1}{2}\right) }{32}+\frac{15015\Gamma \left( \frac{7}{2}\right) }{64}x^{3}-\sin {x^{\frac{3}{2}}}\\&+\,x^2\sqrt{x}\left( -2+x+x^2-4x^3+4x^4+\frac{1}{3}x^5\right) , \end{aligned}$$

where $_{\theta }F_{\tau }\big (\{a_1,\ldots a_\theta \};\{b_1,\ldots ,b_{\tau }\};z\big )$ is the generalized hypergeometric function.

The exact solutions are given by

$$\begin{aligned} y_1(x)= & {} \sin {x^{\frac{3}{2}}},~~ y_2(x)=x^2\sqrt{x}\big (1+2x^3\big ),\\ y_3(x)= & {} x^3\sqrt{x}\big (1+4 x^3\big ),~~ y_4(x)=x^4\sqrt{x}\big (1+\frac{1}{3}x^3\big ), \end{aligned}$$

with the following asymptotic behaviors near the origin

$$\begin{aligned} y_1(x)=O(x^{3/2}), \quad y_2(x)=O(x^{5/2}), \quad y_3(x)=O(x^{7/2}), \quad y_4(x)=O(x^{9/2}), \end{aligned}$$

which are coincident with the results obtained in Theorem 2.

Applying the variable transformation (9) for this problem with $\gamma =2$, the transformed Eq. (10) becomes as follows

$$\begin{aligned} \left\{ \begin{array}{l} \hat{y}_1(v)=\hat{J}^{3/2}\hat{y}_1(v)+3\hat{J}^{3/2}\hat{y}_2(v)-\hat{J}^{3/2}\hat{y}_3(v)+\hat{J}^{3/2}\hat{y}_4(v)+\hat{J}^{3/2}\hat{p}_1(v),\\ \hat{y}_2(v)=2\hat{J}^{5/2}\hat{y}_1(v)-\hat{J}^{5/2}\hat{y}_2(v)+\dfrac{3}{2}\hat{J}^{5/2}\hat{y}_3(v)+\dfrac{5}{2}\hat{J}^{5/2}\hat{y}_4(v) +\hat{J}^{5/2}\hat{p}_2(v),\\ \hat{y}_3(v)=-\hat{J}^{7/2}\hat{y}_1(v)+3\hat{J}^{7/2}\hat{y}_2(v)+\hat{J}^{7/2}\hat{y}_3(v)+4\hat{J}^{7/2}\hat{y}_4(v)+\hat{J}^{7/2}\hat{p}_3(v),\\ \hat{y}_4(v)=\hat{J}^{9/2}\hat{y}_1(v)+2\hat{J}^{9/2}\hat{y}_2(v)-\hat{J}^{9/2}\hat{y}_3(v)-\hat{J}^{9/2}\hat{y}_4(v)+\hat{J}^{9/2}\hat{p}_4(v),\\ \end{array}\right. \end{aligned}$$

(37)

with the following infinitely smooth exact solutions

$$\begin{aligned} \hat{y}_1(v)= & {} \sin {v^3},~~\hat{y}_2(v)=v^5(1+2v^{6}),\\ \hat{y}_3(v)= & {} v^7(1+4v^{6}),~~ \hat{y}_4(v)=v^9\left( 1+\frac{1}{3}v^6\right) . \end{aligned}$$

The transformed Eq. (37) is numerically solved via the proposed scheme and the obtained results are given in Table 1. Obtained numerical errors as well as the CPU-time (s) are reported in Table 1 for different values of N. Indeed, the reported results confirm that the proposed smoothing process removes the existence discontinuity in the derivatives of the exact solutions and produces the reliable approximate solutions, especially for large values of N in a very short CPU time.

Table 1 Obtained errors for Example 1 with different values of N

Example 2

[41] Consider the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{1/2}_Cy_1(x)=y_1(x)+y_2(x)+y_3(x),\\ D^{1/2}_Cy_2(x)=2y_1(x)+y_2(x)-y_3(x),\\ D^{1/2}_Cy_3(x)=-y_2(x)+y_3(x),\\ y_1(0)=1, \quad y_2(0)=2, \quad y_3(0)=3, \end{array}\right. } \end{aligned}$$

(38)

where the exact solutions are given by

$$\begin{aligned} y_1(x)= & {} -\frac{4}{3}E_{\frac{1}{2}}(-\sqrt{x})+\frac{7}{3}E_{\frac{1}{2}}(2\sqrt{x}),\\ y_2(x)= & {} \frac{16}{9}E_{\frac{1}{2}}(-\sqrt{x})+\frac{2}{9}E_{\frac{1}{2}}(2\sqrt{x})+\frac{7}{3}\sqrt{x}E_{\frac{1}{2}}^{\prime }(2\sqrt{x}),\\ y_3(x)= & {} \frac{8}{9}E_{\frac{1}{2}}(-\sqrt{x})+\frac{19}{9}E_{\frac{1}{2}}(2\sqrt{x})-\frac{7}{3}\sqrt{x} E_{\frac{1}{2}}^{\prime }(2\sqrt{x}), \end{aligned}$$

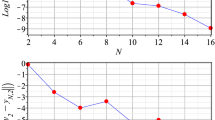
where $E_{\delta }(x)$ is the one parameter Mittag-Leffler function [31]. Clearly, the exact solutions are non-smooth at the origin with the asymptotic behavior $O(\sqrt{x})$. This problem is solved by using the proposed approach, and the obtained results are reported in Table 2 and Fig. 1. To compute the numerical errors, 100-terms of the Mittag-Leffler functions are considered. The presented numerical results indicate the well performance of the proposed scheme in approximating the solutions of (38), especially for large values of N in a very short CPU time. Furthermore, from Fig. 1, the predicted exponential like rate of convergence in Theorem 7 can be confirmed due to the linear variations of semi-log representation of errors versus N.

Table 2 Obtained errors for Example 2 with different values of N

Fig. 1

Semi-log representation of the numerical errors of Example 2 versus N

Example 3

[20] Consider the following system of FDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\alpha }_Cy_{1}(x)=y_{2}(x),\\ D^{\alpha }_Cy_{2}(x)=-y_{1}(x)-y_{2}(x)+x^{\alpha +1}+\frac{\pi \csc (\pi \alpha )x^{1-\alpha }}{\Gamma (-\alpha -1)\Gamma (2-\alpha )}+\frac{\pi x \csc (\pi \alpha )}{\Gamma (-\alpha -1)},\\ y_{1}(0)=0, \quad y_{2}(0)=0, \end{array}\right. } \end{aligned}$$

where the exact solutions are

$$\begin{aligned} y_1(x)=x^{1+\alpha },\quad y_2(x)=\frac{\pi \alpha (\alpha +1) \csc (\pi \alpha )}{\Gamma (1-\alpha )}x. \end{aligned}$$

We have solved this problem via the proposed scheme for values $\alpha =\frac{1}{4}, \frac{1}{2}, \frac{2}{3}$ and obtained the exact solutions for degree of approximation $N \ge 5$. On the other hand, this problem was evaluated in Ref. [20] by applying a hybrid numerical method. In this method, after dividing the integration domain $\Lambda$ into m subintervals, the approximate solutions were considered as a linear combination of non-polynomials in a neighborhood of the origin, and by polynomials in the rest of domain. The presented results in Ref. [20] for various values $\alpha$ and m are listed in Table 3. The listed results in Table 3 approve that our method provides more accurate approximations in comparison with the scheme mentioned in [20].

Table 3 Obtained errors of the hybrid scheme in [20] for Example 3 with degree of approximation $N=4$ and m subintervals

5.1 Application

The following three examples are intended to illustrate the applicability of the proposed scheme in approximating the solutions of some real life and practical problems.

First we consider well-known multi-term Bagley-Torvik equation which has wide applications in engineering. This equation appears in modelling of the movement of a thin, rigid plate in a viscous Newtonian fluid, and the plate is attached to a fixed point via a spring with certain spring constant [3]. Another application of this equation can be seen in studying the performance of a Micro-Mechanical system (MEMS) instrument that is used in measuring the viscosity of fluids that are encountered during oil well exploration [21].

Example 4

Consider the following Bagley-Torvik equation

$$\begin{aligned} {\left\{ \begin{array}{ll} Ay''(x)+BD^{3/2}_Cy(x)+Cy(x)=g(x),\\ y(0)=d_0, \quad y'(0)=d_1, \end{array}\right. } \end{aligned}$$

(39)

in which the constants A, B, C and the function g(x) are known.

Here we set $A=C=1$, $B=\beta \sqrt{\pi }$, $g(x)=0$, $y(0)=1$ and $y'(0)=0$ which is considered in [21] to study the performance of the MEMS system. In this case, the exact solution is given by

$$\begin{aligned} y(x)=1-\sum \limits _{i=0}^{\infty }\sum \limits _{j=0}^{\infty }\dfrac{(-1)^{j}(-\beta \sqrt{\pi })^{i}(i+j)!x^{2+2j+\frac{i}{2}}}{i!j!\left( 2+2j+\frac{i}{2}\right) \Gamma \left( 2+2j+\dfrac{i}{2}\right) }. \end{aligned}$$

From [17], it can be seen that the main problem (39) is equivalent with the following constant coefficients system of multi-order FDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{3/2}_C y_1(x)=y_2(x),\\ D^{1/2}_C y_2(x)=-y_1(x)-\beta \sqrt{\pi }y_2(x),\\ y_1(0)=1,~~y_{1}'(0)=0,~~y_2(0)=0, \end{array}\right. } \end{aligned}$$

(40)

with $y_1(x)=y(x)$. We solve (40) using the presented method and consider $y_{N}(x)=y_{1,N}(x)$ as the approximate solution of the Bagley-Torvik equation (39). The obtained results are given in Table 4 and Fig. 2 which demonstrates the effectiveness and applicability of the proposed scheme.

Table 4 Obtained errors for Example 4 with different values of N and $\beta =\frac{1}{5}$

Fig. 2

Semi-log representation of the numerical errors of Example 4 versus N with $\beta =\frac{1}{5}$

Fig. 3

Electrical circuit

As the second practical example, we consider the following system of multi-order FDEs which arises from modelling of a linear electrical circuit shown in Fig. 3. This circuit consists of resistors, inductors, capacitors, voltage sources with known capacitances $C_{j}$, inductances $L_{j}$, voltages on the capacitances $V_{C_{j}}$, sources voltages $V_{E_{j}}$, currents $i_j$ for $j=1,2$ and resistances $R_{l}$ for $l=1,2,3$.

Example 5

[28] Consider the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\alpha _{1}}_CV_{C_{1}}(x)=\frac{1}{C_{1}}i_{1}(x),\\ D^{\alpha _{2}}_CV_{C_{2}}(x)=\frac{1}{C_{2}}i_{2}(x),\\ D^{\alpha _{3}}_Ci_{1}(x)=-\frac{1}{L_{1}}V_{C_{1}}(x)-\frac{(R_{1}+R_{3})}{L_{1}}i_{1}(x)+\frac{R_{3}}{L_{1}}i_{2}(x)+\frac{V_{E_{1}}}{L_{1}},\\ D^{\alpha _{4}}_Ci_{2}(x)=-\frac{1}{L_{2}}V_{C_{2}}(x)+\frac{R_{3}}{L_{2}}i_{1}(x)-\frac{(R_{2}+R_{3})}{L_{2}}i_{2}(x)+\frac{V_{E_{2}}}{L_{2}},\\ V_{C_{1}}(0)=d_1, \quad V_{C_{2}}(0)=d_2, \quad i_{1}(0)=d_3, \quad i_{2}(0)=d_4, \end{array}\right. } \end{aligned}$$

with $\alpha _{j}=\frac{j}{5}$ for $1 \le j \le 4$. Here we set the parameters $C_{1}=3$, $C_{2}=2$, $L_{1}=5$, $L_{2}=7$, $R_{1}=R_{3}=5/3$, $R_{2}=11/6$, $V_{E_{1}}=3$, $V_{E_{2}}=6$ and $d_1=d_2=d_3=d_4=0$.

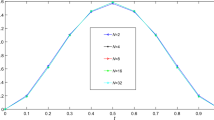
This problem is evaluated by the proposed approach, and the results are reported in Table 5 and Fig. 4.

The numerical results show that the estimated errors are decreased as the degree of approximation N is increased. Moreover, decay of the errors for large values of N in a very short CPU time reveals the well-posedness of the proposed approach in approximating the solutions of this problem.

Table 5 Obtained errors for Example 5 with different values of N

Fig. 4

Semi-log representation of the numerical errors of Example 5 versus N

The next practical example is a fractional model of the Bloch equation which is used to study the spin dynamics and magnetization relaxation, in the simple case of a single spin particle at resonance in a static magnetic field.

Example 6

[33] Consider the following time fractional Bloch equations (TFBE)

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\alpha }_{C} M_x(t)=\omega _0^{\prime }M_y(t)-\dfrac{M_x(t)}{T_2^{\prime }},\\ D^{\alpha }_{C} M_y(t)=-\omega _0^{\prime }M_x(t)-\dfrac{M_y(t)}{T_2^{\prime }},\\ D^{\alpha }_{C} M_z(t)=\dfrac{M_0-M_z(t)}{T_1^{\prime }},\\ M_x(0)=c_1, \quad M_y(0)=c_2, \quad M_z(0)=c_3,\quad \quad 0< \alpha \le 1, \end{array}\right. } \end{aligned}$$

where $1/T_1^{\prime }=\tau _1^{1-\alpha }/T_1$, $1/T_2^{\prime }=\tau _2^{1-\alpha }/T_2$ and $\omega _0^{\prime }=\omega _0/\tau _2^{\alpha -1}$ are parameters with the unit of $(\text {sec})^{-\alpha }$. Here $M_x(t)$, $M_y(t)$ and $M_z(t)$ represent the system magnetization (x, y, and z components), $T_1$ is the spin-lattice relaxation time, $T_2$ is the spin-spin relaxation time, $M_0$ is the equilibrium magnetization, $c_1$, $c_2$ and $c_3$ are given constants, $\omega _0$ is the resonant frequency given by the Larmor relationship $\omega _0=\sigma B_{0}$, where $B_{0}$ is the static magnetic field (z-component) and $\sigma /2\pi$ is the gyromagnetic ratio (42.57 MHz/Tesla for water protons).

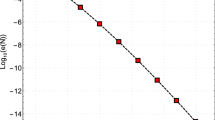
We set the parameters $\alpha =1/6$, $T_1^{\prime }=1$, $T_2^{\prime }=3/2$, $M_0=2$, $c_1=0$, $c_2=2$, $c_3=0$ and $\omega _0=4\pi /15$, and solve the problem via the proposed approach. The numerical results are presented in Table 6 and Fig. 5, which justify efficiency and reliability of the proposed scheme. Indeed, Fig. 5 indicates that the familiar spectral accuracy is achieved because the logarithmic representation of the errors has almost linear behavior versus N. Furthermore, the reported errors as well as the CPU time used, especially for large values of N approve that our implementation process prevents the growth of the rounding errors and its effect on destroying the error of the method.

Table 6 Obtained errors for Example 6 with different values of N

Fig. 5

Semi-log representation of the numerical errors of Example 6 versus N

6 Conclusion

In this paper an efficient formulation of the Chebyshev Tau method for approximating the solutions of constant coefficients system of multi-order FDEs was developed and analyzed. To monitor the smoothness properties of the exact solutions, series representations of the solutions near the origin were obtained which indicate that some derivatives of the exact solutions may suffer from a discontinuity at the origin depending on the fractional derivative orders. To fix this weakness and make the Chebyshev Tau method applicable for obtaining high-order approximation, a regularization strategy proceeded. Convergence analysis of the presented scheme was also investigated, and effectiveness and reliability of the proposed approach were confirmed using some illustrative examples.