1 Introduction

In this paper, we aim to construct new local discontinuous Galerkin (LDG) schemes for solving the following nonlinear convection–diffusion equation

$$\begin{aligned} u_t+f(u)_x=b(u)_{xx}, \end{aligned}$$
(1)

or equivalently

$$\begin{aligned} u_t+f(u)_x=(a^2(u)u_x)_x, \end{aligned}$$
(2)

as well as their two-dimensional versions, where \(a^2(u)=b'(u)\ge 0\). We also assume that \(a(u)\ge 0\). The initial condition is given as \(u(x,0)=u_0(x)\).

The discontinuous Galerkin (DG) method was first introduced in 1973 by Reed and Hill [24] in the framework of neutron linear transport. Subsequently, Cockburn et al. developed Runge-Kutta discontinuous Galerkin (RKDG) methods for hyperbolic conservation laws in a series of papers [5,6,7,8]. In [9], Cockburn and Shu introduced the LDG method to solve the convection–diffusion equations. Their idea was motivated by Bassi and Rebay [1], where the compressible Navier-Stokes equations were successfully solved. As in traditional LDG methods, we introduce an auxiliary variable p to represent \(a(u)u_x\) and thus can rewrite (2) into the following system of first order equations

$$\begin{aligned} \left\{ \begin{array}{l} u_t+f(u)_x=(a(u)p)_x, \\ p=A(u)_x, \end{array} \right. \end{aligned}$$
(3)

where \(A(u)=\int ^u a(t)\ dt\). Usually, u and p are solved on the same mesh.

The LDG method is one of the most important numerical methods for convection–diffusion equations. However, for some special convection–diffusion systems, such as chemotaxis model [19, 22] and miscible displacements in porous media [10, 11], the LDG methods are not easy to construct and analyze. In each of the two models, the convection term is the product of one of the primary variables and the derivatives of the another primary variable. Most of the well established numerical fluxes for the convection terms, such as the upwind fluxes, cannot be applied, since the coefficients of the convection terms turn out to be discontinuous after the spatial discretization. It is well known that hyperbolic equations with discontinuous coefficients are in general not well-posed [13, 18]. Therefore, the DG schemes may not be stable when applied to those model equations. Within the DG framework, there are three different ways to bridge this gap. Firstly, in [15, 20, 30] the authors combined the convection terms and diffusion terms together and obtain the optimal error estimates. The idea was motivated by Wang et. al. [25,26,27], where \(u_x\) and the jump of u across the cell interfaces were proved to be bounded by p. Moreover, to make the numerical solutions to be physically relevant, we have to add a very large penalty which depends on the numerical approximations of the derivatives of the primary variables [16, 20]. The second approach is to applied the flux-free numerical methods such as the Central DG (CDG) methods [21]. However, for CDG methods, we have to solve each equation in (3) on both the primary and dual meshes, which double the computational cost. The last idea is to apply the Staggered DG (SDG) methods [3]. However, the method requires some continuity of the numerical approximations, which is not easy to apply limiters. In this paper, we introduce a new LDG method, and solve u and p on the primitive and dual meshes, respectively, and do not require any continuity across the cell interfaces. Since p is continuous across the cell interfaces in the primitive mesh, we can apply the upwind fluxes for the convection term for the complicated systems discussed above.

Finally, the most significant advantage of the new algorithm is the construction of third-order maximum-principle-preserving (MPP) LDG methods. Recently, in Zhang and Shu [31], genuinely MPP high-order DG schemes for scalar equations and two-dimensional incompressible flows in vorticity-streamfunction formulation have been constructed. Subsequently, positivity-preserving high order DG schemes for compressible Euler equations were given in Zhang and Shu [32]. Later, the technique was applied to other hyperbolic systems, such as pressureless Euler equations [29], Extended MHD equations [34], relativistic hydrodynamics [23], etc, and the \(L^1\) stability was demonstrated. For parabolic equations, the extension was given in Zhang and Shu [33], where second-order MPP discontinuous Galerkin methods were demonstrated, and the construction of third-order schemes seem to be not straightforward. Later another approach based on the flux limiter were discussed in [17, 28]. In Chen et al. [2], the third-order MPP direct DG method was introduced. However, the scheme was not easy to implement and we need to add two penalty terms. In Du and Yang [12], we applied the new LDG method and constructed third-order MPP schemes. There is a mild penalty which does not depend on the numerical approximations. Since the dual meshes can be moved arbitrarily, we also showed that if the dual mesh agree with the primitive mesh, the penalty coefficient turns out to be infinity. Therefore, our algorithm does not violate the results given in Zhang and Shu [33].

In contrast to the above advantages, the new LDG method may not have optimal convergence rates when applied to the pure diffusion equations if the dual mesh is generated by the midpoint in each cell on the primitive mesh and piecewise odd order polynomials are applied. This is the main reason why in the SDG method the numerical approximations are required to be continuous across some of the cell interfaces. In this paper, we will theoretically study the stability and error estimates of new algorithm. We will demonstrate the reason for the accuracy degeneration and introduce several alternatives to gain the optimal convergence rates.

The organization of this paper is as follows. In Sect. 2, we construct the new LDG scheme for nonlinear convection–diffusion equations on overlapping meshes in one space dimension. The stability and error estimates will be given. The extension to problems in two space dimensions will be discussed in Sect. 3. Numerical experiments will be given in Sect. 4 to demonstrate the accuracy and good performance of the new LDG scheme. Finally, we will end in Sect. 5 with concluding remarks.

2 Numerical scheme for one-dimensional case

In this section, we will introduce the new LDG method for solving the one-dimensional nonlinear convection–diffusion equation (3) on overlapping meshes.

2.1 Overlapping meshes

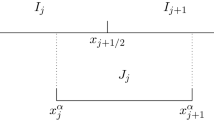
Different from the LDG method introduced in Cockburn and Shu [9], in which u and p are solved on the same mesh, our new method solves (3) on two meshes, as shown in Fig. 1. For simplicity, we consider periodic boundary conditions and the algorithms for other boundary conditions will be discussed in the future.

Fig. 1
figure 1

Overlapping meshes

Full size image

We first define the primitive mesh on which the primary variable u is solved. It is just a decomposition of the computational domain \(\Omega =[0,1]\), which can be non-uniform. We denote the i-th cell as

$$\begin{aligned} I_i=\Big [x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\Big ],\quad i=1,\ldots ,N_x. \end{aligned}$$

The cell length and the cell center of \(I_i\) are denoted as

$$\begin{aligned}&\triangle x_i=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}, \qquad x_i=\frac{x_{i-\frac{1}{2}}+x_{i+\frac{1}{2}}}{2}, \end{aligned}$$

respectively. We define \(\Delta x=\max _i\Delta x_i\). In this paper, we consider regular meshes, i.e. there exists a positive constant \(C\ge 1\) such that \(\Delta x\le C\min _i\Delta x_i\). Clearly, if \(C=1,\) then the mesh is uniformly distributed.

Based on the primitive mesh, we move each cell center within the corresponding cell to obtain a new mesh called the P-mesh, which is used to solve the auxiliary variable p, i.e. in each cell \(I_i\), we choose a point \({\tilde{x}}_i\) given as

$$\begin{aligned} {\tilde{x}}_i=x_i+\frac{\triangle x_i}{2}{\xi _i}_0, \qquad {\xi _i}_0\in [-1,1],\quad i=1,\ldots ,N_x. \end{aligned}$$
(4)

For simplicity, we consider \({\xi _i}_0\) to be a constant independent of i and denoted as \(\xi _0\in [-1,1]\). It is easy to check \({\tilde{x}}_i \in [x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}]\). The \((i-\frac{1}{2})\)-th cell of the dual mesh is defined as

$$\begin{aligned} P_{i-\frac{1}{2}}=[{\tilde{x}}_{i-1},{\tilde{x}}_{i}],\quad i=1,\ldots ,N_x, \end{aligned}$$

where we denote \({\tilde{x}}_0={\tilde{x}}_{N_x}-1.\) We further denote the cell length and the cell center of \(P_{i-\frac{1}{2}}\) as

$$\begin{aligned} \triangle {\tilde{x}}_{i-\frac{1}{2}}={\tilde{x}}_{i}-{\tilde{x}}_{i-1}, \qquad {\tilde{x}}_{i-\frac{1}{2}}=\frac{{\tilde{x}}_{i-1}+{\tilde{x}}_{i}}{2}, \end{aligned}$$

respectively. We can easily check that

$$\begin{aligned} \min \{\Delta x_{i-1},\Delta x_i\}\le \Delta {\tilde{x}}_{i-\frac{1}{2}}\le \max \{\Delta x_{i-1},\Delta x_i\}, \end{aligned}$$

and hence we have \(\max _i\Delta {\tilde{x}}_{i-\frac{1}{2}}\le \Delta x.\) Due to the periodic boundary condition, we can also define \(P_{\frac{1}{2}}=[0,{\tilde{x}}_1]\cup [{\tilde{x}}_{N_x},1]\). Therefore, we consider a polynomial on \(P_{\frac{1}{2}}\) as a polynomial on \([{\tilde{x}}_0,{\tilde{x}}_1]\). We define the dual mesh to be the P-mesh which consists of all these P cells. Notice that when \(\xi _0=0\), we have \({\tilde{x}}_i=x_i\) and \(P_{i+\frac{1}{2}}=[x_{i},x_{i+1}]\). In this case, the cell interfaces of the dual mesh are exactly the cell centers of the primitive mesh. This kind of mesh is the most commonly used overlapping mesh, such as in the central discontinuous Galerkin (CDG) method [21]. When \(\xi _0=1\), we have \({\tilde{x}}_i=x_{i+\frac{1}{2}}\) and hence the P-mesh is the same as the primitive mesh.

2.2 Norms

In this section, we proceed to define some norms to be used throughout the paper.

For any interval I, we define \(\Vert u\Vert _{I}\) and \(\Vert u\Vert _{\infty ,I}\) to be the standard \(L^2\)- and \(L^\infty \)-norm of u on I, respectively. For any natural number \(\ell \), we consider the norm of the Sobolev space \(H^\ell (I)\), defined by

$$\begin{aligned} \Vert u\Vert _{\ell ,I}=\left\{ \sum _{0\le \beta \le \ell }\left\| \frac{\partial ^{\beta } u}{\partial x^\beta }\right\| ^2_I\right\} ^{\frac{1}{2}}. \end{aligned}$$

For convenience, if I is the whole computational domain, then the corresponding subscript will be omitted.

Moreover, for any \(u\in C(I_i)\), we define

$$\begin{aligned} \Vert u\Vert _{\Gamma _i}=|u^-_{i+\frac{1}{2}}|+|u^+_{i-\frac{1}{2}}|, \end{aligned}$$

Similarly, for any \(u\in C(P_{i-\frac{1}{2}})\), we define

$$\begin{aligned} \Vert u\Vert _{\Gamma _{i+\frac{1}{2}}}=|u^-_{i}|+|u^+_{i-1}|. \end{aligned}$$

2.3 LDG method on overlapping meshes

In this section, we introduce the LDG methods for the following pure diffusion equation

$$\begin{aligned} \left\{ \begin{array}{l} u_t=(a(u)p)_x, \\ p=A(u)_x, \end{array} \right. \end{aligned}$$
(5)

where \(A(u)=\int ^u a(t)dt\). We define the finite element spaces to be

$$\begin{aligned}&V_h:=\{u_h: u_h|_{I_{i}}\in P^k(I_{i}),\, i=1,\ldots ,N_x \}, \\&P_h:=\{p_h: p_h|_{P_{i-\frac{1}{2}}}\in P^k(P_{i-\frac{1}{2}}),\, i=1,\ldots ,N_x \}. \end{aligned}$$

By multiplying (5) with test functions and using the integration by parts, our new LDG method on overlapping meshes is defined as follows: find \((u_h,p_h)\in V_h\times P_h\), such that for any test functions \((v,w)\in V_h\times P_h\), we have

$$\begin{aligned}&\int _{I_{i}} (u_h)_t v dx=-\int _{I_{i}} a(u_h) p_h v_x dx + {\hat{a}}_{i+\frac{1}{2}}{\hat{p}}_{i+\frac{1}{2}}v^-_{i+\frac{1}{2}}-{\hat{a}}_{i-\frac{1}{2}}{\hat{p}}_{i-\frac{1}{2}}v^+_{i-\frac{1}{2}}, \end{aligned}$$
(6)
$$\begin{aligned}&\int _{P_{i-\frac{1}{2}}} p_h w dx =-\int _{P_{i-\frac{1}{2}}} A(u_h) w_x dx + A(u_h({\tilde{x}}_{i}))w^-_{i}-A(u_h({\tilde{x}}_{i-1}))w^+_{i-1}. \end{aligned}$$
(7)

where \(v^-_{i+\frac{1}{2}}=v^-({x_{i+\frac{1}{2}}})\) and \(w^-_{i}=w^-({\tilde{x}}_{i})\). Likewise for \(v^+_{i-\frac{1}{2}}\) and \(w^+_{i-1}\). For simplicity, we denote \(v^-_{\frac{1}{2}}=v^-_{N_x+\frac{1}{2}}\) and \(v^+_{N_x+\frac{1}{2}}=v^+_{\frac{1}{2}}.\) The numerical flux \({\hat{a}}\) at the point \(x_{i+\frac{1}{2}}\) is taken as

$$\begin{aligned} {\hat{a}}_{i+\frac{1}{2}}=\frac{[A(u_h)]_{i+\frac{1}{2}}}{[u_h]_{i+\frac{1}{2}}}, \end{aligned}$$
(8)

where \([s]_{i+\frac{1}{2}}:=s^+_{i+\frac{1}{2}}-s^-_{i+\frac{1}{2}}\) denotes the jump of a function s across the cell interface \(x=x_{i+\frac{1}{2}}\). Similarly, we can also denote the jump of w across \(x={\tilde{x}}_{i}\) on the P-mesh as \([w]_i=w^+_i-w^-_i\). Notice that \(p_h\) is continuous at the interfaces of the primitive cells and hence \(p_h(x_{i+\frac{1}{2}})\) is well defined. We choose the numerical flux \({\hat{p}}_{i+\frac{1}{2}}\) as the value of \(p_h\) evaluated at \(x=x_{i+\frac{1}{2}}\) with a penalty term

$$\begin{aligned} {\hat{p}}_{i+\frac{1}{2}}=p_h(x_{i+\frac{1}{2}})+\frac{\alpha _{i+\frac{1}{2}}}{ \triangle {\tilde{x}}_{i+\frac{1}{2}}} [u_h]_{i+\frac{1}{2}}. \end{aligned}$$
(9)

Remark 1

The parameter \(\alpha _{i+\frac{1}{2}}\) in (9) is used for optimal rates of convergence and the maximum-principle-preserving technique introduced in Du and Yang [12].

Finally, we would like to define

$$\begin{aligned} H_u(u_h,p_h,v)&=-\sum _{i=1}^{N_x}\int _{I_{i}} a(u_h) p_h v_x dx - \sum _{i=1}^{N_x}{\hat{a}}_{i-\frac{1}{2}}{\hat{p}}_{i-\frac{1}{2}}[v]_{i-\frac{1}{2}}, \end{aligned}$$
(10)
$$\begin{aligned} H_p(u_h,w)&=-\sum _{i=1}^{N_x}\int _{P_{i-\frac{1}{2}}} A(u_h) w_x dx -\sum _{i=1}^{N_x} A(u_h({\tilde{x}}_{i}))[w]_{i}, \end{aligned}$$
(11)

which would be useful in the stability analysis and error estimates. With the above notations, the LDG scheme can be rewritten as

$$\begin{aligned} \int _\Omega (u_h)_t v dx&=H_u(u_h,p_h,v), \end{aligned}$$
(12)
$$\begin{aligned} \int _\Omega p_h w dx&=H_p(u_h,w). \end{aligned}$$
(13)

2.4 Stability analysis

In this section, we proceed to demonstrate the stability of the new LDG method. We would start with the following lemma.

Lemma 1

Suppose \(H_u\) and \(H_p\) are defined in (10) and (11), respectively, then we have

$$\begin{aligned} H_u(u_h,p_h,u_h)+H_p(u_h,p_h)=&-\sum _{i=1}^{N_x}\frac{[A(u_h)]_{i-\frac{1}{2}}}{[u_h]_{i-\frac{1}{2}}}\frac{\alpha _{i-\frac{1}{2}}[u_h]_{i-\frac{1}{2}}^2}{ \triangle {\tilde{x}}_{i-\frac{1}{2}}}\nonumber \\ =&-\sum _{i=1}^{N_x}\frac{\alpha _{i-\frac{1}{2}}[A(u_h)]_{i-\frac{1}{2}}[u_h]_{i-\frac{1}{2}}}{ \triangle {\tilde{x}}_{i-\frac{1}{2}}}. \end{aligned}$$
(14)

Proof

Taking \(w=p_h\) in (11) and using integration by parts, we obtain

$$\begin{aligned} H_p(u_h,p_h)= & {} -\sum _{i=1}^{N_x}\int _{P_{i-\frac{1}{2}}} A(u_h) (p_h)_x dx -\sum _{i=1}^{N_x} A(u_h({\tilde{x}}_{i}))[p_h]_{i}\nonumber \\= & {} -\sum _{i=1}^{N_x}\int _{{\tilde{x}}_{i-1}}^{x_{i-\frac{1}{2}}} A(u_h) (p_h)_x dx-\sum _{i=1}^{N_x}\int _{x_{i-\frac{1}{2}}}^{{\tilde{x}}_{i}} A(u_h) (p_h)_x dx-\sum _{i=1}^{N_x} A(u_h({\tilde{x}}_{i}))[p_h]_{i}\nonumber \\= & {} \sum _{i=1}^{N_x}\int _{{\tilde{x}}_{i-1}}^{x_{i-\frac{1}{2}}} a(u_h) (u_h)_xp_h dx+\sum _{i=1}^{N_x}\int _{x_{i-\frac{1}{2}}}^{{\tilde{x}}_{i}} a(u_h) (u_h)_x p_h dx+\sum _{i=1}^{N_x}[A(u_h)]_{i{-}\frac{1}{2}}p_h\big (x_{i{-}\frac{1}{2}}\big )\nonumber \\= & {} \sum _{i=1}^{N_x}\int _{I_i} a(u_h)(u_h)_x p_h dx+\sum _{i=1}^{N_x}[A(u_h)]_{i-\frac{1}{2}}p_h\big (x_{i-\frac{1}{2}}\big ). \end{aligned}$$
(15)

Taking \(v=u_h\) in (10), we obtain

$$\begin{aligned} H_u(u_h,p_h,u_h)=&-\sum _{i=1}^{N_x}\int _{I_{i}} a(u_h)p_h (u_h)_x dx \nonumber \\&- \sum _{i=1}^{N_x}\frac{[A(u_h)]_{i-\frac{1}{2}}}{[u_h]_{i-\frac{1}{2}}}\left( p_h\big (x_{i-\frac{1}{2}}\big ) +\frac{\alpha _{i-\frac{1}{2}}}{ \triangle {\tilde{x}}_{i-\frac{1}{2}}} [u_h]_{i-\frac{1}{2}}\right) [u_h]_{i-\frac{1}{2}}. \end{aligned}$$
(16)

Summing (15) and (16), we have (14). \(\square \)

By the definition of A(u) in (5), we can easily check \(\frac{[A(u_h)]_{i+\frac{1}{2}}}{[u_h]_{j+\frac{1}{2}}}\ge 0\), which further leads to the \(L_2\) stability of the LDG method on overlapping meshes. The proof is straightforward, so we omit it and only demonstrate the result as the following theorem.

Theorem 1

The LDG method introduced in (6) and (7) is stable and

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\Vert u_h\Vert ^2+\Vert p_h\Vert ^2 \le 0. \end{aligned}$$

Remark 2

The above theorem is valid for all \(\alpha _{i-\frac{1}{2}}\ge 0\). Especially, we can take the penalty parameter \(\alpha _{i-\frac{1}{2}}=0\) for all \(i=1,2,\ldots ,N_x.\) However, numerical experiments demonstrate that, this may lead to accuracy degeneration in some special cases.

2.5 Error estimates

In this section, we proceed to the error estimates. For simplicity, we consider linear equations only, e.g. \(a(u)=1\) (A(u) = u), then (6) and (7) become

$$\begin{aligned} \int _{I_{i}} (u_h)_t v dx&=-\int _{I_{i}}p_h v_x dx + {\hat{p}}_{i+\frac{1}{2}}v^-_{i+\frac{1}{2}}-{\hat{p}}_{i-\frac{1}{2}}v^+_{i-\frac{1}{2}}, \end{aligned}$$
(17)
$$\begin{aligned} \int _{P_{i-\frac{1}{2}}} p_h w dx =&-\int _{P_{i-\frac{1}{2}}} u_h w_x dx + u_h({\tilde{x}}_{i})w^-_{i}-u_h({\tilde{x}}_{i-1})w^+_{i-1}. \end{aligned}$$
(18)

Moreover, \(H_u\) in (10) can also be written as

$$\begin{aligned} H_u(u_h,p_h,v)=-\sum _{i=1}^{N_x}\int _{I_{i}} p_h v_x dx - \sum _{i=1}^{N_x}{\hat{p}}_{i-\frac{1}{2}}[v]_{i-\frac{1}{2}}. \end{aligned}$$
(19)

We denote the error as \(e_u=u-u_h\) and \(e_p=p-p_h\), then the error equations are

$$\begin{aligned} \int _{I_{i}} (e_u)_t v dx&=-\int _{I_{i}}e_p v_x dx + \widehat{e_p}_{i+\frac{1}{2}}v^-_{i+\frac{1}{2}}-\widehat{e_p}_{i-\frac{1}{2}}v^+_{i-\frac{1}{2}}, \end{aligned}$$
(20)
$$\begin{aligned} \int _{P_{i-\frac{1}{2}}} e_p w dx =&-\int _{P_{i-\frac{1}{2}}} e_u w_x dx + e_u({\tilde{x}}_{i})w^-_{i}-e_u({\tilde{x}}_{i-1})w^+_{i-1}. \end{aligned}$$
(21)

We first study some basic properties of the finite element space. Let us start with the classical inverse properties.

Lemma 2

Assuming \(u_h\in V_h\), then there exists a constant \(C>0\) independent of \(\Delta x\) and \(u_h\) such that for \(\alpha \ge 1\)

$$\begin{aligned} \Vert \partial ^\alpha _xu_h\Vert _{I_i}\le C\Delta x_i^{-\alpha }\Vert u_h\Vert _{I_i},\quad \quad \Vert u_h\Vert _{\Gamma _i}\le C\Delta x_i^{-1/2}\Vert u_h\Vert _{I_i}. \end{aligned}$$

Similarly, for any \(u_h\in P_h\), there exists a constant \(C>0\) independent of \(\Delta x\) and \(u_h\) such that for \(\alpha \ge 1\)

$$\begin{aligned} \Vert \partial ^\alpha _xu_h\Vert _{P_{i+\frac{1}{2}}}\le C\Delta {\tilde{x}}_{i+\frac{1}{2}}^{-\alpha }\Vert u_h\Vert _{P_{i+\frac{1}{2}}}\quad \quad \Vert u_h\Vert _{\Gamma _{i+\frac{1}{2}}}\le C\Delta {\tilde{x}}_{i+\frac{1}{2}}^{-1/2}\Vert u_h\Vert _{P_{i+\frac{1}{2}}}. \end{aligned}$$

We also introduce the standard \(L^2\) projection \(P^1_k\) into \(V_h\) and \(P^2_k\) into \(P_h\) by:

$$\begin{aligned} \int _{I_i} P^1_kuv\ dx= & {} \int _{I_i}uv\ dx\ ,\ \forall v\in P^{k}(I_i),\quad \text {and}\quad \nonumber \\ \int _{P_{i+\frac{1}{2}}} P_k^2uv\ dx= & {} \int _{P_{i+\frac{1}{2}}}uv\ dx\ ,\ \forall v\in P^{k}(P_{i+\frac{1}{2}}), \end{aligned}$$

respectively. By the scaling argument, we obtain the following lemma [4].

Lemma 3

Suppose the function \(u(x)\in C^{k+1}(I_i)\), then there exists a positive constant C independent of \(\Delta x\) and u, such that

$$\begin{aligned} \Vert u-P^1_k u\Vert _{I_i}+\Delta x_i\Vert (u-P^1_k u)_x\Vert _{I_i}+\Delta x_i^\frac{1}{2}\Vert u-P^1_k u\Vert _{\infty ,I_i}\le C\Delta x_i^{k+1}\Vert u\Vert _{k+1,I_i}. \end{aligned}$$

Moreover, if \(u(x)\in C^{k+1}(P_{i+\frac{1}{2}})\), then there exists a positive constant C independent of \(\Delta x\) and u, such that

$$\begin{aligned}&\Vert u-P_k^2 u\Vert _{P_{i+\frac{1}{2}}}+\Delta {\tilde{x}}_{i+\frac{1}{2}}\Vert (u-P_k^2 u)_x\Vert _{P_{i+\frac{1}{2}}}+\Delta {\tilde{x}}_{i+\frac{1}{2}}^\frac{1}{2}\Vert u-P_k^2 u\Vert _{\infty ,P_{i+\frac{1}{2}}}\nonumber \\&\quad \le C\Delta {\tilde{x}}_{i+\frac{1}{2}}^{k+1}\Vert u\Vert _{k+1,P_{i+\frac{1}{2}}}, \end{aligned}$$

where \(\Vert u\Vert _{k+1,I}\) is the standard \(H^{k+1}\)-norm over the interval I.

As the general treatment of the DG methods, we write the errors as

$$\begin{aligned} e_u=\eta _u-\xi _u\quad e_p=\eta _p-\xi _p, \end{aligned}$$

where

$$\begin{aligned} \eta _u=u-P_k^1u,\quad \xi _u=u_h-P_k^1u,\quad \eta _p=p-P_k^2p,\quad \xi _p=p_h-P_k^2p. \end{aligned}$$

With the above notations, we can rewrite the error equations (20) and (21) as

$$\begin{aligned} \int _{I_{i}} (\xi _u)_t v dx&=\int _{I_{i}}e_p v_x dx - \widehat{e_p}_{i+\frac{1}{2}}v^-_{i+\frac{1}{2}}+\widehat{e_p}_{i-\frac{1}{2}}v^+_{i-\frac{1}{2}}, \end{aligned}$$
(22)
$$\begin{aligned} \int _{P_{i+\frac{1}{2}}} \xi _p w dx =&\int _{P_{i+\frac{1}{2}}} e_u w_x dx - e_u({\tilde{x}}_{i+1})w^-_{i+1}+e_u({\tilde{x}}_{i})w^+_{i}. \end{aligned}$$
(23)

Now, we can state the main theorem.

Theorem 2

Suppose the exact solution \(u\in C^{k+2}(\Omega )\) and the finite element space is made up of piecewise polynomial of degree k in each cell. The numerical solutions satisfy (17) and (18). Then the error between the numerical and exact solutions satisfy

$$\begin{aligned} \Vert e_u\Vert +\int _0^T\Vert e_p\Vert \ dt\le C\Delta x^k, \end{aligned}$$

where C is independent of \(\Delta x\).

Proof

Sum up (22) and (23) with \(v=\xi _u\) and \(w=\xi _p\), and then sum up over i to obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert \xi _u\Vert ^2+\Vert \xi _p\Vert ^2= & {} \sum _{i=1}^{N_x}\int _{I_{i}}(\eta _p-\xi _p)(\xi _u)_x dx\nonumber \\&+\sum _{i=1}^{N_x}\left( {\eta _p}_{i-\frac{1}{2}}-{\xi _p}_{i-\frac{1}{2}}+\alpha _{i-\frac{1}{2}}\frac{[\eta _u-\xi _u]_{i-\frac{1}{2}}}{\Delta {\tilde{x}}_{i-\frac{1}{2}}}\right) [\xi _u]_{i-\frac{1}{2}}\nonumber \\&+\sum _{i=1}^{N_x}\int _{P_{i-\frac{1}{2}}} (\eta _u-\xi _u) (\xi _p)_x dx +\sum _{i=1}^{N_x} (\eta _u-\xi _u)({\tilde{x}}_{i})[\xi _p]_{i}\nonumber \\= & {} \sum _{i=1}^{N_x}\int _{I_{i}}\eta _p(\xi _u)_x dx +\sum _{i=1}^{N_x}\left( {\eta _p}_{i-\frac{1}{2}}+\frac{\alpha _{i-\frac{1}{2}}[\eta _u]_{i-\frac{1}{2}}}{\Delta {\tilde{x}}_{i-\frac{1}{2}}}\right) [\xi _u]_{i-\frac{1}{2}}\nonumber \\&+\sum _{i=1}^{N_x}\int _{P_{i-\frac{1}{2}}} \eta _u (\xi _p)_x dx +\sum _{i=1}^{N_x} \eta _u({\tilde{x}}_{i})[\xi _p]_{i}+H_u(\xi _u,\xi _p,\xi _u)\nonumber \\&\qquad +H_p(\xi _u,\xi _p) =R_1+R_2+R_3, \end{aligned}$$
(24)

where

$$\begin{aligned} R_1= & {} \sum _{i=1}^{N_x}\int _{I_{i}}\eta _p(\xi _u)_x dx+\sum _{i=1}^{N_x}\int _{P_{i-\frac{1}{2}}} \eta _u (\xi _p)_x dx, \\ R_2= & {} \sum _{i=1}^{N_x}\frac{\alpha _{i-\frac{1}{2}}[\eta _u]_{i-\frac{1}{2}}}{\Delta {\tilde{x}}_{i-\frac{1}{2}}}[\xi _u]_{i-\frac{1}{2}}+H_u(\xi _u,\xi _p,\xi _u)+H_p(\xi _u,\xi _p),\\ R_3= & {} \sum _{i=1}^{N_x}{\eta _p}_{i-\frac{1}{2}}[\xi _u]_{i-\frac{1}{2}}+\sum _{i=1}^{N_x} \eta _u({\tilde{x}}_{i})[\xi _p]_{i}. \end{aligned}$$

Now we estimate \(R_i\)\(i=1,2,3\) term by term.

$$\begin{aligned} R_1\le & {} \sum _{i=1}^{N_x}\left( \Vert \eta _p\Vert _{I_i}\Vert (\xi _u)_x\Vert _{I_i}+\Vert \eta _u\Vert _{P_{i-\frac{1}{2}}}\Vert (\xi _p)_x\Vert _{P_{i-\frac{1}{2}}}\right) \nonumber \\\le & {} \sum _{i=1}^{N_x}\left( \Vert \eta _p\Vert _{P_{i-\frac{1}{2}}\cup P_{i+\frac{1}{2}}}\Vert (\xi _u)_x\Vert _{k+1,I_i}+\Vert \eta _u\Vert _{k+1,I_{i-1}\cup I_i}\Vert (\xi _p)_x\Vert _{P_{i-\frac{1}{2}}}\right) \nonumber \\\le & {} C\Delta x^k\sum _{i=1}^{N_x}\left( \left( \Vert p\Vert _{k+1,P_{i-\frac{1}{2}}}+\Vert p\Vert _{k+1,P_{i+\frac{1}{2}}}\right) \Vert \xi _u\Vert _{I_i}\right. \nonumber \\&\left. +\left( \Vert u\Vert _{k+1,I_{i-1}}+\Vert u\Vert _{k+1,I_{i}}\right) \Vert \xi _p\Vert _{P_{i-\frac{1}{2}}}\right) \nonumber \\\le & {} C\Delta x^k\left( \Vert p\Vert _{k+1}\Vert \xi _u\Vert +\Vert u\Vert _{k+1}\Vert \xi _p\Vert \right) . \end{aligned}$$
(25)

where in the first step, we applied Cauchy-Schwarz inequality, in the second step we used Lemmas 2 and 3, and the last step follows from Cauchy-Schwarz inequality again. Applying Lemma 1, we obtain the estimate of \(R_2\)

$$\begin{aligned} R_2\le & {} \sum _{i=1}^{N_x}\frac{\alpha _{i-\frac{1}{2}}}{\Delta {\tilde{x}}_{i-\frac{1}{2}}}\left( [\eta _u]_{i-\frac{1}{2}}[\xi _u]_{i-\frac{1}{2}}-[\xi _u]^2_{i-\frac{1}{2}}\right) \nonumber \\\le & {} C\sum _{i=1}^{N_x}\frac{\alpha _{i-\frac{1}{2}}}{\Delta x}[\eta _u]^2_{i-\frac{1}{2}}\nonumber \\\le & {} C\sum _{i=1}^{N_x}\alpha _{i-\frac{1}{2}}\Delta x^{2k}\left( \Vert u\Vert _{I_{i-1}}^2+\Vert u\Vert _{I_{i}}^2\right) ,\nonumber \\\le & {} C\Delta x^{2k}, \end{aligned}$$
(26)

where in step 3, we applied Lemma 3, steps 2 and 4 follow from direct computation. Finally, we estimate \(R_3\).

$$\begin{aligned} R_3\le & {} \sum _{i=1}^{N_x}\Vert \eta _p\Vert _{\infty ,P_{i-\frac{1}{2}}}\big (\Vert \xi _u\Vert _{\Gamma _{i-1}}+\Vert \xi _u\Vert _{\Gamma _{i}}\big )+\sum _{i=1}^{N_x}\Vert \eta _u\Vert _{\infty ,I_i}\left( \Vert \xi _p\Vert _{\Gamma _{i-\frac{1}{2}}}+\Vert \xi _p\Vert _{\Gamma _{i+\frac{1}{2}}}\right) \nonumber \\\le & {} C\Delta x^k\sum _{i=1}^{N_x}\left( \Vert p\Vert _{k+1,P_{i-\frac{1}{2}}}\left( \Vert \xi _u\Vert _{I_{i-1}}+\Vert \xi _u\Vert _{I_i}\right) +\Vert u\Vert _{k+1,I_i}\left( \Vert \xi _p\Vert _{P_{i-\frac{1}{2}}}+\Vert \xi _p\Vert _{P_{i+\frac{1}{2}}}\right) \right) \nonumber \\\le & {} C\Delta x^k\left( \Vert p\Vert _{k+1}\Vert \xi _u\Vert +\Vert u\Vert _{k+1}\Vert \xi _p\Vert \right) , \end{aligned}$$
(27)

where step 1 is straightforward, step 2 follows from Lemmas 2 and 3, and in the last step we applied the Cauchy–Schwarz inequality. Substitute (25)–(27) into (24) to obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert \xi _u\Vert ^2+\Vert \xi _p\Vert ^2\le C\Delta x^{2k}+C\Delta x^k\left( \Vert \xi _u\Vert +\Vert \xi _p\Vert \right) , \end{aligned}$$

which further yields

$$\begin{aligned} \frac{d}{dt} \Vert \xi _u\Vert ^2+\Vert \xi _p\Vert ^2\le C\Delta x^{2k}+\Vert \xi _u\Vert ^2. \end{aligned}$$

Finally, we can apply the Gronwall’s inequality and complete the proof. \(\square \)

In Theorem 2, we only proved suboptimal convergence rate. Numerical experiments in Sect. 4 demonstrate that in some cases the order of accuracy is exactly k. In the traditional error estimates, one would like to study the steady state problem, and construct the elliptic projection. We can show that the elliptic projection may not exist. To explain this point, we use uniform meshes and denote \(\Delta x\) as the mesh size for both the primitive and P-meshes. We consider the following steady state problem

$$\begin{aligned} p_x=0,\quad p=u_x, \end{aligned}$$

subject to periodic boundary condition. To make the problem well-posed, we need another assumption that \(\int _\Omega u(x)\ dx=0\). Then the numerical scheme turns out to be

$$\begin{aligned} 0&=-\int _{I_{i}}p_h v_x dx + {\hat{p}}_{i+\frac{1}{2}}v^-_{i+\frac{1}{2}}-{\hat{p}}_{i-\frac{1}{2}}v^+_{i-\frac{1}{2}}, \end{aligned}$$
(28)
$$\begin{aligned} \int _{P_{i+\frac{1}{2}}} p_h w dx =&-\int _{P_{i+\frac{1}{2}}} u_h w_x dx + u_h({\tilde{x}}_{i+1})w^-_{i+1}-u_h({\tilde{x}}_{i})w^+_{i}. \end{aligned}$$
(29)

We take \(\xi _0=0\) in (4), i.e. the dual mesh is constructed by using the midpoint of the primitive mesh and \(\alpha _{i-\frac{1}{2}}=0\) for all \(i=1,2,\ldots ,N_x\). Moreover, we use \(P^1\) polynomials and assume

$$\begin{aligned} u_h(x)&=u_i^0+u_i^1L_i(x),\quad x\in I_i,\\ p_h(x)&=p_{i+\frac{1}{2}}^0+p_{i+\frac{1}{2}}^1L_{i+\frac{1}{2}}(x),\quad x\in P_{i+\frac{1}{2}}, \end{aligned}$$

where \(L_i(x)\) and \(L_{i+\frac{1}{2}}(x)\) are the scaled Legendre polynomial in cell \(I_i\) and \(P_{i+\frac{1}{2}}\), respectively. Take \(v(x)=1\) and \(v(x)=L_i(x)\) in (28), respectively, to obtain

$$\begin{aligned} 0=p_{i+\frac{1}{2}}^0-p_{i-\frac{1}{2}}^0,\quad 0=-p_{i-\frac{1}{2}}^0-\frac{1}{2}p_{i-\frac{1}{2}}^1-p_{i+\frac{1}{2}}^0+\frac{1}{2}p_{i+\frac{1}{2}}^1+p_{i+\frac{1}{2}}^0+p_{i-\frac{1}{2}}^0,\nonumber \\ \end{aligned}$$
(30)

which further yield

$$\begin{aligned} p_{i+\frac{1}{2}}^0=p_{i-\frac{1}{2}}^0,\quad p_{i+\frac{1}{2}}^1=p_{i-\frac{1}{2}}^1. \end{aligned}$$

Take \(w(x)=1\) and \(w(x)=L_{i+\frac{1}{2}}(x)\) in (29), respectively to obtain

$$\begin{aligned} \Delta xp_{i+\frac{1}{2}}^0=u_{i+1}^0-u_i^0,\quad \frac{\Delta x}{3}p_{i+\frac{1}{2}}^1=-\frac{1}{2}u_i^1+\frac{1}{2}u_{i+1}^1. \end{aligned}$$
(31)

Clearly, (30) and (31) are not uniquely solvable, one nontrivial solution could be \(u_h(x)=L_i(x)\) in \(I_i\) and \(p_h=0\). It is easy to check that \(\int _\Omega u_h\ dx=0.\) Therefore, for the special case given above, the traditional elliptic projection does not exist, and the LDG method cannot be used to solve the steady state problems. For time-dependent problems, though the numerical approximations exist, numerical experiments demonstrate only a suboptimal convergence rate. However, some slight modification of the scheme can yield optimal convergence rates. They are listed as follows:

  1. 1.

    Use even order polynomials, i.e. \(k=0,2,\ldots \);

  2. 2.

    Take \(\xi _0=0\) with \(\alpha \ne 0\);

  3. 3.

    Take \(\xi _0\ne 0\);

Besides the above, for convection–diffusion equations, we can always obtain optimal rates of convergence even though we take \(\xi _0=\alpha =0\).

3 Numerical scheme for two-dimensional case

In this section, we will construct the LDG scheme on overlapping meshes in two space dimensions and study the following PDE over the domain \(\Omega =[0,1]\times [0,1]\),

$$\begin{aligned} \left\{ \begin{array}{l} u_t=(a(u)p)_x+(b(u)q)_y, \\ p=A(u)_x,\\ q=B(u)_y, \end{array} \right. \end{aligned}$$
(32)

subject to periodic boundary conditions, where \(A(u)=\int ^u a(t)dt\) and \(B(u)=\int ^ub(t) dt\).

We first define the primitive mesh for the primary variable u which is a regular rectangular decomposition of \(\Omega \). Let \(0=x_\frac{1}{2}<x_\frac{3}{2}<\cdots <x_{N_x+\frac{1}{2}}=1\) and \(0=y_\frac{1}{2}<y_\frac{3}{2}<\cdots <y_{N_y+\frac{1}{2}}=1\) be the grid points in x and y directions, respectively, and denote the i, j-th cell as

$$\begin{aligned} I_{ij}=I_i\times J_j,\quad i=1,\ldots ,N_x,\ j=1,\ldots ,N_y. \end{aligned}$$

where \(I_i=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]\) and \(J_j=[y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]\). Moreover, we denote

$$\begin{aligned} \Delta x_i=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}},\quad x_i=\frac{x_{i-\frac{1}{2}}+x_{i+\frac{1}{2}}}{2},\quad \Delta y_j=y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}},\quad y_j=\frac{y_{j-\frac{1}{2}}+y_{j+\frac{1}{2}}}{2}. \end{aligned}$$

and

$$\begin{aligned} \Delta x=\max _i\Delta x_i,\quad \Delta y=\max _j\Delta y_j,\quad h=\max \{\Delta x,\Delta y\} \end{aligned}$$

We also move each cell horizontally to obtain the P-mesh: \(P_{i-\frac{1}{2},j}=[{\tilde{x}}_{i-1},{\tilde{x}}_{i}]\times [y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]\), where

$$\begin{aligned} {\tilde{x}}_i=x_i+\frac{\Delta x_i}{2}\xi _0, \qquad \xi _0\in [-1,1],\qquad i=1,2,\ldots ,N_x, \end{aligned}$$
(33)

with \({\tilde{x}}_0={\tilde{x}}_{N_x}-1.\) Similarly, we can define the Q-mesh: \(Q_{i,j-\frac{1}{2}}=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]\times [{\tilde{y}}_{j-1},{\tilde{y}}_{j}]\), where

$$\begin{aligned} {\tilde{y}}_j=y_j+\frac{\Delta y_j}{2}\eta _0, \qquad \eta _0\in [-1,1],\qquad j=1,2,\ldots ,N_y, \end{aligned}$$
(34)

with \({\tilde{y}}_0={\tilde{y}}_{N_y}-1.\) The P-mesh and Q-mesh are used to solve the auxiliary variables p and q, respectively. Similar to the problem in one space dimension, we can also define \(P_{\frac{1}{2},j}=([0,{\tilde{x}}_1]\cup [{\tilde{x}}_{N_x},1])\times J_j\) and \(Q_{j,\frac{1}{2}}=I_i\times ([0,{\tilde{y}}_1]\cup [{\tilde{y}}_{N_y},1]).\)

We define the finite element spaces to be

$$\begin{aligned}&V_h:=\{u_h: u_h|_{I_{ij}}\in P^k(I_{ij}),\, i=1,\ldots ,N_x,\ j=1,\ldots ,N_y \}, \\&P_h:=\{p_h: p_h|_{P_{i+\frac{1}{2},j}}\in P^k(P_{i+\frac{1}{2},j}),\, i=1,\ldots ,N_x,\ j=1,\ldots ,N_y \},\\&Q_h:=\{q_h: q_h|_{Q_{i,j+\frac{1}{2}}}\in P^k(Q_{i,j+\frac{1}{2}}),\, i=1,\ldots ,N_x,\ j=1,\ldots ,N_y \}. \end{aligned}$$

Given \(u\in V_h\), we denote \(u^+_{i-\frac{1}{2},j}\), \(u^-_{i+\frac{1}{2},j}\), \(u^+_{i,j-\frac{1}{2}}\), \(u^-_{i,j+\frac{1}{2}}\) to be the traces of u on the four edges of \(I_{ij}\), respectively. Likewise for the traces of \(P_{i+\frac{1}{2},j}\) along the vertical edges and those of \(Q_{i,j+\frac{1}{2}}\) along the horizontal edges. Moreover, we use \([u]=u^+-u^-\) and \(\{u\}=\frac{1}{2}(u^++u^-)\) as the jump and average of u at the cell interfaces, respectively.

Now, we can introduce the LDG method on overlapping meshes: find \((u_h,p_h,q_h)\in V_h\times P_h\times Q_h\), such that for any test functions \((v,w,z)\in V_h\times P_h\times Q_h\), we have

$$\begin{aligned} \int _{I_{ij}} (u_h)_t v dxdy=&-\int _{I_{ij}} a(u_h) p_h v_x dxdy + \int _{J_j}{\hat{a}}_{i+\frac{1}{2},j}{\hat{p}}_{i+\frac{1}{2},j}v^-_{i+\frac{1}{2},j}dy\nonumber \\&-\int _{J_j}{\hat{a}}_{i-\frac{1}{2},j}{\hat{p}}_{i-\frac{1}{2},j}v^+_{i-\frac{1}{2},j}dy,\nonumber \\&-\int _{I_{ij}} b(u_h) q_h v_y dxdy + \int _{I_i}{\hat{b}}_{i,j+\frac{1}{2}}{\hat{q}}_{i,j+\frac{1}{2}}v^-_{i,j+\frac{1}{2}}dx\nonumber \\&-\int _{I_i}{\hat{b}}_{i,j-\frac{1}{2}}{\hat{q}}_{i,j-\frac{1}{2}}v^+_{i,j-\frac{1}{2}}dx, \end{aligned}$$
(35)
$$\begin{aligned} \int _{P_{i+\frac{1}{2},j}} p_h w dxdy =&-\int _{P_{i+\frac{1}{2},j}} A(u_h) w_x dxdy + \int _{J_j}A(u_h({\tilde{x}}_{i+1}))w^-_{i+1}dy\nonumber \\&-\int _{J_j}A(u_h({\tilde{x}}_{i}))w^+_{i}dy, \end{aligned}$$
(36)
$$\begin{aligned} \int _{Q_{i,j+\frac{1}{2}}} p_h z dxdy =&-\int _{Q_{i,j+\frac{1}{2}}} B(u_h) z_y dxdy + \int _{I_i}B(u_h({\tilde{y}}_{j+1}))z^-_{j+1}dx\nonumber \\&-\int _{I_i}B(u_h({\tilde{y}}_{j}))z^+_{j}dx. \end{aligned}$$
(37)

The numerical flux \({\hat{a}}\) along the edge \(x=x_{i+\frac{1}{2}}\) is taken as

$$\begin{aligned} {\hat{a}}_{i+\frac{1}{2},j}=\frac{[A(u_h)]_{i+\frac{1}{2},j}}{[u_h]_{i+\frac{1}{2},j}} \end{aligned}$$

Similarly, the numerical flux \({\hat{b}}\) along the edge \(y=y_{j+\frac{1}{2}}\) is taken as

$$\begin{aligned} {\hat{b}}_{i,j+\frac{1}{2}}=\frac{[B(u_h)]_{i,j+\frac{1}{2}}}{[u_h]_{i,j+\frac{1}{2}}}, \end{aligned}$$

where \([s]_{i+\frac{1}{2},j}:=s^+_{i+\frac{1}{2},j}-s^-_{i+\frac{1}{2},j}\) denotes the jump of a function s across the cell boundary \(\{x_{i+\frac{1}{2}}\}\times J_j\). Likewise for \([s]_{i,j+\frac{1}{2}}\). Moreover, we choose

$$\begin{aligned} {\hat{p}}_{i+\frac{1}{2},j}&=p_h(x_{i+\frac{1}{2}},y)+\frac{\alpha _{i+\frac{1}{2},j}}{ \Delta {\tilde{x}}_{i+\frac{1}{2},j}} [u_h]_{i+\frac{1}{2},j},\quad \\ {\hat{q}}_{i,j+\frac{1}{2}}&=q_h(x,y_{j+\frac{1}{2}})+\frac{\alpha _{i,j+\frac{1}{2}}}{ \Delta {\tilde{x}}_{i,j+\frac{1}{2}}} [u_h]_{i,j+\frac{1}{2}} \end{aligned}$$
Table 1 Example 1: midpoint, uniform mesh
Full size table
Table 2 Midpoint, random mesh (20%)
Full size table
Table 3 \(\xi _0=0.05\) and \(\xi _0=\sqrt{3}/3\), uniform mesh
Full size table
Table 4 \(\xi _0=0.05\) and \(\xi _0=\sqrt{3}/3\), random mesh (20%)
Full size table
Table 5 Example 2: \(\xi _0=\alpha =0\). random mesh
Full size table
Table 6 Example 3: \(\xi _0=\eta _0=\alpha =\beta =0\), different meshes
Full size table
Table 7 Example 3: \(\xi _0=\eta _0=0\), different \(\alpha \) and \(\beta \), random mesh
Full size table
Table 8 Example 3: different \(\xi _0\) and \(\eta _0\), \(\alpha =\beta =0\), random mesh
Full size table
Table 9 Example 4: \(\xi _0=\eta _0=\alpha =\beta =0\). random mesh
Full size table

Following the same analyses for problems in one space dimension, we can obtain the stability analysis and error estimates. Therefore, we will skip the proof and only demonstrate the results in the following two theorems.

Theorem 3

The LDG methods introduced in (35)–(37) is stable and

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\Vert u_h\Vert ^2+\Vert p_h\Vert ^2+\Vert q_h\Vert ^2 \le 0. \end{aligned}$$

Theorem 4

Suppose the exact solution for linear parabolic equation (32) with \(a(u)=b(u)=1\) satisfies \(u\in C^{k+1}(\Omega )\) and the finite element space is made up of piecewise polynomial of degree k in each cell. The numerical solutions satisfy (35)–(37). Then the error between the numerical and exact solutions satisfy

$$\begin{aligned} \Vert u-u_h\Vert +\int _0^T\left( \Vert p-p_h\Vert +\Vert q-q_h\Vert \right) \ dt\le Ch^{k}, \end{aligned}$$

where C is independent of h.

4 Numerical examples

In this section, we will use numerical experiments to demonstrate the stability and the accuracy of the new LDG method on overlapping meshes. In all the numerical experiments, we use piecewise polynomials of degree \(k=1,2,3,4\). If not otherwise stated we consider third-order SSP Runge-Kutta time discretization [14] with \(\Delta t=0.1\Delta x^2\) if \(k=1,2\) and \(\Delta t=0.01\Delta x^2\) if \(k=3,4\) to reduce the time error, and take the final time \(T=1\). Moreover, the random mesh is generated by randomly and independently perturbing each node in a uniform mesh by up to 20%.

Example 1

We solve the following heat equation in one space dimension

$$\begin{aligned} \left\{ \begin{array}{l} u_t=u_{xx},\\ u(x,0)=\sin (x), \end{array} \right. x\in [0,2\pi ]. \end{aligned}$$
(38)

Clearly, the exact solution is

$$\begin{aligned} u(x,t)=e^{-t}\sin (x). \end{aligned}$$

We consider uniform mesh and take \(\xi _0=0\) in (4), i.e. the dual mesh is generated by using the midpoint of the primitive mesh. We compute the error between the numerical and exact solutions and the results under the \(L^2\)- and \(L^\infty \)-norms are given in Table 1.

From the table, we can only observe suboptimal accuracy if k is an odd number and the penalty parameter \(\alpha =0\). To obtain optimal convergence rates, we can choose \(\alpha \ne 0\) or use even order polynomials. We repeat the same example with random meshes with results given in Table 2, we can observe exactly the same convergence rates discussed above.

Another possible way to recover optimal convergence rates would be taking \(\xi _0\ne 0\). In Tables 3 and 4, we take \(\alpha =0,\) and choose \(\xi _0=0.05\) which is close to 0 and \(\xi _0=\sqrt{3}/3\) which is away from 0. We can clearly observe optimal convergence rates. Moreover, the errors for \(\xi _0=\sqrt{3}/3\) is less than those for \(\xi _0=0.05\).

Example 2

We solve the following convection–diffusion equation

$$\begin{aligned} \left\{ \begin{array}{l} u_t+u_x=u_{xx}, \\ u(x,0)=\sin (x), \end{array} \right. x\in [0,2\pi ]. \end{aligned}$$
(39)

Clearly, the exact solution is

$$\begin{aligned} u(x,t)=e^{-t}\sin (x-t). \end{aligned}$$

We consider random meshes only and use upwind fluxes for the convection term. We take \(\xi _0=\alpha =0\) to test the accuracy and the results are given in Table 5. From the table, we can observe optimal convergence rates.

Example 3

We solve the heat equation in two space dimensions:

$$\begin{aligned} \left\{ \begin{array}{l} u_t=u_{xx}+u_{yy}, \\ u(x,0)=\sin (x)\cos (y), \end{array} \right. (x,y)\in [0,2\pi ]\times [0,2\pi ]. \end{aligned}$$
(40)

Clearly, the exact solution is

$$\begin{aligned} u(x,t)=e^{-2t}\sin (x)\cos (y). \end{aligned}$$

We first test the example with \(\xi _0=0\) in (33), \(\eta _0=0\) in (34) and \(\alpha =\beta =0\). The results are given in Table 6. From the table, we can only observe \((k+1)\)-th order convergence rates for \(k=3\).

To recover the optimal convergence rates, we choose other penalty parameters and the results are listed in Table 7. We use random meshes only and can observe that if both penalty parameters are nonzero, we can obtain optimal rates of convergence. However, if only one of the penalty parameters is nonzero, we still have the accuracy degeneration if piecewise odd order polynomials are applied.

Moreover, following Example 1, we also choose random meshes and take different values of \(\xi _0\) and \(\eta _0\). The results are provided in Table 8. We can observe that, if both of them are nonzero, the optimal convergence rates can be recovered. However, if one of them is zero, (e.g. \(\xi _0=0\)), the optimal rates cannot be obtained for \(k=1\).

Example 4

We solve the convection–diffusion equation in two space dimensions

$$\begin{aligned} \left\{ \begin{array}{l} u_t+u_x+u_y=u_{xx}+u_{yy},\\ u(x,y,0)=\sin (x)\cos (y), \end{array} \right. (x,y)\in [0,2\pi ]\times [0,2\pi ]. \end{aligned}$$
(41)

Clearly, the exact solution is

$$\begin{aligned} u(x,y,t)=e^{-2t}\sin (x-t)\cos (y-t). \end{aligned}$$

We consider random meshes only and use upwind fluxes for the convection term. We take \(\xi _0 =\eta _0= \alpha =\beta = 0\) to test the accuracy and the results are given in Table 9. From the table, we can observe optimal convergence rates.

5 Conclusion

In this paper, we have introduced a new LDG method on overlapping meshes. The scheme is stable but the order of accuracy may not be optimal. We demonstrated a potential reason for the accuracy degeneration and provided several alternatives to recover the optimal convergence rates.