An Adaptive SDG Method for the Stokes System

Abstract

Staggered grid techniques are attractive ideas for flow problems due to their more enhanced conservation properties. Recently, a staggered discontinuous Galerkin method is developed for the Stokes system. This method has several distinctive advantages, namely high order optimal convergence as well as local and global conservation properties. In addition, a local postprocessing technique is developed, and the postprocessed velocity is superconvergent and pointwisely divergence-free. Thus, the staggered discontinuous Galerkin method provides a convincing alternative to existing schemes. For problems with corner singularities and flows in porous media, adaptive mesh refinement is crucial in order to reduce the computational cost. In this paper, we will derive a computable error indicator for the staggered discontinuous Galerkin method and prove that this indicator is both efficient and reliable. Moreover, we will present some numerical results with corner singularities and flows in porous media to show that the proposed error indicator gives a good performance.

1 Introduction

Let $\Omega$ be a polyhedral domain in ${\mathbb {R}}^{2}$ or ${\mathbb {R}}^3$. We consider the Stokes problem

$$\begin{aligned} \left\{ \begin{array}{rcl@{\quad }l} \displaystyle -\Delta \varvec{u}+\nabla p &{} = &{} \varvec{f}, &{} \text {in } \Omega , \\ \displaystyle \nabla \cdot \varvec{u} &{} = &{} 0, &{} \text {in } \Omega , \\ \displaystyle \varvec{u} &{} = &{} {\mathbf {g}}, &{} \text {on } \partial \Omega , \end{array}\right. \end{aligned}$$

(1)

where $\varvec{u}$ is the velocity field, p is the pressure with$\int _{\Omega }p\, dx=0$, $\varvec{f}$ is the given source term, and ${\mathbf {g}}$ is the given boundary term with $\int _{\partial \Omega } {\mathbf {g}} \cdot {\mathbf {n}} =0$. Here ${\mathbf {n}}$ is the unit outward normal vector on the boundary. Throughout the paper, vector fields are denoted by bold faces. The solution of the Stokes system is useful in many applications, and there are many challenges in dealing with the numerical approximations. For example, when the domain of interest has some corners, the solution of the Stokes system will be singular near those corner points. Besides, for Stokes flows in porous media, the flow features are very complicated and require very fine mesh in order to capture these features. In these scenarios, one possible strategy is to apply adaptive mesh refinement technique and refine the mesh at suitable locations in order to reduce the computational cost. For adaptive mesh refinement techniques, the construction of an efficient and reliable error indicator is the key ingredient. The aim of the paper is to derive an error indicator for the recently developed staggered discontinuous Galerkin (SDG) method [30] for the Stokes system and analyze the reliability and efficiency of this error indicator.

Discontinuous Galerkin (DG) methods have been proven to be a class of very successful numerical schemes for the approximation of the Stokes system, due to their high order of approximation, ease of implementation and local conservation. For example, the local DG method [5, 18], the hp DG method [36], the mixed DG method [32, 33] and the HDG method [17, 19, 20] are popular schemes in applications. Recently, the SDG method [30] is proposed and analyzed for the Stokes system. The use of staggered meshes for the Stokes flow is popular in the finite volume and the finite difference communities [1, 2] due to their more enhanced conservation property, which is crucial for Stokes flow. For DG methods, the work in [30] gives the first DG method defined on staggered meshes. The SDG method has several distinctive advantages, namely high order optimal convergence as well as local and global conservation properties. Moreover, shown in [8, 20], a local postprocessing can be applied to the SDG solution to obtain a superconvergent and pointwisely divergence free velocity. The SDG method is also applied to the incompressible Navier-Stokes equations [4], see also [35] for a related work, and a number of other problems, see [6, 7, 9, 12–16, 30].

Adaptive techniques for finite element and discontinuous Galerkin methods are well developed, and there are works that construct error estimators for the Stokes problem, such as [22] and [37]. These estimates typically contain generic (unknown) constants and as such do not provide actual computable error bounds. To overcome this issue, [21] derives constant-free (for the upper bound) a posteriori error estimates for the Crouzeix-Raviart finite element approximation of Stokes flow. In [25], the authors develop a unified framework for a posteriori error estimation for the Stokes problem discretized by various numerical methods, including the conforming divergence-free, DG, conforming (stabilized), nonconforming, mixed, and finite volume methods. This kind of estimates is based on a velocity reconstruction and a locally conservative flux (stress) reconstruction. Moreover, classical residual-based a posteriori error estimates are derived within one unifying framework for lowest-order conforming, nonconforming, and mixed finite element schemes in [3]. In [11], the idea is generalized to more general situations to obtain new a posteriori error estimates for other methods such as mortar and DG methods. Further extensions of this kind of estimators for a wide range of DG methods are derived in [10]. Furthermore, [23] deals with the hp error analysis of a hybrid discontinuous Galerkin (HDG) method for incompressible flow.

As discussed before, adaptive mesh refinement for solving the Stokes problem is important in applications and has been derived for many different finite element methods. For the SDG method, an adaptive mesh refinement is derived for the time-harmonic Maxwell’s equations in [16]. However, the adaptive SDG method has not yet been developed for solving the Stokes problem and hence will be developed in this paper. We will first derive computable error indicator for the estimation of a DG-norm error of the approximate solution. This computable error indicator is composed of local residuals and the jumps of the velocity. We will then show the reliability of this indicator. In particular, we will show that, the DG-norm error of the approximate solution is bounded above by this computable error indicator. The idea of the proof follows from some ideas in [24, 27], and is also based on some new contributions specifically designed for the SDG method. Next, we will prove the efficiency of the error indicator, and we will show that the DG-norm error of the approximate solution is bounded below by this computable error indicator up to a data approximation term. We will apply the standard bubble function technique [38] to prove this result. Based on this error indicator, we will construct an adaptive mesh refinement strategy, which is not the same as the classical one since our method is based on a staggered mesh, and some careful refinement strategies are necessary to retain the staggered structure. We will present several numerical results to show the performance of our method. We will first present an example, with a known exact solution, to show the convergence of our adaptive scheme and compare our scheme to uniform refinement. We see that our adaptive scheme, as predicted, is much better than the uniform refinement, and has an optimal rate of convergence. We also see that, as the mesh is refined, the error indicator becomes close to the true DG-norm error. We will next consider two examples with corner singularities, and show that our adaptive method is able to produce the correct refinement near the corners. Finally, we will present two examples for Stokes flow in porous media. We consider perforated domains with circular perforations, and flows across the domain. For this type of problems, the flow structure is complicated and one cannot refine the mesh locally a-priori. Thus, adaptive mesh refinement is a perfect strategy for this problem. Our results show that the adaptive SDG method is able to give a locally refined mesh at the correct locations and capture the complicated behavior of the solution.

The paper is organized as follows. In Sect. 2, we will have a brief review on the SDG method for the Stokes system. In Sect. 3, we will derive a residual-type a-posteriori error estimator for the SDG method and prove its reliability and efficiency. An adaptive refinement strategy based on this error estimator is also given in Sect. 3. In Sect. 4, we present some numerical examples to show the accuracy and efficiency of the proposed error estimator and the adaptive SDG method. Finally, concluding remarks are provided in Sect. 5.

2 The SDG Method

In this section, we will present a brief review of the SDG method for the Stokes system, which is developed in [30] with a-priori error estimates. We will consider the two-dimensional case for the ease of presentation, and we write $\varvec{u}=(u_1,u_2)$ and $\varvec{f}=(f_1,f_2)$. We also assume $\varvec{g}=\varvec{0}$ for simplicity, and the proposed method can be applied to the nonhomogeneous case.

To begin, we introduce the auxiliary variables

$$\begin{aligned} \varvec{w}= & {} \nabla u_{1},\;\;\;\varvec{z}=\nabla u_{2} \end{aligned}$$

(2)

so that the Stokes system (1) can be written as

$$\begin{aligned} \left\{ \begin{array}{rcl@{\quad }l} \displaystyle -\nabla \cdot \varvec{w}+p_{x} &{} = &{} f_{1}, &{} \text {in }\Omega , \\ \displaystyle -\nabla \cdot \varvec{z}+p_{y} &{} = &{} f_{2}, &{} \text {in }\Omega , \\ \displaystyle \nabla \cdot \varvec{u} &{} = &{} 0, &{} \text {in }\Omega , \\ \displaystyle \varvec{u} &{} = &{} \mathbf {0}, &{} \text {on }\partial \Omega , \end{array}\right. \end{aligned}$$

(3)

together with the constraint that $\int _{\Omega }p\, dx=0$. Throughout the paper, we define the spaces $L^2(\Omega )$ and $H^1(\Omega )$ as usual Sobolev spaces and further define

$$\begin{aligned} \displaystyle H_{0}^{1}(\Omega )= & {} \{v: \, v\in H^1(\Omega ); \, v|_{\partial \Omega }=0\}, \end{aligned}$$

(4)

$$\begin{aligned} \displaystyle L_{0}^{2}(\Omega )= & {} \{v: \, v\in L^2(\Omega ); \,\int _{\Omega }v=0\}. \end{aligned}$$

(5)

We assume that the solution $(\varvec{u},\varvec{w},\varvec{z},p)$ to the problem (3) satisfies $(\varvec{u},\varvec{w},\varvec{z},p)\in [H_{0}^{1}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times L_{0}^{2}(\Omega )$ and that

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \int _{\Omega }\varvec{w}\cdot \nabla v_{1}+\int _{\Omega }\varvec{z}\cdot \nabla v_{2}-\int _{\Omega }p\nabla \cdot \varvec{v} &{} = &{} (\varvec{f},\varvec{v})_{0,\Omega }, \\ \displaystyle \int _{\Omega }\varvec{\psi }_{1}\cdot \nabla u_{1} &{} = &{} (\varvec{w},\varvec{\psi }_{1})_{0,\Omega }, \\ \displaystyle \int _{\Omega }\varvec{\psi }_{2}\cdot \nabla u_{2} &{} = &{} (\varvec{w},\varvec{\psi }_{2})_{0,\Omega }, \\ \displaystyle \int _{\Omega }q\nabla \cdot \varvec{u} &{} = &{} 0, \end{array}\right. \end{aligned}$$

(6)

for all $(\varvec{v},\varvec{\psi }_{1},\varvec{\psi }_{2},q)\in [H_{0}^{1}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times L_{0}^{2}(\Omega )$. Here, $(\cdot ,\cdot )_{0,\Omega }$ denotes the standard $L^2(\Omega )$ inner product.

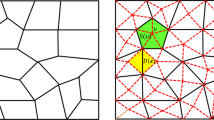
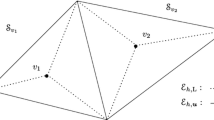
To solve Eq. (3) numerically, we first need to construct a staggered mesh. Let ${\mathcal {T}}_{q}$ be an initial shape regular triangulation of $\Omega$ without hanging nodes, as illustrated by solid lines in Fig. 1. We denote the set of all edges in ${\mathcal {T}}_{q}$ as ${\mathcal {F}}_{u}$ and denote the subset of all interior edges as ${\mathcal {F}}_{u}^{0}$. For the implementation for the SDG scheme, we need to further divide ${\mathcal {T}}_{q}$ to get a staggered mesh. For each triangle, we denote $\nu$ as the center of the triangle, and obtain three subtriangles by connecting $\nu$ to the three vertices of this triangle. The union of these three subtriangles is called ${\mathcal {S}}(\nu )$. We introduce the notation $\mathcal {N}$ to denote the set of all such nodes $\nu$. We then use ${\mathcal {F}}_{p}$ to denote the set of all new edges generated, as illustrated by dotted lines in Fig. 1. Then we define ${\mathcal {T}}$ as the new triangulation after subdivision and define ${\mathcal {F}}$ to be the set of all edges of ${\mathcal {T}}$, and thus we have ${\mathcal {F}}={\mathcal {F}}_{u}\cup {\mathcal {F}}_{p}$. We further denote ${\mathcal {F}}^0={\mathcal {F}}_{u}^0\cup {\mathcal {F}}_{p}$ as the set of all interior edges of ${\mathcal {T}}$.

Fig. 1

An illustration of the triangulation

With the triangulation, we now define the finite element spaces. Let $\tau \in {\mathcal {T}}$ and define $P^{k}(\tau )$ as the space of polynomials of degree up to k on $\tau$. We then define the following spaces with staggered continuity property:

$$\begin{aligned} U^{h}= & {} \left\{ v:\, v|_{\tau }\in P^{k}(\tau ), \, \forall \tau \in {\mathcal {T}};\quad v\text { is continuous over }e\in {\mathcal {F}}_{u}^{0};\; v|_{\partial \Omega }=0\right\} , \end{aligned}$$

(7)

$$\begin{aligned} W^{h}= & {} \left\{ \varvec{w}:\,\varvec{w}|_{\tau }\in [P^{k}(\tau )]^{2},\, \forall \tau \in {\mathcal {T}}; \quad \varvec{w}\cdot \varvec{n}\text { is continuous over }e\in {\mathcal {F}}_{p}\right\} , \end{aligned}$$

(8)

$$\begin{aligned} P^{h}= & {} \left\{ q:\; q|_{\tau }\in P^{k}(\tau ),\,\forall \tau \in {\mathcal {T}};\quad q\text { is continuous over }e\in {\mathcal {F}}_{p};\;\int _{\Omega }q=0\right\} . \end{aligned}$$

(9)

In the above definitions, we define a unit normal vector ${\mathbf {n}}$ on each edge $e \in {\mathcal {F}}$ by the following way. If $e\in \partial \Omega$ is on the boundary, then we define ${\mathbf {n}}$ as the unit normal vector pointing outside of $\Omega$. For an interior edge $e \in {\mathcal {F}}_{u}^0 \cup {\mathcal {F}}_{p}$, we define $K^+$ and $K^-$ as the two triangles sharing this edge. We use notations ${\mathbf {n}}^+$ and ${\mathbf {n}}^-$ to denote the outward unit normal vectors of e taken from $K^+$ and $K^-$, respectively. Then we fix ${\mathbf {n}}$ as one of ${\mathbf {n}}^{\pm }$ for each interior edge e. Next, we give notations to describe the jump of a function over an interior edge. We use notations $v^+$ and $v^-$ to denote the values of a function v on e taken from $K^+$ and $K^-$, respectively. The notation [v] over an edge e for a scalar valued function v is defined as

$$\begin{aligned}{}[v]|_e := (v^+{\mathbf {n}}^+ + v^-{\mathbf {n}}^-)\cdot {\mathbf {n}}. \end{aligned}$$

(10)

For a vector-valued function ${\mathbf {v}}$, the notation $[{\mathbf {v}}\cdot {\mathbf {n}}]$ is defined as

$$\begin{aligned}{}[{\mathbf {v}}\cdot {\mathbf {n}}]|_e := {\mathbf {v}}^+\cdot {\mathbf {n}}^+ + {\mathbf {v}}^-\cdot {\mathbf {n}}^-. \end{aligned}$$

(11)

With the above notations, the SDG scheme [30] for the Stokes system is given as follows: find $(\varvec{u}_{h},\varvec{w}_{h},\varvec{\varvec{z}}_{h},p_{h})\in [U^{h}]^{2}\times W^{h}\times W^{h}\times P^{h}$, such that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle B_{h}(\varvec{w}_{h},v_{h,1})+B_{h}(\varvec{z}_{h},v_{h,2})+b_{h}^{*}(p_{h},\varvec{v}_h) = (\varvec{f},\varvec{v}_h)_{0,\Omega }, \\ \displaystyle B_{h}^{*}(u_{h,1},\varvec{\psi }_{1}) = (\varvec{w}_{h},\varvec{\psi }_{1})_{0,\Omega },\\ \displaystyle B_{h}^{*}(u_{h,2},\varvec{\psi }_{2}) = (\varvec{z}_{h},\varvec{\psi }_{2})_{0,\Omega },\\ \displaystyle b_{h}(\varvec{u}_{h},q_{h}) = 0, \end{array}\right. \end{aligned}$$

(12)

for all $(\varvec{v}_h,\varvec{\psi }_{1},\varvec{\psi }_{2},q_h)\in [U^{h}]^{2}\times W^{h}\times W^{h}\times P^{h}$. Here, $\varvec{u}_{h}=(u_{h,1},u_{h,2})$ and $\varvec{v}_{h}=(v_{h,1},v_{h,2})$. The bilinear forms $B_{h}(\varvec{w}_{h},v_{h})$ and $B_{h}^{*}(u_{h},\varvec{\psi })$ are defined as

$$\begin{aligned} B_{h}(\varvec{w}_{h},v_{h})= & {} \int _{\Omega }\varvec{w}_{h}\cdot \nabla v_{h}-\sum _{e\in {\mathcal {F}}_{p}}\int _{e}\varvec{w}_{h}\cdot \varvec{n}[v_{h}], \end{aligned}$$

(13)

$$\begin{aligned} B_{h}^{*}(u_{h},\varvec{\psi })= & {} -\int _{\Omega }u_{h}\nabla \cdot \varvec{\psi }+\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}u_{h}[\varvec{\psi }\cdot \varvec{n}], \end{aligned}$$

(14)

while the bilinear forms $b_{h}^{*}(p_{h},\varvec{v}_{h})$ and $b_{h}(\varvec{u}_{h},q_{h})$ are defined as

$$\begin{aligned} b_{h}^{*}(p_{h},\varvec{v}_{h})= & {} -\int _{\Omega }p_{h}\nabla \cdot \varvec{v}_{h}+\sum _{e\in {\mathcal {F}}_{p}}\int _{e}p_{h}[\varvec{v}_{h}\cdot \varvec{n}], \end{aligned}$$

(15)

$$\begin{aligned} b_{h}(\varvec{u}_{h},q_{h})= & {} \int _{\Omega }\varvec{u}_{h}\cdot \nabla q_{h}-\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}\varvec{u}_{h}\cdot \varvec{n}[q_{h}]. \end{aligned}$$

(16)

For functions $(\varvec{u},\varvec{w},\varvec{z},p)$ and $(\varvec{v},q)$ defined on $\Omega$, we define the bilinear form ${\mathcal {A}}_{h}$ as

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u},\varvec{w},\varvec{z},p;\varvec{v},q):= & {} B_{h}(\varvec{w},v_{1})+B_{h}(\varvec{z},v_{2})+b_{h}^{*}(p,\varvec{v}) -b_{h}(\varvec{u},q). \end{aligned}$$

(17)

By using this notation, the exact solution of the continuous problem (6) satisfies the following equation

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u},\varvec{w},\varvec{z},p;\varvec{v},q)= & {} (\varvec{f},\varvec{v})_{0,\Omega }, \end{aligned}$$

(18)

for all $(\varvec{v},q)\in [H_{0}^{1}(\Omega )]^{2}\times L_{0}^{2}(\Omega )$. Also, the numerical solution of the discrete problem (12) satisfies

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u}_{h},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}_{h},q_{h})= & {} (\varvec{f},\varvec{v}_{h})_{0,\Omega }, \end{aligned}$$

(19)

for all $(\varvec{v}_{h},q_{h})\in [U^{h}]^{2}\times P^{h}$.

3 An Adaptive SDG Method

In this section, we will derive a reliable and efficient error indicator for the SDG scheme. The error indicator can give a computable estimate of the numerical error in each triangle $\tau \in {\mathcal {T}}$. Thus, we can construct an adaptive refinement strategy by using this error indicator to refine the mesh in locations where the estimated numerical error is large.

Let $(\varvec{u},\varvec{w},\varvec{z},p)\in [H_{0}^{1}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times L_{0}^{2}(\Omega )$ be the exact solution of (6) and we let $(\varvec{u}_{h},\varvec{w}_{h},\varvec{\varvec{z}}_{h},p_{h})\in [U^{h}]^{2}\times W^{h}\times W^{h}\times P^{h}$ be the numerical solution of the SDG scheme (12). Then, we denote the numerical error as

$$\begin{aligned} (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p}):= & {} (\varvec{u-u}_{h},\varvec{w-w}_{h},\varvec{z-z}_{h},p-p_{h}). \end{aligned}$$

(20)

For a vector-valued function $\varvec{v}=(v_{1},v_{2})$, we write $\left| \varvec{v}\right| _{1;\Omega }^{2}:=\left\| \nabla v_{1}\right\| _{0;\Omega }^{2}+\left\| \nabla v_{2}\right\| _{0;\Omega }^{2}$. Here, the gradient operator $\nabla$ means the discrete/broken gradient. Moreover, we define the following norms

$$\begin{aligned} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {cts}}^{2}:= & {} \left| \varvec{e}_u\right| _{1;\Omega }^{2}+\left\| \varvec{e}_w\right\| _{0;\Omega }^{2}+\left\| \varvec{e}_z\right\| _{0;\Omega }^{2}+\left\| e_p\right\| _{0;\Omega }^{2}, \end{aligned}$$

(21)

$$\begin{aligned} \left\| (\varvec{e}_u,\varvec{e}_w,\varvec{e}_z,e_p)\right\| _{\mathrm {DG}}^{2}:= & {} \left\| (\varvec{e}_u,\varvec{e}_w,\varvec{e}_z,e_p)\right\| _{\mathrm {cts}}^{2} +\sum _{e\in {\mathcal {F}}_p} h_{e}^{-1} \left\| [\varvec{e}_u] \right\| _{0;e}^{2}, \end{aligned}$$

(22)

where $\left\| [\varvec{e}_u] \right\| _{0;e}^{2}= \left\| [e_{u,1}] \right\| _{0;e}^{2} +\left\| [e_{u,2}] \right\| _{0;e}^{2}$ and $h_e$ is the length of the edge e. In the above, we adopt standard notations for norms.

In Sect. 3.1, we will prove the reliability of an error estimator with respect to the DG norm $\left\| (\varvec{e}_u,\varvec{e}_w,\varvec{e}_z,e_p)\right\| _{\mathrm {DG}}$. The efficiency of this error estimator will be proved in Sect. 3.2. Finally, we will give the adaptive refinement technique in Sect. 3.3.

3.1 Reliability of the Error Indicator

The aim of the section is to prove the following theorem. It says that the DG error defined in (22) is bounded above by a computable error indicator $\eta$, which is defined in (23) and (24). Throughout the paper, the notation $\alpha \lesssim \beta$ means that $\alpha \le C \beta$ for a constant C independent of the mesh size h. For the analysis below, we define $H^1_P(\Omega )$ as a subspace of $L^2_0(\Omega )$ containing functions that are continuous on ${\mathcal {F}}_p$.

Theorem 3.1

Assuming the exact solution $(\varvec{u},\varvec{w},\varvec{z},p)\in [H_{0}^{1}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times L_{0}^{2}(\Omega )$ of (6) is smooth and denoting $(\varvec{u}_{h},\varvec{w}_{h},\varvec{\varvec{z}}_{h},p_{h})\in [U^{h}]^{2}\times W^{h}\times W^{h}\times P^{h}$ be the numerical solution of the SDG scheme (12), we can estimate the DG norm of the numerical error $(\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})$ defined in Eqs. (20–22) as

$$\begin{aligned} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}^{2}\lesssim & {} \eta ^{2}:=\sum _{\tau \in {\mathcal {T}}}\eta _{\tau }^{2}, \end{aligned}$$

(23)

where for each $\tau \in {\mathcal {T}}$,

$$\begin{aligned} \eta _{\tau }^{2}:= & {} h_{\tau }^{2}\left\| \varvec{R}_1\right\| _{0;\tau }^{2}+\left\| R_{2}\right\| _{0;\tau }^{2}+\left\| R_{3}\right\| _{0;\tau }^{2}+\left\| R_{4}\right\| _{0;\tau }^{2} \nonumber \\&+\sum _{e\in {\mathcal {F}}_{u}^{0}\cap \tau }h_{e}\left( \left\| J_{1}\right\| _{0;e}^{2}+\left\| J_{2}\right\| _{0;e}^{2}\right) +\sum _{e\in {\mathcal {F}}_{p}\cap \tau }h_{e}^{-1}\left\| J_{3}\right\| _{0;e}^{2}, \end{aligned}$$

(24)

with

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \varvec{R}_1 &{} = &{} \varvec{f}+\left( \begin{array}{c} \nabla \cdot \varvec{w}_{h}\\ \nabla \cdot \varvec{z_{h}} \end{array}\right) ^{T}-\nabla p_{h},\\ \displaystyle R_{2} &{} = &{} \varvec{w}_{h}-\nabla u_{h,1},\\ \displaystyle R_{3} &{} = &{} \varvec{z}_{h}-\nabla u_{h,2},\\ \displaystyle R_{4} &{} = &{} \nabla \cdot \varvec{u}_{h},\\ \displaystyle J_{1} &{} = &{} [n_{1}p_{h}-\varvec{w}_{h}\cdot \varvec{n}],\\ \displaystyle J_{2} &{} = &{} [n_{2}p_{h}-\varvec{z}_{h}\cdot \varvec{n}],\\ \displaystyle J_{3} &{} = &{} [\varvec{u}_h]. \end{array} \right. \end{aligned}$$

(25)

Here, $h_{\tau }$ denotes the diameter of the circumcircle of a triangle $\tau$, $h_e$ is the length of an edge e and $\varvec{n}=(n_{1},n_{2})$ is the fixed unit normal vector defined on each e.

The proof of Theorem 3.1 uses some ideas from Houston et al’s idea, see [24, 27]. Firstly, we recall that the exact solution satisfies (18). We will next show that the bilinear form ${\mathcal {A}}_{h}$ satisfies the following condition.

Lemma 3.2

For any $(\varvec{u},\varvec{w},\varvec{z},p)\in [H_{0}^{1}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times H^1_P(\Omega )$, there exists $\varvec{v}^0 \in [H_{0}^{1}(\Omega )]^{2}$ and $q^0 \in H^1_P(\Omega )$ such that

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u},\varvec{w},\varvec{z},p;\varvec{v}^0,q^0)\ge & {} \dfrac{1}{4}\left\| (\varvec{u},\varvec{w},\varvec{z},p)\right\| _{\mathrm {cts}}^{2} \nonumber \\&-\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}-\left\| \nabla u_{2}-\varvec{z}\right\| _{0;\Omega }^{2}, \end{aligned}$$

(26)

with

$$\begin{aligned} \left| \varvec{v}^0\right| _{1;\Omega }+\left\| q^0\right\| _{0;\Omega }\lesssim & {} \left| \varvec{u}\right| _{1;\Omega }+\left\| p\right\| _{0;\Omega }. \end{aligned}$$

(27)

Proof

Since $p\in L_{0}^{2}(\Omega )$, by [24], there exists $\varvec{s}\in H_{0}^{1}(\Omega )^{2}$ such that

$$\begin{aligned} -(p,\nabla \cdot \varvec{s})_{0,\Omega }\ge & {} \left\| p\right\| _{0;\Omega }^{2}, \end{aligned}$$

(28)

$$\begin{aligned} \left| \varvec{s}\right| _{1;\Omega }\le & {} \left\| p\right\| _{0;\Omega }. \end{aligned}$$

(29)

For the above choice of $\varvec{s}$, we take $\varvec{v}^0=2\varvec{u}+\varvec{s}$ and $q^0=2p$. Then we have

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u},\varvec{w},\varvec{z},p;\varvec{v}^0,q^0)= & {} B_{h}(\varvec{w},2u_{1}+s_1)+B_{h}(\varvec{z},2u_{2}+s_2)+b_{h}^{*}(p,2\varvec{u}+\varvec{s}) -b_{h}(\varvec{u},2p) \nonumber \\= & {} 2(\varvec{w},\nabla u_{1})_{0,\Omega }+(\varvec{w},\nabla s_{1})_{0,\Omega } +2(\varvec{z},\nabla u_{2})_{0,\Omega }+(\varvec{z},\nabla s_{2})_{0,\Omega }\nonumber \\&-\,2(p,\nabla \cdot \varvec{u})_{0,\Omega }-(p,\nabla \cdot \varvec{s})_{0,\Omega }\nonumber \\&-\,2(\varvec{u},\nabla p)_{0,\Omega } +2\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}\varvec{u}\cdot \varvec{n}[p]. \end{aligned}$$

(30)

Using integration by parts and the fact that p is continuous over ${\mathcal {F}}_{p}$, it is clear that

$$\begin{aligned} (p,\nabla \cdot \varvec{u})_{0,\Omega }+(\varvec{u},\nabla p)_{0,\Omega }= & {} \sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}\varvec{u}\cdot \varvec{n}[p]. \end{aligned}$$

(31)

Hence, we have

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u},\varvec{w},\varvec{z},p;\varvec{v}^0,q^0)= & {} 2(\varvec{w},\nabla u_{1})_{0,\Omega }+2(\varvec{z},\nabla u_{2})_{0,\Omega } \nonumber \\&+\, (\varvec{w},\nabla s_{1})_{0,\Omega }+(\varvec{z},\nabla s_{2})_{0,\Omega } -(p,\nabla \cdot \varvec{s})_{0,\Omega }. \end{aligned}$$

(32)

Next, we will bound the first four terms in (32) one by one. By the Cauchy-Schwartz inequality, we have

$$\begin{aligned} (\varvec{w},\nabla u_{1})_{0,\Omega }= & {} (\varvec{w},\varvec{w})_{0,\Omega }+(\varvec{w},\nabla u_{1}-\varvec{w})_{0,\Omega }\nonumber \\\ge & {} \left\| \varvec{w}\right\| _{0;\Omega }^{2}-\dfrac{1}{2}\left( \left\| \varvec{w}\right\| _{0;\Omega }^{2}+\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}\right) \nonumber \\= & {} \dfrac{1}{2}\left\| \varvec{w}\right\| _{0;\Omega }^{2}-\dfrac{1}{2}\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}. \end{aligned}$$

(33)

By writing $(\varvec{w},\nabla u_{1})_{0,\Omega } = (\nabla u_1,\nabla u_{1})_{0,\Omega } + (\varvec{w}-\nabla u_1,\nabla u_{1})_{0,\Omega }$, we can bound the same term $(\varvec{w},\nabla u_{1})_{0,\Omega }$ as follows

$$\begin{aligned} (\varvec{w},\nabla u_{1})_{0,\Omega }\ge & {} \dfrac{1}{2}\left\| \nabla u_{1}\right\| _{0;\Omega }^{2}-\dfrac{1}{2}\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}. \end{aligned}$$

(34)

Thus we can bound $2(\varvec{w},\nabla u_{1})_{0,\Omega }$ in using (33–34) with a suitable weighting, namely

$$\begin{aligned} 2(\varvec{w},\nabla u_{1})_{0,\Omega }= & {} \dfrac{3}{2}(\varvec{w},\nabla u_{1})_{0,\Omega }+\dfrac{1}{2}(\varvec{w},\nabla u_{1})_{0,\Omega }\nonumber \\\ge & {} \dfrac{3}{2}\left( \dfrac{1}{2}\left\| \varvec{w}\right\| _{0;\Omega }^{2}-\dfrac{1}{2}\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}\right) \nonumber \\&+\dfrac{1}{2}\left( \dfrac{1}{2}\left\| \nabla u_{1}\right\| _{0;\Omega }^{2}-\dfrac{1}{2}\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}\right) \nonumber \\= & {} \frac{3}{4}\left\| \varvec{w}\right\| _{0;\Omega }^{2}+\frac{1}{4}\left\| \nabla u_{1}\right\| _{0;\Omega }^{2}-\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}. \end{aligned}$$

(35)

Similarly, we have

$$\begin{aligned} 2(\varvec{z},\nabla u_{2})_{0,\Omega }\ge & {} \dfrac{3}{4}\left\| \varvec{z}\right\| _{0;\Omega }^{2}+\frac{1}{4}\left\| \nabla u_{2}\right\| _{0;\Omega }^{2}-\left\| \nabla u_{2}-\varvec{z}\right\| _{0;\Omega }^{2}. \end{aligned}$$

(36)

Again, by the Cauchy-Schwartz inequality, we obtain easily that

$$\begin{aligned} (\varvec{w},\nabla s_{1})_{0,\Omega }\ge & {} -\dfrac{1}{2}\left( \left\| \varvec{w}\right\| _{0;\Omega }^{2}+\left\| \nabla s_{1}\right\| _{0;\Omega }^{2}\right) , \end{aligned}$$

(37)

$$\begin{aligned} (\varvec{z},\nabla s_{2})_{0,\Omega }\ge & {} -\dfrac{1}{2}\left( \left\| \varvec{z}\right\| _{0;\Omega }^{2}+\left\| \nabla s_{2}\right\| _{0;\Omega }^{2}\right) . \end{aligned}$$

(38)

By Eqs. (32) and (35–38), we have

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u},\varvec{w},\varvec{z},p;\varvec{v}^0,q^0)\ge & {} \dfrac{1}{4}\left\| \varvec{w}\right\| _{0;\Omega }^{2}+\dfrac{1}{4}\left\| \varvec{z}\right\| _{0;\Omega }^{2}+\frac{1}{4}\left\| \nabla u_{1}\right\| _{0;\Omega }^{2}+\frac{1}{4}\left\| \nabla u_{2}\right\| _{0;\Omega }^{2}\nonumber \\&-\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}-\left\| \nabla u_{2}-\varvec{z}\right\| _{0;\Omega }^{2}\nonumber \\&-\dfrac{1}{2}\left\| \nabla s_{1}\right\| _{0;\Omega }^{2}-\dfrac{1}{2}\left\| \nabla s_{2}\right\| _{0;\Omega }^{2} \nonumber \\&-(p,\nabla \cdot \varvec{s})_{0,\Omega }. \end{aligned}$$

(39)

Using (28–29), we arrive at the conclusion that

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u},\varvec{w},\varvec{z},p;\varvec{v}^0,q^0)\ge & {} \dfrac{1}{4}\left( \left| \varvec{u}\right| _{1;\Omega }^{2}+\left\| \varvec{w}\right\| _{0;\Omega }^{2}+\left\| \varvec{z}\right\| _{0;\Omega }^{2}+\left\| p\right\| _{0;\Omega }^{2}\right) \nonumber \\&-\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }^{2}-\left\| \nabla u_{2}-\varvec{z}\right\| _{0;\Omega }^{2}, \end{aligned}$$

(40)

which proves the first statement of our lemma. The proof of the second statement is straight forward as

$$\begin{aligned} \left| \varvec{v}^0\right| _{1;\Omega }+\left\| q^0\right\| _{0;\Omega }= & {} \left| 2\varvec{u}+\varvec{s}\right| _{1;\Omega }+\left\| 2p\right\| _{0;\Omega } \nonumber \\\lesssim & {} \left| \varvec{u}\right| _{1;\Omega }+\left| \varvec{s}\right| _{1;\Omega }+\left\| p\right\| _{0;\Omega } \nonumber \\\lesssim & {} \left| \varvec{u}\right| _{1;\Omega }+\left\| p\right\| _{0;\Omega }, \end{aligned}$$

(41)

where the last inequality comes from (29). $\square$

By introducing an auxiliary function $\varvec{u}^{c}\in [H_{0}^{1}(\Omega )]^{2}\cap [U^{h}]^{2}$, the following upper estimate of the error is an immediate consequence of Lemma 3.2.

Corollary 3.3

Under the assumption of Theorem 3.1, for any $\varvec{u}^{c}=(u^c_1,u^c_2)\in [H_{0}^{1}(\Omega )]^{2}\cap [U^{h}]^{2}$, there exists $(\varvec{v}^0,q^0)\in [H_{0}^{1}(\Omega )]^{2}\times H^1_P(\Omega )$ such that

$$\begin{aligned} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {cts}}^{2}\lesssim & {} {\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)+\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }^{2} \nonumber \\&+\left\| R_{2}\right\| _{0;\Omega }^{2}+\left\| R_{3}\right\| _{0;\Omega }^{2}, \end{aligned}$$

(42)

and $\left| \varvec{v}^0\right| _{1;\Omega }+\left\| q^0\right\| _{0;\Omega } \lesssim \left| \varvec{u}-\varvec{u}^{c}\right| _{1;\Omega }+\left\| e_{p}\right\| _{0;\Omega }$.

Proof

It is obvious that $(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p})$ satisfies the assumption of Lemma 3.2. Hence, by the triangle inequality and Lemma 3.2, there exists $(\varvec{v}^0,q^0)\in [H_{0}^{1}(\Omega )]^{2}\times H^1_P(\Omega )$ such that

$$\begin{aligned} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {cts}}^{2}\le & {} \left\| (\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {cts}}^{2}+\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }^{2}\nonumber \\\lesssim & {} {\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)\nonumber \\&+\left\| \nabla (u_{1}-u_{1}^{c})-\varvec{e}_{w}\right\| _{0;\Omega }^{2} +\left\| \nabla (u_{2}-u_{2}^{c})-\varvec{e}_{z}\right\| _{0;\Omega }^{2}\nonumber \\&+\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }^{2}, \end{aligned}$$

(43)

and $\left| \varvec{v}^0\right| _{1;\Omega }+\left\| q^0\right\| _{0;\Omega }\lesssim \left| \varvec{u}-\varvec{u}^{c}\right| _{1;\Omega } +\left\| e_{p}\right\| _{0;\Omega }$. From (6), we have $\left\| \nabla u_{1}-\varvec{w}\right\| _{0;\Omega }=0$ and $\left\| \nabla u_{2}-\varvec{z}\right\| _{0;\Omega }=0$. Therefore, we have

$$\begin{aligned} \left\| \nabla (u_{1}-u_{1}^{c})-\varvec{e}_{w}\right\| _{0;\Omega }= & {} \left\| \nabla u_{1}-\varvec{w}+\varvec{w}_h-\nabla u_{1}^{c}\right\| _{0;\Omega } \nonumber \\\le & {} \left\| \varvec{w}_{h}-\nabla u_{h,1}\right\| _{0;\Omega }+\left| u_{h,1}-u_{1}^{c}\right| _{1;\Omega }, \end{aligned}$$

(44)

and similarly,

$$\begin{aligned} \left\| \nabla (u_{2}-u_{2}^{c})-\varvec{e}_{z}\right\| _{0;\Omega }\le & {} \left\| \varvec{z}_{h}-\nabla u_{h,2}\right\| _{0;\Omega }+\left| u_{h,2}-u_{2}^{c}\right| _{1;\Omega }. \end{aligned}$$

(45)

Combining (43–45) and replacing $\varvec{w}_{h}-\nabla u_{h,1}$ and $\varvec{z}_{h}-\nabla u_{h,2}$ by $R_{2}$ and $R_{3}$ respectively, our result follows. $\square$

We remark that, in (42), the terms ${\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)$ and $\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }$ do not have an upper estimate yet, and we will next derive upper bounds for these terms. Before that, we recall the following lemma from Houston et al [28] on polynomial approximations.

Lemma 3.4

Let $\varvec{v}\in [H_{0}^{1}(\Omega )]^{2}$, there exists $\varvec{v}_{h}\in [U^{h}]^{2}$ satisfying the following conditions:

$$\begin{aligned} \left\| \varvec{v}-\varvec{v}_{h}\right\| _{0;\tau }^{2}\lesssim & {} h_{\tau }^{2}\left\| \nabla \varvec{v}\right\| _{0;\tau }^{2}, \end{aligned}$$

(46)

$$\begin{aligned} \left\| \nabla (\varvec{v}-\varvec{v}_{h})\right\| _{0;\tau }^{2}\lesssim & {} \left\| \nabla \varvec{v}\right\| _{0;\tau }^{2}, \end{aligned}$$

(47)

for all $\tau \in {\mathcal {T}}$, where $\left\| \nabla \varvec{v}\right\| _{0;\tau }^{2}$ means $\left\| \nabla v_{1}\right\| _{0;\tau }^{2}+\left\| \nabla v_{2}\right\| _{0;\tau }^{2}$ for $\varvec{v}=(v_{1},v_{2})$.

With the approximation properties from Lemma 3.4, we are ready to find an upper estimate for ${\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)$.

Lemma 3.5

Let $\varvec{v}^0=(v^0_1,v^0_2) \in [H_{0}^{1}(\Omega )]^{2}$ and $q^0\in H^1_P(\Omega )$ be chosen as in Corollary 3.3, then we have

$$\begin{aligned}&{\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0) \nonumber \\&\quad \lesssim \left( \eta +\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }\right) \left( \left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega } +\Vert (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\Vert _{\mathrm {DG}}\right) . \end{aligned}$$

(48)

Proof

By the fact that $(\varvec{v}^0,q^0)\in [H_{0}^{1}(\Omega )]^{2}\times H^1_P(\Omega )$, we have

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)= & {} {\mathcal {A}}_{h}(\varvec{u},\varvec{w},\varvec{z},p;\varvec{v}^0,q^0) -{\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0,q^0)\nonumber \\= & {} (\varvec{f},\varvec{v}^0)_{0;\Omega }-{\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0,q^0), \end{aligned}$$

(49)

where the second equality comes from (18). Let $\varvec{v}^0_{h}=(v^0_{h,1},v^0_{h,2})\in [U^{h}]^{2}$ be the approximation of $\varvec{v}^0$ chosen as in Lemma 3.4 and $q_{h}^0\in P^{h}$ be arbitrary. Then for the second term in (49), we have

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0,q^0)= & {} {\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0_{h},q^0_{h})\nonumber \\&+\,{\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0-\varvec{v}^0_{h},q^0-q^0_{h})\nonumber \\= & {} {\mathcal {A}}_{h}(\varvec{u}_{h},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0_{h},q^0_{h})\nonumber \\&+\,{\mathcal {A}}_{h}(\varvec{u}^{c}-\varvec{u}_{h},0,0,0;\varvec{v}^0_{h},q^0_{h})\nonumber \\&+\,{\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0-\varvec{v}^0_{h},q^0-q^0_{h})\nonumber \\= & {} (\varvec{f},\varvec{v}^0_{h})_{0;\Omega }-b_{h}(\varvec{u}^{c}-\varvec{u}_{h},q^0_{h})\nonumber \\&+\,{\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0-\varvec{v}^0_{h},q^0-q^0_{h}), \end{aligned}$$

(50)

where the last equality comes from (19) and the definition of ${\mathcal {A}}_{h}$. Hence

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)= & {} (\varvec{f},\varvec{v}^0-\varvec{v}^0_{h})_{0;\Omega }+b_{h}(\varvec{u}^{c}-\varvec{u}_{h},q^0_{h})\nonumber \\&-\,{\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0-\varvec{v}^0_{h},q^0-q^0_{h}), \end{aligned}$$

(51)

by using (49–50). To manipulate the last term in (51), we use the definition

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u}^{c},\varvec{w}_{h},\varvec{z}_{h},p_{h};\varvec{v}^0-\varvec{v}^0_{h},q^0-q^0_{h})= & {} B_{h}(\varvec{w}_{h},v^0_{1}-v^0_{h,1})+B_{h}(\varvec{z}_{h},v^0_{2}-v^0_{h,2})\nonumber \\&+\,b_{h}^{*}(p_{h},\varvec{v}^0-\varvec{v}^0_h)-b_{h}(\varvec{u}^{c},q^0-q^0_{h}),\qquad \end{aligned}$$

(52)

so that each of the first three terms in (52) can be further manipulated using integration by parts, where

$$\begin{aligned} B_{h}(\varvec{w}_{h},v^0_{1}-v^0_{h,1})= & {} -(\nabla \cdot \varvec{w}_{h},v^0_{1}-v^0_{h,1})_{0;\Omega }+\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}(v^0_{1}-v^0_{h,1})[\varvec{w}_{h}\cdot \varvec{n}],\end{aligned}$$

(53)

$$\begin{aligned} B_{h}(\varvec{z}_{h},v^0_{2}-v^0_{h,2})= & {} -(\nabla \cdot \varvec{z}_{h},v^0_{2}-v^0_{h,2})_{0;\Omega }+\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}(v^0_{2}-v^0_{h,2})[\varvec{z}_{h}\cdot \varvec{n}],\end{aligned}$$

(54)

$$\begin{aligned} b_{h}^{*}(p_{h},\varvec{v}^0-\varvec{v}^0_{h})= & {} (\nabla p_{h},\varvec{v}^0-\varvec{v}^0_{h})_{0;\Omega }-\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}(\varvec{v}^0-\varvec{v}^0_{h})\cdot \varvec{n}[p_{h}]. \end{aligned}$$

(55)

Combining (51–55), we arrive at the conclusion that

$$\begin{aligned} {\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)= & {} (\varvec{R}_1,\varvec{v}^0-\varvec{v}^0_{h})_{0;\Omega } \nonumber \\&+\,b_{h}(\varvec{u}^{c}-\varvec{u}_{h},q^0_{h})+b_{h}(\varvec{u}^{c},q^0-q^0_{h})\nonumber \\&+\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}(v^0_{1}-v^0_{h,1})[n_{1}p_{h}-\varvec{w}_{h}\cdot \varvec{n}] \nonumber \\&+\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}(v^0_{2}-v^0_{h,2})[n_{2}p_{h}-\varvec{z}_{h}\cdot \varvec{n}]. \end{aligned}$$

(56)

For the second line of (56), by the last equation in (12) and the fact that $q^0$ is continuous over ${\mathcal {F}}_{p}$, we have

$$\begin{aligned} b_{h}(\varvec{u}^{c}-\varvec{u}_{h},q^0_{h})+b_{h}(\varvec{u}^{c},q^0-q^0_{h})= & {} b_{h}(\varvec{u}^{c},q^0_{h})+b_{h}(\varvec{u}^{c},q^0-q^0_{h})\nonumber \\= & {} b_{h}(\varvec{u}^{c},q^0)\nonumber \\= & {} (\varvec{u}^{c},\nabla q^0)_{0;\Omega }-\sum _{e\in {\mathcal {F}}_{u}^{0}}\int _{e}\varvec{u}^{c}\cdot \varvec{n}[q^0]\nonumber \\= & {} -(\nabla \cdot \varvec{u}^{c},q^0)_{0;\Omega } + \sum _{e\in {\mathcal {F}}_{p}}\int _{e}\varvec{u}^{c}\cdot \varvec{n}[q^0]\nonumber \\= & {} -(\nabla \cdot \varvec{u}_{h},q^0)_{0;\Omega }+(\nabla \cdot (\varvec{u}_{h}-\varvec{u}^{c}),q^0)_{0;\Omega }\nonumber \\= & {} -(R_{4},q^0)_{0;\Omega }+(\nabla \cdot (\varvec{u}_{h}-\varvec{u}^{c}),q^0)_{0;\Omega }.\qquad \end{aligned}$$

(57)

Then from the Cauchy-Schwarz inequality, the trace inequality and (56–57),

$$\begin{aligned}&{\mathcal {A}}_{h}(\varvec{u}_0-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)\nonumber \\&\quad \lesssim \left( \sum _{\tau \in {\mathcal {T}}}h_{\tau }^{2}\left\| \varvec{R}_1\right\| _{0;\tau }^{2}\right) ^{1/2}\left| \varvec{v}^0\right| _{1;\Omega }+\left( \sum _{\tau \in {\mathcal {T}}}\left\| R_{4}\right\| _{0;\tau }^{2}\right) ^{1/2}\left\| q^0\right\| _{0;\Omega }\nonumber \\&\qquad +\left\{ \sum _{e\in {\mathcal {F}}_{u}^{0}}h_{e}\left( \left\| J_{1}\right\| _{0;e}^{2}+\left\| J_{2}\right\| _{0;e}^{2}\right) \right\} ^{1/2}\left| \varvec{v}^0\right| _{1;\Omega }+\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }\left\| q^0\right\| _{0;\Omega }\nonumber \\&\quad \lesssim \left( \eta +\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }\right) \left( \left| \varvec{v}^0\right| _{1;\Omega }+\left\| q^0\right\| _{0;\Omega }\right) . \end{aligned}$$

(58)

Since $(\varvec{v}^0,q^0)$ is chosen as in Corollary 3.3, which satisfies $|\varvec{v}^0|_{1;\Omega }+\left\| q^0\right\| _{0;\Omega } \lesssim |\varvec{u}-\varvec{u}^{c}|_{1;\Omega }+\Vert e_p\Vert _{0;\Omega }$, we have

$$\begin{aligned}&{\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)\nonumber \\&\quad \lesssim \left( \eta +\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }\right) \left( \left| \varvec{u}-\varvec{u}_h\right| _{1;\Omega }+\left| \varvec{u}_h-\varvec{u}^{c}\right| _{1;\Omega }+\Vert e_p\Vert _{0;\Omega } \right) \nonumber \\&\quad \lesssim \left( \eta +\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }\right) \left( \left| \varvec{u}_h-\varvec{u}^{c}\right| _{1;\Omega }+\Vert (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\Vert _{\mathrm {DG}} \right) . \end{aligned}$$

(59)

$\square$

Now, we will derive an upper bound for $\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }$ using the following lemma on polynomial approximations.

Lemma 3.6

For any $\varvec{u}_{h}\in [U^{h}]^{2}$, there exists $\varvec{u}^{c}\in [H_{0}^{1}(\Omega )]^{2}\cap [U^{h}]^{2}$, such that the following inequality holds:

$$\begin{aligned} \left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }^2\lesssim & {} \sum _{e\in {\mathcal {F}}_p }h_{e}^{-1}\left\| [\varvec{u}_{h}]\right\| _{0;e}^2. \end{aligned}$$

(60)

Proof

From Theorem 2.2 of [29], we know that there exists $\varvec{u}^{c}\in [H_{0}^{1}(\Omega )]^{2}\cap [U^{h}]^{2}$ such that

$$\begin{aligned} \left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }^2\lesssim & {} \sum _{e\in {\mathcal {F}}^0} h_{e}^{-1}\left\| [\varvec{u}_{h}]\right\| _{0;e}^2 + \sum _{e\in \partial \Omega }h_{e}^{-1}\left\| \varvec{u}_{h}\right\| _{0;e}^2. \end{aligned}$$

(61)

By the definition of $U^{h}$, we know that $[\varvec{u}_{h}]|_{{\mathcal {F}}_u^0}=\varvec{0}$ and $\varvec{u}_{h}|_{\partial \Omega } =\varvec{0}$. Using the fact that ${\mathcal {F}}^0={\mathcal {F}}_u^0\bigcup {\mathcal {F}}_p$ , we can obtain the conclusion. $\square$

Using all the results above, we are now ready to prove Theorem 3.1.

Lemma 3.7

Theorem 3.1 holds.

Proof

From the definition of ${\displaystyle \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}}$ and by combining Corollary 3.3 and Lemma 3.5, we can easily see that

$$\begin{aligned} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}^{2}\lesssim & {} {\mathcal {A}}_{h}(\varvec{u}-\varvec{u}^{c},\varvec{e}_{w},\varvec{e}_{z},e_{p};\varvec{v}^0,q^0)+\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }^{2} +\eta ^{2} \nonumber \\\lesssim & {} \left( \eta +\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }\right) \left( \left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega } +\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}\right) \nonumber \\&+\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega }^{2} +\eta ^{2}. \end{aligned}$$

(62)

From Lemma 3.6, we know that $\left| \varvec{u}_{h}-\varvec{u}^{c}\right| _{1;\Omega } \lesssim \eta$, hence

$$\begin{aligned} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}^{2}\lesssim & {} \eta \left( \eta +\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}\right) +\eta ^{2}. \end{aligned}$$

(63)

If $\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}\le \eta$, then Theorem 3.1 is trivially satisfied. Otherwise, (63) implies

$$\begin{aligned} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}^{2}\lesssim & {} \eta \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}, \end{aligned}$$

(64)

where Theorem 3.1 clearly holds by dividing both sides of (64) by $\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}$. $\square$

3.2 Efficiency of the Error Indicator

In this section, we will prove the efficiency of the error indicator (24–25) derived in the last section. For our analysis, we denote the space of all piecewise polynomials of an arbitrary order on ${\mathcal {T}}$ by $P({\mathcal {T}})$. Then we have the following theorem, which is the main result of this section.

Theorem 3.8

Using the notations in the previous section, we have

$$\begin{aligned} \eta ^{2}\lesssim & {} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}^{2}+\sum _{\tau \in {\mathcal {T}}}h_{\tau }^{2}\left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }^{2}, \qquad \forall \varvec{f}_{h} \in P({\mathcal {T}}). \end{aligned}$$

(65)

Theorem 3.8 is proved by using the standard bubble function technique proposed by Verfurth [38]. Let $\tau \in {\mathcal {T}}$ be a triangle and $e\in {\mathcal {F}}$ be an edge with $e=\tau _{1}\cap \tau _{2}$. We denote by $\beta _{\tau }$ and $\beta _{e}$ the standard polynomial bubble functions on $\tau$ and e, respectively, which are uniquely defined by the following properties:

$$\begin{aligned} supp \, \beta _{\tau } \subset \tau ,\,\,\, \beta _{\tau } \in P^3(\tau ),\,\,\, \beta _{\tau }\geqslant 0,\,\,\, \max _{x\in \tau } \beta _{\tau }(x)=1, \end{aligned}$$

(66)

and

$$\begin{aligned} supp \, \beta _{e} \subset \tau _1 \cup \tau _2,\,\,\, \beta _{e}|_{\tau _i} \in P^2(\tau _i),\,i=1,2,\,\,\, \beta _{e}\geqslant 0,\,\,\, \max _{x\in \tau _1 \cup \tau _2} \beta _{e}(x)=1. \end{aligned}$$

(67)

Noting that the error indicator $\eta ^2$ is defined as the sum of the element-wise error indicator $\eta _\tau ^2$, we now denote the element-wise norm of the numerical error as

$$\begin{aligned} \left\| (\varvec{e}_u,\varvec{e}_w,\varvec{e}_z,e_p)\right\| _{\mathrm {DG},\tau }^{2}&: =&\left| \varvec{e}_u\right| _{1;\tau }^{2}+\left\| \varvec{e}_w\right\| _{0;\tau }^{2}+\left\| \varvec{e}_z\right\| _{0;\tau }^{2}+\left\| e_p\right\| _{0;\tau }^{2} +\sum _{e\in {\mathcal {F}}_p \bigcap \tau } h_{e}^{-1} \left\| [\varvec{e}_u] \right\| _{0;e}^{2},\nonumber \\ \end{aligned}$$

(68)

To implement the proof of Theorem 3.8, we consider all terms involved in $\eta _\tau ^2$ one by one. It turns out that each term can be bounded by the right-hand side of Equation (65). We will deal with the residual terms in Lemmas 3.9 and 3.10 and the jump terms in Lemma 3.11.

Lemma 3.9

Let $\varvec{f}_{h}\in [P({\mathcal {T}})]^2$ and $\tau \in {\mathcal {T}}$. Then we have

$$\begin{aligned} h_{\tau }^{2}\left\| \varvec{R}_1\right\| _{0;\tau }^{2}\lesssim & {} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau }}^{2}+h_{\tau }^2 \left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }^{2}. \end{aligned}$$

(69)

Proof

Define $\varvec{v}:=\varvec{f}_{h}+\left( \begin{array}{c} \nabla \cdot \varvec{w}_{h}\\ \nabla \cdot \varvec{z_{h}} \end{array}\right) ^{T}-\nabla p_{h}$ which is a polynomial on $\tau$, then $\varvec{R_1}=\varvec{f}-\varvec{f}_h+\varvec{v}$. Hence, we have

$$\begin{aligned} h_{\tau }^{2}\left\| \varvec{R}_1\right\| _{0;\tau }^{2}\le & {} h_{\tau }^{2}\left( \left\| \varvec{v}\right\| _{0;\tau }^2+\left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }^2\right) . \end{aligned}$$

(70)

By defining $\varvec{v}_{b}=\beta _{\tau }\varvec{v}$, we can bound $\left\| \varvec{v}\right\| _{0;\tau }$ by

$$\begin{aligned} \left\| \varvec{v}\right\| _{0;\tau }^{2}\lesssim & {} \left\| \beta _{\tau }^{1/2}\varvec{v}\right\| _{0;\tau }^{2}\nonumber \\= & {} \displaystyle \int _{\tau }\Big \{ \varvec{f}_{h}+\left( \begin{array}{c} \nabla \cdot \varvec{w}_{h}\\ \nabla \cdot \varvec{z_{h}} \end{array}\right) ^{T}-\nabla p_{h}\Big \} \cdot \varvec{v}_{b}\nonumber \\= & {} (\varvec{f}_{h},\varvec{v}_{b})_{0;\tau }-\int _{\tau }\varvec{w}_{h}\cdot \nabla v_{b,1}-\int _{\tau }\varvec{z}_{h}\cdot \nabla v_{b,2}+\int _{\tau }p_{h}\nabla \cdot \varvec{v}_{b}, \end{aligned}$$

(71)

where the first inequality follows from the bubble function technique and the second equality comes from integration by parts. Since $\varvec{v}_{b}\in H_{0}^{1}(\tau )^{2}$, by the variational form (6) we have

$$\begin{aligned} \int _{\tau }\varvec{w}\cdot \nabla v_{b,1}+\int _{\tau }\varvec{z}\cdot \nabla v_{b,2}-\int _{\tau }p\nabla \cdot \varvec{v}_{b}= & {} (\varvec{f},\varvec{v}_{b})_{0;\tau }. \end{aligned}$$

(72)

By Eqs. (71) and (72), we can get

$$\begin{aligned} \left\| \varvec{v}\right\| _{0;\tau }^{2}\lesssim & {} (\varvec{f}_{h}-\varvec{f},\varvec{v}_{b})_{0;\tau }-\int _{\tau }(\varvec{w}_{h}-\varvec{w})\cdot \nabla v_{b,1}\nonumber \\&-\int _{\tau }(\varvec{z}_{h}-\varvec{z})\cdot \nabla v_{b,2}+\int _{\tau }(p_{h}-p)\nabla \cdot \varvec{v}_{b}. \end{aligned}$$

(73)

For the first term in (73), we have

$$\begin{aligned} (\varvec{f}_{h}-\varvec{f},\varvec{v}_{b})_{0;\tau }\le & {} \left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }\cdot \left\| \varvec{v}_{b}\right\| _{0;\tau }\nonumber \\\lesssim & {} \left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }\cdot \left\| \varvec{v}\right\| _{0;\tau }. \end{aligned}$$

(74)

For the second term in (73), we consider

$$\begin{aligned} -\int _{\tau }(\varvec{w}_{h}-\varvec{w})\cdot \nabla v_{b,1}\le & {} \left\| \varvec{w}-\varvec{w}_{h}\right\| _{0;\tau }\cdot \left\| \nabla v_{b,1}\right\| _{0;\tau }\nonumber \\\lesssim & {} h_{\tau }^{-1}\left\| \varvec{w}-\varvec{w}_{h}\right\| _{0;\tau }\cdot \left\| v_{1}\right\| _{0;\tau }\nonumber \\\le & {} h_{\tau }^{-1}\left\| \varvec{w}-\varvec{w}_{h}\right\| _{0;\tau }\cdot \left\| \varvec{v}\right\| _{0;\tau }, \end{aligned}$$

(75)

where the middle inequality holds because $v_{b,1}=\beta _{\tau }v_{1}$. Similarly, we also have

$$\begin{aligned} -\int _{\tau }(\varvec{z}_{h}-\varvec{z})\cdot \nabla v_{b,2}\le & {} h_{\tau }^{-1}\left\| \varvec{z}-\varvec{z}_{h}\right\| _{0;\tau }\cdot \left\| \varvec{v}\right\| _{0;\tau }. \end{aligned}$$

(76)

For the last term in (73), we have

$$\begin{aligned} \int _{\tau }(p_{h}-p)\nabla \cdot \varvec{v}_{b}\le & {} \left\| p-p_{h}\right\| _{0;\tau }\cdot \left\| \nabla \cdot \varvec{v}_{b}\right\| _{0;\tau }\nonumber \\\lesssim & {} h_{\tau }^{-1}\left\| p-p_{h}\right\| _{0;\tau }\cdot \left\| \varvec{v}\right\| _{0;\tau }. \end{aligned}$$

(77)

The remaining part of the proof is straight forward. By (73–77), we have

$$\begin{aligned} \left\| \varvec{v}\right\| _{0;\tau }^{2}\lesssim & {} \left( \left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }+h_{\tau }^{-1}\left\| \varvec{w}-\varvec{w}_{h}\right\| _{0;\tau }+h_{\tau }^{-1}\left\| \varvec{z}-\varvec{z}_{h}\right\| _{0;\tau }\right. \nonumber \\&\left. +\,h_{\tau }^{-1}\left\| p-p_{h}\right\| _{0;\tau }\right) \left\| \varvec{v}\right\| _{0;\tau }. \end{aligned}$$

(78)

Multiplying both sides of (78) by $h_{\tau }\left\| \varvec{v}\right\| _{0;\tau }^{-1}$, we have

$$\begin{aligned} h_{\tau }\left\| \varvec{v}\right\| _{0;\tau }\lesssim & {} h_{\tau }\left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }+\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau }}. \end{aligned}$$

(79)

Hence,

$$\begin{aligned} h_{\tau }^{2}\left\| \varvec{R}_1\right\| _{0;\tau }^{2}\le & {} h_{\tau }^{2}\left( \left\| \varvec{v}\right\| _{0;\tau }^2+\left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }^2\right) \nonumber \\\lesssim & {} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau }}^{2}+h_{\tau }^2\left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau }^{2}. \end{aligned}$$

(80)

$\square$

Lemma 3.10

Let $\tau \in {\mathcal {T}}$, then we have

$$\begin{aligned} \left\| R_{2}\right\| _{0;\tau }^{2}\lesssim & {} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau }}^{2}, \end{aligned}$$

(81)

$$\begin{aligned} \left\| R_{3}\right\| _{0;\tau }^{2}\lesssim & {} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau }}^{2}, \end{aligned}$$

(82)

$$\begin{aligned} \left\| R_{4}\right\| _{0;\tau }^{2}\lesssim & {} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau }}^{2}. \end{aligned}$$

(83)

Proof

Define $\varvec{v}:=R_{2}=\varvec{w}_{h}-\nabla u_{h,1}$, which is a polynomial on $\tau$. Let $\varvec{v}_{b}=\beta _{\tau }\varvec{v}$. Since $\varvec{v}_{b}\in H_{0}^{1}(\tau )^{2}$, by the variational form (6) we have

$$\begin{aligned} \int _{\tau }\varvec{v}_{b}\cdot \nabla u_{1}= & {} (\varvec{w},\varvec{v}_{b}). \end{aligned}$$

(84)

Using the similar trick as in the proof of the previous lemma,

$$\begin{aligned} \left\| \varvec{v}\right\| _{0;\tau }^{2}\lesssim & {} \left\| \beta _{\tau }^{1/2}\varvec{v}\right\| _{0;\tau }^{2}\nonumber \\= & {} \int _{\tau }\varvec{v}_{b}\cdot (\varvec{w}_{h}-\nabla u_{h,1})\nonumber \\= & {} (\varvec{w}_{h}-\varvec{w},\varvec{v}_{b})+\int _{\tau }\varvec{v}_{b}\cdot \nabla (u_{1}-u_{h,1})\nonumber \\\lesssim & {} \left\| \varvec{w}-\varvec{w}_{h}\right\| _{0;\tau }\cdot \left\| \varvec{v}\right\| _{0;\tau }+\left| \varvec{u}-\varvec{u}_{h}\right| _{1;\Omega }\cdot \left\| \varvec{v}\right\| _{0;\tau } \nonumber \\\lesssim & {} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau }} \left\| \varvec{v}\right\| _{0;\tau }, \end{aligned}$$

(85)

which proves (81). Similarly, we can prove (82).

Let us now deal with the last inequality. Define $v:=R_{4}=\nabla \cdot \varvec{u}_{h}$ which is a polynomial on $\tau$. Let $v_{b}=\beta _{\tau }v$. Since $v_{b}\in H_{0}^{1}(\tau )$, by the variational form (6) we have

$$\begin{aligned} \int _{\tau }v_{b}\nabla \cdot \varvec{u}= & {} 0. \end{aligned}$$

(86)

Again, by our standard trick, we have

$$\begin{aligned} \left\| v\right\| _{0;\tau }^{2}\lesssim & {} \left\| \beta _{\tau }^{1/2}v\right\| _{0;\tau }^{2}\nonumber \\= & {} \int _{\tau }v_{b}\nabla \cdot \varvec{u}_{h}\nonumber \\= & {} \int _{\tau }v_{b}\nabla \cdot (\varvec{u}_{h}-\varvec{u})\nonumber \\\lesssim & {} \left| \varvec{u}-\varvec{u}_{h}\right| _{1;\Omega }\cdot \left\| v\right\| _{0;\tau }. \end{aligned}$$

(87)

Our lemma follows as $\varvec{e}_{u}=\varvec{u}-\varvec{u}_{h}$. $\square$

Now, we proceed to the jump terms.

Lemma 3.11

Assume that the exact solution of (6) satisfies $(\varvec{u},\varvec{w},\varvec{z},p)\in [H_{0}^{1}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times [L^{2}(\Omega )]^{2}\times H^1_P(\Omega )$ and let $e\in {\mathcal {F}}_{u}^{0}$ with $e=\tau _{1}\cap \tau _{2}$, then we have

$$\begin{aligned} h_{e}\left\| J_{1}\right\| _{0;e}^{2}+h_{e}\left\| J_{2}\right\| _{0;e}^{2}\lesssim & {} \sum _{i=1,2}\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau _{i}}}^{2} + \sum _{i=1,2} h_{\tau _i}^2 \left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau _i}^{2}.\qquad \end{aligned}$$

(88)

Proof

Since $J_{1}=[n_{1}p_{h}-\varvec{w}_{h}\cdot \varvec{n}]=[n_{1}(p_{h}-p)-(\varvec{w}_{h}-\varvec{w})\cdot \varvec{n}]$ is a polynomial on e, we define $Q_{b,1}\in H_0^1(\tau _{1}\cup \tau _{2})$ be the extension of $\beta _{e}J_1$ on $\tau _{1}\cup \tau _{2}$ such that $Q_{b,1}|_e=\beta _{e}J_1$. Here, we assume $[n_1 p-\varvec{w}\cdot \varvec{n}]=0$ on $e\in {\mathcal {F}}_u^0$. By using the standard bubble function technique, we have

$$\begin{aligned} \left\| J_1\right\| _{0;e}^{2}\lesssim & {} \left\| \beta _{e}^{1/2}J_1\right\| _{0;e}^{2}\nonumber \\= & {} \int _{e}[p_{h}-p]Q_{b,1}n_{1} -\int _{e}[(\varvec{w}_{h}-\varvec{w})\cdot \varvec{n}]Q_{b,1}\nonumber \\= & {} \sum _{i=1,2}\int _{\tau _{i}}(p_{h}-p)(Q_{b,1})_x + \sum _{i=1,2}\int _{\tau _{i}}(p_{h}-p)_xQ_{b,1} \nonumber \\&- \sum _{i=1,2}\int _{\tau _{i}}(\varvec{w}_{h}-\varvec{w})\cdot (\nabla Q_{b,1}) - \sum _{i=1,2}\int _{\tau _{i}}\nabla \cdot (\varvec{w}_{h}-\varvec{w})Q_{b,1}. \end{aligned}$$

(89)

For the first term of (89), we have

$$\begin{aligned} \int _{\tau _{i}}(p_{h}-p)(Q_{b,1})_x\lesssim & {} \left\| p-p_{h}\right\| _{0;\tau _{i}}\cdot \left\| (Q_{b,1})_x\right\| _{0;\tau _{i}}\nonumber \\\lesssim & {} \left\| p-p_{h}\right\| _{0;\tau _{i}}\cdot \left\| \nabla Q_{b,1}\right\| _{0;\tau _{i}}\nonumber \\\lesssim & {} h_{e}^{-1/2}\left\| p-p_{h}\right\| _{0;\tau _{i}}\cdot \left\| J_1\right\| _{0;e}, \end{aligned}$$

(90)

where the last inequality follows from bubble function technique. The bound for the third part of (89) is straight forward as

$$\begin{aligned} -\int _{\tau _{i}}(\varvec{w}_{h}-\varvec{w})\cdot (\nabla Q_{b,1})\lesssim & {} \left\| \varvec{w}-\varvec{w}_{h}\right\| _{0;\tau _{i}}\cdot \left\| \nabla Q_{b,1}\right\| _{0;\tau _{i}}\nonumber \\\lesssim & {} h_{e}^{-1/2}\left\| \varvec{w}-\varvec{w}_{h}\right\| _{0;\tau _{i}}\cdot \left\| J_1\right\| _{0;e}. \end{aligned}$$

(91)

By (89–91), it is easy to see that

$$\begin{aligned} \left\| J_1\right\| _{0;e}^{2}\lesssim & {} h_{e}^{-1/2} \left\| J_1\right\| _{0;e} \sum _{i=1,2} \left( \left\| p-p_{h}\right\| _{0;\tau _{i}}+\left\| \varvec{w}-\varvec{w}_{h}\right\| _{0;\tau _{i}} \right) \nonumber \\&+ \sum _{i=1,2}\int _{\tau _{i}}(p_{h}-p)_xQ_{b,1} - \sum _{i=1,2}\int _{\tau _{i}}\nabla \cdot (\varvec{w}_{h}-\varvec{w})Q_{b,1} \end{aligned}$$

(92)

Similarly, by defining $Q_{b,2}$ as the extension of $\beta _e J_2$, we have

$$\begin{aligned} \left\| J_2\right\| _{0;e}^{2}\lesssim & {} h_{e}^{-1/2} \left\| J_2\right\| _{0;e} \sum _{i=1,2} \left( \left\| p-p_{h}\right\| _{0;\tau _{i}}+\left\| \varvec{z}-\varvec{z}_{h}\right\| _{0;\tau _{i}} \right) \nonumber \\&+ \sum _{i=1,2}\int _{\tau _{i}}(p_{h}-p)_yQ_{b,2} - \sum _{i=1,2}\int _{\tau _{i}}\nabla \cdot (\varvec{z}_{h}-\varvec{z})Q_{b,2}. \end{aligned}$$

(93)

Define $\varvec{J}=(J_1,J_2)$ and $\varvec{Q}_b=(Q_{b,1},Q_{b,2})$. By Summing (92) and (93), we have

$$\begin{aligned} \left\| \varvec{J}\right\| _{0;e}^{2}= & {} \left\| J_1\right\| _{0;e}^{2}+\left\| J_2\right\| _{0;e}^{2} \nonumber \\\lesssim & {} h_{e}^{-1/2} \left\| \varvec{J} \right\| _{0;e} \sum _{i=1,2} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau _{i}}} \nonumber \\&- \sum _{i=1,2}\int _{\tau _{i}} \varvec{R}_1 \cdot \varvec{Q}_b \nonumber \\&+ \sum _{i=1,2}\int _{\tau _{i}} \left\{ \left( \varvec{f}-\nabla p\right) \cdot \varvec{Q}_b + \nabla \cdot \varvec{w} Q_{b,1} +\nabla \cdot \varvec{z}Q_{b,2}\right\} . \end{aligned}$$

(94)

For the second term of (94), we have

$$\begin{aligned} -\int _{\tau _{i}} \varvec{R}_1 \cdot \varvec{Q}_b\lesssim & {} \left\| \varvec{R}_1\right\| _{0;\tau _i} \left\| \varvec{Q}_b\right\| _{0;\tau _i} \nonumber \\\lesssim & {} \left\| \varvec{R}_1\right\| _{0;\tau _i} h_e^{1/2} \left\| \varvec{J}\right\| _{0;e}. \end{aligned}$$

(95)

The third term of (94) is zero by using the variational form. Now we have

$$\begin{aligned} h_e^{1/2} \left\| \varvec{J}\right\| _{0;e} \lesssim \sum _{i=1,2} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau _{i}}} + \sum _{i=1,2} h_{\tau }\left\| \varvec{R}_1\right\| _{0;\tau _i}, \end{aligned}$$

(96)

and our lemma thus follows by using Lemma 3.9:

$$\begin{aligned} h_{e}\left\| J_{1}\right\| _{0;e}^{2}+h_{e}\left\| J_{2}\right\| _{0;e}^{2}= & {} h_e \left\| \varvec{J}\right\| _{0;e}^2 \nonumber \\\lesssim & {} \sum _{i=1,2} \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau _{i}}}^2 + \sum _{i=1,2} h_{\tau }^2\left\| \varvec{R}_1\right\| _{0;\tau _i}^2 \nonumber \\\lesssim & {} \sum _{i=1,2}\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG;\tau _{i}}}^2 + \sum _{i=1,2} h_{\tau _i}^2 \left\| \varvec{f}-\varvec{f}_{h}\right\| _{0;\tau _i}^{2}.\qquad \end{aligned}$$

(97)

$\square$

Lemma 3.12

Theorem 3.8 holds.

Proof

This is trivial by Lemma 3.9–3.11 and the fact that the last term in $\eta$ is also a term in $\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}$. $\square$

3.3 The Adaptive Refinement Strategy

Since $\eta$ is a reliable and efficient error estimator as proved in Sects. 3.1 and 3.2, it is a natural choice to use $\eta$ for a residual-type adaptive refinement scheme. Contrary to standard discontinuous Galerkin methods, our adaptive refinement scheme is constructed based on the initial mesh ${\mathcal {T}}_q$ instead of the final mesh ${\mathcal {T}}$. In particular, we will compute error indicators for the elements in the initial mesh, locate elements with large errors and then refine those elements. After this process, we obtain a new initial mesh, and we will then use the construction of the mesh and function spaces as described in Sect. 2 to form the new SDG system. Specifically, we define the following indicator on the elements of the initial mesh

$$\begin{aligned} \xi _{\rho }^{2}:= & {} \sum _{\tau \in {\mathcal {T}},\,\tau \cap \rho \ne \emptyset }\eta _{\tau }^{2}, \end{aligned}$$

(98)

for each $\rho \in {\mathcal {T}}_{q}$ and

$$\begin{aligned} \xi ^{2}:= & {} \sum _{\rho \in {\mathcal {T}}_{q}}\xi _{\rho }^{2}. \end{aligned}$$

(99)

Now we present the adaptive refinement strategy. The idea is that we find out those elements in ${\mathcal {T}}_{q}$ with higher error using our error indicator and only refine these elements to get a new refinement mesh. With the j-th level initial triangulation denoted as ${\mathcal {T}}_{q}^{j}$, the adaptive refinement scheme is described by the following loop:

• 1. Subdivide each triangle in ${\mathcal {T}}_{q}^{j}$ to get the staggered mesh. Use the SDG scheme (12) to solve for $(\varvec{u}_{h}^{j},\varvec{w}_{h}^{j},\varvec{\varvec{z}}_{h}^{j},p_{h}^{j})$.

• 2. Compute $\xi _{\rho }^2$ for each triangle $\rho \in {\mathcal {T}}_{q}^j$ and thus can compute $\xi ^{2}$.

• 3. If $\xi ^2$ is less than a threshold value $\delta _0$ or the total number of triangles in ${\mathcal {T}}_{q}^{j}$ is larger than a threshold $N_0$, we stop the refinement procedure. Otherwise, we use the following two steps to construct an refinement mesh ${\mathcal {T}}_{q}^{j+1}$.

• 4. We enumerate the triangles in ${\mathcal {T}}_{q}^j$ such that $\xi _{\rho _{1}}\ge \xi _{\rho _{2}}\ge \xi _{\rho _{3}}\ge \cdots$. Choose $0<\theta <1$ and find the least possible value of m such that

  $$\begin{aligned} \theta \xi ^{2}\le & {} \sum _{i=1}^{m}\xi _{\rho _{i}}^{2}. \end{aligned}$$

  (100)

• 5. Get a new mesh ${\mathcal {T}}_{q}^{j+1}$ by refining the m triangles in ${\mathcal {T}}_{q}^{j}$ chosen by Step 4 and any other possible triangles which keep the conformity of ${\mathcal {T}}_{q}^{j+1}$.

3.4 Remarks on the Use of Postprocessing

Recalling that in the DG norm $\left\| (\varvec{e}_u,\varvec{e}_w,\varvec{e}_z,e_p)\right\| _{\mathrm {DG}}$, we compute the $H^1$ semi-norm of the error of the velocity $\varvec{u}$ while compute the $L^2$ norms of the other quantities, including the pressure p. This norm is natural for the Stokes problem (1). However, it was shown in the a priori error analysis of SDG method for the Stokes problem that the numerical solution provides optimal convergence for all the variables. This makes $\left| \varvec{e}_u\right| _{1;\Omega }$ to be the leading term in the above DG norm, converging with order k, while the $L^2$ norms of the velocity gradient and pressure converging with order $k + 1$. Hence, the DG norm defined above seems sub-optimal.

It would be beneficial to investigate on a posteriori error analysis for an optimal energy norm; see, e.g., the relevant work by Larson and Målqvist [31] on optimal a posteriori energy norm control of mixed FEM for diffusion. In the SDG setting, we will use the local postprocessing technique applied to the SDG solution developed in [8, 20]. By doing so, we can obtain a superconvergent velocity ${\tilde{\mathbf {u}}}_h$ converging to $\mathbf {u}$ with order $k+2$. If we consider the following error

$$\begin{aligned} \varvec{\tilde{e}}_{u}:= & {} \varvec{u-\tilde{u}}_{h}, \end{aligned}$$

(101)

then the error norm $\left| \varvec{\tilde{e}}_u\right| _{1;\Omega }$ converges one order higher than $\left| \varvec{e}_u\right| _{1;\Omega }$. If we denote

$$\begin{aligned} \left\| (\varvec{\tilde{e}}_u,\varvec{e}_w,\varvec{e}_z,e_p)\right\| _{new}^{2}:= & {} \left\| (\varvec{\tilde{e}}_u,\varvec{e}_w,\varvec{e}_z,e_p)\right\| _{\mathrm {cts}}^{2} +\sum _{e\in {\mathcal {F}}} h_{e}^{-1} \left\| [\varvec{\tilde{e}}_u] \right\| _{0;e}^{2}, \end{aligned}$$

(102)

then the new norm of the postprocessed solution is optimal. By replacing $\mathbf {u}_h$ with $\tilde{\mathbf {u}}_h$, we can easily prove that

$$\begin{aligned} \left\| (\varvec{\tilde{e}}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{new}^{2}\lesssim & {} \tilde{\eta }^{2}:=\sum _{\tau \in {\mathcal {T}}}\tilde{\eta }_{\tau }^{2}, \end{aligned}$$

(103)

where for each $\tau \in {\mathcal {T}}$,

$$\begin{aligned} \tilde{\eta }_{\tau }^{2}:= & {} h_{\tau }^{2}\left\| \varvec{R}_1\right\| _{0;\tau }^{2}+\left\| \tilde{R}_{2}\right\| _{0;\tau }^{2}+\left\| \tilde{R}_{3}\right\| _{0;\tau }^{2}+\left\| \tilde{R}_{4}\right\| _{0;\tau }^{2} \nonumber \\&+\sum _{e\in {\mathcal {F}}_{u}^{0}\cap \tau }h_{e}\left( \left\| J_{1}\right\| _{0;e}^{2}+\left\| J_{2}\right\| _{0;e}^{2}\right) +\sum _{e\in {\mathcal {F}}\cap \tau }h_{e}^{-1}\left\| \tilde{J}_{3}\right\| _{0;e}^{2}, \end{aligned}$$

(104)

with

$$\begin{aligned} \left\{ \begin{array}{rcl} \displaystyle \varvec{R}_1 &{} = &{} \varvec{f}+\left( \begin{array}{c} \nabla \cdot \varvec{w}_{h}\\ \nabla \cdot \varvec{z_{h}} \end{array}\right) ^{T}-\nabla p_{h},\\ \displaystyle \tilde{R}_{2} &{} = &{} \varvec{w}_{h}-\nabla \tilde{u}_{h,1},\\ \displaystyle \tilde{R}_{3} &{} = &{} \varvec{z}_{h}-\nabla \tilde{u}_{h,2},\\ \displaystyle \tilde{R}_{4} &{} = &{} \nabla \cdot \tilde{\varvec{u}}_{h},\\ \displaystyle J_{1} &{} = &{} [n_{1}p_{h}-\varvec{w}_{h}\cdot \varvec{n}],\\ \displaystyle J_{2} &{} = &{} [n_{2}p_{h}-\varvec{z}_{h}\cdot \varvec{n}],\\ \displaystyle \tilde{J}_{3} &{} = &{} [\tilde{\varvec{u}}_h]. \end{array} \right. \end{aligned}$$

(105)

The proof is almost the same as in Sects. 3.1 and 3.2 and hence we omit the details. Note that $\tilde{R}_{2}$, $\tilde{R}_{3}$, $\tilde{R}_{4}$ and $\tilde{J}_{3}$ converge with one order higher than $R_2$, $R_3$, $R_4$ and $J_3$ in the original error estimator for $\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}^2$, respectively.

4 Numerical Examples

In this section, we provide several numerical examples to show the accuracy and the efficiency of the proposed error indicator and the corresponding adaptive refinement technique. For simplicity, we use piecewise linear elements for all examples. The parameter $\theta$ in Eq. (100) is chosen to be 0.8. For the first three examples, we use structured triangular meshes. Unstructured meshes are used for the last two examples to handel more complicated geometry.

Example 1

To show the order of convergence of our adaptive refinement scheme, we first give an example with analytical solution. Consider the L-shaped domain $\Omega =(-1,1)^{2}\setminus \left( [0,1)\times (-1,0]\right)$, which has a point of singularity at the reentrant corner. The exact solution is given by

$$\begin{aligned} \varvec{u}_{1}= & {} r^{\lambda }\left( \begin{array}{c} (1+\lambda )\sin (\varphi )\psi (\varphi )+\cos (\varphi )\psi '(\varphi )\\ -(1+\lambda )\cos (\varphi )\psi (\varphi )+\sin (\varphi )\psi '(\varphi ) \end{array}\right) ,\end{aligned}$$

(106)

$$\begin{aligned} p_{1}= & {} -r^{\lambda -1}((1+\lambda )\psi '(\varphi )+\psi '''(\varphi ))/(1-\lambda ), \end{aligned}$$

(107)

where $(r,\varphi )$ is the polar coordinate,

$$\begin{aligned} \psi (\varphi )= & {} \sin ((1+\lambda )\varphi )\cos (\lambda \omega )/(1+\lambda )-\cos ((1+\lambda )\varphi ) \nonumber \\&-\sin ((1-\lambda )\varphi )\cos (\lambda \omega )/(1-\lambda )+\cos ((1-\lambda )\varphi ), \end{aligned}$$

(108)

$\lambda \approx 0.54448373678246$ and $\omega =3\pi /2$. Here we have $(\varvec{u}_{1},p_{1})\in \left[ H^{1+\lambda }(\Omega _{1})\right] ^{2}\times H^{\lambda }(\Omega _{2})$, see [26].

Fig. 2

Adaptive mesh with 2206 triangles

Fig. 3

Error plots for Example 1 a comparison of the true error and the error indicator, b comparison of refinement schemes

The adaptive mesh is shown in Fig. 2. We can see that the refinements are more concentrated around the point of singularity as expected. Fig. 3a shows a comparison of the log-log plots of the true error $\left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}$ and the error indicator $\xi$. We can see that the error indicator is very close to the true error and they almost coincide when we keep refining the mesh, which confirms the reliability and efficiency of the error indicator. We also compare our adaptive refinement method with the regular uniform refinement method in Fig. 3b. It is evident that the error of the adaptive refinement scheme is less than the error of the uniform refinement scheme when using the same number of elements. More importantly, we can see that $\log \left\| (\varvec{e}_{u},\varvec{e}_{w},\varvec{e}_{z},e_{p})\right\| _{\mathrm {DG}}$ declines at a rate of 0.5 against $\log (\text {number of elements})$ for the adaptive scheme, which corresponds to order 1 convergence in 2D domains. This shows that our scheme out-performs the uniform refinement scheme and attains an optimal rate of convergence for piecewise linear elements.

Example 2

Consider the square domain $\Omega =(0,1)^{2}$ with a discontinuous boundary condition given by

$$\begin{aligned} \varvec{u}|_{\partial \Omega }= & {} {\left\{ \begin{array}{ll} (1,0), &{} \text {when }y=1,\\ (0,0), &{} \mathrm {elsewhere}. \end{array}\right. } \end{aligned}$$

(109)

This problem is called the lid driven cavity problem as it describes the flow in a rectangular container which is driven by the uniform motion of one lid [34]. Due to the discontinuity of the boundary conditions, there are two singularities at the top corners of the domain.

Fig. 4

Comparison of refinement schemes. a uniform mesh with 8192 triangles, b adaptive mesh with 6090 triangles, c computed $u_{1}$ with uniform mesh, d computed $u_{1}$ with adaptive mesh, e computed $u_{2}$ with uniform mesh, f computed $u_{2}$ with adaptive mesh

Fig. 5

Zoom-in figures at singular point a computed $u_{1}$ with uniform mesh, b computed $u_{1}$ with adaptive mesh

We compare the results with different refinement methods in Figs. 4 and 5. To show the advantage of the adaptive refinement method, we use less number of triangles compared with the uniform refinement mesh, and thus can reduce the size of computation. We can observe that the refinement in the adaptive method is much more reasonable. There are more elements concentrated around the areas of singular points and less elements in the rest region. The minimum length of the edges in ${\mathcal {T}}$ is $4.2426E-6$ for the adaptive method, while it’s 0.0156 for the uniform refinement method. As a result, the recovery of $\varvec{u}$ around the singular point is much finer with the adaptive mesh, as shown in Fig. 5. On the other hand, the recovery of $\varvec{u}$ on the rest region with the adaptive mesh is still similar to the one with uniform mesh, showing that the costly dense mesh used in this area in the uniform refinement method is unnecessary. One can imagine that it will be very costly to reach the same level of resolution near the singular points by using the uniform refinement mesh.

Example 3

Let us consider a slight modification on Example 2, which has a more complicated domain. Consider the square ${\mathcal {S}}=(0,1)^{2}$ divided into 72 identical triangles as shown in Fig. 6a. Our computational domain $\Omega$ is defined by cutting triangles 15, 19–22, 31–34 and 51–57 from ${\mathcal {S}}$. Hence, $\Omega$ together with the initial mesh is given by Fig. 6b.

Fig. 6

Initial mesh a index of triangles in ${\mathcal {S}}$, b computational domain $\Omega$

Furthermore, the boundary condition is given by

$$\begin{aligned} \varvec{u}|_{\partial \Omega }= & {} {\left\{ \begin{array}{ll} (1,0), &{} \text {when }y=5/6\,\text {and }1/6\le x\le 1/2,\\ (0,0), &{} \mathrm {elsewhere}. \end{array}\right. } \end{aligned}$$

(110)

Fig. 7

Comparison of refinement schemes a uniform mesh with 14336 triangles, b adaptive mesh with 13350 triangles, c computed $u_{1}$ with uniform mesh, d computed $u_{1}$ with adaptive mesh, e computed $u_{2}$ with uniform mesh, f computed $u_{2}$ with adaptive mesh

Fig. 8

Zoom-in figures at singular point a computed $u_{2}$ with uniform mesh, b computed $u_{2}$ with adaptive mesh

As in Example 2, the number of triangles used in the adaptive refinement mesh is less than that in the uniform refinement mesh. We compare different refinement methods in Figs. 7 and 8. We can see that the error indicator can capture the corners of the lid and the vertexes of the inside boundary accurately. Here, the minimum length of the edge is $2E-6$ for the adaptive refinement mesh and is 0.0104 for the uniform refinement mesh. The behavior of the numerical solutions is quite similar to Example 2. Although the total number of elements is less, the recovery is much finer around the singular points with the adaptive method while the quality of the recovery remains unaffected on the rest of the domain.

Example 4

Let us consider the lid driven cavity problem in a rectangular perforated domain $\Omega =(0,10)^{2}$ with 19 circular perforations. The boundary condition is given by

$$\begin{aligned} \varvec{u}|_{\partial \Omega }= & {} {\left\{ \begin{array}{ll} (1,0), &{} \text {when }y=10,\\ (0,0), &{} \mathrm {elsewhere}. \end{array}\right. } \end{aligned}$$

(111)

For this problem, contrary to the above examples, there is no clear indication to where to refine the mesh. In particular, we do not know the structure of the solution based on the locations and sizes of the perforations.

We show the initial mesh and the adaptive refinement mesh of level 32 in Fig. 9. It’s clear that the refinements are concentrated around the top corners of the domain where the solution has a singularity and some other regions where the solution has more fine structures. The plots of the velocity are shown in Fig. 10 from which we can observe the flow motion between holes.

Fig. 9

Adaptive mesh for Example 4 a initial mesh, b mesh level 32

Fig. 10

Computed velocity with mesh level 32 a computed $u_{1}$, b computed $u_{2}$

Fig. 11

Adaptive mesh for Example 5 a initial mesh, b mesh level 6

Fig. 12

Computed velocity with mesh level 6 a computed $u_{1}$, b computed $u_{2}$

Example 5

Finally, we consider a rectangular perforated domain $\Omega =(0,10)^{2}$ with 12 circular perforations. We consider a different boundary condition given by

$$\begin{aligned} \varvec{u}|_{\partial \Omega }= & {} {\left\{ \begin{array}{ll} (1,0), &{} \text {when }x=0\, or \, x=10,\\ (0,0), &{} \mathrm {elsewhere}. \end{array}\right. } \end{aligned}$$

(112)

This problem describes the flow passing though a tunnel with obstructions.

We show the initial mesh and the adaptive refinement mesh of level 6 in Fig. 11. It’s clear that the refinements are concentrated in areas where the solution has more fine scale features. The plots of velocity are shown in Fig. 12 from which we can see that the fluid passes though the tunnel from left to right by avoiding the obstructions.

5 Concluding Remarks

In this paper, we derive a residual-type a-posteriori error estimator for the numerical solutions of the Stokes system solved with the SDG method. The reliability and efficiency of this error indicator is proved. By using this error indicator, an adaptive refinement technique is proposed to solve fluid flow problems with singularities and flows in perforated domains, which are computational expensive for the regular uniform refinement method. Numerical examples show that the error indicator is close to the exact numerical error and thus can capture the singular points accurately. Compared with the uniform refinement method, the adaptive refinement method can improve the resolution near the singular points by making the mesh more dense in this area. On the other hand, the accuracy of the rest region remains unchanged even with courser mesh. The total number of elements is still less than that in the uniform refinement mesh and hence the total computational cost can be reduced.

Note that our staggered mesh ${\mathcal {T}}$ is generated from an initial shape regular triangulation ${\mathcal {T}}_{q}$ by dividing each triangle in ${\mathcal {T}}_{q}$ into three sub-triangles. Thus, almost all the sub-triangles in ${\mathcal {T}}$ would be obtuse. Hence, a possible future work is to construct the initial mesh from a macro quadrilateral mesh, or more generally, a macro polygonal mesh, to make the triangles more regular. Also, we should consider the use of hanging nodes in our future works.