1 Introduction

The normal diffusion equation \(\partial _t p(x,t)=\partial _x^2p(x,t)\) can be derived from the Brownian motion which describes the particle’s random walks. Over the last few decades, a large body of literature has demonstrated that anomalous diffusion, in which the mean square variance grows faster (super-diffusion) or slower (sub-diffusion) than in a Gaussian process, offers a superior fit to experimental data observed in many important practical applications, e.g., in physical science [14, 17,18,19], finance [10, 16, 24], biology [4, 12] and hydrology [3, 7, 8]. The anomalous diffusion equation takes the form

$$\begin{aligned} \partial ^\nu _t p(x,t)=\partial _x^\mu p(x,t), \end{aligned}$$
(1.1)

where \(0<\nu \le 1\) and \(0<\mu < 2\) (cf. [17] for a review on this subject), whose solution exhibits heavy tails, i.e., power law decays at infinity. In order to “temper” the power law decay, the authors of [22] incorporated an exponential factor \(e^{-\lambda |x|}\) into the particle jump density, and showed that the Fourier transform of the tempered probability density function p(x, t) takes the form

$$\begin{aligned} {\mathscr {F}}[p](\omega ,t)= e^{-\left[ pA_+^{\mu ,\lambda }(\omega )+qA_-^{\mu ,\lambda }(\omega )\right] Dt},\quad 0<\mu <2, \end{aligned}$$

where \(0\le p\le 1,~q=1-p\), D is a constant and

$$\begin{aligned} A_{\pm }^{\mu ,\lambda }(\omega ):= {\left\{ \begin{array}{ll} (\lambda \pm \mathrm{i}\omega )^\mu -\lambda ^\mu ,&{}0<\mu<1,\\ (\lambda \pm \mathrm{i}\omega )^\mu -\lambda ^\mu -\pm \mathrm{i}\omega \mu \lambda ^{\mu -1},&{}1<\mu <2. \end{array}\right. } \end{aligned}$$
(1.2)

Moreover, they defined tempered fractional derivative operators \(\partial _{\pm ,x}^{\mu ,\lambda }\) through Fourier transform: \(\mathscr {F}{[\partial _{\pm ,x}^{\mu ,\lambda } u]}(\omega )=A_{\pm }^{\mu ,\lambda }(\omega ){\mathscr {F}}[u](\omega )\), and derived the tempered fractional diffusion equation:

$$\begin{aligned} \partial _t u(x,t)=(-1)^k C_T \{ p\partial _{+,x}^{\mu ,\lambda } +q\partial _{-,x}^{\mu ,\lambda } \}u(x,t), \quad \mu \in (k-1,k),~k=1,2. \end{aligned}$$
(1.3)

It is believed that tempered anomalous diffusion models have advantages over the normal diffusion models in some applications in geophysics [15, 30] and finance [5].

It is challenging to numerically solve the tempered fractional diffusion equation (1.3), partially due to (i) the non-local nature of tempered fractional derivatives; and (ii) the unboundedness of the domain. In [22], a finite-difference method was applied to (1.3) on a truncated (finite) interval. In [28], the authors considered tempered derivatives on a finite interval and derived an efficient Petrov–Galerkin method for solving tempered fractional ODEs by using the eigenfunctions of tempered fractional Sturm–Liouville problems. In [11], the authors used Laguerre functions to approximate the substantial fractional ODEs, which are similar to those we consider in Sect. 3, on the half line. In order to avoid the difficulty of assigning boundary conditions at the truncated boundary, we shall deal with the unbounded domain directly in this paper.

Since the tempered fractional diffusion equation is derived from the random walk on the whole line, one is tempted to use Hermite polynomials/functions which are suitable for many problems on the whole line [25]. Unfortunately, due to the exponential factor in the tempered fractional derivatives, Hermite polynomials/functions are not suitable basis functions. Instead, as we will show in Sect. 3, properly defined GLFs enjoy particularly simple form under the action of tempered fractional derivatives, just as the relations between generalized Jacobi functions and usual fractional derivatives [6]. Hence, the main goal of this paper is to design efficient spectral methods using GLFs as basis functions to solve the tempered fractional diffusion equation (1.3) in various situations. However, Laguerre polynomials/functions are mutually orthogonal on the half line, how do we use them to deal with (1.3) on the whole line? We shall first consider special cases of (1.3) with \(p=1, \, q=0\) or \(p=0, \, q=1\). In these cases, we can reduce (1.3) to the half line, and the GLFs can be naturally used. For the general case, we shall employ a two-domain spectral-element method, and use GLFs as basis functions on each subdomain.

The rest of the paper is organized as follows. In the next section, we present the definition of tempered fractional derivatives, and recall some useful properties of Laguerre polynomials. In Sect. 3, we define a class of generalized Laguerre functions, study its approximation properties, and apply it for solving simple one sided tempered fractional equations. In Sect. 4, we develop a spectral-Galerkin method for solving a tempered fractional diffusion equation on the half line. Finally, we present a spectral-Galerkin method for solving the tempered fractional diffusion equation on the whole line in Sect. 5. Some concluding remarks are given in the last section.

2 Preliminaries

Let \({\mathbb {N}}\) and \({\mathbb {R}}\) be respectively the sets of positive integers and real numbers. We further denote

$$\begin{aligned} {\mathbb {N}}_0:=\{0\}\cup {\mathbb {N}}, \;\; {\mathbb {R}}^+:= \{x\in {\mathbb {R}}: x> 0\},\;\; {\mathbb {R}}^-:= \{x\in {\mathbb {R}}: x< 0\},\;\; {\mathbb {R}}_0^\pm :={\mathbb {R}}^\pm \cup \{0\}. \end{aligned}$$
(2.1)

2.1 Usual (Non-tempered) Fractional Integrals and Derivatives

Recall the definitions of the fractional integrals and fractional derivatives in the sense of Riemann–Liouville (see e.g., [20]).

Definition 2.1

(Riemann–Liouville fractional integrals and derivatives) For \(a,b\in {\mathbb {R}} \) or \(a=-\infty , b=\infty ,\) and \(\mu \in {\mathbb {R}}^+,\) the left and right fractional integrals are respectively defined as

$$\begin{aligned}&{}_{a}\mathrm{I}_{x}^{\mu } u(x)=\frac{1}{\Gamma (\mu )}\int _{a}^x \frac{u(y)}{(x-y)^{1-\mu }} \mathrm{d}y,\;\; {}_{x}\mathrm{I}_{b}^{\mu } u(x)=\frac{1}{\Gamma (\mu )}\int _{x}^b \frac{u(y)}{(y-x)^{1-\mu }} \mathrm{d}y,\;\;\;\nonumber \\&\qquad x\in \Lambda :=(a,b). \end{aligned}$$
(2.2)

For real \(s\in [k-1, k)\) with \(k\in {\mathbb {N}},\) the left-sided Riemann–Liouville fractional derivative (LRLFD) of order s is defined by

$$\begin{aligned} {{}_{a}}\mathrm{D}_{x}^{s} u(x)=\frac{1}{\Gamma (k-s)}\frac{d^k}{dx^k}\int _{a}^x \frac{u(y)}{(x-y)^{s-k+1}} \mathrm{d}y,\;\;\; x\in \Lambda , \end{aligned}$$
(2.3)

and the right-sided Riemann–Liouville fractional derivative (RRLFD) of order s is defined by

$$\begin{aligned} {{}_{x}}\mathrm{D}_{b}^{s}u(x)=\frac{(-1)^k}{\Gamma (k-s)}\frac{d^k}{dx^k}\int _{x}^b\frac{u(y)}{(y-x)^{s-k+1}} \mathrm{d}y, \;\;\; x\in \Lambda . \end{aligned}$$
(2.4)

From the above definitions, it is clear that for any \(k\in {\mathbb {N}}_0,\)

$$\begin{aligned} {{}_{a}}\mathrm{D}_{x}^{k}={{}_{}}\mathrm{D}_{}^{k},\quad {{}_{x}}\mathrm{D}_{b}^{k}=(-1)^{k} {{}_{}}\mathrm{D}_{}^{k}, \;\;\; \mathrm{where}\;\;\; {{}_{}}\mathrm{D}_{}^{k}:=\frac{d^k}{dx^k}. \end{aligned}$$
(2.5)

Therefore, we can express the RLFD as

$$\begin{aligned} {{}_{a}}\mathrm{D}_{x}^{s} u(x)={{}_{}}\mathrm{D}_{}^{k}\big \{ {}_{a}\mathrm{I}_{x}^{k-s} u(x)\big \}; \quad \; {{}_{x}}\mathrm{D}_{b}^{s} u(x)=(-1)^k {{}_{}}\mathrm{D}_{}^{k} \big \{ {}_{x}\mathrm{I}_{b}^{k-s} u(x)\big \}. \end{aligned}$$
(2.6)

According to [9, Thm. 2.14], we have that for any finite a and any \(f\in L^1(\Lambda ),\) and real \(s\ge 0,\)

$$\begin{aligned} {{}_{a}}\mathrm{D}_{x}^{s}\, {}_{a}\mathrm{I}_{x}^{s} f(x) = f(x),\quad \text {a.e. in} \;\; \Lambda . \end{aligned}$$
(2.7)

Note that by commuting the integral and derivative operators in (2.6), we define the Caputo fractional derivatives:

$$\begin{aligned} {}_{a}^{C}\mathrm{D}_{x}^{s} u(x)= {}_{a}\mathrm{I}_{x}^{k-s} \big \{{{}_{}}\mathrm{D}_{}^{k} u(x)\big \}; \quad \; {}_{x}^{C}\mathrm{D}_{b}^{s} u(x)= (-1)^k{}_{x}\mathrm{I}_{b}^{k-s} \big \{{{}_{}}\mathrm{D}_{}^{k} u(x)\big \}. \end{aligned}$$
(2.8)

For an affine transform \(x=\lambda t,~\lambda >0\), on account of

$$\begin{aligned} \begin{aligned} {}_{a}\mathrm{I}_{t}^{\mu }v(\lambda t)&=\frac{1}{\Gamma (\mu )}\int _{a}^{ t} \frac{v(\lambda s)}{(t-s)^{1-\mu }} d s =\frac{\lambda ^{-\mu }}{\Gamma (\mu )}\int _{a}^{ t} \frac{v(\lambda s)}{(\lambda t-\lambda s)^{1-\mu }} \lambda d s\\&=\frac{\lambda ^{-\mu }}{\Gamma (\mu )}\int _{\lambda a}^{ x} \frac{v(y)}{(x-y)^{1-\mu }}dy=\lambda ^{-\mu } {}_{\lambda a}\mathrm{I}_{x}^{\mu }v(x), \end{aligned} \end{aligned}$$

and \(\frac{\hbox {d}}{{\hbox {d}}t}=\lambda \frac{\hbox {d}}{{\hbox {d}}x},\) we derive from Definition 2.1 that

$$\begin{aligned} {}_{a}\mathrm{I}_{t}^{\mu }v(\lambda t)= \lambda ^{-\mu } {}_{\lambda a}\mathrm{I}_{x}^{\mu }v(x),\quad {{}_{a}}\mathrm{D}_{t}^{s} v(\lambda t)= \lambda ^{s} {{}_{\lambda a}}\mathrm{D}_{x}^{s} v(x),\quad s,\mu ,\lambda >0. \end{aligned}$$
(2.9)

Similarly, we have the following identities for the right fractional derivative:

$$\begin{aligned} {}_{t}\mathrm{I}_{b}^{\mu }v(\lambda t)= \lambda ^{-\mu } {}_{x}\mathrm{I}_{\lambda b}^{\mu }v(x),\quad {{}_{t}}\mathrm{D}_{b}^{s} v(\lambda t)= \lambda ^{s} {{}_{x}}\mathrm{D}_{\lambda b}^{s} v(x),\quad s,\mu ,\lambda >0. \end{aligned}$$
(2.10)

2.2 Tempered Fractional Integrals and Derivatives on \({\mathbb {R}}\)

Recently, Sabzikar et al. [22, (19)–(23)] introduced the tempered fractional integrals and derivatives on the whole line.

Definition 2.2

(Tempered fractional integrals) For \(\lambda \in {\mathbb {R}}^+_0\), the left tempered fractional integral of a suitable function u(x) of order \(\mu \in {\mathbb {R}}^+\) is defined by

$$\begin{aligned} {}_{-\infty }\mathrm{I}_{x}^{\mu ,\lambda } u(x)=\frac{1}{\Gamma (\mu )}\int _{-\infty }^x \frac{e^{-\lambda (x-y)}}{(x-y)^{1-\mu }}\,u(y)\,\mathrm{d}y,\quad x\in {\mathbb {R}}, \end{aligned}$$
(2.11)

and the right tempered fractional integral of order \(\mu \in {\mathbb {R}}^+\) is defined by

$$\begin{aligned} {}_{x}\mathrm{I}_{\infty }^{\mu ,\lambda } u(x)=\frac{1}{\Gamma (\mu )}\int ^{\infty }_x \frac{e^{-\lambda (y-x)}}{(y-x)^{1-\mu }}\,u(y)\,\mathrm{d}y,\quad x\in {\mathbb {R}}. \end{aligned}$$
(2.12)

It is evident that by (2.2) and (2.11)–(2.12), we have

$$\begin{aligned} {}_{-\infty }\mathrm{I}_{x}^{\mu }={}_{-\infty }\mathrm{I}_{x}^{\mu ,0}, \quad {}_{x}\mathrm{I}_{\infty }^{\mu }={}_{x}\mathrm{I}_{\infty }^{\mu ,0}, \end{aligned}$$
(2.13)

and

$$\begin{aligned} {}_{-\infty }\mathrm{I}_{x}^{\mu ,\lambda } u(x)=e^{-\lambda x}{}_{-\infty }\mathrm{I}_{x}^{\mu }\big \{e^{\lambda x} u(x)\big \},\quad {}_{x}\mathrm{I}_{\infty }^{\mu ,\lambda } u(x)=e^{\lambda x}{}_{x}\mathrm{I}_{\infty }^{\mu }\big \{e^{-\lambda x} u(x)\big \}. \end{aligned}$$
(2.14)

As shown in [22], the tempered fractional derivative can be characterized by its Fourier transform. Recall that, for any \(u\in L^2({\mathbb {R}}),\) its Fourier transform and inverse Fourier transform are defined by

$$\begin{aligned} {{\mathscr {F}}}[u](\omega )=\int _{-\infty }^\infty u(x)e^{-\mathrm{i}\omega x}\,\mathrm{d}x; \quad u(x)={{\mathscr {F}}}^{-1}\big [{{\mathscr {F}}}[u](\omega )\big ](x)=\frac{1}{2\pi }\int _{-\infty }^\infty {{\mathscr {F}}}[u](\omega )e^{\mathrm{i}\omega x}\,\mathrm{d}\omega . \end{aligned}$$
(2.15)

There holds the well-known Parseval’s identity:

$$\begin{aligned} \int _{-\infty }^\infty u(x)\,\overline{v(x)}\, \mathrm{d}x=\frac{1}{2\pi }\int _{-\infty }^\infty {{\mathscr {F}}}[u](\omega )\,\overline{{{\mathscr {F}}}[v](\omega )}\,\mathrm{d}\omega , \end{aligned}$$
(2.16)

where \({\bar{v}}\) is the complex conjugate of v. Let H(x) be the Heaviside function, i.e., \(H(x)=1\) for \(x\ge 0,\) and vanishing for all \(x< 0.\) Then we can reformulate the left tempered fractional integral as

$$\begin{aligned} \begin{aligned} {}_{-\infty }\mathrm{I}_{x}^{\mu ,\lambda } u(x)&=\frac{1}{\Gamma (\mu )}\int _0^\infty y^{\mu -1} e^{-\lambda y} u(x-y)\,\mathrm{d }y {=}\frac{1}{\Gamma (\mu )}\int _{-\infty }^\infty y^{\mu -1} e^{-\lambda y} H(y)\, u(x-y)\,\mathrm{d }y \\ {}&= \big ({ K}*u\big )(x),\quad \mathrm{where}\;\;\; {K}(x):=x^{\mu -1}e^{-\lambda x}H(x)/{\Gamma (\mu )}. \end{aligned} \end{aligned}$$
(2.17)

Note that K(x) is related to the particle jump density (cf. [22, (8)]). Using the formula: \( {{\mathscr {F}}}[K](\omega )= {(\lambda +\mathrm{i}\omega )^{-\mu }},\) and the convolution property of Fourier transform (see, e.g., [23, 26]), we derive

$$\begin{aligned} {{\mathscr {F}}}[{}_{-\infty }\mathrm{I}_{x}^{\mu ,\lambda } u](\omega )={{\mathscr {F}}}[K*u](\omega )= {{\mathscr {F}}}[K](\omega )\, {{\mathscr {F}}}[u](\omega )= {(\lambda +\mathrm{i}\omega )^{-\mu }} {{\mathscr {F}}}[u](\omega ). \end{aligned}$$
(2.18)

Similarly, the Fourier transform of the right tempered fractional integral is

$$\begin{aligned} {{\mathscr {F}}}[{}_{x}\mathrm{I}_{\infty }^{\mu ,\lambda } u](\omega )= {(\lambda -\mathrm{i}\omega )^{-\mu }} {{\mathscr {F}}}[u](\omega ). \end{aligned}$$
(2.19)

In view of (2.18)–(2.19), Sabzikar et al. [22] then introduced the left and right tempered fractional derivatives as follows.

Definition 2.3

(Tempered fractional derivatives) For \( \lambda \in {\mathbb {R}}^+_0\), the left and right tempered fractional derivatives of order \(\mu \in {\mathbb {R}}^+\) of a suitable function u(x),  are defined by

$$\begin{aligned} {{\mathscr {F}}}\big [{{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda } u\big ](\omega )=(\lambda + \mathrm{i}\omega )^{\mu } {{\mathscr {F}}}[u](\omega ),\quad {{\mathscr {F}}}\big [{{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } u\big ](\omega )=(\lambda - \mathrm{i}\omega )^{\mu } {{\mathscr {F}}}[u](\omega ), \end{aligned}$$
(2.20)

that is, for any \(x\in {\mathbb {R}}\),

$$\begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda } u(x)={\mathscr {F}^{-1}}\big [{(\lambda +\mathrm{i}\omega )^{\mu }} {{\mathscr {F}}}[u](\omega )\big ](x),\quad {{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } u(x){=}{\mathscr {F}^{-1}}\big [{(\lambda -\mathrm{i}\omega )^{\mu }} {{\mathscr {F}}}[u](\omega )\big ](x). \end{aligned}$$
(2.21)

Introduce the space

$$\begin{aligned} W^{\mu ,2}_{\lambda }({\mathbb {R}}):=\Big \{u\in L^2({\mathbb {R}})\,:~\int _{{\mathbb {R}}}(\lambda ^2+\omega ^2)^{\mu }\, \big |{{\mathscr {F}}} [u](\omega )\big |^2\mathrm{d}\omega <\infty \Big \},\quad \mu ,\lambda \in {\mathbb {R}}^+. \end{aligned}$$
(2.22)

Thanks to the Parseval’s identity (2.16), the above tempered fractional derivatives are well-defined for any \(u\in W^{\mu ,2}_{\lambda }({\mathbb {R}}).\) Moreover, one verifies from (2.18)–(2.21) that

$$\begin{aligned} \begin{aligned}&{}_{-\infty }\mathrm{I}_{x}^{\mu ,\lambda }{{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda } u(x)=u(x), \;\;\;\;{}_{x}\mathrm{I}_{\infty }^{\mu ,\lambda }{{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } u(x)=u(x), \quad \forall \, u\in W^{\mu ,2}_{\lambda }({\mathbb {R}});\;\;\\&{{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda }{}_{-\infty }\mathrm{I}_{x}^{\mu ,\lambda } u(x)=u(x), \;\;\;\;{{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda }{}_{x}\mathrm{I}_{\infty }^{\mu ,\lambda } u(x)=u(x),\quad \forall \, u\in L^2({\mathbb {R}}). \end{aligned} \end{aligned}$$
(2.23)

Similar to (2.14), we have the following explicit representations (see [13, Lemma 1 and Remark 2]).

Proposition 2.1

For any \(u\in W^{\mu ,2}_{\lambda }({\mathbb {R}}),\) with \( \lambda \in {\mathbb {R}}^+_0\), the left and right tempered fractional derivatives of order \(\mu \in [k-1,k)\) with \(k\in {\mathbb {N}},\) have the explicit representations:

$$\begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda } u(x)=e^{-\lambda x} {{}_{-\infty }}\mathrm{D}_{x}^{\mu } \big \{e^{\lambda x}u(x)\big \},\quad {{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } u(x)=e^{\lambda x} {{}_{x}}\mathrm{D}_{\infty }^{\mu }\big \{e^{-\lambda x}u(x)\big \}, \end{aligned}$$
(2.24)

where \({{}_{-\infty }}\mathrm{D}_{x}^{\mu }\) and \({{}_{x}}\mathrm{D}_{\infty }^{\mu }\) are the Riemann–Liouville fractional derivative operators in Definition 2.1. Alternatively, we have

$$\begin{aligned} \begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda } u(x)&=(\lambda +{{}_{}}\mathrm{D}_{}^{})^k\,\big \{{}_{-\infty }\mathrm{I}_{x}^{k-\mu ,\lambda } u(x)\big \}=(\lambda +{{}_{}}\mathrm{D}_{}^{})^k\,\big \{e^{-\lambda x}{}_{-\infty }\mathrm{I}_{x}^{k-\mu } \big \{e^{\lambda x} u(x)\big \}\big \}; \\ {{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } u(x)&=(\lambda -{{}_{}}\mathrm{D}_{}^{})^k\,\big \{{}_{x}\mathrm{I}_{\infty }^{k-\mu } u(x)\big \}=(\lambda -{{}_{}}\mathrm{D}_{}^{})^k\,\big \{e^{\lambda x}{}_{x}\mathrm{I}_{\infty }^{k-\mu }\big \{e^{-\lambda x} u(x)\big \}\big \}. \end{aligned} \end{aligned}$$
(2.25)

We collect below some useful properties (see [22]).

Lemma 2.1

Given \(\lambda >0\) and \(\mu \in [k-1,k),~k\in {\mathbb {N}}\), the tempered fractional derivative

$$\begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda } u(x)={{}_{-\infty }}\mathrm{D}_{x}^{k,\lambda } {}_{-\infty }\mathrm{I}_{x}^{k-\mu ,\lambda } u(x),\quad {{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } u(x)={{}_{x}}\mathrm{D}_{\infty }^{k,\lambda } {}_{x}\mathrm{I}_{\infty }^{k-\mu ,\lambda } u(x). \end{aligned}$$
(2.26)

In addition, we have

$$\begin{aligned}&{}_{-\infty }\mathrm{I}_{x}^{\mu +\nu ,\lambda } u(x)={}_{-\infty }\mathrm{I}_{x}^{\mu ,\lambda } {}_{-\infty }\mathrm{I}_{x}^{\nu ,\lambda } u(x),\quad \quad {}_{x}\mathrm{I}_{\infty }^{\mu +\nu ,\lambda } u(x)={}_{x}\mathrm{I}_{\infty }^{\mu ,\lambda } {}_{x}\mathrm{I}_{\infty }^{\nu ,\lambda } u(x),\end{aligned}$$
(2.27)
$$\begin{aligned}&{{}_{-\infty }}\mathrm{D}_{x}^{\mu +\nu ,\lambda } u(x)={{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda }{{}_{-\infty }}\mathrm{D}_{x}^{\nu ,\lambda } u(x),\quad {{}_{x}}\mathrm{D}_{\infty }^{\mu +\nu ,\lambda } u(x)={{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda }{{}_{x}}\mathrm{D}_{\infty }^{\nu ,\lambda } u(x),\end{aligned}$$
(2.28)
$$\begin{aligned}&({{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda } u,v)=( u,{{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } v ), \qquad \qquad \qquad ({{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } u,v) =( u, {{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda }v ), \end{aligned}$$
(2.29)

where \( \mu ,\nu \ge 0\).

Remark 2.1

For a suitable function \(f(x),~x\in {\mathbb {R}}^+\), its reflection \(g(y)=f(-y),~y\in {\mathbb {R}}^-\) satisfies

$$\begin{aligned} \begin{aligned} {}_{-\infty }\mathrm{I}_{y}^{\mu ,\lambda }g(y)=&\frac{e^{-\lambda y}}{\Gamma (\mu )} \int _{-\infty }^y e^{\lambda \tau }(y-\tau )^{\mu -1}f(-\tau ){\mathrm{d}} \tau \overset{t=-\tau }{=}\frac{e^{-\lambda y}}{{\Gamma (\mu )}} \int ^{\infty }_{-y} e^{-\lambda t}(y+t)^{\mu -1}f(t) {\mathrm{d}}t\\ \overset{x=-y}{=}&\frac{e^{\lambda x}}{{\Gamma (\mu )}} \int ^{\infty }_{x} e^{-\lambda t}(t-x)^{\mu -1}f(t){\mathrm{d}}t ={}_{x}\mathrm{I}_{\infty }^{\mu ,\lambda }f(x). \end{aligned} \end{aligned}$$
(2.30)

Hence, we can use (2.26) and derivative relation \(\dfrac{{\mathrm{d}}^k}{{\mathrm{d}y^k}}=(-1)^k\dfrac{{\mathrm{d}}^k}{{\mathrm{d}x}^k}\) to obtain the tempered derivative relation

$$\begin{aligned} {{}_{-\infty }}\mathrm{D}_{y}^{\mu ,\lambda }f(-y)={{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda }f(x),\quad y=-x, x\in {\mathbb {R}}^+. \end{aligned}$$
(2.31)

\(\square \)

2.3 Laguerre Polynomials and Some Useful Formulas

For any \(a\in {\mathbb {R}}\) and \(j\in {\mathbb {N}}_0,\) we recall that the rising factorial in the Pochhammer symbol and the Gamma function have the relation:

$$\begin{aligned} (a)_0=1; \;\;\; (a)_j:=a(a+1)\cdots (a+j-1)=\frac{\Gamma (a+j)}{\Gamma (a)},\;\; \mathrm{for}\;\; j\ge 1. \end{aligned}$$
(2.32)

Recall the hypergeometric function (cf. [1]):

$$\begin{aligned} {}_1F_1(a;b; x)=\sum _{j=0}^\infty \frac{(a)_j }{(b)_j}\frac{x^j}{j!},\;\;\; a,b,x\in {\mathbb {R}}^+,\;\; -b\not \in {\mathbb {N}}_0. \end{aligned}$$
(2.33)

If \(b-a>0,\) then \({}_1F_1(a;b; x)\) is absolutely convergent for all \(x\in {\mathbb {R}}.\) If a is a negative integer, then it reduces to a polynomial.

The Laguerre polynomial with parameter \(\alpha >-1\) is defined as in Szegö [27, (5.3.3)]:

$$\begin{aligned} L_n^{(\alpha )}(x)=\frac{(\alpha +1)_n}{n!}~ {}_1F_1\big (-n;\alpha +1;x\big ),\;\;\; n\ge 1,\;\; x\in {\mathbb {R}}^+, \end{aligned}$$
(2.34)

and \(L_0^{(\alpha )}(x)\equiv 1.\) Note that

$$\begin{aligned} L_n^{(\alpha )}(0)=\dfrac{(\alpha +1)_n}{n!}, \end{aligned}$$
(2.35)

and the Laguerre polynomials (with \(\alpha >-1\)) are orthogonal with respect to the weight function \(x^\alpha e^{-x},\) namely,

$$\begin{aligned} \int _{0}^\infty {L}_n^{(\alpha )}(x)~ {L}_m^{(\alpha )}(x) ~x^\alpha e^{-x} \, \mathrm{d}x= \gamma _n^{\alpha }\, \delta _{mn}, \quad \gamma _n^{\alpha } =\frac{\Gamma (n+\alpha +1)}{\Gamma (n+1)}. \end{aligned}$$
(2.36)

They are eigenfunctions of the Sturm–Liouville problem:

$$\begin{aligned} x^{-\alpha }e^x \mathrm{D}\big ( x^{\alpha +1}e^{-x}\mathrm{D} L_n^{(\alpha )}(x)\big )+\lambda _n L_n^{(\alpha )}(x)=0,\quad \lambda _n=n. \end{aligned}$$
(2.37)

We have the following relations:

$$\begin{aligned} L_n^{(\alpha )}(x)= & {} \mathrm{D} L_{n}^{(\alpha )}(x)-\mathrm{D} L_{n+1}^{(\alpha )}(x), \end{aligned}$$
(2.38)
$$\begin{aligned} x\mathrm{D} L_n^{(\alpha )}(x)= & {} nL_{n}^{(\alpha )}(x)-(n+\alpha )L_{n-1}^ {(\alpha )}(x), \end{aligned}$$
(2.39)
$$\begin{aligned} \mathrm{D} L_n^{(\alpha )}(x)= & {} \,- L_{n-1}^{(\alpha +1)}(x)= -\sum _{k=0}^{n-1}L_{k}^{(\alpha )}(x). \end{aligned}$$
(2.40)

In particular, for \(\alpha =-k,~k=1,2,\ldots \) (See Szegö [27, (5.2.1)]),

$$\begin{aligned} L_n^{(-k)}(x)=(-1)^k\frac{\Gamma (n-k+1)}{\Gamma (n+1)}x^k L_{n-k}^{(k)}(x),\quad n\ge k. \end{aligned}$$

For notational convenience, we denote

$$\begin{aligned} {h}_n^{a,b}:=\frac{\Gamma (n+1+a)}{\Gamma (n+1+a-b)}. \end{aligned}$$
(2.41)

We present below some formulas related to Laguerre polynomials and fractional integrals and derivatives, which play an important role in the algorithm development and analysis later. We provide their derivations in “Appendix A”.

Lemma 2.2

For \(\mu \in {\mathbb {R}}^+,\) we have

$$\begin{aligned} {}_{0}\mathrm{I}_{x}^{\mu }\{x^\alpha L_n^{(\alpha )}(x)\}= & {} h^{\alpha ,-\mu }_n\,x^{\alpha +\mu } L_n^{(\alpha +\mu )}(x),\quad \alpha >-1; \end{aligned}$$
(2.42)
$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{\mu }\{x^{\alpha } L_n^{(\alpha )}(x)\}= & {} h^{\alpha ,\mu }_n\, x^{\alpha -\mu } L_n^{(\alpha -\mu )}(x),\quad \alpha >\mu -1, \end{aligned}$$
(2.43)

and

$$\begin{aligned}&{}_{x}\mathrm{I}_{\infty }^{\mu }\{e^{-x} L_n^{(\alpha )}(x)\}= e^{-x} L_n^{(\alpha -\mu )}(x), \quad \alpha >\mu -1; \end{aligned}$$
(2.44)
$$\begin{aligned}&{{}_{x}}\mathrm{D}_{\infty }^{\mu }\{ e^{-x} L_n^{(\alpha )}(x)\}=e^{-x} L_n^{(\alpha +\mu )} (x),\quad \alpha >-1. \end{aligned}$$
(2.45)

Moreover, we have that for \(k\in {\mathbb {N}}\) and \(\alpha >k-1\),

$$\begin{aligned} {{}_{}}\mathrm{D}_{}^{k} \big \{x^\alpha e^{-x} L_{n}^{(\alpha )}(x)\big \}=\frac{\Gamma (n+k+1)}{\Gamma (n+1)} x^{\alpha -k}L^{(\alpha -k)}_{n+k}(x)e^{-x}. \end{aligned}$$
(2.46)

3 Generalized Laguerre Functions

In this section, we introduce the generalized Laguerre functions (GLFs), and study its approximation properties. In what follows, the operators \({}_{0}\mathrm{I}_{x}^{\mu ,\lambda }, {{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda }\) on the half line should be understood as 0 in place of \(-\infty \) in (2.11) and (2.24)–(2.25).

3.1 Definition and Properties

We first introduce the GLFs and their associated properties related to tempered fractional integrals/derivatives.

Definition 3.1

For real \(\alpha \in {\mathbb {R}}\) and \(\lambda >0,\) we define the GLFs as

$$\begin{aligned} {\mathcal {L}}^{(\alpha ,\lambda )}_{n}{(x)}:={\left\{ \begin{array}{ll} x^{-\alpha } e^{-\lambda x}\,{L}_{n}^{(-\alpha )}(2\lambda x),\quad \alpha <0,\\ e^{-\lambda x}\,{L}_{n}^{(\alpha )}(2\lambda x),\qquad \quad \, \alpha \ge 0, \end{array}\right. } \end{aligned}$$
(3.1)

for all \(x\in {\mathbb {R}}^+\) and \(n\in {\mathbb {N}}_0.\)

Remark 3.1

It’s noteworthy that Zhang and Guo [29] introduced the GLFs

$$\begin{aligned} \widetilde{\mathscr {L}}_l^{(\alpha ,\beta )}(x) ={\left\{ \begin{array}{ll} x^{-\alpha }e^{-\frac{\beta }{2}x}L_l^{(-\alpha )}(\beta x), \quad &{}\alpha \le -1,\;\; l\ge \bar{l}_\alpha =[-\alpha ],\\ e^{-\frac{\beta }{2}x}L_l^{(\alpha )}(x),&{}\alpha >-1,\;\; l\ge {\bar{l}}_\alpha =0, \end{array}\right. } \end{aligned}$$
(3.2)

where the scaling factor \(\beta >0.\) It is seen that we modified the definition in the range of \(0<\alpha <1\) (with \(\beta =2\lambda \)). This turns out to be essential for the numerical solution of FDEs of order \(\mu \in (0,1),\) as we shall see in the subsequent sections. \(\square \)

We next present the basic properties of GLFs. Firstly, one verifies readily from the orthogonality (2.36) and Definition 3.1 that for \(\alpha \in {\mathbb {R}}\) and \(\lambda >0,\)

$$\begin{aligned} \int _0^\infty {\mathcal {L}}^{(\alpha ,\lambda )}_{n}{(x)}{\mathcal {L}}^{(\alpha ,\lambda )}_{m}{(x)}\,x^{\alpha }dx =\gamma _n^{{|\alpha |},\lambda }\delta _{nm}, \;\;\; \gamma _n^{|\alpha |,\lambda } =\frac{\gamma _n^{|\alpha |}}{(2\lambda )^{|\alpha | +1}}, \end{aligned}$$
(3.3)

where \(\gamma _n^{|\alpha |}\) is defined in (2.36).

We have the following important (left) “tempered” fractional integral and derivative rules.

Lemma 3.1

For \(\mu ,\nu ,\lambda ,x \in {\mathbb {R}}^+_0,\) we have

$$\begin{aligned} {}_{0}\mathrm{I}_{x}^{\mu ,\lambda } {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}= & {} h^{\nu ,-\mu }_n{\mathcal {L}}^{(-\nu -\mu ,\lambda )}_{n}{(x)},\qquad \quad \end{aligned}$$
(3.4)
$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda } {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}= & {} h^{\nu ,\mu }_n{\mathcal {L}}^{(\mu -\nu ,\lambda )}_{n}{(x)},\quad \nu \ge \mu , \end{aligned}$$
(3.5)

and

$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{\mu +k,\lambda } {\mathcal {L}}^{(-\mu ,\lambda )}_{n}{(x)}=(-2\lambda )^kh^{\mu ,\mu }_n {\mathcal {L}}^{(k,\lambda )}_{n-k}{(x)},\quad n\ge k\in {\mathbb {N}}_0, \end{aligned}$$
(3.6)

where \(h^{a,b}_n\) is defined in (2.41).

Proof

We obtain from (2.11) and (2.24)–(2.25) (with replacing \(-\infty \) by 0) that

$$\begin{aligned} {}_{0}\mathrm{I}_{x}^{\mu ,\lambda }{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}=e^{-\lambda x} {}_{0}\mathrm{I}_{x}^{\mu } \{e^{\lambda x} {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}\}=e^{-\lambda x} {}_{0}\mathrm{I}_{x}^{\mu } \{ x^\nu L^{(\nu )}_n(2\lambda x)\}, \end{aligned}$$

and

$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda }{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}=e^{-\lambda x} {{}_{0}}\mathrm{D}_{x}^{\mu } \{e^{\lambda x} {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}\}=e^{-\lambda x} {{}_{0}}\mathrm{D}_{x}^{\mu } \{x^\nu L^{(\nu )}_n(2\lambda x)\}. \end{aligned}$$

Thus, from (2.9) and Lemma 2.2, we obtain (3.4)–(3.5).

Using (3.5) and the derivative relation (2.40) (with \(\alpha =\mu \)), we obtain

$$\begin{aligned} \begin{aligned} {{}_{0}}\mathrm{D}_{x}^{\mu +k,\lambda } {\mathcal {L}}^{(-\mu ,\lambda )}_{n}{(x)}&={{}_{0}}\mathrm{D}_{x}^{k,\lambda } {{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda } {\mathcal {L}}^{(-\mu ,\lambda )}_{n}{(x)}=e^{-\lambda x}{{}_{}}\mathrm{D}_{}^{k} \big \{e^{\lambda x} h^{\mu ,\mu }_n{\mathcal {L}}^{(0,\lambda )}_{n}{(x)}\big \}\\ {}&=h^{\mu ,\mu }_n\,e^{-\lambda x}{{}_{}}\mathrm{D}_{}^{k} \big \{L_{n}^{(0)}(2\lambda x)\big \}=(-2\lambda )^kh^{\mu ,\mu }_n \,L_{n-k}^{(k)}(2\lambda x)\,e^{-\lambda x}. \end{aligned} \end{aligned}$$

This leads to (3.6). \(\square \)

Similarly, we have the following rules of the (right) “tempered” fractional integrals and derivatives.

Lemma 3.2

For \( \mu ,\nu ,\lambda , x \in {\mathbb {R}}^+_0\), we have

$$\begin{aligned} \quad {}_{x}\mathrm{I}_{\infty }^{\mu ,\lambda }{\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}= & {} (2\lambda )^{-\mu }{\mathcal {L}}^{(\nu -\mu ,\lambda )}_{n}{(x)},\quad \nu \ge \mu , \end{aligned}$$
(3.7)
$$\begin{aligned} {{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda } {\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}= & {} (2\lambda )^{\mu }{\mathcal {L}}^{(\mu +\nu ,\lambda )}_{n}{(x)}.\quad \quad \quad \end{aligned}$$
(3.8)

Proof

Identities (3.7) and (3.8) can be easily derived from (2.9), (2.10) and Lemma 2.2. \(\square \)

We highlight the fractional derivative formulas, which play an important role in the forthcoming algorithm and analysis.

Theorem 3.1

Let \(k\in {\mathbb {N}}\) and \(k-\nu \le 0\),

$$\begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{k,\lambda } \big \{ {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}\big \}= & {} \frac{\Gamma (n+\nu +1)}{\Gamma (n+\nu -k+1)}~{\mathcal {L}}^{(k-\nu ,\lambda )}_{n}{(x)} , \end{aligned}$$
(3.9)
$$\begin{aligned} \qquad {{}_{x}}\mathrm{D}_{\infty }^{k,\lambda } \big \{ {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}\big \}= & {} (-1)^k\frac{\Gamma (n+k+1)}{\Gamma (n+1)} {\mathcal {L}}^{(k-\nu ,\lambda )}_{n+k}{(x)}.\qquad \end{aligned}$$
(3.10)

Proof

From Lemma 2.2 and relations

$$\begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{k,\lambda }u=e^{-\lambda x}{{}_{}}\mathrm{D}_{}^{k}\big \{e^{ \lambda x}u\big \},\quad {{}_{x}}\mathrm{D}_{\infty }^{k,\lambda }u=e^{\lambda x}(-1)^k{{}_{}}\mathrm{D}_{}^{k}\big \{e^{- \lambda x}u\big \}, \end{aligned}$$
(3.11)

we obtain that for \(k-\nu \le 0\),

$$\begin{aligned}\begin{aligned} {{}_{-\infty }}\mathrm{D}_{x}^{k,\lambda }&\big \{x^{\nu } {\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}\big \} =e^{-\lambda x}{{}_{}}\mathrm{D}_{}^{k}\big \{(2\lambda )^{-\nu }(2\lambda x)\ ^\nu L^{(\nu )}_n(2\lambda x)\big \}\\ \overset{(2.43)}{=}&\frac{\Gamma (n+1+\nu )}{\Gamma (n+\nu -k+1)} x^{\nu -k} L^{(\nu -k)}_n(2\lambda x)e^{-\lambda x} =\frac{\Gamma (n+1+\nu )}{\Gamma (n+\nu -k+1)}~{\mathcal {L}}^{(k-\nu ,\lambda )}_{n}{(x)}, \end{aligned}\end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {{}_{x}}\mathrm{D}_{\infty }^{k,\lambda } \big \{x^{\nu } {\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}\big \} =&e^{\lambda x}(-1)^k{{}_{}}\mathrm{D}_{}^{k}\big \{(2\lambda )^{-\nu }(2\lambda x) ^\nu L^{(\nu )}_n(2\lambda x)e^{-2\lambda x}\big \}\\ \overset{(2.46)}{=}&(-1)^k\frac{\Gamma (n+k+1)}{\Gamma (n+1)} x^{\nu -k} L^{(\nu -k)}_{n+k}(2\lambda x)e^{-\lambda x} \\=&(-1)^k\frac{\Gamma (n+k+1)}{\Gamma (n+1)}~{\mathcal {L}}^{(k-\nu ,\lambda )}_{n}{(x)}. \end{aligned}\end{aligned}$$
(3.12)

This ends the proof. \(\square \)

Another attractive property of GLFs is that they are eigenfunctions of Sturm–Liouville problem.

Theorem 3.2

Let \(s,\nu ,x\in {\mathbb {R}}^+_0\) and \(n\in {\mathbb {N}}_0\). Then,

$$\begin{aligned} \qquad x^{\nu }{{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }\{ x^{s-\nu } {{}_{0}}\mathrm{D}_{x}^{s,\lambda }\,{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}\}=\lambda _{n,-}^{s,\nu } \,{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)},\quad \nu -s\ge 0, \end{aligned}$$
(3.13)

and

$$\begin{aligned} x^{-\nu }{{}_{0}}\mathrm{D}_{x}^{s,\lambda }\{ x^{s+\nu } {{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }\,{\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}\}=\lambda _{n,+}^{s,\nu } \,{\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)},\qquad \qquad \, \end{aligned}$$
(3.14)

where the corresponding eigenvalues \(\lambda _{n,-}^{s,\nu }=(2\lambda )^s h_n^{\nu ,s}\) and \(\lambda _{n,+}^{s,\nu }=(2\lambda )^s h_n^{\nu +s,s}\).

Proof

Due to (3.5) and (3.8),

$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{s,\lambda } {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}=h^{\nu ,s}_n{\mathcal {L}}^{(s-\nu ,\lambda )}_{n}{(x)}, \quad {{}_{x}}\mathrm{D}_{\infty }^{s,\lambda } {\mathcal {L}}^{(\nu -s,\lambda )}_{n}{(x)}=(2\lambda )^{s}{\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}. \end{aligned}$$

It’s straightforward to obtain that

$$\begin{aligned}\begin{aligned} x^{\nu }&{{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }\{ x^{s-\nu } {{}_{0}}\mathrm{D}_{x}^{s,\lambda }\,{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}\} =h^{\nu ,s}_n x^{\nu }{{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }\{ x^{s-\nu } {\mathcal {L}}^{(s-\nu ,\lambda )}_{n}{(x)} \} \\ {}&=h^{\nu ,s}_n x^{\nu }{{}_{x}}\mathrm{D}_{\infty }^{s,\lambda } {\mathcal {L}}^{(\nu -s,\lambda )}_{n}{(x)} =(2\lambda )^s h_n^{\nu ,s} \,{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}. \end{aligned}\end{aligned}$$

Similarly, we have

$$\begin{aligned}\begin{aligned} x^{-\nu }&{{}_{0}}\mathrm{D}_{x}^{s,\lambda }\{ x^{s+\nu } {{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }\,{\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}\} =(2\lambda )^s x^{-\nu }{{}_{0}}\mathrm{D}_{x}^{s,\lambda }\{ x^{s+\nu } {\mathcal {L}}^{(s+\nu ,\lambda )}_{n}{(x)} \}\\&=(2\lambda )^s x^{-\nu }{{}_{0}}\mathrm{D}_{x}^{s,\lambda } {\mathcal {L}}^{(-\nu -s,\lambda )}_{n}{(x)}=(2\lambda )^s h_n^{\nu +s,s} \,{\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}. \end{aligned}\end{aligned}$$

This ends the derivation. \(\square \)

Remark 3.2

The above identities can be viewed as an extension of the standard Sturm–Liouville problem of generalized Laguerre functions (cf. (2.37)) to the tempered fractional derivative. We derive immediately from (3.13), (3.14) and the Stirling’s formula (see (3.23)) that for fixed s and \(\nu \),

$$\begin{aligned} \lambda _{n,-}^{s,\nu } =\lambda _{n,+}^{s,\nu }=O\big ((2\lambda n)^s\big ),\quad n\gg 1. \end{aligned}$$

When \(s\rightarrow 1\) and \(\lambda =1/2\), it recovers the O(n) growth of eigenvalues of the standard Sturm–Liouville problem. \(\square \)

3.2 Approximation by GLFs

3.2.1 Approximation by \(\big \{{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}:~\nu >0\big \}_{n=0}^\infty \)

Denote by \({\mathcal {P}}_N\) the set of all polynomials of degree at most N, and define the finite dimensional space

$$\begin{aligned} {\mathcal {F}}^{\nu ,\lambda }_N({\mathbb {R}}^+):=\big \{x^{\nu }e^{-\lambda x} p(x)\,:\, p\in {\mathcal {P}}_N\big \}, \quad N\in {\mathbb {N}}_0. \end{aligned}$$
(3.15)

Define the \(L_\omega ^2({\mathbb {R}}^+)\) with the inner product and norm:

$$\begin{aligned} (f,g)_{\omega }:=\int _{{\mathbb {R}}^+} f\,{\bar{g}}\, \omega \, \mathrm{d}x, \quad \Vert f\Vert _{\omega }^2=(f,f)_{\omega }, \end{aligned}$$
(3.16)

where \(\omega (x)\) be a generic weight function and \({\bar{g}}\) is the conjugate of the function g. In particular, we omit \(\omega \) when \(\omega \equiv 1.\)

To characterize the approximation errors, we define the non-uniformly weighted Sobolev space

$$\begin{aligned} A_{\nu ,\lambda }^m({\mathbb {R}}^+):=\Big \{u\in L^2_{\omega ^{-\nu }}({\mathbb {R}}^+): {{}_{0}}\mathrm{D}_{x}^{\nu +k,\lambda } u \in L^2_{\omega ^{k}}({\mathbb {R}}^+),\;k=0,\ldots ,m\Big \},\quad m\in \mathbb {N}_0, \end{aligned}$$
(3.17)

equipped with the norm and semi-norm

$$\begin{aligned} \Vert u\Vert _{A_{\nu ,\lambda }^m}:=\Big (\Vert u\Vert ^2_{\omega ^{-\nu }} +\sum _{k=0}^{m}\Vert {{}_{0}}\mathrm{D}_{x}^{\nu +k,\lambda }u\Vert ^2_{\omega ^{k}}\Big )^{{1}/{2}}, \quad |u|_{A_{\nu ,\lambda }^m}:=\Vert {{}_{0}}\mathrm{D}_{x}^{\nu +m,\lambda }u\Vert _{\omega ^{m}}, \end{aligned}$$
(3.18)

where the weight function \(\omega ^{a}(x)=x^a.\)

Consider the orthogonal projection \(\pi _N^{-\nu ,\lambda }:\,{L^2_{\omega ^{-\nu }}}({\mathbb {R}}^+)\rightarrow \mathcal {F}^{\nu ,\lambda }_N({\mathbb {R}}^+)\) defined by

$$\begin{aligned} (\pi _N^{-\nu ,\lambda } u-u, ~\phi )_{\omega ^{-\nu }}=0,\quad \forall \phi \in {\mathcal {F}}^{\nu ,\lambda }_N({\mathbb {R}}^+). \end{aligned}$$
(3.19)

Then, by the orthogonality (3.3), u and its \(L^2\)-orthogonal projection can be expanded as

$$\begin{aligned} u(x)=\sum _{n=0}^\infty ~{\hat{u}}_n {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)},\quad (\pi _N^{-\nu ,\lambda } u)(x)=\sum _{n=0}^N ~{\hat{u}}_n {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}, \end{aligned}$$
(3.20)

where

$$\begin{aligned} {\hat{u}}_n=\big (u,~{\mathcal L}_n^{(-\nu ,\lambda )}\big )_{\omega ^{-\nu }}\big /\gamma ^{\nu ,\lambda }_n. \end{aligned}$$

Theorem 3.3

For \(\lambda , \nu >0\), we have that for any \(u\in A^m_{\nu ,\lambda }({\mathbb {R}}^+) \) with \(m\le N+1\),

$$\begin{aligned} \Vert \pi _N^{-\nu ,\lambda } u-u\Vert _{\omega ^{-\nu }}\le ~c~(2\lambda N)^{-\frac{\nu +m}{2}} ~\Vert {{}_{0}}\mathrm{D}_{x}^{\nu +m,\lambda }u\Vert _{\omega ^{m}}, \end{aligned}$$
(3.21)

and for any \(k\le m,\)

$$\begin{aligned} \big \Vert {{}_{0}}\mathrm{D}_{x}^{\nu +k,\lambda }\big (\pi _N^{-\nu ,\lambda } u-u\big )\big \Vert _{\omega ^{k}}\le ~c~({2\lambda }N)^{\frac{k-m}{2}} ~\Vert {{}_{0}}\mathrm{D}_{x}^{\nu +m,\lambda }u\Vert _{\omega ^{m}}, \end{aligned}$$
(3.22)

where \(c\approx 1\) for large N.

Proof

By (3.20), we have

$$\begin{aligned} (u-\pi _N^{-\nu ,\lambda } u)(x)=\sum _{n=N+1}^\infty \,{\hat{u}}_n\, {\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}. \end{aligned}$$

By the orthogonality (3.3) and (3.6),

$$\begin{aligned} \big \Vert {{}_{0}}\mathrm{D}_{x}^{\nu +k,\lambda }{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{}\big \Vert ^2_{\omega ^{k}}=(-2\lambda ) ^{2k}\,(h^{\nu ,\nu }_n)^2\int _{0}^\infty \big (L^{(k)}_{n-k}(2\lambda x)\big )^2\,e^{-2\lambda x}{\omega ^{k}}(x)\mathrm{d}x=(d_{n,k}^{\nu ,\lambda })^2\gamma _{n-k}^{k,\lambda }, \end{aligned}$$

where we denoted \(d_{n,k}^{\nu ,\lambda }:=(2\lambda )^k\,h^{\nu ,\nu }_n\) and used the fact:

$$\begin{aligned} \int _0^\infty L^{(k)}_{n-m}(2\lambda x)L^{(k)}_{n-k}(2\lambda x)\,e^{-2\lambda x} \omega ^{k}dx=\frac{\gamma _{n-k}^{k}}{(2\lambda )^{k+1}} \delta _{km}=\gamma _{n-k}^{k,\lambda }\delta _{km}, \end{aligned}$$

Thus we can obtain

$$\begin{aligned}\begin{aligned}&\Vert \pi _N^{-\nu ,\lambda } u-u\Vert ^2_{\omega ^{-\nu }} =\sum _{n=N+1}^\infty ({\hat{u}}_n)^2\gamma _{n}^{\nu ,\lambda }, \quad \big |\pi _N^{-\nu ,\lambda } u-u\big |^2_{A^k_{\nu ,\lambda }} =\sum _{n=N+1}^\infty ({\hat{u}}_nd_{n,k}^{\nu ,\lambda })^2\gamma _{n-k} ^{k,\lambda }, \\&\big |u\big |^2_{A^m_{\nu ,\lambda }} =\sum _{n=m}^\infty ({\hat{u}}_nd_{n,m}^{\nu ,\lambda })^2\gamma _{n-m}^{m,\lambda }. \end{aligned}\end{aligned}$$

Then one verifies readily that

$$\begin{aligned}\begin{aligned} \Vert \pi _N^{-\nu ,\lambda } u-u\Vert ^2_{\omega ^{-\nu }}&\le \frac{\gamma _{N+1} ^{\nu ,\lambda }}{(d_{N+1,m}^{\nu ,\lambda })^2\gamma _{N+1-m}^{m,\lambda }} \big |u\big |^2_{A^m_{\nu ,\lambda }},\\ \quad \big |\pi _N^{-\nu ,\lambda } u-u\big |^2_{A^k_{\nu ,\lambda }}&\le \left( \frac{d_{N+1,k}^ {\nu ,\lambda }}{d_{N+1,m}^{\nu ,\lambda }}\right) ^2\frac{\gamma _{N+1-k}^{k, \lambda }}{\gamma _{N+1-m}^{m,\lambda }}\big |u\big |^2_{A^m_{\nu ,\lambda }}. \end{aligned}\end{aligned}$$

Recall the property of the Gamma function (see [1, (6.1.38)]):

$$\begin{aligned} \Gamma (x+1)=\sqrt{2\pi } x^{x+1/2}\exp \Big (-x+\frac{\theta }{12x}\Big ),\quad \forall \, x>0,\;\;0<\theta <1. \end{aligned}$$
(3.23)

One can then obtain that for any constants a, b,  and for \(n\ge 1, \) \(n+a>1\) and \(n+b>1,\)

$$\begin{aligned} \frac{\Gamma (n+a)}{\Gamma (n+b)}\le \nu _n^{a,b} n^{a-b}, \end{aligned}$$
(3.24)

where

$$\begin{aligned} \nu _n^{a,b}=\exp \Big (\frac{a-b}{2(n+b-1)}+\frac{1}{12(n+a-1)} +\frac{(a-b)^2}{n}\Big ). \end{aligned}$$
(3.25)

Therefore,

$$\begin{aligned} \begin{aligned} \frac{\gamma _{N+1}^{\nu ,\lambda }}{(d_{N+1,m}^{\nu ,\lambda })^2 \gamma _{N+1-m}^{m,\lambda }}&=\frac{\Gamma (N+2-m)}{(2\lambda ) ^{\nu +m}\Gamma (N+2+\nu )} \le (2\lambda )^{-\nu -m} \nu _n^{2-m,2+\nu } N^{-\nu -m}, \\ \left( \frac{d_{N+1,k}^{\nu ,\lambda }}{d_{N+1,m}^{\nu ,\lambda }}\right) ^2\frac{\gamma _{N+1-k}^{k,\lambda }}{\gamma _{N+1-m}^{m,\lambda }}&=\frac{(2\lambda )^{k}\Gamma (N+2-m)}{(2\lambda )^{m}\Gamma (N+2-k)} <(2\lambda )^{k-m} \nu _n^{2-m,2-k} N^{k-m}, \end{aligned}\end{aligned}$$
(3.26)

where \(\nu _n^{2-m,2+\nu }\approx 1\) and \(\nu _n^{2-m,2-k}\approx 1\) for fixed m and \(n\ge N\gg 1 \). Then (3.21)–(3.22) follow. \(\square \)

3.2.2 Approximation by \(\big \{{\mathcal {L}}^{(\nu ,\lambda )}_{n}{(x)}: \nu \ge 0\big \}_{n=0}^\infty \)

Introduce the non-uniformly weighted Sobolev space:

$$\begin{aligned} B_{\nu ,\lambda }^r({\mathbb {R}}^+):=\Big \{u\in L^2_{\omega ^{\nu }}({\mathbb {R}}^+): {{}_{x}}\mathrm{D}_{\infty }^{s,\lambda } u \in L^2_{\omega ^{\nu +s}}({\mathbb {R}}^+),\;0\le s\le r\Big \},\quad r\in {\mathbb {R}}^+_0, \end{aligned}$$
(3.27)

endowed with the norm and semi-norm

$$\begin{aligned} \Vert u\Vert _{B_{\nu ,\lambda }^r}:=\Big (\Vert u\Vert ^2_{\omega ^{\nu }}+|u|^2_{B_{\nu , \lambda }^r}\Big )^{{1}/{2}},\quad |u|_{B_\nu ^r}:=\Vert {{}_{x}}\mathrm{D}_{\infty }^{\nu +r,\lambda }u\Vert _{\omega ^{\nu +r}}. \end{aligned}$$
(3.28)

Consider the orthogonal projection \(\Pi _N^{\nu ,\lambda }:~{L^2_{\omega ^{\nu }}}({\mathbb {R}}^+)\rightarrow {\mathcal {F}}^{0,\lambda }_N({\mathbb {R}}^+),\) defined by

$$\begin{aligned} \big (\Pi _N^{\nu ,\lambda } u-u, ~\phi \big )_{\omega ^{\nu }}=0,\quad \forall \phi \in {\mathcal {F}}^{0,\lambda }_N({\mathbb {R}}^+),\quad \nu >-1. \end{aligned}$$
(3.29)

Theorem 3.4

Let \(\lambda ,r ,\nu >0\). For any \(u\in B^r_{\nu ,\lambda }({\mathbb {R}}^+) \) with \(0\le s\le r\le N,\) we have

$$\begin{aligned} \big \Vert {{}_{x}}\mathrm{D}_{\infty }^{s,\lambda } \big \{\Pi _N^{\nu ,\lambda } u-u\big \}\big \Vert _{\omega ^{\nu +s}}\le ~c~({2\lambda }{N})^{\frac{s-r}{2}} ~\Vert {{}_{x}}\mathrm{D}_{\infty }^{r,\lambda }u\Vert _{\omega ^{\nu +r}}, \end{aligned}$$
(3.30)

where \(c\approx 1\) for large N.

Proof

Note that by definition,

$$\begin{aligned} u-\Pi _N^{\nu ,\lambda }u =\sum _{n=N+1}^\infty ~{\hat{u}}_n {\mathcal L}_n^{(\nu ,\lambda )}(x),\quad {\hat{u}}_n=\big (u,~ {\mathcal L}_n^{(\nu ,\lambda )}\big )_{\omega ^{\nu }}\big /\gamma ^{\nu ,\lambda }_n. \end{aligned}$$

Then by (3.8), and the orthogonality,

$$\begin{aligned} \Vert {{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }{\mathcal {L}}^{(\nu ,\lambda )}_{n}{}\Vert ^2_{\omega ^{\nu +s}} =\Vert (2\lambda )^s{\mathcal {L}}^{(\nu +s,\lambda )}_{n}{}\Vert ^2_{\omega ^{\nu +s}} =(2\lambda )^{2s}\gamma _{n}^{\nu +s,\lambda }, \end{aligned}$$

we can derive

$$\begin{aligned}\begin{aligned} \big |\Pi _N^{\nu ,\lambda }u-u\big |^2_ {B^s_{\nu ,\lambda }}&=\Big \Vert \sum _{n=N+1}^\infty {\hat{u}}_n (2\lambda )^s{\mathcal {L}}^{(\nu +s,\lambda )}_{n}{} \Big \Vert ^2_{\omega ^{\nu +s}}=\sum _{n=N+1}^\infty ({\hat{u}}_n)^2(2\lambda ) ^{2s}\gamma _{n}^{\nu +s,\lambda },\\ \big |u\big |^2_{B^r_{\nu +r,\lambda }}&= \Big \Vert \sum _{n=0}^\infty {\hat{u}}_n(2\lambda )^r {\mathcal {L}}^{(\nu +r,\lambda )}_{n}{}\Big \Vert ^2_{\omega ^{\nu +r}}=\sum _{n=0}^\infty ({\hat{u}}_n) ^2(2\lambda )^{2r}\gamma _{n}^{\nu +r,\lambda }. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned}\begin{aligned} \big |\Pi _N^{\nu ,\lambda }u-u\big |^2_{B^s_{\nu ,\lambda }}&=\sum _{n=N+1}^ \infty {\hat{u}}_n^2(2\lambda )^{2s}\gamma _{n}^{\nu +s,\lambda } \le (2\lambda )^{2s-2r}\frac{\gamma _{N+1}^{\nu +s,\lambda }}{\gamma _{N+1}^{\nu +r,\lambda }}\sum _{n=N+1}^\infty {\hat{u}}_n^2(2\lambda ) ^{2r}\gamma _{n}^{\nu +r,\lambda }, \end{aligned}\end{aligned}$$

where by (3.24)–(3.25) and an argument similar to (3.26), we obtain

$$\begin{aligned} \dfrac{\gamma _{N+1}^{\nu +s,\lambda }}{\gamma _{N+1}^{\nu +r,\lambda }}=\dfrac{(2\lambda )^r \Gamma (N+\nu +s+2)}{(2\lambda )^s \Gamma (N+\nu +r+2)}\le c ({2\lambda })^{r-s}N^{s-r}. \end{aligned}$$

Consequently, we have

$$\begin{aligned} \Vert {{}_{x}}\mathrm{D}_{\infty }^{s,\lambda } \big \{\Pi _N^{\nu ,\lambda } u-u\big \}\Vert _{\omega ^{\nu +s}}\le ~c\, ({2\lambda }N)^{\frac{s-r}{2}} \,|u|_{B^r_{\nu ,\lambda }}. \end{aligned}$$

This ends the proof. \(\square \)

3.3 A Model Problem and Numerical Results

In what follows, we consider the GLF approximation to a model tempered fractional equation of order \(s\in [k-1,k)\) with \(k\in \mathbb {N}:\)

$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{s,\lambda }u(x)=f(x), \;\; x\in {\mathbb {R}}^+,\;\; \lambda >0; \;\; u^{(j)}(0)=0,\quad j=0,1,\ldots ,k-1, \end{aligned}$$
(3.31)

where \(f\in L^2({\mathbb {R}}^+)\) is a given function. Using the fractional derivative relation (2.7), one can find

$$\begin{aligned} u(x)={}_{0}\mathrm{I}_{x}^{s,\lambda }f(x)+\sum \limits _{i=1}^kc_i\, x^{s-i}e^{-\lambda x}, \end{aligned}$$

where \(\{c_i\}\) can be determined by the conditions at \(x=0.\) In fact, we have all \(c_i=0,\) and

$$\begin{aligned} u(x)={}_{0}\mathrm{I}_{x}^{s,\lambda }f(x)=\frac{e^{-\lambda x}}{\Gamma (s)} \int _0^x (x-\tau )^{s-1} e^{\lambda \tau } f(\tau )\mathrm{d}\tau = \frac{x^s}{\Gamma (s)}\int _0^1 (1-t)^{s-1} e^{-\lambda (1-t)x}f(xt) \mathrm{d}t. \end{aligned}$$
(3.32)

We see that if f(x) is smooth, then \(u(x)=x^s F(x),\) where F(x) is smoother than f(x). With this understanding, we construct the GLF Petrov–Galerkin approximation as: find \(u_N\in {\mathcal {F}}^{s,\lambda }_N({\mathbb {R}}^+)\) (defined in (3.15)) such that

$$\begin{aligned} ({{}_{0}}\mathrm{D}_{x}^{s,\lambda } u_N,v_N)=(f,v_N), \quad \forall \, v_N\in {\mathcal {F}}^{0,\lambda }_N({\mathbb {R}}^+). \end{aligned}$$
(3.33)

We expand f and \(u_N\) as

$$\begin{aligned} f(x)=\sum _{n=0}^\infty ~\hat{f}_n {\mathcal {L}}^{(0,\lambda )}_{n}{(x)}, ~\quad u_N=\sum _{n=0}^N ~{\hat{u}}_n {\mathcal {L}}^{(-s,\lambda )}_{n}{(x)} . \end{aligned}$$
(3.34)

Using the derivative relation (3.5), we find immediately that \(\hat{u}_n={\hat{f}_n}/{h_n^{s,s}}\) for \(n=0,1,\ldots ,N\), which also implies \({{}_{0}}\mathrm{D}_{x}^{s,\lambda } u_N=\pi ^{0,\lambda }_N f.\)

Moreover, we can show that the numerical solution \(u_N\) is precisely the orthogonal projection in the following sense:

$$\begin{aligned} ( u_N-u\,,\,w_N)_{\omega ^{-s}}=0,\quad \forall \, w_N\in {\mathcal {F}}^{s,\lambda }_N({\mathbb {R}}^+). \end{aligned}$$
(3.35)

To this end, we first show

$$\begin{aligned} ( u_N-u\,,\,{{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }v_N)=({{}_{0}}\mathrm{D}_{x}^{s,\lambda } u_N-{{}_{0}}\mathrm{D}_{x}^{s,\lambda } u,v_N)=0,\quad \forall \, v_N\in {\mathcal {F}}^{0,\lambda }_N({\mathbb {R}}^+). \end{aligned}$$
(3.36)

Indeed, thanks to \(u^{(j)}(0)=0\) for \(j=0,\ldots ,k-1\), we have

$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{s,\lambda }\{u_N-u\}=e^{-\lambda x}{{}_{0}}\mathrm{D}_{x}^{s} \{e^{\lambda x} (u_N-u)\}=e^{-\lambda x}{}_{0}\mathrm{I}_{x}^{k-s}{{}_{0}}\mathrm{D}_{x}^{k} \{e^{\lambda x} (u_N-u)\}. \end{aligned}$$

Then,

$$\begin{aligned}\begin{aligned}&\left( {{}_{0}}\mathrm{D}_{x}^{s,\lambda } u_N-{{}_{0}}\mathrm{D}_{x}^{s,\lambda } u\,,\,v_N\right) =\left( {}_{0}\mathrm{I}_{x}^{k-s}{{}_{0}}\mathrm{D}_{x}^{k} \{e^{\lambda x} (u_N-u)\},e^{-\lambda x}v_N\right) \\ {}&\qquad =\left( e^{\lambda x} (u_N-u)\,,\,(-1)^k\mathrm{D}^{k}{}_{x}\mathrm{I}_{\infty }^{k-s,\lambda }v_N\right) =\left( u_N-u\,,\,{{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }v_N\right) , \end{aligned}\end{aligned}$$

so (3.36) is valid. In addition, thanks to Lemma 2.2 and (2.10), we have

$$\begin{aligned} {{}_{x}}\mathrm{D}_{\infty }^{s,\lambda }{\mathcal {L}}^{(0,\lambda )}_{n}{(x)}=e^{\lambda x}{{}_{x}}\mathrm{D}_{\infty }^{s}\big \{e^{-2\lambda x}L^{(0)}_{n}(2\lambda {x})\big \}=(2\lambda )^s e^{-\lambda x}L^{(s)}_{n}(2\lambda {x})=(2\lambda )^sx^{-s}{\mathcal {L}}^{(-s,\lambda )}_{n}{(x)}. \end{aligned}$$

Hence, (3.35) is valid.

Thanks to (3.35), we derive from Theorem 3.3 the following estimate where the convergence rate only depends on the regularity of the source term.

Theorem 3.5

Let u and \(u_N\) be respectively the solutions of (3.31) and (3.33). Then for \({{}_{0}}\mathrm{D}_{x}^{m,\lambda }f\in L^2_{\omega ^m}(I)\) with \(m\in {\mathbb {N}}_0,\) we have

$$\begin{aligned} \Vert u-u_N\Vert _{\omega ^{-s}}\le \,c\,(2\lambda N)^{-\frac{s+m}{2}} \,\Vert {{}_{0}}\mathrm{D}_{x}^{s+m,\lambda }u\Vert _{\omega ^{m}}=c\,(2\lambda N)^{-\frac{s+m}{2}}\,\Vert {{}_{0}}\mathrm{D}_{x}^{m,\lambda }f\Vert _{\omega ^{m}}, \end{aligned}$$
(3.37)

where \(c\approx 1\) for large N.

We provide some numerical results to illustrate the convergence behaviour. We take \(f(x)= e^{-x}\sin x\) and then evaluate the exact solution by (3.32). Note that as \({{}_{0}}\mathrm{D}_{x}^{m,\lambda }f=e^{-\lambda x} {{}_{}}\mathrm{D}_{}^{m}\{e^{\lambda x}f\}\), a direct calculation leads to

$$\begin{aligned} e^{-\lambda x}{{}_{}}\mathrm{D}_{}^{m}\{e^{\lambda x} f\}=e^{-\lambda x}\sum _{k=0}^m {m \atopwithdelims (){k}} \lambda ^{m-k}e^{\lambda x} {{}_{}}\mathrm{D}_{}^{k}f=\sum _{k=0}^m {m \atopwithdelims (){k}} \lambda ^{m-k} {{}_{}}\mathrm{D}_{}^{k}f. \end{aligned}$$

We infer from (3.37) that the spectral accuracy can be achieved by the GLF approximation. Indeed, we observe from Fig. 1 such a convergence behaviour.

Fig. 1
figure 1

Convergence of the GLF approximation to (3.31) with \(f(x)=e^{-x} \sin x\,.\)

Full size image

4 Application to Tempered Fractional Diffusion Equation on the Half Line

In this section, we apply the GLFs to solve a tempered fractional diffusion equation on the half line.

4.1 The Tempered Fractional Diffusion Equation on the Half Line

Consider the tempered fractional diffusion equation of order \(\mu \in (0,1)\) on the half line:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \partial _t u(x,t)+{{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda }u(x,t)-\lambda ^\mu u(x,t) =f(x,t),\quad &{}(x,t)\in {\mathbb {R}}^+\times (0,T],\\ u(0,t)=0,\quad \lim \limits _{x\rightarrow \infty }u(x,t)=0,\quad &{} 0<t\le T, \\ u(x,0)=u_0(x), \quad &{}x\in {\mathbb {R}}^+. \end{array}\right. } \end{aligned} \end{aligned}$$
(4.1)

This equation models the particles jumping on the half line \({\mathbb {R}}^+\) with the probability density function (see [22, (8)]):

$$\begin{aligned} f_{\varepsilon }(x)=C^{-1}_{\varepsilon }x^{-\mu -1}e^{-\lambda x}\mathbf {1}_{({\varepsilon ,\infty })}(x),\quad 0<\mu <1. \end{aligned}$$

Remark 4.1

Note that (4.1) can be viewed as the TFDE (1.3) on the half line with

$$\begin{aligned} \partial _{+,x}^{\mu ,\lambda } u={{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda }u-\lambda ^\mu u,\quad 0<\mu <1. \end{aligned}$$

Indeed, we can show that for \(\mu \in (0,1)\) and real \(\lambda >0\),

$$\begin{aligned} {{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda }u=e^{-\lambda x}{{}_{0}}\mathrm{D}_{x}^{\mu }\big \{e^{\lambda x}{{u}(x)}\big \}=e^{-\lambda x}{{}_{-\infty }}\mathrm{D}_{x}^{\mu }\big \{e^{\lambda x}{\tilde{u}(x)}\big \},\quad x\in {\mathbb {R}}^+, \end{aligned}$$

where \({\tilde{u}}=u\) for \(x\in {\mathbb {R}}^+\) and \(\tilde{u}=0\) for \(x\in (-\infty ,0)\). Moreover, we have

$$\begin{aligned}\begin{aligned} {{\mathscr {F}}}\big [e^{-\lambda x}{{}_{-\infty }}\mathrm{D}_{x}^{\mu }\big \{e^{\lambda x}{\tilde{u}(x)}\big \}\big ](\omega )=&\int _{{\mathbb {R}}} {{}_{}}\mathrm{D}_{}^{}{}_{-\infty }\mathrm{I}_{x}^{1-\mu }\big \{e^{\lambda x}{\tilde{u}(x)}\big \}~e^{-(\lambda +\mathrm{i}\omega ) x}\mathrm{d} x\\ =(\lambda +\mathrm{i}\omega )&\int _{{\mathbb {R}}} {}_{-\infty }\mathrm{I}_{x}^{1-\mu }\big \{e^{\lambda x}{\tilde{u}(x)}\big \}~e^{-(\lambda +\mathrm{i}\omega ) x}\mathrm{d} x\\ {=}(\lambda +\mathrm{i}\omega )&\int _{{\mathbb {R}}}e^{\lambda x} {\tilde{u}(x)}~{}_{x}\mathrm{I}_{\infty }^{1-\mu }e^{-(\lambda +\mathrm{i}\omega ) x}\mathrm{d} x\\ =(\lambda +\mathrm{i}\omega )^\mu&{{\mathscr {F}}}[\tilde{u}](\omega ) \overset{(2.20)}{=}{{\mathscr {F}}}\big [{{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda }{{\tilde{u}(x)}}\big ](\omega ). \end{aligned} \end{aligned}$$

This implies \({\tilde{u}}\in W^{\mu ,2}_\lambda ({\mathbb {R}})\) and the extended tempered fractional derivative \({{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda }u\) can be understood in the sense of the original definition in [22].

4.2 Spectral-Galerkin Scheme

Observe from Remark 4.1 that the identities (2.29) are also valid on \({\mathbb {R}}^+\). A weak form of the problem (4.1) is to find \(u(\cdot ,t)\in W^{\mu /2,2}_{\lambda }({\mathbb {R}}^+)\) such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \big (\partial _tu(\cdot , t),v\big )+a_{\mu ,\lambda }\big (u(\cdot , t),v\big ) =\big (f(\cdot , t),v\big ), \quad \forall v\in W^{\mu /2,2}_{\lambda } ({\mathbb {R}}^+), ~0<t\le T,\\ \big ( u(\cdot ,0),v\big )=(u_0,v), \quad \forall v\in W^{\mu /2,2}_{\lambda } ({\mathbb {R}}^+) \end{array}\right. } \end{aligned}$$
(4.2)

where the space \(W^{\mu /2,2}_{\lambda }({\mathbb {R}}^+)\) consists of all functions whose zero extensions are in \( W_\lambda ^{\mu /2,2}({\mathbb {R}})\) (cf. (2.22)), and the bilinear form reads

$$\begin{aligned} \begin{aligned} a_{\mu ,\lambda }(u,v):&=({{}_{0}}\mathrm{D}_{x}^{\mu /2,\lambda }u,{{}_{x}}\mathrm{D}_{\infty }^{\mu /2,\lambda }v) -\lambda ^\mu (u,v). \end{aligned} \end{aligned}$$
(4.3)

The semi-discrete Galerkin approximation scheme is to find \(u_N(\cdot ,t)\in {\mathcal {F}}^{\nu ,\lambda }_N({\mathbb {R}}^+) \) such that

$$\begin{aligned} \big (\partial _tu_N(\cdot , t),v\big )+a_{\mu ,\lambda }\big (u_N(\cdot , t),v\big )=\big (f(\cdot , t),v\big ), \quad \forall v\in {\mathcal {F}}^{\nu ,\lambda }_N({\mathbb {R}}^+), \end{aligned}$$
(4.4)

with

$$\begin{aligned} u_N(x,0)=\pi _N^{-\nu ,\lambda }u_0(x) =\sum _{n=0}^{N}c_{0,n}\,{\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}, \end{aligned}$$

where the projection operator \(\pi _N^{-\nu ,\lambda }\) is defined in (3.19) with \(\max \big \{0,\mu -1/2\big \}<\nu \le 1.\) Note that the boundary condition \(u(0,t)=0\) is automatically met, and we choose the parameter \(\nu \) is to better fit the singularity behavior of the solution near \(x=0\).

Remark 4.2

We show in next section (see Theorem 5.1 and Remark 5.1) the positivity of the bilinear form, that is, for any \(0\not =v\in W^{\mu /2,2}_{\lambda }({\mathbb {R}}^+)\), \(a_{\mu ,\lambda }(v,v)>0\). Then we can show the stability of the solutions of (4.2) and (4.4) as in (5.9) (with \({\mathbb {R}}^+\) in place of \({\mathbb {R}}\)). Moreover, we can conduct the error analysis of the semi-discrete scheme by using the approximation results in Sect. 3, and following a standard argument for usual diffusion equations. \(\square \)

4.3 Numerical Algorithm

Now, set

$$\begin{aligned} u_N(x,t)=\sum _{n=0}^{N}c_n(t)\, \varphi _{n}({x}), \quad \varphi _{n}({x}):={\mathcal {L}}^{(-\nu ,\lambda )}_{n}{(x)}. \end{aligned}$$
(4.5)

We derive from the scheme (4.4) that

$$\begin{aligned} \mathbf {M}\frac{d}{dt} \mathbf {\mathbf {c}}(t)+{\mathbf {A}}\mathbf {\mathbf {c}}(t)=\mathbf {\mathbf {f}}(t); \quad \mathbf {\mathbf {c}}(0)=\mathbf {\mathbf {c}}_0. \end{aligned}$$
(4.6)

where for fixed \(t>0\), vectors

$$\begin{aligned} \begin{aligned}&\mathbf {\mathbf {c}}(t)=\big (c_0(t),c_1(t),\ldots ,c_N(t)\big )^T, \quad \mathbf {\mathbf {{c}}}_0=\big (c_{0,0}(t),c_{0,1}(t),\ldots c_{0,N}(t)\big )^T, \\&\mathbf {\mathbf {f}}(t)=\big (f_0(t),f_1(t),\ldots f_N(t)\big )^T, \quad f_n(t)=(f,\varphi _{n}),\quad {0\le n\le N}. \end{aligned}\end{aligned}$$
(4.7)

Note that for any \(u,v\in {\mathcal {F}}^{\nu ,\lambda }_N({\mathbb {R}}^+)\), there exists

$$\begin{aligned} ({{}_{0}}\mathrm{D}_{x}^{\mu /2,\lambda }u,{{}_{x}}\mathrm{D}_{\infty }^{\mu /2,\lambda }v)=({{}_{0}}\mathrm{D}_{x}^{\mu ,\lambda }u,v). \end{aligned}$$

The mass matrix \({\mathbf {M}}\) and the stiffness matrix \(\mathbf {S}\) can be computed by Laguerre-Gauss quadrature formula. In fact, by using the tempered fractional derivative relations (3.5), it’s straightforward to obtain that for \(m,n=0,1,2,\ldots ,N\),

$$\begin{aligned} \begin{aligned} \mathbf {M}_{mn}&=(\varphi _{n},\varphi _{m}) =\big ({\mathcal {L}}^{(-\nu ,\lambda )}_{n}{},{\mathcal {L}}^{(-\nu ,\lambda )}_{m}{}\big ),\\ {\mathbf {A}}_{mn}&=a_\mu (\varphi _{n},\varphi _{m}) =h^{\nu ,\mu }_n\big ({\mathcal {L}}^{(\mu -\nu ,\lambda )}_{n}{},{\mathcal {L}}^{(-\nu ,\lambda )}_{m}{}\big ) -\lambda ^\mu \mathbf {M}_{mn}, \end{aligned}\end{aligned}$$
(4.8)

where \(h^{\nu ,\mu }_n=\Gamma (n+1+\nu )/\Gamma (n+1+\nu -\mu )\) was defined in (2.41).

4.4 Numerical Results

Typically, we test three cases as follows.

  1. (i)

    Choose the exact solution to be \(u(x,t)= xe^{-\lambda x}\cos {(t)}\). By a direct calculation, the source term is given by

    $$\begin{aligned} f(x,t)=-xe^{-\lambda x}\sin (t)+\Big (\dfrac{\Gamma (2)}{\Gamma (2-\mu )}x^{1-\mu }-\lambda ^\mu x\Big )e^{-\lambda x}\cos {(t)}. \end{aligned}$$

    Figure 2 (left) illustrates that the error decays to zero rapidly for the spectral method built upon the GLF basis with \(\nu =-1\) and \(N=50\), and the third-order explicit Runge-Kutta method in time with \(\lambda =\mu =2/3\) and time stepping size \(h\in (10^{-3},10^{-1})\).

  2. (ii)

    Set \(f(x,t)=\cos (x)e^{-x}\sin (t),\) and choose \(\lambda , \mu \) as above. Figure 2 (right) verifies that the solution is singular even though f(x, t) is a smooth function. Here, we compare the error with an reference “exact” solution computed with \(N=100.\)

  3. (iii)

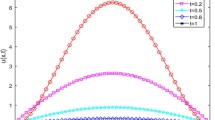
    Consider \(f(x,t)\equiv 0\), and let \(\mu =2/3,~\lambda =2/3\) in (4.1). Figure 3 (left) exhibits the evolution of the tempered fractional diffusion model with the initial distribution \(u_0(x)=xe^{-x}\). Figure 3 (right) shows the convergence rate of the scheme, where the error is compared with the reference solution \(u_{100}(x,t)\) with different \(\nu \) at \(t=10\).

Fig. 2
figure 2

Left \(u=x\exp (-\lambda x)\cos (t)\). Right \(f=\cos (x)\exp (-x)\sin (t)\)

Full size image
Fig. 3
figure 3

TFDE with \(f\equiv 0\), \(\lambda =2/3,~\mu =2/3.\) Left Profiles of the solutions at different time. Right Convergence behavior for different \(\nu \) at \(t=10.\)

Full size image

5 Tempered Fractional Diffusion Equation on the Whole Line

In this section, we present a multi-domain spectral-element method for the tempered fractional diffusion equation on the whole line originally proposed by [22].

5.1 Tempered Fractional Diffusion Equation

Consider the tempered fractional diffusion equation of order \(\mu \in (k-1,k),~k=1,2\) on the whole line:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u(x,t)+ \mathcal {A}^{\mu ,\lambda }_{p,q}u(x,t)=f(x,t), \quad x\in {\mathbb {R}},\;\; 0<t\le T,\\ u(x,0)=u_0(x),\;\; x\in {\mathbb {R}}; \quad \lim \limits _{|x|\rightarrow \infty } u(x,t)=0,\quad 0\le t\le T, \end{array}\right. }\end{aligned}$$
(5.1)

where p, q are nonnegative constants such that \(p+q=1,\) and \(f,u_0\) are given functions. Here, we denote

$$\begin{aligned} {\mathcal {A}}^{\mu ,\lambda }_{p,q}u=(-1)^{k-1} \big \{p\partial _{+,x}^{\mu ,\lambda }+q\partial _{-,x}^{\mu ,\lambda }\big \}u, \end{aligned}$$
(5.2)

where the involved fractional operators are

  1. (i)

    for \(0<\mu <1,\)

    $$\begin{aligned} \begin{aligned} \partial _{+,x}^{\mu ,\lambda }u={{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda }u-\lambda ^\mu u,\quad \partial _{-,x}^{\mu ,\lambda }u={{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda }u-\lambda ^\mu u; \end{aligned}\end{aligned}$$
    (5.3)
  2. (ii)

    for \(1<\mu <2\),

    $$\begin{aligned} \partial _{+,x}^{\mu ,\lambda }u={{}_{-\infty }}\mathrm{D}_{x}^{\mu ,\lambda }u-\mu \lambda ^{\mu -1}\partial _x u-\lambda ^\mu u,\quad \partial _{-,x}^{\mu ,\lambda }u={{}_{x}}\mathrm{D}_{\infty }^{\mu ,\lambda }u+\mu \lambda ^{\mu -1}\partial _x u-\lambda ^\mu u. \end{aligned}$$
    (5.4)

We refer to Definition 2.3 for the tempered derivative operators.

A weak form of (5.1) is to find \(u(\cdot , t)\in V_\lambda ^\mu ({\mathbb {R}})\) for \(0<t\le T,\) such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t (u(\cdot ,t), v)+ a^{\mu ,\lambda }_{p,q}(u(\cdot ,t),v) =(f(\cdot ,t),v),\quad \forall \, v\in V_\lambda ^\mu ({\mathbb {R}}),\; 0<t\le T,\\ (u(\cdot ,0), w)=(u_0,w),\;\;\; \forall \, w\in V_\lambda ^\mu ({\mathbb {R}}), \end{array}\right. } \end{aligned}$$
(5.5)

where \((\cdot , \cdot )\) is the inner product of \(L^2({\mathbb {R}})\) as before. The space \(V_\lambda ^\mu ({\mathbb {R}})\) and the bilinear form \(a^{\mu ,\lambda }_{p,q}(\cdot ,\cdot )\) are defined as

  1. (i)

    for \(0<\mu <1,\) and \(u,v\in V_\lambda ^\mu ({\mathbb {R}})= W_\lambda ^{\mu /2,2}({\mathbb {R}}) \cap L^2({\mathbb {R}})\) (cf. (2.22)),

    $$\begin{aligned} a^{\mu ,\lambda }_{p,q}(u,v)=p\big ({{}_{-\infty }}\mathrm{D}_{x}^{\mu /2,\lambda }u, {{}_{x}}\mathrm{D}_{\infty }^{\mu /2,\lambda } v\big )+q\big ({{}_{x}}\mathrm{D}_{\infty }^{\mu /2,\lambda }u,{{}_{-\infty }}\mathrm{D}_{x}^{\mu /2,\lambda }v\big ) -\lambda ^\mu \, (u,v),\ \end{aligned}$$
    (5.6)
  2. (ii)

    for \(1<\mu <2,\) and \(u,v\in V_\lambda ^\mu ({\mathbb {R}})= W_\lambda ^{\mu -1,2}({\mathbb {R}})\cap H^1({\mathbb {R}})\),

    $$\begin{aligned} \begin{aligned} a^{\mu ,\lambda }_{p,q}(u,v)=&-p({{}_{-\infty }}\mathrm{D}_{x}^{\mu -1,\lambda }u,{{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }v) -q({{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }u,{{}_{-\infty }}\mathrm{D}_{x}^{\mu -1,\lambda }v)\\&+\lambda ^\mu (u,v)+(p-q)\mu \lambda ^{\mu -1}(\partial _xu,v). \end{aligned} \end{aligned}$$
    (5.7)

Note that in (5.7), \({{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }u=\lambda u-\partial _x u\) (cf. (2.25)).

Importantly, we can show that the involved bilinear form is strictly positive, so the well-posedness of (5.5) folows.

Theorem 5.1

For any \(0\not =v \in V_\lambda ^\mu ({\mathbb {R}})\) with \(\mu \in (0,1)\cup (1,2)\) and \(\lambda >0,\) we have

$$\begin{aligned} a^{\mu ,\lambda }_{p,q}(v,v)>0. \end{aligned}$$
(5.8)

If \(u_0\in L^2({\mathbb {R}})\) and \(f\in L^2({\mathbb {R}}\times (0,T)),\) then the problem (5.5) has a unique solution \(u\in L^\infty (0,T; V_\lambda ^\mu ({\mathbb {R}}))\) such that

$$\begin{aligned} \Vert u(\cdot ,t)\Vert ^2_{L^2({\mathbb {R}})}\le e^{t}\Big (\Vert u_0\Vert ^2_{L^2({\mathbb {R}})} + \int _0^t \Vert f(\cdot , s)\Vert _{L^2({\mathbb {R}})}^2ds\Big ),\quad \forall \, 0\le t\le T, \end{aligned}$$
(5.9)

Proof

We first consider \(0<\mu <1.\) Using (2.20) and the Parseval’s identity (2.16), leads to

$$\begin{aligned} \big ({{}_{-\infty }}\mathrm{D}_{x}^{\mu /2,\lambda }v, {{}_{x}}\mathrm{D}_{\infty }^{\mu /2,\lambda } v\big )= & {} \int _{{\mathbb {R}}}(\lambda +\mathrm{i}\omega )^\mu \big |{\mathscr {F}}[v](\omega ) \big |^2 \mathrm{d}\omega \nonumber \\= & {} \int _{{\mathbb {R}}}(\lambda ^2+\omega ^2)^\frac{\mu }{2} e^{\mathrm{i}\mu \Theta (\omega )} \big |{\mathscr {F}}[v](\omega ) \big |^2 \mathrm{d}\omega \end{aligned}$$
(5.10)

where \(\Theta (\omega )\) is the argument of \(\lambda +\mathrm{i}\omega ,\) i.e.,

$$\begin{aligned} \Theta (\omega )=\arccos {(\lambda /\sqrt{\lambda ^2+\omega ^2})}, \;\; \mathrm{if}\;\; \omega >0,\quad \Theta (\omega )=-\arccos {(\lambda /\sqrt{\lambda ^2+\omega ^2})}, \;\; \mathrm{if}\;\; \omega <0. \end{aligned}$$
(5.11)

It is evident that \(\Theta (\omega )\) is odd in \(\omega .\) In fact, for real function v,  \(\big |{\mathscr {F}}[v](\omega ) \big |^2\) is an even function in \(\omega ,\) thanks to the property \({\mathscr {F}}[v](\omega ) =\overline{ {\mathscr {F}}[v](-\omega )}\), which can be derived from the definition (2.15) straightforwardly. Thus, we derive from (5.10) that

$$\begin{aligned} \big ({{}_{-\infty }}\mathrm{D}_{x}^{\mu /2,\lambda }v, {{}_{x}}\mathrm{D}_{\infty }^{\mu /2,\lambda } v\big )=2\int _{0}^\infty (\lambda ^2+\omega ^2)^\frac{\mu }{2} \cos (\mu \Theta (\omega )) \big |{\mathscr {F}}[v](\omega ) \big |^2 \mathrm{d}\omega . \end{aligned}$$
(5.12)

For notational convenience, we denote

$$\begin{aligned} {\mathcal K}_\mu (\omega ):=(\lambda ^2+\omega ^2)^\frac{\mu }{2} \cos (\mu \Theta (\omega )). \end{aligned}$$
(5.13)

Noting that

$$\begin{aligned} \Theta '(\omega )=\frac{\lambda }{\lambda ^2+\omega ^2},\quad \cos \Theta = \frac{\lambda }{\sqrt{\lambda ^2+\omega ^2}},\quad \sin \Theta = \frac{\omega }{\sqrt{\lambda ^2+\omega ^2}}, \end{aligned}$$

we find

$$\begin{aligned} \begin{aligned} {\mathcal {K}}_\mu '(\omega )&={\mu }(\lambda ^2+\omega ^2)^{\frac{\mu -1}{2}} \bigg ( \frac{\omega }{\sqrt{\lambda ^2+\omega ^2}} \cos (\mu \Theta )-\frac{\lambda }{\sqrt{\lambda ^2+\omega ^2}} \sin (\mu \Theta )\bigg )\\&={\mu }(\lambda ^2+\omega ^2)^{\frac{\mu -1}{2}} \sin \big ((1-\mu )\Theta \big ). \end{aligned} \end{aligned}$$
(5.14)

As \(\Theta \in (0, \pi /2),\) \({\mathcal K}_\mu (\omega )\) is ascending with respect to \(\omega ,\) when \(\mu \in (0,1)\). Consequently, for \(\mu \in (0,1)\),

$$\begin{aligned} {\mathcal K}_\mu (\omega )> {\mathcal K}_\mu (0)= \lambda ^\mu ,\quad \forall \, \omega >0. \end{aligned}$$
(5.15)

Combing (5.12) and (5.15) leads to

$$\begin{aligned}\begin{aligned} \big ({{}_{-\infty }}\mathrm{D}_{x}^{\mu /2,\lambda }v, {{}_{x}}\mathrm{D}_{\infty }^{\mu /2,\lambda } v\big )&=2\int _{0}^\infty {\mathcal K}_\mu (\omega ) \big |{\mathscr {F}}[v](\omega )\big |^2 \mathrm{d}\omega \\&> 2\lambda ^\mu \int _{0}^\infty \big |{\mathscr {F}}[v](\omega )\big |^2 \mathrm{d}\omega =\lambda ^\mu \Vert v\Vert ^2_{L^2({\mathbb {R}})}, \end{aligned}\end{aligned}$$

where in the last, we used the property \(|{\mathscr {F}}[v](\omega )|^2\) is even in \(\omega \). As \(p+q=1,\) we obtain from (5.6) and the above that

$$\begin{aligned} a^{\mu ,\lambda }_{p,q}(v,v)=\big ({{}_{-\infty }}\mathrm{D}_{x}^{\mu /2,\lambda }v, {{}_{x}}\mathrm{D}_{\infty }^{\mu /2,\lambda } v\big ) -\lambda ^\mu \,\Vert v\Vert ^2_{L^2({\mathbb {R}})}>0. \end{aligned}$$
(5.16)

For \(1<\mu <2,\) we can follow the same derivation and show that

$$\begin{aligned} ({{}_{-\infty }}\mathrm{D}_{x}^{\mu -1,\lambda }v,{{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }v)=2\int _{0}^\infty {\mathcal K}_\mu (\omega ) \big |{\mathscr {F}}[v](\omega )\big |^2 \mathrm{d}\omega , \end{aligned}$$
(5.17)

but by (5.14), we have \({\mathcal K}_\mu '(\omega )<0,\) so

$$\begin{aligned} {\mathcal {K}}_\mu (\omega )< {\mathcal {K}}_\mu (0)= \lambda ^\mu ,\quad \forall \, \omega >0. \end{aligned}$$
(5.18)

Observe that

$$\begin{aligned} (v',v)=\frac{1}{2} \int _{{\mathbb {R}}} (v^2(x))'\, \mathrm{d}x=0. \end{aligned}$$
(5.19)

From (5.7) and (5.17)–(5.19), we obtain

$$\begin{aligned} a^{\mu ,\lambda }_{p,q}(v,v)=-({{}_{-\infty }}\mathrm{D}_{x}^{\mu -1,\lambda }v,{{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }v) +\lambda ^\mu \,\Vert v\Vert ^2_{L^2({\mathbb {R}})}>0. \end{aligned}$$
(5.20)

This ends the proof of (5.8).

Next, taking \(v=u\) in (5.5), we obtain from the Cauchy–Schwarz inequality that

$$\begin{aligned} \begin{aligned} \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}\Vert u(\cdot ,t)\Vert ^2_{L^2({\mathbb {R}})}&+ a^{\mu ,\lambda }_{p,q}(u(\cdot ,t),u(\cdot ,t)) =(f(\cdot , t), u(\cdot ,t))\\&\le \Vert f(\cdot , t)\Vert _{L^2({\mathbb {R}}^+)}\Vert u(\cdot ,t)\Vert _{L^2({\mathbb {R}})}, \end{aligned} \end{aligned}$$
(5.21)

which, together with (5.8), implies

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\Vert u(\cdot ,t)\Vert ^2_{L^2({\mathbb {R}})}\le \Vert u(\cdot ,t)\Vert _{L^2({\mathbb {R}})}^2+ \Vert f(\cdot , t)\Vert _{L^2({\mathbb {R}}^+)}^2,\quad \forall \, 0\le t\le T.\ \end{aligned}$$
(5.22)

We immediately obtain (5.9), which implies the uniqueness of the solution. The existence follows form the equivalence of uniqueness and existence for linear problems. \(\square \)

Remark 5.1

We see from the proof that the same result is valid for \(\mu \in (0,1)\) and \(u(x,0)=0\) on the half line \({\mathbb {R}}^+\) through zero extension. Therefore, we can show the stability of the model in the previous section (see Remark 4.2). \(\square \)

5.2 A Two-Domain Spectral-Element Method

An interesting observation of the model in [22] (i.e., (5.1)) is its solution might have a limited regularity across \(x=0.\) This motivates us to use the Laguerre polynomial approximations on \((-\infty , 0)\) and \((0,\infty ),\) respectively. Thus, we decompose the whole line as

$$\begin{aligned} {\mathbb {R}}={\Lambda }_1\cup {\Lambda }_2, \quad \Lambda _1=(-\infty ,0),\quad \Lambda _2=[0,\infty ), \end{aligned}$$

and denote \(u_{\Lambda _j}(x,t):=u(x,t)\big |_{\Lambda _j},~j=1,2\). Introduce the approximation space:

$$\begin{aligned} V^{\lambda }_{\varvec{N}}({\mathbb {R}}) :=\big \{\phi \in C({\mathbb {R}})\,:\, \phi (x)=e^{-\lambda |x|} p,\;\; p|_{\Lambda _i} \in {\mathcal {P}}_{N_i-1}(\Lambda _i)\big \}, \end{aligned}$$
(5.23)

and define

$$\begin{aligned} \phi ^{*}(x)=e^{-\lambda |x|},\;\; \phi ^{-}_{n_1}(x)={\left\{ \begin{array}{ll} {\mathcal {L}}^{(-1,\lambda )}_{n_1}{(-x)},&{}x\le 0,\\ 0,&{}x>0, \end{array}\right. } \;\; \phi ^{+}_{n_2}(x)={\left\{ \begin{array}{ll} 0,&{}x\le 0,\\ {\mathcal {L}}^{(-1,\lambda )}_{n_2}{(x)},&{}x>0, \end{array}\right. } \end{aligned}$$
(5.24)

where \({\mathcal {L}}^{(-1,\lambda )}_{n}{(}x)=e^{-\lambda x}xL_n^{(1)}(2\lambda x)\). One verifies readily that

$$\begin{aligned} V^{\lambda }_{\varvec{N}}({\mathbb {R}}) =\mathrm{span}\big \{\phi ^{*}(x); \;\; \phi ^{-}_{n_1}(x), \;\; 0\le n_1\le N_1-1; \;\; \phi ^{+}_{n_2}(x),\;\; 0\le n_2\le N_2-1\big \}. \end{aligned}$$
(5.25)

Then, our semi-discrete spectral-Galerkin method is to find \(u_{\varvec{N}}(\cdot ,t)\in V^{\lambda }_{\varvec{N}}({\mathbb {R}}) \) such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \big (\partial _tu_{\varvec{N}}(\cdot , t),v\big )\ +a^{\mu ,\lambda }_{p,q}\big (u_{\varvec{N}}(\cdot , t),v\big ) =\big (f(\cdot ,t),v\big ), \quad &{} \forall v\in V^{\lambda }_{\varvec{N}} ({\mathbb {R}}),\\ \big (u_{\varvec{N}}(\cdot ,0),v)=(u_{0},v),\quad &{} \forall v\in V^{\lambda }_{\varvec{N}}({\mathbb {R}}). \end{array}\right. } \end{aligned}$$
(5.26)

We provide below some details of the algorithm.

$$\begin{aligned} \begin{aligned} u_{\varvec{N}}(x,t)&=c^{*}(t)\phi ^{*}({x}) +\sum _{n_1=0}^{N_1-1}c^{-}_{n_1}(t)\phi ^{-}_{n_1}({x}) +\sum _{n_2=0}^{N_2-1}c^{+}_{n_2}(t)\phi ^{+}_{n_2}({x}),\\ u_{\varvec{N}}(x,0)&=c^{*}_0\phi ^{*}({x})+\sum _{n_1=0}^{N_1-1}c^{-} _{0,n_1}\phi ^{-}_{n_1}({x})+\sum _{n_2=0}^{N_2-1}c^{+}_{0,n_2}\phi ^{+} _{n_2}({x}). \end{aligned}\end{aligned}$$
(5.27)

Let H(x) be the Heaviside function as before. Thanks to the tempered fractional derivative and integral relations with GLFs, and a reflected mapping from positive half line \({\mathbb {R}}^+\) to negative half line \({\mathbb {R}}^-\), we can derive the following identities (see “Appendix B”):

$$\begin{aligned} \begin{aligned}&{{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }\phi ^{*}(x)=-2\lambda e^{-\lambda x}H(x), \quad {{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }\phi ^{-}_{n_1}(x)=(n_1+1){\mathcal {L}}^{(0,\lambda )}_{n_1}{(-x)}H(-x),\\&{{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{*}(x)= {\left\{ \begin{array}{ll} (2\lambda )^{s}e^{\lambda x},&{}x\le 0,\\ \dfrac{2\lambda e^{\lambda x}}{\Gamma (1-s)}\displaystyle \int _x^{\infty }\dfrac{ e^{-2\lambda t}}{t^s} \mathrm{d}t ,&{}x>0, \end{array}\right. }\\&{{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{-}_{n_1}(x)= {\left\{ \begin{array}{ll} -(2\lambda )^{s-1}(n_1+1)L^{(s-1)}_{n_1+1}{(-2\lambda x)} e^{\lambda x},&{}x\le 0,\\ -e^{\lambda x}\dfrac{{n_1}+1}{\Gamma (1-s)}\displaystyle \int _x^{\infty } \dfrac{L^{(0)}_{{n_1}+1}{(2\lambda (t-x))}e^{-2\lambda t}}{t^s} \mathrm{d}t ,&{}x>0, \end{array}\right. }\\&{{}_{x}}\mathrm{D}_{\infty }^{1,\lambda }\phi ^{+}_{n_2}(x)=-(n_2+1){\mathcal {L}}^{(0,\lambda )}_{n_2+1}{(x)}H(x),\quad \\&{{}_{-\infty }}\mathrm{D}_{x}^{s,\lambda }\phi ^{+}_{n_2}(x)=\dfrac{\Gamma (n_2+2)}{\Gamma (n_2+2-s)}x^{1-s}{\mathcal {L}}^{(1-s,\lambda )}_{n_2}{(x)}H(x). \end{aligned}\end{aligned}$$
(5.28)

Then (5.26) leads to the linear system of ordinary differential equations:

$$\begin{aligned} \mathbf {M}\frac{d}{dt} \overrightarrow{{\mathbf {C}}}(t)+{\mathbf {A}}\overrightarrow{{\mathbf {C}}} (t)=\overrightarrow{{\mathbf {F}}}(t), \end{aligned}$$
(5.29)

where

$$\begin{aligned}\begin{aligned}&\overrightarrow{{\mathbf {C}}}(t)=\big (c^*(t), \overrightarrow{{\mathbf {C}}}^-(t),\overrightarrow{\mathbf {C}}^ +(t)\big )^T,\qquad \overrightarrow{{\mathbf {F}}}(t)=\big (f^*(t), \overrightarrow{{\mathbf {F}}}^-(t),\overrightarrow{\mathbf {F}}^+(t)\big )^T,\\&\overrightarrow{{\mathbf {C}}}^-(t) =\big (c^-_0(t),c^-_1(t),\ldots ,c^-_{N_1-1}(t)\big )^T,\quad \qquad \overrightarrow{{\mathbf {C}}}^+(t)=\big (c^+_0(t),c^+_1(t), \ldots ,c^+_{N_2-1}(t)\big )^T.\\&\overrightarrow{{\mathbf {F}}}^-(t) =\big (f^-_0(t),f^-_1(t),\ldots ,f^-_{N_1-1}(t)\big )^T,~\,\,\quad \quad \overrightarrow{{\mathbf {F}}}^+(t)=\big (f^+_0(t),f^+_1(t), \ldots ,f^+_{N_2-1}(t)\big )^T.\\&f^*(t)=(f,\phi ^*),\quad f^-_{n_1}(t)=(f,\phi ^-_{n_1}), \qquad f^+_{n_2}(t)=(f,\phi ^+_{n_2}),\quad {0\le n_i\le N_i-1},~i=1,2, \end{aligned}\end{aligned}$$

and the matrices

$$\begin{aligned} {\mathbf {M}}=\left( \begin{array}{lll} \mathbf {M}_{1\times 1}^{(*,*)} &{}{\mathbf {M}}_{1\times N_1}^{(*,-)} &{}{\mathbf {M}}_{1\times N_2}^{(*,+)} \\ \\ {\mathbf {M}}_{N_1\times 1}^{(-,*)} &{}\mathbf {M}_{N_1\times N_1}^{(-,-)} &{} \mathbf {M}_{N_1\times N_2}^{(-,+)} \\ \\ {\mathbf {M}}_{N_2\times 1}^{(+,*)} &{} \mathbf {M}_{N_2\times N_1}^{(+,-)} &{} \mathbf {M}_{N_2\times N_2}^{(+,+)} \\ \end{array} \right) , \quad {\mathbf {A}}=\left( \begin{array}{lll} {{\mathbf {A}}}_{1\times 1}^{(*,*)} &{}{{\mathbf {A}}}_{1\times N_1}^{(*,-)} &{} {{\mathbf {A}}}_{1\times N_2}^{(*,+)} \\ \\ {{\mathbf {A}}}_{N_1\times 1}^{(-,*)} &{}{\mathbf {A}}_{N_1\times N_1}^{(-,-)} &{} {\mathbf {A}}_{N_1\times N_2}^{(-,+)} \\ \\ {\mathbf {A}}_{{N_2}\times 1}^{(+,*)} &{} {\mathbf {A}}_{N_2\times N_1}^{(+,-)} &{} {\mathbf {A}}_{N_2\times N_2}^{(+,+)} \\ \end{array} \right) , \end{aligned}$$
(5.30)

with the entries

$$\begin{aligned} \begin{aligned}&\mathbf {M}_{c\times d}^{(a,b)}(i+1,j+1)=(\phi ^b_{j},\phi ^a_{i}),\quad {\mathbf {A}}_{c\times d}^{(a,b)}(i+1,j+1)=a_{p,q}^{\mu ,\lambda }(\phi ^b_{j},\phi ^a_{i}),\\&a,b=*,-,+,\quad c,d=1,N_1,N_2,\qquad 0\le i\le c-1,\quad 0\le j\le d-1, \end{aligned} \end{aligned}$$

and \(\overrightarrow{{\mathbf {C}}}(0)\) is determined by the initial data.

The derivation of the tempered derivative relation (5.28), and of the entries of the matrix \({\mathbf {A}}\) can be found in “Appendix B”. Base on the semi-discrete scheme (5.29), we further use the third-order explicit Runge-Kutta method in time direction with step size \(h=10^{-3}\) to numerically solve the problem.

5.3 Numerical Results

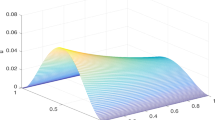
We solve (5.1) with \(C_T=1\) and \(u_0=10e^{-5|x|}\) as the initial distribution by using the proposed method. We first test its accuracy. In Fig. 4, we plot the convergence rate of the spectral method at \(T=5\) with fixed time step \(h=10^{-3}\). We choose a slow decay \(f(x,t)= (1+x^2)^{-1},\) and an exponential decay \(f(x,t)= \cos {t} ~e^{-x^2}\), respectively. Observe from Fig. 4 an exponential convergence for the latter, but an algebraic convergence for the former. In fact, we expect the solution with \(f(x,t)= \cos {t} ~e^{-x^2}\) decays exponentially in space. Indeed, as the Fourier transform of the Gaussian \(e^{-x^2}\) is invariant, so we can use the model by using Fourier transform and then solve the resulted equation. However, the solution with \(f(x,t)= (1+x^2)^{-1}\) should decay very slowly. As a result, we observe a very different convergence behavior.

Fig. 4
figure 4

Left \(f(x,t)= (1+x^2)^{-1}.\) Right \(f(x,t)=\cos {t}~ e^{-x^2}\)

Full size image

Next, we examine behaviors of the solution under various situations. In Fig. 5, we plot the snapshots at different times of the tempered fractional diffusion with \(p=1/3,~q=2/3\) and \(p=3/4,~q=1/4\), respectively. The case with \(p=q=1/2\) is plotted in Fig. 6.

Fig. 5
figure 5

Left \(p=1/3,~q=2/3.\) Right \(p=3/4,~q=1/4.\)

Full size image
Fig. 6
figure 6

Left \(p=q=1/2,~\lambda =5/2.\) Right \(p=q=1/2,~t=2.\)

Full size image

  • The parameters p and q reflect the directional preference of the particle jumping. More precisely, if \(p>q\), the particles tend to jump to the right, and if \(p<q\), the particles tend to jump to the left, see Fig. 5. In particular, \(p=q\) produces a symmetric profile in the case of \(f(x,t)=0\), see the left in Fig.  6.

  • The parameter \(\lambda \) determines the probability of the jump distance of the particles. A larger \(\lambda \) indicates a shorter jump distance, see the right of Fig. 6.

  • To compare with the usual fractional diffusion equation, i.e., \(\lambda =0\), , we plot in Fig. 7 the particle distributions of the usual fractional diffusion and the tempered fractional diffusion with initial distribution \(u_0(x)=10e^{-4 x^2}\) at time \(t=10\). We observe that the tail of the tempered fractional diffusion behaves like \(|x|^{-\mu -1}e^{-\lambda |x|}\) for large |x| while that that of the usual fractional diffusion behaves like \(|x|^{-\mu -1}\).

Fig. 7
figure 7

Initial distribution \(u_0(x)=10e^{-4x^2}\)

Full size image

6 Concluding Remarks

We presented in this paper efficient spectral methods using the generalized Laguerre functions for solving the tempered fractional differential equations on infinite intervals. Our numerical methods and analysis are based on an important observation that the tempered fractional derivative, when restricted to the half line, is intrinsically related to the generalized Laguerre functions that we defined in Sect. 3. By exploring the properties of generalized Laguerre functions, we derived optimal approximation results in properly weighted Sobolev spaces. In Sect. 4, we developed a spectral-Galerkin method for solving a tempered fractional diffusion equation on the half line. Finally, we presented a spectral-Galerkin method for solving the tempered fractional diffusion equation on the whole line in Sect. 5. More importantly, we rigorously showed the well-posedness of the tempered fractional model in [22]. Also to the best of our knowledge, this is perhaps the first attempt in solving this model directly on infinite intervals, and also show the well-posedness of the models in [22]. Indeed, a finite-difference approach on a truncated domain was employed in [22]. Moreover, our numerical results demonstrated some expected properties and behaviors of the underlying solution of such a tempered diffusion model.