Abstract
The tempered fractional calculus has been successfully applied for depicting the time evolution of a system describing non-Markovian diffusion particles. The related governing equations are a series of partial differential equations with tempered fractional derivatives. Using the polynomial interpolation technique, in this paper, we present three efficient numerical formulas, namely the tempered L1 formula, the tempered L1-2 formula, and the tempered L2-\(1_{\sigma }\) formula, to approximate the Caputo-tempered fractional derivative of order \(\alpha \in (0,1)\). The truncation error of the tempered L1 formula is of order 2−\(\alpha\), and the tempered L1-2 formula and L2-\(1_{\sigma }\) formula are of order 3−\(\alpha\). As an application, we construct implicit schemes and implicit ADI schemes for one-dimensional and two-dimensional time-tempered fractional diffusion equations, respectively. Furthermore, the unconditional stability and convergence of two developed difference schemes with tempered L1 and L2-\(1_{\sigma }\) formulas are proved by the Fourier analysis method. Finally, we provide several numerical examples to demonstrate the correctness and effectiveness of the theoretical analysis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The tempered fractional calculus is a generalization of the fractional calculus, and the definition contains both the weak singular kernel and the exponential kernel. It has particular mathematical properties and plays an important role in the actual mathematical physics model. The tempered fractional calculus describes the transition between normal and anomalous diffusions or some anomalous diffusions in finite time or bounded space domain. As we know, the anomalous diffusion phenomena can be seen frequently in the nature world, and the continuous time random walk (CTRW) model has been proved to be a useful tool that describes this phenomenon well [28]. The process of the CTRW model, which is non-Markovian is usually depicted by the waiting time probability density function (PDF) and the jump length PDF. For the CTRW model with tempered power law waiting time, the PDF of diffusion particles obeys the tempered fractional diffusion equation [13, 16, 40]
where \(u(\mathbf{x} ,t)\) denotes the probability density of searching a particle in position \(\mathbf{x}\) at time t, \(\kappa _\alpha >0\) is the diffusion coefficient, the standard Laplace operator \(\Delta =\sum\limits_{i=1}^{d}\frac{\partial ^2}{\partial x^2_i},d=1,2,\) and \(_{0}{\text{D}}_t^{1-\alpha ,\lambda }\,(0<\alpha <1)\) represents the Riemann–Liouville tempered fractional derivative operator. The Riemann–Liouville tempered fractional derivative of order \(\beta\,(n-1<\beta <n)\) gives [18, 31]
Using the properties of the fractional derivative [21], Eq. (1) can be rewritten as
where \(_0^{\text{C}}{}{\text{D}}_t^{\alpha ,\lambda }\) denotes the Caputo-tempered fractional derivative [21, 32, 37]
The more detailed background and application of model (1), we refer to [16, 28] or Appendix A. For the equivalence of models (1) and (2), see [36].
In this paper, without loss of generality, we consider the following time fractional subdiffusion equation:
with the initial condition
and a Dirichlet boundary condition
where \(\varOmega \in R^d\) is a bounded domain in \(\mathbb {R}^d,d=1,2\) with the boundary \(\partial \varOmega\), and \(f,\phi ,\psi\) are given functions.
There are several numerical approaches to the Caputo fractional derivative. The first technique is the piecewise interpolation polynomials, such as the L1 approximation [10, 11, 23, 29, 35, 42], the L1-2 approximation [14, 20], and the L2-\(1_{\sigma }\) approximation [1] and so on. Another widely used technique is the shifted Grünwald–Letnikov approach [2, 6, 19, 26, 30]. The main idea is to approximate the Riemann–Liouville derivative by the Grünwald–Letnikov formula. The third used technique is the so called Lubich’s approach which is introduced by [25]. The main advantages of above-mentioned approaches are simplicity and efficiency. More importantly, the error estimates can be analyzed when above-mentioned approaches are used to approximate the time fractional diffusion equations [22, 38]. More applications of above-mentioned approaches to solve the various kinds of fractional order partial differential equations, see [15, 24, 34] and references, therein.
Recently, there has been a vast interest in the numerical solutions of tempered fractional differential equations due to their wide applications [2, 4, 7, 9, 16, 27, 37, 40, 41]. Several numerical methods, such as the Grünwald–Letnikov approach and the Lubich’s approach, have been used to approximate the tempered fractional derivatives. In [2], Baeumera and Meerschaert presented the finite difference scheme and the particle tracking method for the space-tempered fractional diffusion equation with drift. Applying the spectral method, Zayernouri et al. [39] obtained the eigenfunctions of the tempered fractional Sturm–Liouville problem. Based on the weighted and shifted Grünwald difference (WSGD) operator, Li and Deng [19] constructed a series of high-order numerical forms for the space-tempered fractional diffusion equation, and proved the stability and convergence by the matrix analysis. Using the weighted and shifted Lubich difference operator to approximate the time-tempered fractional derivative, Sun et al. [36] analyzed some local discontinuous Galerkin schemes for a time-tempered fractional diffusion equation. The implicit numerical scheme of the tempered fractional Black–Scholes equation is provided by Zhang et al. [43], and the corresponding theoretical analysis is given. Using the Lubich’s approach for the time-tempered fractional derivative, Chen and Deng [5] derived a high-order algorithm for a time–space fractional Feynman–Kac equation. Dehghan et al. [8] proposed a numerical scheme that is convergent with the second-order accuracy in time for the space–time tempered fractional diffusion–wave equation, and the unconditional stability and convergence of the developed method are also proved. Deng and Zhang [9] developed the finite difference/finite element schemes for a time fractional Feynman–Kac equation. Ding and Li [12] designed a high-order numerical algorithm to solve the space-tempered fractional convection equation with Riemann–Liouville fractional derivatives, and the rigorous stability and convergence analysis of the algorithm are also given. So far, the application of the piecewise interpolation polynomial technique to solve the tempered fractional diffusion equation has not been intensively investigated.
In this paper, we are interested in developing efficient and accurate numerical approximations for the time-tempered fractional diffusion equation. In particular, one of the challenges of this problem lies in the existence of the singular kernel and the smooth kernel. To overcome the difficulty, we discrete the tempered Caputo fractional derivative by transforming it to the conventional Caputo fractional derivative. In Sect. 2, we present three kinds of quadrature formulas for the Caputo-tempered fractional derivative of order \({\alpha} \in (0,1)\). The tempered L1 formula with the order \(2-\alpha\), the tempered L1-2 and L2-\(1_{\sigma }\) formulas with the order \(3-\alpha\). And the corresponding analysis of truncation errors of three formulas are discussed in detail. The presented discrete formulas are applied to solve the time-tempered fractional diffusion equations of one dimension and two dimension in Sects. 3 and 4, respectively. Besides, the unconditional stability and convergence of difference schemes with tempered L1 and L2-\(1_{\sigma }\) formulas are proved by the Fourier method. In Sect. 5, the numerical results in the examples illustrate the effectiveness of the three proposed discrete methods. Finally, we make a brief conclusion in Sect. 6.
2 Interpolation Formulas of Caputo-Tempered Fractional Derivative
In this section, we are concerned with the efficient numerical discretization of the Caputo-tempered fractional derivative. For a given positive integer N, let \(\{t_k\}_{k=0}^{N}\) be an equidistant partition of [0, T], and denote \(t_k=k\tau ,t_{k+1/2}={(t_k+t_{k+1})}/{2}\), where \(\tau =T/N\) is the time step size.
2.1 Tempered L1 Formula
To discrete the Caputo-tempered fractional derivative (3), we introduce the following notations:
then we denote the linear interpolation function of v(t) as \(P_{1,\ell }v(t)\) on each small interval \([t_{\ell -1},t_\ell ]\,(1\leqslant \ell \leqslant k)\), i.e.,
which leads to
and
Denoting \(v(t)={\text{e}}^{\lambda t}u(t)\) and using the piecewise linear approximation on each cell \([t_{\ell -1},t_\ell ]\), then we can get the expression of the tempered L1 formula of the Caputo-tempered fractional derivative, as follows:
By simple calculation, Eq. (4) provides
where
and
We denote \(\mu =\tau ^{\alpha }\Gamma {(2-\alpha )},~U^k\approx u(t_k)\) and
then the tempered L1 approximation operator \(\mathbb {D}_t^{\alpha ,\lambda }U^k\) can be rewritten as the following form:
For coefficients \(\{{a_j^{(\alpha )}}\}\), \(\{\overline{d}_{a,m}^{(\alpha )}\}\), and \(\{\widetilde{d}_{a,m}^{(\alpha )}\}\), we can obtain
Lemma 1
For any \(\alpha \in (0,1), k\geqslant 1\), the coefficients \(a_j^{(\alpha )}(0\leqslant j \leqslant k-1)\) and \(\overline{d}_{a,m}^{(\alpha )},~\widetilde{d}_{a,m}^{(\alpha )}\) \((1\leqslant m\leqslant k)\) defined in Eqs. (6), (7), and (8) satisfy
-
(i)
\(a_j^{(\alpha )}>0;\)
-
(ii)
\(1=a_0^{(\alpha )}>a_1^{(\alpha )}>a_2^{(\alpha )}>\cdots >a_{k-1}^{(\alpha )};\)
-
(iii)
\(\sum\limits _{j=0}^{k-1}a_j^{(\alpha )}=k^{1-\alpha };\)
-
(iv)
\(\overline{d}_{a,m}^{(\alpha )}>0,~\widetilde{d}_{a,m}^{(\alpha )}>0;\)
-
(v)
\(\overline{d}_{a,1}^{(\alpha )}<\overline{d}_{a,2}^{(\alpha )}<\overline{d}_{a,3}^{(\alpha )}<\cdots <\overline{d}_{a,k}^{(\alpha )};\)
-
(vi)
\(\widetilde{d}_{a,1}^{(\alpha )}<\widetilde{d}_{a,2}^{(\alpha )}<\widetilde{d}_{a,3}^{(\alpha )}< \cdots <\widetilde{d}_{a,k}^{(\alpha )};\)
-
(vii)
\(\overline{d}_{a,m+1}^{(\alpha )}-\widetilde{d}_{a,m}^{(\alpha )} \leqslant a_{k-m-1}^{(\alpha )}-a_{k-m}^{(\alpha )},~1\leqslant m\leqslant k-1;\)
-
(viii)
\(\overline{d}_{a,1}^{(\alpha )}\leqslant a_{k-1}^{(\alpha )}.\)
Proof
The proof is provided in Appendix B.
Lemma 2
Assume that \(u(t)\in C^2[0,t_k]\). Then, there is the following error estimate:
for \(R^k\).
Proof
We list the proof in Appendix C.
To see the smoothness of the solution more clearly, we also give the asymptotic expansion formula of the tempered fractional derivative. The asymptotic expansion formula of the tempered L1 approximation is derived from the asymptotic expansion of the L1 approximation. There is the asymptotic expansion of the L1 approximation of the order \(3-\alpha\) [10, 11]
where \(u^k=u(t_k),\,\zeta (s)\) is the Riemann zeta function, and the L1 approximation has weights \(\varpi _0^{(\alpha )}=1,\varpi _k^{(\alpha )}=(k-1)^{1-\alpha }-k^{1-\alpha }\), and \(\varpi _\ell ^{(\alpha )}=(\ell -1)^{1-\alpha }-2\ell ^{1-\alpha }+(\ell +1)^{1-\alpha }\) for \(1\leqslant l \leqslant k-1\).
The tempered L1 approximation (9) has weights \(\widetilde{d}_{a,k}^{(\alpha )}=\varpi _0^{(\alpha )}=1,\overline{d}_{a,1}^{(\alpha )}=-\varpi _k^{(\alpha )}/{\text{e}}^{\lambda k \tau }\), and \(\overline{d}_{a,k-\ell +1}^{(\alpha )} -\widetilde{d}_{a,k-\ell }^{(\alpha )}=-\varpi _\ell ^{(\alpha )}/{\text{e}}^{\lambda \ell \tau }~(1\leqslant \ell \leqslant k-1)\). By applying the asymptotic expansion formula for the function \({\text{e}}^{\lambda s}u(s)\) and multiplying by \({\text{e}}^{-\lambda t_k}\), we obtain the asymptotic expansion formula of the order \(3-\alpha\) of the tempered L1 approximation as follows:
2.2 Tempered L1-2 Formula
To improve the accuracy, we apply the quadratic interpolation \(P_{2,\ell }v(t)\) on each cell \([t_{\ell -1},t_\ell ](\ell \geqslant 2)\) and the linear interpolation \(P_{1,1}v(t)=\delta _t v_{1/2}\) on the first cell \([t_0,t_1]\) to approximate the function v(t) like [14]. For the cells \([t_{\ell -1},t_\ell ] \,(\ell \geqslant 2)\), the quadratic interpolation function \(P_{2,\ell }v(t)\) with three points \((t_{\ell -2},v(t_{\ell -2}))\), \((t_{\ell -1},v(t_{\ell -1}))\), and \((t_\ell ,v(t_\ell ))\) is employed, i.e.,
and it leads to
and
By virtue of Eq. (11), we can obtain
Recalling \(v={\text{e}}^{\lambda t}u\), we have
where \(T^k={_0^{\text{C}}} {\text{D}}_t^{\alpha ,\lambda }u(t)\big |_{t=t_k}-\partial _t^{\alpha ,\lambda }u({t_k}).\) For \(k=1\), there is \(c_0^{(k,\alpha )}=a_0^{(\alpha )}=1\); for \(k\geqslant 2\), the coefficients are given as
and
We call the fractional numerical differentiation formula (12) the tempered L1-2 formula, which adds a correction term \(\frac{{\text{e}}^{-\lambda t_k}\tau ^{2-\alpha }}{\Gamma (2-\alpha )}\sum\limits _{\ell =2}^k b_{(k-\ell )}^{(\alpha )}\delta _t^2v_{\ell -1}\) in the tempered L1 operator \(\mathbb {D}_{t}^{\alpha ,\lambda }u({t_k})\) for \(k\geqslant 2\). Setting
the tempered L1-2 approximation operator \(\partial _t^{\alpha ,\lambda }U^k\) can be rewritten as
The tempered L1-2 approximation operator (16) reduces to the tempered L1 approximation operator (9) for \(k=1\); for \(k=2\), \(c_0^{(k,\alpha )}\in (1,{3}/{2}),~c_1^{(k,\alpha )}\in (-{1}/{2},1)\), then we can obtain \(\overline{d}_{c,2}^{(k,\alpha )}-\widetilde{d}_{c,1}^{(k,\alpha )}\leqslant c_0^{(k,\alpha )}-c_1^{(k,\alpha )}\); as for \(k\geqslant 3\), the properties of \(\overline{d}_{c,m}^{(k,\alpha )}\) and \(\widetilde{d}_{c,m}^{(k,\alpha )}\,(1\leqslant m \leqslant k)\) can be derived with the help of properties of \(c_j^{(k,\alpha )}\), see [14] .
Lemma 3
For any \(\alpha \in (0,1),~k\geqslant 3\), the coefficients \(c_j^{(k,\alpha )}\,(0\leqslant j \leqslant k-1)\) and \(\overline{d}_{c,m}^{(k,\alpha )}\), \(\widetilde{d}_{c,m}^{(k,\alpha )}\) \((1\leqslant m\leqslant k)\) defined in Eqs. (13), (14), and (15) satisfy
-
(i)
\(c_0^{(k,\alpha )}>\big |c_1^{(k,\alpha )}\big |;\)
-
(ii)
\(c_j^{(k,\alpha )}>0,~j\ne 1;\)
-
(iii)
\(c_2^{(k,\alpha )}\geqslant c_3^{(k,\alpha )}\geqslant \cdots \geqslant c_{k-1}^{(k,\alpha )};\)
-
(iv)
\(c_0^{(k,\alpha )}>c_2^{(k,\alpha )};\)
-
(v)
\(\overline{d}_{c,m}^{(k,\alpha )}>0,~\widetilde{d}_{c,m}^{(k,\alpha )}>0,~m\ne k-1;\)
-
(vi)
\(\overline{d}_{c,1}^{(k,\alpha )}\leqslant c_{k-1}^{(k,\alpha )};\)
-
(vii)
\(\overline{d}_{c,m+1}^{(k,\alpha )}>\widetilde{d}_{c,m}^{(k,\alpha )},~1\leqslant m\leqslant k-1,m\ne k-2;\)
-
(viii)
\(\overline{d}_{c,m+1}^{(k,\alpha )}-\widetilde{d}_{c,m}^{(k,\alpha )}\leqslant c_{k-m-1}^{(k,\alpha )}-c_{k-m}^{(k,\alpha )},~1\leqslant m\leqslant k-1,m\ne k-2.\)
It is easy to check that \(c_1^{(k,\alpha )}\in (-1/2,1),~c_2^{(k,\alpha )}\in (0,1)\), the positive and negative of \(c_1^{(k,\alpha )}\) and \(c_1^{(k,\alpha )}-c_2^{(k,\alpha )}\) change with the difference \(\alpha\,(0<\alpha <1)\), which are discussed in the following lemma.
Lemma 4
The coefficients of \(c_1^{(k,\alpha )}\) and \(c_1^{(k,\alpha )}-c_2^{(k,\alpha )}\) for different k and \(\alpha \in (0,1)\) satisfy
-
(i)
\(c_1^{(k,\alpha )}>0,~\overline{d}_{c,1}^{(k,\alpha )} \leqslant c_1^{(k,\alpha )},for~any~\alpha \in (0,\alpha _1),\alpha _1 \approx 0.673\,6~when~k=2;\)
-
(ii)
\(\begin{array}{c} c_1^{(k,\alpha )}-c_2^{(k,\alpha )}>0,~\overline{d}_{c,2}^{(k,\alpha )} -\widetilde{d}_{c,1}^{(k,\alpha )}\leqslant c_1^{(k,\alpha )}-c_2^{(k,\alpha )},~for~any~\alpha \in (0,\alpha _2),\alpha _2 \approx 0.390\,9,~k=3; \end{array}\)
-
(iii)
\(\begin{array}{c} c_1^{(k,\alpha )}-c_2^{(k,\alpha )}> 0,~\overline{d}_{c,k-1}^{(k,\alpha )} -\widetilde{d}_{c,k-2}^{(k,\alpha )}\leqslant c_1^{(k,\alpha )}-c_2^{(k,\alpha )},~for~any~\alpha \in (0,\alpha _3),\alpha _3\approx 0.373\,9,~k>3; \end{array}\)
-
(iv)
\(|c_1^{(k,\alpha )}-c_2^{(k,\alpha )}|<\frac{1}{2}.\)
Proof
The proof is provided in Appendix D.
Lemma 5
Suppose that \(u(t)\in C^3[0,t_k]\), and for the truncation error \(T^k\), we can derive that
Proof
The proof is provided in Appendix E.
2.3 Tempered L2-\(1_{\sigma }\) Formula
By Alikhanov’s work [1], letting \(\sigma =1-\alpha /2\), we discuss the discretization of the tempered fractional derivative at \(t_{k+\sigma }\,(k=0,1,\cdots, N-1)\). The interpolation polynomial based on the quadratic interpolation on each interval \([t_{\ell -1},t_{\ell }]\,(1 \leqslant \ell \leqslant k)\) is constructed to approximate \(v(t)={\text{e}}^{\lambda t}u(t)\) using the three points \((t_{\ell -1},v(t_{\ell -1}))\), \((t_\ell ,v(t_\ell ))\), and \((t_{\ell +1},v(t_{\ell +1}))\), i.e.,
leading to
and
For the last small interval \([t_k,t_{k+\sigma }]\), we use the linear interpolation in the cell \([t_k, t_{k+1}]\) at non-equidistant subdivision points \(t_k,t_{k+\sigma }\), and \(t_{k+1}\). To sum up, we have
where
And for \(k=0\), we have \(s_0^{(k,\alpha ,\sigma )}=p_0^{(\alpha ,\sigma )}=\sigma ^{1-\alpha }\); for \(k\geqslant 1\), we have
Moreover, recalling \(v={\text{e}}^{\lambda t}u\), we have
where \( T^{k+\sigma }={}_0^{\text{C}}{}{\text{D}}_t^{\alpha ,\lambda }u(t)\big |_{t=t_{k+\sigma }}-\Delta_t^{\alpha,\lambda}u({t_{k+\sigma}}).\) Here, we call this numerical differentiation formula (20) the tempered L2-\(1_{\sigma }\) formula. If we adopt the approximate solution \(U^{k}\) and set
then the tempered L2-\(1_{\sigma }\) approximation operator \(\Delta _{t}^{\alpha ,\lambda }U^{\overline{k}}\) is equivalent to the form
It is clear that \(s_0^{(k,\alpha ,\sigma )}=\sigma ^{1-\alpha }>0\) and \(\overline{d}_{s,0}^{(k,\alpha ,\sigma )}<s_0^{(k,\alpha ,\sigma )}, ~\widetilde{d}_{s,0}^{(k,\alpha ,\sigma )}>s_0^{(k,\alpha ,\sigma )}\) for \(k=0\). And, for \(k\geqslant 1\), with the similar fashion given in [1], we can check that the properties of \(\overline{d}_{s,m}^{(k,\alpha ,\sigma )}\) and \(\widetilde{d}_{s,m}^{(k,\alpha ,\sigma )}\,(1\leqslant m \leqslant k)\) hold the following lemma.
Lemma 6
For any \(\alpha \in (0,1),~k\geqslant 1\), \(s_j^{(k,\alpha ,\sigma )}\,(0\leqslant j \leqslant k)\) defined in Eq. (19) and \(\overline{d}_{s,m}^{(k,\alpha ,\sigma )}\), \(\widetilde{d}_{s,m}^{(k,\alpha ,\sigma )}\) \((0\leqslant m\leqslant k)\) defined in Eqs. (21) and (22), we have
-
(i)
\(s_k^{(k,\alpha ,\sigma )}>\frac{1-\alpha }{2}(k+\sigma )^{-\alpha }>0;\)
-
(ii)
\(s_0^{(k,\alpha ,\sigma )}>s_1^{(k,\alpha ,\sigma )}>s_2^{(k,\alpha ,\sigma )}>\cdots>s_{k-1}^{(k,\alpha ,\sigma )}>s_k^{(k,\alpha ,\sigma )};\)
-
(iii)
\(\overline{d}_{s,m}^{(k,\alpha ,\sigma )}>0,~\widetilde{d}_{s,m}^{(k,\alpha ,\sigma )}>0;\)
-
(iv)
\(\overline{d}_{s,m+1}^{(k,\alpha ,\sigma )}>\widetilde{d}_{s,m}^{(k,\alpha ,\sigma )},~0\leqslant m \leqslant k-1;\)
-
(v)
\(\widetilde{d}_{s,k}^{(k,\alpha ,\sigma )}>s_0^{(k,\alpha ,\sigma )};\)
-
(vi)
\(\overline{d}_{s,0}^{(k,\alpha ,\sigma )}<s_k^{(k,\alpha ,\sigma )}.\)
Lemma 7
Suppose that \(u(t)\in C^3[0,t_{k+1}]\,(0\leqslant k \leqslant N-1)\), then the truncation error of the tempered L2-\(1_{\sigma }\) formula gives
Proof
The proof is provided in Appendix F.
3 Implicit Schemes for One-Dimensional Time-Tempered Fractional Diffusion Equation
3.1 Derivation of Difference Schemes
For a given positive integer M, let \(\{x_j\}_{j=0}^{M}\) be a partition of [0, L] with \(x_j=jh_x\) and \(h_x=L/M\). Define a mesh function \(V_h=\{u|u=(u_0,u_1,\cdots, u_M)\}, \mathop {V_h^0}=\{u|u\in V_h,u_0=u_M=0\}\) with the discrete \(L_2\) norm \(\Vert \omega ^k(x)\Vert _2^2=\sum\limits _{j=1}^{M-1}h_x|\omega _j^k|^2\).
Consider the initial boundary value problem as follows:
where the functions \(f,\phi ,\psi _1,\psi _2\) are given, and smooth which satisfy our numerical schemes. Denote \(u_j^k=u(x_j,t_k), f_j^k=f(x_j,t_k)\). Here we consider the spatial variable is approximated by the center difference formula \(\delta _x^2u_j^k= \frac{u_{j+1}^k-2u_j^k+u_{j-1}^k}{h_x^2}+\mathcal{O}(h_x^2),\) and the time variable is discretized by tempered L1, L1-2, and L2-\(1_{\sigma }\) formulas, respectively. Then, the first equation of Eq. (25) at the grid points \((x_j,t_k)\) and \((x_j,t_{k+\sigma })\) holds
where \(f_j^{k+\sigma }=f(x_j,t_{k+\sigma })\) and \(u_j^{k+\sigma }=\Big (\sigma u_j^{k+1}+(1-\sigma )u_j^k\Big )+\mathcal {O}({\tau }^2)\), thus the truncation error
The value of the approximation solution to a function u(x, t) at the grid point \((x_j,t_k)\) is denoted by \(U_j^k\). If the truncation error is omitted and \(U_j^k\) is adopted, then we have the difference schemes
where \(U_j^{k+\sigma }=\sigma U_j^{k+1}+(1-\sigma )U_j^k\).
3.2 Stability Analysis
In this subsection, we will analyze the stability of numerical schemes (30) and (32) using the Fourier analysis [3, 6, 20]. Let \(\tilde{U}_j^k\) be the approximate solution of Eqs. (30) and (32). Then, define \(\varepsilon _j^k=U_j^k-\tilde{U}_j^k,~1\leqslant k\leqslant N,~1\leqslant j\leqslant M-1\), and the error vector \(\varepsilon ^k=[\varepsilon _1^k,\varepsilon _2^k,\varepsilon _3^k,\cdots, \varepsilon _{M-1}^k]^{\mathrm {T}}\in V^0_h.\) To begin the error analysis, we define the grid function
Therefore, \(\varepsilon ^k(x)\) can be expanded by the Fourier series
where \(\xi _m^k=\frac{1}{L}\int _0^L \varepsilon ^k(x) {\text{e}}^{-{\text{i}}2\pi mx/L}\mathrm{d}x, {\text{i}}=\sqrt{-1}.\) According to the definition of the discrete \(L_2\) norm and Parseval’s equality, there exists
From the numerical schemes (30) and (32), we get the following error equations, respectively:
Suppose that the solutions of Eqs. (34) and (35) can be written as the following form:
The main idea of the Fourier analysis method is to check the propagation of the error \(\varepsilon _j^0\) produced in the initial condition. Since the information is exactly given in boundary conditions, we have \(\varepsilon _0^k=\varepsilon _M^k=0\). Now, we check the propagation of the error with the development of time steps. For the stability of the difference scheme (30), we have
Theorem 1
The difference scheme (30) is unconditionally stable, and we can derive that
Proof
Inserting Eq. (36) into Eq. (34), and combining with the Euler formula \({\text{e}}^{{\text{i}}\beta h}=\cos (\beta h)+{\text{i}}\sin (\beta h)\), we arrive at
where \(\widetilde{d}_{a,k}^{(\alpha )}=a_0^{(\alpha )}=1\).
Suppose that \(\xi _m^k(k=1,2,\cdots ,N)\) are the solutions of Eq. (37), we will prove the following inequality by mathematical induction:
The inequality (38) holds obviously for \(k=1\). Now, we suppose that the inequality (38) is true for \(k=1,2,\cdots, n-1\). Thus, for \(k=n\), using Eq. (37) and (vii), (viii) of Lemma 1, we have
and it yeilds
where the relation \(\sum\limits_{\ell =1}^{n-1}(a_{n-\ell -1}^{(\alpha )}-a_{n-\ell }^{(\alpha )})+a_{n-1}^{(\alpha )}=1\) is used. Applying the definition (33) and the inequality (38), we get
which means the difference scheme (30) is unconditionally stable.
With the similar approach, we have the stability of the difference scheme (32).
Theorem 2
The difference scheme (32) is unconditionally stable, and we can derive that
Proof
From Eq. (35), we have
where \(\overline{d}_{s,k}^{(k,\alpha ,\sigma )}=s_0^{(k,\alpha ,\sigma )}{\text{e}}^{\lambda (t_k-t_{k+\sigma })}\), \(s_0^{(k,\alpha ,\sigma )}=\sigma ^{1-\alpha } > 0\,(k=0)\), and \(s_0^{(k,\alpha ,\sigma )}=p_0^{(\alpha ,\sigma )}+q_1^{(\alpha ,\sigma )}>0\,(k\geqslant 1)\).
Suppose that \(\xi _m^{k+1}\,(k=0,1,\cdots , N-1)\) are the solutions of the numerical scheme (39), we shall prove that
For \(k=0\), it holds
and hence
Now, we suppose that Eq. (40) is true for \(k=0,1,\cdots , n-1\). Then, according to Eq. (39), for \(k=n\), we have
In view of the relation \(\sum\limits_{\ell =0}^{n-1}\Big (s_{n-\ell -1}^{(k,\alpha ,\sigma )}-s_{n-\ell }^{(k,\alpha ,\sigma )}\Big ) =s_0^{(k,\alpha ,\sigma )}-s_n^{(k,\alpha ,\sigma )}\), by simple argument, there exists
Finally, using Eqs. (33) and (40), we obtain the difference scheme (32) is unconditionally stable.
3.3 Convergence Analysis
In this subsection, we are dedicated in studying the convergence order of the difference schemes. As an example, we give the complete proof with the tempered L1 approximate and the proofs of other difference schemes are omitted with respect to the length of this paper. Define the truncation error \(\rho _j^k=u(x_j,t_k)-U_j^k=u_j^k-U_j^k,~1\leqslant k\leqslant N,~1\leqslant j\leqslant M-1\), and let the error vectors
Set the grid functions
And \(\rho ^k(x),R^k(x)\) have the following Fourier series expansions:
where \(\eta _m^k=\frac{1}{L}\int _0^L \rho ^k(x) {\text{e}}^{-{\text{i}}2\pi mx/L}\mathrm{d}x, \gamma _m^k=\frac{1}{L}\int _0^L R^k(x) {\text{e}}^{-{\text{i}}2\pi mx/L}\mathrm{d}x.\) From the definition of the \(L_2\) norm and Parseval’s equality, we can obtain
Subtracting numerical schemes (26) from Eq. (30) and multiplying \(h_x^2\) on both sides of the final error equation, we arrive at
where \(\rho _j^0=0,1\leqslant j\leqslant M-1;~\rho _0^k=\rho _M^k,1\leqslant k\leqslant N-1\). Assume that \(\rho _j^k\) and \(R_j^k\) are
Noticing that \(\rho _j^0=0\), we obtain \(\eta _m^0=0\). And we can deduce the following inequality from Eq. (29) and the first equality of Eq. (42):
And from the convergence of the last series of Eq. (42), there exists a positive constant \(\hat{C}\) such that [20]
Lemma 8
There is the following relationship between \(\eta _m^k\) and \(\gamma _m^1\):
Proof
Inserting Eq. (44) into Eq. (43), we arrive at
As for \(k=1\), there is
and we can easily come to
where \(\mu =\tau ^{\alpha }\Gamma {(2-\alpha )}<1\) when \(0<\alpha ,\tau <1\). We suppose that the inequality (47) is true for \(k=1,2,\cdots, n-1\). For \(k=n\), we deduce the following estimate from Eqs. (48) and (46):
i.e.,
Therefore, this lemma is proved.
Let \(C_{x,t}^{4, 2}\) denote the space of function u(x, t) which satisfies \(u(x,t)\in C^2[0,t_k]\cap C^4[0,L]\). Then, there exists the following convergence theorem.
Theorem 3
Suppose \(u(x,t)\in C_{x,t}^{4, 2}\), then the difference scheme with the tempered L1 formula (30) is convergent with the convergence order \(\mathcal {O}(\tau ^{2-\alpha }+h_x^2)\).
Proof
Applying the definition (41)–(42), Eq. (45), and Lemma 8, we arrive at
where \(\tilde{C}={\text{e}}^{T}C_1\hat{C}\sqrt{L}\). Therefore, the difference scheme (30) is \(L_2\) convergent.
The proof of the convergence of the difference scheme with the tempered \({{\rm L}2{\text{-}}1}_{\sigma }\) formula (32) is similar to Theorem 3, so there exists the following result.
Theorem 4
Suppose \(u(x,t)\in C_{x,t}^{4, 3}\), then the difference scheme with the tempered L2-\(1_{\sigma }\) formula (32) is convergent with the convergence order \(\mathcal {O}(\tau ^{2}+h_x^2)\).
4 Implicit ADI Schemes for Two-Dimensional Tempered Fractional Diffusion Equation
In this section, we will discretize the two-dimensional diffusion equation using tempered L1, L1-2, and L2-\(1_{\sigma }\) formulas. From the point of view of computation, we construct ADI schemes by introducing different terms of mixed derivatives similar to [42]. Consider the following two-dimensional initial boundary value problem:
where \(\varOmega =(0,L)\times (0, L)\) and \(\partial \varOmega\) is the boundary of \(\varOmega\). Here, we also assume that functions \(f,\phi ,\psi _1,{\text{and}}\, \psi _2\) are smooth enough for our numerical schemes.
4.1 Construction of Tempered ADI Schemes
For two positive integers \(M_1\) and \(M_2\), denote \(h_x=L/M_1\), \(h_y=L/M_2\) with \(x_j=j h_x\), \(y_m=m h_y\). Let \(\bar{\varOmega }_h=\{(x_j,y_m)| 0 \leqslant j \leqslant M_1, 0 \leqslant m \leqslant M_2\}\), \(\varOmega _h=\bar{\varOmega }_h \cap \varOmega\), \(\varOmega _{\tau }=\{t_k| 0 \leqslant k \leqslant N\}\).
4.1.1 Tempered L1-ADI
For any grid function in \(\bar{\varOmega }_h \times \varOmega _{\tau }\), we define the spatial difference quotients
And denote the grid functions in \(\bar{\varOmega }_h \times \varOmega _{\tau }\), \(u_{j,m}^k=u(x_j,y_m,t_k)\), \(f_{j,m}^k=f(x_j,y_m,t_k),\) \((x_j,y_m)\in \varOmega _h, 0 \leqslant k \leqslant N\). Using the tempered L1 formula (5) to approximate the time derivative in the first equation of Eq. (49) at the grid point \((x_j,y_m,t_k)\), we have
Using Lemma 2 and the Taylor expansion formula, we get
Moreover, add the mixed derivative term \(\mu ^2 {\mathbb {D}_{t}^{\alpha ,\lambda }}\left( \delta _x^2 \delta _y^2 u_{j,m}^k\right)\) to Eq. (50), and there exists
where \((\hat{R}_1)_{j,m}^k=\hat{R}_{j,m}^k+\mu ^2 {\mathbb {D}_{t}^{\alpha ,\lambda }}\Big (\delta _x^2 \delta _y^2 u_{j,m}^k\Big ),~(x_j,y_m)\in \varOmega _h,1\leqslant k\leqslant N.\)
Lemma 9
For the truncation error given in Eq. (52), there is
Proof
If \(v(x)\in C^2[x-h,x+h]\), the Taylor’s formula with the integral remainder implies
Setting \(\delta _x^2 \delta _y^2u_{j,m}^k=P(x_j,y_m,t_k),\) we have
and hence
In addition, combining with Eq. (51), Eq. (53) immediately follows.
Letting \(U_{j,m}^k\) be the approximation solution of \(u(x_j,y_m,t_k)\) and omitting the truncation error in Eq. (52), we have
Because \(\mathbb {D}_{t}^{\alpha ,\lambda }\Big (\delta _x^2 \delta _y^2u_{j,m}^k\Big )\) is the tempered L1 operator of \(_0^{\text{C}}{}{\text{D}}_t^{\alpha ,\lambda }P(x_j,y_m,t_k)\), we call Eq. (55) the tempered L1-ADI scheme. According to the expression of the tempered L1 approximation operator (9) and noting that \(\widetilde{d}_{a,k}^{(\alpha )}=1\), multiplying \(\mu\) on both sides of Eq. (55) and the first equation of Eq. (55) yields
where I is the identical operator. Let \(U_{j,m}^*=(I-\mu \delta _y^2)U_{j,m}^k,~0 \leqslant j \leqslant M_1,~1 \leqslant m \leqslant M_2-1\). Then, we can rewrite the ADI scheme (55) as the following two steps.
Step 1 For fixed \(m=1,2,\cdots ,M_2-1\), using
we get the intermediate variables \(\{U_{j,m}^*\}\).
Step 2 For fixed \(j=1,2,\cdots ,M_1-1\), using
we get the numerical solutions \(\{U_{j,m}^k\}, 0\leqslant k\leqslant N\).
4.1.2 Tempered L1-2-ADI
If the time fractional derivative in problem (49) is approximated by the L1-2 formula (12), we have
With the help of Lemma 5 and the Taylor expansion, we have
Adding the mixed derivatives term \(\mu ^2({\widetilde{d}_{c,k}^{(k,\alpha )}})^{-2} \partial _{t}^{\alpha ,\lambda }\Big (\delta _x^2 \delta _y^2 u_{j,m}^k\Big )\) to the both sides of Eq. (57), and noticing the fact that \(\widetilde{d}_{c,k}^{(k,\alpha)}=c_0^{(k,\alpha)}\), there is
where \((\hat{R}_2)_{j,m}^k=\tilde{R}_{j,m}^k+\mu ^2(c_0^{(k,\alpha )})^{-2} \partial _{t}^{\alpha ,\lambda }\Big (\delta _x^2 \delta _y^2 u_{j,m}^k\Big ),~(x_j,y_m)\in \varOmega _h,1\leqslant k\leqslant N.\) Recalling the truncation error of the small term (54), we deduce that
Omitting the truncation error in Eq. (58), we have the tempered L1-2-ADI scheme
which can be rewritten as
If denote \(U_{j,m}^*=(I-\mu (c_0^{(k,\alpha )})^{-1}\delta _y^2)U_{j,m}^k,~0 \leqslant j \leqslant M_1,~1 \leqslant m \leqslant M_2-1\), then, for the view of computation, it can follow the procedure below.
Step 1 For fixed \(m=1,2,\cdots ,M_2-1\), computing
we can obtain \(\{U_{j,m}^*\}\).
Step 2 For fixed \(j=1,2,\cdots ,M_1-1\), applying
we obtain the numerical solutions \(\{U_{j,m}^k\}, 0 \leqslant k \leqslant N\).
4.1.3 Tempered L2-\(1_{\sigma }\)-ADI
Unlike above two numerical ADI schemes, we consider the numerical method for the first equation in Eq. (49) at the non-integer grid point \((x_j,y_m,t_{k+\sigma })\)
where \(u_{j,m}^{k+\sigma }=u(x_j,y_m,t_{k+\sigma })\). Combining with the tempered L2-\(1_{\sigma }\) formula (20), we have
Using the Taylor expansion, we can check that
which means \(\hat{R}_{j,m}^{k+\sigma }=\mathcal {O}(\tau ^{2}+h_x^2+h_y^2).\)
With the similar method of the tempered L1-ADI and tempered L1-2-ADI schemes, we add another term \(\mu ^2 \sigma ^2({\widetilde{d}_{s,k}^{(k,\alpha ,\sigma )}})^{-2}{\Delta _{t}^{\alpha ,\lambda }}\Big (\delta _x^2 \delta _y^2 u_{j,m}^{k+\sigma }\Big )\) to Eq. (61), which yields
where \((\hat{R}_3)_{j,m}^{k+\sigma }=\hat{R}_{j,m}^{k+\sigma }+\mu ^2 \sigma ^2({\widetilde{d}_{s,k}^{(k,\alpha ,\sigma )}})^{-2}{\Delta_{t}^{\alpha ,\lambda }}\Big (\delta _x^2 \delta _y^2 u_{j,m}^{k+\sigma }\Big )\) with the truncation error
Dropping the truncation error (62), we get the tempered L2-\(1_{\sigma }\)-ADI scheme
Taking into account the expression of the tempered L2-\(1_{\sigma }\) approximation formula (23), we can rewrite the scheme (64) as follows:
The tempered L2-\(1_{\sigma }\)-ADI scheme (65) can be summarized briefly in the following procedure.
Step 1 For fixed \(m=1,2,\cdots ,M_2-1\), using
we get the intermediate variables \(U_{j,m}^*=\Big (I-\mu \sigma ({\widetilde{d}_{s,k}^{(k,\alpha ,\sigma )}})^{-1} \delta _y^2\Big )U_{j,m}^{k+1},~0 \leqslant j \leqslant M_1,~0 \leqslant k \leqslant N-1.\)
Step 2 For fixed \(j=1,2,\cdots ,M_1-1\), using
we can get the numerical solutions \(\{U_{j,m}^{k+1}\}, 0 \leqslant k \leqslant N-1\).
4.2 Stability Analysis
Let \(\tilde{U}_j^k\) be the approximate solution of Eqs. (56) and (65). Then, define \(\hat{\varepsilon }_{j,m}^k=U_{j,m}^k-\tilde{U}_{j,m}^k,~1\leqslant k\leqslant N,1\leqslant j\leqslant M_1-1,1 \leqslant m \leqslant M_2-1,\) and error vectors
Similar to the one-dimensional case, define the function \(\hat{\varepsilon }^k(x,y)\) in the domain \(0 \leqslant x,y \leqslant L\) with the node values \(\hat{\varepsilon }_{j,m}^k\) at \((x_j,y_m,t_k)\). This means
And \(\hat{\varepsilon }^k(x,y)\) can be expanded in the Fourier series
where
According to the definition of the discrete \(L_2\) norm and Parseval’s equality, there exists
From numerical schemes (56) and (65), we have the related error equations
Assume that the solutions of Eqs. (67) and (68) have the following form:
where \(\beta _1=2\pi l_1/L,\beta _2=2\pi l_2/L\), and there are
For the stability of the tempered L1-ADI scheme, we have
Theorem 5
The tempered L1-ADI scheme (56) is unconditionally stable, and we can obtain
Proof
Inserting Eq. (69) and the Euler formula into Eq. (67), the error equation (67) can be rewritten as
where \(\kappa _1=\frac{4}{{h_x}^2}\sin ^2{(\frac{\beta _1 h_x}{2})},~~\kappa _2=\frac{4}{{h_y}^2}\sin ^2{(\frac{\beta _2 h_y}{2})}.\) Suppose that \(\xi _{l_1,l_2}^k(k=1,2,\cdots ,N)\) are the solutions of Eq. (70), then we will use the mathematical induction to proof the following inequality:
For \(k=1\), Eq. (70) clearly deduces that
Now, we assume that Eq. (71) is true for \(k=1,2,\cdots ,n-1\). For \(k=n\), there exists
where the relation \(\sum\limits_{\ell =1}^{n-1}(a_{n-\ell -1}^{(\alpha )}-a_{n-\ell }^{(\alpha )})+a_{n-1}^{(\alpha )}=1\) is utilized. Thus, Eq. (71) is proved. With the help of Eqs. (66) and (71), we obtain
which indicates that the tempered L1-ADI scheme (56) is unconditionally stable.
For the stability of the L2-\(1_{\sigma }\)-ADI difference scheme (65), we have
Theorem 6
The tempered L2-\(1_{\sigma }\)-ADI scheme (65) is unconditionally stable, and we can obtain
Proof
Rewriting the error equation (68) as
Supposing that \(\xi _{l_1,l_2}^{k+1}(k=0,1,\cdots ,N-1)\) are the solutions of Eq. (72), now we will prove the inequality
For \(k=0\), there is
Next, we suppose that
For \(k=n\), using the relation \(\sum\limits_{\ell =0}^{k-1}(s_{k-\ell -1}^{(k,\alpha ,\sigma )}-s_{k-\ell }^{(k,\alpha ,\sigma )})+s_{k}^{(k,\alpha ,\sigma )}={s_0^{(k,\alpha ,\sigma )}}\) and \({\widetilde{d}_{s,k}^{(k,\alpha ,\sigma )}}=s_0^{(k,\alpha ,\sigma )}{\text{e}}^{(\lambda t_{n+1}-t_{n+\sigma })}>s_0^{(k,\alpha ,\sigma )}\), there exists
Thus, according to Eqs. (73) and (66), we have \(\Vert \hat{\varepsilon }^k\Vert _2^2 \leqslant \Vert \hat{\varepsilon }^0\Vert _2^2.\)
4.3 Convergence Analysis
Just like the one-dimensional case, the convergence analysis of the two-dimensional case can be obtained similarly. Let \(C_{x,y,t}^{4, 4, 2}\) denote the space of function u(x, y, t) which satisfies \(u(x,y,t)\in C^2[0,t_k]\cap C^4(\bar{\varOmega })\), \(\bar{\varOmega }= [0,L] \times [0,L]\). Then, the corresponding convergence results are given as follows.
Theorem 7
Suppose \(u(x,y,t)\in C_{x,y,t}^{4, 4, 2}\), then the tempered L1-ADI scheme (56) is convergent with the accuracy \(\mathcal {O}(\tau ^{2\alpha }+h_x^2+h_y^2)\) for \(\alpha \in (0,2/3]\), and \(\mathcal {O}(\tau ^{2-\alpha }+h_x^2+h_y^2)\) for \(\alpha \in (2/3,1)\).
Theorem 8
Suppose \(u(x,y,t)\in C_{x,y,t}^{4, 4, 3}\), then the tempered L2-\(1_{\sigma }\)-ADI scheme (65) is convergent with the accuracy \(\mathcal {O}(\tau ^{2\alpha }+h_x^2+h_y^2)\) for \(\alpha \in (0,1)\).
5 Numerical Experiments
5.1 Truncation Error
In this subsection, we present an example to verify the theoretical results of the three proposed tempered formulas.
Example 1
We calculate the Caputo-tempered fractional derivative of function \(u(t)={\text{e}}^{-\lambda {t}}t^{4+\alpha }\) in [0, 1]. Applying the formula [21]
the exact solution of u(t) is given by
The numerical errors and the convergence orders are calculated with the different parameters \(\alpha =0.1,0.5,0.9\) and \(\lambda =0,6,20,40\). The pointwise maximum norm error and the corresponding convergence order are measured by \(\text{Error}( \tau )=\max\limits _{0 \leqslant j \leqslant N} \big |u(t_j)-U_j\big |~,~~\text{Order}=\log_2\Big (\frac{\text{Error}(\tau )}{\text{Error}(\tau /2)}\Big ),\) where \(U_j\) is the approximate solution of u(t) at the grid point \(t_j\).
Figures 1, 2, 3, where the time steps are 1/10, 1/20, 1/40, 1/80, 1/160, 1/320, 1/640, 1/1 280, and 1/2 560, give the maximum norm errors and convergence orders for different \(\alpha\), \(\lambda\) of the three presented discretization formulas (9), (16), and (23), respectively. Based on the results displayed in Figs. 1, 2, 3, we can easily observe that the convergence orders of tempered L1-2 and L2-\(1_{\sigma }\) formulas are both \(3-\alpha\), which is higher than \(2-\alpha\) order of the tempered L1 formula. These are in accordance with the theoretical analysis.
5.2 One-Dimensional Problem
To further illustrate the effectiveness of the proposed numerical formulas, we test two kinds of equations. The first equation is the initial boundary value problem of the time-tempered fractional diffusion equation and the second one is the time-tempered fractional Burgers equation.
5.2.1 Caputo-Tempered Fractional Diffusion Equation
Example 2
In this example, we solve problem (25) with \(L=1\) using the proposed numerical schemes (30)–(32). The source term f(x, t) was chosen as \(f(x,t)={\text{e}}^{-\lambda t+x}t^{4}\Big [\frac{\Gamma {(5+\alpha )}}{\Gamma {(5)}}-t^{\alpha }\Big ]\) such that the exact solution is \(u(x,t)={\text{e}}^{-\lambda t}{\text{e}}^{x}t^{4+\alpha }\) with \(\phi (x)=0,\psi _1(t)={\text{e}}^{-\lambda t}t^{4+\alpha }\), \(\psi _2(t)={\text{e}}^{-\lambda t+1}t^{4+\alpha }\). The numerical errors can be measured by the maximum norm errors at each discrete point
To demonstrate the numerical accuracy in time direction with a small spatial step size \(h=1/2\,000\), we list the computed results in Table 1. The orders of convergence are identified with theoretical orders of convergence (abbreviated as TOC) in the last row, and the errors of the tempered L1-2 and L2-\(1_{\sigma }\) formulas are significantly smaller than that of the tempered L1 formula. Owing to the interpolation at the non-grid point \(t_{k+\sigma }\), it should be noted that the order of the tempered L2-\(1_{\sigma }\) formula is \(\mathcal {O}(2)\) rather than \(\mathcal {O}(3-\alpha )\). Moreover, the comparisons of CPU times (in seconds) for different implicit difference schemes are exhibited in Fig. 4 of \(\alpha =0.1\) and \(\lambda =6\). From Fig. 4 we can see that the CPU times are proportional to the time steps, while the L2-\(1_{\sigma }\) formula requires more time for this problem than tempered L1 and L1-2 formulas.
5.2.2 Caputo-Tempered Fractional Burgers Equation
Consider the following time-tempered fractional Burgers equation:
where \(\kappa _{\alpha }\) is a positive constant. And denote the difference operator
The time direction is discretized by three proposed difference formulas, and the first and second derivatives of space direction are discretized by central difference. Regarding the nonlinear advection term, we adopt the linearization technique
Then, the following discretization schemes can be obtained, respectively:
where \(\mathcal {N}(U_j^{k+\sigma })=\frac{1}{3}[2U_j^{k}\delta _{\hat{x}}(U_j^{k+\sigma })+U_j^{{k+\sigma }}\delta _{\hat{x}}(U_j^{k})]\), and the initial value and boundary condition are discretized as \(U_j^0=u_0(x_j),~U_0^k=0,~U_M^k=0\).
Example 3
We solve the problem (74) using the numerical schemes (75)–(77) with \(L=1\). The source term is determined by the exact solution \(u(x,t)={\text{e}}^{-\lambda t}t^{3+\alpha }x^3(1-x)\), the initial value and boundary value are both 0.
Without loss of generality, we can get the following numerical results with \(\kappa_{\alpha} =1\). We check the numerical results in both time and space directions with \(\lambda =6\). The computational results about time direction are listed in Table 2 with \(h=1/2\,000\), while the corresponding results are listed in Table 3 for space direction with different ways of selecting \(\tau\) of three difference schemes.
5.3 Two-Dimensional Problem
Example 4
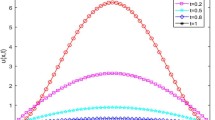
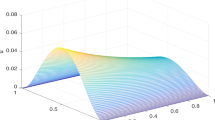
Consider the problem (49) on \(\varOmega =(0,\pi )\times (0,\pi ),\,t\in (0,1/2]\). The exact solution is \(u(x,y,t)={\text{e}}^{-\lambda t}\sin (x)\sin (y)t^2\) with the right source term
The error in this example is measured by
Tables 4 and 5 show the numerical results calculated by the three different implicit ADI schemes with different \(\alpha\) for classic (\(\lambda =0\)) and tempered (\(\lambda =6\)) situation when the spatial step size \(h_x=h_y=\pi /400\) are fixed, respectively. In Fig. 5, we plot the CPU times of the tempered L1-ADI, tempered L1-2-ADI, and tempered L2-\(1_\sigma\)-ADI schemes. From Fig. 5, we observe that the CPU times of L2-\(1_\sigma\)-ADI scheme are bigger than two other schemes, which is almost the same as the one-dimensional case.
6 Conclusion
In this paper, we presented and analyzed the efficient difference schemes for diffusion equations with the Caputo-tempered fractional derivative. To design the difference schemes, we first proposed the tempered L1 formula for the Caputo-tempered fractional derivative of the order \(\alpha \in (0,1)\). The tempered L1 formula is constructed by using the piecewise linear interpolation on each small interval with the order \(2-\alpha\). To improve the numerical accuracy, another two fractional numerical quadrature formulas, called tempered L1-2 and L2-\(1_{\sigma }\) formulas with the order \(3-\alpha\) are presented. The tempered L1-2 formula is established by means of the quadratic interpolation approximation on each cell \([t_{\ell -1},t_\ell ]\,(\ell \geqslant 2)\), while the linear interpolation approximation is applied on the first cell \([t_0,t_1]\). The tempered L2-\(1_{\sigma }\) formula is developed by using the quadratic interpolation approximation on each cell \([t_{\ell -1},t_\ell ]\,(1\leqslant \ell \leqslant k)\), while the linear interpolation in the cell \([t_k,t_{k+1}]\) is applied on the last non-integer grid cell \([t_k,t_{k+\sigma }]\).
We further designed the difference schemes for one- and two-dimensional fractional diffusion equations with the help of the presented interpolation formulas. We checked the stability and convergence of two proposed difference schemes by the Fourier analysis method. The key idea of our method is to examine the weighted coefficients of difference schemes. The analysis shows that the implicit numerical schemes are unconditionally stable and convergent when the tempered L1 formula and L2-\(1_{\sigma }\) formula are used. However, the rigorous theoretical analysis of numerical scheme are not obtained for the tempered L1-2 formula due to the lack of positivity of the weighting coefficients. Finally, several numerical examples are given to validate the theoretical results. As the Caputo fractional derivative, the challenges still exist due to the nonlocal property of tempered fractional derivatives [17]. We expect that a new technique will be needed to construct the fast algorithm for the considered problem.
References
Alikhanov, A.A.: A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 280, 424–438 (2015)
Baeumera, B., Meerschaert, M.M.: Tempered stable Lévy motion and transient super-diffusion. J. Comput. Appl. Math. 233, 2438–2448 (2010)
Cao, J.X., Li, C.P., Chen, Y.Q.: High-order approximation to Caputo derivatives and Caputo-type advection–diffusion equations (II). Fract. Calc. Appl. Anal. 18, 735–761 (2015)
Chen, M.H., Deng, W.H.: High order algorithms for the fractional substantial diffusion equation with truncated Lévy flights. SIAM J. Sci. Comput. 37, A890–A917 (2015)
Chen, M.H., Deng, W.H.: High order algorithm for the time-tempered fractional Feynman–Kac equation. J. Sci. Comput. 76, 867–887 (2018)
Chen, C.M., Liu, F., Burrage, K.: Finite difference methods and a Fourier analysis for the fractional reaction–subdiffusion equation. Appl. Math. Comput. 198, 754–769 (2008)
Chen, S., Shen, J., Wang, L.L.: Generalized Jacobi functions and their applications to fractional differential equations. Math. Comput. 85, 1603–1638 (2016)
Dehghan, M., Abbaszadeh, M., Deng, W.H.: Fourth-order numerical method for the space time tempered fractional diffusion–wave equation. Appl. Math. Lett. 73, 120–127 (2017)
Deng, W.H., Zhang, Z.J.: Numerical schemes of the time tempered fractional Feynman–Kac equation. Comput. Math. Appl. 73, 1063–1076 (2017)
Dimitrov, Y.: A second order approximation for the Caputo fractional derivative. J. Frac. Cal. Appl. 7, 175–195 (2016)
Dimitrov, Y.: Three-point approximation for the Caputo fractional derivative. Comm. Appl. Math. Comput. 31, 413–442 (2017)
Ding, H.F., Li, C.P.: High-order numerical approximation formulas for Riemann–Liouville (Riesz) tempered fractional derivatives: construction and application (II). Appl. Math. Lett. 86, 208–214 (2018)
Gajda, J., Magdziarz, M.: Fractional Fokker–Planck equation with tempered \(\alpha\)-stable waiting times: Langevin picture and computer simulation. Phys. Rev. E 82, 011117 (2010)
Gao, G.H., Sun, Z.Z., Zhang, H.W.: A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259, 33–50 (2014)
Gracia, J.L., Stynes, M.: Central difference approximation of convection in Caputo fractional derivative two-point boundary value problems. J. Comput. Appl. Math. 273, 103–115 (2015)
Henry, B.I., Langlands, T.A.M., Wearne, S.L.: Anomalous diffusion with linear reaction dynamics: from continuous time random walks to fractional reaction–diffusion equations. Phys. Rev. E 74, 031116 (2006)
Jiang, S., Zhang, J., Zhang, Q., Zhang, Z.: Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 21, 650–678 (2017)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equation. Elsevier, Amsterdam (2006)
Li, C., Deng, W.H.: High order schemes for the tempered fractional diffusion equations. Adv. Comput. Math. 42, 543–572 (2016)
Li, C.P., Wu, R.F., Ding, H.F.: High-order approximation to Caputo derivatives and Caputo-type advection–diffusion equations (I). Commun. Appl. Ind. Math. 6, 536 (2014)
Li, C., Deng, W.H., Zhao, L.J.: Well posedness and numerical algorithm for the tempered fractional ordinary differential equations. Discrete Contin. Dyn. Syst. Ser. B 24, 1989–2015 (2019)
Li, C., Sun, X.R., Zhao, F.Q.: LDG schemes with second order implicit time discretization for a fractional sub-diffusion equation. Results Appl. Math. 4, 100079 (2019)
Lin, Y.M., Xu, C.J.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)
Liu, F., Zhuang, P.H., Liu, Q.X.: The Applications and Numerical Methods of Fractional Differential Equations. Science Press, Beijing (2015)
Lubich, Ch.: Discretized fractional calculus. SIAM J. Math. Anal. 17, 704–719 (1986)
Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 172, 65–77 (2004)
Meerschaert, M.M., Zhang, Y., Baeumer, B.: Tempered anomalous diffusion in heterogeneous systems. Geophys. Res. Lett. 35, L17403 (2008)
Metzler, R., Barkai, E., Klafter, J.: Deriving fractional Fokker–Planck equations from generalised master equation. Europhys. Lett. 46, 431–436 (1999)
Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, New York (1974)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Sabzikar, F., Meerschaert, M.M., Chen, J.H.: Tempered fractional calculus. J. Comput. Phys. 293, 14–28 (2015)
Samko, S., Kilbas, A., Marichev, O.: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, London (1993)
Schmidt, M.G.W., Sagués, F., Sokolov, I.M.: Mesoscopic description of reactions for anomalous diffusion: a case study. J. Phys. Condens. Matter. 19, 065118 (2007)
Sousa, E., Li, C.: A weighted finite difference method for the fractional diffusion equation based on the Riemann–Liouville drivative. Appl. Numer. Math. 90, 22–37 (2015)
Sun, Z.Z., Wu, X.N.: A fully discrete difference scheme for a diffusion wave system. Appl. Numer. Math. 56, 193–209 (2006)
Sun, X.R., Li, C., Zhao, F.Q.: Local discontinuous Galerkin methods for the time tempered fractional diffusion equation. Appl. Math. Comput. 365, 124725 (2020)
Tatar, N.: The decay rate for a fractional differential equation. J. Math. Anal. Appl. 295, 303–314 (2004)
Wang, Z.B., Vong, S.W.: Compact difference schemes for the modified anomalous fractional subdiffusion equation and the fractional diffusion–wave equation. J. Comput. Phys. 277, 1–15 (2014)
Zayernouri, M., Ainsworth, M., Karniadakis, G.: Tempered fractional Sturm–Liouville eigenproblems. SIAM J. Sci. Comput. 37, A1777–A1800 (2015)
Zhang, Y.: Moments for tempered fractional advection–diffusion equations. J. Stat. Phys. 139, 915–939 (2010)
Zhang, Z.J., Deng, W.H.: Numerical approaches to the functional distribution of anomalous diffusion with both traps and flights. Adv. Comput. Math. 43, 1–34 (2017)
Zhang, Y.N., Sun, Z.Z.: Alternating direction implicit schemes for the two-dimensional fractional sub-diffusion equation. J. Comput. Phys. 230, 8713–8728 (2011)
Zhang, H., Liu, F., Turner, I., Chen, S.: The numerical simulation of the tempered fractional Black–Scholes equation for European double barrier option. Appl. Math. Model. 40, 5819–5834 (2016)
Acknowledgements
The authors would like to thank Prof. Zhi-Zhong Sun for his various useful discussions on the L1-2 approximation, and pointing out several typos in an earlier version of this paper. We also thank the reviewers for their valuable suggestions and comments to improve this paper. This research was partially supported by the National Natural Science Foundation of China under Grant Nos.11426174,11702214,11972286, the Natural Science Basic Research Plan in Shaanxi Province of China under Grant No.2018JM1016, and the Shaanxi science and technology research projects under Grant No.2015GY004.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Background of Eq. (1)
In particle motion, sometimes the waiting time of particles is too long, however, too long waiting time may not be appropriate for some physical process, therefore, we need to control the waiting time of particles in the finite time domain. To overcome this shortcoming, the PDFs which are exponentially tempered power law are put forward [13, 21]. Therefore, the tempered power law waiting time leads to the time-tempered fractional derivatives, which have proved available in geophysics. And the purpose of tempered fractional differential equations is to more accurately describe the motion behavior of particles in complex dynamic systems. The CTRW model is based on the idea that the length of a given jump, as well as the waiting time elapsing between two successive jumps is drawn from a pdf \(\psi (\mathbf{x} , t)\) which will be referred to as the jump pdf. For \(\psi (\mathbf{x} , t)\), the jump length pdf gives \(\varphi (\mathbf{x} )=\int _{0}^{\infty }\psi (\mathbf{x} , t)\mathrm{d}t,\) and the waiting time pdf obeys \(w(t)=\int _{R^d}\psi (\mathbf{x} , t){\text{d}}\mathbf{x} .\) Thus, \(\varphi (\mathbf{x} ){\text{d}}\mathbf{x}\) produces the probability for a jump length in the interval \((\mathbf{x} , \mathbf{x} +{\text{d}}\mathbf{x} )\) and w(t)dt the probability for a waiting time in the interval \((t, t+\mathrm{d}t)\). If the jump length and waiting time are independent random variables, one finds the decoupled form \(\psi (\mathbf{x} , t)=\varphi (\mathbf{x} )w(t)\) for the jump pdf \(\psi (\mathbf{x} , t)\). The probability density function \(\eta (\mathbf{x} ,t)\) of the positions \(\mathbf{x}\) of the particle, which have just made a jump at time t can be described through an appropriate generalized master equation [16, 33]
The pdf \(u(\mathbf{x} ,t)\) of particle being in \(\mathbf{x}\) at time t is given by
where \(\varPsi (t-t^\prime )\) is the probability of staying at site \(\mathbf{x}\) for a time \(t-t^\prime\) after a jump
The pdf u(x, t) in the Fourier–Laplace space takes the form
where the Laplace and Fourier transforms are defined, respectively, by \(\mathcal {L}(u(t))=\tilde{u}(s)=\int _0^{\infty }u(t){\text{e}}^{-st}\mathrm{d}t,s\in C,Re(s)>0,\) and \(\mathcal {F}(u(\mathbf{x} ))=\widehat{u}(\mathbf{k} )=\frac{1}{(2\pi )^{d}} \int _{R^{d}}{\text{e}}^{-{\text{i}}\mathbf{k} \cdot \mathbf{x} }u(\mathbf{x} ){\text{d}}\mathbf{x} ,\mathbf{k} =(k_{1},k_{2},\cdots ,k_{d})\in R^{d}.\) In the Fourier space, the jump length distribution behaved [28]
where \(\varLambda (\mathbf{k} )\) is the characteristic exponent of \(\varphi (\mathbf{x} )\), the probability distribution for jumps. Taking \(\varLambda (\mathbf{k} )=-C_{\mu }|\mathbf{k} |^{2},\) and a waiting time pdf of a Pareto type [28] \(\widetilde{w}(s)\simeq 1- \Gamma (1-\alpha )\bar{\tau }^{\alpha }s^{\alpha },0<\alpha <1,\) Eq. (A1) can be rewritten in the following form:
Introducing the Riemann–Liouville tempered fractional derivative operator [18, 31]
and the Fourier transform of the standard Laplace operator is \(\mathcal {F}\big (\Delta u(\mathbf{x} )\big ) =-|\mathbf{k} |^{2}\mathcal {F}(u(\mathbf{x} )),\) after inverting the Fourier–Laplace transform on both sides of Eq. (A2), we get that the pdf of diffusion particles obeys the tempered fractional diffusion equation [16]
Appendix B: Proof of Lemma 1
For the proof of (i), (ii), and (iii), see the references [23, 35].
(iv) According to (i) and the definition of Eqs. (7) and (8), it is easy to see that (iv) is true.
(v) Let \(g(x)=[(k-x+1)^{(1-\alpha )}-(k-x)^{1-\alpha }]{\text{e}}^{\lambda (t_{x-1}-t_k)}\). Then, there is
which represents that \(\overline{d}_{a,m}^{(\alpha )}\) is monotone increasing about m.
(vi) \(\widetilde{d}_{a,m}^{(\alpha )}\) is also monotone increasing with the same fashion of (v).
(vii) \(\overline{d}_{a,m+1}^{(\alpha )}-\widetilde{d}_{a,m}^{(\alpha )}=\Big (a_{k-m-1}^{(\alpha )}-a_{k-m}^{(\alpha )}\Big ){\text{e}}^{\lambda (t_m- t_k)}\leqslant a_{k-m-1}^{(\alpha )}-a_{k-m}^{(\alpha )},~~1\leqslant m\leqslant k-1.\)
(viii) \(\overline{d}_{a,1}^{(\alpha )}=a_{k-1}^{(\alpha )}{\text{e}}^{\lambda (t_0- t_k)}\leqslant a_{k-1}^{(\alpha )}.\)
Appendix C: Proof of Lemma 2
By simple calculation, we have the truncation error as follows:
and it yields
On the other hand, for the integral of the right term, we have
with
and
Recalling \(v(t)={\text{e}}^{\lambda t}u(t)\), we have
Combining Eqs. (C3)–(C5) with Eq. (C2) we arrive at Eq. (10).
Appendix D: Proof of Lemma 4
(i) For \(k=2\), \(\overline{d}_{c,1}^{(k,\alpha )}=c_1^{(k,\alpha )}{\text{e}}^{\lambda (t_0-t_2)}\), and
which is strictly monotone decreasing, so \(c_1^{(k,\alpha )}\in (-1/2,1)\). Moreover, \(\alpha _1\approx 0.673\,6\) is the unique zero point for \(\alpha \in (0,1)\), which means
Thus, \(\overline{d}_{c,1}^{(k,\alpha )}\leqslant c_1^{(k,\alpha )}\) for \(\alpha \in (0,\alpha _1)\).
(ii) For \(k=3\), \(\overline{d}_{c,2}^{(k,\alpha ,\sigma )} -\widetilde{d}_{c,1}^{(k,\alpha )}=\Big (c_1^{(k,\alpha )}-c_2^{(k,\alpha )}\Big ){\text{e}}^{\lambda (t_1-t_3)}\) and \(c_1^{(k,\alpha )}-c_2^{(k,\alpha )}=a_1^{(\alpha )}+2b_1^{(\alpha )}-b_0^{(\alpha )}-a_2^{(\alpha )}\). Moreover, the zero point of \(c_1^{(k,\alpha )}-c_2^{(k,\alpha )}\) showed in Fig. 6a is \(\alpha _2 \approx 0.390\,9\), i.e.,
Thus \(\overline{d}_{c,2}^{(k,\alpha )}-\widetilde{d}_{c,1}^{(k,\alpha )}\leqslant c_1^{(k,\alpha )}-c_2^{(k,\alpha )}\) for \(\alpha \in (0,\alpha _2)\).
(iii) For \(k>3\), \(\overline{d}_{c,k-1}^{(k,\alpha )} -\widetilde{d}_{c,k-2}^{(k,\alpha )}=\Big (c_1^{(k,\alpha )}-c_2^{(k,\alpha )}\Big ){\text{e}}^{\lambda (t_{k-2}-t_k)}\leqslant c_1^{(k,\alpha )}-c_2^{(k,\alpha )}\) for \(\alpha \in (0,\alpha _3)\), where the zero point \(\alpha _3\) is about 0.373 9 in Fig. 6b and \(c_1^{(k,\alpha )}-c_2^{(k,\alpha )}=a_1^{(\alpha )}+2b_1^{(\alpha )}-b_0^{(\alpha )}-a_2^{(\alpha )}-b_2^{(\alpha )}\).
(iv) The computed numerically as in the Fig. 6.
Appendix E: Proof of Lemma 5
For \(k=1\), we find that Eq. (12) actually is the tempered L1 formula of the Caputo-tempered fractional derivative and its numerical accuracy is \(\mathcal {O}(\tau ^{2-\alpha })\), i.e.,
thus Eq. (17) is established.
For \(k\geqslant 2\), we get
In [14] there exist
and we have
The substitution of Eqs. (E2)–(E5) into Eq. (E1) can lead to Eq. (18).
Appendix F: Proof of Lemma 7
The error estimate is
Similarly to [1], we have
and
where another term in (F3) besides \(\mathcal {O}(\tau ^{3-\alpha })\) is zero due to the special choice of \(\sigma =1-\alpha /2\), so the order of truncation error \(T^{k+\sigma }\) is \(3-\alpha\). At the same time, there exists
Then substituting Eqs. (F2)–(F4) into Eq. (F1), we have
and using the Taylor expansion
thus Eq. (24) is proved.
Rights and permissions
About this article
Cite this article
Zhao, L., Li, C. & Zhao, F. Efficient Difference Schemes for the Caputo-Tempered Fractional Diffusion Equations Based on Polynomial Interpolation. Commun. Appl. Math. Comput. 3, 1–40 (2021). https://doi.org/10.1007/s42967-020-00067-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42967-020-00067-5