A Kansa-Radial Basis Function Method for Elliptic Boundary Value Problems in Annular Domains

Abstract

We employ a Kansa-radial basis function (RBF) method for the numerical solution of elliptic boundary value problems in annular domains. This discretization leads, with an appropriate selection of collocation points and for any choice of RBF, to linear systems in which the matrices possess block circulant structures. These linear systems can be solved efficiently using matrix decomposition algorithms and fast Fourier transforms. A suitable value for the shape parameter in the various RBFs used is found using the leave-one-out cross validation algorithm. In particular, we consider problems governed by the Poisson equation, the inhomogeneous biharmonic equation and the inhomogeneous Cauchy–Navier equations of elasticity. In addition to its simplicity, the proposed method can both achieve high accuracy and solve large-scale problems. The feasibility of the proposed techniques is illustrated by several numerical examples.

1 Introduction

During the past decade, radial basis function (RBF) collocation methods have attracted great attention in scientific computing and have been widely applied to solve a large class of problems in science and engineering. Among the various types of RBF collocation methods, the Kansa method [15], proposed in early 1990s is the most known. One of the main attractions of this method is its simplicity, since in it neither a boundary nor a domain discretization are required. This feature is especially useful for solving high dimensional problems in complex geometries. Furthermore, we have the freedom of choosing an RBF as the basis function which does not necessary satisfy the governing equation. Hence, the Kansa method is especially attractive for solving nonhomogeneous equations. In general, the multiquadric (MQ) function is the most commonly used RBF in the implementation of the Kansa method. Using the MQ, an exponential convergence rate has been observed and thus high accuracy beyond the reach of the traditional numerical methods such as finite element and finite difference methods can be achieved. Despite all the advantages mentioned above, the Kansa method has a number of unfavorable features. It is known that the determination of the optimal shape parameter of various RBFs is still a challenge. Currently, there are a variety of techniques [5, 11, 16, 26, 32] available for the determination of a suitable shape parameter. In this paper, we will use the so called leave-one-out cross validation (LOOCV) proposed by Rippa [32] to find a sub-optimal shape parameter. Another potential problem of the RBF collocation methods is the ill-conditioning of the resultant matrix. On the one hand, when the number of interpolation points is increased, the accuracy improves, while, on the other hand, the condition number becomes larger. This phenomenon is referred to as the principle of uncertainty by Schaback [33, 34]. Eventually, when the number of interpolation points becomes too large, the condition number becomes enormous and the solution breaks down. When using globally supported RBFs such as the MQ, the resultant matrix of the Kansa method is dense and ill-conditioned. Not only do we have a stability problem, but also the computational cost becomes very high. The Kansa method is thus not suitable for the solution of large-scale problems which require the use of a large number of interpolation points. In recent years, the localized Kansa method [27] has been developed for handling large-scale problems. In this approach, a local influence domain is established for each interpolation point and only a small number of neighbouring points is used to approximate the solution. The resultant matrix is thus sparse allowing for the use of a large number of collocation points. However, the accuracy of the localized Kansa method is rather low because the local influence domain only contains a small number of interpolation points.

In this paper, we couple the Kansa method and a matrix decomposition technique for solving problems using a large number of interpolation points. Since global RBFs are used as basis functions, we can also achieve high accuracy in numerical results. To be more specific, we consider the discretization of elliptic boundary value problems in annular domains using the Kansa method. For any choice of RBF, such appropriate discretizations lead to linear systems in which the coefficient matrices possess block circulant structures and which are solved efficiently using matrix decomposition algorithms (MDAs). An MDA [1] is a direct method which reduces the solution of an algebraic problem to the solution of a set of independent systems of lower dimension with, often, the use of fast Fourier Transforms (FFTs). MDAs lead to considerable savings in computational cost and storage. This decomposition technique not only allows us to handle large-scale matrices but also makes it possible to implement the LOOCV technique to find the sub-optimal shape parameter of the RBFs used. It should be noted that the LOOCV technique is not suitable when the size of the matrix is too large. Such MDAs have been used in the past in various applications of the method of fundamental solutions (MFS) to boundary value problems in geometries possessing radial symmetry, see e.g., [17, 18]. A similar MDA was also applied for the approximation of functions and their derivatives using RBFs in circular domains in [21], see also, [13]. Some preliminary results for the Dirichlet Poisson problem have recently been presented in [20].

The paper is organized as follows. In Sect. 2 we present the Kansa method and the proposed MDA for both the Dirichlet and the mixed Dirichlet–Neumann Poisson problem. The Kansa-RBF discretization for the first and second biharmonic problems is given in Sect. 3. The corresponding discretization and MDA for the Dirichlet and the mixed Dirichlet–Neumann boundary value problems for the more challenging Cauchy–Navier equations of elasticity is described in Sect. 4. In Sect. 5 we present the results of three numerical experiments. In the first example various RBFs are tested and the normalized MQ turns out to be the most effective one. As a result, in the other examples, we focus on using the normalized MQ. We also show that the LOOCV technique is very effective for finding a good shape parameter of the RBFs. All three examples show that we can solve large-scale problems with high accuracy. Finally, in Sect. 6 some conclusions and ideas for future work are outlined.

2 The Poisson Equation

2.1 The Problem

We first consider the Poisson equation

$$\begin{aligned} \Delta u \,=\, f \quad \text{ in } \quad \Omega , \end{aligned}$$

(2.1a)

subject to the Dirichlet boundary conditions

$$\begin{aligned} u= & {} g_1 \quad \text{ on } \quad \partial \Omega _1,\end{aligned}$$

(2.1b)

$$\begin{aligned} u= & {} g_2 \quad \text{ on } \quad \partial \Omega _2, \end{aligned}$$

(2.1c)

in the annulus

$$\begin{aligned} \Omega =\left\{ {\varvec{x} } \in {\mathbb {R}}: {\varrho }_1 <|{\varvec{x} }|< {\varrho }_2 \right\} . \end{aligned}$$

(2.2)

The boundary $\partial \Omega = \partial \Omega _1\cup \partial \Omega _2$, $\partial \Omega _1\cap \partial \Omega _2=\emptyset$ where $\partial \Omega _1=\left\{ {\varvec{x} } \in {\mathbb {R}}^2: |{\varvec{x} }|={\varrho }_1 \right\}$ and $\partial \Omega _2=\left\{ {\varvec{x} } \in {\mathbb {R}}^2: |{\varvec{x} }|={\varrho }_2 \right\}$.

2.2 Kansa’s Method

In Kansa’s method [15] we approximate the solution $u$ of boundary value problem (2.1) by a linear combination of RBFs [3, 7]

$$\begin{aligned} u_{\mathsf{N}}(x,y)=\sum ^{\mathsf{N}}_{\mathsf{n}=1} a_{\mathsf{n}} \phi _\mathsf{n}(x,y),\qquad (x,y) \in \bar{\Omega }. \end{aligned}$$

(2.3)

The RBFs $\phi _\mathsf{n}(x,y), \mathsf{n}=1, \ldots , \mathsf{N}$ can be expressed in the form

$$\begin{aligned} \phi _\mathsf{n}(x,y)=\Phi (r_\mathsf{n}), \quad \text{ where } \quad r_\mathsf{n}^2=(x-x_\mathsf{n})^2+(y-y_\mathsf{n})^2. \end{aligned}$$

(2.4)

Thus each RBF $\phi _\mathsf{n}$ is associated with a point $(x_\mathsf{n}, y_\mathsf{n})$. These points $\left\{ (x_\mathsf{n},y_\mathsf{n})\right\} _{\mathsf{n}=1}^{\mathsf{N}}$ are usually referred to as centers.

The coefficients $\left\{ a_{\mathsf{n}}\right\} _{\mathsf{n}=1}^{\mathsf{N}}$ in Eq. (2.3) are determined from the collocation equations

$$\begin{aligned} \Delta u (x_\mathsf{m},y_\mathsf{m})= & {} f(x_\mathsf{m},y_\mathsf{m}), \quad \mathsf{m}=1, \ldots {\mathsf{M}}_\mathrm{int},\end{aligned}$$

(2.5a)

$$\begin{aligned} u (x_\mathsf{m},y_\mathsf{m})= & {} g_1 (x_\mathsf{m},y_\mathsf{m}), \quad \mathsf{m}={\mathsf{M}}_\mathrm{int}+1, \ldots , {\mathsf{M}}_\mathrm{int}+{\mathsf{M}}_{\mathrm{bry}_1},\end{aligned}$$

(2.5b)

$$\begin{aligned} u (x_\mathsf{m},y_\mathsf{m})= & {} g_2 (x_\mathsf{m},y_\mathsf{m}), \quad \mathsf{m}={\mathsf{M}}_\mathrm{int}+{\mathsf{M}}_{\mathrm{bry}_1}+1, \ldots , {\mathsf{M}}_{\mathrm{int}}+{\mathsf{M}}_{\mathrm{bry}}, \end{aligned}$$

(2.5c)

where ${\mathsf{M}}_{\mathrm{int}}+{\mathsf{M}}_{\mathrm{bry}} = {\mathsf{M}}$ and the points $\left\{ (x_\mathsf{m},y_\mathsf{m})\right\} _{\mathsf{m}=1}^{\mathsf{M}} \in \bar{\Omega }$ are the collocation points. Note that, in general, the collocation points are not the same as the centers and ${\mathsf{M}}\ge {\mathsf{N}}$.

In this work, however, we shall assume that ${\mathsf{M}} = {\mathsf{N}}$ and that the centres are the same as the collocation points. In particular, we define the $M$ angles

$$\begin{aligned} {\vartheta }_m= \dfrac{2\pi (m-1)}{M}, \quad m=1, \ldots , M, \end{aligned}$$

(2.6)

and the $N$ radii

$$\begin{aligned} \mathsf{r}_{n}= {\varrho }_1 + \left( {\varrho }_2-{\varrho }_1\right) \frac{n-1}{N-1}, \quad n=1, \ldots , N. \end{aligned}$$

(2.7)

The collocation points $\left\{ (x_{mn}, y_{mn})\right\} _{m=1,n=1}^{M,N}$ are defined as follows:

$$\begin{aligned}&x_{mn}=\mathsf{r}_{n} \cos \left( {\vartheta }_m + \frac{2\pi \alpha _n}{M}\right) , \quad y_{mn}=\mathsf{r}_{n} \sin \left( {\vartheta }_m + \frac{2\pi \alpha _n}{M}\right) , \quad \nonumber \\&\quad m=1, \ldots , M, \; n=1, \ldots , N.\nonumber \\ \end{aligned}$$

(2.8)

In (2.8) the parameters $\left\{ \alpha _n\right\} _{n=1}^N \in [-1/2, 1/2]$ correspond to rotations of the collocation points and may be used to produce more uniform distributions. Typical distributions of collocation points without rotation ($\alpha _n=0, n=1,\ldots ,n$) and with rotation are given in Fig. 1. In the current application of Kansa’s method, we take

$$\begin{aligned} u_{MN}(x,y)=\sum ^{M}_{m=1} \sum ^{N}_{n=1} a_{mn} \phi _{mn}(x,y),\qquad (x,y) \in \bar{\Omega }, \end{aligned}$$

(2.9)

Fig. 1

Typical discretization of the domain with a no rotation of the collocation points and b with rotation of the collocation points. The crosses ($+$) denote the collocation points

where the ${\mathsf{M}}=MN$ coefficients $\left\{ ({a}_{mn})\right\} _{m=1,n=1}^{M,N}$ are unknown. These coefficients are determined by collocating the differential equation (2.1a) and the boundary conditions (2.1b)–(2.1c) in the following way:

$$\begin{aligned} \Delta u_{MN}(x_{mn},y_{mn})= & {} f (x_{mn},y_{mn}), \quad m=1, \ldots , M, \; n= 2, \ldots , N-1, \nonumber \\ u_{MN}(x_{m1},y_{m1})= & {} g_{1}(x_{m1},y_{m1}), \quad u_{MN}(x_{mN},y_{mN})=g_{2}(x_{mN},y_{mN}), \quad m=1, \ldots , M,\nonumber \\ \end{aligned}$$

(2.10)

yielding a total of ${\mathsf{M}}=MN$ equations.

By vectorizing the arrays of unknown coefficients and collocation points from

$$\begin{aligned}&\mathsf{a}_{(n-1)M+m}=a_{mn}, \quad \mathsf{x}_{(n-1)M+m}=x_{mn}, \quad \mathsf{y}_{(n-1)M+m}=y_{mn}, \quad \nonumber \\&m=1, \ldots , M, \; n=1, \ldots , N, \end{aligned}$$

(2.11)

Equation (2.10) yield a linear system of the form

$$\begin{aligned} A \, {\varvec{a} } = \left( \begin{array}{cccc} A_{1,1} &{}\quad A_{1,2} &{}\quad \ldots &{}\quad A_{1,N}\\ A_{2,1} &{}\quad A_{2,2} &{}\quad \ldots &{}\quad A_{2,N}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ A_{N,1} &{}\quad A_{N,2} &{}\quad \ldots &{}\quad A_{N,N} \end{array} \right) \, \left( \begin{array} [c]{c} {\varvec{a} }_1\\ {\varvec{a} }_2\\ \vdots \\ {\varvec{a} }_N \end{array} \right) \, = \, \left( \begin{array} [c]{c} {\varvec{b} }_1\\ {\varvec{b} }_2\\ \vdots \\ {\varvec{b} }_N \end{array} \right) ={\varvec{b} }\,. \end{aligned}$$

(2.12)

The $M\times M$ submatrices $A_{n_1,n_2}, \; n_1,n_2=1, \ldots , N$ are defined as follows:

$$\begin{aligned} \left( A_{n_1,n_2}\right) _{m_1,m_2}= & {} \Delta \phi _{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1}), \nonumber \\&m_1,m_2=1,\ldots ,M, \; n_1=2, \ldots , N-1, \; n_2=1, \ldots , N,\end{aligned}$$

(2.13a)

$$\begin{aligned} \left( A_{1,n}\right) _{m_1,m_2}= & {} \phi _{m_2,n}(x_{m_1,1},y_{m_1,1}),\nonumber \\&m_1,m_2=1,\ldots ,M, \; n=1, \ldots , N,\end{aligned}$$

(2.13b)

$$\begin{aligned} \left( A_{N,n}\right) _{m_1,m_2}= & {} \phi _{m_2,n}(x_{m_1,N},y_{m_1,N}), \end{aligned}$$

(2.13c)

while the $M\times 1$ vectors ${\varvec{a} }_n, {\varvec{b} }_n, n=1, \ldots , N$ are defined as

$$\begin{aligned}&\left( {\varvec{a} }_n\right) _m=a_{mn}, \; m=1, \ldots , M, \; N=1, \ldots , N,\\&\left( {\varvec{b} }_n\right) _m=f (x_{mn},y_{mn}), \quad m=1, \ldots , M, \; n= 2, \ldots , N-1,\\&\left( {\varvec{b} }_1\right) _m=g_1(x_{m1},y_{m1}), \quad \left( {\varvec{b} }_N\right) _m=g_2(x_{mN},y_{mN}), \quad m=1, \ldots , M. \end{aligned}$$

2.2.1 Neumann Boundary Conditions

Suppose that instead of boundary condition (2.1b) we had the Neumann boundary condition

$$\begin{aligned} \dfrac{\partial u}{\partial \mathrm{n}}\, =\, g_1 \quad \text{ on } \quad \partial \Omega _1, \end{aligned}$$

(2.14)

where $\mathbf{n}(x,y)=(\mathrm{n}_x, \mathrm{n}_y)$ denotes the outward normal vector to the boundary at the point $(x,y)$. The corresponding submatrices $\left( A_{1,n}\right) , \, n=1, \ldots , N$, in (2.13b) are now defined by

$$\begin{aligned} \left( A_{1,n}\right) _{m_1,m_2}= \dfrac{\partial \phi _{m_2,n}}{\partial \mathrm{n}}(x_{m_1,1},y_{m_1,1}), \quad m_1,m_2=1,\ldots ,M. \end{aligned}$$

(2.15)

As proved in the “Appendix” (Lemma 1) each of the $M\times M$ submatrices $A_{n_1,n_2}, \; n_1, n_2=1, \ldots , N$, in the coefficient matrix in (2.12) is circulant [6]. Hence matrix $A$ in system (2.12) is block circulant.

2.3 Matrix Decomposition Algorithm

First, we define the unitary $M \times M$ Fourier matrix

$$\begin{aligned} U_M \,=\, \frac{1}{\sqrt{M}} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 1 &{} 1 &{} \cdots &{} 1 \\ 1 &{} \bar{\omega }&{} \bar{\omega }^2 &{} \cdots &{} \bar{\omega }^{M\!-\!1} \\ 1 &{} \bar{\omega }^2 &{} \bar{\omega }^4 &{} \cdots &{} \bar{\omega }^{2(M\!-\!1)} \\ \vdots &{} \vdots &{} \vdots &{} &{} \vdots \\ 1 &{} \bar{\omega }^{M\!-\!1} &{} \bar{\omega }^{2(M\!-\!1)} &{} \cdots &{} \bar{\omega }^{(M\!-\!1)(M\!-\!1)} \end{array} \right) , \quad \text{ where } \quad \omega =\mathrm{e}^{2\pi \mathrm{i}/M}, \, \mathrm{i}^2=-1. \nonumber \\ \end{aligned}$$

(2.16)

If $I_N$ is the $N \times N$ identity matrix, pre–multiplication of system (2.12) by $I_N \otimes U_M$ yields

$$\begin{aligned} \left( I_N \otimes U_M \right) A \left( I_N \otimes U^*_M \right) \left( I_N \otimes U_M \right) {\varvec{a} } \,=\, \left( I_N \otimes U_M \right) {\varvec{b} } \quad \text{ or } \quad \tilde{A} \tilde{{\varvec{a} }}\,=\, \tilde{{\varvec{b} }}, \end{aligned}$$

(2.17)

where

$$\begin{aligned} \tilde{A} =\left( I_N \otimes U_M \right) A \left( I_N \otimes U^*_M \right) \end{aligned}$$

$$\begin{aligned} =\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} U_M A_{1,1} U^*_M &{} U_M A_{1,2} U^*_M &{} \cdots &{} U_M A_{1,N} U^*_M \\ U_M A_{2,1} U^*_M &{}U_M A_{2,2} U^*_M &{} \cdots &{} U_M A_{2,N} U^*_M \\ \vdots &{} \vdots &{} &{} \vdots \\ U_M A_{N,1} U^*_M &{} U_M A_{N,2} U^*_M &{} \cdots &{} U_M A_{N,N} U^*_M \end{array} \right) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} D_{1,1} &{} D_{1,2} &{} \cdots &{} D_{1,N} \\ D_{2,1} &{} D_{2,2} &{} \cdots &{} D_{2,N} \\ \vdots &{} \vdots &{} &{} \vdots \\ D_{N,1} &{} D_{N,2} &{} \cdots &{} D_{N,N} \end{array} \right) , \!\nonumber \\ \end{aligned}$$

(2.18)

and

$$\begin{aligned} \tilde{{\varvec{a} }}\!= \!\left( I_N \otimes U_M \right) {\varvec{a} }\! =\! \left( \begin{array}{c} \!U_M {\varvec{a} }_1 \!\\ \!U_M {\varvec{a} }_2\! \\ \! \vdots \!\\ \!U_M {\varvec{a} }_N \!\end{array} \right) \! =\! \left( \begin{array}{c} \!\tilde{{\varvec{a} }}_1 \!\\ \! \tilde{{\varvec{a} }}_2 \!\\ \! \vdots \!\\ \!\tilde{{\varvec{a} }}_N \!\end{array} \right) , \quad \tilde{{\varvec{f} }}\!= \! \left( I_N \otimes U_M \right) {\varvec{b} } \!=\!\left( \begin{array}{c}\! U_M {\varvec{b} }_1 \!\\ \!U_M {\varvec{b} }_2\! \\ \! \vdots \!\\ \!U_M {\varvec{b} }_N \!\end{array} \right) \! = \!\left( \begin{array}{c} \!\tilde{{\varvec{b} }}_1\! \\ \!\tilde{{\varvec{b} }}_2\! \\ \!\vdots \! \\ \!\tilde{{\varvec{b} }}_N \!\end{array} \right) . \nonumber \\ \end{aligned}$$

(2.19)

From the properties of circulant matrices [6], each of the $M \times M$ matrices $D_{n_1,n_2}, \; n_1, n_2 = 1, \cdots , N$, is diagonal. If, in particular

$$\begin{aligned} D_{n_1,n_2}= & {} \hbox {diag} \left( D_{n_1,n_{2_{1}}}, D_{n_1,n_{2_2}}, \ldots , D_{n_1,n_{2_M}} \right) \quad \text{ and }\nonumber \\ A_{n_1,n_2}= & {} \text{ circ } \left( A_{n_1,n_{2_1}}, A_{n_1,n_{2_2}} \ldots , A_{n_1,n_{2_M}}\right) , \end{aligned}$$

we have, for $n_1, n_2 = 1, \cdots , N$,

$$\begin{aligned} D_{{n_1, n_2}_m} \,=\, \sum _{k=1}^{M} A_{{n_1, n_2}_k} \omega ^{(k-1)(m-1)}, \; m=1, \cdots , M. \end{aligned}$$

(2.20)

Since the matrix $\tilde{A}$ consists of $N^2$ blocks of order $M$, each of which is diagonal, the solution of system (2.17) can be decomposed into solving the $M$ independent systems of order $N$

$$\begin{aligned} E_m \, {\varvec{x} }_m \,=\, {\varvec{y} }_m, \quad m=1, \cdots , M, \end{aligned}$$

(2.21)

where

$$\begin{aligned} \left( E_m \right) _{n_1,n_2} \,=\, D_{{n_1,n_2}_m}, \; n_1,n_2 = 1, \cdots , N, \end{aligned}$$

and

$$\begin{aligned} \left( {\varvec{x} }_m \right) _{n} = \left( \tilde{{\varvec{a} }}_n \right) _m, \; \left( {\varvec{y} }_m \right) _{n} = \left( \tilde{{\varvec{b} }}_n \right) _m, \; n = 1, \cdots , N. \end{aligned}$$

(2.22)

Having obtained the vectors ${\varvec{x} }_m, \; m=1, \cdots , M$, we can recover the vectors $\tilde{{\varvec{a} }}_n, \; n=1, \cdots , N$ and, subsequently, the vector ${\varvec{a} }$ from (2.19), i.e.

$$\begin{aligned} {\varvec{a} }\! =\! \left( \begin{array}{c} \!{\varvec{a} }_1 \!\\ \! {\varvec{a} }_2 \!\\ \! \vdots \!\\ \!{\varvec{a} }_N \! \end{array} \right) =\!\left( I_N \otimes U_M^* \right) \tilde{{\varvec{a} }}\! =\! \left( \begin{array}{c} \!U_M^* \tilde{{\varvec{a} }}_1 \!\\ \!U_M^* \tilde{{\varvec{a} }}_2\! \\ \! \vdots \!\\ \!U_M^* \tilde{{\varvec{a} }}_N \! \end{array} \right) . \end{aligned}$$

(2.23)

In conclusion, the MDA can be summarized as follows:

In Steps 1, 2 and 4 FFTs are used while the most expensive part of the algorithm is the solution of $M$ linear systems, each of order $N$. The FFTs are carried out using the MATLAB$^{\copyright }$ [35] commands fft and ifft. In addition to the savings in computational cost, considerable savings in storage are achieved since only one row of the circulant matrices involved needs to be stored.

3 The Biharmonic Equation

3.1 The Problem

We next consider the biharmonic equation

$$\begin{aligned} \Delta ^2 u = f \quad \text{ in } \quad \Omega , \end{aligned}$$

(3.1a)

subject to the boundary conditions

$$\begin{aligned} u= & {} g_1 \quad \text{ and } \quad \dfrac{\partial u}{\partial \mathrm{n}}=h_1 \quad \text{ on } \quad \partial \Omega _1,\end{aligned}$$

(3.1b)

$$\begin{aligned} u= & {} g_2 \quad \text{ and } \quad \dfrac{\partial u}{\partial \mathrm{n}}=h_2 \quad \text{ on } \quad \partial \Omega _2, \end{aligned}$$

(3.1c)

where $\Omega$ is the annulus (2.2). This problem is known as the first biharmonic problem.

3.2 Kansa’s Method

We approximate the solution $u$ of boundary value problem (3.1) by (2.9).

The coefficients are determined by collocating the differential equation (3.1a) and the boundary conditions (3.1b)–(3.1c) in the following way:

$$\begin{aligned}&\Delta ^2 u_{MN}(x_{mn},y_{mn})=f (x_{mn},y_{mn}), \quad m=1, \ldots , M, \; n= 3, \ldots , N-2, \nonumber \\&u_{MN}(x_{m1},y_{m1})=g_{1}(x_{m1},y_{m1}) \quad \text{ and } \quad \dfrac{\partial u}{\partial \mathrm{n}}(x_{m1},y_{m1}) =h_{1}(x_{m1},y_{m1}), \quad m=1, \ldots , M,\nonumber \\&u_{MN}(x_{mN},y_{mN})=g_{2}(x_{mN},y_{mN}) \quad \text{ and } \quad \dfrac{\partial u}{\partial \mathrm{n}}u_{MN}(x_{mN},y_{mN})=h_{2}(x_{mN},y_{mN}), \nonumber \\&\quad m=1, \ldots , M, \end{aligned}$$

(3.2)

yielding a total of $MN$ equations.

By vectorizing the arrays of unknown coefficients and collocation points via (2.11), Eq. (3.2) yield a system of the form (2.12). In this case, the $M\times M$ submatrices $A_{n_1,n_2}, \; n_1,n_2=1, \ldots , N$ are defined as follows:

$$\begin{aligned} \left( A_{n_1,n_2}\right) _{m_1,m_2}= & {} \Delta ^2 \phi _{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1}), \nonumber \\&m_1,m_2=1,\ldots ,M, \; n_1=3, \ldots , N-2, \; n_2=1, \ldots , N,\nonumber \\ \left( A_{1,n}\right) _{m_1,m_2}= & {} \phi _{m_2,n}(x_{m_1,1},y_{m_1,1}), \quad \left( A_{2,n}\right) _{m_1,m_2}=\dfrac{\partial \phi _{m_2,n}}{\partial \mathrm{n}}(x_{m_1,1},y_{m_1,1} ),\nonumber \\&m_1,m_2=1,\ldots ,M, \; n=1, \ldots , N,\nonumber \\ \left( A_{N,n}\right) _{m_1,m_2}= & {} \phi _{m_2,n}(x_{m_1,N},y_{m_1,N}), \quad \left( A_{N-1,n}\right) _{m_1,m_2}=\dfrac{\partial \phi _{m_2,n}}{\partial \mathrm{n}}(x_{m_1,N},y_{m_1,N}),\nonumber \\ \end{aligned}$$

(3.3)

while the $M\times 1$ vectors ${\varvec{a} }_n, {\varvec{b} }_n, n=1, \ldots , N$ are defined as

$$\begin{aligned} \left( {\varvec{a} }_n\right) _m= & {} a_{mn}, \; m=1, \ldots , M, \; N=1, \ldots , N,\\ \left( {\varvec{b} }_n\right) _m= & {} f (x_{mn},y_{mn}), \quad m=1, \ldots , M, \; n= 3, \ldots , N-2,\\ \left( {\varvec{b} }_1\right) _m= & {} g_1(x_{m1},y_{m1}), \quad \left( {\varvec{b} }_2\right) _m=h_1(x_{m1},y_{m1}), \quad m=1, \ldots , M,\\ \left( {\varvec{b} }_N\right) _m= & {} g_2(x_{mN},y_{mN}), \quad \left( {\varvec{b} }_{N-1}\right) _m=h_2(x_{mN},y_{mN}), \quad m=1, \ldots , M. \end{aligned}$$

3.2.1 Second Biharmonic Problem

Suppose that instead of boundary conditions (3.1b)–(3.1c) we had the boundary conditions

$$\begin{aligned} u= & {} g_1 \quad \text{ and } \quad \Delta u=h_1 \quad \text{ on } \quad \partial \Omega _1,\end{aligned}$$

(3.4)

$$\begin{aligned} u= & {} g_2 \quad \text{ and } \quad \Delta u=h_2 \quad \text{ on } \quad \partial \Omega _2. \end{aligned}$$

(3.5)

This problem is known as the second biharmonic problem.

The corresponding submatrices $\left( A_{2,n}\right) , \, \left( A_{N-1,n}\right) , \, n=1, \ldots , N$, in (3.3) are now defined by

$$\begin{aligned} \left( A_{2,n}\right) _{m_1,m_2}= & {} \Delta \phi _{m_2,n}(x_{m_1,1},y_{m_1,1}), \nonumber \\ \left( A_{N-1,n}\right) _{m_1,m_2}= & {} \Delta \phi _{m_2,n}(x_{m_1,N},y_{m_1,N}), \quad m_1,m_2=1,\ldots ,M. \end{aligned}$$

(3.6)

As shown in the “Appendix” (Lemma 2), as in the case of the Poisson equation in Sect. 2.2, each of the $M\times M$ submatrices $A_{n_1,n_2}, \; n_1, n_2=1, \ldots , N$, is circulant and hence the matrix $A$ is block circulant. The resulting system can therefore be solved efficiently using the MDA described in Sect. 2.3.

4 The Cauchy–Navier Equations of Elasticity

4.1 The Problem

We finally consider the Cauchy–Navier system for the displacements $(u_1, u_2)$ in the form (see, e.g. [12])

$$\begin{aligned} \left\{ \begin{array}{llr} \mathcal {L}_1 (u_1, u_2)\equiv {\displaystyle \mu \Delta u_1 + \frac{\mu }{1-2\nu }\left( \frac{\partial ^2 u_1}{\partial x^2} + \frac{\partial ^2 u_2}{\partial x \partial y}\right) } = f_1,\\ &{} \text{ in } \quad \Omega ,\\ \mathcal {L}_2 (u_1, u_2) \equiv {\displaystyle \frac{\mu }{1-2\nu }\left( \frac{\partial ^2 u_1}{\partial x \partial y}+ \frac{\partial ^2 u_2}{\partial y^2} \right) +\mu \Delta u_2 } = f_2,&{} \end{array} \right. \end{aligned}$$

(4.1a)

subject to the Dirichlet boundary conditions

$$\begin{aligned} u_1= & {} g_1 \quad \text{ and } \quad u_2=h_1 \quad \text{ on } \quad \partial \Omega _1,\end{aligned}$$

(4.1b)

$$\begin{aligned} u_1= & {} g_2 \quad \text{ and } \quad u_2=h_2 \quad \text{ on } \quad \partial \Omega _2, \end{aligned}$$

(4.1c)

where $\Omega$ in the annulus (2.2). In (4.1a) the constant $\nu \in [0, 1/2)$ is Poisson’s ratio and $\mu >0$ is the shear modulus.

4.2 Kansa’s Method

We approximate the solution $(u_1, u_2)$ of boundary value problem (3.1) by $(u_{MN}^{(1)}, u_{MN}^{(2)})$ where

$$\begin{aligned} u_{MN}^{(\ell )}(x,y)=\sum ^{M}_{m=1} \sum ^{N}_{n=1} a_{mn}^{(\ell )} \phi _{mn}(x,y), \; \ell =1,2, \qquad (x,y) \in \bar{\Omega }, \end{aligned}$$

(4.2)

and the $2MN$ coefficients $\left\{ ({a}_{mn}^{(\ell )})\right\} _{m=1,n=1}^{M,N}, \; \ell =1,2,$ are unknown.

The unknown coefficients are determined by collocating the differential equations (4.1a) and the boundary conditions (4.1b)–(4.1c) in the following way:

$$\begin{aligned} \mathcal {L}_\ell (u_{MN}^{(1)}, u_{MN}^{(2)})(x_{mn},y_{mn})= & {} f_\ell (x_{mn},y_{mn}), \; \ell =1,2, \nonumber \\&m=1, \ldots , M, \; n= 2, \ldots , N-1, \nonumber \\ u_{MN}^{(1)}(x_{m1},y_{m1})= & {} g_{1}(x_{m1},y_{m1}) \; \text{ and } \; u_{MN}^{(2)}(x_{m1},y_{m1})=h_{1}(x_{m1},y_{m1}), \nonumber \\&m=1, \ldots , M,\nonumber \\ u_{MN}^{(1)}(x_{mN},y_{mN})= & {} g_{2}(x_{mN},y_{mN}) \; \text{ and } \; u_{MN}^{(2)}(x_{mN},y_{mN})=h_{2}(x_{mN},y_{mN}),\nonumber \\&m=1, \ldots , M, \end{aligned}$$

(4.3)

yielding a total of $2MN$ equations.

By vectorizing the arrays of unknown coefficients and collocation points as in (2.11), Eq. (4.3) yield a $2 M N \times 2 M N$ system of the form (2.12). The $2M\times 2M$ submatrices $A_{n_1,n_2}, \; n_1,n_2=1, \ldots , N$ are now defined as follows: (note that we are now defining the matrix and vector elements in (2.12) as $2\times 2$ and $2\times 1$ arrays, respectively)

$$\begin{aligned}&\left( A_{n_1,n_2}\right) _{m_1,m_2}\nonumber \\&\quad = {\left( \!\! \begin{array}{c@{\quad }c} \mu \Delta \phi _{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1}) + \dfrac{\mu }{1\!-\!2\nu } \dfrac{\partial ^2 \phi _{m_2,n_2}}{\partial x^2} (x_{m_1,n_1},y_{m_1,n_1}) &{} \dfrac{\mu }{1\!-\!2\nu } \dfrac{\partial ^2 \phi _{m_2,n_2}}{\partial x \partial y} (x_{m_1,n_1},y_{m_1,n_1}) \\ \dfrac{\mu }{1\!-\!2\nu } \dfrac{\partial ^2 \phi _{m_2,n_2}}{\partial x \partial y} (x_{m_1,n_1},y_{m_1,n_1}) &{} \mu \Delta \phi _{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1}) + \dfrac{\mu }{1\!-\!2\nu } \dfrac{\partial ^2 \phi _{m_2,n_2}}{\partial y^2} (x_{m_1,n_1},y_{m_1,n_1}) \end{array}\!\! \right) ,}\nonumber \\&\quad m_1,m_2=1,\ldots ,M, \; n_1=2, \ldots , N-1, \; n_2=1, \ldots , N, \end{aligned}$$

(4.4a)

$$\begin{aligned}&\left( A_{1,n}\right) _{m_1,m_2}= \left( \begin{array}{c c} \phi _{m_2,n}(x_{m_1,1},y_{m_1,1})&{} 0\\ 0 &{} \phi _{m_2,n}(x_{m_1,1},y_{m_1,1}) \end{array} \right) ,\end{aligned}$$

(4.4b)

$$\begin{aligned}&m_1,m_2=1,\ldots ,M, \; n=1, \ldots , N, \nonumber \\&\left( A_{N,n}\right) _{m_1,m_2}= \left( \begin{array}{c c} \phi _{m_2,n}(x_{m_1,N},y_{m_1,N})&{} 0\\ 0 &{} \phi _{m_2,n}(x_{m_1,N},y_{m_1,N}) \end{array} \right) , \end{aligned}$$

(4.4c)

while the $2M\times 1$ vectors ${\varvec{a} }_n, {\varvec{b} }_n, n=1, \ldots , N$ are defined as

$$\begin{aligned} \left( {\varvec{a} }_n\right) _m= & {} \left( \begin{array}{c} a_{mn}^{(1)}\\ a_{mn}^{(2)} \end{array} \right) , \; m=1, \ldots , M, \; n=1, \ldots , N,\\ \left( {\varvec{b} }_n\right) _m= & {} \left( \begin{array}{c} f_1 (x_{mn},y_{mn})\\ f_2 (x_{mn},y_{mn}) \end{array} \right) , \quad m=1, \ldots , M, \; n= 2, \ldots , N-1,\\ \left( {\varvec{b} }_1\right) _m= & {} \left( \begin{array}{c} g_1(x_{m1},y_{m1})\\ h_1(x_{m1},y_{m1})\end{array} \right) , \quad \left( {\varvec{b} }_N\right) _m=\left( \begin{array}{c} g_2(x_{mN},y_{mN})\\ h_2(x_{mN},y_{mN})\end{array} \right) , \quad m=1, \ldots , M. \end{aligned}$$

4.2.1 Neumann Boundary Conditions

Suppose that instead of the Dirichlet boundary conditions (4.1b) we had the Neumann boundary conditions

$$\begin{aligned} t_1 \, =\, g_1 \quad \text{ and } \quad t_2=h_1 \quad \text{ on } \quad \partial \Omega _1, \end{aligned}$$

(4.5)

where $(t_1, t_2)$ are the tractions defined by [12]

$$\begin{aligned} t_1= & {} 2 \mu \left[ \left( \dfrac{1-\nu }{1-2\nu }\right) \dfrac{\partial u_1}{\partial x} + \left( \dfrac{\nu }{1-2\nu }\right) \dfrac{\partial u_2}{\partial y}\right] \mathrm{n}_x + \mu \left[ \dfrac{\partial u_1}{\partial y} +\dfrac{\partial u_2}{\partial x} \right] \mathrm{n}_y,\\ t_2= & {} \mu \left[ \dfrac{\partial u_1}{\partial y} +\dfrac{\partial u_2}{\partial x} \right] \mathrm{n}_x + 2 \mu \left[ \left( \dfrac{\nu }{1-2\nu }\right) \dfrac{\partial u_1}{\partial x} + \left( \dfrac{1-\nu }{1-2\nu }\right) \dfrac{\partial u_2}{\partial y}\right] \mathrm{n}_y. \end{aligned}$$

In this case, we have, instead of (4.4b), that the submatrices $\left( A_{1,n}\right) _{m_1,m_2}, m_1,m_2=1,\ldots ,M, \; n=1, \ldots , N,$ are defined by

$$\begin{aligned}&\left( A_{1,n}\right) _{m_1,m_2}\nonumber \\&\quad = \mu \left( \begin{array}{c c} 2\left( \dfrac{1-\nu }{1-2\nu }\right) \dfrac{\partial \phi _{m_2,n}}{\partial x}\mathrm{n}_x + \dfrac{\partial \phi _{m_2,n}}{\partial y}\mathrm{n}_y &{} \left( \dfrac{2\nu }{1-2\nu }\right) \dfrac{\partial \phi _{m_2,n}}{\partial y}\mathrm{n}_x + \dfrac{\partial \phi _{m_2,n}}{\partial x}\mathrm{n}_y \\ \dfrac{\partial \phi _{m_2,n}}{\partial y}\mathrm{n}_x + \left( \dfrac{2\nu }{1-2\nu }\right) \dfrac{\partial \phi _{m_2,n}}{\partial x}\mathrm{n}_y&{} \dfrac{\partial \phi _{m_2,n}}{\partial x}\mathrm{n}_x + 2\left( \dfrac{1-\nu }{1-2\nu }\right) \dfrac{\partial \phi _{m_2,n}}{\partial y}\mathrm{n}_y \end{array} \right) \nonumber \\&\quad = \mu \left( \dfrac{\partial \phi _{m_2,n}}{\partial x}\mathrm{n}_x + \dfrac{\partial \phi _{m_2,n}}{\partial y}\mathrm{n}_y \right) I_2\nonumber \\&\qquad +\,\dfrac{\mu }{1-2\nu } \left( \begin{array}{ll} \dfrac{\partial \phi _{m_2,n}}{\partial x}\mathrm{n}_x &{} 2\nu \dfrac{\partial \phi _{m_2,n}}{\partial y}\mathrm{n}_x + (1-2\nu ) \dfrac{\partial \phi _{m_2,n}}{\partial x}\mathrm{n}_y \\ (1-2\nu ) \dfrac{\partial \phi _{m_2,n}}{\partial y}\mathrm{n}_x + 2\nu \dfrac{\partial \phi _{m_2,n}}{\partial x}\mathrm{n}_y&{} \dfrac{\partial \phi _{m_2,n}}{\partial y}\mathrm{n}_y \end{array} \right) ,\nonumber \\ \end{aligned}$$

(4.6)

with all the quantities in (4.6) evaluated at the boundary point $(x_{m_1,1},y_{m_1,1})$.

In contrast to the Poisson and biharmonic cases, matrix $A$ in (2.12) does not possess a block circulant structure. However, as described in the context of the MFS, in e.g., [23–25] a block circulant structure can be obtained by means of a simple transformation.

4.3 Matrix Decomposition Algorithm

We introduce the $2M \times 2M$ matrix

$$\begin{aligned} R = \left( \begin{array}{c|c|c|c|c|c} R_{{\vartheta }_1} &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 \\ \hline 0 &{} R_{{\vartheta }_2} &{} 0 &{} \cdots &{} 0 &{} 0 \\ \hline \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots \\ \hline 0 &{} 0 &{} 0 &{} \cdots &{} R_{{\vartheta }_{M \!-\! 1}} &{} 0 \\ \hline 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} R_{{\vartheta }_M} \end{array} \right) \!, \end{aligned}$$

(4.7)

where

$$\begin{aligned} R_{{\vartheta }_k} \,=\, \left( \begin{array}{cc} \cos {\vartheta }_k &{} \sin {\vartheta }_k \\ \sin {\vartheta }_k &{} -\!\cos {\vartheta }_k \end{array} \right) \!, \quad {\vartheta }_k=\displaystyle \frac{2\pi (k-1)}{M}. \end{aligned}$$

Since clearly $R_{{\vartheta }_k}^2=I_2$ then $R^2=I_{2N}$.

We premultiply the $2MN\times 2MN$ system (2.12) ($A{\varvec{a} } = {\varvec{b} }$) by the $2MN\times 2MN$ matrix $I_N \otimes R$ to get

$$\begin{aligned} \left( I_N \otimes R \right) A {\varvec{a} } = \left( I_N \otimes R \right) {\varvec{b} } \quad \text{ or } \quad \tilde{A}\tilde{{\varvec{a} }} = \tilde{{\varvec{b} }}, \end{aligned}$$

(4.8)

where

$$\begin{aligned} \tilde{A}= \left( I_N \otimes R \right) A \left( I_N \otimes R \right) , \quad \tilde{{\varvec{a} }} =\left( I_N \otimes R \right) {\varvec{a} }, \quad \tilde{{\varvec{b} }} = \left( I_N \otimes R \right) {\varvec{b} }. \end{aligned}$$

The $2MN\times 2MN$ matrix $\tilde{A}$ can be written as

$$\begin{aligned} \tilde{A} = \left( \begin{array} [c]{cccc} \tilde{A}_{1,1} &{} \tilde{A}_{1,2} &{} \ldots &{} \tilde{A}_{1,N}\\ \tilde{A}_{2,1} &{} \tilde{A}_{2,2} &{} \ldots &{} \tilde{A}_{2,N}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \tilde{A}_{N,1} &{} \tilde{A}_{N,2} &{} \ldots &{} \tilde{A}_{N,N} \end{array} \right) , \end{aligned}$$

(4.9)

where each of the $2M\times 2M$ submatrices $\tilde{A}_{m,\ell }=RA_{m,\ell }R$.

Moreover, keeping in mind that the elements $\left( \tilde{A}_{n_1,n_2}\right) _{m_1,m_2}=\left( \left( \tilde{A}_{n_1,n_2}\right) _{m_1,m_2}\right) _{i,j=1}^2$ are $2 \times 2$ arrays, we have

$$\begin{aligned} \left( \tilde{A}_{n_1,n_2}\right) _{m_1,m_2}= R_{{\vartheta }_{m_1}} \left( A_{n_1,n_2}\right) _{m_1,m_2} R_{{\vartheta }_{m_2}}, \quad m_1,m_2=1,\ldots ,M, \; n_1, n_2=1, \ldots , N.\nonumber \\ \end{aligned}$$

(4.10)

Further, as proved in the “Appendix” (Lemma 3), each submatrix $\tilde{A}_{n_1,n_2}, n_1, n_2=1, \ldots , N$, has a block $2 \times 2$ block circulant structure. The $2MN\times 1$ vectors $\tilde{{\varvec{a} }}, \tilde{{\varvec{b} }}$ are written as

$$\begin{aligned} \tilde{{\varvec{a} }}=\left( \begin{array} [c]{c} \tilde{{\varvec{a} }}_1\\ \tilde{{\varvec{a} }}_2\\ \vdots \\ \tilde{{\varvec{a} }}_N \end{array} \right) , \quad \tilde{{\varvec{b} }}=\left( \begin{array} [c]{c} \tilde{{\varvec{b} }}_1\\ \tilde{{\varvec{b} }}_2\\ \vdots \\ \tilde{{\varvec{b} }}_N \end{array} \right) , \end{aligned}$$

where the $2M \times 1$ subvectors $\tilde{{\varvec{a} }}_n, \tilde{{\varvec{b} }}_n, n=1,\ldots N$, are defined by $\tilde{{\varvec{a} }}_n =R {\varvec{a} }_n, \tilde{{\varvec{b} }}_n =R {\varvec{b} }_n$ and the $2 \times 1$ subvectors $((\tilde{{\varvec{a} }}_n)_m)_{i=1}^2, \; ((\tilde{{\varvec{b} }}_n)_m)_{i=1}^2,\; m=1,\ldots , M$, are defined by

$$\begin{aligned} \left( \tilde{{\varvec{a} }}_n\right) _m= R_{{\vartheta }_{m}} \left( {{\varvec{a} }}_n\right) _m, \; \left( \tilde{{\varvec{b} }}_n\right) _m= R_{{\vartheta }_{m}} \left( {{\varvec{b} }}_n\right) _m. \end{aligned}$$

We next rewrite system (4.8) in the form

$$\begin{aligned} \left( \begin{array}{c|c} B_{11} &{} B_{12} \\ \hline B_{21} &{} B_{22} \end{array} \right) \left( \begin{array}{c} \!\!{\varvec{c} }_1\!\! \\ \hline \!\!{{\varvec{c} }}_2\!\! \end{array} \right) \,=\, \left( \begin{array}{c} \!\!{\varvec{d} }_1\!\! \\ \hline \!\!{\varvec{d} }_2\!\! \end{array} \right) , \end{aligned}$$

(4.11)

where the $MN \times MN$ matrices $B_{ij}, i,j =1,2,$ are expressed in the form

$$\begin{aligned} B_{ij}= \left( \begin{array} [c]{cccc} \tilde{B}_{1,1}^{ij} &{} \tilde{B}_{1,2}^{ij} &{} \ldots &{} \tilde{B}_{1,N}^{ij}\\ \tilde{B}_{2,1}^{ij} &{} \tilde{B}_{2,2}^{ij} &{} \ldots &{} \tilde{B}_{2,N}^{ij}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \tilde{B}_{N,1}^{ij} &{} \tilde{B}_{N,2}^{ij} &{} \ldots &{} \tilde{B}_{N,N}^{ij} \end{array} \right) . \end{aligned}$$

Each $M\times M$ submatrix $\tilde{B}_{n_1,n_2}^{ij}, i,j =1,2, \; n_1,n_2=1, \dots , N,$ is circulant and defined from

$$\begin{aligned} \left( \tilde{B}_{n_1,n_2}^{ij}\right) _{m_1,m_2} = \left( \left( \tilde{A}_{n_1,n_2}\right) _{m_1,m_2}\right) _{i,j}, \quad m_1,m_2=1,\ldots ,M. \end{aligned}$$

(4.12)

Also, the $MN\times 1$ vectors ${\varvec{c} }_i, {\varvec{d} }_i, i=1,2,$ are defined from

$$\begin{aligned} {\varvec{c} }_i=\left( \begin{array} [c]{c} \tilde{{\varvec{c} }}_1^i\\ \tilde{{\varvec{c} }}_2^i\\ \vdots \\ \tilde{{\varvec{c} }}_N^i \end{array} \right) , \quad {\varvec{d} }_i=\left( \begin{array} [c]{c} \tilde{{\varvec{d} }}_1^i\\ \tilde{{\varvec{d} }}_2^i\\ \vdots \\ \tilde{{\varvec{d} }}_N^i \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} \left( \tilde{c}_{n}^{i}\right) _{m} = \left( \left( \tilde{a}_{n}\right) _{m}\right) _{i}, \quad \left( \tilde{d}_{n}^{i}\right) _{m} = \left( \left( \tilde{b}_{n}\right) _{m}\right) _{i}, {\quad } m=1, \ldots , M. \end{aligned}$$

(4.13)

We premultiply system (4.11) by the matrix $I_2 \otimes I_N \otimes U_M$ to get

$$\begin{aligned}&\left( I_2 \otimes I_N \otimes U_M \right) \left( \begin{array}{c|c} B_{11} &{} B_{12} \\ \hline B_{21} &{} B_{22} \end{array} \right) \left( I_2 \otimes I_N \otimes U_M^* \right) \left( I_2 \otimes I_N \otimes U_M \right) \left( \begin{array}{c} \!\!{\varvec{c} }_1\!\! \\ \hline \!\!{{\varvec{c} }}_2\!\! \end{array} \right) \nonumber \\&\quad = \left( I_2 \otimes I_N \otimes U_M \right) \left( \begin{array}{c} \!\!{\varvec{d} }_1\!\! \\ \hline \!\!{\varvec{d} }_2\!\! \end{array} \right) , \end{aligned}$$

(4.14)

or

$$\begin{aligned} \left( \begin{array}{c|c} \tilde{B}_{11} &{} \tilde{B}_{12} \\ \hline \tilde{B}_{21} &{} \tilde{B}_{22} \end{array} \right) \left( \begin{array}{c} \!\!{{\varvec{p} }}_1\!\! \\ \hline \!\!{{\varvec{p} }}_2\!\! \end{array} \right) \,=\, \left( \begin{array}{c} \!\!{{\varvec{q} }}_1\!\! \\ \hline \!\!{{\varvec{q} }}_2\!\! \end{array} \right) , \end{aligned}$$

(4.15)

where

$$\begin{aligned} \left( \begin{array}{c} \!\!{{\varvec{p} }}_1\!\! \\ \hline \!\!{{\varvec{p} }}_2\!\! \end{array} \right) = \left( I_2 \otimes I_N \otimes U_M \right) \left( \begin{array}{c} \!\!{\varvec{c} }_1\!\! \\ \hline \!\!{{\varvec{c} }}_2\!\! \end{array} \right) , \quad \left( \begin{array}{c} \!\!{{\varvec{q} }}_1\!\! \\ \hline \!\!{{\varvec{q} }}_2\!\! \end{array} \right) = \left( I_2 \otimes I_N \otimes U_M \right) \left( \begin{array}{c} \!\!{\varvec{d} }_1\!\! \\ \hline \!\!{\varvec{d} }_2\!\! \end{array} \right) , \end{aligned}$$

where for $i=1,2$

$$\begin{aligned} {\varvec{p} }_i=\left( \begin{array} [c]{c} \tilde{{\varvec{p} }}_1^i\\ \tilde{{\varvec{p} }}_2^i\\ \vdots \\ \tilde{{\varvec{p} }}_N^i \end{array} \right) , \quad {\varvec{q} }_i=\left( \begin{array} [c]{c} \tilde{{\varvec{q} }}_1^i\\ \tilde{{\varvec{q} }}_2^i\\ \vdots \\ \tilde{{\varvec{q} }}_N^i \end{array} \right) , \quad \text{ with } \quad \tilde{{\varvec{p} }}_n ^i = U_M \tilde{{\varvec{c} }}_n ^i, \; \tilde{{\varvec{q} }}_n ^i= U_M \tilde{{\varvec{d} }}_n ^i, \; n=1, \ldots , N. \end{aligned}$$

The matrices $\tilde{B}_{ij}, i,j =1,2$ are given from

$$\begin{aligned} \tilde{B}_{ij}= \left( I_N \otimes U_M \right) B_{ij} \left( I_N \otimes U_M^* \right) , \end{aligned}$$

and since each of the matrices ${B}_{ij}, i,j =1,2$ is block circulant, from (2.18) it follows that

$$\begin{aligned} \tilde{B}_{ij}= \left( \begin{array}{cccc} D_{1,1}^{ij} &{} D_{1,2}^{ij} &{} \cdots &{} D_{1,N}^{ij} \\ D_{2,1} &{} D_{2,2}^{ij} &{} \cdots &{} D_{2,N}^{ij} \\ \vdots &{} \vdots &{} &{} \vdots \\ D_{N,1}^{ij} &{} D_{N,2}^{ij} &{} \cdots &{} D_{N,N}^{ij} \end{array} \right) , \! \end{aligned}$$

(4.16)

where each $M \times M$ matrix $D_{n_1,n_2}^{ij}, n_1, n_2=1, \ldots , N,$ is diagonal.

More specifically, if

$$\begin{aligned} D_{n_1,n_2}^{ij}= & {} \hbox {diag} \left( D_{{n_1,n_2}_{1}}^{ij}, D_{{n_1,n_2}_2}^{ij}, \ldots , D_{{n_1,n_2}_M}^{ij} \right) \quad \text{ and } \\ \tilde{B}_{n_1,n_2}^{ij}= & {} \text{ circ } \left( \tilde{B}_{{n_1,n_2}_1}^{ij}, \tilde{B}_{{n_1,n_2}_M}^{ij} \ldots , \tilde{B}_{{n_1,n_2}_M}^{ij}\right) , \end{aligned}$$

we have, for $n_1, n_2 = 1, \cdots , N$,

$$\begin{aligned} D_{{n_1,n_2}_{m}}^{ij} \,=\, \sum _{k=1}^{M} \tilde{B}_{{n_1,n_2}_k}^{ij} \omega ^{(k-1)(m-1)}, \; m=1, \cdots , M. \end{aligned}$$

(4.17)

Since each matrix $\tilde{B}_{ij}, i,j =1,2,$ consists of $N^2$ blocks of order $M$ each of which is diagonal, the solution of system (4.15) can be decomposed into solving the $M$ systems of order $2N$

$$\begin{aligned} \left( \begin{array}{c|c} {E}_{11}^m &{} {E}_{12}^m \\ \hline {E}_{21}^m &{} {E}_{22}^m \end{array} \right) \left( \begin{array}{c} {\varvec{x} }_1^m \\ \hline {\varvec{x} }_2^m \end{array} \right) \,=\, \left( \begin{array}{c} {\varvec{y} }_1^m \\ \hline {\varvec{y} }_2^m \end{array} \right) , \quad m=1, \cdots , M, \end{aligned}$$

(4.18)

where

$$\begin{aligned} \left( E_{ij}^m \right) _{n_1,n_2} \,=\, D_{{n_1,n_2}_{m}}^{ij}, \; n_1, n_2 = 1, \cdots , N \end{aligned}$$

and

$$\begin{aligned} \left( {\varvec{x} }_i^m \right) _{n} = \left( \tilde{{\varvec{p} }}_n^i \right) _m, \; \left( {\varvec{y} }_i^m \right) _{n} = \left( \tilde{{\varvec{q} }}_n^i \right) _m, \; \; n = 1, \cdots , N. \end{aligned}$$

(4.19)

From the vectors ${\varvec{x} }_i^m, i=1,2; m=1, \ldots , M$ we can obtain the vectors $p_1, p_2$ and the vectors $c_1, c_2$, and subsequently the vector $\tilde{{\varvec{a} }}$, before finally obtaining the vector ${\varvec{a} }$.

The MDA, in this case, can be summarized as follows:

In Steps 3, 4 and 6 FFTs are used while the most expensive part of the algorithm is the solution of $M$ linear systems, each of order $2N$. Again, substantial savings in storage are obtained as only the first line of the circulant matrices involved needs to be constructed and stored.

5 Numerical Examples

In all numerical examples considered, we took collocation points described by $\alpha _{n}=(-1)^{n}/4, n=1, \ldots , N$ (cf. (2.8)). The inner and outer radii of the annular domain $\Omega$ are ${\varrho }_1 = 0.3, {\varrho }_2 = 1$, respectively. We calculated the maximum relative error $E$ over $\mathcal {M}\mathcal {N}$ test points in $\overline{\Omega }$ defined by

$$\begin{aligned}&\hbox {r}_{n} \left( \cos {\vartheta }_{m}, \sin {\vartheta }_{m}\right) , \; \hbox {where} \; {\vartheta }_{m}= \dfrac{2 \pi (m-1)}{\mathcal {M}}, \; m= 1,\ldots , \mathcal {M}, \; \hbox {r}_{n}= {\varrho }_{1} \nonumber \\&\quad + \left( {\varrho }_{2}-{\varrho }_{1}\right) \frac{n-1}{\mathcal {N}-1}, \; n=1, \ldots , \mathcal {N}. \end{aligned}$$

(5.1)

Unless otherwise stated, we choose $\mathcal {N}=25, \mathcal {M}=50$ so that the test points are different than the collocation points. The maximum relative error $E$ is defined as

$$\begin{aligned} E=\dfrac{||u-u_{N}||_{\infty ,\overline{\Omega }}}{||u||_{\infty ,\overline{\Omega }}}. \end{aligned}$$

(5.2)

The proper selection of an RBF is crucial in obtaining good accuracy. In the first example, we test various commonly used RBFs and then choose the best one to perform the tests for the remaining examples. The determination of a suitable shape parameter remains a major issue in the many applications of RBFs involving such parameters. As we have mentioned earlier, numerous techniques have been proposed for the selection of an appropriate shape parameter. In this work, we apply the so-called LOOCV (leave-one-out cross validation) algorithm proposed by Rippa [32] for the identification of a suitable shape parameter. The MATLAB$^{\copyright }$ codes for LOOCV can be found in [9]. The MATLAB$^{\copyright }$ function fminbnd is used to find the minimum of a function of one variable within a fixed interval. Since fminbnd is a local minimizer, an initial guess of the lower and upper bounds denoted by min and max needs to be provided so that the search takes place in the interval [min, max]. One of the attractive features of using LOOCV is that we do not need to know the exact solution of the given problem for the selection of a (sub-optimal) shape parameter. Typically, in the problems considered, there are $M$ systems of equations of order $N$ to be solved, see, e.g., (2.21). It is clearly not cost-effective to apply the LOOCV to each of the $M$ systems and determine the sub-optimal shape parameter for each. We therefore only apply the LOOCV to a randomly chosen system among the $M$ systems. This adds $O(N^3)$ computational complexity to the proposed technique. The sub-optimal shape parameter thus obtained is then used for all the other systems. This technique, as shown by the results, appears to be working well.

Fig. 2

Example 1: maximum relative error versus shape parameter with $M=128, N=64$

All numerical computations were carried out on a MATLAB$^{\copyright }$ 2010a platform in OS Windows 7 (32 bit) with Intel Core(TM) i5 2.4 GHz CPU and 4 GB memory.

We have considered the following numerical examples.

5.1 Example 1

We consider the Poisson equation (2.1a) with a Neumann boundary condition prescribed on $\partial \Omega _1$ and a Dirichlet boundary condition prescribed on $\partial \Omega _2$. The boundary conditions correspond to the exact solution which is given by $u=\hbox {e}^{x+y}$.

We first perform some tests with the normalized multiquadric (MQ) basis functions

$$\begin{aligned} \phi _{j}(x,y)=\Phi (r_j)=\sqrt{(c r_j)^2+1}, \quad r_{j}^2=(x-x_j)^2+(y-y_j)^2, \end{aligned}$$

where $c$ is the shape parameter. In Fig. 2, we present the maximum relative error in $u$ versus the shape parameter $c$ for the case when $M=128, N=64$ using the normalized MQ basis functions. From this figure, we can observe that the optimal shape parameter is $c = 5.208$ and the corresponding error is $2.940(-8)$. The results in Table 1 are obtained using the LOOCV algorithm for various search intervals [min, max]. When comparing the results in Fig. 2 and Table 1, we can see that the (sub-optimal) shape parameter results obtained for various search intervals are very stable and satisfactorily close to the optimal shape parameter. In terms of accuracy, the errors obtained using the LOOCV algorithm are comparable to the ones obtained using the optimal shape parameter. Moreover, in order to obtain the optimal shape parameter in Fig. 2, one needs to know the exact solution. In contrast, to obtain the sub-optimal shape parameter using the LOOCV algorithm in Table 1, it is not necessary to know the exact solution a priori. The results obtained for the Dirichlet problem (2.1) are very similar.

Table 1 Example 1: sub-optimal shape parameters and the corresponding maximum relative errors for various search intervals using fminbnd with $M=128, N=64$

In Table 2, we present the results obtained using various numbers of collocation points $M = N$. It can be seen that the sub-optimal shape parameter becomes larger when the density of the collocation points increases.

Table 2 Example 1: sub-optimal shape parameter and the maximum relative errors for various $M=N$ with initial search interval [0, 20]

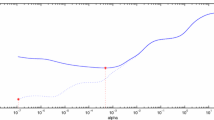
In Fig. 3 we present the error convergence plots for $(M,N) = (16,8), (32,16), (64,32)$ and $(128, 64)$ for varying $c$. From these plots we observe that as the number of degrees of freedom increases, the accuracy improves.

Fig. 3

Example 1: maximum relative error versus shape parameter with different numbers of degrees of freedom

We also compared the performance of the proposed MDA Kansa-RBF versus the full Kansa-RBF solution in which the full system (2.12) is solved. In Table 3, we present the errors $E$, CPU times and condition numbers for the full Kansa-RBF and the corresponding quantities using the proposed MDA Kansa-RBF for various numbers of degrees of freedom, using LOOCV. The most time consuming part in both approaches is the search of a suitable shape parameter using LOOCV, in which systems are solved repeatedly. This makes the advantage of the MDA Kansa-RBF even more pronounced as, for example, the solution of the full Kansa system for $M=N=50$ once requires 2.82 s while with LOOCV the method requires 55.68 s. Clearly, the use of LOOCV with the MDA Kansa approach does not slow the process as considerably. Note that for $M=N=100$ and 150 the size of the full Kansa-RBF matrices becomes prohibitive. From the values of the condition numbers in the two approaches we may infer that the Principle of Uncertainty [32,33] is more pronounced for the full Kansa-RBF than the MDA Kansa-RBF. The sub-optimal shape parameters are not given in Table 3 since the focus is on the CPU time and accuracy. Similar results were observed for the other examples considered.

Table 3 Example 1: comparison of CPU times and $E$ for full Kansa RBF and MDA Kansa RBF solutions for various $M=N$ with initial search interval [0, 8]

Next, we examine and compare the performance of different RBFs using the proposed MDA. The Matérn RBF [30, 31]

$$\begin{aligned} \Phi (r) = (rc)^n K_n (rc), \end{aligned}$$

where $n\in \mathbb {Z}, K_n$ is the modified Bessel function of second kind with order $n$ and $c$ is the shape parameter, is known as a highly effective basis function. In [31], the Kansa method using the Matérn RBF was applied to solve Poisson’s equation. For large-scale problems, domain decomposition was applied to decompose the domain into smaller domains so that the Kansa method can be applied. In this work, instead of domain decomposition, we use matrix decomposition to handle large-scale problems. For (2.1a) with Dirichlet boundary conditions, the profiles of the maximum relative error versus the shape parameter for the Matérn RBF of orders $n=4, 5, 6,$ and 7, with $M=128, N=64$, are shown in Fig. 4. As can be observed, as the order increases so does the value of the optimal shape parameter. Furthermore, the stability of the curve deteriorates as the order becomes higher due to an increase in the higher condition number. As shown in Table 4, when using the Matérn of order 6, the results for various search intervals are compatible with the results in Table 1. Since the value of the optimal shape parameter increases with the order of the Matérn RBF, we use different search intervals for different orders. In Table 5, we present the sub-optimal shape parameters and the corresponding errors for various orders of the Matérn RBF. The accuracy obtained using the Matérn RBF of various orders and the LOOCV algorithm is very close to the results obtained using the actual optimal shape parameters as shown in Fig. 4. Even though the results are highly accurate, the drawback of using the Matérn RBF is the high cost of computation due to the presence of the special function $K_n(cr)$.

Fig. 4

Example 1: maximum relative error versus shape parameter for various orders of the Matérn function with $M=128, N=64$

Table 4 Example 1: sub-optimal shape parameters and the corresponding maximum relative errors for various search intervals using the Matérn function of order 6 with $M=128, N=64$

Table 5 Example 1: sub-optimal shape parameter and the maximum relative errors using various orders of the Matérn function with $M=128$ and $N=64$

The Gaussian RBF

$$\begin{aligned} \Phi (r) = \mathrm{e}^{-cr^2}, \text{ where } \, c ~\text{ is } \text{ the } \text{ shape } \text{ parameter }, \end{aligned}$$

is another popular and widely used RBF. As shown in Fig. 5, we see a very different profile of the shape parameter versus the maximum relative error, for problem (2.1). The errors are fluctuating between $10^{-4}$ and $10^{-6}$. Despite this irregularity, we obtain excellent results using the LOOCV algorithm, as shown in Table 6. We note that all the local minima in Fig. 5 have similar accuracy. The MATLAB$^{\copyright }$ function fminbnd is capable of finding the local minima and, hence, as we can see in Table 6, for different search intervals we may obtain quite different sub-optimal shape parameters and yet the obtained accuracy is very satisfactory. In conclusion, however, it is preferable to use one of the previous two RBFs which are more predictable in finding a suitable shape parameter.

Fig. 5

Example 1: maximum relative error versus shape parameter for Gaussian RBF with $M=128, N=64$

Table 6 Example 1: sub-optimal shape parameters and the corresponding maximum relative errors for various search intervals using the Gaussian RBF with $M=128, N=64$

Finally, we tested the performance of the inverse multiquadric (IMQ) RBF

$$\begin{aligned} \Phi (r) = \dfrac{1}{\sqrt{1+(cr)^2}}, \text{ where } c \text{ is } \text{ the } \text{ shape } \text{ parameter }, \end{aligned}$$

for the same example. The results obtained were very similar to those obtained using the normalized MQ RBF but the best accuracy recorder in this case was slightly worse at around $10^{-7}$.

Among all the RBFs tested in this example, we conclude that the normalized MQ is the best in terms of efficiency, stability, and accuracy. As a result, we will only consider the normalized MQ as an RBF for the next two examples.

Remark 1

We also considered a distribution of the collocation points which renders their concentration near the boundaries denser (see, e.g., [10]). In particular, instead the of the $N$ uniformly distributed radii defined by (2.7) we used the $N$ Chebyshev–Gauss–Lobatto points on the interval $[{\varrho }_1,{\varrho }_2]$, defined by

$$\begin{aligned} \mathsf{r}_{n}= \dfrac{1}{2} \left( {\varrho }_1 +{\varrho }_2 +({\varrho }_1 -{\varrho }_2)\cos \left( \dfrac{n\pi }{N}\right) \right) , \quad n=1, \ldots , N, \end{aligned}$$

(5.3)

while the angles are still defined by (2.6) and the collocation points by (2.8). Extensive experimentation revealed no significant difference in the accuracy of the results with the uniform distribution and the Chebyshev–Gauss–Lobatto point distribution. Moreover, it was observed that there was no significant difference between the size of the errors near the boundaries and the interior of the domain.

5.2 Example 2

We next consider the first biharmonic boundary value problem (3.1) corresponding to the exact solution $u = \sin (\pi x) \cos (\pi y/2)$. In Table 7 we present the sub-optimal shape parameters and their corresponding errors using the LOOCV algorithm with various search intervals for the case $M=128, N=64$. As in Example 1, the results we obtained are very stable irrespective to the initial search interval. Without prior knowledge of the exact solution, we can find a good shape parameter and obtain accuracy which is fairly close to the optimal accuracy, as shown in Fig. 6.

Table 7 Example 2: sub-optimal shape parameters and the corresponding maximum relative errors for various initial search interval using fminbnd for $M=128, N=64$

Fig. 6

Example 2: maximum relative error versus the shape parameter for $M=128, N=64$

In Table 8 we present the sub-optimal shape parameters and errors in $u$ for various values of $M = N$ using the LOOCV algorithm for the case of Dirichlet and Neumann boundary conditions. The initial search internal is set to [0, 20] and obtain stable and accurate results. We also run a similar test for the corresponding second biharmonic boundary value problem (3.1a), (3.4) and (3.5) in which the initial search interval was set to [0, 10]. The results are shown in Table 9.

Table 8 Example 2: sub-optimal shape parameters and the maximum relative errors for various $M=N$

Table 9 Example 2: sub-optimal shape parameters and the maximum relative errors for various $M=N$ for the second biharmonic problem

5.3 Example 3

We finally consider a mixed boundary value problem for the Cauchy–Navier equations of elasticity given by (4.1), (4.5) and (4.1c) and corresponding to the exact solution $u_{1}=\mathrm{e}^{x+y}$, $u_{2}=\sin (x+y)$. We take Poisson’s ratio and the shear modulus to be $\nu =0.3$ and $\mu =1$, respectively. In Fig. 7 we present the errors in $u_{1}$ and $u_{2}$ for various numbers of degrees of freedom versus the shape parameter $c$ when the tractions are prescribed on $\partial \Omega _{1}$ (cf. Sect. 4.2.1). In this case, the optimal shape parameter is $c=5.216$ and the corresponding errors in $u_{1}$ and $u_2$ are $3.530(-8)$ and $1.059(-7)$, respectively. Note that the errors $E_1$ and $E_2$ in $u_{1}$ and $u_2$ are defined using (5.2).

In Table 10 we present results obtained when applying the LOOCV algorithm to find the sub-optimal shape parameter and the corresponding errors in $u_1$ and $u_2$. Overall, accurate results are obtained for various initial search intervals. If we choose the interval properly, the accuracy can be very close to the optimal one as shown in Fig. 7. In Table 11 we present results obtained using various $M=N$ for a search interval of [0,20]. We also considered the corresponding Dirichlet boundary value problem (4.1) and in Table 12 we present results obtained using various $M=N$ for a search interval of [0,20] which are very similar to those in Table 11. Moreover, these results are consistent with the corresponding results obtained in Examples 1 and 2.

Fig. 7

Example 3: maximum relative error versus the shape parameter with $M=128, N=64$

Table 10 Example 3: sub-optimal shape parameters and the corresponding maximum relative errors for various initial search intervals using fminbnd with $M=128, N=64$

Table 11 Example 3: sub-optimal shape parameters and the maximum relative errors for various $M=N$

Table 12 Example 3: sub-optimal shape parameters and the maximum relative errors for various $M=N$ for Dirichlet boundary value problem

6 Conclusions

We have applied a Kansa-RBF method for the solution of elliptic boundary value problems in annular domains. With an appropriate choice of collocation points, the discretization of such problems governed by the Poisson, inhomogeneous biharmonic or the Cauchy–Navier equations of elasticity leads to linear systems in which the coefficient matrices are either block circulant or can be easily transformed into block circulant matrices. Thus these systems may be solved efficiently using MDAs leading to substantial savings in computational cost and storage. In addition, a major advantage of the proposed technique, other than its simplicity, is that it is applicable for any RBF and, as shown in our numerical tests, it is applicable to large-scale problems achieving high accuracy. Moreover, the use of the LOOCV algorithm enables us to select a good shape parameter which is critical to ensure appropriate numerical accuracy. We would like to indicate that the proposed method can be extended to solving a large class of partial differential equations without difficulty. The algorithm proposed in this paper can be easily applied to other RBF collocation methods [4, 8, 29]. In the spirit of reproducible research and for the convenience of interested readers the MATLAB$^{\copyright }$ code for Example 1, as described by Algorithm 1 in Sect. 2.3, maybe accessed at [14].

Possible areas of future research include

• The application of the method using compactly supported RBF, see, e.g., [2].

• The application of the method using a localized RBF collocation, see, e.g., [28].

• The extension of the current method for the solution of three-dimensional axisymmetric elliptic boundary value problems, see, e.g., [22].

• The extension of the current method to problems in which the type of boundary conditions alternates on the circular segments of the boundary, see, e.g., [19].

Appendix

We consider the RBFs $\phi _{mn}, \, m=1, \ldots , M, n=1, \ldots , N$. These satisfy, see, e.g., [7, Appendix D],

$$\begin{aligned} \phi _{mn}(x,y)= \Phi (r_{mn}), \quad r_{mn}^2(x,y)=(x-x_{mn})^2+(y-y_{mn})^2. \end{aligned}$$

(6.1)

It can be easily seen that

$$\begin{aligned} \dfrac{\partial \phi _{mn}}{\partial x} (x,y)= & {} \dfrac{\Phi ^\prime (r_{mn})}{r_{mn}} (x-x_{mn}), \quad \dfrac{\partial \phi _{mn}}{\partial y} (x,y) = \dfrac{\Phi ^\prime (r_{mn})}{r_{mn}}(y-y_{mn}),\end{aligned}$$

(6.2)

$$\begin{aligned} \frac{\partial ^2 \phi _{mn}}{\partial x^2} (x,y)= & {} \dfrac{\Phi ^\prime (r_{mn})}{r_{mn}} + \left( \dfrac{r_{mn}\Phi ^{\prime \prime }(r_{mn})-\Phi ^\prime (r_{mn})}{r_{mn}^3}\right) (x-x_{mn})^2,\end{aligned}$$

(6.3)

$$\begin{aligned} \frac{\partial ^2 \phi _{mn}}{\partial y^2} (x,y)= & {} \dfrac{\Phi ^\prime (r_{mn})}{r_{mn}} + \left( \dfrac{r_{mn}\Phi ^{\prime \prime }(r_{mn})-\Phi ^\prime (r_{mn})}{r_{mn}^3}\right) (y-y_{mn})^2, \end{aligned}$$

(6.4)

and

$$\begin{aligned} \frac{\partial ^2 \phi _{mn}}{\partial x \partial y} (x,y) = \left( \dfrac{r_{mn}\Phi ^{\prime \prime }(r_{mn})-\Phi ^\prime (r_{mn})}{r_{mn}^3}\right) (x-x_{mn}) (y-y_{mn}). \end{aligned}$$

(6.5)

Also,

$$\begin{aligned} \Delta \phi _{mn} (x,y) = \Phi ^{\prime \prime }(r_{mn}) +\dfrac{\Phi ^\prime (r_{mn})}{r_{mn}} \end{aligned}$$

(6.6)

and

$$\begin{aligned} \Delta ^2 \phi _{mn} (x,y) = \Phi ^{\prime \prime \prime \prime }(r_{mn}) +\dfrac{2\Phi ^{\prime \prime \prime }(r_{mn})}{r_{mn}}- \dfrac{\Phi ^{\prime \prime }(r_{mn})}{r_{mn}^2} +\dfrac{\Phi ^{\prime }(r_{mn})}{r_{mn}^3}. \end{aligned}$$

(6.7)

In the sequel, we shall be using the notation (cf. (2.8))

$$\begin{aligned} \delta _{m_1,m_2} x= & {} x_{m_1,n_1}-x_{m_2,n_2} = \mathsf{r}_{n_1} \cos ({\vartheta }_{m_1} + \frac{2\pi \alpha _{n_1}}{N})-\mathsf{r}_{n_2} \cos ({\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}),\nonumber \\ \delta _{m_1,m_2} y= & {} y_{m_1,n_1}-y_{m_2,n_2} = \mathsf{r}_{n_1} \sin ({\vartheta }_{m_1} + \frac{2\pi \alpha _{n_1}}{N})-\mathsf{r}_{n_2} \sin ({\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}). \end{aligned}$$

(6.8)

We shall also need the normal derivatives on the boundary $\partial \Omega _1$ which are given by

$$\begin{aligned} (\mathrm{n}_x, \mathrm{n}_y) (x_{m_1,1},y_{m_1,1}) = -\left( \cos ({\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}),\; \sin ({\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N})\right) . \end{aligned}$$

(6.9)

We next state and prove the following lemmata:

Lemma 1

For any radial function, each submatrix $\left( {A}_{n_1,n_2}\right)$ in (2.12) possesses a circulant structure.

Proof

We first consider the submatrices $\left( {A}_{n_1,n_2}\right) , \; n_1=2, \ldots , N-1, \; n_2=1, \ldots , N,$ which are defined by (2.13a). From (6.6), $\Delta \phi _{m_2,n_2}$ is an RBF, i.e. it is a function of $r_{m_2,n_2}$ (cf. (6.1)). Moreover,

$$\begin{aligned}&r_{m_2,n_2}^2(x_{m_1,n_1},y_{m_1,n_1})= (\delta _{m_1,m_2} x)^2+(\delta _{m_1,m_2} y)^2=\mathsf{r}_{n_1}^2+\mathsf{r}_{n_2}^2\\&\quad - 2\mathsf{r}_{n_1}\mathsf{r}_{n_2} \cos \left( {\vartheta }_{m_1}-{\vartheta }_{m_2} + \frac{2\pi (\alpha _{n_1}-\alpha _{n_2}) }{N}\right) , \end{aligned}$$

shows that for fixed $n_1, n_2$, the quantity $r_{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1})$ only depends on $({\vartheta }_{m_1}-{\vartheta }_{m_2})$, i.e. $({m_1}-{m_2})$ and therefore the submatrices are circulant.

The proof that the submatrices $\left( {A}_{n_1,n_2}\right) , \; n_1=1, N, \; n_2=1, \ldots , N$, defined by (2.13b)–(2.13c), are circulant in the case of Dirichlet boundary conditions is identical since their elements involve the RBFs $\phi _{m_2,n_2}$, which only depend on $r_{m_2,n_2}$.

In the case of a Neumann boundary condition on $\partial \Omega _1$, however, we have that the submatrices $\left( {A}_{1,n}\right) , \; n=1, \ldots , N$, are defined by (2.15), or

$$\begin{aligned} \left( A_{1,n_2}\right) _{m_1,m_2}= & {} \dfrac{\partial \phi _{m_2,n_2}}{\partial x} (x_{m_1,1},y_{m_1,1}) \mathrm{n}_x (x_{m_1,1},y_{m_1,1})\\&+ \,\dfrac{\partial \phi _{m_2,n_2}}{\partial y} (x_{m_1,1},y_{m_1,1}) \mathrm{n}_y (x_{m_1,1},y_{m_1,1}), \end{aligned}$$

and from (6.2) and (6.9) we obtain

$$\begin{aligned}&= - \dfrac{\Phi ^\prime (r_{m_2n_2})(x_{m_1,1},y_{m_1,1})}{r_{m_2n_2}(x_{m_1,1},y_{m_1,1}))} \left[ (x_{m_1,1}-x_{m_2,n_2}) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \right. \nonumber \\&\quad \left. +\, (y_{m_1,1}-y_{m_2,n_2}) \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \right] . \end{aligned}$$

Ignoring the radial part, we examine

$$\begin{aligned}&(x_{m_1,1}-x_{m_2,n_2}) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) + (y_{m_1,1}-y_{m_2,n_2}) \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \nonumber \\&\quad =\left( \mathsf{r}_{1} \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) - \mathsf{r}_{n_2} \cos \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \right) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \nonumber \\&\qquad +\left( \mathsf{r}_{1} \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) - \mathsf{r}_{n_2} \sin \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \right) \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \nonumber \\&\quad =\mathsf{r}_{1}-\mathsf{r}_{n_2} \cos \left( {\vartheta }_{m_2}-{\vartheta }_{m_1} + \frac{2\pi \left( \alpha _{n_2}-\alpha _1\right) }{N}\right) , \end{aligned}$$

(6.10)

which, again, only depends on $(m_2-m_1)$. Hence, this part is also radial and the corresponding submatrices are circulant. $\square$

Following identical arguments we also arrive at the corresponding result for the biharmonic case.

Lemma 2

For any radial function, each submatrix $\left( {A}_{n_1,n_2}\right)$ in (2.12) corresponding to collocation scheme (3.2), for both the first and the second biharmonic problem, possesses a circulant structure.

Finally, we consider the corresponding result for the Cauchy–Navier equations of elasticity.

Lemma 3

For any radial function, each submatrix $\left( \tilde{A}_{n_1,n_2}\right)$ in (4.9) possesses a $2 \times 2$ block circulant structure.

Proof

In order to prove the lemma we need to show that, see, e.g. [23],

$$\begin{aligned} R_{{\vartheta }_{m_1}} \left( A_{n_1,n_2}\right) _{m_1,m_2} R_{{\vartheta }_{m_2}}= & {} R_{{\vartheta }_{m_1+m}} \left( A_{n_1,n_2}\right) _{m_1+m,m_2+m} R_{{\vartheta }_{m_2+m}}, \nonumber \\&m_1,m_2=1,\ldots ,M, \; n_1, n_2=1, \ldots , N, \end{aligned}$$

(6.11)

provided $m_1+m, m_2+m \le M$. In case $m_1+m > M$, $m_1+m$ is replaced by $m_1+m-M$ and in case $m_2+m > M$, $m_2+m$ is replaced by $m_2+m-M$.

Since $R_{{\vartheta }_k}^2=I_2$ proving (6.11) is equivalent to proving

$$\begin{aligned}&R_{{\vartheta }_{m_1+m}} R_{{\vartheta }_{m_1}} \left( A_{n_1,n_2}\right) _{m_1,m_2} R_{{\vartheta }_{m_2}}R_{{\vartheta }_{m_1+m}}=\left( A_{n_1,n_2}\right) _{m_1+m,m_2+m},\nonumber \\&m_1,m_2=1,\ldots ,M, \; n_1, n_2=1, \ldots , N. \end{aligned}$$

(6.12)

However,

$$\begin{aligned} R_{{\vartheta }_{m_1+m}} R_{{\vartheta }_{m_1}}= & {} \left( \begin{array}{cc} \cos {\vartheta }_{m_1+m} &{} \sin {\vartheta }_{m_1+m} \\ \sin {\vartheta }_{m_1+m} &{} -\!\cos {\vartheta }_{m_1+m} \end{array} \right) \! \left( \begin{array}{cc} \cos {\vartheta }_{m_1} &{} \sin {\vartheta }_{m_1} \\ \sin {\vartheta }_{m_1} &{} -\!\cos {\vartheta }_{m_1} \end{array} \right) \! \\= & {} \left( \begin{array}{cc} \cos {\vartheta }_m &{} -\sin {\vartheta }_m \\ \sin {\vartheta }_m &{} \!\cos {\vartheta }_m \end{array} \right) \! = W_{{\vartheta }_m}, \end{aligned}$$

and

$$\begin{aligned} R_{{\vartheta }_{m_1}} R_{{\vartheta }_{m_1+m}}= & {} \left( \begin{array}{cc} \cos {\vartheta }_{m_1} &{} \sin {\vartheta }_{m_1} \\ \sin {\vartheta }_{m_1} &{} -\!\cos {\vartheta }_{m_1} \end{array} \right) \! \left( \begin{array}{cc} \cos {\vartheta }_{m_1+m} &{} \sin {\vartheta }_{m_1+m} \\ \sin {\vartheta }_{m_1+m} &{} -\!\cos {\vartheta }_{m_1+m} \end{array} \right) \! \\= & {} \left( \begin{array}{cc} \cos {\vartheta }_m &{} \sin {\vartheta }_m \\ -\sin {\vartheta }_m &{} \!\cos {\vartheta }_m \end{array} \right) \! = W_{{\vartheta }_m}^{-1}. \end{aligned}$$

Hence proving (6.12) is equivalent to proving that

$$\begin{aligned} W_{{\vartheta }_m} \left( A_{n_1,n_2}\right) _{m_1,m_2} W_{{\vartheta }_m}^{-1} =\left( A_{n_1,n_2}\right) _{m_1+m,m_2+m}. \end{aligned}$$

(6.13)

From (4.4a), for $m_1,m_2=1,\ldots ,M, \; n_1=2, \ldots , N-1, \; n_2=1, \ldots , N$, we can write

$$\begin{aligned}&\left( A_{n_1,n_2}\right) _{m_1,m_2}=\mu \Delta \phi _{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1}) I_2\nonumber \\&\quad +\, \dfrac{\mu }{1-2\nu } \left( \begin{array}{c c} \dfrac{\partial ^2 \phi _{m_2,n_2}}{\partial x^2} (x_{m_1,n_1},y_{m_1,n_1}) &{} \dfrac{\partial ^2 \phi _{m_2,n_2}}{\partial x \partial y} (x_{m_1,n_1},y_{m_1,n_1}) \\ \dfrac{\partial ^2 \phi _{m_2,n_2}}{\partial x \partial y} (x_{m_1,n_1},y_{m_1,n_1}) &{} \dfrac{\partial ^2 \phi _{m_2,n_2}}{\partial y^2} (x_{m_1,n_1},y_{m_1,n_1}) \end{array} \right) . \end{aligned}$$

(6.14)

We first consider the first term in (6.14), namely $\mu \Delta \phi _{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1}) I_2$.

We clearly have that

$$\begin{aligned} \mu \Delta \phi _{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1}) W_{{\vartheta }_m} I_2 W_{{\vartheta }_m}^{-1}= & {} \mu \Delta \phi _{m_2,n_2}(x_{m_1,n_1},y_{m_1,n_1}) I_2\\= & {} \mu \Delta \phi _{m_2+m,n_2}(x_{m_1+m,n_1},y_{m_1+m,n_1}) I_2, \end{aligned}$$

since the Laplacian of $\phi _{m_2,n_2}(x,y)$ is radial from (6.6) and

$$\begin{aligned}&(\delta _{m_1,m_2} x)^2+(\delta _{m_1,m_2} y)^2=\mathsf{r}_{n_1}^2+\mathsf{r}_{n_2}^2- 2\mathsf{r}_{n_1}\mathsf{r}_{n_2} \cos \left( {\vartheta }_{m_1}-{\vartheta }_{m_2} + \frac{2\pi (\alpha _{n_1}-\alpha _{n_2}) }{N}\right) \nonumber \\&\quad =(\delta _{m_1+m,m_2+m} x)^2+(\delta _{m_1+m,m_2+m} y)^2. \end{aligned}$$

(6.15)

Therefore, the first term in (6.14) satisfies (6.13).

For the second term in (6.14), from (6.3)–(6.5) and ignoring the radial parts we only need show that

$$\begin{aligned}&\left( \begin{array}{ll} \cos {\vartheta }_m &{} -\sin {\vartheta }_m \\ \sin {\vartheta }_m &{} \!\cos {\vartheta }_m \end{array} \right) \! \left( \begin{array}{c c} (\delta _{m_1,m_2} x)^2 &{} (\delta _{m_1,m_2} x)(\delta _{m_1,m_2} y)\\ (\delta _{m_1,m_2} x)(\delta _{m_1,m_2} y) &{} (\delta _{m_1,m_2} y)^2 \end{array} \right) \left( \begin{array}{ll} \cos {\vartheta }_m &{} \sin {\vartheta }_m \\ -\sin {\vartheta }_m &{} \!\cos {\vartheta }_m \end{array} \right) \!\nonumber \\&\quad = \left( \begin{array}{c c} (\delta _{m_1+m,m_2+m} x)^2 &{} (\delta _{m_1+m,m_2+m} x)(\delta _{m_1+m,m_2+m} y)\\ (\delta _{m_1+m,m_2+m} x)(\delta _{m_1+m,m_2+m} y) &{} (\delta _{m_1+m,m_2+m} y)^2 \end{array} \right) . \end{aligned}$$

(6.16)

By performing the multiplications on the left hand side of (6.16) we obtain that it is equal to

$$\begin{aligned} \left( \begin{array}{cc} (\cos {\vartheta }_m\delta _{m_1,m_2} x-\sin {\vartheta }_m\delta _{m_1,m_2}y)^2 &{} (\cos {\vartheta }_m\delta _{m_1,m_2} x-\sin {\vartheta }_m\delta _{m_1,m_2}y)(\sin {\vartheta }_m\delta _{m_1,m_2} x +\cos {\vartheta }_m\delta _{m_1,m_2}y) \\ (\cos {\vartheta }_m\delta _{m_1,m_2} x-\sin {\vartheta }_m\delta _{m_1,m_2}y)(\sin {\vartheta }_m\delta _{m_1,m_2} x +\cos {\vartheta }_m\delta _{m_1,m_2}y) &{} (\sin {\vartheta }_m\delta _{m_1,m_2} x+\cos {\vartheta }_m\delta _{m_1,m_2}y)^2 \end{array} \right) \!. \end{aligned}$$

Moreover, it can be easily shown that

$$\begin{aligned} \cos {\vartheta }_m\delta _{m_1,m_2} x-\sin {\vartheta }_m\delta _{m_1,m_2}y= & {} \mathsf{r}_{n_1} \cos \left( {\vartheta }_{m_1+m} + \frac{2\pi \alpha _{n_1}}{N}\right) \\&\quad -\mathsf{r}_{n_2} \cos \left( {\vartheta }_{m_2+m} + \frac{2\pi \alpha _{n_2}}{N}\right) \end{aligned}$$

and

$$\begin{aligned} \sin {\vartheta }_m\delta _{m_1,m_2} x\!+\!\cos {\vartheta }_m\delta _{m_1,m_2}y \!=\!\mathsf{r}_{n_1} \sin \left( {\vartheta }_{m_1+m} \!+ \!\frac{2\pi \alpha _{n_1}}{N}\right) \!-\!\mathsf{r}_{n_2} \sin \left( {\vartheta }_{m_2+m} \!+ \!\frac{2\pi \alpha _{n_2}}{N}\right) , \end{aligned}$$

from which (6.16) follows. Hence, the second term in (6.14) also satisfies (6.13).

We next need to prove that

$$\begin{aligned}&W_{{\vartheta }_m} \left( A_{1,n_2}\right) _{m_1,m_2} W_{{\vartheta }_m}^{-1} =\left( A_{1,n_2}\right) _{m_1+m,m_2+m} \quad \text{ and } \quad \nonumber \\&W_{{\vartheta }_m} \left( A_{N,n_2}\right) _{m_1,m_2} W_{{\vartheta }_m}^{-1} =\left( A_{N,n_2}\right) _{m_1+m,m_2+m}. \end{aligned}$$

(6.17)

Since from (4.4b) we can write

$$\begin{aligned} \left( A_{1,n_2}\right) _{m_1,m_2}=\phi _{m_2,n_2}(x_{m_1,1},y_{m_1,1}) I_2 \quad \text{ and } \quad \left( A_{N,n_2}\right) _{m_1,m_2}=\phi _{m_2,n_2}(x_{m_1,N},y_{m_1,N}) I_2, \end{aligned}$$

from (6.15), following a similar argument to the one used for the first term of (6.14), (6.17) follows.

Finally, we show that if instead of the displacements $u_1, u_2$ we have that the tractions $t_1, t_2$ are prescribed on, say, the boundary $\partial \Omega _1$, cf. Sect. 4.2.1, then

$$\begin{aligned} W_{{\vartheta }_m} \left( A_{1,n_2}\right) _{m_1,m_2} W_{{\vartheta }_m}^{-1} =\left( A_{1,n_2}\right) _{m_1+m,m_2+m} \end{aligned}$$

(6.18)

is still true.

We write

$$\begin{aligned} \left( A_{1,n}\right) _{m_1,m_2}=\left( \begin{array}{cc} T_{11} &{} T_{12} \\ T_{21} &{} T_{22} \end{array}\right) , \end{aligned}$$

(6.19)

where $T_{ij}, i,j=1,2,$ are the appropriate quantities in (4.6).

We can easily show that

$$\begin{aligned}&W_{{\vartheta }_m} \left( \begin{array}{c c} T_{11} &{} T_{12} \\ T_{21} &{} T_{22} \end{array}\right) W_{{\vartheta }_m}^{-1}\\&\quad = \left( \begin{array}{c c} \cos ^2 {\vartheta }_m T_{11} -\cos {\vartheta }_m\sin {\vartheta }_m (T_{21} + T_{12}) + \sin ^2 {\vartheta }_m T_{22}&{} \cos ^2 {\vartheta }_m T_{12} +\cos {\vartheta }_m\sin {\vartheta }_m (T_{11} - T_{22}) - \sin ^2 {\vartheta }_m T_{21} \\ \cos ^2 {\vartheta }_m T_{21} +\cos {\vartheta }_m\sin {\vartheta }_m (T_{11} - T_{22}) - \sin ^2 {\vartheta }_m T_{12} &{} \sin ^2 {\vartheta }_m T_{11} +\cos {\vartheta }_m\sin {\vartheta }_m (T_{21} + T_{12}) + \cos ^2 {\vartheta }_m T_{22} \end{array}\right) . \end{aligned}$$

We shall first show that the first term in (4.6) is radial. Using the notation of (6.8) with $n_1=1$, we have from (6.2) that

$$\begin{aligned}&\dfrac{\partial \phi _{m_2,n}}{\partial x}(x_{m_1,1},y_{m_1,1})\mathrm{n}_x(x_{m_1,1},y_{m_1,1}) + \dfrac{\partial \phi _{m_2,n}}{\partial y}(x_{m_1,1},y_{m_1,1})\mathrm{n}_y (x_{m_1,1},y_{m_1,1})\\&\quad =\dfrac{\Phi ^\prime (r_{m_2n})}{r_{m_2n}} \left[ \delta _{m_1,m_2}x \, \mathrm{n}_x(x_{m_1,1},y_{m_1,1})+\delta _{m_1,m_2}y \, \mathrm{n}_y(x_{m_1,1},y_{m_1,1})\right] , \end{aligned}$$

and ignoring the radial factor, we have, using (6.10) that

$$\begin{aligned}&\delta _{m_1,m_2}x \, \mathrm{n}_x(x_{m_1,1},y_{m_1,1})+\delta _{m_1,m_2}y \, \mathrm{n}_y(x_{m_1,1},y_{m_1,1})\\&\quad =\mathsf{r}_{1}-\mathsf{r}_{n_2} \cos ({\vartheta }_{m_2}-{\vartheta }_{m_1} + \frac{2\pi (\alpha _{n_2}-\alpha _1)}{N}), \end{aligned}$$

which only depends on $(m_2-m_1)$, hence it is radial.

We next consider the second term in (4.6). Dropping the multiplying constants and the obviously radial parts, and with the appropriate notation, we consider the quantities

$$\begin{aligned} \tilde{T}_{11}(m_1,m_2)= & {} \delta _{m_1,m_2}x \, \mathrm{n}_x(x_{m_1,1},y_{m_1,1})= \mathsf{r}_{1} \cos ^2 \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \\&-\,\mathsf{r}_{n_2} \cos \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) ,\\ \tilde{T}_{12}(m_1,m_2)= & {} 2\nu \delta _{m_1,m_2}y \, \mathrm{n}_x(x_{m_1,1},y_{m_1,1}) +(1-2\nu ) \delta _{m_1,m_2}x \, \mathrm{n}_y(x_{m_1,1},y_{m_1,1})\\= & {} \mathsf{r}_{1} \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \\&-\, \mathsf{r}_{n_2} \left( 2 \nu \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \sin \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \right. \\&+\left. (1-2\nu ) \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \right) \\= & {} \mathsf{r}_{1} \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \\&-\, \mathsf{r}_{n_2} \left( 2 \nu \sin \left( {\vartheta }_{m_2}-{\vartheta }_{m_1} + \frac{2\pi (\alpha _{n_2}-\alpha _1)}{N}\right) \right. \\&\left. +\sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \right) ,\\&\tilde{T}_{21}(m_1,m_2)= (1-2\nu ) \delta _{m_1,m_2}y \, \mathrm{n}_x(x_{m_1,1},y_{m_1,1}) \\&\quad +\, 2\nu \delta _{m_1,m_2}x \, \mathrm{n}_y(x_{m_1,1},y_{m_1,1})\\= & {} \mathsf{r}_{1} \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \\&-\, \mathsf{r}_{n_2} \left( (1-2 \nu ) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \sin \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \right. \\&+\left. 2 \nu \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \cos ({\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}) \right) \\= & {} \mathsf{r}_{1} \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \\&-\, \mathsf{r}_{n_2} \left( 2 \nu \sin \left( {\vartheta }_{m_1}-{\vartheta }_{m_2} + \frac{2\pi (\alpha _1-\alpha _{n_2})}{N}\right) \right. \\&+\left. \cos \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \sin \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \right) , \\ \tilde{T}_{22}(m_1,m_2)= & {} \delta _{m_1,m_2}y \, \mathrm{n}_y(x_{m_1,1},y_{m_1,1})= \mathsf{r}_{1} \sin ^2 \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) \\&-\,\mathsf{r}_{n_2} \sin \left( {\vartheta }_{m_2} + \frac{2\pi \alpha _{n_2}}{N}\right) \sin \left( {\vartheta }_{m_1} + \frac{2\pi \alpha _1}{N}\right) . \end{aligned}$$

By using (6.9), we first consider the term

$$\begin{aligned}&\cos ^2 {\vartheta }_m \tilde{T}_{11} -\cos {\vartheta }_m\sin {\vartheta }_m (\tilde{T}_{21} + \tilde{T}_{12}) + \sin ^2 {\vartheta }_m \tilde{T}_{22}\\&\quad = \cos ^2 {\vartheta }_m \delta _{m_1,m_2}x \, \mathrm{n}_x -\cos {\vartheta }_m\sin {\vartheta }_m \left( \delta _{m_1,m_2}y \, \mathrm{n}_x+ \delta _{m_1,m_2}x \, \mathrm{n}_y \right) + \sin ^2 {\vartheta }_m \delta _{m_1,m_2}y \, \mathrm{n}_y\\&\quad =\mathsf{r}_{1} \cos ^2 \left( {\vartheta }_{m_1}\!+\! {\vartheta }_{m} \!+\! \frac{2\pi \alpha _1}{N}\right) -\mathsf{r}_{n_2} \cos \left( {\vartheta }_{m_2} + {\vartheta }_{m} \!+\! \frac{2\pi \alpha _{n_2}}{N}\right) \cos \left( {\vartheta }_{m_1}+ {\vartheta }_{m} \!+\! \frac{2\pi \alpha _1}{N}\right) \\&\quad =\tilde{T}_{11}(m_1+m,m_2+m). \end{aligned}$$

We next consider

$$\begin{aligned}&\cos ^2 {\vartheta }_m \tilde{T}_{12} +\cos {\vartheta }_m\sin {\vartheta }_m (\tilde{T}_{11} - \tilde{T}_{22}) - \sin ^2 {\vartheta }_m \tilde{T}_{21}\\&\quad =\cos ^2 {\vartheta }_m \left( 2\nu \delta _{m_1,m_2}y \, \mathrm{n}_x \!+\!(1\!-\!2\nu ) \delta _{m_1,m_2}x \, \mathrm{n}_y\right) \!+\!\cos {\vartheta }_m\sin {\vartheta }_m (\delta _{m_1,m_2}x \, \mathrm{n}_x \!- \!\delta _{m_1,m_2}y \, \mathrm{n}_y)\\&\quad \quad - \sin ^2 {\vartheta }_m \left( (1-2\nu ) \delta _{m_1,m_2}y \, \mathrm{n}_x + 2\nu \delta _{m_1,m_2}x \, \mathrm{n}_y \right) =-2\nu \mathsf{r}_{n_2} \sin ({\vartheta }_{m_2}-{\vartheta }_{m_1} \\&\qquad + \frac{2\pi (\alpha _{n_2}-\alpha _1)}{N}) +\mathsf{r}_{1} \sin \left( {\vartheta }_{m_1} +{\vartheta }_m + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_1} +{\vartheta }_m + \frac{2\pi \alpha _1}{N}\right) \\&\quad \quad - \mathsf{r}_{n_2} \sin \left( {\vartheta }_{m_1} +{\vartheta }_m + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_2} +{\vartheta }_m + \frac{2\pi \alpha _{n_2}}{N}\right) =\tilde{T}_{12}(m_1+m,m_2+m). \end{aligned}$$

Similarly, we have that

$$\begin{aligned}&\cos ^2 {\vartheta }_m \tilde{T}_{21} +\cos {\vartheta }_m\sin {\vartheta }_m (\tilde{T}_{11} - \tilde{T}_{22}) - \sin ^2 {\vartheta }_m \tilde{T}_{12}=\cos ^2 {\vartheta }_m \\&\qquad \times \left( (1-2\nu ) \delta _{m_1,m_2}y \, \mathrm{n}_x + 2\nu \delta _{m_1,m_2}x \, \mathrm{n}_y\right) +\cos {\vartheta }_m\sin {\vartheta }_m (\delta _{m_1,m_2}x \, \mathrm{n}_x - \delta _{m_1,m_2}y \, \mathrm{n}_y)\\&\qquad - \sin ^2 {\vartheta }_m \left( 2\nu \delta _{m_1,m_2}y \, \mathrm{n}_x + (1-2\nu ) \delta _{m_1,m_2}x \, \mathrm{n}_y \right) =-2\nu \mathsf{r}_{n_2} \sin \left( {\vartheta }_{m_1}-{\vartheta }_{m_2} \right. \\&\qquad \left. + \,\frac{2\pi (\alpha _1-\alpha _{n_2})}{N}\right) +\mathsf{r}_{1} \sin \left( {\vartheta }_{m_1} +{\vartheta }_m + \frac{2\pi \alpha _1}{N}\right) \cos \left( {\vartheta }_{m_1} +{\vartheta }_m + \frac{2\pi \alpha _1}{N}\right) \\&\qquad - \,\mathsf{r}_{n_2} \cos \left( {\vartheta }_{m_1} +{\vartheta }_m + \frac{2\pi \alpha _1}{N}\right) \sin \left( {\vartheta }_{m_2} +{\vartheta }_m + \frac{2\pi \alpha _{n_2}}{N}\right) =\tilde{T}_{21}(m_1+m,m_2+m). \end{aligned}$$

Finally,

$$\begin{aligned}&\sin ^2 {\vartheta }_m \tilde{T}_{11} +\cos {\vartheta }_m\sin {\vartheta }_m (\tilde{T}_{21} + \tilde{T}_{12}) + \cos ^2 {\vartheta }_m \tilde{T}_{22}\\&\quad = \sin ^2 {\vartheta }_m \delta _{m_1,m_2}x \, \mathrm{n}_x +\cos {\vartheta }_m\sin {\vartheta }_m \left( \delta _{m_1,m_2}y \, \mathrm{n}_x+ \delta _{m_1,m_2}x \, \mathrm{n}_y \right) + \cos ^2 {\vartheta }_m \delta _{m_1,m_2}y \, \mathrm{n}_y.\\&\quad =\mathsf{r}_{1} \sin ^2 \left( {\vartheta }_{m_1}\!+\! {\vartheta }_{m} \!+\! \frac{2\pi \alpha _1}{N}\right) \!-\!\mathsf{r}_{n_2} \sin \left( {\vartheta }_{m_2} + {\vartheta }_{m} \!+\! \frac{2\pi \alpha _{n_2}}{N}\right) \sin \left( {\vartheta }_{m_1}\!+\! {\vartheta }_{m} \!+\! \frac{2\pi \alpha _1}{N}\right) \\&\quad =\tilde{T}_{22}(m_1+m,m_2+m). \end{aligned}$$

Therefore (6.18) is satisfied and the proof is complete. $\square$