A Multigrid Method for Helmholtz Transmission Eigenvalue Problems

Abstract

In this paper, we analyze the convergence of a finite element method for the computation of transmission eigenvalues and corresponding eigenfunctions. Based on the obtained error estimate results, we propose a multigrid method to solve the Helmholtz transmission eigenvalue problem. This new method needs only linear computational work. Numerical results are provided to validate the efficiency of the proposed method.

1 Introduction

The transmission eigenvalue problem has important applications in the inverse scattering theory and attracted many researchers’ attention recently [7–9, 11–13, 17, 22]. It arises in the study of inverse scattering by inhomogeneous media. They not only have theoretical importance [11], but also can be used to obtain estimates for the properties of the scattering material [6, 8, 23] since they can be determined from the scattering data.

In the past few years, significant progress of the existence of transmission eigenvalues and applications has been made. We refer the readers to the recent survey paper by Cakoni and Haddar [9]. However, in contrast, the numerical treatment of transmission eigenvalues and the associated interior transmission problem is very limited [1, 12, 15, 16, 21, 24, 26]. To the best of the authors’ knowledge, the recent paper by Colton et al. [12] contains the first numerical study where three finite element methods are proposed. Sun [24] proposes two iterative methods (bisection and secant). Ji et al. [16] construct a mixed finite element method. The technique is employed in [21] to compute Maxwell’s transmission eigenvalues. Most papers do not discuss the convergence due to the difficulty that the problem is neither elliptic nor self-adjoint. Only in [24], a rough error estimate for the eigenvalues is provided. In this paper, we present an accurate error estimate of the eigenvalue and eigenfunction approximations for the Helmhotz transmission eigenvalue problem.

Recently, a new type of multilevel correction method is proposed to solve the eigenvalue problem [18–20, 29]. In the multilevel correction scheme, the solution on a fine mesh can be reduced to a series of solutions of the eigenvalue problem on a very coarse mesh and a series of solutions of the boundary value problem on the multilevel meshes. This multilevel correction method gives a way to construct a type of multigrid scheme for the eigenvalue problem [19]. Based on the obtained error estimate results on the transmission eigenpairs and multilevel correction scheme for the eigenvalue computation, we propose a multigrid method to solve the transmission eigenvalue problem.

The rest of this paper is organized as follows. In Sect. 2, we introduce the transmission eigenvalue problem and derive an equivalent fourth order reformulation. The finite element method and its error estimates are given in Sect. 3. Section 4 introduces the multigrid method. The work estimate of the multigrid method is analyzed in Sect. 5. In Sect. 6, three examples are presented to validate the efficiency of the proposed numerical methods. The last section gives some concluding remarks.

2 Transmission Eigenvalue Problem

First, we introduce some notations and the transmission eigenvalue problem. $C$ (with or without subscripts) denotes a generic positive constant which may be different at its different occurrences through the paper. For convenience, the symbols $\lesssim ,\,\gtrsim$ and $\approx$ will be used in this paper. Notations $x_1\lesssim y_1, x_2\gtrsim y_2$ and $x_3\approx y_3$, mean that $x_1\le C_1y_1,\,x_2 \ge c_2y_2$ and $c_3x_3\le y_3\le C_3x_3$ for some constants $C_1, c_2, c_3$ and $C_3$ that are independent of mesh sizes (see, e.g., [28]).

In this paper, from the physical point of view, we are only concerned with the real transmission eigenvalues corresponding to the scattering of acoustic waves by a bounded simply connected inhomogeneous medium $\varOmega \subset {\mathcal {R}}^2$. The transmission eigenvalue problem is to find $k\in {\mathcal {R}},\,\phi , \varphi \in H^2(\varOmega ),\,\phi -\varphi \in H^2(\varOmega )$ such that

$$\begin{aligned} \left\{ \begin{array}{lcl@{\quad }l} \varDelta \phi +k^2n(x)\phi &{}=&{}0,&{}\mathrm{in}\ \varOmega ,\\ \varDelta \varphi +k^2\varphi &{}=&{}0, &{}\mathrm{in}\ \varOmega ,\\ \phi -\varphi &{}=&{}0,&{}\mathrm{on}\ \partial \varOmega ,\\ \frac{\partial \phi }{\partial \nu }-\frac{\partial \varphi }{\partial \nu }&{}=&{}0,&{}\mathrm{on}\ \partial \varOmega , \end{array}\right. \end{aligned}$$

(1)

where $\nu$ is the unit outward normal to the boundary $\partial \varOmega$. The index of refraction $n(x)$ is assumed to have two cases: $n(x)>\alpha$ a.e. in $\varOmega$ for some constant $\alpha >1$ or $0<n(x)<\tilde{\alpha }_0$ a.e. in $\varOmega$ for some constant $\tilde{\alpha }_0<1$. Values of $k$ such that there exists a nontrivial solution to (1) are called transmission eigenvalues.

Define

$$\begin{aligned} V:=H_0^2(\varOmega )=\Big \{u\in H^2(\varOmega ):\ u=0\ \mathrm{and}\ \frac{\partial u}{\partial {\nu }}=0\ \mathrm{on}\ \partial \varOmega \Big \}. \end{aligned}$$

(2)

Let $u=\phi -\varphi \in V$. Subtracting the second equation from the first one in (1) leads to

$$\begin{aligned} \Big (\varDelta +k^2\Big )u=-k^2\big (n(x)-1\big )\phi . \end{aligned}$$

(3)

Dividing $n(x)-1$ and applying $(\varDelta +k^2n(x))$ to both sides of the above equation, we can rewrite (1) as a fourth order problem

$$\begin{aligned} \big (\varDelta +k^2n(x)\big )\frac{1}{n(x)-1}(\varDelta +k^2)u=0. \end{aligned}$$

(4)

Denote by $(u,v)$ the $L^2(\varOmega )$ inner product. The weak formulation for the transmission eigenvalue problem (4) can be stated as follows: Find $(k^2\ne 0,u)\in {\mathcal {R}}\times V$ such that

$$\begin{aligned} \Big (\frac{1}{n(x)-1}(\varDelta u+k^2u),\varDelta v+k^2n(x)v\Big )=0,\quad \forall v\in V. \end{aligned}$$

(5)

In the rest of this section, we will follow the way in [24] to introduce the associated generalized eigenvalue problem and the existence of transmission eigenvalues. More details can be found in [24].

Let $\tau =k^2$. We define

$$\begin{aligned} {\mathcal {A}}_{\tau }(u,v)=\Big (\frac{1}{n(x)-1}(\varDelta u+\tau u), (\varDelta v+\tau v)\Big )+\tau ^2\big (u,v\big ), \end{aligned}$$

(6)

for $n(x)\ge \alpha _0$ a.e. in $\varOmega$ for some constant $\alpha _0>1$, and

$$\begin{aligned} \widetilde{{\mathcal {A}}}_{\tau }(u,v)&= \Big (\frac{1}{1-n(x)}(\varDelta u+\tau n(x)u), (\varDelta v+\tau n(x)v)\Big )+\tau ^2\big (n(x)u,v\big )\nonumber \\&= \Big (\frac{n(x)}{1-n(x)}(\varDelta u+\tau u),(\varDelta v+\tau v)\Big ) +\big (\varDelta u,\varDelta v\big ), \end{aligned}$$

(7)

for $n(x)\le \tilde{\alpha }_0$ a.e. in $\varOmega$ for some constant $\tilde{\alpha }_0<1$. We also define

$$\begin{aligned} {\mathcal {B}}(u,v)=\big (\nabla u,\nabla v\big ). \end{aligned}$$

(8)

For simplicity, we also call $\tau$ a transmission eigenvalue if $k$ is.

From (5), it is straightforward to show that the transmission eigenvalue problem can be stated as: Find $(\tau , u)\in {\mathcal {R}}\times V$ such that ${\mathcal {B}}(u,u)=1$ and

$$\begin{aligned} {\mathcal {A}}_{\tau }(u,v)=\tau {\mathcal {B}}(u,v),\quad \forall v\in V, \end{aligned}$$

(9)

when $n(x)\ge \alpha _0$ a.e. in $\varOmega$ for some constant $\alpha _0>1$, and

$$\begin{aligned} \mathcal {\tilde{A}}_{\tau }(u,v)=\tau {\mathcal {B}}(u,v),\quad \forall v\in V, \end{aligned}$$

(10)

when $n(x)\le \tilde{\alpha }_0$ a.e. in $\varOmega$ for some constant $\tilde{\alpha }_0<1$.

The bilinear forms ${\mathcal {A}}_{\tau }(\cdot ,\cdot ),\,\mathcal {\tilde{A}}_{\tau } (\cdot ,\cdot )$ and ${\mathcal {B}}_{\tau }(\cdot ,\cdot )$ have the following properties.

Lemma 1

[9, 24] If $\frac{1}{n(x)-1}\ge \gamma$ a.e. in $\varOmega$ for some $\gamma >0$, then the bilinear form ${\mathcal {A}}_\tau (\cdot ,\cdot )$ is coercive on $V\times V$ and if $\frac{n(x)}{1-n(x)}\ge \tilde{\gamma }$ a.e. in $\varOmega$ for some $\tilde{\gamma }>0$, then the bilinear form $\tilde{{\mathcal {A}}}_\tau (\cdot ,\cdot )$ is coercive on $V\times V$. Moreover, ${\mathcal {B}}(\cdot ,\cdot )$ is a symmetric and nonnegative bilinear form on $V\times V$.

Here, in order to give the error analysis, we will use the idea in [24] of transforming the transmission eigenvalue as a fix point of a non-linear function $\lambda (\tau )$ which will be defined by the general eigenvalue problems. We define the following generalized eigenvalue problem: Find $(\lambda (\tau ),u)\in {\mathcal {R}}\times V$ such that ${\mathcal {B}}(u,u)=1$ and

$$\begin{aligned} {\mathcal {A}}_{\tau }(u,v)=\lambda (\tau ){\mathcal {B}}(u,v),\quad \forall v\in V, \end{aligned}$$

(11)

for $n(x)\ge \alpha _0$ a.e. in $\varOmega$ for some constant $\alpha _0>1$, or

$$\begin{aligned} \mathcal {\tilde{A}}_{\tau }(u,v)=\lambda (\tau ){\mathcal {B}}(u,v),\quad \forall v\in V, \end{aligned}$$

(12)

for $n(x)\le \tilde{\alpha }_0$ a.e. in $\varOmega$ for some constant $\tilde{\alpha }_0<1$.

Then $\lambda (\tau )$ is a function of $\tau$. Based on the definitions of $A_{\tau }(\cdot ,\cdot )$ and $\tilde{A}_{\tau }(\cdot ,\cdot )$, it is easy to see that the function $\lambda (\tau )$ is continuous corresponding to $\tau$ based on the eigenvalue perturbation theory (c.f. [2, 3]). From (9) and (10), a transmission eigenvalue is a root of the following nonlinear function

$$\begin{aligned} f(\tau ):= \lambda (\tau )-\tau . \end{aligned}$$

(13)

While our goal is to solve the above non-linear equation numerically, we refer the readers to [9] for more details on the existence result.

3 Error Estimates of the Eigenpair Approximation

In this section, we first introduce the finite element method for the transmission eigenvalue problem. Then we adopt the results in [24] by the bisection method to give the error estimate of the eigenvalue approximations. Finally based on the theory of the finite element method for eigenvalue problems, we derive the error estimates for the eigenfunction approximation.

3.1 Error Estimate of the Eigenvalue Approximation

For simplicity, we only consider the finite element method and error estimates for the case (9). The case (10) follows similarly.

Let $M(\lambda (\tau ))$ denote the following eigenfunction set corresponding to the eigenvalue $\lambda (\tau )$

$$\begin{aligned} M(\lambda (\tau ))=\big \{v\in V:\ v\ \mathrm{is\ an\ eigenfunction\ of\ (11) \ corresponding\ to}\ \lambda (\tau ) \, \mathrm{and}\, {\mathcal {B}}(v,v)\!=\!1\big \}. \end{aligned}$$

We define the operator $T_{\tau }: H^1(\varOmega )\rightarrow V$ as

$$\begin{aligned} {\mathcal {A}}_{\tau }(T_{\tau }f,v)={\mathcal {B}}(f,v),\quad \forall f\in H^1(\varOmega ). \end{aligned}$$

(14)

As we know, the operator $T_{\tau }: V\rightarrow V$ is compact and self-adjoint because of the compact embedding of $V$ into $H^1(\varOmega )$. Therefore the eigenvalue problem (11) can be rewritten as

$$\begin{aligned} \lambda (\tau )T_{\tau }u_{\tau }=u_{\tau }. \end{aligned}$$

(15)

So $\mu =1/\lambda (\tau )$ is an eigenvalue of $T_{\tau }$ associated with the same eigenfunction $u_{\tau }$.

Let ${\mathcal {T}}_h$ be a shape regular mesh over $\varOmega$ which means there exists a constant $\gamma ^*$ such that

$$\begin{aligned} \frac{h_{K}}{\rho _K}\le \gamma ^*,\quad \forall K\in \bigcup \limits _{h}{\mathcal {T}}_h, \end{aligned}$$

where $h_K$ denotes the diameter of the smallest ball containing $K$ for each $K\in {\mathcal {T}}_h$, and $\rho _K$ is the diameter of the biggest ball contained in $K,\,h:=\max \{h_K:K\in {\mathcal {T}}_h\}$. Based on the mesh ${\mathcal {T}}_h$, we define a conforming finite element space $V_h$ (for example Bogner–Fox–Schmit element [4]) such that $V_h\subset V$.

Remark 1

The numerical method proposed in this paper can be used for general conforming finite element spaces for the Sobolev space $H^2(\varOmega )$. For more examples of conforming elements, please read books [5, 10]. The actual implementation of conforming finite element space $V_h$ offers some computational difficulties: Either the dimension of the “local” polynomial spaces is fairly large (at least 18 for triangular elements) or the structure of the polynomial space is complicated. These difficulties mainly come from the fact that the conforming finite element space $V_h$ requires continuity of the function value and the partial derivatives across adjacent finite elements. For more details, please refer [5, 10].

Based on the finite element space $V_h$, we can define the following discrete version of the eigenvalue problem (9) as: Find $(\tau _h,u_h)\in {\mathcal {R}}\times V_h$ such that ${\mathcal {B}}(u_h,u_h)=1$ and

$$\begin{aligned} {\mathcal {A}}_{\tau _h}(u_h,v_h) = \tau _h{\mathcal {B}}(u_h, v_h), \quad \forall v_h\in V_h. \end{aligned}$$

(16)

In order to analyze the error estimates by the finite element method, we adopt the process in [24] to find the roots of a discrete version of (13) which can be defined as: Find $(\lambda _h(\tau ),\hat{u}_h)\in {\mathcal {R}}\times V_h$ such that ${\mathcal {B}}(\hat{u}_h,\hat{u}_h)=1$ and

$$\begin{aligned} {\mathcal {A}}_{\tau }(\hat{u}_h,v_h) = \lambda _{h}(\tau ){\mathcal {B}}(\hat{u}_h, v_h), \quad \forall v_h\in V_h. \end{aligned}$$

(17)

Similarly, we define a discrete operator $T_{\tau ,h}: H^1(\varOmega )\rightarrow V_h$ as

$$\begin{aligned} {\mathcal {A}}_{\tau }(T_{\tau ,h}f,v)={\mathcal {B}}(f,v),\quad \forall f\in V_h. \end{aligned}$$

(18)

Obviously, $T_{\tau ,h}$ is a compact self-adjoint operator and the eigenvalue problem (17) can be rewritten as

$$\begin{aligned} \lambda _h(\tau )T_{\tau ,h}\hat{u}_h=\hat{u}_h. \end{aligned}$$

(19)

Based on the standard theory of the finite element method for the eigenvalue problem, we have the following error estimate (c.f. [2, 3]).

Lemma 2

Assume the index of refraction $n(x)$ satisfies the conditions of Lemma 1. Let $(\lambda _h(\tau ),\hat{u}_h)$ denote a solution of the eigenvalue problem (17). Then there exists a solution of the exact eigenvalue problem (11) such that the following error estimate holds

$$\begin{aligned} |\lambda _h(\tau )-\lambda (\tau )|\lesssim \delta _h^2(\lambda (\tau )), \end{aligned}$$

(20)

where

$$\begin{aligned} \delta _h(\lambda (\tau )):= \sup _{w\in M(\lambda (\tau ))}\inf _{v_h\in V_h}\Vert w-v_h\Vert _V. \end{aligned}$$

(21)

Proof

First, it is obvious that the eigenvalue problem (17) is the discrete version of the eigenvalue problem (11) by the finite element method when we fix the parameter $\tau$. Then the desired result (20) can be obtained by the standard error estimate of the finite element method for eigenvalue problems corresponding to the compact operators (see, e.g., [2, 3]). $\square$

Since the operator $T_{\tau }$ corresponds to the biharmonic operator with a lower order perturbation, the eigenfunction in $M(\lambda )$ has the following regularity estimate

$$\begin{aligned} \Vert u\Vert _{2+\gamma }< \infty ,\quad \mathrm{for}\, u\in M(\lambda ), \end{aligned}$$

(22)

for some $\gamma \,(0<\gamma \le 1)$ which depends on the maximal interior angle of the boundary $\partial \varOmega$ and $\gamma =1$ when the domain $\varOmega$ is convex [14]. Thus the following estimate for $\delta _h(\lambda (\tau ))$ holds

$$\begin{aligned} \delta _h(\lambda (\tau ))\lesssim h^{s}\Vert u\Vert _{2+s}, \end{aligned}$$

(23)

where $s=\min \{\gamma ,k-1\}$ with $k$ denoting the degree of the piecewise polynomial space for the finite element space $V_h$.

From (16) and (17), we know the eigenvalue $\tau _h$ in (16) is a root of the following equation

$$\begin{aligned} f_h(\tau ) := \lambda _h(\tau )-\tau . \end{aligned}$$

(24)

Lemma 3

[24, Lemma 3.2] Let $\lambda _0(\varOmega )$ denote the first Dirichlet eigenvalue of $-\varDelta$ on $\varOmega$. If $|\nabla \frac{1}{n(x)-1}|<c_g$ for some constant $c_g$ when $n(x)\ge \alpha _0$ a.e. in $\varOmega$ for some constant $\alpha _0>1$, or $|\nabla \frac{n(x)}{1-n(x)}|<c_g$ for some constant $c_g$ when $n(x)\le \tilde{\alpha }_0$ a.e. in $\varOmega$ for some constant $\tilde{\alpha }_0<1$. Then we have $f_h'(\tau )<0$ when

$$\begin{aligned} \tau <\frac{\Big (1+\frac{2}{n^*-1}-c_g-\frac{c_g}{\lambda _0(\varOmega )}\Big ) \lambda _0(\varOmega )}{\frac{2n_*}{n_*-1}}, \end{aligned}$$

(25)

for $n(x)\ge \alpha _0$ a.e. in $\varOmega$ with some constant $\alpha _0>1$, or

$$\begin{aligned} \tau <\frac{\Big (1+\frac{2}{1-n_*}-c_g-\frac{c_g}{\lambda _0(\varOmega )}\Big ) \lambda _0(\varOmega )}{\frac{2n^*}{1-n^*}}, \end{aligned}$$

(26)

for $n(x)\le \tilde{\alpha }_0$ a.e. in $\varOmega$ with some constant $\tilde{\alpha }_0<1$. Here $n^{*}=\sup _{x\in \varOmega }n(x)$ and $n_*=\inf _{x\in \varOmega }n(x)$.

The following theorem states that the roots of (24) approximate the roots of (13) well if the mesh size is small enough.

Theorem 1

Assume $\tau _h$ is an eigenvalue solution of (16) approximating the exact eigenvalue $\tau$ of (11) which satisfies the conditions in Lemma 3. Then the following error estimate holds

$$\begin{aligned} |\tau -\tau _h|\lesssim \delta _h^2(\tau ), \end{aligned}$$

(27)

for the small enough $h>0$.

Proof

For small enough $h>0$, from Lemma 3, we have that $f_h'(\tau )<-C <0$ for some $C>0$. From Lemma 2, the following estimate holds

$$\begin{aligned} |f(\tau )- f_h(\tau )|\lesssim \delta _h^2(\lambda (\tau )), \end{aligned}$$

on an interval $[a-\delta _h^2(\lambda (\tau ))/C, b + \delta _h^2(\lambda (\tau ))/C]$ for some $0 < a < b$. Then from Lemma 3.3 in [24] with $\lambda (\tau )=\tau$, we can obtain the desired result (27). $\square$

3.2 Error Estimate of the Eigenfunction Approximation

Based on the above error estimate of the eigenvalue approximation, we now give the convergence analysis for the eigenfunction approximation. Here, we set the eigenvalue $\tau _h$ to be the approximation of the exact eigenvalue $\tau$ defined by (9). So in this subsection, we set $\lambda (\tau )=\tau$.

We construct an auxiliary eigenvalue problem: Find $(\tilde{\lambda },\tilde{u})\in {\mathcal {R}}\times V$ such that ${\mathcal {B}}(\tilde{u},\tilde{u})=1$ and

$$\begin{aligned} {\mathcal {A}}_{\tau _h}(\tilde{u},v)=\tilde{\lambda }{\mathcal {B}}(\tilde{u},v), \quad \forall v\in V. \end{aligned}$$

(28)

Corresponding to this eigenvalue problem and ${\mathcal {A}}_{\tau _h}(\cdot ,\cdot )$, we can also define an operator $T_{\tau _h}:H^1(\varOmega )\rightarrow V$ as

$$\begin{aligned} {\mathcal {A}}_{\tau _h}(T_{\tau _h}f,v)={\mathcal {B}}(f,v),\quad \forall v\in V. \end{aligned}$$

(29)

Then the eigenvalue problem (28) can be written as

$$\begin{aligned} \tilde{\lambda }T_{\tau _h}\tilde{u}=\tilde{u}. \end{aligned}$$

(30)

From Theorem 1, we know $\tau _h\rightarrow \tau$ and the family of compact operators $T_{\tau _h}: V\rightarrow V(0<h\le 1)$ has the property $T_{\tau _h}\rightarrow T_{\tau }$ in the operator norm as $h\rightarrow 0$.

Lemma 4

Assume eigenvalues $\tau$ and $\tau _h$ have the error estimate (27). The two operators $T_{\tau }$ and $T_{\tau _h}$ have the following estimate

$$\begin{aligned} \Vert T_{\tau }-T_{\tau _h}\Vert _V\lesssim |\tau -\tau _h|\lesssim \delta _h(\tau )^2, \end{aligned}$$

(31)

where $\Vert \cdot \Vert _{V}$ means the operator norm on $V\rightarrow V$.

Proof

From the definitions and boundedness of the operators $T_{\tau }$ and $T_{\tau _h}$, the ellipticity and boundedness of ${\mathcal {A}}_{\tau }(\cdot ,\cdot )$ and ${\mathcal {A}}_{\tau _h}(\cdot ,\cdot )$, we have the following estimate

$$\begin{aligned} \Vert T_{\tau }-T_{\tau _h}\Vert _V&= \sup _{f\in V, \Vert f\Vert _V=1}\Vert T_{\tau }f-T_{\tau _h}f\Vert _V\nonumber \\&\lesssim \sup _{f\in V, \Vert f\Vert _V=1}\sup _{v\in V,\Vert v\Vert _V=1}{\mathcal {A}}_{\tau _h}\big (T_{\tau }f- T_{\tau _h}f,v\big )\nonumber \\&= \sup _{f\in V, \Vert f\Vert _V=1}\sup _{v\in V,\Vert v\Vert _V=1}\Big ({\mathcal {A}}_{\tau }\big (T_{\tau }f, v\big ) -{\mathcal {A}}_{\tau }\big (T_{\tau }f, v\big )\nonumber \\&\quad +{\mathcal {A}}_{\tau _h}\big (T_{\tau }f,v\big )-{\mathcal {A}}_{\tau _h} \big (T_{\tau _h}f,v\big )\Big )\nonumber \\&= \sup _{f\in V, \Vert f\Vert _V=1}\sup _{v\in V,\Vert v\Vert _V=1}\Big ({\mathcal {A}}_{\tau _h}\big (T_{\tau }f, v\big ) -{\mathcal {A}}_{\tau }\big (T_{\tau }f, v\big )\Big )\nonumber \\&\lesssim \sup _{f\in V, \Vert f\Vert _V=1}|\tau -\tau _h|\Vert f\Vert _V\nonumber \\&\lesssim |\tau -\tau _h|. \end{aligned}$$

(32)

This is the desired result (31). $\square$

In order to give the estimate $\Vert u-\tilde{u}\Vert _V$, we define $R_z(T_{\tau })=(z-T_{\tau })^{-1},\,R_z(T_{\tau _h})=(z-T_{\tau _h})^{-1}$. Let $\varGamma$ be a circle in the complex plane which is centered at $1/\tau$ and encloses no other eigenvalues of $T_{\tau }$. The spectral projection operator associated with $T_{\tau }$ and $1/\tau$ is defined as

$$\begin{aligned} E_{\tau }=\frac{1}{2\pi i}\int \limits _{\varGamma }R_z(T_{\tau })dz. \end{aligned}$$

(33)

$E_{\tau }$ is a projection onto the space of generalized eigenvectors associated with $1/\tau$ and $T_{\tau }$, i.e., $R(E_{\tau })=N((1/\tau -T_{\tau })^{\alpha })$, where $R$ denotes the range and $\alpha$ is the ascent of $\tau$. For $h$ sufficiently small, the spectral projection

$$\begin{aligned} E_{\tau _h}=\frac{1}{2\pi i}\int \limits _{\varGamma }R_z(T_{\tau _h})dz, \end{aligned}$$

(34)

exists, $E_{\tau _h}$ converges to $E_{\tau }$ in norm and $\mathrm{dim}R(E_{\tau _h})=\mathrm{dim}R(E_{\tau })$. $E_{\tau _h}$ is the spectral projection associated with $T_{\tau _h}$ and the eigenvalues of $T_{\tau _h}$ which lie in $\varGamma$. Furthermore, $E_{\tau _h}$ is a projection onto the direct sum of the spaces of generalized eigenvectors corresponding to these eigenvalues, for more details, please read [3].

Given two closed subspaces $M$ and $N$ of $V$, we define the gap between $M$ and $N$ as

$$\begin{aligned} \delta (M,N)=\max (\hat{\delta }(M,N),\hat{\delta }(N,M)),\, \mathrm{where}\, \hat{\delta }(M,N)=\sup _{v\in M,\Vert v\Vert _V=1}\inf _{\chi \in N}\Vert v-\chi \Vert _V. \end{aligned}$$

Lemma 5

The two finite dimensional spaces $R(E_{\tau })$ and $R(E_{\tau _h})$ have the following estimate

$$\begin{aligned} \delta (R(E_{\tau }),R(E_{\tau _h})) \lesssim \Vert (T_{\tau }-T_{\tau _h})|_{R(E_{\tau })}\Vert _V, \end{aligned}$$

(35)

for small enough $h$, where $(T_{\tau }-T_{\tau _h})|_{R(E_{\tau })}$ denotes the restriction of $T_{\tau }-T_{\tau _h}$ to $R(E_{\tau })$.

Proof

The proof is similar to Theorem 7.1 in [3]. For any $f\in R(E_{\tau })$ with $\Vert f\Vert _V=1$, we have

$$\begin{aligned} \Vert f-E_{\tau _h}f\Vert _V&= \Vert E_{\tau }f-E_{\tau _h}f\Vert _V=\Big \Vert \frac{1}{2\pi i}\int _{\varGamma }[R_z(T_{\tau })-R_z(T_{\tau _h})]fdz\Big \Vert _V\nonumber \\&= \Big \Vert \frac{1}{2\pi i}\int _{\varGamma }[R_z(T_{\tau _h}) (T_{\tau }-T_{\tau _h})R_z(T_{\tau })]fdz\Big \Vert _V\nonumber \\&\lesssim \Vert (T_{\tau }-T_{\tau _h})f\Vert _V\le \Vert (T_{\tau }-T_{\tau _h})|_{R(E_{\tau })}\Vert _V. \end{aligned}$$

(36)

Combination of Theorem 6.1 in [3] and (36) leads to the desired result (35). $\square$

From the standard error estimate theory for the eigenvalue problem by the finite element method, we have the following estimates.

Lemma 6

Assume $\tau _h\rightarrow \tau$. The eigenpair approximations $(\tau ,u)$ of (9) and $(\tilde{\lambda },\tilde{u})$ of (28) have the following estimates

$$\begin{aligned} \Vert u-\tilde{u}\Vert _V&\lesssim \delta _h(\tau ), \end{aligned}$$

(37)

$$\begin{aligned} |\tau - \tilde{\lambda }|&\lesssim \delta _h^2(\tau ). \end{aligned}$$

(38)

Proof

From Lemmas 4 and 5, the following estimate holds

$$\begin{aligned} \delta (R(E_{\tau }),R(E_{\tau _h})) \lesssim \delta _h(\tau ). \end{aligned}$$

(39)

Combining this estimate and the theory in [3], we can obtain the desired estimates (37) and (38). $\square$

The final error estimates of the eigenpair approximation $(\tau _h,u_h)$ can be derived from(37)–(38) and the triangle inequality.

Theorem 2

There exists an eigenpair $(\tau ,u)$ of (9) such that the eigenpair approximation $(\tau _h,u_h)$ of (16) by the finite element method has the following error estimates

$$\begin{aligned} \Vert u_h-u\Vert _V&\lesssim \delta _h(\tau ),\end{aligned}$$

(40)

$$\begin{aligned} \Vert u_h-u\Vert _1&\lesssim \eta _A(h)\delta _h(\tau ),\end{aligned}$$

(41)

$$\begin{aligned} |\tau -\tau _h|&\lesssim \delta _h^2(\tau ), \end{aligned}$$

(42)

where

$$\begin{aligned} \eta _A(h) := \sup _{f\in H^1(\varOmega ),\Vert f\Vert _1=1}\inf _{v_h\in V_h}\Vert T_{\tau }f-v_h\Vert _V. \end{aligned}$$

(43)

Proof

Actually, the discrete eigenvalue problem (16) is the discretization of the linear eigenvalue problem (28) by the finite element method. Then from the standard theory in [3], the following estimates hold

$$\begin{aligned} \Vert \tilde{u}-u_h\Vert _V&\lesssim \delta _h(\tilde{\lambda }),\end{aligned}$$

(44)

$$\begin{aligned} \Vert \tilde{u}-u_h\Vert _1&\lesssim \eta _A(h)\Vert \tilde{u}-u_h\Vert _V, \end{aligned}$$

(45)

$$\begin{aligned} |\tilde{\lambda }- \tau _h|&\lesssim \delta _h^2(\tilde{\lambda }). \end{aligned}$$

(46)

Since for any $w\in M(\tilde{\lambda })$, from (39), there exists an $\tilde{w}\in R(E_{\tau })=M(\tau )$ such that

$$\begin{aligned} \Vert w-\tilde{w}\Vert _V\lesssim \delta _h(\tau ). \end{aligned}$$

(47)

From the definition of $\delta _h(\tau )$, there exists $w_h\in V_h$ such that

$$\begin{aligned} \Vert \tilde{w}-w_h\Vert _V\lesssim \delta _h(\tau ). \end{aligned}$$

(48)

The combination of (47) and (48) leads to

$$\begin{aligned} \Vert w-w_h\Vert _V\lesssim \delta _h(\tau ). \end{aligned}$$

(49)

Then from (49) and the arbitrariness of $w$, we have

$$\begin{aligned} \delta _h(\tilde{\lambda }) =\sup _{w\in M(\tilde{\lambda })}\inf _{v_h\in V_h}\Vert w-v_h\Vert _V \lesssim \delta _h(\tau ). \end{aligned}$$

(50)

The combination of (37)–(38), (44)–(46), (50) and $\delta _h(\tau )\lesssim \eta _A(h)$ leads to the desired results (40)–(42). $\square$

4 A Multigrid Method

In this section, based on the error estimates derived in the previous sections, we propose a multigrid method to solve the discrete transmission eigenvalue problem (16). In order to carry out the scheme, we define a sequence of partitions (triangulation or rectangulation) ${\mathcal {T}}_{h_k}$ of $\varOmega$ as follows: Suppose ${\mathcal {T}}_{h_1}$ (produced from ${\mathcal {T}}_H$ by regular refinement) is given and let ${\mathcal {T}}_{h_k}$ be obtained from ${\mathcal {T}}_{h_{k-1}}$ via regular refinement (produce $\beta ^2$ congruent elements, for example, $\beta =2$ for bisection mesh refinement) such that

$$\begin{aligned} h_k\approx \frac{1}{\beta }h_{k-1}. \end{aligned}$$

Based on this sequence of meshes, we construct the corresponding finite element spaces such that

$$\begin{aligned} V_{H}\subseteq V_{h_1}\subset V_{h_2}\subset \cdots \subset V_{h_n}, \end{aligned}$$

(51)

and the following relation of approximation errors holds

$$\begin{aligned} \eta _A(H)\gtrsim \delta _{h_1}(\tau ),\quad \delta _{h_k}(\lambda )\approx \Big (\frac{1}{\beta }\Big )^{s}\delta _{h_{k-1}}(\tau ), \quad k=2,\ldots ,n, \end{aligned}$$

(52)

where $s$ is defined in (22).

4.1 One Correction Step

Assume we have an eigenpair approximation $(\tau _{h_k},u_{h_k})\in {\mathcal {R}}\times V_{h_k}$. In order to do the correction step, we assume $V_H$ be the background space which is a subset of $V_{h_k}$, i.e., $V_H\subset V_{h_k}$.

Algorithm 1

One Correction Step

• 1. Define the following auxiliary boundary value problem: Find $\widehat{u}_{h_{k+1}}\in V_{h_{k+1}}$ such that

  $$\begin{aligned} {\mathcal {A}}_{\tau _{h_k}}(\widehat{u}_{h_{k+1}},v_{h_{k+1}})=\tau _{h_k}{\mathcal {B}}(u_{h_k},v_{h_{k+1}}), \quad \forall v_{h_{k+1}}\in V_{h_{k+1}}. \end{aligned}$$

  (53)

  Solve this equation with multigrid method to obtain a new eigenfunction approximation $\widetilde{u}_{h_{k+1}}\in V_{h_{k+1}}$ with error estimate

  $$\begin{aligned} \Vert \widehat{u}_{h_{k+1}}-\widetilde{u}_{h_{k+1}}\Vert _V\le C\delta _{h_{k+1}}(\tau ), \end{aligned}$$

  and define

  $$\begin{aligned} \widetilde{u}_{h_{k+1}}:=MG(V_{h_{k+1}},u_{h_k}, \tau _{h_k},m_{k+1}), \end{aligned}$$

  where $u_{h_k}$ is the initial solution and $m_{k+1}$ the iteration time of the multigrid scheme.

• 2. Define a new finite element space $V_{H,h_{k+1}}=V_H+\mathrm{span}\{\widetilde{u}_{h_{k+1}}\}$ and solve the following eigenvalue problem: Find $(\tau _{h_{k+1}},u_{h_{k+1}})\in {\mathcal {R}}\times V_{H,h_{k+1}}$ such that ${\mathcal {B}}(u_{h_{k+1}},u_{h_{k+1}})=1$ and

  $$\begin{aligned} {\mathcal {A}}_{\tau _{h_{k+1}}}(u_{h_{k+1}},v_{H,h_{k+1}})=\tau _{h_{k+1}} {\mathcal {B}}(u_{h_{k+1}},v_{H,h_{k+1}}),\quad \forall v_{H,h_{k+1}}\in V_{H,h_{k+1}}. \end{aligned}$$

  (54)

Summarize the above two steps into $(\tau _{h_{k+1}},u_{h_{k+1}})= Correction (V_H,\tau _{h_k},u_{h_k},V_{h_{k+1}})$, where $\tau _{h_k}$ and $u_{h_k}$ are the given eigenvalue and eigenfunction approximation, respectively.

In order to do the error estimate, we define the finite element projection operator $P_h: V\mapsto V_h$ as follows

$$\begin{aligned} {\mathcal {A}}_{\tau }(u-P_hu,v_h)=0,\quad \forall v_h\in V_h. \end{aligned}$$

(55)

Theorem 3

Assume there exists an eigenpair $(\tau ,u)$ of (9) such that the current eigenpair approximation $(\tau _{h_k},u_{h_k})\in {\mathcal {R}}\times V_{h_k}$ has the following error estimates

$$\begin{aligned} \Vert u-u_{h_k}\Vert _V&\lesssim \varepsilon _{h_k}(\tau ),\end{aligned}$$

(56)

$$\begin{aligned} \Vert u-u_{h_k}\Vert _1&\lesssim \eta _A(H)\varepsilon _{h_k}(\tau ),\end{aligned}$$

(57)

$$\begin{aligned} |\tau -\tau _{h_k}|&\lesssim \varepsilon _{h_k}^2(\tau ). \end{aligned}$$

(58)

Then after one correction step, the resultant approximation $(\tau _{h_{k+1}},u_{h_{k+1}})\in {\mathcal {R}}\times V_{h_{k+1}}$ has the following error estimates

$$\begin{aligned} \Vert u-u_{h_{k+1}}\Vert _V&\lesssim \varepsilon _{h_{k+1}}(\tau ),\end{aligned}$$

(59)

$$\begin{aligned} \Vert u-u_{h_{k+1}}\Vert _1&\lesssim \eta _A(H)\varepsilon _{h_{k+1}}(\tau ),\end{aligned}$$

(60)

$$\begin{aligned} |\tau -\tau _{h_{k+1}}|&\lesssim \varepsilon _{h_{k+1}}^2(\tau ), \end{aligned}$$

(61)

where $\varepsilon _{h_{k+1}}(\tau ):=\varepsilon _{h_k}^2(\tau ) +\eta _A(H)\varepsilon _{h_k}(\tau )+\delta _{h_{k+1}}(\tau )$.

Proof

From problems (9), (53), (55), and inequalities (56), (57), and (58), the following estimates hold

$$\begin{aligned}&\Vert \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u\Vert _V^2\lesssim {\mathcal {A}}_{\tau }(\widehat{u}_{h_{k+1}}-P_{h_{k+1}}u, \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u)\nonumber \\&\quad \lesssim {\mathcal {A}}_{\tau _{h_k}}(\widehat{u}_{h_{k+1}}, \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u)- {\mathcal {A}}_{\tau }(P_{h_{k+1}}u,\widehat{u}_{h_{k+1}}-P_{h_{k+1}}u)\nonumber \\&\quad \quad +|\tau -\tau _{h_k}|\Vert \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u\Vert _V\nonumber \\&\quad ={\mathcal {B}}(\tau _{h_k}u_{h_k}-\tau u,\widehat{u}_{h_{k+1}}-P_{h_{k+1}}u)+|\tau -\tau _{h_k}|\Vert \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u\Vert _V\nonumber \\&\quad \lesssim \Vert \tau _{h_k}u_{h_k}-\tau u\Vert _1\Vert \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u\Vert _V+|\tau -\tau _{h_k}|\Vert \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u\Vert _V\nonumber \\&\quad \lesssim (|\tau _{h_k}-\tau |\Vert u_{h_k}\Vert _1+\tau \Vert u_{h_k}-u\Vert _1)\Vert \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u\Vert _V\nonumber \\&\quad \lesssim \big (\varepsilon _{h_k}^2(\tau )+\eta _A(H)\varepsilon _{h_k}(\tau )\big )\Vert \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u\Vert _V. \end{aligned}$$

Then we have

$$\begin{aligned} \Vert \widehat{u}_{h_{k+1}}-P_{h_{k+1}}u\Vert _V \lesssim \varepsilon _{h_k}^2(\tau )+\eta _A(H)\varepsilon _{h_k}(\tau ). \end{aligned}$$

(62)

Combining (62) and the error estimate of finite element projection

$$\begin{aligned} \Vert u-P_{h_{k+1}}u\Vert _V \lesssim \delta _{h_{k+1}}(\tau ), \end{aligned}$$

we obtain

$$\begin{aligned} \Vert \widehat{u}_{h_{k+1}}-u\Vert _{V}\lesssim \varepsilon _{h_k}^2(\tau )+\eta _A(H) \varepsilon _{h_k}(\tau ) +\delta _{h_{k+1}}(\tau ). \end{aligned}$$

(63)

From (63) and $\Vert \widehat{u}_{h_{k+1}}-\widetilde{u}_{h_{k+1}}\Vert _V\lesssim \delta _{h_{k+1}}(\tau )$, the following estimate holds

$$\begin{aligned} \Vert \widetilde{u}_{h_{k+1}}-u\Vert _{V}\lesssim \varepsilon _{h_k}^2(\tau )+\eta _A(H) \varepsilon _{h_k}(\tau ) +\delta _{h_{k+1}}(\tau ). \end{aligned}$$

(64)

Now we estimate the error for the eigenpair solution $(\tau _{h_{k+1}},u_{h_{k+1}})$ of problem (54). Based on the error estimate theory developed in Sect. 3 (Theorem 2) and the definition of the space $V_{H,h_{k+1}}$, the following estimates hold

$$\begin{aligned} \Vert u-u_{h_{k+1}}\Vert _V\lesssim \sup _{w\in M(\tau )}\inf _{v\in V_{H,h_{k+1}}}\Vert w-v\Vert _V\lesssim \Vert u-\widetilde{u}_{h_{k+1}}\Vert _V. \end{aligned}$$

(65)

The combination of (64) and (65) leads to the desired result (59). Using the same process in Sect. 3 to derive the eigenvalue result (41), we can also obtain

$$\begin{aligned} \Vert u-u_{h_{k+1}}\Vert _1\lesssim \widetilde{\eta }_A(H) \varepsilon _{h_{k+1}}(\tau ), \end{aligned}$$

(66)

where

$$\begin{aligned} \widetilde{\eta }_A(H)=\sup _{f\in V,\Vert f\Vert _V=1}\inf _{v\in V_{H,h_{k+1}}}\Vert Tf-v\Vert _V \le \eta _A(H). \end{aligned}$$

(67)

The estimate (61) can also be derived similarly by Theorem 1. $\square$

4.2 A Multigrid Method by the One Correction Step

In this subsection, we introduce a multigrid scheme based on the One Correction Step defined in Algorithm 1. This method has the same optimal error estimate as solving the transmission eigenvalue problem in the finest finite element space directly which needs much more computation.

Algorithm 2

Eigenvalue Multigrid Scheme

• 1. Construct a series of nested finite element spaces $V_H, V_{h_1}, V_{h_2},\ldots ,V_{h_n}$ such that (51) and (52) hold.

• 2. Solve the following transmission eigenvalue problem: Find $(\tau _{h_1},u_{h_1})\in {\mathcal {R}}\times V_{h_1}$ such that ${\mathcal {B}}(u_{h_1},u_{h_1})=1$ and

  $$\begin{aligned} {\mathcal {A}}_{\tau _{h_1}}(u_{h_1},v_{h_1})=\tau _{h_1}{\mathcal {B}}(u_{h_1},v_{h_1}),\quad \forall v_{h_1}\in V_{h_1}. \end{aligned}$$

  (68)

• 3. Do $k=1,\ldots ,n-1$ Obtain a new eigenpair approximation $(\tau _{h_{k+1}},u_{h_{k+1}})\in {\mathcal {R}}\times V_{h_{k+1}}$ by a correction step

  $$\begin{aligned} (\tau _{h_{k+1}},u_{h_{k+1}})= Correction (V_H,\tau _{h_k},u_{h_k},V_{h_{k+1}}). \end{aligned}$$

  (69)

  End Do

Finally, we obtain an eigenpair approximation $(\tau _{h_n},u_{h_n})\in {\mathcal {R}}\times V_{h_n}$.

In Step 2 of Algorithm 2, $(\tau _{h_1},u_{h_1})$ can be chosen as one of the eigenpair sequences $(\tau _{j,h_1},u_{j,h_1})$ for the discrete eigenvalue (16) on the space $V_{h_1}$ and do the multigrid scheme. But for different $j$, we can do the multigrid scheme parallelly.

Theorem 4

After implementing Algorithm 2, there exists an eigenpair $(\tau ,u)$ of (9) such that the resultant eigenpair approximation $(\tau _{h_n},u_{h_n})$ has the following error estimates

$$\begin{aligned} \Vert u_{h_n}-u\Vert _V&\lesssim \delta _{h_n}(\tau ),\end{aligned}$$

(70)

$$\begin{aligned} \Vert u_{h_n}-u\Vert _1&\lesssim \eta _A(H)\delta _{h_n}(\tau ),\end{aligned}$$

(71)

$$\begin{aligned} |\tau _{h_n}-\tau |&\lesssim \delta _{h_n}^2(\tau ), \end{aligned}$$

(72)

with the condition $C\beta ^s\eta _A(H)<1$ for some constant $C$.

Proof

From $\eta _A(H)\gtrsim \delta _{h_1}(\tau )\ge \delta _{h_2}(\tau )\ge \cdots \ge \delta _{h_n}(\tau )$ and Theorem 3, we have

$$\begin{aligned} \varepsilon _{h_{k+1}}(\tau ) \lesssim \eta _A(H)\varepsilon _{h_k}(\tau )+\delta _{h_{k+1}}(\tau ),\quad \mathrm{for}\ 1\le k\le n-1. \end{aligned}$$

(73)

From Theorem 2 and Algorithm 2, we know there exists an eigenpair $(\tau ,u)$ of (9) such that the following estimates hold

$$\begin{aligned} \Vert u-u_{h_1}\Vert _V&\lesssim \delta _{h_1}(\tau ),\end{aligned}$$

(74)

$$\begin{aligned} \Vert u-u_{h_1}\Vert _1&\lesssim \eta _A(H)\delta _{h_1}(\tau ),\end{aligned}$$

(75)

$$\begin{aligned} |\tau -\tau _{h_1}|&\lesssim \delta _{h_1}^2(\tau ). \end{aligned}$$

(76)

Let $\varepsilon _{h_1}(\tau )=\delta _{h_1}(\tau )$. Based on the proof in Theorem 3, (52), (73), (74)–(76) and $C\beta ^s\eta _A(H)<1$, the final eigenfunction approximation $u_{h_n}$ has the error estimate

$$\begin{aligned} \Vert u_{h_n}-u\Vert _V&\lesssim \eta _A(H)\varepsilon _{h_{n-1}}(\tau ) +\delta _{h_{n}}(\tau )\nonumber \\&\lesssim \eta _A(H)^2\varepsilon _{h_{n-2}}(\tau )+ \eta _A(H)\delta _{h_{n-1}}(\tau )+\delta _{h_n}(\tau )\nonumber \\&\lesssim \sum _{k=1}^n\eta _A(H)^{n-k}\delta _{h_k}(\tau )\nonumber \\&= \sum _{k=1}^n(\beta ^s\eta _A(H))^{n-k}\delta _{h_n}(\tau )\nonumber \\&\lesssim \frac{\beta ^s\eta _A(H)}{1-\beta ^s\eta _A(H)} \delta _{h_n}(\tau )\nonumber \\&\lesssim \delta _{h_n}(\tau ). \end{aligned}$$

(77)

This is the estimate (70). From the proof of Theorem 3 and (70), we can obtain the desired results (71) and (72). $\square$

5 Work Estimate of Eigenvalue Multigrid Scheme

In this section, we turn our attention to the estimate of computational work for Eigenvalue Multigrid Scheme (Algorithm 2). We will show that this algorithm makes solving the eigenvalue problem with almost the same work as solving the corresponding biharmonic boundary value problem.

First, we define the dimension of each level finite element space as $N_k:=\mathrm{dim}V_{h_k}$. Then we have

$$\begin{aligned} N_k \thickapprox \Big (\frac{1}{\beta }\Big )^{2(n-k)}N_n,\quad k=1,2,\ldots , n. \end{aligned}$$

(78)

Theorem 5

Assume the eigenvalue problem solved in the coarse spaces $V_{H}$ and $V_{h_1}$ need work ${\mathcal {O}}(M_H)$ and ${\mathcal {O}}(M_{h_1})$, respectively, and the work of the multigrid solver $MG(V_{h_k},u_{h_{k-1}}, \tau _{h_{k-1}},m_k)$ in each level space $V_{h_k}$ is ${\mathcal {O}}(N_k)$ for $k=2,3,\ldots ,n$. Then the work involved in Algorithm 2 is ${\mathcal {O}}(N_n+M_H\log N_n+M_{h_1})$. Furthermore, the complexity will be ${\mathcal {O}}(N_n)$ provided $M_H\ll N_n$ and $M_{h_1}\le N_n$.

Proof

Let $W_k$ denote the work of the correction step in the $k$th finite element space $V_{h_k}$. Then with the correction definition, we have

$$\begin{aligned} W_k={\mathcal {O}}(N_k+M_H). \end{aligned}$$

(79)

Iterating (79) and using the fact (78), we obtain

$$\begin{aligned} W_n&= \sum _{k=1}^nW_k= {\mathcal {O}}\Big (M_{h_1}+\sum _{k=2}^n\big (N_k+M_H\big )\Big )\nonumber \\&= {\mathcal {O}}\Big (\sum _{k=2}^nN_k+(n-2)M_H+M_{h_1}\Big )\nonumber \\&= {\mathcal {O}}\Big (\sum _{k=2}^n\big (\frac{1}{\beta } \big )^{2(n-k)}N_n+(n-2)M_H+M_{h_1}\Big )\nonumber \\&= {\mathcal {O}}(N_n+M_H\log N_n+M_{h_1}). \end{aligned}$$

(80)

This is the desired result ${\mathcal {O}}(N_n+M_H\log N_n+M_{h_1})$ and ${\mathcal {O}}(N_n)$ can be obtained by the conditions $M_H\ll N_n$ and $M_{h_1}\le N_n$. $\square$

6 Numerical Results

First, we solve the eigenvalue problem (9) on the unit square $\varOmega =(0,1)\times (0,1)$. In this paper, we use the Bogner–Fox–Schmit (BFS) element on the rectangular mesh for the discretization. The BFS element can be defined as follows [4, 31]

$$\begin{aligned} V_h&= \Big \{v_h|_K\in {\mathcal {Q}}_3(K):\ v_h(Z_i), \partial _{x_1}v_h(Z_i), \partial _{x_2}v_h(Z_i), \partial _{x_1}\partial _{x_2}v_h(Z_i)\ \ \mathrm{are\ continuous}, \nonumber \\&\quad i=1,2,3,4\Big \}\bigcap H_0^2(\varOmega ), \end{aligned}$$

(81)

where $Z_i\,(i=1,2,3,4)$ denote the four vertices on the element $K\in {\mathcal {T}}_h$ and ${\mathcal {Q}}_{\ell }(K)$ denotes the space of polynomials with a degree not greater than $\ell$ for each variable.

As predicted in Theorem 4, the convergence order of the eigenvalue approximation is fourth, i.e.,

$$\begin{aligned} |\tau -\tau _h| \lesssim h^4\Vert u\Vert _{6,\varOmega }, \end{aligned}$$

(82)

provided $u\in H^6(\varOmega )$.

6.1 Model Problem with $n=16$

Here we give the numerical results of the multigrid scheme on the unit square. In this example, we choose the index of refraction $n(x) = 16$.

The sequence of finite element spaces are constructed by using the BFS element on the series of rectangular mesh which are produced by regular refinement with $\beta =2$ (connecting the midpoints of each edge). In this example, we use two rectangular partitions with mesh sizes $H=1/4$ and $H=1/8$ as initial meshes and we set ${\mathcal {T}}_{h_1}={\mathcal {T}}_H$ to investigate the convergence behaviors.

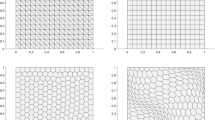
Eigenvalue Multigrid Scheme (Algorithm 2) is applied to solve the eigenvalue problem. The first four eigenvalue approximations $(k_h=\sqrt{\tau _h})$ on the finest mesh are $(1.879591,\,2.444236,\,2.444236,\,2.866439)$ and the corresponding eigenfunction are shown in Fig. 1. Figure 2 present the error estimates of the numerical approximations for the first four eigenvalues corresponding to the two initial meshes. From Fig. 2, we know that the multigrid scheme does obtain the same optimal error estimates as directly solving the eigenvalue problem.

Fig. 1

Eigenfunctions for Example 1

Fig. 2

Example 1: The errors of the multigrid algorithm for the first four eigenvalues

Also, we present the computing time (in seconds) in Fig. 3 to show that the multigrid method has the linear complexity as claimed in Theorem 5.

Fig. 3

Example 1: The computing time

6.2 Model Problem with $n=8+x_1-x_2$

In the second example, we also consider the eigenvalue problem on the unit square $\varOmega =(0,1 )\times (0, 1)$. In this example, the index of refraction is chosen to be $n(x) = 8+x_1-x_2$.

The sequence of finite element spaces are also constructed by using the BFS element on the series of rectangular mesh which are produced by regular refinement with $\beta =2$. We also use two partitions with mesh sizes $H=1/4$ and $H=1/8$ as initial meshes and we set ${\mathcal {T}}_{h_1}={\mathcal {T}}_H$ to investigate the convergence behaviors.

The first four eigenvalue approximations $(k_h=\sqrt{\tau _h})$ on the finest mesh are $(2.823887,\,3.539624,\,3.540073,\,4.118556)$ and the corresponding eigenfunction are shown in Fig. 4. Figure 5 gives the numerical errors for the first four eigenvalues corresponding to the two initial meshes. Figure 5 also shows that the multigrid scheme does obtain the same optimal error estimates as directly solving the eigenvalue problem.

Fig. 4

Eigenfunctions for Example 2

Fig. 5

Example 2: The errors of the multigrid algorithm for the first four eigenvalues

6.3 Model Problem with $n=16$ on $L$ Shape Domain

Here we give the numerical results of the multigrid scheme on the $L$ shape domain $\varOmega =(-1,1)\times (-1,1)\backslash [0, 1)\times (-1, 0]$. In this example, we also choose the index of refraction $n(x) = 16$. Since $\varOmega$ has a reentrant corner, eigenfunctions with singularities are expected. The convergence order for eigenvalue approximation is less than 4 by the BFS element which is the order predicted by the theory for regular eigenfunctions.

The series of finite element spaces are still constructed by using the BFS element on the series of rectangular mesh by regular refinement with $\beta =2$ (connecting the midpoints of each edge). Here we also use two rectangular partitions with mesh sizes $H=1/4$ and $H=1/8$ as initial meshes and we also set ${\mathcal {T}}_{h_1}={\mathcal {T}}_H$ to investigate the convergence behaviors.

Figure 6 gives the numerical errors for the first three eigenvalues corresponding to the two initial meshes. As we have expected the convergence order shown in Fig. 6 is only 1.25 which is less than 4.

Fig. 6

Example 3: The errors of the multigrid algorithm for the first three eigenvalues

7 Concluding Remarks

In this paper, we give a multigrid scheme to solve the transmission eigenvalue problem. The idea is to use the multilevel correction method which can transform the solution of transmission eigenvalue problem to a series of solutions of the corresponding linear boundary value problems that can be solved by the multigrid method.

When the desired eigenvalue $\lambda _i$ has multiplicity $m$, we can choose $\ell \,(\ell \!\ge \! m)$ eigenpairs $(\lambda _{j,h_1},u_{j,h_1}),\ldots , (\lambda _{j+\ell -1,h_1},u_{j+\ell -1,h_1})$ to perform the multigrid scheme. The only requirement for the multigrid method is that the eigenspace of $\lambda _i$ is a subset of the space $\mathrm{span}\{u_{j,h_1},\ldots ,u_{j+\ell -1,h_1}\}$. Since it is independent of each other for the boundary value problems corresponding to different eigenfunction approximations $u_{j,h_k},\ldots ,u_{j+\ell -1}$ in Step 1 of Algorithm 1, we can implement them in the parallel way and the computation work in each processor is still only ${\mathcal {O}}(N_{k+1})$. Furthermore, the computational work in Step 2 of Algorithm 1 is almost the same since the dimension of the space $V_{H,h_{k+1}}=V_H+\mathrm{span}\{\tilde{u}_{j,h_{k+1}},\ldots ,\tilde{u}_{j+\ell -1,h_{k+1}}\}$ will not change much. Finally, we can construct a type of parallel method to compute the eigenvalue problem by the multigrid scheme for the multiple eigenvalues. The computational work involved in the multigrid method is ${\mathcal {O}}(\ell N_n)$, but the work in each processor is still only ${\mathcal {O}}(N_n)$ when we use the parallel method. For some details, please refer [27].

We can replace the multigrid method by other types of efficient iteration schemes such as algebraic multigrid method and the type of preconditioned schemes based on the domain decomposition method (see, e.g., [25, 30]). Furthermore, the framework here can also be coupled with parallel method and the adaptive refinement technique. The multigrid method proposed here can also be extended to the general quadratic eigenvalue problems. These will be investigated in our future work.