An Adaptive Finite Element Method for the Transmission Eigenvalue Problem

Abstract

The classical weak formulation of the Helmholtz transmission eigenvalue problem can be linearized into an equivalent nonsymmetric eigenvalue problem. Based on this nonsymmetric eigenvalue problem, we first discuss the a posteriori error estimates and adaptive algorithm of conforming finite elements for the Helmholtz transmission eigenvalue problem. We give the a posteriori error indicators for primal eigenfunction, dual eigenfunction and eigenvalue. Theoretical analysis shows that the indicators for both primal eigenfunction and dual eigenfunction are reliable and efficient and that the indicator for eigenvalue is reliable. Numerical experiments confirm our theoretical analysis.

1 Introduction

The transmission eigenvalue problem arises in inverse scattering theory for an inhomogeneous medium. They can be used to obtain estimates for the material properties of the scattering object and have theoretical importance in the uniqueness and reconstruction in inverse scattering theory [1, 2].

In recent years, the numerical methods of the transmission eigenvalue problem are hot topics in the field of engineering and computational mathematics. The first numerical study was made by Colton et al. [3] in 2010 and involves three numerical methods. Later on, their works have been developed by [4–10]. These works mentioned above provide some efficient computational approaches. Among them [4, 7, 8, 10] discussed the a priori error estimates for finite element methods of the transmission eigenvalue problem. In 2011, Sun [4] proposed the iterative methods for computing real eigenvalues coupled with a coarse error analysis on the numerical eigenvalues. Based on his work, Ji et al. [7] further proved the accurate error estimates of the iterative methods and put forward an efficient mutigrid method to compute the real transmission eigenvalues. In addition, more recently Cakoni et al. [8] also made an error analysis for eigenvalues by a mixed finite element method. A relatively complete error analysis of an $H^2$ conforming finite element method and a two grid algorithm arose in [10].

The a posteriori error estimates and adaptive finite element methods are always the main streams of scientific and engineering computing. The idea of the a posteriori error estimates were first introduced by Babuska and Rheinboldt [11] in 1978. A few decades later, there have developed many types of a posteriori error estimates such as residual type [12–15] and recovery type [16, 17]. Up to now, many excellent works have been summarized in the books such as [18–20]. A posteriori error estimates of residual type have been applied to conforming or nonconforming finite elements of second and fourth order elliptic eigenvalue problems. But to our knowledge, there does not exist any research on a posteriori error estimates and adaptive algorithms for the transmission eigenvalue problem and so deriving the a posteriori error estimates for the problem is still a new topic. Hence the aim of this paper is to fill in the gap.

The classical weak formulation of the transmission eigenvalue problem is essentially a quadratic and fourth order eigenvalue problem (see, e.g., [3, 4, 8, 27]). Deriving the a posteriori error estimates directly for this quadratic problem is a very challenging task. A feasible way for this purpose, just like the way adopted by the literatures [8, 10], is to linearize the classical weak formulation into a nonsymmetric eigenvalue problem. In recent years, there are many works regarding finite element adaptive algorithms for nonsymmetric eigenvalue problems but mainly for second order elliptic eigenvalue problems, such as the works of Heuveline and Rannacher [21, 22], Carstensen et al. [23–25], and Giani et al. [26].

In this paper, using the linear weak formulation proposed by [10], we aim to study the a posteriori error estimates of residual type for the transmission eigenvalue problem and give an efficient finite element adaptive algorithm. We first give the a posteriori error indicators for the primal eigenfunction and the dual eigenfunction and prove their reliability and efficiency. Thanks to the basic relation between the eigenvalue and its approximate eigenvalue (see Lemma 3.6), we give the a posteriori error indicator for the eigenvalue. The difficulty of theoretical analysis lies in the nonsymmetry, with derivatives, at the right side hand of the eigenvalue problem. Based on the given a posteriori error indicator, we design an efficient adaptive algorithm. This algorithm can be used to compute the multiple and complex eigenvalues. Finally in numerical experiments, we adopt the Argyris element to implement the adaptive algorithm and numerical results not only confirm the efficiency and reliability of the indicator but also indicate that in many cases the error of numerical eigenvalues can achieve the optimal convergence order $O(dof^{-4})$ even on a nonconvex domain.

2 Preliminaries

Let $H^{s}(D)$ be a Sobolev space with norm $\Vert \cdot \Vert _{s}$ ($s=1,2$), and

$$\begin{aligned} H_{0}^{2}(D)=\left\{ v\in H^{2}(D): v|_{\partial D}=\frac{\partial v}{\partial \nu }|_{\partial D}=0\right\} . \end{aligned}$$

Consider the Helmholtz transmission eigenvalue problem: Find $k\in \mathbb {C}$, $\omega , \sigma \in L^{2}(D)$, $\omega -\sigma \in H^{2}(D)$ such that

$$\begin{aligned}&\varDelta \omega +k^{2}n(x)\omega =0,~~~in~ D, \end{aligned}$$

(2.1)

$$\begin{aligned}&\varDelta \sigma +k^{2}\sigma =0,~~~in~ D, \end{aligned}$$

(2.2)

$$\begin{aligned}&\omega -\sigma =0,~~~on~ \partial D, \end{aligned}$$

(2.3)

$$\begin{aligned}&\frac{\partial \omega }{\partial \nu }-\frac{\partial \sigma }{\partial \nu }=0,~~~ on~\partial D, \end{aligned}$$

(2.4)

where $D\subset \mathbb {R}^{t}~(t=2,3)$ is an bounded Lipschitz polyhedron, and $\nu$ is the unit outward normal to $\partial D$.

Let $u=\omega -\sigma$. Then the eigenvalue problem (2.1)–(2.4) can be stated as the classical weak formulation below (see, e.g., [1, 3, 27]): Find $k^{2}\in \mathbb {C}$, $k^{2}\not =0$, nontrivial $u\in H_{0}^{2}(D)$ such that

$$\begin{aligned} \left( \frac{1}{n(x)-1}(\varDelta u+k^{2} u),\varDelta v+\overline{k}^{2} n(x)v \right) _{0}=0,~~~\forall v \in ~H_{0}^{2}(D), \end{aligned}$$

(2.5)

where $(\cdot ,\cdot )_0$ is the inner product of $L^2(D)$. As usual, we define $\lambda =k^{2}$ as the transmission eigenvalue in this paper. We suppose that the index of refraction $n\in L^{\infty }(D)$ satisfying the following assumption

$$\begin{aligned} 1+\delta \le n(x)~a.e.~in~\varOmega , \end{aligned}$$

for some constant $\delta >0$, although, with obvious changes, the theoretical analysis in this paper also holds for n strictly less than 1. For simplicity, throughout this paper we assume n(x) $\in$ $W^{1,\infty }(D)$ $\bigcap H^2(D)$.

Define Hilbert spaces $\mathbf {H}=H_{0}^{2}(D)\times L^{2}(D)$ and $\mathbf {H}^{s}(K)=H^{s}(K)\times H^{s-2}(K)$. Let $\Vert \cdot \Vert _{s,K}$ be the norm in $H^{s}(K)$ for a given $K\subseteq D$. Using the same notation, we define the norm in $\mathbf {H}^{s}(K)$ as $\Vert (u,w)\Vert _{s,K}=\Vert u\Vert _{s,K}+\Vert w\Vert _{s-2,K}$. We write $\mathbf {H}^{1}:=\mathbf {H}^{1}(D)$ for simplicity.

From (2.5) we derive that

$$\begin{aligned}&\left( \frac{1}{n-1}\varDelta u, \varDelta v\right) _{0}-\lambda \left( \nabla \left( \frac{1}{n-1}u\right) , \nabla v\right) _{0}\nonumber \\&~~~~~~-\lambda \left( \nabla u, \nabla \left( \frac{n}{n-1}v\right) \right) _{0}+\lambda ^{2} \left( \frac{n}{n-1}u,v \right) _{0}=0,~~~\forall v \in ~H_{0}^{2}(D). \end{aligned}$$

Let $w=\lambda u$, then we arrive at a linear weak formulation: Find $(\lambda , u, w)\in \mathbb {C}\times H_{0}^{2}(D)\times L^{2}(D)$ such that

$$\begin{aligned}&\left( \frac{1}{n-1}\varDelta u, \varDelta v\right) _{0}=\lambda \left( \nabla \left( \frac{1}{n-1}u\right) , \nabla v\right) _{0}\nonumber \\&~~~~~~+\lambda \left( \nabla u, \nabla \left( \frac{n}{n-1}v\right) \right) _{0}-\lambda \left( \frac{n}{n-1}w, v \right) _{0},~~~\forall v \in ~H_{0}^{2}(D), \end{aligned}$$

(2.6)

$$\begin{aligned}&(w, z)_{0}=\lambda (u,z)_{0},~~~\forall z\in L^{2}(D). \end{aligned}$$

(2.7)

We introduce the following sesquilinear forms

$$\begin{aligned}&A((u,w),(v,z))=\left( \frac{1}{n-1}\varDelta u, \varDelta v\right) _{0}+(w, z)_{0},\\&B((u,w),(v,z))\nonumber \\&~~~=\left( \nabla \left( \frac{1}{n-1}u\right) , \nabla v\right) _{0}+\left( \nabla u, \nabla \left( \frac{n}{n-1}v\right) \right) _{0}- \left( \frac{n}{n-1}w, v \right) _{0}+(u,z)_{0}, \end{aligned}$$

then (2.5) can be rewritten as the following problem (primal problem): Find $\lambda \in \mathbb {C}$, nontrivial $(u,w)\in \mathbf {H}$ such that

$$\begin{aligned} A((u,w),(v,z)) =\lambda B((u,w),(v,z)),~~~\forall (v,z)\in \mathbf {H}. \end{aligned}$$

(2.8)

Let norm $\Vert \cdot \Vert _A$ be induced by the inner product $A(\cdot ,\cdot )$, then it is clear $\Vert \cdot \Vert _A$ is equivalent to $\Vert \cdot \Vert _{2,D}$ in $\mathbf {H}$.

One can easily verify that for any given $(f,g)\in \mathbf {H}^{1}$, B((f, g), (v, z)) is a continuous bilinear form on $\mathbf {H}^1$:

$$\begin{aligned} B((f,g), (v, z))\lesssim \Vert (f,g)\Vert _{1,D}\Vert (v,z)\Vert _{1,D},~\forall (v,z)\in \mathbf {H}^1. \end{aligned}$$

(2.9)

Here and hereafter we use the symbols $x \lesssim y$ to mean $x \le Cy$ for a constant C that is independent of the mesh size and may be different at different occurrences.

Consider the dual problem of (2.8): Find $\lambda ^{*}\in \mathbb {C}$, nontrivial $(u^{*},w^{*})\in \mathbf {H}$ such that

$$\begin{aligned} A((v,z), (u^{*},w^{*})) =\overline{\lambda ^{*}} B((v,z), (u^{*},w^{*})),~~~\forall (v,z)\in \mathbf {H}, \end{aligned}$$

(2.10)

or equivalently,

$$\begin{aligned}&\left( \frac{1}{n-1}\varDelta u^*, \varDelta v\right) _{0}=\lambda ^* \left( \nabla u^*, \nabla \left( \frac{1}{n-1} v\right) \right) _{0}\nonumber \\&~~~~~~+\lambda ^*\left( \nabla \left( \frac{n}{n-1}u^*\right) , \nabla v\right) _{0}+\lambda ^* (w^*, v )_{0},~~~\forall v \in ~H_{0}^{2}(D), \end{aligned}$$

(2.11)

$$\begin{aligned}&(w^*, z)_{0}=-\lambda ^*\left( \frac{n}{n-1}u^*,z\right) _{0},~~~\forall z\in L^{2}(D). \end{aligned}$$

(2.12)

Note that the primal and dual eigenvalues are connected via $\lambda =\overline{\lambda ^{*}}$.

Define the corresponding solution operator $T^{*}: \mathbf {H}^{1}\rightarrow \mathbf {H}$ by

$$\begin{aligned} A((v,z), T^{*}(f,g)) =B((v,z), (f,g)),~~~\forall (v,z)\in \mathbf {H}. \end{aligned}$$

In order to discretize the space $\mathbf {H}$, we need two finite element spaces to discretize $H_{0}^{2}(D)$ and $L^{2}(D)$ respectively. Since $H^2_0(D)\subset L^2(D)$ here we can construct only one conforming finite element space $S^h\subset H_{0}^{2}(D)$ of the piecewise polynomial degree $\le l$ such that $\mathbf {H}_{h}:=S^h\times S^h\subset H_{0}^{2}(D) \times L^{2}(D)$. For example, $S^h$ can be taken as the Argyris element or the Bell element space. Let $\{\pi _h\}_{h>0}$ be a sequence of shape regular meshes of D and $\kappa$ be an element on $\pi _h$ with the diameter $h_\kappa$.

The conforming finite element approximation of (2.8) is given by the following: Find $\lambda _{h}\in \mathbb {C}$, nontrivial $(u_{h},w_{h})\in \mathbf {H}_{h}$ such that

$$\begin{aligned} A((u_{h},w_{h}),(v,z)) =\lambda _{h} B((u_{h},w_{h}),(v,z)),~~~\forall (v,z)\in \mathbf {H}_{h}. \end{aligned}$$

(2.13)

To give the error of eigenfunction $(u_h,w_h)$ in the norm $\Vert \cdot \Vert _{1,D}$ we make the following regularity assumption:

R(D).   For any $\xi \in H^{-1}(D)$, there exists $\psi \in H^{2+r_{1}}(D)$ satisfying

$$\begin{aligned} \varDelta \left( \frac{1}{n-1}\varDelta \psi \right)= & {} \xi ,~~~in~D,\\ \psi= & {} \frac{\partial \psi }{\partial \nu }=0,~~~ on~\partial D, \end{aligned}$$

and

$$\begin{aligned} \Vert \psi \Vert _{2+r_{1}}\le C_{p} \Vert \xi \Vert _{-1}, \end{aligned}$$

(2.14)

where $r_{1}\in (0,1]$, $C_{p}$ denotes the prior constant dependent on the equation and D but independent of the right-hand side $\xi$ of the equation.

It is easy to know that (2.14) is valid with $r_1 = 1$ when n and $\partial D$ are appropriately smooth. When n is a constant and $D \subset \mathbb {R}^2$ is a convex polygon, from Theorem 2 in [28] we can get $r_1 = 1$.

The conforming finite element approximation of (2.10) is given by: Find $\lambda _{h}^{*} \in \mathbb {C}$, $(u_{h}^{*},w_{h}^{*})\in \mathbf {H}_{h}$ such that

$$\begin{aligned} A((v,z), (u_{h}^{*},w_{h}^{*})) =\overline{\lambda _{h}^{*}} B((v,z), (u_{h}^{*},w_{h}^{*})),~~~\forall (v,z)\in \mathbf {H}_{h}. \end{aligned}$$

(2.15)

Note that the primal and dual eigenvalues are connected via $\lambda _{h}=\overline{\lambda _{h}^{*}}$.

Define the corresponding solution operator $T_{h}^{*}: \mathbf {H}^{1}\rightarrow \mathbf {H}_{h}$ satisfying

$$\begin{aligned} A((v,z), T_{h}^{*}(f,g))=B((v,z), (f,g)),~~~\forall ~(v,z)\in \mathbf {H}_{h}. \end{aligned}$$

For reading convenience we adopt the following notation in this paper. Let $\lambda$ be the ith eigenvalue of (2.8) with the ascent $\alpha$. Assume there are q eigenvalues $\lambda _{j,h}$ ($j=i,\cdots ,i+q-1$) of (2.13) converging to $\lambda$. Let $M(\lambda )$ be the space spanned by all generalized eigenfunctions corresponding to the eigenvalue $\lambda$. Let $M_h(\lambda )$ be the space spanned by all generalized eigenfunctions of (2.13) corresponding to the eigenvalues $\{\lambda _{j,h}\}_{j=i}^{i+q-1}$. As for the dual problems (2.10) and (2.15), the definitions of $M^*(\lambda ^*)$ and $M^*_h(\lambda ^*)$ are made similarly to $M(\lambda )$ and $M_h(\lambda )$, respectively. In what follows, to characterize the approximation relation of the finite element space $\mathbf {H}_h$ to $M({\lambda })$ and $M^*({\lambda }^*)$, we introduce the following quantities

$$\begin{aligned} {\delta }_{h}({{\lambda }})= & {} {\mathop {\mathop {\sup }\limits _{(v,z)\in M({\lambda })}}\limits _{\Vert (v,z)\Vert _{2,D}=1}} \inf \limits _{(v_h,z_h)\in \mathbf {H}_{h}}\Vert (v,z)-(v_h,z_h)\Vert _{2,D} , \\ {\delta }^*_{h}({{\lambda }}^*)= & {} {\mathop {\mathop {\sup }\limits _{(v,z)\in M^*({\lambda }^*)}}\limits _{\Vert (v,z)\Vert _{2,D}=1}}\inf \limits _{(v_h,z_h)\in \mathbf {H}_{h}}\Vert (v,z)-(v_h,z_h)\Vert _{2,D}. \end{aligned}$$

Using the spectral approximation theory [29, 30], [10] established the following a priori error estimates for the finite element approximation (2.13).

Lemma 2.1

Let $\lambda _h$ be an eigenvalue of the problem (2.13) that converges to $\lambda$. Let $(u_{h},w_{h})$ be an eigenfunction of the problem (2.13) and $\Vert (u_{h},w_{h})\Vert _A=1$, then there exists a primal eigenfunction (u, w) such that

$$\begin{aligned}&\Vert (u_{h},w_{h})-(u,w)\Vert _{2,D}\lesssim \delta _{h}(\lambda )^{1/\alpha } , \end{aligned}$$

(2.16)

$$\begin{aligned}&\Vert (u_{h},w_{h})-(u,w)\Vert _{1,D}\lesssim h^{r_1} \Vert (u_{h},w_{h})-(u,w)\Vert _{2,D} ~for~\alpha =1, \end{aligned}$$

(2.17)

$$\begin{aligned}&|\lambda -\lambda _{h}|\lesssim ( \delta _{h}(\lambda )\delta _{h}^{*}(\lambda ^{*}))^{1/\alpha }. \end{aligned}$$

(2.18)

For any $(u_h^*,w_h^*)\in M_h^*(\lambda ^*)$ satisfying $\Vert (u_h^*,w_h^*)\Vert _A=1$, there exists $(u^*,w^*)\in M^*(\lambda ^*)$ such that

$$\begin{aligned}&\Vert (u^*_h,w^*_h)-(u^*,w^*)\Vert _{2,D} \lesssim \delta ^*_{h}(\lambda ^*), \end{aligned}$$

(2.19)

$$\begin{aligned}&\Vert (u^*_h,w^*_h)-(u^*,w^*)\Vert _{1,D} \lesssim h^{r_1} \Vert (u^*_h,w^*_h)-(u^*,w^*)\Vert _{2,D}~for~\alpha =1. \end{aligned}$$

(2.20)

Remark 2.1

The similar estimates as (2.16)–(2.18) are valid for the finite element approximation (2.15) of the dual problem (2.10) (see [10]).

3 A Posteriori Error Estimates

In this section, we aim to derive the a posteriori error estimates for the transmission eigenvalue problem. First of all, we give the local a posteriori error indicators $\eta _\kappa$ and $\eta ^*_\kappa$ for the primal eigenfunction $(u_h,w_h)$ and the dual eigenfunction $(u^*_h,w^*_h)$. Here we use the symbol $\widetilde{f}$ to denote the polynomial interpolation for the function f on its definition domain G, which is bounded from a Sobolev space between $H^2(\widehat{G})$ and $H^1(\widehat{G})$ into $H^2(\widehat{G})$ with $\widehat{G}$ being the reference element of G, into polynomial space of degree $\le m_G$, G $= e,k$. Throughout this section, the symbol e represents an edge in $\mathbb {R}^2$ or an face in $\mathbb {R}^3$ on the mesh $\pi _h$. On one hand, we define the local error indicator of the primal eigenfunction $(u_h,w_h)$

$$\begin{aligned} \eta _{\kappa }^2(u_h,w_h):= \eta _{T_\kappa }^2(u_h,w_h)+\eta _{E_\kappa }^2(u_h). \end{aligned}$$

For any element $\kappa \in \pi _h$, we define the element residual

$$\begin{aligned} \eta _{T_\kappa }(u_h,w_h):= h_\kappa ^2\Vert \widehat{R}_{\kappa }(u_h,w_h) \Vert _{0,\kappa } \end{aligned}$$

with

$$\begin{aligned} \widehat{R}_{\kappa }(u_h,w_h) =\varDelta \left( \widetilde{\frac{1}{n-1}}\varDelta u_h\right) +\varDelta \left( \widetilde{\frac{\lambda _h}{n-1}}u_h\right) +\widetilde{\frac{\lambda _h n}{n-1}}\varDelta u_h+ \widetilde{\frac{\lambda _h n}{n-1}} w_h \end{aligned}$$

being an approximation of

$$\begin{aligned} R_{\kappa }(u_h,w_h) =\varDelta \left( {\frac{1}{n-1}}\varDelta u_h\right) +\varDelta \left( {\frac{\lambda _h}{n-1}}u_h\right) + {\frac{\lambda _h n}{n-1}}\varDelta u_h+ {\frac{\lambda _h n}{n-1}} w_h. \end{aligned}$$

Note that $\widetilde{\frac{ n}{n-1}}$ and $\widetilde{\frac{1}{n-1}}$ are well defined since we have assumed n(x) $\in$ $W^{1,\infty }(D)$ $\bigcap H^2(D)$. In what follows, the definition of $\widehat{R}_{e,1},\widehat{R}_{e,2},\widehat{R}^*_{\kappa ,1},\widehat{R}^*_{\kappa ,2}$ are similar and thus omitted. For any edge (in $\mathbb {R}^2$) or face (in $\mathbb {R}^3$) $e\subset \partial \kappa \cap D$, we define the element edge or face residual

$$\begin{aligned} \eta _{E_\kappa }(u_h):= \Big \{ \sum \limits _{ e\subset \partial \kappa \cap D} \Big ( h_e\Vert \widehat{R}_{e,1}(u_h) \Vert ^2_{0,e} +h_e^3\Vert \widehat{R}_{e,2}(u_h) \Vert _{0,e}^2 \Big ) \Big \}^{1/2} \end{aligned}$$

with

$$\begin{aligned} R_{e,1}(u_h)=\left[ \left[ \frac{1}{n-1}\varDelta u_h\right] \right] _e \end{aligned}$$

and

$$\begin{aligned} R_{e,2}(u_h)=\left[ \left[ \nabla (\frac{1}{n-1}\varDelta u_h)\cdot \nu _e\right] \right] _e, \end{aligned}$$

where the symbol $[[\cdot ]]_e$ represents the jump across the edge or face e.

On the other hand, we define the local error indicator of the dual eigenfunction $(u^*_h,w^*_h)$

$$\begin{aligned} \eta _{\kappa }^{*2}(u^*_h,w^*_h):= \eta _{T_\kappa }^{*2}(u^*_h,w^*_h)+\eta _{E_\kappa }^{*2}(u^*_h). \end{aligned}$$

(3.1)

For any element $\kappa \in \pi _h$, we define the element residual

$$\begin{aligned} \eta _{T_\kappa }^{*2}(u^*_h,w^*_h):= h_\kappa ^4\Vert \widehat{R}^*_{\kappa ,1}(u^*_h,w^*_h) \Vert ^2_{0,\kappa }+h_\kappa ^4\Vert \widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h) \Vert ^2_{0,\kappa } \end{aligned}$$

with

$$\begin{aligned}&R^*_{\kappa ,1}(u^*_h,w^*_h)=\varDelta \left( \frac{1}{n-1}\varDelta u^{*}_h\right) +\varDelta \left( \frac{\lambda ^*_h}{n-1}u^{*}_h\right) +\frac{\lambda ^*_h n}{n-1}\varDelta u^{*}_h- \lambda ^*_h w^{*}_h, \end{aligned}$$

(3.2)

$$\begin{aligned}&R^*_{\kappa ,2}(u^*_h,w^*_h)= w^*_h+\frac{\lambda ^*_h n}{n-1}u^{*}_h. \end{aligned}$$

(3.3)

For any edge or face $e\subset \partial \kappa \cap D$, we define the element edge or face residual

$$\begin{aligned} \eta _{E_\kappa }^*(u_h^*):= \Big \{ \sum \limits _{ e\subset \partial \kappa \cap D} \Big ( h_e\Vert \widehat{R}_{e,1}(u^*_h) \Vert ^2_{0,e} +h_e^3\Vert \widehat{R}_{e,2}(u^*_h) \Vert _{0,e}^2 \Big ) \Big \}^{1/2}. \end{aligned}$$

Finally the global error indicators can be given as

$$\begin{aligned} {\eta }_h( {u}_h,w_h)=\left\{ \sum \limits _{\kappa \in \pi _h} {\eta }_\kappa ^2( {u}_h,w_h)\right\} ^{1/2},\\ {\eta }^*_h( {u}^*_h,w^*_h)=\left\{ \sum \limits _{\kappa \in \pi _h} {\eta }_\kappa ^{*2}( {u}^*_h,w^*_h)\right\} ^{1/2}. \end{aligned}$$

The following interpolation error estimate of projection-mean operator (see [20]) is a powerful tool to analyze the reliability of the indicators $\eta _h(u_h,w_h)$ and ${\eta }^*_h( {u}^*_h,w^*_h)$.

Lemma 3.1

Assume $S^h$ is the finite element space with at most third order derivative in every node and non-zero dimensional face (edge in $\mathbb {R}^2$ or edge and face in $\mathbb {R}^3$) degrees of freedom. Then there exists a linear bounded operator $I_h: L^2(D)\rightarrow {S}^h$ such that the following estimates hold for any element $\kappa \in \pi _h$ and any edge or face $e\subset \partial \kappa \cap D$

$$\begin{aligned}&\Vert \phi -I_h \phi \Vert _{j,\kappa }\lesssim h^{s-j}_\kappa \Vert \phi \Vert _{s,\omega _\kappa },~1\le s\le l+1,~ 0\le j\le s,~\forall \phi \in H^s(D), \end{aligned}$$

(3.4)

$$\begin{aligned}&\Vert \phi -I_h \phi \Vert _{0,e}+h_{e}\Vert \nu _e\cdot \nabla (\phi -I_h \phi )\Vert _{0,e}\lesssim h^{3/2}_e\Vert \phi \Vert _{2,\omega _\kappa },~\forall \phi \in H^2(D), \end{aligned}$$

(3.5)

where $\omega _\kappa$ is the union of elements sharing at least one node with $\kappa$.

The following two theorems shows respectively the global reliability of the indicators $\eta _h(u_h,w_h)$ and $\eta ^*_h(u^*_h,w^*_h)$.

Theorem 3.1

Let $(u_h,w_h,\lambda _h)$ be an eigenpair of the discrete problem (2.13), then there exists an eigenpair $(u,w,\lambda )$ of the primal problem (2.8) such that

$$\begin{aligned}&\Vert (u,w)-(u_h,w_h)\Vert _A\lesssim {\eta }_h( {u}_h,w_h)+\Vert \lambda (u,w)-\lambda _h(u_h,w_h)\Vert _{1,D}\nonumber \\&~~~~~~+ \Big \{\sum \limits _{\kappa \in \pi _h} \Big [h_\kappa ^4\Vert \widehat{R}_{\kappa }(u_h,w_h)-R_{\kappa }(u_h,w_h) \Vert _{0,\kappa }^2\nonumber \\&~~~~~~+ \sum \limits _{ e\subset \partial \kappa \cap D} \Big ( h_e\Vert \widehat{R}_{e,1}(u_h)-R_{e,1}(u_h)\Vert ^2_{0,e}\nonumber \\&~~~~~~+h_e^3\Vert \widehat{R}_{e,2}(u_h)-R_{e,2}(u_h)\Vert _{0,e}^2 \Big )\Big ]\Big \}^{1/2}. \end{aligned}$$

(3.6)

Proof

Denote $\mathbf {e}_h=(u,w)-(u_h,w_h)$ and $I\mathbf {e}_h=(I_h (u-{u}_h),I_h (w-{w}_h))$. A direct calculation shows that

$$\begin{aligned}&\Vert (u,w)-(u_h,w_h)\Vert ^2_A = A((u,w)-(u_h,w_h),\mathbf {e}_h-I\mathbf {e}_h)\nonumber \\&~~~~~~ +A((u,w)-(u_h,w_h), I\mathbf {e}_h) \nonumber \\&~~~=B(\lambda (u,w),\mathbf {e}_h-I\mathbf {e}_h)-A((u_h,w_h),\mathbf {e}_h-I\mathbf {e}_h)\nonumber \\&~~~~~~+ B(\lambda (u,w)-\lambda _h(u_h,w_h),I\mathbf {e}_h)\nonumber \\&~~~=B(\lambda (u,w),\mathbf {e}_h)- B(\lambda _h(u_h,w_h),I\mathbf {e}_h) -A((u_h,w_h),\mathbf {e}_h-I\mathbf {e}_h)\nonumber \\&~~~=B(\lambda _h(u_h,w_h),\mathbf {e}_h-I\mathbf {e}_h)-A((u_h,w_h),\mathbf {e}_h-I\mathbf {e}_h)\nonumber \\&~~~~~~+B(\lambda (u,w)-\lambda _h(u_h,w_h),\mathbf {e}_h). \end{aligned}$$

(3.7)

For any $(v,z)\in \mathbf {H}$, the integration by parts leads to

$$\begin{aligned}&B((u_h,w_h),(v,z))\\&~~~=\left( \nabla \left( \frac{1}{n-1}u_h\right) , \nabla v\right) _{0}+\left( \nabla u_h, \nabla \left( \frac{n}{n-1}v\right) \right) _{0}- \left( \frac{n}{n-1}w_h, v \right) _{0}+(u_h,z)_{0}\\&~~~=\left( -\varDelta \left( \frac{1}{n-1}u_h\right) -\frac{n}{n-1}\varDelta u_h - \frac{n}{n-1}w_h, v\right) _{0}+(u_h,z)_{0} \end{aligned}$$

and

$$\begin{aligned}&A((u_h,w_h),(v,z)) =\left( \frac{1}{n-1}\varDelta u_h, \varDelta v\right) _{0}+(w_h, z)_{0}\\&~~~=\sum \limits _{\kappa \in \pi _h} \Big \{\int _{\kappa } \varDelta \left( \frac{1}{n-1}\varDelta u_h\right) \overline{v}+\frac{1}{2}\sum \limits _{ e\subset \partial \kappa \cap D}\Big ( \big [\big [ (\frac{1}{n-1}\varDelta u_h) \nabla \overline{v}\cdot \nu _e\big ]\big ]_e\\&~~~~~~-\big [\big [\overline{v}\nabla \left( \frac{1}{n-1}\varDelta u_h\right) \cdot \nu _e\big ]\big ]_e\Big )\Big \} +(w_h,z)_{0}. \end{aligned}$$

It is immediate that

$$\begin{aligned}&A((u_h,w_h),(v,z))-B(\lambda _h(u_h,w_h),(v,z))\\&=\sum \limits _{\kappa \in \pi _h} \Big \{\int _{\kappa }\Big ( \varDelta (\frac{1}{n-1}\varDelta u_h)+\varDelta \left( \frac{\lambda _h}{n-1}u_h\right) +\frac{\lambda _h n}{n-1}\varDelta u_h+ \frac{n}{n-1}\lambda _h w_h\Big ) \overline{v} \\&~~~+\frac{1}{2}\sum \limits _{ e\subset \partial \kappa \cap D} \int _e\Big ( \big [\big [(\frac{1}{n-1}\varDelta u_h) \nabla \overline{v}\cdot \nu _e\big ]\big ]_e -\big [\big [\overline{v}\nabla \left( \frac{1}{n-1}\varDelta u_h\right) \cdot \nu _e\big ]\big ]_e\Big )\Big \}. \end{aligned}$$

Hence taking $(v,z)=\mathbf {e}_h-I\mathbf {e}_h$ and using Lemma 3.1 we have

$$\begin{aligned}&~~ |A((u_h,w_h),(v,z))-B(\lambda _h(u_h,w_h),(v,z))| \lesssim \sum \limits _{\kappa \in \pi _h} \Big \{\Vert R_{\kappa }(u_h,w_h) \Vert _{0,\kappa }\Vert v \Vert _{0,\kappa }\\&~~~~~~+ \sum \limits _{ e\subset \partial \kappa \cap D} \Big ( \Vert R_{e,1}(u_h)\Vert _{0,e} \Vert \nu _e\cdot \nabla v\Vert _{0,e} +\Vert R_{e,2}(u_h)\Vert _{0,e}\Vert v \Vert _{0,e}\Big )\Big \}\\&~~~\lesssim \Vert \mathbf {e}_h\Vert _{2,D}\Big \{\sum \limits _{\kappa \in \pi _h} \Big [h_\kappa ^4\Vert R_{\kappa }(u_h,w_h) \Vert _{0,\kappa }^2\\&~~~~~~+ \sum \limits _{ e\subset \partial \kappa \cap D} \Big ( h_e\Vert R_{e,1}(u_h)\Vert ^2_{0,e} +h_e^3\Vert R_{e,2}(u_h)\Vert _{0,e}^2 \Big )\Big ]\Big \}^{1/2}. \end{aligned}$$

By virtue of triangle inequality, (3.7) together with the above inequality and (2.9) yields (3.6). $\square$

Theorem 3.2

Let $(u^*_h,w^*_h,\lambda ^*_h)$ be an eigenpair of the discrete problem (2.15), then there exists an eigenpair $(u^*,w^*,\lambda ^*)$ of the dual problem (2.10) such that

$$\begin{aligned}&\Vert (u^*,w^*)-(u^*_h,w^*_h)\Vert _A\lesssim {\eta }^*_h( {u}^*_h,w^*_h)+\Vert \lambda ^*(u^*,w^*)-\lambda ^*_h(u^*_h,w^*_h)\Vert _{1,D}\nonumber \\&~~~~~~+ \Big \{\sum \limits _{\kappa \in \pi _h} \Big [h_\kappa ^4\sum _{i=1,2}\Vert \widehat{R}^*_{\kappa ,i}(u^*_h,w^*_h)-R^*_{\kappa ,i}(u^*_h,w^*_h) \Vert _{0,\kappa }^2\nonumber \\&~~~~~~+ \sum \limits _{ e\subset \partial \kappa \cap D} \Big ( h_e\Vert \widehat{R}_{e,1}(u^*_h)-R_{e,1}(u^*_h)\Vert ^2_{0,e}\nonumber \\&~~~~~~+h_e^3\Vert \widehat{R}_{e,2}(u^*_h)-R_{e,2}(u^*_h)\Vert _{0,e}^2 \Big )\Big ]\Big \}^{1/2}. \end{aligned}$$

(3.8)

Proof

Notice that for all $(v,z)\in \mathbf {H}$, $\overline{A((v,z),(u^*_h,w^*_h))}=A((u^*_h,w^*_h),(v,z))$ and

$$\begin{aligned}&\overline{B((v,z),\lambda _h^*(u^*_h,w^*_h))}\\&=(\nabla (\frac{\lambda ^*_hn}{n-1}u^*_h),\nabla v)_0+(\lambda ^*_h\nabla u^*_h,\nabla (\frac{1}{n-1}v))_0-(\frac{\lambda ^*_hn}{n-1}u^*_h,z)_0+(\lambda ^*_hw^*_h,v)_0\\&=(\nabla (\frac{\lambda ^*_h}{n-1}u^*_h),\nabla v)_0+(\lambda ^*_h\nabla u^*_h,\nabla (\frac{n}{n-1}v))_0-(\frac{\lambda ^*_hn}{n-1}u^*_h,z)_0+(\lambda ^*_hw^*_h,v)_0. \end{aligned}$$

We set $\mathbf {e}^*_h=(u^*,w^*)-(u^*_h,w^*_h)$ and $I\mathbf {e}^*_h=(I_h (u^*-{u}^*_h),I_h(w^*-{w}^*_h))$. Using the similar argument to show (3.7) yields

$$\begin{aligned}&\Vert (u^*,w^*)-(u^*_h,w^*_h)\Vert ^2_A\nonumber \\&~~~=\overline{B(\mathbf {e}^*_h,\lambda ^*(u^*,w^*)-\lambda ^*_h(u^*_h,w^*_h))} +\overline{B(\mathbf {e}^*_h-I\mathbf {e}^*_h,\lambda ^*_h(u^*_h,w^*_h))}\nonumber \\&~~~~~~ -\overline{A(\mathbf {e}^*_h-I\mathbf {e}^*_h,(u^*_h,w^*_h))}. \end{aligned}$$

(3.9)

It is immediate that

$$\begin{aligned}&\overline{A((v,z),(u^*_h,w^*_h))-B((v,z),\lambda ^*_h(u^*_h,w^*_h))}\\&=\sum \limits _{\kappa \in \pi _h} \Big \{\int _{\kappa }\Big (\big (\varDelta (\frac{1}{n-1}\varDelta u^*_h)+\varDelta (\frac{\lambda ^*_h}{n-1}u^*_h)+\frac{\lambda ^*_h n}{n-1}\varDelta u^*_h-\lambda ^*_h w^*_h\big ) \overline{v} \\&~~~+ (w^*_h+\frac{\lambda ^*_hn}{n-1}u^*_h)\overline{z}\Big ) \\&~~~+\frac{1}{2}\sum \limits _{ e\subset \partial \kappa \cap D}\int _e\Big ( \big [\big [(\frac{1}{n-1}\varDelta u^*_h) \nabla \overline{v}\cdot \nu _e\big ]\big ]_e -\big [\big [\overline{v}\nabla (\frac{1}{n-1}\varDelta u^*_h)\cdot \nu _e\big ]\big ]_e\Big )\Big \}. \end{aligned}$$

The similar argument used in the proof of Theorem 3.1 can show (3.8). $\square$

Next we shall prove the local efficiency of the indicator $\eta _k$ for the primal problem (2.8). We need to estimate the upper bound of the terms with respect to $\widehat{R}_{\kappa }(u_h,w_h),\widehat{R}_{e,1}(u_h)$ and $\widehat{R}_{e,2}(u_h)$ step by step.

Lemma 3.2

The following estimate of element residual holds for the primal eigenpair $(u,w,\lambda )$ and its approximate eigenpair $(u_h,w_h,\lambda _h)$

$$\begin{aligned}&h_\kappa ^{2}\Vert \widehat{R}_{\kappa }(u_h,w_h)\Vert _{0,\kappa } \lesssim \Vert u_h-u\Vert _{2,\kappa } +h_\kappa ^{2}\Vert w_h-w\Vert _{0,\kappa } +h_\kappa |\lambda _h-\lambda | \nonumber \\&~~~+h_\kappa ^{2}\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\kappa } . \end{aligned}$$

(3.10)

Proof

Define the $H_0^2(\kappa )$ function $w_\kappa =b_\kappa ^2\widehat{R}_{\kappa }(u_h,w_h)$ with the bubble function $b_\kappa =(t+1)^{t+1} L_{\kappa ,1}L_{\kappa ,2}\cdots L_{\kappa ,t+1}$ where $L_{\kappa ,1}, L_{\kappa ,2},\cdots , L_{\kappa ,t+1}$ are the barycentric coordinates of $\kappa$. Using (2.6) with $v=w_\kappa$ we have

$$\begin{aligned}&\int \limits _{\kappa } R_{\kappa }(u_h,w_h)w_\kappa =\int \limits _{\kappa }\Big \{\frac{1}{n-1}\varDelta u_h \varDelta w_\kappa -\nabla (\frac{\lambda _h}{n-1}u_h )\cdot \nabla w_\kappa \\&~~~~~~-\lambda _h\nabla u_h \cdot \nabla (\frac{n}{n-1}w_\kappa )+\frac{n}{n-1}\lambda _h w_hw_\kappa \Big \}\\&~~~\lesssim \Vert u_h-u\Vert _{2,\kappa }\Vert w_\kappa \Vert _{2,\kappa }+\Vert w_h-w\Vert _{0,\kappa }\Vert w_\kappa \Vert _{0,\kappa } +|\lambda _h-\lambda |\Vert w_\kappa \Vert _{1,\kappa }\\&~~~\lesssim (h_\kappa ^{-2}\Vert u_h-u\Vert _{2,\kappa } +\Vert w_h-w\Vert _{0,\kappa } +h_\kappa ^{-1}|\lambda _h-\lambda |)\Vert w_\kappa \Vert _{0,\kappa }, \end{aligned}$$

hence

$$\begin{aligned}&\Vert \widehat{R}_{\kappa }(u_h,w_h)\Vert _{0,\kappa }^2\lesssim \int \limits _{\kappa }\Big ( R_{\kappa }(u_h,w_h)+\widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h))w_\kappa \\&~~~\lesssim (h_\kappa ^{-2}\Vert u_h-u\Vert _{2,\kappa } +\Vert w_h-w\Vert _{0,\kappa } +h_\kappa ^{-1}|\lambda _h-\lambda |)\Vert w_\kappa \Vert _{0,\kappa }\\&~~~~~~+\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\kappa }\Vert w_\kappa \Vert _{0,\kappa }. \end{aligned}$$

And (3.10) follows. $\square$

Lemma 3.3

Assume $n(x)\in W^{2,\infty }(\kappa )$ for all $\kappa \in \pi _h$. The following estimates of element edge or face residual holds for the primal eigenpair $(u,w,\lambda )$ and its approximate eigenpair $(u_h,w_h,\lambda _h)$

$$\begin{aligned}&h_e^{1/2}\Vert \widehat{R}_{e,1}(u_h)\Vert _{0,e} \lesssim \Vert u_h-u\Vert _{2,\omega _e} +h_e^{2}\Vert w_h-w\Vert _{0,\omega _e} +h_e|\lambda _h-\lambda |\nonumber \\&~~~~~~+h_e^{2}\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\omega _e}\nonumber \\&~~~~~~+h^{1/2}_e\Vert \widehat{R}_{e,1}(u_h)-R_{e,1}(u_h)\Vert _{0,e},~e\subset \partial \kappa \cap D, \end{aligned}$$

(3.11)

$$\begin{aligned}&h_e^{3/2}\Vert \widehat{R}_{e,2}(u_h)\Vert _{0,e} \lesssim \Vert u_h-u\Vert _{2,\omega _e} +h_e^{2}\Vert w_h-w\Vert _{0,\omega _e} +h_e|\lambda _h-\lambda |\nonumber \\&~~~~~~+ h_e^{2}\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\omega _e}\nonumber \\&~~~~~~+h_e^{1/2}\Vert \widehat{R}_{e,1}(u_h)-R_{e,1}(u_h)\Vert _{0,e}\nonumber \\&~~~~~~+ h_e^{3/2}\Vert \widehat{R}_{e,2}(u_h)- R_{e,2}(u_h)\Vert _{0,e},~e\subset \partial \kappa \cap D, \end{aligned}$$

(3.12)

where $\omega _e$ is the union of elements sharing the edge or face e.

Proof

First we shall estimate $\widehat{R}_{e,1}(u_h)$. Define the $H_0^2(\omega _e)$ function $w_{e,1}=(b_{\kappa _2}-b_{\kappa _1})b_e \widehat{R}_{e,1}(u_h)$ which vanishes on the edge or face e, where $b_e$ is defined by enumerating the the vertices of $\kappa _1$ and $\kappa _2$ such that the vertices of e are numbered first:

$$\begin{aligned} b_e= \Big \{\begin{array}{ll} t^t L_{\kappa _i,1}L_{\kappa _i,2}\cdots L_{\kappa _i,t},&{}in ~\kappa _i,\\ 0,&{}D\setminus \omega _e. \end{array} \end{aligned}$$

Note that $w_{e,1}$ is continuously differentiable across e and that

$$\begin{aligned} \nu _e\cdot \nabla w_{e,1}=\frac{(t+1)^{t+1}}{t^{t+1}}\left( \frac{|e|}{|\kappa _2|}+\frac{|e|}{|\kappa _1|}\right) b_e^2 \widehat{R}_{e,1}(u_h)~on~e, \end{aligned}$$

(3.13)

where $\nu _e$ is fixed as the unit inward normal of $\kappa _2$ on the edge or face e; in fact, note that

$$\begin{aligned} \nabla L_{\kappa _2,t}\cdot \nu _e=\frac{|e|}{t|\kappa _2|},~~\nabla L_{\kappa _1,t}\cdot \nu _e=\frac{-|e|}{t|\kappa _1|}, \end{aligned}$$

then (3.13) can be obtained by the equality below

$$\begin{aligned} \nu _e\cdot \nabla w_{e,1}= (t+1)^{t+1}\nu _e \cdot ( \nabla L_{\kappa _2,t}-\nabla L_{\kappa _1,t}) \frac{b_e^2}{t^t} \widehat{R}_{e,1}(u_h)~\mathrm {on}~e. \end{aligned}$$

It is obtained by (2.6) and the estimate (3.10) that

$$\begin{aligned}&|\int _{e} R_{e,1}(u_h)\nu _e\cdot \nabla \overline{w}_{e,1}|=|\int _{\omega _e}\frac{1}{n-1}\varDelta u_h\varDelta \overline{w}_{e,1}-\varDelta (\frac{1}{n-1}\varDelta u_h) \overline{w}_{e,1}|\nonumber \\&~~~=|\int _{\omega _e}\frac{1}{n-1}\varDelta (u_h-u)\varDelta \overline{w}_{e,1}- \int _{\omega _e}\big (R_{\kappa }(u_h,w_h)- \varDelta (\frac{1}{n-1}(\lambda _h u_h-\lambda u))\nonumber \\&~~~~~~- \frac{n}{n-1}\varDelta (\lambda _h u_h-\lambda u)-\frac{n}{n-1}(\lambda _h w_h-\lambda w)\big )\overline{w}_{e,1}|\nonumber \\&~~~\lesssim \big (h_e^{-2}\Vert u_h-u\Vert _{2,\omega _e} +\Vert w_h-w\Vert _{0,\omega _e} +h_e^{-1}|\lambda _h-\lambda |\nonumber \\&~~~~~~+ \Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\omega _e} \big )\Vert w_{e,1}\Vert _{0,e}h_e^{1/2}. \end{aligned}$$

(3.14)

We deduce from (3.13) and the above estimate that

$$\begin{aligned}&h_e^{-1}\Vert \widehat{R}_{e,1}(u_h)\Vert ^2_{0,e} \lesssim \int _{e}\big (R_{e,1}(u_h)+ \widehat{R}_{e,1}(u_h)-R_{e,1}(u_h)\big )\nu _e\cdot \nabla \overline{w}_{e,1}\\&~~~\lesssim \big (h_e^{-2}\Vert u_h-u\Vert _{2,\omega _e} +\Vert w_h-w\Vert _{0,\omega _e} +h_e^{-1}|\lambda _h-\lambda |\\&~~~~~~+\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\omega _e}\big )\Vert w_{e,1}\Vert _{0,e}h_e^{1/2}\\&~~~~~~+\Vert \widehat{R}_{e,1}(u_h)-R_{e,1}(u_h)\Vert _{0,e}\Vert w_{e,1}\Vert _{0,e}h^{-1}_e. \end{aligned}$$

This yields (3.11).

It remains to estimate $\widehat{R}_{e,2}(u_h)$. Define the function $w_{e,2}=b'_{e}{P} \widehat{R}_{e,2}(u_h)$, where the prolongation operator $P:C^1(e)\rightarrow C^1(\omega _e)$ and the bubble function $b'_e$ are defined as follows respectively. Enumerate the vertices of $\kappa _1$ and $\kappa _2$ such that the vertices of e are numbered first. Then we set

$$\begin{aligned} b'_e=\Big \{\begin{array}{ll} \big (t^{2t}\prod _{i=1}^t(L_{\kappa _1,i}L_{\kappa _2,i})\big )^{2},&{} \mathrm {on}~\omega _e,\\ 0,&{}\mathrm {on}~ D\backslash \omega _e. \end{array} \end{aligned}$$

Denote by $x_e=(x_{e,1},\cdots ,x_{e,t})$ an Euclidean coordinate system such that e is contained in the hyperplane $\{x_{e,t}=0\}$. Set $x'_e=(x_{e,1},x_{e,2},\cdots ,x_{e,t-1})$ and define

$$\begin{aligned} {P}\delta (x_e):=\Big \{\begin{array}{ll} b'_e(x'_e,0) \delta (x'_e,0),&{} \mathrm {if}~(x'_e,0)\in e,\\ 0,&{} \mathrm {if}~(x'_e,0) \overline{\in } e. \end{array} \end{aligned}$$

Such construction of P can guarantee that ${P}\varrho \in C^1(\omega _e)$ if $\varrho \in C^1(e)$. Hence $w_{e,2}\in H_0^2(\omega _e)$. According to the definition of $R_{e,2}(u_h)$, using the Green’s formula we have

$$\begin{aligned}&\int _{e} R_{e,2}(u_h) \overline{w}_{e,2} =\int _{\omega _e}\big ( \varDelta (\frac{1}{n-1}\varDelta u_h) \overline{w}_{e,2}+\nabla (\frac{1}{n-1}\varDelta u_h) \cdot \nabla \overline{w}_{e,2}\big )\\&~~~=\int _{\omega _e}\big ( \varDelta (\frac{1}{n-1}\varDelta u_h) \overline{w}_{e,2}- \frac{1}{n-1}\varDelta u_h \varDelta \overline{w}_{e,2}\big ) +\int _{e}R_{e,1}(u_h)\nu _e \cdot \nabla \overline{w}_{e,2}. \end{aligned}$$

Using the similar way to show (3.14) yields

$$\begin{aligned}&|\int _{\omega _e}\frac{1}{n-1}\varDelta u_h\varDelta \overline{w}_{e,2}-\varDelta (\frac{1}{n-1}\varDelta u_h) \overline{w}_{e,2}|\\&~~~\lesssim \big (h_e^{-2}\Vert u_h-u\Vert _{2,\omega _e} +\Vert w_h-w\Vert _{0,\omega _e} +h_e^{-1}|\lambda _h-\lambda |\\&~~~~~~+ \Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\omega _e} \big )\Vert w_{e,2}\Vert _{0,e}h_e^{1/2}. \end{aligned}$$

Hence

$$\begin{aligned}&| \int _{e} R_{e,2}(u_h) \overline{w}_{e,2}| \lesssim \big (h_e^{-2}\Vert u_h-u\Vert _{2,\omega _e} +\Vert w_h-w\Vert _{0,\omega _e} +h_e^{-1}|\lambda _h-\lambda |\\&~~~~~~+ \Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\omega _e} \big )\Vert w_{e,2}\Vert _{0,e}h_e^{1/2}\\&~~~~~~+\Vert R_{e,1}(u_h)\Vert _{0,e}\Vert w_{e,2}\Vert _{0,e}h_e^{-1}. \end{aligned}$$

It is immediate that

$$\begin{aligned}&\Vert \widehat{R}_{e,2}(u_h)\Vert _{0,e}^2\lesssim \int _{e} ( R_{e,2}(u_h)+\widehat{R}_{e,2}(u_h)- R_{e,2}(u_h))w_{e,2}\\&~~~\lesssim \big (h_e^{-3/2}\Vert u_h-u\Vert _{2,\omega _e} +h_e^{1/2}\Vert w_h-w\Vert _{0,\omega _e} +h_e^{-1/2}|\lambda _h-\lambda |\\&~~~~~~+ h^{1/2}_e\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\omega _e}+\Vert R_{e,1}(u_h)\Vert _{0,e}h_e^{-1} \big )\Vert w_{e,2}\Vert _{0,e}\\&~~~~~~+ \Vert \widehat{R}_{e,2}(u_h)- R_{e,2}(u_h)\Vert _{0,e}\Vert w_{e,2}\Vert _{0,e}, \end{aligned}$$

from which we deduce

$$\begin{aligned}&h_e^{3/2}\Vert \widehat{R}_{e,2}(u_h)\Vert _{0,e} \lesssim \Vert u_h-u\Vert _{2,\omega _e} +h_e^{2}\Vert w_h-w\Vert _{0,\omega _e} +h_e|\lambda _h-\lambda |\\&~~~~~~+ h_e^{2}\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\omega _e}+h_e^{1/2}\Vert R_{e,1}(u_h)\Vert _{0,e} \\&~~~~~~+ h_e^{3/2}\Vert \widehat{R}_{e,2}(u_h)- R_{e,2}(u_h)\Vert _{0,e}. \end{aligned}$$

This together with (3.11) yields (3.12). $\square$

Notice that the dual problem (2.11)–(2.12) has a similar form as the primal problem (2.6)–(2.7). By the similar argument used in Lemmas 3.2–3.3, we can also prove the following two lemmas for the dual problem (2.10).

Lemma 3.4

The following estimates of element residual hold for the dual eigenpair $(u^*,w^*,\lambda ^*)$ and its approximate eigenpair $(u^*_h,w^*_h,\lambda ^*_h)$

$$\begin{aligned}&h_\kappa ^{2}\Vert \widehat{R}^*_{\kappa ,1}(u^*_h,w^*_h)\Vert _{0,\kappa } \lesssim \Vert u^*_h-u^*\Vert _{2,\kappa } +h_\kappa ^{2}\Vert w^*_h-w^*\Vert _{0,\kappa } +h_\kappa |\lambda _h-\lambda |\nonumber \\&~~~+h_\kappa ^{2}\Vert \widehat{R}^*_{\kappa ,1}(u^*_h,w^*_h)- R_{\kappa ,1}(u^*_h,w^*_h)\Vert _{0,\kappa }, \end{aligned}$$

(3.15)

$$\begin{aligned}&\Vert \widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h)\Vert _{0,\kappa } \lesssim \Vert u^*_h-u^*\Vert _{2,\kappa } + \Vert w^*_h-w^*\Vert _{0,\kappa } + |\lambda _h-\lambda | \nonumber \\&~~~+ \Vert \widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h)- R_{\kappa ,1}(u^*_h,w^*_h)\Vert _{0,\kappa }. \end{aligned}$$

(3.16)

Proof

(3.15) can be obtained by the similar proof used in (3.10). In order to prove (3.16), we define the $H_0^2(\kappa )$ function $w_{\kappa ,2}=b_\kappa ^2\widehat{R}_{\kappa ,2}(u^*_h,w^*_h)$. Then by (2.12) we have

$$\begin{aligned}&\int _\kappa \widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h)w_{\kappa ,2}=\int _\kappa \big ({R}^*_{\kappa ,2}(u^*_h,w^*_h)+\widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h)- {R}^*_{\kappa ,2}(u^*_h,w^*_h)\big )w_{\kappa ,2}\\&~~~\lesssim \int _\kappa (w_h^*+\frac{\lambda _h^*n}{n-1}u_h^*) w_{\kappa ,2}+\Vert \widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h)- {R}^*_{\kappa ,2}(u^*_h,w^*_h)\Vert _{\kappa ,0}\Vert w_{\kappa ,2}\Vert _{\kappa ,0}\\&~~~ \lesssim (\Vert u^*_h-u^*\Vert _{0,\kappa } + \Vert w^*_h-w^*\Vert _{0,\kappa } + |\lambda _h-\lambda |\\&~~~~~~+\Vert \widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h)- {R}^*_{\kappa ,2}(u^*_h,w^*_h)\Vert _{\kappa ,0})\Vert w_{\kappa ,2}\Vert _{\kappa ,0}, \end{aligned}$$

which together with $\Vert \widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h)\Vert ^2_{0,\kappa }\lesssim \int _\kappa \widehat{R}^*_{\kappa ,2}(u^*_h,w^*_h) w_{\kappa ,2}$ yields (3.16). $\square$

Lemma 3.5

Assume $n(x)\in W^{2,\infty }(\kappa )$ for all $\kappa \in \pi _h$. The following estimates of element edge or face residual hold for the dual eigenpair $(u^*,w^*,\lambda ^*)$ and its approximate eigenpair $(u^*_h,w^*_h,\lambda ^*_h)$

$$\begin{aligned}&h_e^{1/2}\Vert \widehat{R}_{e,1}(u^*_h)\Vert _{0,e} \lesssim \Vert u^*_h-u^*\Vert _{2,\omega _e} +h_e^{2}\Vert w^*_h-w^*\Vert _{0,\omega _e} +h_e|\lambda _h-\lambda |\nonumber \\&~~~~~~+h_\kappa ^{2}\sum _{i=1,2}\Vert \widehat{R}^*_{\kappa ,i}(u^*_h,w^*_h)- R_{\kappa ,i}^*(u^*_h,w^*_h)\Vert _{0,\omega _e}\nonumber \\&~~~~~~+h^{1/2}_e\Vert \widehat{R}_{e,1}(u^*_h)-R_{e,1}(u^*_h)\Vert _{0,e},~ e\subset \partial \kappa \cap D, \end{aligned}$$

(3.17)

$$\begin{aligned}&h_e^{3/2}\Vert \widehat{R}_{e,2}(u^*_h)\Vert _{0,e} \lesssim \Vert u^*_h-u^*\Vert _{2,\omega _e} +h_e^{2}\Vert w^*_h-w^*\Vert _{0,\omega _e} +h_e|\lambda _h-\lambda |\nonumber \\&~~~~~~+ h_\kappa ^{2}\sum _{i=1,2}\Vert \widehat{R}^*_{\kappa ,i}(u^*_h,w^*_h)- R^*_{\kappa ,i}(u^*_h,w^*_h)\Vert _{0,\omega _e}\nonumber \\&~~~~~~+h_e^{1/2}\Vert \widehat{R}_{e,1}(u^*_h)-R_{e,1}(u^*_h)\Vert _{0,e} \nonumber \\&~~~~~~+ h_e^{3/2}\Vert \widehat{R}_{e,2}(u^*_h)- R_{e,2}(u^*_h)\Vert _{0,e}, ~ e\subset \partial \kappa \cap D. \end{aligned}$$

(3.18)

Combining Lemmas 3.2 and 3.3, we naturally have the following.

Theorem 3.3

Assume $n(x)\in W^{2,\infty }(\kappa )$ for all $\kappa \in \pi _h$. The following efficiency of the error indicator $\eta _\kappa$ holds for the primal eigenpair $(u,w,\lambda )$ and its approximate eigenpair $(u_h,w_h,\lambda _h)$

$$\begin{aligned}&\eta _{\kappa }(u_h,w_h) \lesssim \Vert u_h-u\Vert _{2,\widehat{\omega }_{\kappa }} +h_\kappa ^{2}\Vert w_h-w\Vert _{0,\widehat{\omega }_{\kappa }} +h_\kappa |\lambda _h-\lambda |\nonumber \\&~~~~~~+ h_\kappa ^{2}\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\widehat{\omega }_{\kappa }}\nonumber \\&~~~~~~+\sum \limits _{e\subset \partial \kappa \cap D}h_e^{1/2}\Vert \widehat{R}_{e,1}(u_h)-R_{e,1}(u_h)\Vert _{0,e} \nonumber \\&~~~~~~+\sum \limits _{e\subset \partial \kappa \cap D} h_e^{3/2}\Vert \widehat{R}_{e,2}(u_h)- R_{e,2}(u_h)\Vert _{0,e}, \end{aligned}$$

(3.19)

where $\widehat{\omega }_\kappa$ is the union of elements sharing at least one edge in $\mathbb {R}^2$ or at least one face in $\mathbb {R}^3$ with the element $\kappa$.

Combing Lemmas 3.4 and 3.5, we can also give the following upper bound of $\eta ^*_\kappa$.

Theorem 3.4

Assume $n(x)\in W^{2,\infty }(\kappa )$ for all $\kappa \in \pi _h$. The following efficiency of the error indicator $\eta ^*_\kappa$ holds for the dual eigenpair $(u^*,w^*,\lambda ^*)$ and its approximate eigenpair $(u^*_h,w^*_h,\lambda ^*_h)$

$$\begin{aligned}&\eta ^*_{\kappa }(u^*_h,w^*_h) \lesssim \Vert u^*_h-u^*\Vert _{2,\widehat{\omega }_{\kappa }} +h_\kappa ^{2}\Vert w^*_h-w^*\Vert _{0,\widehat{\omega }_{\kappa }} +h_\kappa |\lambda _h-\lambda |\nonumber \\&~~~~~~+ h_\kappa ^{2} \sum _{i=1,2}\Vert \widehat{R}^*_{\kappa ,i}(u^*_h,w^*_h)- R^*_{\kappa ,i}(u^*_h,w^*_h)\Vert _{0, \widehat{\omega }_{\kappa }} \nonumber \\&~~~~~~+\sum \limits _{e\subset \partial \kappa \cap D}h_e^{1/2}\Vert \widehat{R}_{e,1}(u^*_h)-R_{e,1}(u^*_h)\Vert _{0, e} \nonumber \\&~~~~~~+\sum \limits _{e\subset \partial \kappa \cap D} h_e^{3/2}\Vert \widehat{R}_{e,2}(u^*_h)- R_{e,2}(u^*_h)\Vert _{0, e}. \end{aligned}$$

(3.20)

Thanks to Lemma 2.1, we know in (3.6) and (3.19) $\Vert \lambda (u,w)-\lambda _h(u_h,w_h)\Vert _{1,D}$ ($\lesssim |\lambda - \lambda _h|+\Vert (u,w) -(u_h,w_h)\Vert _{1}$) and $h_\kappa |\lambda _h-\lambda |$ are terms of higher order, and the similar assert is valid for (3.8) and (3.20). In what follows, we shall point out that in (3.6) and (3.19) the small quantities with $h_\kappa ^{2}\Vert \widehat{R}_{\kappa }(u_h,w_h)- R_{\kappa }(u_h,w_h)\Vert _{0,\kappa }$, $h_e^{1/2}\Vert \widehat{R}_{e,1}(u_h)-R_{e,1}(u_h)\Vert _{0,e}$ and $h_e^{3/2}\Vert \widehat{R}_{e,2}(u_h)- R_{e,2}(u_h)\Vert _{0,e}$ are of higher order than $\Vert (u_h,w_h)-(u,w)\Vert _{A}$, which implies $\eta _\kappa$ is a reliable and efficient error indicator of $\Vert (u_h,w_h)-(u,w)\Vert _{A}$. The similar assertion is valid for (3.8) and (3.20). Here, as an special case to specify this point, we take the symbol $\widetilde{f }$ to be the Lagrange interpolation of f or the $L^2$-projection onto the polynomial space of degree $\le$ $m_G$.

For simplicity, hereafter we assume the ascent $\alpha$ of $\lambda$ is equal to 1.

Let the primal eigenfunction satisfy the piecewise smoothness $(u,w)|_{\omega _\kappa }\in \mathbf {H}^{2+r_\kappa }(\omega _\kappa ),\forall \kappa \in \pi _h$. Let $n\in H^{2+\widehat{r}_\kappa }(\kappa ), \forall \kappa \in \pi _h$ with $\widehat{r}_\kappa > 0$ to be determined.

Condition A. $\min (\widehat{r}_{\kappa }+3/2,m_\kappa +1,\min \limits _{e\subset \partial \kappa \cap D} m_e+1)>\min (r_{\kappa },l-1)$, $\forall \kappa \in \pi _h$.

By (2.16) and Lemma 3.1 we get the following a priori error estimate

$$\begin{aligned} \Vert (u_h,w_h)-(u,w)\Vert _{A}\lesssim \left( \sum \limits _{\kappa \in \pi _h}h_\kappa ^{2\min (r_\kappa ,l-1)}\Vert (u,w)\Vert ^2_{2+r_\kappa ,\omega _\kappa }\right) ^{1/2}. \end{aligned}$$

(3.21)

By the interpolation error estimate, $\widehat{R}_{\kappa }(u_h,w_h)- {R}_{\kappa }(u_h,w_h)$ can be bounded as follows.

$$\begin{aligned}&\Vert \widehat{R}_{\kappa }(u_h,w_h)- {R}_{\kappa }(u_h,w_h)\Vert _{0,\kappa }\nonumber \\&~~~\lesssim \sum \limits _{i=0}^{2}|\widetilde{\frac{1}{n-1}}-\frac{1}{n-1}|_{i,\kappa }\Vert u_h\Vert _{4-i,\kappa } +|\widetilde{\frac{1}{n-1}}-\frac{1}{n-1}|_{0,\kappa }\Vert w_h\Vert _{0,\kappa }\nonumber \\&~~~\lesssim \Big (\sum \limits _{i=0}^{2}h^{2+\min (\widehat{r}_{\kappa },m_\kappa -1)-i}_{\kappa } h^{i-2}_{\kappa }\Vert u_h\Vert _{2,\kappa } +h^{2+\min (\widehat{r}_{\kappa },m_\kappa -1)}_{\kappa }\Vert w_h\Vert _{0,\kappa }\Big )\nonumber \\&~~~~~~\cdot |\frac{1}{n-1}|_{2+\widehat{r}_{\kappa },\kappa }\nonumber \\&~~~\lesssim h^{\min (\widehat{r}_{\kappa },m_\kappa -1)}_{\kappa }\Vert (u_h,w_h)\Vert _{2,\kappa }. \end{aligned}$$

(3.22)

Using the interpolation error estimate and the inverse inequality again, $\widehat{R}_{e,i}(u_h)- {R}_{e,i}(u_h)~(i=1,2, e\subset \partial \kappa \cap D$) can be bounded as follows.

$$\begin{aligned}&\Vert \widehat{R}_{e,1}(u_h)- {R}_{e,1}(u_h)\Vert _{0,e} \lesssim |\widetilde{\frac{1}{n-1}}-\frac{1}{n-1}|_{0,e}\Vert [[u_h]]_e\Vert _{2,e}\nonumber \\&~~~\lesssim h^{3/2+\min (\widehat{r}_{\kappa },m_e-1/2)}_e |\frac{1}{n-1}|_{2+\widehat{r}_{\kappa },\kappa }\sum \limits _{\kappa \subset \omega _e}\Vert u_h\Vert _{5/2,\kappa }\nonumber \\&~~~\lesssim h^{1+\min (\widehat{r}_{\kappa },m_e-1/2)}_e |\frac{1}{n-1}|_{2+\widehat{r}_{\kappa },\kappa }\sum \limits _{\kappa \subset \omega _e}\Vert u_h\Vert _{2,\kappa }, \end{aligned}$$

(3.23)

and

$$\begin{aligned}&\Vert \widehat{R}_{e,2}(u_h)- {R}_{e,2}(u_h)\Vert _{0,e} \lesssim \sum \limits _{i=0}^{1}|\widetilde{\frac{1}{n-1}}-\frac{1}{n-1}|_{i,e}\Vert [[u_h]]_e\Vert _{3-i,e}\nonumber \\&~~~\lesssim \sum \limits _{i=0}^{1}h^{3/2+\min (\widehat{r}_{\kappa },m_e-1/2)-i}_{\kappa }|\frac{1}{n-1}|_{2+\widehat{r}_{\kappa },\kappa } h^{i-1}_{\kappa }\Vert [[u_h]]_e\Vert _{2,e}\nonumber \\&~~~\lesssim h^{1/2+\min (\widehat{r}_{\kappa },m_e-1/2)}_{\kappa }|\frac{1}{n-1}|_{2+\widehat{r}_{\kappa },\kappa } \sum \limits _{\kappa \subset \omega _e}\Vert u_h\Vert _{5/2,\kappa }\nonumber \\&~~~\lesssim h^{\min (\widehat{r}_{\kappa },m_e-1/2)}_{\kappa }|\frac{1}{n-1}|_{2+\widehat{r}_{\kappa },\kappa } \sum \limits _{\kappa \subset \omega _e}\Vert u_h\Vert _{2,\kappa }. \end{aligned}$$

(3.24)

To summarize, we know from Theorems 3.1 and 3.3 and (3.21)–(3.24) the following conclusion:

Let $(u_h,w_h)$ be an approximate eigenfunction of the primal eigenfunction (u, w). If Condition A is valid, $\eta _h(u_h,w_h)$ is a globally reliable and efficient error indicator of $\Vert (u_h,w_h)-(u,w)\Vert _{A}$.

Let the dual eigenfunction satisfy the piecewise smoothness $(u^*,w^*)|_{\omega _\kappa }\in \mathbf {H}^{2+r^*_\kappa }(\omega _\kappa ) , \forall \kappa \in \pi _h$.

Condition B. $\min (\widehat{r}_{\kappa }+3/2,m_\kappa +1,\min \limits _{e\subset \partial \kappa \cap D} m_e+1)>\min (r^*_{\kappa },l-1)$, $\forall \kappa \in \pi _h$.

By the similar argument as above, we can also have the following conclusion:

Let $(u^*_h,w^*_h)$ be an approximate eigenfunction of the dual eigenfunction $(u^*,w^*)$. If Condition B is valid, $\eta _h^*(u^*_h,w^*_h)$ is a globally reliable and efficient error indicator of $\Vert (u^*_h,w^*_h)-(u^*,w^*)\Vert _{A}$.

It is clear that Conditions A and B can be easily satisfied when $\widehat{r}_{\kappa } , m_\kappa$ and $m_e$ are relatively large compared with $r_\kappa ,r^*_\kappa$ and l.

The following lemma improves Lemma 3.2 in [31], which builds the basic relation between the eigenvalue and its approximate eigenvalue.

Lemma 3.6

Let $(\lambda _h,u_h,\omega _h)$ be an approximate eigenpair of the primal eigenpair $(\lambda ,u,\omega )$, $(\lambda ^*,u^*,w^*)$ be an dual eigenpair with $\lambda ^*=\overline{\lambda }$, and $\lambda _h^*=\overline{\lambda }_h$. Let $(u_h^{-},w_{h}^{-})$ be the orthogonal projection of $(u_{h},w_{h})$ onto $M^*_h(\lambda ^{*})$ in the sense of the inner product $A(\cdot ,\cdot )$, and

$$\begin{aligned} (u_{h}^{*},w_{h}^{*})=\frac{(u_{h}^{-},w_h^{-})}{\Vert (u_{h}^{-},w_h^{-})\Vert _{A}}. \end{aligned}$$

(3.25)

Then $|A((u_h,w_h),(u_h^*,w_h^*))|$ has a positive lower bound uniformly with respect to h and

$$\begin{aligned}&|A((u_h,w_h),(u_h^*,w_h^*))||\lambda -\lambda _h | \lesssim \Vert (u_h,w_h)-(u,w)\Vert _A^2+\Vert (\varphi _h^*,\psi _h^*)-(\varphi ^*,\psi ^*)\Vert _A^2\nonumber \\&~~~~~~+\Vert \lambda ^*(u^*,w^*)-\lambda _h^*(u_h^*,w_h^*)\Vert _{1,D}^2, \end{aligned}$$

(3.26)

where $(\varphi ^*,\psi ^*)\in \mathbf {H}$ and $(\varphi _h^*,\psi _h^*)\in \mathbf {H}_h$ are respectively defined by

$$\begin{aligned} A((v,z),(\varphi ^*,\psi ^*))=B((v,z),\lambda ^*_h(u^*_h,w^*_h)),~\forall (v,z)\in \mathbf {H},\nonumber \\ A((v,z),(\varphi _h^*,\psi _h^*))=B((v,z),\lambda ^*_h(u^*_h,w^*_h)),~\forall (v,z)\in \mathbf {H}_h. \end{aligned}$$

(3.27)

Proof

From Lemma 4.1 in [10] we know $|A((u_h,w_h),(u_h^*,w_h^*))|$ has a positive lower bound uniformly with respect to h. Then the assertion can be proved by the similar proofs of Theorem 3.2 in [31, lines 5-32 on page 56]. $\square$

We need to estimate the upper bound of $\Vert (\varphi ^*,\psi ^*)-(\varphi ^*_h,\psi ^*_h)\Vert _A$ in (3.26). Similar to the proof of Theorem 3.2, we have

Theorem 3.5

Under the conditions of Lemma 3.6, there holds

$$\begin{aligned}&\Vert (\varphi ^*,\psi ^*)-(\varphi ^*_h,\psi ^*_h)\Vert _A\lesssim {\underline{\eta }}^*_h( {u}^*_h,w^*_h)\nonumber \\&~~~~~~+ \Big \{\sum \limits _{\kappa \in \pi _h} \Big [h_\kappa ^4\sum _{i=1,2}\Vert \widehat{\underline{R}}^*_{\kappa ,i}(u^*_h,w^*_h)-\underline{R}^*_{\kappa ,i}(u^*_h,w^*_h) \Vert _{0,\kappa }^2\nonumber \\&~~~~~~+ \sum \limits _{ e\subset \partial \kappa \cap D} \Big ( h_e\Vert \widehat{R}_{e,1}(\varphi ^*_h)-R_{e,1}(\varphi ^*_h)\Vert ^2_{0,e}\nonumber \\&~~~~~~+h_e^3\Vert \widehat{R}_{e,2}(\varphi ^*_h)-R_{e,2}(\varphi ^*_h)\Vert _{0,e}^2 \Big )\Big ]\Big \}^{1/2}, \end{aligned}$$

(3.28)

where ${\underline{\eta }}^{*2}_h( {u}^*_h,w^*_h) = \sum \limits _{\kappa \in \pi _h} {\underline{\eta }}_\kappa ^{*2}( {u}^*_h,w^*_h)$; $\underline{\eta }_{\kappa }^*(u^*_h,w^*_h)$ is defined similarly as ${\eta }_{\kappa }^*(u^*_h,w^*_h)$ in (3.1) by only replacing $\eta _{E_\kappa }^*(u_h^*)$ with $\eta _{E_\kappa }^*(\varphi _h^*)$, and replacing $R^*_{\kappa ,1}(u^*_h,w^*_h)$ and $R^*_{\kappa ,2}(u^*_h,w^*_h)$ with $\underline{R}^*_{\kappa ,1}(u^*_h,w^*_h)$ and $\underline{R}^*_{\kappa ,2}(u^*_h,w^*_h)$ respectively; $\underline{R}^*_{\kappa ,1}(u^*_h,w^*_h)$ and $\underline{R}^*_{\kappa ,2}(u^*_h,w^*_h)$ are defined by replacing ${u}^*_h$ and ${w}^*_h$ in the first term of the right hand side of (3.2)–(3.3) with ${\varphi }^*_h$ and ${\psi }^*_h$ respectively.

Remark 3.1

Theorem 3.5 indicates that ${\underline{\eta }}^*_h( {u}^*_h,w^*_h)$ is a reliable indicator of $\Vert (\varphi ^*,\psi ^*)-(\varphi ^*_h,\psi ^*_h)\Vert _A$ if the ascent $\alpha =1$. In fact, let $(u^*_h,w^*_h)$ and $(u^*,w^*)$ satisfy Lemma 3.6 then

$$\begin{aligned}&\Vert (\varphi ^*,\psi ^*)-(\varphi ^*_h,\psi ^*_h)\Vert _A =\Vert \lambda _h^*(T^*-T_h^*)(u^*_h,w^*_h)\Vert _A,\\&|\Vert \lambda _h^*(T^*-T_h^*)(u^*_h,w^*_h)\Vert _A-\Vert \lambda ^*(T^*-T_h^*)(u^*,w^*)\Vert _A|\\&~~~\le \Vert (T^*-T_h^*)(\lambda _h^*(u^*_h,w^*_h)-\lambda ^*(u^*,w^*))\Vert _A\\&~~~\lesssim \Vert T^*-T_h^*\Vert _{\mathbf {H}\rightarrow \mathbf {H}}\Vert \lambda _h^*(u^*_h,w^*_h)-\lambda ^*(u^*,w^*)\Vert _A. \end{aligned}$$

From [10] we know $\Vert T^*-T_h^*\Vert _{\mathbf {H}\rightarrow \mathbf {H}}\rightarrow 0$; hence from the above estimate and (2.18)–(2.20) we have $\Vert (\varphi ^*,\psi ^*)-(\varphi ^*_h,\psi ^*_h)\Vert _A$ has the same order as $\Vert \lambda ^*(T^*-T_h^*)(u^*,w^*)\Vert _A$. Notice that $\Vert (\varphi ^*_h,\psi ^*_h)\Vert _A=\Vert \lambda _h^*T_h^*(u^*_h,w^*_h)\Vert _A\lesssim \Vert (u^*_h,w^*_h)\Vert _A$; then by the similar argument as in (3.21)–(3.24), we can prove that if $(u^*,w^*)$ satisfies Condition B then the second term at right hand side of (3.28) is a small quantity of higher order than $\Vert \lambda ^*(T^*-T_h^*)(u^*,w^*)\Vert _A$ as well as $\Vert (\varphi ^*,\psi ^*)-(\varphi ^*_h,\psi ^*_h)\Vert _A$.

Theorem 3.6

Let $\lambda _h$ be an eigenvalue of the primal problem (2.13) which converges to the eigenvalue $\lambda$, and let the approximate eigenfunction $(u_h,w_h)$ and $(u^*_h,w^*_h)\in M^*_h(\lambda ^{*})$ be defined in Lemma 3.6. Suppose the ascent $\alpha =1$ and that the primal eigenfunction (u, w) and the dual eigenfunction $(u^*,w^*)$ satisfy Conditions A and B respectively. Then

$$\begin{aligned}&|\lambda _h-\lambda |\lesssim \eta ^2_h(u_h,w_h)+\underline{\eta }_h^{*2}(u^*_h,w^*_h). \end{aligned}$$

(3.29)

Proof

From (2.19)–(2.20) and Remark 3.1 we know the third term at the right side hand of (3.26) is a small quantity of higher order. According to Conditions A and B and Remark 3.1, we know the second term at right hand side of (3.28) is a small quantity of higher order. Hence (3.29) can be derived from (3.6), (3.26) and (3.28). $\square$

Remark 3.2

When using (3.29) to estimate $|\lambda -\lambda _h|$, it seems that one needs to solve the boundary value problem (3.27) for $(\varphi _h^*,\psi _h^*)$. However, if the ascent of the eigenvalues $\lambda _{j,h}(j=i,\ldots ,i+q-1)$ is 1, then

$$\begin{aligned} (\varphi _h^*,\psi _h^*)=\sum \limits _{j=i}^{i+q-1} \frac{\lambda ^*_h \lambda ^{*-1}_{j,h} a_j(u^*_{j,h},w^*_{j,h})}{\Vert (u^-_{h},w^-_{h})\Vert _A},~(u^*_{j,h},w^*_{j,h})\in M^*(\lambda ^*_{j,h}), \end{aligned}$$

where $(u^-_h,w^-_h)=\sum \limits _{j=i}^{i+q-1}a_j(u^*_{j,h},w^*_{j,h})$ with $\Vert (u^*_{j,h},w^*_{j,h})\Vert _A=1$ is the orthogonal projection of $(u_{h},w_{h})$ onto $M^*_h(\lambda ^{*})$.

Remark 3.3

Theorem 3.6 shows only the reliability of the indicator $\eta ^2_h(u_h,w_h)+\underline{\eta }_h^{*2}(u^*_h,w^*_h)$ of $\lambda _h$. To our knowledge, up to now, there does not exist any work regarding residual type a posteriori error estimates of finite elements for nonsymmetric eigenvalue problems that has proved the efficiency of the indicator of $\lambda _h$ therein.

4 Adaptive Algorithm and Numerical Experiment

The following algorithm is a standard adaptive procedure (e.g., see Algorithm C in [32]).

Algorithm 1

• Step 1. Set $it=0$ and Pick any initial mesh $\pi _{h_{it}}$ with the mesh size ${h_{it}}$.

• Step 2. Solve (2.13) on $\pi _{h_{it}}$ for the discrete solution $(\lambda _{h_{it}},u_{h_{it}},w_{h_{it}})$ and find $(u^*_{h_{it}},w^*_{h_{it}})\in M_{h_{it}}(\lambda ^*)$ by (3.25) such that $\Vert (u_{h_{it}},w_{h_{it}})\Vert _A=\Vert (u^*_{h_{it}},w^*_{h_{it}})\Vert _A=1$.

• Step 3. Compute the local indicators ${\eta }_{\kappa }(u_{h_{it}},w_{h_{it}})$ and ${\underline{\eta }}^*_{\kappa }(u^*_{h_{it}},w^*_{h_{it}})$.

• Step 4. Construct $\widehat{\pi }_{h_{it}}\subset \pi _{h_{it}}$ by Marking Strategy E and parameter $\theta$.

• Step 5. Refine $\pi _{h_{it}}$ to get a new mesh $\pi _{h_{it+1}}$ by Procedure REFINE.

• Step 6. Let ${it} = {it} + 1$ and go to Step 2.

Marking Strategy E

Given parameter $0< \theta < 1$:

Step 1. Construct a minimal subset $\widehat{\pi }_{h_{it}}\subset \pi _{h_{it}}$ by selecting some elements in $\pi _{h_{it}}$ such that

$$\begin{aligned} \sum \limits _{{\kappa }\in \widehat{\pi }_{h_{it}}}({ {\eta }}_{\kappa }^2(\mathbf {u}_{h_{it}},w_{h_{it}})+{ {\underline{\eta }}}^{*2}_{\kappa }(\mathbf {u}_{h_{it}},w_{h_{it}}))\ge \theta ( { {\eta }}_{h_{{it}}}^2(\mathbf {u}_{h_{it}},w_{h_{it}})+{ {\underline{\eta }}}^{*2}_{h_{it}}(\mathbf {u}_{h_{it}},w_{h_{it}})). \end{aligned}$$

Step 2. Mark all the elements in $\widehat{\pi }_{h_{it}}$.

In this section, we will report some numerical experiments for solving the transmission eigenvalue problem (2.8) by the Argyris element to validate our theoretical results. We consider the case when D is the unit square $(0,1)^2$ or the L-shaped domain $(-1,1)^2\backslash ([0,1)\times (-1, 0])$ and the index of refraction $n=16, 8+x_1-x_2,1.005$.

We use Matlab 2012a to solve (2.1)–(2.4) on a Lenovo G480 PC with 4G memory. Our program is made in the environment of Matlab together with the package of iFEM [33]. In steps 2 of Algorithm 1, we use the sparse solver eigs in Matlab to solve the matrix eigenvalue problem. We adopt the quadrature formula with sixth order algebraic precision to numerically compute the integral on elements and edges. We use the effective index $\frac{\eta ^2_h(u_h,w_h)+\underline{\eta }_h^{*2}(u^*_h,w^*_h)}{|k-k_h|}$ to investigate the reliability of the indicator of $\lambda _h$. For reading convenience, we denote by $k_{j}=\sqrt{\lambda _{j}}$ and $k_{j,h}=\sqrt{\lambda _{j,h}}$ the jth eigenvalue and the jth numerical eigenvalue obtained by Algorithm 1 on $\mathbf {H}_{h}$.

Fig. 1

Error curves on the unit square with $\theta =0.25$ for the 1st (left top) and 2nd (right top) eigenvalues with $n=16$ and the 1st (left bottom) and 5th (right bottom) eigenvalues with $n=8+x_1-x_2$

4.1 Model Problem on the Unit Square

In the computation of errors, we take $k_1\approx 1.879591173147$ and $k_2\approx 2.444236099229$ (the multiplicity of $k_2$ is 2) for $n=16$, $k_1\approx 2.82218934089$ and $k_5\approx 4.496551954471 - 0.871481780427i$ for $n=8+x_1-x_2$, $k_1\approx 5.579320511651 - 2.442978884001i$ and $k_3\approx 8.280617372950 - 2.806336620282i$ (the multiplicity of $k_3$ is 2) for $n=1.005$, all of which are obtained by our adaptive procedure and are relatively accurate.

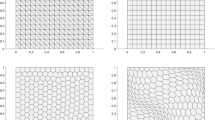
The initial mesh on the unit square is made up of congruent triangles, the mesh size $h_0$ being respectively $\frac{\sqrt{2}}{16}$ and $\frac{\sqrt{2}}{8}$. We set the different parameter $\theta$ to compute the numerical eigenvalues, varying according to the setting of n and the domain D. We depict the error curves (see Figs. 1 and 5) and some adaptively refined meshes (see Fig. 2) for the numerical eigenvalues. We see from Fig. 1 that the error curve of the uniform refinement is not a straight line; we are confused for this phenomena since there is no singularity in that case and we cannot explain it at present.

According to the regularity theory, we know $u, w\in H^{4}(D)$ if D is a square. When the ascent of k is equal to 1: according to (2.18), using the uniform meshes, the accuracy of the numerical eigenvalue $k_{j,h}$ on the unit square can achieve $O(dof^{-2})$ (where dof denotes the number of degrees of freedom of finite element equation). It is seen from Figs. 1, 5 and 6 that all of the a posteriori error indicators of the numerical eigenvalues are reliable, which coincides with the theoretical result. When setting $h_0=\frac{\sqrt{2}}{4}$, using Algorithm 1 after 3 iterations we obtain the first two eigenvalues 1.87965 and 2.44455 with $dof=374$ and 356 respectively. Table 3 in [3] shows that the first two eigenvalues by continuous method are 1.9094, 2.5032 with $dof = 330$ and those by mixed method are 1.8954, 2.4644 with $dof= 513$; hence the advantage of adaptive Algorithm in this paper is obvious. Also it is easy to know that our adaptive Algorithm is efficient compared with the numerical results on the unit square in [8].

Fig. 2

Adaptive meshes on the unit square after 20 iterations for the 1st (left top) and 2nd (right top) eigenvalues with $n=16$ and the 1st (left bottom) and 5th (right bottom) eigenvalues with $n=8+x_1-x_2$

Fig. 3

Error curves on the L-shaped for the 1st (left top) and 2nd (right top) eigenvalues with $n=16$ and $\theta =0.75$ and the 1st (left bottom, $\theta =0.75$) and 5th (right bottom, $\theta =0.5$) eigenvalues with $n=8+x_1-x_2$

Fig. 4

Adaptive meshes on the L-shaped after 20 iterations for the 1st (left top) and 2nd (right top) eigenvalues with $n=16$ and the 1st (left bottom) and 5th (right bottom) eigenvalues with $n=8+x_1-x_2$

Fig. 5

Error curves on the unit square with $\theta =0.25$ for the 1st (left top) and 2nd (right top) eigenvalues with $n=1.005$ and on the L-shaped for the 1st (left bottom, $\theta =0.75$) and 3rd (right bottom, $\theta =0.5$) eigenvalues with $n=1.005$

Fig. 6

Effective indexes for eigenvalues on the unit square (left) and on the L-shaped (right)

In addition, we can see from Fig. 2 that the weak singularities of the eigenfunctions corresponding to $k_1,k_2$ for $n=16$ and $k_1$ for $n=8+x_1-x_2$ mainly center on the corner points.

4.2 Model Problem on the L-Shaped

In the computation of errors, we take $k_1\approx 1.476100561$ and $k_2\approx 1.56972574409$ for $n=16$, $k_1\approx 2.30212057$ and $k_5\approx 2.9242325-0.5645906i$ for $n=8+x_1-x_2$, $k_1\approx 4.11589607 - 2.06786337i$ and $k_3\approx 4.795653396 - 2.0361001266i$ for $n=1.005$, all of which are obtained by our adaptive procedure and are relatively accurate.

The initial meshes on the L-shaped are made up of congruent triangles, the mesh size $h_0$ being $\frac{\sqrt{2}}{8}$. We depict the error curves (see Fig. 3) and some adaptively refined meshes (see Fig. 4) for the numerical eigenvalues.

Since the problem on the L-shaped has the singularity in general so that the accuracy of the numerical eigenvalue $k_{j,h}$ is not less than $O(dof^{-2})$. It is seen from Figs. 3, 5 and 6 that all of the a posteriori error indicators of the numerical eigenvalues are reliable, which coincides with the theoretical result. The phenomena that the curves of effective indexes go upward may lie in the insufficiently exact eigenvalues provided in this paper. Moreover, the most numerical eigenvalues in numerical examples can achieve the nearly optimal convergence order $O(dof^{-4})$. The convergence order of the numerical eigenvalues $k_{5,h}$ on the L-shaped with $n=8+x_1-x_2$ is $O(dof^{-3})$. Note that for all cases on the L-shaped with $n=8+x_1-x_2$ the accuracy of the numerical eigenvalue on adaptive meshes is better than that on uniform meshes. We can see from the numerical results in [7, 10] that the convergence order of numerical eigenvalues on the L-shaped on uniform meshes by the BFS element is less than 1 with respect to $dof^{-1}$.

In addition, we can see from Fig. 4 that the eigenfunctions corresponding to all computed eigenvalues on the L-shaped have singularities towards the L corner point and change abruptly near the midpoints of two longest sides of this domain.