1 Introduction

By definition, a porous media consists of pores or void spaces between some particulate phases within a vessel or conduit. Understanding the characteristics of the fluid flows through fully or partially porous media is critical to a wide range of fields, including hydrology (ground water quality), hydrogeology (mineral processing), extract of fossil energies and weathering (pollution transport) and other engineering applications. For example, porous media are crucial for groundwater flows in various aquifers, like sedimentary deposits, fractured rock or karst systems [1]. Aquifers are characterized by a network of porous conduits resulting from geological formations and allow significant amounts of water to move through it under ordinary field conditions. All aquifers can be considered to fall on a continuum between porous media systems and conduit systems.

A key variable to describe the void spaces in porous media is porosity, which denotes the fraction of the volume of pores over the total control volume. The smallest volume to obtain a meaningful value for the porosity of a system is called representative elementary volume (REV), which contains the minimum number of pores necessary to establish a porosity value valid for the whole system. In many studies, due to the complex nature of the porous media, the simulations are performed by models based on the volume-averaging at the REV scale. The Darcy, the Brinkman–Darcy and the Forchheimer–Darcy equations are common models in the simulation of the flow through the porous media [1, 2].

Darcy’s law is valid for laminar flows, and the validity of this hypothesis depends upon the particle size of media. It has been found that flows through fine-grained soils are laminar whenever the Reynolds number is less than unity [2]. As a result, the flow is dominated by fluid viscous forces, such that the pressure gradient responsible for the flow is linearly proportional to the superficial velocity. Weak inertial flow, often named creeping flow in porous media, can be also described by Darcy’s law properly [3]. But, by increasing the pressure gradient, Darcy’s law may fail, as it does not account for the increased influence of inertial effects at the higher pressures.

The Darcy–Brinkman model is a governing equation for flows through porous media with an extra viscous term, namely the Brinkman term, added to the Darcy equation [4]. This equation is adequate for the simulation of high-porosity porous media and thus it enables the description of the fluid flow where velocities are high enough for the momentum transport by shear stress to be of importance [5]. This model is used to account for transitional flows between boundaries, but the validity of the Darcy–Brinkman model has been a subject of investigation in many applications [6].

The inertia effect can be very important for high velocity flows through porous media. In order to consider the effect of inertia, a quadratic velocity term (inertia term) was added to the Darcy’s equation by Forchheimer in 1914. This term is able to account for the non-linear behavior of the pressure gradient versus velocity. The resulting equation is known as the Darcy-Forchheimer equation and is solved in order to include non-Darcy effects [7]. Despite many researches on the suitability of this model [8, 9], the Forchheimer equation has made the object of several criticisms, questioning the ability of the quadratic velocity term (Forchheimer coefficient) to capture all regimes beyond the Darcy flow [10].

As mentioned above, the Brinkman’s equation is valid only for high porosity media and on the other hand, in such cases the validity of the Forchheimer’s equation is not clear. In order to overcome such problems, a generalized model, namely the Brinkman–Forchheimer model, has been proposed [11]. In this model, the viscous and inertial forces are considered in the momentum equation by a local volume averaging. The other models can be seen as limiting cases of the Brinkman–Forchheimer model, which has been successfully applied to solve transient flows in porous media [12–14].

In this paper, the Brinkman–Forchheimer model is coupled with a finite volume Lattice Boltzmann model (LBM) to simulate flows in porous media of practical interest. The LBM [15, 16] is based on a minimal form of Boltzmann’s kinetic equation in which a set of representative fluid particles move and interact on the nodes of a uniform lattice according to a synchronous stream-collide dynamics. Streaming is the free flight of the particles along the links of the lattice, whereas collisions are typically represented as a relaxation around a local equilibrium [17]. The simple form of the governing equations, the space-time locality, the straightforward parallelism, the easy grid generation and the capability of incorporating complex microscopic interactions are the main advantages of the LBM. Thanks to these advantages, this method has been successfully applied to a wide variety of flow problems across scales of motion, as turbulent flows in complex geometry, multiphase and multi-component flows, free surface flows, biological flows [17–24].

Porous flows on pore-scale made the object of very early LBM simulations [18, 25, 26] and still represent one of its main applications [27–29]. Recently, LBM has also been combined with the REV-scale approach to simulate fluid flows in porous media [11, 30–33]. In the REV-scale approach, the standard LBM is modified by including an additional term to account for the presence of a porous medium [12, 19]. The usual REV models are based on the Darcy, the Brinkman–Darcy and the Forchheimer–Darcy equations and therefore have some intrinsic limitations. Recently, the Brinkman–Forchheimer equation has been proposed for modeling fluid flows through porous media [12, 34].

The most used form of the LBM is based on the Bhatnagar–Gross–Krook (BGK) [35] approximation of the collision, which is a single relaxation time model. Though very robust, the LBGK is affected by linear and non-linear stability problems [36–39] for moderately low viscosities. Much progress has been made in this direction in the last two decades and several alternative options for the collision operator are available.

The so-called multi-time relaxation method [40–42], an optimized version of early LB models in scattering form, has been proposed by d’Humieres [41]. In this model, the collision step is performed in a moment space whereas the propagation step is done in the discrete velocity space. The MRT models are more stable than the standard BGK as they overcome some limitations, such as the fixed ratio between kinematic and bulk viscosities [43], but increase computational costs and still presents some stability problems [44, 45].

Another heuristic method, recently introduced [46, 47], is the so-called quasi-equilibrium method, which differs from MRT, as no collision is actually performed in the moment space, thus making it computationally more efficient. This method satisfies the H-theorem and features an additional free-tunable parameter, that allows enhanced stability by controlling the bulk viscosity, whenever the incompressible limit is the only concern [47].

The LBM can be also improved by constructing the collision integral on the basis of the entropy function, and by stabilizing the updates on the basis of the discrete-time H-theorem [48, 49]. The novelty of ELBM is represented by the definition of local equilibrium, which is computed by minimizing the H-function, under the constraint of local conservation laws. This makes the method thermodynamically consistent and the simulations non-linearly stable [48–50]. However, ELBM is known only on highly symmetric lattices (i.e. D3Q27) and, as for the MRT, implies a computational overhead [51].

The physical spatial structure of the lattice in the standard LB scheme is coupled to the velocity discretization, which results into a Lagrangian, exact treatment of advective propagation and hence, to virtually zero numerical diffusion. On the other hand, straightforward integration of the LBE is not possible on non-uniform meshes. This leads to difficulties in adapting the mesh in many practical applications with complex geometry. Furthermore, the use of locally refined meshes is mandatory for an efficient solution of CFD problems.

Recently, many studies have been dedicated to the extension of the standard LBM on non-uniform mesh. Among the others, we could cite the characteristic Galerkin finite element method for the discrete Boltzmann equation (CGDBE) [52] and the interpolation supplemented LBM [30], both giving good results with limited numerical dissipation. Imamura et al. [53] applied the local time step method to the generalized form of the interpolation supplemented LBM and obtained steady-state solutions with a higher computational efficiency.

Among recent advances to overcome the above limitations, a particularly valuable option is to change the solution procedure from the original ‘stream and collide’ lattice dynamics to a finite difference (FD), finite element (FE) and finite volume (FV) formulation.

Cao et al. [54] combined the first LBM and FD based on the central difference scheme in Cartesian coordinates. Their scheme was later extended to curvilinear coordinates with non-uniform grids [55].

Finite element methods allowed simulating complex and realistic geometries. Least-squares finite element (LSFE) method has shown a better stability and robustness in comparison with Taylor–Galerkin based FE schemes [56]. Li et al. [57] presented a new LSFE scheme on unstructured mesh to simulate flow in porous media with fourth order accuracy in space and second order accuracy in time.

The advection term in the FV-LBM is solved in an Eulerian framework, and the problem of treatment of the advective terms re-enters the solution procedure. This problem may be effectively addressed by suitably adapting the mesh resolution [58–60].

However, early FV-LBM methods [61–63] usually suffer from substantial numerical instability compared to the standard LBM models with improved stability [64, 66]. Also, the computational efficiency of the previous FV formulations seems to be only marginally competitive with standard methods. This stability problem may be overcome by suitably adapting the various schemes. Patil and Lakshmisha [67] proposed a FV formulation of LBM on triangular meshes based on Total Variation Diminishing (TVD) scheme. They validated their results for some benchmark problems and demonstrated that their model features a better stability than the scheme based on central discretization of the convection term. Also in [68] they enhanced the accuracy of their scheme to simulate unsteady flows. They used the quadratic least squares (QLS) procedure to extract the first-order derivatives of the distribution functions up to second-order accuracy and validated the results for flows over two circular cylinders in tandem and side-by-side.

In this paper, we further develop a stable finite volume formulation of the LBM to study the behavior of fluid flow through porous media. In this formulation, the combination of the finite volumes and weighting factors is carried out in the momentum fluxes [69]. Suitable application of these factors allows to improve stability and convergence. The effect of porous media is considered by introducing the porosity into the equilibrium distribution function, and incorporating viscous and inertial effects as momentum source terms (Brinkman–Forchheimer equation) in the Boltzmann equation.

The outline of this paper is as follows. In Sect. 2, we give a description of the lattice Boltzmann method for porous media, using the Brinkman–Forchheimer model. Section 3 describes the mathematical formulation of the proposed scheme. In Sect. 3, we discuss the computational results and comparisons with previous studies and, finally in Sect. 4, we present some closing remarks.

2 Numerical Model

In the presence of an external force \({\mathop {F}\limits ^{\rightharpoonup }}_i\), the LBM can be viewed as a special discrete scheme for the Boltzmann equation with discrete velocities. The usual framework starts from an evolution equation for particle distribution functions of the form:

$$\begin{aligned} f_i \left( {\mathop {x}^{\rightharpoonup }}+ {\mathop {e}\limits ^{\rightharpoonup }}_{i} \Delta t,t+\Delta t \right) -f_i \left( {x,t} \right) =-\frac{1}{\tau }\left( {f_i -f_i^{eq} } \right) +\Delta t\, {\mathop {F}\limits ^{\rightharpoonup }}_i, \end{aligned}$$
(1)

where \(\tau \) is the relaxation time, \(\Delta t\) is the time step, \({\mathop {e}\limits ^{\rightharpoonup }}_i\) is the lattice velocity vector in the i-th direction,\(f_i \) is the probability distribution for the particles speed along the i-th direction and \(f_i^{eq}\) is the corresponding equilibrium.

The first term of the right hand-side of Eq. (1) is the so-called Bhatnagar–Gross–Krook (BGK) operator [35], which describes particles collision through a single time relaxation \((\tau _f)\) to local equilibrium \((f_i^{eq})\).

The corresponding kinematic viscosity is calculated as \(\nu =c_s^2 \tau \) [70–72] and the discrete velocities for the so-called D2Q9 lattice are given by \({\mathop {e}\limits ^{\rightharpoonup }}_{0}=0\) and \({\mathop {e}\limits ^{\rightharpoonup }}_i =\lambda _i \left( {\cos \theta _i ,\sin \theta _i } \right) \) with \(\lambda _i =1,\, \theta _i ={\left( {i-1} \right) \pi }/2\) for \(i=1\sim 4\) and \(\lambda _i =\sqrt{2},\,\theta _i ={\left( {i-5} \right) \pi }/2+\pi /4\) for \(i=5\sim 8\) [16]. The order numbers \(i=1\sim 4\) and \(i=5\sim 8\) represent the Cartesian and the diagonal directions of the lattice, respectively. The force vector \({\mathop {F}\limits ^{\rightharpoonup }}_i\) in Eq. (1) causes an additional momentum change extra to the momentum exchange due to collisions.

2.1 The LBM for Porous Media

The forcing term \({\mathop {F}\limits ^{\rightharpoonup }}_i\) in Eq. (1) represents the total body force including viscous diffusion, inertia related to the presence of a porous medium, and external forces. The suitable choice for \({\mathop {F}\limits ^{\rightharpoonup }}_i\) to obtain the correct equations of hydrodynamics is as follows [12]:

$$\begin{aligned} {\mathop {F}\limits ^{\rightharpoonup }}_i =\omega _i \rho \left( {1-\frac{1}{2\tau }} \right) \left[ {\frac{3{\mathop {e}\limits ^{\rightharpoonup }}_i \cdot {\mathop {E}\limits ^{\rightharpoonup }}}{c^{2}}+\frac{9\left[ {\left( {\mathop {u}\limits ^{\rightharpoonup }}\cdot {\mathop {e}\limits ^{\rightharpoonup }}_i \right) \,\left( {{\mathop {E}\limits ^{\rightharpoonup }}\cdot {\mathop {e}\limits ^{\rightharpoonup }}_i } \right) } \right] }{\varepsilon \, c^{4}}-\frac{3{\mathop {u}\limits ^{\rightharpoonup }}\cdot {\mathop {E}\limits ^{\rightharpoonup }}}{\varepsilon \,c^{2}}} \right] _{i=1\sim 9} , \end{aligned}$$
(2)

where \({\mathop {u}\limits ^{\rightharpoonup }}\) is the fluid velocity, \(\varepsilon \) is the porosity and \({\mathop {E}\limits ^{\rightharpoonup }}\) is a forcing term accounting for the presence of a porous medium and for other external force fields. This term can be calculated through the Ergun’s equation, as follows [73]:

$$\begin{aligned} {\mathop {E}\limits ^{\rightharpoonup }}=- \frac{\varepsilon \nu }{K}{\mathop {u}\limits ^{\rightharpoonup }}- \frac{\varepsilon \,F_\varepsilon }{\sqrt{K}}\left| {{\mathop {u}\limits ^{\rightharpoonup }}} \right| {\mathop {u}\limits ^{\rightharpoonup }} +\varepsilon \, {\mathop {\hbox {G}}\limits ^{\rightharpoonup }} , \end{aligned}$$
(3)

where \(F_\varepsilon ={1.75}{\bigg /}{\sqrt{150\varepsilon ^{3}}}\) is the geometric function, \({\mathop {G}\limits ^{\rightharpoonup }}\) is the acceleration due to the body force, and \(K\) is the porous media permeability. The latter is calculated as \(K=\hbox {Da}\cdot H^{2}\), being \(H\) the characteristic length and Da the Darcy number, a dimensionless quantity describing the ability of a fluid to flow through porous media. The permeability is traditionally assumed to be a constant material property and a function of the porous material’s pore shape and size. Physically, the permeability can be perceived as an inverse effective resistance of the fluid flow.

It is worth noting that the total body force \({\mathop {E}\limits ^{\rightharpoonup }}\) in Eq. (3) encompasses the viscous diffusion (1st term) and inertia due to the presence of a porous medium (2nd term) and an external force (3rd term). The equilibrium density distribution functions, \(f_i^{eq}\), for a \(\hbox {D}_{2}\hbox {Q}_{9}\) lattice-speed model are given by:

$$\begin{aligned} f_i^{eq} =w_i \rho \,\left[ {1+\frac{3}{2}\left( {{\mathop {e}\limits ^{\rightharpoonup }}_i\cdot {\mathop {u}\limits ^{\rightharpoonup }}} \right) +\frac{9}{2\varepsilon }\left( {{\mathop {e}\limits ^{\rightharpoonup }}_i\cdot {\mathop {u}\limits ^{\rightharpoonup }}} \right) ^{2}-\frac{3}{2\varepsilon }\left| {\mathop {u}\limits ^{\rightharpoonup }}\right| ^{2}} \right] _{i=1\sim 9}, \end{aligned}$$
(4)

where \(\rho =\sum _i {f_i } \) is the macroscopic density and \(w_i\) are the weighting factors, equal to 4/9 for \(i=0\), 1/9 for \(i=1\sim 4\) and 1/36 for \(i=5\sim 8\). Accordingly, the pressure is calculated as \(p={\rho \,c_s^2 }/\varepsilon \) and the macroscopic fluid velocity is defined as:

$$\begin{aligned} {\mathop {u}\limits ^{\rightharpoonup }} =\sum _i {{{\mathop {e}\limits ^{\rightharpoonup }}_i f_i }/\rho } +\frac{\delta _t }{2}{\mathop {E}\limits ^{\rightharpoonup }}. \end{aligned}$$
(5)

Since \({\mathop {E}\limits ^{\rightharpoonup }}\) contains the velocity term, Eqs. (3) and (5) represent a 2-equations non-linear system in \({\mathop {E}\limits ^{\rightharpoonup }}\) and \({\mathop {u}\limits ^{\rightharpoonup }}\). However, this nonlinearity may be ignored by the introduction of an auxiliary velocity, \({\mathop {\vartheta }\limits ^{\rightharpoonup }}\), and by explicitly calculating the velocity \({\mathop {u}\limits ^{\rightharpoonup }}\) as follows [12]:

$$\begin{aligned} {\mathop {u}\limits ^{\rightharpoonup }} =\frac{{\mathop {\vartheta }\limits ^{\rightharpoonup }}}{c_0 +\sqrt{c_0^2 +c_1 \left| {{\mathop {v}\limits ^{\rightharpoonup }}} \right| }}, \end{aligned}$$
(6)

where \(c_0 =0.5\left[ {1+{\varepsilon \delta _t \nu }/{2K}} \right] \), \(c_1 =0.5{\varepsilon \delta _t F_\varepsilon }/{\sqrt{K}}\) and \({\mathop {\vartheta }\limits ^{\rightharpoonup }}\) defined as:

$$\begin{aligned} {\mathop {\vartheta }\limits ^{\rightharpoonup }}=\frac{1}{\rho }\sum \nolimits _i {{\mathop {e}\limits ^{\rightharpoonup }}_{i} f_i } +\frac{\delta _t }{2}{\mathop {G}\limits ^{\rightharpoonup }} \varepsilon . \end{aligned}$$
(7)

The standard lattice Boltzmann equation is derived from Eq. (1) upon explicit time marching along the characteristics \(\Delta {\mathop {x}\limits ^{\rightharpoonup }}_{i} -{\mathop {e}\limits ^{\rightharpoonup }}_{i} \Delta t=0\) leading to a fully discrete formulation in which space and time are linked one-to-one through the discrete velocities. In other words, the particles always land on a lattice site, leading to a very simple and highly efficient synchronous computational scheme. As discussed in the introduction, the downside is the inability to cluster grid points around regions where a higher resolution is required. This is precisely the limitation lifted by the finite volume formulation presented in the following section.

2.2 Finite Volume Formulation

In this section, the cell-centered finite volume formulation of the Eq. (1) on an equilateral mesh system is briefly described. The lattice Boltzmann equation in its continuum form reads as follows [71]:

$$\begin{aligned} \frac{\partial f_i }{\partial t}+{\mathop {e}\limits ^{\rightharpoonup }}_{i}\cdot \nabla f_i =-\frac{1}{\tau }\left( {f_i -f_i^{eq} } \right) , \end{aligned}$$
(8)

The integration of the collision term is performed through the following formulation:

$$\begin{aligned}&-\int \limits _{abcd} {\frac{1}{\tau }(f_i -f_i^{eq} )dA} \nonumber \\&\quad =-\frac{A_{I,J} }{\tau }\left[ \frac{1}{4}\left[ {f_i^{ne} } \right] _{I,J} + \frac{1}{8}\left\{ { \left[ {f_i^{ne} } \right] _{I+1,J} +\left[ {f_i^{ne} } \right] _{I,J+1} +\left[ {f_i^{ne} } \right] _{I-1,J} +\left[ {f_i^{ne} } \right] _{I,J-1} } \right\} \nonumber \right. \\&\quad \quad + \left. \frac{1}{16}\left\{ { \left[ {f_i^{ne} } \right] _{I+1,J-1} +\left[ {f_i^{ne} } \right] _{I+1,J+1} +\left[ {f_i^{ne} } \right] _{I-1,J+1} +\left[ {f_i^{ne} } \right] _{I-1,J-1} } \right\} \right] \end{aligned}$$
(9)

where \(A_{I,J} \) is the area of cell and \(f_i^{ne} =f_i -f_i^{eq} \) is the non-equilibrium component of the distribution function. After applying an upwind scheme, the convective fluxes may be written as follows [73]:

$$\begin{aligned} \int \limits _{abcd} {{\mathop {e}\limits ^{\rightharpoonup }}_{i} .\nabla f_i\, dA}&\approx {\mathop {e}\limits ^{\rightharpoonup }}_{i} \cdot N_{ab} \left( {\zeta _{ab} \left[ {f_i } \right] _{I,J} +\left( {1-\zeta _{ab} } \right) \,\left[ {f_i } \right] _{I+1,J} } \right) \nonumber \\&+{\mathop {e}\limits ^{\rightharpoonup }}_{i} \cdot N_{bc} \left( {\zeta _{bc} \left[ {f_i } \right] _{I,J} +\left( {1-\zeta _{bc} } \right) \,\left[ {f_i } \right] _{I,J+1} } \right) \nonumber \\&+{\mathop {e}\limits ^{\rightharpoonup }}_{i} \cdot N_{cd} \left( {\zeta _{cd} \left[ {f_i } \right] _{I,J} +\left( {1-\zeta _{cd} } \right) \,\left[ {f_i } \right] _{I-1,J} } \right) \nonumber \\&+{\mathop {e}\limits ^{\rightharpoonup }}_{i}\cdot N_{da} \left( {\zeta _{da} \left[ {f_i } \right] _{I,J} +\left( {1-\zeta _{da} } \right) \,\left[ {f_i } \right] _{I,J-1} } \right) , \end{aligned}$$
(10)

where \(N_k =\left( {\Delta y\, {\mathop {i}\limits ^{\rightharpoonup }}-\Delta x\hbox { }{\mathop {j}\limits ^{\rightharpoonup }} } \right) _k \) is the outward unit vector normal to the edge, \(k = ab, bc, cd\) and \(da\) is the side of cell. The parameters \(\zeta _{ab} ,\zeta _{bc} ,\zeta _{cd} \) and \(\zeta _{da} \) are weighting factors defined as follows [69]:

$$\begin{aligned} \zeta _{ab} =\frac{\Delta p_{ab} }{\sum {p_{horizental} } }, \,\,\zeta _{bc} =\frac{\Delta p_{bc} }{\sum {p_{vertical} } }, \,\,\zeta _{cd} =\frac{\Delta p_{cd} }{\sum {p_{horizental} } }, \,\,\zeta _{da} =\frac{\Delta p_{da} }{\sum {p_{vertical} } }, \end{aligned}$$
(11)

being \(\sum {p_{horizental} } =\sum {\left( {p_{I+1,J} +2p_{I,J} +p_{I-1,J} } \right) } \), \(\sum {p_{vertical} } =\sum {\Big ( {p_{I,J+1+}}} {{2p_{I,J}}}\) \( {+p_{I,J-1} \Big )} \) and \(\Delta p_{ab} =p_{I+1,J} -p_{I,J} \), \(\Delta p_{bc} =p_{I,J+1} -p_{I,J} \), \(\Delta p_{cd} =p_{I,J} -p_{I-1,J} \), \(\Delta p_{da} =p_{I,J} -p_{I,J-1} \) The heuristic meaning of these coefficients is to enhance transport downhill the pressure gradient and reduce it uphill and they allow improving stability and computational efficiency, without numerical diffusion, as demonstrated in previous works [72, 74].

It is important to note that the employed approach to numerically solve Eq. (8) is a cell-centred finite-volume scheme based on a space discretization into quadrilateral elements. The scheme is here employed for a structured grid, but the method could be easily extended to unstructured grids, as for any finite volume scheme. Obviously unstructured grids would require a connectivity list for each vertex to identify the mesh elements.

For hydrodynamic boundary conditions, additional D2Q9 lattices at the edge of each boundary cell are introduced as described in [72]. Then, boundary nodes are treated like internal nodes, except that the fluxes through the boundary edges are also taken into account.

Physical boundaries of the computational domain are defined to be aligned with the lattice grid lines (on-grid formulation). Assuming that the velocity on the inlet boundary (\(u_{in}, v_{in}=0\)) is known, the inlet boundary conditions at \(I=1\) are given by \(f_1 =f_3 +{2u_{in} }/3\), \(f_5 =f_7 +0.5\left( {f_4 -f_2 } \right) +{u_{in} }/6\) and \(f_8 =f_6 +0.5\left( {f_2 -f_4 } \right) +{u_{in} }/6\) where \(\rho _{\mathrm{in}} ={\left[ {f_0 +f_2 +f_4 +2\left( {f_3 +f_6 +f_7 } \right) } \right] }/{\left( {1-u_{in} } \right) }\), as proposed by Zou and He [74]. At the outlet boundary i.e. \(I=N_{x}\), the distribution functions are extrapolated as follows: \(f_i \left( {N_x ,J} \right) =2f_i \left( {N_x -1,J} \right) -f_i \left( {N_x -2,J} \right) \).

Wall boundary conditions, including the corners, are implemented by applying the so-called bounce-back rule, which states that the component of the distribution function that would propagate into the solid node is bounced back and ends up back at the fluid node, but pointing in the opposite direction. Therefore, the unknown distribution functions are calculated as \(f_{6}=f_{8}, f_{4}=f_{2}\) and \(f_{7}=f_{5}\). For further details about the mathematical formulation and boundary conditions we refer the reader to our previous works [72, 75].

3 Results and Discussion

At first, in order to validate the proposed scheme, we apply the model to three fully porous problems, namely: the Poiseuille flow, the Couette flow and the lid driven cavity flow. In all cases, the results are compared to numerical data available in the literature. Then we perform simulations for flows through partially porous channels.

3.1 Fluid Flow in Fully Porous Conduits

3.1.1 Porous Poiseuille Flow

One of the basic benchmark hydrodynamics problems is the Poiseuille flow, in which a fluid laterally flows through a plane duct with constant cross section. Here, we consider a channel with height \(H\) and aspect ratio \(L/H=8\) where \(L\) is the length of channel. The lattice used is a \(640\times 80\) square mesh. The channel filled with a porous media of porosity \(\varepsilon =0.1\). The Reynolds number is defined by \(Re={Hu_0 }/\nu \), where \(u_{0}\) is the characteristic velocity. An important parameter which influences the accuracy and stability of the solution is the compressibility error which is related to the fact that the LBE recovers the Navier–Stokes in the limit of weakly-compressible flows (\(\mathrm{{Ma}}\ll 1\)). This means that it describes a slightly compressible regime to solve the pressure equation of the fluid. Compressibility effects are kept under control by choosing the Mach number, defined as \(u_{0}/c_{s}\), below 0.1. The selected computational parameters for the simulations are listed in Table 1. The convergence criterion is set to \(\max \left| {{\left( {u^{n+1}-u^{n}} \right) }/{u^{n}}} \right| \le 10^{-6}\), where superscripts \(n\) and \(n+1\) indicate old and new time levels, respectively.

Table 1 Selected computational parameters for the channel flow simulation
Full size table

Figure 1 compares present numerical results with literature data given in [12] at four different Reynolds numbers, Re = 0.01, 10, 50 and 100, and at \(\hbox {Da} =10^{-5}\). The velocity profiles are normalized by \(u_{Br}\), which is the maximum velocity of the flow along the centerline in the Brinkman model [12]:

$$\begin{aligned} u_{Br} =\frac{G_x K}{\nu }\left[ {1-\left( {\cosh \left( {\frac{rH}{2}} \right) } \right) ^{-1}} \right] \end{aligned}$$
(12)

where \(r=\sqrt{{\nu \varepsilon }/{K\nu _e }}\). Here, \(\nu _e \) is the effective viscosity, which accounts for flows through porous media where the grains are porous themselves. In the present simulations, the effective viscosity is assumed to be equal to \(\nu \). In the whole Reynolds number range under consideration, we observe an excellent agreement of present results with literature data [12], obtained with a finite difference solution of the Navier–Stokes equations and a discrete LBM approach, respectively.

Fig. 1
figure 1

Stream-wise velocity profiles of the porous Poiseuille flow at \(\hbox {Da} =10^{-5}\) and different Reynolds numbers, Re = 0.01, 10, 50 and 100. Results are compared with finite difference and standard LBM solutions presented in [12]

Full size image

Figure 2 represents the velocity profiles for a porous Poiseuille flow for different Darcy numbers, \(\mathrm{{Da}}= 10^{-3}\), \(10^{-4}\) and \(10^{-6}\), and at \(\mathrm{{Re}} =0.1\), compared with the finite difference solution reported in [12]. It is observed that, by increasing the Darcy number at a constant porosity, the value of the permeability (K) is increased, and the velocity profile approaches a parabolic shape.

Fig. 2
figure 2

Stream-wise velocity profiles of the porous Poiseuille flow at Re = 0.1 and different Darcy numbers, \(\mathrm{{Da}}= 10^{-3}\), \(10^{-4}\) and \(10^{-6}\). Results are compared with the finite difference solution proposed in [12]

Full size image

3.1.2 Porous Couette Flow

The numerical model is here tested against the Couette flow, an axial laminar flow induced in the space between parallel plates that move relative to one another. In the present case, the flow is driven by the upper plate moving in the stream-wise direction with a constant velocity \(u_{0}\) instead of constant force. Periodic boundary conditions are applied to the entrance and exit of the channel and the resulting Reynolds number is defined as \(Re={Hu_0 }/\nu \), where \(H\) is the distance between the two parallel plates. The computations are based on a \(640\times 80\) lattice in all cases and the aspect ratio is the same used in Poiseuille flow. The other main flow parameters are set as \(\varepsilon =0.4\), Da = 0.01 and tests have been carried out at four different Reynolds numbers, i.e. 0.1, 5, 10 and 100. The other computational are the same of those reported in Table 1.

Without considering the Forchheimer (inertia) term, the governing equations of the flow at steady state have the following analytical solution [12]:

$$\begin{aligned} u=u_0 \exp \left[ {r\left( {\frac{y}{H}-1} \right) } \right] \frac{\sinh \left( {\varphi \cdot y/H} \right) }{\sinh \left( \varphi \right) }, \quad v=v_0 \end{aligned}$$
(13)

where \(r\) and \(\varphi \) are calculated as:

$$\begin{aligned} r=\frac{\hbox {Re}}{2\varepsilon \nu /{\nu _e }}, \quad \varphi =\frac{1}{2\varepsilon \nu /{\nu _e }}\sqrt{\hbox {Re}^{2}+\frac{4\varepsilon \nu /{\nu _e }}{\hbox {Da}}} \end{aligned}$$
(14)

Figure 3 shows the normalized stream-wise velocity profiles at the three different Reynolds numbers, Re = 0.1, 5 and 100, compared with the analytical solution and, again, a very good agreement is observed.

Fig. 3
figure 3

Velocity profiles of the porous Couette flow at Da = 0.01 and different Re numbers, Re = 0.1, 5 and 100. Results are compared with the finite difference solution proposed in [12]

Full size image

The same flow test has been also performed using the Brinkman–Forchheimer model, namely by adding the Forchheimer term to the force term. Figure 4 presents the velocity profiles of the Couette flow, calculated by the present method at Re = 10, \(\varepsilon =0.1\) and three different Darcy numbers, \(10^{-2}\), \(10^{-3}\), and \(10^{-5}\). Good agreement is found between the FV-LBM and the finite difference solution presented in [12]. The graph reported in Fig. 4 clearly shows that, by decreasing the Darcy number, the steadiness of the velocity profiles is enhanced.

Fig. 4
figure 4

Velocity profiles of the porous Couette flow at Re = 10 and different Darcy numbers. Results are compared with the finite difference solution proposed in [12]

Full size image

By definition the Darcy number decreases when the permeability is reduced \((\hbox {Da}=K/H^{2})\). As we mentioned before, permeability measures the ability of the porous media to allow fluid flow through it. Therefore, if the pores are very small, or if they are poorly connected, the permeability is low and the fluid does not flow through easily. Therefore, by decreasing the permeability and consequently the Darcy number, the collisions between the fluid particles and the pores increase. In other words, the pores act as a damping force on the fluid flow velocity. Thus, by decreasing the Darcy number, the porous layer become denser, more pressure drop builds up, the velocity profile becomes steadier and shear stress in the fluid is limited to the fluid layers near the moving plate, as at \(\hbox {Da}=10^{-5}\) most part of fluid layers remain static.

3.1.3 Porous Lid-driven Cavity Flow

The lid driven cavity flow is a steady laminar incompressible flow that sets up in a square box where one of the walls (i.e. bottom wall) translates with constant velocity. It is a standard benchmark problem in which the non-linear component of the Navier–Stokes equation plays a major role, as, despite the simplicity of the geometry, the flow has a complicated behavior with counter rotating vortices appearing at the corners of the cavity. In this section we apply the present scheme to a 2D lid-driven square of side \(H\) filled up with a porous media. The upper wall of the cavity moves from left to right with a constant velocity \(u_{0}\) and the other walls are fixed. Fixing the viscosity and the cavity shape, the complexity of the flow depends only on the Reynolds number calculated in terms of cavity width and of moving plate speed, \(\hbox {Re}={Hu_0 }/\nu \).

As a first validation step, we simulated the cavity flow with \(\varepsilon =0.99\), which practically corresponds to the standard non-porous cavity flow, \(\hbox {Da}=10^{-4}\) and Re = 100 and 1,000. The comparisons between FV-LBM solutions with the benchmark solutions of Ref. [76] are plotted in Fig. 5. In this figure, the stream-wise and span-wise velocity components through the cavity center agree well with the benchmark solutions.

Fig. 5
figure 5

a Stream-wise and b span-wise velocity components through the cavity center with \(\varepsilon =0.99\), \(\hbox {Da}=10^{-4}\) and Re = 100 and 1,000. Results are compared with Ghia et al. [76]

Full size image

Then we perform simulations with porosity \(\upvarepsilon =0.1\), Re = 10 and two different Darcy numbers, \(10^{-2}\) and \(10^{-4}\). Figure 6 compares the present velocity profiles through the cavity center with the finite difference solution reported in [12]. The results show that, by decreasing the Darcy number, the boundary layer thickness near the moving lid decreases, and the vortex in the cavity becomes weaker.

Fig. 6
figure 6

a Stream-wise and b span-wise velocity components through the cavity center with \(\varepsilon =0.1\), \(\hbox {Da} =10^{-2}\) and \(10^{-4}\) and Re = 10. Results are compared with the finite difference solution proposed in [12]

Full size image

3.2 Fluid Flow in Partially Porous Conduits

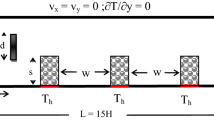
The proposed numerical method is here applied to simulate the flow in a selected partially porous conduit, represented in Fig. 7, together with its coordinate system. The flow enters the channel with a uniform velocity profile, \(u_{0}\). The channel aspect ratio is set to \(L/H=8\), where \(L\) and \(H\) are the channel length and width, respectively. The Reynolds number is defined as \(\hbox {Re}={Hu_0 }/\nu \) and a homogeneous porous layer of width \(y_{p}\) is attached to the walls. This type of configuration can be selected as a model for fractured porous aquifers. All aquifers can be regarded to fall on a continuum between porous media systems and conduit systems. In homogeneous porous media aquifers, groundwater flows through the gaps between the sand grains. In purely fractured media, groundwater flows only in conduits, and the aquifer matrix (porous media) between the conduits is impermeable and has no porosity. But in fractured porous aquifers, the water flows both in the open channel and in the aquifer matrix [77]. In reality, most fractured rock aquifers are of the fractured porous media type.

Fig. 7
figure 7

Schematic of partially porous conduits with homogenous porous layer attached the walls

Full size image

Here, similarly to many groundwater flow models, we assume that the porous media is homogeneous and that fractures are planar and parallel [77]. While these assumptions are unlikely to hold in reality, they provide a useful starting point for our understanding of groundwater behavior in fractured rocks.

3.2.1 Mesh Refinement

Numerical test were performed to determine the grid size needed to resolve the flow field and generate grid-independency solutions for the present problems. Several tests were performed using four meshes of three types, i.e. uniform square grid with \(1,440\times 180\) nodes, uniform rectangular grid with \(850\times 90\) nodes, mapped or non-uniform rectangular grids with \(850\times 90\) nodes, shown in Fig. 8, and another uniform square grid with \(720\times 90\) nodes. Here, an algebraic mapping [78] has been used to cluster the nodes around the walls. This type of mapped grid has been chosen to properly capture the boundary layer effects, as well as the porous media layer effects for the selected configuration. More details about the selected grid sizes are presented in Table 2. The results obtained on the uniform square grid with \(1,440\times 180\) nodes are selected as the reference case and used to benchmark the results obtained with the other meshes.

Fig. 8
figure 8

Mapped rectangular grid with \(850\times 90\) nodes

Full size image
Table 2 Details of the four grids employed in the mesh test
Full size table

Figure 9 shows the profiles of non-dimensional stream-wise velocity profile in partially porous channels at \(x=0.15H\) and \(x=H\) using three different meshes with Re = 100, \(\hbox {Da}=10^{-4}\), \(y_{p}=0.2H\) and \(\varepsilon =0.9\). As shown in the figure, the numerical results with reference square and mapped rectangular mesh grids agree well with each other, as the maximum velocity error is less than 1.4 %, against a 5.8 % deviation obtained with the uniform rectangular grid in both selected stations. On the other hand, by using the mapped grid with about 70 % nodes less than the uniform square grid, almost the same result is obtain. To avoid crowding the graph, the plots of the \(720\times 90\) uniform square grid are not reported in Fig. 9, but the maximum error was calculated around 6 % in comparison with the reference case in both stations.

Fig. 9
figure 9

Stream-wise velocity profiles in the channel with porous media attached to the walls with Re = 100, \(\hbox {Da}=10^{-4}\), \(y_{p}=0.2H \) and \(\varepsilon =0.9\) a \(x=0.15H\) and b \(x=H\)

Full size image

Figure 10 shows the convergence of the relative velocity error estimates in log scale for the selected grid sizes based on the following equation:

$$\begin{aligned} E_v =\frac{\sum \limits _{I,J} {\left| {\sqrt{\left( {{\mathop {u}\limits ^{\rightharpoonup }}_{I,J}^{2} +{\mathop {v}\limits ^{\rightharpoonup }}_{I,J}^2 } \right) ^{n+1}}-\sqrt{\left( {{\mathop {u}\limits ^{\rightharpoonup }}_{I,J}^{2} +{\mathop {v}\limits ^{\rightharpoonup }}_{I,J}^2 } \right) ^{n}}} \right| } }{\sum \limits _{I,J} {\left| {\sqrt{\left( {{\mathop {u}\limits ^{\rightharpoonup }}_{I,J}^2 +{\mathop {v}\limits ^{\rightharpoonup }}_{I,J}^2 } \right) ^{n}}} \right| } } \end{aligned}$$
(15)

where \(n\) and \(n+1\) indicate the reference and under test conditions, respectively. Also \({\mathop {u}\limits ^{\rightharpoonup }}\) and \({\mathop {v}\limits ^{\rightharpoonup }}\) are the stream-wise and the span-wise velocity component, respectively. The error decay clearly shows that the mapped grid provides almost the same accuracy of the reference grid, and it is then used in the following simulations.

Fig. 10
figure 10

Convergence of error in log scale for the selected grids

Full size image

Numerical tests are also performed to determine the allowable value of the grid size aspect ratio, defined as \({\hbox {AR}=\Delta x}/{\Delta y_{\min } }\), for the mapped rectangular grid. For a first set of simulations, we employed six types of meshes, whose characteristics are reported in Table 3. The number of nodes in vertical \((y)\) direction is equal to 90 for all the tested meshes, in order to keep constant the distance of the nodes in the y-direction, \(\Delta y_{\min } \). Again, the result obtained on the uniform square mesh with \(1,440\times 180\) nodes is used to calculate the maximum velocity error \({\left( {u-u_{ref} } \right) }/{u_{ref} }\) and to benchmark the results. The numerical results in terms of maximum and relative velocity error are reported in Table 3, which clearly shows that, by increasing the aspect ratio, the velocity error increases. Note that the velocity profile for AR = 3 is not completely smooth and the simulation diverged for \(\mathrm{{AR}}>3\).

Table 3 Mesh refinement test results for the mapped rectangular grid
Full size table

It is important to note that the limitation to an AR\(<\) 3 is due to the fact that, by keeping constant \(\Delta y_{\min }\), an increase in the AR produces a reduction of the number of nodes, as clearly shown in the first column of Table 3. Therefore, other numerical tests have been performed with a variable AR and a constant number of nodes (144,000). In this case we could limit the maximum velocity error to about 1 % up to an AR slightly lower than 4 and we could reach an AR as high as 6. The results are summarized in Table 4.

Table 4 Aspect ratio analysis results for the different grids with constant number of elements (=144,000 nodes)
Full size table

Being finite volume schemes relatively new in the LB framework, this particular scheme has been developed and successfully demonstrated for isothermal fluid dynamics only recently [68, 71, 73]. Several theoretical and practical issues still need to be addressed and a fair comparison with the standard LBM scheme is not trivial and beyond the scope of the present paper. However, as regards the computational efficiency, the present method is at least one order of magnitude computationally more expensive than the standard scheme. In fact, on a single-node basis, streaming and collision steps are no more local and the maximum time step for a stable computation is much lower, given that the time step is equal to the spatial resolution in the traditional LBM. On the other hand the above results suggest that this gas could be partially filled up as long as the geometrical complexity increases, where non uniform grids would require fewer nodes for a given spatial resolution. A combination of the present method with the standard LBM would also be possible to exploit the advantages of both approaches.

3.2.2 Fractured Homogenous Porous Conduit

As pointed out before, the porous media adds extra flow resistance, drag and friction between the flow and solid surfaces, which mainly depends on flow velocity and permeability. Figure 11 shows the normalized developing stream-wise velocity profile for \(\hbox {Da}=10^{-4}\), \(y_p =0.2H\), \(\varepsilon =0.2\) and Re = 100. So, due to the mentioned forces, the magnitude of the stream-wise velocity is relatively low in the porous layer and the slowdown of the flow in the porous media enhances the fluid velocity in the clear region. The magnitude of the axial velocity in the porous layer decreases along the conduit, especially at the fully developed region. Here, the starting point of fully developed region was considered as a point in the channel centerline in which the velocity reaches 99 % of the velocity at the outlet. The region after this point is named fully developed region.

Fig. 11
figure 11

Stream-wise velocity profile for \(\hbox {Da}=10^{-4}\), \(y_{p}=0.2H\), \(\varepsilon = 0.2\), and Re = 100

Full size image

Figure 12 compares the normalized stream-wise velocity profiles at fully developed region for two different porosities, 0.2 and 0.9, at Re = 100. According to this figure, the velocity is strongly influenced by the porous substrate porosity. By increasing the porosity, the resistance exerted by the insert decreases and the velocity profile is similar to that one found between two parallel plates. But by decreasing the porosity, eventually the insert acts like an impermeable and the velocity magnitude increases in the clear region.

Fig. 12
figure 12

Stream-wise velocity profiles at fully developed region for two different porosities

Full size image

The effect of the Darcy number on the fully developed stream-wise velocity is shown in Fig. 13. By increasing the Darcy number, the ease with which the fluid flows through the porous layer increases as well and the velocity in the porous layer is enhanced. Consequently, the peak of the velocity decreases and the profiles tend to assume a parabolic shape in the fully clear channel.

Fig. 13
figure 13

Stream-wise velocity profiles at fully developed region for different Darcy numbers and \(y_p =0.2H\)

Full size image

3.2.3 Fractured Non-homogenous Porous Conduit

All porous aquifers exhibit some degree of heterogeneity, in which a systematic variation in the size of the sand grains leads to the existence of preferential flow zones. In many cases, the degree of heterogeneity is relatively low, and does not need to be explicitly considered in groundwater investigations [77]. Here, in order to consider the minimum degree of heterogeneity of a porous layer, we add a non-homogeneous layer with random porosity as shown in Fig. 14. The first layer has constant thickness \((y_{p1}=0.1H)\), low porosity \((\varepsilon _{p1} =0.2)\) and low permeability \((\hbox {Da}_{p1}=10^{-5})\). This part of porous layer can be considered as an aquitard layer, which is a partly permeable geologic formation and has very low porosity, thus transmitting water at a slow rate.

Fig. 14
figure 14

Schematic of the partially porous conduit with homogenous and non-homogenous layers

Full size image

The permeability for the second non-homogenous porous layer has been considered equal to \(\hbox {Da}_{p2}=10^{-4}\) and the range of porosity is set to \(0.2<\varepsilon _{p2} <0.5\). This layer may feature an aquiclude which is composed of different materials such as rocks or sediments that act as a barrier to the groundwater flow.

Figure 15 shows the gradual development of the velocity at different stations through the channel with \(y_{p1}=y_{p2}=0.1 \,H\). By approaching the fully developed region, the velocity magnitude in the porous layers decreases whereas it increases in the clear region. Also, it is clear that the porous layers, especially the first one, play a negligible role in the fluid transport.

Fig. 15
figure 15

Behavior of the velocity profile through the channel with two porous layers

Full size image

In order to show the effect of random porosity, the velocity profiles, for \(y_{p2}=0.3H\) and Re = 100, at \(x=0\) and \(x=0.1H\), are reported in Fig. 16 and the random behavior of the velocity profile in the second layer is clearly visible.

Fig. 16
figure 16

Velocity profiles for \(y_{p2}=0.3H\) and Re = 100, a inlet and b \(x/H=0.1\)

Full size image

The effect of non-homogenous porous layer thickness on the fluid flow is also investigated. Figure 17 shows the velocity profiles for \(y_{p1}=0.1H\) and three different non-homogenous layer thicknesses i.e. \(y_{p2}=0.1H\), \(y_{p2}=0.2H\) and \(y_{p2}=0.3H\) at \(x=0.5H\). By increasing the porous layer thickness, the peak value of the velocity in the clear region increases. The random porosity produces a non-symmetric speed profile, as clearly visible especially in the thicker layer.

Fig. 17
figure 17

Fully developed velocity profiles with different non-homogenous porous layer thickness

Full size image

3.2.4 Layered Porous Conduit

Here we consider a layered fully porous channel of the same geometry of the one characterized in the previous section, except for the central layer, which is here filled up with a porous media with \(\varepsilon _s =0.6\) and \(\hbox {Da}_\mathrm{s}=10^{-3}\). The parameters for other layers are the same as described before, i.e. for the first layer: \(y_{p1}=0.1H, \varepsilon _{p1} =0.2\) and \(\hbox {Da}_{p1}=10^{-5}\); and for the second layer: \(y_{p2}=0.3H, 0.2<\varepsilon _{p2} <0.5\) and \(\hbox {Da}_{p2}=10^{-4}\). This configuration can represent a multi-layer aquifer which is usual in many real aquifer systems. So, we can consider the first layer as an aquiclude layer with very low permeability and the second layer as a heterogeneous aquitard layer with low permeability. So, the heterogeneous layer and also the core layer with higher porosity and permeability are the major water transmitting zones. This subject is clearly found from Fig. 18 which shows the velocity profile in the layered conduit obtained at Re = 25.

Fig. 18
figure 18

Stream-wise velocity profile in the layered porous conduit at Re = 25

Full size image

One of the most important parameters for porous layers is the hydraulic conductivity, which is a property of porous media that describes the ease with which the water can move through pore spaces or fractures. The hydraulic conductivity is defined as:

$$\begin{aligned} \mathbb{K }=Kg/v, \end{aligned}$$
(16)

being \(g\) is the gravity acceleration. The total thicknesses of the first layer, the non-homogenous layer and the core layer are \(d_{1}=2y_{p1}=0.2H, d_{2}=2y_{p2}=0.6H\) and \(d_{3}= 0.2H\), respectively.

By converting the lattice units into real units, the resulting hydraulic conductivities for the first, the second and the core layer are calculated as \(\mathbb{K }_{d1}\approx 5\times 10^{-8} \mathrm{{cm}}/\mathrm{{s}}, \mathbb{K }_{d2}\approx 4.5\times 10^{-6} \mathrm{{cm}}/\mathrm{{s}}\) and \(\mathbb{K }_{d3}\approx 5\times 10^{-6} \mathrm{{cm}}/\mathrm{{s}}\), respectively. By comparing with the measured hydraulic conductivity of real materials in nature [79], we can find that the present multi-layer channel can be classified as a layered clay aquifer, which consist of very fine sand, silt and loess. Moreover, the first layer describes a non-pervious layer, whereas the other layers define semi-pervious media with low permeability. Another important parameter in hydrology is the transmissivity, defined as the hydraulic conductivity multiplied by the porous layer thickness,

$$\begin{aligned} T=\mathbb{K }d, \end{aligned}$$
(17)

expressing \(\mathbb{K }\) in meter per day and \(d\) in meter. Thus, \(T\) is a measure of how much water can be horizontally transmitted through a porous layer. The transmissivity of multi-layered porous conduit is calculated as follows:

$$\begin{aligned} T_{total}=\sum _{i=1}^n\mathbb{K }_id_i \end{aligned}$$
(18)

where \(i=1,{\ldots },n\) denotes the layer. So, the transmissivity for the above described layered conduit is approximately equal to \(3.5\times 10^{-3}\mathrm{{m}}^{2}/\mathrm{{day}}\) which shows that the conduit transmits very few amount of water within a day.

The total discharge \((Q)\) of a porous channel can be calculated through the Darcy’s law, which is a relationship between the instantaneous discharge rate through a porous medium, the viscosity of the fluid and the pressure drop over a given distance. In other words, the discharge passing through a porous tube of cross sectional area \((A)\) is proportional to the hydraulic conductivity \((\mathbb{K })\), the difference of the hydraulic head between the two end points \(\Delta h_{12} =(h_2 -h_1 )\) and inversely proportional to the flow length \((L)\), as follows

$$\begin{aligned} Q=\mathbb{K }A[(h_2-h_1)/L], \end{aligned}$$
(19)

being the hydraulic head calculated as \(h=z+p/\gamma +v^{2}/2g\). Since, the conduit is horizontal and the average velocity of the flow is small and constant, the vertical distance above an established datum (\(z)\) and the averaged fluid velocity \((v)\) are negligible. So, the hydraulic head between two end points is calculated as \(\Delta h_{12} =(p_2 -p_1 )/\gamma \) where \(p\) is the pressure and \(\gamma \) is the specific weight of the fluid. Therefore, the discharge flow rates for the first, the second and the core layer are calculated as \(Q_{d1} =4.4\times 10^{-10}{\mathrm{{m}}^{3}}/\mathrm{{s}}\), \(Q_{d2} =1.8\times 10^{-7}{\mathrm{{m}}^{3}}/\mathrm{{s}}\) and \(Q_{d3} =6.8\times 10^{-8}{\mathrm{{m}}^{3}}/\mathrm{{s}}\), respectively, and the total discharge of the conduit is \(Q_t =\sum {Q_i =} 2.48\times 10^{-7}{\mathrm{{m}}^{3}}/\mathrm{{s}}\).

If we divide \(Q\) by the sectional area, we obtain the so-called apparent or Darcy’s velocity, which is not to be confused with the effective water velocity, as the water flows through pore-paths (interconnected pores). Therefore, the average water velocity is greater than the apparent velocity, as the fluid is moving through a much smaller area. However, both quantities are related to each other, through the concept of effective porosity, \(\varepsilon _{eff} \). The definition of effective porosity can be stated in a similar way to porosity, but considering only interconnected pores instead of void volume and is measured using laboratory techniques.

In other words, to convert the apparent velocity, measured in a flow through an aquifer, into the actual velocity, also called seepage or average velocity, one must divide specific discharge by the effective porosity as follows:

$$\begin{aligned} V_{seepage} =Q_t /(\varepsilon _{eff} A). \end{aligned}$$
(20)

Note that the effective porosity occurs because a fluid in a saturated porous media will not flow through all voids, but only through interconnected voids. Unconnected pores are often called dead-end pores. Particle size, shape, and packing arrangement are among the factors that determine the occurrence of dead-end pores. In addition, some fluid contained in interconnected pores is held in place by molecular and surface-tension forces. This immobile fluid volume also does not participate to the mass transport [80].

4 Conclusions

In this paper, we propose and validate a novel numerical method to effectively simulate the fluid flow in media with non-homogeneous porosity, to be applied for modeling fractured porous aquifers. To this aim, we further developed a finite volume formulation of the lattice Boltzmann method previously applied to non-porous isothermal flows. In this formulation, a cell-centered scheme is used to discretize the convection term and the correction factors are considered in order to improve the numerical stability of the method. The porous media effects at the REV scale and based on the Brinkman–Forchheimer model are incorporated, by introducing the porosity and flow resistance effects in the equilibrium distribution function and Boltzmann’s equation, respectively. The proposed numerical formulation is validated against literature results for several fully porous channel flows, namely Poiseuille flow, Couette flow and lid driven cavity flow, and the results demonstrate the validity of the numerical approach. The scheme has then been extended to simulate partially porous channels, as a model for fractured porous ducts with homogenous and non-homogenous (random) porosities. A mesh analysis clearly shows the effectiveness of the finite volume discretisation, which allows a grid refinement in critical regions with a 70 % reduction in the number of nodes with almost the same accuracy.

The effects of Darcy number, porosity and porous layer thickness are also investigated. It is shown that, when the Darcy number or porosity is high, the fluid flows more easily through the porous layer and the velocity magnitude in the porous layer increases. Consequently, the peak of velocity in the clear region decreases and the profiles approach a parabolic shape in the fully clear channel. Furthermore, the random porosity leads to a non-symmetric behavior of the velocity profile in the layers. Finally, the fluid flow through a porous layered conduit was simulated and the corresponding hydraulic parameters, as hydraulic conductivity, transmissivity and discharge rate, were computed.