Introduction

Karst aquifers are often considered as resulting from two interconnected flow systems that correspond to (1) a fracture network developed within the limestone and (2) a large conduit network that is specific to a karst system. The fractured limestone has a high storage capacity due to the low mobility of water located in the cracks and to the presence of almost stagnant water in the porous matrix (Hauns et al. 2000). Thus, in karstified media, a large range of pore sizes is present, from fine pores and fractures to large fractures and karst conduits.

Over the past several decades, three types of approach have been developed to quantify groundwater flow in multi-porous media:

  1. 1.

    The black-box approach that investigates karst spring responses to the rainfall and water surface infiltration process considering the karst system as a whole. The flows are modeled by a transfer function (Dreiss 1982, 1989; Barrett and Charbeneau 1996; Zhang et al. 1996).

  2. 2.

    The analytical approach that describes the karst system by its hydrological functioning. Based on a better understanding of the groundwater flow regime and knowledge of the hydraulic parameters, simple hydrological conditions are then integrated into a simple analytical expression (Lin and Chen 1988).

  3. 3.

    Finally, the numerical approach that is the most powerful in studying the impact of heterogeneities on the hydraulic parameters and consequently on the karst hydrological functioning. Usually, there are three ways to characterize karst media. The simplest and most commonly used assumes that the karst aquifer is an equivalent porous media in which conduits and wide fractures are treated as a high hydraulic conductivity region (Teutsch 1993; Eisenlohr et al. 1997; Scanlon et al. 2003). The second approach is to use a dual porosity or double permeability model (Mohrlok et al. 1997; Cornaton and Perrochet 2002). The karst system is described using two overlapping continua in hydraulic interaction: a matrix continuum of low hydraulic conductivity, and a conduit domain with high hydraulic conductivity (Cornaton and Perrochet 2002). The third approach is the coupling of linear flow with nonlinear flows by using the concept of equivalent hydraulic conductivity in Darcy’s law (Cheng and Chen 2004). It was shown that the key to modeling karst groundwater is still dependent on the chosen approach to couple the conduit flow with the flow in the calcareous formation (Scanlon et al. 2003).

The coupling of flow equations and advection-dispersion models is commonly used to bring the quantitative approach of pollution transport to karstic aquifers (Hauns et al. 2000; Massei et al. 2006; Goldscheider et al. 2007). Many studies presented both fluid flow and solute transport in the karst system to describe dye tracer tests (Ford and Williams 1989). Water tracer tests and breakthrough tracer curves (BTC) were used to validate numerical hydrodynamic-transport models. Maloszewski et al. (1999) performed two multitracer tests in the major cross fault zones of the Lange Bramke in Germany. They compared the measured BTC with that simulated from the coupling between the advection-dispersion equation and Darcy’s law. They showed that the hydraulic conductivity in the fault zone was several orders of magnitude larger than that of the remaining fractured zone of the aquifer. The relationship between the geometry of the karst conduits and breakthrough curves was established by Hauns et al. (2000). They used a one-dimensional advection-dispersion equation to calculate the breakthrough curve using the mean flow velocity and observed that the dispersion coefficient depended linearly on the average flow velocity in the karst conduit under homogeneous flow conditions. Other studies about solute transport in a karst system were carried out using Darcy’s law and a multi-porous approach to show that water flow in the conduits is the key parameter to describe transport in these heterogeneous aquifers (Morales et al. 1995; Couturier and Fourneaux 1998; Rivard and Delay 2004; Massei et al. 2006; Goppert and Goldscheider 2007). However, Darcy’s law is not well adapted to model flow in conduits of large diameter.

In this study, it is proposed to use Darcy’s law to describe the water flow within the fractured calcareous rock where the pores are small and the Brinkman equation to describe the water flow in the karstic conduits. The latter equation enables flow description in the domain where the porosity is high (i.e. >90%) and is used in domains where velocities are high enough to produce an important momentum transport by shear stress (Brinkman 1947; Durlofsky and Brady 1987; Nield and Bejan 1992; Parvazinia et al. 2006). The Brinkman equation is classically applied to calculate the flow fields in many domains such as in porous squeeze film, and in porous heterogeneous materials with more than one typical pore size (Lin et al. 2001; Nicos 2001; Cheng and Chen 2004; Albert and Yuan 2004). The first objective of this paper was to describe the water flow in the karst aquifer of the Val d’Orléans by using a two-dimensional numerical model. This model applies the Brinkman equation within karst conduit flow and Darcy’s law within the hosting calcareous rock. The flow model results were coupled to the transport equation in order to simulate solute transport in the karst. A BTC was simulated at the spring points and compared to real tracer tests to validate the model. The six dye tracer tests used for the calibration of the simulation allow the validation of the model for different hydrological conditions. Finally the model established (discrete continuum approach) was compared to a double permeability continuum model (i.e. Darcy’s law will be used to model flow in the karstic conduit). The comparison was used to investigate the significance of the momentum transport by shear stress on the behaviour of BTCs at the spring points.

Method

Study area

The Val d’Orléans consists of a vast depression along the main route of the Loire River, 37 km long and from 4 to 7 km wide (Fig. 1). The karst aquifer is hosted within an Oligocene carbonate lacustrine limestone occurring in the center of the Paris basin and called the Beauce limestone (Guillocheau et al. 2000). This latter formation displays a variable habit with a significant primary porosity except for the micritic facies. This porosity is increased by karstification leading to a relatively high permeability (5 × 10−11 to 2 × 10−9 m2) at a hectometric scale (Martin and Noyer 2003). The Beauce limestone is overlain by the Quaternary alluvia of the Loire River.

Fig. 1
figure 1

Water flow in the karst aquifer of the Val d’Orléans (Albéric and Lepiller, modified 1998)

Full size image

The Loire River supplies more than 80% of the water held in the carbonate karstic aquifer developed within the upper Beauce limestone underlying the alluvia of the Loire River. The estimated inflow of the Loire River into the swallow hole located near the town of Jargeau varies from 15 to 20 m3/s and can reach 100 m3/s when the Loire River is in flood (Chéry 1983). The karst network is well known on the south bank of the Loire River. The water runs from Jargeau through the karst network toward the springs of the Loiret River (Fig. 1) (Zunino 1979; Chéry 1983; Lepiller and Mondain 1986). The main springs of the Loiret River are called Bouillon and Abîme. These springs are the main emergences of the water lost from the Loire River at Jargeau with flow rates of 0.3–5 m3/s. There are also several smaller springs along the Loiret River called Béchets, Saint-Nicolas, Bellevue and Pie (Fig. 1). All these springs are surface overflows of the karstic aquifer. The mean aquifer outflow is an underground emergence in the Loire River located around the confluence of the Loire-Loiret (Fig. 1). Previous studies showed the relation between these springs and the swallow-hole points at Jargeau within the Loire River (Zunino 1979; Chéry 1983; Alberic and Lepiller 1998; Lepiller 2001).

Desprez (1967) established piezometric maps of the study area for periods of low and high water levels (using more than 700 boreholes). Every year, the difference in water level between the high and low water periods is usually about 1 m. The main conduits were located according to the depressions of the piezometric surface and to the different connections identified by the tracer tests presented in Fig. 1.

Tracer tests

Tracer tests were conducted to study the conduit karst system of the Val d’Orléans, particularly the relation between the swallow-hole point and the different springs. The injection point was the swallow hole located near Jargeau 15 km west of Bouillon Spring (Fig. 1). The tests were performed in Feb 1973, Feb 1998, May 2001, Nov 2001, Nov 2006 and Nov 2007. A solution of 15 kg of uranine diluted with 80 L of water was injected in Feb 1973, 2 kg of uranine diluted with 5 L of water in May 2001 and Nov 2001, 1 kg diluted with 5 L of water on Feb 1998, Nov 2006 and Nov 2007 (Table 1). Uranine was used for groundwater dye tracing in the karst system of the Val d’Orléans because of its great detection sensitivity and weak propensity to adsorption. The tracer was analysed by using fluorescence spectrofluorimetry (mark Hitachi HITACHI F-2500 and F 2000, and Turner). The excitation and emission for uranine were 491 and 512 nanometres (nm), respectively. The fluorescence is proportional to the dye concentration (Société Suisse Hydrogéologie 2002). Uranine concentration was determined at several spring points in the Loiret River. Samples were taken automatically at each spring point at 1.5 m depth underneath the water surface. Figure 2 shows the tests performed for different hydrological conditions. The datasets recorded at the different dates enable the simulation of several combined injection protocols and hydraulic conditions (Table 1). Moreover, Fig. 2 shows the variation of the concentration as a function of time, and presents the tracer recovery curves for each spring depending on the existence of a sampler at the spring.

Fig. 2
figure 2

a Tracer tests at 6/02/1973, b Tracer tests at 20/02/1998, c Tracer tests at 25/05/2001, d Tracer tests at 15/11/2001, e Tracer tests at 16/11/2006 and f Tracer tests at 14/11/2007

Full size image
Table 1 Principal information from tracer tests realized at Jargeau
Full size table

The BTCs enable the calculation of several parameters related to the transit time and velocity (leading edge, trailing edge and peak velocity), to the tracer concentration (maximum and average), and to the duration of the recovery (Table 2). Times were measured by taking the injection time (t = 0) as reference. The distance used to calculate the velocities is the straight line between the injection point on one hand and the sampling point on the other. Consequently, the velocity values obtained are minimum values, the real values depending on the tortuousness of the conduits (Field and Nash 1997; Worthington 1999) and estimated as being from 1.3 to 1.5 times higher (Field 1999; Field and Pinsky 2000). The curve of the tracer mass flow rate enables the calculation of the mass of the tracer recovery. The ratio between this recovered mass and the initially injected mass is the recovery rate.

Table 2 Parameters obtained from the tracer tests data (Lepiller and Mondain 1986; Morales et al. 2007)
Full size table

The residence time distribution (RTD) was obtained by relating the mass flow to the recovered tracer mass (Table 2). It has inverse time units and represents the probability density function that a traced water element stays in the system for a time between t and t + dt (Molinari 1976). The variance of the residence time is an indication of the dispersion around the mean residence time. There is no mixing if the variance nears zero and complete mixing if the variance tends toward infinity. All parameters which can be calculated from the tracer tests are shown in Table 2.

Development of the coupled model

In the light of the previous description of the karst system with flow within a fractured porous aquifer and karst conduits, it was necessary to find an adapted mathematical model describing the water flux and solute transport between swallow holes and springs.

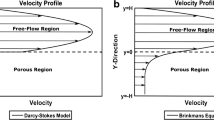
Darcy’s law

Darcy’s law describes fluid flow in porous media and it is well adapted to an aquifer with small porosity. This equation describes the flow behaviours in porous media as driven by pressure gradients as follows:

$$ {u_{\text{D}}} = - \frac{{{k_{\text{D}}}}}{\mu }\nabla p $$
(1)

where u D is the Darcy flow velocity (m/s), k D the intrinsic permeability related to Darcy’s law (m²), µ the fluid viscosity (Pa.s) and p the pressure (Pa).

Brinkman equation

The Brinkman equation describes the fluid flow in porous media where velocities are high and include momentum transport by shear stress. In Darcy’s law, it is indeed assumed that all stress within the flow is negligible compare to the stress carried by the interface of the liquid and the solid porous media. This assumption cannot be regarded to be physically realistic for high permeability porous media where at least part of the viscous stress is limited within the fluid domain. The Brinkman equation, which accounts for the transition from Darcian flow to viscous free flow, is ideal to be used for high permeability porous regimes (Brinkman 1947; Parvazinia et al. 2006). This equation is adapted to describe the flow in porous media if the porosity is greater than 90% (Durlofsky and Brady 1987). The Brinkman equation is written as follows (Brinkman 1947; Laptev 2003):

$$ {u_{\text{Br}}} = \frac{{{k_{\text{Br}}}}}{\mu }\left[ { - \nabla p + {\mu_{\text{e}}}\Delta u_{\text{Br}}^2} \right] $$
(2)
$$ \nabla .{u_{\text{Br}}} = 0 $$

where u Br is the Brinkman fluid velocity vector (m/s), μ the fluid viscosity (Pa.s), k Br the intrinsic permeability related to the Brinkman equation (m2), μ e the effective viscosity that theoretically takes into account the stress within the fluid as it flows through a porous medium. However experimental measurement of μ e is not trivial (Nield and Bejan 1992). Therefore, with respect to the literature, μ e is set to be equal to the fluid viscosity μ (Hsu and Cheng 1985; Kaviany 1986; Allan and Hamdan 2002; Parvazinia et al. 2006). In the following section, the subscripted D and Br refer to Darcy’s law and the Brinkman equation, respectively, as the model deals with the two flow equations.

Solute transport equation

This equation describes the migration of chemicals in multi-porous media. The phenomenon which govern solute movement are advection and dispersion. They are described by the solute transport equation as follows:

$$ \theta \frac{{\partial c}}{{\partial t}} + \nabla u.c = \nabla \left[ {{D_{\text{hyd}}}\nabla c} \right] + R $$
(3)

where c is the solute concentration (kg/m3), θ the media porosity, D hyd the hydrodynamic dispersion tensor (m2/s), u the velocity vector (m/s) originating from Darcy’s law or the Brinkman equation, and R the source term (kg/m3.s). Thus, this equation relates the concentration change with time and the advection term on one hand, and the hydrodynamic dispersion of the concentration on the other.

The advection describes the transport of solute such as a pollutant, at the same velocity as the groundwater flow. Hydrodynamic dispersion in a porous medium occurs as a consequence of two processes: (1) the molecular diffusion which originates from the random molecular motion of solute molecules, and (2) the mechanical dispersion which is caused by non-uniform velocities and flow path direction. Molecular diffusion and mechanical dispersion cannot be separated in a flow regime (Bear 1979) and the summation of these two coefficients is called the hydrodynamic dispersion. The hydrodynamic dispersion tensor for isotropic porous media is defined in the following x-y components form as follows:

$$ \begin{array}{*{20}{c}} {{{\left( {{D_{\text{xx}}}} \right)}_{\text{hyd}}} = {\alpha_{\text{L}}}\frac{{{u^2}}}{{\left| u \right|}} + {\alpha_{\text{T}}}\frac{{{v^2}}}{{\left| u \right|}} + {D_{\text{m}}}} \hfill \\ {{{\left( {{D_{\text{yy}}}} \right)}_{\text{hyd}}} = {\alpha_{\text{L}}}\frac{{{v^2}}}{{\left| v \right|}} + {\alpha_{\text{T}}}\frac{{{u^2}}}{{\left| v \right|}} + {D_{\text{m}}}} \hfill \\ {{{\left( {{D_{\text{xy}}}} \right)}_{\text{hyd}}} = \left[ {{\alpha_{\text{L}}} - {\alpha_{\text{T}}}} \right]\frac{{uv}}{{\left| u \right|}}} \hfill \\ \end{array} $$
(4)

where (D ii ) hyd are the principal components of the hydrodynamic dispersion tensor (m2/s), α L the longitudinal dispersivity coefficient (m), which is parallel to the direction velocity, α T the transverse dispersivity coefficient (m), D m the effective molecular diffusion coefficient (≈10−9 m2/s), u and v components of the velocity vector along the x,y direction originating from Darcy’s law or the Brinkman equation.

Coupling

Darcy’s law and the Brinkman equation are fundamentally compatible since both describe fluid velocities and pressure distributions. The dependent variable in Darcy’s law and the Brinkman equation is the pressure alone. The advantage of using the Brinkman equation is its similarity to Darcy’s law. Consequently this similarity can facilitate identification of the boundary conditions at the interface between the conduits and the fractures by assuming continuous pressures. The analysis begins by creating a hydrodynamic model using Darcy’s law in the porous massive limestone and the Brinkman equation in the karst conduits. Next, the model examines the tracer transport in the karst system by coupling the solute transport equation with Darcy’s law and the Brinkman equation.

Geometry and boundary conditions

The application of the hydrodynamic-transport model was used to simulate a reach of 24 km from the site of Jargeau down to the confluence of the Loire-Loiret. The model is based on a two-dimensional (x,y) description of the hydrogeological system. This simulation considers the water table as a boundary condition, so well extractions and the effect of infiltrated precipitation in the karst aquifer were considered as constant parameters, to keep the water table stable (Chéry 1983; Lepiller and Mondain 1986).

The locations of the karstic conduits between Jargeau and the springs of the Loiret River to the confluence of the Loire-Loiret were deduced from the piezometric contours describing a valley at the piezometric surface. These linear depressions suggest the presence of karstic conduits. Therefore, two hydrodynamic domains could be defined: (1) a Darcy domain where the piezometric map is not perturbed, and (2) a Brinkman domain in the karstic conduit area (size will be discussed below).

In the Darcy domain, the pressure variation was deduced from the piezometric maps (Desprez 1967) and adapted for simulation during low and high water periods. These pressures were used as the boundary condition for the Darcy and Brinkman domains, as follows:

$$ p = \rho g\left( {H - {H_{\text{o}}}} \right) $$
(5)

where p is the pressure of each water isoline, H the water level isoline (m), and H o the reference water level isoline (m). In this study, the reference water level isoline was taken at the confluence of the Loire-Loiret. Then this equation was used to calculate the pressure head for each water isoline between the swallow hole points and the confluence of the Loire-Loiret. For a continuous solution across the interface between the Darcy and Brinkman domains, the pressures given by Darcy’s law equalled those given by the Brinkman equation and thus at the Darcy–Brinkman interface:

$$ {p_{\text{D}}} = {p_{\text{Br}}} $$
(6)

Then, the assumed boundary conditions in the external zones surrounding the study area are in symmetry, i.e. the integrated flow velocity on this boundary can be considered as equal to zero because the flow is perpendicular to the piezometric contours.

For the Brinkman flow in the conduits, the pressures at the swallow holes and spring points are set as the Dirichlet boundary conditions. For the swallow-hole points (points 1, 2 and 3) the pressures were 88,200, 49,250 and 49,000 Pa, respectively. The pressure value for the swallow-hole points area (Fig. 3) is 93,100 Pa. For the spring points which discharge in the Loire River (points 4, 5 and 6) the pressures were –550, −2,600 and −3,425 Pa, as shown in Fig. 3. This figure shows the boundary conditions and numerical scheme for the Darcy-Brinkman model. A finite element method was used to solve the equations by breaking the problem area into many small triangular elements. The domain was meshed into 67,300 triangular finite elements, with higher refinement surrounding the conduits. The intent was to achieve higher computation accuracy near the interface between the matrix (diffuse) and conduit systems.

Fig. 3
figure 3

Darcy-Brinkman boundary conditions and finite element mesh for low water level periods. Pressure is constant along each isoline

Full size image

To compare the tracer recovery realised from the field and the simulation, the transport equation was solved using the velocity given in the Darcy and Brinkman domains. At t 0 the tracer concentrations are everywhere equal to zero except at the injection point where the concentration equals the initial concentration injected for some minutes. The continuity tracer flux is implemented in the Darcy domain where the tracer is transported. At the Darcy-Brinkman interface, the tracer concentrations are equal, and an advective flux condition is taken for the spring points and the boundaries of the study area. Finally, the defined boundary conditions are a mix of Dirichlet, Neumann and Cauchy conditions.

Numerical solutions

Numerical solutions were obtained with COMSOL Multiphysics (formerly FEMLAB) software, a general purpose finite element code developed for the MATLAB environment. Benchmark tests were carried out to valid the numerical model. COMSOL Multiphysics (COMSOL Multiphysics, Earth Science Module, Model Library Version 3.2b, 2006) have made some benchmark models and that of Hossain and Wilson (2002) is one such model. These authors performed a simulation of unsteady natural convection flow in a rectangular enclosure with non-isothermal walls using the Brinkman equation and the convection-conduction equation. The results obtained by COMSOL Multiphysics match those obtained from the published study.

In this work, a benchmark test was performed using the model originating from Birk et al. (2005) which was established for a karst system by using MODFLOW-96 (a modular finite difference groundwater model code). These authors applied a Darcy-Weisbach equation in order to simulate the conduit flow. In this benchmark model, the same conditions were used but the Brinkman equation was applied in the conduit. The results obtained were in excellent agreement with Birk et al. (2005).

The tracer transport model was generated in two steps. First, the steady-state water flow was generated and a stable hydrodynamic solution was stored. In the second step, this result was inserted to solve the solute transport equation and to follow the transient migration of the tracer.

Double permeability continuum approach and discrete-continuum approach

In order to compare the discrete-continuum approach and the double permeability continuum approach, a model was established by using Darcy’s law in the fractures and in the conduit systems. Applying this model to similar geometry, boundary conditions and numerical solution, the tracer test was compared to those obtained in the field, and by the double permeability model.

Results and discussion

Tracer tests

The amount of the tracer recovered at the spring is highly variable according to the hydrological conditions, the amount of tracer mass injected and the circulating flow rate. The percentage of tracer recovered increases at the spring in conditions of low water and with an increasing mass of tracer injected. The tracer was first detected at Bouillon Spring 70, 84, 74, 81, 72 and 57 h after the tracer injection in Feb 1973, Feb 1998, May 2001, Nov 2001, Nov 2006 and Nov 2007, respectively. The uranine concentration reached its maximum of 5.91 ng/ml after 92 h for the test of Feb 1973, 0.56 ng/ml after 100 h for the test of Feb 1998, 0.39 ng/ml after 87 h for the test of May 2001, 0.56 ng/ml after 104.5 h for the test of Nov. 2001, 0.072 ng/ml after 88 h for the test of Nov 2006 and 0.1 ng/ml after 79 h for the test of Nov 2007. These differences will be investigated using the parametric tests of the proposed model developed in the discussion. Table 3 gives the different characteristic values for the six tracer tests with injection at Jargeau and recovery at Bouillon Spring.

Table 3 Parameters obtained by the tracer tests for Bouillon Spring
Full size table

First calibration of hydrodynamic parameters

The result produced by the model needs to be calibrated, and a first step was necessary to estimate roughly the hydrodynamic parameters. The validity of the model is based on the comparison with the velocity flow rates recorded during the tracer tests (0.04–0.06 m/s). In the Brinkman domain (conduits), the principal parameters are the conduit size and the permeability. In the Darcy domain, the permeability is the main parameter that controls flow and it was assumed constant.

Conduit diameter

The variations of the mean velocity in the karst conduits in the case of steady-state flow with different conduit diameters as a function of hydraulic parameters are presented in Fig. 4. Generally, in the karst conduits the mean velocity (Vm) increases when the diameter decreases and when the permeability increases. The diameter of the conduit does not influence the mean velocity when the permeability of the fractured zone is very low (Fig. 4a). The influence of the Brinkman permeability for conduits of 5 and 10 m diameter is not significant (Fig. 4b). The diameter of the conduits observed by the speleologists between the swallow-hole points at Jargeau and the spring points of the Loiret River varies between 2 and 10 m, therefore a diameter of 5 m provided the best results compared with the mean velocity measured in the channels by the tracer tests.

Fig. 4
figure 4

Mean velocity (Vm) in the conduit with different diameter a as the function of fractured zone permeability, b as the function of conduit permeability

Full size image

Permeability

The best results were achieved when the Darcy permeability varies from 8 × 10−11 to 6 × 10−10 m2 and the Brinkman permeability from 5 × 10−6 to 5.5 × 10−5 m2. Figure 5 shows the pressure distribution along the karst system of the Val d’Orléans (surface plot) in the case of steady-state flow for low water levels. It also shows some values of the conduit water velocity. Generally, the mean velocity obtained in the conduits is 0.05 and 0.06 m/s for low water levels and high water levels, respectively. These results clearly show that the velocity in the Brinkman domain is greater than that in the Darcy domain. This can be attributed to the effect of shear stress and the high permeability in the Brinkman equation.

Fig. 5
figure 5

Water flow for steady-state solution. Surface plot represents the pressure distribution (Pa), and the values represent the water velocity in the conduit (m/s) with permeability in the Darcy domain = 5.7 × 10−10 m2 and in the Brinkman domain = 1.65 × 10−5 m2

Full size image

Simulation of tracer transport (steady and unsteady problem)

One week is needed for the tracer to reach the spring from the injected point. During this period, the variation of flow rate could be evaluated by the variation of water level with the time in the Loire River. The water levels of the Loire River at the Orléans Bridge during the tracer tests are shown in Fig. 6a–f. In general, the water level variation is less than 0.3 m. Chéry (1983) and Lepiller and Mondain (1986) noted that the variation of flow rate in the springs is negligible during the period of tracer transport. Therefore, the hydrodynamic equations are solved for the steady state. The flow and velocity fields were generated in the Darcy and Brinkman domains, and these solutions were inserted in the solute transport equation.

Fig. 6
figure 6

Water level for the Loire River at the Orléans Bridge a Feb 1973, b from 13 Feb to 10 March 1998, c from 16 May to 11 Jun 2001, d Nov 2001, e from 9 to 25 Nov 2006, f from 3 to 24 Nov 2007

Full size image

To simulate tracer transport it is necessary to solve the transport equation for a temporal model, i.e. for the unsteady state. The analysis period is 10 days and the output time-step settings were simulated by means of similar vectors of time starting at zero with steps of 2 h up to 10 days. The parameters that require adjustment in the hydrodynamic-transport model include permeabilities and dispersivity coefficients in the Darcy and Brinkman domains.

The resolution of this transient problem allows the plotting of the breakthrough curves (BTCs) corresponding to the tests considered. The fitting between breakthrough curves and experimental data is evaluated by assessing the magnitude of the error generated. To compare the results obtained with the model, six tracer tests were chosen, conducted during low and high water level periods.

Sensitivity of the model to the main parameters

Several simulations of tracer recovery were compared to the six tracer tests presented before. In these simulations, the Darcy and Brinkman permeabilities are constant and the boundary condition is given by the piezometric map of a low water level period, or for the tests of Feb 1973, Nov 2006 and Nov 2007 which were performed during a high water level period, by the high water piezometric map.

Many parameters influence the tracer transport process such as permeabilities, longitudinal and transverse dispersivity coefficients in the Darcy and Brinkman domains, the level of the water table and the mass of tracer injected. Therefore, it was important to study the effect of the variations of these parameters separately to describe the rate and pattern of transport and to prioritize their influences.

Permeability

A comparison between the theoretical BTCs for different values of Darcian permeability (Fig. 7a) shows the decrease of tracer concentration recovery with permeability increases. Thus, the increasing of Darcy velocity leads to an increase in the tracer concentrations toward Darcy domain. Conversely, an increase in the Brinkman permeability causes an increase in the conduit water velocity and consequently an increase in the tracer recovery (Fig. 7b).

Fig. 7
figure 7

The effect of hydrodynamic-transport parameters on the behaviour of BTC at Bouillon Spring: a behaviour of BTC curve (conduit permeability = 1.65 × 10−5 m2, α D = 5 m and α Br = 53 m), b behaviour of BTC curve (fractured permeability = 5.7 × 10−10 m2, α D = 5 m and α Br = 53 m), c behaviour of BTC curve (conduit permeability = 1.65 × 10−5 m2, fractured permeability = 5.7 × 10−10 m2, α D = 5 m), d behaviour of BTC curve (conduit permeability = 1.65 × 10−5 m2, fractured permeability = 5.7 × 10−10 m2, α Br = 53 m), e behaviour of BTC curve as a function of water level in Loire River (conduit permeability = 1.65 × 10−5 m2, fractured permeability = 5.7 × 10−10 m2, α D = 5 m and α Br = 53 m,), f behaviour of BTC curve as a function of injection time (conduit permeability = 1.65 × 10−5 m2, fractured permeability = 5.7 × 10−10 m2, α D = 5 m and α Br = 53 m)

Full size image

Dispersivity

The dispersivity coefficients play a significant role in the behaviour of tracer transport. These coefficients are affected by the mean velocity and karst geometry (Majid and Leijnse 1995; Faidi et al. 2002; Ham et al. 2004; Gaganis et al. 2005). Concerning the problem of transport, the authors who used the transport equation in porous media were forced to apply different values for the ratio α T/α L (El-Mansouri et al. 1999; Younes et al. 1999; Kim et al. 2003; Ham et al. 2004). In open channels, Mohan and Muthukumaran (2004) found that the best value for the α T/α L ratio was 1 when they simulated the pollutant transport in the river bed. In this study, the ratio was taken as equal to 1.

The results suggest that the increase in the dispersivity coefficients in the Brinkman domain causes a decrease in the recovery of tracer concentration (Fig. 7c). The tracer dispersion toward the fractured zone increases with an increase in the dispersivity coefficients in the Brinkman domain. In the same way, the increase in dispersivity coefficients in the Darcy domain causes an increase in concentration levels in this domain and, consequently, decreases the concentration levels at Bouillon Spring (Fig. 7d). A good agreement was recorded when α L = α T whatever the domain. Herein, four values were examined.

Piezometric surface

The effect of water level change on the behaviour of tracer recovery at Bouillon Spring is shown in Fig. 7e. This figure shows four different values of water level at Jargeau (h = 96.5, 97, 97.5 and 98 masl). It can be clearly seen that when the water level along the study area increases, low tracer recovery at the spring is found. This can be attributed to the effect of tracer dispersion toward the fractured zone which increases with the water level. This suggests an important dilution during high water levels periods.

Mass of tracer injected

The mass of tracer injected influences the maximum tracer concentration at the spring as shown in Fig. 7f. When the injected mass increases, the concentration of tracer recovery increases, and the tests performed in Feb 1973 and Nov 2007 confirm this because the injected mass of tracer for the test performed in Feb 1973 and Nov 2007 was 15 and 1 kg, respectively. This can be caused by the dilution process.

Table 4 summarises the effect of hydrodynamic-transport parameters on the tracer recovery parameters (mean residence time, recovery time, recovery rate and variance).The hydrodynamic transport parameters are the permeabilities and dispersivity coefficients. This table shows that all tracer recovery parameters are influenced by the variations of hydrodynamic-transport parameters but not with the same magnitude, because it can be observed that the permeability and the ratio between the longitudinal and transverse dispersivity coefficients influence strongly the tracer recovery parameters. Moreover, the water level along the study area influences the mean residence time and recovery rate.

Table 4 Summary of the effect of hydrodynamic-transport parameters on the tracer recovery parameters
Full size table

Parameters corresponding to the best fit

The best fit recorded when the simulated concentrations were compared to the measured BTCs at Bouillon, Pie, Béchets and Sanit Nicolas springs shown in Fig. 8. In the figure, it can be found that the predicted recovery times are slightly smaller than that measured. This can be attributed to the 2-h time accuracy of the model. Moreover, Fig. 8 shows the best fit corresponding to the measured BTC due to the calibration processes which yield a permeability of 5.7 × 10−10 m2 in the fractures. This value is compatible with the double permeability continuum model established by Martin and Noyer (2003) in which they found that the permeability in the fractures ranges from 2.04 × 10−10 to 1.02 × 10−9 m2. In the conduits, the more appropriate permeability was 1.65 × 10−5 m2 between Jargeau and Bouillon Spring, and 5.5 × 10−5 m2 between Bouillon Spring and the confluence of the Loire-Loiret. The best fit was recorded when α L = α T = 5 m in the Darcy domain for the tests of Nov 2006, May 2001, Nov 2001, Feb 1998 and Feb 1973, and equal to 1 m for the test of Nov 2007. In the Brinkman domain, α L = α T = 43 m for the test of Nov 2007, 28 m for the test of Nov 2006, 53 m for the test of Nov 2001, 23 m for the test of May 2001, 50 m for the test of Feb 1998 and 20 m for the test of Feb 1973.

Fig. 8
figure 8

Comparison between simulated and measured BTCs for the tracer tests when conduit permeability = 1.65 × 10−5 m2 between Jargeau and Bouillon Spring, and 5.5 × 10−5 m2 between Bouillon Spring and the confluence Loire-Loiret, fractured permeability = 5.7 × 10−10 m2. a Test 6/02/1973, b test 20/02/1998, c test 25/05/2001, d test 15/11/2001, e test 16/11/2006, f test 14/11/2007

Full size image

Table 5 presents a summary of the measured and predicted tracer parameters for each tracer test at Bouillon Spring. It can be found that the calculated water flow at the spring is close to that measured and the predicted tracer parameters are very close to those measured with different hydrological conditions.

Table 5 Comparison between predicted and measured tracer test parameters at Bouillon Spring
Full size table

Comparison between double permeability continuum approach and discrete-continuum approach

In order to investigate the differences between the discrete-continuum approach and the double continuum approach, a model was established by using Darcy’s law alone in the fractures and conduit systems. When the same calibration parameters were used with this model, the recovery of the tracer concentrations at Bouillon Spring are retarded by around 20 h compared with the Darcy-Brinkman model.

The Darcy-Darcy model was applied using four tests. In the first, calibration of the parameters gave a better curve shape (t 1, t 2 and C max) compared with the measured data. In the second test, the parameters were calibrated to get the best mass balance and tracer quantity (spring flow rate and total tracer recovery). In the third test, the diameter of Bouillon Spring was increased to adjust the flow rate. The last test was performed with an increased diameter in the conduit.

To optimize the first and second tests, it was necessary to increase the permeability in the conduit between Jargeau and Bouillon Spring to 1.8 × 10−5 m2 and 3 × 10−5 m2, respectively. For the third test, Bouillon Spring diameter was raised from 1 to 1.2 m. In the last test, the conduit diameter was raised from 5 to 10 m. For all the tests, the dispersivity coefficients in the conduit and fractured rocks were equal to 25 and 5 m, respectively. Table 6 shows the tracer parameters calculated from the measured and the whole simulated results for the tracer test of November 2001.

Table 6 Predicted and measured tracer test parameters obtained at Bouillon Spring for Nov 2001 for the Darcy–Brinkman model (D-B), and the four tests for the Darcy-Darcy model (D-D)
Full size table

When the first test was applied, the simulated recovery time (t 1) and the maximum concentration are similar to those measured, but the results for the flow rate and total tracer recovery are not admissible. If the second test is applied, the tracer recovers very early and the recovery duration is very short, but the calculated spring flow rate and the total tracer recovery are very good. The best results for the Darcy-Darcy model were recorded when the third test was applied. In this test all simulated tracer parameters are good compared with the measured parameters except the total recovery rate which was far from reality. The simulated results of the fourth test are close to the results of second test.

However, Fig. 9 shows the best agreement between the calculated and measured BTC that corresponds to the use of the Darcy-Brinkman model for the test performed in Nov 2001. When Darcy’s law was applied in the conduits, the dispersion toward the fractures (diffuse system) was low compared with its value when the Brinkman equation was applied in the conduits. This may be attributed to the small interactions observed between the fractures and conduits when Darcy’s law was applied in the latter.

Fig. 9
figure 9

Comparison between measured tracer concentrations for the experience Nov 2001 with simulated results when Darcy’s law is used in the fractures and the Brinkman equation is used in the conduits (D-B), best simulated test when Darcy’s law is used in the fractures and conduits (third test, with the permeability in the conduit = 1.65 × 10−5 m2 and the dispersivity coefficients equal to 25 and 5 m in the conduits and fractures, respectively)

Full size image

Conclusions

The results showed that the presented model enabled estimation of the solute transport in a karstic aquifer. The water flows in the conduits were described by the Brinkman equation to be compatible in a domain where the porosity is high (>90%) and thus enabling the description of the fluid flow in the karst conduits where velocities are high enough to create important momentum transport by shear stress. On the other hand, Darcy’s law was applied to describe the water flows in the surrounding rock domain. These two domains were connected through their boundary condition where a continuous pressure was assigned.

The hydrodynamic analysis enables the generation of a solute transport solution with the aim of analyzing the uranine tracer transport in the karst aquifer of the Val d’Orléans. The COMSOL Multiphysics finite element analysis software was used to solve the governing equations. Six tracer tests were employed to investigate the accuracy of the calculated parameters. The calibration of the model indicated that it was possible to find parameters corresponding to the breakthrough tracer curves when the conduit permeability (Brinkman permeability) ranged from 5 × 10−6 to 5.5 × 10−5 m2, and the limestone permeability (Darcy permeability) from 8 × 10−11 to 6 × 10−10 m2. A 5-m diameter for the conduit gave representative results. Finally, the best fit was recorded when the dispersivity coefficients were isotropic and ranged in the conduits from 23 to 53 m and in the limestone from 1 to 5 m The results analysis showed that the use of Darcy’s law in the conduit system minimises the importance of the interactions between fractures and conduits. Adding momentum transport by shear stress in conduits with the Brinkman equation reduces greatly this underestimation.