Comparative study of elastic properties of some inorganic and organic molecular crystals from EOS

Abstract

In the present work we have perform a comparative study of structural and elastic properties of some inorganic and organic molecular crystals viz. Realgar As₄S₄, As₄S₃, C₁₄H₁₀ (anthracene), C₁₀H₈ (naphthalene). For theoretical prediction, four different EOSs have been used viz. modified Lenard-Jones EOS (M-L Jones EOS), Brennan-Stacey EOS, Hamma—Suito EOS and Thomsen EOS. Further, we have checked the applicability of these EOSs for calculation of Grüneisen parameter at different compressions. Experimental data and theoretical facts give the validity of our work.

1 Introduction

Equation of states is a theoretical topic of great interest for theoretical researcher because from EOS we can predict some thermal and structural properties without using any experimental setup. This technique of predicting elastic properties of bulk materials have been used to predict the structural and thermo elastic properties of some inorganic and organic crystal. These crystals are Realgar As₄S₄, As₄S₃, C₁₄H₁₀ (anthracene), C₁₀H₈ (naphthalene). Chalcogenides of Arsenic have become the topic of great interest for high pressure researcher. In As–S system, both inorganic molecular As₄S₄, As₄S₃ and ordinary covalent As₂S₃ are realized. All these inorganic compounds are minerals of the Earth’s upper mantle. Glasses of chalcogenide are the topic of high interest in the reference of their photo structural sensitivity, high infrared transparency, and their doping ability [1]. In the recent years, glasses of the regular As₄S₄ like composition have been obtained under high pressure [2, 3]. Organic materials such as naphthalene, anthracene have potential application in the area of organic semiconductors, smokes screens, production of dyes. Present study of these crystals open a new field for researcher because at high pressure, materials can change their fundamental structural properties and new materials with unique properties can emerge [4].

As temperature and chemical composition is a variable of great interest for condense phase, pressure have become very important quantity for high pressure techniques. High pressure can change the atomic spacing, Gibbs free energy and chemical bonding of materials [5, 6]. Grüneisen parameter ($\gamma$) is another very important parameter for geophysicist because it is approximately constant under the application of high temperature and pressure [7, 8]. The experimental determination of Grüneisen parameter is very difficult, so this is a theoretical topic of great interest for researcher. In the present work we have established the theoretical graph between Grüneisen parameter and volume compression ratio and will observe that for which EOS the variation of Grüneisen parameter with V/V₀ is in agreement with the available fact that Grüneisen parameter is almost constant under high pressure [7, 8]. To investigate the variation of Grüneisen parameter with compression under high pressure for Realgar As₄S₄, As₄S₃, C₁₄H₁₀ (anthracene) and C₁₀H₈ (naphthalene), we have used four different EOSs viz. modified Lenard-Jones EOS (M-L Jones EOS), Brennan-Stacey EOS, Hamma—Suito EOS and Thomsen EOS. These EOS will be probably give an accurate idea about variation of Grüneisen parameter under high pressure and this work will also be able to predict about which EOS is best to explain the thermo elastic properties of these inorganic and organic crystals.

2 Method of analysis

To investigate thermo elastic properties of Realgar As₄S₄, As₄S₃, C₁₄H₁₀ (anthracene) and C₁₀H₈ (naphthalene), we have used four different EOSs viz. modified Lenard-Jones EOS (M-L Jones EOS), Brennan-Stacey EOS, Hamma—Suito EOS and Thomsen EOS. These EOSs are given below.

2.1 The modified Lenard Jones EOS (M L-Jones EOS) [9]

This EOS is based on generalized Lenard-Jones potential and is given below:

$$P = \left( {\frac{{K_{0} }}{m}} \right)\left( s \right)^{ - m} \left[ {s^{ - m} - 1} \right]$$

(1)

where $m = \frac{{{K_{0}}^{\prime} }}{3}$ and $s = \left( {\frac{V}{{V_{0} }}} \right)$.

2.2 Brennan-Stacey EOS [10, 11]

Brennan-Stacey EOS have derived an EOS using thermodynamic formulation for Gruneisen parameter

$$P = \frac{{3K_{0} x^{ - 4} }}{{({3K_{0}}^{\prime} - 5)}}\left[ {\exp \left\{ {\frac{{({3K_{0}}^{\prime} - 5)(1 - x^{3} )}}{3}} \right\} - 1} \right]\quad$$

(2)

where $x= \left( {\frac{V}{{V_{0} }}} \right)^{\frac{1}{3}}$

2.3 Thomsen EOS [12, 13]

Using the finite strain concept, where strains are uniquely determined by hydrostatic pressure, Thomsen suggested new EOSs given as:

$$P = \frac{{3K_{0} }}{2}\left[ {\left( s \right)^{{ - \frac{1}{3}}} - \left( s \right)^{\frac{1}{3}} } \right]\quad \left[ {1 + \frac{3}{4}{K_{0}}^{\prime} \left( {1 - \left( s \right)^{\frac{2}{3}} } \right)} \right]\quad \quad \quad \quad \quad \quad \quad \quad$$

(3)

where $s = \frac{V}{{V_{0} }}$.

2.4 Hama–Suito EOS [7, 14]

Hama and Suito used first principles method based on QSMs and APW method and obtained new EOS known as Hama-Suito EOS.

$$P = 3K_{O} s^{ - 5} (1 - s)\exp \quad \left[ {\frac{3}{2}\left( {{K_{0}}^{\prime} - 3} \right)\left( {1 - s} \right) + \left( {z - \frac{3}{2}} \right)\left( {1 - s} \right)^{2} } \right]\quad \quad \quad \quad \quad \quad \quad \quad$$

(4)

where $s = \left( {\frac{V}{{V_{0} }}} \right)^{\frac{1}{3}}$

$$z = \frac{3}{8}\left( {{K_{0}}^{\prime} - 1} \right)\left( {K_{0}^{\prime} + 3} \right) - \frac{3}{5}{K_{0}}^{{\prime}^{2}} + \frac{1}{3}$$

The value of Bulk modulus can be computed by the formula $K{}_{T} = - V\left( {\frac{\partial P}{{\partial V}}} \right){}_{T}$ using Eqs. (1), (2), (3) and (4). The first pressure derivative of bulk modulus can be calculated by using formula ${K_{T}}^{\prime} = \left( {\frac{{\partial K_{T} }}{\partial P}} \right)_{T}$.

2.5 Grüneisen parameter

Borton and Stacey suggest a formula to calculate the value of Gruneisen parameter $(\gamma )$ at different compressions [15]:

$$\gamma = \frac{{\left( \frac{1}{2} \right)K^{\prime} - \frac{1}{6} - \frac{h}{3}\left[ {1 - \frac{1}{3}\left( {\frac{P}{{K_{T} }}} \right)} \right]}}{{1 - \left( \frac{4}{3} \right)\left( {\frac{P}{{K_{T} }}} \right)}}$$

(5)

where $h$ = 2.35.

3 Result and discussion

For predicting the thermo elastic properties of inorganic and organic crystal from EOSs we have used two input parameter K₀ and ${K_{0}}^{\prime}$ known as bulk modulus and pressure derivative of bulk modulus respectively at zero pressure. The value of these parameter is depend on materials, so different materials have different value of K₀ and ${K_{0}}^{\prime}$. The value of input parameters used in the present study is given in the following table:

Crystals	K0(GPa)	${K_{0}}^{\prime}$	Reference
Realgar As4S4	8.1	9	[3]
As4S3	17	5.5	[16]
C14H10 (anthracene)	7.5	7.3	[17]
C10H8 (naphthalene)	6.727	7.13	[17]

3.1 Theoretical prediction for Realgar As₄S₄

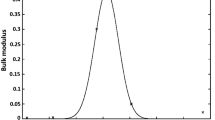
We have tried to predict the elastic properties of Realgar As₄S₄ using four different EOSs namely modified Lenard-Jones EOS (M-L Jones EOS), Brennan-Stacey EOS, Hamma—Suito EOS and Thomsen EOS. The theoretically calculated values are shown in the Figs. 1, 2, 3 and 4.

Fig. 1

Graph between pressure and volume compression ratio for realgar As₄S₄

Fig. 2

Graph between bulk modulus and volume compression ratio for realgar As₄S₄

Fig. 3

Graph between pressure derivative of bulk modulus and volume compression ratio for realgar As₄S₄

Fig. 4

Graph between Grüneisen parameter and volume compression ratio for realgar As₄S₄

Figure 1 represents the theoretical graph plotted between Pressure and corresponding volume compression ratio. All the four EOSs give exactly same results up to compression ratio of 0.85. This implies that if realgar As₄S₄ is compressed up to 15% of its initial volume, all the EOSs can be equally apply for computation of pressure at different compressions. But after that it shows the abrupt behaviour. If we compress As₄S₄ beyond the compression ratio 0.85, Thomsen EOS start deviating from other three EOS viz. modified Lenard-Jones EOS (M-L Jones EOS), Brennan-Stacey EOS and Hamma–Suito EOS. Further, the Hama–Suito EOS deviates with modified Lenard-Jones EOS (M-L Jones EOS) and Brennan-Stacey EOS beyond compression ratio 0.75. Also, from Figs. 2 and 3 it is clear that modified Lenard Jones EOS and Brennan Stacey EOS gives very similar result both at low compression ratio as well as at moderate pressure but at high pressure they shows deviation with each other.

Further from Fig. 4 we notice that Grüneisen parameter decreases as the volume of realgar As₄S₄ decrease but the decrement from modified Lenard Jones EOS is very slow. The slope of curve obtained from modified Lenard Jones EOS is minimum in comparison to other three EOSs [7, 8]. The above discussion signifies that modified Lenard Jones EOS is best EOS to explain the elastic properties of realgar As₄S₄. Also from Fig. 4, We notice that the values of Grüneisen parameter obtained from Thomsen EOS gives negative result beyond compression ratio of 0.7. Graph from Thomsen EOS is not a straight line, so it is not applicable for calculation of compression dependence of Grüneisen parameter even at low compression range for realgar As₄S₄. The values obtained from Thomsen EOS also deviate from the available fact that the ratio γ/Ω (where Ω = V/V₀) of Gruneisen parameter to volume is constant for solids [18].

3.2 Theoretical prediction for As₄S₃

Modified Lenard-Jones EOS (M-L Jones EOS), Brennan-Stacey EOS, Hamma–Suito EOS and Thomsen EOS have been used to predict the elastic properties of As₄S₃. The theoretically calculated values are shown in the Figs. 5, 6, 7 and 8.

Fig. 5

Graph between pressure and volume compression ratio for As₄S₃

Fig. 6

Graph between bulk modulus and volume compression ratio for As₄S₃

Fig. 7

Graph between pressure derivative of bulk modulus and volume compression ratio for As₄S₃

Fig. 8

Graph between Grüneisen parameter and volume compression ratio for As₄S₃

Figure 5 corresponds to graph between pressure and volume compression ratio. The results obtained from all the four EOSs are very similar up to compression ratio of 0.85. So, all the four EOSs are equally applicable for calculations of pressure in compression of As₄S₃ up to 15% of its initial volume. After the compression ratio of 0.85, Thomsen EOS start deviating from other three EOS viz. modified Lenard-Jones EOS (M-L Jones EOS), Brennan-Stacey EOS and Hamma–Suito EOS. Further, the Hama-Suito EOS deviates with M-L Jones EOS and Brennan-Stacey EOS beyond compression ratio 0.75. Also, from Figs. 6 and 7 it is clear that modified Lenard Jones EOS and Brennan Stacey EOS gives very similar result both at low compression ratio as well as at moderate pressure but at high pressure they shows deviation with each other.

Further from Fig. 8 we notice that Grüneisen parameter declines as the compression on As₄S₃ increases. The slope of straight line obtained from modified Lenard Jones EOS is minimum in comparison to other three EOSs. The above discussion signifies that modified Lenard Jones EOS is best EOS to explain the elastic properties of As₄S₃. The values obtained from Thomsen EOS also deviate from the available fact that the ratio γ/Ω (where Ω = V/V₀) of Gruneisen parameter to volume is constant for solids [18].

3.3 Theoretical prediction for anthracene

Figures 9, 10, 11 and 12 represent the thermo elastic properties of anthracene at different value of compressions.

Fig. 9

Graph between pressure and volume compression ratio for anthracene

Fig. 10

Graph between bulk modulus and volume compression ratio for anthracene

Fig. 11

Graph between pressure derivative of bulk modulus and volume compression ratio anthracene

Fig. 12

Graph between Grüneisen parameter and volume compression ratio for anthracene

Further from Fig. 12, we notice that Grüneisen parameter declines as the volume of anthracene decrease The slope of straight line obtained from modified Lenard Jones EOS is minimum in comparison to other three EOSs. The above discussion indicates that modified Lenard Jones EOS is best EOS to explain the thrmo elastic properties of anthracene. Also from Fig. 12, we notice that the values of Grüneisen parameter obtained from Thomsen EOS gives negative result beyond compression ratio of 0.75. Graph from Thomsen EOS is not a straight line, so it is not applicable for calculation of compression dependence of Grüneisen parameter even at low compression range for anthracene. The values obtained from Thomsen EOS also deviate from the available fact that the ratio γ/Ω (where Ω = V/V₀) of Gruneisen parameter to volume is constant for solids [18].

3.4 Theoretical prediction for Naphthalene

Thermo elastic properties of Naphthalene can be studied from Figs. 13, 14, 15 and 16 shown below.

Fig. 13

Graph between pressure and volume compression ratio for naphthalene

Fig. 14

Graph between bulk modulus and volume compression ratio for naphthalene

Fig. 15

Graph between pressure derivative of bulk modulus and volume compression ratio for naphthalene

Fig. 16

Graph between Grüneisen parameter and volume compression ratio for naphthalene

From Figs. 13, 14, 15 and 16, we can see that the best EOS to explain the thermo elastic properties of naphthalene is modified Lenard Jones EOS because the graph plotted between Thomsen EOS and volume compression ratio (Fig. 16) is straight line as well as have minimum slope. The values obtained from Thomsen EOSs are negative at high compression range and the graph is also not a straight line, so Thomsen EOS is less useful to calculate thermo elastic properties of naphthalene. The values obtained from Thomsen EOS also deviate from the available fact that the ratio γ/Ω (where Ω = V/V₀) of Grüneisen parameter to volume is constant for solids [18].

The values obtained for Grüneisen parameter at different compressions from modified Lenard-Jones EOS (M-L Jones EOS), Brennan-Stacey EOS, Hamma—Suito EOS are in agreement with the work of S. Srivastava et al. on Grüneisen parameter [19].

4 Conclusions

The overall discussion leads to the result that Thomsen EOS is not useful to calculate the Grüneisen parameter even at low compression range. Thomsen EOS give negative value of Grüneisen parameter at high compression range (beyond compression value of 0.75). Further, modified Lenard Jones EOS is best EOS in compression to other three (Brennan-Stacey EOS, Hamma–Suito EOS and Thomsen EOS) to explain thermo elastic properties of Realgar As₄S₄, As₄S₃, C₁₄H₁₀ (anthracene), C₁₀H₈ (naphthalene).