1 Introduction

Perovskites are a family of materials that may be differentiated from other types of materials due to the crystal structures of their perovskite crystals, which are analogous to CaTiO3 crystal structures. It was first found in Russia in 1839 by Gustave Rose, and the name "perovskite" was given to the mineral in honour of a Russian mineralogist who went by the name L.A. Perovski [1]. The class of naturally occurring compounds known as perovskites can be identified by their overarching chemical formula, which is written as ABX3, and they are given the name perovskite. Perovskite oxides, on the other hand, have structures that are denoted by the generic formula ABO3 [2,3,4,5]. The formation of perovskite occurred spontaneously and took the form of halides and oxides, both of which can be found in significant amounts. In the realm of technology, the most cutting-edge ones have a big impact and can be applied in a variety of contexts. The structural and compositional diversity of these materials greatly influences their characteristics [6,7,8]. Both experimentalists and theoreticians are currently looking for perovskite compounds that can improve their performance for specific functionalities and suit the needs of specific applications [9,10,11]. This is of paramount importance to the field of materials science; halide perovskites, for instance, are being put to use in solar cell applications [4,5,6,7]. Transducers, solar cells, ferroelectric, and piezoelectric devices all benefit greatly from the use of oxide-based perovskites because of the material's versatility. There is a wide variety of perovskites, all of which share the general formula ABO3 (where the A atom is 9–12-fold coordinated by oxygen, the B atom is sixfold coordinated by oxygen, and BO6 octahedra are corner-connected. The majority of these devices are made from lead-based materials like PbTiO3, Pb(Zr,Ti)O3, and Pb(Mg,Nb)O3. The fact that lead is poisonous restricts the ways in which it can be used in modern gadgets. It is necessary to develop alternatives to lead-based materials that have the same structure as well as other physical qualities [12, 13]. There has been a lot of research done on lead-free perovskites because of their high strain capacities and wide range of practical applications [14,15,16,17]. Examples of these uses can be found in aeroplanes, nanoelectronics devices, waveguides, actuators, and sensors. Furthermore, these materials have received a lot of attention due to the ease with which they can be synthesized, the unique electrical structure findings that they provide, and their physical properties. These desirable qualities can be attributed, in large part, to the highly correlated electrons in the d and f bands as well as the strong electron-lattice couplings [18]. These materials have found significant use in a wide range of devices and industries, including optoelectronics, thermoelectric, and laser frequency doubling waveguide, making them ideal for cutting-edge technological applications [19,20,21]. Other examples of applications include laser frequency doubling waveguides. High-temperature superconductors, colossal magneto-resistors, and multiferroic materials are only some of the out-of-the-ordinary uses proposed for these materials [22,23,24,25]. The aforementioned studies highlight the advancement in the precision of first-principles calculations on ABO3 perovskite compounds. Although these compounds initially seem to have many degrees of freedom and complexity, first-principle calculations have made it simpler to comprehend the structure and several distinctive properties of these compounds. Possibilities for the creation of innovative materials are opened up by understanding at the microscopic level. First-principles calculations can provide a more accurate link between the real system and the simplified model to comprehend the underlying physics, resulting in conceptual advancements and greater interaction between theory and experiment. In the current study, we examined two distinct ABO3-based perovskite compounds that include XReO3 (where X = Na and K). This study presents a comparative analysis of the aforementioned content. Utilizing Density Functional Theory, we examined its elastic, mechanical, and thermodynamic properties for industrial purposes (DFT). In addition, properties are investigated under FP-LAPW-GGA (PBE). The recommended materials were examined for the first time. First investigations have been carried out into the cubic compounds NaReO3 and KReO3. There is currently no data available for the suggested materials.

2 Computational method

The density functional theory (DFT) has been shown to be the most influential, acceptable, and approximate method for describing the physical properties of solids [26, 27]. The Full-potential Linearized Augmented Plane Wave (FPLAPW) method [28], which is built into WIEN2k [29], is used to determine the physical properties of the present perovskite oxide XReO3 (where X = Na and K). Within the framework of the Perdew, Burke, and Ernzerhof (PBE) method [30], the generalized gradient algorithm (GGA) was used to optimize the structures of the perovskite compounds XReO3 (where X = Na and K). The structural properties of XReO3 perovskites were examined and measured at a mesh size of 1000 k-points (10 × 10 × 10). The value of Kmax × RMT can be predicted with the help of the convergence test. This test assumes that the calculation has converged if (Kmax × RMT = 7.0), where RMT is the diameter of the muffin tin and Kmax is the cut-off for plane waves in the reciprocal lattice vector. The following expressions that represent the radius of a muffin tin for each atom were chosen to be: RMT  = 2.22, Na = 2.01, Re = 1.98, and O = 2.06 The Charpin method [31] was employed for the elastic constants. The calculation was done at the equilibrium lattice constants, which are found by plotting the total energy against the unit cell volume and fitting that to the Birch–Murnaghan equation of state [32]. To compute the elastic properties of the studied XReO3 (where X = Na and K) compounds IRELAST method as implemented in WIEN2K code [33, 34]. The quasi-harmonic Debye model [35] is presented here in order to determine the thermodynamic characteristics of the cubic compound XReO3 (where X = Na and K).

3 Results and discussion

3.1 Structural properties

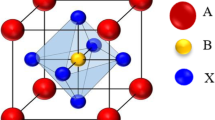
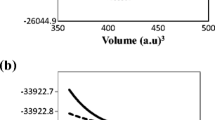
In this set of computations, the ground-state stable structure at 0 GPa pressure is taken into consideration. This structure has the atomic positions (X = Na and K) at (0, 0, 0); O at (1/2, 1/2, 0); (1/2, 0, 1/2); and (0, 1/2, 1/2); and Re at (1/2, 1/2, 1/2) in its cubic Pm-3m structure as shown in Fig. 1. The energy-volume optimization was accomplished by using the Birch–Murnaghan equation to determine the lattice parameters, which were then used to calculate the thermodynamic properties of the present oxides NaReO3 and KReO3 within the quasi-harmonic Debye model [36]. This allowed for the achievement of the energy-volume optimization goal. In order to determine the ground state parameters of NaReO3 and KReO3, we fit the data to Murnaghan's equation of state [32], which is depicted in Fig. 2 as the total energy as a function of the volume of the unit cell. These ground state properties include the equilibrium lattice parameter (a0), total energies (E0), bulk modulus (B0), and its pressure derivatives (B0'). Table 1 provides a summary of the previously acquired results as well as the computed parameters of the ground state that were obtained by applying the GGA approach. When we compare our findings to those of earlier theoretical calculations, we find that there is a high degree of congruence between the two sets of data. This was discovered when we performed an analysis of the results of B0 and B’. As a result of our work, we have determined that the optimized lattice parameters for NaReO3 are a = 3.887 Å, whereas the optimized lattice parameters for KReO3 are a = 3.930 Å, respectively. It is important to keep in mind that when the atomic number increases from K to Na, the lattice parameters also increase. The accumulation of electron layers is to blame for this phenomenon. It is thought that the equilibrium volume of XReO3 (X = Na, K) cubic perovskite will be controlled by a certain type of XRe sub-lattice. Figure 2 demonstrates that the ground state of KReO3 is the most energy-efficient compared to NaReO3. In NaReO3ant perovskites, the inter-atomic distances are Na–O = 2.74 Å, Re–O = 1.94 Å and Na–Re = 3.36 Å, whereas in KReO3, the inter-atomic distances are K–O = 2.78 Å, Re–O = 1.96 Å and K–Re = 3.41 Å. This indicates that the directional O–Re bonds in (NaReO3 or KReO3) ought to be the strongest. The formation energy (Ef) is written as the difference between the total energy (ET) and the sum of the atomic energies of all the individual atoms at the stable crystal structure as follows:

$$E_{{{\text{form}}}}^{{{\text{XReO}}_{3} }} = E_{{\text{T}}} - \left[ {E_{{X = {\text{Na}},\;{\text{K}}}} + E_{{{\text{Re}}}} + 3E_{{\text{O}}} } \right]$$
(1)
Fig. 1
figure 1

Crystal structure of XReO3(X = Na, K)

Full size image
Fig. 2
figure 2

Energy versus volume in PBE-GGA: a NaReO3, b KReO3

Full size image
Table 1 Ground state structural parameters of the XReO3 (X = Na, K) by PBE-GGA
Full size table

The computed values of formation energies are − 1.932 eV/atom, − 1.920 eV/atom, which is conducive to the crystal favourable allowing stability for the cubic oxide perovskite XReO3 (X = Na, K).

3.2 Electronic properties

Electronic results (band structure and density of state results) for all of these materials have been calculated in PBE-GGA. The bandgap in the band structure may have a role in the explanation for the electron transition [38,39,40]. Band structures are depicted in the region of maximum symmetry defined by the Brillouin zone. Figure 3a, b shows the band structure results for XReO3 (X = Na, K). Results from the study of the band structure show that both compounds are metallic with no energy separation between the conduction and valence bands. Both compounds were discovered to have electrons at the Fermi level. The density of states (DOS) provides illustrative evidence of the band structure conclusions reached for these substances [41, 42]. DOS diagrams (Fig. 3a, b) have been produced for XReO3 (X = Na, K) to help make the band results more evident. DOS data for Na–p, K–p, Re–p, d, and O–p have been plotted. DOS readings reveal nearly identical metallic characteristics for both compounds. It was observed that both the Re–d and O–p states pass the Fermi level in each of these compounds, which explains why they have a metallic quality. Bands generated by Na and K atoms at X sites are located in the valence or conduction band, respectively. The Na-p states of NaReO3 can be seen in the 1–4 eV conduction band region of Fig. 3a. Figure 3b shows that the Cs–d states of KReO3 are in the 0–4 eV region of the conduction band. Figure 3a, b shows the nature of compound is metallic.

Fig. 3
figure 3

Band structure, Total and partial density of states within PBE-GGA: a NaReO3 and b KReO3

Full size image

3.3 Elastic and mechanical properties

The mechanical stability, hardness, plastic twist, and other aspects of a material's mechanical properties can all be greatly impacted by the material's elastic constants, which are always considered to be fundamental for the purpose of understanding the essential features that comprise its mechanical properties. The elasticity values for XReO3 (where X = Na and K) perovskite compounds have been computed using the Charpin technique [31], which has been implemented in the WIEN2k package [29]. These calculations have been done under ambient pressure. Elastic constants have been computed with the assistance of the GGA. Because both compounds are stable in the cubic phase, the mechanical stability has been proven by lowering the number of dependent elastic constants from 21 to just three independent elastic constants. These three independent elastic constants are represented by the symbols C11, C12, and C44. The stability requirements for the cubic phase are as follows, and it was discovered that the computed values of these elastic constants [43, 44] match those requirements.

$$\left( {{\text{C}}_{{{11}}} {-}{\text{C}}_{{{12}}} } \right) > 0,$$
(2)
$${\text{C}}_{{{11}}} > 0,$$
(3)
$${\text{C}}_{{{44}}} > 0,$$
(4)
$$\left( {{\text{C}}_{{{11}}} + {\text{ 2C}}_{{{12}}} } \right) > 0,$$
(5)
$${\text{C}}_{{{12}}} < {\text{B}} < {\text{C}}_{{{11}}}$$
(6)

The computed values of elastic constants are shown in Table 2, and it is evident that the mentioned restrictions of the elastic value are properly followed by both of the compounds; as a result, they are mechanically stable [45]. This is because both compounds adhere to the mentioned restrictions of the elastic value. There are many mechanical properties that may be calculated with the use of the elastic constants and their values. The Young's modulus (Y), the shear modulus (G), the bulk modulus (B), and the Poisson's ratio are all examples of such characteristics (v). In order to examine the material's stiffness, plastic twist, and strength, certain conditions must be met. Utilizing the computed values of elastic constants is required in order to derive Hill's shear modulus GH; this modulus is an arithmetic mean of the (GR) Reuss and (GV) Voigt approximations [46].

Table 2 Values of elastic constants (Cij), bulk modulus (B), shear modulus (G), Young’s modulus (Y), Poisson’s ratio (σ), Pugh ratio, Frantsevich ratio, Shear anisotropy factor (A) Cauchy pressure CP, sound velocities (m/s), Debye Temperature ΘD (K) of XReO3(X = Na, K)
Full size table

These mechanical characteristics and their derived values are listed in Table 2. It is necessary to measure the Young's modulus (Y) and bulk modulus (B) of the material in order to get its hardness and strength. Calculated values for XReO3 (X = Na and K) are 289.63 and 270.89 GPa, respectively. We have also determined the bulk modulus for these substances. In the case of XReO3 (X = Na and K), the computed values of B are 216.17 and 151.206 GPa, respectively. Young's modulus and bulk modulus measurements show that both compounds are sufficiently stiff and robust. Therefore, these compounds can be used to create electrode materials for fuel cells and may play an essential role in the production of ultra-hard devices. The ductility of these materials was determined by calculating the ratio of their bulk modulus to their shear modulus (B/G), which was a concept put forth by Pugh [47]. Pugh's criteria state that a material is considered to have ductile behaviour if the B/G ratio of the material is more than 1.75; otherwise, the material is considered to have brittle behaviour [47]. The computed value of B/G for XReO3 (where X = Na and K) came out to be 1.89, and the respective value for G was found to be 1.34. As a result of this, it is evident from the B/G value that NaReO3 will have a ductile nature, but KReO3 would behave in a brittle manner. Cauchy's pressure (C12–C44) value has been examined further in order to gain a better understanding of the ductility and brittleness of this material. If the value of this parameter is positive, it indicates that the material is ductile; otherwise, it indicates that the material is brittle [48]. The value that was computed for (C12–C44) turned out to be positive for NaReO3, while the value that was calculated for KReO3 turned out to be negative. Therefore, it was determined, based on Pugh's criteria as well as Cauchy's pressure that NaReO3 will exhibit a ductile character, whereas KReO3 will demonstrate a brittle nature. Poisson's ratio is an additional characteristic that helps to designate the ductility and brittleness of a material. The Frantsevich rule states that brittle behaviour is exhibited by a material if it is less than 0.26 and the substance is not otherwise ductile. It was determined that the value of for NaReO3 was greater than or equal to 0.26, but the value for KReO3 was less than or equal to 0.26. Therefore, according to, NaReO3 should be considered ductile, whereas KReO3 should be considered brittle, as seen in Table 2. Also, Poisson's ratio can be used to learn about the bonding structure of a substance. If the value of this ratio is less than 0.10, the bonding in the material is said to be covalent; if it is between 0.25 and 0.33, the bonding is said to be ionic; and if it is larger than 0.33, the material is said to be metallic. The value of drops to 0.277 as a consequence of our experiments, which is extremely near to 0.25 for NaReO3 and 0.201 for KReO3; thus, NaReO3 and KReO3 will exhibit ionic bonding. We have determined the anisotropic factor A, stands for the elastic anisotropy and isotropy. This is part of our ongoing effort to gain a better understanding of the characteristics of elasticity in various directions. If a material is isotropic, then its value of A will be equal to unity; if it is anisotropic, then it will have a value that deviates from unity. For the NaReO3 compound, the calculated value of A is non-unity, but for the KReO3 compound, it is 1. In this way, NaReO3 will exhibit elastic anisotropy, whereas KReO3 maintains elastic isotropy. We have also determined the melting point (Tm) for these substances. In terms of its physical qualities, as shown by Cauchy's pressure CP, it has been demonstrated that KReO3 is more brittle than NaReO3. Another illustrative way to demonstrate the elastic anisotropy of any material is by visualizing the mechanical moduli in three-dimensional (3D) surface. For a cubic crystal, the crystallographic direction dependence of the bulk modulus B, Young’s modulus E and shear modulus G are computed by using the following expressions:

$$\frac{1}{B} = \left( {S_{11} + 2S_{12} } \right)\left( {l_{1}^{2} + l_{2}^{2} + l_{3}^{2} } \right)$$
(7)
$$\frac{1}{E} = S_{11} - 2\left( {S_{11} - S_{12} - \frac{1}{2}S_{44} } \right)\left( {l_{1}^{2} l_{2}^{2} + l_{2}^{2} l_{3}^{2} + l_{3}^{2} l_{1}^{2} } \right)$$
(8)
$$\frac{1}{G} = S_{44} - 4\left( {S_{11} - S_{12} - \frac{1}{2}S_{44} } \right)\left( {\sin^{2} \theta \cdot \cos^{2} \theta + 0.125\sin^{4} } \right)\left( {1 - \cos 4\varphi } \right)$$
(9)

Here, Sij are the contents of the elastic compliance constants matrix, which are obtained from the inverse of the elastic constant matrix (\(S_{ij} = C_{ij}^{ - 1}\)), and their values are depicted in Table 2. l1, l2 and l3 are the direction cosines in accordance with the x-, y- and z-axes, respectively. If the 3D directional-dependent surface is exactly of spherical shape, the material is characterized as isotopic, but if the surfaces are non-spherical, indicating their character as anisotropic. The three-dimensional surfaces with their 2D projections of different planes [100], [010] and [001] of the bulk, Young’s and shear moduli for the studied compounds are illustrated in Fig. 4a, b, respectively. As shown in Fig. 4a, b, the 3D plot surface of the bulk modulus represents a perfect spherical form for the title compounds, revealing them as isotropic materials. We can note substantial deviation from the shape of the sphere for the shear modulus and Young's modulus, hence revealing that the shear modulus demonstrates a larger degree of anisotropy. From the 2D plane projections, it is clear that bulk moduli values at different planes have an isotropic character, while the non-circular shape of Young’s modulus and shear modulus reveals greater anisotropic behaviour for G than E.

Fig. 4
figure 4figure 4

a 3D-directional representation of the Bulk modulus (B, in GPa), Young modulus (E in GPa) and Shear modulus (G, in GPa) and their projections in different planes (100), (010) and (001) for NaReO3. b 3D-directional representation of the Bulk modulus (B, in GPa), Young modulus (E in GPa) and Shear modulus (G, in GPa) and their projections in different planes (100), (010) and (001) for KReO3

Full size image

Through the use of elastic constant values, melting temperature (Tm) value has been determined. The melting point values reported in Table 2 show that both the compounds under study have sufficiently high melting points with values 3366.42 for NaReO3 K and 2334.13 K for KReO3 compounds. Table 2 displays the computed values for the melting temperature, the Debye temperature, the average sound velocity, and the transverse sound velocity. According to the results, NaReO3 has a greater Debye temperature than KReO3. As a result, NaReO3 is superior to KReO3 in terms of energy storage capacity. Our calculated values of average sound velocity and are 7117.11 m/s, 3951.04 m/s, 4400.74 m/s and 576.13 K for NaReO3, respectively, while it is 6351.54 m/s, 3883.79 m/s, 4288.28 m/s and 555.44 K for KReO3 within PBE-GGA.

3.4 Thermodynamic properties

The thermodynamic characteristics of XReO3 (X = Na and K) materials are studied here using the quasi-harmonic Debye approximation [49,50,51,52] Thermodynamic properties including specific heat at constant volume (Cv), thermal expansion (\(\alpha\)), and the Debye temperature (\({\theta }_{\mathrm{D}}\)) have been determined as a function of a pressure range of 0–161 GPa and a temperature range of 0–1200 K (200 K steps) (step size of 20 GPa). It has been shown that the quasi-harmonic Debye model works well for temperatures between 0 and 1200 K. Unit cell volume changes for XReO3 (X = Na and K) as a function of pressure and temperature are shown in Fig. 5a, b. Temperature and pressure have opposite impacts on cell volume for both substances. When the pressure is raised, the volume decreases, but when the temperature rises, the volume expands. It is important to note that, in general, all solids tend to get smaller when they are pressed and bigger when they are heated.

Fig. 5
figure 5

a, b Volume (V), c, d Bulk modulus (B) as a function of temperature and pressure for XReO3 (X = Na, K)

Full size image

It is commonly known that the stiffness resistance of a material is related to a material's bulk modulus, or B. In Fig. 5c, d, the fluctuation in the value of B has been displayed as a function of both the temperature and the pressure, respectively, for XReO3 (X = Na, K). It can be seen quite linearly from Fig. 5c, d that the value of B remains unaffected by changes in temperature, but it demonstrates an ascending trend in response to reductions in pressure. This holds true for both of the materials that are being taken into account. This increase and decrease in B with pressure and temperature is due to the fact that volume decreases with rising pressure and volume increases with lowering temperature. At 0 GPa of pressure and all temperatures, the calculated value of B for XReO3 (where X = Na and K) was obtained to be 210 and 200 GPa, respectively.

Figure 6a, b depicts the entropy of the proposed materials, which was measured to be 12.0 J/molK at 100 K temperature and maximum at 0 GPa pressure for NaReO3 and 12.5 J/molK at 100 K temperature for the KReO3 compound. Both of these values were found to be maximums. A plot of the thermal expansion coefficient "α" versus temperature and pressure is shown in Fig. 6c, b. These statistics make it very easy to see that the value climbs sharply under low temperatures up to 300 K, whereas it climbs steadily and linearly under high temperatures. This can be seen by comparing the two sets of data. It is possible that this is because of the saturation of up to 300 K. The value for NaReO3 was calculated to be 2.4 × 10−5 per Kelvin, but the value for KReO3 was 3 × 10−5 per Kelvin. It has been discovered that pressure may bring the value down. However, when the temperature is raised, the effect of pressure on the value becomes more prominent and falls more quickly. This is because the quasi-harmonic model does not work well when low pressure and high temperature are both present.

Fig. 6
figure 6

a, b Entropy (S), c, d thermal expansion (α) as a function of temperature and pressure for XReO3 (X = Na, K)

Full size image

The Gruneisen parameter (γ) was used in order to determine the thermodynamic properties of the material when it was subjected to high temperatures and pressures [53]. This parameter reflects the anharmonicity that exists within the crystal. In addition to this, it depicts the relationship between temperature and pressure in terms of phonon frequencies, also known as vibrational frequencies. As a result, we were finally able to calculate the pressure and temperature dependence of XReO3 (X = Na and K) as shown in Fig. 8a, b. The value of g gradually climbs upward as the temperature continues to rise, while it heads downward as pressure continues to rise. For NaReO3, the value that was estimated under ambient circumstances was found to be 1.73295, and this value remains the same across all temperatures and pressures up to 100 GPa.

There are several additional thermodynamic parameters, such as the solid heat capacity and melting temperature, that are connected to the Debye temperature (θD). As shown in Fig. 7c, d, the Debye temperature of XReO3 (X = Na and K) varies with both temperature and pressure. When comparing the two graphs, it is evident that the value of θD decreases extremely slowly but nearly becomes constant across a wide range of temperatures and high pressures. At 0 GPa pressure, it is decreasing with rising temperature for both the compounds. The value of θD is observed to grow with pressure at a certain temperature. For X = Na and K, the calculated value of θD for XReO3 at 0 GPa pressure and 300 K temperature is 575 and 570.05 K, respectively.

Fig. 7
figure 7

a, b Gruneisen parameter (γ) c, d Debye temperature (θD) as a function of temperature and pressure for XReO3 (X = Na, K)

Full size image

The effect of temperature and pressure on the specific heat capacity (CV) is shown graphically in Fig. 8a, b. One find striking similarities when comparing the CV diagrams of various substances. At temperatures below 300 Kelvin (K), CV increases at an exponential rate; from 300 to 700 K, CV increases at a slower rate; and at temperatures beyond 700 K, CV is nearly constant. The well-known Debye model (CV(T)/T3) predicts that CV will increase at low temperatures. This is because it is only the long-wavelength vibration modes of the lattice that are occupied, and it is possible to approach these modes if the lattice is treated as a continuum [54]. However, the classical conduct (CV(T)/3R for mono-atomic materials) is found at sufficiently high temperatures, as predicted by Petit and Dulong's law [55]. The computed values of CV at 0 GPa and 300 K were found to be 104 and 105 (J mol−1 K), respectively, for XReO3 (X = Na and K).

Fig. 8
figure 8

a, b Specific heat capacity at constant volume (Cv), c, d specific heat capacity at constant pressure (Cp) as a function of temperature and pressure for XReO3 (X = Na, K)

Full size image

The heat capacity Cp temperature diagram is depicted in Fig. 8c, d, which shows the relationship between the two variables at varying pressures. The fluctuation characteristics of Cp values at lower temperatures, which are comparable to those of Cv, become more pronounced as the temperature rises. The change in Cp, on the other hand, behaves differently from the change in Cv when the temperature is high. The critical pressure (Cp) values drop when the pressure is increased and do not converge to a single value. When the temperature is raised, there is a discernible rise in the heat capacity.

4 Conclusions

In this work, we have performed ab initio calculations on the structural, elastic, and thermodynamic properties for the cubic XReO3 (X = Na and K) using the FP-LAPW method. The exchange correlations PBE-GGA has been used to predict the structural ground state details. The structural ground state details have been predicted using the exchange correlation PBE-GGA. The computed lattice constant and bulk modulus, as well as other ground-state parameters, are in good agreement with the other available theoretical results. According to the electrical structure calculations, cubic XReO3 (X = Na and K) has a zero-band gap and show metallic behaviour. Young’s modulus and bulk modulus are two measures of the brittleness of the materials in both the compounds, and both can be used in the construction of fuel cell electrodes. The cubic compound NaReO3 is found to be ductile, whereas KReO3 was found brittle from the Poisson’s ratio (ν), Cauchy’s pressure (C12–C44), and Pugh ratio (B/G). The NaReO3 compound was found to be elastically anisotropic, whereas KReO3 maintains elastic isotropy. Through the quasi-harmonic Debye model, the dependence of the bulk modulus, lattice constant, specific heat capacities and Debye temperature on pressure and temperature have been predicted.