1 Introduction

Research on Nanomaterials is very hot topic for the researcher because of their demand in different sectors (Industrial area, Biological area, application in electrical area etc.). Nanomaterials not just nano sized materials but this is a entirely different area because at this level a lot of properties of materials are governed by quantum mechanics. In this paper our main concern is on carbon nanotubes (CNTs) because in the field of nanotechnology CNTs are unique and are material of future. In the present work we have theoretically predicted the thermo elastic properties of carbon nanotubes. We have used three different Equation of states (The modified Lenard Jones EOS, Birch–Murnaghan (3rd) EOS, Vinet–Rydburg EOS) for calculation. These equations of states (EOSs) are sufficient to describe almost all the thermo elastic properties of CNTs.

2 Method of analysis

To investigate thermo elastic properties of carbon nanotubes (CNTs) under high pressure we have used three different EOSs. They are given below:

  1. (a)

    The modified Lenard Jones EOS [1]: the modified Lenard Jones EOS is given below,

    $$ P = \left( {\frac{{K_{0} }}{n}} \right)\left( y \right)^{ - n} \left[ {y^{ - n} - 1} \right] $$
    (1)

    where \(n = \frac{{K_{0}{\prime} }}{3}\) and \(y = \left( {\frac{V}{{V_{0} }}} \right)\).

    Isothermal Bulk modulus can be found by Eq. (1) using the formula \(K{}_{T} = - V\left( {\frac{\partial P}{{\partial V}}} \right){}_{T}\)

    $$ K_{T} = K_{0} y^{ - n} [2y^{ - n} - 1] $$
    (2)

    First order pressure derivative of Bulk Modulus (\(K_{T}^{\prime}\)) can be obtained by equation \(K_{T}^{\prime} = \left( {\frac{{\partial K_{T} }}{\partial P}} \right)_{T}\)

    $$ K_{T}^{\prime} = n\left[ {\frac{{ - 4y^{ - n} + 1}}{{ - 2y^{ - n} + 1}}} \right] $$
    (3)
  2. (b)

    Birch–Murnaghan (3rd) EOS [2]: the Birch–Murnaghan (3rd) EOS have been derived using finite strain theory is given below:

    $$ P = \frac{3}{2}K_{0} [x^{ - 7} - x^{ - 5} ][1 + \frac{3}{4}(K_{0}^{\prime} - 4)(x^{ - 2} - 4)] $$
    (4)

    where \(x = \left( {\frac{V}{{V{}_{0}}}} \right)^{\frac{1}{3}}\).

    Isothermal Bulk modulus can be found by Eq. (4) using the formula \(K{}_{T} = - V\left( {\frac{\partial P}{{\partial V}}} \right){}_{T}\)

    $$ K_{T} = \frac{{K_{0} }}{2}[7x^{ - 7} - 5x^{ - 5} ] + \frac{3}{8}K_{0} (K_{0}^{\prime} - 4)(9x^{ - 9} - 14x^{ - 7} + 5x^{ - 5} ) $$
    (5)

    First order pressure derivative of Bulk Modulus (\(K_{T}^{\prime}\)) can be obtained by equation \(K_{T}^{\prime} = \left( {\frac{{\partial K_{T} }}{\partial P}} \right)_{T}\)

    $$ K_{T}^{\prime} = \frac{{K_{0} }}{{8K_{T} }}[(K_{0}{\prime} - 4)(81x^{ - 9} - 98x^{ - 7} + 25x^{ - 5} ) + \frac{4}{3}(49x^{ - 7} - 25x^{ - 5} )] $$
    (6)
  3. (c)

    (c) Vinet–Rydburg EOS [3, 4]: The Vinet–Rydburg EOS is based on universal relationship between binding energy and interatomic separation for solids, the Vinet–Rydburg EOS is given below:

    $$ P = 3K{}_{0}x^{ - 2} (1 - x)\exp [\eta (1 - x)]\quad \quad $$
    (7)

    where \(x = \left( {\frac{V}{{V{}_{0}}}} \right)^{\frac{1}{3}}\) and \(\eta = \frac{3}{2}(K^{\prime}{}_{0} - 1)\).

    Isothermal Bulk modulus can be found by Eq. (7) using the formula \(K{}_{T} = - V\left( {\frac{\partial P}{{\partial V}}} \right){}_{T}\)

    $$ K_{T} = K_{0} x^{ - 2} [1 + (\eta x + 1)(1 - x)]\exp \{ \eta (1 - x)\} \quad $$
    (8)

    First order pressure derivative of Bulk Modulus (\(K_{T}^{\prime}\)) can be obtained by equation \(K_{T}^{\prime} = \left( {\frac{{\partial K_{T} }}{\partial P}} \right)_{T}\)

    $$ K_{T}^{\prime} = \frac{1}{3}\left[ {\frac{{x(1 - \eta ) + 2\eta x^{2} }}{1 + (1 + \eta x)(1 - x)} + \eta x + 2} \right] $$
    (9)

    For doing calculation we can also use another EOS like Brennan–Stacey [5, 6] EOS but in the present work we are interested to find some thermo elastic properties of CNT so three EOS will be sufficient for calculations.

2.1 Relative isothermal expansion coefficient (\(\alpha_{r}\))

\(\alpha_{r} = \left( {\frac{\alpha }{{\alpha_{0} }}} \right)\), coefficient of thermal expansion is the ratio of relative change of volume and change in temperature [7]:

The value of \(\alpha_{r}\) can be calculated as follows:

$$ \alpha_{r} = \left( {\frac{{K_{0} }}{{K_{T} }}} \right) $$
(10)

2.2 The Gruneisen parameter

The value of Gruneisen parameter \((\gamma )\) can be calculated by using the formula given by Borton and Stacey [8]:

$$\gamma =\frac{\left(\frac{1}{2}\right){K}^{\prime}-\frac{1}{6}-\frac{f}{3}\left[1-\frac{1}{3}\left(\frac{P}{{K}_{T}}\right)\right]}{1-\left(\frac{4}{3}\right)\left(\frac{P}{{K}_{T}}\right)}$$
(11)

where \(f\)=2.35.

3 Result and discussion

Generally we use EOSs for Bulk materials but in this paper we have used EOSs for nanomaterials (CNTs). The input parameter used in this paper for performing calculations are given in the Table 1.

Table 1 Input parameter used in theoretical analysis
Full size table

Here we have calculated the effect of pressure or compression on thermoelastic properties of carbon nano tubes. Figure 1 represents variation of pressure with respect to compression (V/V0) by using different equation of states and we notice that all the three EOSs used in these calculations gives exactly identical results and the theoretically obtained values from EOSs gives complete agreement with experimental data [10].

Fig. 1
figure 1

Plot between pressure and V/V0

Full size image

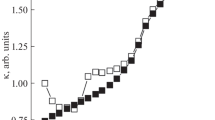
Figure 2 represents the variations of isothermal bulk modulus with respect to temperature and we notice bulk modulus is increasing with the increase in pressure and this completely agree with the work of Stacey that bulk modulus increases with the increase in pressure [11].

Fig. 2
figure 2

Plot between KT and P

Full size image

Figure 3 represents the variations of \(K_{T}^{\prime}\) with respect to pressure, we can notice that \(K_{T}^{\prime}\) is decreasing with increase in pressure with all the three EOSs used in the calculation and this also completely agree with the work of Stacey that \(K_{T}^{\prime}\) is decreases with increase in pressure [11]. Here we notice that Vinet–Rydburg EOS give very small deviation from other two.

Fig. 3
figure 3

Plot of \(K_{T}^{\prime}\) and P

Full size image

Figure 4 represent the variations of Relative isothermal expansion coefficient \(\alpha_{r}\) with respect to pressure for CNT and we notice that it also decreasing with increase in pressure from theoretical point of view in all the three EOSs used in this calculations.

Fig. 4
figure 4

Plot of \(\alpha_{r}\) and P

Full size image

Figure 5 represents the variation of Gruneisen parameter with respect to different compression V/V0. Here we notice that the graph between \(\gamma\) and V/V0 is straight line in all the three EOSs used in this calculation. So such type of variation of \(\gamma\) with V/V0 completely agree with the fact that for a good approximation the ratio of Gruneisen parameter to V/V0 is constant [12]. Here we see that Vinet–Rydburg EOS is showing disagreement from the other two EOSs this is due to this EOS was showing was also showing deviation in value of \(K_{T}^{\prime}\).

Fig. 5
figure 5

Plot between \((\gamma )\) and V/V0

Full size image

In the present study we have used EOSs for calculations of thermo elastic properties of carbon nanotubes which is nanomaterials so this leads the conclusion that the EOSs which are commonly used for calculation of Bulk materials can also used for calculation of properties of nanomaterials [13]. So EOSs can be used to study the properties of nanomaterials at high pressure or compression [14, 15].