1 Introduction

The key goal of the study is to apply Pareto multi-objective optimization methods to the problems of chemical kinetics. The purpose of modeling of any process, including a complex catalyzed reaction, is to find the optimal conditions for conducting the process. Here we present a procedure for determining the optimal conditions of a chemical reaction such that the extreme values of several criteria are attained simultaneously. Determination of the optimal reaction conditions is based on the kinetic model of the reaction.

We consider the catalytic reaction of DMC with alcohols catalyzed by W(CO)6 or Co2(CO)8. DMC is a green chemistry reagent. According to green chemistry principles [1], hazardous chemicals used in the syntheses must be replaced by less toxic and more efficient compounds, which give either less by-products or more readily utilizable by-products. DMC complies with the green chemistry principles as both a solvent and a reactant. It is synthesized using CO2 as a starting compound. Reactions involving DMC require only a catalytic amount of a base and give no wastes. The reaction gives the methyl ethers of alcohols and alkyl methyl carbonates, which are widely used as solvents and intermediates for the synthesis of pharmaceuticals, herbicides, antifreezes, etc. The DMC reactivity is moderate; therefore, the reaction is carried out in the presence of catalysts [2, 3].

Previously [4], alkyl dimethyl ethers and alkyl methyl carbonates have been synthesized by the reactions of diols with dimethyl carbonate in the presence of W(CO)6 or Co2(CO)8. The tungsten carbonyl W(CO)6 and the cobalt carbonyl Co2(CO)8 show high catalytic activities towards the reaction of DMC with alcohols. The W(CO)6-catalyzed reaction affords alkyl methyl ethers ROMe with a 95-98% selectivity. When the catalyst is replaced by Co2(CO)8, alkyl methyl carbonates ROCO2Me are formed. The DMC activation towards the reactions with alcohols is accomplished by the metal complex catalysts, dicobalt octacarbonyl (Co2(CO)8) and tungsten hexacarbonyl (W(CO)6).

$$ {\text{ROH}} + ({\text{MeO}})_{2} {\text{CO}}{\xrightarrow{{{\text{Co}}({\text{CO}})_{8}},W({\text{CO}})_{6} }}{\text{ROMe}} + {\text{ROCO}}_{2} {\text{Me}} + {\text{CO}}_{2} + {\text{MeOH}} $$

The observable compounds are ROH, ROMe, and ROCO2Me (R = C6H13).

The conditions of this kinetically complex reaction should be optimized on the basis of a kinetic model that reflects the key reaction regularities: the reaction mechanism, equations for the rates of single steps, and quantitative characteristics including kinetic constants, activation energies, and additional simplifying assumptions for the roles of particular steps.

2 Kinetic model of the catalytic reaction between dimethyl carbonate and alcohols

The kinetic models for the possible chemical transformation schemes have been reported in [5,6,7,8]. By comparative analysis of the calculated kinetic parameters and rates of steps, the possible reaction pathways were elucidated and an adequate mechanism was chosen.

The scheme of transformations involved in the reaction of DMC with alcohols in the presence of Co2(CO)8 and the relevant ranges of kinetic parameters are summarized in Table 1.

Table 1 Kinetic parameters of the Co2(CO)8-catalyzed reaction of DMC with alcohols
Full size table

The scheme of transformations involved in the reaction of DMC with alcohols in the presence of W(CO)6 and the relevant ranges of kinetic parameters are summarized in Table 2.

Table 2 Kinetic parameters of the W(CO)6-catalyzed reaction of DMC with alcohols (the rate constants are reduced to the min−1 units)
Full size table

The uncertainty of the values of kinetic parameters (Tables 1, 2) appears because the inverse kinetic problem has a non-unique solution. The parameters were determined by processing a large array of experimental data collected at various temperatures and initial amounts of the catalyst [4,5,6]. The kinetic parameters thus obtained vary over the indicated ranges.

This kinetic model can be used to solve the optimization problem for the reaction conditions. Setting up the optimization problem implies the presence of objective functions, variable parameters, and some constraints on the variable parameters.

3 Objective functions of the optimization of chemical reaction conditions based on a kinetic model

In the general case, objective functions of optimization based on a kinetic model have the form

$$ Z(y,y^{0} ,t*,\eta ,\mu ,T) \to \hbox{max} , $$
(1)

As a rule, the optimization functional for problems of chemical kinetics is the maximized product yield. However, the most general setting up of the optimization problem is to express the objective function as some economic evaluation. This evaluation may be done using some economic criterion (profitability, productivity).

Optimization of the reaction conditions according to (1) on the basis of the kinetic model can be performed using the following objective functions [9, 10]:

  1. 1.

    Product yield

    $$ Z = y_{prod} (t*,T,y^{0} ) \to \hbox{max} $$
    (2)

    This objective function can be used to determine the reaction conditions to maximize the yield of the target product.

  2. 2.

    Productivity criterion: production output per unit time

    $$ Z = B = N \cdot y_{i}^{0} \cdot \xi_{{y_{i} }} (t*,T) \cdot M_{{y_{i} }} \to { \hbox{max} } $$
    (3)

The objective function can be used to determine the reaction conditions that would maximize the productivity. The productivity maximum does not necessarily coincide with the highest product yield, as the product formation slows down with time, and the reaction can be arrested after high productivity has been attained. In this case, the number of cycles N is greater.

  1. 3.

    Profitability criterion equal to the ratio of the income amount to the capital investment:

    $$ {{Z}} = {{P}} = \frac{{\sum\nolimits_{{{{prod}} = 1}}^{ Pr } {{{y}}_{{prod}} ( {{t*,T,}}y^{ 0} )\cdot \eta_{{prod}} } }}{{\sum\nolimits_{{{{source}} = 1}}^{{Sr}} {{{y}}_{{source}} ( {{t*,T,}}y^{ 0} )\cdot \eta_{{source}} + \psi ( {{t*,T)}} + {{A}}} }} \to { {max} } $$
    (4)

This objective function defines the reaction conditions to maximize the profitability.

Simultaneous investigation of several objective functions requires multi-objective optimization, which provides the optimal values of variable parameters.

4 Setting up and methods of solution of multi-objective optimization problem for the conditions of reaction based on the kinetic model

The mathematical model of the problems of chemical kinetics is given by a nonlinear system of ordinary differential equations for the variation of the compound concentrations with time with known kinetic parameters, that is, pre-exponential factors and activation energies of particular steps [11,12,13]

$$ \frac{{dy_{i} }}{dt} = \sum\limits_{j = 1}^{J} {v_{ij} w_{j} ,i = 1, \ldots I} ;\quad w_{j} = k_{j} \cdot \prod\limits_{i = 1}^{I} {(y_{i} )^{{\left| {\alpha_{ij} } \right|}} } - k_{ - j} \cdot \prod\limits_{i = 1}^{I} {(y_{i} )^{{\beta_{ij} }} } ;\quad k_{j} = k_{j}^{0} \cdot \exp \left( { - \frac{{E_{j} }}{GT}} \right);\quad t \ {\in}\ \left[ {0,t*} \right] $$
(5)

The optimal conditions for conducting the reaction can be identified by analysis of the specified objective functions (2)-(4) within the framework of model (5).

Setting up the multi-objective optimization problem for the conditions of chemical reaction on the basis of the kinetic model has the following form [10, 14, 15].

Vector of variable parameters X = (x1, x2, x3). x1 is the reaction temperature, T; x2 is the initial amount of the catalyst, yct (Co2(CO)8) or W(CO)6); x3 is the reaction time, t*. Dimensionality of the vector of variable parameters |X| = 3. Objective function vector F(X) = (f1(X), f2(X)). f1 is the yield of the target product (2) (the target product is ROCO2Me for Co2(CO)8 as the catalyst or ROMe in the case of W(CO)6); alternatively, f1 is productivity (3); f2 is the profitability of the reaction (4).

F(X) with the values {F} = R(F)= R2 in the objective space is defined in the region DX⊂ {X} = R|X|= R3: T ∈ [Tmin; Tmax], yct ∈ [yct min; yt max], t* ∈ [t*min; t*max].

Then the maximization of the objective function in the region DX can be written in the form

$$ \mathop {\hbox{max} F(X)}\limits_{{X \in D_{X} }} = F(X*) = F* $$
(6)

The two-objective optimization problem (6) for the catalytic reaction of DMC with alcohols was first solved separately for each objective function (single-objective optimization) in order to evaluate the influence of variable parameters on the objective functions with the following constraints on the variable parameters: \( T \in [150,200],y_{kt} \in [0.001;0.005],{{t*}} \in [1;300] \). The solution was found by the Hooke and Jeeves direct search method in combination with the multistart method using the Matlab software [16].

It was found (Table 3) that the extreme values for the reactions with Co2(CO)8 and W(CO)6 and objective functions (2)-(4) are attained at the highest temperature, but at different xct and t* values, which is indicative of the inconsistency of the optimization quality functional. Therefore, the multi-objective optimization (MOO) problem was solved with the assumption that Tmin= Tmax= 200 °C.

Table 3 Variable parameters for the case of single-objective optimization (t* is the reaction time, xct is the initial amount of the catalyst, T is the reaction temperature)
Full size table

The MOO problem was solved by the Pareto approximation using the NSGA-II algorithm [16] in the Matlab software with parallelization [17, 18]. The condition for exiting the algorithm was the minimum change in the objective function (less than 10−6). The quality of Pareto approximation was evaluated considering the following factors [14]:

  1. 1.

    Average distance between solutions, that is, the Euclidean distances for all pairs of solutions of the obtained agglomerations

    $$ \bar{d}(A) = \frac{1}{{\left| {C_{1} } \right|*\left| {C_{2} } \right|}}\sum\limits_{{i \in C_{1} ,j \in C_{2} }} {d(i,j)} , $$
    (7)

    i ∊ C1, j ∊ C2 where the pairs of C1, C2 solutions are aggregations, agglomerations, clusters and d(i, j) is the Euclidean distance between solutions i and j.

  2. 2.

    Average scattering as a measure of homogeneity of distribution of solutions

    $$ I_{S} (A) = \sqrt {\frac{1}{\left| A \right| - 1}\sum\limits_{j = 1}^{\left| A \right|} {(\bar{d} - d_{j} )^{2} } } , $$
    (8)

where |A| = |C1| + |C2| is the size of the solution set.

These characteristics were applied to evaluate the Pareto set (genotype), that is, the optimal values of the variable parameters, and the Pareto front (phenotype), that is, the corresponding optimal values of the objective functions.

5 Results and discussion

While solving the multi-objective optimization problem, we took into account the ranges of kinetic parameters (Tables 1 and 2) by interpolating the parameters for the conditions of interest.

The results of Pareto set and front approximations for elucidation of the optimal conditions of the catalytic reaction of DMC with alcohols in the presence of the Co2(CO)8, and W(CO)6 catalysts with objective functions (2)–(4) are summarized below:

  1. 1.

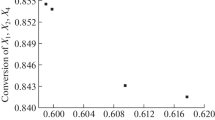
    Pareto front approximations for the yield (2) and profitability (4), and productivity (3) and profitability (4) objective functions F are shown in Figs. 1 and 2.

    Fig. 1
    figure 1

    Pareto front approximation for the MOO problem for the reaction of alcohols with DMC catalyzed by Co2(CO)8. a Objective functions: product yield-profitability, b Objective functions: productivity-profitability

    Full size image
    Fig. 2
    figure 2

    Pareto front approximation for the MOO problem for the reaction of alcohols with DMC catalyzed by W(CO)6. a Objective functions: product yield-profitability. b Objective functions: productivity-profitability

    Full size image

When productivity is taken as an objective function, the resulting profitability values are higher (Figs. 1b, 2b) than with the target product yield (Figs. 1a, 2a). This is due to the fact that the highest productivity is attained over a shorter time, resulting in higher profitability according to (4). The profitability is higher for the Co2(CO)8 catalyst (Fig. 1) than for W(CO)6 (Fig. 2), which can serve to compare the performances of various catalysts.

  1. 2.

    The Pareto set approximations (variable parameters) for the use of yield (2) and profitability (4), and productivity (3) and profitability (4) objective functions F are presented in Figs. 3 and 4.

    Fig. 3
    figure 3

    Pareto set approximations (variable parameters) for the MOO problem for the reaction of alcohols with DMC catalyzed by Co2(CO)8. a Variable parameters for objective functions: product yield-profitability. b Variable parameters for objective functions: productivity-profitability

    Full size image
    Fig. 4
    figure 4

    Pareto set approximations (variable parameters) for the MOO problem for the reaction of alcohols with DMC catalyzed by W(CO)6. a Variable parameters for objective functions: product yield-profitability. b Variable parameters for objective functions: productivity-profitability

    Full size image

Figures 3 and 4 show the following trends: the optimized variable parameters (amount of the catalyst and reaction time) are lower for the case of productivity-profitability objective functions (Figs. 3b, 4b) than for the yield-profitability case (Figs. 3a, 4a). This allows one to evaluate the process performance.

The evaluation of the quality of Pareto approximations according to (7), (8) is given in Table 4.

Table 4 Evaluation of the quality of Pareto approximations
Full size table

Relying on the solution of the MOO problem and the obtained values, one can consider an assembly of points in which DM can assume practical values of reaction conditions. It is possible to choose conditions for maximized target characteristics (by Pareto front approximation) or some compromise decision. Also, on the basis of the existing Pareto set, it is possible to choose acceptable conditions for variable parameters (i.e., minimal values of the Pareto set that are matched by approximations of the Pareto front).

6 Conclusion

Thus, using the NSGA-II algorithm, we determined the Pareto set and front for the MOO problem for the reaction of alcohols with DMC for two catalysts. The areas of variation of parameters in the Pareto set with the corresponding extrema of the Pareto front are provided for the DM.

As regards the practical process design, the application of the above methods provides exhaustive sets of conditions for conducting chemical processes, with both economic and production requirements being taken into account in any production cycle.