Multicriteria Interval Optimization of Conditions for Complex Chemical Reactions Based on a Kinetic Model

Abstract

The problem of multicriteria interval optimization of the conditions for complex chemical reactions is formulated based on an interval kinetic model. A solution method is proposed, based on evolutionary optimization algorithms, in the form of an interval Pareto front. An interval kinetic model is developed for the reaction of dimethyl carbonate with alcohols in the presence of a Co₂(CO)₈ metal complex catalyst, and two-sided limits on component concentrations and kinetic parameters have been determined. For this process, the effect of temperature and its possible disturbance on the values of the optimality criteria is calculated: the yield of the target product and productivity, with appropriate restrictions on changing the width of the interval.

1 INTRODUCTION

In applied problems of chemical kinetics, uncertainty arises in the calculation of parameters. This uncertainty affects the solution of the multicriteria optimization (MCO) problem, since the MCO is based on a kinetic model. The mathematical model of the problem of chemical kinetics is a system of ordinary nonlinear differential equations (SONDEs) of large dimensions. Uncertainty in the solution of the SONDEs may arise due to the interval values of the kinetic parameters of the model or due to controlling the process with variable parameters in the form of intervals [1, 2]. For example, in practice, the temperature of a complex chemical reaction cannot be constantly maintained at the same value, but some allowable variation interval is set. Therefore, it is topical to solve MCO problems using the interval analysis of the kinetic model of the SONDEs.

There are methods for solving SONDEs with interval parameters, such as the direct replacement of arithmetic operations and functions in the numerical method with the corresponding interval ones or the use of two-sided and interval methods for solving the Cauchy problem [3, 4].

The object of the study is the reaction of dimethyl carbonate (DMC) with alcohols in the presence of a metal complex catalyst octacarbonyldicobalt. The reaction of DMC with alcohols leads to the production of ethers and esters with high selectivity using the metal complex catalyst Co₂(CO)₈ [5]. In the works [6, 7], full-scale chemical experiments were carried out to study this reaction, and alkyl methyl ethers and alkyl methyl carbonates were obtained. Experiments were carried out with varying temperature and amount of catalyst in a closed stainless steel autoclave at 150, 160, 170, 180, and 200°C with sampling every 10 min for 8 h, at a concentration of Co₂(CO)₈ of 1, 2, 3, and 5 mol %. The reaction’s reagents are used in a ratio of one to three (100 mmol 1-hexanol per 300 mmol DMC). The experimentally observed substances are ROH, ROCO₂Me, and ROMe (R = C₆H₁₃). The target product of the reaction is ROCO₂Me (predominantly formed in Co₂(CO)₈). For the analysis reaction conditions during the subsequent introduction into production, it is necessary to determine the interval of the optimal conduction conditions, providing the maximum yield of the target product and maximum productivity, which does not have a directly proportional dependence on the conversion of the initial reagent. At the same time, fundamental knowledge about the process in the form of a kinetic model developed in [8, 9] is the base of the base optimization. For the catalytic reaction of dimethyl carbonate with alcohols, it is important to determine the optimal temperature intervals when solving the problem of multicriteria interval optimization (MCIO).

2 INTERVAL MATHEMATICAL MODEL OF COMPLEX CHEMICAL REACTIONS

The interval mathematical model of complex chemical reactions in the form of the SONDEs has the form

$$\begin{gathered} d{{y}_{i}}{\text{/}}dt = {{\varphi }_{i}}({{y}_{1}},{{y}_{2}},...,{{y}_{i}},{{{\mathbf{k}}}_{{\mathbf{1}}}},{{{\mathbf{k}}}_{{\mathbf{2}}}}, \ldots ,{{{\mathbf{k}}}_{{\mathbf{j}}}}),\quad i = 1,...,I,{\kern 1pt} \quad j = 1,...,J, \\ {{y}_{i}}(0) = y_{i}^{0},\quad t \in [0,t^*], \\ \end{gathered} $$

(1)

where y_i is the concentration of the chemical reaction of substances, mol/L; t* is the reaction time, min; φ_i are the functions of the right-hand sides with respect to the rate of the reaction stages; I is the number of substances in a chemical reaction; J is the number of stages of a chemical reaction; and ${{{\mathbf{k}}}_{{\mathbf{1}}}},{{{\mathbf{k}}}_{{\mathbf{2}}}}{\text{,}} \ldots {\text{,}}{{{\mathbf{k}}}_{{\mathbf{j}}}}$ are the interval values of the rate constants of the stages,

$${\text{\{ }}{{{\mathbf{k}}}_{{\mathbf{j}}}} = [{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{k} }_{j}},{{\bar {k}}_{j}}]\,|\,{{\underline k }_{j}} < {{\bar {k}}_{j}}\} ,\quad {{\underline k }_{j}},{{\bar {k}}_{j}} \in R,$$

(2)

$${{{\mathbf{k}}}_{{\mathbf{j}}}} = {\mathbf{k}}_{j}^{0}\exp ( - {{{\mathbf{E}}}_{{\mathbf{j}}}}{\text{/}}RT).$$

(3)

Equation (3) is the interval Arrhenius equation, where ${\mathbf{k}}_{j}^{0}$ are the interval values of the preliminary exponential factors; E_j are the interval values of the activation energies of the stages, kcal/mol; R is the universal gas constant, 2 cal/(mol K); and T is temperature, K.

The interval parameters of the mathematical model (1) arise due to the ambiguity of the solution of the inverse kinetic restoration problem k_j according to the calculated concentrations y_i with the experimental data, which, among other things, is due to the insufficient information content of the experiment: not all concentrations of the intermediate substances of a complex chemical reaction can be observed experimentally and an insufficient number of time measurements are carried out.

The reaction conditions can be set with an allowable interval $T \in (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} ,\bar {T})$; then according to formula (3) the rate constants will also have interval values. Thus, when solving the direct kinetic problem (1), it is necessary to use the methods of interval analysis.

The use of numerical interval methods, such as methods based on Taylor series [10] and its modifications, difference methods with polar remainder terms [11], leads to the appearance of the unwinding effect (or packing, the Moore effect) in the solution. This effect consists of a significant increase in the interval of the solution of the SONDE with time relative to the true one. It should be noted that the spin-up effect depends on the interval methods themselves and does not arise due to the error in the numerical solution [3].

3 TWO-SIDED METHOD FOR SOLVING THE INTERVAL KINETIC PROBLEM

According to [3], for the SONDE of chemical kinetics, we can introduce the following concepts: the function of the right-hand sides ${{\varphi }_{i}}$ is isotonic in parameter k_j if $\partial {{\varphi }_{i}}{\text{/}}\partial {{k}_{j}} > 0$ and antitonic in k_j if $\partial {{\varphi }_{i}}{\text{/}}\partial {{k}_{j}} < 0$; otherwise φ_i does not depend on k_j.

Assume that in (1) φ_i is isotonic in k_l and antitonic in k_m, where $l = 1,...,L;$ $m = 1,...,{\kern 1pt} M$, and $L + M = J$. Then the original SONDE (1) can be represented as a two-sided system

$$\begin{gathered} \left\{ \begin{gathered} d{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} }}_{i}}{\text{/}}dt = {{\varphi }_{i}}({{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} }}_{1}},{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} }}_{2}},...,{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} }}_{i}},{{\underline {\mathbf{k}} }_{l}}{\mathbf{,}}{{{{\mathbf{\bar {k}}}}}_{m}}), \hfill \\ d{{{\bar {y}}}_{i}}{\text{/}}dt = {{\varphi }_{i}}({{{\bar {y}}}_{1}},{{{\bar {y}}}_{2}},...,{{{\bar {y}}}_{i}},{{{{\mathbf{\bar {k}}}}}_{l}}{\mathbf{,}}{{\underline {\mathbf{k}} }_{m}}), \hfill \\ \end{gathered} \right. \\ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} }}_{i}}(0) = {{{\bar {y}}}_{i}}(0) = y_{i}^{0}. \\ \end{gathered} $$

(4)

The solutions of system (4), and, accordingly, (1), are interval changes in the concentrations of the components ${{y}_{i}} = [{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} }_{i}};{{\bar {y}}_{i}}]$.

4 INTERVAL KINETIC MODEL OF THE CATALYTIC REACTION OF ALCOHOLS WITH DIMETHYL CARBONATE

Chemical experiments to study the kinetics of the catalytic reaction of alcohols with dimethyl carbonate in the presence of a Co₂(CO)₈ catalyst is studied in [7].

The mathematical model of the process was developed based on the law of acting masses [8, 9] and has the form of a system of ordinary nonlinear differential equations (1). Due to the fact that there is a series of chemical experiments with different initial ratios of the catalyst, there is an uncertainty in the values of the kinetic parameters and their values must be determined in the intervals [12]. The numerical solution of such a system of equations is a direct interval problem of chemical kinetics [13–15]. Determining the kinetic parameters of the reaction stages by comparing the calculated values of the concentrations of substances with their experimental values is an inverse problem of chemical kinetics. The interval problem is mathematically represented as the minimization of the functional’s deviation of the calculated values from the experimental data. The minimization functional is defined as the sum over the maxima of the absolute deviations of the calculated concentrations of the upper and lower values from the experimental data

$$\begin{gathered} F\left( {\underline {k_{j}^{0}} ,\overline {k_{j}^{0}} ,\underline {{{E}_{j}}} ,\overline {{{E}_{j}}} } \right) = \sum\limits_{i = 1}^n {\sum\limits_{p = 1}^P {\left[ {\max \left\{ {{{\left| {y_{{ip}}^{{\exp }} - \underline {y_{{ip}}^{{{\text{calc}}}}} (\underline {k_{j}^{0}} ,\overline {k_{j}^{0}} ,\underline {{{E}_{j}}} ,\overline {{{E}_{j}}} )} \right|} \mathord{\left/ {\vphantom {{\left| {y_{{ip}}^{{\exp }} - \underline {y_{{ip}}^{{{\text{calc}}}}} (\underline {k_{j}^{0}} ,\overline {k_{j}^{0}} ,\underline {{{E}_{j}}} ,\overline {{{E}_{j}}} )} \right|} {y_{{ip}}^{{\exp }}}}} \right. \kern-0em} {y_{{ip}}^{{\exp }}}},} \right.} \right.} } \\ \left. {\left. {{{\left| {y_{{ip}}^{{\exp }} - \overline {y_{{ip}}^{{{\text{calc}}}}} (\underline {k_{j}^{0}} ,\overline {k_{j}^{0}} ,\underline {{{E}_{j}}} ,\overline {{{E}_{j}}} )} \right|} \mathord{\left/ {\vphantom {{\left| {y_{{ip}}^{{\exp }} - \overline {y_{{ip}}^{{{\text{calc}}}}} (\underline {k_{j}^{0}} ,\overline {k_{j}^{0}} ,\underline {{{E}_{j}}} ,\overline {{{E}_{j}}} )} \right|} {y_{{ip}}^{{\exp }}}}} \right. \kern-0em} {y_{{ip}}^{{\exp }}}}} \right\}} \right] \to \min . \\ \end{gathered} $$

(5)

The direct interval kinetic problem was solved using the two-sided method in combination with the multistep Gear method of variable order [16]. To solve the inverse kinetic problem, a combination of global and local optimization methods was used: a genetic algorithm and the Hooke–Jeeves direct search method [17].

The scheme of chemical transformations of the reaction and the corresponding ranges of values of the kinetic parameters are given in Table 1.

Table 1. Stages of chemical transformations and values of intervals of kinetic parameters of the catalytic reaction of alcohols with DMC ([ln k₀] = [L/(mol min)], [E_j] = [kcal/mol])

The activation energy of the first stage of the interaction of the catalyst with alcohol is quite large (E_j = 24.10 ± 0.01 kcal/mol), which indicates that this stage limits the entire reaction. The formation stages of the byproducyt of the simple ROMe ether reaction have larger activation energies (E₄ = 15.00 ± 0.01 kcal/mol, E₆ = 21.5 ± 1.5 kcal/mol) than for the target product ROCO₂Me (E₅ = 5.6 ± 0.1 kcal/mol), which corresponds to the experimental data, according to which ROMe appears only with an increase in temperature or amount of catalyst [9].

Figures 1 and 2 show the correspondence between the experimental data and the ranges of the calculated values of the measured substrates of the catalytic reaction of alcohols with dimethyl carbonate in the presence of Co₂(CO)₈ (two-sided concentration limits). The observed substrates are the initial alcohol ROH (Y₁) and the reaction products ROMe (Y₄) and ROCo₂Me (Y₅) (Y₄ is not shown on the graphs due to its insignificant yield). The graphs show the concentrations of the initial alcohol Y₁ and ether Y₅ in relation to the sum of all values of the observed substances (mole fractions) at temperatures T = 180 and 200°C.

Fig. 1.

Correspondence graphs of experimental data (points) and intervals of calculated values (lines) of changes in the concentration of observed substrates at T = 180°C of the reaction of dimethyl carbonate with alcohols in the presence of Co₂(CO)₈.

Fig. 2.

Correspondence graphs of experimental data (points) and intervals of calculated values (lines) of changes in the concentration of observed substrates at T = 200°C of the reaction of dimethyl carbonate with alcohols in the presence of Co₂(CO)₈.

The experimental data on the concentrations of the components are included in the calculated interval (Figs. 1, 2). Thus, the interval values of the parameters obtained according to the scheme from Table 1 describe the experimental data within the permissible error. This gives grounds to conclude that this mechanism is reliable for the catalytic reaction of alcohols with dimethyl carbonate.

The subsequent introduction of the process into production requires determining the optimal reaction conditions in order to obtain the highest yield of the target ether ROCO₂Me and the smallest byproduct of ROMe. Based on the calculated values of the intervals of the kinetic parameters and a comparative analysis of the activation energies of possible stages of the scheme of chemical transformations with the determination of possible reaction pathways, it is possible to formulate an MCIO problem [18–20].

5 STATEMENT OF THE PROBLEM OF MULTICRITERIAL INTERVAL OPTIMIZATION

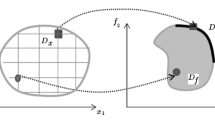
The formulation of the MCIO problem makes it possible to take into account direct restrictions on the parameters to be varied rather than singling them out separately, as was done earlier [19–21]. The MCIO solution covers all admissible reaction conditions that make it possible to reach the extrema of the optimality criteria. For practical problems, this determines the entire range of acceptable values of the variable parameters.

The vector of interval variable parameters

$$\begin{gathered} X = ({{x}_{1}},{{x}_{2}},{{x}_{3}}) \in {{D}_{X}}, \\ {{x}_{1}} \in [{{\underline x }_{1}},\overline {{{x}_{1}}} ];\quad {{x}_{2}} \in [{{\underline x }_{2}},{{{\bar {x}}}_{2}}];\quad {{x}_{3}} \in [{{\underline x }_{3}},\overline {{{x}_{3}}} ];\quad \ldots . \\ \end{gathered} $$

(6)

The vector function of the interval optimality criteria

$$F(X) = ({{f}_{1}}(x),{{f}_{2}}(x),{{f}_{3}}(x),...) \in {{D}_{F}};$$

(7)

${{f}_{1}}(x),{{f}_{2}}(x),{{f}_{3}}(x)$ consists of particular interval optimality criteria.

To solve the MCIO, it is necessary to determine the desired characteristics of the interval variable parameters and optimality criteria. An interval can be uniquely defined by its midpoint and width.

Then for x_i

$$\operatorname{mid} {{x}_{i}} = (\overline {{{x}_{i}}} + {{\underline x }_{i}}){\text{/2}}\quad {\text{is the middle of the interval}},$$

(8)

and

$$\operatorname{wid} {{x}_{i}} = \overline {{{x}_{i}}} - {{\underline x }_{i}}\quad {\text{is the interval width}}{\text{.}}$$

(9)

The variable parameters can be the reaction temperature, the initial concentrations of the reagents, the reaction time, etc. The optimality criteria can be the maximization of the yield of the target product, minimization of the byproduct, and economic or production criteria. However, when calculating the interval values of F, there is a requirement for an acceptable interval width. For example, the output of the target product should be maximum and should not change by more than some given value ${{\rho }_{n}}$, where ${{\rho }_{n}}$ is the stability radius of the MCIO (engineering stability) according to criterion n, n = 1, 2, 3, …. Then, for MCIO it is necessary to set restrictions on the change of the width of the interval of each criterion

$$\left| {\operatorname{wid} {{f}_{n}} - {{\rho }_{n}}} \right| < {{\varepsilon }_{n}},$$

(10)

and determine the extremum of the middle of the interval of values of the optimality criterion

$$\mathop {\operatorname{extr} \operatorname{mid} F(X)}\limits_{X \in {{D}_{X}}} = F(X*) = F{\kern 1pt} ^*{\kern 1pt} .$$

(11)

6 MULTICRITERIA INTERVAL PROBLEM OF OPTIMIZING THE CATALYTIC REACTION OF DIMETHYL CARBONATE WITH ALCOHOLS

The products of the catalytic reaction of alcohols with dimethyl carbonate in the presence of a Co₂(CO)₈ catalyst are alkyl methyl carbonate ROCO₂Me (the target product) and alkyl methyl ether ROMe (a byproduct) [7]. In the chemical experiments, the initial amount of the catalyst and the reaction temperature were selected [9], varying which led to different product yields. The optimal conditions for the reaction of DMC with alcohols are determined by the following criteria:

(1) Yield of the target reaction product (y_prod). The output depends on the given variable parameters

$${{f}_{1}}(X) = {{y}_{{{\text{prod}}}}}(t^*,T,{{{\mathbf{y}}}^{{\mathbf{0}}}}) \to \max .$$

(12)

The scheme of chemical transformations of the reaction of DMC with alcohols (Table 1) does not take into account the decomposition of the target product. The concentration of the target product does not change further when the maximum is reached (Figs. 1, 2).

(2) Productivity is the number of products produced per unit of time, [g/(L day)]. For a selective reaction, when the amount of the product is directly proportional to the conversion of the initial reagent, the productivity is estimated by the conversion of the initial reagent [22]:

$${{f}_{2}}(X) = Ny_{i}^{0}{{\xi }_{{{{Y}_{i}}}}}(t^*,T){{M}_{{{{Y}_{i}}}}} \to {\text{max}}{\text{,}}$$

(13)

$$N(t*) = 1440{\text{/}}(t{\kern 1pt} ^* + \;{{t}_{{{\text{idle}}}}}),$$

(14)

where M_Yprod is the molar mass of the target product [g/mol], N is the number of cycles per day [days^–1] (it is determined according to (14)); t_idle is the idle time between cycles; and ξ_Yi is the conversion of the initial reagent. The increase in productivity is not directly proportional to the increase in conversion. Since the conversion directly depends on t* and an in increase t* leads to a decrease in the number of cycles.

The change in the performance criterion passes through a maximum and decreases with the time of the reaction. At t* = 0 performance value is 0 (13). At t* → ∞, performance tends to 0, since in formula (13) the number of cycles N → 0 by formula (14). Then, for the catalytic reaction of dimethyl carbonate with alcohols, the effect of the process temperature will be calculated (x₁, °C) on the values of the optimality criteria. The variable parameters are midx₁ ∈ [140, 180] and wid x₁ ∈ [1, 15]. The optimization criteria F(X) = ( f₁(X), f₂(X)). The values of the optimality criteria are subject to restrictions on the change of the width of the interval depending on the temperature variation being no more than the given value for each criterion according to formula (10). It is necessary to maximize the optimality criteria according to formula (11).

The problem posed was solved in the form of Pareto approximation using the evolutionary algorithm of multicriteria optimization NSGA-II (nondominated sorting genetic algorithm) [23–25], which allows solving the problem of a compromise of the optimality criteria values and calculating the entire set of unimprovable solutions. The simultaneous and independent calculation of the values of contradictory optimality criteria makes it possible to obtain a solution to the MCO problem without applying the convolution of the partial criteria and assigning the appropriate weight parameters. The solution of the MCIO problem is the interval Pareto front in the area of the optimality criteria.

Figure 3 shows the dependence of the calculated values of the optimality criteria for the catalytic reaction of dimethyl carbonate with alcohols: the yield of the target product ROCO₂Me ( f₁) and the productivity of the process ( f₂). The values of mid f₁ and mid f₂ are highlighted by a black marker. The gray marker shows the lower and upper limits of the change in the optimality criteria that are possible for the given temperature fluctuations. Moreover, with an increase in the yield of the product and a decrease in productivity, the possible intervals of changes decrease and tend to the same value.

Fig. 3.

Approximation of the interval Pareto front of the MCIO problem for the reaction of dimethyl carbonate with alcohols in the presence of Co₂(CO)₈.

Figure 4 shows the dependence of the temperature change intervals on the product yield and productivity. With an increase in the concentration of the target product, the interval of the change in temperature decreases, and with an increase in productivity, it increases, which appears to be related to the lower dependence of productivity on the kinetics of the process, in contrast to the concentration of the product.

Fig. 4.

Reaction temperature ranges for ROCO₂Me (a) and productivity (b) of the reaction of dimethyl carbonate with alcohols in the presence of Co₂(CO)₈.

7 CONCLUSIONS

This paper proposes an algorithm for solving the problem of multicriterial optimization using the interval analysis of the kinetic model of the SONDE. This algorithm makes it possible to take into account the uncertainty in the solution of the SONDE and possible disturbances in the values of the variable parameters in practice, as well as to obtain a possible interval of variation of the optimality criteria.

For the catalytic reaction of dimethyl carbonate with alcohols, an interval kinetic model has been developed, and bilateral limits on the concentrations of the components have been determined. Based on the kinetic model, the problem of MCIO of the conditions of the process was posed and solved. Calculations using the interval kinetic model showed the possible maximum yield of the ROCO₂Me product of up to 3–4 mol/L in the acceptable mode of 155 to 175°C. This approach makes it possible in practice to have a complete picture of the process, as well as evaluate the possible values of the optimality criteria and the allowable intervals of variation for the variable technological parameters, which determines an exhaustive solution to the problem of multicriteria interval optimization using a kinetic model.