1 Introduction

In the last 2 decades, many scientists have studied physical properties of low-dimensional semiconductor nanostructures. The research on the low-dimensional structures is an interesting challenge due to their important applications in physics, chemistry and engineering. There are a number of ways devised to fabricate nanostructures such as molecular-beam epitaxy, droplet epitaxy, chemical vapor deposition and lithography [1,2,3]. In addition, these techniques have the capability to produce structures of different geometries such as rectangular, cylindrical, spherical, rings, single quantum ring and double quantum ring [4,5,6,7,8,9,10].

Among the low-dimensional structures, quantum dots, in particular, have extensively been studied both experimentally and theoretically in the last few years [11,12,13,14]. The confinement of charge carriers in quantum dots generates discrete energy levels with spacing of a few meV or more. The theoretical study of quantum dots with different geometries such as parabolic, lens-shape, cone-like, Gaussian, modified Gaussian and spheroidal has been the subject of much discussion for the last decade [15,16,17,18,19,20].

The prediction of confinement potential in quantum dots plays an important role in the physics of low-dimensional semiconductor structures. It is worth mentioning that the knowledge of the realistic profile of the confinement potential is important in theoretical studies of the physical properties of quantum dots. To study theoretically physical properties of quantum dots, researches have used different models for the confinement potential like parabolic potential, spherical harmonic oscillator, non-spherical oscillator, ring-shaped oscillator, ring-shaped non-spherical oscillator and double ring-shaped oscillator [21,22,23,24,25,26].

An important challenge in the physics science is to study electronic and optical properties of quantum dots because these structures have interesting potential applications. In the past few years, electronic and optical properties of quantum dots have been extensively investigated under external factors such as spin–orbit interaction, electron–phonon interaction, magnetic field, electric field, temperature, impurity and pressure [27,28,29,30,31]. For example, Ciftja and Faruk [32] have studied a two-dimensional quantum dot helium confined by parabolic potential in the presence of weak and strong magnetic field using variational theory. Chen et al. [33] have studied the effect of SOI in the double ring-shaped oscillator. Boda et al. [34] have studied the effect of electron–electron interaction on the magnetic moment and susceptibility of a parabolic GaAs quantum dots.

Among the physical properties of quantum dots, there are few studies on thermodynamics properties of quantum dots [35,36,37,38,39,40,41,42,43]. For example, Sukirti et al. [44] have studied thermodynamic behavior of Rashba quantum dots in the presence of magnetic field. Ibragimov [45] has investigated thermodynamic properties of asymmetric parabolic quantum dot. Since thermodynamics properties of nanostructures are an interesting subject in physics science, we intend to study thermodynamics quantities such as energy, entropy, heat capacity and magnetic susceptibility of the double ring-shaped quantum dot.

2 Theory and Model

We consider an electron confined in a double ring-shaped quantum dot under magnetic and electric fields. The Hamiltonian of the system is given by

$$\begin{aligned} H=\frac{\left( {{\varvec{P}}+e{\varvec{A}}} \right) ^{2}}{2m^{*}}+V\left( {r,\theta } \right) -e{\varvec{F}}.{\varvec{r}}, \end{aligned}$$
(1)

where \(m^{*}\) is the effective mass of the electron, \(A=\frac{B}{2}\left( {-y,x, 0} \right) \) is the vector potential induced by the magnetic field which is taken in the symmetric gauge and F is the electric field. The second term in Eq. (1) is the confinement potential which is given by [26] (see Fig. 1)

$$\begin{aligned} V\left( {r,\theta } \right) =\frac{1}{2}m^{*}\omega _0^2 r^{2}+\frac{\hbar ^{2}}{2m^{*}}\left( {\frac{B}{r^{2}\sin ^{2}\theta }+\frac{C}{r^{2}\cos ^{2}\theta }} \right) . \end{aligned}$$
(2)

Here B and C are two potential parameters, \(\omega _0 \) is the frequency of confinement potential and \(\hbar \) is the Plank constant. For \(C=0\) and \(B=C=0\), Eq. (2) reduces to the ring-shaped oscillator and spherical harmonic oscillator, respectively.

In the cylindrical coordinates, the Schrödinger equation with the potential Eq. (2) is written as

$$\begin{aligned}&\left[ -\frac{\hbar ^{2}}{2m^{*}}\nabla ^{2}+\frac{1}{8}m^{*}\omega _c^2 \rho ^{2}+\frac{1}{2}\omega _c L_z +\frac{1}{2}m^{*}\omega _0^2 \left( {\rho ^{2}+z^{2}} \right) \right. \nonumber \\&\left. \quad +\frac{\hbar ^{2}}{2m^{*}}\left( {\frac{B}{\rho ^{2}}+\frac{C}{z^{2}}} \right) -eFz \right] \psi \left( {\rho ,\varphi ,z} \right) =E\psi \left( {\rho ,\varphi ,z} \right) . \end{aligned}$$
(3)

Substituting the wave function in the form \(\psi \left( {\rho ,\varphi ,z} \right) = R\left( \rho \right) F\left( z \right) {e^{im\varphi }}\) in Eq. (3), we obtain the following equations

$$\begin{aligned}&\frac{\mathrm{d}^{2}R\left( \rho \right) }{\mathrm{d}\rho ^{2}}+\frac{1}{\rho }\frac{\mathrm{d}R\left( \rho \right) }{\mathrm{d}\rho }\nonumber \\&\quad -\frac{m^{2}+B}{\rho ^{2}}R\left( \rho \right) -\frac{m^{*^{2}}{\Omega }^{2}}{\hbar ^{2}}\rho ^{2}R\left( \rho \right) +\left( {\frac{2m^{*}E_\rho }{\hbar ^{2}}-\frac{m^{*}m\omega _c }{\hbar }} \right) R\left( \rho \right) =0, \end{aligned}$$
(4)

and

$$\begin{aligned} \frac{\mathrm{d}^{2}F\left( z \right) }{\mathrm{d}z^{2}}-\left( {\frac{m^{*^{2}}\omega _0^2 }{\hbar ^{2}}z^{2}+\frac{C}{z^{2}}-\frac{2m^{*}E_z }{\hbar ^{2}}-\frac{2m^{*}}{\hbar ^{2}}eFz} \right) F\left( z \right) =0. \end{aligned}$$
(5)

where \(\omega _c =eB/m^{*}\) is the cyclotron frequency and \({\Omega }=\sqrt{\omega _0^2 +\frac{\omega _c^2 }{4}}\).

Considering the change of variable as \(\eta = \kappa {\rho ^2} (\kappa = \frac{{{m^{*}}\mathrm{{\Omega }}}}{\hbar })\), Eq. (4) can be written as

$$\begin{aligned} \left[ {\frac{\mathrm{d}^{2}}{\mathrm{d}\eta ^{2}}+\frac{1}{\eta }\frac{\mathrm{d}}{\mathrm{d}\eta }-\frac{m^{2}+B}{4\eta ^{2}}+\frac{\lambda }{4\kappa \eta }-\frac{1}{4}} \right] R\left( \eta \right) =0. \end{aligned}$$
(6)

Here \(\lambda =\left( {\frac{2m^{*}E_\rho }{\hbar ^{2}}-\frac{m^{*}m\omega _c }{\hbar }} \right) \). The radial wave function \(R\left( \rho \right) \) needs to be finite as \(R\left( 0 \right) \rightarrow 0\) and \(R\left( \infty \right) \rightarrow 0\). To make the solution satisfying the above conditions, we have considered the solution of the wave function as \(R\left( \eta \right) =e^{-\frac{\eta }{2}}\eta ^{\frac{\left| {\sqrt{m^{2}+B}} \right| }{2}}F\left( \eta \right) \). Inserting the wave function into Eq. (6), we obtain the following equation

$$\begin{aligned} \left[ {\eta \frac{\mathrm{d}^{2}}{\mathrm{d}\eta ^{2}}+\left( {\left| {\sqrt{m^{2}+B}} \right| +1-\eta } \right) \frac{\mathrm{d}}{\mathrm{d}\eta }-\left( {\frac{\left| {\sqrt{m^{2}+B}} \right| }{2}+\frac{1}{2}-\frac{\lambda }{4\kappa }} \right) } \right] F\left( \eta \right) =0.\nonumber \\ \end{aligned}$$
(7)

The above equation is the confluent hypergeometric differential equation, and it has the solution as \(F\left( \eta \right) =F\left( {\frac{\left| {\sqrt{m^{2}+B}} \right| }{2}+\frac{1}{2}-\frac{\lambda }{4\kappa },\left| {\sqrt{m^{2}+B}} \right| +1;\eta } \right) \). The quantum condition of polynomial confluent function requires that \(-n_\rho =\frac{\left| {\sqrt{m^{2}+B}} \right| }{2}+\frac{1}{2}-\frac{\lambda }{4\kappa }\). Using the values of parameters \(\lambda \) and \(\kappa \), we can obtain the energy levels as

$$\begin{aligned} E_\rho =\hbar {\Omega }\left( {2n_\rho +1+\sqrt{m^{2}+B}} \right) +\frac{m\hbar \omega _c }{2}. \end{aligned}$$
(8)

Considering the solution of Eq. (5) as \(F\left( z \right) =z^{\frac{1+\sqrt{1+4C}}{2}}\mathrm{exp}\left( {-\frac{m^{*}\omega _0 }{2\hbar }z^{2}} \right) \hbox {exp}\left( {\frac{eF}{\hbar \omega _0 }z} \right) g\left( z \right) \), one can obtain the following equation

$$\begin{aligned}&\frac{\mathrm{d}^{2}g\left( z \right) }{\mathrm{d}z^{2}}-\frac{\left( {2z^{2}+\beta z-\alpha -1} \right) }{z}\frac{\mathrm{d}g\left( z \right) }{\mathrm{d}z}\nonumber \\&\quad -\frac{1}{2}\frac{\left[ {\left( {2\alpha -2\gamma +4} \right) z+\delta +\beta +\beta \alpha } \right] }{z}g\left( z \right) =0. \end{aligned}$$
(9)

Above equation is the HeunB differential equation with \(\alpha =\sqrt{1+4C}\), \(\beta =\frac{2eF}{\hbar \omega _0 }\sqrt{\frac{m^{*}\omega _0 }{\hbar }}\), \(\gamma =\frac{2E_z }{\hbar \omega _0 }+\frac{e^{2}F^{2}}{\hbar m^{*}\omega _0^2 }\) and \(\delta =0\). Using the boundary conditions, we obtain

$$\begin{aligned} E_z =\left( {n_z +1} \right) \hbar \omega _0 +\frac{\hbar \omega _0 }{2}\sqrt{1+4C}-\frac{\hbar eF}{2m^{*}\omega _0 }. \end{aligned}$$
(10)

Employing Eqs. (8) and (10), we have

$$\begin{aligned} E= & {} \hbar {\Omega }\left( {2n_\rho +1+\sqrt{m^{2}+B}} \right) \nonumber \\&+\,\frac{m\hbar \omega _c }{2}+\left( {n_z +1} \right) \hbar \omega _0 +\frac{\hbar \omega _0 }{2}\sqrt{1+4C}-\frac{\hbar eF}{2m^{*}\omega _0 }. \end{aligned}$$
(11)

From a theoretical point of view, there are many effective techniques to calculate the energy levels of nanostructured systems. Examples of the techniques are the density of function and the variational method of Pekar type. For example, Chen and Xiao [43, 46] have studied the temperature effects on the parabolic quantum dot qubit in the presence of electric and magnetic fields using the variational method of Pekar type. Chen and Xiao [47] have calculated electronic and excitonic properties of two-dimensional InN crystals using density of function. The aforementioned methods have been performed numerically. The variational method of Pekar type is based on trial wave functions, and the method is usually an approximate approach. In this work, we have solved the Schrödinger equation and obtained the energy levels analytically. The advantage of the method used in the present paper is to obtain analytical wave functions and energy levels.

3 Thermodynamic Properties

A starting point to derive thermodynamic properties of the system is the partition function. The partition function can be calculated by direct summation over all possible states available to the system,

$$\begin{aligned} Q=\mathop \sum \limits _{n_\rho } \mathop \sum \limits _{n_z } \mathop \sum \limits _m \hbox {exp}\left( {-\beta E_{n_\rho ,n_z ,m} } \right) \end{aligned}$$
(12)

where \(\beta =\frac{1}{k_B T}\), \(k_B \) is the Boltzmann constant and T is the temperature. Substituting expression (11) into Eq. (12), we can obtain the partition function. After obtaining the partition function, one can calculate the thermodynamic functions of the system using the following relations,

  1. (i)

    Mean energy \(U=-\frac{\partial \mathrm{ln}Q}{\partial \beta },\)

  2. (ii)

    Specific heat \(C_v =\frac{\partial U}{\partial T}=k_B \beta ^{2}\frac{\partial ^{2}}{\partial \beta ^{2}}\hbox {ln}Q\),

  3. (iii)

    Free energy \(F=-k_B T\mathrm{ln}Q\),

  4. (iv)

    Entropy \(S=k_B \mathrm{ln}Q-k_B \beta \frac{\partial \mathrm{ln}Q}{\partial \beta }\),

  5. (v)

    Susceptibility \(\chi =-\frac{\partial ^{2}F}{\partial B^{2}},\)

4 Results and Discussions

In this part, we have selected a typical GaAs as an example to present our numerical results with \({m^*} = ~0.067\,{m_0}\). Also, in our calculations, we have defined the following parameters:

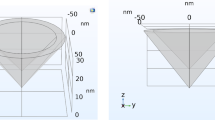
$$\begin{aligned} {l_0} = \sqrt{\frac{\hbar }{{{m^*}{\omega _0}}}} \hbox { and }{l_B} = \sqrt{\frac{\hbar }{{{m^*}{\omega _c}}}} . \end{aligned}$$

In Fig. 1, we have plotted a schematic diagram of the double ring-shaped quantum dot.

Figure 2a, b shows the mean energy as a function of the temperature for different magnetic fields with \(l_0 =20\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). It is seen from the figures that the mean energy increases with enhancing the temperature at low and high temperatures. At low temperatures (Fig. 2b), the variation of mean energy is more than that at high temperatures. At high temperatures, the mean energy increases slowly with temperature, whereas it increases rapidly at low temperatures. At a fixed temperature, the mean energy increases with enhancing the magnetic field. This increment at low temperatures is higher than high temperatures. There is a competition between thermal energy and magnetic energy in the system. At low temperatures, however, the magnetic energy wins. In the case of quantum dots, the energy levels are discrete, and therefore, the mean energy can be said to depend on the distribution of energy levels.

Fig. 1
figure 1

A schematic diagram of double ring-shaped quantum dot (Color figure online)

Full size image
Fig. 2
figure 2

Mean energy as a function of temperature for different magnetic fields with \(l_0 =20\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). The curves in (a) and (b) correspond to high and low temperatures (Color figure online)

Full size image

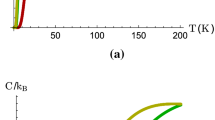
Figure 3a, b displays the specific heat as a function of the temperature for different magnetic fields with \(l_0 =20\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). It is observed from Fig. 3a that the specific heat increases until it reaches a maximum and then reduces with increasing the temperature. We observe that the specific heat shows a peak structure at low temperatures. The peak position of the specific heat shifts toward higher temperatures with increasing the magnetic field. Also, the width of the specific heat curve increases with raising the magnetic field. There is an interesting point in these figures. At low temperatures, the specific heat reduces with increasing the magnetic field (see Fig. 3b), whereas at high temperatures, it increases with enhancing the magnetic field (see Fig. 3a). Also, for \(T<2\,\mathrm{K}\), the magnetic field has no effect on the specific heat (see Fig. 3b). At low temperatures, the occupation probability of the higher states decreases. The application of the magnetic field enhances the quantum confinement effects, and thereby, the occupation probability of the levels increases. Consequently, the specific heat capacity should depend on both the energy level distribution and the temperature dependence of the occupation probability of the states.

Fig. 3
figure 3

Specific heat as a function of temperature for different magnetic fields with \(l_0 =20\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). The curves in (a) and (b) correspond to high and low temperatures (Color figure online)

Full size image

The variations of entropy have been plotted in Fig. 4a, b as a function of the temperature and the magnetic field, respectively, with \(l_0 =20\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). As seen from Fig. 4a, the entropy increases with raising the temperature at a fixed magnetic field, as is generally expected. This is because the occupation probability of the levels changes and thereby the system disorder increases with raising the temperature. At a fixed temperature, the entropy decreases with increasing the magnetic field due to the increase in quantum confinement effects and thereby the reduction of the system disorder. The obtained order in the system by the magnetic field might be counterbalanced by the kinetic energy due to confinement together with the thermodynamic disorder at higher temperatures. It is observed from Fig. 4b that the entropy decreases with increasing magnetic field at a fixed value of temperature. It is worth mentioning that there are two kinds of energies: kinetic energy due to confinement and heat energy due to the thermodynamic disorder. At low and high temperatures, these energies are competed. We have compared our results with a GaAs quantum dot with Gaussian potential [21].

Fig. 4
figure 4

Entropy as a function of temperature for different magnetic fields with \(l_0 =20\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). The curves in (a) and (b) correspond to high and low temperatures (Color figure online)

Full size image
Fig. 5
figure 5

The susceptibility as a function of temperature for different magnetic fields with \(l_0 =20\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). The curves in (a) and (b) correspond to high and low temperatures (Color figure online)

Full size image
Fig. 6
figure 6

Mean energy as a function of temperature for different confinement lengths with \(l_B =5\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). The curves in (a) and (b) correspond to high and low temperatures (Color figure online)

Full size image

In Fig. 5a, we have presented the magnetic susceptibility as a function of the temperature for different magnetic fields with \(l_0 =20\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). It is seen from the figure that the susceptibility shows a peak structure at low temperatures (\(T<50\,\mathrm{K})\). The paramagnetic peak position shifts toward higher temperatures with increasing the magnetic field. The magnetic susceptibility for the selected magnetic fields approaches a constant value with enhancing temperature. The peak width of the magnetic susceptibility increases with raising the magnetic field, whereas the height of magnetic susceptibility increases with reducing the magnetic field. To obtain more information, the magnetic susceptibility has been plotted in Fig. 5b at low temperatures (\(T<10\,\mathrm{K})\). As seen from the figure, below 4 K, the susceptibility shows a transition between diamagnetic and paramagnetic. The transition temperature increases with raising the magnetic field.

Figure 6a, b shows the mean energy as a function of the temperature for different confinement lengths with \(l_B =5\,\mathrm{nm}\) and \(F=1\,\mathrm{V/m}\). It is observed from the figures that the mean energy enhances with increasing the temperature. At high temperatures, the mean energy increases linearly with temperature, whereas it increases nonlinearly at low temperatures. At low temperatures (Fig. 6b), the variation of mean energy is more than that at high temperatures. It is to be noted that the energy level distribution depends strongly on the temperature. This causes to change the occupation probability of the energy levels by the electron. At a fixed temperature, the mean energy increases with enhancing the confinement length. This is because the quantum confinement effect decreases with increasing the confinement length and thereby the energy spacing reduces. Therefore, the occupation probability of the levels increases, and thereby, the mean energy enhances.

5 Conclusion

We have studied theoretically the thermodynamic properties of a double ring-shaped quantum dot as a function of temperature under the magnetic and electric fields. The results have been presented at low and high temperatures. We have found that the entropy is increased with the temperature. The entropy increases monotonically for all values of the magnetic fields at low temperatures, whereas it depends on the magnetic field at high temperatures. The heat capacity and magnetic susceptibility show a peak structure. The heat capacity decreases with increasing the magnetic field at low temperatures. The magnetic susceptibility shows a transition between diamagnetic and paramagnetic below 4 K. The transition temperature depends on the magnetic field.