Stability and Double-Hopf Bifurcations of a Gause–Kolmogorov-Type Predator–Prey System with Indirect Prey-Taxis

Abstract

In this paper, we deal with the Gause–Kolmogorov-type predator–prey system with indirect prey-taxis, which means that directional movement of predators is stimulated by some chemicals emitted by preys. The existence of the positive equilibrium, the effect of the indirect prey-taxis on the stability and the related bifurcations are investigated. The critical values for the occurrence of the Hopf bifurcation, Turing bifurcation, Turing–Hopf bifurcation and double-Hopf bifurcation are explicitly determined. An algorithm for calculating the normal form of the double-Hopf bifurcation for the non-resonance and weak resonance is derived. Moreover, we apply the theoretical results to the system with Holling-II type functional response, the stable region and the bifurcation curves are completely determined in the plane of the indirect prey-taxis and self saturation coefficient. The dynamical classification near the double-Hopf bifurcation point is explicitly determined. In the neighborhood of the double-Hopf bifurcation, there are stable spatially homogeneous/inhomogeneous periodic solutions, stable spatially inhomogeneous quadi-periodic solutions and the pattern transitions from one spatial–temporal patterns to another one with the changes of the indirect taxis and semi saturation coefficients. The results show that spatially inhomogeneous Hopf bifurcations are induced by an indirect prey-taxis parameter $\chi >0$, which is impossible for the reaction–diffusion predator–prey model with a direct prey-taxis.

1 Introduction

Since the pioneer work of Lotka [32] and Volterra [50], predator–prey interactions have been one of the hottest topics in mathematics and ecology and exhibited the rich biodiversity of ecosystem [3]. Spatiotemporal heterogeneity plays an important role in ecological systems, directly accounting for ecosystem biodiversity and species interactions. The reaction–diffusion models including taxis terms provide effective theoretical and practical tools in describing the spatiotemporal heterogeneity in ecosystems [6, 7, 29, 33, 34, 46]. The prey-taxis describes active movement of predators towards the area of higher prey density, which was first observed in the experiment and treated as biased random walks by Karevia and Odell [25].

In view of the random diffusion of predator and prey and biased random walks to prey, a general reaction–diffusion equation with direct prey-taxis is the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial N}{\partial t}=Nf(N)-Pg(N)+\delta _N\triangle N,~~x\in \Omega ,~t>0,\\ \frac{\partial P}{\partial t}=\gamma Pg(N)-mP+\nabla \cdot (-\chi (P)\nabla N+\delta _P\nabla P),~~x\in \Omega ,~t>0, \end{array}\right. } \end{aligned}$$

(1.1)

where N(x, t),  P(x, t) are the densities of prey and predator populations at space x and time t, Pg(N) denotes the inter-specific interaction, f(N) is the per capita growth rate of the prey population in the absence of predator. m is the mortality rate of the predator population. $\gamma$ is the conversion coefficient. In particular, g(N) is the functional response which reflects the intake rate of predators to preys. $\delta _N,~\delta _P$ are the diffusion coefficients of the prey and predator. $\nabla \cdot (-\chi (P) \nabla N)$ denotes the tendency of predator moving upward or downward the prey gradient direction. The existence and uniqueness of weak solutions of system (1.1) were obtained by [2]. Tao [44] investigated the existence and uniqueness of classical solutions of system (1.1) in a smooth bounded domain $\Omega \subset R^n,~1\le n\le 3$. Pattern formation induced by prey-taxis was studied for different functional responses in [29]. The existence, bifurcation of nonconstant steady state and pattern formations of system (1.1) are investigated in [52]. Wu et al. [53] focused on a more general form of system (1.1) and obtained the global existence and boundness of the solutions. Wang et al. [51] studied the existence and boundedness of the solutions of the three-species predator–prey model with two prey-taxis in bounded domain of arbitrary spatial domain. Yousefnezhad et al. [54] studied the global stability of the constant positive equilibrium of a predator–prey system with prey-taxis and special functional responses by constructing a Lyapunov function. The existence of nonconstant steady state and Turing instability induced by direct prey-taxis has also been widely investigated in the literatures (see [5, 24, 27, 30, 55, 56]), which show that the prey-taxis term can destabilize the constant equilibrium.

Direct taxis models as (1.1) to simulate the active movement of predators to preys are fraught since such models can not result in stable spatially heterogeneous dynamical behaviors in the absence of nonlinear terms, illustrated in [4, 19, 47]. Instead of a direct influence of prey-taxis and assuming that the taxis is stimulated by some chemicals that are continuously emitted by prey (e.g., odour, pheromones, exometabolites), the predator–prey model with the indirect prey-taxis has attracted the great attention of the researchers. Compared with the direct prey-taxi, there is a little work on the predator–prey system with indirect prey-taxis.

It has been shown that intensive indirect prey-taxis results in the spatial heterogeneity in the predator–prey models even in the absence of predator’s reproduction and mortality processes [4, 9, 45]. Recently, Tyutyunov et al. [49] investigated the influence of the indirect prey-taxis on the dynamics for the diffusive Gause–Kolmogorov-type predator–prey model, where the predator ability to pursue the prey is modelled by the Patlak–Keller–Segel taxis model and the movement velocities of predators are proportional to the gradients of specific cues emitted by the prey population. And it has been shown that the prey-taxis destabilizes the constant steady state and induces Hopf bifurcation. Tyutyunov et al. [48] considered the indirect prey-taxis model based on the Rosenzweig–MacArthur predator–prey model with Allee effect in predator population growth. They found that the indirect prey-taxis activity of the predator can destabilize both the stationary and periodic spatially-homogeneous regimes of the species coexistence. The results in [48, 49] are mainly based on the numerical investigation and the assumption. More recently, Ahn et al. [1] proved the global existence and uniform boundedness of solutions of system (1.2) with indirect taxis in any spatial domain and the global stability of semi-trivial equilibrium, And the simulations reveal that indirect prey-taxis can result in complex spatial patterns.

In the present paper, we consider the following Gause–Kolmogorov-type predator–prey system with indirect prey-taxis as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial N}{\partial t}=Nf(N)-Pg(N)+\delta _N\triangle N,~~x\in \Omega ,~t>0,\\ \frac{\partial P}{\partial t}=\gamma Pg(N)-mP+\nabla \cdot (-\chi P\nabla S+\delta _P\nabla P),~~x\in \Omega ,~t>0,\\ \frac{\partial S}{\partial t}=\xi N-\eta S+\delta _S\triangle S,~~x\in \Omega ,~t>0,\\ \frac{\partial N}{\partial \nu }=\frac{\partial P}{\partial \nu }= \frac{\partial S}{\partial \nu }=0,~~x\in \partial \Omega ,~t>0,\\ N(x,0)=N_0(x)\ge 0, ~P(x,0)=P_0(x)\ge 0,~S(x,0)=S_0(x)\ge 0,~x\in \Omega , \end{array}\right. } \end{aligned}$$

(1.2)

where S(x, t) is the taxis stimulus concentration, $\delta _S$ is the constant diffusion coefficient of stimulus, $\chi$ is the taxis coefficient of the predator population. When $\chi =0$, there is no indirect prey-taxis. Generally, $\chi >0$ (known as the attractive taxis), which implies that the prey-taxis movements of predator density are positively stimulated by some chemical emitted by the prey and show the tendency to the high prey area. When the predator may retreat from high prey area, $\chi$ can be negative (known as the repulsive taxis), which occurs in the case when the prey act anti-predator defensive behaviors and show chemical defences [31]. Other parameters are as the same as system (1.1). Here, we choose $\Omega =(0,l\pi )$ for simplicity and convenience in computing the normal forms and carrying out the numerical simulations. $\nu$ is the outer normal direction. The zero-flux boundary condition is imposed to imply that the system is close to the exterior environment.

The primary purpose in this paper is to investigate mathematically what interesting dynamical behaviors for system (1.2). Especially, we investigate the occurrence of the codimension-two double-Hopf bifurcation and Turing–Hopf bifurcation and determine the dynamical classification near the double-Hopf bifurcation by calculating the normal form of the double-Hopf bifurcation. System (1.2) has been proposed in [49], however, to the best of our knowledge, the study for the stability and codimension-two bifurcation is the first mathematical investigation.

As we all know, the codimension-one Hopf bifurcation and Turing bifurcation have been extensively studied in various reaction–diffusion systems (e.g. [8, 17, 23, 40, 49, 57] ). However, the interactions of double-Hopf bifurcations may generate spatially homogeneous and nonhomogeneous periodic solutions, quasi-periodic solutions, coexisting of several periodic solutions [13, 20, 21]. Interactions of Turing and Hopf bifurcations may generate spatiotemporal periodic pattern, bistability between spatial and temporal patterns [38, 40, 42, 43]. Following the outstanding work of Faria [16, 18], the general frame of calculating the normal forms of double-Hopf bifurcations has been derived by Jiang and Song [22] for the delay differential equations under the case of non-resonance and weak resonance and by Du et al. [13] for the reaction–diffusion with delay, where is no prey-taxis, and by Song et al. [39] for the resource-consumer model with random and memory-based diffusions.

In comparison with other existing results, we roughly summarize our main results as follows:

• The spatially inhomogeneous Hopf bifurcations induced by the indirect prey-taxis for the predator–prey model are found.

• Taking the indirect taxis coefficient and other parameter as the bifurcation parameters, we mathematically investigate the existence of double-Hopf bifurcations and Turing–Hopf bifurcations of system (1.2), which reflect that indirect prey-taxis can bring about rich dynamical behaviors.

• An algorithm for calculating the normal form of the double-Hopf bifurcation for the non-resonance and weak resonance is derived, which guarantees the exact regional divisions with different dynamics near double-Hopf bifurcation points.

• Our theoretical results are applied to the predator–prey system (1.2) with Holling-II functional response and some interesting pattern formations are illustrated.

We would like to mention that spatially inhomogeneous Hopf bifurcations do not occur for the reaction–diffusion predator–prey model with a direct prey-taxi like (1.1) when $\chi >0$, and here it is shown that an indirect prey-taxi can generate spatially inhomogeneous Hopf bifurcations. The spatially inhomogeneous Hopf bifurcations are also proved in [31] for the attraction-repulsion Keller–Segel system. The mechanism there is to have both attractive and repulsive chemotaxis, while the mechanism here is to have indirect prey-taxi. Both of them need three equations. However, when the delay is involved into the diffusion terms, spatially inhomogeneous Hopf bifurcations can occur even for the single population model with memory-based diffusion [36, 37, 41]. In [37], the authors first proposed this spatial memory model and it has been shown that the delay-induced spatially inhomogeneous Hopf bifurcations are always unstable. However, the delay-induced stable spatially inhomogeneous Hopf bifurcations are possible in the models proposed in [36, 41]. In [41], the mechanism of spatially inhomogeneous Hopf bifurcations comes from the interaction of the memory delay and the nonlocal reaction, while in [36], it comes from the interaction of the memory delay and maturation delay. For classical Keller–Segel equation with logistic growth, spatially inhomogeneous periodic orbits are also found, but which are not the results of Hopf bifurcation from the positive constant equilibrium [15, 35].

The rest of this article is as follows. In Sect. 2, we investigate the stability of the positive equilibrium and existence of spatially homogeneous and nonhomogeneous Hopf bifurcations and Turing bifurcations, and the critical values of the double-Hopf bifurcation and Turing–Hopf bifurcation points are explicitly obtained. Besides, our results are applied to the system (2.12) with Holling-II functional response and the corresponding results are derived. In Sect. 3, the normal form of double-Hopf bifurcation for a general reaction–diffusion system with indirect prey-taxis is derived and rich dynamical behaviors near the double-Hopf bifurcation points are discussed. In Sect. 4, numerical simulations are illustrated to verify and expand our theoretical results and complex spatial patterns are exhibited. Conclusion and further discussion are given in Sect. 5.

2 Stability and Bifurcation Analysis

In this article, we further assume the absence of the Allee effect in the prey population. Moreover, the functional response of predators is only prey-dependent, which implies that f(N) and g(N) satisfy the following conditions formulated by Kolmogorov [26]:

$(H1)~~~f(0)>0,~~f_N'<0$ and there exists a constant $K>0$ such that $f(K)=0$;

$(H2)~~~g(0)=0,~~g_N'>0$ and there exists a constant $N_2^*>0$ such that $g(N_2^*)=\frac{m}{\gamma }$.

It is shown that the system (1.2) has the zero equilibrium $E_0(0,0,0)$ and the boundary equilibrium $E_1(K,0,\frac{\xi K}{\eta })$ (extinction of predator) and the unique positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ (coexistence of prey and predator), where

$$\begin{aligned} N_2^*=g^{-1}\left( \frac{m}{\gamma }\right) ,~P_2^*=\frac{N_2^*f(N_2^*)}{g(N_2^*)}=\frac{\gamma N_2^*f(N_2^*)}{m},~S_2^*=\frac{\xi N_2^*}{\eta }. \end{aligned}$$

(2.1)

The corresponding ordinary differential equation of system (1.2) is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dN}{dt}=Nf(N)-Pg(N),\\ \frac{dP}{dt}=\gamma Pg(N)-mP,\\ \frac{dS}{d t}=\xi N-\eta S. \end{array}\right. } \end{aligned}$$

(2.2)

From [49], we have the following result:

Lemma 2.1

[49] System (2.2) has a unique positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ defined by (2.1), which is locally asymptotically stable if $f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)<0$ and unstable if $f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)>0$. And system (2.2) undergoes a Hopf bifurcation at $E_2(N_2^*,P_2^*,S_2^*)$ when $f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)=0$.

Through this section, we assume the following condition holds:

$(H3)~~~ f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)\le 0.$

The linearization of the system (1.2) at $E_2(N_2^*,P_2^*,S_2^*)$ is as follows:

$$\begin{aligned} \left( \begin{array}{c} \frac{\partial N}{\partial t}\\ \frac{\partial P}{\partial t}\\ \frac{\partial S}{\partial t} \end{array}\right) =D\left( \begin{array}{c}\triangle N\\ \triangle P\\ \triangle S\end{array}\right) +A\left( \begin{array}{c} N\\ P\\ S \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} D=\left( \begin{array}{c@{\quad }c@{\quad }c}\delta _N&{}0&{}0\\ 0&{}\delta _P&{}-\chi P_2^*\\ 0&{}0&{}\delta _S\end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} A=\left( \begin{array}{c@{\quad }c@{\quad }c} a_{11}&{}-g(N_2^*)&{}0\\ \gamma P_2^*g'(N_2^*)&{} \gamma g(N_2^*)-m&{}0\\ \xi &{}0&{}-\eta \end{array}\right) =\left( \begin{array}{c@{\quad }c@{\quad }c} a_{11}&{}-\frac{m}{\gamma }&{}0\\ \gamma P_2^*g'(N_2^*)&{}0&{}0\\ \xi &{}0&{}-\eta \end{array}\right) , \end{aligned}$$

where $a_{11}=f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)\le 0$.

It is well-known that the eigenvalue problem

$$\begin{aligned} \begin{aligned} -\triangle u(x)=\mu u(x),~~~&x\in (0,l\pi ),\\ u_x(0)=u_{x}(l\pi )=0, \end{aligned} \end{aligned}$$

has the eigenvalues $\mu _n=\frac{n^2}{l^2},~n=0,1,2,\ldots$, with the corresponding normalized eigenfunctions

$$\begin{aligned} \beta _n^{(j)}(x)=r_n(x)e_j,~r_n(x)=\frac{\cos {\frac{nx}{l}}}{\Vert \cos {\frac{nx}{l}}\Vert }_{2,2}=\left\{ \begin{array}{cc}\frac{1}{\sqrt{l\pi }},&{}n=0,\\ \sqrt{\frac{2}{l\pi }}\cos {\frac{nx}{l}},&{}n\ne 0.\end{array}\right. \end{aligned}$$

(2.3)

The characteristic equations corresponding to the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ are

$$\begin{aligned} \lambda ^3+P(\chi ,n)\lambda ^2+Q(\chi ,n)\lambda +R(\chi ,n)=0, \end{aligned}$$

(2.4)

where

$$\begin{aligned} \begin{aligned} P(\chi ,n)=&\,(\delta _N+\delta _S+\delta _P)\left( \frac{n}{l}\right) ^2+\eta -a_{11},\\ Q(\chi ,n)=&\,(\delta _N\delta _S+(\delta _S+\delta _N)\delta _P)\left( \frac{n}{l}\right) ^4+(\eta (\delta _N+\delta _P)-(\delta _S+\delta _P)a_{11})\left( \frac{n}{l}\right) ^2\\ {}&-\eta a_{11}+mP_2^*g'(N_2^*),\\ R(\chi ,n)=&\,\delta _N\delta _S\delta _P\left( \frac{n}{l}\right) ^6+(\delta _N\delta _P\eta -a_{11}\delta _S\delta _P)\left( \frac{n}{l}\right) ^4+\eta mP_2^*g'(N_2^*)\\&+\left( -\eta \delta _Pa_{11}+mP_2^*g'(N_2^*)\delta _S+\frac{m\xi }{\gamma }\chi P_2^*\right) \left( \frac{n}{l}\right) ^2. \end{aligned} \end{aligned}$$

(2.5)

2.1 Stability, Hopf and Double-Hopf Bifurcations

In this section, we consider the stability and Hopf bifurcation of the system (1.2) by analyzing the characteristic values. By the Routh–Hurwitz criterion, $E_2(N_2^*,P_2^*,S_2^*)$ is locally asymptotically stable if and only if for all $n=0,1,2,\ldots ,$

$$\begin{aligned} \triangle _{1n}>0,~\triangle _{2n}>0,~\triangle _{3n}>0, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \triangle _{1n}=&\,P(\chi ,n)=(\delta _N+\delta _S+\delta _P)\left( \frac{n}{l}\right) ^2+\eta -a_{11}>0,\\ \triangle _{2n}=&\,\left| \begin{array}{cc}P(\chi ,n)&{}1\\ R(\chi ,n)&{}Q(\chi ,n)\end{array}\right| =P(\chi ,n)Q(\chi ,n)-R(\chi ,n)\\ =&\,b_1\left( \frac{n}{l}\right) ^6+b_2\left( \frac{n}{l}\right) ^4+b_3\left( \frac{n}{l}\right) ^2-\frac{m\xi }{\gamma }\chi P_2^*\left( \frac{n}{l}\right) ^2+b_4,\\ \triangle _{3n}=&\,\left| \begin{array}{c@{\quad }c@{\quad }c}P(\chi ,n)&{}1&{}0\\ R(\chi ,n)&{}Q(\chi ,n)&{}P(\chi ,n)\\ 0&{}0&{}R(\chi ,n)\end{array}\right| =R(\chi ,n)\triangle _{2n}, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} b_1=&\,(\delta _s+\delta _N)\delta _P^2+\delta _S^2(\delta _P+\delta _N)+\delta _N^2(\delta _S+\delta _P)+2\delta _N\delta _S\delta _P>0,\\ b_2=&\,\eta (\delta _N^2+\delta _P^2+2\delta _P(\delta _S+\delta _N)+2\delta _S\delta _N)\\ {}&-a_{11}(\delta _S^2+\delta _P^2+2((\delta _N+\delta _S)\delta _P+\delta _N\delta _S))>0,\\ b_3=&\,a_{11}^2(\delta _S+\delta _P)-2a_{11}\eta (\delta _S+\delta _P)-2a_{11}\eta \delta _N+\eta ^2(\delta _N+\delta _P)\\ {}&+mP_2^*g'(N_2^*)(\delta _N+\delta _P)>0,\\ b_4=&\,a_{11}^2\eta -a_{11}\eta ^2-a_{11}mP_2^*g'(N_2^*)\left\{ \begin{array}{l@{\quad }l} =0, &{} a_{11}=0,\\ >0, &{} a_{11}<0. \end{array}\right. \end{aligned} \end{aligned}$$

(2.6)

Clearly, the sign of $\triangle _{3n}$ agrees with $\triangle _{2n}$ since $R(\chi ,n)>0$ for all $n\in N_0\triangleq \{0,1,2,\ldots \}$. Thus, the stability of $E_2(N_2^*,P_2^*,S_2^*)$ and the existence of Hopf bifurcation are determined only by the sign of $\triangle _{2n}$. It is easy to check that, when $a_{11}<0$, system (1.2) has no Hopf bifurcation for any $\chi \le 0$ since $\triangle _{2n}>0$ for $n\in N_0$. Thus, when $a_{11}<0$, we can obtain the existence of Hopf bifurcation only when $\chi >0$. In this case, $\lambda =0$ is not a root of the characteristic Eq. (2.4).

The necessary condition for Hopf bifurcation to occur is $\triangle _{2n}=0$ for a fixed $n\in N_0$, which is equivalent to

$$\begin{aligned} \chi \triangleq \chi _n^H=\frac{\gamma }{m\xi P_2^*}\left( b_1\left( \frac{n}{l}\right) ^4+b_2\left( \frac{n}{l}\right) ^2+b_3+b_4\left( \frac{l}{n}\right) ^2\right) >0,~n=1,2,\ldots , \end{aligned}$$

(2.7)

or

$$\begin{aligned} a_{11}=0,~n=0. \end{aligned}$$

Remark 2.1

The Hopf bifurcation curve $a_{11}=f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)=0,~n=0$ of the diffusive system (1.2) is exactly the Hopf bifurcation of the corresponding ODE (2.2).

Hence, for fixed $n\in \{1,2,\ldots \}$, Eq. (2.4) has a pair of purely imaginary roots,

$$\begin{aligned} \lambda _n=\pm i\omega _n=\pm i\sqrt{Q(\chi ,n)}~\text {at}~\chi =\chi _n^H. \end{aligned}$$

(2.8)

Next, we verify that the transversality condition holds.

Taking the derivative of both sides of Eq. (2.4) with respect to $\chi$ at $\chi =\chi _n^H$, we have that,

$$\begin{aligned} \left. \frac{d\lambda }{d\chi }(3\lambda ^2+2\lambda P(\chi ,n)+Q(\chi ,n))\right| _{\chi =\chi _n^H}=-\frac{m\xi }{\gamma }P_2^*\left( \frac{n}{l}\right) ^2, \end{aligned}$$

which implies that

$$\begin{aligned} \left. Re\left( \frac{d\lambda }{d\chi }\right) ^{-1}\right| _{\chi =\chi _n^H}=-\left. \frac{\gamma Re(3\lambda ^2+2\lambda P(\chi ,n)+Q(\chi ,n))}{\xi mP_2^*\left( \frac{n}{l}\right) ^2}\right| _{\chi =\chi _n^H}=\frac{2\gamma Q(\chi ,n)}{m\xi P_2^*\left( \frac{n}{l}\right) ^2}>0. \end{aligned}$$

Thus, $\left. \frac{dRe\lambda }{d\chi }\right| _{\chi =\chi _n^H}>0$ since the sign of $Re\left( \frac{d\lambda }{d\chi }\right) ^{-1}$ is consistent with the sign of $\frac{dRe\lambda }{d\chi }$.

In the sequel, we show the monotonicity of the critical values $\chi _n^H$ with respect to n.

Lemma 2.2

Let $x_0$ be a unique positive root of the cubic equation $2b_1x^3+b_2x^2-b_4=0$, where $b_1,b_2,b_4$ are defined in (2.6). Set

(2.9)

Then $\chi _n^H$ is decreasing in $n\le n_H^*$ and increasing in $n>n_H^*$. That is, $\chi _{n_H^*}^H=\min \limits _{n\in \{1,2,\ldots \}}\{\chi _n^H\}$, where $\chi _n^H$ is defined by (2.7).

In particular, when $a_{11}=0$, $\chi _n^H$ is increasing in n, that is, $\chi _{1}^H=\min \limits _{n\in \{1,2,\ldots \}}\{\chi _n^H\}$.

Proof

(i) When $a_{11}\ne 0$, let $G(x)=b_1x^2+b_2x+b_3+\frac{b_4}{x}$. Then $G'(x)=2b_1x+b_2-\frac{b_4}{x^2}$.

Clearly, $G'(x)=0$ is equivalent to $W(x)\doteq 2b_1x^3+b_2x^2-b^4=0$.

Obviously, W(x) is increasing in $(0,+\infty )$ since $b_1,b_2>0$ and $W(0)=-b^4<0$. Thus, there exists a unique $x_0>0$ such that $W(x_0)=0$ and $W(x)<0$ on $(0,x_0)$ and $W(x)>0$ on $(x_0,+\infty )$. Since $G'(x)=W(x)/x^2$, G(x) is decreasing on $(0,x_0)$ and increasing on $(x_0,+\infty )$. By the definition (2.9) of $n_H^*$, the result is confirmed.

(ii) When $a_{11}=0$, $\chi _n^H=\frac{\gamma }{m\xi P_2^*}\left( b_1\left( \frac{n}{l}\right) ^4+b_2\left( \frac{n}{l}\right) ^2+b_3\right)$ is increasing in n since $b_1>0,~b_2>0,~b_3>0$. Clearly, $\chi _{1}^H=\min \limits _{n\in \{1,2,\ldots \}}\{\chi _n^H\}$. $\square$

From the analysis above, we obtain the following results:

Theorem 2.1

Assume that the conditions (H1)–(H3) hold and $\chi _n^H,~n=1,2,\ldots ,$ are defined by (2.7). Then the following results are true:

• (I) when $f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)<0$ and $\chi \le 0$, system (1.2) has no Hopf bifurcation;

• (II) when $f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)<0$ and $\chi > 0$, for fixed $\delta _N,~\delta _P,~\delta _S,~\gamma ,~m,~\xi ,~\eta ,~a_{11}$ and l,

  • (i) if for any $j\in N_0$ and $j\ne n$ such that $\chi _j^H\ne \chi _n^H$, system (1.2) undergoes spatially inhomogeneous Hopf bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _n^H$, and a family of spatially inhomogeneous periodic solutions bifurcate from the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$;

  • (ii) if there exists $n_1,~n_2,\ldots ,~n_s\in N_0$ such that $\chi _{n_1}^H=\chi _{n_2}^H=\cdots =\chi _{n_s}^H$ and $\chi _j^H\ne \chi _{n_1}^H$ for $j\ne n_1,~n_2,\ldots ,n_s$, system (1.2) undergoes spatially inhomogeneous $s-$multiple Hopf bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _{n_i}^H,~i=1,2,\ldots ,s$;

    In particular, if $s=2$, 2-multiple Hopf bifurcation is often called double-Hopf bifurcation;

  • (iii) the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ is locally asymptotically stable for $\chi \in [0,\chi _{n_H^*}^H)$ and unstable for $\chi \in (\chi _{n_H^*}^H,+\infty )$, where $n_H^*$ is defined by (2.9);

• (III) if $f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)=0$, system (1.2) undergoes double-Hopf bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _n^{DH}$, where

  $$\begin{aligned} \chi _n^{DH}=\frac{\gamma }{m\xi P_2^*}\left( b_1\left( \frac{n}{l}\right) ^4+b_2\left( \frac{n}{l}\right) ^2+b_3\right) >0,~n=1,2,\ldots , \end{aligned}$$

  and $\chi _1^{DH}=\min \limits _{n\in \{1,2,\ldots \}}\{\chi _n^{DH}\}$.

Remark 2.2

Hopf bifurcation in the predator–prey models has been widely studied in [43, 57], where Hopf bifurcation at the first critical value is always homogenous. In fact, it is exactly Hopf bifurcation of the corresponding ODE. However, the indirect-taxis-induced Hopf bifurcation at the first critical value is spatially inhomogeneous.

2.2 Turing Instability and Turing–Hopf Bifurcation

From the above analysis, we know that when $a_{11}<0$, system (1.2) has no Turing pattern for any $\chi \ge 0$ since $\lambda =0$ is not a root of the characteristic Eq. (2.4). Thus, we can obtain the existence of Turing bifurcation only when $\chi <0$.

The necessary condition for Turing bifurcation to occur is $R(\chi ,n)=0$, which is equivalent to

$$\begin{aligned} \begin{aligned} \chi =\chi _n^T\triangleq&-\frac{\gamma }{m\xi P_2^*}\left( \delta _N\delta _S\delta _P\left( \frac{n}{l}\right) ^4+(\delta _N\eta \delta _P-a_{11}\delta _S\delta _P)\left( \frac{n}{l}\right) ^2\right. \\&\left. +\eta mP_2^*g'(N_2^*)\left( \frac{l}{n}\right) ^2-\eta \delta _Pa_{11}+mP_2^*g'(N_2^*)\delta _S\right) , ~n=1,2,\ldots . \end{aligned} \end{aligned}$$

(2.10)

Clearly, for fixed $n\in \{1,2,\ldots \}$, Eq. (2.4) has a simple zero root at $\chi =\chi _n^T$ since $R(\chi ,n)=0,~Q(\chi ,n)>0$. Next, we verify the transversality condition.

Taking the derivative of both sides of Eq. (2.4) with respect to $\chi$ at $\chi =\chi _n^T$, we have that,

$$\begin{aligned} \left. \frac{d\lambda }{d\chi }(3\lambda ^2+2\lambda P(\chi ,n)+Q(\chi ,n))\right| _{\chi =\chi _n^T}=-\frac{m\xi }{\gamma }P_2^*\left( \frac{n}{l}\right) ^2, \end{aligned}$$

which implies that

$$\begin{aligned} \left. \left( \frac{d\lambda }{d\chi }\right) ^{-1}\right| _{\chi =\chi _n^T}=-\left. \frac{\gamma (3\lambda ^2+2\lambda P(\chi ,n)+Q(\chi ,n))}{\xi mP_2^*\left( \frac{n}{l}\right) ^2}\right| _{\chi =\chi _n^T}=-\frac{\gamma Q(\chi ,n)}{m\xi P_2^*\left( \frac{n}{l}\right) ^2}<0. \end{aligned}$$

Thus, $\left. \frac{d\lambda }{d\chi }\right| _{\chi =\chi _n^T}<0$ since the sign of $\left( \frac{d\lambda }{d\chi }\right) ^{-1}$ is consistent with the sign of $\frac{d\lambda }{d\chi }$.

Next, we give the monotonicity of $\chi _n^T$ on n.

Lemma 2.3

Let $x^*$ be a unique positive root of cubic equation

$$\begin{aligned} 2\delta _N\delta _S\delta _Px^3+(\delta _N\eta \delta _P-a_{11}\delta _S\delta _P)x^2-\eta mP_2^*g'(N_2^*)=0. \end{aligned}$$

Set

(2.11)

Then $\chi _n^T$ is increasing in $n\le n_T^*$ and decreasing in $n>n_T^*$. That is, $\chi _{n_T^*}^T=\max \limits _{n\in \{1,2,\ldots \}}\{\chi _n^T\}$, where $\chi _n^T$ is defined by (2.10).

Proof

Let

$$\begin{aligned} L(x)=\delta _N\delta _S\delta _Px^2+(\delta _N\eta \delta _P-a_{11}\delta _S\delta _P)x+\frac{\eta mP_2^*g'(N_2^*)}{x}. \end{aligned}$$

Clearly,

$$\begin{aligned} \begin{aligned} L'(x)=&2\delta _N\delta _S\delta _Px+(\delta _N\eta \delta _P-a_{11}\delta _S\delta _P)-\frac{\eta mP_2^*g'(N_2^*)}{x^2},\\ L''(x)=&2\delta _N\delta _S\delta _P+\frac{2\eta mP_2^*g'(N_2^*)}{x^3}. \end{aligned} \end{aligned}$$

That is, $L'(x)$ is increasing in $(0,+\infty )$ and $L'(0^+)=-\infty ,~L'(+\infty )=+\infty$. Hence, there exists a unique $x^*>0$ such that $L'(x^*)=0$ and $L'(x)<0$ for $x\in (0,x^*)$ and $L'(x)>0$ for $x\in (x^*,+\infty )$.

By the definition of $n_T^*$, the result is confirmed. $\square$

In addition, it is clear that $\triangle _{1n}>0,~\triangle _{2n}>0$ when $\chi <0,~a_{11}\le 0$. Hence, the positive equilibrium $E_2$ is unstable only when $R(\chi ,n)<0$, which is equivalent to

$$\begin{aligned} \chi <\max \limits _{n\in N}\{\chi _n^T\}=\chi _{n_T^*}^T. \end{aligned}$$

From the analysis results above and combining Lemmas 2.1 and 2.3, we have the following results:

Theorem 2.2

Assume that the conditions (H1)–(H3) hold and $\chi _n^T,~n=1,2,\ldots ,$ are defined by (2.10). Then the following results are true:

• (I) when $\chi \ge 0$, system (1.2) has no Turing bifurcation;

• (II) when $\chi < 0$, for fixed $\delta _N,~\delta _P,~\delta _S,~\gamma ,~m,~\xi ,~\eta ,~a_{11}$ and l,

  • (i) if for any $j\in N_0$ and $j\ne n$ such that $\chi _j^T\ne \chi _n^T$, system (1.2) undergoes Turing bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _n^T$;

  • (ii) if there exists $n_1,~n_2,\ldots ,~n_s\in N_0$ such that $\chi _{n_1}^T=\chi _{n_2}^T=\cdots =\chi _{n_s}^T$ and $\chi _j^T\ne \chi _{n_1}^T$ for $j\ne n_1,n_2,\ldots ,n_s$, system (1.2) undergoes $s-$multiple Turing bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _{n_1}^T$;

    In particular, if $s=2$, $2-$multiple Turing bifurcation is often called Turing–Turing bifurcation;

  • (iii) the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ of system (1.2) is asymptotically stable for $\chi _{n_T^*}^T<\chi \le 0$ and unstable for $\chi <\chi _{n_T^*}^T$, where $n_T^*$ is defined in (2.11);

• (III) when $f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)=0$, system (1.2) undergoes Turing–Hopf bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _n^{TH}$, where

  $$\begin{aligned} \begin{aligned} \chi _{n_T^*}^{TH}=&-\frac{\gamma }{m\xi P_2^*}\left( \delta _N\delta _S\delta _P\left( \frac{n_T^*}{l}\right) ^4+(\delta _N\eta \delta _P-a_{11}\delta _S\delta _P)\left( \frac{n_T^*}{l}\right) ^2\right. \\&\left. +\eta mP_2^*g'(N_2^*)\left( \frac{l}{n_T^*}\right) ^2-\eta \delta _Pa_{11}+mP_2^*g'(N_2^*)\delta _S\right) . \end{aligned} \end{aligned}$$

2.3 Application to the Predator–Prey Model with Logistic Growth and Holling-II Functional Response

In this subsection, we consider the following predator–prey model with Logistic growth and Holling-II functional response:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial N}{\partial t}=rN\left( 1-\frac{N}{k}\right) -\frac{\beta NP}{1+\sigma N}+\delta _N\triangle N,~~x\in (0,l\pi ),~t>0,\\ \frac{\partial P}{\partial t}=\beta \left( \frac{\gamma NP}{1+\sigma N}-\rho P\right) +\nabla \cdot (-\chi P\nabla S+\delta _P\nabla P),~~x\in (0,l\pi ),~t>0,\\ \frac{\partial S}{\partial t}=\xi N-\eta S+\delta _S\triangle S,~~x\in (0,l\pi ),~t>0,\\ N_x(x,t)=P_x(x,t)=S_x(x,t)=0,~~x=0,~l\pi ,~t>0,\\ N(x,0)=N_0(x)\ge 0, ~P(x,0)= {P_0}\text {(}x\text {)}\ge 0,~S(x,0)=S_0(x)\ge 0,~x\in [0,l\pi ]. \end{array}\right. } \end{aligned}$$

(2.12)

Assume that

$$\begin{aligned} (A1) ~~~0<\rho <\frac{\gamma k}{\sigma k+1}, \end{aligned}$$

then system (2.12) has a unique positive steady state $E_2(N_2^*,P_2^*,S_2^*)$, where

$$\begin{aligned} N_2^*=\frac{\rho }{\gamma -\sigma \rho },~P_2^*=\frac{r\gamma }{\beta (\gamma -\sigma \rho )^2}\left( \gamma -\rho \left( \sigma +\frac{1}{k}\right) \right) ,~S_2^*=\frac{\xi N_2^*}{\eta }. \end{aligned}$$

For system (2.12), we have

$$\begin{aligned} f(N)=r\left( 1-\frac{N}{k}\right) ,~~g(N)=\frac{\beta N}{1+\sigma N},~m=\beta \rho , \end{aligned}$$

and then

$$\begin{aligned} \begin{aligned}&a_{11}=\rho r\left( \frac{1}{\gamma }\left( \sigma +\frac{1}{k}\right) -\frac{2}{k(\gamma -\sigma \rho )}\right) , ~a_{12}=-\frac{\beta \rho }{\gamma },\\&a_{21}=r\left( \gamma -\rho \left( \sigma +\frac{1}{k}\right) \right) ,~a_{22}=0. \end{aligned} \end{aligned}$$

It is easy to verify that,

$$\begin{aligned} a_{11}<0,~~\text {if}~\sigma \le \frac{1}{k}, \end{aligned}$$

(2.13)

and when $\sigma >\frac{1}{k}$,

$$\begin{aligned} a_{11}=f(N_2^*)-P_2^*g'(N_2^*)+N_2^*f'(N_2^*)\left\{ \begin{array}{l@{\quad }l}<0, &{} \rho>\rho _1(\sigma ),\\ =0, &{} \rho =\rho _1(\sigma ),\\ >0, &{} \rho <\rho _1(\sigma ), \end{array}\right. \end{aligned}$$

(2.14)

where

$$\begin{aligned} \rho =\rho _1(\sigma )\triangleq \frac{\gamma (k\sigma -1)}{\sigma ^2k+\sigma }~\text {for fixed}~\gamma ,~k. \end{aligned}$$

(2.15)

Therefore, for the following corresponding ODE of system (2.12),

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dN}{dt}=rN\left( 1-\frac{N}{k}\right) -\frac{\beta NP}{1+\sigma N},\\ \frac{dP}{dt}=\beta \left( \frac{\gamma NP}{1+\sigma N}-\rho P\right) ,\\ \frac{d S}{dt}=\xi N-\eta S, \end{array}\right. } \end{aligned}$$

(2.16)

we have the following results on the stability and Hopf bifurcation for system (2.16):

Theorem 2.3

Assume that the condition (A1) holds and $\rho =\rho _1(\sigma )$ is defined by (2.15). Then the following results are true:

• (i) if $\sigma \le \frac{1}{k}$, the positive steady state $E_2(N_2^*,P_2^*,S_2^*)$ of system (2.16) is always stable for any $\rho >0$;

• (ii) if $\sigma >\frac{1}{k}$, the positive steady state $E_2(N_2^*,P_2^*,S_2^*)$ of system (2.16) is stable for $\rho >\rho _1(\sigma )$ and unstable for $\rho <\rho _1(\sigma )$;

• (iii) for fixed $k,~\gamma$ and $0<\rho <\rho ^*_{max}$, where

  $$\begin{aligned} \rho ^*_{max}=\frac{\sqrt{2}\gamma k}{4+3\sqrt{2}}, \end{aligned}$$

  (2.17)

  system (2.16) undergoes Hopf bifurcations at $\sigma =\sigma _j, ~j=1,2$, where $\sigma _1$ and $\sigma _2$ are two roots of (2.15) for fixed $\rho$. And when $\rho ^*_{max}<\rho <\frac{\gamma k}{\sigma k+1}$, there is no Hopf bifurcation for system (2.16).

Proof

From Lemma 2.1 and (2.13), (2.14), (i) and (ii) are confirmed. Next we only verify the result (iii).

(iii) It follows from Eq. (2.15) that

$$\begin{aligned} \frac{\partial \rho _1(\sigma )}{\partial \sigma }=\frac{(-k^2\sigma ^2+2\sigma k+1)\gamma }{(\sigma ^2k+\sigma )^2}, \end{aligned}$$

which implies that there exists a unique $\sigma ^*=\frac{1+\sqrt{2}}{k}$ such that $\frac{\partial \rho _1(\sigma )}{\partial \sigma }|_{\sigma =\sigma ^*}=0, ~\frac{\partial \rho _1(\sigma )}{\partial \sigma }>0$ for $\sigma \in \left( \frac{1}{k},\frac{1+\sqrt{2}}{k}\right)$ and $\frac{\partial \rho _1(\sigma )}{\partial \sigma }<0$ for $\sigma \in \left( \frac{1+\sqrt{2}}{k},+\infty \right)$.

Thus, for fixed $k,~\gamma$, the function $\rho _1(\sigma )$ is increasing for $\sigma \in \left( \frac{1}{k},\frac{1+\sqrt{2}}{k}\right)$ and decreasing for $\sigma \in \left( \frac{1+\sqrt{2}}{k},+\infty \right)$ with respect to $\sigma$. And $\rho _1(\sigma )$ reaches its maximum value

$$\begin{aligned} \rho ^*_{max}\triangleq \rho _1(\sigma ^*)=\frac{\sqrt{2}\gamma k}{4+3\sqrt{2}}. \end{aligned}$$

Therefor, for fixed $k,\gamma$ and $\rho \in (0,\rho ^*_{max})=(0,\frac{\sqrt{2}\gamma k}{4+3\sqrt{2}})$, there exists two possible Hopf bifurcation points $\sigma _1,~\sigma _2$ with $\sigma _1<\frac{1+\sqrt{2}}{k}<\sigma _2$ such that

$$\begin{aligned} \rho =\frac{\gamma (k\sigma _j-1)}{\sigma _j^2k+\sigma _j},~j=1,2. \end{aligned}$$

(2.18)

The characteristic equation of the linearized system of (2.16) at $E_2(N_2^*,P_2^*,S_2^*)$ is

$$\begin{aligned} (\lambda +\eta )(\lambda ^2-a_{11}\lambda -a_{12}a_{21})=0, \end{aligned}$$

which means that $\lambda _0=-\eta <0$, and

$$\begin{aligned} \lambda ^2-a_{11}\lambda -a_{12}a_{21}=0. \end{aligned}$$

(2.19)

Clearly, Eq. (2.19) has a pair of purely imaginary roots $\lambda _{1,2}=\pm i\sqrt{-a_{12}a_{21}}$ at $\sigma =\sigma _j,~j=1,2$. In addition, taking the derivative of both sides of Eq. (2.19) with respect to $\sigma$ at $\sigma =\sigma _j$ and combining (2.18), we have that,

$$\begin{aligned} \frac{d\lambda }{d\sigma }=\frac{\lambda \frac{\partial a_{11}}{\partial \sigma }+a_{12}\frac{\partial a_{21}}{\partial \sigma }}{2\lambda -a_{11}}, \end{aligned}$$

which implies that,

$$\begin{aligned} \begin{aligned} \left. Re\left( \frac{d\lambda }{d\sigma }\right) ^{-1}\right| _{\sigma =\sigma _j}&=\left. Re\left( \frac{\rho r \left( \lambda \left( \frac{1}{\gamma }-\frac{2\rho }{k(\gamma -\sigma \rho )^2}\right) -a_{12}\right) }{2\lambda -a_{11}}\right) \right| _{\sigma =\sigma _j}\\&=\left. \frac{\rho r}{2}\left( \frac{1}{\gamma }-\frac{2\rho }{k(\gamma -\sigma \rho )^2}\right) \right| _{\sigma =\sigma _j}\\&=-\frac{\rho rk}{4\gamma \sigma _j}\left( \sigma _j-\frac{1+\sqrt{2}}{k}\right) \left( \sigma _j+\frac{\sqrt{2}-1}{k}\right) ,~j=1,2. \end{aligned} \end{aligned}$$

By $\sigma _1<\frac{1+\sqrt{2}}{k}<\sigma _2$, we have that,

$$\begin{aligned} \left. Re\left( \frac{d\lambda }{d\sigma }\right) ^{-1}\right| _{\sigma =\sigma _1}>0,~~\left. Re\left( \frac{d\lambda }{d\sigma }\right) ^{-1}\right| _{\sigma =\sigma _2}<0. \end{aligned}$$

Hence, system (2.18) undergoes Hopf bifurcation at $\sigma _j,~j=1,2$. Theorem 2.3 is confirmed. $\square$

We apply the results of Sects. 2.1,2.2 to the taxis-induced predator–prey model with Logistic growth and Holling-II functional response under the condition (A1).

By Theorems 2.1, 2.2 and  2.3, we have the following results:

Theorem 2.4

Assume that the condition (A1) holds and $\chi _n^H, \chi _n^T$ are defined by (2.7) and (2.10) respectively. Then when one of the following three conditions (i) $\sigma \le \frac{1}{k}$, (ii) $\rho ^*_{max}<\rho <\frac{\gamma k}{\sigma k+1}$ and $\sigma >\frac{1}{k}$, (iii) $0<\rho <\rho _{max}^*$ and $\sigma \in (1/k, \sigma _1)\cup (\sigma _2, \frac{\gamma k-\rho }{k\rho })$ holds, where $\sigma _1,~\sigma _2$ are homogenous Hopf bifurcation points defined by Theorem 2.3(iii), the following results are true:

• (I) the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ is locally asymptotically stable for $\chi \in (\chi _{n_T^*}^T,\chi _{n_H^*}^H)$ and unstable for $\chi \in (-\infty , \chi _{n_T^*}^T)\cup (\chi _{n_H^*}^H, +\infty )$;

• (II) if for any $j\in N_0$ and $j\ne n$ such that $\chi _j^H\ne \chi _n^H$, system (1.2) undergoes spatially inhomogeneous Hopf bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _n^H>0$; and if there exists $n_1,~n_2,~\ldots ,~n_s$ such that $\chi _{n_1}^H=\chi _{n_2}^H=\cdots =\chi _{n_s}^H$ and $\chi _j^H\ne \chi _{n_1}^H$, system (1.2) undergoes $s-$multiple Hopf bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _{n_1}^H>0$. In particular, if $s=2$, system (1.2) undergoes double-Hopf bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$;

• (III) if for any $j\in N_0$ and $j\ne n$ such that $\chi _j^T\ne \chi _n^T$, system (1.2) undergoes Turing bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _n^T<0$; and if there exists $n_1,~n_2,~\ldots ,~n_s$ such that $\chi _{n_1}^T=\chi _{n_2}^T=\cdots =\chi _{n_s}^T$ and $\chi _j^T\ne \chi _{n_1}^T$, system(1.2) undergoes $s-$multiple Turing bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _{n_1}^T>0$. In particular, if $s=2$, system (1.2) undergoes Turing–Turing bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$.

Theorem 2.5

Assume that the condition (A1) holds and $\chi _n^H, \chi _n^T$ are defined by (2.7) and (2.10) respectively. Then when $\sigma =\sigma _1$ or $\sigma =\sigma _2$, and $0<\rho <\rho _{max}^*$, where $\sigma _1,~\sigma _2$ are homogenous Hopf bifurcation points defined by Theorem 2.3(iii), system (1.2) undergoes double-Hopf bifurcations near the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ at $\chi =\chi _n^H>0,~n=1,2,\ldots$, and Turing–Hopf bifurcations at $\chi =\chi _n^T<0,~n=1,2,\ldots$, and $\chi _1^H=\min \limits _{n=1,2,\ldots }\{\chi _n^H\}$.

3 Normal Form of Double–Hopf Bifurcations on the Center Manifold

In this section, we follow the normal form theory developed in [16, 42] for the reaction–diffusion system with/without delay and use the same notations as in [16, 42] and derive the normal form of double-Hopf bifurcations for the non-resonance or weak resonance case. This section is also motivated by the works on the double-Hopf bifurcations in [11, 12, 22] for the delay differential equations without diffusion, in [13, 14, 39] for the reaction–diffusion with delay but without indirect prey-taxis.

3.1 Decomposition of Phase Space

From Theorem 2.2, we know that system (2.12) undergoes double-Hopf bifurcations at the interaction points $(\sigma ,\chi ^H_n)$ of two Hopf bifurcation curves near the positive steady state $E_2(N_2^*,P_2^*,S_2^*)$. We assume that at the interaction point $(\sigma ,\chi ^H_n)=(\sigma ^*,\chi ^*)$, Eq. (2.4) has two pairs of purely imaginary roots $\pm i \omega _{n_1},~\pm i\omega _{n_2}$ for $n=n_1$ and $n=n_2$ with $n_1<n_2$, respectively, which only requires that the ratio of $\omega _{n_1}$ and $\omega _{n_2}$ is not 1 : 1, 1 : 2, 1 : 3, 1 : 4, that is non-resonance or weak resonance case. And all other eigenvalues have negative real parts. Define the real-value Sobolev space:

$$\begin{aligned} X=\{(u_1,u_2,u_3)\in (W^{2,2}(0,l\pi ))^3| \frac{\partial u_i}{\partial x}=0,~x=0,l\pi ,\,~i=1,2,3\} \end{aligned}$$

with the inner product

$$\begin{aligned}{}[u,v]=\int _0^{l\pi }(u_1v_1+u_2v_2+u_3v_3)dx,~\text {for}~u=(u_1,u_2,u_3),~v=(v_1,v_2,v_3). \end{aligned}$$

(3.1)

To investigate codimension-2 bifurcation, we introduce two parameters $\epsilon _1$ and $\epsilon _2$. Set $\epsilon _1=\sigma -\sigma ^*,~\epsilon _2=\chi -\chi ^*$ such that $\epsilon _1=\epsilon _2=0$ are double-Hopf bifurcation values. Thus, the positive equilibrium $E_2(N_2^*,P_2^*,S_2^*)$ can be written into a parameter-dependent form $E_{2\epsilon _1}(N_2^*(\epsilon _1),P_2^*(\epsilon _1),S_2^*(\epsilon _1))$ with

$$\begin{aligned} \begin{aligned}&N_2^*(\epsilon _1)=\frac{\rho }{\gamma -(\sigma ^*+\epsilon _1)\rho },~P_2^*(\epsilon _1)=\frac{r\gamma }{\beta (\gamma -(\sigma ^*+\epsilon _1)\rho )^2}\left( \gamma -\rho \left( \sigma ^*+\epsilon _1+\frac{1}{k}\right) \right) ,\\ {}&S_2^*(\epsilon _1)=\frac{\xi N_2^*(\epsilon _1)}{\eta }. \end{aligned} \end{aligned}$$

Letting ${\tilde{N}}(\cdot ,t)=N(\cdot ,t)-N_2^*(\epsilon _1),~{\tilde{P}}(\cdot ,t)=P(\cdot ,t)-P_2^*(\epsilon _1),~{\tilde{S}}(\cdot ,t)=S(\cdot ,t)-S_2^*(\epsilon _1)$ and ${\tilde{U}}(t)=({\tilde{N}}(\cdot ,t),{\tilde{P}}(\cdot ,t),{\tilde{S}}(\cdot ,t))$, then dropping the tildes for simplification, system (2.12) can be rewritten into the following abstract form:

$$\begin{aligned} \frac{dU(t)}{dt}=D(\epsilon ) U_{xx}+L(\epsilon _1)U+F(U,\epsilon _1), \end{aligned}$$

(3.2)

where

$$\begin{aligned} F(U,\epsilon _1)=(f^{(1)}(N,P,S,\epsilon _1),f^{(2)}(N,P,S,\epsilon _1),f^{(3)}(N,P,S,\epsilon _1))^T-L(\epsilon _1)U, \end{aligned}$$

(3.3)

with

$$\begin{aligned} \begin{aligned}&f^{(1)}(N,P,S,\epsilon _1)=r(N+N_2^*(\epsilon _1))\left( 1-\frac{N+N_2^*(\epsilon _1)}{k}\right) -\frac{\beta (N+N_2^*(\epsilon _1))(P+P_2^*(\epsilon _1))}{1+(\sigma ^*+\epsilon _1)(N+N_2^*(\epsilon _1))},\\&f^{(2)}(N,P,S,\epsilon _1)=\beta \left( \frac{\gamma (N+N_2^*(\epsilon _1))(P+P_2^*(\epsilon _1))}{1+(\sigma ^*+\epsilon _1)(N+N_2^*(\epsilon _1))}-\rho (P+P_2^*(\epsilon _1))\right) ,\\&f^{(3)}(N,P,S,\epsilon _1)=\xi (N+N_2^*(\epsilon _1))-\eta (S+S_2^*(\epsilon _1)), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} D(\epsilon )U_{xx}=DU_{xx}+G^d(U,\epsilon ), \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} G^d(U,\epsilon )=&\left( \begin{array}{c}0\\ chi^*P_xS_x\\ 0\end{array}\right) +\epsilon _1D_1U_{xx}+\epsilon _2D_2U_{xx}\\ {}&-\epsilon _2\left( \begin{array}{c}0\\ P_xS_{x}\\ 0\end{array}\right) -\epsilon _1\epsilon _2\left( \begin{array}{c}0\\ {P_2^*}'(0)S_{xx}\\ 0\end{array}\right) +o(\epsilon ), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} D=\left( \begin{array}{c@{\quad }c@{\quad }c}\delta _N&{}0&{}0\\ 0&{}\delta _P&{}-\chi ^*P_2^*\\ 0&{}0&{}\delta _S\end{array}\right) ,~~ D_1=\left( \begin{array}{c@{\quad }c@{\quad }c}0&{}0&{}0\\ 0&{}0&{}-\chi ^*{P_2^*}'(0)\\ 0&{}0&{}0\end{array}\right) ,~~D_2=\left( \begin{array}{c@{\quad }c@{\quad }c}0&{}0&{}0\\ 0&{}0&{}-P_2^*\\ 0&{}0&{}0\end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} L(\epsilon _1)U=\left( \begin{array}{c@{\quad }c@{\quad }c}a_{11}(\epsilon _1)&{}a_{12}(\epsilon _1)&{}0\\ a_{21}(\epsilon _1)&{}a_{22}(\epsilon _1)&{}0\\ \xi &{}0&{}-\eta \end{array}\right) \triangleq AU+\epsilon _1QU+o(\epsilon _1), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&a_{11}(\epsilon _1)=\rho r\left( \frac{1}{\gamma }\left( \sigma ^*+\epsilon _1+\frac{1}{k}\right) -\frac{2}{k(\gamma -(\sigma ^*+\epsilon _1)\rho )}\right) ,~a_{12}=-\frac{\beta \rho }{\gamma },\\&a_{21}(\epsilon _1)=r\left( \gamma -\rho \left( \sigma ^*+\epsilon _1+\frac{1}{k}\right) \right) ,~a_{22}(\epsilon _1)=0, \end{aligned} \end{aligned}$$

(3.4)

and

$$\begin{aligned} A=\left( \begin{array}{c@{\quad }c@{\quad }c}a_{11}(0)&{}a_{12}(0)&{}0\\ a_{21}(0)&{}a_{22}(0)&{}0\\ \xi &{}0&{}-\eta \end{array}\right) ,~Q=\left( \begin{array}{c@{\quad }c@{\quad }c}{a_{11}}'(0)&{}0&{}0\\ {a_{21}}'(0)&{}0&{}0\\ 0&{}0&{}0\end{array}\right) . \end{aligned}$$

Noticing that $\epsilon _1,\epsilon _2$ are the parameters, we can obtain another form of (3.2) as follows:

$$\begin{aligned} \frac{dU(t)}{dt}=DU_{xx}+AU+{\tilde{F}}(U,\epsilon _1,\epsilon _2), \end{aligned}$$

(3.5)

where

$$\begin{aligned} \begin{aligned} {\tilde{F}}(U,\epsilon _1,\epsilon _2)=F(U,\epsilon _1)+\epsilon _1QU+G^d(U,\epsilon )+o(\epsilon _1). \end{aligned} \end{aligned}$$

(3.6)

The linearized system of system (2.12) at the origin is

$$\begin{aligned} \frac{dU}{dt}=DU_{xx}+AU. \end{aligned}$$

(3.7)

By Theorem 2.5, the operator $D+A$ has two pairs of purely imaginary eigenvalues $\pm i\omega _{n_1},~\pm i \omega _{n_2}~(\omega _{n_1}\ne \omega _{n_2})$ for $n=n_1$ and $n=n_2$ and all other eigenvalues have negative real parts.

Set

$$\begin{aligned} {\mathfrak {B}}_n=Span\{[\phi (\cdot ),\beta _n^{(j)}]\beta _n^{(j)}|\phi \in X,j=1,2,3\}, \end{aligned}$$

where $\beta _n^{(j)}(x),~j=1,2,3$ are defined in (2.3).

On ${\mathfrak {B}}_n$, the linear equation (3.7) is equivalent to the ODE on $R^3$:

$$\begin{aligned} \left( \begin{array}{c}{\dot{N}}\\ {\dot{P}}\\ {\dot{S}}\end{array}\right) =\left( \begin{array}{c@{\quad }c@{\quad }c}-\delta _N\left( \frac{n}{l}\right) ^2&{}0&{}0\\ 0&{}-\delta _P\left( \frac{n}{l}\right) ^2&{}\chi ^*P_2^*\left( \frac{n}{l}\right) ^2\\ 0&{}0&{}-\delta _S\left( \frac{n}{l}\right) ^2\end{array}\right) \left( \begin{array}{c}N\\ P\\ S\end{array}\right) +A\left( \begin{array}{c}N\\ P\\ S\end{array}\right) , \end{aligned}$$

(3.8)

where $(N,P,S)\in R^3$. It is easy to check that (3.8) has the same characteristic equation as the linearized equation (3.7).

Let

$$\begin{aligned} \begin{aligned} {\mathscr {M}}_n=\left( \frac{n}{l}\right) ^2D+A \end{aligned} \end{aligned}$$

(3.9)

be the characteristic matrix of (3.8). Let $\Lambda$ be the finite set of all eigenvalues of the matrix (3.9) with zero real parts. We have known, when $n=n_1,~n_2$, ${\mathscr {M}}_n$ has two pairs of purely imaginary roots $\pm i\omega _{n_1},\pm i\omega _{n_2}$, i.e. $\Lambda =\{i\omega _{n_1},-i\omega _{n_1},i\omega _{n_2},-i\omega _{n_2}\}$. And P is the generalized eigenspace corresponding to $\Lambda$. $P^*$ is the dual space of P.

Define the scalar product

$$\begin{aligned} \langle \psi ^T,\phi \rangle =\psi ^T\phi ,~\text {for}~\psi ,\phi \in R^3. \end{aligned}$$

Denote

$$\begin{aligned} \begin{aligned}&\Phi _{n_1}=(\phi _1,\phi _2),~\Phi _{n_2}=(\phi _3,\phi _4),\\&\Psi _{n_1}=col(\psi _1^T,\psi _2^T),\Psi _{n_2}=col(\psi _3^T,\psi _4^T). \end{aligned} \end{aligned}$$

Let $\Phi \doteq (\Phi _{n_1},\Phi _{n_2})=(\phi _1,\phi _2,\phi _3,\phi _4),~\Psi \doteq diag(\Psi _{n_1},\Psi _{n_2})$ be the basis of P and $P^*$ associated with the eigenvalues $i\omega _{n_1}$ and $i\omega _{n_2}$ satisfying

$$\begin{aligned} {\mathscr {M}}_n\Phi _n=\Phi _nB_n,~ {\mathscr {M}}_n^T\Psi _n=B_n\Psi _n, \langle \Psi _n,\Phi _n\rangle =I,~n=n_1,n_2, \end{aligned}$$

with $B_{n_1}=diag(i\omega _{n_1},-i\omega _{n_1}),~B_{n_2}=diag(i\omega _{n_2},-i\omega _{n_2})$.

By virtue of ${\mathscr {M}}_{n_1}\Phi _{n_1}=\Phi _{n_1}B_{n_1},~ {\mathscr {M}}_{n_1}^T\Psi _{n_1}=B_{n_1}\Psi _{n_1}$, i.e.

$$\begin{aligned} {\mathscr {M}}_{n_1}\phi _1=i\omega _{n_1}\phi _1,~{\mathscr {M}}_{n_1}\phi _2=-i\omega _{n_1}\phi _2,~ {\mathscr {M}}_{n_1}^T\psi _1^T=i\omega _{n_1}\psi _1^T,~{\mathscr {M}}_{n_1}^T\psi _2^T=-i\omega _{n_1}\psi _2^T, \end{aligned}$$

we choose that

$$\begin{aligned} \begin{aligned}&\phi _1=\left( \begin{array}{c}\phi _{11}\\ \phi _{12}\\ \phi _{13}\end{array}\right) =\left( \begin{array}{c}1 \\ \ \frac{i\omega _{n_1}+\delta _N\left( \frac{n_1}{l}\right) ^2-a_{11}(0)}{a_{12}(0)}\\ \frac{\xi }{i\omega _{n_1}+\delta _S\left( \frac{n_1}{l}\right) ^2+\eta }\end{array}\right) ,\\&\psi _1=\left( \begin{array}{c}\psi _{11}\\ \psi _{12}\\ \psi _{13}\end{array}\right) =\overline{M_1}\left( \begin{array}{c}\frac{i\omega _{n_1}+\delta _p\left( \frac{n_1}{l}\right) ^2-a_{22}(0)}{a_{12}(0)}\\ 1\\ \frac{\chi ^*P_2^*\left( \frac{n_1}{l}\right) ^2}{i\omega _{n_1}+\delta _S\left( \frac{n_1}{l}\right) ^2+\eta }\end{array}\right) ,\\&\phi _2=\overline{\phi _1},~~\psi _2=\overline{\psi _1}, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \overline{M_1}=\left( \frac{2i\omega _{n_1}+(\delta _P+\delta _N)\left( \frac{n_1}{l}\right) ^2-a_{11}(0)-a_{22}(0)}{a_{12}(0)}+\frac{\xi \chi ^*P_2^*\left( \frac{n_1}{l}\right) ^2}{(i\omega _{n_1}+\delta _S\left( \frac{n_1}{l}\right) ^2+\eta )^2}\right) ^{-1}. \end{aligned}$$

By the same way, in terms of ${\mathscr {M}}_{n_2}\Phi _{n_2}=\Phi _{n_2}B_{n_2},~ {\mathscr {M}}_{n_2}^T\Psi _{n_2}=B_{n_2}\Psi _{n_2}$, i.e.

$$\begin{aligned} {\mathscr {M}}_{n_2}\phi _3=i\omega _{n_2}\phi _3,~{\mathscr {M}}_{n_2}\phi _4=-i\omega _{n_2}\phi _4,~ {\mathscr {M}}_{n_2}^T\psi _3^T=i\omega _{n_2}\psi _3^T,~{\mathscr {M}}_{n_2}^T\psi _4^T=-i\omega _{n_2}\psi _4^T, \end{aligned}$$

we choose that

with

$$\begin{aligned} \overline{M_2}=\left( \frac{2i\omega _{n_2}+(\delta _P+\delta _N)\left( \frac{n_2}{l}\right) ^2-a_{11}(0)-a_{22}(0)}{a_{12}(0)}+\frac{\xi \chi ^*P_2^*\left( \frac{n_2}{l}\right) ^2}{(i\omega _{n_2}+\delta _S\left( \frac{n_2}{l}\right) ^2+\eta )^2}\right) ^{-1}. \end{aligned}$$

Now, we decompose the Sobolev space X into a center subspace P and its orthocomplement, i.e.

$$\begin{aligned} X=P\oplus ker\pi , \end{aligned}$$

where $\pi :X\rightarrow P$ is the projection defined by

$$\begin{aligned} \pi (\phi )=\Phi _{n_1}\langle \Psi _{n_1},[\phi (\cdot ),\beta _{n_1}]\rangle \cdot \beta _{n_1}+\Phi _{n_2}\langle \Psi _{n_2},[\phi (\cdot ),\beta _{n_2}]\rangle \cdot \beta _{n_2}, \end{aligned}$$

(3.10)

with

$$\begin{aligned} \left[ \phi (\cdot ),\beta _{n_j}\right] =\left( \begin{array}{c} \left[ \phi (\cdot ),\beta _{n_j}^{(1)}\right] \\ \left[ \phi (\cdot ),\beta _{n_j}^{(2)}\right] \end{array}\right) , ~j=1, 2. \end{aligned}$$

By (3.10), $U=(N,P,S)^T\in X$ can be rewritten as

$$\begin{aligned} \begin{aligned} U&=\Phi _{n_1}{\tilde{z}}_{n_1}\cdot \beta _{n_1}+\Phi _{n_2}{\tilde{z}}_{n_2}\cdot \beta _{n_2}+w\\&=(z_1\phi _1+z_2{\overline{\phi }}_1)r_{n_1}(x)+(z_3\phi _3+z_4{\overline{\phi }}_3)r_{n_2}(x)+w\\&\doteq \Phi z_x+w, \end{aligned} \end{aligned}$$

(3.11)

where ${\tilde{z}}_{n_1}=\langle \Psi _{n_1},[U,\beta _{n_1}]\rangle =(z_1,z_2),~{\tilde{z}}_{n_2}=\langle \Psi _{n_2},[U,\beta _{n_2}]\rangle =(z_3,z_4),$ and

$$\begin{aligned} \begin{aligned}&z_x=(z_1r_{n_1}(x),z_2r_{n_1}(x),z_3r_{n_2}(x),z_4r_{n_2}(x))^T,\\&w=(w_1,w_2,w_3)^T\in Q\triangleq C^1\cap Ker\pi =\{\phi \in Ker\pi |{\dot{\phi }}\in C\}. \end{aligned} \end{aligned}$$

For convenience, denote $z\doteq ({\tilde{z}}_{n_1},{\tilde{z}}_{n_2})^T=(z_1,z_2,z_3,z_4)$ and $B=diag(i\omega _{n_1},-i\omega _{n_1},i\omega _{n_2},-i\omega _{n_2})$. Then system (3.5) is decomposed as a system of abstract ODEs on $R^4\times Ker\pi$:

(3.12)

where $L_1$ is the restriction of the linear operator $D+A$ in Q.

3.2 Center Manifold Reduction

Consider the formal Taylor expansion

$$\begin{aligned} {\tilde{F}}(U,\epsilon )=\sum \limits _{j\ge 2}\frac{1}{j!}{\tilde{F}}_j (U,\epsilon ),~~F(U,\epsilon _1)=\sum \limits _{j\ge 2}\frac{1}{j!}F_j(U,\epsilon _1), \end{aligned}$$

where ${\tilde{F}}_j$ is the $j\hbox {th}$ $\hbox {Fr}\acute{e}\hbox {chet}$ derivative of ${\tilde{F}}$. And

$$\begin{aligned} G^d(U,\epsilon )=\frac{1}{2}G_2^{d}(U,\epsilon )+\frac{1}{3!}G_3^{d}(U,\epsilon )+o(\epsilon ), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} G_2^{d}(U,\epsilon )&=G_2^{d(0,0)}(U)+\epsilon _1G_2^{d(1,0)}(U)+\epsilon _2G_2^{d(0,1)}(U),\\ G_3^{d}(U,\epsilon )&=\epsilon _1G_3^{d(1,0)}(U)+\epsilon _2G_3^{d(0,1)}(U)+\epsilon _1\epsilon _2G_3^{d(1,1)}(U), \end{aligned} \end{aligned}$$

(3.13)

with

$$\begin{aligned} \begin{aligned} G_2^{d(0,0)}(U)&=2\left( \begin{array}{c}0\\ -\chi ^*P_xS_x\\ 0\end{array}\right) ,~~G_2^{d(1,0)}(U)=2D_1U_{xx},\\ G_2^{d(0,1)}(U)&=2D_2U_{xx},~~G_3^{d(1,0)}(U)=0,~~\\ G_3^{d(0,1)}(U)&=-6\left( \begin{array}{c}0\\ P_xS_x\\ 0\end{array}\right) ,~~G_3^{d(1,1)}(U)=-6\left( \begin{array}{c}0\\ {P_2^*}'(0)S_{xx}\\ 0\end{array}\right) . \end{aligned} \end{aligned}$$

(3.14)

From (3.6), we have that,

$$\begin{aligned} {\tilde{F}}_2(U,\epsilon _1,\epsilon _2)=2\epsilon _1QU+G_2^d(U,\epsilon )+F_2(U,\epsilon _1), \end{aligned}$$

(3.15)

and

$$\begin{aligned} {\tilde{F}}_3(U,\epsilon _1,\epsilon _2)=G_3^d(U,\epsilon )+F_3(U,\epsilon _1). \end{aligned}$$

(3.16)

Then (3.12) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{z}}=Bz+\sum \limits _{j\ge 2}\frac{1}{j!}{\tilde{f}}_j^1(z,w,\epsilon ),\\ {\dot{w}}=L_1w+\sum \limits _{j\ge 2}\frac{1}{j!}{\tilde{f}}_j^2(z,w,\epsilon ), \end{array}\right. } \end{aligned}$$

(3.17)

where

(3.18)

Let $V_j^6(R^4)$ denote the space of homogeneous polynomials of degree j in 6 variables $z=(z_1,z_2,z_3,z_4)^T,~\epsilon =(\epsilon _1,\epsilon _2)^T$ with coefficients in $R^4$ as follows:

$$\begin{aligned}&V_j^6(R^4)=Span\{z_1^{q_1}z_2^{q_2}z_3^{q_3}z_4^{q_4}\epsilon _2^{p_1}\epsilon _1^{p_2}\vartheta _k,~q_1,q_2,q_3,q_4,p_1,p_2\in N_0,\\&\qquad \text {and}~q_1+q_2+q_3+q_4+p_1+p_2=j\}, \end{aligned}$$

where $\vartheta _k (k=1,2,3,4)$ are unit coordinate vector of $R^4$.

Define the operator $M_j=(M_j^1,M_j^2),~j\ge 2$ by

$$\begin{aligned} \begin{aligned}&M_j^1:~V_j^6(R^4)\rightarrow V_j^6(R^4),~M_j^2:~V_j^6(Q_1)\rightarrow V_j^6(Ker\pi ),\\&(M_j^1p)(z,\epsilon )=D_zp(z,\epsilon )Bz-Bp(z,\epsilon ),\\&(M_j^2h)(z,\epsilon )=D_zh(z,\epsilon )Bz-L_1h(z,\epsilon ). \end{aligned} \end{aligned}$$

(3.19)

It is easy to verify that,

$$\begin{aligned} \begin{aligned}&M_j^1(z^q\epsilon ^p\vartheta _k)=(i\omega _{n_1}(q_1-q_2)+i\omega _{n_2}(q_3-q_4)+(-1)^ki\omega _{n_1})z^q\epsilon ^p\vartheta _k,~k=1,2,\\&M_j^1(z^q\epsilon ^p\vartheta _k)=(i\omega _{n_1}(q_1-q_2)+i\omega _{n_2}(q_3-q_4)+(-1)^ki\omega _{n_2})z^q\epsilon ^p\vartheta _k,~k=3,4, \end{aligned} \end{aligned}$$

(3.20)

where $z^q\epsilon ^p=z_1^{q_1}z_2^{q_2}z_3^{q_3}z_4^{q_4}\epsilon _2^{p_1}\epsilon _1^{p_2}$.

Then from (3.20), we have that,

$$\begin{aligned} Ker(M_2^1)=Span\left\{ \left( \begin{array}{c}z_1\epsilon _i\\ 0\\ 0\\ 0 \end{array}\right) ,\left( \begin{array}{c}0\\ z_2\epsilon _i\\ 0\\ 0\end{array}\right) ,\left( \begin{array}{c}0\\ 0\\ z_3\epsilon _i\\ 0\end{array}\right) , \left( \begin{array}{c}0\\ 0\\ 0\\ z_4\epsilon _i\end{array}\right) \right\} ,~i=1,2, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} Ker(M_3^1)=Span\{&z_1z_3z_4\vartheta _1,z_1\epsilon _i^2\vartheta _1,z_1^2z_2\vartheta _1,z_1\epsilon _2\epsilon _1\vartheta _1,\\&z_2z_3z_4\vartheta _2,z_2\epsilon _i^2\vartheta _2,z_1z_2^2\vartheta _2,z_2\epsilon _2\epsilon _1\vartheta _2,\\&z_1z_2z_3\vartheta _3,z_3\epsilon _i^2\vartheta _3,z_3^2z_4\vartheta _3,z_3\epsilon _2\epsilon _1\vartheta _3,\\&z_1z_2z_4\vartheta _4,z_4\epsilon _i^2\vartheta _4,z_3z_4^2\vartheta _4,z_4\epsilon _2\epsilon _1\vartheta _4,i=1,2\}. \end{aligned} \end{aligned}$$

Remark 3.1

If $\omega _{n_1}:\omega _{n_2}$ is 1 : 1, 1 : 2, 1 : 3 or 1 : 4, that is the strong resonance case, the base forms of the space $Ker(M_2^1)$, $Ker(M_3^1)$ will be more complex, which is not considered here.

For autonomous ODEs in the finite dimension space [10], by a recursive transformation of variables

$$\begin{aligned} (z,w)=({\tilde{z}},{\tilde{w}})+\frac{1}{j!}(U_j^1({\tilde{z}}, \epsilon ),U_j^2({\tilde{z}},\epsilon )),~j\ge 2, \end{aligned}$$

where $U_j^1$ and $U_j^2$ are homogeneous polynomials of j in ${\tilde{z}}$ and $\epsilon$, and dropping the tilde, the normal form on the center manifold for (3.17) is

$$\begin{aligned} {\dot{z}}=Bz+\frac{1}{2}g_2^1(z,0,\epsilon )+\frac{1}{3!}g_3^1(z,0,\epsilon )+o(\epsilon |z|^2), \end{aligned}$$

(3.21)

where $g_2^1$ and $g_3^1$ are the second and third terms in $(z,\epsilon )$, defined by

$$\begin{aligned} g_2^1(z,0,\epsilon )=Proj_{Ker(M_2^1)}{\tilde{f}}_2^1(z,0,\epsilon ),~ g_3^1(z,0,\epsilon )=Proj_{Ker(M_3^1)}\bar{f_3^1}(z,0,0)+o(\epsilon |z|^2), \end{aligned}$$

(3.22)

where

$$\begin{aligned} \begin{aligned} \bar{f_3^1}(z,0,0)=&\tilde{f_3^1}(z,0,0)+\frac{3}{2}[(D_z\tilde{f_2^1})(z,0,0)U_2^1(z,0)+(D_w\tilde{f_2^1})(z,0,0)U_2^2(z,0)\\ {}&-(D_zU_2^1(z,0))g_2^1(z,0,0)]. \end{aligned} \end{aligned}$$

(3.23)

3.3 Second Order Terms of the Normal Form

It follows from (3.18) that,

(3.24)

From (3.11) and (3.14), we have that,

(3.25)

From (3.3), it is easy to check that for any $\epsilon \in R^2_+$,

$$\begin{aligned} F_2(\Phi z_x,\epsilon )=F_2(\Phi z_x,0), \end{aligned}$$

which, together with (3.15), (3.22), (3.25) results in

$$\begin{aligned} \frac{1}{2}g_2^1(z,0,\epsilon )= \frac{1}{2}Proj_{Ker(M_2^1)}{\tilde{f}}_2^1(z,0,\epsilon )=\left( \begin{array}{c}B_{n_11}z_1\epsilon _1+B_{n_12}z_1\epsilon _2\\ \overline{B_{n_11}}z_2\epsilon _1+\overline{B_{n_12}}z_2\epsilon _2\\ B_{n_21}z_3\epsilon _1+B_{n_22}z_3\epsilon _2\\ \overline{B_{n_21}}z_4\epsilon _1+\overline{B_{n_22}}z_4\epsilon _2\end{array}\right) , \end{aligned}$$

(3.26)

where

$$\begin{aligned} \begin{aligned}&B_{n_11}=\psi _1^T\left( Q\phi _1-\left( \frac{n_1}{l}\right) ^2D_1\phi _1\right) ,~~B_{n_12}=-\left( \frac{n_1}{l}\right) ^2\psi _1^TD_2\phi _1,\\&B_{n_21}=\psi _3^T\left( Q\phi _3-\left( \frac{n_2}{l}\right) ^2D_1\phi _3\right) ,~~B_{n_22}=-\left( \frac{n_2}{l}\right) ^2\psi _3^TD_2\phi _3. \end{aligned} \end{aligned}$$

3.4 Third Order Terms of the Normal Form

Since $o(|z|\epsilon ^2)$ is irrelevant to determine the generic Hopf bifurcation, it is sufficient to compute $g_3^1(z,0,0)$ for determining the properties of Hopf bifurcation.

By (3.22), (3.23) and $g_2^1(z,0,0)=(0,0,0,0)^T$, we have that,

$$\begin{aligned} g_3^1(z,0,0)=Proj_{Ker(M_3^1)}\bar{f_3^1}(z,0,0), \end{aligned}$$

(3.27)

where

$$\begin{aligned} \bar{f_3^1}(z,0,0)=\tilde{f_3^1}(z,0,0)+\frac{3}{2}[(D_z\tilde{f_2^1})(z,0,0)U_2^1(z,0)+(D_w\tilde{f_2^1})(z,0,0)U_2^2(z,0)], \end{aligned}$$

and

$$\begin{aligned} U_2^1=(M_2^1)^{-1} \tilde{f_2^1}(z,0,0),~ U_2^2=(M_2^2)^{-1} \tilde{f_2^2}(z,0,0). \end{aligned}$$

(3.28)

Next we calculate the third order terms $g_3^1(z,0,0)$ in three steps.

Step 1. The calculation of $Proj_{Ker(M_3^1)}\tilde{f_3^1}(z,0,0)$.

By (3.13) and (3.16), we have that,

$$\begin{aligned} \begin{aligned} {\tilde{F}}_3(\Phi z_x,0)=F_3(\Phi z_x,0). \end{aligned} \end{aligned}$$

Expand $F_3(\Phi z_x,0)$ in Taylor series described as follows:

$$\begin{aligned} {\tilde{F}}_3(\Phi z_x,0)=F_3(\Phi z_x,0)=\sum \limits _{q_1+q_2+q_3+q_4=3}F_{q_1q_2q_3q_4}r_{n_1}^{q_1+q_2}(x)r_{n_2}^{q_3+q_4}(x)z_1^{q_1}z_2^{q_2}z_3^{q_3}z_4^{q_4}, \end{aligned}$$

where $F_{q_1q_2q_3q_4}=(F^{(1)}_{q_1q_2q_3q_4},F^{(2)}_{q_1q_2q_3q_4},F^{(3)}_{q_1q_2q_3q_4})^T$. Hence, from (3.18), we have that,

$$\begin{aligned} \begin{aligned} {\tilde{f}}_3^1(z,0,0)&=\Psi \left( \begin{array}{c}\left[ {\tilde{F}}_3(\Phi z_x,0),\beta _{n_1}\right] \\ \left[ {\tilde{F}}_3(\Phi z_x,0),\beta _{n_2}\right] \end{array}\right) =\Psi \left( \begin{array}{c}\left[ F_3(\Phi z_x,0),\beta _{n_1}\right] \\ \left[ F_3(\Phi z_x,0),\beta _{n_2}\right] \end{array}\right) \\&=\Psi \left( \begin{array}{c}\sum \limits _{q_1+q_2+q_3+q_4=3}F_{q_1q_2q_3q_4}\int _0^{l\pi }r_{n_1}^{q_1+q_2+1}(x)r_{n_2}^{q_3+q_4}(x)dxz_1^{q_1}z_2^{q_2}z_3^{q_3}z_4^{q_4}\\ \sum \limits _{q_1+q_2+q_3+q_4=3}F_{q_1q_2q_3q_4}\int _0^{l\pi }r_{n_1}^{q_1+q_2}(x)r_{n_2}^{q_3+q_4+1}(x)dxz_1^{q_1}z_2^{q_2}z_3^{q_3}z_4^{q_4}\end{array}\right) . \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \frac{1}{3!}Proj_{Ker(M_3^1)}{\tilde{f}}_3^1(z,0,0)=\left( \begin{array}{c}C_{2100}z_1^2z_2+C_{1011}z_1z_3z_4\\ \overline{C_{2100}}z_1z_2^2+\overline{C_{1011}}z_2z_3z_4\\ C_{0021}z_3^2z_4+C_{1110}z_1z_2z_3\\ \overline{C_{0021}}z_3z_4^2+\overline{C_{1110}}z_1z_2z_4 \end{array}\right) , \end{aligned}$$

(3.29)

where, combining with the fact $\int _0^{l\pi }r_{n_1}^2(x)r_{n_2}^2(x)dx=\frac{1}{l\pi },$

$$\begin{aligned} \begin{aligned} C_{2100}&=\left\{ \begin{array}{cc}\frac{1}{6l\pi }\psi _1^TF_{2100},&{}n_1=0,\\ \\ \frac{1}{4l\pi }\psi _1^TF_{2100},&{}n_1\ne 0,\end{array}\right. ~~ C_{1011}=\frac{1}{6l\pi }\psi _1^TF_{1011},\\ C_{0021}&=\frac{1}{4l\pi }\psi _3^TF_{0021},~~~~~~~~~~~~~~~~~~~ C_{1110}=\frac{1}{6l\pi }\psi _3^TF_{1110}. \end{aligned} \end{aligned}$$

Step 2. The calculation of $Proj_{Ker(M_3^1)}(D_z\tilde{f_2^1})(z,0,0)U_2^1(z,0)$.

It follows from (3.13),(3.15) that

$$\begin{aligned} {\tilde{F}}_2(\Phi z_x,0)=G_2^d(\Phi z_x,0)+F_2(\Phi z_x,0)=G_2^{d(0,0)}(\Phi z_x)+F_2(\Phi z_x,0). \end{aligned}$$

(3.30)

Since for all $\epsilon \in R^2,$ $F(0,\epsilon )=DF(0,\epsilon )U=(0,0,0)^T$. Then we have that,

$$\begin{aligned} \begin{aligned}&F_2(\Phi z_x+w,\epsilon )=F_2(\Phi z_x+w,0)\\&=\sum \limits _{q_1+q_2+q_3+q_4=2}F_{q_1q_2q_3q_4}r_{n_1}^{q_1+q_2}(x)r_{n_2}^{q_3+q_4}(x)z_1^{q_1}z_2^{q_2}z_3^{q_3}z_4^{q_4}+S_2(\Phi z_x+w,0)+o(|w|^2), \end{aligned} \end{aligned}$$

(3.31)

where $S_2(\Phi z_x+w,0)$ is the cross term of $\Phi z_x$ and w.

Besides, denote $G_2^{d(0,0)}(\Phi z_x)=(0,G_2^{d(0,0)(2)}(\Phi z_x),0)^T$ for convenience. From (3.14), we have that,

$$\begin{aligned} \begin{aligned} G_2^{d(0,0)(2)}&(\Phi z_x)\\=&\,-\frac{4}{l\pi }\chi ^*\left\{ \left( \frac{n_1}{l}\right) ^2(\phi _{12}\phi _{13}z_1^2+2Re(\phi _{12}\overline{\phi _{13}})z_1z_2+\overline{\phi _{12}\phi _{13}}z_2^2)\left( \sin {\frac{n_1x}{l}}\right) ^2\right. \\&+\frac{n_1n_2}{l^2}((\phi _{12}\phi _{33}+\phi _{13}\phi _{32})z_1z_3+(\phi _{12}\overline{\phi _{33}}+\phi _{13}\overline{\phi _{32}})z_1z_4\\&+(\overline{\phi _{12}}\phi _{33}+\overline{\phi _{13}}\phi _{32})z_2z_3+ (\overline{\phi _{12}\phi _{33}}+\overline{\phi _{13}\phi _{32}})z_2z_4)\sin {\frac{n_1x}{l}}\sin {\frac{n_2x}{l}} \\&\left. +\left( \frac{n_2}{l}\right) ^2(\phi _{32}\phi _{33}z_3^2+2Re(\phi _{32}\overline{\phi _{33}})z_3z_4+\overline{\phi _{32}\phi _{33}}z_4^2)\left( \sin {\frac{n_2x}{l}}\right) ^2\right\} . \end{aligned} \end{aligned}$$

(3.32)

Noticing that,

$$\begin{aligned} \begin{aligned}&\int _0^{l\pi }r_{m}^2(x)r_{n}(x)dx=\left\{ \begin{array}{cc}\frac{1}{\sqrt{l\pi }},&{}m\ne 0,~n=0,\\ \frac{1}{\sqrt{2l\pi }},&{}2m=n\ne 0,\\ 0, &{}\text {otherwise}, \end{array}\right. \\&\int _0^{l\pi }\left( \sin {\frac{mx}{l}}\right) ^2r_{n}(x)dx=\left\{ \begin{array}{cc}\frac{\sqrt{l\pi }}{2},&{}m\ne 0,~n=0,\\ -\frac{\sqrt{2l\pi }}{4},&{}2m=n\ne 0,\\ 0,&{}\text {otherwise}, \end{array}\right. \\&\int _0^{l\pi }\sin {\frac{mx}{l}}\sin {\frac{nx}{l}}r_{k}(x)dx=\left\{ \begin{array}{cc}\frac{\sqrt{2l\pi }}{4},&{}k=n-m,~m\ne 0,\\ -\frac{\sqrt{2l\pi }}{4},&{}k=n+m,\\ 0,&{}\text {otherwise},\end{array}\right. \\&\int _0^{l\pi }r_{m}(x)r_{n}(x)r_{k}(x)dx=\left\{ \begin{array}{cc}\frac{1}{\sqrt{2l\pi }},&{}k=m+n,~\text {or}~k=n-m.\\ 0,&{}\text {otherwise}. \end{array}\right. \\ \end{aligned} \end{aligned}$$

(3.33)

by (3.24), (3.30), (3.33), direct calculation results in

where

$$\begin{aligned} \begin{aligned} E_1&=(0,2\chi ^*\phi _{32}\phi _{33}\left( \frac{n_2}{l}\right) ^2,0)^T,~E_2=(0,4\chi ^* Re(\phi _{32}\overline{\phi _{33}})\left( \frac{n_2}{l}\right) ^2,0)^T,\\ E_3&=(0,2\chi ^*(\phi _{12}\phi _{33}+\phi _{13}\phi _{32})\frac{n_1n_2}{l^2},0)^T,~E_4=(0,2\chi ^*(\phi _{12}\overline{\phi _{33}}+\phi _{13}\overline{\phi _{32}})\frac{n_1n_2}{l^2},0)^T,\\ E_5&=(0,2\chi ^*\phi _{12}\phi _{13}\left( \frac{n_1}{l}\right) ^2,0)^T,~E_6=(0,4\chi ^*Re(\phi _{12}\overline{\phi _{13}})\left( \frac{n_1}{l}\right) ^2,0)^T. \end{aligned} \end{aligned}$$

(3.34)

Thus, for $n_2\ne 2n_1,~n_1\ne 0$, $U_2^1(z,0)=(0,0,0,0)^T$.

For $n_1=0,n_2\ne 0$, we can compute that $U_2^1(z,0)=(U_2^{1(1)},U_2^{1(2)},U_2^{1(3)},U_2^{1(4)})^T$ from $U_2^1=(M_2^1)^{-1} \tilde{f_2^1}(z,0,0)$ as follows:

$$\begin{aligned} \begin{aligned} U_2^{1(1)}=&\,\frac{1}{\sqrt{l\pi }}\psi _1^T\left( \frac{1}{i\omega _{n_1}}F_{2000}z_1^2-\frac{1}{3i\omega _{n_1}}\overline{F_{2000}}z_2^2 +\frac{1}{2i\omega _{n_2}-i\omega _{n_1}}(F_{0020}-E_1)z_3^2\right. \\&\left. -\frac{1}{2i\omega _{n_2}+i\omega _{n_1}}(\overline{F_{0020}}-\overline{E_1})z_4^2-\frac{1}{i\omega _{n_1}}F_{1100}z_1z_2-\frac{1}{i\omega _{n_1}}(F_{0011}-E_2)z_3z_4\right) ,\\ U_2^{1(2)}=&\,\frac{1}{\sqrt{l\pi }}\overline{\psi _1}^T\left( \frac{1}{3i\omega _{n_1}}F_{2000}z_1^2-\frac{1}{i\omega _{n_1}}\overline{F_{2000}}z_2^2 +\frac{1}{2i\omega _{n_2}+i\omega _{n_1}}(F_{0020}-E_1)z_3^2\right. \\&\left. -\frac{1}{2i\omega _{n_2}-i\omega _{n_1}}(\overline{F_{0020}}-\overline{E_1})z_4^2+\frac{1}{i\omega _{n_1}}F_{1100}z_1z_2+\frac{1}{i\omega _{n_1}}(F_{0011}-E_2)z_3z_4\right) ,\\ U_2^{1(3)}=&\,\frac{1}{\sqrt{l\pi }}\psi _3^T\left( \frac{F_{1010}}{i\omega _{n_1}}z_1z_3-\frac{F_{1001}}{2i\omega _{n_2}-i\omega _{n_1}}z_1z_4-\frac{F_{0110}}{i\omega _{n_1}}z_2z_3-\frac{F_{0101}}{2i\omega _{n_2}+i\omega _{n_1}}z_2z_4\right) ,\\ U_2^{1(4)}=&\,\frac{1}{\sqrt{l\pi }}\overline{\psi _3}^T\left( \frac{F_{1010}}{i\omega _{n_1}+2i\omega _{n_2}}z_1z_3+\frac{F_{1001}}{i\omega _{n_1}}z_1z_4-\frac{F_{0110}}{i\omega _{n_1}-2i\omega _{n_2}}z_2z_3-\frac{F_{0101}}{i\omega _{n_1}}z_2z_4\right) . \end{aligned} \end{aligned}$$

For $2n_1=n_2\ne 0$, $U_2^1(z,0)=(U_2^{1(1)},U_2^{1(2)},U_2^{1(3)},U_2^{1(4)})$ denoted by

Thus,

$$\begin{aligned} \frac{1}{3!}Proj_{Ker(M_3^1)}[(D_z\tilde{f_2^1})U_2^1](z,0,0)=\left( \begin{array}{c}D_{2100}z_1^2z_2+D_{1011}z_1z_3z_4\\ \overline{D_{2100}}z_1z_2^2+\overline{D_{1011}}z_2z_3z_4\\ D_{0021}z_3^2z_4+D_{1110}z_1z_2z_3\\ \overline{D_{0021}}z_3z_4^2+\overline{D_{1110}}z_1z_2z_4\end{array}\right) , \end{aligned}$$

(3.35)

where for $n_2\ne 2n_1,~n_1\ne 0$, $D_{2100}=D_{1011}=D_{0021}=D_{1110}=0$. And for $n_1=0,n_2\ne 0$,

$$\begin{aligned} \begin{aligned} D_{2100}=&\,\frac{1}{6l\pi i\omega _{n_1}}\left( -(\psi _1^TF_{2000})(\psi _1^TF_{1100})+\frac{2}{3}|\psi _1^TF_{2000}|^2+|\psi _1^TF_{1100}|^2 \right) ,\\ D_{1011}=&\,\frac{1}{6l\pi }\left( -\frac{2}{i\omega _{n_1}}(\psi _1^TF_{2000})(\psi _1^T(F_{0011}-E_2))+\frac{1}{i\omega _{n_1}}(\psi _1^TF_{1100})(\overline{\psi _1}^T(F_{0011}-E_2))\right. \\&\left. -\frac{2}{2i\omega _{n_2}-i\omega _{n_1}}(\psi _1^T(F_{0020}-E_1))(\psi _3^TF_{1001})+\frac{1}{i\omega _{n_1}}(\psi _1^T(F_{0011}-E_2))(\psi _3^TF_{1010})\right. \\&\left. +\frac{2}{2i\omega _{n_2}+i\omega _{n_1}}(\psi _1^T(\overline{F_{0020}}-\overline{E_1}))(\overline{\psi _3}^TF_{1010})+\frac{1}{i\omega _{n_1}}(\psi _1^T(F_{0011}-E_2))(\overline{\psi _3}^TF_{1001})\right) ,\\ D_{0021}=&\,\frac{1}{6l\pi }\left( -\frac{1}{i\omega _{n_1}}(\psi _3^TF_{1010})(\psi _1^T(F_{0011}-E_2))+\frac{1}{2i\omega _{n_2}-i\omega _{n_1}}(\psi _3^TF_{1001})(\psi _1^T(F_{0020}-E_1))\right. \\&\left. +\frac{1}{i\omega _{n_1}}(\psi _3^TF_{0110})(\overline{\psi _1}^T(F_{0011}-E_2))+\frac{1}{2i\omega _{n_2}+i\omega _{n_1}}(\psi _3^TF_{0101})(\overline{\psi _1}^T(F_{0020}-E_1))\right) ,\\ D_{1110}=&\,\frac{1}{6l\pi }\left( \frac{1}{i\omega _{n_1}}(\psi _3^TF_{0110})(\overline{\psi _1}^TF_{1100})-\frac{1}{i\omega _{n_1}}(\psi _3^TF_{1010})(\psi _1^TF_{1100})-\frac{1}{i\omega _{n_1}}(\psi _3^TF_{1010})(\psi _3^TF_{0110})\right. \\&\left. +\frac{1}{i\omega _{n_1}}(\psi _3^TF_{0110})(\psi _3^TF_{1010})+\frac{|\psi _3^TF_{1001}|^2}{2i\omega _{n_2}-i\omega _{n_1}}+\frac{|\psi _3^TF_{0101}|^2}{i\omega _{n_1}+2i\omega _{n_2}}\right) . \end{aligned} \end{aligned}$$

For $2n_1=n_2\ne 0$,

$$\begin{aligned} \begin{aligned} D_{2100}=&\,\frac{1}{12l\pi }\left( -\frac{(\psi _1^T(F_{1010}-E_3))(\psi _3^T(F_{1100}+\overline{E_6}))}{i\omega _{n_2}}+\frac{(\psi _1^T(F_{0110}-\overline{E_4})(\psi _3^T(F_{2000}+E_5))}{2i\omega _{n_1}-i\omega _{n_2}}\right. \\&\left. +\frac{(\psi _1^T(F_{1001}-E_4))(\overline{\psi _3}^T(F_{1100}+\overline{E_6}))}{i\omega _{n_2}}+\frac{(\psi _1^T(F_{0101}-\overline{E_3}))(\overline{\psi _3}^T(F_{2000}+E_5))}{2i\omega _{n_1}+i\omega _{n_2}}\right) ,\\ D_{1011}=&\,\frac{1}{12l\pi }\left( -\frac{(\psi _1^T(F_{1010}-E_3))(\psi _1^T(F_{1001}-E_4))}{i\omega _{n_2}}+\frac{(\psi _1^T(F_{1001}-E_4))(\psi _1^T(F_{1010}-E_3))}{i\omega _{n_2}}\right. \\&\left. +\frac{1}{2i\omega _{n_1}-i\omega _{n_2}}|\psi _1^T(F_{0110}-\overline{E_4})|^2+\frac{1}{2i\omega _{n_1}+i\omega _{n_2}}|\psi _1^T(F_{0101}-\overline{E_3})|^2\right) ,\\ D_{0021}=&\,0,\\ D_{1110}=&\,\frac{1}{12l\pi }\left( \frac{2\psi _3^T(F_{2000}+E_5)(\psi _1^T(F_{0110}-\overline{E_4})}{i\omega _{n_2}-2i\omega _{n_1}} +\frac{(\psi _3^T(F_{1100}+\overline{E_6})(\psi _1^T(F_{1010}-E_3))}{i\omega _{n_2}}\right. \\&\left. +\frac{2\psi _3^T(\overline{F_{2000}}+\overline{E_5})(\overline{\psi _1}^T(F_{1010}-E_3))}{2i\omega _{n_1}+i\omega _{n_2}}+\frac{(\psi _3^T(F_{1100}+\overline{E_6})(\overline{\psi _1}^T(F_{0110}-\overline{E_4}))}{i\omega _{n_2}}\right) . \end{aligned} \end{aligned}$$

Step 3. The calculation of $Proj_{Ker(M_3^1)}(D_w\tilde{f_2^1})(z,0,0)U_2^2(z,0)$.

By (3.13), (3.14), (3.15) and (3.18), we have that,

$$\begin{aligned} (D_w\tilde{f_2^1})(z,0,0)U_2^2(z,0)=\Psi \left( \begin{array}{c}\left[ D_w{\tilde{F}}_2(\Phi z_x+w,0)|_{w=0}U_2^2(z,0),\beta _{n_1}\right] \\ \left[ (D_w{\tilde{F}}_2(\Phi z_x+w,0)|_{w=0}U_2^2(z,0),\beta _{n_2}\right] \end{array}\right) , \end{aligned}$$

(3.36)

where

$$\begin{aligned} {\tilde{F}}_2(\Phi z_x+w,0)=G_2^{d(0,0)}(\Phi z_x+w)+F_2(\Phi z_x+w,0). \end{aligned}$$

(3.37)

Direct computation shows that

$$\begin{aligned} D_w G_2^{d(0,0)}(\Phi z_x+w)|_{w=0}U_2^2(z,0)=0, \end{aligned}$$

(3.38)

since $G_2^{d(0,0)}(\Phi z_x+w)$ is independent on w.

From (3.31),

$$\begin{aligned} \begin{aligned}&F_2(\Phi z_x+w,0)=S_2(\Phi z_x+w,0)+O(z^2,w^2)\\&=\sum _{j=1}^{3}\left( \sum _{k=1}^2S_{jk}w_jz_kr_{n_1}(x)+\sum _{k=3}^4S_{jk}w_jz_kr_{n_2}(x)\right) +O(z^2,w^2), \end{aligned} \end{aligned}$$

where $S_{jk}=2\frac{\partial ^2F_2(\Phi z_x+w,0)}{\partial w_j\partial z_k}|_{z_k=0,~w=0},~(j=1,2,3,~k=1,2,3,4)$, which induces that

$$\begin{aligned} \begin{aligned} D_wF_2(\Phi z_x+w,0)|_{w=0}w=&\,\left( \sum _{k=1}^2(S_{1k}~ S_{2k}~ S_{3k})z_kr_{n_1}(x)+\sum _{k=3}^4(S_{1k}~ S_{2k}~ S_{3k})z_kr_{n_2}(x)\right) w. \end{aligned} \end{aligned}$$

(3.39)

Let

$$\begin{aligned} U_2^2(z,0)\doteq h(z)=\sum \limits _{n\ge 0}h_n(z)r_n(x), \end{aligned}$$

(3.40)

with

$$\begin{aligned} h_n\doteq h_n(z)=\left( \begin{array}{c}h_n^{(1)}(z)\\ h_n^{(2)}(z)\\ h_n^{(3)}(z)\end{array}\right) =\sum \limits _{q_1+q_2+q_3+q_4=2} \left( \begin{array}{c}h_{nq_1q_2q_3q_4}^{(1)}\\ h_{nq_1q_2q_3q_4}^{(2)}\\ h_{nq_1q_2q_3q_4}^{(3)}\end{array}\right) z_1^{q_1}z_2^{q_2}z_3^{q_3}z_4^{q_4}. \end{aligned}$$

According to (3.36)–(3.40), we have that,

where $n=0,1,2,\ldots$ and

$$\begin{aligned} \begin{aligned} b_{nn_1n_1}&=\int _0^{l\pi }r_n(x)r_{n_1}^2(x)dx={\left\{ \begin{array}{ll}\frac{1}{\sqrt{l\pi }},&{}n=0,\\ \frac{1}{\sqrt{2l\pi }},&{}n=2n_1\ne 0,\\ 0,&{}otherwise.\end{array}\right. } \\ b_{nn_1n_2}&=\int _0^{l\pi }r_n(x)r_{n_1}(x)r_{n_2} (x)dx={\left\{ \begin{array}{ll}\frac{1}{\sqrt{l\pi }},&{}n=n_2\ne 0,n_1=0,\\ \frac{1}{\sqrt{2l\pi }},&{}0<n_1<n_2,~n=n_2+n_1 ~\text {or}~n=n_2-n_1,\\ 0,&{}otherwise.\end{array}\right. } \\ \end{aligned} \end{aligned}$$

Thus, for $n_1=0,n_2\ne 0,$

$$\begin{aligned} (D_w\tilde{f_2^1})(z,0,0)U_2^2(z,0)=\Psi \left( \begin{array}{c}\frac{1}{\sqrt{l\pi }}\left( \sum _{k=1}^{2}(S_{1k}~ S_{2k}~ S_{3k})h_0z_k+\sum _{k=3}^{4}(S_{1k}~ S_{2k}~ S_{3k})h_{n_2}z_k\right) \\ \frac{1}{\sqrt{l\pi }}\left( \sum _{k=1}^{2}(S_{1k}~ S_{2k}~ S_{3k})h_{n_2}z_k+\sum _{k=3}^{4}(S_{1k}~ S_{2k}~ S_{3k})h_{0}z_k\right) \\ +\frac{1}{\sqrt{2l\pi }}\sum _{k=3}^{4}(S_{1k}~ S_{2k}~ S_{3k})h_{(2n_2)}z_k \end{array}\right) . \end{aligned}$$

For $0<n_1\le n_2,$

$$\begin{aligned} \begin{aligned}&(D_w\tilde{f_2^1})(z,0,0)U_2^2(z,0)\\ {}&=\Psi \left( \begin{array}{c}\frac{1}{\sqrt{2l\pi }}\left( \sum _{k=1}^{2}(S_{1k}~ S_{2k}~ S_{3k})h_{2n_1}z_k+\sum _{k=3}^{4}(S_{1k}~ S_{2k}~ S_{3k})h_{n_1+n_2}z_k\right) \\ +\frac{1}{\sqrt{l\pi }}\sum _{k=1}^{2}(S_{1k}~ S_{2k}~ S_{3k})h_0z_k+\delta _{n_1n_2}\sum _{k=3}^{4}(S_{1k}~ S_{2k}~ S_{3k})h_{n_2-n_1}z_k\\ \frac{1}{\sqrt{2l\pi }} \left( \sum _{k=1}^{2}(S_{1k}~ S_{2k}~ S_{3k})h_{n_1+n_2}z_k +\sum _{k=3}^{4}(S_{1k}~ S_{2k}~ S_{3k})h_{2n_2}z_k\right) \\ +\frac{1}{\sqrt{l\pi }}\sum _{k=3}^{4}(S_{1k}~ S_{2k}~ S_{3k})h_{0}z_k+\delta _{n_1n_2}\sum _{k=1}^{2}(S_{1k}~ S_{2k}~ S_{3k})h_{n_2-n_1}z_k \end{array}\right) , \end{aligned} \end{aligned}$$

where $\delta _{n_1n_2}=\left\{ \begin{array}{cc}\frac{1}{\sqrt{2l\pi }},&{}n_1<n_2\\ \frac{1}{\sqrt{l\pi }},&{}n_1=n_2\end{array}\right.$. Then,

$$\begin{aligned} \frac{1}{3!}Proj_{Ker(M_3^1)}(D_w\tilde{f_2^1})(z,0,0)U_2^2(z,0)=\left( \begin{array}{c}E_{2100}z_1^2z_2+E_{1011}z_1z_3z_4\\ \overline{E_{2100}}z_1z_2^2+\overline{E_{1011}}z_2z_3z_4\\ E_{0021}z_3^2z_4+E_{1110}z_1z_2z_3\\ \overline{E_{0021}}z_3z_4^2+\overline{E_{1110}}z_1z_2z_4\end{array}\right) , \end{aligned}$$

(3.41)

where for $n_1=0,~n_2\ne 0$,

$$\begin{aligned} \begin{aligned} E_{2100}=&\,\frac{1}{6\sqrt{l\pi }}\psi _1^T((S_{11}~ S_{21}~ S_{31})h_{01100}+(S_{12}~ S_{22}~ S_{32})h_{02000}),\\ E_{1011}=&\,\frac{1}{6\sqrt{l\pi }}\psi _1^T((S_{11}~ S_{21}~ S_{31})h_{00011}+(S_{13}~ S_{23}~ S_{33})h_{n_21001}+(S_{14}~ S_{24}~ S_{34})h_{n_21010}),\\ E_{0021}=&\,\frac{1}{6}\psi _3^T\left( \frac{1}{\sqrt{l\pi }}((S_{13}~ S_{23}~ S_{33})h_{00011}+(S_{14}~ S_{24}~ S_{34})h_{00020})\right. \\&\left. +\frac{1}{\sqrt{2l\pi }}((S_{13}~ S_{23}~ S_{33})h_{(2n_2)0011}+(S_{14}~ S_{24}~ S_{34})h_{(2n_2)0020})\right) ,\\ E_{1110}=&\,\frac{1}{6}\psi _3^T\left( \frac{1}{\sqrt{l\pi }}((S_{11}~ S_{21}~ S_{31})h_{n_20110}+(S_{12}~ S_{22}~ S_{32})h_{n_21010}\right. \\&\left. +(S_{13}~ S_{23}~ S_{33})h_{01100})+\frac{1}{\sqrt{2l\pi }}(S_{13}~ S_{23}~ S_{33})h_{(2n_2)1100}\right) , \end{aligned} \end{aligned}$$

and for $0<n_1\le n_2,$

Obviously, we still need to compute $h_{n1100},~h_{n2000},~h_{n0011},~h_{n1001},~h_{n1010},~h_{n0020}, h_{n0110}$.

By (3.19), we have that,

$$\begin{aligned} (M_2^2)(h_n(z)r_n(x))=(D_z)(h_n(z)r_n(x))Bz-L_1(h_n(z)r_n(x)), \end{aligned}$$

which, combining (3.1), (3.9), (3.12), leads to

$$\begin{aligned} \begin{aligned} \left[ ( M_2^2)(h_n(z)r_n(x)),\beta _n\right] =&\,i\omega _{n_1}(2h_{n2000}z_1^2+h_{n1010}z_1z_3+h_{n1001}z_1z_4\\&-2h_{n0200}z_2^2-h_{n0101}z_2z_4-h_{n0110}z_2z_3)\\&+i\omega _{n_2}(2h_{n0020}z_3^2+h_{n1010}z_1z_3+h_{n0110}z_2z_3\\&-2h_{n0002}z_4^2-h_{n1001}z_1z_4-h_{n0101}z_2z_4)-{\mathscr {M}}_nh_n(z), \end{aligned} \end{aligned}$$

(3.42)

where ${\mathscr {M}}_n$ is defined in (3.9). According to (3.10), (3.12), (3.30), we have that,

$$\begin{aligned} \begin{aligned} {\tilde{f}}_2^2(z,0,0)=&\,(I-\pi ){\tilde{F}}_2(\Phi z_x,0)\\ =&{\tilde{F}}_2(\Phi z_x,0)-(\psi _1^T[{\tilde{F}}_2(\Phi z_x,0),\beta _{n_1}]\phi _1+\overline{\psi _1}^T[{\tilde{F}}_2(\Phi z_x,0),\beta _{n_1}]\overline{\phi _1})r_{n_1}(x)\\&-(\psi _3^T[{\tilde{F}}_2(\Phi z_x,0),\beta _{n_2}]\phi _3+\overline{\psi _3}^T[{\tilde{F}}_2(\Phi z_x,0),\beta _{n_2}]\overline{\phi _3})r_{n_2}(x),\\ {\tilde{F}}_2(\Phi z_x,0)=&\,G_2^{d(0,0)}(\Phi z_x)+F_2(\Phi z_x,0), \end{aligned} \end{aligned}$$

which, combining (3.33), induces that, for $n_1=0,~n_2\ne 0$,

$$\begin{aligned} \begin{aligned} \left[ {\tilde{f}}_2^2(z,0,0),\beta _0\right] =&\,\frac{1}{\sqrt{l\pi }}\left( (F_{2000}-\psi _1^TF_{2000}\phi _1-\overline{\psi _1}^TF_{2000}\overline{\phi _1})z_1^2\right. \\&+(\overline{F_{2000}}-\psi _1^T\overline{F_{2000}}\phi _1-\overline{\psi _1}^T\overline{F_{2000}}\overline{\phi _1})z_2^2\\&+(F_{1100}-\psi _1^TF_{1100}\phi _1-\overline{\psi _1}^TF_{1100}\overline{\phi _1})z_1z_2\\&+(F_{0020}-E_1-\psi _1^T(F_{0020}-E_1)\phi _1-\overline{\psi _1}^T(F_{0020}-E_1)\overline{\phi _1})z_3^2\\&+(\overline{F_{0020}}-\overline{E_1}-\psi _1^T(\overline{F_{0020}}-\overline{E_1})\phi _1-\overline{\psi _1}^T(\overline{F_{0020}}-\overline{E_1})\overline{\phi _1})z_4^2\\&\left. +(F_{0011}-E_2-\psi _1^T(F_{0011}-E_2)\phi _1-\overline{\psi _1}^T(F_{0011}-E_2)\overline{\phi _1})z_3z_4\right) ,\\ [{\tilde{f}}_2^2(z,0,0),\beta _{n_2}]=&\,\frac{1}{\sqrt{l\pi }}\left( (F_{1010}-\psi _3^TF_{1010}\phi _3-\overline{\psi _3}^TF_{1010}\overline{\phi _3})z_1z_3\right. \\&+(F_{1001}-\psi _3^TF_{1001}\phi _3-\overline{\psi _3}^TF_{1001}\overline{\phi _3})z_1z_4\\&+(\overline{F_{1001}}-\psi _3^T\overline{F_{1001}}\phi _3-\overline{\psi _3}^T\overline{F_{1001}}\overline{\phi _3})z_2z_3\\&\left. +(\overline{F_{1010}}-\psi _3^T\overline{F_{1010}}\phi _3-\overline{\psi _3}^T\overline{F_{1010}}\overline{\phi _3})z_2z_4\right) ,\\ [{\tilde{f}}_2^2(z,0,0),\beta _{2n_2}]=&\,\frac{1}{\sqrt{2l\pi }}\left( (F_{0020}+E_1)z_3^2+(\overline{F_{0020}}+\overline{E_1})z_4^2+(F_{0011}+E_2)z_3z_4\right) , \end{aligned} \end{aligned}$$

(3.43)

where $E_1,~E_2$ are defined by (3.34).

For $0<n_1<n_2$,

$$\begin{aligned} \begin{aligned}&\left[ {\tilde{f}}_2^2(z,0,0),\beta _n\right] \\ =&\,{\left\{ \begin{array}{ll}\frac{1}{\sqrt{l\pi }}\left( (F_{2000}-E_5)z_1^2+(\overline{F_{2000}}-\overline{E_5})z_2^2+(F_{0020}-E_1)z_3^2\right. \\ +\left. (\overline{F_{0020}}-\overline{E_1})z_4^2+(F_{1100}-E_6)z_1z_2+(F_{0011}-E_2)z_3z_4\right) ,&{}n=0,\\ \frac{1}{\sqrt{2l\pi }}\left( (F_{0020}+E_1)z_3^2+(\overline{F_{0020}}+\overline{E_1})z_4^2+(F_{0011}+E_2)z_3z_4\right) ,&{}n=2n_2,\\ \end{array}\right. } \end{aligned} \end{aligned}$$

(3.44)

$$\begin{aligned} \begin{aligned}&\left[ {\tilde{f}}_2^2(z,0,0),\beta _n\right] \\ =&\,{\left\{ \begin{array}{ll} \frac{1}{\sqrt{2l\pi }}\left( (F_{1010}+E_3)z_1z_3+(\overline{F_{1010}}+\overline{E_3})z_2z_4\right. \\ +\left. (F_{1001}+E_4)z_1z_4+(\overline{F_{1001}}+\overline{E_4})z_2z_3\right) ,~~~~~~~~~~~~~~~~n=n_1+n_2,\\ \frac{1}{\sqrt{2l\pi }}\left( (F_{1010}-E_3)z_1z_3+(\overline{F_{1010}}-\overline{E_3})z_2z_4\right. \\ +\left. (F_{1001}-E_4)z_1z_4+(\overline{F_{1001}}-\overline{E_4})z_2z_3\right) , ~~~~~~~~~~~~~~~~n=n_2-n_1,~n_2\ne 2n_1,~n_2\ne 3n_1,\\ \frac{1}{\sqrt{2l\pi }}\left( (F_{1010}-E_3-\psi _1^T(F_{1010}-E_3)\phi _1-\overline{\psi _1}^T(F_{1010}-E_3)\overline{\phi _1}))z_1z_3\right. \\ +(F_{1001}-E_4-\psi _1^T(F_{1001}-E_4)\phi _1-\overline{\psi _1}^T(F_{1001}-E_4)\overline{\phi _1}))z_1z_4\\ +(\overline{F_{1001}}-\overline{E_4}-\psi _1^T(\overline{F_{1001}}-\overline{E_4})\phi _1-\overline{\psi _1}^T(\overline{F_{1001}}-\overline{E_4})\overline{\phi _1}))z_2z_3\\ +\left. (\overline{F_{1010}}-\overline{E_3}-\psi _1^T(\overline{F_{1010}}-\overline{E_3})\phi _1-\overline{\psi _1}^T(\overline{F_{1010}}-\overline{E_3})\overline{\phi _1}))z_2z_4\right) ,n=n_2-n_1,~n_2=2n_1,\\ \frac{1}{\sqrt{2l\pi }}\left( (F_{2000}+E_5)z_1^2+(\overline{F_{2000}}+\overline{E_5})z_2^2+(F_{1100}+E_6)z_1z_2\right. \\ +(F_{1010}-E_3)z_1z_3+(F_{1001}-E_4)z_1z_4+(\overline{F_{1010}}-\overline{E_3})z_2z_4\\ \left. +(\overline{F_{1001}}-\overline{E_4})z_2z_3\right) ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~n=n_2-n_1,~n_2=3n_1, \end{array}\right. } \end{aligned} \end{aligned}$$

(3.45)

and

$$\begin{aligned} \begin{aligned}&\left[ {\tilde{f}}_2^2(z,0,0),\beta _n\right] \\ =&\,{\left\{ \begin{array}{ll} \frac{1}{\sqrt{2l\pi }}\left( (F_{2000}+E_5)z_1^2+(\overline{F_{2000}}\right) \\ + \frac{1}{\sqrt{2l\pi }}\left( \overline{E_5})z_2^2+(F_{1100}+E_6)z_1z_2\right) , ~~~~~~~~~~~~~~~~~~~~~~~ n=2n_1,~n_2\ne 2n_1,~n_2\ne 3n_1, \\ \frac{1}{\sqrt{2l\pi }}\left( (F_{2000}+E_5-\psi _3^T(F_{2000}+E_5)\phi _3-\overline{\psi _3}^T(F_{2000}+E_5)\overline{\phi _3})z_1^2\right. \\ +(\overline{F_{2000}}+\overline{E_5}-\psi _3^T(\overline{F_{2000}}+\overline{E_5})\phi _3-\overline{\psi _3}^T(\overline{F_{2000}}+\overline{E_5})\overline{\phi _3})z_2^2\\ \left. +(F_{1100}+E_6-\psi _3^T(F_{1100}+E_6)\phi _3-\overline{\psi _3}^T(F_{1100}+E_6)\overline{\phi _3})z_1z_2\right) , ~n=2n_1,n_2=2n_1,\\ \frac{1}{\sqrt{2l\pi }}\left( (F_{2000}+E_5)z_1^2+(\overline{F_{2000}}+\overline{E_5})z_2^2+(F_{1100}+E_6)z_1z_2\right. \\ +(F_{1010}+E_3)z_1z_3+(F_{1001}+E_4)z_1z_4+(\overline{F_{1010}}+\overline{E_3})z_2z_4\\ \left. +(\overline{F_{1001}}+\overline{E_3})z_2z_4\right) , ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ n=2n_1,~n_2=3n_1. \end{array}\right. } \end{aligned} \end{aligned}$$

(3.46)

From (3.28), we have that,

$$\begin{aligned}{}[( M_2^2)(h_n(z)r_n(x)),\beta _n]=[{\tilde{f}}_2^2(z,0,0),\beta _n],~n=0,1,2,\ldots . \end{aligned}$$

(3.47)

Next, we compute $h_{nq_1q_2q_3q_4}$ in three cases.

Case 1. For $n_1=0,~n_2\ne 0$, from (3.42),(3.43), (3.47) and matching the coefficients $z_1^2,~z_3^2, ~z_1z_2,~z_3z_4$, we have that,

$$\begin{aligned} n=0, {\left\{ \begin{array}{ll} 2i\omega _{n_1}h_{02000}-{\mathscr {M}}_0h_{02000}=\frac{1}{\sqrt{l\pi }}(F_{2000}-\psi _1^TF_{2000}\phi _1-\overline{\psi _1}^TF_{2000}\overline{\phi _1}),\\ 2i\omega _{n_2}h_{00020}-{\mathscr {M}}_0h_{00020}=\frac{1}{\sqrt{l\pi }}(F_{0020}-E_1-\psi _1^T(F_{0020}-E_1)\phi _1-\overline{\psi _1}^T(F_{0020}-E_1)\overline{\phi _1}),\\ -{\mathscr {M}}_0h_{01100}=\frac{1}{\sqrt{l\pi }}(F_{1100}-\psi _1^TF_{1100}\phi _1-\overline{\psi _1}^TF_{1100}\overline{\phi _1}),\\ -{\mathscr {M}}_0h_{00011}=\frac{1}{\sqrt{l\pi }}(F_{0011}-E_2-\psi _1^T(F_{0011}-E_2)\phi _1-\overline{\psi _1}^T(F_{0011}-E_2)\overline{\phi _1}). \end{array}\right. } \end{aligned}$$

Therefore,

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{02000}=\frac{1}{\sqrt{l\pi }}(2i\omega _{n_1}I-{\mathscr {M}}_0)^{-1}(F_{2000}-\psi _1^TF_{2000}\phi _1-\overline{\psi _1}^TF_{2000}\overline{\phi _1}),\\ h_{00020}=\frac{1}{\sqrt{l\pi }}(2i\omega _{n_2}I-{\mathscr {M}}_0)^{-1}(F_{0020}-E_1-\psi _1^T(F_{0020}-E_1)\phi _1-\overline{\psi _1}^T(F_{0020}-E_1)\overline{\phi _1}),\\ h_{01100}=-\frac{1}{\sqrt{l\pi }}{\mathscr {M}}_0^{-1}(F_{1100}-\psi _1^TF_{1100}\phi _1-\overline{\psi _1}^TF_{1100}\overline{\phi _1}),\\ h_{00011}=-\frac{1}{\sqrt{l\pi }}{\mathscr {M}}_0^{-1}(F_{0011}-E_2-\psi _1^T(F_{0011}-E_2)\phi _1-\overline{\psi _1}^T(F_{0011}-E_2)\overline{\phi _1}). \end{array}\right. } \end{aligned}$$

Similarly, when $n=n_2$ and $n=2n_2$, by matching the coefficients $z_1z_3,~z_1z_4, ~z_2z_3,$ we have that,

Case 2. For $0<n_1<n_2$, from (3.42), (3.44), (3.46), (3.47) and matching the coefficients $z_1^2,~z_3^2, ~z_1z_2,~z_3z_4$, we have that,

$$\begin{aligned} n=0, {\left\{ \begin{array}{ll} 2i\omega _{n_1}h_{02000}-{\mathscr {M}}_0h_{02000}=\frac{1}{\sqrt{l\pi }}(F_{2000}-E_5),\\ 2i\omega _{n_2}h_{00020}-{\mathscr {M}}_0h_{00020}=\frac{1}{\sqrt{l\pi }}(F_{0020}-E_1),\\ -{\mathscr {M}}_0h_{01100}=\frac{1}{\sqrt{l\pi }}(F_{1100}-E_6),\\ -{\mathscr {M}}_0h_{00011}=\frac{1}{\sqrt{l\pi }}(F_{0011}-E_2). \end{array}\right. } \end{aligned}$$

Therefore,

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{02000}=\frac{1}{\sqrt{l\pi }}(2i\omega _{n_1}I-{\mathscr {M}}_0)^{-1}(F_{2000}-E_5),\\ h_{00020}=\frac{1}{\sqrt{l\pi }}(2i\omega _{n_2}I-{\mathscr {M}}_0)^{-1}(F_{0020}-E_1),\\ h_{01100}=-\frac{1}{\sqrt{l\pi }}{\mathscr {M}}_0^{-1}(F_{1100}-E_6),\\ h_{00011}=-\frac{1}{\sqrt{l\pi }}{\mathscr {M}}_0^{-1}(F_{0011}-E_2). \end{array}\right. } \end{aligned}$$

Similarly, when $n=2n_1,~n=n_1+n_2,~n=n_2-n_1$ and $n=2n_2$, by matching the coefficients $z_1^2,~z_3^2,~z_1z_2,~z_1z_3,~z_1z_4, ~z_2z_3,~z_3z_4$, we have that,

For $n=2n_1,~n_2\ne 2n_1,$

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{(2n_1)1100}=-\frac{1}{\sqrt{2l\pi }}({\mathscr {M}}_{2n_1})^{-1}(F_{1100}+E_6),&{}h_{(2n_1)0011}=\vec {0},\\ h_{(2n_1)2000}=\frac{1}{\sqrt{2l\pi }}(2i\omega _{n_1}I-{\mathscr {M}}_{2n_1})^{-1}(F_{2000}+E_5),&{}h_{(2n_1)0020}=\vec {0}.\\ \end{array}\right. } \end{aligned}$$

For $n=2n_1,~n_2=2n_1,$

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{(2n_1)1100}=-\frac{1}{\sqrt{2l\pi }}({\mathscr {M}}_{2n_1})^{-1}(F_{1100}+E_6-\psi _3^T(F_{1100}+E_6)\phi _3-\overline{\psi _3}^T(F_{1100}+E_6)\overline{\phi _3}),\\ h_{(2n_1)2000}=\frac{1}{\sqrt{2l\pi }}(2i\omega _{n_1}I-{\mathscr {M}}_{2n_1})^{-1}(F_{2000}+E_5-\psi _3^T(F_{2000}+E_5)\phi _3-\overline{\psi _3}^T(F_{2000}+E_5)\overline{\phi _3}),\\ h_{(2n_1)0011}=h_{(2n_1)0020}=\vec {0}. \end{array}\right. } \end{aligned}$$

For $n=n_2-n_1,~n_2\ne 2n_1,$

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{(n_2-n_1)1001}=\frac{1}{\sqrt{2l\pi }}(i(\omega _{n_1}-\omega _{n_2})I-{\mathscr {M}}_{n_2-n_1})^{-1}(F_{1001}-E_4),\\ h_{(n_2-n_1)1010}=\frac{1}{\sqrt{2l\pi }}(i(\omega _{n_1}+\omega _{n_2})I-{\mathscr {M}}_{n_2-n_1})^{-1}(F_{1010}-E_3),\\ h_{(n_2-n_1)0110}=\frac{1}{\sqrt{2l\pi }}(i(\omega _{n_2}-\omega _{n_1})I-{\mathscr {M}}_{n_2-n_1})^{-1}(\overline{F_{1001}}-\overline{E_4}). \end{array}\right. } \end{aligned}$$

For $n=n_2-n_1,~n_2=2n_1,$

$$\begin{aligned} {\left\{ \begin{array}{ll} h_{(n_2-n_1)1001}= &{}\,\frac{1}{\sqrt{2l\pi }}(i(\omega _{n_1}-\omega _{n_2})I-{\mathscr {M}}_{n_2-n_1})^{-1}(F_{1001}-E_4\\ &{}-\psi _1^T(F_{1001}-E_4)\phi _1-\overline{\psi _1}^T(F_{1001}-E_4)\overline{\phi _1})),\\ h_{(n_2-n_1)1010}= &{}\,\frac{1}{\sqrt{2l\pi }}(i(\omega _{n_1}+\omega _{n_2})I-{\mathscr {M}}_{n_2-n_1})^{-1}(F_{1010}-E_3\\ &{}-\psi _1^T(F_{1010}-E_3)\phi _1-\overline{\psi _1}^T(F_{1010}-E_3)\overline{\phi _1})),\\ h_{(n_2-n_1)0110}= &{}\,\frac{1}{\sqrt{2l\pi }}(i(\omega _{n_2}-\omega _{n_1})I-{\mathscr {M}}_{n_2-n_1})^{-1}(\overline{F_{1001}}-\overline{E_4}\\ &{}-\psi _1^T(\overline{F_{1001}}-\overline{E_4})\phi _1-\overline{\psi _1}^T(\overline{F_{1001}}-\overline{E_4})\overline{\phi _1})). \end{array}\right. } \end{aligned}$$

Hence, by (3.21), (3.26), (3.27), (3.29), (3.35) and (3.41), the norm form to third order for double bifurcation is as follows:

$$\begin{aligned} {\dot{z}}=Bz+\left( \begin{array}{c}B_{n_11}z_1\epsilon _1+B_{n_12}z_1\epsilon _2\\ \overline{B_{n_11}}z_2\epsilon _1+\overline{B_{n_12}}z_2\epsilon _2\\ B_{n_21}z_3\epsilon _1+B_{n_22}z_3\epsilon _2\\ \overline{B_{n_21}}z_4\epsilon _1+\overline{B_{n_22}}z_4\epsilon _2\end{array}\right) +\left( \begin{array}{c}B_{2100}z_1^2z_2+B_{1011}z_1z_3z_4\\ \overline{B_{2100}}z_1z_2^2+\overline{B_{1011}}z_2z_3z_4\\ B_{0021}z_3^2z_4+B_{1110}z_1z_2z_3\\ \overline{B_{0021}}z_3z_4^2+\overline{B_{1110}}z_1z_2z_4 \end{array}\right) , \end{aligned}$$

(3.48)

where,

$$\begin{aligned} \begin{aligned} B_{2100}=&\,C_{2100}+\frac{3}{2}(D_{2100}+E_{2100}),~~B_{1011}=C_{1011}+\frac{3}{2}(D_{1011}+E_{1011}),\\ B_{0021}=&\,C_{0021}+\frac{3}{2}(D_{0021}+E_{0021}),~~B_{1110}=C_{1110}+\frac{3}{2}(D_{1110}+E_{1110}). \end{aligned} \end{aligned}$$

Making double polar coordinates transformation by

$$\begin{aligned} z_1=\rho _1e^{i\theta _1},~z_2=\rho _1e^{-i\theta _1},~z_3=\rho _2e^{i\theta _2},~z_4=\rho _2e^{-i\theta _2}, \end{aligned}$$

system (3.48) is equivalent to the following equation:

$$\begin{aligned} \begin{aligned} {\dot{\rho }}_1&=\rho _1(c_1\epsilon _1+c_2\epsilon _2+d_1\rho _1^2+k_1\rho _2^2),\\ {\dot{\rho }}_2&=\rho _2(c_3\epsilon _1+c_4\epsilon _2+d_2\rho _1^2+k_2\rho _2^2), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} c_1&=Re(B_{n_11}),~c_2=Re(B_{n_12}),~c_3=Re(B_{n_21}),~c_4=Re(B_{n_22}),\\ d_1&=Re(B_{2100}),~d_2=Re(B_{1110}),~k_1=Re(B_{1011}),~k_2=Re(B_{0021}). \end{aligned} \end{aligned}$$

4 Numerical Simulations

In this section, we numerically investigate the spatiotemporal patterns of system (2.12). Firstly, for the local system (2.16) with

$$\begin{aligned} r=1,~k=2,~\beta =1.2,~\gamma =1,~\xi =2,~\eta =0.5, \end{aligned}$$

it follows from (A1) that the positive equilibrium $E_2$ exists for $0<\rho <2/(2\sigma +1)$ and from (2.17) that system (2.16) has no Hopf bifurcation for $\rho >\rho ^*_{max}\approx 0.3431$. By (2.15), we have the Hopf bifurcation curve $\text{ H: }~ \rho =(2\sigma -1)/(2\sigma ^2+\sigma )$ and $E_2$ is asymptotically stable for $\rho >(2\sigma -1)/(2\sigma ^2+\sigma )$ and unstable for $\rho <(2\sigma -1)/(2\sigma ^2+\sigma ).$ The stability region $D_1$ and the Hopf bifurcation curve H for system (2.16) in the $\sigma$–$\rho$ plane are illustrated in Fig. 1a for $0<\sigma <4.2$ and $0<\rho <2$.

For fixed $\rho =0.2<\rho ^*_{max}$, we have $\sigma _1\simeq 0.6492$ and $\sigma _2\simeq 3.8508$. Thus, the positive equilibrium $E_2$ is asymptotically stable for $0<\sigma <\sigma _1$ or $\sigma >\sigma _2$ and unstable for $\sigma _1<\sigma <\sigma _2$, and system (2.16) undergoes Hopf bifurcations at $\sigma =\sigma _j, j=1, 2$, which are also the critical values of the spatially homogeneous Hopf bifurcation of the diffusive system (2.12). Then, for (2.12), choosing the diffusive coefficients and the spatial interval $(0, l\pi )$ as

$$\begin{aligned} \delta _N=0.5,~\delta _P=0.8,~\delta _S=0.5,~l=4, \end{aligned}$$

we investigate the spatiotemporal dynamics taking the parameters $\chi$ and $\sigma$ as two bifurcation parameters. It follows from Lemma 2.2 that $[\sqrt{x_0}l]=1$ if $\sigma \in (0,4.2)$. A further calculation shows that $\chi _{1}^H(\sigma )>\chi _{2}^H(\sigma )$ for $\sigma \in (0,0.1837)\cup (4.0146,4.2)$ and $\chi _{1}^H(\sigma )<\chi _{2}^H(\sigma )$ for $\sigma \in (0.1837,4.0146)$. Thus,

$$\begin{aligned} n_H^*=\left\{ \begin{array}{ll} 1, &{} \sigma \in (0.1837,4.0146),\\ 2, &{} \sigma \in (0,0.1837)\cup (4.0146,4.2). \end{array} \right. \end{aligned}$$

Denote the Hopf bifurcation curves in the $\sigma$–$\chi$ plane by

$$\begin{aligned} H_0^{(1)}: \sigma =\sigma _1\simeq 0.6492,~~H_0^{(2)}: \sigma =\sigma _2\simeq 3.8508, \end{aligned}$$

which correspond to the spatially homogeneous Hopf bifurcations, and by Theorem 2.1,

$$\begin{aligned} \begin{aligned}&H_1: \chi =\chi _{1}^H(\sigma )=\frac{2.5(1-0.2\sigma )^2(9.3a_{11}^2-(9.4429-0.768\sigma )a_{11}+0.7058-0.0624\sigma )}{0.9-0.2\sigma },\\&H_2: \chi =\chi _{2}^H(\sigma )=\frac{2.5(1-0.2\sigma )^2(3.3a_{11}^2-(4.4115-0.192\sigma )a_{11}+1.0852-0.0624\sigma )}{0.9-0.2\sigma }, \end{aligned} \end{aligned}$$

where $a_{11}=0.2(\sigma +0.5-1/(1-0.2\sigma ))$, which correspond to the spatially inhomogeneous Hopf bifurcations, for wave numbers $n=1$ and $n=2$, respectively.

Similarly, by Lemma 2.3, we have

$$\begin{aligned} n_T^*=\left\{ \begin{array}{ll} 3, &{} \sigma \in (0, 2.857),\\ 2, &{} \sigma \in (2.857, 4.2). \end{array} \right. \end{aligned}$$

Then, by Theorems 2.1 and 2.2, the boundaries of the stability regions of system (2.12) consist of the spatially inhomogeneous Hopf bifurcation curves $H_1$ and $H_2$, the spatially homogeneous Hopf bifurcation lines $H_0^{(1)}$ and $H_0^{(2)}$ and the Turing bifurcation curves $T_3$ and $T_2$, as shown in Fig. 1b, where

$$\begin{aligned} \begin{aligned}&T_2: \chi =\chi _{2}^T(\sigma )=-\frac{2.5(1-0.2\sigma )^2}{0.9-0.2\sigma }\left( -0.22\sigma +0.5525+\frac{1}{10-2\sigma }\right) ,\\&T_3:\chi =\chi _{3}^T(\sigma )=-\frac{2.5(1-0.2\sigma )^2}{0.9-0.2\sigma }\left( -0.1917\sigma +0.4133+\frac{0.125}{1-0.2\sigma }\right) , \end{aligned} \end{aligned}$$

according to Theorem 2.2.

Fig. 1

a The existence and stability regions of the positive equilibrium $E_2$ of the local system (2.16); b Stability regions and bifurcation diagrams for the diffusive system (2.12) in the $\chi -\sigma$ for $\rho =0.2$ and other parameters are the same as in (a). The shaded regions SR1 and SR2 are stable regions, $H_0^{(1)}$ and $H_0^{(2)}$ are homogeneous Hopf bifurcation lines. $H_1,~H_2$ are spatially inhomogeneous Hopf bifurcation curves and $T_3,~T_2$ are critical Turing bifurcation curves

The spatially inhomogeneous Hopf bifurcation curves $H_1$ and $H_2$ intersect at two points $Q_3(0.1837,3.7633)$ and $Q_4(4.0146,1.2837)$. The spatially inhomogeneous Hopf bifurcation curve $H_1$ intersects with the straight Hopf bifurcation lines $H_0^{(1)}$ and $H_0^{(2)}$ at the point $Q_1(0.6492,1.6353)$ and $Q_2(3.8508,0.4736)$, respectively. These double-Hopf bifurcation points $Q_j, (j=1,2,3,4)$ lie on the the boundaries of the stability regions of system (2.12).

The critical Turing bifurcation curves $T_3$ and $T_2$ intersect with the straight Hopf bifurcation lines $H_0^{(1)}$ and $H_0^{(2)}$ at the points $R_1(0.6492,-1.063)$ and $R_2(3.8508, -0.1428)$, respectively. By Theorem 2.5, system (2.12) undergoes Turing–Hopf bifurcations near the positive constant equilibrium $E_2$ at $R_1$ and $R_2$, which also lie on the the boundaries of the stability regions of system (2.12).

In what follows, we are interested in the dynamical classification of system (2.12) near the double-Hopf bifurcation points.

4.1 The Double-Hopf Bifurcations Due to the Intersection of the Spatially Homogeneous and Inhomogeneous Hopf Bifurcations

For the double-Hopf bifurcation point $Q_2(3.8508,0.4736)$, which is the intersection point of the spatially homogeneous Hopf bifurcation line $H_0^{(2)}$ and the spatially inhomogeneous Hopf bifurcation curves $H_1$, we have $n_1=0,~n_2=1$ and it follows from (2.5) and (2.8) that

$$\begin{aligned} \omega _0=0.1765,~~\omega _1=0.2755. \end{aligned}$$

Letting $\epsilon _1=\sigma -3.8508,~\epsilon _2=\chi -0.4736$ and employing the procedure developed in Sect. 3, we obtain the normal form truncated to the third order terms as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\rho }}_1=\rho _1 (-0.2786\epsilon _1-0.03075\rho _1^2-10.0633\rho _2^2),\\ {\dot{\rho }}_2=\rho _2 (-0.2396\epsilon _1+0.0681\epsilon _2-0.0464\rho _1^2-0.057\rho _2^2). \end{array}\right. } \end{aligned}$$

(4.1)

System (4.1) has a zero equilibrium $E_0^*(0,0)$ for any $\epsilon _1,~\epsilon _2\in R$, and two boundary equilibria

$$\begin{aligned} E_1^*(\sqrt{-9.0594\epsilon _1},0),~\epsilon _1<0;~ E_2^*(0,\sqrt{-4.2006\epsilon _1+1.1943\epsilon _2}),~\epsilon _2>3.5173\epsilon _1, \end{aligned}$$

and a positive equilibrium

$$\begin{aligned} E^*(\sqrt{-5.1462\epsilon _1+1.4728\epsilon _2},\sqrt{-0.01196\epsilon _1-0.00401\epsilon _2}), ~3.4941\epsilon _1<\epsilon _2<-2.6569\epsilon _1. \end{aligned}$$

By analyzing the stability and bifurcation of these equilibria, the normal form (4.1) is the so-called simple case, illustrated in [28]. The phase portrait is easy to be obtained in Fig. 2, where the curves $H_0^{(2)}, ~{\widetilde{H}}_1,~L_2^1,~L_2^2$ are denoted by

$$\begin{aligned} \begin{aligned}&H_0^{(2)}:~\sigma =3.8508,~{\widetilde{H}}_1:~\chi =0.4736+3.5173(\sigma -3.8508),\\&L_2^1:~\chi =0.4736+3.4941(\sigma -3.8508),~(\sigma<3.8508),\\&L_2^2:~\chi =0.4736-2.6569(\sigma -3.8508),~(\sigma <3.8508). \end{aligned} \end{aligned}$$

The lines $H_0^{(2)}, ~{\widetilde{H}}_1,~L_2^1,~L_2^2$ divide the $(\sigma , \chi )$ plane into six regions with different dynamics.

Remark 4.1

The Hopf bifurcation line ${\widetilde{H}}_1$ obtained by the normal form (4.1) is tangent to the Hopf bifurcation curve $H_1$ due to the linear analysis at the point $Q_2(3.8508,0.4736)$.

Fig. 2

The phase portrait near the double-Hopf bifurcation point $Q_2$ in Fig. 1

According to the phase portrait Fig. 2, there are three stable patterns near the double-Hopf bifurcation point $Q_2$ as follows:

• (i) when $(\sigma , \chi )=(3.858, 0.44)\in \textcircled {{1}}$, (4.1) has a stable equilibrium $E_0^*$, which implies that the positive equilibrium $E_2(0.8757,2.0511,3.5026)$ of system (2.12) is asymptotically stable, as shown in Fig. 3a, d;

• (ii) when $(\sigma , \chi )=(3.848, 0.44)\in \textcircled {{6}}$, (4.1) has a stable boundary equilibrium $E_1^*$, which implies that system (2.12) has a stable spatially homogeneous periodic solution, as shown in Fig. 3b, e;

• (iii) when $(\sigma , \chi )=(3.8608, 0.5096)\in \textcircled {{2}}$, (4.1) has a stable boundary equilibrium $E_2^*$, which implies that system (2.12) has a stable spatially inhomogeneous periodic solution with the spatial shape like $\cos (x/4)$, as shown in Fig. 3c, f.

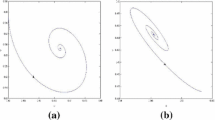
Except for these stable patterns, there are two types of pattern transitions: (i) from unstable spatially homogeneous periodic solution to stable spatially inhomogeneous periodic solution, which exists in the region $\textcircled {{3}}$, (see Fig. 4a); (ii) from unstable spatially inhomogeneous periodic solution to stable spatially homogeneous periodic solution, which exists in the region $\textcircled {{5}}$, (see Fig. 5a). Figures 4a and 5a are the projections of N(x, t) on the x–t plane for $(\sigma , \chi )=(3.85, 0.49)\in \textcircled {{3}}$ and $(\sigma , \chi )=(3.842, 0.4438)\in \textcircled {{5}}$, respectively. Figure 4b, c are the truncated sections of Fig. 4a for short-term and long-term behaviors, respectively. Figure 5b, c are the truncated sections of Fig. 5a for short-term and long-term behaviors, respectively.

When $(\sigma , \chi )$ lies in the region $\textcircled {{4}}$, two stable spatially homogeneous and inhomogeneous periodic solutions coexist.

Fig. 3

Spatiotemporal dynamics of (2.12) for different parameters $\sigma$ and $\chi$ near the point $Q_2$: a, b and c are the projections of N(x, t) on the x–t plane for $(\sigma , \chi )=(3.858, 0.44)\in \textcircled {{1}}$, $(\sigma , \chi )=(3.848, 0.44)\in \textcircled {{6}}$, $(\sigma , \chi )=(3.8608, 0.5096)\in \textcircled {{2}}$, respectively. d, e and f are the spatial profiles for fixed time $t=1500$ of (a), (b) and (c), respectively

Fig. 4

a The projection of N(x, t) on the x–t plane for $(\sigma , \chi )=(3.85, 0.49)\in \textcircled {{3}}$, which shows the existence of the pattern transition from unstable spatially homogeneous periodic solution to stable spatially inhomogeneous periodic solution. b and c are the truncated section of (a) for short-term and long-term behaviors, respectively

Fig. 5

a The projection of N(x, t) on the x–t plane for $(\sigma , \chi )=(3.842, 0.4438)\in \textcircled {{5}}$, which shows the existence of the pattern transition from unstable spatially inhomogeneous periodic solution to stable spatially homogeneous periodic solution. b, c are the truncated section of (a) for short-term and long-term behaviors, respectively

4.2 The double-Hopf bifurcations due to the intersection of two spatially inhomogeneous Hopf bifurcations

For the double-Hopf bifurcation point $Q_3(0.1837,3.7633)$, which is the intersection point of two spatially inhomogeneous Hopf bifurcation curves $H_1$ and $H_2$, we have $n_1=1, n_2=2$ and $\omega _1=0.5414,~\omega _2=0.7027$, and the normal form truncated to the third order terms is

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\rho }}_1=\rho _1 (0.08387\epsilon _1+0.0153\epsilon _2-0.0902\rho _1^2-0.1524\rho _2^2),\\ {\dot{\rho }}_2=\rho _2 (0.08896\epsilon _1+0.03029\epsilon _2+0.1093\rho _1^2-0.1886\rho _2^2). \end{array}\right. } \end{aligned}$$

(4.2)

System (4.2) has a zero equilibrium $M_0(0,0)$ for any $\epsilon _1,~\epsilon _2\in R$, and two boundary equilibria

$$\begin{aligned} M_1(\sqrt{0.9296\epsilon _1+0.1696\epsilon _2},0),~\epsilon _2>-5.4822\epsilon _1;~ M_2(0,\sqrt{0.4716\epsilon _1+0.1605\epsilon _2}),~\epsilon _2>-2.9373\epsilon _1, \end{aligned}$$

and a positive equilibrium

$$\begin{aligned} M(\sqrt{0.06715\epsilon _1-0.05138\epsilon _2},\sqrt{0.5105\epsilon _1+0.1308\epsilon _2}),~\text {for}~-3.9033\epsilon _1<\epsilon _2<1.3069\epsilon _1. \end{aligned}$$

And the phase portrait for (4.2) is plotted in Fig. 6, where the curves ${\widetilde{H}}_{31}, ~{\widetilde{H}}_{32},~L_3^1,~L_3^2$ are denoted by

$$\begin{aligned} \begin{aligned}&{\widetilde{H}}_{31}:~\chi =3.7633-5.4822 (\sigma -0.1837),~{\widetilde{H}}_{32}:~\chi =3.7633-2.9373(\sigma -0.1837),\\&L_3^1:~\chi =3.7633-3.9033(\sigma -0.1837),~(\sigma>0.1837),\\&L_3^2:~\chi =3.7633+1.3069(\sigma -0.1837),~(\sigma >0.1837). \end{aligned} \end{aligned}$$

The lines ${\widetilde{H}}_{31}, ~{\widetilde{H}}_{32},~L_3^1,~L_3^2$ divide the $(\sigma ,\chi )$ plane into six regions with different dynamics.

Fig. 6

The phase portrait near the double-Hopf bifurcation point $Q_3$ in Fig. 1

Remark 4.2

The Hopf bifurcation curves ${\widetilde{H}}_{31}$ and ${\widetilde{H}}_{32}$ obtained by the normal form (4.2) are tangent to the Hopf bifurcation curves $H_1$ and $H_2$, respectively, due to the linear analysis at the point $Q_3(0.1837,3.7633)$.

According to the phase portrait Fig. 6, there are four stable patterns near the double-Hopf bifurcation point $Q_3$:

• (i) when $(\sigma , \chi )=(0.18, 3.685)\in \textcircled {{1}}$, system (4.2) has a stable equilibrium $M_0$, which means that the positive equilibrium $E_2(0.2075,0.7748,0.8299)$ of system (2.12) is asymptotically stable, as shown in Fig. 7a, e;

• (ii) when $(\sigma , \chi )=(0.19, 3.736)\in \textcircled {{2}}$, system (4.2) has a stable boundary equilibrium $M_1$, which means that system (2.12) has a stable spatially inhomogeneous periodic solution with the spatial shape like $\cos (x/4)$, as shown in Fig. 7b, f;

• (iii) when $(\sigma , \chi )=(0.18, 3.78)\in \textcircled {{6}}$, system (4.2) has a stable boundary equilibrium $M_2$, which means that system (2.12) has a stable spatially inhomogeneous periodic solution with the spatial shape like $\cos (x/2)$, as shown in Fig. 7c, g;

• (iv) when $(\sigma , \chi )=(0.19, 3.752)\in \textcircled {{4}}$, system (4.2) has a stable positive equilibrium M and two unstable boundary equilibria $M_1,~M_2$, which means that system (2.12) has a stable spatially inhomogeneous quasi-periodic solution with the spatial shape like the combination of $\cos (x/4)$ and $\cos (x/2)$, as shown in Fig. 7d, h.

For fixed space variable $x=\pi /5$, Fig. 8a–c are the time evolutions of N(x, t), and (d), (e) and (f) are the orbits of system (2.12) in the phase space corresponding to Fig. 7b–d.

In addition, besides these four stable patterns, there are still three types of pattern transitions: (i) from unstable spatially inhomogeneous periodic solution with the spatial shape like $\cos (x/4)$ to stable spatially inhomogeneous quasi-periodic solution for $(\sigma , \chi )\in \textcircled {{3}}$; (ii) from unstable spatially inhomogeneous periodic solution with the spatial shape like $\cos (x/2)$ to stable spatially inhomogeneous quasi-periodic solution for $(\sigma , \chi )\in \textcircled {{4}}$; (iii) from unstable spatially inhomogeneous periodic solution with the spatial shape like $\cos (x/4)$ to stable spatially inhomogeneous periodic solution with the spatial shape like $\cos (x/2)$ for $(\sigma , \chi )\in \textcircled {{5}}$.

Remark 4.3

Compared with the case of $Q_2$, the stable spatially inhomogeneous quasi-periodic solution newly appears, but there is no the existence of stable spatially homogeneous and inhomogeneous periodic solutions.

Fig. 7

Spatiotemporal dynamics of (2.12) for different parameters $\sigma$ and $\chi$ near the point $Q_3$: a–d are the projections of N(x, t) on the x–t plane for $(\sigma , \chi )=(0.18, 3.685)\in \textcircled {{1}}$, $(\sigma , \chi )=(0.19, 3.736)\in \textcircled {{2}}$, $(\sigma , \chi )=(0.18, 3.78)\in \textcircled {{6}}$, $(\sigma , \chi )=(0.19, 3.752)\in \textcircled {{4}}$, respectively. e–h are the spatial profiles for fixed time $t=1500$ of a–d, respectively

Fig. 8

For fixed space variable $x=\pi /5$, a–c are the time evolution of N(x, t), and d–f are the orbit of system (2.12) in the phase space with the same parameters $\sigma$ and $\chi$ as in Fig. 7b–d, respectively. d–e show the existence of stable periodic orbit and f shows the existence of the quasi-periodic orbit

5 Conclusion

In this paper, we investigate the effect of the indirect prey-taxis on the dynamics of the Gause–Kolmogorov-type predator–prey system. The stability of the positive equilibrium and the possible bifurcations are studied. We obtain the conditions guaranteeing the occurrence of the Hopf bifurcation, double-Hopf bifurcation and Turing–Hopf bifurcation and the explicit critical values for these bifurcations are determined.

For this system and under the assumption that the positive equilibrium of the corresponding ordinary differential system is stable, there is no diffusion-driven Turing instability when there is no indirect prey-taxis ($\chi =0$). For the repulsive indirect taxis ($\chi <0$), there exists only taxis-driven Turing bifurcation but no Hopf bifurcations and the boundaries of the stability region consist of the Turing bifurcation curves and the spatially homogeneous Hopf bifurcation curve. The intersection points of these boundary curves are Turing–Turing bifurcation and Turing–Hopf bifurcation points, which may result in the occurrence of the spatially inhomogeneous steady state, spatially homogeneous/inhomogeneous periodic solutions and the coexistence of multiple stable steady states.

For the attractive indirect taxis ($\chi >0$), there exists only prey-taxis-driven spatially Hopf bifurcation but no Turing bifurcation, which do not occur for the reaction–diffusion predator–prey model with a direct prey-taxi like (1.1), and the boundaries of the stability region consist of the Hopf bifurcation curves. The intersection points of these boundary curves are double-Hopf bifurcation points, which leads to the occurrence of the spatially homogeneous/inhomogeneous periodic solutions and quasi-periodic solutions. To theoretically investigate the dynamical classification near the double-Hopf bifurcation point, we take the indirect prey-taxis and other parameter in the reaction term as the perturbation parameters, and then derive an algorithm for calculating the normal form of codimension-2 double-Hopf bifurcation for the non-resonance and weak resonance.

We also apply the obtained theoretical results to the system with the Holling-II functional response. The stable region and the bifurcation curves are completely determined in the $\sigma -\chi$ plane, where $\sigma$ is the self saturation coefficient. Employing the normal form of the double-Hopf bifurcation, the dynamical classification near this double-Hopf bifurcation point is explicitly determined. For the double-Hopf bifurcation derived from the interaction of the spatially homogeneous and inhomogeneous Hopf bifurcations, there are three kinds of stable patterns: constant equilibrium, spatially homogeneous periodic solutions and spatially inhomogeneous periodic solutions. Except for these stable spatial–temporal patterns, there are two types of pattern transitions: one is from unstable spatially homogeneous periodic solution to stable spatially inhomogeneous periodic solution, the other is from unstable spatially inhomogeneous periodic solution to stable spatially homogeneous periodic solution.

For the double-Hopf bifurcation derived from the interaction of two spatially inhomogeneous Hopf bifurcations, there are four kinds of stable patterns: constant equilibrium, two kinds of spatially inhomogeneous periodic solutions with different spatial profiles and spatially inhomogeneous quasi-periodic solutions. Besides these four stable spatial–temporal patterns, there are pattern transitions either between two spatially inhomogeneous periodic solution with different spatial profiles or between spatially inhomogeneous periodic solution and spatially inhomogeneous quasi-periodic solution.

There are other interesting but challenging bifurcation problems worthy of investigation for this system with indirect prey-taxis: the spatial–temporal dynamics induced by the other codimension-two bifurcations such as Turing–Turing bifurcation and Turing–Hopf bifurcation or by the strong resonance double-Hopf bifurcation which may be the codimension-three bifurcation.