1 Introduction

Numerous studies show that diffusive predator-prey system can exhibit richer dynamics in space and time [1,2,3,4,5,6,7]. If the interactions among individuals are local, in many previous investigations, Hopf bifurcation is regarded as an effective tool to capture the temporal oscillation, and a general result was found that when the positive constant steady state is destabilized, the time-periodic solution bifurcated through the Hopf bifurcation are always spatially homogeneous, which is first concluded in [8]. However, this may be not realistic since it is common that a species can distribute in different patches in the environment, putting it another way, for some reasons the species can aggregate in the habitat, for this motivation, many researchers explicated such spatial heterogeneity through Turing bifurcations or Turing instability [9]. Accordingly, the combination of Hopf and Turing bifurcations can always be regarded as one of the mechanisms to interpret spatio-temporal oscillations [10, 11].

There will be a breakthrough if the interaction between individuals is not limited to be local, the spatially nonhomogeneous solution is probable to emerge even though only Hopf bifurcation occurs. Furter and Grinfeld [12] argued that populations may share common resources or communicate visually and chemically, it means that taking the nonlocal interaction into account in reaction-diffusion systems may be more realistic in population systems. Britton [13] proposed the following single population model

$$\begin{aligned} u_t=D\varDelta u+\frac{\alpha }{K}\left( u-(1+\alpha )\int _\varOmega K(x,y)u(y,t)\text {d}y\right) . \end{aligned}$$
(1)

If a species encounters some natural causes, for instance the depletion of food resources, then the intraspecific competition not only depends on the population density at the current location but also depends on the population density near the origin. A interesting result was carried out in [14, 15], i.e. under the influence of the nonlocal interaction merely in the form of purely spatial convolution, complex spatio-temporal dynamics can occur as well in the reaction-diffusion system, including bifurcations to spatially nonhomogeneous steady states, spatially nonhomogeneous periodic solution and periodic travelling wave solutions, more studies on nonlocal interactions refer to [16,17,18,19,20] and references therein.

Recently, the nonlocal intraspecific competition of prey was introduced to the Holling-Tanner predator prey system by Merchant and Nagata [21], they put forward the following model

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=d_{1}\varDelta {u}+au\left( 1-\dfrac{1}{k} \displaystyle \int _{\varOmega } K(x,y)u(y,t)\,\mathrm {d}y\right) -\dfrac{buv}{u+m},&{}x\in \varOmega ,\,t>0,\\ v_t=d_{2}\varDelta {v}+cv\left( 1-\dfrac{ev}{u}\right) , &{}x\in \varOmega ,\,t>0.\\ \end{array}\right. } \end{aligned}$$
(2)

here u(x, t) and v(x, t) model the densities of the prey and predator, respectively, \( d_{1} \) and \( d_{2} \) are corresponding diffusive rates, k expresses the carrying capacity of the prey, a, c measure the corresponding intrinsic growth rates, b, e measure the strength of Interaction between predator and prey, m measures the ability of the prey evading predation. the prey species adopts Holling type-II functional response. They considered three common kernel functions in a unbounded domain: Laplace kernel, Gaussian kernel and uniform kernel, and numerically verified complex spatio-temporal pattern formations from viewpoints of Hopf, Turing and Turing-Hopf bifurcations.

For a bounded domain, it is worth noticing that if the kernel function is chosen as \( K(x,y)=\delta (x-y) \), then the system (2) is reduced to the classic diffusive Holling-Tanner predater prey model, which has been extensively studied, see [6, 7, 22,23,24]. From the viewpoint of the predator species invading prey habitats without predators, a symmetric stepfunction kernel is considered in [25], where the authors found that such invasion process can induce complex spatio-temporal structures of species. Chen et. al [26] study the system (2) with Neumann boundary conditions on a bounded spatial domain and \( K(x,y)=\frac{1}{|\varOmega |} \), i.e. spatial average kernel function, they found that the system can produce stable spatially nonhomogeneous periodic solution through Hopf bifurcation, this is completely distinct with the previous works on systems with local interaction. Furthermore, there are some other studies for (2) with spatial average kernel, for example, considering the combination of Hopf and Turing bifurcation, Turing-Hopf bifurcation and double-Hopf bifurcation are discussed in [27], the results showed that in addition to stable spatially nonhomogeneous periodic solution and steady states, spatially nonhomogeneous tristability phenomenon can also emerge.

A natural question arises, whether the system (2) can exhibit more complex spatio-temporal patterns if the kernel is not spatially average on a bounded spatial region? In this paper, we will study the following Holloing-Tanner predator prey system with the nonlocal prey intraspecific competition and a spatial dependently kernel,

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=d_{1}{u}_{xx}+au\Big (1-\dfrac{1}{k} \displaystyle \int _0^{l\pi }K(x,y) u(y,t)\,\mathrm {d}y\Big )-\dfrac{buv}{u+m}, \ &{}t>0,\\ v_t=d_{2}{v}_{xx}+cv\left( 1-\dfrac{ev}{u}\right) ,\ &{}t>0,\\ u_{x}(0, t)=v_{x}(0, t)=0,\ u_{x}(l\pi , t)=v_{x}(l\pi , t)=0, \ &{}t>0, \\ u(x, 0)=u_{0}(x)>0, \quad v(x, 0)=v_{0}(x)>0. \end{array}\right. } \end{aligned}$$
(3)

with

$$\begin{aligned} K(x,y)=\frac{1}{l\pi } +\frac{2}{l\pi }\sum _{k=1 }^{\infty }\text {cos}\frac{kx}{l}\text {cos}\frac{ky}{l}e^{-\frac{\alpha k^2}{l^2}}, \end{aligned}$$
(4)

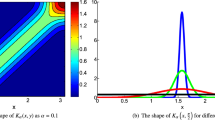
here \(x\in (0, l\pi )\), \( l>0 \) is a positive constant. The kernel function (4) was put forward in [28] where a single reaction diffusion equation model with time delay and nonlocal effect was studied in a one-dimension domain. Considering homogeneous Neumann boundary condition, Su et. al. [29] investigated a diffusive nonlocal Nicholson’s blowflies equation with time delay, they gave detailed analyses of Hopf bifurcations, the results revealed that the nonlocal effect can promote more complex spatial distributions of the species since spatially nonhomogeneous transient patterns appeared. As in [21], Gaussian kernel function was considered in the system (2) on a unbounded domain, this kernel can more realistically describe the strength varying of intraspecific interaction between individuals with the distance. Since homogeneous Neumann boundary conditions is included. Compared to the case of Gaussian kernel in [21], based on the nonlocal term \( \int _{\varOmega }K(x,y) u(y,t)\,\mathrm {d}y \), it can be verified that the effect of the kernel (4) for the system (3) is mathematically equivalent to the Gaussian kernel function in the unbounded domain. It is still worth noting that the kernel (4) is actually a general form, which includes the local kernel for \( \alpha \rightarrow 0 \) and the spatial average kernel for \( \alpha \rightarrow \infty \). Throughout this paper, the parameters \( d_{1} \), \( d_{2} \), a, b, c, d, e, k, \(\alpha \), l are positive constants.

This paper is devoted to study spatio-temporal patterns of system (3). We find the kernel function (4) can induce more complex spatio-temporal patterns with spatial multi-peaks for the system (3) than corresponding Dirac and spatial average kernels. Firstly, we establish the existence criteria of Turing, Hopf, Turing-Hopf and double-Hopf bifurcations, based on these, we accurately characterize the stable and unstable regions of the positive constant steady state. Importantly, when the positive constant steady state loses the stability, the system (3) could undergo any k-mode Hopf bifurcation for different values, which means that bifurcating periodic solution can be not only spatially nonhomogeneous, it also can possess multiple spatial peaks corresponding to multiple space wave frequencies. As a consequence, the complexity of double-Hopf bifurcations increases as well, i.e. stable \( (k,k+1) \)-mode double-Hopf bifurcation with the nonnegative integer k can occur for the system (3). It extremely differs from the cases of Dirac kernel and spatial average kernel, as is well known, it is impossible to undergo double-Hopf bifurcations for the system (2) with Dirac kernel, and for the system (2) with spatial average kernel, only (0, 1) -mode double-Hopf bifurcation can be stable, see [27]. Furthermore, we still find that the stable parameter region of the positive constant steady state decreases as the parameter \( \alpha \) increases, which implies that the region of pattern formations for the kernel (4) is smaller than the spatial average case. Biologically, if the scope of such intraspecific interaction among individuals is farther, then the positive equilibrium The farther the scope of such intraspecific interaction among individuals is, the more likely the positive equilibrium will be destabilized, accordingly, the system is morel likely to generate complex spatio-temporal patterns.

As is well known, double-Hopf bifurcation plays an important role in demonstrating periodic, quasi-periodic or multi-periodic oscillations [30,31,32]. In this paper, on account of the bifurcation theory for partial differential equations in [33] and the frame of the normal form computation given in [34,35,36], we calculate the normal form up to the third order term of \( (k,k+1) \)-mode double-Hopf bifurcation for the positive integer k, which is expressed by original system parameters, it is beneficial for analyzing the influence of original parameters on pattern formations. By studying the equivalent amplitude system near the double-Hopf singularity, we theoretically and numerically demonstrate the existence of two stable spatially nonhomogeneous periodic solutions with different spatial peaks and the bistability of them, as well as a unstable spatially nonhomogeneous quasi-periodic solution. Interestingly, we also numerically find a strange periodic solution and a strange attractor with multi-period near the double-Hopf singularity.

The rest of this paper is organized as follows. In Sect. 2, we perform a linear stability analysis near the positive equilibrium, the existences of Turing, Hopf, Turing-Hopf and double-Hopf bifurcations are established, the stability of positive equilibrium is derived as well. In Sect. 3, we calculate the third order normal form of the \((k,k+1)\)-mode double-Hopf bifurcation for \( k\in {\mathbb {N}} \), complex spatio-temporal dynamics of system (3) near the double-Hopf bifurcation point are illustrated theoretically. Appropriate numerical simulations are carried out to complete the theoretical analyses. Finally, conclusions and discussions are given in Sect. 4.

2 Stability of Positive Equilibrium and Bifurcation Analysis

In this section, the first purpose of is to establish the existence criteria for Turing, Hopf bifurcations, considering the interaction of Turing and Hopf bifurcations, we further discuss the existences of Turing-Hopf bifurcation and double-Hopf bifurcation. Then the second purpose is to determine the stable and unstable regions for the unique positive constant steady state of (3). Our results show that when the positive constant steady state is destabilized, \((k,k+1)\)-mode double-Hopf bifurcation occurs for (3), which leads to complex spatio-temporal periodic, quasi-periodic or multi-periodic phenomena. Throughout this paper we denote the set of all positive integers by \( {\mathbb {N}}\) and denote the set of all nonnegative integers by \( {\mathbb {N}}_{0}\).

2.1 Hopf Bifurcation and Turing Bifurcation

This subsection is devoted to investigate the existence and non-existence of Turing bifurcation and Hopf bifurcation for system (5). By transforming as in [26], \( {\tilde{t}}=at,\ {\tilde{u}}=\frac{u}{m},\ {\tilde{v}}=\frac{ev}{m}, \)

denoting

$$\begin{aligned} {\tilde{\beta }}=\frac{m}{k}, \ {\tilde{b}}=\frac{b}{ae}, \ {\tilde{c}}=\frac{c}{a},\ {\tilde{d}}_{1}=\frac{d_{1}}{a},\ {\tilde{d}}_{2}=\frac{d_{2}}{a}, \end{aligned}$$

ignoring the tilde, system (3) can be transformed into

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=d_{1}u_{xx}+u\Big (1-\beta \displaystyle \int _{0}^{l\pi } K(x,y)u(y,t)\,\mathrm {d}y\Big )-\dfrac{buv}{u+1},&{}x\in (0, l\pi ),\,t>0, \\ v_t=d_{2}v_{xx}+cv\left( 1-\dfrac{v}{u}\right) , &{}x\in (0, l\pi ),\,t>0, \\ u_{x}(0, t)=v_{x}(0, t)=0,\quad u_{x}(l\pi , t)=v_{x}(l\pi , t)=0, &{}t>0, \\ u(x, 0)=u_{0}(x)>0, \quad v(x, 0)=v_{0}(x)>0, \end{array}\right. } \end{aligned}$$
(5)

with \(K(x,y)=\frac{1}{l\pi } +\frac{2}{l\pi }\sum _{k=1 }^{k=\infty }\text {cos}\frac{kx}{l}\text {cos}\frac{ky}{l}e^{-\frac{\alpha k^2}{l^2}}\).

For any given \(\beta >0\) and \(b>0\), as in [27], the system (5) has a unique positive constant steady state, denoted by \( (u^{*}, v^{*})\) with

$$\begin{aligned} u^*=v^*:=\frac{1}{2\beta }\left( 1-\beta -b+\sqrt{(1-\beta -b)^{2}+4\beta }\right) . \end{aligned}$$
(6)

The linearized system of (5) at \( (u^{*}, v^{*}) \) is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _t=d_{1}\phi _{xx}-\beta u^* \displaystyle \int _{0}^{l\pi } K(x,y)\phi (y, t) \mathrm {d}y+\dfrac{ u^* (1-\beta u^*)}{1 + u^*} \phi -(1-\beta u^*)\psi , \\ \psi _t=d_{2}\psi _{xx}+c\phi -c\psi , \\ \phi _{x}(0, t)=\psi _{x}(0, t)=0,\quad \phi _{x}(l\pi , t)=\psi _{x}(l\pi , t)=0, \end{array}\right. } \end{aligned}$$
(7)

with \(K(x,y)=\frac{1}{l\pi } +\frac{2}{l\pi }\sum _{k=1 }^{k=\infty }\text {cos}\frac{kx}{l}\text {cos}\frac{ky}{l}e^{-\frac{\alpha k^2}{l^2}}\) for \(x\in (0, l\pi )\), \(t>0\). Let \( \{\frac{k^{2}}{l^{2}}\}_{k\in {\mathbb {N}}_{0}} \) be the eigenvalues of \(-\mathrm {d}^2/\mathrm {d}x^2\) with zero Neumann boundary condition.

Then the characteristic equations of (7) are given by

$$\begin{aligned} {\mathcal {P}}_{k}(\lambda ) := \lambda ^{2}-T_{k}(c)\lambda +D_{k}(c)=0,\quad k\in {\mathbb {N}}_{0}, \end{aligned}$$
(8)

where for \( k\in {{\mathbb {N}}_0} \),

$$\begin{aligned} \begin{aligned} T_{k}(c)&=-c-d_{2}\frac{k^{2}}{l^{2}}+r u^*-\beta u^* e^{-\frac{\alpha k^2}{l^2}}-d_{1}\frac{k^{2}}{l^{2}},\\ D_{k}(c)&= c\left( r +\beta u^*e^{-\alpha \frac{k^2}{l^2}}+d_1 \frac{k^2}{l^2}\right) -d_2\frac{k^2}{l^2}\left( r u^*-\beta u^*e^{-\alpha \frac{k^2}{l^2}}-d_1 \frac{k^2}{l^2}\right) , \end{aligned} \end{aligned}$$
(9)

with r denoted by

$$\begin{aligned} r:=\frac{1-\beta u^*}{1+ u^*}>0. \end{aligned}$$

As is well known that the stability of the positive equilibrium can be determined if the existences of Turing and Hopf bifurcations are established by analyzing the critical situations of \( T_k(c) \) and \( D_k(c) \). To facilitate comparison with the system with the spatial average kernel in [27], we introduce the following sets of \( \beta \)

$$\begin{aligned} \begin{aligned} \mathbf{B }_1&:=\{(\beta ,b)\ |\ \beta \ge 1, b>0\} \cup \left\{ (\beta , b)\ |\ 0<\beta< 1, 0<b\le \tfrac{(1+\beta )^2}{2(1-\beta )}\right\} , \\ \mathbf{B }_2&:=\left\{ (\beta ,b)\ |\ 0<\beta < 1, b> \tfrac{(1+\beta )^2}{2(1-\beta )}\right\} , \end{aligned} \end{aligned}$$
(10)

which are defined by computing the sign of \( T_0(\beta ,b) \). As in [27], the \((\beta ,b)\)-plane can be divided into two regions \( \mathbf{B }_1 \) and \( \mathbf{B }_2\). It is obviously that when \( (\beta , b) \in \mathbf{B }_1\), i.e. \( r\le \beta \), for any other positive parameters, the positive constant steady state is locally asymptotically stable for the ordinary differential equations corresponding to (5). To further define Hopf and Turing bifurcations curves, we denote

$$\begin{aligned} h(x)=r u^*-\beta u^* e^{-\alpha x}-d_{1}x, \end{aligned}$$
(11)

if \( h(x)=0 \) has two different roots, then we denote them by \( {\underline{x}} \) and \( {\bar{x}} \) with \( {\underline{x}} <{\bar{x}}\), based on this, we address the following result.

Lemma 1

For any \(l,~ \alpha >0\), if one of following conditions holds:

  1. (i)

    \((\beta ,b)\in \mathbf{B }_1\), \(d_1<\alpha \beta u^*\) and \(ru^*-\beta u^* e^{-\alpha \frac{k_H^2}{l^2} }-d_1\frac{k_H^2}{l^2}>0\), where \( k_H \) is defined as in (13), i.e. the positive integer that maximizes h(x) ;

  2. (ii)

    \((\beta ,b)\in \mathbf{B }_2\), \( d_1>0 \),

then there exists a set \( \varLambda \) such that \(ru^*-\beta u^* e^{-\alpha \frac{k^2}{l^2} }-d_1\frac{k^2}{l^2}>0\) for \( k\in \varLambda \) with

$$\begin{aligned} \varLambda :=\{k\in {\mathbb {N}}_0 \ | \ {\underline{k}} \le k \le {\overline{k}} \}, \end{aligned}$$
(12)

where \( {\underline{k}} ={\left\{ \begin{array}{ll} \lfloor l\sqrt{{\underline{x}}}\rfloor +1, \ \text {{for condition (i)}}\\ \ 0,\ \qquad \ \text {{for condition (ii)}} \end{array}\right. }\), \( {\overline{k}}= \lfloor l\sqrt{{\bar{x}}}\rfloor \), where \( \lfloor \cdot \rfloor \) is the floor function.

Proof

For any \(l,~ \alpha >0\), we claim that \( \varLambda \) is nonempty since at least \( k_H \) or 0 belongs to \( \varLambda \).

For the proof of part (i), \((\beta ,b)\in \mathbf{B }_1\) is equivalent to \( r\le \beta \), according to (11), the derivative of h(x) with respect to x is

$$\begin{aligned} h'(x)=\alpha \beta u^* e^{-\alpha x }-d_1, \end{aligned}$$

if \(d_1<\alpha \beta u^*\), then there exists a unique positive constant \(\frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1} \) such that

$$\begin{aligned} {\left\{ \begin{array}{ll} h'(x)>0,\ \ \ \ \text {for}\ x\in \left( {\underline{x}}, \frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}\right) ,\\ h'(x)=0,\ \ \ \ \text {for} \ x= \frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1},\\ h'(x)<0,\ \ \ \ \text {for} \ x\in \left( \frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}, {\bar{x}}\right) . \end{array}\right. } \end{aligned}$$

Hence h(x) is monotonically increasing in \( ({\underline{x}}, \frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1} ) \) and monotonically decreasing in \( ( \frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}, {\bar{x}})\), and it will attain the maximum at \( \frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1} \). Hence, let \( x=\frac{k^2}{l^2} \), considering \( k\in {\mathbb {N}} \), if \(ru^*-\beta u^* e^{-\alpha \frac{k_H^2}{l^2} }-d_1\frac{k_H^2}{l^2}>0\) with

$$\begin{aligned} k_H:= {\left\{ \begin{array}{ll} \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor , \ \qquad \text {for} \ h\left( \frac{1}{l^2}\left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor ^2\right) > h\left( \frac{1}{l^2}\left( \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor +1\right) ^2\right) ,\\ \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor +1, \ \ \text {for} \ h\left( \frac{1}{l^2}\left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor ^2\right) \le h\left( \frac{1}{l^2}\left( \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor +1\right) ^2\right) ,\\ \end{array}\right. } \end{aligned}$$
(13)

where h(x) defined in (11), \( \lfloor \cdot \rfloor \) is the floor function, then \(ru^*-\beta u^* e^{-\alpha \frac{k^2}{l^2} }-d_1\frac{k^2}{l^2}>0\) for k belongs to \(\{k\in {\mathbb {N}}_0\ | \ {\underline{k}}\le k\le {\bar{k}}\} \).

For the proof of part (ii), \((\beta ,b)\in \mathbf{B }_2\) ia equivalent to \( r> \beta \). It is obviously that \(h(x)=0\) has a unique solutions \( {\bar{x}} \), thus let \( x=\frac{k^2}{l^2} \), \( k\in {\mathbb {N}}_0 \),we have \(ru^*-\beta u^* e^{-\alpha \frac{k^2}{l^2} }-d_1\frac{k^2}{l^2}>0\) for any \(\{k\in {\mathbb {N}}_0\ | \ 0\le k\le {\bar{k}}\} \).

Therefore, if one of the condition (i) and (ii) holds, \(ru^*-\beta u^* e^{-\alpha \frac{k^2}{l^2} }-d_1\frac{k^2}{l^2}>0\) for \( k\in \varLambda \) with \( \varLambda \) defined as in (12). \(\square \)

As the definitions of Hopf, Turing, Turing-Hopf and double-Hopf bifurcations given in [27], corresponding existence conditions can be obtained by the linear stability analysis. Next we will address the existences of Turing and Hopf bifurcation.

Proposition 1

For any \( l,~\alpha ,~d_2>0 \), the following statements hold:

  1. (i)

    If \((\beta ,b)\in \mathbf{B }_1\), \(d_1\ge \alpha \beta u^*\) or \(d_1<\alpha \beta u^*\) and \(ru^*-\beta u^* e^{-\alpha \frac{k_H^2}{l^2} }-d_1\frac{k_H^2}{l^2}\le 0\) with \( k_H \) defined as in (13), then there are no Hopf bifurcations and Turing bifurcations of (5) for all \( c>0 \).

  2. (ii)

    If \((\beta ,b)\in \mathbf{B }_2\), \(d_1\ge ru^*l^2-\beta u^*l^2 e^{-\frac{\alpha }{l^2} }\), then there are no Turing bifurcations of (5) for all \( c>0 \) and only 0-mode Hopf bifurcation occurs for (5) when \( c=ru^*-\beta u^* \) (see Fig. 1a).

Following Lemma 1 and Proposition 1, as \( k_H \) is defined in (13), we can define the following sets

$$\begin{aligned} \begin{aligned} \varSigma _1=\{(\beta ,b,d_1) \ | \&(\beta ,b)\in \mathbf{B }_1, d_1<\alpha \beta u^* \text {and} \ ru^*-\beta u^* e^{-\alpha \frac{k_H^2}{l^2} }-d_1\frac{k_H^2}{l^2}>0\ \\&\text {for any}\ \alpha ,~l>0 \}, \\ \varSigma _2=\{(\beta ,b,d_1) \ | \&(\beta ,b)\in \mathbf{B }_2,~0<d_1< ru^*l^2-\beta u^*l^2 e^{-\frac{\alpha }{l^2} }\ \text {for any}\ \alpha ,~l>0 \}. \end{aligned} \end{aligned}$$
(14)

In the view of (9), we denote

$$\begin{aligned} \begin{aligned} c_k^H(d_2)&:=-d_2 \frac{k^2}{l^2}+r u^*-\beta u^*e^{-\alpha \frac{k^2}{l^2}}-d_1 \frac{k^2}{l^2},\\ c_k^T(d_2)&:=\frac{\left( r u^*-\beta u^*e^{-\alpha \frac{k^2}{l^2}}-d_1 \frac{k^2}{l^2}\right) \frac{k^2}{l^2} d_2}{r +\beta u^*e^{-\alpha \frac{k^2}{l^2}}+d_1 \frac{k^2}{l^2}}, \end{aligned} \end{aligned}$$
(15)

then we can define Hopf and Turing bifurcation curves according to Lemma 1 as follows

$$\begin{aligned} \begin{aligned} {\mathcal {H}}_k: c&=c_k^H(d_2), \ \ 0<d_2<{d_2}_k^M,\ \ {d_2}_k^M=\tfrac{r u^*l^2}{k^2}-\tfrac{\beta u^*l^2}{k^2}e^{-\alpha \frac{k^2}{l^2}}-d_1,\ \ k\in \varLambda , \\ {\mathcal {T}}_k: c&=c_k^T(d_2),\ \ d_2>0,\ \ k\in \varLambda \setminus \{0\}. \end{aligned} \end{aligned}$$
(16)

Next we will establish the existence of Turing bifurcation.

Lemma 2

For any \( l,~\alpha ,~d_2>0 \), if \( (\beta ,b,d_1)\in \varSigma _1\cup \varSigma _2 \), then there exists the unique \( k_T^*\in (\text {max}\{0, \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor \}, {\overline{k}}] \), such that the slop of \({\mathcal {T}}_k \) reaches the maximum at \( k=k_T^* \) with

$$\begin{aligned} k_T^*:= {\left\{ \begin{array}{ll} \kappa , \ \qquad \text {for} \ c_{\kappa }^T(d_2)>c_{\kappa +1}^T(d_2),\\ \kappa +1, \ \ \text {for} \ c_{\kappa }^T(d_2)\le c_{\kappa +1}^T(d_2), \end{array}\right. } \ \ \text {with}\ \kappa =\lfloor l\sqrt{x^*}\rfloor ,\ \end{aligned}$$
(17)

where \( x^* \) is the maximum of f(x) on \( x\in (\text {max}\{0,{\underline{x}}\}, {\bar{x}}) \) with f(x) defined in (18).

Proof

Denote that

$$\begin{aligned} f(x)=\frac{(r u^*-\beta u^*e^{-\alpha x}-d_1 x)x}{r +\beta u^*e^{-\alpha x}+d_1 x},\ \ \end{aligned}$$
(18)

it is obviously equivalent to

$$\begin{aligned} f(x)=\frac{r( 1+u^*)x}{r +\beta u^*e^{-\alpha x}+d_1 x}-x. \end{aligned}$$

Now let

$$\begin{aligned} f_1(x)=\frac{r( 1+u^*)x}{r +\beta u^*e^{-\alpha x}+d_1 x}, \quad f_2(x)=x. \end{aligned}$$

It is easy to derive

$$\begin{aligned} f(x) {\left\{ \begin{array}{ll}>0,\ \ \ \ \text {for} \ \text {max}\{0,{\underline{x}}\}<x<{\bar{x}},\\ =0, \ \ \ \ \text {for} \ x={\bar{x}},\\ < 0, \ \ \ \ \text {for} \ x>{\bar{x}}, \end{array}\right. } \end{aligned}$$

which means \( f'({\bar{x}})<0 \), i.e. \(f'({\bar{x}}) = f_1'({\bar{x}})-f_2'({\bar{x}})<0 \) with \( {\bar{x}} \) defined as in (11). By direct calculations,

$$\begin{aligned} f_1'(x)= & {} \frac{r( 1+u^*)(r+\beta u^*e^{-\alpha x}+\alpha \beta u^*e^{-\alpha x}x)}{(r +\beta u^*e^{-\alpha x}+d_1 x)^2}>0, \quad f_2'(x)=1.\\ f_1''(x)= & {} \frac{-r( 1+u^*)[\alpha ^2\beta u^*e^{-\alpha x}x+2(r+\beta u^*e^{-\alpha x}+\alpha \beta u^*e^{-\alpha x}x)(d_1-\alpha \beta u^*e^{-\alpha x})]}{(r +\beta u^*e^{-\alpha x}+d_1 x)^3}. \end{aligned}$$

The rest of proof is divided into two parts.

  1. (i)

    For \( d_1\ge \alpha \beta u^* \), we just need consider \( x\in (0, {\bar{x}}) \). It is obviously that \( f_1''(x)\le 0 \), \( f_1'(x)>0 \) and \( f_1'(x)\rightarrow 0 \) as \( x\rightarrow +\infty \). In this case, we know that only \((\beta ,b)\in \mathbf{B }_2\) is possible, that is \( r>\beta \), then

    $$\begin{aligned} f_1'(0)=\frac{r(1+u^*)}{r+\beta u^*}>1, \end{aligned}$$

    i.e. \( f'(0)=f_1'(0)-f_2'(0)>0 \), therefore, there exists a unique \( x^*\in (0, {\bar{x}}) \) such that \( f'(x^*)=0\), and f(x) is monotonically increasing on \( [0, x^*) \) and monotonically decreasing on \( (x^*, {\bar{x}}) \).

  2. (ii)

    For \( d_1< \alpha \beta u^* \), we consider \( x\in (\text {max}\{0,{\underline{x}}\}, {\bar{x}}] \) with \( {\underline{x}} \), \( {\bar{x}} \) defined as in (11) and we know that \( r u^*-\beta u^*e^{-\alpha x}-d_1 x>0\). We can compute the derivative of f(x) as

    $$\begin{aligned} \begin{aligned} f'(x)&= \frac{1}{(r +\beta u^*e^{-\alpha x}+d_1 x)^2}\biggl \{(r+\beta u^*e^{-\alpha x} +\alpha \beta u^*e^{-\alpha x}x)[(r u^* -\beta u^*e^{-\alpha x} \\&\quad -d_1 x) +x(\alpha \beta u^*e^{-\alpha x} -d_1)] +x(r u^*-\beta u^*e^{-\alpha x}-d_1 x)(\alpha \beta u^*e^{-\alpha x}-d_1)\biggr \}. \end{aligned} \end{aligned}$$

    Obviously, \( x=\frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1} \) solves \( d_1-\alpha \beta u^*e^{-\alpha x}= 0 \). When \( x\in (\text {max}\{0,{\underline{x}}\} ,\frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}] \), we have

    $$\begin{aligned} \alpha \beta u^*e^{-\alpha x}-d_1\ge 0, \end{aligned}$$

    hence \( f'(x)>0 \) in \( x\in (\text {max}\{0,{\underline{x}}\},\frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}] \). When \(x \in (\frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1},{\bar{x}}) \), under this condition \( \alpha \beta u^*e^{-\alpha x}-d_1< 0 \), by utilizing the same argument as the part (i), we can prove that there exists a unique \( x^*\in (\frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}, {\bar{x}}) \) such that \( f'(x^*)=0\), and f(x) is monotonically increasing on \( [\frac{1}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}, x^*) \) and monotonically decreasing on \( [x^*, {\bar{x}}) \).

In conclusion, let \( x=\frac{k^2}{l^2} \), above results imply that for any \( d_2>0 \), \( c_k^T(d_2) \) reaches its maximum in \( (\text {max}\{0, \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor \}, {\overline{k}}] \), denoted by \( k_T^* \) and it is monotonically increasing on \( (\text {max}\{0, {\underline{k}}\}, k_T^*) \) and monotonically decreasing on \( (k_T^*, {\bar{k}}] \).

\(\square \)

Subsequently, we denote the intersection of \( c_i^H(d_2) \) and \( c_j^H(d_2) \) by \( (d_2^{i,j}, c^H_{i,j} ) \) for \( i,~j \in \varLambda \), where

$$\begin{aligned} d_2^{i,j} := \frac{\beta u^*\left( e^{-\alpha \frac{i^2}{l^2}}-e^{-\alpha \frac{j^2}{l^2}}\right) }{\frac{j^2}{l^2}-\frac{i^2}{l^2}}-d_1,\quad c^H_{i,j}:=c_i^H(d_2^{i,j}), \end{aligned}$$
(19)

and denote the the intersection of \( c_k^H(d_2) \) and \( c_{k^*_T}^T(d_2) \) by \( (d_2^{k}, c_k^H({d_2}_{k}^*) ) \) with \( k \in \varLambda \) and \( k^*_T \) defined as in Lemma 2, where

$$\begin{aligned} \begin{aligned} {d_2}_{k}^*:=\frac{\left( r u^*-\beta u^*e^{-\alpha \frac{{k}^2}{l^2}}-d_1 \frac{{k}^2}{l^2}\right) \left( r +\beta u^*e^{-\alpha \frac{{k_T^*}^2}{l^2}}+d_1 \frac{{k_T^*}^2}{l^2}\right) }{\left( r +\beta u^*e^{-\alpha \frac{{k_T^*}^2}{l^2}}+d_1 \frac{{k_T^*}^2}{l^2}\right) \frac{{k}^2}{l^2}+\left( r u^*-\beta u^*e^{-\alpha \frac{{k_T^*}^2}{l^2}}-d_1 \frac{{k_T^*}^2}{l^2}\right) \frac{{k_T^*}^2}{l^2}}. \end{aligned} \end{aligned}$$
(20)

It is well known that Turing bifurcations can theoretically interpret the emergence of nonconstant steady state solutions. As in Theorem 1, the system (5) will undergo \( k_T^* \)-mode Turing bifurcation at first, and other Turing bifurcations can also occurs near the equilibrium for \( k\in \varLambda \setminus \{0, k_T^*\} \), but the bifurcating solutions must be unstable since there have been unstable flows. Moreover, when the condition \(c_{\kappa }^T=c_{\kappa +1}^T\) holds, more generally, when \( c_{k_1}^{T}=c_{k_2}^{T} \) for \( k_1,k_2 \in \varLambda \), \( (k_1,k_2) \)-mode Turing-Turing bifurcation for the system (5), in this situation the parameter \( d_2 \) is not enough to describe the existence of Turing-Turing bifurcation, it can be further study thus we ignore this case in following discussions. Our next theorem determines the first Turing bifurcation.

Theorem 1

For any \(l,~\alpha >0\), if \( (\beta ,b,d_1)\in \varSigma _1\cup \varSigma _2 \), \( c_{\kappa }^T\not = c_{\kappa +1}^T \), then for \( d_2>0 \), \( d_2\not ={d_2}_{k}^* \), the system (5) undergoes a \( k^*_T \)-mode Turing bifurcation near \(( u^*, v^*) \) at \( c=c_{k^*_T}^{T} ({d_2})\) (see Figs. 1b–e), where \( c_{k^*_T}^{T} ({d_2}) \), \( \kappa \), \( {d_2}_{k}^* \) are defined as in (15), (17) and (20), respectively.

Proof

If \( (\beta ,b,d_1)\in \varSigma _1\cup \varSigma _2 \), by (9), (15) and (16), we know that \( D_k(c_k^T(d_2))=0 \) for \( d_2>0 \), \( k\in \varLambda \), in particular, \( D_{k^*_T}(c_{k^*_T}^T(d_2))=0 \). Since \( c_{k^*_T}^T({d_2}_{k}^*)=c_{k}^H({d_2}_{k}^*) \) when \(d_2={d_2}_{k}^* \), that implies \( T_{k}(c_{k}^H({d_2}_{k}^*))=0 \), hence when \( d_2>0 \), \( d_2\not ={d_2}_{k}^* \), we have

$$\begin{aligned} D_{k^*_T}(c_{k^*_T}^T(d_2))=0 \ \ \text {and}\ \ T_{k}(c_{k^*_T}^H({d_2}))\not =0,\ \ k\in \varLambda . \end{aligned}$$

By utilizing Lemma 2, for any \( k\in \varLambda \), \( k\not =k^*_T \) and \( d_2>0 \), we know that \( c_{k^*_T}^T(d_2)> c_k^T(d_2) \) , then

$$\begin{aligned} D_k(c_{k^*_T}^T(d_2))<D_{k^*_T}(c_{k^*_T}^T(d_2))=0, \end{aligned}$$

provided by \( c_{\kappa }^T\not = c_{\kappa +1}^T \). Therefore, \( {\mathcal {P}}_{k_T^*}(\lambda )=0 \) has a simple zero eigenvalue, all other eigenvalues have nonzero real parts.

Moreover, suppose that \(\lambda (c)=\alpha (c)+i\gamma (c) \) is a complex root of the characteristic equation \( P_{k_T^*}(\lambda )=0 \) near \( c=c_{k_T^*}^{T}(d_2) \) with \( \alpha (c_{k_T^*}^{T}(d_2))=0, \gamma (c_{k_T^*}^{T}(d_2))=0\). By direct calculations,

$$\begin{aligned} \frac{\partial \alpha (c_{k^*_T}^{T}(d_2))}{\partial c}= \frac{r+\beta u^*e^{-\alpha \tfrac{{k^*_T}^{2}}{l^{2}}}+d_{1}\tfrac{{k^*}^{2}}{l^{2}}}{T_{k^*_T}(c_{k^*}^{T}(d_2))}\not =0, \end{aligned}$$
(21)

i.e. the transversality condition holds. Therefore, system (5) undergoes a \( k^*_T \)-mode Turing bifurcation near \(( u^*, v^*) \) at \( c=c_{k^*_T}^{T} ({d_2})\) \(\square \)

Next we will concern the existence of Hopf bifurcation.

Theorem 2

For any \( l,~\alpha >0\), if \( (\beta ,b,d_1)\in \varSigma _1\), then system (5) undergoes a k-mode Hopf bifurcation near \(( u^*, v^*) \) at \( c=c_{k}^{H} (d_2)\) for \( 0<d_2<{d_2}_{k}^* \), \( d_2\not =d_2^{k,j} \) with \(k, j~\in \varLambda \) (see Fig. 1b,c). Moreover the bifurcating periodic orbits are spatially nonhomogeneous, where \( \varLambda ,~c_k^H(d_2)\), \( {d_2}_k^* \), \(d_2^{k,j} \) are defined as in (12), (15), (19) respectively.

Proof

For any \( l,~\alpha >0\), when \( (\beta ,b,d_1)\in \varSigma _1\), by Lemma 1, \( c_k^H(d_2)>0 \) \( 0<d_2<\tfrac{r u^*l^2}{k^2}-\tfrac{\beta u^*l^2}{k^2}e^{-\alpha \frac{k^2}{l^2}}-d_1\) for \( k\in \varLambda \). \((\beta ,b)\in \mathbf{B }_1\) is equivalent to \( r\le \beta \), in view of \( c_k^H(d_2) \) in (15), we know \( c_0^H(d_2)=ru^*-\beta u^*\le 0 \), i.e. there is no 0-mode Hopf bifurcation.

Let \( T_k(c)=0 \), we obtain \( c=c_{k}^{H}(d_2) \) with \(c_{k}^{H}(d_2)\) defined as in (15), which means for each \( k\in \varLambda \), \(T_k(c_{k}^{H}(d_2))=0 \), and \( (d_2^{k,j}, c^H_{k,j} ) \) is the unique intersection of \( c_{k}^{H}(d_2) \) and \( c_{j}^{H}(d_2) \), which is defined as in (19) with \( 0<d_2^{k,j}< {d_2}_k^M \), then for the case of \( d_2^{k,j}>0 \), we know that \( T_k(c_{k}^{H}(d_2^{k,j}))=T_j(c_{j}^{H}(d_2^{k,j}))=0 \). Hence, if \( 0<d_2<{d_2}_{k}^* \) and \( d_2\not =d_2^{k,j} \) with \( d_2^{k,j}>0 \), then \( T_j(c_{k}^{H}(d_2))\not =0\) for any \( j\in \varLambda \).

On the other hand, by direct calculation, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} c_{k}^{H}(d_2)>c_{k^*_T}^{T} (d_2), \qquad \text {for}\ 0<d_2<{d_2}_{k}^*,\\ c_{k}^{H}(d_2)=c_{k_T^*}^{T} (d_2), \qquad \text {for}\ d_2={d_2}_{k}^*,\\ c_{k}^{H}(d_2)<c_{k_T^*}^{T} (d_2), \qquad \text {for}\ d_2>{d_2}_{k}^*, \end{array}\right. } \end{aligned}$$
(22)

where \( {d_2}_{k}^* \) is defined as in (20). By Lemma 2, we know that if \( c>c_{k^*_T}^T(d_2) \) for \( d_2>0\), then \(D_j(c)>0 \) for any \(j\in \varLambda \). Thus if \(0<d_2<{d_2}_{k^*}^k\), then \(D_j(c_k^H(d_2))>0 \) for any \(j\in \varLambda \).

Therefore, all other eigenvalues of \( {\mathcal {P}}_{k}(\lambda )=0 \) have nonzero real parts, except a pair of purely imaginary eigenvalues. Moreover, suppose \(\lambda (c)=\alpha (c)\pm i\omega (c) \) is a pair of roots of characteristic equations \( {\mathcal {P}}_{k}(\lambda ) =0\) near \( c=c_{k}^{H}(d_2) \) with \( \alpha (c_{k}^{H}(d_2))=0, \omega (c_{k}^{H}(d_2))>0\), the transversality condition holds, since

$$\begin{aligned} \frac{\partial \alpha (c_{k}^{H})}{\mathrm {d}c}=\frac{1}{2}\frac{\partial T_k(c_{k}^{H})}{\partial c}=-\frac{1}{2}<0. \end{aligned}$$
(23)

The proof is complete. \(\square \)

Theorem 3

For any \(l,~\alpha >0\), if \( (\beta ,b,d_1)\in \varSigma _2 \), then the followings hold:

  1. (i)

    If \( d_1> \alpha \beta u^*e^{-\frac{\alpha }{l^2}}\), then when \( 0<d_2<{d_2}_{k}^* \) for \( k\in \varLambda \) then system (5) undergoes a k-mode Hopf bifurcation near \(( u^*, v^*) \) at \( c=c_{k}^{H} (d_2)\) (see Fig. 1d), where \( \varLambda ,~c_k^H(d_2)\) are defined as in (12), (15) respectively.

  2. (ii)

    If \(0< d_1\le \alpha \beta u^*e^{-\frac{\alpha }{l^2}}\), then when \( 0<d_2<{d_2}_{k}^* \) and \( d_2\not =d_2^{k,j} \) for \(k,~ j\in \varLambda \) with \( 0<d_2^{k,j}< {d_2}_k^M \), then system (5) undergoes a k-mode Hopf bifurcation near \(( u^*, v^*) \) at \( c=c_{k}^{H} (d_2)\) (see Fig. 1e), where \( \varLambda ,~c_k^H(d_2) \), \( {d_2}_k^M \), \(d_2^{k,j} \) are defined as in (12), (15), (19) respectively.

Moreover, the bifurcating periodic orbit is spatially homogeneous for \( k=0 \) and spatially nonhomogeneous for \( k\not =0 \).

Proof

For any \(l>0\) and \((\beta ,b)\in { \mathbf{B }_2} \), we know \(r>\beta \), i.e. \(c_0^H(d_2)>0\). In view of \( c_k^H(d_2) \) in (15), we can obtain

$$\begin{aligned} c_k^H(0)=ru^*-\beta u^* e^{-\alpha \frac{k^2}{l^2}}-d_1\frac{k^2}{l^2}, \end{aligned}$$

then

$$\begin{aligned} \frac{\text {d}c_k^H(0)}{\text {d}(\tfrac{k^2}{l^2})}=\alpha \beta u^*e^{-\alpha \frac{k^2}{l^2}}-d_1. \end{aligned}$$
(24)

It is easy to verify that \(\alpha \beta u^*e^{-\frac{\alpha }{l^2}}< ru^*l^2-\beta u^*l^2 e^{-\frac{\alpha }{l^2} } \), so the rest of the proof is divided into two parts.

For the proof of part (i), if \( d_1> \alpha \beta u^*e^{-\frac{\alpha }{l^2}}\), then \( \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor \le 0\), thus for any \( k\in \varLambda \), \( c_k^H(0) \) is monotonically decreasing with respect to k. Moreover, since \( c_0^H(d_2)>0 \), \( (\beta ,b,d_1)\in \varSigma _2 \) and the slop of \( c_k^H(d_2) \) is monotonically decreasing, so \( c_{k+1}^H(d_2)<c_k^H(d_2) \) for each \( k\in \varLambda \).

By (9), \( T_k(c_k^H(d_2))=0 \), \( D_0(c_k^H(d_2))>0 \). If \( 0<d_2<{d_2}_{k}^* \), then by the monotonicity of \( c_k^H(d_2) \), \( T_j(c_k^H(d_2))\not =0 \) for any \( j\in \varLambda ,~j\not =k \). On the other hands, according to (22), we derive \(D_j(c_k^H(d_2))>0 \) for any \(j\in \varLambda \). Therefore, \( {\mathcal {P}}_{k}(\lambda )=0 \) has a pair of purely imaginary eigenvalues and all other eigenvalues have nonzero real parts, the transversality condition is satisfied as well by (23).

For the proof of part (ii), If \( 0<d_1\le \alpha \beta u^*e^{-\frac{\alpha }{l^2}}\), then \( \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor > 0\). Since \( c_0^H(d_2)>0 \), thus for any \( k\in \varLambda \), \( c_k^H(0) \) is monotonically increasing for \( 0\le k\le \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor \), and monotonically increasing for \( \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor <k\le {\bar{k}}\). Similarly, the slop of \( c_k^H(d_2) \) is monotonically decreasing with k, then there exists some \( j \in \varLambda \), \( j\not =k \) such that \( 0<d_2^{k,j}< {d_2}_k^M \) and \( T_k(c_{k}^{H}(d_2^{k,j}))=T_j(c_{j}^{H}(d_2^{k,j}))=0 \). Therefore, if \( 0<d_2<{d_2}_{k}^* \) and \( d_2\not =d_2^{k,j} \) for \(k,~ j\in \varLambda \) with \( 0<d_2^{k,j}< {d_2}_k^M \), then by using the similar argument as the Proof of Theorem 2, we can prove that all other eigenvalues of the characteristic equation \( {\mathcal {P}}_{k}(\lambda )=0 \) have nonzero real parts, except a pair of purely imaginary eigenvalues, and the transversality condition holds. \(\square \)

2.2 Turing-Hopf Bifurcation and Double-Hopf Bifurcation

In this subsection, we consider the interactions of Turing and Hopf bifurcations and derive sufficient conditions for the existence of Turing-Hopf bifurcation and double-Hopf bifurcation. First we define the following notation

$$\begin{aligned} k^*_H:=\text {max}\{k\in \varLambda \ | \ {d_2}_k^*\ \text {attains the maximum in}\ \varLambda \ \text {with} \ {d_2}_k^* >0\}. \end{aligned}$$
(25)

Remark 1

We can assert that \( k^*_H \) defined as in (25) satisfies \( k^*_H\le k_H \) with \( k_H \) defined in (13), since when \( k\in \varLambda , ~ k\ge k_H\), \( c_k^H(d_2) \) is monotonically decreasing for any \( d_2>0 \) as the argument in Theorem 3, this means all \( c_k^H(d_2) \) for any \( k\in \varLambda ,~k> k_H \) completely lay below \( c_{k_H}^H(d_2) \).

Theorem 4

For any \( l,~\alpha >0\), if \( (\beta ,b,d_1)\in \varSigma _1\), \( c_{\kappa }^T\not = c_{\kappa +1}^T \), \( k^*_H \) is defined as in (25), then the following hold:

  1. (i)

    The system (5) undergoes a \( (k^*_T,k^*_H) \)-mode Turing-Hopf bifurcation near \(( u^*, v^*) \) at \( (d_2,c)=({d_2}^{*}, c^* ) \), provided by \( k^*_T\not =k^*_H \) and \( {d_2}^{*}\not =d_2^{k^*_H,k^*_H+1} \) (see Fig. 1b, c), where

    $$\begin{aligned} {d_2}^{*}:={d_2}_{k^*_H}^{*},\quad c^*:=c_{k^*_H}^H({d_2}_{k^*_H}^{*}). \end{aligned}$$
    (26)

    Moreover, the real parts of other eigenvalues for the characteristic Eq. (8) are negative except a pair of purely imaginary eigenvalues and a simple zero eigenvalue.

  2. (ii)

    If \( {k}_H^*<k_H \), the system (5) undergoes a \( (k,k+1) \)-mode double-Hopf bifurcation near \(( u^*, v^*) \) at \( (d_2,c)=(d_2^{k,k+1}, c^H_{k,k+1} ) \) for all \( k\in \varLambda ,~ k^*_H\le k< k_H\) (see Fig. 1b,c), where \(d_2^{k,k+1}, ~ c^H_{k,k+1} \) are defined as (19). Moreover, the real parts of other eigenvalues for the characteristic Eq. (8) are negative except two pairs of purely imaginary eigenvalues. In particular, there is no double-Hopf bifurcation if \( {k}_H^*=k_H \).

Proof

If \( (\beta ,b,d_1)\in \varSigma _1\), then \( r\le \beta \), i.e. \( c_0^H(d_2)\le 0 \) for any \( d_2>0 \). For the proof of part (i), denote

$$\begin{aligned} {d_2}^{*}:={d_2}_{k^*_H}^{*},\quad c^*:=c_{k^*_H}^H({d_2}_{k^*_H}^{*}). \end{aligned}$$

By Theorem 2, we know that \((d_2,c)=({d_2}^{*}, c^{*})\), and for each \( k\in \varLambda \),

$$\begin{aligned} T_k({d_2}^{*}, c^{*})<T_{k^*_H}({d_2}^{*}, c^{*})=0. \end{aligned}$$
(27)

In addition, since \( c_{\kappa }^T\not = c_{\kappa +1}^T \), applying Theorem 1, we derive that when \((d_2,c)=({d_2}^{*}, c^{*})\), for \( k\in \varLambda \)

$$\begin{aligned} D_k({d_2}^{*}, c^{*})>D_{k^*_T}({d_2}^{*}, c^{*})=0, \end{aligned}$$
(28)

As results of \( k^*_T\not =k^*_H \) and \( {d_2}^{*}\not =d_2^{k,k+1} \), when \( (d_2,c)=({d_2}^{*}, c^{*}) \), \({\mathcal {P}}_{k^*_H}(\lambda )=0\) has two purely imaginary roots, and \({\mathcal {P}}_{k^*_T}(\lambda )=0\) has a zero eigenvalue. Moreover, (27) and (28) also imply that \( T_k({d_2}^{*}, c^{*})<0,\ D_k({d_2}^{*}, c^{*})>0 \) for each \( k\in \varLambda \), \( k\not =k^*_H,~ k^*_T \), i.e. all the eigenvalues of \({\mathcal {P}}_{k}(\lambda )=0\) for \( k\in \varLambda \), \( k\not =k^*_H,~ k^*_T \) have negative real part, and the transversality conditions hold via (23) and (21). Therefore, system (5) undergoes \( (k^*_T,k^*_H) \)-mode Turing-Hopf bifurcation near \(( u^*, v^*) \) when \( (d_2,c)=({d_2}^{*}, c^* ) \).

For the proof of part (ii), as in (19), by setting \( x=\frac{i^2}{l^2} \), \( y=\frac{j^2}{l^2} \) we define g(x, y) as

$$\begin{aligned} g(x,y)=\frac{\beta u^*(e^{-\alpha x}-e^{-\alpha y}) }{y-x}-d_1, \end{aligned}$$

then for fixed \( y>0 \),

$$\begin{aligned} \frac{\partial g(x,y)}{\partial x}= \frac{-\alpha \beta u^*e^{-\alpha x}(y-x)+\beta u^*(e^{-\alpha x}-e^{-\alpha y}) }{(y-x)^2}, \end{aligned}$$

by direct calculation, when \( y\ge x \),

$$\begin{aligned} \begin{aligned}&-\alpha \beta u^*e^{-\alpha x}(y-x)+\beta u^*(e^{-\alpha x}-e^{-\alpha y})\\&\quad =\beta u^*e^{-\alpha x}[-\alpha (y-x)+1-e^{-\alpha (y-x)}]\le 0, \end{aligned} \end{aligned}$$

thus \( \frac{\partial g(x,y)}{\partial x}\ge 0 \) when \( y\ge x \), which implies that \( d_2^{i,j} \) is monotonically decreasing with \( i\in \varLambda \) for fixed j. Similarly, it can be proved that \( d_2^{i,j} \) is monotonically decreasing with \( j\in \varLambda \) for fixed i. As a consequence,

$$\begin{aligned} d_2^{k-1,k}>d_2^{k,k+1}>d_2^{k+1,k+2}, \ \text {for}\ k\in \varLambda \setminus \{0\}, \end{aligned}$$
(29)

and \( (d_2^{k,k+1}, c_{k,k+1}^H) \) is the first double-Hopf bifurcation point as \( (d_2,c) \) crosses \( {\mathcal {H}}_k \) from top to bottom. For each \( k\in \varLambda \), if \( {k}_H^*=k_H \), then \( D_k(d_2^{k,k+1}, c_{k,k+1}^H)<0 \) for any \( k\in \varLambda \), this implies double-Hopf bifurcation can not occur. If \( {k}_H^*<k_H \), for \( k\le k^*_H\), then \( d_2^{k,k+1}<{d_2}^*\), by (9), (15), (19) and Lemma 2, we obtain

$$\begin{aligned}&T_k(d_2^{k,k+1}, c_{k,k+1}^H)=0, \ \ \ D_k(d_2^{k,k+1}, c_{k,k+1}^H)>0,\\&T_{k+1}(d_2^{k,k+1}, c_{k,k+1}^H)=0, \ \ \ D_{k+1}(d_2^{k,k+1}, c_{k,k+1}^H)>0, \end{aligned}$$

and for any \( j\in \varLambda ,~j\not = k,k+1 \),

$$\begin{aligned}&T_j(d_2^{k,k+1}, c_{k,k+1}^H)\le T_k(d_2^{k,k+1}, c_{k,k+1}^H)=0,\\&D_j(d_2^{k,k+1}, c_{k,k+1}^H)>D_k(d_2^{k,k+1}, c_{k,k+1}^H)>0. \end{aligned}$$

Therefore, when \( (d_2,c)=(d_2^{k,k+1}, c_{k,k+1}^H) \), both of \({\mathcal {P}}_{k}(\lambda )=0\) and \({\mathcal {P}}_{k+1}(\lambda )=0\) have two pairs of purely imaginary roots, all the other eigenvalues of \({\mathcal {P}}_{j}(\lambda )=0\) for \( j\in \varLambda \), \( j\not =k\) have negative real part, and the transversality conditions hold via (23). Therefore, system (5) undergoes \( (k,k+1) \)-mode double-Hopf bifurcation near \(( u^*, v^*) \) when \( (d_2,c)=(d_2^{k,k+1}, c_{k,k+1}^H) \). \(\square \)

Theorem 5

For any \( l,~\alpha >0\), if \( (\beta ,b,d_1)\in \varSigma _2\) and \( d_1> \alpha \beta u^*e^{-\frac{\alpha }{l^2}}\), \( c_{\kappa }^T\not = c_{\kappa +1}^T \), \( k^*_H \) is defined as in (25), then the followings hold:

  1. (i)

    The system (5) undergoes a \( (k^*_T,0) \)-mode Turing-Hopf bifurcation near \(( u^*, v^*) \) at \( (d_2,c)=({d_2}^{*}, c^* ) \), where \( {d_2}^{*}, ~c^* \) are defined as in (26) with \( k^*_H=0 \) (see Fig. 1d). Moreover, the real parts of other eigenvalues for the characteristic Eq. (8) are negative except a pair of purely imaginary eigenvalues and a simple zero eigenvalue.

  2. (ii)

    There is no double-Hopf bifurcation of system (5) for any \( d_2>0, ~c>0 \).

Proof

If \( (\beta ,b,d_1)\in \varSigma _2\) and \( d_1> \alpha \beta u^*e^{-\frac{\alpha }{l^2}}\), then \( c_0^H(d_2)>0 \), as a consequence of Theorem 3-(i), for any \( k\in \varLambda \), \( c_{k+1}^H(d_2)<c_k^H(d_2)<c_0^H(d_2)\) since \( c_k^H(0) \) is monotonically decreasing with k, which means for any \( i,j\in \varLambda \), \( c_i^H(d_2) \) and \( c_j^H(d_2) \) can not intersect for any \( d_2>0 \). Therefore, There is no double-Hopf bifurcation of system (5) for any \( d_2>0, ~c>0 \).

In addition, by Lemma 2 and Theorem 1, we know that when \( (d_2,c)=({d_2}^{*}, c^* ) \) with \( {d_2}^{*}, ~c^* \) defined as (26) for \( k^*_H=0 \), for each \( k\in \varLambda \),

$$\begin{aligned} T_k({d_2}^{*}, c^{*})<T_{0}({d_2}^{*}, c^{*})=0. \end{aligned}$$

and

$$\begin{aligned} D_k({d_2}^{*}, c^{*})>D_{k^*_T}({d_2}^{*}, c^{*})=0. \end{aligned}$$

So the characteristic equation \({\mathcal {P}}_{0}(\lambda )=0\) has two purely imaginary roots, \({\mathcal {P}}_{k^*_T}(\lambda )=0\) has a zero eigenvalue, and for \( k\in \varLambda \), \( k\not =0,~ k^*_T \), all the eigenvalues of \({\mathcal {P}}_{k}(\lambda )=0\) have negative real part. Furthermore, the transversality conditions hold via (23) and (21). Therefore, system (5) undergoes \( (k^*_T,0) \)-mode Turing-Hopf bifurcation near \(( u^*, v^*) \). \(\square \)

Theorem 6

For any \( l,~\alpha >0\), if \( (\beta ,b,d_1)\in \varSigma _2\) and \( 0<d_1\le \alpha \beta u^*e^{-\frac{\alpha }{l^2}}\), \( c_{\kappa }^T\not = c_{\kappa +1}^T \), \( k^*_H \) is defined as in (25), then the followings hold:

  1. (i)

    The system (5) undergoes a \( (k^*_T,k^*_H) \)-mode Turing-Hopf bifurcation near \(( u^*, v^*) \) at \( (d_2,c)=({d_2}^{*}, c^* ) \), provided by \( k^*_T\not =k^*_H \) and \( {d_2}^{*}\not =d_2^{k,k+1} \) with \( k=k^*_H \) (see Fig. 1e), where \( {d_2}^{*}, ~c^* \) are defined as (26). Moreover, the real parts of other eigenvalues for the characteristic Eq. (8) are negative except a pair of purely imaginary eigenvalues and a simple zero eigenvalue.

  2. (ii)

    If \( {k}_H^*<k_H \), system (5) undergoes a \( (k,k+1) \)-mode double-Hopf bifurcation near \(( u^*, v^*) \) at \( (d_2,c)=(d_2^{k,k+1}, c^H_{k,k+1} ) \) for all \( k\in \varLambda ,~ k^*_H\le k< k_H\) (see Fig. 1e), where \(d_2^{k,k+1}, ~ c^H_{k,k+1} \) are defined as (19). Moreover, the real parts of other eigenvalues for the characteristic equation (8) are negative except two pairs of purely imaginary eigenvalues. In particular, there is no double-Hopf bifurcation if \( {k}_H^*=k_H \).

Proof

The part (i) can be proved by utilizing the same argument as the Proof of Theorem 4-(i), we omit here.

For the proof of part (ii), the case of \( k^*_H=k_H \) is simple, we just give the proof for \( k^*_H<k_H \). If \( (\beta ,b,d_1)\in \varSigma _2\) and \( 0<d_1\le \alpha \beta u^*e^{-\frac{\alpha }{l^2}}\), then \( c_0^H(d_2)>0 \), as a consequence of Theorem 3-(ii), then \( \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor > 0\), for \( k\in \varLambda \), \( c_k^H(0) \) is monotonically increasing for \( 0\le k< \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor \), and monotonically increasing for \( \left\lfloor \sqrt{\frac{l^2}{\alpha }\text {ln}\frac{\alpha \beta u^*}{d_1}} \right\rfloor <k\le {\bar{k}}\), and there exists \( d_2^{k,k+1}>0 \) for each \( k\in \varLambda ,~ k^*_H\le k< k_H\). Similar to the proof of Theorem 4-(ii), we can derive that when \( (d_2,c)=(d_2^{k,k+1}, c_{k,k+1}^H) \), both of \({\mathcal {P}}_{k}(\lambda )=0\) and \({\mathcal {P}}_{k+1}(\lambda )=0\) have two pairs of purely imaginary roots, and all the eigenvalues of \({\mathcal {P}}_{j}(\lambda )=0\) for \( j\in \varLambda \), \( j\not =k\) have negative real part. Furthermore, the transversality conditions can be verified by (23), therefore, system (5) undergoes \( (k,k+1) \)-mode double-Hopf bifurcation near \(( u^*, v^*) \) when \( (d_2,c)=(d_2^{k,k+1}, c_{k,k+1}^H) \). \(\square \)

Remark 2

Theorems 4 and 6 exhibit similar results on the existences of Turing-Hopf bifurcation and double-Hopf bifurcation, nevertheless, there still exist some major differences, i.e. under the conditions in Theorem 4, 0-mode Hopf bifurcation is nonexistent, that is \( k^*_H\not =0 \), this means all bifurcating solutions through Turing-Hopf or double-Hopf bifurcations are spatially nonhomogeneous. In particular, they could have more than two spatial peaks.

Remark 3

In Theorems 4–6, we neglect the situation of \(k^*_H =k^*_T\) and \( {d_2}^{*}=d_2^{k,k+1} \). Actually, if \(k^*_H =k^*_T\), we can claim that a Bogdanov-Takens may occur for the system (5) when parameter cross some critical values. If \( {d_2}^{*}=d_2^{k,k+1} \), the system (5) may undergoes a more highly degenerated Turing-double-Hopf bifurcation. We will not give more corresponding investigations in this paper.

Fig. 1
figure 1

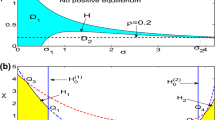
Graphs (a)–(e) characterize the stable and unstable regions of the positive equilibrium in \( (d_2,c) \)- plane, which correspond to Corollary 1-(ii)(iii). Where TH represents Turing-Hopf bifurcation point, HH represents double-Hopf bifurcation point, \( {\mathcal {H}}_k \) and \( {\mathcal {T}}_k \) for integer k are Hopf and Turing bifurcation curves defined as in (16), respectively

Full size image

The existences criteria for Hopf, Turing, Turing-Hopf and double-Hopf bifurcation are contribute to further characterize the stability of the unique positive equilibrium. For the sake of comparing to the case of the spatial average kernel in [27], we define the first Hopf bifurcation curve \( {\mathcal {C}}^{H} \) for \( (\beta ,b,d_1)\in \varSigma _1\cup \varSigma _2 \), it is given by

$$\begin{aligned} {\mathcal {C}}^{H}(d_{2}) := {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} c_{k_H}^{H}(d_{2}),\quad 0<d_{2}\le d_2^{k_H-1,k_H},\\ c_{k}^{H}(d_{2}),\ \quad d_2^{k,k+1}<d_{2}<d_2^{k-1,k} \ \text {for}\ k\in \varLambda , \ k^*_H<k< k_H, \\ c_{k^*_H}^{H}(d_{2}),\quad d_2^{k^*_H,k^*_H+1}\le d_{2}<{d_2}^*, \end{array}\right. } \text {if} \ k^*_H<k_H-1,\\ {\left\{ \begin{array}{ll} c_{k_H}^{H}(d_{2}),\quad 0<d_{2}\le d_2^{k_H-1,k_H},\\ c_{k^*_H}^{H}(d_{2}),\quad d_2^{k_H-1,k_H}< d_{2}<{d_2}^*, \end{array}\right. } \qquad \qquad \qquad \qquad \qquad \qquad \text {if} \ k^*_H=k_H-1,\\ \ c_{k_H}^{H}(d_{2}),\ \ \quad 0<d_{2}< d_2^{*}, \ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \ \ \ \text {if} \ k^*_H=k_H, \end{array}\right. }\nonumber \\ \end{aligned}$$
(30)

then we define the following sets in the first quadrant of \(( d_{2},c) \)-plane:

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_{1}&:=\{(d_{2},c)\in {\mathbb {R}}_{+}^{2}\ |\ c>c_{0}^{H}(d_{2})\ \mathrm {for}\ d_{2}>0\},\\ {\mathcal {S}}_{2}&:=\{(d_{2},c)\in {\mathbb {R}}_{+}^{2}\ |\ c>{\mathcal {C}}^{H}(d_{2})\ \mathrm {for}\ 0<d_{2}<{d_2}^*\ \mathrm {and}\ c>c_{k^{*}_T}^{T}(d_{2})\ \mathrm {for}\ d_{2}\ge {d_2}^*\}. \end{aligned} \end{aligned}$$

As consequences of Proposition 1, Theorems 2, 3, 1 and 4–6, the stability of the positive equilibrium can be determined as follows:

Corollary 1

Denote the closure of \({\mathcal {S}}_{i}\) by \(\overline{{\mathcal {S}}_{i}}\), \(1\le i \le 2\), \( k_H \) is defined as in (13). For any \( l, \alpha >0\), the following statements hold:

  1. (i)

    If \((\beta ,b)\in \mathbf{B }_1\), \(d_1\ge \alpha \beta u^*\) or \(d_1<\alpha \beta u^*\) and \(ru^*-\beta u^* e^{-\alpha \frac{k_H^2}{l^2} }-d_1\frac{k_H^2}{l^2}\le 0\), then \( ( u^*,v^*) \) is locally asymptotically stable;

  2. (ii)

    If \((\beta ,b)\in \mathbf{B }_2\), \( d_1\ge ru^*l^2-\beta u^*l^2 e^{-\frac{\alpha }{l^2} }\), then \( ( u^*,v^*) \) is locally asymptotically stable for \( (d_{2},c)\in {\mathcal {S}}_{1} \) and unstable for \( (d_{2},c)\in \ {\mathbb {R}}_{+}^{2}\backslash \overline{{\mathcal {S}}_{1} }\);

  3. (iii)

    If \( (\beta ,b,d_1)\in \varSigma _1\cup \varSigma _2 \), then \( ( u^*,v^*) \) is locally asymptotically stable for \( (d_{2},c)\in {\mathcal {S}}_{2} \) and unstable for \( (d_{2},c)\in \ {\mathbb {R}}_{+}^{2}\backslash \overline{{\mathcal {S}}_{2} }\).

We provide respective figures in \( (d_2,c) \)-plane to illustrate Corollary 1; see Fig. 1, where the colored regions match with the stable parameter regions of \( (u^*,v^*) \), and Fig. 1 can also be used to illustrate Proposition 1,Theorems 1–3 and 4–6.

Remark 4

To explore the effect of the kernels on the spatio-temporal dynamics of the system (3), we review the situation of (3) with the spatial average kernel,

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=d_{1}u_{xx}+u\Big (1-\dfrac{\beta }{l\pi } \displaystyle \int _{0}^{l\pi } u(y,t)\,\mathrm {d}y\Big )-\dfrac{buv}{u+1},&{}x\in (0, l\pi ),\,t>0,\\ v_t=d_{2}v_{xx}+cv\left( 1-\dfrac{v}{u}\right) , &{}x\in (0, l\pi ),\,t>0,\\ u_{x}(0, t)=v_{x}(0, t)=0,\quad u_{x}(l\pi , t)=v_{x}(l\pi , t)=0, &{}t>0,\\ u(x, 0)=u_{0}(x)>0, \quad v(x, 0)=v_{0}(x)>0. \end{array}\right. } \end{aligned}$$
(31)

In [27], if the positive equilibrium of (31) loses the stability through Hopf bifurcation, which only can be 0-mode Hopf or 1-mode Hopf bifurcation, the system (31) can exhibit spatially nonhomogeneous periodic solutions quasi-periodic solutions induced by Hopf, Turing-Hopf or double-Hopf bifurcations, but there is only one spatial wave frequency, this means when the positive equilibrium is destabilized through Hopf, double-Hopf or Turing-Hopf bifurcations, the bifurcating solutions can only have one spatial peak for (31). Whereas, according to Theorems 1, 2–3 and 4–6, when taking the kernel (4) into account instead of spatial average kernel, the phenomena will be distinct, that is spatially nonhomogeneous periodic solutions or quasi-periodic solutions can possess any spatial wave frequencies, i.e. there can be multiple spatial peaks in one space period, this leads to the system can exhibit more complex spatio-temporal patterns.

Remark 5

It is worth noting that the kernel function (4) may be more reasonable, the effect of which is equivalent to Gaussian kernel on a unbounded domain in [21], and it includes spatial average kernel and Dirac kernel through parameter \( \alpha \). In view of \( \int _{\varOmega }K(x,y) u(y,t)\,\mathrm {d}y \) and Neumann boundary condition, let \( u(y,t)=\varSigma _{k=1}^{k=\infty } e^{\lambda t}\text {cos}\frac{kx}{l}\), then

$$\begin{aligned} \int _{\varOmega }K(x,y) u(y,t)\,\mathrm {d}y=u(x,t), \end{aligned}$$

which indicates that the effect of the kernel (4) is equivalent to Dirac kernel when \( \alpha \rightarrow 0 \), i.e. the classic Holling-Tanner predator prey system. In this case, only the spatially homogeneous periodic solution generated by Hopf bifurcation could be stable, and double-Hopf bifurcations are impossible, this also means that there is no the peak alternating periodic solution.

On the other hand, it is obvious that

$$\begin{aligned} K(x,y)=\frac{1}{l\pi } +\frac{2}{l\pi }\sum _{k=1 }^{k=\infty }\text {cos}\frac{kx}{l}\text {cos}\frac{ky}{l}e^{-\frac{\alpha k^2}{l^2}}\rightarrow \frac{1}{l\pi } \ \text {as }\ \alpha \rightarrow +\infty , \end{aligned}$$

i.e. the system (5) is equivalent to the system (31) when \( \alpha \rightarrow +\infty \). In view of (15), it is easy to calculate the derivative of \( c_k^H(d_2) \) and \( c_k^T(d_2) \) with respective to \( \alpha \),

$$\begin{aligned} \frac{\partial c_k^H(d_2)}{\partial \alpha } =\beta u^*\frac{k^2}{l^2} e^{-\frac{\alpha k^2}{l^2} }>0,\ \ \ \ \frac{\partial c_k^T(d_2)}{\partial \alpha } =\frac{(r+ru^*)d_2\beta u^*\frac{k^4}{l^4} e^{-\frac{\alpha k^2}{l^2} }}{(r+\beta u^* e^{-\frac{\alpha k^2}{l^2} }+d_1\frac{k^2}{l^2})^2}>0. \end{aligned}$$

Hence Hopf bifurcations curve \( c_k^H(d_2) \) and Turing bifurcation curve \( c_k^T(d_2) \) are monotonically increasing on \( \alpha \), which imply that the stable region of positive constant steady state will be smaller as \( \alpha \) increases. Thus to some extent, we can assert that the pattern formation region of the positive equilibrium may be smaller for the system (5) than (31), but spatio-temporal patterns are more diverse. Ecologically, For the kernel (4), when the range of nonlocal interaction is wider, the system is more likely to produce complex spatio-temporal patterns.

3 Spatio-Temporal Patterns Near the Double-Hopf Singularity

In this section we investigate the spatio-temporal patterns of system (5) near the double-Hopf singularity by the method of center manifold theory and the normal form reduction. we first calculate the normal form up to third-order term by applying the formulas of the normal form at double-Hopf singularity in [37]. Subsequently, the dynamics of system (5) near the double-Hopf bifurcation point is illustrated by analyzing the reduced normal form, and appropriate numerical simulations are carried out to support the theoretically results.

3.1 Normal Form of Double-Hopf Bifurcation

Introduce perturbation parameters \( (\varepsilon _1,\varepsilon _{2} )\) by plugging \( d_2=d_2^{k,k+1}+\varepsilon _1,~ c= c_{k,k+1}^H+\varepsilon _2 \) into (5), and translate \((u^{*},v^{*})\) to (0, 0) , consequently, the system (5) can be transformed into

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t=d_{1}u_{xx}+(u+ u^*)\Big (1-\beta \displaystyle \int _{0}^{l\pi } K(x,y)(u(y,t)+ u^*)\,\mathrm {d}y\Big ) -\dfrac{b(u+ u^*)(v+ u^*)}{(1+u+ u^*)}, \\ v_t=(d_2^{k,k+1}+\varepsilon _{1})v_{xx}+( c_{k,k+1}^H+\varepsilon _{2})(v+ u^*)\Big (1-\dfrac{v+ u^*}{u+ u^*}\Big ) , \end{array}\right. }\nonumber \\ \end{aligned}$$
(32)

where \(x\in (0, l\pi )\), \(t>0\), K(x, y) is given by (4). Via denoting

$$\begin{aligned} U(t)=\left( u(t), v(t)\right) ^{T},~~ {\hat{U}}(t)=\displaystyle {\int _{0}^{l\pi }K(x,y)U(y,t)\mathrm {d}y}, \end{aligned}$$

we can abstract (32) as

$$\begin{aligned} {\dot{U}}(t)=D_{0}(\varepsilon )\varDelta U(t)+L(\varepsilon )U(t)+{\hat{L}}(\varepsilon ){\hat{U}}(t)+G(U(t),{\hat{U}}(t), \varepsilon ), \end{aligned}$$
(33)

where

$$\begin{aligned} D(\varepsilon )= & {} \begin{pmatrix} d_{1} &{} 0\\ 0 &{} d_2^{k,k+1}+\varepsilon _1 \end{pmatrix},\quad L(\alpha )= \begin{pmatrix} \frac{u^* (1-\beta u^*)}{1 + u^*} &{} -(1-\beta u^*) \\ c_{k,k+1}^H+\varepsilon _2 &{} -c_{k,k+1}^H+\varepsilon _2 \end{pmatrix},\quad {\hat{L}}(\varepsilon )= \begin{pmatrix} -\beta u^* &{} 0\\ 0&{}0 \end{pmatrix}, \quad \\ G(\xi , {\hat{\xi }}, \alpha )= & {} \begin{pmatrix} (\xi _{1}+u^*) (1-\beta u^*-\beta {\hat{\xi }}_1)-\frac{b(\xi _{1}+u^*)(\xi _{2}+u^*)}{(1+\xi _{1}+u^*)}+\beta u^*{\hat{\xi }}_1-\frac{u^* (1-\beta u^*)}{1 + u^*}\xi _{1}+(1-\beta u^*)\xi _{2} \\ (c^{*}+\varepsilon _{2})(\xi _{2}+u^*)\left( 1-\frac{\xi _{2}+u^*}{\xi _{1}+u^*}\right) -(c^{*}+\varepsilon _{2})(\xi _{1}-\xi _{2}) \end{pmatrix}. \end{aligned}$$

where \(\xi =(\xi _{1},\xi _{2})^T\), \({\hat{\xi }}=({\hat{\xi }}_{1},{\hat{\xi }}_{2})^T\triangleq \int _0^{l\pi }K(x,y)\xi (y,t)\mathrm {d}y\) and \( \varepsilon =(\varepsilon _{1},\varepsilon _{2}) \). and

$$\begin{aligned}&D(0)= \begin{pmatrix} d_{1} &{} 0\\ 0 &{} d_2^{k,k+1} \end{pmatrix},\qquad D_{1}(\varepsilon )= \begin{pmatrix} 0 &{} 0\\ 0 &{} \varepsilon _{1} \end{pmatrix},\nonumber \\&L(0)= \begin{pmatrix} \frac{u^* (1-\beta u^*)}{1 + \lambda } &{} -(1-\beta u^*) \\ c_{k,k+1}^H &{} \end{pmatrix}, \quad {\hat{L}}(0)= \begin{pmatrix} -\beta u^* &{} 0\\ 0&{}0 \end{pmatrix},\quad \nonumber \\&L_{1}(\varepsilon )= \begin{pmatrix} 0 &{} 0\\ \varepsilon _{2} &{} -\varepsilon _{2} \end{pmatrix}, \quad {\hat{L}}_{1}(\varepsilon )= \begin{pmatrix} 0 &{} 0\\ 0 &{} 0 \end{pmatrix}. \end{aligned}$$
(34)
$$\begin{aligned}&Q(X, Y)= \begin{pmatrix} -\beta x_{1}{\hat{y}}_1 -\beta y_{1}{\hat{x}}_1+\frac{2bu^*}{(1+u^*)^{3}}x_1y_1-\frac{b}{(1+u^*)^{2}}(x_1y_2+x_2y_1) \\ -\frac{2c}{u^*}x_1y_1+\frac{2c}{u^*}(x_1y_2+x_2y_1)-\frac{2c}{u^*}x_2y_2 \end{pmatrix}, \end{aligned}$$
(35)
$$\begin{aligned}&C(X, Y, Z)\nonumber \\&\quad = \begin{pmatrix}\ -\frac{6bu^*}{(1+u^*)^{4}}x_1y_1z_1+\frac{2b}{(1+u^*)^{3}}(x_1y_1z_2+x_1y_2z_1+x_1y_1z_1)\\ \frac{6c}{{u^*}^{2}}x_1y_1z_1-\frac{4c}{{u^*}^{2}}(x_1y_1z_2+x_1y_2z_1+x_2y_1z_1)+\frac{2c}{{u^*}^{2}}(x_1y_2z_2+x_2y_2z_1+x_2y_1z_2) \end{pmatrix}.\nonumber \\ \end{aligned}$$
(36)

where \(X=(x_1,x_2)^T\), \(Y=(y_1,y_2)^T\), \(Z=(z_1,z_2)^T\), \({\hat{x}}_1=\int _0^{l\pi }K(x,y)x_1(y,t)\mathrm {d}y\), and \({\hat{y}}_1=\int _0^{l\pi }K(x,y)y_1(y,t)\mathrm {d}y\). As

$$\begin{aligned} \int _{0}^{l\pi }K(x,y) \beta _{k}(y) d y =e^{-\alpha \mu _k}\beta _{k}, \ \text {for} \ k\in {\mathbb {N}}_0, \end{aligned}$$
(37)

with \( \mu _{k}=\frac{k^2}{l^2} \) and \( \beta _{k} \) are the eigenvalues and corresponding eigenfunctions of Laplace operator \(- \text {d}^2/\text {d}x^2 \), then the characteristic equation of (33) is equivalent to a sequence of characteristic equations

$$\begin{aligned} \mathrm {det}\triangle _k(\lambda )=0 \ \ \text{ with }\ \ \triangle _k(\lambda )=\lambda I+\mu _k D_0-(L(0)+e^{-\alpha \mu _k}{\hat{L}}(0))(e^{\lambda \cdot }I), \;\; k\in {\mathbb {N}}_0,\nonumber \\ \end{aligned}$$
(38)

For any \(k\in {\mathbb {N}}_0\), denote the \(m\times m\) matrix-valued function of bounded variation on \([-r,0]\) by \(\eta _k\in BV([-r,0],{\mathbb {C}}^{m\times m})\), which satisfies

$$\begin{aligned} -\mu _kD_0 \psi (0)+(L(0)+e^{-\alpha \mu _k}{\hat{L}}(0))\psi = \int _{-r}^0 \mathrm {d}\eta _k(\theta )\psi (\theta ),\ ~\psi \in C. \end{aligned}$$
(39)

Denote the eigenfunctions of characteristic Eq. (38) for \( k, k+1\in {\mathbb {N}}_0\) by \( \phi _{i} \), \( {\bar{\phi }}_{i} \), and \( \psi _{i} \), \( {\bar{\psi }}_{i} \), \( i=1,2 \) represent eigenfunctions of adjoint characteristic equations, which satisfy \( \psi _i\phi _i=1\), \( \psi _i\phi _j=0\) for \( i,j=1,2, j\not =i \). Denote corresponding purely imaginary eigenvalues by \( \pm i\omega _1 \) and \( \pm i\omega _2 \), here

$$\begin{aligned} \omega _1=\sqrt{D_k(d_2^{k,k+1}, c^H_{k,k+1})}, \ \ \ \omega _2=\sqrt{D_{k+1}(d_2^{k,k+1}, c^H_{k,k+1})}. \end{aligned}$$
(40)

By direct calculating as in [38], we derive that

$$\begin{aligned} \phi _{1}= \begin{pmatrix} 1 \\ p_{1} \end{pmatrix}, \quad \phi _{2}= \begin{pmatrix} 1 \\ p_{2} \end{pmatrix},\quad \psi _{1}= \begin{pmatrix} \tfrac{1}{{N_{1}}} \\ \tfrac{q_{1}}{N_{1}} \end{pmatrix}^{T}, \quad \psi _{2}= \begin{pmatrix} \tfrac{1}{N_{2}}\\ \tfrac{q_{2}}{N_{2}} \end{pmatrix}^{T}, \end{aligned}$$
(41)

with

$$\begin{aligned} p_{1}= & {} \frac{-i\omega _1+ r u^*-\beta u^*e^{-\alpha \frac{k}{l^2}}-d_1 \frac{k}{l^2}}{1-\beta u^*}, \ \ q_{1}=-\frac{1-\beta u^*}{i\omega _1+ c_{k,k+1}^H+\tfrac{d_2^{k,k+1}k^2}{ l^{2}}},\\ p_{2}= & {} \frac{-i\omega _2+ r u^*-\beta u^*e^{-\alpha \frac{k+1}{l^2}}-d_1 \frac{k+1}{l^2}}{1-\beta u^*}, \ \ q_{2}=-\frac{1-\beta u^*}{i\omega _2+ c_{k,k+1}^H+\tfrac{d_2^{k,k+1}(k+1)^2}{ l^{2}}},\\ N_{1}= & {} 1-\frac{i\omega _1- r u^*+\beta u^*e^{-\alpha \frac{k}{l^2}}+d_1 \frac{k}{l^2}}{i\omega _1+ c_{k,k+1}^H+\tfrac{d_2^{k,k+1}k^2}{ l^{2}}}, \quad N_{2}=1-\frac{i\omega _2-r u^*+\beta u^*e^{-\alpha \frac{k+1}{l^2}}+d_1 \frac{k+1}{l^2}}{i\omega _2+ c_{k,k+1}^H+\tfrac{d_2^{k,k+1}(k+1)^2}{ l^{2}}}. \end{aligned}$$

So far we have derived the Q, C, and corresponding eigenfunctions \( \phi _i \), \( \psi _i \), \( i=1,~2 \), as a consequent of (37) and utilizing the formulas of the normal form for double-Hopf bifurcation in [37], we derive the normal form up to third-order of (5) at \( (k_1,k_2) \)-mode double-Hopf bifurcation point as in the following proposition.

Proposition 2

For any \( l,~\alpha >0 \), \( (\beta ,b,d_1)\in \varSigma _1\cup \varSigma _2 \), \( k_1\),\( k_2 \in \varLambda \) with \( \varLambda \) defined as in (12), the normal form up to third-order term restricted on the center manifold of (5) at \( (k_1,k_2) \)-mode double-Hopf singularity \( (d_2^{k,k+1}, c^H_{k,k+1}) \) is given by

$$\begin{aligned} \begin{aligned} {\dot{z}}_1&=\mathrm {i}\omega _1z_1+a_{1}(\varepsilon )z_1+ a_{2100}z_1^2{\bar{z}}_1+a_{1011}z_1z_2{\bar{z}}_2+ h.o.t.,\\ \dot{{\bar{z}}}_1&=-\mathrm {i}\omega _1{\bar{z}}_1+\overline{a_{1}(\varepsilon )}{\bar{z}}_1+ \overline{a_{2100}}z_1{\bar{z}}_1^2+\overline{a_{1011}}{\bar{z}}_1z_2{\bar{z}}_2+h.o.t.,\\ {\dot{z}}_2&=\mathrm {i}\omega _2z_2+b_{2}(\varepsilon )z_2+b_{0021}z_2^2{\bar{z}}_2+b_{1110}z_1{\bar{z}}_1z_2+ h.o.t.,\\ \dot{{\bar{z}}}_2&=-\mathrm {i}\omega _2{\bar{z}}_2+\overline{b_{2}(\varepsilon )}{\bar{z}}_2+\overline{b_{0021}}z_2{\bar{z}}_2^2+\overline{b_{1110}}z_1{\bar{z}}_1{\bar{z}}_2+h.o.t., \end{aligned} \end{aligned}$$
(42)

where

$$\begin{aligned} a_{1}(\varepsilon )= & {} \frac{1}{2}\psi _1 (0)((L_1(\varepsilon )+e^{-\alpha \mu _k}{\hat{L}}_1(\varepsilon ))(\phi _1) -\mu _{k_1}D_1(\varepsilon )\phi _1(0)),\nonumber \\ b_{2}(\varepsilon )= & {} \frac{1}{2}\psi _2 (0)( (L_1(\varepsilon )+e^{-\alpha \mu _k}{\hat{L}}_1(\varepsilon ))(\phi _2)-\mu _{k_2}D_1(\varepsilon )\phi _2(0)),\end{aligned}$$
(43)
$$\begin{aligned} a_{2100}= & {} \frac{3}{4}\psi _1 (0)C_{\phi _1\phi _1{\bar{\phi }}_1} +\frac{1}{4}\delta (k_2-2k_1) \psi _1 (0) \left[ \frac{1}{i\omega _2}(-Q_{\phi _1\phi _2}\psi _2 (0) +Q_{\phi _1{\bar{\phi }}_2}{\bar{\psi }}_2 (0) ) Q_{\phi _1{\bar{\phi }}_1} \nonumber \right. \\&\left. +\left( \frac{1}{i(2\omega _1-\omega _2)}Q_{{\bar{\phi }}_1\phi _2}\psi _2 (0)+\frac{1}{i(2\omega _1+\omega _2)} Q_{{\bar{\phi }}_1{\bar{\phi }}_2} {\bar{\psi }}_2 (0)\right) Q_{\phi _1\phi _1}\right] \nonumber \\&+ \psi _1 (0)[Q_{\phi _1}(h^0_{1100} \nonumber \\&+\frac{1}{\sqrt{2}}h^{2k_1}_{1100}) +Q_{{\bar{\phi }}_1}(h^0_{2000}+\frac{1}{\sqrt{2}}h^{2k_1}_{2000})],\nonumber \\ a_{1011}= & {} \psi _1(0)C_{\phi _1\phi _2{\bar{\phi }}_2} +\frac{1}{2}\delta (k_2-2k_1)\psi _1(0)\left[ \left( \frac{1}{i\omega _2}Q_{\phi _1{\bar{\phi }}_2}\psi _1 (0) \nonumber \right. \right. \\&\left. +\frac{1}{i(2\omega _1+\omega _2)}Q_{{\bar{\phi }}_1{\bar{\phi }}_2}{\bar{\psi }}_1(0)\right) Q_{\phi _1\phi _2} +\left( -\frac{1}{i\omega _2}Q_{\phi _1\phi _2}\psi _1 (0) \nonumber \right. \\&\left. \left. +\frac{1}{i(2\omega _1-\omega _2)}Q_{{\bar{\phi }}_1\phi _2}{\bar{\psi }}_1 (0)\right) Q_{\phi _1{\bar{\phi }}_2}\right] +\frac{1}{2}\delta (k_1-2k_2)\psi _1(0)\left[ \left( \frac{1}{i\omega _1}Q_{\phi _2{\bar{\phi }}_2}\psi _2(0) \nonumber \right. \right. \\&\left. +\frac{1}{i(\omega _1+2\omega _2)}Q_{{\bar{\phi }}_2{\bar{\phi }}_2}{\bar{\psi }}_2 (0)\right) Q_{\phi _1\phi _2} +\left( \frac{1}{i(\omega _1-2\omega _2)}Q_{\phi _2\phi _2} \psi _2(0) \nonumber \right. \\&\left. \left. +\frac{1}{i\omega _1}Q_{\phi _2{\bar{\phi }}_2}{\bar{\psi }}_2 (0)\right) Q_{\phi _1{\bar{\phi }}_2}\right] +\psi _1 (0)\left[ Q_{\phi _1}h^0_{0011}+Q_{\phi _2}\left( \frac{1}{\sqrt{2}}h^{|k_1-k_2|}_{1001} \nonumber \right. \right. \\&\left. \left. +\frac{1}{\sqrt{2}}h^{k_1+k_2}_{1001}\right) +Q_{{\bar{\phi }}_2}\left( \frac{1}{\sqrt{2}}h^{|k_1-k_2|}_{1010} +\frac{1}{\sqrt{2}}h^{k_1+k_2}_{1010}\right) \right] ,\nonumber \\ b_{0021}= & {} \frac{3}{4}\psi _2 (0)C_{\phi _2\phi _2{\bar{\phi }}_2} +\frac{1}{4}\delta (k_1-2k_2)\psi _2 (0) \left[ \frac{1}{i\omega _1}(-Q_{\phi _1\phi _2}\psi _1 (0)+Q_{{\bar{\phi }}_1\phi _2}{\bar{\psi }}_1 (0)) \right] Q_{\phi _2{\bar{\phi }}_2} \nonumber \\&+\left( \frac{1}{i(2\omega _2-\omega _1)}Q_{\phi _1{\bar{\phi }}_2}\psi _1 (0)+\frac{1}{i(2\omega _2+\omega _1)}Q_{{\bar{\phi }}_1{\bar{\phi }}_2}{\bar{\psi }}_1 (0)\right) Q_{\phi _2\phi _2}]\nonumber \\&+\psi _2 (0)\left[ Q_{\phi _2}(h^0_{0011} \nonumber \right. \\&\left. +\frac{1}{\sqrt{2}}h^{2k_2}_{0011}) +Q_{{\bar{\phi }}_2}\left( h^0_{0020}+\frac{1}{\sqrt{2}}h^{2k_2}_{0020}\right) \right] ,\nonumber \\ b_{1110}= & {} \psi _2(0)C_{\phi _1{\bar{\phi }}_1\phi _2} +\frac{1}{2}\delta (k_2-2k_1) \psi _2(0)\left[ \left( \frac{1}{i(\omega _2-2\omega _1)}Q_{\phi _1\phi _1}\psi _1(0) \nonumber \right. \right. \\&\left. \left. +\frac{1}{i\omega _2}Q_{\phi _1{\bar{\phi }}_1}{\bar{\psi }}_1 (0)\right) Q_{{\bar{\phi }}_1\phi _2} +\left( \frac{1}{i\omega _2}Q_{\phi _1{\bar{\phi }}_1}\psi _1 (0) +\frac{1}{i(\omega _2+2\omega _1)}Q_{{\bar{\phi }}_1{\bar{\phi }}_1}{\bar{\psi }}_1 (0)\right) Q_{\phi _1\phi _2}\right] \nonumber \\&+\frac{1}{2}\delta (k_1-2k_2) \psi _2(0) \left[ \left( -\frac{1}{i\omega _1}Q_{\phi _1\phi _2}\psi _2 (0) +\frac{1}{i(2\omega _2-\omega _1)}Q_{\phi _1{\bar{\phi }}_2}{\bar{\psi }}_2 (0)\right) Q_{{\bar{\phi }}_1\phi _2} \nonumber \right. \\&\left. +\left( \frac{1}{i\omega _1}Q_{{\bar{\phi }}_1\phi _2}\psi _2 (0)+ \frac{1}{i(2\omega _2+\omega _1)}Q_{{\bar{\phi }}_1{\bar{\phi }}_2}{\bar{\psi }}_2 (0) \right) Q_{\phi _1\phi _2}\right] +\psi _2(0) \left[ Q_{\phi _2}h^0_{1100} \nonumber \right. \\&\left. +Q_{\phi _1}\left( \frac{1}{\sqrt{2}}h^{|k_1-k_2|}_{0110} +\frac{1}{\sqrt{2}}h^{k_1+k_2}_{0110}\right) +Q_{{\bar{\phi }}_1}\left( \frac{1}{\sqrt{2}}h^{|k_1-k_2|}_{1010} +\frac{1}{\sqrt{2}}h^{k_1+k_2}_{1010}\right) \right] , \end{aligned}$$
(44)

here

\(h_{q_1q_2q_3q_4}~(q_1+q_2+q_3+q_4=2,~q_1,q_2,q_3,q_4\in {\mathbb {N}}_0)\) given by

$$\begin{aligned} h^0_{2000}(\theta )= & {} \frac{1}{2}[2i\omega _1I-\int _{-r}^0e^{2i\omega _1\theta } \mathrm {d} \eta _{0}(\theta )]^{-1} Q_{\phi _1\phi _1} e^{2i\omega _1\theta }, \nonumber \\ h^{2k_1}_{2000}(\theta )= & {} \frac{1}{2\sqrt{2}}\delta (k_2-2k_1) \left( \frac{1}{i(\omega _2-2\omega _1)}\phi _2(\theta )\psi _2 (0)-\frac{1}{i(\omega _2+2\omega _1)}{\bar{\phi }}_2(\theta ){\bar{\psi }}_2 (0)\right) Q_{\phi _1\phi _1} \nonumber \\&+\frac{1}{2\sqrt{2}}[2i\omega _1I-\int _{-r}^0e^{2i\omega _1\theta } \mathrm {d} \eta _{2k_1}(\theta )]^{-1} Q_{\phi _1\phi _1} e^{2i\omega _1\theta }, \nonumber \\ h^0_{1100}(\theta )= & {} -\left[ \int _{-r}^0 \mathrm {d} \eta _{0}(\theta ) \right] ^{-1} Q_{\phi _1{\bar{\phi }}_1} , \qquad h^{2k_2}_{1100}(\theta ) \equiv 0,\nonumber \\ h^{2k_1}_{1100}(\theta )= & {} \frac{1}{\sqrt{2}}\left[ \int _{-r}^0 \mathrm {d} \eta _{2k_1}(\theta ) \right] ^{-1} [-I+ \delta (k_2-2k_1)(\phi _2(0)\psi _2 (0) +{\bar{\phi }}_2(0){\bar{\psi }}_2 (0)) ]Q_{\phi _1{\bar{\phi }}_1} , \nonumber \\ h^{0}_{0020}(\theta )= & {} \frac{1}{2} \left[ 2i\omega _2I-\int _{-r}^0e^{2i\omega _2\theta } \mathrm {d} \eta _{0}(\theta )\right] ^{-1} Q_{\phi _2\phi _2}e^{2i\omega _2\theta }, \nonumber \\ h^{2k_2}_{0020}(\theta )= & {} \frac{1}{2\sqrt{2}} \delta (k_1-2k_2) \left( \frac{1}{i(\omega _1-2\omega _2)}\phi _1(\theta )\psi _1 (0)-\frac{1}{i(\omega _1+2\omega _2)}{\bar{\phi }}_1(\theta ){\bar{\psi }}_1 (0)\right) Q_{\phi _2\phi _2} \nonumber \\&+\frac{1}{2\sqrt{2}}[2i\omega _2I -\int _{-r}^0e^{2i\omega _2\theta } \mathrm {d} \eta _{2k_2}(\theta )]^{-1} Q_{\phi _2\phi _2} e^{2i\omega _2\theta },\nonumber \\ h^{0}_{0011}(\theta )= & {} -\left[ \int _{-r}^0 \mathrm {d} \eta _{0}(\theta ) \right] ^{-1} Q_{\phi _2{\bar{\phi }}_2}, \qquad h^{2k_1}_{0011}(\theta ) \equiv 0,\nonumber \\ h^{2k_2}_{0011}(\theta )= & {} \frac{1}{\sqrt{2}}[\int _{-r}^0 \mathrm {d} \eta _{2k_2}(\theta ) ]^{-1} [-I+ \delta (k_1-2k_2)(\phi _1(0)\psi _1 (0) +{\bar{\phi }}_1(0){\bar{\psi }}_1 (0)) ]Q_{\phi _2{\bar{\phi }}_2} ,\nonumber \\ h^{0}_{1010}(\theta )\equiv & {} 0, \qquad h^{0}_{1001}(\theta ) \equiv 0,\nonumber \\ h^{k_1+k_2}_{1010}(\theta )= & {} \frac{1}{\sqrt{2}}[i(\omega _1+\omega _2)I-\int _{-r}^0e^{i(\omega _1+\omega _2)\theta } \mathrm {d} \eta _{k_1+k_2}(\theta )]^{-1} Q_{\phi _1\phi _2} e^{i(\omega _1+\omega _2)\theta }, \nonumber \\ h^{k_1+k_2}_{1001}(\theta )= & {} \frac{1}{\sqrt{2}} [i(\omega _1-\omega _2)I-\int _{-r}^0e^{i(\omega _1-\omega _2)\theta } \mathrm {d} \eta _{k_1+k_2}(\theta )]^{-1} Q_{\phi _1{\bar{\phi }}_2}e^{i(\omega _1-\omega _2)\theta }, \nonumber \\ h^{|k_1-k_2|}_{1010}(\theta )= & {} \frac{1}{\sqrt{2}} [i(\omega _1+\omega _2)I-\int _{-r}^0e^{i(\omega _1+\omega _2)\theta } \mathrm {d} \eta _{|k_1-k_2|}(\theta )]^{-1} Q_{\phi _1\phi _2} e^{i(\omega _1+\omega _2)\theta } \nonumber \\&-\frac{1}{\sqrt{2}} \left[ \delta (k_2-2k_1) \left( \frac{1}{i\omega _2}\phi _1(\theta )\psi _1 (0) +\frac{1}{i(2\omega _1+\omega _2)}{\bar{\phi }}_1(\theta ){\bar{\psi }}_1 (0)\right) \nonumber \right. \\&\left. +\delta (k_1-2k_2) \left( \frac{1}{i\omega _1}\phi _2(\theta )\psi _2 (0) +\frac{1}{i(\omega _1+2\omega _2)}{\bar{\phi }}_2(\theta ){\bar{\psi }}_2 (0) \right) \right] Q_{\phi _1\phi _2} ,\nonumber \\ h^{|k_1-k_2|}_{1001}(\theta )= & {} \frac{1}{\sqrt{2}} [i(\omega _1-\omega _2)I-\int _{-r}^0e^{i(\omega _1-\omega _2)\theta } \mathrm {d} \eta _{|k_1-k_2|}(\theta )]^{-1} Q_{\phi _1{\bar{\phi }}_2} e^{i(\omega _1-\omega _2)\theta } \nonumber \\&+\frac{1}{\sqrt{2}} \left[ \delta (k_2-2k_1) \left( \frac{1}{i\omega _2}\phi _1(\theta )\psi _1 (0) -\frac{1}{i(2\omega _1+\omega _2)}{\bar{\phi }}_1(\theta ){\bar{\psi }}_1 (0)\right) \nonumber \right. \\&\left. -\delta (k_1-2k_2) \left( \frac{1}{i\omega _1}\phi _2(\theta )\psi _2 (0) +\frac{1}{i(\omega _1+2\omega _2)}{\bar{\phi }}_2(\theta ){\bar{\psi }}_2 (0) \right) \right] Q_{\phi _1{\bar{\phi }}_2},\nonumber \\ h^0_{0110}(\theta )= & {} \overline{ h^0_{1001}(\theta )}, \quad h^{|k_1-k_2|}_{0110}(\theta )=\overline{ h^{|k_1-k_2|}_{1001}(\theta )}, \quad h^{k_1+k_2}_{0110}(\theta )=\overline{ h^{k_1+k_2}_{1001}(\theta )},\nonumber \\ h^0_{0101}(\theta )= & {} \overline{ h^0_{1010}(\theta )}, \quad h^{|k_1-k_2|}_{0101}(\theta )=\overline{ h^{|k_1-k_2|}_{1010}(\theta )}, \quad h^{k_1+k_2}_{0101}(\theta )=\overline{ h^{k_1+k_2}_{1010}(\theta )}, \end{aligned}$$
(45)

\(\theta \in [-r, 0]\), and \( \delta (x) =0 \) for \( x\not =0 \); \( \delta (x)=1 \) for \( x=0 \), and \( \phi _{1}, \phi _{2}, \psi _{1}(0)=\psi _{1}, \psi _{2}(0)=\psi _{2} \) and \( \eta _{k} \) are defined as in (41) and (39).

Remark 6

The formula of the third normal form restricted on the center manifold of double-Hopf bifurcation is also applicable to the system without time delay. As we did not consider the effect of time delay in (32), the formulas in Proposition 2 satisfy \( r=0 \), this implies \( \theta =0 \) and \( \phi _{i}(\theta )=\psi _{i} \), \( \psi _{i}(0)=\psi _{i} \), \(i=1,~2\) in all formulas. Therefore, the normal form of (5) can be directly derived by Proposition 2.

3.2 Pattern Formation Induced by Double-Hopf Bifurcation

In this subsection, we will investigate the spatio-temporal dynamics of system (5) near the \( (k, k+1) \)-mode double-Hopf bifurcation point. Based on the formulas of the normal form given in the Sect. 3.1, the general third normal form of (5) at \( (k, k+1) \)-mode double-Hopf bifurcation point have been derived, Next we fix the parameters

$$\begin{aligned} l=5,~ \alpha =0.5,~\beta =0.15, b=0.8 ,~d_{1}=0.4, \end{aligned}$$

then the positive equilibrium \((u^{*},v^{*})=(2.7540,2.7540) \), utilizing the results in Sect. 2, the system (5) can undergo (2, 3) -mode double-Hopf bifurcation near \( (u^{*},v^{*}) \) at \( (d_2,c)=(d_2^{2,3},c^H_{2,3}) \) with \( (d_2^{2,3},c^H_{2,3})=(0.0945, 0.0515)\). According to (40), we can figure out \( \omega _1= 0.2931\), \( \omega _2= 0.2826\). Corresponding 2-mode and 3-mode Hopf bifurcation curves in \(( d_{2},c) \)-plane are characterized as

$$\begin{aligned} \begin{aligned} {\mathcal {H}}_{2} :\ c&=-0.16d_{2}+0.0666,\ 0<d_{2}<0.4162,\\ {\mathcal {H}}_{3} : \ c&=- 0.36d_{2}+0.0855,\ 0<d_2<0.2375.\\ \end{aligned} \end{aligned}$$

Through applying Lemma 2, the third-order truncated normal form of (5) near (2, 3) -mode double-Hopf bifurcation point \( (d_2^{2,3},c^H_{2,3}) \) can be figured out, corresponding coefficients in (42) are given by

$$\begin{aligned} \begin{aligned} a_{1}(\varepsilon )&=-(0.08 + 0.02034i)\varepsilon _{1} - (0.5 - 0.9955i)\varepsilon _2; \\ b_{2}(\varepsilon )&=-(0.18 + 0.0602i)\varepsilon _{1} - (0.5 - 0.9802i)\varepsilon _2; \\ a_{2100}&=- 0.0410 + 0.0145i;\ \ a_{1011}=- 0.0617 + 0.0288i;\\ b_{0021}&=- 0.0422 + 0.0195i;\ \ b_{1110}=- 0.0649 + 0.0338i . \end{aligned} \end{aligned}$$
(46)

By the transformation

$$\begin{aligned} z_{1}=\rho _1\mathrm {cos}(\theta )+\text {i}\rho _1\mathrm {sin}(\theta ),\ z_{2}=\rho _2\mathrm {cos}(\theta )-\text {i}\rho _2\mathrm {sin}(\theta ), \end{aligned}$$

and let \( \sqrt{|Re(a_{2100})|}\rho _1\rightarrow \rho _1,\ \sqrt{|b_{0021}|}\rho _2\rightarrow \rho _2, \) ignoring the equations of \( \theta \), the normal form is transformed into the following planar system,

$$\begin{aligned} \begin{aligned} {\dot{\rho }}_1&=\rho _1(-0.08\varepsilon _1-0.5\varepsilon _2+\rho _1^2+1.4618\rho _2^2),\\ {\dot{\rho }}_2&=\rho _2(-0.18\varepsilon _1-0.5\varepsilon _2+1.583 \rho _1^2+\rho _2^2). \end{aligned} \end{aligned}$$
(47)
Table 1 The correspondence between (5) and (47)
Full size table

Via direct calculations, there are four equilibria for (47), denoted by \( E_0 \), \( E_1 \), \( E_2 \) and \( E_3 \),which are given by

$$\begin{aligned} \begin{aligned} E_0&=(0,0),~E_1=\left( \sqrt{-0.08\varepsilon _1-0.5\varepsilon _2},0\right) ,\ \text {for}\ \varepsilon _2<-0.16\varepsilon _1,\\ E_2&=\left( 0,\sqrt{-0.18\varepsilon _1-0.5\varepsilon _2}\right) ,\ \text {for}\ \varepsilon _2<-0.36\varepsilon _1,\\ E_3&=\left( \sqrt{- 0.1393\varepsilon _1-0.1757\varepsilon _2}, \sqrt{0.0406\varepsilon _1-0.2219\varepsilon _2}\right) ,\\&\quad \text {for}\ \varepsilon _2+0.7931\varepsilon _1<0 \ \text {and}\ \varepsilon _2-0.1829\varepsilon _1<0 . \end{aligned} \end{aligned}$$

Similar to [27], we give Table 1 to illustrate the correspondence of these equilibria and the solutions of (5), including the positive constant steady state, periodic solutions and the quasi-periodic solution. It follows from the twelve unfoldings classifications given in [39, Chap.7.5], the Case Ib occurs for (47), and the critical bifurcation curves in \((d_2,c)\)-plane are characterized as

$$\begin{aligned} \begin{aligned} {\mathcal {H}}_2^+: c&=c_{2,3}^H-0.16(d_2-d_2^{2,3}),\ \ \text {for} \ d_2>d_2^{2,3},\\ {\mathcal {H}}_2^-: c&=c_{2,3}^H-0.16(d_2-d_2^{2,3}),\ \ \text {for} \ 0<d_2<d_2^{2,3},\\ {\mathcal {H}}_3^+: c&=c_{2,3}^H-0.36(d_2-d_2^{2,3}),\ \ \text {for} \ d_2>d_2^{2,3},\\ {\mathcal {H}}_3^-: c&=c_{2,3}^H-0.36(d_2-d_2^{2,3}),\ \ \text {for} \ 0<d_2<d_2^{2,3},\\ {\mathcal {L}}_1: c&=c_{2,3}^H-0.7931(d_2-d_2^{2,3}), \ \ \text {for} \ d_2>d_2^{2,3},\\ {\mathcal {L}}_2: c&=c_{2,3}^H+0.1829(d_2-d_2^{2,3}), \ \ \text {for} \ 0<d_2<d_2^{2,3}. \end{aligned} \end{aligned}$$
(48)
Fig. 2
figure 2

HH and TH represent double-Hopf bifurcation point and Turing-Hopf bifurcation point, \( {\mathcal {H}}_0\), \( {\mathcal {H}}_1\), \( {\mathcal {H}}_2\), \( {\mathcal {H}}_3\) are corresponding 0-mode, 1-mode, 2-mode, 3-mode Hopf bifurcation curves, \( {\mathcal {T}}_4\) is 4-mode Turing bifurcation curve. \( {\mathcal {H}}_{2}^+ \), \( {\mathcal {H}}_{2}^- \), \( {\mathcal {H}}_{3}^+ \), \( {\mathcal {H}}_{3}^- \), \( {\mathcal {L}}_{1} \) and \( {\mathcal {L}}_{2} \) represent critical bifurcation curves defined as in (48)

Full size image
Fig. 3
figure 3

The solution of (5), for parameters \( (d_{2},c)=( 0.1445, 0.1015)\in D_{1} \) with initial conditions \(u(x,0)=2.7540+0.2\mathrm {cos}(\frac{2x}{5})\), \(v(x,0)=2.7540+0.2\mathrm {cos}(\frac{2x}{5})\) Figures show that the constant steady state is locally asymptotically stable

Full size image
Fig. 4
figure 4

The solution of (5), for parameters \( (d_{2},c)=(0.1445,0.0415)\in D_{2} \) with initial conditions \(u(x,0)=v(x,0)= 2.7540+0.2\mathrm {cos}\frac{2x}{5}\). The left figure shows that the spatially nonhomogeneous periodic solution with two spatial wave frequencies is locally asymptotically stable, the right figure is corresponding projections in (x, t) -plane. Here we omit the graphs of v for simplification since it is similar to the graphs of u

Full size image

The bifurcation set and corresponding phase are shown in Fig. 2. As in Fig. 2b, the \((d_2,c)\)- plane is divided into six regions near \((d_2^{2,3},c^H_{2,3})\), corresponding phase portraits in each region are portrayed in Fig. 2b. Next we will elaborate the spatio-temporal dynamics of (5) near the (2, 3) -mode double-Hopf singularity, which are summarized in the following proposition.

Proposition 3

For \(l=5,~ \alpha =0.5,~\beta =0.15, ~b=0.8 ,~d_{1}=0.4\), the unique positive equilibrium \( E^*=(2.7540,2.7540) \), when \( (d_2,c) \) perturb near \( (d_2^{2,3},c^H_{2,3})=(0.0945, 0.0515)\) with frequencies \(\omega _1=0.3014 \) and \( \omega _2= 0.2199 \), (5) exhibits following dynamics near \( E^* \) :

  1. (i)

    When \( (d_2,c)\in D_1 \), \( E^* \) is locally asymptotically stable and a 2-mode Hopf bifurcation of (5) occurs when \( (d_2, c) \) crosses \( {\mathcal {H}}_2^+ \).

  2. (ii)

    When \( (d_2,c)\in D_2 \), \( E^* \) becomes unstable, a locally asymptotically stable spatially nonhomogenoes periodic solution with two spatial frequencies \( {\tilde{E}}_1 \) bifurcates from \( E^* \), which can be approximated by

    $$\begin{aligned} E^*+(\rho _{11}\phi _{1}(0)e^{\omega _1 t}+{\bar{\rho }}_{11}{\bar{\phi }}_{1}(0)e^{-\omega _1 t})\text {cos}\frac{2x}{l}, \end{aligned}$$

    with \( \rho _{11} \rightarrow 0\) for \( (d_2,c) \) approaching \( (d_2^{2,3},c_{2,3}^H)\). Moreover, (5) undergoes a 3-mode Hopf bifurcation from \( E^*\) when \( (d_2, c) \) crosses \( {\mathcal {H}}_3^{+} \).

  3. (iii)

    When \( (d_2,c)\in D_3 \), \( E^* \) is unstable, spatially nonhomogenoes periodic solution \( {\tilde{E}}_1 \) remains stable, a spatially nonhomogenoes periodic solution with three spatial frequencies \( {\tilde{E}}_2 \) appears through 3-mode Hopf bifurcation, it is unstable and shaped like

    $$\begin{aligned} E^*+(\rho _{21}\phi _{2}(0)e^{\omega _2 t}+{\bar{\rho }}_{21}{\bar{\phi }}_{2}(0)e^{-\omega _2 t})\text {cos}\frac{3x}{l}, \end{aligned}$$

    with \( \rho _{21}\rightarrow 0\) when \( (d_2,c) \) close to \( (d_2^{2,3},c_{2,3}^H)\).

  4. (iv)

    When \( (d_2,c)\in D_4 \), \( E^* \) is unstable, spatially nonhomogeneous periodic solution \( {\tilde{E}}_1\) still remains the stability, \( {\tilde{E}}_2 \) becomes locally asymptotically stable through a 2-mode Hopf bifurcation when \( (d_2, c) \) crosses \( {\mathcal {L}}_1 \), and a spatially nonhomogeneous quasi-periodic solution bifurcates from \( {\tilde{E}}_2 \), which is unstable and close to

    $$\begin{aligned} E^*+(\rho _{12}\phi _{1}(0)e^{\omega _1 t}+{\bar{\rho }}_{12}{\bar{\phi }}_{1}(0)e^{-\omega _1 t})\text {cos}\frac{2x}{l}+(\rho _{22}\phi _{2}(0)e^{\omega _2 t}+{\bar{\rho }}_{22}{\bar{\phi }}_{2}(0)e^{-\omega _2 t})\text {cos}\frac{3x}{l}, \end{aligned}$$

    with \( \rho _{12}\rightarrow 0\), \( \rho _{22}\rightarrow 0\) for \( (d_2,c) \) closing to \( (d_2^{2,3},c_{2,3}^H)\).

  5. (v)

    When \( (d_2,c)\in D_5 \), \( E^* \) and spatially nonhomogeneous periodic solution \( {\tilde{E}}_1\) are unstable, the spatially nonhomogeneous periodic solution \( {\tilde{E}}_2 \) persists stable, and spatially nonhomogeneous quasi-periodic solution \( {\tilde{E}}_3 \) disappears (through a 3-mode Hopf bifurcation at \( {\tilde{E}}_1 \) on \({\mathcal {L}}_2\)), .

  6. (vi)

    When \( (d_2,c)\in D_6 \), \( E^* \) is still unstable, the spatially nonhomogenoes periodic solution \( {\tilde{E}}_3 \) remains the stability, the spatially nonhomogenoes periodic solution \( {\tilde{E}}_2 \) disappears (through 3-mode Hopf bifurcation on \({\mathcal {H}}_3^{-}\) from \( E^* \)).

Fig. 5
figure 5

The solution of (5), for parameters \( (d_{2},c)=( 0.1445,0.0315)\in D_{3} \) with initial conditions \( u(x,0)=v(x,0)=2.7540+0.3\mathrm {cos}\frac{3x}{5}\). The left and middle figures exhibit the transition from spatially nonhomogeneous periodic solution with three spatial wave frequencies to the stable spatially nonhomogeneous periodic solution with two spatial wave frequencies. The right shows the spatio-temporal patterns with two spatial wave frequencies. Here we omit the graphs of v

Full size image
Fig. 6
figure 6

The solution of (5), for parameters \( (d_{2},c)=(2.4587,0.1512)\in D_{4} \). The left figures show the bistability of spatially nonhomogeneous periodic solutions with two and three spatial wave frequencies, and the right are corresponding spatio-temporal patterns. Here we omit the graphs of v

Full size image
Fig. 7
figure 7

The solution of (5), for parameters \( (d_{2},c)=( 0.0445,0.0465)\in D_{3} \) with initial conditions \( u(x,0)=v(x,0)=2.7540+0.02\mathrm {cos}\frac{3x}{5}+0.3\mathrm {cos}\frac{2x}{5}\). The left and middle figures exhibit the transition from the spatially nonhomogeneous periodic solution with three spatial wave frequencies to the stable spatially nonhomogeneous periodic solution with three spatial wave frequencies. The right shows the spatio-temporal patterns with three spatial wave frequencies. Here we omit the graphs of v

Full size image
Fig. 8
figure 8

The solution of (5), for parameters \( (d_{2},c)=(0.0445, 0.0615)\in D_{6} \) with initial conditions \( u(x,0)=v(x,0)=2.7540+0.3\mathrm {cos}\frac{3x}{5}\), the spatially nonhomogeneous periodic solution with three spatial wave frequencies is locally asymptotically stable. Here we omit the graphs of v

Full size image
Fig. 9
figure 9

The solution of (5), for parameters \( (d_{2},c)=( 0.1445, 0.0015)\) with initial conditions \( u(x,0)=v(x,0)=2.7540+0.2\mathrm {cos}\frac{2x}{5}\), Figures exhibit strange spatially homogeneous periodic solutions

Full size image
Fig. 10
figure 10

The solution of (5), for parameters \( (d_{2},c)=( 0.1445, 0.0015)\) with initial conditions \( u(x,0)=v(x,0)=2.7540+0.2\mathrm {cos}\frac{2x}{5}\). Figures show spatially nonhomogeneous multi-periodic solutions emerge

Full size image

Proposition 3 illustrates complex spatio-temporal dynamics near the double-Hopf bifurcation point, some numerical simulations with bifurcation parameters \( (d_{2}, c) \) fixed in regions \( D_{1}\)-\(D_{6} \) are carried out to support the theoretical results; see Figs. 3,  4,  5,  6,  7 and 8. Figure 5 show the locally asymptotically stable constant steady state in \( D_1 \). As shown in Figs. 4 and 5, the spatially nonhomogeneous periodic solution with two spatial wave frequencies is locally asymptotically stable in \( D_2 \) and \( D_3 \), in particular, when \( (d_{2}, c) \) belongs to \( D_3 \), there exist a transition from spatially nonhomogeneous periodic solution with spatial three-peaks to the one with spatial two-peaks. In \( D_{4}\), Fig. 6 show that the system exhibits the bistability, that is the coexistence of spatially nonhomogeneous periodic solution with two and three spatial wave frequencies, both of them are peak alternating, this is the distinct phenomenon revealed by double-Hopf bifurcation for the system with kernel (4). Analogously,  8 illustrates a transition from spatially nonhomogeneous periodic solution with spatial two-peaks to the one with spatial three -peaks in \( D_5 \), and the system will eventually convergent to the tree-peaks one in both of \( D_5 \) and \( D_6 \). Corresponding spatio-temporal patterns are addressed in Fig. 4, 5, 6, 7 and 8 as well.

4 Conclusion

This paper investigated the spatio-temporal dynamics of Holling-Tanner predator prey system with nonlocal intraspecific prey competition and homogeneous Neumann boundary conditions. The main distinction with previous investigations is that a spatial dependently kernel \(K(x,y)=\frac{1}{l\pi } +\frac{2}{l\pi }\sum _{k=1 }^{k=\infty }\text {cos}\frac{kx}{l}\text {cos}\frac{ky}{l}e^{-\frac{\alpha k^2}{l^2}}\) is considered. Our results reveals that the system can undergo more complex bifurcations when the unique positive equilibrium is destabilized, which implies that such kernel can induce more diverse teme-periodic patterns with spatial multi-peaks.

We establish the existences of Turing bifurcation, Hopf bifurcation, Turing-Hopf bifurcation and double-Hopf bifurcation in the current paper. As usual, double-Hopf bifurcations occurs in the system with time delay, Our results reveal that it could occur under the effect of the nonlocal interaction. If the nonlocal cometition is spatial average, i.e. the system (31), double-Hopf bifurcation only can be (0, 1) -mode, which was argued in [27]. As in Remark 5, if other system parameters are fixed, then the region of pattern formations in \( (d_2,c)\)-plane will be smaller for the system (5) than the system (31). Based on the similar progress in [37], the normal form up to the third-order at double-Hopf singularity is derived, in particular, it is expressed by the original parameters of the system. Via analyzing the reduced normal form, rich spatio-temporal dynamics near the double-Hopf bifurcation point are shown when the positive constant steady state is destabilized. Especially, the system could exhibit periodic oscillations with multiple spatial peaks alternating. In addition, bistability of such periodic solutions with different spatial wave frequencies could appear as well.

Biologically, we can assert that the farther scope of such intraspecific interaction can lead to complex spatio-temporal patterns. As a consequently of the existence of \( (k,k+1) \)-mode double-Hopf bifurcations for any \( k\in {\mathbb {N}} _0\) for the system (5), the coexistence states of the prey and predator species will be more diverse, especially in spatially nonhomogeneous states.

Finally, we still find that some novel simulations for the system (5), see Figs. 9 and 10. Under the influence of the nonlocal effect, the system (5) can undergo more multiplicate Hopf and double-Hopf bifurcations, the bifurcating periodic solutions could transshape when bifurcation parameters vary from one critical value to another. As a result, Fig. 9 could illustrate the periodic solution when the bifurcation parameter is away from the 0-mode Hopf bifurcation singularity. Figure 10 exhibits the strange attractor with multiple time-periods, which generally can be induced by double-Hopf bifurcations. It will be of interest to analytically investigate these phenomena as the bifurcation parameter varying from a global perspective.