The Sliding Bifurcations in Planar Piecewise Smooth Differential Systems

Abstract

In this paper we are mainly interested in the bifurcation phenomena for a class of planar piecewise smooth differential systems, where a new phenomenon, i.e. sliding heteroclinic bifurcation, is found. Furthermore we will show that the involved systems can present many interesting bifurcation phenomena, such as the (sliding) heteroclinic bifurcation, sliding (homoclinic) cycle bifurcation and semistable limit cycle bifurcation and so on. The system can have two hyperbolic limit cycles, which are bifurcated in one way from a semistable limit cycle, and in another way from a heteroclinic cycle and a sliding cycle. In the proof of our main results, we will use the geometric singular perturbation theory to analyze the dynamics near the sliding region.

1 Introduction

Piecewise smooth dynamical systems have been widely applied to model real systems, such as the automatical control, the mechanical systems with dry frictions, biology, economics and so on (see e.g. [2, 4, 8, 16, 17] and [19] and the references therein). These kinds of systems can have richer dynamical phenomena than the smooth ones (see e.g. [5–15, 21, 22] and [25] and the references therein). For example the sliding phenomena has appeared only in non–smooth dynamical systems. In [12] and [13] Gannakopoulos and Pliete have studied the existence of sliding cycles and sliding homoclinic cycles for a planar relay control feedback systems which is modelled by a piecewise linear system. These kinds of systems have also many applications in engineering such as Coulomb friction, valve oscillators and so on, see e.g. [18] and [24]. In [3] Battelli and Fečkan studied the homoclinic trajectories of discontinuous systems. Recently in [23] we have investigated the sliding homoclinic and sliding cycle bifurcations. We proved that a sliding homoclinic cycle can be bifurcated into a sliding cycle and a sliding cycle can be bifurcated into a limit cycle.

In this paper we find a new bifurcation phenomenon in piecewise smooth differential systems, which we call the sliding heteroclinic cycle bifurcation. We should mention that the sliding vector fields appearing in this paper have some singularities in the interior of the sliding section. The appearance of the singularities inside the sliding region will bring some difficulties in the study of the sliding bifurcation phenomena. In Sect. 3 we will use the geometric singular perturbation theory to study the dynamics of system (4) near the sliding region. This method was developed in [5, 20].

Consider a planar piecewise smooth vector field with discontinuity on the $y$ axis

$$\begin{aligned} X(x,y)= \left\{ \begin{array}{ll} X_r(x,y), &{}\quad (x,y)\in G_r, \\ X_l(x,y), &{}\quad (x,y)\in G_l, \end{array}\right. \end{aligned}$$

(1)

where $X_i = (f_i,g_i ) \in C^{k}(\mathbb{R }^2)$ with $k\in \mathbb{N }\cup \{\infty \},\, i \in \{r, l\}$, and

$$\begin{aligned} G_r=\{(x,y)\in \mathbb{R }^2:\,\,\, x>0\},\qquad G_l=\{(x,y)\in \mathbb{R }^2:\quad x<0\}. \end{aligned}$$

Associated to (1) we define a set–valued map in $\mathbb{R }^2$ by

$$\begin{aligned} X^F(x,y)= \left\{ \begin{array}{ll} \{X_l(x,y)\}, &{}(x,y)\in G_l,\\ \overline{co}\{X_r(0,y),X_l(0,y)\}, &{}(x,y)\in Y,\\ \{X_r(x,y)\}, &{}(x,y)\in G_r, \end{array}\right. \end{aligned}$$

where $Y$ denotes the set of points on the $y$ axis, and

$$\begin{aligned} \overline{co} \{X_r(0,y),X_l(0,y)\}\!\!=\!\{v(y)\in \mathbb{R }^{2}: v(y)\!=\!\alpha X_r(0,y)\!+\!(1\!-\!\alpha )X_l(0,y), \alpha \in [0,1]\}\!,\quad \end{aligned}$$

(2)

is the convex hull of the vectors $X_r(0,y)$ and $X_l(0,y)$. We get the differential inclusion

$$\begin{aligned} \left( \begin{array}{l} \dot{x} \\ \dot{y} \\ \end{array} \right) \in X^F(x,y),\qquad (x,y) \in \mathbb{R }^2, \end{aligned}$$

(3)

where the dot denotes the derivative with respect to the time $t$.

In what follows we will specify the function $\alpha$ in $y$ for which the vector $v$ given in (2) is uniquely defined in terms of $X_r$ and $X_l$. Consequently $X^F(x,y)$ will be a well defined vector field in $\mathbb{R }^2$, which is called the Filippov system [11].

According to Filippov [11], a solution of (1) or of the Filippov system is an absolutely continuous function $\left( x(t),\, y(t)\right)$ defined on an interval $I\subset \mathbb{R }$ which satisfies $\left( \dot{x}(t),\,\dot{y}(t) \right) \in X^F(x(t),y(t))$ for almost all $t\in I$.

For a Filippov system there may appear three kinds of subregions of $Y$, which are extremely important in the study of the dynamics of piecewise smooth differential systems (see [5, 9, 22]):

• (a) A sewing region is a subset $M_1\subset Y$ on which $f_r\cdot f_l>0$. In this case, if a trajectory of (1) can meet $M_1$, it must pass through $M_1$ transversally. Recall that $f_r$ and $f_l$ are the first components of $X_r$ and $X_l$, respectively.

• (b) A sliding region is a subset of $M$ on which $f_r\cdot f_l\le 0$. More precisely,

  • If $f_r<0$ and $f_l>0$, the sliding region is called attracting or an attracting region, denoted by $M_2$. If the vector fields meet $M_2$, they will point inward to $M_2$. On the attracting region any orbit remains being tangent to $M_2$.

  • If $f_r>0$ and $f_l<0$, the sliding region is called repulsive or an escaping region, denoted by $M_3$. On the escaping region the trajectories may stay on it for a while, and also may leave it at some time. In this case the solution is not unique.

On the sewing region the vector fields $X^F$ are defined directly from $X_r$ and $X_l$ by choosing either $\alpha \equiv 0$ or $\alpha \equiv 1$ if either $f_r<0$ or $f_r>0$. On the sliding region (see e.g., [5]) a sliding vector field associated to $X$, denoted by $X_s$, is tangent to $M_i$ for $i=2,3$ and is defined at $q \in M_i$ by $X_s(q) = m-q$ with $m$ being the point on $Y$ where the segment joining $q + X_r(q)$ and $q +X_l(q)$ is tangent to $M_i$. For distinguishing the two cases, the sliding vector field on $M_3$ will be called the escaping vector field; and the one on $M_2$ is also called a sliding vector field. Depending on the vector fields on the discontinuity $Y$, there occur two possible things: when an orbit meets $Y$ it either crosses $Y$ or stays on it for a while. The latter is called sliding phenomena. If an orbit has a segment on the sliding region, we call it a sliding orbit, or an orbit with sliding motion.

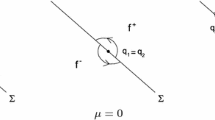
A limit cycle of the piecewise smooth vector field $X$ is a closed orbit, and in some neighborhood of which other orbits are either all positively approach it or all negatively approach it. This definition follows from that of smooth vector fields, see e.g. [26]. A sliding cycle is a closed orbit with sliding motion, see Fig. 1a. A sliding–zero cycle is a closed orbit having a unique point of the sliding region, see Fig. 1b. We mention that the unique point of the sliding region on a sliding–zero cycle should be one of the end points of the sliding region. By the very definition a limit cycle is neither a sliding cycle nor a sliding–zero cycle. Closed orbits are central nested if they surround the same singularity.

Fig. 1

The sliding phenomena a sliding cycle b sliding–zero cycle c sliding heteroclinic d sliding–zero heteroclinic

A sliding heteroclinic orbit (or cycle) is a heteroclinic one with sliding motion, see Fig. 1c. A sliding–zero heteroclinic orbit (or cycle) is a heteroclinic one which possesses an end point of the sliding region, see Fig. 1d. Of course, the saddles in Fig. 1c, d can be located in the different sides of the $y$ axis.

A piecewise smooth dynamical system with a parameter $\alpha$ has a sliding cycle bifurcation at $\alpha =\alpha _0$ if the system has a sliding–zero cycle when $\alpha =\alpha _0$, while for $0<|\alpha -\alpha _0|\ll 1$ the sliding–zero cycle disappears, instead there appears a limit cycle in its small neighborhood when $\alpha$ varies in one direction, and there appears a sliding cycle when $\alpha$ goes in another direction.

The system with a parameter $\alpha$ has a sliding heteroclinic bifurcation at $\alpha =\alpha _0$ if the system has a sliding (or sliding–zero) heteroclinic cycle when $\alpha =\alpha _0$, while for $0<|\alpha -\alpha _0|\ll 1$ the sliding (or sliding–zero) heteroclinic cycle disappears, instead there appears a sliding (or sliding–zero) cycle in its small neighborhood when $\alpha$ varies in one direction, and there is neither sliding heteroclinic orbits nor sliding cycles in its suitable neighborhood when $\alpha$ goes in another direction.

A sliding Hopf bifurcation is the phenomena that the system has a small sliding cycle for either $0<\alpha -\alpha _0\ll 1$ or $0<\alpha _0-\alpha \ll 1$, and the sliding cycle shrinks to a singularity when $\alpha =\alpha _0$.

In this paper we investigate a class of piecewise smooth differential systems which can present sliding heteroclinic cycle. As we know, this is a new phenomena that we first find. The known sliding phenomena are sliding cycles and sliding homoclinic cycles, see e.g. [23]. Furthermore we show that these kinds of systems can also present the sliding cycle bifurcation, the sliding heteroclinic cycle bifurcation and the multiplicity 2 limit cycle bifurcation and so on. The sliding heteroclinic cycle bifurcation is also a kind of new bifurcation phenomenon that we first find. In the study of these results we will use the theory of singular perturbation to study the dynamics of the piecewise smooth differential systems near the sliding region.

Consider the following piecewise smooth differential systems with non–smoothness appearing on the $y$ axis

$$\begin{aligned} \begin{array}{l} \left( \begin{array}{l} \dot{x} \\ \dot{y} \\ \end{array} \right) =\left( \begin{array}{c} F_{1}(x,y)\\ F_{2}(x,y) \\ \end{array} \right) \end{array} \end{aligned}$$

(4)

with

$$\begin{aligned} \left( \begin{array}{l} F_{1}(x,y)\\ F_{2}(x,y) \\ \end{array} \right) = \begin{array}{l} \left( \begin{array}{c} y-x-b_1\\ -px-b_2 \\ \end{array} \right) \end{array}\triangleq X_l(x,y), \quad \text{ for } (x,y)\in \overline{G}_{l}, \end{aligned}$$

(5)

and

$$\begin{aligned} \left( \begin{array}{l} F_{1}(x,y)\\ F_{2}(x,y) \\ \end{array} \right) = \begin{array}{l} \left( \begin{array}{l} \left( \dfrac{1}{3}-2x\right) y \\ -3x^2-x+y^2 \\ \end{array} \right) \end{array}\triangleq X_r(x,y), \quad \text{ for } (x,y)\in \overline{G}_{r}, \end{aligned}$$

(6)

where $b_1,b_2,p$ are real parameters. In what follows we call Eq. (4) with (5) the left system of (4) and Eq. (4) with (6) the right system of (4). We should mention that the left system (5) is a linear one, which appeared in [12] and [13] for modelling the existence of sliding cycles of piecewise smooth linear systems. The right system (6) is a quadratic Hamiltionian one with the Hamiltonian

$$\begin{aligned} H(x,y)=\left( \dfrac{1}{6}-x\right) y^2+\frac{x^2}{2}+x^3, \end{aligned}$$

which is given in [1] as one of the full classification of the cubic Hamiltonians.

For studying the dynamics of system (4), we need the set–valued vector field in $\mathbb{R }^2$

$$\begin{aligned} \mathcal X (x,y)= \left\{ \begin{array}{ll} \{X_l(x,y)\}, &{}(x,y)\in G_l,\\ \overline{co}\{X_r(0,y),X_l(0,y)\}, &{}(x,y)\in Y,\\ \{X_r(x,y)\}, &{}(x,y)\in G_r, \end{array}\right. \end{aligned}$$

(7)

with $\overline{co}$ being defined in (2).

This paper is organized as follows. In the next section we will state our main results. Section 3 is a preparation to the proof of our main result, where we make use of the theory of singular perturbation to study the dynamics of system (4) near the sliding region. The proof of our main results will be given in Sect. 4. The last section is an appendix, which illustrates the conditions of our main results.

2 Statement of the Main Results

For stating our main results we need some basic facts on the left and right systems of (4). In order for the system to present sliding phenomena, we require that the left system has a focus. So we need $b_2>0$ and $p>\frac{1}{4}$, which implies that the left system has a unique singularity $F_l=(-\frac{b_2}{p},-\frac{b_2}{p}+b_1)$ in $G_l$, which is a focus, see Fig. 2a.

Fig. 2

The phase portrait of the subsystems of (4) a phase portrait of the left system b phase portrait of the right system

The right system of (4) has four singularities in the full plane: $O(0,0)$ a center and three saddles $S_1=(-\frac{1}{3},0),\, S_2=(\frac{1}{6},\frac{1}{2})$ and $S_3=(\frac{1}{6},-\frac{1}{2})$. Set ${\tilde{x}}=x-\frac{1}{6}, \, {\tilde{y}}=y+\frac{1}{2}$. Then system (4) with (6) becomes

$$\begin{aligned} \dot{x}=x-2xy, \quad \dot{y}=-2x-y-3x^2+y^2, \end{aligned}$$

(8)

where we still use $x$ and $y$ to represent ${\tilde{x}}$ and ${\tilde{y}}$. System (8) has the phase portrait given in VULPE 10 of [1]. Hence the right system of (4) has the phase portrait Fig. 2b.

For $b_1>0$, we can check that system (4) has the (repulsive) sliding region $M_3=\{(0,y)\in M|\,\, 0 \le y\le b_1\}$. We now establish the sliding vector field on $M_3$. By the very definition, the sliding vector field $X_s=\alpha X_r(0,y)+(1-\alpha )X_l(0,y)$ should be tangent to the $y$ axis, it implies that

$$\begin{aligned} \alpha \frac{y}{3}+(1-\alpha )(y-b_1)=0, \quad \text{ for } \alpha \in [0,1]. \end{aligned}$$

So we have

$$\begin{aligned} \alpha =\dfrac{b_1-y}{b_1-\frac{2}{3}y}. \end{aligned}$$

This shows that the sliding vector field on $M_3$ is

$$\begin{aligned} X_s=\left( 0,\dfrac{y(b_1y-y^2-\frac{b_2}{3})}{b_1-\frac{2}{3}y}\right) . \end{aligned}$$

We remark that the sliding vector field $X_s$ is well defined on $M_3$.

The following properties about the sliding vector field $X_s$ can be checked easily, the details are omitted.

Proposition 1

For the sliding vector field $X_s$ with $b_1,b_2>0$, the following hold.

• (a) In any case $X_s$ has the singularity $O=(0,0)$, which is stable.

• (b) If $b_2=\dfrac{3b_1^2}{4}$, $X_s$ has another singularity $S=\left( 0,\dfrac{b_1}{2}\right)$, which is semi–stable.

• (c) If $b_2<\dfrac{3b_1^2}{4}$, except $O$ the sliding vector field $X_s$ has another two singularities

  $$\begin{aligned} S^{+}=\left( 0,\dfrac{b_1+\sqrt{b_1^2-\frac{4b_2}{3}}}{2}\right) \text{ and }\, S^{-}=\left( 0,\dfrac{b_1-\sqrt{b_1^2-\frac{4b_2}{3}}}{2}\right) , \end{aligned}$$

  which are stable and unstable respectively.

According to the above analysis, for studying the existence of sliding heteroclinic phenomena we need the following basic assumptions on the values of the parameters of (4):

$$\begin{aligned} (\mathcal{A }) \,b_1>0, \,b_2>0\,{and}\,p>1/4. \end{aligned}$$

Our first result shows the existence of the sliding heteroclinic bifurcation, of the sliding cycle bifurcation and of the multiplicity 2 limit cycle bifurcation for the piecewise smooth differential systems (4).

Theorem 2

Suppose that system (4) satisfies the basic assumption $(\mathcal{A })$ and $0<b_1<\frac{1}{3}$. Then there exist $0<b_2^h<b_2^{sc}<b_2^m<\infty$ together with the assumption $\frac{3b_1^2}{4}<b_2^h$ for which the following statements hold.

• (a) If $b_2>b_{2}^m$, system (4) has a heteroclinic orbit connecting $F_l$ and $S_3$, and has no closed orbit.

• (b) If $b_2=b_{2}^{m}$, system (4) has a unique limit cycle of multiplicity 2, which is stable from outside and is unstable from inside.

• (c) If $b_{2}^{sc}<b_2<b_{2}^m$, system (4) has two hyperbolic limit cycles, which are central nested. The inner one is unstable and contains the sliding region in its interior enclosed by the limit cycle.

• (d) If $b_2=b_{2}^{sc}$, system (4) has the stable hyperbolic limit cycle and a sliding–zero cycle. They are central nested. The inner sliding–zero cycle contains the sliding region in its interior limited by the cycle.

• (e) If $b_2^h<b_2<b_{2}^{sc}$, system (4) has the stable hyperbolic limit cycle and a unique sliding cycle, which are central nested.

• (f) If $b_2=b_2^h$, system (4) has the sliding cycle and a heteroclinic cycle.

• (g) If $\frac{3b_1^2}{4}<b_2<b_2^h$, system (4) has the sliding cycle, and has neither homoclinic nor heteroclinic orbits.

• (h) If $b_2=\frac{3b_1^2}{4}$, for the different choice of $b_1\in (0,\frac{1}{3})$ system (4) may have either a sliding cycle or a sliding homoclinic cycle, which consists of the sliding motion and the regular orbit arcs of both the left and right subsystems of (4).

Furthermore, there exists a $\hat{b}_2\in (0,\frac{3b_1^2}{4})$ for which we have

• (i) If $\hat{b_2}<b_2<\frac{3b_1^2}{4}$, for the different choice of $b_1\in (0,\frac{1}{3})$ system (4) may have either a sliding cycle or a sliding homoclinic cycle or a sliding heteroclinic oribits, which consists of the sliding motion and the regular orbit arcs of both the left and right subsystems of (4).

• (j) If $0<b_2\le \hat{b_2}$, system (4) may have either a sliding cycle or a sliding homoclinic cycle or a sliding heteroclinic oribits, which consists of the sliding motion and the regular orbit arc of only the left subsystems of (4).

Figure 3 shows all the topological structures of system (4) around the sliding region.

Fig. 3

The topological structures of trajectories in Theorem 2 a $b_2>b_2^m$ b $b_2=b_2^m$ c $b_2^{sc}<b_2<b_2^m$ d $b_2=b_2^{sc}$ e $b_2^h<b_2<b_2^{sc}$ f $b_2=b_2^{h}$ g $\frac{3b_1^2}{4}<b_2<b_2^h$ h $b_2=\frac{3b_1^2}{4}<b_2^{h}$ i $\hat{b}^{2}_2<b_2<\frac{3b_1^2}{4}$ j $b_2\le \hat{b}_2$

In Theorem 2 we have an addition assumption $\frac{3b_1^2}{4}<b_2^h$. Lemmas 10 and 11 in Appendix shows that there does exist $b_1>\frac{1}{3}$ such that the additional condition holds. Of course, it is possible that there is $b_1>\frac{1}{3}$ such that $\frac{3b_1^2}{4}\in [b_2^h,\infty )$. But we will not pursue these analysis because the computation is tedious and the idea is similar to the present ones.

From Theorem 2 and its proof we can get easily the following results. Its proof will be omitted.

Corollary 3

Under the assumptions of Theorem 2 system (4) has a heteroclinic bifurcation at $b_2=b_2^h$, where a unique limit cycle is bifurcated from the heteroclinic cycle. At $b_2=b_2^{sc}$ there appears a sliding–zero bifurcation, where a limit cycle is bifurcated from the sliding–zero cycle and the system will have two limit cycles. At $b_2=b_2^m$ there appears a multiple two limit cycle bifurcation. In the cases $(e),\, (f)$ and $(g)$ of Theorem 2, system (4) undergoes a sliding Hopf bifurcation at $b_1= 0$.

We remark that the sliding Hopf bifurcation happens, because in the cases $(e),\, (f)$ and $(g)$ of Theorem 2, $b_2^h$ and $b_2^{sc}$ are multiplication of $b_1$ by positive functions in $p$, when $b_1\rightarrow 0$ we have $b_2\rightarrow 0$, the sliding cycle together with the focus $F_l$ shrinks to $O$.

The second result provides the conditions for the existence of sliding cycle and sliding heteroclinic orbits.

Theorem 4

Assume that system (4) satisfies $(\mathcal{A })$ and $b_1> \frac{1}{3}$. Let $t_0$ be the largest negative root of $\cos (\omega t_0)+\frac{1}{2\omega }\sin (\omega t_0)=\exp \left( \frac{t_0}{2}\right)$ and let

$$\begin{aligned} b_2^*=\exp \left( \frac{t_0}{2}\right) \frac{\omega (\frac{1}{3}+b_1)}{\sin (\omega t_0)} \quad \text{ with } \,\,\, \omega =\frac{\sqrt{4p-1}}{2}. \end{aligned}$$

Suppose $\frac{3b_1^2}{4}<b_2^*$, the following statements hold.

• (a) If $b_2>b_2^*$, system (4) has a heteroclinic orbit connecting $S_3$ and $F_l$, which has no sliding motion. The system has neither closed orbits nor homoclinic orbits.

• (b) If $b_2=b_2^*$, system (4) has a unique sliding heteroclinic cycle connecting $S_2$ and $S_3$, and has infinitely many sliding heteroclinic orbits connecting $S_3$ and $F_l$. The system has no closed orbits.

• (c) If $\frac{3b_1^2}{4}<b_2<b_2^*$, system (4) has a unique sliding cycle. And the system has neither other closed orbits nor homoclinic and heteroclinic orbits which connect two finite singularities.

• (d) If $b_2=\frac{3b_1^2}{4}$, for the different choice of $b_1$ system (4) can have either a unique sliding cycle or a sliding homoclinic cycle to the saddle–node $S$ of the sliding vector field. These sliding cycles consist of the sliding motion and the orbit arcs of both the left and right subsystem of (4).

• (e) If $\widetilde{b}_2<b_2<\frac{3b_1^2}{4}$, system (4) can have either a sliding cycle or a sliding homoclinic cycle to $S^+$ or a sliding heteroclinic orbit from $S^-$ to $S^+$. These sliding orbits are composed of the sliding motion and the orbit arcs of both the left and right subsystem of (4).

• (f) If $0<b_2\le \tilde{b_2}$, system (4) can have either a sliding homoclinic orbit from $S^-$ to $S^+$ or a sliding homoclinic cycle to $S^+$ or a sliding cycle. These sliding orbits are formed by the sliding motion and the orbit arc of only the left subsystem of (4).

Figure 4 shows all the topological structures of system (4) around the sliding region.

Fig. 4

The topological structures of trajectories in Theorem 4 a $b_2>b_2^*$ b $b_2=b_2^*$ c $\frac{3b_1^2}{4}<b_2<b_2^*$ d $b_2=\frac{3b_1^2}{4}$ e $\widetilde{b}_2<b_2<\frac{3b_1^2}{4}$ f $b_2\le \widetilde{b}_2$

In Theorem 4, there is the additional assumption $\frac{3b_1^2}{4}<b_2^*$. Lemma 12 in Appendix shows that this assumption can be realized. Of course, it is also possible that $\frac{3b_1^2}{4}\in [b_2^*,\infty )$ for some $b_1> \frac{1}{3}$ and $p>\frac{1}{4}$. We will not study these cases in this paper because the computation is tedious and the idea is similar.

We note that in the last theorem system (4) has the sliding heteroclinic bifurcation at $b_2=b_2^*$. Figure 4 illustrates the topological structures of the trajectories of system (4) involved in Theorem 4.

From Theorems 2 and 4 and their proofs, we get easily the following two results.

Corollary 5

Let $b_2^*$ be that defined in Theorem 4. Assume that system (4) satisfies $(\mathcal{A })$, $b_1= \frac{1}{3}$ and $\frac{3b_1^2}{4}<b_2^*$. Then the statements $(a)$ to $(f)$ of Theorem 4 hold.

As the comments stated after Theorems 2 and 4, we will not consider the cases $\frac{3b_1^2}{4}\in [b_2^*,\infty )$.

Corollary 6

System (4) has at most two closed orbits, and the maximum number can be achieved. The two ones may be either both hyperbolic limit cycles, or one hyperbolic limit cycle and a sliding ($sliding-zero$) cycle.

3 Dynamics Near the Sliding Region Via Singular Perturbation Theory

In this section, we will study the local structure of trajectories of system (4) near the sliding region via the geometrical singular perturbation theory, see e.g [10]. The results of this section will be used in the proof of our main results. Before studying system (4), we first give a general description for piecewise smooth vector fields (1) on how to transforming (1) near the sliding region to a singular perturbation problem. We should mention that our approach is based on the techniques developed in [5].

Let $\epsilon \ge 0$ be sufficiently small. A singular perturbation problem in $\mathbb{R }^2$ is a differential system which can be written as

$$\begin{aligned} x'=\frac{dx}{d\tau }=f(x,y,\epsilon ),\quad y'=\frac{dy}{d\tau }=\epsilon g(x,y,\epsilon ),\quad (x,y)\in \mathbb{R }^2, \end{aligned}$$

(9)

or equivalently, after the time rescaling $t=\epsilon \tau$,

$$\begin{aligned} \epsilon \dot{x}=\epsilon \frac{dx}{dt}=f(x,y,\epsilon ),\quad \dot{y}=\frac{dy}{dt}=g(x,y,\epsilon ), \quad (x,y)\in \mathbb{R }^2, \end{aligned}$$

(10)

where $f,g$ are smooth in their variables. We note that for $\epsilon >0$ systems (9) and (10) are the same. Systems (9) and (10) are called respectively the fast and slow systems of the singular perturbation problem. The set $SM=\{(x,y): f(x,y,0)=0\}$ is called the slow manifold of the singular perturbation problem. We say that $p\in SM$ is normally hyperbolic if $\frac{\partial f}{\partial x}(p,0)\ne 0$. By the Fenichel’s geometric singular perturbation theory [10] the slow manifold will be preserved and it is invariant by the flow of (10) for $0<\epsilon \ll 1$.

Consider the piecewise smooth vector field (1). Let $\phi :\mathbb{R }\rightarrow \mathbb{R }$ be a $C^{\infty }$ transition function satisfying $\phi (x)=-1$ for $x\le -1$, $\phi (x)=1$ for $x\ge 1, \,\phi (0)=0$ and $\phi '(x)>0$ if $x\in (-1,1)$. The $\phi$–regularization of the vector field $X$ defined in (1) is a $1$-parameter family of $C^k$ vector fields $X_{\epsilon }$ defined in $\mathbb{R }^2$ for $k\in \mathbb{N }\cup \{\infty \}$ by

$$\begin{aligned} X_{\epsilon }=\left( \frac{1}{2}+\frac{\phi _{\epsilon }(x)}{2}\right) X_{r}+\left( \frac{1}{2}-\frac{\phi _{\epsilon }(x)}{2}\right) X_{l}, \end{aligned}$$

where $\phi _{\epsilon }(x)=\phi (\frac{x}{\epsilon })$ for $\epsilon >0$.

The trajectories of $X_{\epsilon }$ in $\mathbb{R }^2$ satisfy the differential system

$$\begin{aligned} \dot{x}&= \frac{f_r+f_l}{2}+\phi \left( \frac{x}{\epsilon }\right) \frac{f_r-f_l}{2},\nonumber \\ \dot{y}&= \frac{g_r+g_l}{2}+\phi \left( \frac{x}{\epsilon }\right) \frac{g_r-g_l}{2},\nonumber \\ \dot{\epsilon }&= 0, \end{aligned}$$

(11)

for $\epsilon >0$, where $f_r$ and $f_l$ are the first components of $X_r$ and $X_l$ and $g_r$ and $g_l$ are the second components of $X_r$ and $X_l$, respectively. Observe that system (11) is not defined at $\epsilon =0$. Taking the directional blow-up $\beta :\mathbb{R }^3\rightarrow \mathbb{R }^3$ given by $(x,y,\epsilon )=\beta (\bar{x},y,{\epsilon })=(\bar{x}{\epsilon },y, {\epsilon })$, system (11) can be written in

$$\begin{aligned} {\epsilon }\dot{\bar{x}}&= \frac{f_r+f_l}{2}+\phi (\bar{x})\frac{f_r-f_l}{2},\nonumber \\ \dot{y}&= \frac{g_r+g_l}{2}+\phi (\bar{x})\frac{g_r-g_l}{2},\nonumber \\ \dot{{\epsilon }}&= 0. \end{aligned}$$

(12)

Clearly, system (12) is a singular perturbation one, and is well–defined at $\epsilon =0$.

In addition we take the polar coordinate blow-up

$$\begin{aligned} \alpha :\,\,[0,\infty )\times \left[ \frac{\pi }{4},\frac{3\pi }{4}\right] \times \mathbb{R }&\longrightarrow \mathbb{R }^3\\ (r,\theta ,y)\qquad&\longrightarrow (x,y,\epsilon )=(r\cos \theta ,y,r\sin \theta ). \end{aligned}$$

Then (11) can be written in

$$\begin{aligned} \theta '&= -\sin \theta \left( \frac{f_r+f_l}{2}+\phi (\cot \theta )\frac{f_r-f_l}{2}\right) ,\nonumber \\ y'&= r\left( \frac{g_r+g_l}{2}+\phi (\cot \theta )\frac{g_r-g_l}{2}\right) ,\nonumber \\ r'&= r\cos \theta \left( \frac{f_r+f_l}{2}+\phi (\cot \theta )\frac{f_r-f_l}{2}\right) , \end{aligned}$$

(13)

where we have used the time rescaling $dt=rd\tau$, and the prime denotes the derivative with respect to $\tau$. We mention that the interval of $\theta$ is different from that of [5], because $\phi (\cot \theta )$ is constant on either $(0,\frac{\pi }{4})$ or $(\frac{3\pi }{4},\pi )$, and is not defined at $\theta =0$ and $\pi$.

We note that system (13) is not a singular perturbation one, but instead of $r$ we use the first integral $r\sin \theta =c$ of (13) as a new variable, then system (13) can be written in an equivalent way as a singular perturbation one. For this reason, in what follows we will say (13) a singular perturbation system.

Since $\theta \in \left[ \frac{\pi }{4},\frac{3\pi }{4}\right]$, so $r\sin \theta =0$ if and only if $r=0$. Consequently, the parameter value $\epsilon =0$ corresponds to $r=0$. As shown in [5] the directional blow-up and the polar blow-up are essentially the same. In fact, it follows from the map $G:[0,\infty )\times \left[ \frac{\pi }{4},\frac{3\pi }{4}\right] \times \mathbb{R }\rightarrow \mathbb{R }^3$ given by $G(r,\theta ,y)=(\cot \theta ,y,r\sin \theta )$ satisfying $\beta \circ G=\alpha$ and $\det \left( \frac{\partial G}{\partial (r,\theta ,y)}\right) =\csc \theta \ne 0$. More information on the method of blowing up for families of vector fields can be found in [7] and [6].

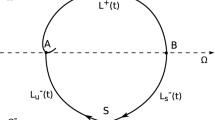
The fast flow of (13) on $S_{+}^{1}\times \mathbb{R }=\{(\cos \theta ,\sin \theta ,y):\,\theta \in \left[ \frac{\pi }{4},\frac{3\pi }{4}\right] ,y\in \mathbb{R })\}$ is given by the solutions of

$$\begin{aligned} \theta '=-\sin \theta \left( \frac{f_r+f_l}{2}+\phi (\cot \theta ) \frac{f_r-f_l}{2}\right) ,\quad y'=0. \end{aligned}$$

(14)

The slow flow of (13) is given by the solutions of

$$\begin{aligned} 0=\frac{f_r+f_l}{2}+\phi (\cot \theta )\frac{(f_r-f_l)}{2},\quad \dot{y}=\left( \frac{g_r+g_l}{2}+\phi (\cot \theta )\frac{g_r-g_l}{2}\right) . \end{aligned}$$

(15)

According to Theorem 2.2 of [22], we know that the sliding region $(0,b_1)$ of the discontinuous vector fields $X$ given in (1) is homeomorphic to the slow manifold

$$\begin{aligned} \left\{ (\theta ,y)\in (0,\pi )\times (0,b_1):\,\sin \theta \left( \frac{f_r+f_l}{2}+\phi (\cot \theta ) \frac{f_r-f_l}{2}\right) =0\right\} . \end{aligned}$$

The sliding vector field $X_s$ is topologically equivalent to the reduced problem (15) on the slow manifold.

We now turn to the concrete system (4). Corresponding to the general singular perturbation system (13), we have the following singular perturbation system

$$\begin{aligned} r\dot{\theta }&= -\sin \theta \left[ \frac{(\frac{4}{3}-2r\cos \theta )y -(r\cos \theta +b_1)}{2}+\phi (\cot \theta )\frac{b_1+r\cos \theta -(\frac{2}{3}+2r\cos \theta )y}{2}\right] ,\nonumber \\ \dot{y}&= \frac{y^2-r(p+1)\cos \theta -b_2-3r^2\cos ^2\theta }{2} +\phi (\cot \theta )\frac{r(p-1)\cos \theta +b_2-3r^2\cos ^2\theta +y^2}{2},\nonumber \\ \dot{r}&= \cos \theta \left[ \frac{(\frac{4}{3}-2r\cos \theta )y -(r\cos \theta +b_1)}{2}+\phi (\cot \theta )\frac{b_1+r\cos \theta -(\frac{2}{3}+2r\cos \theta )y}{2}\right] .\qquad \quad \end{aligned}$$

(16)

The slow manifold of (16) is

$$\begin{aligned} \left\{ (\theta ,y)\in \left[ \frac{\pi }{4},\frac{3\pi }{4}\right] \times \mathbb{R }: \frac{2y}{3}-\frac{b_1}{2}+\phi (\cot \theta )\left( \frac{b_1}{2} -\frac{y}{3}\right) =0\right\} , \end{aligned}$$

which can be written in

$$\begin{aligned} y(\theta )=\frac{b_1(1-\phi (\cot \theta ))}{\frac{4}{3}-\frac{2}{3}\phi (\cot \theta )},\quad \theta \in \left[ \frac{\pi }{4},\frac{3\pi }{4}\right] . \end{aligned}$$

(17)

The reduced flow is

$$\begin{aligned} \frac{2y}{3}-\frac{b_1}{2}+\phi (\cot \theta )\left( \frac{b_1}{2}-\frac{y}{3}\right) =0,\quad \dot{y}=\frac{y^2-b_2}{2}+\phi (\cot \theta )\frac{y^2+b_2}{2}. \end{aligned}$$

That is, on the slow manifold we have

$$\begin{aligned} \dot{y}=\frac{b_1y^2-y^3-\frac{b_1}{3}y}{b_1-\frac{2}{3}y}, \end{aligned}$$

(18)

which is the same as the sliding vector field $X_s$. This implies that if $\phi _1$ and $\phi _2$ are different transition functions then the phase portrait in the blow up loci (16) are the same.

The fast flow is given by the solutions of the system

$$\begin{aligned} \theta '=-\sin \theta \left[ \frac{2y}{3} -\frac{b_1}{2}+\phi (\cot \theta )\left( \frac{b_1}{2}-\frac{y}{3}\right) \right] ,\quad y'=0. \end{aligned}$$

(19)

Clearly the fast vector field satisfies $\theta '>0$ for $\{(\theta ,y):\, \theta \in [\frac{\pi }{4},\frac{3\pi }{4}], 0<y<y(\theta )\}$, and $\theta '<0$ for $\{(\theta ,y):\, \theta \in [\frac{\pi }{4},\frac{3\pi }{4}], y(\theta )<y<b_1\}$, where $y(\theta )$ is given in (17).

Notice that $(\theta ,y)=(\frac{\pi }{4},0)$ and $(\theta ,y)=(\frac{3\pi }{4},b_1)$ are not normally hyperbolic for the slow manifold, because

$$\begin{aligned} \left. \frac{\partial }{\partial \theta }\left( \frac{2y}{3}-\frac{b_1}{2}+\phi (\cot \theta )\left( \frac{b_1}{2}-\frac{y}{3}\right) \right) \right| _{(\frac{\pi }{4},0) \text{ or } (\frac{3\pi }{4},b_1)}=0. \end{aligned}$$

In order to study the dynamics of the fast flow near $(\theta ,y)=(\frac{\pi }{4},0)$, we take an additional blow-up at this point given by

$$\begin{aligned} \theta =s\cos \psi +\frac{\pi }{4},\quad y=s\sin \psi , \end{aligned}$$

(20)

with $s\ge 0$ and $\psi \in [-\frac{\pi }{2},\frac{\pi }{2}]$. Then we get from (19) that

$$\begin{aligned} s'=-\cos \psi \sin \left( s\cos \psi +\frac{\pi }{4}\right) H(s,\psi ),\quad \psi '=\frac{\sin \psi }{s}\sin \left( s\cos \psi +\frac{\pi }{4}\right) H(s,\psi ), \end{aligned}$$

where

$$\begin{aligned} H(s,\psi )=\frac{2s}{3}\sin \psi -\frac{b_1}{2}+\phi \left( \cot \left( s\cos \psi +\frac{\pi }{4}\right) \right) \left( \frac{b_1}{2} -\frac{s\sin \psi }{3}\right) . \end{aligned}$$

Since

$$\begin{aligned} \lim _{s\rightarrow 0}\psi ' =\frac{\sqrt{2}}{6}\sin ^2\psi , \end{aligned}$$

it implies that for $s>0$ suitably small, the function $\psi$ is increasing for $\psi \in (-\frac{\pi }{2},\frac{\pi }{2})$.

Analogously, for studying the dynamics of (19) at the point $(\theta ,y)=(\frac{3\pi }{4},b_1)$, we take the following transformation

$$\begin{aligned} \theta =s\cos \psi +\frac{3\pi }{4},\quad \bar{y}=s\sin \psi +b_1, \end{aligned}$$

(21)

where $s\ge 0$ and $\psi \in [\frac{\pi }{2},\frac{3\pi }{2}]$. A direct calculation shows that

$$\begin{aligned} s'=-\cos \psi \sin \left( s\cos \psi +\frac{3\pi }{4}\right) G(s,\psi ),\quad \psi '=\frac{1}{s}\sin \psi \sin \left( s\cos \psi +\frac{3\pi }{4}\right) G(s,\psi ), \end{aligned}$$

where

$$\begin{aligned} G(s,\psi )=\frac{2}{3}s\sin \psi +\frac{b_1}{6} +\phi \left( \cot \left( s\cos \psi +\frac{3\pi }{4}\right) \right) \left( \frac{b_1}{6}-\frac{s}{3}\sin \psi \right) . \end{aligned}$$

Since

$$\begin{aligned} \lim _{s\rightarrow 0}\psi ' =\frac{\sqrt{2}}{2}\sin ^2\psi , \end{aligned}$$

for $s>0$ suitably small, the function $\psi$ is increasing for $\psi \in (\frac{\pi }{2},\frac{3\pi }{2})$.

Combining the above results with Proposition 1, if $\epsilon =0$, i.e $r=0$, we have the phase portraits of the fast and slow dynamics of the singular perturbation problem (16), which are shown in Fig. 5, where the double arrow means that the trajectories are the ones of the fast system, and the single arrow means that the trajectories are the ones of the slow system.

Fig. 5

Phase portrait of the fast and slow dynamics of system (16) a $b_2>\frac{3b_1^2}{4}$ b $b_2=\frac{3b_1^2}{4}$ c $b_2<\frac{3b_1^2}{4}$

In Fig. 5b, the sliding vector field (18) has a saddle–node in the interior of the sliding region, and in Fig. 5c the sliding vector field (18) has a stable and an unstable singularities inside the sliding region, the trajectories of the sliding vector field can slide only on the segments separated by these singularities.

From Fig. 5 and the Fenichel’s geometric singular perturbation theory we can get the following

Proposition 7

A positive orbit of (4) starting at a point of the sliding region can either slide along the sliding region until reaching a singularity, or leave the sliding region at any time from its left or right side.

4 Proof of the Main Results

4.1 Proof of Theorem 2

Under the assumption $(\mathcal{A })$, the left system of (4) has the focus $F_l$, and the right system has three saddles and a center $O$, the latter is located on $Y$. Recall that the right system has the analytic Hamiltonian

$$\begin{aligned} H(x,y)=\frac{(1-6x)y^2}{6}+\frac{x^2}{2}+x^3. \end{aligned}$$

So, any orbit of the right system must be contained in the level curve of $H(x,y)$. At $S_1$ the Hamiltonian $H$ has the value $h_s=\frac{1}{54}$. The level curve $H=h_s$ has two branches intersecting the $y$ axis at the points $P^+=(0,\frac{1}{3})$ and $P^-=(0,-\frac{1}{3})$. These two branches are also one of the separatrices of $S_2$ and $S_3$, respectively. We denote by $\Gamma _{r}^+$ and $\Gamma _{r}^-$ the separatrices of $S_2$ and $S_3$ which pass through $P^+$ and $P^-$, respectively. Of course, $\Gamma _r^+$ and $\Gamma _r^-$ are also the separatrices of $S_1$.

Since $0<b_1<\frac{1}{3}$, the sliding region is located in between $P^-$ and $P^+$. If system (4) has a closed orbit, it must intersect the $y$ axis and the orbit arc on the left hand side of the $y$ axis should be located in between $\Gamma _{r}^+$ and $\Gamma _{r}^-$.

Suppose that system (4) has a closed orbit or a heteroclinic cycle, denoted by $\Gamma _h$. Its right half part should be contained in the level curve $H(x,y)=h$ for some $h\in \mathbb{R }$. Let $C=(0,y_+)$ with $y_+>0$ and $D=(0,y_-)$ with $y_-<0$ be the two intersection points of $\Gamma _h$ with the $y$ axis. Then we have $y_+=-y_-$.

We now study the orbits of the left system. The orbit of system (4) in $G_l$ starting at $A=(0,s_1)$ at $t=0$ is given by

$$\begin{aligned} x^+(t)&= \exp \left( -\frac{t}{2}\right) \left[ \frac{b_2}{p}\cos (\omega t)+\frac{2ps_1-2p b_1+b_2}{2p\omega }\sin (\omega t)\right] -\frac{b_2}{p},\\ y^+(t)&= \exp \left( -\frac{t}{2}\right) \left[ \frac{ps_1-b_1p+b_2}{p}\cos (\omega t)+\frac{ps_1-2b_2p-b_1p+b_2}{2p\omega }\sin (\omega t)\right] \\&-\frac{b_2}{p}+b_1, \end{aligned}$$

where $\omega =\frac{\sqrt{4p-1}}{2}$. Denote by $\Gamma _A$ this orbit. Assume that after a certain time $t_1>0$, the orbit $\Gamma _A$ arrives at $y$ axis at $B=(0,s_2)$. Then $s_2\ge b_1$ and $A$ is located under $B$ and

$$\begin{aligned} x^+(t_1)=0,\qquad y^+(t_1)=s_2. \end{aligned}$$

(22)

Of course, we ask the $t_1>0$ to be the minimum time for which (22) holds. From the expression of $x^+(t)$ we get that $\sin (\omega t_1)\ne 0$. The following result due to Gannakopoulos and Pliete [12] will be used in the proof of Theorem 2.

Lemma 8

The intersection points $A=(0,s_1)$ and $B=(0,s_2)$ with $s_1<s_2$ of an orbit of the left system of (4) with the $y$ axis at the time $t_1>0$ satisfy

$$\begin{aligned} \begin{array}{l} \displaystyle s_1=\frac{-b_2\omega }{p\sin (\omega t_1)}\left[ \cos (\omega t_1)+\frac{\sin (\omega t_1)}{2\omega }-\exp \left( \frac{t_1}{2}\right) \right] +b_1,\\ \displaystyle s_2=\frac{b_2\omega }{p\sin (\omega t_1)}\left[ \cos (\omega t_1)-\frac{\sin (\omega t_1)}{2\omega }-\exp \left( -\frac{t_1}{2}\right) \right] +b_1. \end{array} \end{aligned}$$

(23)

Recall that the sliding region is located in between $O$ and $P^+$. So, the closed orbits (if exist) may have three possibilities: a sliding cycle, a sliding–zero cycle, or a limit cycle containing the sliding region in its interior enclosed by the limit cycle, see Fig. 1.

If system (4) has a limit cycle or a sliding–zero cycle or a heteroclinic cycle, we must have $A=D$ and $B=C$. These require that

$$\begin{aligned} s_1=-s_2 \quad \text{ and } \quad s_2\in \left[ b_1,\frac{1}{3}\right] . \end{aligned}$$

The condition $s_1=-s_2$ is equivalent to that the functional equation

$$\begin{aligned} b_2=\dfrac{2b_1 p\sin (\omega t_1)}{\sin (\omega t_1)-\omega \exp (\frac{t_1}{2})+\omega \exp (-\frac{t_1}{2})} \end{aligned}$$

(24)

has roots in $t_1$ with $t_1>0$ for given $b_1,b_2$ and $p$ satisfying the assumptions of the theorem.

We now study the number of roots of (24) in $t_1>0$. Set $s=\omega t_1$ and $v=\frac{1}{2\omega }$, and define

$$\begin{aligned} q(s)=\sin s-\omega \exp (vs)+\omega \exp (-vs), \quad f(s)=\dfrac{\sin s}{q(s)}. \end{aligned}$$

Recall from [23] that $q(s)<0$ for $s\in (0,\infty )$ and it is decreasing. Equation (24) becomes the following functional equation in $s>0$

$$\begin{aligned} b_2=2b_1 pf(s). \end{aligned}$$

(25)

Since $b_1,b_2>0$, we get from [23] that $s\in (\pi , 2\pi )\,(\text{ mod }2\pi )$ and the equation

$$\begin{aligned} \exp (vs)(\cos s-v\sin s)-1=0, \end{aligned}$$

has a unique root in $(\pi , 2\pi )$, denoted by $s_0$. Next we investigate the number of roots of equation (25) in $s\in (\pi ,s_0)$. Since $b_1,\,b_2,\, p>0$, we get from (25) that

$$\begin{aligned} f(s)>0. \end{aligned}$$

If $s=s_0$, it follows from the second equation of (23) that $s_2=b_1$. For any fixed $b_1,p$, set $b_2^{sc}=2b_1pf(s_0)$. So if $s=s_0$ and $b_2=b_2^{sc}$, we have $s_2=-s_1=b_1$. Consequently system (4) has a sliding–zero cycle, which passes through the points $(0,-b_1)$ and $(0,\,b_1)$.

Next we consider the existence of closed orbits passing through $(0,\,s_2)$ with $s_2\in (b_1,\frac{1}{3})$. In this case we have $s\in (\pi ,s_0)$. We will prove the existence of closed orbits and that if the closed orbits exist, they must be limit cycles. By (23) we have

$$\begin{aligned} s_2=\frac{b_2\omega }{p\sin s}(\cos s-v\sin s-\exp (-vs))+b_1. \end{aligned}$$

(26)

The function $s_2$ in $s$ is decreasing for $s\in (\pi , s_0)$, and $\lim \limits _{s\rightarrow \pi ^+}s_2=\infty$. This shows that there exists a unique $s_h\in (\pi ,s_0)$ such that $s_2(s_h)=\frac{1}{3}$; $s_2(s)>\frac{1}{3}$ if $s\in (\pi , s_h)$; and $s_2(s)\in \left( b_1,\frac{1}{3}\right)$ if $s\in (s_h, s_0)$.

Set $b_2^h=2b_1pf(s_h)$. The above proof shows that if $b_2=b_2^h$, system (4) has a heteroclinic cycle connecting $S_2$ and $S_3$, which contains the sliding region in its interior.

For $s\in (\pi ,s_h)$, since $s_2(s)>\frac{1}{3}$ it is not possible to have closed orbits or sliding cycles or heteroclinic cycles, which are composed of both the left and the right orbits. Hence, to investigate the existence of closed orbits is equivalent to find the miximal number of roots of the functional Eq. (25) in $(s_h,\,s_0)\subset (\pi ,\, s_0)$. For this purpose, we study the graph of the function $f(s)$.

Some calculations show that $f(\pi )=0, \,f(s_0)>0$ and

$$\begin{aligned} f'(s)=\dfrac{\omega (-\exp (sv)+\exp (-sv)) \cos s+\omega v( \exp (sv)+ \exp (-sv))\sin s}{(\sin s-\omega \exp (sv)+\omega \exp (-sv))^2}. \end{aligned}$$

(27)

From $1-\exp (-v s_0)(\cos s_0+v\sin s_0)=1-(\cos s_0+v\sin s_0)(\cos s_0-v\sin s_0)=\sin ^2 s_0(v^2+1)>0$ we have

$$\begin{aligned} f'(s_0)=\dfrac{-\omega [1-\exp (-v s_0)(\cos s_0+v\sin s_0)]}{(\sin s_0-\omega \exp (s_0v)+\omega \exp (-s_0v))^2}<0. \end{aligned}$$

Since $f'(\pi )>0$, there exists an $s^*\in (\pi ,s_0)$ such that $f'(s^*)=0$. We claim that $s^*$ is the unique extreme point of $f$ in $(\pi , s_0)$. Indeed, set

$$\begin{aligned} u(s)= (-\exp (sv)+\exp (-sv)) \cos s+ v( \exp (sv)+ \exp (-sv))\sin s. \end{aligned}$$

(28)

We have

$$\begin{aligned} u'(s)=(1+ v^2)(\exp (vs)-\exp (-vs))\sin s<0 \quad \text{ for } s\in (\pi ,s_0). \end{aligned}$$

(29)

So $s^*$ is the unique zero point of $f'(s)$, and that $f(s)$ is strictly increasing on $(\pi ,s^*)$ and is strictly decreasing on $(s^*,s_0)$. This proves the claim and so $s^*$ is the maximum point of $f$ in $(\pi ,\,s_0)$.

Set $b_2^{m}= 2b_{1} pf(s^*)$, we have $b_2^{sc}<b_2^m$. Without loss of generality we assume that $b_2^h<b_2^{sc}$. Otherwise, the case $b_2^{sc}\le b_2$ can be similarly studied. The following result presents the root of Eq. (25) in $s$.

Proposition 9

The functional Eq. (25) in $s$ has a unique root if $b_2^h<b_2<b_2^{sc}$; two roots with one of which is the $s_0$ if $b_2=b_2^{sc}$; two roots if $b_2^{sc}<b_2<b_{2}^m$; a multiple two root if $b_2=b_{2}^{m}$; and no roots if $b_2>b_{2}^{m}$.

We mention that each root of Eq. (25), except $s_0$, corresponds to a closed orbit without sliding motion of system (4). Since the closed orbit is isolated, it is a limit cycle. We next study the stability of the limit cycles of the piecewise smooth differential system (4). For doing so, we need to compute the derivative of the Poincaré map defined on the $y$ axis of system (4). Define

$$\begin{aligned} \quad P_r:[0,+\infty )\longrightarrow (-\infty ,0] \end{aligned}$$

to be the map induced by the flow of the right Hamiltonian system, which maps the points on the positive $y$ axis to the negative $y$ axis, and define

$$\begin{aligned} P_l:(-\infty ,0]\longrightarrow [0, +\infty ), \end{aligned}$$

to be the map induced by the left linear flow, which maps the negative $y$ axis to the positive $y$ axis. Then the Poincaré map of system (4) defined on the $y$ axis is

$$\begin{aligned} P=P_r\circ P_l:\,\,(-\infty , 0]\rightarrow (-\infty ,0]. \end{aligned}$$

The derivative of the Poincaré map $P$ with respect to $s_1$ is

$$\begin{aligned} \frac{dP}{ds_1}-1&= \frac{dP_r}{dP_l}\frac{dP_l}{ds_1}-1=-\frac{dP_l}{ds_1}-1=-\frac{ds_2/ds}{ds_1/ds}-1\\&= \frac{(\exp (-vs)-\exp (vs))\cos s+v (\exp (-vs)+\exp (vs))\sin (s)}{(\cos s-v\sin s)\exp (vs)-1}. \end{aligned}$$

Recall that $s_0$ is the unique root of $(\cos s-v\sin s)\exp (vs)-1=0$. For $s<s_0$, we have $(\cos s-v\sin s)\exp (vs)-1<0$ and $u(s_0)<0$. Hence

$$\begin{aligned} \frac{dP}{ds_1}|_{s=s_0}=\lim _{s\rightarrow s_0-}\frac{dP}{ds_1}=+\infty ; \end{aligned}$$

It follows from the property of the function $u(s)$ defined in (28) and $l(s)<0$ for $s\in (\pi , s_0)$ that

$$\begin{aligned} \frac{dP}{ds_1}>1 \text{ for } s\in (s^*,s_0]; \quad \frac{dP}{ds_1}=1 \text{ for } s=s^*;\quad \text{ and } \quad 0\le \frac{dP}{ds_1}<1 \text{ for } s\in (\pi ,s^*). \end{aligned}$$

Combining the above proof and Proposition 7, we get the following facts:

• (a) If $b_2>b_{2}^{m}$, system (4) has a heteroclinic orbit connecting $S_3$ and $F_l$, see Fig. 3a.

• (b) If $b_2=b_{2}^{m}$, system (4) has a limit cycle of multiplicity two, which is semistable. Here the multiplicity 2 limit cycle bifurcation happens, see Fig. 3b.

• (c) If $b_2^{sc}<b_2<b_{2}^{m}$, system (4) has two hyperbolic limit cycles. The outside one is stable, and the inside one is unstable. The unstable limit cycle contains the sliding region in its interior, see Fig. 3c.

• (d) If $b_2=b_2^{sc}$, system (4) has the stable limit cycle and a sliding–zero cycle. The two cycles are central nested, and the inner sliding–zero cycle passes through the upper end point of the sliding region $\{(x,y)\in M| \,\, y\in [0,b_1]\}$. Here the sliding cycle bifurcation happens, see Fig. 3d.

• (e) If $b_2^h<b_2<b_2^{sc}$, system (4) has the stable limit cycle and a sliding cycle. The limit cycle surrounds the sliding cycle, see Fig. 3e.

• (f) If $b_2=b_2^h$, system (4) has the sliding cycle and a heteroclinic orbit. The sliding cycle is located in the interior of the region limited by the heteroclinic orbit. Here a heteroclinic bifurcation happens, see Fig. 3f.

• (g) If $\frac{3b_1^2}{4}<b_2<b_2^h$, system (4) has a unique closed orbit, which is the sliding cycle, see Fig. 3g.

Finally we consider the case $0<b_2\le \frac{3b_1^2}{4}$, in which the sliding vector field has singularities in the interior of the sliding region. The above proof of this theorem shows that for $b_2<b_2^h$, we have $-s_1<s_2$ if $s_1<0$. Recall that $(0,s_1)$ is the starting point of an orbit of the left system of (4), and that $(0,s_2)$ is the first intersection point of the orbit from $(0,s_1)$. Hence system (4) has neither closed orbits including limit cycles and sliding–zero cycles nor heteroclinic cycles passing through $S_2$ and $S_3$.

Now the possible interesting orbits are the sliding ones. A sliding orbit should pass through $(0,b_1)$ and is tangent to the $y$ axis at this point. From Lemma 8 we must have $s=s_0$, and so $s_2=b_1$. It follows that $s_1>-b_1$.

Assume that $b_2=\frac{3b_1^2}{4}$. We will show that for the different choice of $b_1\in (0,\frac{1}{3})$, all the possibilities $s_1<-\frac{b_1}{2}, \,s_1=-\frac{b_1}{2}$ and $s_1<-\frac{b_1}{2}$ can be realized.

From Lemma 8 and the fact that $s_0$ is the unique root of $\cos s-v\sin s-\exp (-vs)=0$ in $(\pi ,2\pi )$, we get that $s_1<-\frac{b_1}{2}$ is equivalent to

$$\begin{aligned} \frac{b_1}{p}>2K(s_0), \end{aligned}$$

where

$$\begin{aligned} K(s)=\frac{\sin s}{\omega (\cos s+v\sin s-\exp (vs))}. \end{aligned}$$

We claim that

$$\begin{aligned} K(s_0)<\frac{2}{3}. \end{aligned}$$

Indeed, direct calculations show that

$$\begin{aligned} K(s_0)\!-\!\frac{2}{3}\!=\!\left. \frac{2\sin s\!+\!2\omega \exp (vs)\!-\!2\omega \cos s}{3\omega (\cos s\!+\!v\sin s-\exp (vs))}\right| _{s=s_0} \!=\!\frac{2\omega (v\sin s_0\!+\!\exp (vs_0)-\exp (-vs_0))}{3\omega (\cos s_0+v\sin s_0-\exp (vs_0))}. \end{aligned}$$

For $s\in [\pi ,s_0]$, we have

$$\begin{aligned} (v\sin s+\exp (vs)-\exp (-vs))'=v\cos s+v(\exp (vs)+\exp (-vs))\ge 2v +v\cos s >0. \end{aligned}$$

So, $v\sin s_0+\exp (vs_0)-\exp (-vs_0)\ge \exp (v\pi )-\exp (-v\pi )>0$. Note that $\cos s_0+v\sin s_0-\exp (vs_0)<0$, the claim follows.

In addition, $K(s)$ is strictly monotone increase for $s\in [\pi ,s_0]$ and $K(\pi )=0$, we have $0<K(s_0)<\frac{2}{3}$.

Since $0<b_1<\frac{1}{3}$ and $p>\frac{1}{4}$, we have $\frac{b_1}{p}\le \frac{4}{3}$. By the definition, $K(s)$ is independent of $b_1$. So for the suitable choice of the values of $b_1$ and $p$, denoted by $b_1^0$ and $p^0$ respectively, we can have $2K(s_0)<\frac{b_1^0}{p^0}$, i.e. $s_1<-\frac{b_1^0}{2}$. These facts and Proposition 7 imply that system (4) has a sliding cycle, which consists of the right part of the level curve of $H(x,y)=H(0,s_1)$, the orbit arc from $(0,s_1)$ to $(0,b_1)$ of the left system and the sliding motion from $(0,b_1)$ to $(0,-s_1)$. The phase portrait is given in Fig. 3(${h}_1$).

For the given $p^0$, we can choose $b_1<b_1^0$ such that $2K(s_0)=\frac{b_1}{p^0}$ and $2K(s_0)>\frac{b_1}{p^0}$. Hence we can have $s_1=-\frac{b_1}{2}$ and $s_1>-\frac{b_1^0}{2}$, respectively. In the former, system (4) has a sliding homoclinic cycle, which consists of the right part of the level curve of $H(x,y)=H(0,-b_1/2)$, the orbit arc from $(0,-b_1/2)$ to $(0,b_1)$ of the left system and the sliding motion from $(0,b_1)$ to $(0,b_1/2)$. In the latter, system (4) has a sliding homoclinic cycle, which consists of the sliding motion from $(0,\frac{b_1}{2})$ down to $(0,-s_1)$, the right part of the level curve of $H(x,y)=H(0,s_1)$, the orbit arc from $(0,s_1)$ to $(0,b_1)$ of the left system and the sliding motion from $(0,b_1)$ to $(0,\frac{b_1}{2})$. Consequently we have the phase portrait given in Fig. 3(${h}_2$), (${h}_3$), respectively.

We now consider the case $0<b_2<\frac{3b_1^2}{4}$, under which the sliding vector field has the two hyperbolic singularities $S^+$ and $S^-$. The former is stable and the latter is unstable.

For the different choice of $b_1$ in the last case $(h)$, it follows from Lemma 8 that we can determine a $b_2$, denoted by $\hat{b}_2$, depending on $b_1$ and $p$ such that $s_1=0$. So for $\hat{b}_2<b_2<\frac{3b_1^2}{4}$, by the continuation of solutions with respect to the parameters of the system we can get the five phase portraits given in Fig. 3i. In Fig. 3(${i}_1$), (${i}_2$) we have respectively the sliding cycle and the sliding homoclinic cycle, which are composed of the left orbit, sliding motion and the right orbit. In Fig. 3(${i}_3$)–(${i}_5$) we have three different types of sliding heteroclinic orbits, which connect the two singularities on the sliding region.

For $0<b_2\le \hat{b}_2$, we have $0\le s_1<b_1$. With the decreasing of $b_2$ from $\hat{b}_2$ to $0$ we can have respectively the phase portraits (${j}_1$) to (${j}_5$) given in Fig. 3j. In $({j}_1), ({j}_2)$ and (${j}_3$) we have sliding heteroclinic orbits connecting $S^+$ and $S^-$, which consist of the left orbit arc and the sliding motion. In (${j}_4$) and (${j}_5$) we have respectively a sliding homoclinic cycle and a sliding cycle. Of course, in all phase portraits of Fig. 3j we also have a heteroclinic orbit, which connects $S_2$ and one of the singularities on the sliding region.

We complete the proof of Theorem 2.

4.2 Proof of Theorem 4

For simplicity we will use the notations given in the proof of Theorem 2. Denote by $\Gamma _r^+$ and $\Gamma _r^-$ the orbit arcs of the separatrices from the saddles $S_2$ and $S_3$ to $P^+$ and $P^-$ on the $y$ axis, respectively. Since $b_1>\frac{1}{3}$, it follows that $P^+$ is located in the interior of the sliding region.

Let $\Gamma _l$ be the negative orbit of the left system starting at $(0,\,b_1)$ at the time $t=0$. Then $\Gamma _l$ will return back to the $y$ axis. Let $(x^-_l(t),\,y^-_l(t))$ for $t<0$ be the expression of the orbit $\Gamma _l$. Some computations show that

$$\begin{aligned} x_l^-(t)&= \frac{b_2}{p} \exp \left( -\frac{t}{2}\right) \left[ \cos (\omega t)+\frac{1}{2\omega }\sin (\omega t)\right] -\frac{b_2}{p},\\ y_l^-(t)&= \frac{b_2}{p} \exp \left( -\frac{t}{2}\right) \left[ \cos (\omega t)-\frac{2p-1}{2\omega }\sin (\omega t)\right] -\frac{b_2}{p}+b_1, \end{aligned}$$

Assume that it is at a time $t_0<0$ that $\Gamma _l$ firstly returns back to the $y$ axis. Let $(0,\,y_l^-)$ be the intersection point of $\Gamma _l$ with the $y$ axis. Then the time $t_0$ satisfies

$$\begin{aligned} \cos (\omega t_0)+\frac{1}{2\omega }\sin (\omega t_0)=\exp \left( \frac{t_0}{2}\right) ,\qquad y_l^-=-b_2\frac{\sin (\omega t_0)}{\omega }\exp \left( -\frac{t_0}{2}\right) +b_1. \end{aligned}$$

(30)

Clearly the first equation of (30) has negative solutions. Moreover, by the assumption $t_0$ is the largest negative solution of the first equation in $t$ of (30). Since $y_l^-<b_1$, it follows that $\sin (\omega t_0)>0$, i.e. $\omega t_0\in (-2\pi ,-\pi )\,{mod}\,(2\pi )$. In what follows, we simply say $\omega t_0\in (-2\pi ,-\pi )$. For any fixed $b_1,p,b_2$ satisfying $(\mathcal{A })$, set

$$\begin{aligned} b_2^*=\exp \left( \frac{t_0}{2}\right) \left( \frac{1}{3}+b_1\right) \frac{\omega }{\sin (\omega t_0)}. \end{aligned}$$

$(a)$ If $b_2>b_2^*$, then $y_l^-<-\frac{1}{3}$. The separatrix $\Gamma _r^-$ from $S_3$ passes through $P^-$ will go to the focus $F_l$ of the left subsystem. We have Fig. 4a.

$(b)$ If $\frac{3b_1^2}{4}<b_2=b_2^*$, then $y_l^-=-\frac{1}{3}$. Denote by $\Gamma _0$ the sliding motion on $M_3$ from $(0,b_1)$ down to $(0,\frac{1}{3})$ of the sliding vector field $X_s$, and by $\Gamma ^*$ the separatrix connecting $S_2$ and $S_3$. Then we get from Proposition 7 that $\Gamma =\Gamma _l\cup \Gamma _0\cup \Gamma _{l}^+\cup \Gamma ^*\cup \Gamma _l^-$ form a sliding heteroclinic cycle, see Fig. 4b. Moreover it follows from the previous proof that system (4) has no closed orbits. This proves statement $(b)$.

$(c)$ If $\frac{3b_1^2}{4}<b_2<b_2^*$, we get from the second equation of (30) that $y_l^->-\frac{1}{3}$. Then $\Gamma _l$ together with the level curve passing through $(0,\,y_l^-)$ of the Hamiltonian $H(x,y)$ and the sliding motion on $M_3$ from $(0,b_1)$ down to $\left( 0,-y_l^-\right)$ of the sliding vector field $X_s$ form a sliding cycle, see Fig. 4c. Furthermore, it follows from the structure of the trajectories of the left and right systems that system (4) has neither other closed orbits nor heteroclinic and homoclinic orbits. Of course, we do not consider the heteroclinic ones going to infinity. This proves statement $(c)$.

$(d)$ If $b_2=\frac{3b_1^2}{4}$, then $y_l^->-\frac{1}{3}$. We will show that for the different choice of $b_1\in (\frac{1}{3},\infty )$, all the possibilities $y_l^-< (=,>)-\frac{b_1}{2}$ can appear. These are equivalent to

$$\begin{aligned} b_1>\,(=,\,<)\frac{2\omega }{\sin (\omega t_0)}\exp \left( \frac{t_0}{2}\right) . \end{aligned}$$

That is, $\frac{b_1}{3}+b_1^2>\,(=,\,<)\,2b_2^*$.

For $b_1\ge \frac{2}{3}$, we have $\frac{3}{2} b_1^2\ge \frac{b_1}{3}+b_1^2$. Since $\frac{3}{4}b_1^2<b_2^*$, it follows that $2b_2^*> \frac{b_1}{3}+b_1^2$. This proves the existence of the third possibility.

For $b_1\in (\frac{1}{3}, \frac{2}{3})$, by the definition of $b_2^*$ the inequality $2b_2^*\le \frac{b_1}{3}+b_1^2$ is equivalent to

$$\begin{aligned} b_1\ge 2\exp \left( \frac{t_0}{2}\right) \frac{\omega }{\sin (\omega t_0)}. \end{aligned}$$

(31)

Recall that $\omega =\sqrt{4p-1}$ and $\omega t_0\in (-2\pi ,-\pi )$. So if we choose $p>\frac{1}{4}$ with $p-\frac{1}{4}\ll 1$, i.e. $\omega$ sufficiently small, we will have $-t_0$ large enough because $\omega t_0\in (-2\pi ,-\pi )$. This proves that for the suitable choice of $p$ and $b_1$, if $b_2=\frac{3b_1^2}{4}$, we can have $y_l^-< (=,>)-\frac{b_1}{2}$.

In the case $y_l^-<-\frac{b_1}{2}$ we have a sliding cycle consisting of the sliding motion and the orbit arcs of both the left and right subsystems of (4), see Fig. 4(d$_1)$.

In the case $y_l^-\ge -\frac{b_1}{2}$ we have a sliding homoclinic cycle to $S$, which consists of the sliding motion and the orbit arcs of both the left and right subsystems of (4), see Fig. 4(${d}_2$), (${d}_3$). Now we have also a sliding heteroclinic orbit to $S$ and $S_2$.

From the second equation of (30), it follows that there exists a $\widetilde{b}_2\in (0,\frac{3b_1^2}{4})$ for which $y_l^-=0$.

$(e)$ $\widetilde{b}_2<b_2<\frac{3b_1^2}{4}$. We have $-\frac{1}{3}<y_l^-<0$. The sliding vector field $X_s$ has the two hyperbolic singularities $S^+$ and $S^-$. Similar to the proof of the last statement $(d)$ and the statement $(i)$ of Theorem 2, we can get the dynamics of system (4) as shown in Fig. 4e, where the system can have either a sliding cycle, or a sliding homoclinic cycle to $S^+$, or a sliding heteroclinic orbit to $S^+$ and $S^-$, which are composed of the sliding motion and the orbit arcs of both the left and right subsystem of (4). Note that in the phase portrait Fig. 4(${e}_2$) we have also a sliding heteroclinic orbit connecting $S^+$ and $S_2$. In Fig. 4(${e}_3$)–(${e}_5$) the system has a sliding heteroclinic orbit to $S^-$ and $S_2$.

$(f)$ $b_2\le \widetilde{b}_2$. We have $y_l^-\ge 0$. The sliding vector field $X_s$ has also the singularities $S^+$ and $S^-$. Similar to the proof of the case $(d)$ and the statement $(j)$ of Theorem 2, we can get the dynamics of system (4) as shown in Fig. 4f, where the system can have either a sliding cycle, or a sliding homoclinic cycle to $S^+$, or a sliding heteroclinic orbit to $S^+$ and $S^-$, which are composed of the sliding motion and the orbit arc of only the left subsystem of (4). Note that the phase portraits given in Fig. 4 $({f}_1)$–(${f}_3$) have also a sliding heteroclinic orbit connecting $S^-$ and $S_2$. Figure 4(${f}_4$) has a sliding heteroclinic orbit to $S^+$ and $S_2$.

We complete the proof of the theorem.

5 Appendix

In this appendix, we will show that the additional conditions of Theorem 2, of Theorem 4 and of Corollary 5 can be realized.

Lemma 10

There exists a $b_1\in (0,\frac{1}{3})$ such that for $b_2\ge \frac{3b_1^2}{4}$ we have $\frac{3b_1^2}{4}<b_2^h$.

Proof

By the definition we have

$$\begin{aligned} \left. b_2^h=\frac{2b_1p\sin s}{\sin s-\omega \exp (vs)+\omega \exp (-vs)}\right| _{s=s_h}, \end{aligned}$$

where $s_h\in (\pi ,s_0)\subseteq (\pi ,2\pi )$ satisfying

$$\begin{aligned} \frac{b_2\omega \left( \cos s-v\sin s-\exp (-vs)\right) }{p\sin s}+b_1=\frac{1}{3}. \end{aligned}$$

$\square$

We turn to show that

$$\begin{aligned} \left. \frac{3}{4}b_1\left( \frac{1}{3}-b_1\right) <\frac{2b_2\omega (\cos s-v\sin s-\exp (-vs))}{\sin s-\omega \exp (vs)+\omega \exp (-vs)}\right| _{s=s_h}. \end{aligned}$$

(32)

Choose $b_2\ge \frac{3}{4}b_1^2$, then $\frac{3b_1(\frac{1}{3}-b_1)}{4b_2}\le \frac{1}{3b_1}-1$. So we only need to prove that there exists a $b_1\in (0,\frac{1}{3})$ such that

$$\begin{aligned} 3b_1>C(s_h), \end{aligned}$$

(33)

where

$$\begin{aligned} C(s)=\frac{\sin s-\omega \exp (vs)+\omega \exp (-vs)}{\omega (2\cos s-\exp (vs)-\exp (-vs))}. \end{aligned}$$

We claim that for $s\in [\pi ,s_0)$,

$$\begin{aligned} C(s)\in (0,1). \end{aligned}$$

Indeed, for the function $q(s)=\sin s-\omega \exp (vs)+\omega \exp (-vs)$, we have $q'(s)=\cos s-\frac{1}{2}(\exp (vs)+\exp (-vs))\le 0$ for $s\in [\pi ,2\pi ]$. This shows that

$$\begin{aligned} q(s)\in [\omega \exp (-2\pi v)-\omega \exp (2\pi v),\omega \exp (-\pi v)-\omega \exp (\pi v)],\qquad s\in [\pi ,2\pi ]. \end{aligned}$$

(34)

In addition, $2\cos s-\exp (vs)-\exp (-vs)\le 2\cos s-2 \le 0$ for $s\in [\pi ,2\pi ]$. Hence we have

$$\begin{aligned} C(s)>0, \quad s\in [\pi ,2\pi ]. \end{aligned}$$

The rest is to show

$$\begin{aligned} C(s)<1, \quad s\in [\pi ,s_0]. \end{aligned}$$

Since

$$\begin{aligned} C(s)-1=\frac{\sin s-2\omega \cos s+2\omega \exp (-vs)}{\omega (2\cos s-\exp (vs)-\exp (-vs))}, \end{aligned}$$

we shall show that

$$\begin{aligned} \frac{\sin s-2\omega \cos s+2\omega \exp (-vs)}{\omega (2\cos s-\exp (vs)-\exp (-vs))}<0. \end{aligned}$$

(35)

Observe that

$$\begin{aligned} \left( (\sin s-2\omega \cos s)\exp (vs)+2\omega \right) '= (v+2\omega )\sin s\exp (vs)\le 0. \end{aligned}$$

So for $s\in (\pi , s_0)$, we have

$$\begin{aligned} (\sin s-2\omega \cos s)\exp (vs)+2\omega&\ge (\sin s_0-2\omega \cos s_0)\exp (vs_0)+2\omega \\&= \frac{1}{v}\left( (v\sin s_0-2\omega v\cos s_0)\exp (vs_0)+2\omega v\right) . \end{aligned}$$

From Lemma 8, we know that $\exp (vs_0)(\cos s_0-v\sin s_0)=1$ and $\exp (vs)(\cos s-v\sin s)-1$ is increasing in $s$. So for $s\in (\pi ,s_0)$, we have $\exp (vs)(\cos s-v\sin s)-1<0$, and consequently $(\sin s-2\omega \cos s)\exp (vs)+2\omega >0$, where we have used the fact $2\omega v=1$. This proves (35) and consequently the lemma.

Lemma 11

There exists a $b_1\in (0,\frac{1}{3})$ such that for $b_2<\frac{3b_1^2}{4}$ we also have $\frac{3b_1^2}{4}<b_2^h$.

Proof

We can choose $b_2>\frac{1}{4}b_1^2$, then $\frac{3b_1(\frac{1}{3}-b_1)}{4b_2}<\frac{1-3b_1}{b_1}$. By the inequality (32), we only need to prove that there exists a $b_1\in (0,\frac{1}{3})$ such that

$$\begin{aligned} \left. b_1>\frac{\sin s-\omega \exp (vs)+\omega \exp (-vs)}{2\omega \cos s+2\sin s+\omega \exp (-vs)-3\omega \exp (vs)}\right| _{s=s_h}. \end{aligned}$$

(36)

We claim that for $s\in [\pi ,s_0)$,

$$\begin{aligned} B(s):=\frac{\sin s-\omega \exp (vs)+\omega \exp (-vs)}{2\omega \cos s+2\sin s+\omega \exp (-vs)-3\omega \exp (vs)}\in \left( 0,\frac{1}{3}\right) . \end{aligned}$$

$\square$

Set

$$\begin{aligned} q(s)&= \sin s-\omega \exp (vs)+\omega \exp (-vs),\\ \eta (s)&= 2\omega \cos s+2\sin s+\omega \exp (-vs)-3\omega \exp (vs). \end{aligned}$$

Then for $s\in [\pi ,s_0)$, we have $q(s)<0$ and

$$\begin{aligned} \eta (s)=2\omega (\cos s+2v\sin s-\exp (-vs))+3\omega (\exp (-vs)-\exp (vs))<0. \end{aligned}$$

Hence we have $B(s)>0$ for $s\in [\pi ,s_0)$. The rest is to show $B(s)<\frac{1}{3}$.

Rewrite $\eta (s)$ as

$$\begin{aligned} \eta (s) =3\sin s-3\omega \exp (vs)+3\omega \exp (-vs)+2\omega (\cos s-v\sin s-\exp (-vs)). \end{aligned}$$

For $s\in [\pi ,s_0)$, we have $\cos s-v\sin s-\exp (-vs)<0$. Hence

$$\begin{aligned} \eta (s)<3\sin s-3\omega \exp (vs)+3\omega \exp (-vs)<0. \end{aligned}$$

It follows that $B(s)<\frac{1}{3}$ for $s\in (\pi ,s_0)$. The lemma follows.

Lemma 12

There exits a $b_1\ge \frac{1}{3}$ such that $\frac{3b_1^2}{4}<b_2^*$, where

$$\begin{aligned} b_2^*=\exp \left( \frac{t_0}{2}\right) \frac{\omega (\frac{1}{3}+b_1)}{\sin (\omega t_0)},\quad \omega t_0\in (-2\pi ,-\pi ) \end{aligned}$$

and $t_0$ is the largest root of the equation

$$\begin{aligned} \cos (\omega t_0)+\frac{1}{2\omega }\sin (\omega t_0)=\exp \left( \frac{t_0}{2}\right) . \end{aligned}$$

Proof

Set

$$\begin{aligned} g(b_1)=\frac{\frac{3b_1^2}{4}}{\frac{1}{3}+b_1}. \end{aligned}$$

Then for $b_1\ge \frac{1}{3}$ we have

$$\begin{aligned} g'(b_1)=\frac{\frac{b_1}{2}+\frac{3b_1^2}{4}}{(\frac{1}{3}+b_1)^2}>0, \end{aligned}$$

and consequently $g(b_1)\ge \frac{1}{8}$ and the minimum is taken at $b_1=1/3$. $\square$

Since $t_0<0$ and $\omega t_0\in (-2\pi ,-\pi )$, we have

$$\begin{aligned} \frac{\omega \exp \left( \frac{t_0}{2}\right) }{\sin (\omega t_0)}\ge \omega \exp (\frac{t_0}{2})> \omega \exp \left( -\frac{\pi }{\omega }\right) . \end{aligned}$$

So if

$$\begin{aligned} \omega \exp \left( -\frac{\pi }{\omega }\right) \ge \frac{1}{8}, \end{aligned}$$

(for instance by choosing $\omega =\frac{\sqrt{4p-1}}{2}=2$, the assumption holds) there exists a $b_1\ge \frac{1}{3}$ such that

$$\begin{aligned} g(b_1)<\frac{\omega \exp \left( \frac{t_0}{2}\right) }{\sin (\omega t_0)}, \end{aligned}$$

and consequently $\frac{3b_1^2}{4}<b_2^*$. This proves the lemma.