1 Introduction

Problems in nonlinear dynamics have fascinated scientists for several hundred years. With the development of nonlinear science, piecewise smooth systems sometimes are ideal mathematical models for the successful analysis of practical nonlinear problems observed in many fields, such as, switching in electronic circuits, impacting motion in mechanical systems, epidemic control in biology, hybrid dynamics in control theory and non-smooth models in economics (see, for instance [1,2,3,4,5,6,7,8,9]). Although classical theoretical results and methods cannot be directly generalized to piecewise smooth system because of the discontinuities of the vector field, fortunately, quite a few innovative methods and theoretical results have been proposed and established, respectively, we refer to the monographs [2,3,4].

Like for smooth systems, the study of bifurcation phenomena in piecewise smooth system has been significantly increasing in recent years, and almost all of the main research interest of bifurcation problems have focused on the bifurcations induced by the discontinuity, which cannot exist in smooth systems. Except for Hopf bifurcation and homoclinic bifurcation that can be obtained by generalizing the classical methods for treating smooth systems to piecewise smooth cases, piecewise smooth systems also can exhibit new and complicated phenomena, for example, grazing bifurcation, sliding bifurcation, border-collision bifurcation and so on. It is worth mentioning that a great deal of efforts have focused on the especial bifurcations, such as, generalized homoclinic bifurcation [10,11,12,13] and sliding homoclinic bifurcation [14,15,16]. The generalized homoclinic loop is a closed curve containing generalized singular point lying on the switching boundary [10] and the sliding homoclinic loop is a solution homoclinic to a hyperbolic critical point with a part on the discontinuity boundary [16]. In considering a closed orbit with some degenerate points or sliding points (generalized singular points in [10]), more complicated calculations and parameterization techniques are needed. Fortunately, the Melnikov method is also the powerful analytical tool enabling us to understand how the generalized homoclinic loop and sliding homoclinic loop were affected by the perturbations. Naturally, heteroclinic loop bifurcation is not a topic that can be circumvented. As early as 1988, the Melnikov method has been extended to the analysis of heteroclinic bifurcations by Bertozzi in [17]. Recently, many attempts have been made to generalized heteroclinic loop [13, 18,19,20], in which more complex phenomena of bifurcation can be exhibited than homoclinic ones undergo. This is also the subject of our work.

Owing to the emergence of non-autonomous forces in many real applications, the non-autonomous vector fields, which could be periodic, quasi-periodic, almost periodic in time or without any periodicity in time, have become very active in the development of dynamical system research. In smooth system, perturbing homoclinic or heteroclinic loop with time periodical is an common route for the occurrence of chaos in differential systems (see [21, 22] and the references therein), thus many efforts have been made to discuss how the non-smooth systems are so affected (see, for instance [23,24,25,26,27,28,29,30,31]). In particular, by extending the classical Melnikov method to a class of periodic perturbed planar piecewise smooth systems with two zones, [23] obtains the persistence of the homoclinic loop transversally crossing the switching manifold, moreover, the presented Melnikov functions are used to detect the chaotic dynamics for a concrete oscillator. In [26], the authors consider a piecewise Hamiltonian system separated by y-axis with a heteroclinic orbit connecting two saddles and fully covered by periodic orbits surrounding the origin, the existence of nT-periodic orbit under a small periodic perturbation and the impact maps are obtained by the Melnikov method. [25] focuses on the reversible piecewise smooth system with a closed trajectory connecting a visible two-fold singularity to itself. Under a periodic perturbation, by using the Melnikov’s ideas and the geometric singular perturbation theory, the sufficient conditions of the existence of sliding and crossing periodic solutions are obtained. Besides, the Shilnikov loop, an important connection in describing complex behavior in 3 dimensional applied model [32], was also considered for non-smooth systems [29,30,31]. To our knowledge, few attentions have been paid to generalized heteroclinic bifurcations in these systems, therefore, we shall work with this in our paper.

The purpose of this work is to discuss the T-periodic perturbation of the generalized heteroclinic loop connecting a hyperbolic critical point with a quadratic tangential singularity of the upper vector field in a planar piecewise smooth system separated by the x-axis. Among the various kinds of behaviours leaded by the non-autonomous perturbations, we are mainly concerned with the global bifurcation related to the hyperbolic critical point. More specifically, in terms of the continuous dependence on perturbation parameter, we give some preliminary lemmas to look for the intersections with the switching manifold of the invariant manifolds of hyperbolic critical point and of the trajectory passing through the quadratic tangential singularity of the upper subsystem. By measuring the distances of each pair of intersections and using the implicit function theorem, the related function depending on perturbation parameter \(\varepsilon \) and time t can be obtained to detect the existence of homoclinic loop of perturbed system. In particular, when we deal with the existence of sliding generalized heteroclinic loop (a generalized heteroclinic loop a part of which lies on the switching manifold), the points p on the sliding region can be parameterized by the spending time \(\varepsilon \tau \) of sliding flow starting from the tangential singularity to p, therefore the sufficient conditions can be obtained by taking the new variable \(\tau \) into account. Finally, an example is given to illustrate how to use our main results to get the existence of the corresponding phenomena of a concrete planar piecewise smooth system.

The rest of this paper is structured as follows. Section 2 is dedicated to the description of the piecewise smooth system involving time-periodic perturbation and basic assumptions. In Section 3, we state and prove our main results in Theorem 1 by using Melnikov’s ideas with perturbation techniques. Additionally, the analytic result Theorem 1 is applied in a concrete planar piecewise smooth system in Section 4. Finally, brief conclusions on our results are provided in Sect. 5.

2 Preliminaries

Assume that the switching line \(\Omega =\{(x,y)\in {\mathbb {R}}^2: y=0\}\) divides the plane \({\mathbb {R}}^2\) into two zones as

$$\begin{aligned} \Omega ^+=\{(x,y)\in {\mathbb {R}}^2: y>0\}~~\mathrm{and}~~\Omega ^-=\{(x,y)\in {\mathbb {R}}^2: y<0\}. \end{aligned}$$

We consider the following non-autonomous piecewise smooth differential system

$$\begin{aligned} ({\dot{x}},{\dot{y}})= \left\{ \begin{array}{cc} X^+(x,y)+\varepsilon Y^+(t,x,y),~\mathrm{if}~(x,y)\in \Omega ^+,\\ X^-(x,y)+\varepsilon Y^-(t,x,y),~\mathrm{if}~(x,y)\in \Omega ^-, \end{array}\right. \end{aligned}$$
(2.1)

where \(\varepsilon >0\) is a small parameter, \(X^\pm (x,y)=(f^\pm _1(x,y), f^\pm _2(x,y))\) with \(f^\pm _{i}\in {\mathbf {C}}^r({\mathbb {R}}^2, {\mathbb {R}})\) \((i=1,2, r\ge 2)\) and \(Y^\pm (t,x,y)=(g^\pm _1(t,x,y), g^\pm _2(t,x,y))\) with \(g^\pm _{i}\in {\mathbf {C}}^r({\mathbb {R}}^3, {\mathbb {R}})\) \((i=1,2, r\ge 2)\) are T-periodic in t. Let the following assumption hold.

H1

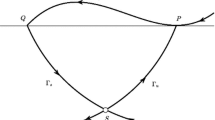
System (2.1) \(|_{\varepsilon =0}\) has a generalized heteroclinic loop \(\Gamma (t)\) (see Fig. 1), which contains a visible quadratic tangential singularity (i.e. fold point) \(A=(x_a,0)\) of the vector field \(X^+\) and a real hyperbolic critical point \(S=(x_s, y_s)\) of the vector field \(X^-\), crossing the switching line \(\Omega \) clockwise at point \(B=(x_b,0)\) in a transverse way, where \(x_a<x_b\).

Fig. 1
figure 1

The generalized heteroclinic loop \(\Gamma (t)\)

Full size image

Denote the solutions of system (2.1) \(|_{\varepsilon =0}\) restricted to \(\Omega ^\pm \) by \(\gamma ^\pm (t,x,y)=(\gamma ^\pm _1(t,x,y), \gamma ^\pm _2(t,x,y))\), which satisfy \(\gamma ^\pm (0,x,y)=(x,y)\).

Remark 1

For \(\varepsilon =0\), the generalized heteroclinic loop \(\Gamma (t)\) can be expressed as \(\Gamma (t)=L^-_u(t)\cup L^+(t)\cup L^-_s(t)\) (see Fig. 1), where

$$\begin{aligned}&L^-_u(t)={\widehat{SA}}:=\gamma ^-_u(t,A)=\{\gamma ^-(t,A): t\le 0\},\\&L^+(t)={\widehat{AB}}:=\{\gamma ^+(t,A): 0\le t\le \tau _0\},\\&L^-_s(t)={\widehat{BS}}:=\gamma ^-_s(t-\tau _0,B)=\{\gamma ^-(t,B): t\ge \tau _0\} \end{aligned}$$

and \(\tau _0>0\) is the flying time of \(\gamma ^+\) from A to B, moreover, \(\gamma ^-_u(0,A)=\gamma ^+(0, A)=A\), \(\gamma ^-_s(0,B)=\gamma ^+(\tau _0,A)=B\) and \( \lim _{{t \rightarrow + \infty }} \gamma ^-_{u}(t,A)= \lim _{{t \rightarrow + \infty }} \gamma ^-_{s}(t-\tau _0,B)=S\).

Remark 2

From the assumption (H1), for the points \(A=(x_a,0)\) and \(B=(x_b,0)\) we have

$$\begin{aligned} x_a<x_b,~f^+_1(A)<0,~f^+_2(A)=0,~f^-_2(A)>0,~f^+_{2x}(A)<0~~\mathrm{and}~~f^\pm _2(B)<0. \end{aligned}$$

Moreover, for the hyperbolic critical point \(S=(x_s, y_s)\), we have \(f^-_{i}(S)=0,~i=1,2\),

$$\begin{aligned} y_s<0~~\mathrm{and}~~f^-_{1x}(S)f^-_{2y}(S)-f^-_{1y}(S)f^-_{2x}(S)<0, \end{aligned}$$

where the subscripts x and y denote the partial derivative with respect to x and y respectively.

In order to study the non-autonomous periodic differential system (2.1), we append the time \(\theta =t\) to the phase space and obtain the equivalent system in the extended phase space as

$$\begin{aligned} \left\{ \begin{array}{ll} ({\dot{x}}, {\dot{y}})= \left\{ \begin{array}{cc} X^+(x,y)+\varepsilon Y^+(\theta ,x,y),~\mathrm{if}~(x, y)\in \Omega ^+,\\ X^-(x,y)+\varepsilon Y^-(\theta ,x,y),~\mathrm{if}~(x, y)\in \Omega ^-, \end{array}\right. \\ {\dot{\theta }}=1, \end{array}\right. \end{aligned}$$
(2.2)

where \((x,y,\theta )\in {\mathbb {R}}^2\times {\mathbb {S}}^1\), \({\mathbb {S}}^1={\mathbb {R}}(\mathbf{mod}~T)\) is the unite circle of period T and \(\theta =t(\mathbf{mod}~T)\in {\mathbb {S}}^1\). The system (2.2) is also a piecewise smooth system with switching plane \({\widetilde{\Omega }}=\Omega \times {\mathbb {S}}^1\). We denote \(\phi ^\pm (t,x,y,\theta ;\varepsilon )=(\varphi ^\pm (t,x,y,\theta ;\varepsilon ),t+\theta )\) by the solutions of (2.2) restricted to \(\Omega ^\pm \times {\mathbb {S}}^1\) such that \(\phi ^\pm (0,x,y,\theta ;\varepsilon )=(x,y,\theta )\), where \(\varphi ^\pm (t,x,y,\theta ;\varepsilon )=(\varphi ^\pm _1(t,x,y,\theta ;\varepsilon ), \varphi ^\pm _2(t,x,y,\theta ;\varepsilon ))\subset {\mathbb {R}}^2\) are the solutions of system

$$\begin{aligned} ({\dot{x}}, {\dot{y}})= \left\{ \begin{array}{cc} X^+(x,y)+\varepsilon Y^+(t+\theta ,x,y),~\mathrm{if}~(x, y)\in \Omega ^+,\\ X^-(x,y)+\varepsilon Y^-(t+\theta ,x,y),~\mathrm{if}~(x, y)\in \Omega ^-, \end{array}\right. \end{aligned}$$
(2.3)

with \(\varphi ^\pm (0,x,y,\theta ;\varepsilon )=(x,y)\) restricted to \(\Omega ^\pm \).

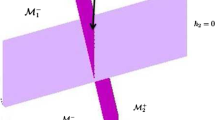
When \(\varepsilon =0\), let \(A_\theta :=\{(A,\theta ): \theta \in {\mathbb {S}}^1\}\), \(S_\theta :=\{(S, \theta ): \theta \in {\mathbb {S}}^1\}\), \(B_\theta :=\{(B,\theta ): \theta \in {\mathbb {S}}^1\}\), and \(W^s(S_\theta )\) and \(W^u(S_\theta )\) be the stable and unstable invariant manifold of \(S_\theta \) respectively. Thus there exists a generalized heteroclinic manifold \({\widetilde{\Gamma }}(t):=\{(\Gamma (t), \theta ): \theta \in {\mathbb {S}}^1\}\) formed by the coincidence of three two-dimensional surfaces: a branch of \(W^s(S_\theta )\), a branch of \(W^u(S_\theta )\) and a branch of \(\Gamma ^+_\theta (t):=\{(\gamma ^+(t,A), \theta ): 0\le t\le \tau _0~\mathrm{and}~\theta \in {\mathbb {S}}^1\}\), see Fig. 2.

Fig. 2
figure 2

The generalized heteroclinic manifold \({\widetilde{\Gamma }}(t)\)

Full size image

Proposition 1

Suppose that the assumption (H1) holds. Then for sufficiently small \(\varepsilon >0\), the system (2.2) has a curve \(A^+_{\varepsilon }(\theta )=(x^+_{a,\varepsilon }(\theta ),0,\theta )\) consisting of visible folds and nearing \(A_\theta \) of the field vectors in \(\Omega ^+\times {\mathbb {S}}^1\), where

$$\begin{aligned}&x^+_{a,\varepsilon }(\theta )=x_a-\varepsilon \frac{g^+_2(\theta ,A)}{f^+_{2x}(A)}+{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$
(2.4)

and a hyperbolic critical curve \(S_{\varepsilon }(\theta )=S_\theta +{\mathcal {O}}(\varepsilon )\) nearing \(S_\theta \) of the field vectors in \(\Omega ^-\times {\mathbb {S}}^1\). Moreover, the stable manifold \(W^s(S_{\varepsilon }(\theta ))\) and the unstable manifold \(W^u(S_{\varepsilon }(\theta ))\) of \(S_{\varepsilon }(\theta )\) are \(\varepsilon \)-closed to \(W^s(S_{\theta })\) and \(W^u(S_{\theta })\), respectively. (see Fig. 3)

Proof

The calculation of the tangency singularities of system (2.2) is equivalent to the discussion of the zeros of the vector field \(f^+_2(x,0)+\varepsilon g^+_2(\theta ,x,0)\). Let

$$\begin{aligned} P(x,\varepsilon ,\theta ):=f^+_2(x,0)+\varepsilon g^+_2(\theta ,x,0). \end{aligned}$$

Noticing \(P(x_a,0,\theta )=f^+_2(A)=0\) and \(\frac{\partial P}{\partial x}(x_a,0,\theta )=f^+_{2x}(A)\ne 0\), by using the implicit function theorem, there exists a function

$$\begin{aligned}&x^+_{a,\varepsilon }(\theta )=x_a-\varepsilon \frac{g^+_2(\theta ,A)}{f^+_{2x}(A)}+{\mathcal {O}}(\varepsilon ^2) \end{aligned}$$

such that \(P(x^+_{a,\varepsilon }(\theta ),\varepsilon ,\theta )=0\). The remaindering results can be obtained by the Theorem 3.6.4 in [21]. \(\square \)

Fig. 3
figure 3

(colour online) Under the small perturbation. Purple shaded area represents the local sliding region near \(A^+_\varepsilon (\theta )\)

Full size image

This paper allows the possibility of sliding motion. Firstly, we distinguish three different subregions on the switching plane \({\widetilde{\Omega }}\) as crossing region \({\widetilde{\Omega }}_c\), escaping region \({\widetilde{\Omega }}_e\) and sliding region \({\widetilde{\Omega }}_s\), respectively, where

$$\begin{aligned} \begin{aligned} {\widetilde{\Omega }}_c&=\{(x,0,\theta )\in {\widetilde{\Omega }}:\left( f^+_2(x,0)+\varepsilon g^+_2(\theta ,x,0)\right) \left( f^-_2(x,0)+\varepsilon g^-_2(\theta ,x,0)\right)>0\},\\ {\widetilde{\Omega }}_e&=\{(x,0,\theta )\in {\widetilde{\Omega }}:f^+_2(x,0)+\varepsilon g^+_2(\theta ,x,0)>0>f^-_2(x,0)+\varepsilon g^-_2(\theta ,x,0)\},\\ {\widetilde{\Omega }}_s&=\{(x,0,\theta )\in {\widetilde{\Omega }}:f^+_2(x,0)+\varepsilon g^+_2(\theta ,x,0)<0<f^-_2(x,0)+\varepsilon g^-_2(\theta ,x,0)\}. \end{aligned} \end{aligned}$$
(2.5)

In the crossing region, the orbits are concatenated in the natural way. Additionally, by using the Filippov convention method [2], the local solution of system (2.2) on escaping or sliding regions can be define by the sliding vector field

$$\begin{aligned} Z^s(x,\theta ,\varepsilon )=\left( \frac{(f^-_2+\varepsilon g^-_2)(f^+_1+\varepsilon g^+_1)-(f^-_1+\varepsilon g^-_1)(f^+_2+\varepsilon g^+_2)}{(f^-_2+\varepsilon g^-_2)-(f^+_2+\varepsilon g^+_2)},0,1\right) , \end{aligned}$$
(2.6)

where \(f_i=f_i(x,0)\) and \(g_i=g_i(\theta ,x,0)\), \(i=1,2\).

Since \(f^-_2(A)>0\) and \({\mathbb {S}}^1\) is compact, for sufficient small \(\varepsilon >0\) and every \(\theta \in {\mathbb {S}}^1\), \(f^-_2(A)+\varepsilon g^-_2(\theta ,A)>0\). Accordingly, from (2.5) there has only sliding region \({\widetilde{\Omega }}_s\) and crossing region \({\widetilde{\Omega }}_c\) on the switching plane \({\widetilde{\Omega }}\) of system (2.2) in a neighborhood of \(A_\theta \times {\mathbb {S}}^1\). Similarly, by \(f^-_2(B)f^+_2(B)>0\), in a neighborhood of \(B_\theta \times {\mathbb {S}}^1\) there has only crossing region. Let \({\widetilde{\Omega }}^{loc}_{s}=\{(x,0,\theta )\in {\widetilde{\Omega }}:x^+_{a,\varepsilon }(\theta )<x <x^+_{a,\varepsilon }(\theta )+\delta \}\subset {\widetilde{\Omega }}_s\), where \(\delta >0\) is a sufficient small constant, denote the sliding region in a small neighborhood of curve \(A^+_\varepsilon (\theta )\), see the purple shaded area in Fig. 3. Therefore, we can get the following proposition.

Proposition 2

Under the assumption (H1), on the sliding region \({\widetilde{\Omega }}^{loc}_{s}\) the orbits of (2.6) will arrive at \(A^+_\varepsilon (\theta )\) and then enter into \(\Omega ^+\times {\mathbb {S}}^1\).

Proof

Obviously, from (2.6) we have

$$\begin{aligned} \pi _{x}(Z^s(x,\theta ,\varepsilon ))&=\frac{(f^-_2+\varepsilon g^-_2)(f^+_1+\varepsilon g^+_1)-(f^-_1+\varepsilon g^-_1)(f^+_2+\varepsilon g^+_2)}{(f^-_2+\varepsilon g^-_2)-(f^+_2+\varepsilon g^+_2)}, \end{aligned}$$

where \(f_i=f_i(x,0)\), \(g_i=g_i(\theta ,x,0)\), \(i=1,2\), \(x^+_{a,\varepsilon }(\theta )<x <x^+_{a,\varepsilon }(\theta )+\delta \) and \(\pi _x\) denotes the projection onto x-axis. Therefore, by \(f^+_2(A)=0\), we have

$$\begin{aligned} \pi _{x}(Z^s(x_a,\theta ,\varepsilon ))=f^+_1(A)+{\mathcal {O}}(\varepsilon ). \end{aligned}$$

Since \(f^+_1(A)<0\) and \({\mathbb {S}}^1\) is compact, there exists \(\varepsilon _0>0\) such that \(\pi _{x}(Z^s(x_a,\theta ,\varepsilon ))<0\) for every \(\theta \in {\mathbb {S}}^1\) and \(\varepsilon \in (0,\ varepsilon_0]\). In addition, since the set \(C=\{(x_a,0,\theta ):\theta \in {\mathbb {S}}^1\}\) is compact, there exists a compact neighborhood U of C such that \(\pi _{x}(Z^s(x,\theta ,\varepsilon ))<0\) for every \((x,0,\theta )\in U\) and \(\varepsilon \in (0,\varepsilon _1]\). By taking \(\varepsilon , \delta >0\) small enough, we can get \({\widetilde{\Omega }}^{loc}_{s}\subset U\), accordingly, \(Z^s\) has no singularities in \({\widetilde{\Omega }}^{loc}_{s}\) and \(\pi _{x}(Z^s(x,\theta ,\varepsilon ))<0\). This can prove the proposition. \(\square \)

3 Periodic Solutions Bifurcated from Generalized Heteroclinic Loop

For \(\theta \in {\mathbb {S}}^1\), let \(A^-_{\varepsilon }(\theta )\) and \(B^-_{\varepsilon }(\theta )\) be the intersections of \(W^u(S_{\varepsilon }(\theta ))\) and \(W^s(S_{\varepsilon }(\theta ))\) with \({\widetilde{\Omega }}=\Omega \times {\mathbb {S}}^1\), respectively, and assume that the flow of system (2.2) in \(\Omega ^+\times {\mathbb {S}}^1\) passing through point \(A^+_{\varepsilon }(\theta )\) will reach the switching manifold \({\widetilde{\Omega }}=\Omega \times {\mathbb {S}}^1\) transversally at \(B^+_{\varepsilon }(\theta )\). Obviously, as \(\theta \) varies in \({\mathbb {S}}^1\), \(A^-_{\varepsilon }(\theta )\), \(B^-_{\varepsilon }(\theta )\) and \(B^+_{\varepsilon }(\theta )\) are also three curves in switching manifold \({\widetilde{\Omega }}=\Omega \times {\mathbb {S}}^1\) (see Fig. 3). In order to discuss the periodic solutions bifurcated from the generalized heteroclinic loop \(\Gamma (t)\) under the small periodic perturbations, several propositions are given to the presentations of the curves \(B^+_{\varepsilon }(\theta )\), \(A^-_{\varepsilon }(\theta )\) and \(B^-_{\varepsilon }(\theta )\) firstly.

Proposition 3

Let \((x^+_{b,\varepsilon }(\theta ),0)\) be the coordinates of \(B^+_{\varepsilon }(\theta )\) on the (x, y)-plane and

$$\begin{aligned} \begin{aligned} w(\tau _0,\theta )&=\mathrm{exp}\left( \int ^{\tau _0}_0 f^+_{1x}+f^+_{2y}\mathrm{d}s\right) \int ^{\tau _0}_0 \left( f^+_2g^+_1 -f^+_1g^+_2\right) \mathrm{exp}\left( -\int ^s_0 f^+_{1x}+f^+_{2y}\mathrm{d}\tau \right) \mathrm{d}s, \end{aligned} \end{aligned}$$
(3.1)

where \(f^+_{iz}=f^+_{iz}(\gamma ^+(t,A))\), \(f^+_i=f^+_i(\gamma ^+(t,A))\) and \(g^+_i=g^+_i(t+\theta ,\gamma ^+(t,A))\), \(i=1,2\), \(z\in \{x,y\}\). For sufficient small \(\varepsilon >0\), we have

$$\begin{aligned} x^+_{b,\varepsilon }(\theta )=x_b+\varepsilon \frac{w(\tau _0,\theta )}{f^+_2(B)}+{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$
(3.2)

Proof

Notice that \(\phi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon )=(\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ),t+\theta )\) is the solution of (2.2) restricted to \(\Omega ^+\times {\mathbb {S}}^1\) with initial point \(A^+_{\varepsilon }(\theta )\). For the sufficient small \(\varepsilon >0\), we can expand \(\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon )\) as

$$\begin{aligned} \varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon )=\gamma ^+(t,A)+\varepsilon p^+(t,\theta )+{\mathcal {O}}(\varepsilon ^2), \end{aligned}$$

where \(p^+=(p^+_1,p^+_2)=\frac{\partial \varphi ^+}{\partial \varepsilon }|_{\varepsilon =0}\) satisfying

$$\begin{aligned} \frac{\partial }{\partial t}p^+(t,\theta )=DX^+(\gamma ^+(t,A))p^+(t,\theta )+Y^+(t+\theta ,\gamma ^+(t,A)) \end{aligned}$$
(3.3)

and \(p^+(0,\theta )=(-\frac{g^+_2(\theta ,A)}{f^+_{2x}(A)},0)\) by (2.3) and (2.4). The \(DX^+\) is the Jacobian matrix of vector filed \(X^+\) and \(\frac{\partial }{\partial t}\) denotes the partial derivative with respect to t. Let \(t^+(\varepsilon )\) be the spending time of trajectory \(\phi ^+\) from \(A^+_{\varepsilon }(\theta )\) to \(B^+_{\varepsilon }(\theta )\), that is

$$\begin{aligned} \varphi ^+_1(t^+(\varepsilon ), A^+_{\varepsilon }(\theta );\varepsilon )=\gamma ^+_1(t^+(\varepsilon ),A)+\varepsilon p^+_1(t^+(\varepsilon ),\theta )+{\mathcal {O}}(\varepsilon ^2)=x^+_{b,\varepsilon }(\theta ) \end{aligned}$$
(3.4)

and

$$\begin{aligned} \varphi ^+_2(t^+(\varepsilon ), A^+_{\varepsilon }(\theta );\varepsilon )=\gamma ^+_2(t^+(\varepsilon ),A)+\varepsilon p^+_2(t^+(\varepsilon ),\theta )+{\mathcal {O}}(\varepsilon ^2)=0, \end{aligned}$$
(3.5)

such that \(t^+(0)=\tau _0\), where \(\tau _0\) is the flying time of trajectory \(\gamma ^+\) from A to B assumed in Remark 1. Therefore, \(t^+(\varepsilon )\) can be expanded as

$$\begin{aligned} t^+(\varepsilon )=\tau _0+\varepsilon \frac{\mathrm{d} t^+(\varepsilon )}{\mathrm{d} \varepsilon }|_{\varepsilon =0}+{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$
(3.6)

Substituting (3.6) into (3.5), and comparing the coefficients of \(\varepsilon \) yields

$$\begin{aligned} \frac{\mathrm{d} t^+(\varepsilon )}{\mathrm{d} \varepsilon }|_{\varepsilon =0}=-\frac{p^+_2(\tau _0,\theta )}{f^+_2(B)}. \end{aligned}$$
(3.7)

From (3.4), (3.6) and (3.7), we have

$$\begin{aligned} \begin{aligned} x^+_{b,\varepsilon }(\theta )=x_b+\varepsilon \frac{w(\tau _0,\theta )}{f^+_2(B)}+{\mathcal {O}}(\varepsilon ^2), \end{aligned} \end{aligned}$$
(3.8)

where

$$\begin{aligned} w(\tau _0,\theta )=f^+_2(B)p^+_1(\tau _0,\theta )-f^+_1(B)p^+_2(\tau _0,\theta ). \end{aligned}$$

Let

$$\begin{aligned} w(t,\theta )=f^+_2(\gamma ^+(t,A))p^+_1(t,\theta )-f^+_1(\gamma ^+(t,A))p^+_2(t,\theta ). \end{aligned}$$

By (3.3), it is not difficult to obtain that

$$\begin{aligned} \frac{\partial }{\partial t}w(t,\theta )&=\left( f^+_{1x}(\gamma ^+(t,A))+f^+_{2y}(\gamma ^+(t,A))\right) w(t,\theta )\\&~~+f^+_2(\gamma ^+(t,A))g^+_1(t+\theta ,\gamma ^+(t,A))\\&\quad -f^+_1(\gamma ^+(t,A))g^+_2(t+\theta ,\gamma ^+(t,A)) \end{aligned}$$

and \(w(0,\theta )=0\), thus the formula of constant variation implies

$$\begin{aligned} \begin{aligned} w(t,\theta )&=\mathrm{exp}\left( \int ^{t}_0 f^+_{1x}(\gamma ^+(s,A))+f^+_{2y}(\gamma ^+(s,A))\mathrm{d}s\right) \cdot \\&\quad \int ^{t}_0 \left( f^+_2(\gamma ^+(s,A))g^+_1(s+\theta ,\gamma ^+(s,A))\right. \\&\quad \left. -f^+_1(\gamma ^+(s,A))g^+_2(s+\theta ,\gamma ^+(s,A))\right) \cdot \\&\qquad \mathrm{exp}\left( -\int ^s_0 f^+_{1x}(\gamma ^+(\tau ,A))+f^+_{2y}(\gamma ^+(\tau ,A))\mathrm{d}\tau \right) \mathrm{d}s. \end{aligned} \end{aligned}$$
(3.9)

According to (3.8) and (3.9), the (3.1) and (3.2) can be obtained. \(\square \)

For fixed \(\theta _0\in (0,T]\), let

$$\begin{aligned} \Sigma _{\theta _0}=\{(x,y,\theta )\in {\mathbb {R}}^2\times {\mathbb {S}}^1:\theta =\theta _0\} \end{aligned}$$

and denote \(A^-_{\varepsilon }(\theta _0)=(x^-_{a,\varepsilon }(\theta _0),0,\theta _0)\) and \(B^-_{\varepsilon }(\theta _0)=(x^-_{b,\varepsilon }(\theta _0),0,\theta _0)\) the intersections of unstable manifolds \(W^u(S_{\varepsilon }(\theta ))\) and stable manifolds \(W^s(S_{\varepsilon }(\theta ))\) with \({\widetilde{\Omega }}\cap \Sigma _{\theta _0}\), respectively, hence the following results hold.

Proposition 4

Let

$$\begin{aligned} \begin{aligned} \kappa (0,\theta _0)&=-\int ^{-\infty }_{0}(f^-_1g^-_2-g^-_1f^-_2)\mathrm{exp} \left( -\int ^s_{0}f^-_{1x}+f^-_{2y}\mathrm{d}\tau \right) \mathrm{d}s \end{aligned} \end{aligned}$$
(3.10)

with \(f^-_{i}=f^-_{i}(\gamma ^-_u(s,A))\), \(f^-_{iz}=f^-_{iz}(\gamma ^-_u(\tau ,A))\) and \(g^-_{i}=g^-_{i}(s+\theta _0,\gamma ^-_u(s,A))\), \(i=1,2\), \(z\in \{x,y\}\), and

$$\begin{aligned} \rho (0,\theta _0)=-\int ^{+\infty }_{0}(f^-_1g^-_2-g^-_1f^-_2)\mathrm{exp}\left( -\int ^s_{0}f^-_{1x}+f^-_{2y}\mathrm{d}\tau \right) \mathrm{d}s \end{aligned}$$
(3.11)

with \(f^-_{i}=f^-_{i}(\gamma ^-_s(s,B))\), \(f^-_{iz}=f^-_{iz}(\gamma ^-_s(\tau ,B))\) and \(g^-_{i}=g^-_{i}(s+\theta _0,\gamma ^-_s(s,B))\), \(i=1,2\), \(z\in \{x,y\}\). For sufficient small \(\varepsilon >0\), we have

$$\begin{aligned} x^-_{a,\varepsilon }(\theta _0)=x_a+\varepsilon \frac{\kappa (0,\theta _0)}{f^-_2(A)}+{\mathcal {O}}(\varepsilon ^2) \end{aligned}$$
(3.12)

and

$$\begin{aligned} x^-_{b,\varepsilon }(\theta _0)=x_b+\varepsilon \frac{\rho (0,\theta _0)}{f^-_2(B)}+{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$
(3.13)

Proof

Let \(l_u\) be the normal line of invariant manifold \(W^u(S_{\theta })\) at \((A,\theta _0)\) on the plane \(\Sigma _{\theta _0}\). Hence there is a intersection of perturbed unstable manifold \(W^u(S_{\varepsilon }(\theta ))\) with \(l_u\) at time \(t=\theta _0\), denoted by \({\hat{A}}^-_{\varepsilon }(\theta _0)\). Define the solution passing through point \({\hat{A}}^-_{\varepsilon }(\theta _0)\) by \((\varphi ^-_u(t, {\hat{A}}^-_{\varepsilon }(\theta _0);\varepsilon ), t+\theta _0)\) with \(\varphi ^-_u=(\varphi ^-_{u1},\varphi ^-_{u2})\), which lies in manifold \(W^u(S_{\varepsilon }(\theta ))\). The continuous dependence on parameter implies that there exists a time \(t^-_u(\theta _0,\varepsilon )\) such that \(\varphi ^-_u(t^-_u(\theta _0,\varepsilon ), {\hat{A}}^-_{\varepsilon }(\theta _0);\varepsilon )=(x^-_{a,\varepsilon }(\theta _0),0)\) and \(t^-_u(\theta _0,0)=0\). From the Lemma 28.1.3 in [21] or Lemma 4.5.2 in [22], we know

$$\begin{aligned} \varphi ^-_u(t,{\hat{A}}^-_{\varepsilon }(\theta _0);\varepsilon )=\gamma ^-_u(t,A)+\varepsilon p^-_u(t,\theta _0)+{\mathcal {O}}(\varepsilon ^2),~~t\in (-\infty , \theta _0+t^-_u(\theta _0,\varepsilon )], \end{aligned}$$

where \(p^-_{u}=(p^-_{u1},p^-_{u2})=\frac{\partial \varphi ^-_{u}}{\partial \varepsilon }|_{\varepsilon =0}\) satisfying

$$\begin{aligned} \frac{{\partial }}{{\partial }t}p^-_u(t,\theta _0)=DX^-(\gamma ^-_u(t,A))p^-_u(t,\theta _0) +Y^-(t+\theta _0,\gamma ^-_u(t,A)). \end{aligned}$$
(3.14)

Therefore

$$\begin{aligned} \varphi ^-_{u1}(t^-_u(\theta _0,\varepsilon ),{\hat{A}}^-_{\varepsilon }(\theta _0);\varepsilon )&=\gamma ^-_{u1}(t^-_u(\theta _0,\varepsilon ),A)+\varepsilon p^-_{u1}(t^-_u(\theta _0,\varepsilon ),\theta _0)+{\mathcal {O}}(\varepsilon ^2)\nonumber \\ {}&=x^-_{a,\varepsilon }(\theta _0) \end{aligned}$$
(3.15)

and

$$\begin{aligned} \varphi ^-_{u2}(t^-_u(\theta _0,\varepsilon ),{\hat{A}}^-_{\varepsilon }(\theta _0);\varepsilon ) =\gamma ^-_{u2}(t^-_u(\theta _0,\varepsilon ),A)+\varepsilon p^-_{u2}(t^-_u(\theta _0,\varepsilon ),\theta _0)+{\mathcal {O}}(\varepsilon ^2)=0. \end{aligned}$$
(3.16)

Expand \(t^-_{u}(\theta _0,\varepsilon )\) in Taylor series as

$$\begin{aligned} t^-_u(\theta _0,\varepsilon )=\varepsilon \frac{\partial t^-_u(\theta _0,\varepsilon )}{\partial \varepsilon }|_{\varepsilon =0}+{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$
(3.17)

Substituting (3.17) into (3.16) and comparing the coefficients of \(\varepsilon \) yields

$$\begin{aligned} \frac{\partial t^-_u(\theta _0,\varepsilon )}{\partial \varepsilon }|_{\varepsilon =0}=-\frac{p^-_{u2}(0,\theta _0)}{f^-_2(A)}. \end{aligned}$$
(3.18)

From (3.15), (3.17) and (3.18), we have

$$\begin{aligned} \begin{aligned} x^-_{a,\varepsilon }(\theta _0)=x_a+\varepsilon \frac{\kappa (0,\theta _0)}{f^-_2(A)}+{\mathcal {O}}(\varepsilon ^2), \end{aligned} \end{aligned}$$
(3.19)

where

$$\begin{aligned} \kappa (0,\theta _0)=f^-_2(A)p^-_{u1}(0,\theta _0)-f^-_1(A)p^-_{u2}(0,\theta _0). \end{aligned}$$

Let

$$\begin{aligned} \kappa (t,\theta _0)=f^-_2(\gamma ^-_u(t,A))p^-_{u1}(t,\theta _0)-f^-_1(\gamma ^-_u(t,A))p^-_{u2}(t,\theta _0), \end{aligned}$$

which satisfies

$$\begin{aligned} \frac{\partial }{\partial t}\kappa (t,\theta _0)&=\left( f^-_{1x}(\gamma ^-_u(t,A))+f^-_{2y}(\gamma ^-_u(t,A))\right) \kappa (t)\\&\qquad +f^-_2(\gamma ^-_u(t,A))g^-_1(t+\theta _0, \gamma ^-_u(t,A))\\ {}&\qquad -f^-_1(\gamma ^-_u(t,A))g^-_2(t+\theta _0, \gamma ^-_u(t,A)) \end{aligned}$$

from (3.14). By the formula of constant variation, we can get

$$\begin{aligned} \kappa (t,\theta _0)&=\mathrm{exp}\left( \int ^t_{0}f^-_{1x}(\gamma ^-_u(s,A))+f^-_{2y}(\gamma ^-_u(s,A))\mathrm{d}s\right) \cdot \\&\quad \left[ \kappa (0,\theta _0)+ \int ^t_{0}\left[ f^-_1(\gamma ^-_u(s,A))g^-_2(s+\theta _0, \gamma ^-_u(s,A))\right. \right. \\&\qquad \left. \left. -g^-_1(s+\theta _0, \gamma ^-_u(s,A))f^-_2(\gamma ^-_u(s,A))\right] \right. \cdot \\&\qquad \left. \mathrm{exp}\left( -\int ^s_{0}f^-_{1x}(\gamma ^-_u(\tau ,A))+f^-_{2y}(\gamma ^-_u(\tau ,A))\mathrm{d}\tau \right) \mathrm{d}s\right] . \end{aligned}$$

Letting \(t\rightarrow -\infty \), it follows from Lemma 4.2.2 of [33] that

$$\begin{aligned} \kappa (t,\theta _0)\mathrm{exp}\left( -\int ^t_{0}f^-_{1x}(\gamma ^-_u(s,A))+f^-_{2y}(\gamma ^-_u(s,A))\mathrm{d}s\right) \rightarrow 0, \end{aligned}$$

thus

$$\begin{aligned} \begin{aligned} \kappa (0,\theta _0)&=-\int ^{-\infty }_{0}\left[ f^-_1(\gamma ^-_u(s,A))g^-_2(s+\theta _0, \gamma ^-_u(s,A))\right. \\&\qquad \left. -g^-_1(s+\theta _0, \gamma ^-_u(s,A))f^-_2(\gamma ^-_u(s,A))\right] \cdot \\&\quad \mathrm{exp}\left( -\int ^s_{0}f^-_{1x}(\gamma ^-_u(\tau ,A))+f^-_{2y}(\gamma ^-_u(\tau ,A))\mathrm{d}\tau \right) \mathrm{d}s. \end{aligned} \end{aligned}$$
(3.20)

According to (3.19) and (3.20), (3.10) and (3.12) are completed. Similarly, we can derive (3.11) and (3.13) by the same manner. This ends the proof. \(\square \)

Additionally, assume that the orbit starting from \(A^\prime _{\varepsilon }(\theta ,\xi )=(x_{a^\prime ,\varepsilon }(\theta ,\xi ),0,\theta )\) on \({\widetilde{\Omega }}\), where \(x_{a^\prime ,\varepsilon }(\theta ,\xi )=x^+_{a,\varepsilon }(\theta )-\xi \) and \(0<\xi<\varepsilon _0<\varepsilon \) for some \(\varepsilon _0\), can intersect the switching manifold \({\widetilde{\Omega }}\) at point \(B^\prime _{\varepsilon }(\theta ,\xi )\), the coordinates on (x, y)-plane denoted by \((x_{b^\prime ,\varepsilon }(\theta ,\xi ),0)\), thus we have the following proposition.

Proposition 5

Let

$$\begin{aligned} \begin{aligned} u(t^+(\varepsilon ),\theta ,\varepsilon )&=\mathrm{exp}\left( \int ^{t^+(\varepsilon )}_0(f^+_{1x}+\varepsilon g^+_{1x})+(f^+_{2y}+\varepsilon g^+_{2y})\mathrm{d}s\right) \cdot \\&\qquad \left( \int ^{t^+(\varepsilon )}_0 V(s,\theta ,\varepsilon )\mathrm{exp}\left( -\int ^{s}_0(f^+_{1x}+\varepsilon g^+_{1x})+(f^+_{2y}+\varepsilon g^+_{2y})\mathrm{d}\tau \right) \mathrm{d}s\right) , \end{aligned} \end{aligned}$$

where \(f^+_{iz}=f^+_{iz}\) \((\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(g^+_{iz}=g^+_{iz}(t+\theta ,\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(i=1,2\), \(z\in \{x,y\}\), and \(V(s,\theta ,\varepsilon )\) is expressed in (3.32). Thus we have

$$\begin{aligned}&x_{b^\prime ,\varepsilon }(\theta ,\xi )=x^+_{b,\varepsilon }(\theta ) +\frac{1}{2}\frac{u(t^+(\varepsilon ),\theta ,\varepsilon )}{f^+_2(x^+_{b,\varepsilon }(\theta ),0)+\varepsilon g^+_2(t^+(\varepsilon )+\theta ,x^+_{b,\varepsilon }(\theta ),0)}\xi ^2+{\mathcal {O}}(\xi ^3), \end{aligned}$$
(3.21)

where \(t^+(\varepsilon )=\tau _0-\varepsilon \frac{p^+_2(\tau _0,\theta )}{f^+_2(B)}+{\mathcal {O}}(\varepsilon ^2)\) is the spending time of trajectory \(\phi ^+\) from \(A^+_{\varepsilon }(\theta )\) to \(B^+_{\varepsilon }(\theta )\) and \(x^+_{b,\varepsilon }(\theta )\) is expressed in (3.2).

Proof

We denote the trajectory of the subsystem in \(\Omega ^+\times {\mathbb {S}}^1\) passing through \(A^\prime _{\varepsilon }(\theta ,\xi )=(x_{a^\prime ,\varepsilon }(\theta ,\xi ),0,\theta )\), where \(x_{a^\prime ,\varepsilon }(\theta ,\xi )=x^+_{a,\varepsilon }(\theta )-\xi \) with \(0<\xi<\varepsilon _0<\varepsilon \), by \(\phi ^+(t,A^\prime _{\varepsilon }(\theta ,\xi );\varepsilon )=(\varphi ^+(t,A^\prime _{\varepsilon }(\theta ,\xi );\varepsilon ),t+\theta )\), the continuous dependence on initial values implies that \(\varphi ^+(t,A^\prime _{\varepsilon }(\theta ,\xi );\varepsilon )\) can be expended in Taylor series around \(\xi =0\) as

$$\begin{aligned} \varphi ^+(t,A^\prime _{\varepsilon }(\theta ,\xi );\varepsilon )=\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon )+ q^+(t,\theta ,\varepsilon )\xi +\frac{1}{2}k^+(t,\theta ,\varepsilon )\xi ^2+{\mathcal {O}}(\xi ^3), \end{aligned}$$

where \(q^+=(q^+_1,q^+_2)=\frac{\partial \varphi ^+}{\partial \xi }|_{\xi =0}\) and \(k^+=(k^+_1,k^+_2)=\frac{\partial ^2 \varphi ^+}{\partial \xi ^2}|_{\xi =0}\) satisfying

$$\begin{aligned} \frac{\partial }{\partial t}q^+(t,\theta ,\varepsilon )&=\begin{pmatrix} f^+_{1x}+\varepsilon g^+_{1x}&{} f^+_{1y}+\varepsilon g^+_{1y}\\ f^+_{2x}+\varepsilon g^+_{2x}&{} f^+_{2y}+\varepsilon g^+_{2y} \end{pmatrix}q^+(t,\theta ,\varepsilon ) \end{aligned}$$
(3.22)

with \(q^+(0,\theta ,\varepsilon )=(-1,0)\) and

$$\begin{aligned}&\frac{\partial }{\partial t}k^+(t,\theta ,\varepsilon )\\&\quad =\begin{pmatrix} f^+_{1x}+\varepsilon g^+_{1x}&{} f^+_{1y}+\varepsilon g^+_{1y}\\ f^+_{2x}+\varepsilon g^+_{2x}&{} f^+_{2y}+\varepsilon g^+_{1y} \end{pmatrix}k^+(t,\theta ,\varepsilon )\\&\qquad +\begin{pmatrix} (f^+_{1xx}+\varepsilon g^+_{1xx})q^+_1+(f^+_{1xy}+\varepsilon g^+_{1xy})q^+_2 &{} (f^+_{1xy}+\varepsilon g^+_{1xy})q^+_1+(f^+_{1yy}+\varepsilon g^+_{1yy})q^+_2\\ (f^+_{2xx}+\varepsilon g^+_{2xx})q^+_1+(f^+_{2xy}+\varepsilon g^+_{2xy})q^+_2 &{} (f^+_{2xy}+\varepsilon g^+_{2xy})q^+_1+(f^+_{2yy}+\varepsilon g^+_{2yy})q^+_2 \end{pmatrix}\\&\qquad q^+(t,\theta ,\varepsilon ) \end{aligned}$$

with \(k^+(0,\theta ,\varepsilon )=(0,0)\), respectively, and \(f^+_{iz}=f^+_{iz}\) \((\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(f^+_{izz}=f^+_{izz}\) \((\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(g^+_{iz}=g^+_{iz}(t+\theta ,\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\) and \(g^+_{izz}=g^+_{izz}(t+\theta ,\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(i=1,2\), \(z\in \{x,y\}\). Let \(s^+(\xi ,\varepsilon )\) be the spending time of trajectory \(\phi ^+\) from \(A^\prime _{\varepsilon }(\theta ,\xi )\) to \(B^\prime _{\varepsilon }(\theta ,\xi )\), that is

$$\begin{aligned} \varphi _1^+(s^+(\xi ,\varepsilon ),A^\prime _{\varepsilon }(\theta ,\xi );\varepsilon ) =x_{b^\prime ,\varepsilon }(\theta ,\xi ) \end{aligned}$$
(3.23)

and

$$\begin{aligned} \varphi _2^+(s^+(\xi ,\varepsilon ),A^\prime _{\varepsilon }(\theta ,\xi );\varepsilon )=0, \end{aligned}$$
(3.24)

where \(s^+(0,\varepsilon )=t^+(\varepsilon )\) and \(t^+(\varepsilon )\) is the spending time of trajectory \(\phi ^+\) from \(A^+_{\varepsilon }(\theta )\) to \(B^+_{\varepsilon }(\theta )\), see (3.5). Thus we can expend \(s^+(\xi ,\varepsilon )\) around \(\xi =0\) as

$$\begin{aligned} s^+(\xi ,\varepsilon )=t^+(\varepsilon )+\frac{\partial s^+}{\partial \xi }(0,\varepsilon )\xi +\frac{1}{2}\frac{\partial ^2 s^+}{\partial \xi ^2}(0,\varepsilon )\xi ^2+ {\mathcal {O}}(\xi ^3). \end{aligned}$$
(3.25)

Substituting (3.25) into (3.24) and comparing the coefficients of \(\xi \) and \(\xi ^2\) respectively, we can obtain

$$\begin{aligned} \frac{\partial s^+}{\partial \xi }(0,\varepsilon )=-\frac{q^+_2(t^+(\varepsilon ),\theta ,\varepsilon )}{f^+_2(x^+_{b,\varepsilon }(\theta ),0)+\varepsilon g^+_2(t^+(\varepsilon )+\theta ,x^+_{b,\varepsilon }(\theta ),0)} \end{aligned}$$
(3.26)

and

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 s^+}{\partial \xi ^2}(0,\varepsilon )\\&\quad =-\frac{\frac{\partial ^2 \varphi ^+_2}{\partial t^2}(t^+(\varepsilon ),A^+_{\varepsilon }(\theta );\varepsilon )(\frac{\partial s^+}{\partial \xi }(0,\varepsilon ))^2+2\frac{\partial }{\partial t}q^+_2(t^+(\varepsilon ),\theta ,\varepsilon )\frac{\partial s^+}{\partial \xi }(0,\varepsilon )+k^+_2(t^+(\varepsilon ),\theta ,\varepsilon )}{f^+_2(x^+_{b,\varepsilon }(\theta ),0)+\varepsilon g^+_2(t^+(\varepsilon )+\theta ,x^+_{b,\varepsilon }(\theta ),0)}, \end{aligned} \end{aligned}$$
(3.27)

where \(\frac{\partial ^2 \varphi ^+_2}{\partial t^2}(t^+(\varepsilon ),A^+_{\varepsilon }(\theta );\varepsilon )\) also satisfies differential equation (3.22). According to (3.23), (3.25), (3.26) and (3.27), one gets

$$\begin{aligned} x_{b^\prime ,\varepsilon }(\theta ,\xi )&=x^+_{b,\varepsilon }(\theta ) +\frac{v(t^+(\varepsilon ),\theta ,\varepsilon )}{f^+_2(x^+_{b,\varepsilon }(\theta ),0)+\varepsilon g^+_2(t^+(\varepsilon )+\theta ,x^+_{b,\varepsilon }(\theta ),0)}\xi \nonumber \\&\quad +\frac{1}{2}\frac{u(t^+(\varepsilon ),\theta ,\varepsilon )}{f^+_2(x^+_{b,\varepsilon }(\theta ),0)+\varepsilon g^+_2(t^+(\varepsilon )+\theta ,x^+_{b,\varepsilon }(\theta ),0)}\xi ^2+{\mathcal {O}}(\xi ^3), \end{aligned}$$
(3.28)

where

$$\begin{aligned} v(t^+(\varepsilon ),\theta ,\varepsilon )&=(f^+_2+\varepsilon g^+_2)q^+_1(t^+(\varepsilon ),\theta ,\varepsilon )-(f^+_1+\varepsilon g^+_1)q^+_2(t^+(\varepsilon ),\theta ,\varepsilon ) \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} u(t^+(\varepsilon ),\theta ,\varepsilon )&=(f^+_2+\varepsilon g^+_2)k^+_1(t^+(\varepsilon ),\theta ,\varepsilon )-(f^+_1+\varepsilon g^+_1)k^+_2(t^+(\varepsilon ),\theta ,\varepsilon )\\&\quad -\frac{q^+_2(t^+(\varepsilon ),\theta ,\varepsilon )}{(f^+_2+\varepsilon g^+_2)^2}\left[ (f^+_2+\varepsilon g^+_2)(f^+_{1x}+\varepsilon g^+_{1x})\right. \\&\quad \left. -(f^+_1+\varepsilon g^+_1)(f^+_{2x}+\varepsilon g^+_{2x})\right] v(t^+(\varepsilon ),\theta ,\varepsilon ) \end{aligned} \end{aligned}$$

with notations \(f^+_{i}=f^+_{i}(\varphi ^+(t^+(\varepsilon ),A^+_{\varepsilon }(\theta );\varepsilon ))\), \(f^+_{iz}=f^+_{iz}(\varphi ^+(t^+(\varepsilon ),A^+_{\varepsilon }(\theta );\varepsilon ))\), \(g^+_{i}=g^+_{i}(t^+(\varepsilon )+\theta ,\varphi ^+(t^+(\varepsilon ),A^+_{\varepsilon }(\theta );\varepsilon ))\) and \(g^+_{iz}=g^+_{iz}(t^+(\varepsilon )+\theta ,\varphi ^+(t^+(\varepsilon ),A^+_{\varepsilon }(\theta );\varepsilon ))\), \(i=1,2\), \(z\in \{x,y\}\). Considering

$$\begin{aligned} v(t,\theta ,\varepsilon )&=(f^+_2+\varepsilon g^+_2)q^+_1(t,\theta ,\varepsilon )-(f^+_1+\varepsilon g^+_1)q^+_2(t,\theta ,\varepsilon ), \end{aligned}$$
(3.29)

we have

$$\begin{aligned} \frac{\partial }{\partial t}v(t,\theta ;\varepsilon )=\left( (f^+_{1x}+\varepsilon g^+_{1x})+(f^+_{2y}+\varepsilon g^+_{2y})\right) v(t,\theta ,\varepsilon ) \end{aligned}$$

with \(v(0,\theta ;\varepsilon )=0\), accordingly,

$$\begin{aligned} v(t,\theta ;\varepsilon )=0. \end{aligned}$$
(3.30)

Moreover, from (3.22), (3.29) and (3.30), we can calculate that

$$\begin{aligned} \begin{aligned}&q^+_1(t,\theta ,\varepsilon )=-\mathrm{exp}\begin{pmatrix}\int ^{t}_0(f^+_{1x}+\varepsilon g^+_{1x})+(f^+_{1y}+\varepsilon g^+_{1y})\frac{f^+_{2}+\varepsilon g^+_{2}}{f^+_{1}+\varepsilon g^+_{1}}\mathrm{d}s\end{pmatrix},\\&q^+_2(t,\theta ,\varepsilon )=\frac{f^+_{2}+\varepsilon g^+_{2}}{f^+_{1}+\varepsilon g^+_{1}}q^+_1(t,\theta ,\varepsilon ), \end{aligned} \end{aligned}$$
(3.31)

where \(f^+_{i}=f^+_{i}(\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(f^+_{iz}=f^+_{iz}(\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(g^+_{i}=g^+_{i}(t+\theta ,\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\) and \(g^+_{iz}=g^+_{iz}(t+\theta ,\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(i=1,2\), \(z\in \{x,y\}\). In what follows, considering

$$\begin{aligned} \begin{aligned} u(t,\theta ,\varepsilon )&=(f^+_2+\varepsilon g^+_2)k^+_1(t,\theta ,\varepsilon )-(f^+_1+\varepsilon g^+_1)k^+_2(t,\theta ,\varepsilon )\\&\quad -\frac{q^+_2(t,\theta ,\varepsilon )}{(f^+_2+\varepsilon g^+_2)^2}\left( (f^+_2+\varepsilon g^+_2)(f^+_{1x}+\varepsilon g^+_{1x})\right. \\&\quad \left. -(f^+_1+\varepsilon g^+_1)(f^+_{2x}+\varepsilon g^+_{2x})\right) v(t,\theta ,\varepsilon ), \end{aligned} \end{aligned}$$

one gets

$$\begin{aligned} \frac{\partial }{\partial t}u(t,\theta ,\varepsilon )&=\left( (f^+_{1x}+\varepsilon g^+_{1x})+(f^+_{2y}+\varepsilon g^+_{2y})\right) u(t,\theta ,\varepsilon )+V(t,\theta ,\varepsilon ) \end{aligned}$$

with \(u(0,\theta ,\varepsilon )=0\), where

$$\begin{aligned} \begin{aligned} V(t,\theta ,\varepsilon )&=(f^+_2+\varepsilon g^+_2)\left[ (f^+_{1xx}+\varepsilon g^+_{1xx})(q^+_1(t,\theta ,\varepsilon ))^2\right. \\&\quad \left. +2(f^+_{1xy}+\varepsilon g^+_{1xy})q^+_1(t,\theta ,\varepsilon )q^+_2(t,\theta ,\varepsilon )+(f^+_{1yy}+\varepsilon g^+_{1yy})(q^+_2(t,\theta ,\varepsilon ))^2\right] \\&\quad -(f^+_1+\varepsilon g^+_1)\left[ (f^+_{2xx}+\varepsilon g^+_{2xx})(q^+_1(t,\theta ,\varepsilon ))^2\right. \\&\quad \left. +2(f^+_{2xy}+\varepsilon g^+_{2xy})q^+_1(t,\theta ;\varepsilon )q^+_2(t,\theta ,\varepsilon )+(f^+_{2yy}+\varepsilon g^+_{2yy})(q^+_2(t,\theta ,\varepsilon ))^2\right] \end{aligned} \end{aligned}$$
(3.32)

with \(f^+_{i}=f^+_{i}\) \((\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(f^+_{izz}=f^+_{izz}\) \((\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(g^+_{i}=g^+_{i}(t+\theta ,\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(g^+_{izz}=g^+_{izz}(t+\theta ,\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(i=1,2\), \(z\in \{x,y\}\), and \(q^+_1(t,\theta ;\varepsilon )\) and \(q^+_2(t,\theta ;\varepsilon )\) are expressed in (3.31). The formula of constant variation yields

$$\begin{aligned} \begin{aligned} u(t^+(\varepsilon ),\theta ,\varepsilon )&=\mathrm{exp}\begin{pmatrix}\int ^{t^+(\varepsilon )}_0(f^+_{1x}+\varepsilon g^+_{1x})+(f^+_{2y}+\varepsilon g^+_{2y})\mathrm{d}s\end{pmatrix}\cdot \\&\quad \begin{pmatrix} \int ^{t^+(\varepsilon )}_0 V(s,\theta ,\varepsilon )\mathrm{exp}\begin{pmatrix}-\int ^{s}_0(f^+_{1x}+\varepsilon g^+_{1x})+(f^+_{2y}+\varepsilon g^+_{2y})\mathrm{d}\tau \end{pmatrix}\mathrm{d}s \end{pmatrix}, \end{aligned} \end{aligned}$$
(3.33)

where \(f^+_{iz}=f^+_{iz}\) \((\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\) and \(g^+_{iz}=g^+_{iz}(t+\theta ,\varphi ^+(t,A^+_{\varepsilon }(\theta );\varepsilon ))\), \(i=1,2\), \(z\in \{x,y\}\). By (3.28), (3.30) and (3.33), we can complete the proof. \(\square \)

By using aforementioned results we able to obtain the sufficient conditions of the periodic orbits of system (2.1) bifurcated from the generalized heteroclinic loop under the influence of the small periodic perturbations.

Theorem 1

Let

$$\begin{aligned} M(\theta )=f^-_2(B)w(\tau _0,\theta )-f^+_2(B)\rho (0, \theta +\tau _0) \end{aligned}$$

and

$$\begin{aligned} R(\theta )=f^+_{2x}(A)\kappa (0,\theta )+f^-_2(A)g^+_2(\theta ,A), \end{aligned}$$

where \(w(\tau _0,\theta )\), \(\kappa (0,\theta )\) and \(\rho (0, \theta +\tau _0)\) are expressed in (3.1), (3.10) and (3.11), respectively. Under the assumption (H1), if we suppose that there exists a \(\theta ^*\in (0,T]\) such that \(M(\theta ^*)=0\) and \(\frac{\mathrm{d}M(\theta ^*)}{\mathrm{d}\theta }\ne 0\), then for sufficiently small \(\varepsilon >0\), the following statements hold.

  1. (i)

    When \(R(\theta ^*)>0\), the system (2.1) has a homoclinic loop connecting the hyperbolic critical point to itself;

  2. (ii)

    When \(R(\theta ^*)<0\),

    $$\begin{aligned} f^-_2(A)f^+_{1x}(A)-f^+_{2x}(A)(f^-_1(A)-f^+_1(A))\ne 0 \end{aligned}$$
    (3.34)

    and

    $$\begin{aligned} \left( f^-_2(f^-_2g^+_1+\kappa (0,\theta ^*)f^+_{1x})-(f^-_1-f^+_1)R(\theta ^*)\right) \left( g^+_1f^+_{2x}-g^+_2f^+_{1x}\right) <0, \end{aligned}$$
    (3.35)

    where \(f^\pm _i=f^\pm _i(A)\), \(f^+_{ix}=f^+_{ix}(A)\) and \(g^+_i=g^+_i(\theta ^*,A)\), \(i=1,2\), the system (2.1) has a sliding generalized heteroclinic loop connecting the hyperbolic critical point and the visible fold.

Proof

For any fixed \(\theta \in (0,T]\), let

$$\begin{aligned} \xi =x^+_{a,\varepsilon }(\theta )-x^-_{a,\varepsilon }(\theta ) =-\varepsilon \left( \frac{\kappa (0,\theta )}{f^-_2(A)} +\frac{g^+_2(\theta ,A)}{f^+_{2x}(A)}\right) +{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$
(3.36)

From Proposition 5, we can assume that the orbit \(\phi ^+\) starting from \(A^-_{\varepsilon }(\theta )\) can return to the switching manifold \({\widetilde{\Omega }}\) at point \(B^\prime _{\varepsilon }(\theta ,\xi )\), and then define a distance between \(B^\prime _{\varepsilon }(\theta ,\xi )\) and \(B^-_{\varepsilon }(\theta +s^+(\xi ,\varepsilon ))\) in the plane \(\Sigma _{\theta +s^+(\xi ,\varepsilon )}\) as follows

$$\begin{aligned} d(\theta ,\varepsilon )&:=\pi _x(B^\prime _{\varepsilon }(\theta ,\xi ) -B^-_{\varepsilon }(\theta +s^+(\xi ,\varepsilon ))), \end{aligned}$$

where \(s^+(\xi ,\varepsilon )\) is the spending time of trajectory \(\phi ^+\) from \(A^\prime _{\varepsilon }(\theta ,\xi )\) to \(B^\prime _{\varepsilon }(\theta ,\xi )\). According to (3.2), (3.6), (3.13), (3.21), (3.25) and (3.36), we have

$$\begin{aligned} x_{b^\prime ,\varepsilon }(\theta ,\xi ) -x^+_{b,\varepsilon }(\theta )&=\frac{1}{2}\frac{u(t^+(\varepsilon ),\theta ,\varepsilon )}{f^+_2(x^+_{b,\varepsilon }(\theta ),0)+\varepsilon g^+_2(t^+(\varepsilon )+\theta ,x^+_{b,\varepsilon }(\theta ),0)}\xi ^2 +{\mathcal {O}}(\xi ^3)\\ {}&={\mathcal {O}}(\varepsilon ^2) \end{aligned}$$

and

$$\begin{aligned} x^+_{b,\varepsilon }(\theta )-x^-_{b,\varepsilon }(\theta +s^+(\xi ,\varepsilon )) =\varepsilon \left( \frac{w(\tau _0,\theta )}{f^+_2(B)} -\frac{\rho (0, \theta +\tau _0)}{f^-_2(B)}\right) +{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$

Accordingly,

$$\begin{aligned} d(\theta ,\varepsilon )&=\pi _x(B^\prime _{\varepsilon }(\theta ,\xi ) -B^+_{\varepsilon }(\theta )+B^+_{\varepsilon }(\theta )-B^-_{\varepsilon }(\theta +s^+(\xi ,\varepsilon )))\\&=x_{b^\prime ,\varepsilon }(\theta ,\xi ) -x^+_{b,\varepsilon }(\theta )+x^+_{b,\varepsilon }(\theta )-x^-_{b,\varepsilon }(\theta +s^+(\xi ,\varepsilon ))\\&=\varepsilon \left( \frac{w(\tau _0,\theta )}{f^+_2(B)} -\frac{\rho (0, \theta +\tau _0)}{f^-_2(B)}\right) +{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$

Notice that the existence of homoclinic loops in system (2.1) is equivalent to the existence of the zeros of \(d(\theta ,\varepsilon )\) when \(\xi >0\). From Remark 2 that \(f^-_2(B)f^+_2(B)>0\), we can denote

$$\begin{aligned} F(\theta ,\varepsilon ):=f^-_2(B)f^+_2(B)\frac{d(\theta ,\varepsilon )}{\varepsilon }=M(\theta )+{\mathcal {O}}(\varepsilon ), \end{aligned}$$

where

$$\begin{aligned} M(\theta )=f^-_2(B)w(\tau _0,\theta )-f^+_2(B)\rho (0, \theta +\tau _0). \end{aligned}$$
(3.37)

Under the assumption that there exists a \(\theta ^*\in (0,T]\) such that \(M(\theta ^*)=0\) and \(\frac{\mathrm{d} M(\theta )}{\mathrm{d} \theta }|_{\theta =\theta ^*}\ne 0\), that is \(F(\theta ^*,0)=0\) and \(\frac{\partial F(\theta ,\varepsilon )}{\partial \theta }|_{(\theta ^*,0)}\ne 0\), then we can find a function \(\theta (\varepsilon )\in {\mathbb {S}}^1\) such that \(F(\theta (\varepsilon ),\varepsilon )=0\), equivalently, \(d(\theta (\varepsilon ),\varepsilon )=0\), by using the implicit function theorem, moreover, \(\theta (\varepsilon )\rightarrow \theta ^*\) as \(\varepsilon \rightarrow 0\). Additionally, \(R(\theta ^*)>0\) implies \(\xi >0\). This completes the statement (i).

In what follows, we discuss the existence of sliding periodic orbits. To start with, we define two distances between \(A^+_\varepsilon (\theta )\) and \(A^-_{\varepsilon }(\theta )\) in the plane \(\Sigma _\theta \) and \(B^+_\varepsilon (\theta )\) and \(B^-_{\varepsilon }(\theta )\) in the plane \(\Sigma _{\theta +t^+(\varepsilon )}\), where \(t^+(\varepsilon )\) is the shortest spending time of the trajectory of \(\phi ^+\) from \(A^+_{\varepsilon }(\theta )\) to \(B^+_\varepsilon (\theta )\), as

$$\begin{aligned} d_1(\theta ,\varepsilon )&:=\pi _x(A^+_{\varepsilon }(\theta )-A^-_{\varepsilon }(\theta ))\\&=x^+_{a,\varepsilon }(\theta )-x^-_{a,\varepsilon }(\theta )\\&=-\varepsilon \left( \frac{\kappa (0,\theta )}{f^-_2(A)}+\frac{g^+_2(\theta ,A)}{f^+_{2x}(A)}\right) +{\mathcal {O}}(\varepsilon ^2) \end{aligned}$$

by (2.4) and (3.12), and

$$\begin{aligned} d_2(\theta ,\varepsilon )&:=\pi _x(B^+_{\varepsilon }(\theta )-B^-_{\varepsilon }(\theta +t^+(\varepsilon )))\\&=x^+_{b,\varepsilon }(\theta )-x^-_{b,\varepsilon }(\theta +t^+(\varepsilon ))\\&=\varepsilon \left( \frac{w(\tau _0,\theta )}{f^+_2(B)} -\frac{\rho (0, \theta +\tau _0)}{f^-_2(B)}\right) +{\mathcal {O}}(\varepsilon ^2) \end{aligned}$$

by (3.2), (3.6) and (3.13), respectively. Next, consider the orbits on the sliding region. Given a point \(p\in {\widetilde{\Omega }}^{loc}_s\), letting \(\phi ^s(\tau ,\theta ,\varepsilon )=(\varphi _1^s(\tau ,\theta ,\varepsilon ),0,\theta ^s(\tau ,\theta ,\varepsilon ))\) be a solution of sliding vector field (2.6) starting from \(A^+_\varepsilon (\theta )\) and arriving p by spending time \(\varepsilon \tau <0\), where \(\theta ^s(\tau ,\theta ,\varepsilon )=\theta +\varepsilon \tau \) and \(\phi ^s(0,\theta ,\varepsilon )=(x^+_{a,\varepsilon }(\theta ),0,\theta )\), and expending \(\varphi _1^s(\tau ,\theta ,\varepsilon )\) as

$$\begin{aligned} \varphi _1^s(\tau ,\theta ,\varepsilon )=x_a+\varepsilon \beta (\tau ,\theta )+{\mathcal {O}}(\varepsilon ^2), \end{aligned}$$

where \(\beta (\tau ,\theta )=\frac{\partial \varphi _1^s}{\partial \varepsilon }|_{\varepsilon =0}\) satisfying

$$\begin{aligned} \frac{\partial \beta }{\partial \tau }(\tau ,\theta )=K\beta (\tau ,\theta )+N(\theta )~~\mathrm{and}~~\beta (0,\theta )=-\frac{g^+_2(\theta ,A)}{f^+_{2x}(A)} \end{aligned}$$

with

$$\begin{aligned} K=\frac{1}{f^-_2(A)}\left( f^-_2(A)f^+_{1x}(A)-f^+_{2x}(A)(f^-_1(A)-f^+_1(A))\right) \ne 0 \end{aligned}$$

and

$$\begin{aligned} N(\theta )=\frac{1}{f^-_2(A)}\left( f^-_2(A)g^+_{1}(\theta ,A)-g^+_{2}(\theta ,A)(f^-_1(A)-f^+_1(A))\right) , \end{aligned}$$

accordingly,

$$\begin{aligned} \beta (\tau ,\theta )&=-\frac{N(\theta )}{K}+\left( \frac{N(\theta )}{K}-\frac{g^+_2(\theta ,A)}{f^+_{2x}(A)}\right) \mathrm{exp}(K\tau ). \end{aligned}$$

Set

$$\begin{aligned} d_3(\tau ,\theta ,\varepsilon )&:=\varphi _1^s(\tau ,\theta ,\varepsilon ) -x^-_{a,\varepsilon }\left( \theta ^s(\tau ,\theta ,\varepsilon )) =\varepsilon (\beta (\tau ,\theta )-\frac{\kappa (0,\theta )}{f^-_2(A)}\right) +{\mathcal {O}}(\varepsilon ^2). \end{aligned}$$

The existence of sliding generalized loop will be proved if we can find a \((\theta ,\tau )\) such that for sufficient small \(\varepsilon >0\), \(d_1(\theta ,\varepsilon )<0\), \(d_2(\theta ,\varepsilon )=0\) and \(d_3(\tau ,\theta ,\varepsilon )=0\). Since \(f^-_2(A)f^+_{2x}(A)<0\), \(f^-_2(B)f^+_2(B)>0\) and \(f^-_2(A)>0\), we can denote

$$\begin{aligned} F_1(\theta ,\varepsilon )&:=-f^-_2(A)f^+_{2x}(A)\frac{d_1(\theta ,\varepsilon )}{\varepsilon }=R(\theta )+{\mathcal {O}}(\varepsilon ),\\ F_2(\theta ,\varepsilon )&:=f^-_2(B)f^+_2(B)\frac{d_2(\theta ,\varepsilon )}{\varepsilon }=M(\theta )+{\mathcal {O}}(\varepsilon ),\\ F_3(\tau ,\theta ,\varepsilon )&:=f^-_2(A)\frac{d_3(\tau ,\theta ,\varepsilon )}{\varepsilon }=G(\tau ,\theta )+{\mathcal {O}}(\varepsilon ) \end{aligned}$$

where

$$\begin{aligned} R(\theta )=f^+_{2x}(A)\kappa (0,\theta )+f^-_2(A)g^+_2(\theta ,A), \end{aligned}$$

\(M(\theta )\) is expressed in (3.37) and

$$\begin{aligned} G(\tau ,\theta )=f^-_2(A)\beta (\tau ,\theta )-\kappa (0,\theta ). \end{aligned}$$

From \(M(\theta ^*)=0\), \(\frac{\mathrm{d}M(\theta ^*)}{\mathrm{d}\theta }\ne 0\), \(R(\theta ^*)<0\), (3.34) and (3.35), for this fixed \(\theta ^*\), there exists a

$$\begin{aligned} \tau ^*=\frac{1}{K}\ln \frac{\left( f^-_2(A)N(\theta ^*)+\kappa (0,\theta ^*)K\right) f^+_{2x}(A)}{\left( f^+_{2x}(A)N(\theta ^*)-g^+_2(\theta ^*,A)K\right) f^-_{2}(A)}<0 \end{aligned}$$

such that \(G(\tau ^*,\theta ^*)=0\) and \(d_1(\theta ^*,\varepsilon )<0\) for sufficient small \(\varepsilon >0\). Noticing

$$\begin{aligned}&\begin{pmatrix} \frac{\partial F_2(\theta ,\varepsilon )}{\partial \tau } &{} \frac{\partial F_2(\theta ,\varepsilon )}{\partial \theta }\\ \frac{\partial F_3(\tau ,\theta ,\varepsilon )}{\partial \tau } &{} \frac{\partial F_3(\tau ,\theta ,\varepsilon )}{\partial \theta } \end{pmatrix}|_{(\tau ^*,\theta ^*,0)} =\begin{pmatrix} \frac{\partial M(\theta )}{\partial \tau } &{} \frac{\partial M(\theta )}{\partial \theta }\\ \frac{\partial G(\tau ,\theta )}{\partial \tau } &{} \frac{\partial G(\tau ,\theta )}{\partial \theta } \end{pmatrix}|_{(\tau ^*,\theta ^*)}\\&\quad =\begin{pmatrix}0 &{} \frac{\mathrm{d} M(\theta ^*)}{\mathrm{d} \theta }\\ f^-_2(A)K\left( \frac{N(\theta ^*)}{K}-\frac{g^+_2(\theta ^*,A)}{f^+_{2x}(A)}\right) \mathrm{exp}(K\tau ^*) &{} \# \end{pmatrix}\\&\quad =\frac{f^-_2(A)}{f^+_{2x}(A)}\left( f^+_{2x}(A)N(\theta ^*)-g^+_2(\theta ^*,A)K\right) \mathrm{exp}(K\tau ^*)\frac{\mathrm{d} M(\theta ^*)}{\mathrm{d} \theta }\ne 0, \end{aligned}$$

hence by using the implicit function theorem, for sufficient small \(\varepsilon >0\), there exist \(\theta (\varepsilon )\in (0,T]\) and \(\tau (\varepsilon )<0\) such that \(F_2(\theta (\varepsilon ),\varepsilon )=0\) and \(F_3(\tau (\varepsilon ),\theta (\varepsilon ),\varepsilon )=0\), that is \(d_2(\theta (\varepsilon ),\varepsilon )=0\) and \(d_3(\tau (\varepsilon ),\theta (\varepsilon ),\varepsilon )=0\), moreover, \(\tau (\varepsilon )\rightarrow \tau ^*\) and \(\theta (\varepsilon )\rightarrow \theta ^*\) as \(\varepsilon \rightarrow 0\). This can conclude the statement (ii). \(\square \)

Remark 3

The case of \(R(\theta ^*)=0\) needs to approximate the calculations in Propositions 1-5 to the higher order, which seems to be a complicated process, we leave it for future consideration.

4 Application

In this section, we give the following example to illustrate how to use our results in Theorem 1 to get the exact periodic orbits.

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{pmatrix}{\dot{x}}\\ {\dot{y}} \end{pmatrix}=\begin{pmatrix}2y+n\\ -x+y-1 \end{pmatrix}+\varepsilon \begin{pmatrix}\alpha _1\sin {t}\\ 0 \end{pmatrix},~~~~~&{}\mathrm{if}~y>0,\\ \begin{pmatrix}{\dot{x}}\\ {\dot{y}} \end{pmatrix}=\begin{pmatrix}-1-\frac{1}{2}x-\frac{1}{2}y\\ -x \end{pmatrix}+\varepsilon \begin{pmatrix}\alpha _2\sin {t}\\ 0 \end{pmatrix},~&\mathrm{if}~y<0, \end{array}\right. \end{aligned}$$
(4.1)

where \(n<0\) and \(\alpha _i,~i=1,2\), are real parameters with \(\alpha _2\ne 0\).

When \(\varepsilon =0\), the upper subsystem (i.e., the subsystem in \(y>0\)) has a real unstable focus \((-\frac{n}{2}-1, -\frac{n}{2})\) with eigenvalues \(\lambda ^\pm =\frac{1}{2}\pm \mathrm{i}\frac{\sqrt{7}}{2}\) and a visible fold \(A=(-1,0)\). However, for the lower system (i.e., the subsystem in \(y<0\)), there have an invisible fold \(O=(0,0)\) and a saddle \(S=(0,-2)\) with two eigenvalues \(\lambda _1=\frac{1}{2}\) and \(\lambda _2=-1\). Moreover, the corresponding unstable manifold and stable manifold of S are

$$\begin{aligned} W^u(S)=\{(x,y):y\le 0~\mathrm{and}~y=-2x-2\}~~\mathrm{and}~~W^s(S)=\{(x,y):y\le 0~\mathrm{and}~y=x-2\}, \end{aligned}$$

which intersect the x-axis at points \(A=(-1,0)\) and \(B=(2,0)\), respectively. The solutions in two subsystems of (4.1) can be expressed as

$$\begin{aligned} \gamma ^+(t,x,y)&=\left( \frac{\sqrt{7}}{14}(-2+3n+8y-2x)e^{\frac{1}{2}t}\sin {\left( \frac{\sqrt{7}}{2}t\right) }\right. \\&\qquad \left. +\left( 1+\frac{n}{2}+x\right) e^{\frac{1}{2}t}\cos {\left( \frac{\sqrt{7}}{2}t\right) }-1-\frac{n}{2},\right. \\&\quad \left. \frac{\sqrt{7}}{28}(-8x+4y-2n-8)e^{\frac{1}{2}t}\sin {\left( \frac{\sqrt{7}}{2}t\right) }\right. \\&\qquad \left. +\frac{1}{2}(n+2y) e^{\frac{1}{2}t}\cos {\left( \frac{\sqrt{7}}{2}t\right) }-\frac{n}{2}\right) ,~y>0 \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \gamma ^-(t,x,y)&=\left( \frac{1}{3}(e^{-t}(y+2x+2)-e^{\frac{1}{2}t}(y-x+2)),\right. \\&\quad \left. \frac{1}{3}(e^{-t}(y+2x+2)+2e^{\frac{1}{2}t}(y-x+2))-2\right) ,~y<0, \end{aligned} \end{aligned}$$
(4.2)

respectively. Accordingly, the orbit of the upper subsystem passing through point \(A=(-1,0)\) is

$$\begin{aligned} \begin{aligned} \gamma ^+(t,A)&=\left( \frac{n}{2}e^{\frac{1}{2}t}\left( \cos {\left( \frac{\sqrt{7}}{2}t\right) } +\frac{3\sqrt{7}}{7}\sin {\left( \frac{\sqrt{7}}{2}t\right) }\right) -1-\frac{n}{2},\right. \\&\quad \left. \frac{n}{2}e^{\frac{1}{2}t} \left( \cos {\left( \frac{\sqrt{7}}{2}t\right) }-\frac{\sqrt{7}}{7}\sin {\left( \frac{\sqrt{7}}{2}t\right) }\right) -\frac{n}{2}\right) . \end{aligned} \end{aligned}$$
(4.3)

Therefore, there exists a \(\tau _0\approx 3.4177\), which is the smallest positive root of equation \(\cos (\frac{\sqrt{7}}{2}t)-\frac{\sqrt{7}}{7}\sin (\frac{\sqrt{7}}{2}t)=e^{-\frac{1}{2}t}\), such that \(\gamma ^+(\tau _0,A)=(2,0)=B\) for \(n=\frac{3\sqrt{7}}{2}e^{-\frac{1}{2}\tau _0}\frac{1}{\sin ({\frac{\sqrt{7}}{2}\tau _0})}\approx -0.7320\). Namely, the system (4.1) has a generalized heteroclinic loop \(\Gamma (t)\) (see Fig. 4) connecting the saddle \(S=(0,-2)\) with the fold \(A=(-1,0)\) and crossing the x-axis at \(B=(2,0)\) when \(n=\frac{3\sqrt{7}}{2}e^{-\frac{1}{2}\tau _0}\frac{1}{\sin ({\frac{\sqrt{7}}{2}\tau _0})}\approx -0.7320\). So that the assumption (H1) is established.

Fig. 4
figure 4

A generalized heteroclinic loop \(\Gamma (t)\)

Full size image

Clearly, by (4.2) the solutions of the lower system on the unstable and stable manifolds are

$$\begin{aligned} \gamma ^-_u(t,A)&=\left( -e^{\frac{1}{2}t},~e^{\frac{1}{2}t}-2\right) ,~~t\in (-\infty ,0], \end{aligned}$$
(4.4)

and

$$\begin{aligned} \gamma ^-_s(t-\tau _0,B)&=\left( 2e^{-(t-\tau _0)},~2e^{-(t-\tau _0)}-2\right) ,~~t\in [\tau _0,+\infty ), \end{aligned}$$
(4.5)

respectively. Moreover, from (4.3), (4.4) and (4.5), the corresponding \(w(\tau _0,\theta )\), \(\kappa (0,\theta )\) and \(\rho (0,\theta +\tau _0)\) in Propositions 3 and 4 can be calculated as

$$\begin{aligned}&w(\tau _0,\theta )=-\frac{3e^{\frac{1}{2}\tau _0}}{\sin {\left( \frac{\sqrt{7}}{2}\tau _0\right) }}\alpha _1\int ^{\tau _0}_0e^{-\frac{1}{2}s}\sin {(s+\theta )} \sin {\left( \frac{\sqrt{7}}{2}s\right) }\mathrm{d}s,\\&\kappa (0,\theta )=\alpha _2\int ^{-\infty }_0e^s\sin {(s+\theta )}\mathrm{d}s,\\&\rho (0,\theta +\tau _0)=-2\alpha _2\int ^{+\infty }_{\tau _0}e^{-\frac{1}{2}s}\sin {(s+\theta +\tau _0)}\mathrm{d}s. \end{aligned}$$

By Theorem 1, we have

$$\begin{aligned} \begin{aligned} M(\theta )&=\frac{6e^{\frac{1}{2}\tau _0}}{\sin {\left( \frac{\sqrt{7}}{2}\tau _0\right) }}\alpha _1\int ^{\tau _0}_0e^{-\frac{1}{2}s}\sin {(s+\theta )} \sin {\left( \frac{\sqrt{7}}{2}s\right) }\mathrm{d}s\\&\quad -6\alpha _2\int ^{+\infty }_{\tau _0}e^{-\frac{1}{2}s}\sin {(s+\theta +\tau _0)}\mathrm{d}s,\\&=\frac{3}{4\sin {\left( \frac{\sqrt{7}}{2}\tau _0\right) }}\alpha _1\left( 2\sqrt{7}e^{\frac{1}{2}\tau _0}(\cos \theta +\sin \theta )-(3+\sqrt{7})\cos {\left( \frac{(\sqrt{7}-2)\tau _0}{2}-\theta \right) }\right. \\&\quad +(3-\sqrt{7})\cos {(\frac{(\sqrt{7}+2)\tau _0}{2}+\theta )}+(1+\sqrt{7})\sin {\left( \frac{(\sqrt{7}-2)\tau _0}{2}-\theta \right) }\\&\quad \left. +(1-\sqrt{7})\sin {\left( \frac{(\sqrt{7}+2)\tau _0}{2}+\theta \right) }\right) \\&\quad -\frac{12}{5}e^{-\frac{1}{2}\tau _0}\alpha _2\left[ (2\cos {(2\tau _0)} +\sin (2\tau _0))\cos {\theta } +(\cos {(2\tau _0)}-2\sin (2\tau _0))\sin {\theta }\right] \end{aligned} \end{aligned}$$
(4.6)

and

$$\begin{aligned} R(\theta )&=-\alpha _2\int ^{-\infty }_0e^s\sin {(s+\theta )}\mathrm{d}s=-\frac{\alpha _2}{2}(\cos {\theta }-\sin {\theta }), \end{aligned}$$
(4.7)

it follows that

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}M(\theta )}{\mathrm{d}\theta }&=M(\theta +\frac{\pi }{2}). \end{aligned} \end{aligned}$$

Observe that \(M(\theta )\) is \(2\pi \)-periodic in \(\theta \), if there exists a \(\theta \in (0,2\pi ]\) such that \(M(\theta )=0\) then \(\frac{\mathrm{d}M(\theta )}{\mathrm{d}\theta }\ne 0\).

In what follows, based on both theoretical analysis and numerical simulations, we will discuss the existence of the sliding generalized heteroclinic loop and the homoclinic loop in system (4.1) by using our main results Theorem 1 .

Without loss of generality, we assume \(\alpha _2<0\), the case of \(\alpha _2>0\) can be discussed similarly. From (4.7) we have

$$\begin{aligned} \begin{aligned} R(\theta ) \left\{ \begin{array}{cc} >0,~~&{}\mathrm{if}~~\theta \in \left( 0, \frac{\pi }{4}\right) \cup (\frac{5\pi }{4}, 2\pi ],\\ =0,~~&{}\mathrm{if}~~\theta \in \{\frac{\pi }{4},\frac{5\pi }{4}\},\\ <0,~~&{}\mathrm{if}~~\theta \in \left( \frac{\pi }{4},\frac{5\pi }{4}\right) . \end{array}\right. \end{aligned} \end{aligned}$$

(4.6) can be rewritten as

$$\begin{aligned} \begin{aligned} M(\theta )&=\frac{3}{4\sin {(\frac{\sqrt{7}}{2}\tau _0})}\alpha _1\Lambda _2(\theta ) -\frac{12}{5}e^{-\frac{1}{2}\tau _0}\alpha _2\Lambda _1(\theta ), \end{aligned} \end{aligned}$$
(4.8)

where

$$\begin{aligned} \Lambda _1(\theta )&=(2\cos {(2\tau _0)} +\sin (2\tau _0))\cos {\theta } +(\cos {(2\tau _0)}-2\sin (2\tau _0))\sin {\theta },\\ \Lambda _2(\theta )&=2\sqrt{7}e^{\frac{1}{2}\tau _0}(\cos \theta +\sin \theta )-(3+\sqrt{7})\cos {\left( \frac{(\sqrt{7}-2)\tau _0}{2}-\theta \right) }\\&\quad +(3-\sqrt{7})\cos {\left( \frac{(\sqrt{7}+2)\tau _0}{2}+\theta \right) }\\&\quad +(1+\sqrt{7})\sin {\left( \frac{(\sqrt{7}-2)\tau _0}{2}-\theta \right) } +(1-\sqrt{7})\sin {\left( \frac{(\sqrt{7}+2)\tau _0}{2}+\theta \right) }. \end{aligned}$$

By (4.8), if there exists a \(\theta ^*\) such that \(\Lambda _2(\theta ^*)=0\), then \(M(\theta ^*)=0\) is equivalent to \(\Lambda _1(\theta ^*)=0\), however, it is impossible since that \(\Lambda _1(\theta )\) and \(\Lambda _2(\theta )\) have no common zeros in \((0,2\pi ]\) (see Fig. 5). Therefore, we can suppose \(\Lambda _2(\theta )\ne 0\). The zeros of \(M(\theta )\) in \((0,2\pi ]\) has a one-to-one correspondence to the zeros of the following \(m(\frac{\alpha _1}{\alpha _2},\theta )\) in \((0,2\pi ]\).

$$\begin{aligned} m(\frac{\alpha _1}{\alpha _2},\theta ):=\frac{\alpha _1}{\alpha _2}-\Lambda _3(\theta ), \end{aligned}$$

where

$$\begin{aligned} \Lambda _3(\theta )=\frac{16}{5}e^{-\frac{1}{2}\tau _0}\sin {\left( \frac{\sqrt{7}}{2}\tau _0\right) }\frac{\Lambda _1(\theta )}{\Lambda _2(\theta )}. \end{aligned}$$

Noticing

$$\begin{aligned} \mu _1:&=\Lambda _3(0)=\Lambda _3(\pi )=\Lambda _3(2\pi )=\frac{16}{5}e^{-\frac{1}{2}\tau _0}\sin {\left( \frac{\sqrt{7}}{2}\tau _0\right) } \frac{\Lambda _1(0)}{\Lambda _2(0)}\approx -0.0448,\\ \mu _2:&=\Lambda _3(\frac{\pi }{4})=\Lambda _3(\frac{5\pi }{4})=\frac{16}{5}e^{-\frac{1}{2}\tau _0}\sin {\left( \frac{\sqrt{7}}{2}\tau _0\right) } \frac{\Lambda _1\left( \frac{\pi }{4}\right) }{\Lambda _2(\frac{\pi }{4})}\approx -0.0228, \end{aligned}$$

from Fig. 6, we can found that for any fixed \(\frac{\alpha _1}{\alpha _2}\), there always exist two \(\theta \in (0,2\pi ]\), denoted by \(\theta ^*_1\) and \(\theta ^*_2\) with \(0<\theta ^*_1<\theta ^*_2\le 2\pi \), such that \(m(\frac{\alpha _1}{\alpha _2},\theta ^*_i)=0, i=1,2\), equivalently, \(M(\theta ^*_i)=0\), \(i=1,2\).

Fig. 5
figure 5

(colour online) The red and blue curves represent the \(\Lambda _1(\theta )\) and \(\Lambda _2(\theta )\), respectively

Full size image
Fig. 6
figure 6

(colour online) The blue and green lines represent the curves \(m(\frac{\alpha _1}{\alpha _2},\theta )=0\) and \(n(\frac{\alpha _1}{\alpha _2},\theta )=0\), respectively

Full size image

Additionally, by some simple calculations (3.34) is clear. When \(R(\theta )<0\), that is \(\theta \in (\frac{\pi }{4},\frac{5\pi }{4})\), from Theorem 1, we must take the condition (3.35) into consideration. Let

$$\begin{aligned} C(\theta ):&=\left[ f^-_2(f^-_2g^+_1+\kappa (0,\theta )f^+_{1x})-(f^-_1-f^+_1)R(\theta )\right] \left( g^+_1f^+_{2x}-g^+_2f^+_{1x}\right) \\&=-\left( \alpha _1\sin \theta -(1+3\sqrt{7}e^{-\frac{1}{2}\tau _0}\frac{1}{\sin ({\frac{\sqrt{7}}{2}\tau _0})}) \alpha _2(\cos \theta -\sin \theta )\right) \alpha _1\sin \theta . \end{aligned}$$

Clearly, if \(\sin \theta =0\), that is \(\theta =\pi \), then \(C(\theta )=0\). However, when \(\theta \ne \pi \), we can denote

$$\begin{aligned} n\left( \frac{\alpha _1}{\alpha _2},\theta \right) :=\frac{\alpha _1}{\alpha _2}-\Lambda _4(\theta ), \end{aligned}$$

where

$$\begin{aligned} \Lambda _4(\theta )=\left( 1+3\sqrt{7}e^{-\frac{1}{2}\tau _0} \frac{1}{\sin ({\frac{\sqrt{7}}{2}\tau _0})}\right) \left( \frac{1}{\tan \theta }-1\right) , \end{aligned}$$

thus

$$\begin{aligned} \mathrm{sign}(C(\theta ))=-\mathrm{sign}\left( n\left( \frac{\alpha _1}{\alpha _2},\theta \right) \right) \mathrm{sign}(\alpha _1\sin \theta ). \end{aligned}$$

Noticing \(\Lambda _4(\pi )=\Lambda _4(\frac{5\pi }{4})=0\), from Fig. 6, for \(\theta \in (\frac{\pi }{4},\frac{5\pi }{4})\) there exist two intersections \((\theta _1,\mu _4)\) and \((\theta _2,\mu _3)\) of \(m(\frac{\alpha _1}{\alpha _2},\theta )=0\) and \(n(\frac{\alpha _1}{\alpha _2},\theta )=0\), where \(\theta _1\in (\frac{\pi }{4},2.2393)\), \(\theta _2\in (\pi , \frac{5\pi }{4})\) and \(\mu _4>0>\mu _2>\mu _3>\mu _1\).

From aforementioned analysis, considering the two zeros \(\theta ^*_1\) and \(\theta ^*_2\) (\(\theta ^*_1<\theta ^*_2\)) of \(M(\theta )\) and \(\alpha _2<0\), we have the following cases.

(a):

If \(\frac{\alpha _1}{\alpha _2}>\mu _4\), then \(\theta ^*_1\in (\theta _1,2.2393)\), \(\theta ^*_2\in (\frac{5\pi }{4},5.3810)\), \(R(\theta ^*_1)<0\), \(R(\theta ^*_2)>0\) and \(C(\theta ^*_1)>0\);

(b):

If \(\frac{\alpha _1}{\alpha _2}=\mu _4\), then \(\theta ^*_1=\theta _1\), \(\theta ^*_2\in (\frac{5\pi }{4},5.3810)\), \(R(\theta ^*_1)<0\), \(R(\theta ^*_2)>0\) and \(C(\theta ^*_1)=0\);

(c):

If \(\mu _2<\frac{\alpha _1}{\alpha _2}<\mu _4\), then \(\theta ^*_1\in (\frac{\pi }{4},2.2393)\), \(\theta ^*_2\in (\frac{5\pi }{4},5.3810)\), \(R(\theta ^*_1)<0\), \(R(\theta ^*_2)>0\) and \(C(\theta ^*_1)<0\);

(d):

If \(\frac{\alpha _1}{\alpha _2}=\mu _2\), then \(\theta ^*_1=\frac{\pi }{4}\), \(\theta ^*_2=\frac{5\pi }{4}\), \(R(\theta ^*_1)=0\) and \(R(\theta ^*_2)=0\);

(e):

If \(\mu _3<\frac{\alpha _1}{\alpha _2}<\mu _2\), then \(\theta ^*_1\in (0,\frac{\pi }{4})\), \(\theta ^*_2\in (\theta _2,\frac{5\pi }{4})\), \(R(\theta ^*_1)>0\), \(R(\theta ^*_2)<0\) and \(C(\theta ^*_2)<0\);

(f):

If \(\frac{\alpha _1}{\alpha _2}=\mu _3\), then \(\theta ^*_1\in (0,\frac{\pi }{4})\), \(\theta ^*_2=\theta _2\), \(R(\theta ^*_1)>0\), \(R(\theta ^*_2)<0\) and \(C(\theta ^*_2)=0\);

(g):

If \(\mu _1<\frac{\alpha _1}{\alpha _2}<\mu _3\), then \(\theta ^*_1\in (0,\frac{\pi }{4})\), \(\theta ^*_2\in (\pi ,\theta _2)\), \(R(\theta ^*_1)>0\), \(R(\theta ^*_2)<0\) and \(C(\theta ^*_2)>0\);

(h):

If \(\frac{\alpha _1}{\alpha _2}=\mu _1\), then \(\theta ^*_1=\pi \), \(\theta ^*_2=2\pi \), \(R(\theta ^*_1)<0\), \(R(\theta ^*_2)>0\) and \(C(\theta ^*_1)=0\);

(i):

If \(\frac{\alpha _1}{\alpha _2}<\mu _1\), then \(\theta ^*_1\in (2.2393,\pi )\), \(\theta ^*_2\in (5.3810,2\pi )\), \(R(\theta ^*_1)<0\), \(R(\theta ^*_2)>0\) and \(C(\theta ^*_1)>0\).

Below, we summarize the dynamical behaviours of system (4.1).

(i):

When \(\frac{\alpha _1}{\alpha _2}\ge \mu _4\) or \(\frac{\alpha _1}{\alpha _2}\le \mu _3\), there exists a homoclinic loop;

(ii):

When \(\mu _3<\frac{\alpha _1}{\alpha _2}<\mu _2\) or \(\mu _2<\frac{\alpha _1}{\alpha _2}<\mu _4\), there exist a homoclinic loop and a sliding generalized heteroclinic loop.

5 Conclusions

In this paper, an autonomous planar piecewise smooth system having a generalized heteroclinic loop connecting a hyperbolic critical point and a visible fold is perturbed by the small non-autonomous periodic functions. With the aim to study the dynamics behavior near the unperturbed generalized heteroclinic loop, the \(\hbox {Melnikov}^\prime \)s ideas are used to obtain the existence of homoclinic and sliding generalized heteroclinic loops. It can be noticed that unlike the autonomous perturbation, except for perturbation parameter \(\varepsilon \) the displacement functions here also depend on time t, which makes the analysis more complicated. In addition, the appearance of the tangential singularities increases the degeneracy of the system, which also directly leads to the generation of the sliding generalized heteroclinic loop in our paper .