On the edge metric dimension of convex polytopes and its related graphs

Abstract

Let $G=(V, E)$ be a connected graph. The distance between the edge $e=uv\in E$ and the vertex $x\in V$ is given by $d(e, x) = \min \{d(u, x), d(v, x)\}$. A subset $S_{E}$ of vertices is called an edge metric generator for G if for every two distinct edges $e_{1}, e_{2}\in E$, there exists a vertex $x\in S_{E}$ such that $d(e_{1}, x)\ne d(e_{2}, x)$. An edge metric generator containing a minimum number of vertices is called an edge metric basis for G and the cardinality of an edge metric basis is called the edge metric dimension denoted by $\mu _{E}(G)$. In this paper, we study the edge metric dimension of some classes of plane graphs. It is shown that the edge metric dimension of convex polytope antiprism $A_{n}$, the web graph ${\mathbb {W}}_{n}$, and convex polytope ${\mathbb {D}}_{n}$ are bounded, while the prism related graph $D^{*}_{n}$ has unbounded edge metric dimension.

1 Introduction

The metric dimension was first introduced independently by Slater (1975) and by Harary and Melter (1976), which has been widely investigated in a number of papers, see Cáceres et al. (2007), Hallaway et al. (2014), Chartrand et al. (2000), Sebő and Tannier (2004), Guo et al. (2012) and Chartrand and Zhang (2003) for more details. It was appeared in various areas including pharmaceutical chemistry (Chartrand et al. 2000), combinatorial optimization (Sebő and Tannier 2004), robot navigation (Khuller et al. 1996), and sonar (Slater 1975), etc. Let G be a finite, simple, and connected graph with the vertex set V(G) and the edge set E(G). Throughout the paper, when there is no scope for ambiguity, we write V and E instead of the vertex set V(G) and the edge set E(G), respectively. For every distinct vertices $u, v\in V$, the distance between the vertices u and v, denoted by d(u, v), is the number of edges in a shortest path between them in G. A vertex $x\in V$ is said to distinguish a pair of vertices $u, v\in V$ if $d(u, x)\ne d(v, x)$. A set $S\subseteq V$ is a metric generator for G if every pair of vertices of G can be distinguished by some vertex in S. A metric basis of G is a metric generator of minimum cardinality. The cardinality of a metric basis, denoted by $\mu (G)$, is called the metric dimension of G. It was shown that computing the metric dimension of a graph is NP-hard (Khuller et al. 1996).

The edge metric dimension is a new variant of the metric dimension. It was introduced by Kelenc et al. (2018) and further investigated by Zubrilina (2018), Peterin and Yero (2018), Kratica et al. (2017) and Zhu et al. (2019). The distance between an edge $e = uv$ and a vertex x is defined as follows:

$$\begin{aligned} d(e, x) = \min \{d(u, x), d(v, x)\}. \end{aligned}$$

A vertex $x\in V$ is said to distinguish two distinct edges $e_{1}, e_{2}\in E$ if $d(e_{1}, x)\ne d(e_{2}, x)$. A set $S_{E}\subseteq V$ is an edge metric generator of a graph G if every two distinct edges are distinguished by some vertex of $S_{E}$. An edge metric generator with the smallest number of vertices is called an edge metric basis of G. The edge metric dimension of G, denoted by $\mu _{E}(G)$, is the cardinality of its edge metric basis. Kelenc et al. (2018) proved that computing the edge metric dimension of a graph is NP-hard.

For an ordered subset $S_{E}=\{x_{1}, x_{2}, \ldots , x_{k}\}$ of the vertex set V, the k-tuple $r(e|S_{E})=(d(e, x_{1}), d(e, x_{2}), \ldots , d(e, x_{k}))$ is called the edge metric representation of an edge e with respect to $S_{E}$. In this sense, $S_{E}$ is an edge metric generator for G if and only if for every pair of different edges $e_{1}, e_{2}$ of G, we have $r(e_{1}|S_{E})\ne r(e_{2}|S_{E})$.

An edge metric generator $S_{E}$ is not necessarily a metric generator. In Kelenc et al. (2018), the authors proposed an realization question for edge metric dimension and metric dimension. Specifically, they stated that it is possible to find graphs for which the metric dimension equals the edge metric dimension, as well as other graphs G for which $\mu (G)<\mu _{E}(G)$ or $\mu (G)>\mu _{E}(G)$. In this paper, using four classes of plane graphs convex polytope antiprism $A_{n}$, the web graph ${\mathbb {W}}_{n}$, the prism related graph $D^{*}_{n}$ and convex polytope ${\mathbb {D}}_{n}$, we further explore such situations by comparing the value of $\mu (G)$ and $\mu _{E}(G)$, where G denotes one of plane graphs $A_{n}$, ${\mathbb {W}}_{n}$, $D^{*}_{n}$ and ${\mathbb {D}}_{n}$.

This paper is organized as follows. In Sect. 2, we recall some results related to the edge metric dimension of graphs. In Sect. 3, we study the edge metric dimension of antiprism $A_{n}$. In Sect. 4, the explicit expression for $\mu _{E}({\mathbb {W}}_{n})$ and $\mu _{E}(D^{*}_{n})$ are obtained. The edge metric dimension convex polytope ${\mathbb {D}}_{n}$ is determined in Sect. 5. In the last section, we conclude the obtained results.

Throughout this paper, all vertex indices are taken to be module n.

2 Preliminaries

In this section, we recall some results on the edge metric dimension of graphs.

Let $G=(V,E)$ be a simple connected graph with the vertex set V and the edge set E. For a vertex v, let $N(v)=\{u\in V|uv\in E\}$ denote the neighborhood of the vertex v. |N(v)| is called the degree of the vertex v, denoted by $deg_{G}(v)$. The maximum degree and the minimum degree of G are denoted by $\Delta (G)$ and $\delta (G)$, respectively. Let ${\mathbb {R}}$ be a real number set and ${\mathbb {Z}}$ be the integer set. If $i, j\in {\mathbb {R}}$, we let $\llbracket i, j\rrbracket :=\{x\in {\mathbb {Z}}|\ i\le x\le j\}$ stand for the discrete interval between i and j.

It is known that if G is a connected graph of order n, we have $1 \le \mu _{E}(G) \le n-1$.

Now, we recall the lower bounds of the edge metric dimension of a connected graph.

Proposition 1

(Kelenc et al. 2018) If G is a connected graph and $\Delta (G)$ is the maximum degree of G, then we have $\mu _{E}(G)\ge \lceil log_{2}\Delta (G)\rceil$.

Proposition 2

(Kratica et al. 2017) Let G be a connected graph and let $\delta (G)$ be the minimum degree of G. Then $\mu _{E}(G) \ge 1 + \lceil log_{2}\delta (G)\rceil$.

For a family ${\mathscr {F}}$ of connected graphs, we say that ${\mathscr {F}}$ has bounded edge metric dimension, if for every graph G of ${\mathscr {F}}$ there exists a constant $C>0$ such that $\mu _{E}(G)\le C$ ; otherwise ${\mathscr {F}}$ has unbounded edge metric dimension.

If all graphs in ${\mathscr {F}}$ have the same edge metric dimension, then ${\mathscr {F}}$ is called a family with constant edge metric dimension. Paths $P_{n}$, cycles $C_{n}$ for $n\ge 2$ and prism $D_{n}$ are families of graphs with constant edge metric dimension.

We end this section with some useful facts about the metric dimension of antiprism $A_{n}$, the web graph ${\mathbb {W}}_{n}$, the prism related graph $D^{*}_{n}$ and convex polytope ${\mathbb {D}}_{n}$.

Lemma 1

(Javaid et al. 2008) Let $A_{n}$ be an antiprism with $n\ge 3$. Then we have $\mu (A_{n})=3$.

Lemma 2

(Imran et al. 2016) For $n\ge 3$, let ${\mathbb {W}}_{n}$ be a web graph. Then we have

$$\begin{aligned} \mu ({\mathbb {W}}_{n})= & {} \left\{ \begin{array}{lll} 2, \ \ n \ is \ odd, \\ 3, \ \ n \ is \ even. \end{array} \right. \end{aligned}$$

Lemma 3

(Ali et al. 2012) For $n\ge 6$, we have $\mu (D^{*}_{n})=3$.

Lemma 4

(Imran et al. 2012) Let ${\mathbb {D}}_{n}$ be the graph of convex polytope with $n\ge 3$. Then we have $\mu ({\mathbb {D}}_{n})=3$.

3 The graph of convex polytope antiprism $A_{n}$

In this section, we present the edge metric dimension of antiprism $A_{n}$ with $n\ge 3$.

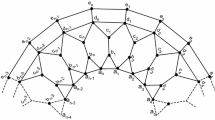
The antiprism $A_{n}$ defined in Bača (1988) is a 4-regular graph which has 2n 3-sided faces, and a pair of n-sided faces respectively, see Fig. 1. It consists of an outer cycle $b_{1}, b_{2}, \ldots , b_{n}$, an inner cycle $a_{1}, a_{2}, \ldots , a_{n}$, and a set of 2n spokes $a_{i}b_{i}$ and $a_{i}b_{i+1}$. We have the vertex set $V(A_{n})=\{a_{i}, b_{i}|1\le i \le n\}$, and the edge set $E(A_{n})=\{a_{i}a_{i+1}, a_{i}b_{i}, a_{i}b_{i+1}, b_{i}b_{i+1} |1\le i \le n\}$.

Fig. 1

Antiprism $A_{n}$

Lemma 5

For any edge metric generator $S_{E}$ of $A_{n}$, $S_{E}$ contains at least one vertex of outer cycle and one vertex of inner cycle, respectively.

Proof

Without loss of generality, assume $\{b_{1}, b_{2}, \ldots , b_{n}\}\bigcap S_{E}=\emptyset$. Since $S_{E}\ne \emptyset$, there exist some elements of inner cycle in $S_{E}$. In this case, we have $r(a_{i}b_{i}|S_{E})=r(a_{i}b_{i+1}|S_{E})$ for $1\le i\le n$. It implies that $S_{E}$ is not an edge metric generator. A contradiction. So there exists at least one vertex of outer cycle in $S_{E}$.

Similarly, we can show that there exists at least one vertex of inner cycle in $S_{E}$. $\square$

Lemma 6

If an edge metric generator $S_{E}$ for $A_{n}$ contains two vertices of one cycle, then $S_{E}$ contains at least two vertices of the another cycle.

Proof

The result will be proved by showing that if an edge metric generator $S_{E}$ for $A_{n}$ contains $n-1$ vertices of one cycle, then $S_{E}$ contains at least two vertices of the another cycle. Because of symmetry of the antiprism $A_{n}$, it is enough to show that if an edge metric generator $S_{E}$ for $A_{n}$ contains $n-1$ vertices of inner cycle, then $S_{E}$ contains at least two vertices of the outer cycle. By Lemma 5, there exists at least one vertex of outer cycle in $S_{E}$. Assume that there is only one vertex, say $b_{j}$ for $1\le j\le n$, such that $b_{j}\in S_{E}$. Without loss of generality, we assume that $a_{i}\notin S_{E}$ and $a_{k}\in S_{E}$ ($1\le k\le n, k\ne i$). We divide the proof into two cases.

• (1) If j or $j+n\in \llbracket i+1, i+\lceil \frac{n}{2}\rceil \rrbracket$, then we have $r(a_{i}b_{i+1}|S_{E})=r(b_{i}b_{i+1}|S_{E})$;

• (2) If j or $j+n\in \llbracket i+\lceil \frac{n}{2}\rceil +1, i+n\rrbracket$, then we have $r(a_{i}b_{i}|S_{E})=r(b_{i}b_{i+1}|S_{E})$.

Any of case above contradicts that $S_{E}$ is an edge metric generator for $A_{n}$.

The lemma follows immediately from what we have proved. $\square$

In the following, we give a lower bound for the edge metric dimension of antiprism $A_{n}$.

Corollary 1

If $A_{n}$ is an antiprism with $n\ge 3$, then $\mu _{E}(A_{n})\ge 4$.

Proof

Immediate from Proposition 2 and Lemma 6. $\square$

The metric dimension of antiprism $A_{n}$ was investigated in Javaid et al. (2008), see Lemma 1. In the following, we determine the exact value of the edge metric dimension for antiprism $A_{n}$.

Theorem 1

Let $A_{n}$ be an antiprism with $n\ge 3$. Then we have

$$\begin{aligned} \mu _{E}(A_{n})= & {} \left\{ \begin{array}{lll} 4, \ \ n \ is \ even, \\ 5, \ \ otherwise. \end{array} \right. \end{aligned}$$

Proof

We divide our proof into two cases.

Case (I)n is even. Set $n=2l$, where $l\in {\mathbb {Z}}$. Let $S_{E}=\{a_{1}, a_{l}, b_{1}, b_{l+1}\}$. To show that $S_{E}$ is an edge metric generator for $A_{n}$, we give representations of any edge of $E(A_{n})$ with respect to $S_{E}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{E})= & {} \left\{ \begin{array}{l@{\quad }l} (i-1, l-i-1,i, l-i), &{} 1\le i\le l-1, \\ (l-1, 0, l, 1), &{} i=l, \\ (2l-i, i-l, 2l-i, i-l), &{} l+1\le i\le 2l-1, \\ (0, l-1, 1, l), &{} i=2l. \end{array} \right. \\ r(a_{i}b_{i}|S_{E})= & {} \left\{ \begin{array}{l@{\quad }l} (i-1, l-i,i-1, l-i+1), &{} 1\le i\le l, \\ (2l-i+1, i-l, 2l-i+1, i-l-1), &{} l+1\le i\le 2l. \\ \end{array} \right. \\ r(a_{i}b_{i+1}|S_{E})= & {} \left\{ \begin{array}{l@{\quad }l} (i-1, l-i,i, l-i), &{} 1\le i\le l, \\ (2l-i+1, i-l, 2l-i, i-1), &{} l+1\le i\le 2l. \\ \end{array} \right. \\ r(b_{i}b_{i+1}|S_{E})= & {} \left\{ \begin{array}{l@{\quad }l} (1, l-1, 0, l-1), &{} i=1, \\ (i-1, l-i, i-1, l-i), &{} 2\le i\le l-1(l\ge 3), \\ (l-1, 1, l-1, 0), &{} i=l, \\ (2l-i+1, i-l, 2l-i, i-l-1), &{} l+1\le i\le 2l. \\ \end{array} \right. \end{aligned}$$

We note that there are no two edges having the same edge metric representations. So we have $\mu _{E}(A_{n})\le 4$. Using the Corollary 1 we obtain $\mu _{E}(A_{n})= 4$.

Case (II)n is odd. Set $n=2l+1$, where $l\in {\mathbb {Z}}$. Let $S_{E}=\{a_{1}, a_{l+1}, a_{l+2}, b_{1}, b_{l+2}\}$. To show that $S_{E}$ is an edge metric generator for $A_{n}$, we give representations of any edge of $E(A_{n})$ with respect to $S_{E}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (i-1, l-i,l-i+1, i, l-i+1), &{} 1\le i\le l, \\ (l, 0, 0, l, 1), &{} i=l+1, \\ (2l-i+1, i-l-1, i-l-2, 2l-i+1, i-l-1), &{} l+2\le i\le 2l, \\ (0, l, l-1, 1, l), &{} i=2l+1. \end{array} \right. \\ r(a_{i}b_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (0, l, l, 0, l), &{} i=1, \\ (i-1, l-i+1, l-i+2, i-1, l-i+2), &{} 2\le i\le l+1, \\ (2l-i+2, i-l-1, i-l-2, 2l-i+2, i-l-2), &{} l+2\le i\le 2l+1. \end{array} \right. \\ r(a_{i}b_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (0, l, l, 1, l), &{} i=1, \\ (i-1, l-i+1, l-i+2, i, l-i+1), &{} 2\le i\le l, \\ (l, 0, 1, l, 0), &{} i=l+1, \\ (2l-i+2, i-l-1, i-l-2, 2l-i+1, i-l-1), &{} l+2\le i\le 2l+1. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (1, l, l, 0, l), &{} i=1, \\ (i-1, l-i+1, l-i+2, i-1, l-i+1,), &{} 2\le i\le l(l\ge 2), \\ (l, 1, 1, l, 0), &{} i=l+1, \\ (l, 1, 1, l-1, 0), &{} i=l+2,\\ (2l-i+2, i-l-1, i-l-2, 2l-i+1, i-l-2), &{} l+3\le i\le 2l+1. \\ \end{array} \right. \end{aligned}$$

Note that there are no two edges having same edge metric representation, which implies that $\mu _{E}(A_{n})\le 5$. On the other hand, we show that $\mu _{E}(A_{n})\ge 5$. Suppose on contrary that $\mu _{E}(A_{n})= 4$. Then there are following possibilities to be discussed. Using Lemma 6, we know that an edge metric generator $S_{E}$ for $A_{n}$ contains at least two vertices of two cycles respectively.

Let $a_{1}, a_{i}$ be two vertices on inner cycle and $b_{j}, b_{k}$ be two vertices on outer cycle, where $2 \le i \le n$, $1 \le j\ne k \le n$. For $2 \le i \le l+1$, we only consider the following cases.

• (1) If both of j, k aren’t equal to $l+2$, then we have $r(a_{l+1}a_{l+2}|S_{E})=r(a_{l+1}b_{l+2}|S_{E})$.

• (2) If one of the j, k equals $l+2$, we assume $j=l+2$. we only consider the following two cases.

  • (i) If $k=1$, then we have $r(a_{l+1}a_{l+2}|S_{E})=r(a_{l+1}b_{l+1}|S_{E})$;

  • (ii) If $k\ne 1$, then we obtain $r(a_{1}a_{n}|S_{E})=r(a_{1}b_{1}|S_{E})$.

Thus, in every case we get a contradiction.

For $l+2 \le i \le n$, we can rename vertices and situation will be same as discussed above.

Hence, it follows from the above that there is no edge metric generator with four vertices for $A_{n}$ implying that $\mu _{E}(A_{n})= 5$ in this case. $\square$

Remark 1

If $A_{n}$ is an antiprism with $n\ge 3$, then $\mu (A_{n})<\mu _{E}(A_{n})$ by Lemma 1.

4 The prism related graphs

The prism $D_{n}$ is a 3-regular graph which is obtained by the Cartesian product of a cycle $C_{n}$ and the path $P_{2}$. It consists of an outer cycle $b_{1}, b_{2}, \ldots , b_{n}$, an inner cycle $a_{1}, a_{2}, \ldots , a_{n}$, and a set of n spokes $a_{i}b_{i}$. We have the vertex set $V(D_{n})=\{a_{i}, b_{i}|1\le i \le n\}$, and the edge set $E(D_{n})=\{a_{i}a_{i+1}, a_{i}b_{i}, b_{i}b_{i+1} |1\le i \le n\}$. The edge metric dimension of the prism $D_{n}$ has been studied recently in Kratica et al. (2017). In this section, we extend this study to two classes prism related graphs which obtained from prism $D_{n}$ by slight modifications. Furthermore, we consider how the edge metric dimension of prism $D_{n}$ is affected by adding a single vertex.

4.1 The web graph ${\mathbb {W}}_{n}$

Koh et al. (1980) defined a web graph ${\mathbb {W}}_{n}$ (Fig. 2) as a stacked prism graph $P_{3}\times C_{n}$ with the edges of the outer cycle removed. The web graph ${\mathbb {W}}_{n}$ also can be obtained from prism $D_{n}$ by attaching a pendant edge $b_{i}c_{i}$ at each vertex $b_{i}$ of outer cycle of prism $D_{n}$. We have the vertex set $V({\mathbb {W}}_{n})=\{a_{i}, b_{i}, c_{i}|1\le i \le n\}$, and the edge set $E({\mathbb {W}}_{n})=\{a_{i}a_{i+1}, a_{i}b_{i}, b_{i}b_{i+1}, b_{i}c_{i} |1\le i \le n\}$. For convenience, we call vertices $c_{i}$ where $1\le i\le n$, the pendent vertices.

Fig. 2

The web graph ${\mathbb {W}}_{n}$

Theorem 2

For the web graph ${\mathbb {W}}_{n}$ with $n\ge 3$, we have $\mu _{E}({\mathbb {W}}_{n})=3$.

Proof

We consider the following two cases.

Case (I)n is even. Set $n=2l$, where $l\in {\mathbb {Z}}$. Let $S_{E}=\{a_{1}, a_{2}, a_{l+1}\}$. To show that $S_{E}$ is an edge metric generator for ${\mathbb {W}}_{n}$, we give representations of any edge of $E({\mathbb {W}}_{n})$ with respect to $S_{E}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (0, 0, l-1), &{} i=1, \\ (i-1, i-2, l-i), &{} 2\le i \le l, \\ (l-1, l-1, 0), &{} i=l+1, \\ (2l-i, 2l-i+1, i-l-1), &{} l+2 \le i \le 2l. \end{array} \right. \\ r(a_{i}b_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (0, 1, l), &{} i=1, \\ (i-1, i-2, l-i+1), &{} 2\le i \le l+1, \\ (2l-i+1, 2l-i+2, i-l-1), &{} l+2 \le i \le 2l. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (1, 1, l), &{} i=1, \\ (i, i-1, l-i+1), &{} 2\le i \le l, \\ (l, l, 1), &{} i=l+1, \\ (2l-i+1, 2l-i+2, i-l), &{} l+2 \le i \le 2l. \end{array} \right. \\ r(b_{i}c_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (1, 2, l+1), &{} i=1, \\ (i, i-1, l-i+2), &{} 2\le i \le l+1, \\ (2l-i+2, 2l-i+3, i-l), &{} l+2 \le i \le 2l. \end{array} \right. \end{aligned}$$

Note that there are no two edges having same edge metric representation, which implies that $\mu _{E}({\mathbb {W}}_{n})\le 3$.

It remains to show that $\mu _{E}({\mathbb {W}}_{n})\ge 3$. The result will be proved by showing that there is no edge metric generator $S_{E}$ with $|S_{E}|=2$. Assume for a contradiction that $|S_{E}|=2$, then there are the following possibilities to be discussed.

• (1) Both vertices are in the inner cycle. Without loss of generality, we assume that one vertex is $a_{1}$, and the other is $a_{i}\ (2\le i\le l+1)$. For $2\le i\le l$, we have $r(a_{1}a_{n}|S_{E})=r(a_{1}b_{1}|S_{E})=(0, i-1)$. And for $i=l+1$, we have $r(a_{1}a_{2}|S_{E})=r(a_{1}a_{n}|S_{E})=(0, l-1)$. A contradiction.

• (2) Both vertices are in the outer cycle. Without loss of generality, we assume that one vertex is $b_{1}$, and the other is $b_{i}\ (2\le i\le l+1)$. For $2\le i\le l$, we have $r(b_{1}b_{n}|S_{E})=r(b_{1}c_{1}|S_{E})=(0, i-1)$. And for $i=l+1$, we have $r(b_{1}b_{2}|S_{E})=r(b_{1}b_{n}|S_{E})=(0, l-1)$. A contradiction.

• (3) Both vertices are in the set of pendent vertices. Without loss of generality, we assume that one vertex is $c_{1}$, and the other is $c_{i}\ (2\le i\le l+1)$. For $2\le i\le l$, we have $r(a_{1}b_{1}|S_{E})=r(b_{1}b_{n}|S_{E})=(1, i)$. And for $i=l+1$, we have $r(a_{2}b_{2}|S_{E})=r(a_{n}b_{n}|S_{E})=(2, l)$. A contradiction.

• (4) One vertex is in the inner cycle, and the other is in the outer cycle. Consider the vertex $a_{1}$, and the other is $b_{i}\ (1\le i\le l+1)$. For $1\le i\le l$, we have $r(b_{1}c_{1}|S_{E})=r(b_{1}b_{n}|S_{E})=(1, i-1)$. And for $i=l+1$, we have $r(a_{2}b_{2}|S_{E})=r(a_{n}b_{n}|S_{E})=(1, l-1)$. A contradiction.

• (5) One vertex is in the inner cycle, and the other is in the set of pendent vertices. Consider the vertex $a_{1}$, and the other is $c_{i}\ (1\le i\le l+1)$. For $i=1$, we have $r(b_{1}b_{2}|S_{E})=r(b_{1}b_{n}|S_{E})=(1, 1)$. And for $2\le i\le l+1$, we have $r(b_{1}b_{2}|S_{E})=r(a_{2}b_{2}|S_{E})=(1, i-1)$. A contradiction.

• (6) One vertex is in the outer cycle, and the other is in the set of pendent vertices. Consider the vertex $b_{1}$, and the other is $c_{i}\ (1\le i\le l+1)$. For $1\le i\le l$, we have $r(a_{1}b_{1}|S_{E})=r(b_{1}b_{n}|S_{E})=(0, i)$. And for $i=l+1$, we have $r(a_{2}b_{2}|S_{E})=r(a_{n}b_{n}|S_{E})=(1, l)$. A contradiction.

So from above we conclude that there is no edge metric generator with two vertices for ${\mathbb {W}}_{n}$ implying that $\mu _{E}({\mathbb {W}}_{n})=3$ in this case.

Case (II)n is odd.

Set $n=2l+1$, where $l\in {\mathbb {Z}}$. Let $S_{E}=\{a_{1}, a_{2}, a_{l+2}\}$. To show that $S_{E}$ is an edge metric generator for ${\mathbb {W}}_{n}$, we give representations of any edge of $E({\mathbb {W}}_{n})$ with respect to $S_{E}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (0, 0, l), &{} i=1, \\ (i-1, i-2, l-i+1), &{} 2\le i \le l+1, \\ (2l-i+1, 2l-i+2, i-l-2), &{} l+2 \le i \le 2l+1. \end{array} \right. \\ r(a_{i}b_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (0, 1, l), &{} i=1, \\ (i-1, i-2, l-i+2), &{} 2\le i \le l+1, \\ (l, l, 0), &{} i=l+2, \\ (2l-i+2, 2l-i+3, i-l-2), &{} l+3 \le i \le 2l+1. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (1, 1, l+1), &{} i=1, \\ (i, i-1, l-i+2), &{} 2\le i \le l+1, \\ (2l-i+2, 2l-i+3, i-l-1), &{} l+2 \le i \le 2l+1. \end{array} \right. \\ r(b_{i}c_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (1, 2, l+1), &{} i=1, \\ (i, i-1, l-i+3), &{} 2\le i \le l+1, \\ (l+1, l+1, 1), &{} i=l+2, \\ (2l-i+3, 2l-i+4, i-l-1), &{} l+3 \le i \le 2l+1. \end{array} \right. \end{aligned}$$

Again we see that there are no two edges having same edge metric representation, which implies that $\mu _{E}({\mathbb {W}}_{n})\le 3$.

By the similar arguments to Case (I), we have $\mu _{E}({\mathbb {W}}_{n})\ge 3$. Thus, we obtain $\mu _{E}({\mathbb {W}}_{n})=3$. This completes the proof. $\square$

Remark 2

Let ${\mathbb {W}}_{n}$ be a web graph with $n\ge 3$. If n is odd, then $\mu ({\mathbb {W}}_{n})<\mu _{E}({\mathbb {W}}_{n})$; if n is even, then $\mu ({\mathbb {W}}_{n})=\mu _{E}({\mathbb {W}}_{n})$ by Lemma 2,

4.2 The prism related graph $D^{*}_{n}$

The plane graph $D^{*}_{n}$ (Fig. 3) defined in Ali et al. (2012) is also an extension of the prism $D_{n}$. It can be obtained from prism $D_{n}$ by adding a new vertex $c_{i}$ between the vertices $b_{i-1}$ and $b_{i}$ of the outer cycle with the vertex $c_{i}$ joining to vertices $b_{i-1}$ and $b_{i}$ for $1\le i\le n$, where $b_{0} = b_{n}$. We have the vertex set $V(D^{*}_{n})=\{a_{i}, b_{i}, c_{i}|1\le i \le n\}$, and the edge set $E(D^{*}_{n})=\{a_{i}a_{i+1}, a_{i}b_{i}, b_{i}b_{i+1}, b_{i}c_{i}, b_{i}c_{i+1}|1\le i \le n\}$.

Fig. 3

The prism related graph $D^{*}_{n}$

Lemma 7

Let $W=\{c_{1}, c_{2}, \ldots , c_{n}\}$ be a subset of $V(D^{*}_{n})$. For arbitrary edge metric generator $S_{E}$ of $D^{*}_{n}$, $S_{E}$ contains at least $\lceil \frac{n}{2}\rceil$ vertices of W.

Proof

Suppose that $S_{E}$ contains at most $\lceil \frac{n}{2}\rceil -1$ vertices of W for a contradiction. Without loss of generality, we assume vertices $c_{i}, c_{i+1}\notin S_{E}$. Then we have $r(b_{i}c_{i}|S_{E})=r(b_{i}c_{i+1}|S_{E})$, a contradiction. $\square$

Remark 3

Let $S_{E}$ be any edge metric basis for $D^{*}_{n}$. We note that $S_{E}$ contains all odd vertices (vertex indices are odd ) of W for odd n, while $S_{E}$ contains either all odd vertices or even vertices (vertex indices are even) of W for even n.

In the next lemma, we give a lower bound for the edge metric dimension of $D^{*}_{n}$.

Lemma 8

For $n\ge 5$, we have $\mu _{E}(D^{*}_{n})\ge \lceil \frac{n}{2}\rceil +1$.

Proof

We assume for a contradiction that the cardinality of subset $S_{E}$ is equal to $\lceil \frac{n}{2}\rceil$ by Lemma 7. Using Remark 3, we take $S_{E}=\{c_{i}\in W|$ vertex indices i is odd $\}$ such that $|S_{E}|=\lceil \frac{n}{2}\rceil$. For even $i\in [n]$, we have $r(a_{i}b_{i}|S_{E})=r(b_{i}c_{i}|S_{E})$ and $r(a_{i-1}b_{i-1}|S_{E})=r(b_{i-1}c_{i}|S_{E})$, a contradiction. $\square$

Theorem 3

For the prism related graph $D^{*}_{n}$ with $n\ge 3$, we have

$$\begin{aligned} \mu _{E}(D^{*}_{n})= & {} \left\{ \begin{array}{ll} 4,\ &{} n=3,\ 4, \\ \lceil \frac{n}{2}\rceil +1,\ &{} otherwise. \end{array} \right. \end{aligned}$$

Proof

For $n=3$ or $n=4$, we have found the edge metric dimension by total enumeration and given edge metric bases of $D^{*}_{n}$ in Table 1.

Table 1 Edge metric bases of $D^{*}_{n}$

For $n\ge 5$, we consider the following four cases.

Let $S_{E}=\{a_{1}, c_{1}, c_{3}, c_{5}, \ldots , c_{2l-1}\}$. We will show that $S_{E}$ is an edge metric basis of $D^{*}_{n}$ in Case (I) and (II), respectively.

Case (I)$n\equiv 0\ (mod \ 4)$.

In this case, we can write $n=2l$, where $l\in {\mathbb {Z}}$. Let $S_{1}=\{a_{1}, c_{1}, c_{3}, c_{l+1}, c_{2l-1}\}$. Next, we give representations of any edge of $E(D^{*}_{n})$ with respect to $S_{1}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (i-1, i+1, 2, l-i+1, i+3), &{} 1\le i \le 2, \\ (i-1, i+1, i-1, l-i+1, i+3), &{} 3\le i \le l-2, \\ (i-1, i+1, i-1, 2, 2l-i-1), &{} l-1 \le i \le l,\\ (2l-i, 2l-i+1, i-l, i-l+1, 2l-i-1), &{} l+1 \le i \le l+2,\\ (2l-i, 2l-i+1, 2l-i+3, i-l+1, 2l-i-1), &{} l+3\le i \le 2l-3,\\ (2l-i, 2l-i+1, 2l-i+3, i-l+1, 2), &{} 2l-2 \le i \le 2l-1,\\ (0, 2, 3, l+1, 3), &{} i=2l. \end{array} \right. \\ r(a_{i}b_{i}|S_{1})= & {} \left\{ \begin{array}{ll} (i-1, i, 3-i, l-i+1, i+2), &{} 1\le i \le 2, \\ (i-1, i, i-2, l-i+1, i+2), &{} 3\le i \le l-2, \\ (i-1, i, i-2, l-i+1, 2l-i-1), &{} l-1 \le i \le l,\\ (2l-i+1, 2l-i+1, i-2, i-l, 2l-i-1), &{} l+1 \le i \le l+2,\\ (2l-i+1, 2l-i+1, 2l-i+3, i-l, 2l-i-1), &{} l+3 \le i \le 2l-2,\\ (2l-i+1, 2l-i+1, 2l-i+3, i-l, i-2l+2), &{} 2l-1 \le i \le 2l. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (i, i, 1, l-i, i+2), &{} 1\le i \le 2, \\ (i, i, i-2, l-i, i+2), &{} 3\le i \le l-2, \\ (i, i, i-2, 1, 2l-i-2), &{} l-1 \le i \le l,\\ (2l-i+1, 2l-i, i-2, i-l, 2l-i-2), &{} l+1 \le i \le l+2,\\ (2l-i+1, 2l-i, 2l-i+2, i-l, 2l-i-2), &{} l+3 \le i \le 2l-3,\\ (2l-i+1, 2l-i, 2l-i+2, i-l, 1), &{} 2l-2 \le i \le 2l-1,\\ (1, 1, 2, l, 2), &{} i=2l. \end{array} \right. \\ r(b_{i}c_{i}|S_{1})= & {} \left\{ \begin{array}{ll} (1, 0, 2, l, 3), &{} i=1, \\ (i, i, 3-i, l-i+1, i+2), &{} 2\le i \le 3, \\ (i, i, i-2, l-i+1, i+2), &{} 4 \le i \le l-2,\\ (i, i, i-2, l-i+1, 2l-i-1), &{} l-1 \le i \le l,\\ (2l-i+2, 2l-i+1, i-2, 2i-2l-2, 2l-i-1), &{} l+1 \le i \le l+2,\\ (2l-i+2, 2l-i+1, 2l-i+3, i-l, 2l-i-1), &{} l+3 \le i \le 2l-1,\\ (2, 1, 3, l, 2), &{} i=2l. \end{array} \right. \\ r(b_{i}c_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (1, 1, 2, l, 3), &{} i=1, \\ (i, i, i-2, l-i+1, i+2), &{} 2\le i \le l-2, \\ (l-1, l-1, l-3, 2, l), &{} i=l-1,\\ (i, l, i-2, i-l, 2l-i-1), &{} l \le i \le l+1,\\ (l, l-1, i-2, 2, l-3), &{} i=l+2,\\ (2l-i+2, 2l-i+1, 2l-i+3, i-l, 2l-i-1), &{} l+3 \le i \le 2l-3,\\ (2l-i+2, 2l-i+1, 2l-i+3, i-l, i-2l+2), &{} 2l-2 \le i \le 2l-1,\\ (2, 0, 3, l, 2), &{} i=2l. \end{array} \right. \end{aligned}$$

When $1\le i\le n$ and $i\ne 1, 2, 3, l, l+1, 2l-2, 2l-1, 2l$, we have $r(b_{i}c_{i}|S_{1})=r(b_{i}c_{i+1}|S_{1})$. In other cases, there are no two edges having same edge metric representation. For odd i, where $1\le i\le n$ and $i\ne 1, 3, l+1, 2l-1$, we have $r(b_{i-1}c_{i-1}|S_{1}\cup \{c_{i}\})\ne r(b_{i-1}c_{i}|S_{1}\cup \{c_{i}\})$ and $r(b_{i}c_{i}|S_{1}\cup \{c_{i}\})\ne r(b_{i}c_{i+1}|S_{1}\cup \{c_{i}\})$. It follows that $r(b_{i}c_{i}|S_{E})\ne r(b_{i}c_{i+1}|S_{E})$ for $1\le i\le n$. Combining the above and Lemma 8, we obtain that $S_{E}$ is an edge metric generator for $D^{*}_{n}$, which implies that $\mu _{E}(D^{*}_{n})=\lceil \frac{n}{2}\rceil +1$.

Case (II)$n\equiv 2\ (mod \ 4)$.

In this case, we can write $n=2l$, where $l\in {\mathbb {Z}}$. Let $S_{1}=\{a_{1}, c_{1}, c_{3}, c_{l+2}\}$. Next, we give representations of any edge of $E(D^{*}_{n})$ with respect to $S_{1}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (i-1, i+1, 2, l-i+2), &{} 1\le i \le 2, \\ (i-1, i+1, i-1, l-i+2), &{} 3\le i \le l, \\ (l-1, l, l, 2), &{} i=l+1,\\ (2l-i, 2l-i+1, 2l-i+3, i-l), &{} l+2 \le i \le 2l-1,\\ (0, 2, 3, l), &{} i=2l. \end{array} \right. \\ r(a_{i}b_{i}|S_{1})= & {} \left\{ \begin{array}{ll} (i-1, i, 3-i, l), &{} 1\le i \le 2, \\ (i-1, i, i-2, l-i+2), &{} 3\le i \le l, \\ (2l-i+1, 2l-i+1, i-2, 1), &{} l+1 \le i \le l+2,\\ (2l-i+1, 2l-i+1, 2l-i+3, i-l-1), &{} l+3 \le i \le 2l. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (i, i, 1, l-i+1), &{} 1\le i \le 2, \\ (i, i, i-2, l-i+1), &{} 3\le i \le l, \\ (l, l-1, l-1, 1), &{}i=l+1,\\ (2l-i+1, 2l-i, 2l-i+2, i-l-1), &{} l+2 \le i \le 2l-1,\\ (1, 1, 2, l-1), &{} i=2l. \end{array} \right. \\ r(b_{i}c_{i}|S_{1})= & {} \left\{ \begin{array}{ll} (1, 0, 2, l), &{} i=1, \\ (i, i, 3-i, l-i+2), &{} 2\le i \le 3, \\ (i, i, i-2, l-i+2), &{} 4 \le i \le l,\\ (2l-i+2, 2l-i+1, i-2, l-i+2), &{} l+1 \le i \le l+2,\\ (2l-i+2, 2l-i+1, 2l-i+3, i-l-1), &{} l+3 \le i \le 2l. \end{array} \right. \\ r(b_{i}c_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (1, 1, 2, l), &{} i=1, \\ (i, i, i-2, l-i+2), &{} 2\le i \le l, \\ (2l-i+2, 2l-i+1, i-2, i-l-1), &{} l+1 \le i \le l+2,\\ (2l-i+2, 2l-i+1, 2l-i+3, i-l-1), &{} l+3 \le i \le 2l-1,\\ (2, 0, 3, l-1), &{} i=2l. \end{array} \right. \end{aligned}$$

When $1\le i\le n$ and $i\ne 1, 2, 3, l+1, l+2, 2l$, we have $r(b_{i}c_{i}|S_{1})=r(b_{i}c_{i+1}|S_{1})$. In other cases, there are no two edges having same edge metric representation. For odd i, where $1\le i\le n$ and $i\ne 1, 3, l+2$, we have $r(b_{i-1}c_{i-1}|S_{1}\cup \{c_{i}\})\ne r(b_{i-1}c_{i}|S_{1}\cup \{c_{i}\})$ and $r(b_{i}c_{i}|S_{1}\cup \{c_{i}\})\ne r(b_{i}c_{i+1}|S_{1}\cup \{c_{i}\})$. It follows that $r(b_{i}c_{i}|S_{E})\ne r(b_{i}c_{i+1}|S_{E})$ for $1\le i\le n$. Combining the above and Lemma 8, we see that $S_{E}$ is an edge metric generator for $D^{*}_{n}$, which implies that $\mu _{E}(D^{*}_{n})=\lceil \frac{n}{2}\rceil +1$.

Let $S_{E}=\{a_{1}, c_{1}, c_{3}, c_{5}, \ldots , c_{2l-1}, c_{2l+1}\}$. We will show that $S_{E}$ is an edge metric basis of $D^{*}_{n}$ in Case (III) and (IV), respectively.

Case (III)$n\equiv 1\ (mod \ 4)$.

In this case, we can write $n=2l+1$, where $l\in {\mathbb {Z}}$. Let $S_{1}=\{a_{1}, c_{1}, c_{3}, c_{l+3}\}$. Next, we give representations of any edge of $E(D^{*}_{n})$ with respect to $S_{1}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (i-1, i+1, 2, l+1), &{} 1\le i \le 2, \\ (i-1, i+1, i-1, l-i+3), &{} 3\le i \le l, \\ (2l-i+1, 2l-i+2, i-l, 2), &{} l+1 \le i \le l+2,\\ (2l-i+1, 2l-i+2, 2l-i+4, i-l-1), &{} l+3 \le i \le 2l,\\ (0, 2, 3, l), &{} i=2l+1. \end{array} \right. \\ r(a_{i}b_{i}|S_{1})= & {} \left\{ \begin{array}{ll} (i-1, i, 3-i, l+i-1), &{} 1\le i \le 2, \\ (i-1, i, i-2, l-i+3), &{} 3\le i \le l+1, \\ (l, l, l, 1), &{} i=l+2,\\ (2l-i+2, 2l-i+2, 2l-i+4, i-l-2), &{} l+3 \le i \le 2l+1. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (i, i, 1, l), &{} 1\le i \le 2, \\ (i, i, i-2, l-i+2), &{} 3\le i \le l, \\ (2l-i+2, 2l-i+1, i-2, 1), &{} l+1 \le i \le l+2,\\ (2l-i+2, 2l-i+1, 2l-i+3, i-l-2), &{} l+3 \le i \le 2l,\\ (1, 1, 2, l-1), &{} i=2l+1. \end{array} \right. \\ r(b_{i}c_{i}|S_{1})= & {} \left\{ \begin{array}{ll} (1, 0, 2, l), &{} i=1, \\ (i, i, 3-i, l-i+3), &{} 2\le i \le 3, \\ (i, i, i-2, l-i+3), &{} 4 \le i \le l+1,\\ (2l-i+3, 2l-i+2, i-2, l-i+3), &{} l+2 \le i \le l+3,\\ (2l-i+3, 2l-i+2, 2l-i+4, i-l-2), &{} l+4 \le i \le 2l+1. \end{array} \right. \\ r(b_{i}c_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (1, 1, 2, l), &{} i=1, \\ (i, i, i-2, l-i+3), &{} 2\le i \le l+1, \\ (2l-i+2, 2l-i+1, i-2, i-l-2), &{} l+2 \le i \le l+3,\\ (2l-i+2, 2l-i+1, 2l-i+3, i-l-2), &{} l+4 \le i \le 2l,\\ (2, 0, 3, l-1), &{} i=2l+1. \end{array} \right. \end{aligned}$$

Again we see that when $1\le i\le n$ and $i\ne 1, 2, 3, l+2, l+3, 2l+1$, we have $r(b_{i}c_{i}|S_{1})=r(b_{i}c_{i+1}|S_{1})$. In other cases, there are no two edges having same edge metric representation. For odd i, where $1\le i\le n$ and $i\ne 1, 3, l+3$, we have $r(b_{i-1}c_{i-1}|S_{1}\cup \{c_{i}\})\ne r(b_{i-1}c_{i}|S_{1}\cup \{c_{i}\})$ and $r(b_{i}c_{i}|S_{1}\cup \{c_{i}\})\ne r(b_{i}c_{i+1}|S_{1}\cup \{c_{i}\})$. It follows that $r(b_{i}c_{i}|S_{E})\ne r(b_{i}c_{i+1}|S_{E})$ for $1\le i\le n$. Combining the above and Lemma 8, we see that $S_{E}$ is an edge metric generator for $D^{*}_{n}$, which implies that $\mu _{E}(D^{*}_{n})=\lceil \frac{n}{2}\rceil +1$.

Case (IV)$n\equiv 3\ (mod \ 4)$.

In this case, we can write $n=2l+1$, where $l\in {\mathbb {Z}}$. Let $S_{1}=\{a_{1}, c_{1}, c_{3}, c_{l+2}\}$. Next, we give representations of any edge of $E(D^{*}_{n})$ with respect to $S_{1}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (i-1, i+1, 2, l-i+2), &{} 1\le i \le 2, \\ (i-1, i+1, i-1, l-i+2), &{} 3\le i \le l, \\ (2l-i+1, 2l-i+2, i-1, 2), &{} l+1 \le i \le l+2,\\ (2l-i+1, 2l-i+2, 2l-i+4, i-l), &{} l+3 \le i \le 2l,\\ (0, 2, 3, l+1), &{} i=2l+1. \end{array} \right. \\ r(a_{i}b_{i}|S_{1})= & {} \left\{ \begin{array}{ll} (i-1, i, 3-i, l-i+2), &{} 1\le i \le 2, \\ (i-1, i, i-2, l-i+2), &{} 3\le i \le l+1, \\ (l, l, l, 1), &{} i=l+2,\\ (2l-i+2, 2l-i+2, 2l-i+4, i-l-1), &{} l+3 \le i \le 2l+1. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (i, i, 1, l-i+1), &{} 1\le i \le 2, \\ (i, i, i-2, l-i+1), &{} 3\le i \le l, \\ (2l-i+2, 2l-i+1, i-2, 1), &{} l+1 \le i \le l+2,\\ (2l-i+2, 2l-i+1, 2l-i+3, i-l-1), &{} l+3 \le i \le 2l,\\ (1, 1, 2, l), &{} i=2l+1. \end{array} \right. \\ r(b_{i}c_{i}|S_{1})= & {} \left\{ \begin{array}{ll} (1, 0, 2, l+1), &{} i=1, \\ (i, i, 3-i, l-i+2), &{} 2\le i \le 3, \\ (i, i, i-2, l-i+2), &{} 4 \le i \le l+1,\\ (l+1, l, l, 0), &{} i=l+2,\\ (2l-i+3, 2l-i+2, 2l-i+4, i-l-1), &{} l+3 \le i \le 2l+1. \end{array} \right. \\ r(b_{i}c_{i+1}|S_{1})= & {} \left\{ \begin{array}{ll} (1, 1, 2, l+1), &{} i=1, \\ (i, i, i-2, l-i+2), &{} 2\le i \le l, \\ (l+1, 2l-i+2, i-2, i-l-1), &{} l+1 \le i \le l+2,\\ (2l-i+3, 2l-i+2, 2l-i+4, i-l-1), &{} l+3 \le i \le 2l,\\ (2, 0, 3, l), &{} i=2l+1. \end{array} \right. \end{aligned}$$

When $1\le i\le n$ and $i\ne 1, 2, 3, l+1, l+2, 2l+1$, we have $r(b_{i}c_{i}|S_{1})=r(b_{i}c_{i+1}|S_{1})$. In other cases, there are no two edges having same edge metric representation. For odd i, where $1\le i\le n$ and $i\ne 1, 3, l+2$, we have $r(b_{i-1}c_{i-1}|S_{1}\cup \{c_{i}\})\ne r(b_{i-1}c_{i}|S_{1}\cup \{c_{i}\})$ and $r(b_{i}c_{i}|S_{1}\cup \{c_{i}\})\ne r(b_{i}c_{i+1}|S_{1}\cup \{c_{i}\})$. It follows that $r(b_{i}c_{i}|S_{E})\ne r(b_{i}c_{i+1}|S_{E})$ for $1\le i\le n$. Combining the above and Lemma 8, we see that $S_{E}$ is an edge metric generator for $D^{*}_{n}$, which implies that $\mu _{E}(D^{*}_{n})= \lceil \frac{n}{2}\rceil +1$. $\square$

Remark 4

For $n\ge 6$, we obtain $\mu (D^{*}_{n})<\mu _{E}(D^{*}_{n})$ by Lemma 3.

5 The graph of convex polytope ${\mathbb {D}}_{n}$

The graph of convex polytope ${\mathbb {D}}_{n}$ (Fig. 4) defined in Bača (1988) is the trivalent plane graph which consists of 2n 5-sided faces and a pair of n-sided faces, respectively. We have the vertex set $V({\mathbb {D}}_{n})=\{a_{i}, b_{i}, c_{i}, d_{i}|1\le i \le n\}$, and the edge set $E({\mathbb {D}}_{n})=\{a_{i}a_{i+1}, a_{i}c_{i}, c_{i}d_{i}, c_{i+1}d_{i}, b_{i}d_{i}, b_{i}b_{i+1}|1\le i \le n\}$.

Fig. 4

The graph of convex polytope ${\mathbb {D}}_{n}$

It has been proved in Imran et al. (2012) that the metric dimension of the convex polytope ${\mathbb {D}}_{n}$ is constant. In the following, we will prove that the edge metric dimension of ${\mathbb {D}}_{n}$ is the same as the metric dimension of ${\mathbb {D}}_{n}$.

Theorem 4

Let the graph of convex polytope ${\mathbb {D}}_{n}$ be defined above. Then we have $\mu _{E}({\mathbb {D}}_{n})=3$

Proof

We consider the following two cases.

Case (I)n is even.

In this case, we set $n=2l$, where $l\in {\mathbb {Z}}$. Let $S_{E}=\{a_{1}, b_{1}, c_{l}\}$. To show that $S_{E}$ is an edge metric generator for ${\mathbb {D}}_{n}$, we give representations of any edge of $E({\mathbb {D}}_{n})$ with respect to $S_{E}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (0, 3, l-1), &{} i=1, \\ (i-1, i+1, l-i), &{} 2\le i \le l-1, \\ (l-1, l+1, 1), &{} i=l, \\ (2l-i, 2l-i+3, i-l+1), &{} l+1 \le i \le 2l-1,\\ (0, 3, l), &{} i=2l. \\ \end{array} \right. \\ r(a_{i}c_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (0, 2, l), &{} i=1, \\ (i-1, i, l-i+1), &{} 2\le i \le l-1, \\ (l-1, l, 0), &{} i=l, \\ (l, l+1, 2), &{} i=l+1, \\ (2l-i+1, 2l-i+3, i-l+1), &{} l+2 \le i \le 2l. \end{array} \right. \\ r(c_{i}d_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (i, i, l-i+2), &{} 1\le i \le l-3, \\ (l-2, l-2, 3), &{} i=l-2, \\ (l-1, l-1, 1), &{} i=l-1, \\ (l, l, 0), &{} i=l, \\ (l+1, l+1, 2), &{} i=l+1, \\ (2l-i+2, 2l-i+2, i-l+2), &{} l+2 \le i \le 2l. \end{array} \right. \\ r(d_{i}c_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (i+1, i, l-i+1), &{} 1\le i \le l-3, \\ (l-1, l-2, 2), &{} i=l-2, \\ (l, l-1, 0), &{} i=l-1, \\ (l+1, l, 1), &{} i=l, \\ (l, l+1, 3), &{} i=l+1, \\ (2l-i+1, 2l-i+2, i-l+3), &{} l+2 \le i \le 2l-1,\\ (l, 2, l+1), &{} i=2l. \end{array} \right. \\ r(b_{i}d_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (i+1, i-1, l-i+1), &{} 1\le i \le l-2, \\ (l, l-2, 1), &{} i=l-1, \\ (l+1, l-1, 1), &{} i=l, \\ (2l-i+2, 2l-i+1, i-l+2), &{} l+1 \le i \le 2l-1\\ (2, 1, l+1), &{} i=2l. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (i+2, i-1, l-i), &{} 1\le i \le l-2, \\ (l+1, l-2, 2), &{} i=l-1, \\ (l+1, l-1, 2), &{} i=l, \\ (2l-i+2, 2l-i, i-l+2), &{} l+1 \le i \le 2l-1\\ (3, 0, l), &{} i=2l. \end{array} \right. \end{aligned}$$

Note that there are no two edges having same edge metric representation, which implies that $\mu _{E}({\mathbb {D}}_{n})\le 3$. It follows from Proposition 2 that $\mu _{E}({\mathbb {D}}_{n})=3$ in this case.

Case (II)n is odd.

In this case, we set $n=2l+1$, where $l\in {\mathbb {Z}}$. Let $S_{E}=\{a_{1}, b_{1}, c_{l+1}\}$. To show that $S_{E}$ is an edge metric generator for ${\mathbb {D}}_{n}$, we give representations of any edge of $E({\mathbb {D}}_{n})$ with respect to $S_{E}$. They are

$$\begin{aligned} r(a_{i}a_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (0, 3, l), &{} i=1, \\ (i-1, i+1, l-i+1), &{} 2\le i \le l, \\ (l, l+2, 1), &{} i=l+1, \\ (2l-i+1, 2l-i+4, i-l), &{} l+2 \le i \le 2l+1. \end{array} \right. \\ r(a_{i}c_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (0, 2, l+1), &{} i=1, \\ (i-1, i, l-i+2), &{} 2\le i \le l, \\ (l, l+1, 0), &{} i=l+1, \\ (2l-i+2, 2l-i+4, i-l), &{} l+2 \le i \le 2l+1. \end{array} \right. \\ r(c_{i}d_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (i, i, l-i+3), &{} 1\le i \le l-2, \\ (l-1, l-1, 3), &{} i=l-1, \\ (l, l, 1), &{} i=l, \\ (l+1, l+1, 0), &{} i=l+1, \\ (l+1, l+1, 2), &{} i=l+2, \\ (2l-i+3, 2l-i+3, i-l+1), &{} l+3 \le i \le 2l+1. \end{array} \right. \\ r(d_{i}c_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (i+1, i, l-i+2), &{} 1\le i \le l-2, \\ (l, l-1, 2), &{} i=l-1, \\ (l+1, l, 0), &{} i=l, \\ (l+1, l+1, 1), &{} i=l+1, \\ (l, l+1, 3), &{} i=l+2, \\ (2l-i+2, 2l-i+3, i-l+2), &{} l+3 \le i \le 2l,\\ (l, 2, l+2), &{} i=2l+1. \end{array} \right. \\ r(b_{i}d_{i}|S_{E})= & {} \left\{ \begin{array}{ll} (i+1, i-1, l-i+2), &{} 1\le i \le l-1, \\ (l+1, l-1, 1), &{} i=l, \\ (l+2, l, 1), &{} i=l+1, \\ (2l-i+3, 2l-i+2, i-l+1), &{} l+2 \le i \le 2l+1. \end{array} \right. \\ r(b_{i}b_{i+1}|S_{E})= & {} \left\{ \begin{array}{ll} (i+2, i-1, l-i+1), &{} 1\le i \le l-1, \\ (l+2, l-1, 2), &{} i=l, \\ (2l-i+3, 2l-i+1, i-l+1), &{} l+1 \le i \le 2l\\ (3, 0, l+1), &{} i=2l+1. \end{array} \right. \end{aligned}$$

Again we see that there are no two edges having same edge metric representation, which implies that $\mu _{E}({\mathbb {D}}_{n})\le 3$. It follows from Proposition 2 that $\mu _{E}({\mathbb {D}}_{n})=3$ in this case. $\square$

Remark 5

For the graph of convex polytope ${\mathbb {D}}_{n}$ with $n\ge 3$, then we have $\mu ({\mathbb {D}}_{n})=\mu _{E}({\mathbb {D}}_{n})$ by Lemma 4.

6 Conclusion

In this paper, we have determined the exact value of the edge metric dimension of convex polytopes antiprism $A_{n}$, the web graph ${\mathbb {W}}_{n}$, the prism related graph $D^{*}_{n}$ and convex polytope ${\mathbb {D}}_{n}$. We conclude that the edge metric dimension of web graph ${\mathbb {W}}_{n}$ and convex polytope ${\mathbb {D}}_{n}$ are constant, and antiprism $A_{n}$ has bounded edge metric dimension while the prism related graph $D^{*}_{n}$ has unbounded edge metric dimension.