Mixed Metric Dimension of Some Plane Graphs

Abstract

Let G be a finite undirected simple connected graph with vertex set V(G) and edge set E(G). A vertex $u \in V(G)$ resolves two elements (vertices or edges) $v, w \in V(G)\cup E(G)$ if $d(u, v)\ne d(u,w)$. A subset $S_m$ of vertices in G is called a mixed metric generator for G if every two distinct elements (vertices and edges) of G are resolved by some vertex of $S_m$. The minimum cardinality of a mixed metric generator for G is called the mixed metric dimension and is denoted by $dim _m (G)$. In this paper, we study the mixed metric dimension for the plane graph of web graph $\mathbb {W}_n$ and convex polytope $\mathbb {D}_n$.

1 Introduction

The concept of the metric dimension of graph G was introduced independently by Slater [18] and Harary and Melter [6]. After these two seminal papers, several works concerning applications, as well as some theoretical properties, of this invariant were published. For instance, applications to the navigation of robots in networks were discussed in [14] and applications to chemistry were discussed in [2, 3, 10, 11].

Let G be a finite undirected simple connected graph with vertex set V(G) and edge set E(G). The distance d(u, v) between two vertices $u, v \in V(G)$ is the number of edges in a shortest path between them in G. A vertex $x \in V(G)$ resolves or distinguishes two vertices $u, v \in V(G)$ if $d(u, x) \ne d(v, x)$. A set $S\subset V(G)$ is a metric generator for G if every two distinct vertices of G can be distinguished by some vertex in S. A metric basis of G is a metric generator of minimum cardinality. The cardinality of a metric basis, denoted by dim(G) is called the metric dimension of G.

Similar to metric dimension, edge metric dimension was introduced by [12] which uniquely identifies the edges related to a graph. The distance between the vertex u and edge $e=vw$ is defined as $d(e,\,u)=min\{d(v,\,u),d(w,\,u)\}$. The vertex $u\in V(G)$ resolves or distinguishes two edges of a graph $e_1,\,e_2\in E(G)$ if $d(e_1,\,u)\ne d(e_2,\,u)$. A set $S_e\subset V(G)$ is an edge metric generator for G if every two distinct edges of G can be distinguished by some vertex of $S_e$. An edge metric basis of G is an edge metric generator of minimum cardinality. The cardinality of an edge metric basis, denoted by $dim_e(G)$ is called the edge metric dimension of G. Recently, this variant has been investigated by [15, 19, 20].

The mixed metric dimension is the combination of well studied metric and edge metric dimension. It was introduced by Kelenc et al. [11]. A vertex $v \in V(G)$ resolves or distinguishes two elements (vertices or edges) $a, b \in V(G) \cup E(G)$ if $d(v, a)\ne d(v, b)$. A set $S_m\subset V(G)\cup E(G)$ is a mixed metric generator for G if every two distinct elements (vertices or edges) of G can be distinguished by some vertex in $S_m$. A mixed metric basis of G is a mixed metric generator of minimum cardinality. The cardinality of a mixed metric basis, denoted by $dim_m(G)$ is called the mixed metric dimension of G. Let $S_m=\{v_1,\ v_2, \ldots ,\ v_k\}$ be an ordered subset of V(G). Let a be an element (vertex or edge) of G. The k-tuple $r(a|S_m ) = (d(a,\,v_1 ),\ d(a,\,v_2 ), \ldots ,\ d(a,\,v_k ))$ is called mixed metric representation of a with respect to $S_m$. Clearly, $S_m$ is a mixed metric generator if and only if for every two distinct elements (vertices or edges) a, b of G we have $r(a|S_m )\ne r(b|S_m )$. Calculation of the mixed metric dimension of a graph G can be found in [4, 5, 16, 17].

In this paper, we study the mixed metric dimension of two classes of plane graphs: web graph $\mathbb {W}_n$, plane graph (convex polytope) $\mathbb {D}_n$. We show that the mixed metric dimension of $\mathbb {W}_n$ is not constant and the mixed metric dimension of $\mathbb {D}_n$ is constant. For $\mathbb {W}_n$, $dim_m(\mathbb {W}_n)\, = n\,+1$ when $n\geqslant 3$. For $\mathbb {D}_n$, $dim_m(\mathbb {D}_n)\,=\,4$ when $n\geqslant 3$.

The organization of the paper is as follows. In the following section, we recall some results concerning plane graphs: $\mathbb {W}_n$, $\mathbb {D}_n$. In Sect. 3, we study the mixed metric dimension of $\mathbb {W}_n$. In Sect. 4, we study the mixed metric dimension of $\mathbb {D}_n$. In the last section, we conclude this paper.

2 Preliminaries

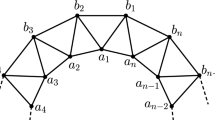
The web graph $\mathbb {W}_n$ [13] (Fig. 1) has 3n vertices and 4n edges. We have the vertex set

$$V(\mathbb {W}_n)=\{a_i, b_i, c_i | 1\leqslant i\leqslant n\},$$

and all edges $E(\mathbb {W}_n)\,=\,\{a_ia_{i+1}, a_ib_i, b_ib_{i+1},$ $b_ic_i | 1\leqslant i\leqslant n\} \ (a_{n+1}\,=\,a_1, b_{n+1}\,=\,b_1).$

Fig. 1.

The web graph $\mathbb {W}_n$

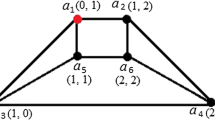
The plane graph (convex polytope) $\mathbb {D}_n$ [1] (Fig. 2) has 4n vertices and 6n edges. We have the vertex set

$$V(\mathbb {D}_n)\,=\,\{a_i, b_i, c_i, d_i | 1\leqslant i\leqslant n\},$$

and all edges $E(\mathbb {D}_n)\,=\,\{a_ia_{i+1}, a_ic_i, c_id_i, c_{i+1}d_i, b_id_i, b_ib_{i+1} | 1\leqslant i\leqslant n\} \ (a_{n+1}\,=\,a_1, b_{n+1}\,=\,b_1, c_{n+1}=c_1).$ Let $A\,=\,\{a_i:1\leqslant i\leqslant n\}$, $B=\{b_i:1\leqslant i\leqslant n\}$, $C\,=\,\{c_i:1\leqslant i\leqslant n\}$, $D\,=\,\{d_i:1\leqslant i\leqslant n\}$.

Fig. 2.

The plane graph $\mathbb {D}_n$

Lemma 1

[8] For $n\geqslant 5$, let $\mathbb {W}_n$ be a web graph. Then $dim(\mathbb {W}_n)$ is equal to 2 if n is odd and 3 if n is even.

Lemma 2

[7] Let $\mathbb {D}_n$ be the graph of convex polytope with $n\geqslant 4$, then we have $dim(\mathbb {D}_n)\,=\,3$.

Lemma 3

[21] For the web graph $\mathbb {W} _n$ with $n \geqslant 3$, we have $dim_e(\mathbb {W}_n)\,=\,3$.

Lemma 4

[21] For the graph of convex polytope $\mathbb {D}_ n$ with $n\geqslant 3$, then we have $dim_e(\mathbb {D}_n ) \,=\,3$.

3 The Mixed Metric Dimension of Web Graph $\mathbb {W}_n$

In this section we intend to present the mixed metric dimension of web graph $\mathbb {W}_n$ (Fig. 1).

Lemma 5

Let $\mathbb {W}_n$ be the web graph, where $n\geqslant 3$. Let $W=\{c_1,\ c_2, \ldots , \ c_n \}$ be a subset of $V(\mathbb {W}_n)$. For arbitrary mixed metric generators $S_m$ of $\mathbb {W}_n$, we have $W\subseteq S_m$.

Proof

Suppose that $c_i\notin S_m$. Then we have $r(b_ic_i|S_m)\,=\,r(b_i|S_m)$, which is a contradiction to the fact that $S_m$ is a mixed metric generator. Therefore we have $W\subseteq S_m$.

Lemma 6

Let $\mathbb {W}_n$ be the web graph, where $n\geqslant 3$. Then $dim_m(\mathbb {W}_n)\geqslant n+1$.

Proof

Let $S_m$ be any mixed metric generators for $\mathbb {W}_n$. By Lemma 5, we get $|S_m|\geqslant n$. If $|S_m|=n$, then we have $S_m\,=\,\{c_1,\ c_2, \ldots ,\ c_n \}$. Note that $r(a_ib_i|S_m)\,=\,r(b_i|S_m)$, which is a contradiction to the fact that $S_m$ is a mixed metric generator. Thus, we have $dim_m(\mathbb {W}_n)\geqslant n+1$.

Theorem 1

Let $\mathbb {W}_n$ be the web graph, where $n\geqslant 3$. Then $dim_m(\mathbb {W}_n)\,=\,n+1$.

Proof

For $3\leqslant n\leqslant 5$, we find that $\{a_1,\ c_1,\ c_2,\ldots ,\ c_n \}$ is the mixed metric basis of $\mathbb {W}_n$ by total enumeration, and hence the mixed metric dimension of $\mathbb {W}_n$ is $n+1$.

For $n\geqslant 6$, let $S_m\,=\,\{a_1,\ c_1,\ c_2, \ldots , c_n \}$. We will show that $S_m$ is a mixed metric generator of $\mathbb {W}_n$ in Cases (I) and (II), respectively.

Case (I) n is odd. In this case, we can write $n \,=\, 2l+1$, where $l\geqslant 3$ is an integer. Let $S_1\,=\,\{a_1,\ c_1,\ c_3,\ c_{l+3}\}.$ We give mixed metric representations of any element of $V(\mathbb {W}_n) \cup E(\mathbb {W}_n)$ with respect to $S_1$.

$$\begin{aligned} r(a_i|S_1)={\left\{ \begin{array}{ll} (i-1,\ i+1,\ 5-i,\ l+i), &{} 1\leqslant i\leqslant 2; \\ (i-1,\ i+1,\ i-1,\ l+5-i), &{} 3\leqslant i\leqslant l+1;\\ (2l+2-i,\ 2l+4-i,\ i-1,\ l+5-i), &{} l+2 \leqslant i \leqslant l+3;\\ (2l+2-i,\ 2l+4-i,\ 2l+6-i,\ i-l-1), &{} l+4 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_i|S_1)={\left\{ \begin{array}{ll} (i,\ i,\ 4-i,\ l+i-1), &{} 1\leqslant i\leqslant 2; \\ (i,\ i,\ i-2,\ l-i+4), &{} 3\leqslant i\leqslant l+1;\\ (2l-i+3,\ 2l-i+3,\ i-2,\ l-i+4), &{} l+2\leqslant i\leqslant l+3;\\ (2l+3-i,\ 2l+3-i,\ 2l+5-i,\ i-l-2), &{} l+4 \leqslant i \leqslant 2l+1.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(c_i|S_1)={\left\{ \begin{array}{ll} (2,\ 0,\ 4,\ l+1), &{} i\,=\,1; \\ (3,\ 3,\ 3,\ l+2), &{} i\,=\,2;\\ (4,\ 4,\ 0,\ l+2), &{} i\,=\,3;\\ (i+1,\ i+1,\ i-1,\ l+5-i), &{} 4\leqslant i\leqslant l+1;\\ (l+2,\ l+2,\ l+1,\ 3), &{} i\,=\,l+2;\\ (l+1,\ l+1,\ l+2,\ 0), &{} i\,=\,l+3;\\ (2l+4-i,\ 2l+4-i,\ 2l+6-i,\ i-l-1), &{} l+4\leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(a_ia_{i+1}|S_1)\,=\,{\left\{ \begin{array}{ll} (i-1,\ i+1,\ 4-i,\ l+i), &{} 1\leqslant i\leqslant 2; \\ (i-1,\ i+1,\ i-1,\ l-i+4), &{} 3\leqslant i\leqslant l+1;\\ (l-1,\ l+1,\ l+1,\ 2), &{} i\,=\,l+2;\\ (2l+1-i,\ 2l+3-i,\ 2l+5-i,\ i-l-1), &{} l+3\leqslant i\leqslant 2l+1.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(a_ib_i|S_1)\,=\,{\left\{ \begin{array}{ll} (i-1,\ i,\ 4-i,\ l-1+i), &{} 1\leqslant i\leqslant 2; \\ (i-1,\ i,\ i-2,\ l+4-i), &{} 3\leqslant i\leqslant l+1;\\ (2l+2-i,\ 2l+3-i,\ i-2,\ l+4-i), &{} l+2\leqslant i\leqslant l+3;\\ (2l+2-i,\ 2l+3-i,\ 2l+5-i,\ i-l-2), &{} l+4\leqslant i\leqslant 2l+1.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_ib_{i+1}|S_1)\,=\,{\left\{ \begin{array}{ll} (i,\ i,\ 3-i,\ l-1+i), &{} l\leqslant i\leqslant 2; \\ (i,\ i,\ i-2,\ l+3-i), &{} 3\leqslant i\leqslant l+1;\\ (l,\ l,\ l,\ 1), &{} i\,=\,l+2;\\ (2l-i+2,\ 2l-i+2,\ 2l+4-i,\ i-l-2), &{} l+3\leqslant i\leqslant 2l+1.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_ic_i|S_1)={\left\{ \begin{array}{ll} (1,\ 0,\ 3,\ l), &{} i\,=\,1; \\ (2,\ 2,\ 2,\ l+1), &{} i\,=\,2;\\ (3,\ 3,\ 0,\ l+1), &{} i\,=\,3;\\ (i,\ i,\ i-2,\ l+4-i), &{} 4\leqslant i\leqslant l+1;\\ (l+1,\ l+1,\ l,\ 2), &{} i\,=\,l+2;\\ (l,\ l,\ l+1,\ 0), &{} i\,=\,l+3;\\ (2l+3-i,\ 2l+3-i,\ 2l+5-i,\ i-l-2), &{} l+4\leqslant i\leqslant 2l+1.\\ \end{array}\right. } \end{aligned}$$

Note that when $1\leqslant i\leqslant n$ and $i\ne 1, 3, l+3$, we have $r(b _i c_ i |S_ 1 ) \,=\, r(b _i |S_ 1 )$. In other cases, all mixed metric representations with respect to $S_1$ are pairwise different. Therefore, in other cases, all mixed metric representations with respect to $S_m$ are pairwise different. However, when $1\leqslant i\leqslant n$ and $i\ne 1, 3, l+3,$ we have $r(b_ic_i|S_1\cup c_i)\ne r(b_i|S_1\cup c_i).$ It follows that $r(b _i c _i |S_m) \ne r(b _i|S_m)$ for $1\leqslant i\leqslant n$. Hence $S_m$ is a mixed metric generator and therefore $dim_m(\mathbb {W}_n)\leqslant n+1$. By Lemma 6 we have $dim_m(\mathbb {W}_n)\geqslant n+1$. Thus, we obtain that $dim_m(\mathbb {W}_n)\,=\,n+1$.

Case (II) n is even. In this case, we can write $n \,=\, 2l$, where $l\geqslant 3$ is an integer. Let $S_1\,=\,\{a_1,\ c_1,\ c_3,\ c_{l+2}\}$. We give mixed metric representations of any element of $V(\mathbb {W}_n) \cup E(\mathbb {W}_n)$ with respect to $S_1$.

$$\begin{aligned} r(a_i|S_1)\,=\,{\left\{ \begin{array}{ll} (i-1,\ i+1,\ 5-i,\ l+i), &{} 1\leqslant i\leqslant 2; \\ (i-1,\ i+1,\ i-1,\ l+4-i), &{} 3\leqslant i\leqslant l+1;\\ (l-1,\ l+1,\ l+1,\ 2), &{} i\,=\,l+2;\\ (2l-i+1,\ 2l-i+3,\ 2l-i+5,\ i-l), &{} l+3 \leqslant i\leqslant 2l. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_i|S_1)\,=\,{\left\{ \begin{array}{ll} (i,\ i,\ 4-i,\ l-1+i), &{} 1\leqslant i\leqslant 2;\\ (i,\ i,\ i-2,\ l+3-i), &{} 3\leqslant i\leqslant l+1;\\ (l,\ l,\ l,\ 1), &{} i\,=\,l+2;\\ (2l-i+2,\ 2l-i+2,\ 2l-i+4,\ i-l-1), &{} l+3\leqslant i\leqslant 2l.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(c_i|S_1)\,=\,{\left\{ \begin{array}{ll} (2,\ 0,\ 4,\ l+1), &{} i\,=\,1; \\ (3,\ 3,\ 3,\ l+2), &{} i\,=\,2;\\ (4,\ 4,\ 0,\ l+1), &{} i\,=\,3;\\ (i+1,\ i+1,\ i-1,\ l+4-i), &{} 4\leqslant i\leqslant l+1;\\ (l+1,\ l+1,\ l+1,\ 0), &{} i\,=\,l+2;\\ (2l-i+3,\ 2l-i+3,\ 2l-i+5,\ i-l), &{} l+3\leqslant i\leqslant 2l.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(a_ia_{i+1}|S_1)\,=\,{\left\{ \begin{array}{ll} (0,\ 2,\ 3,\ l+1), &{} i\,=\,1;\\ (1,\ 3,\ 2,\ l+1), &{} i\,=\,2;\\ (i-1,\ i+1,\ i-1,\ l+3-i), &{} 3\leqslant i\leqslant l;\\ (l-1,\ l+1,\ l,\ 2), &{} i\,=\,l+1; \\ (l-2,\ l,\ l+1,\ 2), &{} i\,=\,l+2;\\ (2l-i,\ 2l-i+2,\ 2l-i+4,\ i-l), &{} l+3\leqslant i\leqslant 2l.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(a_ib_i|S_1)={\left\{ \begin{array}{ll} (i-1,\ i,\ 4-i,\ l-1+i), &{} 1\leqslant i\leqslant 2;\\ (i-1,\ i,\ i-2,\ l+3-i), &{} 3\leqslant i\leqslant l+1;\\ (l-1,\ l,\ l,\ 1), &{} i\,=\,l+2;\\ (2l-i+1,\ 2l-i+2,\ 2l-i+4,\ i-l-1), &{} l+3\leqslant i\leqslant 2l.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_ib_{i+1}|S_1)\,=\,{\left\{ \begin{array}{ll} (1,\ 1,\ 2,\ l), &{} i\,=\,1;\\ (2,\ 2,\ 1,\ l), &{} i\,=\,2;\\ (i,\ i,\ i-2,\ l+2-i), &{} 3\leqslant i\leqslant l;\\ (2l-i+1,\ 2l-i+1,\ i-2,\ 1), &{} l+1\leqslant i\leqslant l+2;\\ (2l-i+1,\ 2l-i+1,\ 2l-i+3,\ i-l-1), &{} l+3\leqslant i\leqslant 2l.\\ \end{array}\right. }\end{aligned}$$

$$\begin{aligned} r(b_ic_i|S_1)\,=\,{\left\{ \begin{array}{ll} (1,\ 0,\ 3,\ l), &{} i\,=\,1;\\ (2,\ 2,\ 2,\ l+1), &{} i\,=\,2;\\ (3,\ 3,\ 0,\ l), &{} i\,=\,3;\\ (i,\ i,\ i-2,\ l+3-i), &{} 4\leqslant i\leqslant l+1;\\ (l,\ l,\ l,\ 0), &{} i\,=\,l+2;\\ (2l-i+2,\ 2l-i+2,\ 2l-i+4,\ i-l-1), &{} l+3\leqslant i\leqslant 2l.\\ \end{array}\right. } \end{aligned}$$

Note that when $1\leqslant i\leqslant n$ and $i\ne 1, 3, l+2$, we have $r(b _i c_ i |S_ 1 ) \,=\, r(b _i |S_ 1 )$. In other cases, all mixed metric representations with respect to $S_1$ are pairwise different. Thus, in other cases, all mixed metric representations with respect to $S_m$ are pairwise different. However, when $1\leqslant i\leqslant n$ and $i\ne 1, 3, l+2$, we have $r(b_ic_i|S_1\cup c_i)\ne r(b_i|S_1\cup c_i)$. It follows that $r(b _i c _i |S_m) \ne r(b _i|S_m)$ for $1\leqslant i\leqslant n$. Hence $S_m$ is a mixed metric generator and therefore $dim_m(\mathbb {W}_n)\leqslant n+1$. By Lemma 6 we have $dim_m(\mathbb {W}_n)\geqslant n+1$. Thus, we obtain that $dim_m(\mathbb {W}_n)\,=\,n+1$.

Therefore, for $n\geqslant 3$ we have $dim_m(\mathbb {W}_n)\,=\,n+1$.

4 The Mixed Metric Dimension of Plane Graph (Convex Polytope) $\mathbb {D}_n$

In this section, we intend to present the mixed metric dimension of plane graph (convex polytope) $\mathbb {D}_n$ (Fig. 2).

Lemma 7

Let $\mathbb {D}_n$ be the plane graph (convex polytope), where $n\geqslant 10$. Then $dim_m(\mathbb {D}_n)\leqslant 4$.

Proof

We consider two cases.

Case (I) n is odd. In this case, we can write $n \,=\, 2l +1$, where $l\geqslant 5$ is an integer. Let $S_m\,=\,\{a_1,\ a_{l+1},\ b_2,\ b_{l+2}\}$. We will show that $S_m$ is a mixed metric generator of $\mathbb {D}_n$. We give mixed metric representations of any element of $V(\mathbb {D}_n) \cup E(\mathbb {D}_n)$ with respect to $S_m$.

$$\begin{aligned} r(a_i|S_m)\,=\,{\left\{ \begin{array}{ll} (i-1,\ l-i+1,\ 5-i,\ l+i+1), &{}\ 1\leqslant i\leqslant 2; \\ (i-1,\ l-i+1,\ i,\ l-i+5), &{}\ 3\leqslant i\leqslant l+1;\\ (l,\ 1,\ l+2,\ 3), &{}\ i\,=\,l+2; \\ (2l-i+2,\ i-l-1,\ 2l-i+6,\ i-l), &{}\ l+3 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_i|S_m)\,=\,{\left\{ \begin{array}{ll} (3,\ l+2,\ 1,\ l), &{}\ i\,=\,1; \\ (i+2,\ l-i+3,\ i-2,\ l-i+2), &{}\ 2\leqslant i\leqslant l;\\ (2l-i+4,\ i-l+2,\ i-2,\ l-i+2), &{}\ l+1 \leqslant i\leqslant l+2; \\ (2l-i+4,\ i-l+2,\ 2l-i+3,\ i-l-2), &{}\ l+3 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(c_i|S_m)\,=\,{\left\{ \begin{array}{ll} (i,\ l-i+2,\ 4-i,\ l+i), &{}\ 1\leqslant i\leqslant 2;\\ (i,\ l-i+2,\ i-1,\ l-i+4), &{}\ 3\leqslant i\leqslant l+1;\\ (l+1,\ 2,\ l+1,\ 2), &{}\ i\,=\,l+2; \\ (2l-i+3,\ i-l,\ 2l-i+5,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(d_i|S_m)\,=\,{\left\{ \begin{array}{ll} (2,\ l+1,\ 2,\ l+1), &{}\ i\,=\,1; \\ (i+1,\ l-i+2,\ i-1,\ l-i+3), &{}\ 2\leqslant i\leqslant l;\\ (2l-i+3,\ i-l+1,\ i-1,\ l-i+3), &{}\ l+1 \leqslant i\leqslant l+2; \\ (2l-i+3,\ i-l+1,\ 2l-i+4,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(a_ia_{i+1}|S_m)\,=\,{\left\{ \begin{array}{ll} (i-1,\ l-1,\ 3,\ l+2), &{}\ 1\leqslant i\leqslant 2;\\ (i-1,\ l-i,\ i,\ l-i+4), &{}\ 3\leqslant i\leqslant l;\\ (2l-i+1,\ i-l-1,\ i,\ 3), &{}\ l+1 \leqslant i\leqslant l+2; \\ (2l-i+1,\ i-l-1,\ 2l-i+5,\ i-l), &{}\ l+3 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(a_ic_i|S_m)\,=\,{\left\{ \begin{array}{ll} (i-1,\ l-i+1,\ 4-i,\ l+i), &{}\ 1\leqslant i\leqslant 2;\\ (i-1,\ l-i+1,\ i-1,\ l-i+4), &{}\ 3\leqslant i\leqslant l+1;\\ (l,\ 1,\ l+1,\ 2), &{}\ i\,=\,l+2; \\ (2l-i+2,\ i-l-1,\ 2l-i+5,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(c_id_i|S_m)\,=\,{\left\{ \begin{array}{ll} (1,\ l+1,\ 2,\ l+1), &{}\ i\,=\,1; \\ (i,\ l-i+2,\ i-1,\ l-i+3), &{}\ 2\leqslant i\leqslant l+1;\\ (l+1,\ 2,\ l+1,\ 1), &{}\ i\,=\,l+2; \\ (2l-i+3,\ i-l,\ 2l-i+4,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(c_{i+1}d_i|S_m)\,=\,{\left\{ \begin{array}{ll} (2,\ l,\ 2,\ l+1), &{}\ i\,=\,1; \\ (i+1,\ l-i+1,\ i-1,\ l-i+3), &{}\ 2\leqslant i\leqslant l;\\ (2l-i+2,\ i-l+1,\ i-1,\ l-i+3), &{}\ l+1\leqslant i\leqslant l+2;\\ (2l-i+2,\ i-l+1,\ 2l-i+4,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l; \\ (1,\ l+1,\ 3,\ l ), &{}\ i\,=\,2l+1.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_id_i|S_m)\,=\,{\left\{ \begin{array}{ll} (2,\ l+1,\ 1,\ l), &{}\ i\,=\,1; \\ (i+1,\ l-i+2,\ i-2,\ l-i+2), &{}\ 2\leqslant i\leqslant l;\\ (2l-i+3,\ i-l+1,\ i-2,\ l-i+2), &{}\ l+1\leqslant i\leqslant l+2;\\ (2l-i+3,\ i-l+1,\ 2l-i+3,\ i-l-2), &{}\ l+3 \leqslant i\leqslant 2l+1. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_ib_{i+1}|S_m)\,=\,{\left\{ \begin{array}{ll} (3,\ l+1,\ 0,\ l), &{}\ i\,=\,1; \\ (i+2,\ l-i+2,\ i-2,\ l-i+1), &{}\ 2\leqslant i\leqslant l-1;\\ (l+2,\ 3,\ i-2,\ l+1-i), &{}\ l\leqslant i\leqslant l+1;\\ (2l-i+3,\ i-l+2,\ 2l-i+2,\ i-l-2), &{}\ l+2 \leqslant i\leqslant 2l; \\ (3,\ l+2,\ 1,\ l-1), &{}\ i\,=\,2l+1. \\ \end{array}\right. } \end{aligned}$$

Note that all mixed metric representations with respect to $S_m$ are pairwise different. We deduce that $S_m$ is a mixed metric generator for $\mathbb {D}_n$.

Case (II) n is even. In this case, we can write $n = 2l$, where $l\geqslant 5$ is an integer. Let $S_m\,=\,\{a_1,\ a_{l+1},\ b_2,\ b_{l+2}\}$. We will show that $S_m$ is a mixed metric generator of $\mathbb {D}_n$. We give mixed metric representations of any element of $V(\mathbb {D}_n) \cup E(\mathbb {D}_n)$ with respect to $S_m$.

$$\begin{aligned} r(a_i|S_m)\,=\,{\left\{ \begin{array}{ll} (i-1,\ l-i+1,\ 5-i,\ l+i), &{}\ 1\leqslant i\leqslant 2; \\ (i-1,\ l-i+1,\ i,\ l-i+5), &{}\ 3\leqslant i\leqslant l+1;\\ (l-1,\ 1,\ l+2,\ 3), &{}\ i\,=\,l+2; \\ (2l-i+1,\ i-l-1,\ 2l-i+5,\ i-l), &{}\ l+3 \leqslant i\leqslant 2l.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_i|S_m)\,=\,{\left\{ \begin{array}{ll} (i+2,\ l-i+3,\ 2-i,\ l+i-2), &{}\ 1\leqslant i\leqslant 2; \\ (i+2,\ l-i+3,\ i-2,\ l-i+2), &{}\ 3\leqslant i\leqslant l;\\ (2l-i+3,\ i-l+2,\ i-2,\ l-i+2), &{}\ l+1 \leqslant i\leqslant l+2;\\ (2l-i+3,\ i-l+2,\ 2l-i+2,\ i-l-2), &{}\ l+3 \leqslant i\leqslant 2l.\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(c_i|S_m)\,=\,{\left\{ \begin{array}{ll} (i,\ l-i+2,\ 4-i,\ l+i-1), &{}\ 1\leqslant i\leqslant 2;\\ (i,\ l-i+2,\ i-1,\ l-i+4), &{}\ 3\leqslant i\leqslant l+1;\\ (l,\ 2,\ l+1,\ 2), &{}\ i=l+2; \\ (2l-i+2,\ i-l,\ 2l-i+4,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(d_i|S_m)\,=\,{\left\{ \begin{array}{ll} (2,\ l+1,\ 2,\ l), &{}\ i\,=\,1;\\ (i+1,\ l-i+2,\ i-1,\ l-i+3), &{}\ 2\leqslant i\leqslant l;\\ (2l-i+2,\ i-l+1,\ i-1,\ l-i+3), &{}\ l+1 \leqslant i\leqslant l+2; \\ (2l-i+2,\ i-l+1,\ 2l-i+3,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(a_ia_{i+1}|S_m)\,=\,{\left\{ \begin{array}{ll} (i-1,\ l-1,\ 3,\ l+i), &{}\ 1\leqslant i\leqslant 2;\\ (i-1,\ l-i,\ i,\ l-i+4), &{}\ 3\leqslant i\leqslant l;\\ (2l-i,\ i-l-1,\ i,\ l-i+4), &{}\ l+1\leqslant i\leqslant l+2; \\ (2l-i,\ i-l-1,\ 2l-i+4,\ i-l), &{}\ l+3 \leqslant i\leqslant 2l. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(a_ic_i|S_m)\,=\,{\left\{ \begin{array}{ll} (i-1,\ l-i+1,\ 4-i,\ l+i-1), &{}\ 1\leqslant i\leqslant 2;\\ (i-1,\ l-i+1,\ i-1,\ l-i+4), &{}\ 3\leqslant i\leqslant l+1;\\ (l-1,\ 1,\ l+1,\ 2), &{}\ i\,=\,l+2; \\ (2l-i+1,\ i-l-1,\ 2l-i+4,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(c_id_i|S_m)\,=\,{\left\{ \begin{array}{ll} (1,\ l+1,\ 2,\ l), &{}\ i=1; \\ (i,\ l-i+2,\ i-1,\ l-i+3), &{}\ 2\leqslant i\leqslant l+1;\\ (l,\ 2,\ l+1,\ 1), &{}\ i\,=\,l+2; \\ (2l-i+2,\ i-l,\ 2l-i+3,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(c_{i+1}d_i|S_m)\,=\,{\left\{ \begin{array}{ll} (2,\ l,\ 2,\ l), &{}\ i=1; \\ (i+1,\ l-i+1,\ i-1,\ l-i+3), &{}\ 2\leqslant i\leqslant l;\\ (2l-i+1,\ i-l+1,\ i-1,\ l-i+3), &{}\ l+1\leqslant i\leqslant l+2;\\ (2l-i+1,\ i-l+1,\ 2l-i+3,\ i-l-1), &{}\ l+3 \leqslant i\leqslant 2l. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_id_i|S_m)\,=\,{\left\{ \begin{array}{ll} (2,\ l+1,\ 1,\ l-1), &{}\ i=1; \\ (i+1,\ l-i+2,\ i-2,\ l-i+2), &{}\ 2\leqslant i\leqslant l;\\ (2l-i+2,\ i-l+1,\ i-2,\ l-i+2), &{}\ l+1\leqslant i\leqslant l+2;\\ (2l-i+2,\ i-l+1,\ 2l-i+2,\ i-l-2), &{}\ l+3 \leqslant i\leqslant 2l. \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} r(b_ib_{i+1}|S_m)\,=\,{\left\{ \begin{array}{ll} (3,\ l+1,\ 0,\ l-1), &{}\ i\,=\,1; \\ (i+2,\ l-i+2,\ i-2,\ l-i+1), &{}\ 2\leqslant i\leqslant l-1;\\ (l+2,\ 3,\ l-2,\ 1), &{}\ i\,=\,l;\\ (l+1,\ 3,\ l-1,\ 0), &{}\ i\,=\,l+1;\\ (2l-i+2,\ i-l+2,\ 2l-i+1,\ i-l-2), &{}\ l+2 \leqslant i\leqslant 2l-1; \\ (3,\ l+2,\ 1,\ l-2), &{}\ i\,=\,2l. \\ \end{array}\right. } \end{aligned}$$

Note that all mixed metric representations with respect to $S_m$ are pairwise different. We deduce that $S_m$ is a mixed metric generator for $\mathbb {D}_n$.

Therefore, for $n\geqslant 10$ we have $dim_m(\mathbb {D}_n)\leqslant 4$.

Lemma 8

Let $\mathbb {D}_n$ be the plane graph (convex polytope), where $n\geqslant 10$. Let $C_i=\{c_i, c_{i+1}, d_i\}\subset C\cup D$, $D_i\,=\,\{ d_{i-1}, d_i, c_i\}\subset C\cup D$. Then the following $\mathrm (i)$ and $\mathrm (ii)$ hold.

• (i) $r(b_i|B\cup C\cup D\setminus C_i)=r(b_id_i|B\cup C\cup D\setminus C_i)$ for $1\leqslant i\leqslant n$;

• (ii) $r(a_i|A\cup C\cup D\setminus D_i)=r(a_ic_i|A\cup C\cup D\setminus D_i)$ for $1\leqslant i\leqslant n$.

Proof

$\mathrm (i)$ We consider the subsequent two cases depending upon n.

Case (I) n is odd. In this case, we can write $n \,=\, 2l + 1$, where $l\geqslant 5$ is an integer. Now, we calculate the distance between the vertexs $b_i$ and $x_j$, and the distance between the edges $b_id_i$ and the vertex $x_j$, where $x_j\in B\cup C\cup D$, $1\leqslant i,j\leqslant n$.

$$\begin{aligned} \left\{ \begin{array}{ll} d(b_i,b_j)\,=\,d(b_id_i,b_j)\,=\,|i-j|, &{}\ |i-j|\leqslant l;\\ d(b_i,b_j)\,=\,d(b_id_i,b_j)\,=\,n-|i-j|, &{}\ l+1\leqslant |i-j|\leqslant 2l.\\ \end{array}\right. \end{aligned}$$

$$\begin{aligned} \left\{ \begin{array}{ll} d(b_i,c_j)\,=\,2, d(b_id_i,c_j)\,=\,1, &{}\ j\,=\,i,j\,=\,i+1;\\ d(b_i,c_j)\,=\,d(b_id_i,c_j)=|i-j|+1, &{}\ |i-j|\leqslant l\ and \ j>i,j\leqslant i,j\leqslant i+1;\\ d(b_i,c_j)\,=\,d(b_id_i,c_j)=|i-j|+2, &{}\ |i-j|\leqslant l\ and \ j<i,j\leqslant i,j\leqslant i+1;\\ d(b_i,c_j)\,=\,d(b_id_i,c_j)=n-|i-j|+2, &{}\ l+1\leqslant |i-j|\leqslant 2l\ and \ i\leqslant l;\\ d(b_i,c_j)\,=\,d(b_id_i,c_j)=n-|i-j|+1, &{}\ l+1\leqslant |i-j|\leqslant 2l\ and \ l+1\leqslant i\leqslant 2l+1.\\ \end{array}\right. \end{aligned}$$

$$\begin{aligned} \left\{ \begin{array}{ll} d(b_i,d_j)\,=\,1, d(b_id_i,d_j)\,=\,0 ,&{}\ j\,=\,i;\\ d(b_i,d_j)\,=\,d(b_id_i,d_j)\,=\,|i-j|+1, &{}\ |i-j|\leqslant l\ and \ j\leqslant i;\\ d(b_i,d_j)\,=\,d(b_id_i,d_j)\,=\,n-|i-j|+1, &{}\ l+1\leqslant |i-j|\leqslant 2l.\\ \end{array}\right. \end{aligned}$$

In this case, it is not hard to see that $r(b_i|B\cup C\cup D\setminus C_i)=r(b_id_i|B\cup C\cup D\setminus C_i)$.

Case (II) n is even. Similar to the proof of Case (I) we may obtain $r(b_i|B\cup C\cup D\setminus C_i)=r(b_id_i|B\cup C\cup D\setminus C_i)$.

So $\mathrm (i)$ holds.

$\mathrm (ii)$ We consider the subsequent two cases depending upon n.

Case (I) n is odd. In this case, we can write $n = 2l + 1$, where $l\geqslant 5$ is an integer. Now, we calculate the distance between the vertexs $a_i$ and the vertex $x_j$, and the distance between the edges $a_ic_i$ and the vertex $x_j$, where $x_j\in A\cup C\cup D$, $1\leqslant i,j\leqslant n$.

$$\begin{aligned} \left\{ \begin{array}{ll} d(a_i,a_j)\,=\,d(a_ic_i,a_j)\,=\,|i-j|, &{}\ |i-j|\leqslant l;\\ d(a_i,a_j)\,=\,d(a_ic_i,a_j)\,=\,n-|i-j|, &{}\ l+1\leqslant |i-j|\leqslant 2l.\\ \end{array}\right. \end{aligned}$$

$$\begin{aligned} \left\{ \begin{array}{ll} d(a_i,c_j)\,=\,1, d(a_ic_i,c_j)\,=\,0, &{}\ j\,=\,i;\\ d(a_i,c_j)\,=\,d(a_ic_i,c_j)\,=\,|i-j|+1, &{}\ |i-j|\leqslant l\ and \ j\leqslant i;\\ d(a_i,c_j)\,=\,d(a_ic_i,c_j)\,=\,n-|i-j|+1, &{}\ l+1\leqslant |i-j|\leqslant 2l.\\ \end{array}\right. \end{aligned}$$

$$\begin{aligned} \left\{ \begin{array}{ll} d(a_i,d_j)\,=\,2, d(a_ic_i,d_j)\,=\,1, &{}\ j\,=\,i,j\,=\,i-1;\\ d(a_i,d_j)\,=\,d(a_ic_i,d_j)\,=\,|i-j|+2, &{}\ |i-j|\leqslant l\ and \ j>i,j\leqslant i,j\leqslant i-1;\\ d(a_i,d_j)\,=\,d(a_ic_i,d_j)\,=\,|i-j|+1, &{}\ |i-j|\leqslant l\ and \ j<i,j\leqslant i,j\leqslant i-1;\\ d(a_i,d_j)\,=\,d(a_ic_i,d_j)\,=\,n-|i-j|+1, &{}\ l+1\leqslant |i-j|\leqslant 2l\ and \ i\leqslant l;\\ d(a_i,d_j)\,=\,d(a_ic_i,d_j)\,=\,n-|i-j|+2, &{}\ l+1\leqslant |i-j|\leqslant 2l\ and \ l+1\leqslant i\leqslant 2l+1.\\ \end{array}\right. \end{aligned}$$

In this case, it is not hard to see that $r(a_i|A\cup C\cup D\setminus D_i)\,=\,r(a_ic_i|A\cup C\cup D\setminus D_i)$.

Case (II) n is even. Similar to the proof of Case (I) we may obtain $r(a_i|A\cup C\cup D\setminus D_i)\,=\,r(a_ic_i|A\cup C\cup D\setminus D_i)$.

So $\mathrm (ii)$ holds.

Lemma 9

Let $\mathbb {D}_n$ be the plane graph (convex polytope), where $n\geqslant 10$. Then each mixed metric basis $S_m$ of $\mathbb {D}_n$ contains at least one vertex of A and one vertex of B.

Proof

We first show that $S_m$ contains at least one vertex of A. Suppose on the contrary that $S_m$ does not contain any vertex of A. Then $S_m\subset B\cup C\cup D$. By Lemma 8$\mathrm (i)$, we have $r(b_i|B\cup C\cup D\setminus C_i)\,=\,r(b_id_i|B\cup C\cup D\setminus C_i)$, where $C_i\,=\,\{c_i, c_{i+1}, d_i\}\subset C\cup D$. This means that $S_m$ contains at least one vertex of $C_i$. Also, we observe that

$$\begin{aligned} |C_i\cap C_j|={\left\{ \begin{array}{ll} 1,&{}\ |i-j|\,=\,1;\\ 0, &{}\ |i-j|\ne 1.\\ \end{array}\right. } \end{aligned}$$

From which it follows that $S_m$ contains at least $\lceil \frac{n}{2}\rceil$ vertices of $C\cup D$. Since $n\geqslant 10$, then $dim_m(\mathbb {D}_n)\geqslant 5$. But, $dim_m(\mathbb {D}_n)\leqslant 4$ by Lemma 7. This is a contradiction.

Secondly, we show that $S_m$ contains at least one vertex of B. Suppose on the contrary that $S_m$ does not contain any vertex of B. Then $S_m\subset A\cup C\cup D$. By Lemma 8$\mathrm (ii)$, we have $r(a_i|A\cup C\cup D\setminus D_i)=r(a_ic_i|A\cup C\cup D\setminus D_i)$, where $D_i=\{d_{i-1}, d_i, c_i\}\subset C\cup D$. This means that $S_m$ contains at least one vertex of $D_i$. Also, we observe that

$$\begin{aligned} |D_i\cap D_j|\,=\,{\left\{ \begin{array}{ll} 1,&{}\ |i-j|\,=\,1;\\ 0, &{}\ |i-j|\ne 1.\\ \end{array}\right. } \end{aligned}$$

From which it follows that $S_m$ contains at least $\lceil \frac{n}{2}\rceil$ vertices of $C\cup D$. Since $n\geqslant 10$, then $dim_m(\mathbb {D}_n)\geqslant 5$. But, $dim_m(\mathbb {D}_n)\leqslant 4$ by Lemma 7. This is a contradiction.

Thus, each mixed metric basis $S_m$ of $\mathbb {D}_n$ contains at least one vertex of A and one vertex of B. $\square$

Theorem 2

Let $\mathbb {D}_n$ be the plane graph (convex polytope), where $n\geqslant 3$. Then $dim_m(\mathbb {D}_n)=4$.

Proof

For $n \,=\, 3$, we find that $\{a_1,\ a_2,\ d_3,\ b_2 \}$ is the mixed metric basis of $\mathbb {D}_n$ by total enumeration, and hence the mixed metric dimension of $\mathbb {D}_n$ is 4. For $n = 4$, we find that $\{a_1,\ a_2,\ d_3,\ b_2 \}$ is the mixed metric basis of $\mathbb {D}_n$ by total enumeration, and hence the mixed metric dimension of $\mathbb {D}_n$ is 4. For $5\leqslant n\leqslant 9$, we find that $\{a_1,\ a_{l+1},\ b_2,\ b_{l+2} \}$ is the mixed metric basis of $\mathbb {D}_n$ by total enumeration, and hence the mixed metric dimension of $\mathbb {D}_n$ is 4. For $n \geqslant 10$, we consider the following two cases.

Case (I) n is odd. We show that $dim_m(\mathbb {D}_n)\ne 3$. By Lemma 9 we know that a mixed metric basis $S_m$ for $\mathbb {D}_n$ contains at least one vertex of A and one vertex of B. Since the vertices of graph $\mathbb {D}_n$ are symmetric, without loss of generality, we assume that $a_1$ and $b_i$ are these two vertices, where $1\leqslant i\leqslant l+1$. By calculating, there are following four possibilities to be discussed.

(1) If $S_m\,=\,\{a_1,\ b_i,\ a_j\}$, where $1\leqslant i\leqslant l+1\$ and $2\leqslant j\leqslant 2l+1,\$ then we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} r(c_{l+1}|S_m)\,=\,r(c_{l+1}d_{l+1}|S_m), &{}\ 1\leqslant i\leqslant l\ and \ 2\leqslant j\leqslant 2l+1;\\ r(c_{2l+1}|S_m)\,=\,r(c_{2l+1}d_{2l+1}|S_m), &{}\ i=l+1 \ and \ 2\leqslant j\leqslant 2l+1.\\ \end{array}\right. \end{aligned}$$

(2) If $S_m\,=\,\{a_1,\ b_i,\ b_j\}$, where $1\leqslant i\leqslant l+1\$and $2\leqslant j\leqslant 2l+1,$ then we obtain $r(d_{2l+1}|S_m)\,=\,r(c_{2l+1}d_{2l+1}|S_m).$

(3) If $S_m\,=\,\{a_1,\ b_i,\ c_j\}$, where $1\leqslant i\leqslant l+1\$and $1\leqslant j\leqslant 2l+1,$ then we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} r(a_1|S_m)\,=\,r(a_1a_{2l+1}|S_m), &{}\ 1\leqslant i\leqslant l\ and \ 1\leqslant j\leqslant l+1;\\ r(a_1|S_m)\,=\,r(a_1a_2|S_m), &{}\ 1\leqslant i\leqslant l\ and \ l+2\leqslant j\leqslant 2l+1;\\ r(d_{2l+1}|S_m)\,=\,r(c_{2l+1}d_{2l+1}|S_m), &{}\ i\,=\,l+1 \ and \ 1\leqslant j\leqslant l;\\ r(c_{2l+1}|S_m)\,=\,r(c_{2l+1}d_{2l+1}|S_m), &{}\ i\,=\,l+1 \ and \ l+1\leqslant j\leqslant 2l+1.\\ \end{array}\right. \end{aligned}$$

(4) If $S_m=\{a_1,\ b_i,\ d_j\}$, where $1\leqslant i\leqslant l+1$ and $1\leqslant j\leqslant 2l+1,$ then we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} r(b_1|S_m)\,=\,r(b_1b_{2l+1}|S_m), &{}\ i\,=\,1\ and \ 1\leqslant j\leqslant l+1;\\ r(b_1|S_m)\,=\,r(b_1b_2|S_m), &{}\ i\,=\,1 \ and \ l+2\leqslant j\leqslant 2l+1;\\ r(d_{l+2}|S_m)\,=\,r(c_{l+2}d_{l+2}|S_m), &{}\ 2\leqslant i\leqslant l\ and\ 1\leqslant j\leqslant 2l+1\ and\ j\ne l,l+1;\\ r(c_{l+2}|S_m)\,=\,r(c_{l+2}d_{l+2}|S_m), &{}\ 2\leqslant i\leqslant l\ and ~ j\,=\,l, l+1.\\ \end{array}\right. \end{aligned}$$

By the above we see that there is no resolving set with three vertices for $V(\mathbb {D}_n)$, then $dim_m(\mathbb {D}_n)\geqslant 4$. By Lemma 7 we know that $dim_m(\mathbb {D}_n)\leqslant 4$, so $dim_m(\mathbb {D}_n)=4$ holds.

Case (II) n is even. We show that $dim_m(\mathbb {D}_n)\ne 3$. By Lemma 9 we know that a mixed metric basis $S_m$ for $\mathbb {D}_n$ contains at least one vertex of A and one vertex of B. Since the vertices of graph $\mathbb {D}_n$ are symmetric, without loss of generality, we assume that $a_1$ and $b_i$ are these two vertices, where $1\leqslant i\leqslant l$. By calculating, there are following four possibilities to be discussed.

(1) If $S_m=\{a_1,\ b_i,\ a_j\}$, where $1\leqslant i\leqslant l\$ and $2\leqslant j\leqslant 2l,$ then we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} r(c_l|S_m)\,=\,r(c_ld_l|S_m), &{}\ 1\leqslant i\leqslant l-1\ and \ 2\leqslant j\leqslant 2l;\\ r(c_{2l}|S_m)\,=\,r(c_{2l}d_{2l}|S_m), &{}\ i\,=\,l \ and \ 2\leqslant j\leqslant 2l.\\ \end{array}\right. \end{aligned}$$

(2) If $S_m\,=\,\{a_1,\ b_i,\ b_j\}$, where $1\leqslant i\leqslant l\$ and $2\leqslant j\leqslant 2l,$ then we obtain $r(d_{2l}|S_m)\,=\,r(c_{2l}d_{2l}|S_m).$

(3) If $S_m\,=\,\{a_1,\ b_i,\ c_j\}$, where $1\leqslant i\leqslant l\$ and $1\leqslant j\leqslant 2l,$ then we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} r(d_{2l}|S_m)\,=\,r(c_{2l}d_{2l}|S_m), &{}\ 1\leqslant i\leqslant l\ and \ 1\leqslant j\leqslant l;\\ r(d_l|S_m)\,=\,r(c_ld_l|S_m), &{}\ 1\leqslant i\leqslant l\ and ~ l+1\leqslant j\leqslant 2l.\\ \end{array}\right. \end{aligned}$$

(4) If $S_m\,=\,\{a_1,\ b_i,\ d_j\}$, where $1\leqslant i\leqslant l\$ and $1\leqslant j\leqslant 2l,$ then we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} r(a_1|S_m)\,=\,r(a_1a_{2l}|S_m), &{}\ i\,=\,1\ and \ 1\leqslant j\leqslant l;\\ r(a_1|S_m)\,=\,r(a_1a_2|S_m), &{}\ i\,=\,1 \ and \ l+1\leqslant j\leqslant 2l;\\ r(d_{l+2}|S_m)\,=\,r(c_{l+2}d_{l+2}|S_m), &{}\ 2\leqslant i\leqslant l\ and\ 1\leqslant j\leqslant 2l\ and\ j\ne l,l+1;\\ r(c_{l+2}|S_m)\,=\,r(c_{l+2}d_{l+2}|S_m), &{}\ 2\leqslant i\leqslant l\ and ~ j\,=\,l, l+1.\\ \end{array}\right. \end{aligned}$$

From the above we know that there is no resolving set with three vertices for $V(\mathbb {D}_n)$, then $dim_m(\mathbb {D}_n)\geqslant 4$. By Lemma 7 we know that $dim_m(\mathbb {D}_n)\leqslant 4$, so $dim_m(\mathbb {D}_n)=4$ holds.

5 Conclusion

In this paper, we studied the mixed metric dimension for two families of plane graphs (web graphs and convex polytopes) in metric graph theory. For web graphs, a lower bound for the mixed metric dimension was proved and a mixed metric basis was then obtained to determine the mixed metric dimension. For convex polytopes, an upper bound for the mixed metric dimension was discovered and the above bound was then proved to be tight. The future research can be thought of as finding the mixed metric dimension for other families of plane graphs, especially rotationally symmetric ones.