Introduction

Since the twentieth century, with the rapid development of industrial technology, especially in the fields of micro-electromechanical system (MEMS) and electrical devices, the demand and requirement for materials have been increasing accordingly. In order to take full advantage of the metallic material capability, it has been more and more necessary to understand the heterogeneous plastic deformation mechanisms, and to establish the models linking the microstructure evolution with the macroscopic mechanical performance that are used to characterize the corresponding deformation behavior in service under complex loading conditions.

The crystal plasticity theory has increasingly attracted considerable interests as it has the capability of describing the heterogeneous mechanical responses of metallic materials by reproducing the grain-scale microstructural features and incorporating microscale deformation physics and mechanisms [1]. Sachs [2] proposed the first crystal plasticity model based on the iso-stress assumption that the resolved stresses of all the deformed grains are identical and are equal to the macroscopically imposed stresses. The second crystal plasticity model was proposed by Taylor [3] based on the iso-strain assumption that all grains accommodate the same plastic strain equal to the macroscopically imposed strain. Hill and Rice [4,5,6] then established the models used for describing the geometry and kinematics of crystal plastic deformation, and applied the models to analyze the rate-independent elastic–plastic deformation. Based on the crystal plasticity theory, Asaro [7, 8] and Peirce [9] further developed the numerical computation frame of crystal plastic constitutive model, and the rate-dependent elasto-viscoplastic deformation behavior was analyzed accordingly. In recent years, with the development of finite element method, the numerical implementation of crystal plasticity by taking the advantage of the finite element method (CPFEM) has been conducted by many researchers [10,11,12,13,14,15,16], and a large number of open source codes and software were developed resultantly [17,18,19,20,21]. The wide applications of these codes and software have considerably improved the developments of crystal plasticity theory.

Within the framework of crystal plasticity finite element method (CPFEM), a single-crystal plasticity constitutive model is developed firstly to describe the elastic–plastic deformation at the grain level. According to the classic plasticity theory, the plastic deformation of materials is attributed to the crystallographic slip of dislocation on the discrete slip systems. Schmid [22] proposed a criterion for starting the slip systems that the plastic slip occurs when the resolved shear stress on a glide plane reaches the critical resolved shear stress (CRSS). As a result, the plastic deformation of crystals is related to the orientation of the crystal lattice relative to the loading axis; crystallographic slip may occur on one or more slip systems. Besides the dislocation slipping, there are some other mechanisms of the plastic deformation, such as twinning and phase transformation, which are not taken into consideration in this work.

Similar to the conventional macroscopic plasticity theory, the material mechanical responses described by the crystal plasticity constitutive model are also based on the flow rule, the hardening law and the evolution of internal state variable. The flow rule establishes the relation between the resolved shear stress and the shear strain rate, such as the well-known power law [23] and thermally activated formula [24]. The hardening law expresses the evolution of slip resistance, which can be generally divided into two categories: the phenomenological model and the physically based model. The typical phenomenological hardening laws include: Peirce–Asaro–Needleman (PAN) hardening law [25], Anand–Kalidindi hardening law [26], Voce hardening law [27, 28], etc. In the phenomenological hardening law, the hardening effects are generally dominated by two parts: self-hardening and latent hardening [29, 30], and the latent hardening is usually taken into consideration by a latent-hardening factor defined by the ratio between the latent-hardening rate and self-hardening rate. The different hardening laws would have a significant impact on the predictability of the crystal plasticity model in terms of the stress–strain responses and texture evolutions [31]. Guo et al. [32] employed the Taylor model and Affine model to study the large strain behavior of OFHC copper in terms of stress–strain responses and deformed textures, and the role of latent hardening was comprehensively investigated resultantly.

When compared with the physically based hardening law, the crystal plasticity models in conjunction with the phenomenological hardening laws are computationally more efficient, since these hardening laws are not related to any physical processes associated with the plastic deformation. In order to capture the microstructural evolution that develops in the process of the large plastic deformation, a large number of physically based hardening laws have been developed for taking into account the microstructural evolutions of metallic materials [33, 34].

Most recently, many microstructurally based crystal plasticity models have been focused on the hardening laws by developing the internal state variables such as dislocation densities [35,36,37]. According to the physical mechanism of the plastic deformation, the mechanical responses of materials are dependent on the competition between the multiplication, storage, rearrangement and annihilation of dislocations [38], the plastic flow is mainly due to the movement of mobile dislocations, and the work-hardening intrinsically is the increase in required stress to activate the motion of the stored dislocations. In the process of the plastic deformation dominated by the dislocations slipping, the dislocation evolution tends to pattern the well-known cellular substructures or subgrains, which consist of cell walls with higher dislocation density and cell interiors with lower dislocation density [39, 40]. Estrin et al. [41,42,43] considered the fundamental microstructural feature as a dislocation cell structure, the metallic materials are accordingly dealt with as a “composite” two-phase structure, i.e., cell walls and cell interiors, and the work hardening is related to the evolution of the dislocation densities in the two “phases.” Roters and Gottstein et al. [44, 45] developed a hardening law based on the mobile and immobile dislocation density in the cell walls and cell interiors. Zhang et al. [46] developed a unified physically based crystal plasticity model, which takes into account the mobile dislocation density, immobile dislocation densities in the cell walls and interiors, to describe the plastic deformation of FCC materials over a wide range of temperatures and strain rates.

On the other hand, the polycrystalline aggregate comprises many single crystals with the different crystallographic orientations, and the initial orientations can be obtained from experimental characterizations by using electron backscatter diffraction (EBSD) technique [47]. There are generally two ways to create the finite element model of polycrystalline aggregate: (1) each element represents a set of grains, i.e., the mean-field crystal plasticity model, (2) several elements describe an individual grain, i.e., the full-field crystal plasticity model. There is a special case that each element represents an individual grain, which can be obtained by both the two ways [48, 49].

For the finite element calculation of polycrystal plasticity, the mechanical response of each grain within the polycrystalline aggregate is calculated by employing the single-crystal plasticity constitutive model, and the macroscopic mechanical response of the polycrystalline aggregate is generally obtained by using a homogenization scheme, rather than the direct full-field crystal plasticity finite element calculation of the polycrystalline aggregate which are too computationally expensive to simulate laboratory-scale components with complete microstructural information. The homogenization scheme is capable to take into account the influences of the single-crystal properties and the texture and is similar to the concept of representative volume element (RVE). The homogenization ideas of the polycrystal plasticity were firstly taken from the pioneer work of Taylor [3], and Hill and Rice [4,5,6] developed the precise mathematical implementation. The homogenization scheme is widely used in the crystal plasticity finite element method (CPFEM) to improve the computation efficiency and satisfy the equilibrium and compatibility with the FEM framework. Nowadays, there are a considerable number of homogenization schemes that have been developed to calculate the macroscopic mechanical response of a polycrystalline aggregate by incorporating the evolutions of the texture and microstructure, including the classic Taylor-type model [50], fast Fourier transform (FFT) models [51, 52], crystal plasticity finite element models [53], self-consistent [54] and grain-cluster homogenization scheme [55, 56].

Due to the rapid development and wide application of the high-performance computing, material identification equipment and experimental technology, there are increasing efforts to study the crystal plasticity models in conjunction with either the phenomenological hardening law or the physically based hardening law so far. In this work, an innovative crystal plasticity model in conjunction with the dislocation density-based hardening law was developed and implemented into the finite element codes, the classic crystal plasticity model incorporated with the saturation-type phenomenological hardening law was employed as well, to simulate the large plastic deformation of OFHC copper single crystals and polycrystals, and then a comprehensive comparison study on the two hardening laws was accordingly carried out in terms of the stress–strain responses and texture evolutions. By using the crystal plasticity finite element method, attempts have been made to apply the Taylor-type mean-field crystal plasticity models to simulate the process of single shot impact and to investigate the microstructural evolutions and mechanical responses of the impacted surface, which would be conducive to providing a significant insight into the microscopic strengthening mechanisms of shot peening or surface mechanical attrition treatment and the new ideas for relevant modeling.

Crystal plasticity model

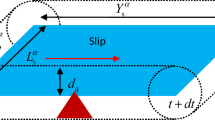
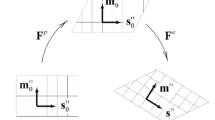
According to the crystal plasticity theory on the crystallographic slip of dislocation, consisting of dislocation motion and crystal rotation, as shown in Fig. 1, the deformation gradient (\({\mathbf{F}} = {{\partial {\varvec{X}}} \mathord{\left/ {\vphantom {{\partial {\varvec{X}}} {\partial {\varvec{Y}}}}} \right. \kern-\nulldelimiterspace} {\partial {\varvec{Y}}}}\), wherein \({\varvec{X}}\) and \({\varvec{Y}}\) are the two vectors representing the coordinates in the current and initial configurations, respectively, and \({\varvec{X}} = {\varvec{X}}\left( {{\mathbf{Y}},\;t} \right)\), and t represents the time.) can be multiplicatively decomposed into the elastic and plastic components

$${\varvec{F}} = {\varvec{F}}^{{\text{e}}} {\varvec{F}}^{{\text{p}}}$$
(1)

Where \({\varvec{F}}^{{\text{p}}}\) represents the inelastic shear deformation along the crystalline slip planes, mapping the initial configuration into the intermediate configuration; \({\varvec{F}}^{{\text{e}}}\) represents the rotation and elastic distortion of the lattice, mapping the intermediate configuration into the current configuration.

Figure 1
figure 1

Multiplicative decomposition of deformation gradient

Full size image

The velocity gradient can be expressed with deformation gradient

$${\varvec{L}} = {\dot{\mathbf{F}}\mathbf{F}}^{ - 1} = {\dot{\mathbf{F}}}^{{\text{e}}} {\mathbf{F}}^{{{\text{e}} - {1}}} + {\mathbf{F}}^{{\text{e}}} {\dot{\mathbf{F}}}^{{\text{p}}} {\mathbf{F}}^{{{\text{p}} - {1}}} {\mathbf{F}}^{{{\text{e}} - {1}}}$$
(2)

where \({\varvec{L}}^{{\text{p}}} = {\dot{\mathbf{F}}}^{{\text{p}}} {\mathbf{F}}^{{{\text{p}} - 1}}\) represents the plastic velocity gradient which is dependent on the sum of shear strain rates on all slip systems, i.e.,

$${\mathbf{L}}^{{\text{p}}} = \sum\limits_{\alpha }^{{N_{s} }} {\dot{\gamma }^{\alpha } {\mathbf{m}}^{\alpha } \otimes {\mathbf{n}}^{\alpha } }$$
(3)

where \(N_{{\text{s}}}\) represents the number of slip systems and \(N_{{\text{s}}} = 12\) for the face-centered cubic (fcc) metals, \(\dot{\gamma }^{\alpha }\) is the slip rate of the \(\alpha\) slip system, the unit vectors \({\mathbf{m}}^{\alpha }\) and \({\mathbf{n}}^{\alpha }\) are the slip direction and normal to the slip plane, respectively, and the symbol \(\otimes\) represents the dyadic product. In the initial configuration \({\mathbf{L}}_{{0}}^{{\text{p}}} = \sum\limits_{\alpha }^{{N_{s} }} {\dot{\gamma }^{\alpha } {\mathbf{m}}_{0}^{\alpha } \otimes {\mathbf{n}}_{0}^{\alpha } }\), and \({\mathbf{m}}^{\alpha } = {\mathbf{F}}^{{\text{e}}} {\mathbf{m}}_{0}^{\alpha }\) and \({\mathbf{n}}^{\alpha } = {\mathbf{n}}_{0}^{\alpha } {\mathbf{F}}^{{{\text{e}} - {1}}}\).

For the rate-dependent crystal plasticity model, the well-known power-law flow rule was used to establish the relation between the shear strain rate and the resolved shear stress.

$$\dot{\gamma }^{\alpha } = \dot{\gamma }_{0} \left| {\frac{{\tau^{\alpha } }}{{g^{\alpha } }}} \right|^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}}} {\text{sgn}} \left( {\tau^{\alpha } } \right)$$
(4)

where \(\dot{\gamma }_{0}\) represents the reference shear strain rate, \(\tau^{\alpha }\) is the resolved shear stress on the \(\alpha\) slip system, \(g^{\alpha }\) is the slip resistance on the \(\alpha\) slip system, m is the rate-sensitivity exponent.

The resolved shear stress (\(\tau^{\alpha }\) on the \(\alpha\) slip system) is calculated from the Cauchy stress

$$\tau^{\alpha } = {{\varvec{\upsigma}}}:({\mathbf{m}}^{\alpha } \otimes {\mathbf{n}}^{\alpha } )$$
(5)

The Cauchy stress is correlated to the 2nd Piola–Kirchhoff stress through the relationship as

$${\varvec{\sigma}} = {{{\mathbf{F}}^{{\text{e}}} {\mathbf{TF}}^{{{\text{eT}}}} } \mathord{\left/ {\vphantom {{{\mathbf{F}}^{{\text{e}}} {\mathbf{TF}}^{{{\text{eT}}}} } {\det ({\mathbf{F}})}}} \right. \kern-\nulldelimiterspace} {\det ({\mathbf{F}})}}$$
(6)

For the hyperelastic law, the 2nd Piola–Kirchhoff stress can be calculated as

$${\varvec{T}} = \Re :{\mathbf{E}}^{{\text{e}}}$$
(7)

where \(\Re\) is the elastic matrix consisting of \(C_{11}\), \(C_{12}\) and \(C_{44}\), \({\mathbf{E}}^{{\text{e}}}\) is the Green strain and is calculated as \({\varvec{E}}^{{\text{e}}} = {{\left( {{\mathbf{F}}^{{{\text{eT}}}} {\mathbf{F}}^{{\text{e}}} - {\mathbf{I}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{F}}^{{{\text{eT}}}} {\mathbf{F}}^{{\text{e}}} - {\mathbf{I}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\).

Phenomenological hardening law

The evolution of \(g^{\alpha }\) has the general form

$$\dot{g}^{\alpha } = \sum\limits_{\beta }^{{N_{{\text{s}}} }} {h^{\alpha \beta } \left| {\dot{\gamma }^{\beta } } \right|}$$
(8)

where \(g_{0}^{\alpha }\) is the initial hardness and is assumed to be a constant, \(h^{\alpha \beta }\) is the hardening modulus and is described phenomenologically by a saturation-type law [26, 57]

$$h^{\alpha \beta } = h_{0} \left[ {q + \left( {1 - q} \right)\delta^{\alpha \beta } } \right] \cdot \left| {1 - \frac{{g^{\beta } }}{{g_{s} }}} \right|^{a} \cdot {\text{sgn}} \left( {1 - \frac{{g^{\beta } }}{{g_{s} }}} \right)$$
(9)

where \(h_{0}\), a and \(g_{{\text{s}}}\) are the slip system hardening parameters which are taken to be identical for all slip systems, \(h_{0}\) is the initial hardening rate and \(g_{{\text{s}}}\) is the saturation value of the slip resistance, q is the ratio of the latent hardening rate to the self-hardening rate, \(q = 1\) for coplanar slip system and \(q = 1.4\) for non-coplanar slip systems. The relevant material parameters of the crystal plasticity model incorporated with the saturation-type phenomenological hardening law are listed in Table 1 [58].

Table 1 Parameters of crystal plasticity model incorporated with the saturation-type phenomenological hardening law for OFHC copper [58]
Full size table

Dislocation density-based hardening law

For the dislocation density-based hardening law, an equivalent slip resistance (\(\overline{g}\)) was used. The simplest form of \(\overline{g}\) is an isotropic hardening model which assumes that the slip resistances on all slip systems are identical, it indicates that the latent hardening rate is equal to the self-hardening rate, i.e., \(q = 1\), and some works have indicated that the better prediction of the plastic deformation behavior of OFHC copper could be obtained by using \(q = 1\) rather than using others [31]. One classic example of isotropic hardening models is the power-law hardening model [59],\(\overline{g} = a_{1} + a_{2} \left( {\overline{\varepsilon }^{p} } \right)^{{n^{*} }}\), where \(a_{1}\), \(a_{2}\) and \(n^{*}\) are the hardening parameters and \(\overline{\varepsilon }^{p}\) represents the equivalent plastic strain. Based on the dislocation density-based material model [41,42,43], the equivalent slip resistance (\(\overline{g}\)), which is related to the resolved shear strain (\(\gamma^{r}\)) and resolved shear strain rate (\(\dot{\gamma }^{r}\)), can be explicitly expressed as

$$\overline{g} = \eta Gb\left[ {f\sqrt {\rho_{w} } + \left( {1 - f} \right)\sqrt {\rho_{c} } } \right] \cdot \left( {\frac{{\dot{\gamma }^{r} }}{{\dot{\gamma }_{0} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {m^{*} }}} \right. \kern-\nulldelimiterspace} {m^{*} }}}}$$
(10)

where G is the shear modulus, \(\eta\) is a material constant, b is the magnitude of the Burgers vector, \(\dot{\gamma }_{0}\) is a reference shear rate, \({1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}^{*}\) is a strain rate-sensitivity parameter, \(\dot{\gamma }^{r}\) is the resolved shear strain rate and is correlated to the equivalent strain (\(\dot{\overline{\varepsilon }}^{p}\)) via the Taylor factor, \(\dot{\gamma }^{r} = M\dot{\overline{\varepsilon }}^{p}\), M is the Taylor factor, \(\rho_{w}\) and \(\rho_{c}\), respectively, represent the dislocation densities in the cell walls and the cell interiors, and f represents the volume fraction of the cell walls. The total dislocation density is calculated by \(\rho_{{\text{t}}} = f\rho_{{\text{w}}} + \left( {1 - f} \right)\rho_{{\text{c}}}\), and the evolutions of \(\dot{\overline{\varepsilon }}^{p}\), f, \(\rho_{{\text{w}}}\) and \(\rho_{c}\) are, respectively, expressed as [41,42,43].

$$\dot{\overline{\varepsilon }}^{p} = \sqrt {\frac{2}{3}{\dot{\mathbf{\varepsilon }}}^{p} :{\dot{\mathbf{\varepsilon }}}^{p} } ,\quad {\dot{\mathbf{\varepsilon }}}^{p} = \sum\limits_{\alpha }^{{N_{s} }} {{{\dot{\gamma }^{\alpha } \left( {{\mathbf{m}}^{\alpha } \otimes {\mathbf{n}}^{\alpha } + {\mathbf{n}}^{\alpha } \otimes {\mathbf{m}}^{\alpha } } \right)} \mathord{\left/ {\vphantom {{\dot{\gamma }^{\alpha } \left( {{\mathbf{m}}^{\alpha } \otimes {\mathbf{n}}^{\alpha } + {\mathbf{n}}^{\alpha } \otimes {\mathbf{m}}^{\alpha } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}}$$
(11)
$$f = f_{\infty } + \left( {f_{0} - f_{\infty } } \right)\exp \left( {{{ - \gamma^{r} } \mathord{\left/ {\vphantom {{ - \gamma^{r} } {\tilde{\gamma }^{r} }}} \right. \kern-\nulldelimiterspace} {\tilde{\gamma }^{r} }}} \right)$$
(12)
$$\dot{\rho }_{w} = \frac{{\sqrt 3 \beta^{*} \dot{\gamma }^{r} \left( {1 - f} \right)\sqrt {\rho_{w} } }}{fb} + \frac{{6\beta^{*} \dot{\gamma }^{r} \left( {1 - f} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} }}{bdf} - k_{{0}} \dot{\gamma }^{r} \rho_{w} \left( {\frac{{\dot{\gamma }^{r} }}{{\dot{\gamma }_{0} }}} \right)^{{ - {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}}}$$
(13)
$$\dot{\rho }_{c} = \frac{{\alpha^{*} \dot{\gamma }^{r} \sqrt {\rho_{w} } }}{\sqrt 3 b} - \frac{{6\beta^{*} \dot{\gamma }^{r} }}{{bd\left( {1 - f} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} - k_{{0}} \dot{\gamma }^{r} \rho_{c} \left( {\frac{{\dot{\gamma }^{r} }}{{\dot{\gamma }_{0} }}} \right)^{{ - {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}}}$$
(14)

where \(f_{0}\) and \(f_{\infty }\), respectively, represent the initial and saturation values of f, \(f_{0} > f_{\infty }\), f decreases monotonically from the initial value to the saturation value with shear deformation increasing, which implies that the dislocation cell walls become sharper and more narrow with plastic deformation, and the parameter \(\tilde{\gamma }^{r}\) is a constant that quantifies the descent rate of the values of \(f\) [41,42,43], the coefficients \(\alpha^{*}\), \(\beta^{*}\) and \(k_{{0}}\) are the three material constants, which are, respectively, related to the generation, motion and annihilation of dislocations in the process of plastic deformation, and the exponent \(n\) is a constant based on the assumption of the isothermal treatment processes.

The average cell size is inversely proportional to the square root of the total dislocation density, i.e.,

$$d = \frac{K}{{\sqrt {\rho_{t} } }}$$
(15)

where K is a material constant. More detailed descriptions about the dislocation density-based material model can be found from the works of Estrin et al. [41,42,43]. The relevant material parameters of the crystal plasticity model in conjunction with the dislocation-based hardening law are listed in Table 2 [41,42,43, 60].

Table 2 Parameters of dislocation-based hardening law for OFHC copper [41,42,43, 60]
Full size table

Numerical implementation in ABAQUS/Explicit

Based on the Green–Naghdi material co-rotational coordinate system in the ABAQUS/Explicit codes, which is a set of moving coordinate systems in which the basis systems rotate with the material, the deformation gradient is then represented as \({\mathbf{F}}_{{{\text{cor}}}}\), and \({\mathbf{F}}_{{{\text{cor}}}} = {\mathbf{F}}_{{{\text{cor}}}}^{{\text{e}}} {\mathbf{F}}^{{\text{p}}}\). According to the polar decomposition of the deformation gradient (\({\mathbf{F}} = {\mathbf{RU}}\)), it can be obtained that \({\mathbf{F}}_{{{\text{cor}}}} = {\mathbf{U}}\) since the rotation component is taken into account in the Green–Naghdi material co-rotational coordinate system. Therefore, the following equation is further obtained

$${\mathbf{F}}_{{{\text{cor}}}}^{{\text{e}}} {\mathbf{F}}^{{\text{p}}} = {\mathbf{U}}$$
(16)

where \({\mathbf{F}}_{{{\text{cor}}}}^{{\text{e}}}\) is the elastic component of deformation gradient in the Green–Naghdi material co-rotational coordinate system, and \({\mathbf{F}}_{{{\text{cor}}}}^{{\text{e}}} = {\mathbf{UF}}^{{{\text{p}} - {1}}}\) according to Eq. (16).

Combining Eqs. (5), (6), (7) and (16), the 2nd Piola–Kirchhoff stress (\({\mathbf{T}}\)), the co-rotational stress (\({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }}\)) and resolved stress on the \(\alpha\) slip system (\(\tau^{\alpha }\)) can be rewritten as

$${\mathbf{T}} = \Re :{{\left( {{\mathbf{F}}_{{{\text{cor}}}}^{{{\text{eT}}}} {\mathbf{F}}_{{{\text{cor}}}}^{{\text{e}}} - {\mathbf{I}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{F}}_{{{\text{cor}}}}^{{{\text{eT}}}} {\mathbf{F}}_{{{\text{cor}}}}^{{\text{e}}} - {\mathbf{I}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2} = \Re :{{\left( {{\mathbf{F}}^{{{\text{p}} - {\text{T}}}} {\mathbf{UUF}}^{{{\text{p}} - {1}}} - {\mathbf{I}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{F}}^{{{\text{p}} - {\text{T}}}} {\mathbf{UUF}}^{{{\text{p}} - {1}}} - {\mathbf{I}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}$$
(17)
$${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }} = {{{\mathbf{UF}}^{{{\text{p}} - {1}}} {\mathbf{TF}}^{{{\text{p}} - {\text{T}}}} {\mathbf{U}}} \mathord{\left/ {\vphantom {{{\mathbf{UF}}^{{{\text{p}} - {1}}} {\mathbf{TF}}^{{{\text{p}} - {\text{T}}}} {\mathbf{U}}} {\det ({\mathbf{U}})}}} \right. \kern-\nulldelimiterspace} {\det ({\mathbf{U}})}}$$
(18)
$$\tau^{\alpha } = ({\mathbf{F}}^{{{\text{p}} - {\text{T}}}} {\mathbf{UUF}}^{{{\text{p}} - {1}}} {\mathbf{T}}):\left( {{\mathbf{m}}_{0}^{\alpha } \otimes {\mathbf{n}}_{0}^{\alpha } } \right)$$
(19)

According to the evolution of \({\mathbf{F}}^{{\text{p}}}\), \({\dot{\mathbf{F}}}^{{\text{p}}} {\mathbf{F}}^{{{\text{p}} - {1}}} = \sum\limits_{\alpha }^{{N_{s} }} {\dot{\gamma }^{\alpha } \cdot \left( {{\mathbf{m}}_{0}^{\alpha } \otimes {\mathbf{n}}_{0}^{\alpha } } \right)}\), the value of \({\mathbf{F}}^{{\text{p}}}\) at the time of \(t + \Delta t\) can be calculated as

$${\mathbf{F}}_{t + \Delta t}^{{\text{p}}} = \exp \left( {\Delta t \cdot {\mathbf{L}}_{0}^{{\text{p}}} } \right) \cdot {\mathbf{F}}_{t}^{{\text{p}}}$$
(20)

where the subscript t and \(t + \Delta t\), respectively, represent the end and start of an increment, and the unknown tensor \({\mathbf{F}}_{t + \Delta t}^{{\text{p}}}\) is accordingly expressed by the known tensor \({\mathbf{F}}_{t}^{{\text{p}}}\). Therefore, Eq. (19) can be rewritten as

$$\tau_{t + \Delta t}^{\left( \alpha \right)} = \left[ {\left( {{\mathbf{I}} - \sum\limits_{\alpha }^{{N_{s} }} {\Delta \gamma^{\alpha } {\mathbf{S}}_{0}^{{\alpha {\text{T}}}} } } \right){\mathbf{F}}_{t}^{{{\text{p}} - {\text{T}}}} {\mathbf{U}}_{t + \Delta t} {\mathbf{U}}_{t + \Delta t} {\mathbf{F}}_{t}^{{{\text{p}} - 1}} \left( {{\mathbf{I}} - \sum\limits_{\alpha }^{{N_{s} }} {\Delta \gamma^{\alpha } {\mathbf{S}}_{0}^{\alpha } } } \right)} \right] \cdot \left[ {\Re :{{\left( {{\mathbf{F}}^{{{\text{p}} - {\text{T}}}} {\mathbf{UUF}}^{{{\text{p}} - {1}}} - {\mathbf{I}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{F}}^{{{\text{p}} - {\text{T}}}} {\mathbf{UUF}}^{{{\text{p}} - {1}}} - {\mathbf{I}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}} \right]:{\mathbf{S}}_{0}^{\alpha }$$
(21)

where \({\mathbf{S}}_{0}^{\alpha } = {\mathbf{m}}_{0}^{\alpha } \otimes {\mathbf{n}}_{0}^{\alpha }\).

The Bunge's Euler angles \(\left\{ {\varphi_{1} ,\;\Phi ,\;\varphi_{2} } \right\}\) were employed to define the crystallographic orientation

$${\mathbf{Q}} = \left[ {\begin{array}{*{20}l} {\cos \varphi_{1} \cos \varphi_{2} - \sin \varphi_{1} \sin \varphi_{2} \cos \Phi } \hfill & {\sin \varphi_{1} \cos \varphi_{2} + \cos \varphi_{1} \sin \varphi_{2} \cos \Phi } \hfill & {\sin \varphi_{2} \sin \Phi } \hfill \\ { - \cos \varphi_{1} \sin \varphi_{2} - \sin \varphi_{1} \cos \varphi_{2} \cos \Phi } \hfill & { - \sin \varphi_{1} \sin \varphi_{2} + \cos \varphi_{1} \cos \varphi_{2} \cos \Phi } \hfill & {\cos \varphi_{2} \sin \Phi } \hfill \\ {\sin \varphi_{1} \sin \Phi } \hfill & { - \cos \varphi_{1} \sin \Phi } \hfill & {\cos \Phi } \hfill \\ \end{array} } \right]$$
(22)

The current crystallographic orientation can be updated by

$${\mathbf{Q}} = {\mathbf{R}}^{{\text{e}}} {\mathbf{Q}}_{0}$$
(23)

where \({\mathbf{Q}}_{0}\) is the initial crystallographic orientation, \({\mathbf{R}}^{{\text{e}}}\) is a lattice rotation tensor resulting from the polar decomposition of \({\mathbf{F}}^{{\text{e}}}\). The updated Q is used for texture analysis.

Based on the Green–Naghdi material co-rotational coordinate frame in ABAQUS/Explicit, the crystal plasticity models in conjunction with the saturation-type phenomenological hardening law and the dislocation density-based hardening law were, respectively, implemented into the finite element codes by developing the user material subroutines VUMAT for finite element computation, and detailed description for the numerical implementation method and the relevant explicit integration algorithm of VUMAT can be seen in the literature [49, 57].

Results and discussion

Deformation of single crystals

By using the crystal plasticity models in conjunction with the saturation-type phenomenological hardening law and the dislocation density-based hardening law, the uniaxial compression tests of the copper cylindrical single-crystal specimens taken from the literature [61] were simulated. As shown in Fig. 2, the cylindrical single-crystal specimen was compressed along its axis direction by two platens of the testing machine, and the contacts between the cylindrical single-crystal specimen and platens were considered to be frictionless. The two platens were treated as rigid bodies, the fixed constraint was applied on the reference point of the lower platen, and a velocity load was applied on the reference point of the upper platen. Four cylindrical single-crystal specimens with different geometrical dimensions and crystallographic orientations were used to simulate the large plastic deformation behavior of copper single crystals under the uniaxial compression. Each cylindrical single-crystal specimen associated with the identical initial crystallographic orientation was meshed by C3D8R elements (three-dimensional eight-node linear brick elements with reduced integration and hourglass control), which were assigned the crystal plastic constitutive models by the user material subroutines (VUMAT in ABAQUS/Explicit). The element size used for meshing the cylindrical single-crystal specimen was determined as 0.44 mm by the trail calculations. Table 3 presents the dimensions and orientations of the four copper cylindrical single-crystal specimens, and the symbols of S1, S2, S3 and S4 in the table denote the specimen numbers. The detailed experimental description of the uniaxial compressions of the cylindrical single-crystal specimens can be seen in the literature [61].

Figure 2
figure 2

Finite element model of the cylindrical single-crystal specimen for the uniaxial compression

Full size image
Table 3 Dimensions and Euler angles of the copper cylindrical single-crystal specimens [61]
Full size table

The predicted macroscopic mechanical responses of the copper cylindrical single-crystal specimens under the uniaxial compression loads are shown in Fig. 3. In general, the predicted relations between the “Load/Initial Cross section” and “Crosshead displacement/Initial length” (i.e., macroscopic stress–strain responses) of the four cylindrical single-crystal specimens are consistent with the experimental measurement results, especially for the specimen of S1, the predicted macroscopic stress–strain response is in good agreement with the experimental results by using the crystal plasticity model in conjunction with the saturation-type phenomenological hardening law.

Figure 3
figure 3

Predictions and experimental results [61] of the mechanical responses of the copper cylindrical single-crystal specimens under the uniaxial compression loads

Full size image

Compared with the predictions results of the crystal plasticity model incorporated with the saturation-type phenomenological hardening law, when the macroscopic strain is smaller than 0.2 for S1, 0.23 for S2, 0.25 for S3 and 0.24 for S4, the larger macroscopic stresses are predicted by the crystal plasticity model in conjunction with the dislocation density-based hardening law, whereas after the macroscopic strains exceed these critical values, the predicted macroscopic stresses by the dislocation density-based hardening law become smaller. The reasons are related to the dislocation evolution. In the plastic deformation process, the cell walls are increasingly sharpening, and the cell sizes and the relative volume fraction of the cell walls decrease. As more and more dislocations are confined into the less and less space, the storage process of dislocations gradually changes in the cell walls. Zehetbauer et al. [62] suggested the gradual change of the character of the dislocation cell walls from the polarized dipole walls to the polarized tilted walls. However, the process, which develops the increasing misorientations between adjacent cells, has not been yet incorporated into the present dislocation density-based hardening law [63].

As seen in Fig. 3, in the cases of specimens S2, S3 and S4, the predicted macroscopic stresses are larger than the experimental data with respect to the same macroscopic strains; the reason for explaining the deviation between the prediction results and experimental data is mainly attributed to the influence of non-Schmid effects. For some orientations, non-Schmid stresses favor the formation of constriction and promote cross-slip resulting in higher macroscopic flow stress; while for other orientations, non-Schmid stresses hinder cross-slip resulting in lower macroscopic flow stress [61]. The non-Schmid effects can be quantitatively analyzed by the ratio (\(R_{{{\text{ns}}}}\)) between \(\tau_{{{\text{eff}}}}^{\alpha }\) and \(\tau_{s}^{\alpha }\) as suggested by Patra et al. [64]. Paik et al. [61] estimated the values of \(R_{{{\text{ns}}}}\) are 1.112, 0.922, 0.967, 0.944 at the point of initial yield and 1.05, 0.93, 0.93, 0.84 at the macroscopic compressive strain of 0.4 for the specimens of S1, S2, S3 and S4, respectively, which deviate from 1.0 for all the specimens. As a result, the predictions resulting from the crystal plasticity model based on the Schmid’s law deviate the experimentally measured mechanical responses of copper single crystals. Additionally, since the values of \(R_{{{\text{ns}}}}\) are smaller than 1.0 for the specimens of S2, S3 and S4, the predicted macroscopic stresses by the crystal plasticity models in conjunction with the saturation-type phenomenological hardening law and the dislocation density-based hardening law, which do not take into account the influences of non-Schmid effects in this work, are over-estimated therefore.

Figure 4 compares the simulated and experimental crystallographic textures of copper single crystals for the cylindrical specimens of S1, S2, S3 and S4 at a macroscopic compressive strain of 0.4. The crystallographic textures were calculated according to the Euler angles by using the open source codes (MTEX). As seen from the figures, the predicted pole figures accord well with the experimental measurement results [61] on the whole, which provides indirect support for the validations of the numerical computation of the crystal plasticity model in conjunction with the saturation-type phenomenological hardening law and the dislocation density-based hardening law (VUMAT). However, careful observation reveals that there are some differences between them. The differences mainly come from two aspects: (1) the crystal plasticity models in conjunction with the saturation-type phenomenological hardening law and the dislocation density-based hardening law do not take into consideration the influences of non-Schmid effects; (2) the finite element computation was carried out by using the explicit dynamic finite element algorithm (ABAQUS/Explicit codes), and it is difficult to simulate the uniaxial compression process associated with a quasi-static strain rate ranging from \(2.83 \times 10^{ - 4} {\text{s}}^{ - 1}\) to \(4.93 \times 10^{ - 4} {\text{s}}^{ - 1}\). In order to improve the calculation's rate and efficiency of the explicit finite element method, the loading strain rate of \(5{\text{0s}}^{{ - {1}}}\) was then used to simulate the uniaxial compression processes of the cylindrical single-crystal copper associate with a quasi-static rate. The differences between the loading strain rate of \(5{\text{0s}}^{{ - {1}}}\) used in the finite element simulation and the quasi-static rates used in experiments could have an impact on the simulated crystallographic textures, but the influence was not taken into account in this work due to the consideration of the computation cost.

Figure 4
figure 4figure 4

Predicted crystallographic textures of the copper cylindrical single-crystal specimens at a uniaxial compression engineering strain of 0.4

Full size image

Deformation of polycrystalline aggregate

In order to study the plastic deformation behavior of copper polycrystals, two homogenization schemes were employed to conduct the transition from the microscopic mechanical response of the individual grains to the macroscopic mechanical response of the polycrystalline aggregate:

  1. (1)

    Taylor-type model, which belongs to the mean-field crystal plasticity model and assumes that all grains accommodate the same plastic strain equal to the macroscopically imposed strain, and with the assumption in this work that the volumes of all grains are the same, the volume average of co-rotational stress in a material point with respect to an element can be simplified as

    $${\mathbf{\overline{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }}} = \frac{1}{{N_{g} }}\sum\limits_{g = 1}^{{N_{g} }} {{}^{g}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }}}$$
    (24)

    where \(N_{g}\) denotes the number of grains in a material point and \({}^{g}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }}\) represents the co-rotational stress of a grain.

  2. (2)

    Voronoi-type model, which belongs to the full-field crystal plasticity model and uses the MPT codes in MATLAB to create Voronoi tessellations at first, the geometrical coordinate information of the Voronoi tessellations is then transferred into ABAQUS/CAE, and the finite element model of polycrystalline aggregate is accordingly created by a routine written by Python, as a result, individual grains are discretized by many finite elements.

The Taylor-type mean-field homogenization scheme satisfies the deformation compatibility condition, but the stress equilibrium at the grain boundaries cannot be guaranteed, the microstructure is represented in a statistical way where each grain is considered to be homogeneous, thus disregarding realistic microstructural in-grain morphologies and specific local grain interactions. Compared with the Taylor-type mean-field model, the Voronoi-type full-field model is capable to take into account the interaction between grains and the effects of grain boundaries, grain sizes and grain shapes, whereas these crystal plasticity models are too computationally expensive to simulate laboratory-scale components with complete microstructural information.

The Taylor-type and Voronoi-type models with the same dimensions of 1 × 1 × 1 mm are created, as shown in Fig. 5. A single element (C3D8R) was used to mesh the Taylor-type model, and the single material point consisted of 10 grains with initial random orientation, as shown in Fig. 5a. The Voronoi-type model was created by MPT codes and was discretized into 1000 elements, and was also composed of 10 grains with initial random orientation, as shown in Fig. 5b. The element size of 0.1 mm in the Voronoi-type model was determined by the trail calculations. The bottom surfaces of the Taylor-type and Voronoi-type models were constrained completely, and the same velocity load was imposed on the top surfaces of the two cubic finite element models.

Figure 5
figure 5

Cubic finite element models consisting of 10 grains

Full size image

Figure 6 shows the plastic deformations and mechanical responses of Taylor-type and Voronoi-type models under the uniaxial tensile load, in which the symbols of S33 and LE33 represent the stress component of \(\sigma_{z}\) and the logarithmic strain component of \(\varepsilon_{z}\), respectively, and the z-axial direction is the loading direction. As seen in Fig. 6a and b, which are corresponding to the Taylor-type models conjuncted with the saturation-type phenomenological hardening law and the dislocation density-based hardening law, respectively, the dimensions of the top surfaces of the cubic finite element models decrease under the uniaxial tensile load, and a square pyramid is resultantly produced. However, as seen in Fig. 6c and d, which corresponds to the Voronoi-type models conjuncted with the saturation-type phenomenological hardening law and the dislocation density-based hardening law, respectively, the significant inhomogeneous plastic deformation can be found owing to the interaction between grains and the effects of grain boundaries, grain sizes, grain shapes, and the directional necking occurs due to the relative position relation between the initial crystallographic orientation and the loading direction.

Figure 6
figure 6

Plastic deformations and mechanical responses of Taylor-type and Voronoi-type models under the uniaxial tensile load

Full size image

The similar phenomena can be observed in Fig. 7, which shows the plastic deformations and mechanical responses of Taylor-type and Voronoi-type models under the uniaxial compression load. As seen in Fig. 7a and b, the relative regular plastic deformation can be obtained by the Taylor-type model, and the single element and single material point are responsible for the relative regular plastic deformation. However, for the Voronoi-type model, the significant inhomogeneous plastic deformation can be seen from Fig. 7c and d, which is also mainly attributed to the interaction between grains and the effects of grain boundaries, grain sizes, grain shapes and initial crystallographic orientations.

Figure 7
figure 7

Plastic deformations and mechanical responses of Taylor-type and Voronoi-type models under the uniaxial compression load

Full size image

Figure 8 compares the stress–strain relations resulting from Taylor-type and Voronoi-type models. As seen in the figures, when compared with Taylor-type model, the stress–strain relations predicted by Voronoi-type model are closer to the experimental data [58], and the predictions resulting from Voronoi-type model incorporated with the dislocation density-based hardening law are in good agreement with the experimental data [58]. Since Taylor-type model does not take into account the interaction between grains and the effects of grain boundaries, grain sizes and grain shapes, the predictions resulting from Taylor-type model are larger than that resulting from Voronoi-type model with respect to the same strain.

Figure 8
figure 8

Stress–strain relations resulting from the Taylor-type and Voronoi-type models

Full size image

In order to further investigate the effects of grain number on the Taylor-type homogenization scheme, the Taylor-type cubic finite element model was discretized into \(2^{3}\), \(3^{3}\), \(4^{3}\), \(5^{3}\) and \(6^{3}\) elements (C3D8R), and the material point in each element consisted of 10 grains; as a result, the number of the total grains within Taylor-type model is corresponding to 80, 270, 640, 1250 and 2160, respectively. Figure 9 shows the stress–strain relations resulting from Taylor-type model associated with different grain numbers under the uniaxial tensile load. As seen in Fig. 9a, which makes the use of the crystal plasticity model incorporated with the saturation-type phenomenological hardening law, with the increase in total grain number, the stress–strain relations tend to be stable gradually, and the same conclusion can be obtained for the crystal plasticity model incorporated with the dislocation density-based hardening law, as shown in Fig. 9b. By comparing Fig. 9a and b, it reveals that both the predictions of the stress–strain relations resulting from Taylor-type models conjuncted with the saturation-type phenomenological hardening law and dislocation density-based hardening law agree well with the experimental data [58] when the cubic finite element model consists a large number of grains, and the sensitivity of stress–strain relations to grain number is relatively smaller for the dislocation density-based hardening law than the saturation-type phenomenological hardening law.

Figure 9
figure 9

Stress–strain relations resulting from Taylor-type model considering different grain numbers

Full size image

Figure 10 compares the simulated crystallographic textures by Taylor-type model incorporated with the saturation-type phenomenological hardening law and the dislocation density-based hardening law at the uniaxial tensile strain of 0.37. The two resultant simulation textures are visually similar for the same total grain number, and with the increase in total grain number, the simulated textures become closer and closer to the experimental measurement results [58]. As seen from Figs. 9 and 10, the stress–strain responses and crystallographic textures of the homogenized polycrystalline aggregate are no longer dependent on the grain number if a sufficient number of grains with random crystallographic orientation distribution are used [65].

Figure 10
figure 10figure 10

Crystallographic textures simulated by Taylor-type model at the uniaxial tensile strain of 0.37

Full size image

Modeling of single shot impact

Shot peening (SP) and surface mechanical attrition treatment (SMAT) are two well-known surface modification techniques of metallic materials; the surface strengthening layers produced by SP and SMAT are attributed to the severe plastic deformation induced by shot impact. In order to study the shot impact-induced plastic deformation mechanism, which is very significant for the developments of SP and SMAT techniques, the single impact experiments of OFHC copper along a given direction were carried out, and the crystal plasticity models in conjunction with the saturation-type phenomenological hardening law and the dislocation density-based hardening law were used to simulate the process of single shot impact on the copper polycrystalline aggregate, respectively.

A cylinder-shaped impactor made of high-speed steel, with the diameter of 6 mm and height of 10 mm, was accelerated by an electromagnetic driver, as shown in Fig. 11. The impact velocity was measured by magnetic inductive method, and the impact angle was adjusted by the multi-axial rotatable fixture. Three impact experiments were carried out that the velocity of impactor remained a constant of 8 m/s, while the impact angles were, respectively, set to 70°, 80° and 90°. The resultant indentation profiles were measured by Keynes 3D microscopic system.

Figure 11
figure 11

Schematic diagram of single shot impact experiment and simplified finite element model

Full size image

The front of the impactor was processed into a hemisphere with a diameter of 1 mm, as shown in Fig. 11. An analytical rigid shot with the diameter of 1 mm was modeled to impact the OFHC copper target instead of the cylinder-shaped impactor in the finite element model of single impact. The mass of the analytical rigid shot was equal to the mass of cylinder-shaped impactor, and the shot impact velocity was also equal to the measured velocity of cylinder-shaped impactor. The initial velocity of 8 m/s was applied on the reference point of the analytical rigid shot, which was located at the sphere center of rigid shot. The contact between the shot and the target surface was numerically computed by using the penalty method with Coulomb friction coefficient of 0.3 [66, 67]. In the case of single shot impact, three impact angles of 70°, 80° and 90° were taken into consideration.

In order to reduce the computation cost, a symmetrical finite element model of the target to be impacting was created, as shown in Fig. 12. The geometrical dimensions of target model are 5 mm length, 2.5 mm width and 5 mm height. The elements of C3D8R in ABAQUS/Explicit codes were adopted to mesh the target model, and the finest elements size of \(40{\mu m}\) were used to mesh the shot-impacted region. The Taylor-type mean-field model, in which each material point of the target model consists of 10 grains, was used to homogenize the calculation results of the copper polycrystalline aggregate. The center local region of the target model with the dimension of 1.5 × 0.75 × 1.5 mm was regarded as the reference region for analyzing the calculation results, as shown in Fig. 12.

Figure 12
figure 12

Finite element model of single shot impact on OFHC copper polycrystalline aggregate

Full size image

As seen in Fig. 13, under the single shot impact, the predicted indentation profiles by the dislocation density-based hardening law are well consistent with the predictions resulting from the saturation-type phenomenological hardening law. Therefore, the dislocation density-based hardening law is validated by the saturation-type phenomenological hardening law. However, no matter for the dislocation density-based hardening law or for the saturation-type phenomenological hardening law, the predicted depths of the indentations are larger than the experimentally measured data. The reasons for explaining the differences between the predicted indentation profiles and the experimental results can be concluded that: (1) the Taylor-type mean-field model used to homogenize the OFHC copper polycrystalline aggregate does not take into account the effects of grain boundaries, grain sizes, grain shapes and the interaction between grains, which could cause the reduction of plastic deformation resistance for the target model; (2) the differences in geometries between the cylinder-shaped impactor used for experiments and the rigid shot simplified for finite element simulations could result in the different distributions of the contact stresses imposing on the target surface; (3) there could be some dispersion and error in the experimental measurement.

Figure 13
figure 13

Comparison between the predicted indentation profiles and experimental results

Full size image

Figure 14 presents the crystallographic textures of the impacted surface; the data of Euler angles used for plotting the crystallographic textures were all taken from the first element layer of the reference region as shown in Fig. 12. It can be seen from Fig. 14 that the simulated textures by crystal plasticity model conjuncted with the saturation-type phenomenological hardening law and the dislocation density-based hardening law look similar for all the impact conditions. However, careful observation can be found that the maximum texture intensity decreases with the increase in the impact angle from 70° to 90°. The crystallographic textures are used to characterize the plastic deformation behaviors, which are dependent on the evolution of dislocation density. Figure 15 shows the dislocation densities resulting from the single shot impact associated with the different impact angles. The larger dislocation densities are located in the subsurface layer and the local surface region close to the indentation edge, as shown in Fig. 15a, b and c. Figure 15d shows the in-depth dislocation densities of the reference region, and the “area-averaged” method [68, 69] was used to calculate the average value of the resultant dislocation density with respect to the thickness direction of the reference region. It can be concluded that the averaged dislocation density in the impacted surface decreases with the increase in the impact angle from 70° to 90°, which accord well with the maximum texture intensity as shown in Fig. 14. However, for the depth larger than 0.2 mm, as seen in Fig. 15d, the averaged dislocation density with respect to the same depth is smallest for the impact angle of 70°, and the averaged dislocation density in the case of 90° impact angle is slightly larger than that in the case of 80° impact angle. The refined cell sizes are inversely proportional to the square root of the increased dislocation density, as shown in Fig. 15d.

Figure 14
figure 14

Crystallographic textures of the impacted surface of the copper polycrystalline aggregate

Full size image
Figure 15
figure 15

Dislocation densities induced by single shot impact associated with different impact angles

Full size image

Conclusions

In this paper, based on the two crystal plasticity models in conjunction with the saturation-type phenomenological hardening law and the dislocation density-based hardening law, a comparative study on the large plastic deformation behaviors of OFHC copper single crystals and polycrystals in terms of stress–strain responses and texture evolutions was carried out. The two crystal plasticity models incorporated with the saturation-type phenomenological hardening law and the dislocation density-based hardening law were implemented into the finite element codes (ABAQUS/Explicit) as the user material subroutine (VUMAT). The three-dimensional finite element models of the cylindrical specimens were created to simulate the uniaxial compression-induced plastic deformation behaviors of copper single crystals associated with the different geometrical dimensions and initial crystallographic orientations. Two homogenization schemes, Taylor-type mean-field model and Voronoi-type full-field model, were used to calculate the macroscopic mechanical responses of the polycrystalline aggregate of copper under the uniaxial compression and uniaxial tension loads. The process of single shot impact was further simulated and analyzed by using the Taylor-type mean-field homogenization scheme. From the simulation results, the obtained conclusions can be drawn as follows:

  1. (1)

    The simulated stress–strain responses and texture evolutions by the developed crystal plasticity model in conjunction with the dislocation density-based hardening law accord well with the simulation results of the crystal plasticity model incorporated with the classic saturation-type phenomenological hardening law, and both the predictions of the two crystal plasticity models agree well with the experimental results whether for OFHC copper single crystals or for polycrystalline aggregate in general.

  2. (2)

    The calculations resulting from the Voronoi-type full-field homogenization are more close to the experimental results than the results of the Taylor-type mean-field homogenization for the polycrystalline aggregate of OFHC copper under the uniaxial compression and tension loads.

  3. (3)

    With the increase in grain number, the mechanical responses of the homogenized polycrystalline aggregate become stable gradually and closer to the experimental results for the Taylor-type mean-field model.

  4. (4)

    Both the dislocation density and the maximum texture intensity in the single shot impacted surface increase with the decrease in the impact angle from 90° to 70°.