1 Introduction

Crystal structures play an important role on the localized plastic flow in metals [1]. Variations in grain orientation and morphology within single-phase metals are among the key causes of strain inhomogeneity in sheet metals even under macroscopically uniform boundary conditions. Inhomogeneous microscopic strain field is the onset of macroscopic localized plastic flow. Free surface roughening and non-uniform deformation of grains at the microscopic level are among the commonly observed indications of such strain inhomogeneity [2]. Moreover, it is observed that the deformation not only varies amongst grains in a polycrystal, but also deformation within a grain is not uniform. Based on the grain orientation and surrounding conditions, the grain itself may divided to several regions which rotate differently after deformation [3]. The absence of heterogeneous microstructure considerations in macroscopic phenomenological models of plasticity makes them incapable of predicting the localized deformation. These theories, with the assumption that materials are homogenous, generally consider an artificial imperfection in the geometry for analysis of the plastic instability [4,5,6,7,8,9], such as the groove considered in Marciniak–Kuczynski procedure for sheet metal forming limits analysis [6, 10, 11].

Crystal plasticity formulation of a single crystal incorporates slips in each slip system of the crystal to map the plastic deformation of the material [12,13,14]. For analyzing polycrystalline metals, there are some homogenization methods such as Sachs, Taylor [15], and self-consistent [16] methods. In these methods, each material point considered to contain many grains with the overall texture characteristic of the crystalline aggregate. The characteristics of all material points are determined using averaging techniques. These averaging approaches, consequently, lead to a homogeneous model, similar to the conventional plasticity theories, which are also incapable of demonstrating heterogeneous strain field in the polycrystalline metals. It should be mentioned that such homogenization methods were successfully applied in determination of texture evolution [14, 17], shear band formation [18, 19], and forming limits diagrams [20] of sheets in textured metals. In these applications, an artificial imperfection is applied to the model to localize the deformation. It is evident that the effects of grain boundary and grain morphology on micro-scale strain distributions cannot be mapped in these methods.

With the aid of the crystal plasticity finite-element method, it is possible to follow the details of strain field in grain scale, and hence, the heterogeneous deformation in the polycrystalline aggregates [21,22,23]. Considering individual grain structure in models, similar to real microstructures, localized flow is likely to arise without the aid of the artificial imperfection. To overcome computational aspects, crystal plasticity finite-element method was sometimes implemented in 2D plane-strain or plane-stress simulation models [2, 18, 23, 24]. However, it has been shown by Simha et al. [25] that the state of stress in necking is three-dimensional, and two-dimensional analyses cannot satisfactorily model the localized plastic flow. Three-dimensional crystal plasticity finite-element simulations, on the other hand, are limited to a few number of grains. In this regard, several studies investigated effects of different finite-element modeling parameters on the micro- and macro-scale fields. Analyses demonstrated that the localized strains mostly occurred in areas close to grain boundaries [26,27,28,29,30,31,32]. Effects of second-phase material and inclusion also have been reported [33,34,35]. These simulations suffered from prediction of the locations where microvoids nucleate without considering damage effects in the analyses.

Extensive experimental investigations of heterogeneous strain and misorientation fields have been conducted on crystalline aggregates [1, 3, 33, 36,37,38,39,40,41,42,43]. Although the experimental methods are limited to the surface deformation measurements, they provide valuable insight into the strain field in grain scale. Chandrasekaran and Nygards [37] examined the misorientation and out-of-plane deformation of a single-phase ultra-low carbon steel with the aid of Electron Backscatter Diffraction (EBSD) and Atomic Force Microscopy (AFM) techniques. They showed that in the vicinity of grain boundaries, both rotation and deformation are increased. Using high-resolution Digital Image Correlation (DIC) measurement, Stinville et al. [38] gave a more-detailed understanding of the sub-grain straining process where the localized plastic strain was directly correlated with physical slip bands in relatively small applied macroscopic strain. They showed that without using high-resolution DIC measurement, the resulted strain fields would be more diffused and sharp localization of plastic strain along the slip traces cannot be captured. In another study, Lim et al. [44] showed that the slip lines observed in the early stages of the loading in the high-resolution DIC measurement were not captured by the employed crystal plasticity model for tantalum oligocrystal. Moreover, the crystal plasticity simulation was incapable in handling grain boundary effects.

Void nucleation sites have been the subject of interest for a wide experimental investigations in the grain scale. It is believed that in a high-purity, single-phase metal, void nucleation is associated with grain boundaries, triple junctions, twin interactions, or deformation-induced dislocation boundaries [41, 45,46,47]. Although the current models for single-crystal plasticity are used acceptably to capture localized deformation at grain boundaries, they have to be developed, so that they can be used in predicting deformation-induced dislocation boundaries [40]. Furthermore, most of the studies on predicting the sites of void nucleation rely on the strain and misorientation fields predicted by crystal plasticity, and damage theories are rarely applied in the analysis in conjunction with crystal plasticity finite-element method [48, 49].

Damage behavior of crystalline metals has been assessed on the basis of the crystal plasticity formulation incorporating scalar [48, 50,51,52] and anisotropic [49, 53, 54] damage models. Kim and Yoon [50] used a scalar damage model to investigate necking behavior of aluminum alloy in tensile loading using different evolution relations for the damage parameter. In the simulations, they focused on the macroscopic response of polycrystalline model with regular octahedron grain shape; each of them was discretized by different element sizes. Without imposing artificial imperfection in the models, the analyses reasonably predicted the post-necking softening and sudden drop in load-carrying capacity due to incorporating damage effects [55]. However, in their analysis due to using a scalar model, the damage evolutions in different directions are not considered. Moreover, the microscopic behavior of strain and damage at grain level have not been considered. In this paper, the focus is on the micromechanical distribution of anisotropic damage at grain-scale level. Zhao et al. [49] proposed a coupled model of crystal plasticity and anisotropic continuum damage mechanics to numerically investigate creep in Cr-based steel. In their model, a damage tensor is considered in the formulation of the crystal plasticity, and the damage evolution formulation is presented which is dependent on the history of damage and the state of stress.

In this paper, a rate-dependent coupled model of crystal plasticity and anisotropic continuum damage mechanics is developed. This model is extracted using thermodynamically consistent finite deformation theory. The damage evolution is considered to be dependent on the damage history, equivalent plastic strain, stress triaxiality, and Lode parameter. Using this formulation, the potential damage sites in a single-phase polycrystalline model are predicted. This formulation is implemented numerically in general-purpose finite-element analysis software Abaqus 6.14 using user material subroutine UMAT. Experimental tensile test of single crystal of stainless steel 316L [56] is utilized to identify model parameters. This model is employed to investigate damage initiation and growth in polycrystalline aggregate with random texture. The effect of grain boundaries and individual grain orientation is considered.

2 Constitutive model

2.1 Continuum damage mechanics

The underlying principle of continuum damage mechanics is embedded in the assumption of material degradation through strength and stiffness reduction due to existence of voids and micro-cracks. This results in the reduction of effective load-carrying surface areas inside the material. The effective Cauchy stress in damaged material for one-dimensional case \(\overline{\mathbf{T}}\) can be expressed as:

$$\overline{\mathbf{T}}=\frac{\mathbf{T}}{1-\mathscr{D}},$$
(1)

in which \(\mathbf{T}\) is Cauchy stress in the same imaginary undamaged body [6]. The scalar variable \(\mathscr{D}\) is called damage variable and defined as the proportion of defected area \({A}_{d}\) to the total area \({A}_{0}\):

$$\mathscr{D}=\frac{{A}_{d}}{{A}_{0}}.$$
(2)

The damage variable evolves from \(\mathscr{D}=0\) for intact area to \(\mathscr{D}=1\) for total rapture. In practice, rupture happens when the damage variable reaches a critical value much less than its theoretical value \(\mathscr{D}={\mathscr{D}}_{c}<1\). The effective stress tensor in a general three-dimensional body may be expressed as [7, 8]:

$$\overline{\mathbf{T}}={\mathbb{M}}\mathbf{T}.$$
(3)

The fourth-order tensor \({\mathbb{M}}={\mathbb{M}}(\mathcal{D})\) is called the damage effect tensor. The second-order tensor \(\mathcal{D}\) is the damage tensor. In the following, the kinematic and thermodynamics formulation of the rate-dependent crystal plasticity coupled with the anisotropic continuum damage mechanics for finite deformations is presented.

2.2 Kinematics of finite deformation crystal plasticity

In the finite deformation plasticity, the deformation gradient \(\mathbf{F}\) is decomposed as follows [57]:

$$\mathbf{F}={\mathbf{F}}^{e}{\mathbf{F}}^{p},$$
(4)

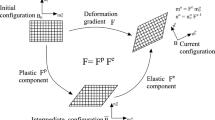
in which \({\mathbf{F}}^{e}\) is the part of deformation which includes stretch and rotation and is cited as the elastic part, and \({\mathbf{F}}^{p}\) is the part of deformation due to slide of slip planes in crystalline materials and is called the plastic part. A schematic representation of this multiplicative decomposition of the deformation gradient is depicted in Fig. 1. The velocity gradient \(\mathbf{L}\) is expressed as:

Fig. 1
figure 1

Multiplicative decomposition of deformation gradient

Full size image
$$\mathbf{L}=\dot{\mathbf{F}}{\mathbf{F}}^{-1}={{\dot{\mathbf{F}}}^{e}\mathbf{F}}^{e-1}+{\mathbf{F}}^{e}{{\dot{\mathbf{F}}}^{p}\mathbf{F}}^{p-1}{\mathbf{F}}^{e-1}={\mathbf{L}}^{e}+{\mathbf{F}}^{e}{\mathbf{L}}_{0}^{p}{\mathbf{F}}^{e-1}.$$
(5)

In this equation, \({\mathbf{L}}^{e}={\dot{\mathbf{F}}}^{e}{\mathbf{F}}^{e-1}\) is the velocity gradient for the elastic part of deformation, and \({\mathbf{L}}_{0}^{p}={\dot{\mathbf{F}}}^{p}{\mathbf{F}}^{p-1}\) is the velocity gradient for the plastic part of deformation which, for a single crystal, is given by [58]:

$${\mathbf{L}}_{0}^{p}=\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }{\mathbf{s}}_{0}^{\alpha }\otimes {\mathbf{m}}_{0}^{\alpha }=\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }{\mathbf{S}}_{0}^{\alpha },$$
(6)

where \({\mathbf{s}}_{0}^{\alpha }\) and \({\mathbf{m}}_{0}^{\alpha }\) are slip direction and slip normal of the slip system \(\alpha\) in the reference configuration, respectively. \(N\) is the total number of slip systems in the single crystal, \({\dot{\gamma }}^{\alpha }\) is the rate of shear strain in the slip system \(\alpha\), and \({\mathbf{S}}_{0}^{\alpha }={\mathbf{s}}_{0}^{\alpha }\otimes {\mathbf{m}}_{0}^{\alpha }\) is the Schmid tensor in the reference configuration. Thus, Eq. (5) can be rewritten as:

$$\mathbf{L}={\mathbf{L}}^{e}+\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }{\mathbf{S}}^{\alpha }={\mathbf{L}}^{e}+{\mathbf{L}}^{p},$$
(7)

where \({\mathbf{L}}^{p}=\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }{\mathbf{S}}^{\alpha }\). The Schmid tensor in the current configuration is defined as \({\mathbf{S}}^{\alpha }={\mathbf{s}}^{\alpha }\otimes {\mathbf{m}}^{\alpha }\). Relation between slip direction and slip normal in the current configuration with their associated reference vectors is:

$${\mathbf{s}}^{\alpha }={\mathbf{F}}^{e}{\mathbf{s}}_{0}^{\alpha },{\mathbf{m}}^{\alpha }={\mathbf{F}}^{e-T}{\mathbf{m}}_{0}^{\alpha }.$$
(8)

The velocity gradient can be decomposed into the symmetric \(\mathbf{D}\) and skew-symmetric \(\mathbf{W}\) parts:

$$\mathbf{L}=\mathbf{D}+\mathbf{W},$$
(9)

which are related to \({\mathbf{L}}^{e}\) and \({\mathbf{L}}^{p}\) as follows:

$$\mathbf{D}=\frac{1}{2}\left({\mathbf{L}}^{e}+{\mathbf{L}}^{eT}\right)+\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }\frac{1}{2}\left({\mathbf{S}}^{\alpha }+{\mathbf{S}}^{\alpha T}\right)={\mathbf{D}}^{e}+{\mathbf{D}}^{p}\mathbf{W}=\frac{1}{2}\left({\mathbf{L}}^{e}-{\mathbf{L}}^{eT}\right)+\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }\frac{1}{2}\left({\mathbf{S}}^{\alpha }-{\mathbf{S}}^{\alpha T}\right)={\mathbf{W}}^{e}+{\mathbf{W}}^{p},$$
(10)

where:

$$\begin{aligned}{\mathbf{D}}^{e}&=\mathrm{sym }{\mathbf{L}}^{e},{\mathbf{D}}^{p}=\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }\mathrm{sym} {\mathbf{S}}^{\alpha }\\{\mathbf{W}}^{e}&=\mathrm{skw }{\mathbf{L}}^{e}, {\mathbf{W}}^{p}=\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }\mathrm{skw} {\mathbf{S}}^{\alpha }.\end{aligned}$$
(11)

2.3 Energy balance and second law of thermodynamics

Ignoring thermal energy and assuming uniform temperature throughout the body, the internal and external powers must be equivalent [57]:

$$\begin{aligned} {\mathcal{W}}_{int}\left({\mathcal{P}}_{t}\right)&={\int}_{{\mathcal{P}}_{t}}\mathbf{T}:\mathrm{grad }\mathbf{v}\mathrm{d}v={\int}_{{\mathcal{P}}_{t}}\mathbf{T}:\mathbf{L}\mathrm{d}v\\ {\mathcal{W}}_{ext}\left({\mathcal{P}}_{t}\right)&={\int}_{{\partial \mathcal{P}}_{t}}\mathbf{t}\left(\mathbf{n}\right). \mathbf{v}\mathrm{d}a+{\int}_{{\mathcal{P}}_{t}}\mathbf{b}.\mathbf{v}\mathrm{d}v. \end{aligned}$$
(12)

The \({\mathcal{P}}_{t}\) is occupied by a part of the body at the current configuration. The vector \(\mathbf{b}\) is the body force per unit current volume and includes inertia forces. The traction on the part surface per unit area is shown by \(\mathbf{t}\left(\mathbf{n}\right).\) It is assumed that elastic and plastic responses are separable, and the internal power is rewritten as the summation of two separate elastic and plastic power:

$$\begin{aligned} {\mathcal{W}}_{int}\left({\mathcal{P}}_{t}\right)&={\int}_{{\mathcal{P}}_{t}}\mathbf{T}:\mathbf{L}\mathrm{d}v\\& ={\int}_{{\mathcal{P}}_{t}}\left({\mathbf{T}}^{e}:{\mathbf{L}}^{e}+{\sum }_{\alpha =1}^{N}{\pi }^{\alpha }{\dot{\gamma }}^{\alpha } \right)\mathrm{d}v, \end{aligned}$$
(13)

in which \({\mathbf{T}}^{e}\) is the elastic stress tensor work-conjugate to elastic velocity gradient \({\mathbf{L}}^{e}\), and \({\pi }^{\alpha }\) is the so-called plastic force work-conjugate to plastic shear strain rate \({\dot{\gamma }}^{\alpha }\) in each slip system \(\alpha\).

Using the frame indifference principle, it is concluded that:

$${\mathbf{T}}^{e}={\mathbf{T}}^{eT},\quad {\mathbf{T}}^{e*}={\mathbf{Q}}^{T}{\mathbf{T}}^{e}\mathbf{Q}.$$
(14)

The tensor \({\mathbf{T}}^{e*}\) is the elastic stress tensor in new frame and \(\mathbf{Q}\) is the frame rotation tensor. Thus, the elastic stress tensor is symmetric and frame-indifferent. Plastic forces \({\pi }^{\alpha }\) are scalar quantities and they are frame-invariant. Moreover, the principle of power balance dictates the following:

$${\mathbf{t}\left(\mathbf{n}\right)=\mathbf{T}}^{e}\mathbf{n}.$$
(15)

It is concluded from the above equation that \({\mathbf{T}}^{e}\) is the same as Cauchy stress tensor \({\mathbf{T}}^{e}=\mathbf{T}\). Furthermore, the plastic forces are obtained to be equal to resolved shear stress \({\tau }^{\alpha }\) in the direction of associated slip system:

$${\pi }^{\alpha }={\tau }^{\alpha }=\mathbf{T}:{\mathbf{S}}^{\alpha }.$$
(16)

Now, the elastic stress power can be rewritten as:

$$\begin{aligned} {\mathbf{T}}^{e}:{\mathbf{L}}^{e}&=\mathbf{T}:{\mathbf{L}}^{e}\\ &=\mathbf{T}:{\mathbf{D}}^{e}\\ &=\mathbf{T}:{{\mathbf{F}}^{e-T}\dot{\mathbf{E}}}^{e}{\mathbf{F}}^{e-1}\\ &={\mathbf{F}}^{e-1}\mathbf{T}{\mathbf{F}}^{e-T}:{\dot{\mathbf{E}}}^{e}\\ &={{J}^{-1}\mathbf{T}}_{RR}^{e}:{\dot{\mathbf{E}}}^{e} \end{aligned}$$
(17)

where \({\mathbf{T}}_{RR}^{e}\) is the elastic second Piola–Kirchhoff stress tensor:

$${\mathbf{T}}_{RR}^{e}=J{\mathbf{F}}^{e-1}\mathbf{T}{\mathbf{F}}^{e-T},$$
(18)

and \({\dot{\mathbf{E}}}^{e}\) is the rate of the elastic Green strain tensor \({\mathbf{E}}^{e}=\frac{1}{2}({\mathbf{F}}^{eT}{\mathbf{F}}^{e}-\mathbf{I})\):

$${\dot{\mathbf{E}}}^{e}={\mathbf{F}}^{eT}{\mathbf{D}}^{e}{\mathbf{F}}^{e}.$$
(19)

Second law of thermodynamics for mechanical system in single crystals in view of isothermal deformation with uniform temperature distribution is expressed locally in the following:

$${J}^{-1}\dot{\psi }-{{J}^{-1}\mathbf{T}}_{RR}^{e}:{\dot{\mathbf{E}}}^{e}-\sum_{\alpha =1}^{N}{\tau }^{\alpha }{\dot{\gamma }}^{\alpha }\le 0.$$
(20)

Here, \(\psi\) is the Helmholtz free energy per unit volume of structural space.

2.4 Constitutive relations

With determination of dependence of the Helmholtz free energy in Eq. (20) on the internal variables, it is possible to combine the large deformation plasticity of single crystals with continuum damage mechanics. Assuming isothermal deformation, free energy in a crystalline material without considering damage is considered to be dependent on the Green strain tensor \({\mathbf{E}}^{e}\). Moreover, the reference configuration is assumed to be natural in which the Helmholtz free energy has a local minimum. The consequence of this assumption is that the reference configuration is stress-free. In the continuum damage mechanics, based on the equivalency hypothesis of the strain energy, free energy also depends on the damage tensor \(\mathcal{D}\) in addition to Green strain tensor \({\mathbf{E}}^{e}\):

$$\psi =\widehat{\psi }\left({\mathbf{E}}^{e}, \mathcal{D}\right).$$
(21)

Substituting Eq. (21) into Eq. (20), and applying the time derivatives:

$$\left(\frac{\partial \widehat{\psi }}{\partial {\mathbf{E}}^{e}}-{\mathbf{T}}_{RR}^{e}\right):{\dot{\mathbf{E}}}^{e}+\frac{\partial \widehat{\psi }}{\partial \mathcal{D}}:\dot{\bf{\mathcal{D}}}-\sum_{\alpha =1}^{N}J{\tau }^{\alpha }{\dot{\gamma }}^{\alpha }\le 0.$$
(22)

For every admissible process, the following equation must satisfy:

$${\mathbf{T}}_{RR}^{e}=\frac{\partial \widehat{\psi }}{\partial {\mathbf{E}}^{e}}.$$
(23)

To derive the constitutive equations without violating the second law of the thermodynamics, the damage evolution takes the following form:

$$\mathbf{Y}=-\frac{\partial \widehat{\psi }}{\partial \bf{\mathcal{D}}}$$
$$\dot{\mathcal{D}}={\dot{\lambda }}_{\mathscr{D}}\frac{\partial {F}^{\mathscr{D}}}{\partial \mathbf{Y}}.$$
(24)

The potential function \({F}^{\mathcal{D}}\) is a function of damage driving force \(\mathbf{Y}\) and it is a convex function of \(\mathbf{Y}\). The following form is adopted from [59]:

$${F}^{\mathscr{D}}=\frac{1}{2}\mathbf{Y}:{\mathbb{J}}\mathbf{Y}-\mathrm{constant},$$
(25)

in which \({\mathbb{J}}\) is a fourth-order positive-definite tensor which assures that the following law will be always satisfied:

$$\mathbf{Y}:\dot{\mathcal{D}}\ge 0.$$
(26)

The tensor \({\mathbb{J}}\) takes the form of [60]:

$${\mathbb{J}}=\left(1-\zeta \right){\mathbb{I}}^{s}+\zeta \mathbf{I}\otimes \mathbf{I},$$
(27)

where \(\zeta\) is a material constant that represents the ratio of increments of second and third principal values of damage tensor to the first principal value in a uniaxial tensile loading [61]. The value of \(\zeta\) is related to the effective elastic modulus and Poisson ratio of isotropic elastic material [62], and is calculated based on experimental measurements of these variables for a damaged material. Its theoretical values lays between \(0\le \zeta \le 1;\) with \(\zeta =1\) corresponding to isotropic damage evolution [63]. The reported values for \(\zeta\) are very divers, but it mostly takes a value less than 0.6. This value is chosen to be \(\zeta =0.2\) in the following calculations. The fourth-order tensor \({\mathbb{I}}^{s}={\frac{1}{2}(\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}){\mathbf{e}}_{i}\otimes {\mathbf{e}}_{j}\otimes {\mathbf{e}}_{k}\otimes {\mathbf{e}}_{l}\) is symmetric unit tensor, and \(\mathbf{I}\) is a unit tensor of second order. The variable \({\dot{\lambda }}_{\mathcal{D}}\) is a positive variable known as damage multiplier which will be discussed further for rate-dependent models in Sect. 3. Substituting Eq. (25) into Eq. (24) gives:

$$\dot{\mathcal{D}}={\dot{\lambda }}_{\mathscr{D}}\frac{\partial {F}^{\mathscr{D}}}{\partial \mathbf{Y}}={\dot{\lambda }}_{\mathscr{D}}\frac{{\mathbb{J}}\mathbf{Y}}{2{Y}_{eq}}={\dot{\lambda }}_{\mathscr{D}}{\mathbf{N}}_{\mathscr{D}}.$$
(28)

Here, the tensor \({\mathbf{N}}_{\mathcal{D}}\) is normal to damage surface:

$${\mathbf{N}}_{\mathscr{D}}=\frac{{\mathbb{J}}\mathbf{Y}}{2{Y}_{eq}},$$
(29)

in which \({Y}_{eq}\) is defined as:

$${Y}_{eq}={\left(\frac{1}{2}\mathbf{Y}:{\mathbb{J}}\mathbf{Y}\right)}^\frac{1}{2}.$$
(30)

It is assumed that the Helmholtz free energy takes the following form:

$$\psi =\widehat{\psi }\left({\mathbf{E}}^{e}, \mathcal{D}\right)=\frac{1}{2}{\mathbf{E}}^{e}:\overline{\mathbb{C}}{\mathbf{E}}^{e},$$
(31)

in which [60]:

$${\overline{\mathbb{C}}}^{-1}\left(\mathcal{D}\right)={\mathbb{M}}^{T}\left(\mathcal{D}\right):{\mathbb{C}}^{-1}:{\mathbb{M}}\left(\mathcal{D}\right).$$
(32)

The fourth-order tensor \({\mathbb{C}}\) is the elastic tensor which is assumed to be constant isotropic tensor:

$${\mathbb{C}}=2\mu {\mathbb{I}}^{s}+\lambda \mathbf{I}\otimes \mathbf{I},$$
(33)

and components of the inverse of the damage effect tensor \({\mathbb{M}}^{-1}\) are taken to have the following relation [63, 64]:

$${M}_{ijkl}^{-1}={\frac{1}{2}(\Phi }_{ik}{\Phi }_{jl}+{\Phi }_{il}{\Phi }_{jk}),$$
(34)

where the tensor \({\varvec{\Phi}}={\Phi }_{ij}{\mathbf{e}}_{i} \otimes {\mathbf{e}}_{j}\) is a positive-definite tensor defined as:

$${\varvec{\Phi}}={\left(\mathbf{I}-\mathcal{D}\right)}^\frac{1}{2},$$
(35)

and \({\mathbb{M}}:{\mathbb{M}}^{-1}={\mathbb{I}}^{s}\) and \({M}_{ijkl}^{T}={M}_{klij}\). The power \(\frac{1}{2}\) in Eq. (35) is defined using spectral decomposition of tensor \(\left(\mathbf{I}-\mathcal{D}\right)\) [57, 59].

The damage driving force can be obtained:

$$\mathbf{Y}=-\frac{\partial \widehat{\psi }}{\partial \mathcal{D}}=-\frac{1}{2}{\mathbf{E}}^{e}:\frac{\partial \overline{\mathbb{C}}}{\partial \mathcal{D}}{\mathbf{E}}^{e}=-{\mathbf{E}}^{e}:\mathrm{sym}\left(\frac{\partial {\mathbb{M}}^{-1}}{\partial \mathcal{D}}:{\mathbb{C}}:{\mathbb{M}}^{-T}\right){\mathbf{E}}^{e},$$
(36)

in which:

$$\frac{\partial \overline{\mathbb{C}}}{\partial \mathcal{D}}=2\mathrm{sym}\left(\frac{\partial {\mathbb{M}}^{-1}}{\partial \mathcal{D}}:{\mathbb{C}}:{\mathbb{M}}^{-T}\right)=2\mathrm{sym}\left(\frac{\partial {\mathbb{M}}^{-1}}{\partial \mathcal{D}}:{\mathbb{M}}:\overline{\mathbb{C}}\right).$$
(37)

From Eq. (23), it could be concluded [57]:

$${\mathbf{T}}_{RR}^{e}=\frac{\partial \widehat{\psi }}{\partial {\mathbf{E}}^{e}}=\overline{\mathbb{C}}{\mathbf{E}}^{{\varvec{e}}}.$$
(38)

The only remaining constitutive part is the plastic part. In the rate-dependent crystal plasticity formulation utilized here, rate of the shear strain is expressed in terms of resolved shear stress in each slip system \(\alpha\) as:

$${\dot{\gamma }}^{\alpha }={\dot{\gamma }}_{0}{\left(\frac{{\tau }^{\alpha }}{{g}^{\alpha }}\right)}^\frac{1}{m}\mathrm{sgn}\left({\tau }^{\alpha }\right).$$
(39)

The constant \({\dot{\gamma }}_{0}\) is the reference flow rate and \(m\) is the rate-sensitivity parameter. The function \({g}^{\alpha }\) is the current strength of the slip system \(\alpha\) which evolves during slip of the slip systems in accordance with:

$${\dot{g}}^{\alpha }=\sum_{\beta =1}^{N}{h}_{\alpha \beta }\left|{\dot{\gamma }}^{\beta }\right|,$$
(40)

where \({h}_{\alpha \beta }\) is the hardening factor incorporating self and latent hardening of slip systems:

$${h}_{\alpha \beta }=\left[q+\left(1-q\right){\delta }_{\alpha \beta }\right]{h}_{\alpha \alpha }.$$
(41)

The function \({h}_{\alpha \alpha }\) is the self-hardening function, and the parameter \(q\) is an interaction constant between latent slip systems. Asaro [12] proposed hyper-secant function for self-hardening \({h}_{\alpha \alpha }\) which is a function of total shear strain in the slip system:

$${h}_{\alpha \alpha }={h}_{\alpha \alpha }\left(\gamma \right)={h}_{0}{\mathrm{sech}}^{2}\left|\frac{{h}_{0}\gamma }{{\tau }_{s}-{\tau }_{0}}\right|,$$
(42)

where \({h}_{0}\), the initial hardening modulus, \({\tau }_{0}\), the yield stress which equals the initial value of current strength, \({\tau }_{s}\), the break-through stress where large plastic flow initiates, are hardening parameters used to calibrate the single-crystal stress–strain curve.

Although the constitutive equation [Eq. (23)] is frame-invariant and convenient to express the rate form of the constitutive equations [14], the UMAT subroutine in Abaqus software uses Cauchy stress, and it is appropriate to express rate equations in terms of Cauchy stress. Substituting Eq. (23) into Eq. (18) and performing time derivative:

$$\dot{J}\mathbf{T}+J\dot{\mathbf{T}}=\dot{\overline{{\mathbf{F}}^{e}{\mathbf{T}}_{\mathrm{RR}}^{e}{\mathbf{F}}^{eT}}}={\dot{\mathbf{F}}}^{e}{\mathbf{T}}_{\mathrm{RR}}^{e}{\mathbf{F}}^{eT}+{\mathbf{F}}^{e}{\dot{\mathbf{T}}}_{\mathrm{RR}}^{e}{\mathbf{F}}^{eT}+{\mathbf{F}}^{e}{\mathbf{T}}_{\mathrm{RR}}^{e}{\dot{\mathbf{F}}}^{eT}$$
(43)

Recognizing that \({\dot{\mathbf{E}}}^{e}={\mathbf{F}}^{eT}{\mathbf{D}}^{e}{\mathbf{F}}^{e}\):

$${\dot{\mathbf{T}}}_{\mathrm{RR}}^{e}=\overline{\mathbb{C}}{\dot{\mathbf{E}}}^{e}+\dot{\overline{\mathbb{C}}}{\mathbf{E}}^{e}=\overline{\mathbb{C}}\left({\mathbf{F}}^{eT}{\mathbf{D}}^{e}{\mathbf{F}}^{e}\right)+\left(\frac{\partial \overline{\mathbb{C}}}{\partial \mathcal{D}}:\dot{\mathcal{D}}\right){\mathbf{E}}^{e}$$
(44)

and using \(\dot{J}=J \mathrm{tr}\mathbf{L}=J \mathrm{tr}\mathbf{D}\), it results in the following relation:

$$\dot{\mathbf{T}}+\left(\mathrm{tr}\mathbf{D}\right)\mathbf{T}={\mathbf{L}}^{e}\mathbf{T}+\mathbf{T}{\mathbf{L}}^{eT}+{J}^{-1}{\mathbf{F}}^{e}\left[\overline{\mathbb{C}}{\mathbf{F}}^{eT}{\mathbf{D}}^{e}{\mathbf{F}}^{e}+\left(\frac{\partial \overline{\mathbb{C}}}{\partial \mathcal{D}}:\dot{\mathcal{D}}\right){\mathbf{E}}^{e}\right]{\mathbf{F}}^{eT}.$$
(45)

Using \({\mathbf{L}}^{e}={\mathbf{D}}^{e}+{\mathbf{W}}^{e}\) and Eq. (17), the following equation is obtained:

$$\dot{\mathbf{T}}-{\mathbf{W}}^{e}\mathbf{T}+\mathbf{T}{\mathbf{W}}^{e}+\left(\mathrm{tr}\mathbf{D}\right)\mathbf{T}={\mathbf{D}}^{e}\mathbf{T}+\mathbf{T}{\mathbf{D}}^{e}+{J}^{-1}{\mathbf{F}}^{e}\left[\overline{\mathbb{C}}{\mathbf{F}}^{eT}{\mathbf{D}}^{e}{\mathbf{F}}^{e}+\left(\frac{\partial \overline{\mathbb{C}}}{\partial \mathcal{D}}:\dot{\mathcal{D}}\right){\mathbf{E}}^{e}\right]{\mathbf{F}}^{eT}.$$
(46)

The first three terms on the LHS of Eq. (46) is corotational rate of Cauchy stress based on axes that rotate at the lattice spin \({\mathbf{W}}^{e}\):

$${\stackrel{\nabla }{\mathbf{T}^{e}}}=\dot{\mathbf{T}}-{\mathbf{W}}^{e}\mathbf{T}+\mathbf{T}{\mathbf{W}}^{e}.$$
(47)

The first three term on the RHS of Eq. (46) can be combined into one term as follows:

$${\mathbf{D}}^{e}\mathbf{T}+\mathbf{T}{\mathbf{D}}^{e}+{J}^{-1}{\mathbf{F}}^{e}\left[\overline{\mathbb{C}}\left({\mathbf{F}}^{eT}{\mathbf{D}}^{e}{\mathbf{F}}^{e}\right)\right]{\mathbf{F}}^{eT}=\overline{\mathbb{L}}{\mathbf{D}}^{e},$$
(48)

where \(\overline{\mathbb{L}}\) is a fourth-order tensor whose components in indicial form are expressed as:

$$\begin{aligned} {\overline{L}}_{ijmn}&={J}^{-1}{F}_{iI}^{e}{F}_{jJ}^{e}{F}_{mM}^{e}{F}_{nN}^{e}{\overline{C}}_{IJMN}+{T}_{im}{\delta }_{jn}+{T}_{jn}{\delta }_{im}\\ &={J}^{-1}{F}_{iI}^{e}{F}_{jJ}^{e}{F}_{mM}^{e}{F}_{nN}^{e}{\overline{C}}_{IJMN}\\&+\frac{1}{2}({T}_{im}{\delta }_{jn}+{T}_{jn}{\delta }_{im}+{T}_{in}{\delta }_{jm}+{T}_{jm}{\delta }_{in}). \end{aligned}$$
(49)

To have a consistent relation, the minor symmetry of tensor \(\overline{\mathbb{L}}\) is taken into account in the second part of Eq. (49). The scalars \({\overline{C}}_{IJMN}\) are the components of effective elasticity tensor \(\overline{\mathbb{C}}\), and \({\delta }_{ij}\) is Kronecker delta. Thus, knowing that \(\mathrm{tr }\mathbf{D}=\mathrm{tr }{\mathbf{D}}^{e}\), Eq. (46) can be rewritten as:

$${\stackrel{\nabla }{\mathbf{T}^{e}}}+\left(\mathrm{tr}{\mathbf{D}}^{e}\right)\mathbf{T}=\overline{\mathbb{L}}{\mathbf{D}}^{e}+{J}^{-1}{\mathbf{F}}^{e}\left(\frac{\partial \overline{\mathbb{C}}}{\partial \mathcal{D}}:\dot{\mathcal{D}}\right){\mathbf{E}}^{e}{\mathbf{F}}^{eT}.$$
(50)

Using \({\mathbf{W}}^{e}=\mathbf{W}-{\mathbf{W}}^{p}\), \({\mathbf{D}}^{e}=\mathbf{D}-{\mathbf{D}}^{p}\) and Eq. (48), after some manipulations, Eq. (50) becomes:

$$\stackrel{\nabla }{\mathbf{T}}=\overline{\mathbb{L}}\mathbf{D}-\left(\mathrm{tr}\mathbf{D}\right)\mathbf{T}+{J}^{-1}{\mathbf{F}}^{e}\left(\frac{\partial \overline{\mathbb{C}}}{\partial \mathcal{D}}:\dot{\mathcal{D}}\right){\mathbf{E}}^{e}{\mathbf{F}}^{eT}-\sum_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }\left(\overline{\mathbb{L}}{\mathbf{A}}^{\alpha }+{\mathbf{B}}^{\alpha }\mathbf{T}+\mathbf{T}{\mathbf{B}}^{\alpha T}\right),$$
(51)

where:

$$\begin{aligned} {\mathbf{A}}^{\alpha }&=\mathrm{sym}{\mathbf{S}}^{\alpha }=\frac{1}{2}({\mathbf{S}}^{\alpha }+{\mathbf{S}}^{\alpha T})\\{\mathbf{B}}^{\alpha }&=\mathrm{skw}{\mathbf{S}}^{\alpha }=\frac{1}{2}\left({\mathbf{S}}^{\alpha }-{\mathbf{S}}^{\alpha T}\right), \end{aligned}$$
(52)

and \(\stackrel{\nabla }{\mathbf{T}}=\dot{\mathbf{T}}-\mathbf{W}\mathbf{T}+\mathbf{T}\mathbf{W}\) is the corotational rate of Cauchy stress. In Eq. (51), the effect of damage is incorporated by \(\overline{\mathbb{L}}\) and the third term on right-hand side \({J}^{-1}{\mathbf{F}}^{e}\left(\frac{\partial \overline{\mathbb{C}}}{\partial \mathcal{D}}:\dot{\mathcal{D}}\right){\mathbf{E}}^{e}{\mathbf{F}}^{eT}\).

3 Damage evolution

Damage evolution in metals has been shown to be dependent on the equivalent plastic strain \(p\), equivalent plastic strain rate \(\dot{p}\), stress triaxiality \(\eta\), and Lode parameter \(\xi\) [65, 66]. Since, in the present study, a rate-dependent model is applied for damage, the damage evolution considered to be in the form of:

$$\dot{\mathcal{D}}\propto {\left[\frac{p}{{\epsilon }_{d}^{p}}f\left(\eta ,\xi \right)\right]}^{n}{\mathbf{N}}_{\mathscr{D}},$$
(53)

where \(p\) is the cumulative equivalent plastic strain \(p={\int }_{0}^{t}\dot{p}dt\), and \(\dot{p}\) is defined as:

$$\dot{p}=\left|{\mathbf{D}}^{p}\right|={\left({\mathbf{D}}^{p}:{\mathbf{D}}^{p}\right)}^\frac{1}{2}.$$
(54)

Rate of damage tensor is considered to have a linear dependence on the equivalent plastic strain rate \(\dot{p}\). In addition, the macroscopic equivalent fracture stain is heavily dependent on the stress triaxiality \(\eta\) [67] and Lode parameter \(\xi\) [68]. These two parameters are defined as:

$$\begin{aligned} \eta &=\frac{{T}_{m}}{{T}_{e}}\\ \xi &=\frac{\frac{27}{2}\mathrm{det}\left(\mathbf{T}-{T}_{m}\mathbf{I}\right)}{{T}_{e}^{3}} \end{aligned}$$
$$\begin{aligned} {T}_{m}&=\frac{1}{3}\mathrm{tr}\mathbf{T}\\{T}_{e}&=\sqrt{\frac{3}{2}\left(\mathbf{T}-{T}_{m}\mathbf{I}\right):\left(\mathbf{T}-{T}_{m}\mathbf{I}\right)}. \end{aligned}$$
(55)

In consequence, the damage evolution assumed to be:

$$\dot{\mathcal{D}}={\dot{\lambda }}_{\mathscr{D}}{\mathbf{N}}_{\mathscr{D}}={\dot{p}\left({Y}_{eq}\frac{p}{{\epsilon }_{d}^{p}}f\left(\eta ,\xi \right)\right)}^{n}{\mathbf{N}}_{\mathscr{D}}.$$
(56)

Following the formulation given in Ref. [65], a similar phenomenological expression for damage evolution is used to incorporate stress triaxiality and Lode parameter in Eq. (56):

$$\dot{\mathcal{D}}={\dot{\lambda }}_{\mathscr{D}}{\mathbf{N}}_{\mathscr{D}}=\dot{p}{\left\{\frac{{Y}_{eq}}{A}\left[3\left|\eta \right|+\frac{A}{B}\left(1-{\xi }^{2}\right)\right]\frac{p}{{\epsilon }_{d}^{p}}\right\}}^{n}{\mathbf{N}}_{\mathscr{D}}.$$
(57)

To determine the parameters \(A\) and \(B\), pure tensile and pure shear tests are necessary. However, due to lack of experimental data on austenitic stainless steel 316L single crystal for these parameters, the ratio of \(\frac{A}{B}\) is chosen based on the values given in Ref. [65]. This value is approximately \(\frac{A}{B}=0.72\) for two different materials with different crystal structure; aluminum 2024-T351 (FCC crystal structure) and steel AISI 1045 (BCC crystal structure). Thus, the value of 0.72 is chosen for this ratio in the following calculations.

The main parameter influencing damage evolution is the equivalent plastic strain. However, the coefficient itself is affected by a factor which is a function of stress triaxiality and Lode parameter.

4 Numerical implementation

The proposed model in the previous sections is implemented in Abaqus finite-element software via user material subroutine (UMAT). The code is constructed on the basis of Huang’s crystal plasticity UMAT [69]. Besides adding damage relations to Huang’s UMAT, a thermodynamically consistent hyperelastic relation is used for the elastic part of the constitutive equations [70]. The main difference made by this assumption manifests itself in the calculation of elastic tensor relation in Eq. (48).

4.1 Incremental relations

The numerical procedure for implementing the formulations given in Sect. 2 is outlined in this section. A summary of the plastic and damage variable evolution laws are given in Table 1. Some new tensors are defined in this table to compact the relations.

Table 1 Evolution relations of the variables in the presented model
Full size table

All the variables are dependent, directly or through other relations, on the \(\Delta {\gamma }^{\alpha }\). The \(\Delta {\gamma }^{\alpha }\) is calculated by utilizing the following set of Eq’s [69, 71]:

$$\Delta {\gamma }^{\alpha }=\Delta t\left[\left(1-\theta \right){\dot{\gamma }}_{t}^{\alpha }+\theta {\dot{\gamma }}_{t+\Delta t }^{\alpha }\right],$$
(58)

in which \(\Delta {\gamma }^{\alpha }={\gamma }^{\alpha }\left(t+\Delta t\right)-{\gamma }^{\alpha }(t)\). The parameter \(\theta\) can vary from \(0\) to \(1\), with \(\theta =0\) corresponding to forward (explicit) Euler time integration scheme and \(\theta =1\) corresponding to backward (implicit) Euler time integration scheme. It is shown in [71] that the stable solution is obtained for values of \(\theta\) in the range of 0.5 to 1. The rate of the plastic shear strain \({\dot{\gamma }}_{t+\Delta t }^{\alpha }\) can be expressed in the following form:

$${\dot{\gamma }}_{t+\Delta t }^{\alpha }={\dot{\gamma }}_{0}{\left(\frac{{\tau }^{\alpha }+\Delta {\tau }^{\alpha }}{{g}^{\alpha }+\Delta {g}^{\alpha }}\right)}^\frac{1}{m}\mathrm{sgn}\left({\tau }^{\alpha }+\Delta {\tau }^{\alpha }\right),$$
(59)

The increment \(\Delta {g}^{\alpha }\) is a direct function of the increments \(\Delta {\gamma }^{\beta }\) as a consequence of Eq. (40). In addition, the increment of the shear stress \(\Delta {\tau }^{\alpha }\) is also a function of \(\Delta {\gamma }^{\beta }\) through \({\mathbf{D}}^{e}\Delta t\) and \(\Delta \mathcal{D}\) relations. The elastic part of rate of strain:

$${\mathbf{D}}^{e}\Delta t=\mathbf{D}\Delta t-{\mathbf{D}}^{p}\Delta t=\Delta {\varvec{\upepsilon}}-\sum_{\beta =1}^{N}{\Delta \gamma }^{\beta }\mathrm{sym} {\mathbf{S}}^{\beta }.$$
(60)

The \(\Delta {\varvec{\upepsilon}}=\mathbf{D}\Delta t=\mathrm{DSTRAN}\) is known and provided by Abaqus at time \(t+\Delta t\). Moreover, \(\Delta \mathcal{D}\) is a function of \(\Delta p\) which is also dependent on \(\Delta {\gamma }^{\beta }\) through Eqs. (54) and (11). Thus, all the increments specified in Eq. (57) are functions of \(\Delta {\gamma }^{\beta }\). Substituting Eq. (57) into Eq. (58), the following equation is obtained:

$$\Delta {\gamma }^{\alpha }-\Delta t\left(1-\theta \right){\dot{\gamma }}_{t}^{\alpha }-\Delta t\theta {\dot{\gamma }}_{0}{\left(\frac{{\tau }^{\alpha }+\Delta {\tau }^{\alpha }}{{g}^{\alpha }+\Delta {g}^{\alpha }}\right)}^\frac{1}{m}\mathrm{sgn}\left({\tau }^{\alpha }+\Delta {\tau }^{\alpha }\right)=0.$$
(61)

This equation is solved using Newton–Raphson procedure to obtain \(\Delta {\gamma }^{\beta }\) in time \(t+\Delta t\). Having the increment of the plastic shear strains, it is a simple updating procedure to obtain all other variables at time \(t+\Delta t\). These variables include stress tensor and other required variables which are saved as state variables in the UMAT. A flowchart of showing the UMAT algorithm is demonstrated in Fig. 2.

Fig. 2
figure 2

The numerical procedure in the Written UMAT in Abaqus Software (*state variables include: \({\gamma }^{\alpha }\), \({\tau }^{\alpha }\), \({g}^{\alpha }\), \(p\), \({\mathbf{s}}^{\alpha }\), \({\mathbf{m}}^{\alpha }\), \(\mathcal{D}\), \({\mathbf{F}}^{e}\), \({\mathscr{D}}_{I}\), \({\mathscr{D}}_{II}\), \({\mathscr{D}}_{III}\), Schmid factors)

Full size image

4.2 Parameters’ identification

The single-crystal tensile stress–strain curve presented in Ref. [56] is used to calibrate the crystal plasticity and damage parameters. Calibrating all these parameters based on solely a tensile curve is not a normal procedure. However, due to lack of experimental data on damage evolution of single crystals, some assumption has been made to evaluate the parameters. Moreover, the suggested procedure of testing and calibrating the parameters of damage evolution and slip hardening of the model has been presented in the references given in their respective sections [65, 70]. The assumptions made here are now discussed. It is assumed that damage evolution at early stages of plastic deformation is small. This assumption is in accordance with the experimental results in which the damage is not effective until reaching a strain threshold [72, 73]. Using Eq. (53), it is possible to diminish, not entirely ignore, the effect of damage on the single-crystal tensile response prior to the strain \({\epsilon }_{d}^{p}\) by selecting a sufficiently large value for the parameter \(n\). Moreover, the increase in damage at final stages of the loading subsequent to \({\epsilon }_{d}^{p}\) can be captured using this relation [74]. Thus, the crystal plasticity hardening parameters can be calibrated based on the tensile behavior before the strain value \({\epsilon }_{d}^{p}\), and damage evolution parameters are calibrated based on the tensile behavior after the strain value \({\epsilon }_{d}^{p}\) in Eq. (52). The crystal plasticity parameters can be calibrated, so that the numerical stress–strain curve and experimental curve before necking coincides. The damage parameter can be chosen, so that the numerical curve follows the experimental one after necking. The model used to calibrate the parameters is shown in Fig. 3. This model is prepared based on data given in [56]. The displacement boundary conditions are applied to the end surfaces of the model in cylinder axis direction. On the diameter of the fixed end, there also applied zero displacement condition and the center of the face is fixed to prevent rigid body motion. The model is meshed with total number of 850 linear brick elements C3D8.

Fig. 3
figure 3

Model used to calibrate single-crystal parameters according available data in [56]. Left: applied displacement boundary conditions. Right: meshed model

Full size image
Fig. 4
figure 4

Graph showing the effect of damage in the crystal plasticity analysis on the stress–strain curve for a single crystal [56]

Full size image

The identified values for damage evolution and slip hardening parameters are presented in Table 3. These values are calculated by taking \({\dot{\gamma }}_{0}=0.001\) and \(m=20.0\) [75]. The elastic properties of the 316L material are assumed to be anisotropic with elastic tensor components given in Table 2 for its FCC crystal structure. The interaction constant \(q\) is taken to be equal to unity \(q=1.4\).

Table 2 Elasticity tensor components of the 316L single crystal [76]
Full size table
Table 3 Calibrated values of crystal plasticity and damage parameters for a single-crystal stainless steel 316L
Full size table

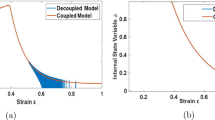
The resulted stress–strain curve is compared to the experimental one in Fig. 3. There also depicted is a curve which is calculated using the crystal plasticity without the damage effect taken into account. It is obvious that although the curve without damage shows a softening behavior, the drop of the experimental curve after necking is not captured and the results begin to deviate near to necking point of the experimental curve (Table 3; Fig. 4).

5 Results and discussion

5.1 Principal values of damage growth with increasing equivalent plastic strain

Figure 5 shows how principal damage values increase with loading. As seen, the first principal component of the damage tensor \({\mathscr{D}}_{I}\) starts to grow rapidly approximately at \({\epsilon }_{d}^{p}=0.38\). The two other principal components of the damage tensor coincide with each other and the growths are similar in manner to the growth of \({\mathscr{D}}_{I}\) but different in their rates. The growth of the second and third principal compared to the first principal is dependent on the value chosen for the parameter \(\zeta\) which in this case is \(\zeta =0.86\) [77]. It is apparent in the figure that at large strains, the ratio of \({\mathscr{D}}_{II}\) and \({\mathscr{D}}_{III}\) to \({\mathscr{D}}_{I}\) is about 0.86. The critical damage value, in which the numerical stress–strain curve reaches the break point on the experimental curve, is \({\mathscr{D}}_{c}=0.18\).

Fig. 5
figure 5

Variations of three principal damage components in uniaxial test model of 316L single crystal

Full size image

5.2 Damage distribution in a polycrystalline model

To investigate the application of the presented model in the prediction of damage initiation and growth in FCC polycrystalline aggregates, a 316L foil model with random grain shape and orientation is prepared. Dimensions of the model are \(4 \mathrm{mm}\times 2\mathrm{mm}\times 0.25\mathrm{mm}\). As shown in Fig. 6a, the model is discretized with 8-node linear brick elements C3D8 and uniaxial tensile loading is imposed on the model. Since, in the finite-element crystal plasticity analysis, the strains may increase up to 2.0, it is found convenient to use models with the initial well-shaped mesh elements. These elements endure more deformation without failing the analysis due to the excess distortion. As it is shown in Fig. 6b, the model contains 40 grains with different volumes from 1 (in grain number 10) to 750 (in grain number 28) elements per grain. In a recent study by the authors [70], it is demonstrated that increasing the average number of elements per grain results in softer behavior of the model. With the average number of elements per grain greater than 200, the differences between results of the similar models become less than 1%. In this study, the average number of elements per grain is 320 which is considered to have a negligible influence on the overall stress and strain distributions in the model.

Fig. 6
figure 6

A polycrystalline foil model with random grain shape and orientation. a Meshed model; b assigned grain numbers

Full size image

Maximum values of grains Schmid factor are displayed in Fig. 7a for back view (\(-z\) axis) of the model.

Fig. 7
figure 7

The back view of the polycrystalline model: a Schmid factor of each grain before loading, b equivalent plastic strain \(p\), and c first principal value of the damage tensor \({\mathscr{D}}_{I}\)

Full size image

From Eq. (55), it is obvious that the damage tensor evolution is dependent on the evolution of equivalent plastic strains as well as stress triaxiality and Lode parameter. Thus, it is expected that in a polycrystalline aggregate, damage components vary across the model as a result of the non-uniform distribution of these parameters. The distribution of the equivalent plastic strain \(p\) and first principal value of the damage tensor \({\mathscr{D}}_{I}\) at macroscopic engineering strain 17% are shown in Fig. 7b, c, respectively. At the first glance, it can be noticed from Fig. 7b that the regions of high magnitude of the equivalent plastic strains arise in the vicinity of grain boundaries. In addition, they are more severe at triple junctions. Strain distribution in this polycrystalline models is affected by the loading conditions of grains, their shapes, and relative positions in the model.

The distribution of the first principal value of the damage tensor \({\mathscr{D}}_{I}\) is shown in Fig. 7c. The \({\mathscr{D}}_{I}\) distribution is similar to the equivalent plastic strain distribution; in the regions with high amplitude of the equivalent plastic distribution, \({\mathscr{D}}_{I}\) is more severe than other regions. In the single-crystal simulation implemented in the previous section, at the point of break, the amount of \({\mathscr{D}}_{I}\) reached the amount of ~ 0.18. Thus, the values above 0.18 are greyed out in Fig. 7c to demonstrate the potential sites of failure and void nucleation. Beside some grain boundaries and triple junctions, there are other spots inside grains which \({\mathscr{D}}_{I}\) grows considerably. For instance, in grain 23, a region with high values of \({\mathscr{D}}_{I}\) can be observed. The grains with this condition are mostly located at the boundaries of the polycrystalline model. Since these grains experience a different surrounding conditions, damage occurrence inside the grains could not be generalized.

Considering adjacent grains, the grains with larger Schmid factor suffer more damage in the sense that the high-magnitude damage \({\mathscr{D}}_{I}\) covers more volume in these grains. For instance, note the potential void nucleation area in the grains 26, 31, 24, and 25 with compared to their adjacent grains. Although the adjacent grains are affected by damage, literally, all damaged areas are concentrated in the nearby grains with higher Schmid factor. The local softening effect of damage is partly a cause for damage growth in a specific region. When, in a point at the grain boundaries, damage begins to grow, there will be an influential softening effect which cause the near vicinity of the softened area undergo more loads. This phenomenon adds on the individual grain orientation effects and they lead to damage growth happens mostly inside only one grain between two neighboring grains. In general, initially, comparative low Schmid factor grains, for example grains 22 and 28, which are adjacent to high Schmid factor grains endure lower amount of plastic deformation and damage.

One interesting feature of the damage distribution arises in the colony of grains with the same Schmid factor. Consider grains 28, 29, 33, and 36 as a colony of grains with comparatively low Schmid factor (colored in shades of green). Another colony with high Schmid factor next to this colony is comprised four grains 33, 24, 25, and 40 (colored in shades of red). Regarding the amount of damage, these two adjacent colonies receive different effects from loading. The colony with higher values of Schmid factors suffers more from damage which is apparent from Fig. 7c. For the other side, the colony remains almost intact by the damage.

The void nucleation in grains microstructure begins at early stages of plastic deformation and before reaching the macroscopic rupture strain. In the case of the model presented, it is observed that at 17% of macroscopic strain, and even at values less than it, multiple sites of damage at grain boundaries nucleate and grow. This strain is smaller than the macroscopic strain at which a macroscopic rupture occurs. As predicted by the presented model, the microscopic void nucleation mechanism is clearly inter-granular mechanism. In this mechanism, the voids nucleate at grain boundaries. In trans-granular failure mechanisms, on the other hand, there exist particles which trigger the void nucleation inside grains. Incorporation of second-phase particles needs more complicated models which is not considered here. However, the coupled model can be used to investigate stress and strain state around the second-phase particles inside grains. As mentioned earlier, the voids nucleated at grain boundaries mostly grow alongside grain boundaries and toward inside higher Schmid factor grains.

6 Conclusion

In this study, a thermodynamically consistent anisotropic continuum damage mechanics model coupled with the crystal plasticity theory was presented. The finite-element analysis of the model was implemented in Abaqus/Standard software using a user material subroutine (UMAT). The damage evolution was considered to be dependent on the equivalent plastic strain, stress triaxiality, and Lode parameter. Aside from capturing the drop in the stress–strain curve of 316L single crystal after necking, the incorporated damage model made it possible to see the damage evolution in different directions. Moreover, the presented formulation was employed to investigate damage initiation sites in a three-dimensional 316L polycrystalline aggregate foil model with randomly sized and oriented grains. In grains with high Schmid factor, the damage grows rapidly into the interior of the grains. On the other hand, for neighboring grains with comparatively lower Schmid factor, the initial damage on the boundary virtually remains intact. In addition to damage growth in single grains, grains colonies with close Schmid factors behave in the similar manner. In other words, damage growth in the high Schmid factor colonies is more noticeable than the low Schmid factor colonies. The presented formulation is able to capture the damage initiation and grow in a polycrystalline aggregate. One of the challenges of using this model was the parameters’ calibration. Damage and crystal plasticity parameters depend on several microscopic characteristics of the crystalline material. In the absence of such microscopic characteristics’ measurements, the parameters are calibrated using macroscopic characteristics.