Abstract
Image registration under small displacements is the keystone of several image analysis tasks such as optical flow estimation, stereoscopic imaging, or full-field displacement estimation in photomechanics. A popular approach consists in locally modeling the displacement field between two images by a parametric transformation and performing least-squares estimation afterward. This procedure is known as “digital image correlation” in several domains as in photomechanics. The present article is part of this approach. First, the estimated displacement is shown to be impaired by biases related to the interpolation scheme needed to reach subpixel accuracy, the image gradient distribution, as well as the difference between the hypothesized parametric transformation and the true displacement. A quantitative estimation of the difference between the estimated value and the actual one is of importance in application domains such as stereoscopy or photomechanics, which have metrological concerns. Second, we question the extent to which these biases could be eliminated or reduced. We also present numerical assessments of our predictive formula in the context of photomechanics. Software codes are freely available to reproduce our results. Although this paper is focused on a particular application field, namely photomechanics, it is relevant to various scientific areas concerned by image registration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Two images \({\mathcal {I}}\) and \({\mathcal {I}}'\) of a scene being given, image registration consists in estimating a bidimensional displacement field \({\varvec{\phi }}\) which permits to map pixels from one image to the corresponding pixels in the other image. Assuming that corresponding pixels have the same intensity, for any pixel \({{\mathbf {x}}}\), the following relation thus holds: \({{\mathcal {I}}}({{\mathbf {x}}}) = {{\mathcal {I}}}'({{\mathbf {x}}}+{\varvec{\phi }}({{\mathbf {x}}})) \). When small displacements are sought (typically below one pixel), the displacement field is often estimated locally by imposing the preceding relation over corresponding subsets of the domains of \({\mathcal {I}}\) and \({\mathcal {I}}'\). While image registration is the very first step of many image analysis tasks, the case of small amplitude displacements is of particular interest in optical flow estimation [11, 12], disparity estimation in stereoscopic imaging [9, 31, 33, 34], or extensometry in experimental mechanics [20, 43], to mention some representative examples. Although we will focus our presentation on displacement estimation in photomechanics, which is a branch of experimental solid mechanics dedicated to full-field measurements from images, many aspects of the problem discussed in this paper are of general interest. However, in this latest application domain, no occlusions are present, in contrast to stereoscopic imaging or optical flow estimation.
1.1 Problem Statement
In photomechanics, digital image correlation (DIC) [20, 43] is of prime interest to measure displacement fields on the surface or in the bulk of materials subjected to thermo-mechanical loads. The term DIC equally refers to methods which are based on cross-correlation (CC), on sum of squared differences (SSD), or on normalized CC or SSD as well [27]. DIC methods are based on two images \({\mathcal {I}}\) and \({{\mathcal {I}}}'\) of the surface of the specimen taken before and after deformation, respectively. The specimen shall be marked beforehand with a contrasted random pattern, called a speckle pattern, as shown in Sect. 3. The aim is to retrieve the displacement field \({{\mathbf {u}}}\) such that for any \({{\mathbf {x}}}\), \(\mathcal{I}({{\mathbf {x}}})={{\mathcal {I}}}'({{\mathbf {x}}}+{{\mathbf {u}}}({{\mathbf {x}}}))\). Strain fields are then deduced by differentiation. These fields are used to observe various phenomena, which occur on the surface of deformed specimens, and which are revealed by displacement or strain heterogeneities. They can eventually be used to identify parameters governing constitutive equations, which are then used to design structural components [19]. It is therefore of prime importance to retrieve displacement and strain maps affected by the lowest possible measurement errors, so that the resulting identified parameters are themselves as reliable as possible. The displacement field usually features values well-below one pixel. The so-called local subset-based DIC consists in registering \({{\mathcal {I}}}'\) on \({\mathcal {I}}\) by optimizing some criterion as the above-mentioned CC or SSD over subsets of the image domains. These criteria being equivalent under mild assumptions [27], we focus on the sum of squared differences (SSD), which is also used in block matching for stereoscopic imaging [31]. Since \(\mathcal I\) and \({{\mathcal {I}}}'\) are known only at integer pixel coordinates and since subpixel accuracy of \({{\mathbf {u}}}\) is sought, interpolation is required. In order to estimate the displacement \({{\mathbf {u}}}\) at a pixel \({{\mathbf {x}}}\), the following SSD, defined over a subset \(\varOmega _{{\mathbf {x}}}\) of the image of the specimen surface centered at \({{\mathbf {x}}}\), is minimized with respect to a displacement \({\varvec{\phi }}^{{\mathbf {x}}}\) defined over \(\varOmega _{{\mathbf {x}}}\):
Here, \(\widetilde{{{\mathcal {I}}}'}\) denotes a continuous interpolation of \({{\mathcal {I}}}'\) (\({{\mathcal {I}}}'\) being sampled at integer coordinates), and \(\varOmega _{{\mathbf {x}}}\) is a set of M pixels \(({{\mathbf {x}}}_1,\dots ,{{\mathbf {x}}}_M)\). Minimization is performed with respect to a displacement field \({\varvec{\phi }}^{{\mathbf {x}}}\) expected to approximate the actual unknown displacement \({{\mathbf {u}}}\) over \(\varOmega _{{\mathbf {x}}}\). We do not consider a weighted SSD criterion, but the formulas in the remainder of the paper would easily adapt.
An estimation \({\varvec{\phi }}({{\mathbf {x}}})\) of the displacement field over the whole specimen surface is eventually obtained by taking, at any pixel \({{\mathbf {x}}}\), the value of \({\varvec{\phi }}^{{\mathbf {x}}}\) at the center of the subset \(\varOmega _{{\mathbf {x}}}\).
Displacement estimation is an ill-posed problem because of under-determination. Indeed, at each pixel, a bidimensional displacement must be retrieved. Moreover, information is lost from the component of the displacement orthogonal to the image gradient. This is the so-called aperture problem [11, 12]. Consequently, in experimental mechanics (and in general applications as well [7]), the displacement \({\varvec{\phi }}^{{\mathbf {x}}}\) is usually sought as the linear combination of N shape (or basis) functions \(({\varvec{\phi }}_j)_{1\le j \le N}\), such that the parameters \((\lambda _j)_{1\le j \le N}\) minimize
It may be noted that classic ways to deal with the aperture problem are either to consider a constant displacement \({\varvec{\phi }}^{{\mathbf {x}}}\) over \(\varOmega _{{\mathbf {x}}}\) and a first-order Taylor expansion of the preceding equation, giving fast approaches à la Lucas-Kanade [25], or to consider global smoothing with regularization constraints, giving approaches à la Horn-Schunck [21]. In experimental mechanics, it is often preferred to numerically minimize SSD because an accurate estimation of \({\varvec{\phi }}\) is required and setting the hyperparameter involved by regularization is not an easy task, which rules out such approaches.
From now on, we assume that \({{\varvec{\varLambda }}} = (\lambda _1,\dots ,\lambda _N)^T \) minimizes the expression of SSD given by Equation 2, and \({\varvec{\phi }}^{{\mathbf {x}}}=\sum _{j=1}^N \lambda _j {\varvec{\phi }}_j\) denotes the corresponding local displacement field. For example, as recalled in [5], zero-order shape functions are such that \(N=2\) and \({\varvec{\phi }}_1({{\mathbf {x}}}) = (1\; 0)^T \), \({\varvec{\phi }}_2({{\mathbf {x}}}) = (0 \;1)^T \), giving a constant \({\varvec{\phi }}^{{\mathbf {x}}}\) over \(\varOmega _{{\mathbf {x}}}\). First-order shape functions are such that \(N=6\) and functions \({\varvec{\phi }}_3({{\mathbf {x}}}) = (x\; 0)^T \), \({\varvec{\phi }}_4({{\mathbf {x}}}) = (0 \;x)^T \), \({\varvec{\phi }}_5({{\mathbf {x}}}) = (y \;0)^T \), \({\varvec{\phi }}_6({{\mathbf {x}}}) = (0\; y)^T \) are added to \({\varvec{\phi }}_1\) and \({\varvec{\phi }}_2\). Second-order shape functions are such that \(N=12\) and embed the following additional functions: \({\varvec{\phi }}_7({{\mathbf {x}}})=(x^2,0)^T\), \({\varvec{\phi }}_8({{\mathbf {x}}})=(xy,0)^T\), \({\varvec{\phi }}_9({{\mathbf {x}}})=(y^2,0)^T\), \({\varvec{\phi }}_{10}({{\mathbf {x}}})=(0,x^2)^T\), \({\varvec{\phi }}_{11}({{\mathbf {x}}})=(0,xy)^T\), \({\varvec{\phi }}_{12}({{\mathbf {x}}})=(0,y^2)^T\).
The origin of the axis is often the center of the subset \(\varOmega _{{\mathbf {x}}}\), so that the displacement estimated at \({{\mathbf {x}}}\) by minimizing the SSD criterion over \(\varOmega _{{\mathbf {x}}}\) is given by \({\varvec{\phi }}({{\mathbf {x}}})={\varvec{\phi }}^{{\mathbf {x}}}(0,0)=(\lambda _1,\lambda _2)^T\) for any order. Moreover, one can see that first- and second-order shape functions satisfy \(\partial {\varvec{\phi }}^{{\mathbf {x}}}/ \partial x (0,0)= (\lambda _3,\lambda _4)^T\) and \(\partial {\varvec{\phi }}^{{\mathbf {x}}}/ \partial y(0,0) = (\lambda _5,\lambda _6)^T\).
The displacement field is supposed to be smooth enough so that approximating \({{\mathbf {u}}}\) by \({\varvec{\phi }}\) makes sense. In particular, no occlusions (an object hide the part of another object in stereoscopy) or missing parts (as a mechanical fracture) are allowed. Displacement is locally invertible if the mapping from \({{\mathbf {x}}}\) to \({{\mathbf {x}}}+{\varvec{\phi }}({{\mathbf {x}}})\) has a non-singular Jacobian matrix, thanks to the inverse function theorem. In the case of polynomial shape functions, the determinant of this matrix at the center of the subset is \((1+\lambda _3)(1+\lambda _6) -\lambda _4\lambda _5 = 1+\lambda _3+\lambda _6 + \lambda _3\lambda _6-\lambda _4\lambda _5\). Of course, zero-order shape functions (corresponding to simple translations) give invertible displacement since, in this case, \(\lambda _i=0\) for \(i\in \{3,4,5,6\}\) and the determinant is non-zero. Higher-order shape functions also yield locally invertible displacement fields if the \(\lambda _i\)’s are small with respect to 1, which holds true under the classic small strain hypothesis in photomechanics.
1.2 Motivation
The motivation of our work is the observation that, in photomechanics, displacement fields are often impaired by spurious small fluctuations. These fluctuations are often believed, in this community, to be caused by sensor noise, interpolation bias, or the numerical scheme minimizing the DIC criterion. Nevertheless, recent works consider the random marking on the surface of the specimen [14, 24, 45], in addition to the aforementioned causes, the authors of [10] coining the term pattern-induced bias. From a different perspective, it is known that the local parametric estimation of a displacement field is intrinsically biased, the retrieved displacement being merely the convolution of the true displacement by a Savitzky–Golay filter [36]. In this latter approach, specimen marking does not play any role, which is contradictory with the presence of a pattern-induced bias. The main motivation of this study is thus to see if this contradiction can be removed.
1.3 Contributions
The goal of the present paper is to provide a theoretical basis for these different viewpoints and thus to show that they can coexist. More precisely, we shall give the relation between the retrieved \({\varvec{\varLambda }}\) (thus, the retrieved displacement \({\varvec{\phi }}\)) and the actual unknown displacement \({{\mathbf {u}}}\) over any subset \(\varOmega _{{\mathbf {x}}}\). By revisiting papers dealing with disparity estimation in stereo-imaging [1, 9, 31, 34], we show in Sect. 2 that the estimation of \({\varvec{\varLambda }}\) is mainly the sum of two terms, namely a term depending on the unknown displacement \({{\mathbf {u}}}\) and the approximation induced by the shape functions, and a term caused by the interpolation error. We propose a characterization of these terms, which actually depend on the gradient distribution over the imaged specimen. This unifies the points of view of stereoscopy (fattening effect) and photomechanics (pattern-induced bias). In Sect. 3, numerical experiments validate the theoretical developments and assess their limitations. To limit the size of the paper, we discuss how sensor noise propagates from the images to the estimated displacement field in a separate companion research report [42].
1.4 Related Work
Stereoscopy and photomechanics share the same objective, namely estimating displacement fields very accurately. The proposed contribution echoes different papers from these research areas.
First, the proposed approach relies on the calculation presented in [31] (and, to some extent, in [9]) in the context of disparity estimation in stereo-imaging. In this research field, disparity plays the role of the displacement field considered in the present paper. On the one hand, disparity may be estimated at any pixel as a constant monodimensional displacement between small patches extracted from the stereo image pair. Indeed, disparity is collinear with a given direction, since images are rectified so that the epipolar lines are parallel to each other. In this context, the authors of [9, 31] give predictive formulas for quantifying the fattening effect, i.e., the bias in disparity estimation caused by image gradient distribution. On the other hand, in experimental mechanics, local non-constant displacements are estimated as linear combinations of shape functions and they are not constrained to be collinear with a given direction. The main difference with disparity is that displacement fields are usually smooth and have tiny fluctuations, the strain components (defined from the partial derivatives of the displacement) being below \(10^{-2}\) for many materials and load intensity. Gradient distribution is also likely to affect displacement estimation, giving pattern-induced bias. A first attempt at characterizing this bias in photomechanics is available in [24].
In addition to pattern-induced bias or fattening effect, the interpolation scheme required for registration is certainly a source of error. It is a common assumption in stereo-imaging that the input images satisfy Shannon–Nyquist sampling conditions, cf. [9, 31, 34]. This involves that continuous images can be perfectly interpolated from the Fourier coefficients without any interpolation bias. However, it is mentioned in [29, 40] that aliasing, although hardly noticeable to the naked eye on the raw input images, may strongly affect the estimated displacement and strain fields in photomechanics. This motivates the use of bilinear or bicubic interpolation schemes in this field [43] instead of Fourier interpolation. The drawback is that \(\widetilde{{{\mathcal {I}}}'}\) matches \({{\mathcal {I}}}'\) only at integer pixel coordinates: non-integer pixel coordinates are thus affected by interpolation error, as numerically illustrated in [6]. Seeing interpolation as a convolution filter, the authors of [35] have proposed a characterization of the interpolation-induced bias giving rise to the famous “S-shape function”. The authors of [38] reduce the interpolation bias by sampling the subset \(\varOmega \) at non-integer pixels.
As mentioned in the introduction, the most popular approach in experimental mechanics is certainly to locally approximate the displacement field by a linear combination of shape functions, which may in turn undermatch the true displacement. This is another source of error discussed in [36], where it is shown that the retrieved displacement field is the convolution of the true displacement with a Savitzky–Golay filter characterized by the order of the shape functions and the size of the subset. This characterization is used in [14] and [46] to define some metrological parameters, and in [16] to restore displacement fields through a dedicated deconvolution procedure.
1.5 Notation and Reminder
In what follows, \(\left\langle \cdot , \cdot \right\rangle \) and \(|\cdot |\) denote the bidimensional Euclidean product and norm, respectively. The gradient of any 2D function is denoted by \(\nabla \). We identify any vector with the corresponding column matrix, in boldface letters. The transpose of any matrix A is denoted by \(A^T\).
We denote by \({{\mathcal {O}}}\) Landau’s “big-O” for a variable tending to 0. We recall that if \({\mathbf {f}}\) and \({\mathbf {g}}\) are 2D-valued functions, \({{\mathbf {f}}}={{\mathcal {O}}}(|{\mathbf{g}}|)\) means that for some \(K>0\), any small enough \({{\mathbf {x}}}\) satisfies \(|{{\mathbf {f}}}({{\mathbf {x}}})|\le K|{\mathbf{g}}({{\mathbf {x}}})|\). If \({{\mathbf {f}}}=\mathcal{O}(|{{\mathbf {g}}}|)\) and A is some two-column matrix, then \(A{{\mathbf {f}}}=\mathcal{O}(|{ {\mathbf {g}}}|)\) and in particular \(\langle {{\mathbf {h}}},{{\mathbf {f}}}\rangle ={{\mathcal {O}}}(|{\mathbf{g}}|)\) for any constant 2-D vector \({\mathbf {h}}\).
In the remainder of this paper, we will make use of partial derivatives of interpolated 2-D functions. While some interpolation schemes, such as bilinear interpolation, do not provide us with derivatives at integer pixel coordinates, it should be noted that derivatives of the interpolated functions will be calculated at points like \({{\mathbf {x}}}_i+{\varvec{\phi }}({{\mathbf {x}}}_i)\), \({{\mathbf {x}}}_i\) being an integer pixel coordinate. In most situations, \({\varvec{\phi }}({{\mathbf {x}}}_i)\) has a subpixel value, thus \({{\mathbf {x}}}_i+{\varvec{\phi }}({{\mathbf {x}}}_i)\) has a non-integer value and the derivatives are well-defined.
2 Estimating Displacements by Minimizing SSD
This section gives a closed-form expression of the displacement \({\varvec{\phi }}\) estimated by minimizing the SSD criterion (defined in Equation 2) as a function of the actual unknown displacement \({{\mathbf {u}}}\). The aim is to emphasize the role of systematic errors caused by image texture and interpolation scheme.Non-noisy images are considered in this section. Images affected by signal-dependent noise are investigated in a separate research report [42].
Since the present section deals with the minimization problem at a given pixel \({{\mathbf {x}}}\) and in order to simplify notations, we do not write the index \({{\mathbf {x}}}\) to remind that the subset is centered at a pixel \({{\mathbf {x}}}\), and we simply write \(\varOmega \) and \({\varvec{\phi }}\) instead of \(\varOmega _{{\mathbf {x}}}\) and \({\varvec{\phi }}^{{\mathbf {x}}}\).
2.1 Relation Between Retrieved and Actual Displacement Fields
The goal here is to express \({\varvec{\varLambda }}\) as a function of the images \({\mathcal {I}}\) and \({{\mathcal {I}}}'\), of the interpolated continuous image \(\widetilde{{{\mathcal {I}}}'}\), and of the unknown displacement field \({{\mathbf {u}}}\).
By definition, \({\varvec{\varLambda }}= (\lambda _1,\dots ,\lambda _N)^T \) is a stationary point of the SSD given by Equation 2. For any \(j\in \{1,\dots ,N\}\), taking the derivative with respect to \(\lambda _j\) thus gives:
Let \({\varvec{\delta }}\) be the difference between the unknown displacement field and the retrieved one, such that for any \({{\mathbf {x}}}_i\in \varOmega \), \({\varvec{\delta }}({{\mathbf {x}}}_i)={{\mathbf {u}}}({{\mathbf {x}}}_i) - {\varvec{\phi }}({{\mathbf {x}}}_i)\). It quantifies the undermatching of shape functions mentioned in [36].
First,
By definition of \({{\mathbf {u}}}\),
A first-order Taylor series expansion allows writing:
Denoting by \({{\mathbf {D}}}{{\mathcal {I}}}'={{\mathcal {I}}}'-\widetilde{{{\mathcal {I}}}'}\) the interpolation error (equal to 0 at integer coordinates), we conclude from Equation 4 that
Second, another Taylor series expansion gives:
where \(H\mathcal{I}'\left( {{\mathbf {x}}}_i+{\varvec{\phi }}({{\mathbf {x}}}_i)\right) \) is the Hessian matrix of \(\mathcal{I}'\) at \({{\mathbf {x}}}_i+{\varvec{\phi }}({{\mathbf {x}}}_i)\).
Consequently,
where \({{\mathbf {D}}}\nabla {{\mathcal {I}}}'=\nabla {{\mathcal {I}}}'-\nabla \widetilde{{{\mathcal {I}}}'}\) is the gradient interpolation error.
Plugging Equations 7 and 10 into Equation 3 gives:
For any \(i\in \{1,\dots ,M\}\) and \(j\in \{1,\dots ,N\}\), let \(L^{{\mathbf {u}}}_{i,j}= \left\langle \nabla {{\mathcal {I}}}'\left( {{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i)\right) ,{\varvec{\phi }}_j({{\mathbf {x}}}_i) \right\rangle \), such that \(L^{{\mathbf {u}}}\) is a \(M\times N\) matrix. We eventually obtain:
or in a simpler way:
where \({{\mathcal {O}}}(|{{\mathbf {f}}}|)\) denotes \(\sum _{{{\mathbf {x}}}_i\in \varOmega }(\mathcal{O}|{{\mathbf {f}}}({{\mathbf {x}}}_i)|)\).
Since \({\varvec{\delta }}({{\mathbf {x}}}_i)={{\mathbf {u}}}({{\mathbf {x}}}_i) - {\varvec{\phi }}({{\mathbf {x}}}_i) = {{\mathbf {u}}}({{\mathbf {x}}}_i) - \sum _{k=1}^N \lambda _k{\varvec{\phi }}_k({{\mathbf {x}}}_i)\), the preceding equation gives:
If we denote by \({{\mathbf {G}}}\) the vector of components \({{\mathbf {G}}}_i = \left\langle \nabla {{\mathcal {I}}}' ({{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i)), {{\mathbf {u}}}({{\mathbf {x}}}_i)\right\rangle \) for any \(i\in \{1,\dots ,M\}\), we obtain with Equation 14 the following matrix relation:
Matrix \((L^{{\mathbf {u}}})^T L^{{\mathbf {u}}}\) is invertible as soon as the columns of \(L^{{\mathbf {u}}}\) are linearly independent (it is a Gramian matrix), which holds if the \({\varvec{\phi }}_j\) form a valid basis and if the gradient is not equal to zero over the whole subset \(\varOmega \). We assume in the following that these assumptions hold.
We have finally demonstrated the following theorem.
Theorem 1
If \({\varvec{\varLambda }}\) minimizes the SSD criterion of Equation 2 registering image \({{\mathcal {I}}}'\) over \({\mathcal {I}}\), then the following equality holds:
where \({{\mathbf {u}}}\) is the actual displacement field, and for any \(i\in \{1,\dots ,M\}\) and \(j\in \{1,\dots ,N\}\), the following notations hold: \(L^{{\mathbf {u}}}_{i,j}= \left\langle \nabla \mathcal{I}'\left( {{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i)\right) ,{\varvec{\phi }}_j({{\mathbf {x}}}_i) \right\rangle \), \({{\mathbf {G}}}_i = \left\langle \nabla {{\mathcal {I}}}' ({{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i)), {{\mathbf {u}}}({{\mathbf {x}}}_i)\right\rangle \), \({{\mathbf {D}}}\mathcal{I}'={{\mathcal {I}}}'-\widetilde{{{\mathcal {I}}}'}\), \({{\mathbf {D}}}\nabla {{\mathcal {I}}}'=\nabla {{\mathcal {I}}}'-\nabla \widetilde{{{\mathcal {I}}}'}\), \(\widetilde{{\mathcal {I}}}'\) denotes the interpolation of \({{\mathcal {I}}}'\) at non-integer coordinates, and \({\varvec{\delta }}={{\mathbf {u}}}-{\varvec{\phi }}\).
With this presentation, it is not straightforward to see how the estimation of \({\varvec{\varLambda }}\) is affected by a systematic error.
Let us now decompose (for instance, in the least-squares sense) the unknown, true displacement \({{\mathbf {u}}}\) over the basis functions \(({\varvec{\phi }}_k)\). We introduce the N-dimensional vector \({\varvec{\varLambda }}^{{\mathbf {u}}}= (\lambda ^{{\mathbf {u}}}_1,\dots ,\lambda ^{{\mathbf {u}}}_N)^T\) such that \({{\mathbf {u}}}= \sum _{k=1}^N \lambda ^{{\mathbf {u}}}_k {\varvec{\phi }}_k + {\varvec{\epsilon }}\) where \({\varvec{\epsilon }}\) is the residual in the decomposition of \({{\mathbf {u}}}\) over the basis \(({\varvec{\phi }}_k)_{k\in \{1,\dots ,N\}}\). Consequently, for any \(i\in \{1,\dots ,M\}\),
If we denote by \({{\mathbf {E}}}\) the vector of components \({{\mathbf {E}}}_i = \left\langle \nabla {{\mathcal {I}}}' ({{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i)), {\varvec{\epsilon }}({{\mathbf {x}}}_i)\right\rangle \), we obtain \({{\mathbf {G}}}= L^{{\mathbf {u}}}{\varvec{\varLambda }}+ {{\mathbf {E}}}\). Consequently, Theorem 1 gives the following corollary.
Corollary 1
If \({\varvec{\varLambda }}\) minimizes the SSD criterion of Equation 2 registering image \({{\mathcal {I}}}'\) over \({\mathcal {I}}\), then the following equality holds:
with, in addition to the notations of Theorem 1, \({{\mathbf {E}}}_i = \left\langle \nabla {{\mathcal {I}}}' ({{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i)), {\varvec{\epsilon }}({{\mathbf {x}}}_i)\right\rangle \) for any \(i\in \{1,\dots ,M\}\), where \({\varvec{\epsilon }}\) is the component of \({{\mathbf {u}}}\) out of the basis \(({\varvec{\phi }}_k)\).
2.2 Discussion
Skipping second-order terms from Theorem 1 gives:
and from Corollary 1:
It is easy to see that if interpolation is perfect (\({{\mathbf {D}}}{{\mathcal {I}}}' = {{\mathbf {0}}}\)), and if the function basis is expressive enough to perfectly represent the true displacement \({{\mathbf {u}}}\) (\({{\mathbf {E}}}={{\mathbf {0}}}\)) or at least if the degree of the polynomial basis is large enough (\({{\mathbf {E}}}\simeq {{\mathbf {0}}}\)) , then \({\varvec{\varLambda }}\) is equal to the sought \({\varvec{\varLambda }}^{{\mathbf {u}}}\).
These assumptions are, however, optimistic. They are discussed in the remainder of this section.
2.2.1 Interpolation Bias
In Equation 19, the term \(((L^{{\mathbf {u}}})^T L^{{\mathbf {u}}})^{-1}(L^{{\mathbf {u}}})^T {{\mathbf {D}}}{{\mathcal {I}}}'\) quantifies the effect of subpixel interpolation error. Since the underlying image \({{\mathcal {I}}}'\) is unknown, it is not possible to bound a priori this error, except if some additional information is available. For instance, well-sampled images satisfying the Shannon–Nyquist condition give no interpolation error when using Fourier interpolation as in [31, 44] and in this case, \({{\mathbf {D}}}\mathcal{I}'=0\). As discussed in the introduction, real images from photomechanical experiments probably do not satisfy these hypotheses.
It should be noted that most image interpolation schemes (such as Fourier, bilinear, bicubic, or Lanczos interpolations) are actually linear, in the sense that any interpolated value is a weighted mean of image values at integer pixel coordinates [13, 23]. For any \({{\mathbf {x}}}\in {{\mathbb {R}}}^2\), there exists a row matrix \(P({{\mathbf {x}}})\) of size M such that the interpolation of \({{\mathcal {I}}}'\) at \({{\mathbf {x}}}\) is given by \(\widetilde{{\mathcal {I}}}'({{\mathbf {x}}}) = P({{\mathbf {x}}}) {{\mathcal {I}}}'\), where \({{\mathcal {I}}}'\) momentarily denotes the matrix of image values reshaped as a column vector. For instance, row-vector \(P({{\mathbf {x}}})\) has four nonzero entries in bilinear interpolation, sixteen in bicubic or bicubic spline interpolation [13, 23], which are the most popular schemes in photomechanics.
The interpolation bias thus writes:
It has been derived by another approach in [2] (refining [30, 43]), and experimentally assessed in [3]. It can be noted that the image gradient is involved in \(L^{{\mathbf {u}}}\) and affects the interpolation bias. While interpolation error may be neglected (either by assuming the Shannon–Nyquist condition to be satisfied or by using high-order interpolation schemes), the next section deals with the so-called “undermatched subset shape functions” which potentially gives pattern-induced bias.
2.2.2 Undermatched Shape Functions and Pattern-Induced Bias
In Equation 19, the term \(((L^{{\mathbf {u}}})^T L^{{\mathbf {u}}})^{-1}(L^{{\mathbf {u}}})^T {{\mathbf {G}}}\) links \({\varvec{\varLambda }}\) with the gradient of \({{\mathcal {I}}}'\) and the actual displacement \({{\mathbf {u}}}\). Let us recall that, for any \(i\in \{1,\dots ,M\}\) and \(j\in \{1,\dots ,N\}\),
and
We can see that we find again the well-known aperture problem: only the displacement component collinear with the image gradient plays a role in \({{\mathbf {G}}}_i\). Moreover, Theorem 1 (Corollary 1, respectively) shows that each component (the error on each component, respectively) of \({\varvec{\varLambda }}\) is a weighted mean of \({{\mathbf {G}}}_i\) (of the undermatching error \({{\mathbf {E}}}\), respectively), the weights being proportional to the squared components of the gradient along the shape functions (here, \(((L^{{\mathbf {u}}})^T L^{{\mathbf {u}}})^{-1}\) acts as a normalization).
For didactic purposes, we explicit the relation in a simple, yet realistic case, where displacements is sought as a pure translation along the x-direction. This situation corresponds to disparity estimation in stereo-imaging with rectified images. We have \({{\mathbf {u}}}({{\mathbf {x}}}_i)=(u({{\mathbf {x}}}_i)\; 0)^T\), \(N=1\) and \({\varvec{\phi }}_1({{\mathbf {x}}})=(1\; 0)^T \). In this case, \(L^{{\mathbf {u}}}=({{\mathcal {I}}}'_x({{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i)))_{1\le i \le M}\) is a column-vector, and:
where \({{\mathcal {I}}}'_x\) denotes the partial derivative of \({{\mathcal {I}}}'\) along direction x.
In this case, the term related to the interpolation error simplifies into:
When \({{\mathbf {u}}}=(u,0)\) is a constant displacement, Equation 25 simplifies to u. This observation is consistent with Corollary 1 since in this case, the displacement is perfectly represented by the basis function \({\varvec{\phi }}_1\) as, for any \({{\mathbf {x}}}\), \({{\mathbf {u}}}({{\mathbf {x}}}) = u\,{\varvec{\phi }}_1({{\mathbf {x}}})\).
It should be noted that Equation 25 is exactly the relation given in [1, 31]. When the sought displacement is not constant over \(\varOmega \), it is a weighted mean of the actual displacement, the weights being the squared image derivatives. This justifies the well-known fattening effect in stereo-imaging (also called adhesion effect in [9]): points lying in the neighborhood of edges have a disparity essentially governed by the edge points, which have large gradient values. Fattening effects can be seen for example in [31, 34]: foreground objects (which have a larger disparity than the background) appear fatter than they are because background pixels near their edges inherit their disparity.
In experimental mechanics the relevant formula is given by Theorem 1. The estimated displacement field given by \({\varvec{\varLambda }}\) is biased since it is a weighted sum of the actual displacement at the pixels belonging to the subset, the weights increasing with the squared gradient at the pixels (more precisely, with the squared component of the gradient collinear with the shape functions). In particular, the displacement returned at the center of the considered subset is essentially the average of the actual displacement taken at high-gradient points, even if the actual displacement is different at the considered point. Although this corresponds to the intuition, we are not aware of earlier papers giving a rigorous description of the phenomenon in the context of experimental mechanics. As a consequence, we keep on calling this phenomenon “pattern-induced bias” after [10], since the expression “fattening effect” does not seem to be adequate in experimental mechanics, nothing really becoming “fatter”.
Note that the relation between \({\varvec{\varLambda }}\) and \({{\mathbf {G}}}\) in Theorem 1 can be seen as a generalized convolution, with a spatially varying kernel.
2.3 From Pattern-Induced Bias to Savitzky–Golay Filtering
The authors of [36] claim that the estimated displacement is simply the convolution product between the true displacement and the Savitzky–Golay (SG) kernel (a low-pass filter [26, 32]), causing the so-called matching bias [14]. The SG filter only depends on the degree of the polynomial shape functions and on the size of the considered subset \(\varOmega \) [32]. In particular, it does not depend on the gradient of the underlying image. Moreover, the discussion of Sect. 2.2.2 concludes that the relation between the estimated displacement and the true one can be seen as a convolution with a spatially varying kernel. The claim of [36], backed by results from [14] or [16], therefore seems to contradict Theorem 1 and pattern-induced bias discussed in the preceding section. In the remainder of this section, we explain how these two viewpoints can be accomodated.
2.3.1 The Case of Stationary Random Patterns
To establish the relation with the SG filter, the ground hypothesis of [36] is that, with our notations, \({\varvec{\phi }}\) minimizes
over a subset \(\varOmega _{{\mathbf {x}}}\) centered at pixel \({{\mathbf {x}}}\), for any \({{\mathbf {x}}}\). Let us write for a while the x- and y-components of \({\varvec{\phi }}\) as:
where d is the maximum degree of the shape functions. Thus, \(\lambda _1=\alpha _{0,0}\), \(\lambda _2=\beta _{0,0}\), \(\lambda _3=\alpha _{1,0}\), \(\lambda _4=\beta _{1,0}\), \(\lambda _5=\alpha _{0,1}\), \(\lambda _6=\beta _{0,1}\), etc.
With \(J_{{\mathbf {x}}}= (1,x,\dots ,x^d,y, \dots ,yx^{d-1},y^2, \dots ,y^2x^{d-2},\) \(\dots ,y^d)^T\), \(\alpha =(\alpha _{0,0},\alpha _{1,0},\dots ,\alpha _{d,0},\alpha _{1,0},\dots ,\alpha _{1,d-1},\alpha _{2,0},\) \(\dots ,\alpha _{2,d-2},\dots ,\alpha _{d,0})^T\), and \(\beta =(\beta _{0,0},\beta _{1,0},\dots ,\beta _{d,0},\beta _{1,0},\) \(\dots ,\beta _{1,d-1},\beta _{2,0},\dots ,\beta _{2,d-2},\dots ,\beta _{d,0})^T\), Equation 27 writes:
Consequently, minimizing Equation 27 with respect to \(\alpha \) and \(\beta \) amounts to solving the normal equations \(J^T\alpha = u_1\) and \(J^T\beta = u_2\) where matrix J collects all column vectors \(J_{{\mathbf {x}}}\). In other words, \(\alpha = (JJ^T)^{-1}J u_1\) and \(\beta = (JJ^T)^{-1}J u_2\). Since the displacement estimated over the subset \(\varOmega \) is simply \((\lambda _1,\lambda _2)=(\alpha _{0,0},\beta _{0,0})\), each component of the retrieved displacement is the convolution of the components of \({{\mathbf {u}}}\) by a Savitzky–Golay [32] filter of order equal to the degree of the shape functions and of support given by the dimensions of \(\varOmega \). With first- and second-degree shape functions, the partial derivatives of the displacement field being given by \((\lambda _3,\lambda _4,\lambda _5,\lambda _6)\), they are also given by SG filters, as explained in [26, 32].
The justification that the sought \({\varvec{\phi }}\) minimizes Equation 27 is only based on heuristic arguments in [36]. We shall see that the very specific nature of the speckle patterns used in experimental mechanics permits to justify this claim.
Since \({{\mathcal {I}}}({{\mathbf {x}}}_i) = {{\mathcal {I}}}'\left( {{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i)\right) \), if we neglect interpolation error and identify \(\widetilde{{{\mathcal {I}}}'}\) with \({{\mathcal {I}}}'\), we obtain the following first-order approximation as in Equation 6:
Provided this first-order approximation holds (for instance because an initial guess of the solution is available), minimizing the SSD criterion thus amounts to minimizing:
with \(g_i\) the norm of \(\nabla {{\mathcal {I}}}'({{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i))\) and \(\theta _i\) the angle between \(\nabla {{\mathcal {I}}}'({{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i))\) and the error \({{\mathbf {u}}}({{\mathbf {x}}}_i)-{\varvec{\phi }}({{\mathbf {x}}}_i)\). As can be seen, this is not Equation 27. It can be noted that the component of \({{\mathbf {u}}}-{\varvec{\phi }}\) orthogonal to the gradient of \({{\mathcal {I}}}'\) does not play any role, which is consistent with the preceding discussion about the aperture problem. This was also mentioned in [24].
As explained in the introduction, specimens tested in experimental mechanics are marked with random speckle patterns which can be modeled as stationary textures. We can thus safely assume that the gradient norms \((g_i)_{{{\mathbf {x}}}_i\in \varOmega }\) are indentically distributed random variables, as well as the angles \((\theta _i)_{{{\mathbf {x}}}_i\in \varOmega }\), and that at each pixel \({{\mathbf {x}}}_i\), \(g_i\) and \(\theta _i\) are independent. Nevertheless, these random variables are spatially correlated. A common assumption is that spatial correlation vanishes with the distance between pixels as in natural images [37].
Let \(X_i = g_i^2 \cos ^2(\theta _i) \left| {{\mathbf {u}}}({{\mathbf {x}}}_i)-{\varvec{\phi }}({{\mathbf {x}}}_i) \right| ^2\) for any \(1\le i \le M\). The classic law of large numbers does not hold here because of spatial correlations. However, generalizations such as Bernstein’s weak law of large numbers [8, Ex. 254 p. 67] still hold. Assuming that the variance of the \(X_i\) is bounded, i.e., there exists \(c>0\) such that \(\text {Var}(X_i)\le c\), and assuming also that spatial correlations vanish with distance, i.e., \(\text {Cov}(X_i,X_j)\rightarrow 0\) when \(|{{\mathbf {x}}}_i-{{\mathbf {x}}}_j|\rightarrow +\infty \), we obtainFootnote 1:
where for any \(\varepsilon >0\), \(V_i\) is the set of indices j such that for any i and \(j\in V_i\), \(\text{ Cov }(X_i,X_j) \le \varepsilon \). Here, \(B\backslash A\) denotes the relative complement of a set A with respect to B. Let \(N_i\) be the cardinality of \({{\mathbb {N}}}\backslash V_i\) which is a finite set since \(\text {Cov}(X_i,X_j)\rightarrow 0\) when \(|{{\mathbf {x}}}_i-{{\mathbf {x}}}_j|\rightarrow +\infty \), and \(N=\max _i N_i\).
Since for any i, j, \(\text {Cov}(X_i,X_j) \le c\) by Cauchy–Schwartz inequality, the following upper bound holds:
Thus,
Chebyshev’s inequality implies that the random variable \(\frac{1}{M}\sum _{i=1}^M X_i - \frac{1}{M} \sum _{i=1}^M E(X_i)\) tends to 0 in probability as \(M\rightarrow + \infty \).
In other words, this justifies that minimizing Equation 32 amounts to minimizing
as soon as the size M of the domain \(\varOmega \) is “large enough.” Equation 35 states that for a given M, the approximation is as tight as the bound c on the variance is small, or as the spatial correlation of the image gradients quickly vanishes, giving a small N.
2.3.2 Toward an Optimum Pattern with Respect to Pattern-Induced Bias?
The result of the preceding section can be interpreted as follows: minimizing Equation 32 to estimate \({\varvec{\phi }}\) is similar to minimizing Equation 27, provided that the size M of the subset \(\varOmega \) is large enough. From Equation 35, this is all the more valid as the speckle pattern is fine (giving quickly vanishing spatial correlations, thus a small N for a given \(\varepsilon \)) and as the variance of the \(X_i\) is small (giving a small c). Since \(\text {Var}(X_i)\) is proportional to \(\text {Var}(g_i^2\cos ^2(\theta _i)) = E(g_i^4)E(\cos ^4(\theta _i)) - E^2(g_i^2)E^2(\cos ^2(\theta _i)) = 3E(g_i^4)/8 - E^2(g_i^2)/4\) (assuming that the \(\theta _i\) are uniformly distributed in the interval \((0,2\pi )\), which is sound with an isotropic speckle pattern, we indeed obtain \(E(\cos ^2(\theta ))=1/2\) and \(E(\cos ^4(\theta ))=3/8\)). As a consequence,
A fine pattern minimizing this quantity should have lower pattern-induced bias. One can see that a concentrated gradient distribution with a low gradient average value is of interest. However, such a speckle pattern is still to be designed.
2.3.3 Link with a Fattening-Free Criterion in Stereoscopic Imaging
Disparity in stereo-imaging being a 1-D displacement, \(\theta _i=0\) in Equation 32 and \(g_i=\widetilde{\mathcal{I}'}_x({{\mathbf {x}}}_i+{{\mathbf {u}}}({{\mathbf {x}}}_i))\) where \(\widetilde{{{\mathcal {I}}}'}_x\) denotes the partial derivative of \(\widetilde{{{\mathcal {I}}}'}\) along the epipolar line.
This motivates the authors of [1] to estimate \({\varvec{\phi }}\) by minimizing the following weighted SSD criterion, denoted \(\widetilde{\text {SSD}}\) in what follows:
where \(\kappa >0\) avoids divisions by zero.
In stereo-imaging, \({\varvec{\phi }}\) is sought as a constant displacement. The solution of \(\widetilde{\text {SSD}}\) minimizes \(\sum _i |{{\mathbf {u}}}({{\mathbf {x}}}_i) - {\varvec{\phi }}|^2\) and does not depend on the image gradient. It is shown in [1] that estimating \({\varvec{\phi }}\) by minimizing \(\widetilde{\text {SSD}}\) at any pixel gives an estimated displacement at \({{\mathbf {x}}}\) which is the mean of the \({{\mathbf {u}}}({{\mathbf {x}}}_i)\) over \(\varOmega _{{\mathbf {x}}}\). Interestingly, this is consistent with the preceding section, since a zero-order Savitzky–Golay filter is a simple moving average with a kernel constant over its domain.
3 Numerical Assessment
The goal of this section is to provide the reader with illustrative didactic experiments, and to assess the validity of the predictive formulas given by Theorem 1 and Corollary 1. We also discuss to what extent PIB can be eliminated or decreased. In the proposed numerical assessments, the real displacement fields are known, and we are able to compare the estimated displacement to this ground truth. It should be noted that the numerical scheme actually used to minimize the SSD criterion over the subsets (Equation 2) (see, e.g., [28]) is not important here. Nevertheless, the stopping criterion must be set carefully so that the stationarity assumption, which is the ground of Sect. 2, is valid. In practice, we use the Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton method with a cubic line search implemented in Matlab’s fminunc function.
Since the predictive formulas are based on the ideal, continuous images \({\mathcal {I}}\) and \({{\mathcal {I}}}'\) whose derivatives are required, we shall first consider in Sect. 3.1 images and deformation fields expressed as simple closed-form expressions. We also assess the effect of gray-level quantization. Nevertheless, the true derivatives of quantized images are, of course, unknown. Section 3.2 deals with synthetic speckle images which mimic real images used in experimental solid mechanics.
The numerical experiments proposed in this section can be reproduced with datasets and Matlab codes available at the following URL:https://members.loria.fr/FSur/software/PIB/ The interested reader can also easily modify the parameters and datasets for further investigations.
3.1 Image Pairs Given by a Closed-Form Expression
In this section, we make use of images defined by closed-form expressions in order to assess the proposed formulas in a controlled experimental setting.
3.1.1 Displacement Estimation
We define the image \({\mathcal {I}}\) of the reference state and the image \({{\mathcal {I}}}'\) of the deformed state at any pixel of coordinates (x, y) as sine waves by the following equations:
where (x, y) spans a \(200\times 15\) pixel domain, \(b=8\) (so that the gray level of both images spans an 8-bit range), \(\gamma =0.9\) is the contrast, \(p=50\) pixels governs the varying period of the sine wave, and u(x) is the ground-truth displacement field, supposed to be restricted along the x-axis See Fig. 1. Note that in this section, images are not quantized over b bits.
For displacement a) (constant displacement of 0.2 pixel): 1) closed-form expression (first column), 2) bilinear interpolation (second column), and 3) bicubic interpolation (third column). In each of these three cases, the first row depicts, superimposed on the same graph: the ground truth u, the displacement \({\varvec{\phi }}(x)\) estimated from SSD, the displacement \({\widetilde{{\varvec{\phi }}}}(x)\) estimated from \(\widetilde{\text {SSD}}\), the displacement predicted by Theorem 1, and Savitzky–Golay filtering of u. In each of the three cases, the second row depicts, superimposed on the same graph: the differences (bias estimations) between u on the one hand, and displacement retrieved with SSD, predicted displacement, displacement retrieved with \(\widetilde{\text {SSD}}\), output of the SG filter on the other hand
For displacement b) (sine wave of amplitude 0.2 pixel and period 90 pixels): 1) closed-form expression (first column), 2) bilinear interpolation (second column), and 3) bicubic interpolation (third column). In each of these three cases, the first row depicts, superimposed on the same graph: the ground truth u, the displacement \({\varvec{\phi }}(x)\) estimated from SSD, the displacement \(\widetilde{{\varvec{\phi }}}(x)\) estimated from \(\widetilde{\text {SSD}}\), the displacement predicted by Theorem 1, and Savitzky–Golay filtering of u. In each of the three cases, the second row depicts, superimposed on the same graph: the differences (bias estimations) between u on the one hand, and displacement retrieved with SSD, predicted displacement, displacement retrieved with \(\widetilde{\text {SSD}}\), output of the SG filter on the other hand
We seek for a constant displacement field \((\phi ,0)\) on each subset \(\varOmega _{{\mathbf {x}}}\) of size \(15\times 15\) \(\hbox {pixels}^2\) distributed along the x-axis. The size of the subset is chosen in accordance with the characteristic scale of the modulated sine wave giving images \({\mathcal {I}}\) and \({{\mathcal {I}}}'\). Such a constant displacement corresponds to zero-order shape functions. We therefore calculate at any abscissa x the quantity \({\varvec{\phi }}(x)=(\phi (x),0)\) minimizing the SSD criterion:
The numerical assessment in the present section deals with a 1-D displacement along the x-axis in an image which varies only along the x-axis. The gradient is thus always collinear with the displacement. Consequently, the aperture problem manifests itself only because of vanishing image gradients; there is no loss of information orthogonally to the gradient as in the general 2-D case.
The 1-D displacement considered here is the case of interest of stereoscopy. It is possible to also implement the \(\widetilde{\text {SSD}}\) criterion of [1], recalled in Sect. 2.3.3 above. We set the value of \(\kappa \) to achieve the best trade-off between reducing the fattening effect and numerical stability, see Sect. 3.2.5.
In the SSD and \(\widetilde{\text {SSD}}\) criteria, \(\widetilde{{{\mathcal {I}}}'}\) denotes a continuous image. Since we use images given by closed-form expressions, image values at non-integer pixels are available. Real experiments require, however, to interpolate images. In this illustrative experiment, we consider three possibilities: 1) using Equation 40 which allows avoiding any interpolation scheme (in this case we also use the closed-form expression of the gradient in the quasi-Newton scheme), 2) using bilinear interpolation, or 3) using bicubic interpolation.
We also consider two displacement fields: a) a constant \(u(x)=0.2\) pixel, b) a low-frequency sine wave \(u(x) = 0.2\,\sin (2\pi x/q)\) where \(q=90\) pixels. We also discuss in [42] the case of a high-frequency sine wave (not shown here). In all cases, the largest displacement value is 0.2 pixel.
Figures 2 and 3 show various plots. Each of these figures permits discussing displacement fields on the top and biases (systematic errors) on the bottom, as a function of the interpolation scheme (from left to right: closed-form expression, bilinear interpolation, and bicubic interpolation). Concerning the displacement, we plot the ground truth u (thin green line), the displacement \({\varvec{\phi }}(x)\) retrieved by minimizing the SSD criterion (blue), the displacement \({\widetilde{{\varvec{\phi }}}}(x)\) retrieved from the modified criterion \(\widetilde{\text {SSD}}\) defined in Equation 38 (red), the predicted displacement (cf. Theorem 1, yellow) and the filtering of the ground-truth displacement by the Savitzky–Golay filter of order 0 and frame length 15 (purple). Concerning the biases, we plot the differences between the ground truth displacement on the one hand, and the retrieved displacement with SSD, the predicted displacement, the retrieved displacement with \(\widetilde{\text {SSD}}\), and the output of the SG filter on the other hand.
Concerning the constant displacement a) in Fig. 2, since it can be represented with zero-order shape functions, the error \({\varvec{\epsilon }}\) (thus \({{\mathbf {E}}}\)) in Corollary 1 is null: no marking bias should be noticed. With the closed-form expression of image \({{\mathcal {I}}}'\) (case 1), the interpolation error \({{\mathbf {D}}}{{\mathcal {I}}}'\) is also null. It can be seen, indeed, that all curves are superimposed in this case. With bilinear interpolation (case 2), Theorem 1 predicts an error term caused by the interpolation error. We can see that the retrieved displacement fits well the prediction, the blue and yellow curves being superimposed. We can also see that correcting the marking bias (which is, here, non-existent) significantly amplifies the interpolation error, giving the erratic red curve. When looking closely at the curves showing the biases, we can notice a small difference between the retrieved bias and the predicted bias, which could probably be explained by higher-order error terms than the first-order terms of the present calculation. With bicubic interpolation (case 3), the interpolation error is very small, all the curves being close to each other. With the constant displacement considered here, we can see that interpolation still causes a very small drift in the estimation, giving the increasing bias. Correcting the marking bias with \(\widetilde{\text {SSD}}\) does not give an erratic red curve but a few spurious estimations can be seen. Interpolation errors seem to be amplified.
Concerning the low-frequency sine displacement b) in Fig. 3, it cannot be represented by zero-order shape functions, thus marking bias should affect the retrieved displacement, the error term \({{\mathbf {E}}}\) being non-null in Theorem 1. We can see that with closed-form expression (case 1), thus no interpolation error, the retrieved displacement fits perfectly the prediction, the blue and yellow curves being superimposed. The marking bias causes departures from the ground truth displacement, whose amplitude is governed by the gradient of the underlying image, giving a rather chaotic bias curve. The marking bias is perfectly removed with the \(\widetilde{\text {SSD}}\) criterion: the retrieved displacement indeed fits the output of the SG filter, as predicted by the theory. With bilinear interpolation (case 2), an additional interpolation error is predicted by Theorem 1, although it is difficult to see a difference between the blue and yellow curves. The retrieved displacement globally fits the prediction. With bicubic interpolation (case 3), the curves are close to case 1. When using the \(\widetilde{\text {SSD}}\) criterion, we can see that cases 1 and 3 fit well the predicted Savitzky–Golay filtering (green and red curves are superimposed), but as for displacement a), bilinear interpolation error (case 2) is amplified, giving an erratic red curve.
3.1.2 Effect of Quantization
In the preceding section, image intensity is not quantized. We now perform experiments with quantized images in order to illustrate its impact on the predictive formulas. Bicubic interpolation is used in order to minimize interpolation bias, as illustrated earlier. We perform the same experiment as the one described in Fig. 3.
Effect of gray-level quantization. From left to right: 8-bit images, 10-bit images, 12-bit images, 14-bit images. First row: displacements. Second row: biases (difference between the predicted or retrieved displacements and the ground truth displacement)
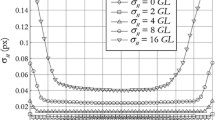
Figure 4 shows the result of displacement estimation by minimizing SSD and \(\widetilde{\text {SSD}}\). The former estimation should match the predicted one, and the latter should match the output of SG filter. We can see that the proposed predictive formulas are quite accurate as soon as quantization is performed over 10 bits (the yellow and blue curves are superimposed), and that retrieving the output of the SG filter with \(\widetilde{\text {SSD}}\) requires to quantize image intensity over 12 bits (so that red and purple curves are superimposed).
Two speckle images (size: \(500\times 100\) pixels) and y-component \(u_y\) of the prescribed displacement field. There is no displacement along the x-direction (\(u_x=0\)). The first image shows the large speckle pattern discussed in Sect. 3.2.2, and the second one the fine speckle pattern of Sect. 3.2.3
Fine speckle, zero-order shape functions. From left to right: \(7\times 7\), \(19\times 19\), \(31\times 31\), and \(43\times 43\) subset \(\varOmega \). On the top, displacement following x-axis; on the bottom, displacement following y-axis (difference between retrieved displacement field and output of SG filter, and cross section along the line \(y=50\))
Large speckle, \(7\times 7\) subset \(\varOmega \) and zero-order shape functions. Displacement along x- (left) and y-axis (right), and corresponding cross-section plots
3.2 Speckle Patterns: Assessing the Prediction for Pattern-Induced Bias
The previous section shows numerical assessments with smooth images and simple ground-truth displacement fields. The present section presents numerical assessments based on speckle pattern images corresponding to typical usage cases in experimental mechanics. BSpeckleRender softwareFootnote 2 [41] is used to render synthetic speckle images of size \(500\times 100\) pixels: one image corresponds to a reference state and another one corresponds to a deformed state. Speckles are designed to mimic real patterns such as the ones that can be seen in [22, 38, 39] for instance. The displacement field \({{\mathbf {u}}}=(u_x,u_y)\) is given by the following closed formula:
The speckle pattern is deformed along the y-direction, the prescribed displacement being a sine wave along the x-direction of maximum amplitude of 0.5 pixel, whose period ranges from 5 pixels (\(x=0\)) to 50 pixels (\(x=500\)). Such a deformation field is relevant in order to highlight the frequency response of the SG filter, see [10, 16,17,18] for instance. A 12-bit quantization is used, following the prescription of Sect. 3.1.2. Note that these images are smaller than in assessment datasets used in some recent works [14, 15, 17, 18] because of the time needed to render 12-bit images, and in order to facilitate the reading of the graphs. Because of the discrete nature of the rendered speckle images, interpolation is also required. Bicubic interpolation is used, following Sect. 3.1.1. Consequently, estimation error is likely to be only caused by the \(((L^{{\mathbf {u}}})^T L^{{\mathbf {u}}})^{-1}(L^{{\mathbf {u}}})^T {{\mathbf {E}}}\) term in Corollary 1.
Figure 5 shows two speckle images and the imposed (ground truth) displacement field. Images (before and after deformation) with the large speckle pattern are discussed in Sect. 3.2.2. Section 3.2.3 concerns images with the fine speckle pattern. The goal here is to compare the displacement field retrieved with SSD minimization to its counterpart given by the predictive formula for the pattern-induced bias (PIB). For didactic purpose, several values are tested for both the subset size and the order of the shape functions. In the remainder of this section, we show the displacement maps (in each direction) retrieved by SSD minimization, the maps predicted by Theorem 1, the ground-truth (GT) displacement, and the output of the Savitzky–Golay filtering of the GT displacement. We also show a cross-section plot of the displacement field along its middle-line \(y=50\) where GT displacement is constant, either null along the x-direction, or equal to 0.5 pixel along the y-direction.
3.2.1 Influence of the Subset Size
Figure 6 shows the evolution of the difference between the retrieved displacement and the output of the Savistzky–Golay filter as a function of the subset size, for zero-order shape functions used in stereoscopy. The results (not shown) for first-order shape functions are similar. The fine speckle pattern images are used here. As discussed in the following sections, the predictive formulas for the retrieved displacement are quite accurate. These figures illustrate the convergence of the retrieved displacement toward the output of the SG filter, as predicted in Sect. 2.3. It also illustrates that PIB shows a large amplitude over areas where the gradient of the displacement has a large value (here, on the left of the \(u_y\) displacement field). We can also see that large subsets give very smooth displacement fields, the corresponding low-pass SG filter having the same support as the subset (see [14, 36]). Such large subsets are not used in practice. Small subsets are required to avoid a large Savitzky–Golay smoothing, but they also give a potentially large PIB.
Large speckle, \(13\times 13\) subset \(\varOmega \) and first-order shape functions. The cross-section plots show, from left to right and top to bottom, \(\lambda _1\), \(\lambda _3\), \(\lambda _5\), \(\lambda _2\), \(\lambda _4\), \(\lambda _6\), such that the x-component of the displacement over a subset (giving fields shown on the upper left) is \(\lambda _1 + \lambda _3 x +\lambda _5 y\) and the y-component (on the upper right) is \(\lambda _2 + \lambda _4 x +\lambda _6 y\)
Large speckle, \(19\times 19\) subset \(\varOmega \) and second-order shape functions. Displacement along x- (left) and y-axis (right)
Large speckle, \(19\times 19\) subset \(\varOmega \) and second-order shape functions. From left to right and top to bottom: \(\lambda _1\), \(\lambda _3\), \(\lambda _5\), \(\lambda _7\), \(\lambda _9\), \(\lambda _{11}\) concerning x-displacement, and \(\lambda _2\), \(\lambda _4\), \(\lambda _6\), \(\lambda _8\), \(\lambda _{10}\), \(\lambda _{12}\) concerning y-displacement
3.2.2 Large Speckle Pattern
Figure 7 shows the results for a subset \(\varOmega \) of size \(7\times 7\) and zero-order shape functions (that is, a constant displacement is estimated over each subset). We can see that the seemingly random fluctuations in the retrieved displacement fields are actually caused by PIB (thus not by sensor noise) and are well-predicted by our formulas. In particular, the cross-section plots of the displacement maps confirm that the seemingly random fluctuations of the estimated displacement along the SG filtering of the GT displacement are caused by PIB, the retrieved and predicted curves being superimposed. Interestingly, despite the null GT displacement along the x-direction, the x-component of the retrieved displacement is still affected by PIB. We can see that the amplitude of the PIB is quite large compared to the true displacement. It can be noticed that PIB is large where displacement gradient is large (that is, on the left-hand side of the displacement field). Since the retrieved displacement is a weighted mean of the true displacement in the considered subset, PIB is indeed likely to be larger if the displacement strongly varies within the subset.
Figure 8 shows results for \(13\times 13\) subsets and first-order shape functions. It turns out that higher-order shape functions require larger subsets, since numerical issues affect smaller subsets (not shown here). With first-order shape functions, \({\varvec{\varLambda }}\) has six components. The first two components correspond to the displacement \({\varvec{\phi }}(x)\) at the center of the subset \(\varOmega _{{\mathbf {x}}}\) and can thus be compared to the convolution of the true displacement with SG filter. The four other components correspond to partial derivatives of the displacement field. They also correspond to the output of (other) SG filters, as recalled in Sect. 2.3.Footnote 3 In all cases, we can see fluctuations of the estimated displacement around the output of the SG filter, these fluctuations being due to PIB. Because of the transfer function of the SG filter, the retrieved displacement field vanishes for certain values. It has even a wrong sign, as discussed in detail in [14]. It is quite surprising that the PIB give such large spurious measurements.
Figures 9 and 10 show results for \(19\times 19\) subsets and second-order shape functions. Even if second-order shape functions are rarely used in commercial DIC software programs for experimental mechanics, it can be seen that predictive formulas are still valid in this case.
Fine speckle, \(7\times 7\) subset \(\varOmega \) and 0-order shape functions. Displacement maps along x- (left) and y-axis (right), and cross-section plots
Fine speckle, \(13\times 13\) subset \(\varOmega \) and first-order shape functions. Displacement maps along x- (left) and y-axis (right). Cross-section plots, from left to right and top to bottom: \(\lambda _1\), \(\lambda _3\), \(\lambda _5\), \(\lambda _2\), \(\lambda _4\), \(\lambda _6\)
3.2.3 Fine Speckle Pattern
Figures 11, 12, 13, 14 show the results of the same experiments as in the preceding section, but with the fine speckle pattern. Although such a pattern makes it difficult to reliably estimate the image gradients, we can see that PIB is still accurately predicted. With the same shape functions and subset sizes, we can see that the fine speckle pattern gives a PIB with a smaller amplitude, as discussed in Sect. 2.3.
Fine speckle, \(19\times 19\) subset \(\varOmega \) and second-order shape functions. Displacement maps along x- (left) and y-axis (right)
Fine speckle, \(19\times 19\) subset \(\varOmega \) and second-order shape functions. From left to right and top to bottom: \(\lambda _1\), \(\lambda _3\), \(\lambda _5\), \(\lambda _7\), \(\lambda _9\), \(\lambda _{11}\) concerning x-displacement, and \(\lambda _2\), \(\lambda _4\), \(\lambda _6\), \(\lambda _8\), \(\lambda _{10}\), \(\lambda _{12}\) concerning y-displacement
3.2.4 A Remark on Checkerboard Patterns
While random speckle patterns have a huge popularity in photomechanics, very recent papers show that checkerboard patterns give less random noise in the retrieved displacement, see [4, 18]. The reason is that the average gradient norm within a subset has larger values than with any typical random speckle patterns. Figure 15 shows a checkerboard pattern of pitch equal to 6 (that is, it is made of juxtaposed black and white squares of width 3 pixels). Such a pattern has been used in the experimental assessment of [15, 18]. In these papers, less spurious fluctuations have been observed in the displacement with checkerboard than with random speckle.
This is confirmed by Figs. 16 and 17 which show estimation of the \({\varvec{\varLambda }}\) parameters with checkerboards patterns, with the same settings as in Figs. 7, 8 with large speckle and 11, 12 with fine speckle. While predictive formulas are not fully satisfied here, the curves being not perfectly superimposed, it can be noted that the amplitude of the spurious fluctuations is much smaller than with speckle patterns. The amplitude of the high-frequency spurious displacement on the x-component of the displacement is less than \(5\,10^{-3}\), an order of magnitude smaller than with speckles. This high-frequency phenomenon is caused by aliasing; it cannot be seen with large checkerboard pitches (not shown here). Moreover, with such a fine pattern, the numerical estimation of the gradient needed in the predictive formulas is certainly not consistent. While spurious fluctuations cannot be seen, contrary to the fluctuations caused by random speckle patterns, the PIB still plays a role, giving displacement fields which do not fit the output of the SG filter, as can be seen in the cross-section plots in Figs. 16 and 17 . The difference caused by PIB reaches, however, values smaller than with random speckle patterns.
This experiment illustrates that a periodic and fine pattern such as a checkerboard gives a smaller difference with the output of the SG filter than the classic speckle patterns.
3.2.5 Toward a PIB-Free SSD Criterion?
This section discusses the extent to which it is possible to get rid of PIB, after Blanchet et al.’s approach [1]. We can see from Sect. 2.3.3 that if \({\varvec{\phi }}\) minimizes the following GT-\(\widetilde{\text {SSD}}\) criterion:
(with the notations of Sect. 2.3.3), then it is also the least-squares estimate of \({{\mathbf {u}}}\) over \(\varOmega \). In this section, \(\kappa =10^{-2}\) for the large speckle pattern, and \(\kappa =10^{-4}\) for the fine one.
Figure 18 shows the representative of results obtained with the large speckle pattern. We can see that the displacement retrieved with this criterion is much less impaired by the spurious fluctuations caused by PIB. Here, it is possible to estimate \(g_i^2\cos ^2(\theta _i)\) since the GT displacement is known. However, Fig. 19 shows that this approach is much less efficient with the fine speckle pattern. The reason is that the GT-\(\widetilde{\text {SSD}}\) criterion requires an estimation of the gradient \(g_i\) and of the angle \(\theta _i\), which is less accurate with the fine speckle than with the smooth softly-varying speckle pattern. For the same reason, similar results are obtained with the checkerboard pattern discussed in Sect. 3.2.4.
We now discuss two approaches to PIB-free estimation which do not require the knowledge of the true displacement \({{\mathbf {u}}}\). In the present experiment, \({{\mathbf {u}}}\) is actually a 1-D displacement along the x-axis. It is thus possible to use Blanchet et al.’s approach to fattening-free block matching, and estimate \({\varvec{\phi }}\) over \(\varOmega _x\) by minimizing (again with Matlab’s fminunc function) the following 1D-\(\widetilde{\text {SSD}}\) criterion:
where \(\widetilde{{{\mathcal {I}}}'}_x\) denotes the partial derivative along x of the interpolated image \({{\mathcal {I}}}'\), an initial guess of \({\varvec{\phi }}\) being given by the classic SSD criterion.
Checkerboard pattern
The result is shown in Figs. 20 and 21 (to be compared to Figs. 18 and 19 ). PIB significantly decreases: 1D-\(\widetilde{\text {SSD}}\) gives a displacement that roughly follows the output of the SG filter.
Nevertheless, realistic displacements in experimental mechanics are bidimensional. We also introduce and test the following 2D-\(\widetilde{\text {SSD}}\) criterion:
Figure 22 is representative of results generally obtained: this approach only marginally allows us to decrease PIB, contrary to the case of 1D-\(\widetilde{\text {SSD}}\). A slight decreasing of the amplitude of PIB can be noticed. As noted earlier in the 1-D case, displacement information is lost only at points where the derivative of the image vanishes. On the contrary, in the 2-D case the aperture problems manifests itself at any pixel since the component of the displacement orthogonal to the gradient always vanishes. This probably leads here to an incomplete correction of the criterion.
Checkerboard, \(7\times 7\) subset \(\varOmega \) and 0-order shape functions. Displacement maps along x- (left) and y-axis (right), and cross-section plots
Checkerboard, \(13\times 13\) subset \(\varOmega \) and first-order shape functions. Displacement maps along x- (left) and y-axis (right). Cross-section plots, from left to right and top to bottom: \(\lambda _1\), \(\lambda _3\), \(\lambda _5\), \(\lambda _2\), \(\lambda _4\), \(\lambda _6\)
Large speckle, \(19\times 19\) subset \(\varOmega \), zero-order shape functions, and displacement estimation (along x- on the left and y-axis on the right) with the GT-\(\widetilde{\text {SSD}}\) criterion
Fine speckle, \(19\times 19\) subset \(\varOmega \), zero-order shape functions, and displacement estimation (along x- on the left and y-axis on the right) with the GT-\(\widetilde{\text {SSD}}\) criterion
Large speckle, \(19\times 19\) subset \(\varOmega \), zero-order shape functions, and displacement estimation (along x-axis) with the 1D-\(\widetilde{\text {SSD}}\) criterion. To be compared to Fig. 18
Fine speckle, \(19\times 19\) subset \(\varOmega \), first-order shape functions, and displacement estimation (along x-axis) with the 1D-\(\widetilde{\text {SSD}}\) criterion. To be compared to Fig. 19
Large speckle, \(19\times 19\) subset \(\varOmega \), zero-order shape functions, and displacement estimation (along x- on the left and y-axis on the right) with the 2D-\(\widetilde{\text {SSD}}\) criterion
4 Conclusion and Open Questions
This paper discusses several bias sources in image registration with local parametric estimation via a sum of squared differences criterion, with a focus on photomechanics. A predictive formula is proposed in Theorem 1 for biases caused by interpolation and undermatched shape functions. These sources of errors all depend on the gradient distribution in the underlying images. In particular, the pattern-induced bias (PIB), known as fattening effect in stereoscopic imaging, is caused by the gradient distribution and by the difference between the true displacement field and its local approximation by shape functions. In addition to these biases, the retrieved displacement is affected by spatially correlated random fluctuations caused by sensor noise propagation. This point is discussed in [42].
Several results from the literature are extended or presented in a unifying way. In Sect. 2.3, we have also completed the contribution of [36] by establishing a rigorous link between the estimated displacement and the true displacement through the Savitzky–Golay (SG) filter, whose parameters depends on the order of the shape functions and on the size of the analysis subset. The link holds because of the very random nature of speckle images.
A numerical assessment of the predictive formulas is discussed as well. First, we have noticed that bicubic interpolation gives biases well below PIB in amplitude, in contrast to bilinear interpolation. Second, it is shown that PIB may have a large amplitude, either if zero-order (used in stereo-imaging) or first- and second-order (used in DIC for experimental mechanics applications) shape functions are used. This bias term gives fluctuations around the output of the SG filter of the true displacement. It is striking to note that these fluctuations may have an amplitude of twice the true displacement. As mentioned in Sect. 2.3, the effect of PIB is equivalent to a spatially varying convolution. A fine understanding of this question would permit to go beyond the deconvolution procedure that is proposed in [16] in order to reduce the measurement bias.
In experimental mechanics applications, defining a marking pattern which is optimal with respect to relevant metrological criteria still remains an open question. Some guidelines are given in Sect. 3.2.5. In addition, first results discussed in [18] show that checkerboards give a smaller measurement bias than classic speckle patterns used in DIC, and suggest that checkerboards indeed give lower PIB than random speckle patterns. This was numerically verified and illustrated in Sect. 3.2.4.
Besides, the set of shape functions used to parameterize the local displacement also plays a role: we have shown that PIB involves the scalar product of the image gradient and the difference between the true and the retrieved displacements. It could be of interest to select shape functions minimizing PIB, by improving statistical criteria such as the ones discussed in [7].
Concerning modifications of the sum of squared differences criterion permitting to get rid of pattern-induced bias, we have verified that the approach proposed by Blanchet et al. [1] is an effective method for 1-D displacements met in stereo-imaging. Our numerical experiments show that it is also a valid approach with higher-order shape functions than the constant local displacement considered in [1]. We have shown that the resulting fattening-free estimation approximates the output of a SG filter, which generalizes [1]. However, the case of 2-D displacements is much more complicated because of the aperture problem, which discards displacement information at any pixel. A PIB-free estimation is still to be designed in this case.
Notes
The proposed calculation is adapted from https://math.stackexchange.com/questions/245327/.
We use BSpeckleRender_b which renders speckle images with patterns of intensity at pixel \({{\mathbf {x}}}\) varying as \(\exp (-4|{{\mathbf {x}}}-{{\mathbf {x}}}_0|^2/R^2) \) with a center \({{\mathbf {x}}}_0\) given by a Poisson point process and a random radius R, instead of random black disks over a white background, so that the image gradient is a smooth function. Matlab software code is available at the following URL: https://members.loria.fr/FSur/software/BSpeckleRender/.
It should be noted that these four components are the derivatives of the local displacement field \({\varvec{\phi }}^{{\mathbf {x}}}\) estimated over \(\varOmega _{{\mathbf {x}}}\). In photomechanics, the derivatives of the displacement field, which are related to strain components, are rather computed from the derivatives of the global displacement \({\varvec{\phi }}\).
References
Blanchet, G., Buades, A., Coll, B., Morel, J.M., Rougé, B.: Fattening free block matching. J. Math. Imaging Vis. 41(1), 109–121 (2011)
Blaysat, B., Grédiac, M., Sur, F.: Effect of interpolation on noise propagation from images to DIC displacement maps. Int. J. Numer. Methods Eng. 108(3), 213–232 (2016)
Blaysat, B., Grédiac, M., Sur, F.: On the propagation of camera sensor noise to displacement maps obtained by DIC—an experimental study. Exp. Mech. 56(6), 919–944 (2016)
Bomarito, G., Hochhalter, J., Ruggles, T., Cannon, A.: Increasing accuracy and precision of digital image correlation through pattern optimization. Opt. Lasers Eng. 91, 73–85 (2017)
Bornert, M., Brémand, F., Doumalin, P., Dupré, J.C., Fazzini, M., Grédiac, M., Hild, F., Mistou, S., Molimard, J., Orteu, J.J., Robert, L., Surrel, Y., Vacher, P., Wattrisse, B.: Assessment of digital image correlation measurement errors: methodology and results. Exp. Mech. 49(3), 353–370 (2009)
Bornert, M., Doumalin, P., Dupré, J.C., Poilâne, C., Robert, L., Toussaint, E., Wattrisse, B.: Shortcut in DIC error assessment induced by image inerpolation used for subpixel shifting. Opt. Lasers Eng. 91, 124–133 (2017)
Bouthemy, P., Toledo-Acosta, B., Delyon, B.: Robust model selection in 2D parametric motion estimation. J. Math. Imaging Vis. 61(7), 1022–1036 (2019)
Cacoullos, T.: Exercices in Probability. Springer, Berlin (1989)
Delon, J., Rougé, B.: Small baseline stereovision. J. Math. Imaging Vis. 28(3), 209–223 (2007)
Fayad, S., Seidl, D., Reu, P.: Spatial DIC errors due to pattern-induced bias and grey level discretization. Exp. Mech. 60, 249–263 (2020)
Fleet, D., Weiss, Y.: Optical flow estimation. In: Handbook of Mathematical Models in Computer Vision. Springer, pp. 237–257 (2006)
Fortun, D., Bouthemy, P., Kervrann, C.: Optical flow modeling and computation: a survey. Comput. Vis. Image Underst. 134, 1–21 (2015)
Getreuer, P.: Linear methods for image interpolation. Image Process. On Line 1, 238–259 (2011)
Grédiac, M., Blaysat, B., Sur, F.: A critical comparison of some metrological parameters characterizing local digital image correlation and grid method. Exp. Mech. 57(6), 871–903 (2017)
Grédiac, M., Blaysat, B., Sur, F.: Extracting displacement and strain fields from checkerboard images with the localized spectrum analysis. Exp. Mech. 59(2), 207–218 (2019)
Grédiac, M., Blaysat, B., Sur, F.: A robust-to-noise deconvolution algorithm to enhance displacement and strain maps obtained with local DIC and LSA. Exp. Mech. 59(2), 219–243 (2019)
Grédiac, M., Blaysat, B., Sur, F.: Comparing several spectral methods used to extract displacement fields from checkerboard images. Opt. Lasers Eng. 127, 105984 (2020)
Grédiac, M., Blaysat, B., Sur, F.: On the optimal pattern for displacement field measurement: Random speckle and DIC, or checkerboard and LSA? Exp. Mech. 60(4), 509–534 (2020)
Grédiac, M., Hild, F. (eds.): Full-Field Measurements and Identification in Solid Mechanics. Wiley, Hoboken (2012)
Hild, F., Roux, S.: Digital image correlation: from displacement measurement to identification of elastic properties: a review. Strain 42(2), 69–80 (2006)
Horn, B., Schunck, B.: Determining optical flow. Artif. Intell. 17(1–3), 185–203 (1981)
Lavatelli, A., Balcaen, R., Zappa, E., Debruyne, D.: Closed-loop optimization of DIC speckle patterns based on simulated experiments. IEEE Trans. Instrum. Meas. 68(11), 4376–4386 (2019)
Lehmann, T., Gonner, C., Spitzer, K.: Survey: interpolation methods in medical image processing. IEEE Trans. Med. Imaging 18(11), 1049–1075 (1999)
Lehoucq, R., Reu, P., Turner, D.: The effect of the ill-posed problem on quantitative error assessment in digital image correlation. Exp. Mech. (2017)
Lucas, B., Kanade, T.: An iterative image registration technique with an application to stereo vision. In: Proceedings of the 7th International Joint Conference on Artificial Intelligence (IJCAI), pp. 674–679. Vancouver (BC, Canada) (1981)
Luo, J., Ying, K., He, P., Bai, J.: Properties of Savitzky–Golay digital differentiators. Digit. Signal Process. 15(2), 122–136 (2005)
Pan, B., Xie, H., Wang, Z.: Equivalence of digital image correlation criteria for pattern matching. Appl. Opt. 49(28), 5501–5509 (2010)
Passieux, J.C., Bouclier, R.: Classic and inverse compositional Gauss–Newton in global DIC. Int. J. Numer. Methods Eng. 119(6), 453–468 (2019)
Reu, P.: All about speckles: aliasing. Exp. Tech. 38(5), 1–3 (2014)
Réthoré, J., Besnard, G., Vivier, G., Hild, F., Roux, S.: Experimental investigation of localized phenomena using digital image correlation. Philos. Mag. 88(28–29), 3339–3355 (2008)
Sabater, N., Morel, J.M., Almansa, A.: How accurate can block matches be in stereo vision? SIAM J. Imaging Sci. 4(1), 472–500 (2011)
Savitzky, A., Golay, M.: Smoothing and differentiation of data by simplified least-squares procedures. Anal. Chem. 36(3), 1627–1639 (1964)
Scharstein, D., Hirschmüller, H., Kitajima, Y., Krathwohl, G., Nesic, N., Wang, X., Westling, P.: High-resolution stereo datasets with subpixel-accurate ground truth. In: Proceedings of the 36th German Conference on Pattern Recognition (GCPR), pp. 31–42. Münster (Germany) (2014)
Scharstein, D., Szeliski, R.: A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 47(1), 7–42 (2002)
Schreier, H., Braasch, J., Sutton, M.: Systematic errors in digital image correlation caused by intensity interpolation. Opt. Eng. 39(11), 2915–2921 (2000)
Schreier, H., Sutton, M.: Systematic errors in digital image correlation due to undermatched subset shape functions. Exp. Mech. 42(3), 303–310 (2002)
Su, Y., Gao, Z., Fang, Z., Liu, Y., Wang, Y., Zhang, Q., Wu, S.: Theoretical analysis on performance of digital speckle pattern: uniqueness, accuracy, precision, and spatial resolution. Opt. Express 27(16), 22439–22474 (2019)
Su, Y., Zhang, Q., Fang, Z., Wang, Y., Liu, Y., Wu, S.: Elimination of systematic error in digital image correlation caused by intensity interpolation by introducing position randomness to subset points. Opt. Lasers Eng. 114, 60–75 (2019)
Su, Y., Zhang, Q., Xu, X., Gao, Z.: Quality assessment of speckle patterns for DIC by consideration of both systematic errors and random errors. Opt. Lasers Eng. 86, 132–142 (2016)
Sur, F., Blaysat, B., Grédiac, M.: Determining displacement and strain maps immune from aliasing effect with the grid method. Opt. Lasers Eng. 86, 317–328 (2016)
Sur, F., Blaysat, B., Grédiac, M.: Rendering deformed speckle images with a Boolean model. J. Math. Imaging Vis. 60(5), 634–650 (2018)
Sur, F., Blaysat, B., Grédiac, M.: On biases in displacement estimation for image registration, with a focus on photomechanics—Extended version. Technical Report hal-02862808, HAL (2020). https://hal.archives-ouvertes.fr/hal-02862808
Sutton, M., Orteu, J.J., Schreier, H.: Image Correlation for Shape. Motion and Deformation Measurements. Springer, Berlin (2009)
Szeliski, R., Scharstein, D.: Sampling the disparity space image. IEEE Trans. Pattern Anal. Mach. Intell. 26(3), 419–425 (2004)
Wang, Y., Lava, P., Reu, P., Debruyne, D.: Theoretical analysis on the measurement errors of local 2D DIC: part I temporal and spatial uncertainty quantification of displacement measurements. Strain 52(2), 110–128 (2016)
Xu, X., Su, Y., Zhang, Q.: Theoretical estimation of systematic errors in local deformation measurements using digital image correlation. Opt. Lasers Eng. 88, 265–279 (2017)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported in part by the French National Research Agency (ANR) under Grant ANR-18-CE08-0028-01 (ICAReS project).
Rights and permissions
About this article
Cite this article
Sur, F., Blaysat, B. & Grédiac, M. On Biases in Displacement Estimation for Image Registration, with a Focus on Photomechanics. J Math Imaging Vis 63, 777–806 (2021). https://doi.org/10.1007/s10851-021-01032-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-021-01032-4