Robust Model Selection in 2D Parametric Motion Estimation

Abstract

Parametric motion models are commonly used in image sequence analysis for different tasks. A robust estimation framework is usually required to reliably compute the motion model over the estimation support in the presence of outliers, while the choice of the right motion model is also important to properly perform the task. However, dealing with model selection within a robust estimation setting remains an open question. We define two original propositions for robust motion-model selection. The first one is an extension of the Takeuchi information criterion. The second one is a new paradigm built from the Fisher statistic. We also derive an interpretation of the latter as a robust Mallows’ $C_P$ criterion. Both robust motion-model selection criteria are straightforward to compute. We have conducted a comparative objective evaluation on computer-generated image sequences with ground truth, along with experiments on real videos, for the parametric estimation of the 2D dominant motion in an image due to the camera motion. They demonstrate the interest and the efficiency of the proposed robust model-selection methods.

1 Introduction

Adopting 2D parametric models is a common practice in motion estimation, motion segmentation, image registration, and more generally in dynamic scene analysis. Video stabilization [25], video summarization [9], image stitching [41], motion detection with a free-moving camera [47], motion layer segmentation [8], optical flow computation [5, 10, 50], tracking [39, 51], time-to-collision estimation for obstacle detection [27], action recognition and localization [16], crowd motion analysis [30], to name a few, all may rely on 2D polynomial motion estimation. A key issue then arises: how to choose the right motion model when adopting a robust estimation setting?

This problem is most often circumvented by settling for empirical choice. The affine motion model is for instance claimed as a good trade-off between efficiency and representativeness without any available information on the dynamic scene. However, a principled method is more powerful and satisfying to properly solve the motion-model selection problem [11, 13, 44]

The most known statistical criteria for model selection are without doubt Akaike information criterion (AIC) [2], Bayesian information criterion (BIC) [38], or Takeuchi information criterion (TIC) [7]. Broadly speaking, it starts from the maximum likelihood and amounts to add to the model fit, a weighted penalty term on the model complexity or dimension, e.g., given by the number of the model parameters. The definition of the weight depends on the statistical information criterion. The likelihood term accounts for a Gaussian distribution of the residuals involved in the regression issue. A comparative study of several of them is reported in [46] for classification in pattern recognition. Let us add the Mallows’ C$_P$ criterion [23] and the minimum description length criterion (MDL) [32], respectively, equivalent to AIC and BIC under certain hypotheses. Finally, let us mention the Akaike criterion with a correction for finite sample sizes (AICc) [7].

However, outliers are usually present whatever the motion estimation support, the entire frame or a more local one. It may be due to local independent motions, occlusions, or any local violation of the assumptions associated with motion computation. Robust estimation [14, 15] is then required in many situations [5, 26, 29, 39] to cope with the presence of outliers. Indeed, least-square estimation finds oneself biased in these cases. As a consequence, the aforementioned information criteria involving a quadratic (i.e., Gaussian) likelihood term are no more exploitable as they stand. Model selection must be revisited in the context of the robust estimation setting.

So far, combining model selection and robust estimation for parametric motion computation has rarely been investigated [44]. In this paper, we propose two different statistical criteria for robust motion-model selection. The first one is an extension of the Takeuchi information criterion (TIC). The second one tackles this problem from a different perspective based on the Fisher statistic. An interpretation as a robust version of the Mallows’ C$_P$ criterion [23] is also provided.

We need a use case to validate the proposed methods in real situations. We want to handle a single-model fitting task, so that we can focus on the robust model-selection problem. We take the task of estimating the global (or dominant) motion in the image due to the camera motion for a shallow scene, which is of primary interest for many applications, e.g., video stabilization or action recognition. In that context, the dominant motion in the image can be represented by a 2D parametric motion model. Indeed, this task is merely an estimation problem in the presence of outliers constituted by the independently moving objects in the scene. It is not interwoven with other involved issues as in motion detection, motion segmentation, or object tracking. On the other hand, the multiple-model fitting issue investigated in [22, 42, 43] is a different problem. The goal is to fit multiple instances of a given type of model over (unknown) subsets of data. These works do not address the selection of the motion model type.

We described a preliminary version of this work in the short conference paper [6]. The present paper is a significant extension of the latter. We have added several contributions: a new criterion -the robust TIC-, improvements in the Fisher-based criterion, an augmented related-work section, a revisited objective comparative evaluation, and more experiments on real videos.

The remainder of the paper is organized as follows. Section 2 is devoted to related work and positioning of our approach. In Sect. 3, we recall a classical robust estimation method of 2D motion models and formulate the model fit. Section 4 describes our first robust motion-model selection method called robust Takeuchi information criterion (RTIC). In Sect. 5, we present our second original method for robust motion-model selection, called Fisher-based robust information criterion (FRIC). Objective comparisons on computer-generated examples with ground truth are reported in Sect. 6, along with experiments on real videos, to assess the performance of our two criteria. Concluding remarks are given in Sect. 7.

2 Related Work and Positioning

2.1 Review of Related Research

Statistical information criteria have been exploited in computer vision for years [13], sometimes with specific formulations and characteristics. Geometric counterparts of AIC and MDL, respectively, termed GAIC and GMDL, were proposed in [18] to take into account a different formulation of model fitting along with the dimension of the manifold involved in a 3D geometric transformation. AIC and BIC were tested in [11] for 2D affine motion-model classification, but they were experimentally proven less efficient than a succession of hypothesis tests deciding in turn on the nonzero parameters of the affine motion model. Indeed, AIC tends to overestimate the complexity of the underlying model. In [49], the most appropriate model among 2D polynomial motion models for motion estimation from normal flows was selected with a penalization factor given by the Vapnik’s measure; the resulting algorithm was favorably compared to AIC, BIC, and generalized cross-validation. In [37], a MDL-based criterion was designed for model selection in 3D multi-body structure and motion from images. A MDL principle is also adopted in [24] for non-rigid image registration. On the other hand, the small-sample-size-corrected version of Akaike information criterion (AICc) was used in [4] for a pixel-wise motion-model selection with a view to crowd motion analysis in video sequences.

Robust model selection on its own was explored in the robust statistics literature along several directions [1, 19, 28, 31, 33, 36]. In [33], a robust extension of AIC (RAIC) was defined, coming up with substituting a general robust estimator $\rho$ of the model parameters $\theta$ for the maximum likelihood estimator. M-estimators are incorporated in BIC, and the asymptotic performance is studied in [21]. A special case is the use of the Huber robust function [15], leading to the RBIC criterion. The Mallows’ C$_P$ criterion is revisited in [34] to yield a robust version. The generalized information criterion (GIC), described in [19], can be applied to evaluate statistical models constructed by other procedures than maximum likelihood, such as robust estimation or maximum penalized likelihood.

In contrast, to the best of our knowledge, very few similar investigations have been undertaken regarding motion analysis in image sequences. In [3], the authors designed a global energy function for both the robust estimation of mixture models and the validation of a MDL criterion. The overall goal is to get a layering representation of the moving content of an image sequence. The MDL encoding acts on the overall cost of the representation comprising the number of layers, residuals, and motion parameters. However, the primary purpose was parsimonious motion segmentation and not motion-model selection on its own. In [44], a robust extension of the geometric information criterion (GIC) [17], termed GRIC, is proposed in the vein of RAIC. It was applied to the selection of the 3D geometric transformation attached to a rigid motion and estimated through the matching of image interest points. Geometrical and physical constraints are also explored in [12] for image motion segmentation, with the so-called surface selection criterion (SSC) primarily designed by the authors for range data segmentation. Better performance is reported than with several information criteria, but the use of SSC here is comparable to a regularization approach.

Since we start with a set of 2D parametric motion models meant to provide us with an approximation of the unknown optical flow, we naturally adopt a parametric approach for the robust motion-model selection problem. We are looking for the simplest model among the set, able to describe the motion of the maximum amount of image points. An alternative could be to follow a nonparametric approach by modeling the outliers themselves. This can be done by representing the distribution of the noise as a mixture of two distributions, the second one having small probability and taking large values. More specifically, in [20], robust Gaussian process regression is investigated. However, comparing mixture of distributions seems intricate. We believe that it is much easier to compare directly parametric motion models. The authors of [52] address the related problem of image stitching when the projective assumption may be locally violated. The aim is to estimate a globally projective warp while adjusting it on the data to improve the fit. However, this data-driven method leads to a different problem, that is, the adequacy of a given model, and not the selection among several different models.

2.2 Our Approach

In computer vision and in particular in dynamic scene analysis, for instance when estimating the global image motion, the concern is not only to choose the best model, but also to get the largest possible inlier set. Selecting a simple global motion model that only fits the apparent motion of a too limited part of the static scene is not appropriate. As a consequence, the size of the inlier set must be properly taken into account in the robust model-selection criterion.

The problem of robust motion-model selection is then threefold: (1) maximizing the motion model fit to the data, (2) penalizing the motion-model complexity, (3) accounting for the largest possible set of inlier points in the estimation support. Indeed, the two latter ones must be simultaneously satisfied, which might be contradictory. By definition, this is an issue specific to robust model selection. It apparently did not draw interest in the robust statistics literature, while it is of key importance in motion analysis. In this paper, we introduce two robust motion-model selection methods in that perspective. The first one is in the vein of approaches extending the non-robust model-selection criteria, but here, we start, in an original way, with the Takeuchi criterion [7]. The second method promotes a new paradigm based on Fisher statistic [35].

To make the robust motion-model selection problem concrete, we will deal with the dominant image motion estimation issue. The dominant (or global) image motion is usually due to the camera motion, and then corresponds to the background motion, i.e., the apparent motion of the static scene in the image sequence. Computing the dominant motion has many important applications such as video stabilization, background subtraction in case of a free-moving camera, action recognition, image stitching, and image registration in general. Of course, the proposed framework could be applied to other issues as well, for instance, to select the right motion model in each image region for motion layer segmentation.

3 Robust Motion-Model Estimation

First, we briefly recall the main principles of the robust estimation of parametric motion models. The estimation process relies on the brightness constancy assumption and is embedded in a coarse-to-fine scheme to handle large displacements. We will present it in the frame of the motion-model computation over the whole image domain $\Omega$, but it can be straightforwardly adapted to the computation of the motion model over a given area in the image. Then, we will define the motion-model fit for the estimated motion model parameters. Finally, we will describe the set of 2D parametric motion models that will be considered, appertaining to the category of polynomial models.

Table 1 Set of 2D polynomial motion models

3.1 Computation of Motion-Model Parameters

We consider a set of 2D polynomial motion models. They will be precisely defined in Sect. 3.3 and Table 1. Let $\theta _m$ denote the parameters of model m, that is, the polynomial coefficients for the two components of the velocity vector. Parameters of the full model will be denoted by $\theta _M$, if we have M models to test. $\mathbf{w}_{\theta _m}(p)$ is the velocity vector supplied by the motion model m at point $p=(x,y)$ of the image domain $\Omega$.

We exploit the usual brightness constancy assumption [10] to estimate the parameters of the motion model between two consecutive images of the video sequence. It leads to the linear regression equation relating the motion-model parameters, through the velocity vector, and the space–time derivatives of the image intensity I:

$$\begin{aligned} \nabla I(p)\cdot \mathbf{w}_{\theta _m}(p) + I_t(p) = 0. \end{aligned}$$

(1)

Let us denote $r_{\theta _m}(p)$ the left member of (1). The robust estimation of the motion-model parameters can be defined by:

$$\begin{aligned} {\hat{\theta }}_m = \arg \min _{\theta _m} \sum _{p\in \Omega } \rho (r_{\theta _m}(p)), \end{aligned}$$

(2)

where $\rho$ denotes any robust penalty function. To quote a few examples of penalty function among M-estimators, the Lorentzian function is used in [5], whereas the Hampel estimator is preferred in [39], and the Tukey’s function is adopted in [29].

Equation (1) is in fact the linearization of the more general constraint $I(p+\mathbf{w}_{\theta _m}(p)) - I(p,t) = 0$. As a consequence, it only holds for small displacements. A usual way to overcome this problem is to follow a coarse-to-fine scheme based on image multi-resolution and incremental motion estimation [10]. More specifically, we compute two image pyramids by applying a Gaussian filter and subsampling by two in row and column the two consecutive images of the pair, from level to level. The minimization of (2) is achieved by an iterative algorithm, the iterated reweighting least squares (IRLS) method [14]. The IRLS method iteratively updates weights at every point $p\in \Omega$. The weights express the influence of each point p in the estimation of the motion-model parameters. These weights can be further exploited to determine the inlier set associated with the estimated motion model m.

Regarding the initialization of the IRLS algorithm, we proceed as follows. At the very first iteration of the iterative estimation, at the coarsest resolution level, we initialize all the weights to one and perform a first estimation of the motion parameters. This of course amounts to a classical least mean-square estimation. However, this is a very common practice, and it works well in practice, especially since we use it only once at the coarsest image resolution. Afterward, since we switch to the incremental mode, we initialize the IRLS algorithm at every step of the incremental estimation, by taking zero as initial value of the motion parameter increment. Indeed, the latter is supposed to be small. In other words, we start by updating the weights with the current estimate of the motion-model parameters. We usually need only a few iterations of the IRLS algorithm to converge. For more information on estimation issues like initialization of IRLS, definition of the scale parameter of the penalty function, impact of the outlier rate, estimation accuracy, we refer the reader to [29].

3.2 Motion-Model Fit

Once we compute an estimate ${\hat{\theta }}_m$ of the motion-model parameters, we get the residuals $r_{\hat{\theta }_m}(p)$, for all $p \in \Omega$, measuring the discrepancy between the input data and the estimated motion model. To evaluate how the estimated motion model fits the input data over the associated inlier set, we consider the residual sum of squares (RSS) obtained for the robustly estimated parameters ${\hat{\theta }}_m$ of the motion model m, given by:

$$\begin{aligned} \mathrm{RSS}_m = \sum _{p\in {\mathcal {I}_m}} r^2_{\hat{\theta }_m}(p), \end{aligned}$$

(3)

where $\mathcal {I}_m$ represents the set of inliers associated with the estimated motion model m. The way the inlier set is computed will be further explained in Sect. 5.1. The residual is formally defined by:

$$\begin{aligned} r_{\hat{\theta }_m}(p) = I(p+\mathbf{w}_{\hat{\theta }_m}(p),t+1)-I(p,t), \end{aligned}$$

(4)

knowing that the left member of (1) is a linearized version of (4) as aforementioned.

We compute RSS$_m$ on the inlier set $\mathcal {I}_m$ and not on the overall domain $\Omega$, to obtain the model fit evaluation precisely on the subset of points whose motion conforms to the estimated motion model. In [45], the authors designed a method for estimating deformable registration from feature correspondences between two images. The outlying correspondences are removed once for all by first estimating a simple parametric model. The rationale is that the outlier deviations are much larger than the inaccuracies of the simple model fit for relevant correspondences. However, on our side, we need to achieve the outlier removal for every model, since the inlier set depends upon each motion model, and its cardinality is one of the key ingredients of our robust motion-model selection criteria.

Furthermore, we need to introduce the expression RSS$_m^{+}$, which represents the residual sum of squares computed for the full model M over the inlier set $\mathcal {I}_m$ attached to model m. The full model, that is, the most complex one in the set of the parametric motion models, will be specified in the next Sect. 3.3. We have:

$$\begin{aligned} \mathrm{RSS}_m^{+} = \sum _{p\in {\mathcal {I}_m}} r^2_{\hat{\theta }_M}(p). \end{aligned}$$

(5)

As recall in Sect. 3.1, the minimization in (2) is solved by applying the iteratively reweighted least squares algorithm within a coarse-to-fine framework. At convergence, the final weights $\alpha _m(p), p\in \Omega$ are given by:

$$\begin{aligned} \alpha _m(p) = \frac{\psi (r_{\hat{\theta }_m}(p))}{r_{\hat{\theta }_m}(p)}, \end{aligned}$$

(6)

where the influence function $\psi (.)$ is the derivative of the robust function $\rho (.)$, $\psi (r)=\frac{d \rho (r)}{dr}$. In practice, we adopt the robust estimation method defined in [29], and we use the publicly available Motion2D¹ software implementing this method.

3.3 Set of Parametric Motion Models

We are dealing with 2D polynomial motion models ranging from translation (polynomial of degree 0) to quadratic models (polynomials of degree 2), including different affine models (polynomials of degree 1). They are forming a set of models which is partly nested. The model complexity ranges from dimension 2 to dimension 12. The full set of motion models is given in Table 1 with their main features. The explicit equivalence, when available, between the 2D polynomial models and 3D physical motions assumes a perspective projection for the image formation and 3D rigid motion.

To make it easier to understand the relationship between 2D motion models and 3D motion, let us briefly recall the mathematical relations which link them. The 2D velocity vector $\mathbf{w}(p)=(u(p),v(p))^T$ is the projection of the 3D velocity vector of point $P=(X,Y,Z)^T$ in the scene, whose point p is the projection onto the image plane. We follow the classical perspective projection assumption, and we take a focal length of unity. We get:

$$\begin{aligned} \left\{ \begin{array}{lll} u(p) &{} = &{} \frac{U}{Z} - x \frac{W}{Z} - A xy + B (x^2+1) - C y \\ ~\\ v(p) &{} = &{} \frac{V}{Z} - y \frac{W}{Z} - A (y^2+1) + B xy + C x, \end{array} \right. \end{aligned}$$

(7)

where the instantaneous rigid motion is specified by the translational and rotational velocities, respectively, $(U,V,W)^T$ and $(A,B,C)^T$ in the 3D coordinate systems, whose origin is located at the camera projection center and the Z-axis aligned with the camera axis of view. We refer the reader, for instance, to [48] for mathematical details. If we further assume that the scene is planar, then any depth Z is given by the plane equation: $Z = Z_0 + \gamma _1 X + \gamma _2 Y$, and knowing that $x=\frac{X}{Y}$ and $y=\frac{Y}{Z}$, we come up with:

$$\begin{aligned} \left\{ \begin{array}{lll} u(p) &{} = B + \frac{U}{Z_0} + x \left( -\gamma _1 \frac{U}{Z_0} - \frac{W}{Z_0}\right) + y \left( - \gamma _2 \frac{U}{Z_0} - C\right) \\ ~\\ &{}\quad +\, x^2 \left( \gamma _1 \frac{W}{Z_0} + B\right) + xy \left( \gamma _2 \frac{W}{Z_0} - A\right) \\ ~\\ v(p) &{} = -A + \frac{V}{Z_0} + x \left( -\gamma _1 \frac{V}{Z_0} +C\right) + y \left( - \frac{W}{Z_0} + \gamma _2 \frac{V}{Z_0}\right) \\ ~\\ &{}\quad +\, xy \left( \gamma _1 \frac{W}{Z_0} + B\right) + y^2 \left( \gamma _2 \frac{W}{Z_0} - A\right) . \end{array} \right. \end{aligned}$$

(8)

A pan–tilt–camera motion is a pure rotation of component A around the X-axis, and component B around the Y-axis, and then, C, U, V, W are all equaling zero. Applying this to equations (8) gives the expression of the 2D motion model PT, with $a_1=B$ and $a_4=-A$. A rotation in the plane, i.e., around the Z-axis, means that only $C\ne 0$, which explains the expression of motion model TR, with $a_3=C$. A translation along the axis of view implies that only $W\ne 0$, which leads to the expression of motion model TS, with $a_2=-W/Z_0$. Finally, we can easily infer from Eq. (8) that the eight-parameter PSRM model precisely accounts for a rigid motion between a planar surface and the camera. Let us add that the constant monomial of models PT, TR, TS, and TRS does not necessarily mean that the underlying physical motion has actually a translation component. Indeed, the constant part is merely the velocity vector given by the motion model at the origin of the image coordinate system. The in-plane rotation is not necessarily centered at the origin. The same holds for the focus of expansion in case of scaling motion, knowing that the scaling motion in the image is due to a translation of the camera along its axis of view. Finally, let us recall that our 2D motion models are defined in the velocity field space, not in the point-to-point geometrical transformation space. Nevertheless, parallels can be drawn. For instance, the eight-parameter quadratic motion model is the counterpart of the homography.

The FQ model corresponding to the full polynomial of degree 2 has no specific physical interpretation. It will act in the sequel as the full model M, that is, the most complex model in the set of the tested parametric motion models.

Let us stress that this 3D motion interpretation is just given to motivate the set of 2D parametric motion models, which incidentally are of common use in many applications of video processing and dynamic scene analysis. Indeed, we are not concerned with any 3D scene recovery goal. The latter is a different task. The motion-model selection is still relevant, even if no physical interpretation is sought, that is, just finding the right 2D motion model to represent the (unknown) optical flow field in the image, in other words, finding the right polynomial to represent an unknown function. Besides, we do not claim that there is a correct model on its own. We just aim to select the most appropriate one among the set of predefined motion models.

4 Robust Motion-Model Selection with RTIC

An intuitive approach for defining a robust motion-model selection framework is to draw from classical statistical information criteria. However, instead of starting from AIC or BIC, we consider the Takeuchi information criterion (TIC) which is a more general derivation of Akaike’s information criterion [7].

4.1 TIC Criterion

TIC can be written as follows:

$$\begin{aligned} \mathrm{TIC}(m) = 2 \mathcal {K}(\hat{\theta }_m) + 2 \; \mathrm{tr}(P(\theta _m)Q(\theta _m)^{-1}), \end{aligned}$$

(9)

where $\mathcal {K}$ denotes the contrast function. Equivalently, it could be referred to as the negated logarithm of the likelihood, or the pseudo-likelihood function. “tr” is the trace of the matrix. The two $m\times m$ matrices $P(\theta _m)$ and $Q(\theta _m),$ respectively, involve first and second mixed partial derivatives of the likelihood function w.r.t. model parameters. In the regression case, the two matrices P and Q are defined by:

$$\begin{aligned} P(\theta _m)&= E\left[ \frac{\partial }{\partial _{\theta _i}}g(r_{\theta }(p)) \frac{\partial }{\partial _{\theta _j}}g(r_{\theta }(p))^T\right] _{|\theta =\hat{\theta }_m} \nonumber \\ Q(\theta _m)&= E\left[ \frac{\partial ^2}{\partial _{\theta _i}\partial _{\theta _j}}g(r_{\theta }(p))\right] _{|\theta =\hat{\theta }_m}, \end{aligned}$$

(10)

where $\{\theta _i, i=1,m\}$ and $\{\theta _j, j=1,m\}$ denote components of the parameter vector $\theta _m$, function g(.) is defined by $\mathcal {K}(\theta _m) = \sum _p g(r_{\theta _m}(p))$, $r_{\theta _m}(p)$ acts as the regression residual, and E denotes expectation.

4.2 Robust TIC

In the context of robust estimation, the g function is now specified as a robust penalty function $\rho (.)$, which was introduced in Eq. (2). We come up with the following expression of the Takeuchi information criterion, which we will call robust Takeuchi information criterion (RTIC) to make it short:

$$\begin{aligned} \mathrm{RTIC}(m) = 2 \sum _{p\in \Omega } \rho (r_{\hat{\theta }_m}(p)) + 2q_m \frac{E[\psi (r_{\theta }(p))^2]}{E[\psi '(r_{\theta }(p))]}_{|\theta =\hat{\theta }_m}, \end{aligned}$$

(11)

where $q_m$ is the dimension (i.e., number of parameters) of model m, $\psi (.)$ is the influence function as defined in Sect. 3.2, and $\psi '$ its derivative.

We develop two versions of RTIC for the Talwar and Huber penalty functions, which are well-known simple enough robust functions. The Talwar function is defined by:

$$\begin{aligned} \rho _{\mathrm{tal}}(r) = \left\{ \begin{array}{ll} r^2/2 &{} \text{ if } \; |r| \le \alpha \\ \alpha ^2/2 &{} \text{ if } \; |r| > \alpha \end{array} \right. \end{aligned}$$

(12)

Knowing that the inlier set $\mathcal {I}_m$ corresponds to points p such that $|r_{\theta _m}(p)| \le \alpha$, we estimate the expectation as:

$$\begin{aligned} E[\psi (r_{\theta }(p))^2] \simeq&\frac{1}{|\Omega |} \sum _{p\in \Omega } \psi (r_{\theta }(p))^2 = \frac{1}{|\Omega |} \sum _{p\in \mathcal {I}_m} r_{\theta }^2(p),\nonumber \\ \text{ and } \; \; E[\psi '(r_{\theta }(p))] \simeq&\frac{|\mathcal {I}_m|}{|\Omega |}, \end{aligned}$$

(13)

where |.| denotes the cardinality of the set. We get the following expression of RTIC for the Talwar penalty function:

$$\begin{aligned} \mathrm{RTIC}_{\mathrm{tal}}(m) = 2 \sum _{p\in \Omega } \rho (r_{\hat{\theta }_m}(p)) + \frac{2q_m}{|\mathcal {I}_m|} \sum _{p\in \mathcal {I}_m} r_{\hat{\theta }_m}^2(p). \end{aligned}$$

(14)

We make the same development for the Huber function defined as follows:

$$\begin{aligned} \rho _{\mathrm{hub}}(r) = \left\{ \begin{array}{ll} \frac{1}{2}r^2 &{} \quad \text{ if } \; |r| \le \alpha \\ \alpha (|r| - \frac{1}{2}\alpha ) &{} \quad \text{ if } \; |r| > \alpha , \end{array} \right. \end{aligned}$$

(15)

and the RTIC expression turns out to write for the Huber function:

$$\begin{aligned} \mathrm{RTIC}_{\mathrm{hub}}(m)&= 2 \sum _{p\in \Omega } \rho (r_{\hat{\theta }_m}(p))\nonumber \\&\quad + \frac{2q_m}{|\mathcal {I}_m|} \left( \sum _{p\in \mathcal {I}_m} r_{\hat{\theta }_m}^2(p) + \sum _{p\in \Omega {\setminus } \mathcal {I}_m} \alpha ^2\right) . \end{aligned}$$

(16)

The selected model $\tilde{m}$ is the one minimizing RTIC$_{\mathrm{tal}}(m)$ (respectively, RTIC$_{\mathrm{hub}}(m)$) among the tested models. The parameters $\hat{\theta }_m$ are obtained from (2) with the Talwar (resp. Huber) $\rho$-penalty function. In contrast to RAIC and RBIC, the size $|\mathcal {I}_m|$ of the inlier set explicitly intervenes in the second term of the expression of the two RTIC variants (14) and (16). Minimizing RTIC implies to maximize the size of the inlier set.

5 Robust Motion-Model Selection with FRIC

On the other hand, we have investigated a very different approach than those proposed so far for robust model selection. As in [11], we adopt now a two-class hypothesis test approach. This is first motivated by the fact that we are dealing with a non-nested set of parametric motion models. For instance, both the rotation and the scaling models involve three parameters as described in Sect. 3.3, but they account for quite different motions. Moreover, we aim to select the model m which explains the motion of the maximum number of points in the estimation support, that is, with the largest possible inlier set. Let us stress that taking the simplest motion model, while maximizing the size of the inlier set, may be contradictory in most tasks of dynamic scene analysis. Then, it is beneficial to explicitly tackle this issue from the off.

5.1 Fisher Statistic

The first step is to compare any model m of the set of tested models to the full model M. To this end, we consider the Fisher statistic [35], which can be expressed as follows:

$$\begin{aligned} \mathcal {F}(m) = \frac{(\mathrm{RSS}_m - \mathrm{RSS}_m^{+}) / (q_M-q_m)}{\mathrm{RSS}_m^{+} / (|\mathcal {I}_m|-q_M)}, \end{aligned}$$

(17)

where again |.| designates the set cardinality and $q_m$ represents the number of parameters of model m. Both $RSS_m$ and $RSS_m^{+}$ are evaluated on the inlier set $\mathcal {I}_m$ attached to the tested model m. To really deal with Fisher statistic, both model parameters, $\theta _m$ and $\theta _M$, must be estimated on the same set too. Therefore, we reestimate $\theta _m$ and $\theta _M$ over $\mathcal {I}_m$ in a least-square setting, before evaluating $\mathcal {F}(m)$. By the way, it also improves the estimated parameters of model m, and consequently, the model fit.

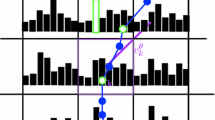
In addition, we must check that the estimate of $|I_m|$ has no noticeable variability, so that it has no impact on the Fisher statistic. An image point p belongs to the inlier set if its attached weight at the end of the IRLS procedure is greater than a given threshold. We can at least empirically assess the absence of significant variability, by providing histograms of weights computed for the estimation of the motion parameters in the IRLS procedure, as explained in Sect. 3.1. Samples are supplied in Fig. 1, with the Tukey function used in the robust motion-model parameter estimation. Similar behavior was observed in many experiments. The plots show that the weight histograms are clearly bimodal, with one mode close to 0 and the second one close to 1, after normalization of the weights. Then, it is easy to get the inlier set $\mathcal {I}_m$. The threshold used to determine the inlier set is not critical at all, and this step does not introduce any randomness in $|I_m|$. Indeed, the range of values for the threshold value is large. In practice, we will set it to 0.5. Then, we can assume that the cardinality of the inlier set is as legitimate as the fit residual and the model complexity in the definition of the robust model-selection criterion. The configuration is even simpler in the case of the Talwar and Tukey functions, since the weights are null for outliers and strictly positive for inlier points.

Fig. 1

Examples of histograms of weights supplied by the IRLS procedure in the robust estimation of the image dominant motion model for two different experiments

The denominator of expression (17) can be interpreted as a non-biased empirical estimate of the full model variance computed on $\mathcal {I}_m$. It will be denoted by:

$$\begin{aligned} {\hat{\sigma }}^2_{M}(\mathcal {I}_m) = \frac{\mathrm{RSS}_m^{+}}{|\mathcal {I}_m|-q_M}. \end{aligned}$$

(18)

The statistic $\mathcal {F}(m)$ allows us to decide whether model m is a more significant representation of the unknown true motion than the full model M over $\mathcal {I}_m$ which is the validity domain of model m in $\Omega$. However, it will supply all the models m of that type. We need to take into account the dimension $q_m$ of model m to further select the right one.

5.2 Fisher-Based Robust Information Criterion (FRIC)

Starting from (17), and penalizing the complexity of the model expressed by the number $q_m$ of model parameters, we define the Fisher-based robust information criterion:

$$\begin{aligned} \mathrm{FRIC}_1(m) = \mathcal {F}(m) (q_M-q_m) + 2q_m. \end{aligned}$$

(19)

Under the assumption of validity of model m, $\mathcal {F}(m)$ follows a Fisher distribution $F(q_M-q_m,|\mathcal {I}_m|-q_M)$. Then, the first term of the right member of (19) (approximately) follows a $\chi ^2$ distribution with $q_M-q_m$ degrees of freedom.

We can now write the test for selecting the best motion model $\tilde{m}$ in this robust model-selection framework:

$$\begin{aligned} {\tilde{m}} = \arg \min _m \mathrm{FRIC}_1(m). \end{aligned}$$

(20)

The theoretical behavior of this test can be qualitatively described as follows. $FRIC_1(m)$ is supposed to decrease when evaluating in turn the first successive models in decreasing (or equivalently increasing) complexity order up to the optimal model $m^{*}$, and then to increase for the subsequent models. This is confirmed by Fig. 2 which contains plots of $FRIC_1(m)$ values for several experiments.

Fig. 2

Plots of $FRIC_1(m)$ values corresponding to the set of tested motion models for several experiments. Tested motion models are those listed in Table 1, and ordered according to the number of parameters. The true model is FA

We design a second version of the Fisher-based robust model selection criterion, by incorporating the number of inliers in the model complexity penalization as in the BIC criterion, that is:

$$\begin{aligned} \mathrm{FRIC}_2(m) = \mathcal {F}(m) (q_M-q_m) + 2 \log (|\mathcal {I}_m|) q_m. \end{aligned}$$

(21)

5.3 Interpretation of FRIC as Robust C$_p$

We now provide another interpretation of the Fisher-based robust information criterion (FRIC) defined in (19). Let us first make ${\hat{\sigma }}^2_{M}(\mathcal {I}_m)$ appear in the expression of $\mathrm{FRIC}_1(m)$ as follows:

$$\begin{aligned} \mathrm{FRIC}_1(m) = \frac{(\mathrm{RSS}_m - \mathrm{RSS}_m^{+})}{{\hat{\sigma }}^2_{M}(\mathcal {I}_m)} + 2q_m, \end{aligned}$$

(22)

By exploiting (3) and (18), it can be further developed into:

$$\begin{aligned} \mathrm{FRIC}_1(m) = \frac{1}{{\hat{\sigma }}^2_{M}(\mathcal {I}_m)} \sum _{p\in \mathcal {I}_m}r^2_{\hat{\theta }_m}(p) - |\mathcal {I}_m| + q_M + 2q_m. \end{aligned}$$

(23)

If we neglect $q_M$ which is a constant term for the test (20), expression (23) can be viewed as the Mallows’ C$_P$ criterion [23], computed over the inlier set attached to model m with $|\mathcal {I}_m|$ as the number of observations. Then, our test (20) could also be interpreted as a robust version of the Mallows’ C$_P$ criterion.

Let us point out that (23) explicitly involves the aforementioned trade-off between maximizing the size $|\mathcal {I}_m|$ of the inlier set and minimizing the complexity (i.e., the number $q_m$ of parameters) of the selected motion model. In contrast, for existing robust model-selection criteria such as RAIC or RBIC which write

$$\begin{aligned} \mathrm{RAIC} = \sum _{p\in \Omega }\rho (r_{\hat{\theta }_m}(p)) + q_m, \end{aligned}$$

(24)

and

$$\begin{aligned} \mathrm{RBIC} = \sum _{p\in \Omega }\rho (r_{\hat{\theta }_m}(p)) + \log |\Omega | \; q_m, \end{aligned}$$

(25)

the model selection is only implicitly influenced by the size of the inlier set attached to model m through the values of the robust function $\rho (.)$ at the outlier points. Hence, the impact depends on the asymptotic behavior of the robust function. The same holds for [34] where in addition the penalty term requires additional expensive computation to be evaluated.

Fig. 3

From left to right: the input image, the second image generated from the first one, by applying a translation as dominant motion and a different translation on the outlier rectangular area in the middle of the image, as plotted in the right part

Table 2 Range of parameter values for the different motion models

6 Experimental Results

As pointed out in the introduction, we take the computation of the dominant image motion to experimentally validate our robust motion selection methods. In contrast to motion segmentation for instance, it is a pure estimation problem. Furthermore, it must tackle the presence of outliers consisting in independently moving objects in the scene, since the dominant motion in the image is (most generally) induced by the camera movement. Thus, it is a robust estimation problem. Finally, choosing the right 2D motion model to properly approximate the dominant image motion is an issue, since the camera motion and the scene depth are most often unknown. In addition, it is a typical and very frequently needed task in dynamic scene analysis. However, there is no available benchmark for this purpose, and inferring ground truth on real videos may be not that easy. Since we focus on the model selection issue, we will report selection results only. The accuracy of the estimated motion model is conveyed by the model fit term of the criterion, and it is not a concern on its own for this work.

6.1 Objective Evaluation on Synthetic Examples

To quantitatively assess the performance of the model selection criteria, we carried out a comparative objective evaluation on a synthetic dataset. We generated a series of image pairs by applying a velocity field to a real image, as shown in Fig. 3. The velocity field involves two parametric subfields chosen from the list given in Table 1. The first parametric motion subfield is the dominant motion, and the outliers, forming a rectangular region in the middle of the image, undergo the second one. We used bilinear intensity interpolation when needed to reconstruct the second image. We used border replication to deal with image boundaries. We generated outlier motion in the synthetic examples with a parametric motion model for the sake of efficiency. However, when estimating the global motion and computing the robust selection criteria, we never model the outlier motion nor estimate it. It could be anything, as the dust cloud in the real example of Fig. 8, or many independently moving cars in Fig. 9.

Three groups of 3000 synthetic image pairs were generated, each group formed by different dominant and secondary motions. The first group involves a translation (T) motion model as dominant motion model and a full affine (FA) as secondary motion. The second set has a FA model as dominant motion and a planar surface rigid motion (PSRM) as secondary motion model. The last group has a PSRM model as the dominant one and a T model as the secondary one. Each group is divided in two subgroups of 1500 image pairs each depending on the range used for the values of the parameters of the dominant motion, as summarized in Table 2. For each motion model used to create the image pairs, the value of its parameters is randomly selected in the interval given in Table 2.

Fig. 4

Rates of correct classification for each group of experiments obtained with the four model-selection criteria (given in percentage of the total number of examples in each experiment). S1 stands for FRIC$_1$ and S2 for FRIC$_2$

We proceed to the selection of the dominant motion model in each experiment for each compared criterion. Rates of correct selection are summarized in Fig. 4. For a fair comparison, we decided to use the same penalty function for all the compared criteria in all the experiments, that is, to estimate the parametric motion models and to compute the four robust motion-model selection criteria. For implementation issues, we took the Talwar penalty function, with $\alpha$ set to 2.795 as recommended in [40]. It is available in the Motion2D software, which is not the case for the Huber function. Still, we will refer to the compared existing method as RBIC. In addition, for the sake of notation simplicity, we will write RTIC instead of $\mathrm{RTIC}_{\mathrm{tal}}$. Scores are given in percentage of the total number of the images in each experiment.

Overall, the proposed criteria $\mathrm{FRIC}_1$, $\mathrm{FRIC}_2,$ and RTIC outperform the existing one RBIC. Regarding $\mathrm{FRIC}_2$, the rate of successful motion-model selection is rather stable at a high level, ranging from a minimum of 74.4$\%$ of frames to a maximum of 83.4$\%$. $\mathrm{FRIC}_1$ also provides good results, but it has a lowest success rate with a minimum of 61.2$\%$ and a maximum of 82.1$\%$. In general, RBIC has a close but lower success rate than the three new criteria, and even reaches down to a very low rate at 38.6$\%$ for the FA2 experiment. RTIC has the lowest success rate in the T2 experiment by a small margin, while being the best performing criterion for all the other experiments.. Especially, when the complexity of the dominant motion models increases, RTIC yields the best results, even scoring over a 94$\%$ success rate in a couple of experiments.

Tables 3 and 4 detail the scores obtained with $\mathrm{FRIC}_2$ and RTIC, respectively, the two best criteria, for all the tested models and for the six subsets of experiments. Wrong selections are spread, but mostly concern more complex models than the true one.

Table 3 Scores obtained with criterion $\mathrm{FRIC}_2$ for all the tested models and for the six experiments, in percentage of the total number of examples in each experiment

Table 4 Scores obtained with criterion $\mathrm{RTIC}$ for all the tested models and for the six experiments, in percentage of the total number of examples in each experiment

We conducted complementary experiments to analyze the behavior of the criteria in the presence of noise. We corrupted the two images with independent Gaussian noise of increasing variances (5, 10, 15, 20) for a series of 100 pairs of images with T model as dominant motion and PSRM model as secondary motion. When adding independent noise on the pixel intensities, the brightness constancy assumption is no more strictly valid. Table 5 supplies the relative performance change of the robust motion-selection criteria in the presence of noise of varying levels. The percentage of relative variation is given with respect to the selection score of the true model T obtained with a reference small noise of variance 2. We can observe that RBIC is not robust to noise. RTIC is slightly and smoothly affected (as one could expect) by noise up to a variance of 15. Somewhat surprisingly, the FRIC criteria have a more irregular behavior, especially $\mathrm{FRIC}_1$, knowing that the absolute performance score of $\mathrm{FRIC}_1$ is much lower than those of RTIC and $\mathrm{FRIC}_2$.

Table 5 Relative change in performance of selecting the true model, with added Gaussian noise of increasing variance

To compare the selection criteria on the same fair basis, as aforementioned, we used the simple Talwar robust function to estimate the motion model, since it is implemented in the Motion2D software. The Tukey function is also available in the Motion2D software. Then, we rerun the experiments on the synthetic dataset for the FRIC criteria, to know if their performance may depend on the robust fitting stage. From Table 6, we can observe that results are similar apart from experiment PSRM1 where results are a bit different. Then, there is no evidence for any dependence on the robust function used.

Table 6 Comparison of FRIC criteria results for two different robust functions, Talwar (Tw) and Tukey (Tk) functions, respectively, for the same experiments as those of Fig. 4

6.2 Results on Real-Image Sequences

To evaluate the performance of the proposed criteria on real cases, we carried out experiments on two sets of video sequences. The first one contains videos acquired with a robot setup in our laboratory, the second set gathers videos collected on the web.

For the real experiments, we keep a subset of five motion models of Table 1: $\{$T, TR, TS, PSRM, FQ$\}$. FA was removed since it does not precisely correspond to any given camera motion. Clearly, inferring the ground-truth motion models in real sequences is harder. As a consequence, we limited the set of motion models to models representative of real physical camera motion. In addition, FQ still serves as the full model. PT is removed since it involves the same two parameters as T, and the perceived motion is quite similar for the two respective camera motions.

Let us make a cautious observation on the ground-truth issue when dealing with real videos. In contrast to the experiments with computer-generated sequences reported in the preceding Sect. 6.1, we cannot state right away which motion model is the true one. We can just try to infer it from the 3D motion of the camera and the 3D structure of the scene, given the relation between the 3D (rigid) motion of the camera, and the 2D image motion recalled in Sect. 3.3. For the videos acquired with our robot setup, we control the robot motion and the scene layout, but to a certain extent. As a consequence, the ground truth cannot be established with $100\%$ confidence. For the experiments on the video sequences downloaded on the net, reported later on in this subsection, we deduced the ground truth only from the visual inspection of the sequences. It is definitively subject to even greater uncertainty on the exact 3D motion of the camera and the pose of the scene.

The first set of real-image sequences were acquired with a camera mounted on a Cartesian coordinate robot available in our laboratory. The setup enables to apply a given motion type to the robot. Ideally, the motion applied to the robot, and then to the camera, induces the dominant motion of the image sequence. Since we estimate one single motion model to account for the dominant image motion, we need to assume a planar scene so that the ground-truth motion model can be inferred unambiguously for the dominant image motion. Otherwise, in case of a non-shallow scene, we would need multiple motion models and a segmentation framework to fit a motion model to each part of the scene, since depth and surface orientation impact on the resulting image motion. However, this is beyond the scope of this work. For these laboratory video sequences, a poster depicting an aerial view of a city constitutes the scene background. In addition, we introduce an independent motion in the scene using an additional single axis robot bearing a flat object and moving in the field of view of the camera. The complete setup is drawn on Fig. 5. A sample of acquired images is given in Fig. 6 showing that the outlier moving region may occupy a substantial part of the image (on the left of the image).

We report two experiments. In the first experiment, a rotation around the view axis is applied to the robot to produce an image sequence of 146 frames as illustrated in Fig. 6. Since the rotation axis does not pass by the optical center, the expected dominant motion model is the combination of a translation and a in-plane rotation (TR).

Fig. 5

Robotic setup for the acquisition of video sequences. The camera is mounted at the robot end effector. The scene background is a planar surface formed by a poster. The outlier object is a square flat object translating along an axis put on the poster

Fig. 6

First and last frames of the first robot sequence, and the dominant flow between frames 0 and 1 computed with TR model. The outlier area is framed in red in the first image

Table 7 contains the model selection results provided by our criteria $\mathrm{FRIC}_1$, $\mathrm{FRIC}_2$ and RTIC, along with RBIC. $\mathrm{FRIC}_2$ and RTIC select the true motion model (TR) with a good percentage rate of 64.8$\%$ and 76$\%,$ respectively. Let us observe that the motion models without rotation (T and TS) are never selected, demonstrating that the key component of the dominant motion is consistently well identified. $\mathrm{FRIC}_1$ selection is more balanced between TR and the full model FQ. RBIC selects the full model in almost the whole sequence. For this experiment, RTIC is the best criterion by a large margin.

Table 7 Selected motion models over the sequence of Fig. 6 for the four compared criteria (in percentage of the total number of frames)

Fig. 7

First and last frames of the second robot sequence, and the dominant flow between frames 0 and 1 computed with TS model

For the second experiment with the robotic setup, a translation is applied along the axis of the Cartesian robot, parallel to the camera line of sight (the Z-axis), producing a divergent motion in the image, as displayed in Fig. 7. However, the focus of expansion is not at the center of the image plane. Then, the expected dominant motion model is TS. A sequence of 170 frames was acquired. Results are collected in Table 8. The most frequent choice of our three selection criteria throughout the sequence is the PSRM model. The TS model is the second most frequent selected model for the two FRIC criteria, while RBIC selects the full model over almost all the frames. The FRIC criteria yield a better performance than RTIC. However, the real robot motion may not be perfectly aligned with the camera axis of view, thereof the possible occurrence of the PSRM configuration (component U or V of the 3D translation would not be strictly equal to 0), which may explain the results. If we add the scores for TS and PSRM, we get a cumulated score of 71.2%, 77.6%, and 58.2%, for $\mathrm{FRIC}_1$, $\mathrm{FRIC}_2$, and RTIC, respectively, whereas RBIC stagnates at a score of 7.6%. For this experiment, we can conclude that $\mathrm{FRIC}_2$ is the best criterion by a large margin.

Table 8 Motion models selected by the compared criteria over the second robot sequence (in percentage of the total number of frames)

We now report results on three video sequences taken from the net. The first one depicts a field scene acquired from an airborne camera. The sequence contains 84 frames and the scene is almost planar. The outlier moving object is the reaping machine with the dust cloud behind it (Fig. 8). It is difficult to infer the precise ground truth from the video alone, we do not know the camera orientation with respect to the ground and its exact motion. However, it can be assumed that the PRSM model should be the most relevant one. Since in previous experiments, $\mathrm{FRIC}_2$ systematically outperforms $\mathrm{FRIC}_1$, we only include $\mathrm{FRIC}_2$ in the next experiments.

Fig. 8

First and last frames of the field scene sequence, and the dominant flow between frames 2 and 3 computed with PSRM model

Table 9 shows that both proposed criteria $\mathrm{FRIC}_2$ and RTIC first select PSRM as the dominant motion of the sequence. However, $\mathrm{FRIC}_2$ achieves a greater correct classification rate of 73.8$\%$ of the image pairs, than RTIC which obtains a rate of 54.8$\%$. In contrast, RBIC selects the full model as dominant motion, with PSRM in second place.

Table 9 Selected motion models over the field sequence of Fig. 8 for the three compared criteria

The second real video consists of a sequence of 54 frames (Fig. 9). Visually, the camera moves away from the scene, which leads to consider TS as the true dominant motion model. As in the previous sequence, the scene is almost planar and the vehicles present in it constitute the outliers to the dominant motion.

Fig. 9

First and last frames of the roundabout sequence and the dominant motion between the first and second images computed with TS model

We report in Table 10 the selection scores of the compared criteria for the five tested motion models in the sequence of Fig. 9. The right motion model TS is correctly selected by $\mathrm{FRIC}_2$, but not by RTIC nor RBIC, both selecting the FQ model.

Table 10 Motion models selected by the three compared criteria over the roundabout sequence of Fig. 9

The last real video example involves a sequence where a partly planar scene is recorded from an aerial camera (Fig. 10). A passing train introduces outliers to the dominant motion, The camera motion is apparently parallel to the ground with a slight rotation. We can assume that the TR motion model is the true one.

Fig. 10

First and last frames of the train sequence and the dominant motion between the first and second frames computed with TR model

We can observe in Table 11 that $\mathrm{FRIC}_2$ selects TR as dominant motion, both with a rate of 45.9$\%$. They also select T and TS in almost half of the sequence, which are still reasonable choices. RTIC and RBIC incorrectly select the full model for most of the sequence.

For these three real-image videos, $\mathrm{FRIC}_2$ is the one which consistently supplies good results. Let us add that the RAIC criterion will not give better results than RBIC which is almost always stuck on the full model FQ when dealing with real-image sequences. Indeed, the RAIC penalty of the model dimension [Eq. (24)] is far lower than the one of RBIC [Eq. (25)].

Table 11 Motion models selected by the three compared criteria over the train sequence of Fig. 10

7 Conclusion

We have proposed two new robust motion-model selection criteria. The first one is a robust version of the Takeuchi information criterion called RTIC. The second one departs from the usual approach by starting from the Fisher statistic. We designed two variants of the latter, $\mathrm{FRIC}_1$ and $\mathrm{FRIC}_2$. All three are easy to compute. The three criteria explicitly tackle the trade-off between the size of the inlier set (to be maximized) and the complexity of the motion model (to be minimized). In addition, $\mathrm{FRIC}_1$ can be viewed as a proposition for a robust Mallows’ $C_P$ criterion.

Experiments on synthetic and real-image sequences, along with comparison with RBIC, demonstrate that our criteria achieve superior performance. RTIC supplied the best performance on the synthetic dataset, whereas $\mathrm{FRIC}_2$ performed the best on the tested real videos. This demonstrates that the two proposed robust motion selection criteria, RTIC and FRIC, are complementary and bring valuable contributions. The proposed robust motion-selection criteria could be also applied to other tasks involving parametric models.