Abstract
In this paper, we present a framework for computing dissimilarities between surfaces which is based on the mathematical model of normal cycle from geometric measure theory. This model allows to take into account all the curvature information of the surface without explicitly computing it. By defining kernel metrics on normal cycles, we define explicit distances between surfaces that are sensitive to curvature. This mathematical framework also has the advantage of encompassing both continuous and discrete surfaces (triangulated surfaces). We then use this distance as a data attachment term for shape matching, using the large deformation diffeomorphic metric mapping for modelling deformations. We also present an efficient numerical implementation of this problem in PyTorch, using the KeOps library, which allows both the use of auto-differentiation tools and a parallelization of GPU calculations without memory overflow. We show that this method can be scalable on data up to a million points, and we present several examples on surfaces, comparing the results with those obtained with the similar varifold framework.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This article takes place in the context of computational anatomy, an active research field which aims at providing a mathematical framework to study the variability of anatomical structures among a population of subjects. The term “computational anatomy” was first introduced by Grenander and Miller [28].
In the past decades, the development of acquisition techniques (among which magnetic resonance imaging, coherence tomography, diffusion-tensor imaging, functional MRI) opens the way to an early diagnosis of diseases that cause or are caused by unexpected deformations. A qualitative approach is not anymore sufficient and one necessitates an automatized procedure for an analysis that fully exploits the size of the database. This automation implies a quantitative approach, and thus, a mathematical modelling of shape variability and how to measure it.
This problematic is at the heart of computational anatomy. Formally, one estimates from a “healthy” data set a statistical model of the shapes’ variability. From there, it is possible to provide statistical tests to discriminate between a pathological and a normal shape variation. Of course, this is a very large and complex problem. From a mathematical point of view, the measure of shapes variability necessitates a framework that provides theoretical and numerical guarantees. From a medical point of view, the relevance and the interpretation of such applications need to be evaluated depending on the anatomical structure at stake. Yet, numerous studies have shown promising results. Let us quote, for example, works on Alzheimer’s disease [17, 18, 39, 45, 48], DTI images [20, 29, 38], heart malformations [34], Down syndrome [19, 21] and retina layer for glaucoma diagnosis [7, 31, 32].
An elementary brick for carrying out such statistical analyses is the pairwise registration of geometric structures. This matching problem is often addressed as a variational problem, with a cost functional which is the sum of two terms: a data attachment term that measures how close the deformed shape is to the target shape, and a regularization term on the deformation that ensures that the problem is well posed. In this context, the construction of a data attachment term to measure the residual distance between the deformed shape and the target is of importance. Indeed, depending on the features of the shapes it takes into account, this term will drive the registration procedure in a certain way. Ideally, we want a mathematical setting to represent the shapes (e.g. the surfaces) in a common framework for discrete and continuous shapes, and with theoretical guarantees of the kind of information that we are able to retrieve through this representation. Last but not least, this setting should provide an explicit metric between shapes, which is implementable numerically for discrete shapes.
In the past decade, several models for defining such data attachment terms for curves, surfaces or points clouds have been proposed, based on mathematical tools coming from geometric measure theory. The first of these models consisted of defining kernel metrics on spaces of currents [27, 47] to provide an explicit distance between shapes, for both continuous and discrete cases.
This setting is now commonly used in computational anatomy; its advantages lie in its simple implementation, its parameterization-free representation and the fact that it provides a common framework for continuous and discrete shapes. However, currents are oriented objects, and thus, a consistent orientation of shapes is needed for a coherent matching. Moreover, due to this orientation property, artificial cancellation can occur with shapes with high local variations. To deal with this problem, a more advanced model based on varifolds has been introduced more recently [10, 30]. Such framework provides a non-oriented distance between shapes, which contains first-order information. Note that optimal transport has also been used to construct a data attachment term for diffeomorphic registration in the same spirit [25].
The idea of using curvature information to improve the registration motivated authors in [41]. In this article, they make use of a modification of the varifolds representation of surfaces to be sensitive to the mean curvature, coupled with a spatially varying metric, depending on the mean curvature of the shape.
In [43], we have introduced another shape representation in computational anatomy, using the mathematical model of normal cycle, and we have applied it to curves. The notion of normal cycle has been introduced by Zähle in [50], based on the work on curvature measures developed by Federer earlier [22]. The theory of normal cycles relies on the representation of shapes through their unit normal bundle: more precisely, the normal cycle of a shape is the current associated with its unit normal bundle. The benefit of such a model is that the normal cycle contains all the curvature information of the underlying shape, as it was shown in [50, 51]. The idea is that the current associated with a shape contains only first-order information. Considering the current of the unit normal bundle, we get first-order information of a first-order model and thus curvature information. One can find a more detailed explanation in [43, 46]. Defining kernel metrics on normal cycles, one gets an explicit data attachment term between shapes which is sensitive to curvature and also to singularities of the shapes, such as branching points and boundaries. Taking into account, the curvature during the registration process is an interesting property, since in most application regions with high curvature are features that we want to be matched together.
In this article, we propose to extend the construction of kernel metrics on normal cycles seen in [43] to surfaces of \({\mathbb {R}}^3\) (note that we presented preliminary work on surfaces in a short article [44]). The contributions of this paper are twofold: first, the extension of the previous work to surfaces requires a fine decomposition of normal bundle in the case of triangulated surfaces. The choice of the kernel defining the metric is also crucial, so that the distance can be calculated, and contains non-trivial curvature information. We also present an implementation of this algorithm, which makes extensive use of recent software developments in the neural networks community. More precisely, our implementation takes full advantage of the automatic differentiation module of the PyTorch library [37], together with a seamless use of parallelization of generic convolution operations on Graphics Processing Units (GPU) provided by the recent KeOps module [8, 9], developed by Benjamin Charlier, Joan Glaunès and Jean Feydy. This allows to have a linear memory footprint memory on GPU for kernel convolutions, and thus to avoid memory overflows that happen because of the usual quadratic memory footprint. All these elements lead to a code for the matching problem that is both very efficient (because the parallelization of the calculations is optimized) and simple (because the calculation of the gradients is painless). In addition, the computation times presented are significantly improved because of the automatic and efficient calculation of the gradient. By doing so, we are able to define distances that are sensitive to curvature, with an efficient implementation and that significantly improve matching results.
The article is organized as follows: in Sect. 2, we present the bases of the representation of shapes with normal cycles, after which we describe the normal cycle in the case of triangulated surfaces. In Sects. 3 and 4, we define the kernel metrics on normal cycles and express the associated distance in the case of discrete surfaces. We will see that we can interpret what type of curvature is encoded in these distances. In Sect. 5, we detail the diffeomorphic deformation model that we will use for the inexact registration problem, namely the large deformation diffeomorphic mapping metric (LDDMM, [49]) framework. Section 6 focuses on the numerical aspects of the registration problem. We detail the implementation in PyTorch and provide benchmarks for computation times of the distance on normal cycles, as well as the gradient evaluation. We compare this computation times with the ones on varifolds, and we observe that they are of the same order of magnitude, despite the greater complexity of the normal cycle model. Finally, in Sect. 7, we present many examples of matching on surfaces using kernel metrics on normal cycles as a data attachment term. The various examples aim to show the advantages of introducing curvature into the data attachment term.
2 Representation of Shapes with Normal Cycles
The question of shapes representation is a central point in geometric measure theory whose reference book is from Federer [23]. This field was motivated in the second half of the twentieth century by the calculus of variation, and more specifically by the Plateau’s problem of finding a minimal area surface with constrained boundary: given a closed \((m-1)\)-dimensional surface \(\varGamma \subset {\mathbb {R}}^d\), find an m-dimensional surface S of least area such that \(\partial S = \varGamma \). Solving this problem was a conceptual breakthrough. Indeed if the formulation is a classical minimization problem with constraint, the main difficulty was to provide a theoretical setting to embed surfaces in a topological space with nice properties. The specifications of this framework are the following: define a space where the surfaces can be represented, with a topology that allows some compactness properties for a minimizing sequence of the Plateau’s problem. The representation of oriented surfaces with integral currents [24] and later the representation of non-oriented surfaces with varifolds [1, 2] were introduced for this purpose.
As convenient as these two settings may be, in this article we investigate the finer shape representations of normal cycles. The theory of normal cycles was originated from Federer’s work on curvature measures [22] and was pushed forward by Zähle [50] who gave integral representation of these measures: this is the normal cycle. It provides another theoretical tool to represent surfaces and more generally shapes, encoding higher-order information such as curvature.
The theory of normal cycles had already been used in the applied mathematics community, to perform curvature estimation from triangulations: in [15], the authors use the Lipschitz–Killing forms to generalize the mean and Gaussian curvatures in a mathematical setting that encompasses the polyhedral case as well as the continuous case. They also use vector-valued differential forms to extend the notion of second fundamental form operator and get finer results: the principal curvatures as well as the principal directions may be estimated from this. Moreover, an upper bound of the error of the estimated curvature from a triangulated approximation of a smooth shape is proven. The estimation of the second fundamental form is refined in [16] in a Riemannian framework. [13] extends the stability result of [15] that was valid only for approximation of smooth hypersurfaces. Introducing the \(\mu \)-reach of a set, they provide curvature stability with respect to the Hausdorff distance of compact subset that has positive \(\mu \)-reach, still using the theory of normal cycles. For example, a finite set of points in \({\mathbb {R}}^3\) has a positive \(\mu \)-reach and the authors derived an algorithm to explicit the curvature measure in this case from a description of its normal bundle. Some of the previous curvature estimation with normal cycles are summed up in [36].
In this section, we detail the representation of shapes with normal cycles. We start with a brief recall of currents, as it is underpinning for the theory of normal cycles. Then, we define the normal cycle of a shape with positive reach as the current associated with its unit normal bundle, and we explain how to extend this definition to sets that are union of sets with positive reach. These kinds of sets encompass the case of discrete shapes, such as triangulations. The next step is then to describe the normal cycles for elementary objects as a triangle and a union of triangle. The latter relies on a decomposition of the unit normal bundle into spherical, cylindrical and planar part, each part being associated with a precise kind of curvature.
2.1 Currents
We present the framework for m-dimensional currents in \({\mathbb {R}}^d\).
Let \(0 \le m \le d\) be an integer. In the following, we consider \(\varOmega ^m_0({\mathbb {R}}^d):= {\mathscr {C}}_0\big ({\mathbb {R}}^d, (\varLambda ^m {\mathbb {R}}^d)^*\big )\) the space of continuous differential forms on M, vanishing at infinity, endowed with the uniform norm. Here \(\varLambda ^m {\mathbb {R}}^d\) is the space of m-vector in \({\mathbb {R}}^d\) and \( (\varLambda ^m {\mathbb {R}}^d)^*\) is its algebraic dual.
In this article, a current will simply be an element of the topological dual of \(\varOmega _0^m({\mathbb {R}}^d)\):
Definition 1
(Currents) The space of m-currents in \({\mathbb {R}}^d\) is defined as the topological dual of \(\varOmega _0^m({\mathbb {R}}^d)\), denoted \(\varOmega _0^m({\mathbb {R}}^d)'\). \(T \in \varOmega _0^m({\mathbb {R}}^d)'\) maps every differential form \(\omega \) to \(T(\omega ) \in {\mathbb {R}}\) and \(T(\omega ) \le C_T \left\| \omega \right\| _{\infty }\).
Note 1
This definition differs from the original one of Federer that was introduced similarly to Schwartz’ theory of distribution [24]. However, we do not need such refinements for our applications.
A current can be seen as an object that integrates differential forms, and if we consider X an oriented, m-dimensional submanifold of \({\mathbb {R}}^d\), we can associate with X a current, denoted [X], through the integration of differential forms over X: if \(\omega \in \varOmega _0^m({\mathbb {R}}^d)\),
where \(\tau _X(x)\) is the m-vector associated with a positively oriented, orthonormal basis of \(T_xX\) (if \((e_1(x), \dots , e_m(x))\) is an orthonormal frame of \(T_xX\), then \(\tau _X(x) := e_1(x) \wedge \dots \wedge e_m(x)\)), \(\left\langle . \big | .\right\rangle \) stands for the dual pairing between \(\omega (x) \in (\varLambda ^m {\mathbb {R}}^d)^*\) and \(\tau _X(x) \in \varLambda ^m {\mathbb {R}}^d\), and \(\sigma _X\) is the volume form of X (that coincides with the m-dimensional Hausdorff measure of \({\mathbb {R}}^d\), \({\mathscr {H}}^m\)). We have seen here that the space of m-dimensional currents contains, among others, all the m-dimensional submanifolds.
Another interesting object living in \(\varOmega _0^m({\mathbb {R}}^d)'\) is the Dirac current. Considering \(x \in {\mathbb {R}}^d\) and \(\alpha \in \varLambda ^m {\mathbb {R}}^d\), we define \(\delta _x^\alpha \) as:
These types of currents are useful to have compact approximation of currents, especially for discrete shapes.
2.2 Representation of Surfaces with Normal Cycles
The convenient setting for introducing normal cycles is the one of sets with positive reach. In this section, we give basic definitions and results of the theory and refer to [22, 51] for proofs and more developments.
Definition 2
(Reach of a set) The reach of a set \(X\subset {\mathbb {R}}^3\) is the supremum of the \(r > 0\) for which we can define a unique projection from \(\partial X_r\) on X, where \(\partial X_r = \{x \in {\mathbb {R}}^3 | \mathrm {d}(x,X) = r\}\).
One can find in Fig. 1 an illustration of a set X with zero reach and a set X with positive reach.
In these two figures, we consider a black curve X. The black dotted line represents the medial axis of the curve, i.e. the set of points which do not have a unique projection on X. This is illustrated with the orthogonal projections from the medial axis to X (red dotted lines) . The reach is the distance between the medial axis and the curve. Left: a black curve X with positive reach. Right: the curve X has not a positive reach. The medial axis is at distance 0 from the curve (Color figure online)
Example 1
-
For a convex set X, \(\mathrm {Reach}(X) = +\infty \).
-
If X is a \({{\mathcal {C}}}^2\)-submanifold, compact, \(\mathrm {Reach}(X) >0\).
One can prove that for any \(r<\mathrm {Reach}(X)\), \(\partial X_r\) is a closed surface of class \(\mathcal {C}^1\) in \({\mathbb {R}}^3\).
Definition 3
(Unit normal bundle for sets with positive reach in\({\mathbb {R}}^3\)) Let \(X \subset {\mathbb {R}}^3\) be a set with positive reach, and \(0<r<\mathrm {Reach}(X)\), and let \(x \in X\). The unit normal bundle of X, denoted \({{\mathscr {N}}}_X\), is defined as:
It can be proven that this set \({{\mathscr {N}}}_X\) does not depend on r and that \(g_r:(x,n)\mapsto x+r n\) defines a bi-Lipschitz bijection between \({{\mathscr {N}}}_X\) and \(\partial X_r\). Since \( \partial X_r\) is a \(\mathcal {C}^1\) closed surface in \({\mathbb {R}}^3\), it is canonically oriented, and this orientation transfers via \(g_r\) to a canonical orientation of \({{\mathscr {N}}}_X\). In order to consider the current associated with \({{\mathscr {N}}}_X\), it is interesting to describe the tangent space \(T_{(x,n)}{{\mathscr {N}}}_X\) of the normal bundle at point (x, n). Let us start by considering \(\partial X_r\). It is a smooth hypersurface without border, and thus, it is canonically oriented. For \((x,n) \in {{\mathscr {N}}}_X\), \(x +r n \in \partial X_{r}\) and we denote \(\Big (b_i^r(x,n)\Big )_{1\le i \le d-1}\) the directions of principal curvatures of \(\partial X_r\) associated with the curvatures \((k_i^r(x,n))_{1 \le i \le d-1}\). As explained in [50], \(b_i^r(x,n)\) is independent of r and we write it \(b_i(x,n)\). Moreover, we define \(k_i(x,n) := \lim _{r \rightarrow 0} k_i^r(x,n)\). \(k_i(x,n)\) expresses the curvature of X at point x, seen with n as the reference direction. For example, if X is a closed smooth surface of \({\mathbb {R}}^3\), oriented with a normal vector field \(x \mapsto n(x)\), then we have \(k_i(x,n(x)) = \kappa _i(x)\) where \(\kappa _i(x)\) is the ith principal curvature (signed). And one can show that
This means that the curvature considered with \(-n(x)\) as reference direction is opposite of the one considered with n(x) as reference direction. [50] showed that an orthonormal basis of \(T_{(x,n)}{{\mathscr {N}}}_X\) is then:
If \(k_i(x,n) = \infty \), we set \(\frac{1}{\sqrt{1 + \infty ^2}} = 0\) and \(\frac{\infty }{\sqrt{1 + \infty ^2}} = 1\).
We see with this remark that the information on the curvatures of the set X can be read on the expression of the orthonormal basis of \(T_{(x,n)}{{\mathscr {N}}}_X\).
In the following, we denote \(\tau _{{{\mathscr {N}}}_X}(x,n) = \wedge _{i = 1}^{d-1} a_i(x,n)\) the \((d-1)\)-vector associated with the tangent frame of \({{\mathscr {N}}}_X\) at point (x, n).
Definition 4
(Normal cycles for sets with positive reach in\({\mathbb {R}}^3\)) Let \(X \subset {\mathbb {R}}^3\) be a set with positive reach. The normal cycle of X, denoted N(X), is the 2-current associated with the surface \({{\mathscr {N}}}_X\subset {\mathbb {R}}^3\times {\mathbb {S}}^2\), endowed with the canonical orientation. If \(\omega \in \varOmega _0^2({\mathbb {R}}^3 \times {\mathbb {S}}^2)\),
The representation of a shape with its normal cycle is thus equivalent to consider the shape as an object which integrates differential forms over the unit normal bundle. As explained in [46, 50], and later in [43], there exists differential forms \(\omega _0, \omega _1, \omega _2\) such that \(N(X)(\omega _i)\) retrieves the integral of the ith curvature of X when X is a smooth surface of \({\mathbb {R}}^3\). These differential forms are called the Lipschitz–Killing differential forms. This is why we can say that the representation of shapes with normal cycles encodes all the curvature information.
Let us illustrate this fact with an example on surface: consider a global parameterization of a surface S, with
S is oriented with a normal vector field defined as
where \(\partial _u \gamma (u,v) = \frac{\partial \gamma }{\partial u}(u,v)\). The normal bundle of S has two connected component, \({{\mathscr {N}}}_S^1\) and \({{\mathscr {N}}}_S^2\) with parameterization
Using these parameterizations, we compute \(N(S)(\omega )\)
where we omit the dependence of \(\gamma , n\) and \(\varGamma \) in u, v. We can suppose that \(\gamma \) is a parameterization such that \((\partial _u \gamma , \partial _v \gamma )\) is an orthogonal frame of the tangent space and such that \(\partial _u \gamma \) is the direction of first principal curvature \(\kappa _1\), and \(\partial _v \gamma \) is the direction of second principal curvature \(\kappa _2\), so that:
with \((b_1= \frac{\partial _u \gamma }{\left\| \partial _u \gamma \right\| },b_2 = \frac{\partial _v \gamma }{\left\| \partial _v \gamma \right\| })\) an orthonormal frame of principal directions. With the previous expression, we see that:
where the \(\varepsilon _i = \begin{pmatrix} b_i\\ 0 \end{pmatrix} \) and \({\tilde{\varepsilon }}_j = \begin{pmatrix} 0\\ b_j \end{pmatrix} \). This last expression is interesting because it specifies how the tangent space of the normal bundle (represented via \(\partial _u \varGamma \wedge \partial _v \varGamma \) and \(\partial _u {\tilde{\varGamma }} \wedge \partial _v {\tilde{\varGamma }}\)) contains the different curvature information. Now, we define the following subspaces of \(\varLambda ^2({\mathbb {R}}^3 \times {\mathbb {R}}^3)\):
and \(W_i\) the spaces of differential forms with value in \(F_i^*\).
Note 2
-
The subspaces \(F_i\) are orthogonal with respect to the canonical scalar product on \(\varLambda ^2({\mathbb {R}}^3 \times {\mathbb {R}}^3)\).
-
With the previous notation, \(\varepsilon _1 \wedge \varepsilon _2 \in W_2\), \( {\tilde{\varepsilon }}_1 \wedge \varepsilon _2, \varepsilon _1 \wedge {\tilde{\varepsilon }}_2 \in W_1\), \( {\tilde{\varepsilon }}_1 \wedge {\tilde{\varepsilon }}_2 \in W_0\).
With the expression of \(\partial _u \varGamma \wedge \partial _v \varGamma \), and with 2, one can show that
This makes clear that the normal cycle contains all the (unsigned) curvature information.
2.2.1 Description of the Unit Normal Bundle of a Triangle
Let T be a solid triangle of \({\mathbb {R}}^3\) with vertices \(x_1,x_2,x_3\) and edges: \(f_1 = x_2-x_1\), \(f_2 = x_3-x_2\), \(f_3 = x_1-x_3\). The normal vectors of the face are: \(n_T = \frac{f_1 \times f_2}{|f_1 \times f_2|}\) and \(-n_T\).
Note that the description of the normal cycle of a 2-dimensional polyhedral has been studied in [15]. The description of the normal bundle of a triangle is quite straightforward. As illustrated in Fig. 2, it can be decomposed into a planar part (associated with the unit normal vectors at the relative interior of T), composed of two triangles (in cyan), a cylindrical part (associated with the generalized unit normal vectors at the edges), composed of three “half” cylinders located at the edges (in red), and a spherical part (associated with the generalized unit normal vectors at the vertices), composed of three portions of sphere located at the vertices (in green).
This description of the unit normal bundle can be summed up as follows. Let us define
\( {{\mathscr {N}}}_T^\mathrm{pln}, {{\mathscr {N}}}_T^\mathrm{cyl}, and {{\mathscr {N}}}_T^\mathrm{sph}\) stand for, respectively, for the planar, cylindrical and spherical part of the unit normal bundle. Here, for any non zero vectors \(\alpha , \beta \in {\mathbb {R}}^3\), we denote the semicircle \(S^{\perp +}_{\alpha ,\beta }:= \big ({\mathbb {S}}^2 \cap \alpha ^\perp \big ) \cap \left\{ u | \left\langle u,\beta \right\rangle \ge 0 \right\} \), and the portion of sphere \(S^+_{\alpha ,\beta }:= \left\{ u\in {\mathbb {S}}^2, \left\langle u,\alpha \right\rangle \ge 0, \left\langle u,\beta \right\rangle \ge 0 \right\} \). Note that \(f_i\) and \(n_T\) depend on an orientation of T, but this is not the case for \(f_i \times n_T\) which is always oriented outward from the triangle. We define the associated currents:
We have straightforwardly
because the sets \({{\mathscr {N}}}_T^\mathrm{pln}\), \({{\mathscr {N}}}_T^\mathrm{cyl}\) and \({{\mathscr {N}}}_T^\mathrm{sph}\) intersect only along 1-dimensional subsets and their union equals \({{\mathscr {N}}}_T\).
Notice that as previously said, every part of the triangle appears in the unit normal bundle: for a triangle, the edges are associated with half cylinders and the vertices with portions of spheres. Starting from this description, we will see how to consider the normal cycle of a polyhedral mesh.
2.2.2 Decomposition of the Normal Cycle for Triangulation Meshes
The theory of normal cycles can be extended to a class of sets containing unions of sets with positive reach, as developed in [40, 46, 51]. We briefly introduce this extension here, referring to these works for all details. The \(\mathcal {U}_{PR}\) class is defined as the class of sets X which can be written as a locally finite union of sets \(X_i\), \(i\in {\mathbb {N}}\), such that for any finite subset of indices \(I\subset {\mathbb {N}}\), \(\cap _{i\in I}X_i\) is of positive reach. In particular sets of positive reach belong of course to this class, and it contains also all finite unions of non-empty closed convex sets. The normal cycle N(X) associated with a set \(X\in \mathcal {U}_{PR}\) can be defined in a recursive way so that the following fundamental additive property is satisfied:
Definition 5
(Additive property) Assume that sets X, Y, \(X\cap Y\) are with positive reach. Then, we define
In the case where \(X \cup Y\) is with positive reach, this definition is coherent: the left-hand side and the right-hand side in the definition are equal. In the case of a finite union of sets with positive reach: \(X=\cup _{i=1}^nX_i\), belonging to \(\mathcal {U}_{PR}\), it is easy to see that any combination of unions and intersections of the \(X_i\) also belongs to \(\mathcal {U}_{PR}\). Hence, the additive formula allows to write a recursive expression for the normal cycle of X, which can serve as a definition for normal cycle in this case: for \(1\le k\le n\), one has
Since this formula is not ready to use, we will rather explicit a decomposition of the unit normal bundle such that the additive property is straightforward. This work has already been done for discrete curves in [43]. We recall it briefly here for convenience, starting with union of segments and considering union of triangles after.
If we start with a single segment, \(C = [a,b]\), we define the normal cycle of its relative interior, the “open segment” \({\tilde{C}} := [a,b]{\setminus }\{a,b\}\) as
where \(N(\{a\}) = \{ a\} \times {\mathbb {S}}^2, \, N(\{ b\}) = \{b \} \times {\mathbb {S}}^2\).
Now, let \(C_1 \cup \dots \cup C_n\) be a union of n segments in \({\mathbb {R}}^d\). We can consider without loss of generality that two segments \(C_i\) and \(C_j\) for \(i\ne j\) either do not intersect or intersect at one of their end points. Using the additive property eq. (3), it can be easily seen that the normal cycle of a union of segments can be obtained by summing the normal cycles associated with open segments and vertices. More precisely, if we denote \(\{v_1, \ldots , v_N\}\) the vertices of \(\cup _{i = 1}^n C_i\), our decomposition of the normal bundle satisfies:
Even though the additive property is now straightforward, we will go a bit further in this decomposition, as it will prove to be more efficient with the kernel metric. We can decompose (4) into cylindrical and spherical parts as follows:
This decomposition is sketched in Fig. 3.
Decomposition of the normal bundle of a union of segments. In green, the spherical part (of a single point and of an extremity) and in red the cylindrical part. Note that this representation is only illustrative, as the true normal bundle belongs to the space \({\mathbb {R}}^2\times {\mathbb {S}}^1\) in this case (Color figure online)
A slightly more complex decomposition is necessary for a union of triangles in \({\mathbb {R}}^3\). We apply the same process as for the union of segments. Let T be a triangle of \({\mathbb {R}}^3\) with vertices \(x_1,x_2,x_3\) and edges: \(f_1 = x_2-x_1\), \(f_2 = x_3-x_2\), \(f_3 = x_1-x_3\). We denote by \(e_i\) the geometrical edges (i.e. the segments \([x_1,x_2]\), etc.) of the triangle. The normal vectors of the face are: \(n_T = \frac{f_1 \times f_2}{|f_1 \times f_2|}\) and \(-n_T\). First, we define the normal cycle of the relative interior of T, the “open triangle” \({\tilde{T}}:=T{\setminus }\partial T\) where \(\partial T:=(e_1\cup e_2\cup e_3)\):
\(\partial T\) is a union of the edges \((e_i)_{1 \le i \le 3}\), and the description of its normal bundle has been done right above:
Thus
Since we know an explicit description of N(T), \(N(\tilde{e_i})\) and \(N(\{x_i\})\), we can express \(N({\tilde{T}})\) as a sum of a spherical part, cylindrical part and planar part:
with
where \(S^{+}_{\alpha , \beta } = \{u \in {\mathbb {S}}^2 \, | \, \left\langle u,\alpha \right\rangle \ge 0 \, , \, \left\langle u,\beta \right\rangle \le 0\}\), and
In Fig. 4, one can find an illustration of the normal bundle of an open triangle.
“Normal bundle” of an open triangle \({\tilde{T}}\) in dark blue. The normal bundle above the interior of the triangle, \({{\mathscr {N}}}_{{\tilde{T}}}^\mathrm{pln}\), is two triangles in cyan. The normal bundle above the edges, \({{\mathscr {N}}}_{{\tilde{T}}}^\mathrm{cyl}\), is three half cylinders in red. The normal bundle over the vertices, \({{\mathscr {N}}}_{{\tilde{T}}}^\mathrm{sph}\), is portions of sphere in green (Color figure online)
After the introduction of \(N({\tilde{T}})\), we can proceed as for a union of segments. Suppose that \({{\mathscr {T}}}= \cup _{i = 1}^{n_T} T_i\) is a triangulation where we require that the intersection of two triangles is either empty, or a single edge or a single vertex. We denote \((e_j)_{1 \le j \le n_e}\) the edges and \((v_k)_{1 \le k \le n_v}\) the vertices of the triangulation. Then, one has:
With this decomposition, the additive property is straightforward. Moreover, one can guess that the different parts of the unit normal bundle contain different kinds of discrete curvature information: the area form for the planar part, the mean curvature for the cylindrical part and the Gaussian curvature for the spherical part. This will be clearer when introducing kernel metrics.
Decomposition of the normal bundle for two triangles with a common edge. In this figure, the two normal bundles of the open triangles appear. Then, we add (only once) the normal bundle of the open edge (the red cylinder and the two green half spheres). Then, we add (only once) the normal bundle of the vertices of the edge (the two green spheres). Note that if the triangulation is reduced to this two triangles, we should add the normal bundle of the other edges of the triangles (Color figure online)
In this section, we have developed the representation of shapes through normal cycles, in a common setting that encompasses both the smooth and the discrete case. We are left to design metric on such representations, so that we have a distance between shapes that is sensitive to curvature.
3 Kernel Metrics on Normal Cycles
The idea of normal cycles (resp. current) is convenient because it embeds shapes in a vectorial space: the space of 2-currents in \({\mathbb {R}}^3 \times {\mathbb {S}}^{2}\) (resp. the space of 2-current in \({\mathbb {R}}^2\)). These spaces, defined as dual to spaces of differential forms, come with a dual norm: if \(T \in \varOmega ^m_0({\mathbb {R}}^d)'\), we define \(M(T) := \sup \left\{ T(\omega ), \omega \in \varOmega ^m_0({\mathbb {R}}^d), \left\| \omega \right\| _{\infty } \le 1 \right\} \), called the mass norm in geometric measure theory. It would be tempting to use this norm as a distance between shapes. However, it is not interesting for a matching purpose. Indeed, if C and S are two shapes, non-intersecting, then one can show that \(M([S]-[C]) = {\mathscr {H}}^m(C) + {\mathscr {H}}^m(S)\) and this independently of any closeness between the two sets. This happens because the set of test functions \(\omega \) is too large and thus discriminates completely the two shapes.
For our numerical purpose, we need a computable expression for the dissimilarity between shapes. In the very same spirit of [26] for currents and [11] for varifolds, we will use the theory of reproducing kernel Hilbert space (RKHS, see [4] for the original article) to provide kernel metrics on normal cycles as dissimilarity measures. This work has already been presented in [43], and we present here the basis for self-completeness.
Example 2
We illustrate this with the example of two curves C and S in \({\mathbb {R}}^2\). Representing these two curves as currents [C] and [S] (Fig. 6), a kernel metric allows to consider a scalar product between those curves that takes explicit expression as integral over the curves:
Now, if we represent the two curves as normal cycles (Fig. 7), the kernel metric will consider integrals over the normal bundle rather than integrals over the curves themselves. Precisely, we will construct two scalar kernels \(k_p\) and \(k_n\) where \(k_p\) takes into account the relative spatial position of the curves and \(k_n\) the relative position of the normal vectors u and v at point \(x \in C\) and \(y \in S\).
It has been shown in [43] (in \({\mathbb {R}}^d\) and as a consequence in our framework of surface in \({\mathbb {R}}^3\)) that by choosing scalar kernels \(k_n\) and \(k_p\) such that: \(\forall x \in {\mathbb {R}}^3, \, k_p(x,.) \in {\mathscr {C}}_0({\mathbb {R}}^d)\) and \(\forall n \in {\mathbb {S}}^2,\, k_n \in {\mathscr {C}}({\mathbb {S}}^2)\), then we generate a RKHS W of differential forms such that \(W \hookrightarrow \varOmega _0^{2}({\mathbb {R}}^3 \times {\mathbb {S}}^2)\). This will always be the case in the following. The space W is generated through elementary differential forms:
By considering the topological dual of these spaces, we obtain the inclusion: \(\varOmega _0^2({\mathbb {R}}^3 \times {\mathbb {S}}^2)' \subset W'\). We recall that the normal cycle N(S) of a surface \(S \subset {\mathbb {R}}^3\) is an element of \(\varOmega _0^2({\mathbb {R}}^3 \times {\mathbb {S}}^2)'\). The inclusion \(\varOmega _0^2({\mathbb {R}}^3 \times {\mathbb {S}}^2)' \subset W'\) allows to have an explicit representation of N(S) in \(W'\) through the kernels \(k_p\) and \(k_n\).
Note 3
The question whether the dual inclusion \(\varOmega _0^2({\mathbb {R}}^3 \times {\mathbb {S}}^2)' \subset W'\) is an injection is called the universality property. It can be shown that it is equivalent to W being dense in \(\varOmega _0^2({\mathbb {R}}^3 \times {\mathbb {S}}^2)\) [6]. We have already shown that if \(k_n\) is a Sobolev kernel, then we have indeed \(\varOmega _0^2({\mathbb {R}}^3 \times {\mathbb {S}}^2)' \hookrightarrow W'\) [43]. However, this will not be the case with the normal kernels \(k_n\) that we will chose in this article.
In \(W'\), the scalar product between two normal cycles N(S) and N(C) associated with two surfaces S and C is explicit:
Proposition 1
[43] With such spatial scalar kernel \(k_p\) and normal scalar kernel \(k_n\), we generate a RKHS of differential forms \(W \hookrightarrow \varOmega _0^2({\mathbb {R}}^3 \times {\mathbb {S}}^2)\). In \(W'\), the scalar product between the normal cycles N(C) and N(S) associated with two surfaces (discrete or smooth) C and S is:
The unit normal bundles \({{\mathscr {N}}}_C\) and \({{\mathscr {N}}}_S\) have been described for smooth surfaces and triangulations in the previous section. Our aim in the following is to specify some kernels \(k_n\) and \(k_p\) that allow for a computable scalar product between two triangulations. The main limitation for the choice of the kernels will be our ability to compute explicitly the scalar product, and to do so, we will chose two simple normal kernels: \(k_n(u,v) = 1\) and \(k_n(u,v) = \left\langle u,v\right\rangle \). We will see that even though these kernels may seem coarse at first, we are able to retrieve curvature-related information. For the spatial kernel \(k_p\), we will use a Gaussian kernel \(k_p(x,y) = \exp \left( \frac{-|x-y|^2}{\sigma _W^2}\right) \).
4 Expression of the Kernel Metric for Discrete Surfaces with Constant and Linear Normal Kernel
Note 4
We derive expression of the kernel metrics on normal cycles with the linear normal kernel and the constant normal kernel \(k_n\). However, for the moment and for the linear normal kernel we are limited to the implementation phase which is more delicate than for the constant kernel. This is why we only present experiments with the constant normal kernel in this article. It is, however, interesting to see that the normal linear kernel gives Gaussian curvature information as it will be seen in Proposition 4
In this section, we derive the expression of the kernel metric for discrete surfaces in \({\mathbb {R}}^3\), with constant and linear normal kernels. For this, we will use the decomposition of the unit normal bundle that has been presented in Sect. 2.2. The computation of the scalar product between two triangulations [Eq. (6)] involves integration over the planar part (in cyan in Fig. 5), the cylindrical part (in red) and the spherical part (in green). After introducing the notations in 4.1, we will detail the computation and the approximation of Eq. (6) for each part of the normal bundle. One can find the scalar product with the constant and linear normal kernel \(k_n\) in 4.2 and 4.3. In Sect. 6.2, we present an implementation of such metrics in PyTorch, using automatic differentiation libraries in order to compute the gradient of the metric without implementing it.
4.1 Notations for Triangulated Surfaces and General Remarks
Let us first introduce the notations that we will use in the following.
Let \({{\mathscr {T}}}= \cup _{i = 1}^N T_i\) and \({{\mathscr {T}}}' = \cup _{i = 1}^M T'_i\) be two triangulated meshes. We denote \(x_1, \dots , x_{n_v}\) (resp. \(y_1, \ldots , y_{m_v}\)) the vertices of \({{\mathscr {T}}}\) (resp. of \({{\mathscr {T}}}'\)). Given a triangle \(T_i\) (resp. \(T'_j\)), \(v_i^1, v_i^2,v_i^3\) are its three vertices and \(b_i\) its barycentre: \(b_i = \frac{1}{3}(v_i^1 + v_i^2 + v_i^3)\) (resp. \(b'_j\)). \((f_l)_{1 \le l \le n_e}\) (resp \((g_l)_{1 \le l \le m_e}\)) are the edges of \({{\mathscr {T}}}\) (resp. \({{\mathscr {T}}}'\)). \(\pm n_{T_i}\) are the unit normal vectors of the triangle \(T_i\). Moreover:
-
\(x_{f_i^1}\) and \(x_{f_i^2}\) are the two vertices of \(f_i\): \(f_i = x_{f_i^2}-x_{f_i^1}\).
-
\(c_i\) (resp. \(d_j\)) is the middle of the edge \(f_i\) (resp. \(g_j\)).
-
\(n_{T,f_i}\) is the normal vector of the triangle T such that \(n_{T, f_i} \times f_i\) is oriented inward for the triangle T.
We recall that with the kernel metric, the planar, cylindrical and spherical parts are orthogonal to one another [43, Prop. 36].
Proposition 2
[43, prop. 36] For any two triangulations \({{\mathscr {T}}}\) and \({{\mathscr {T}}}'\), the planar part \(N({{\mathscr {T}}})^\mathrm{pln}\), the cylindrical part \(N({{\mathscr {T}}})^\mathrm{cyl}\) and the spherical part \(N({{\mathscr {T}}})^\mathrm{sph}\) are orthogonal with respect to the kernel metric:
The calculation of the expression of (6) in this case is simplified, and we see here how convenient the decomposition introduced in Sect. 2.2 is: we only need to compute scalar products between spherical parts, cylindrical parts and planar parts. This will be done below.
We start with \(\left\langle N({{\mathscr {T}}})^\mathrm{pln},N({{\mathscr {T}}}')^\mathrm{pln}\right\rangle _{W'}\). We would like to compute
We have seen in Sect. 2.2 and illustrated in Fig. 5 that
with
\({{\mathscr {N}}}_{{\mathscr {T}}}^\mathrm{pln}\) corresponds to the cyan triangles in Fig. 5. Since the planar parts are disjoint, we can restrict ourselves to the computation of the scalar product for the planar part associated with a single triangle \(T \in {{\mathscr {T}}}\) and \(T' \in {{\mathscr {T}}}'\).
For a point \((x,u) \in {{\mathscr {N}}}_T^\mathrm{pln}\), we denote \(\tau _{(x,u)}\) the 2-tangent vector of \({{\mathscr {N}}}_T^\mathrm{pln}\). We recall that this is a 2-vector associated with a positively oriented, orthonormal basis of \(T_{(x,u)}{{\mathscr {N}}}_T^\mathrm{pln}\). One can show that
where \((e_1(x,u),e_2(x,u),u)\) is a positively oriented orthonormal basis of \({\mathbb {R}}^3\). Moreover, if \(\tau _{(y,v)}\) is a 2-tangent vector of \({{\mathscr {N}}}_T^\mathrm{pln}\) at point (y, v), then we have \(\left\langle \tau _{(x,u)},\tau _{(y,v)}\right\rangle = \left\langle u,v\right\rangle \). Combining all these quantities, we have:
In order to have a fast implementation, we approximate the integrals over T and \(T'\) with a single evaluation of the spatial kernel at the barycentres of the triangles \(c_T\) and \(c'_{T'}\):
where \(|T| = \mathrm {Area(T)}\). For the whole triangulation:
Note 5
If we choose \(k_n(u,v) = \left\langle u,v\right\rangle \), we obtain:
which is exactly the kernel metric on varifolds for the linear kernel on the Grassmanian [11]. We see here that with the planar part, we retrieve the metric on varifolds. This shows that the metric on normal cycles contains more information about the shape that the one on varifolds.
The same work can be done for the cylindrical and the spherical part.
We consider two cylinders (or half cylinders) \(C_i = f_i \times S_i\) and \(C'_j = g_j \times S'_j\), where \(S_i\) (resp. \(S'_j\)) is a circle or a half circle, in a plane orthogonal to \(f_i\) (resp. \(g_j\)). \(C_i\) represents a generic elementary of the cylindrical part of the unit normal bundle for a triangulation, as it is illustrated in Fig. 5. Thus, \([C_i]\), the current associated with \(C_i\) represents a typical contribution of the cylindrical part in the normal cycle.
For a point \((x,u) \in {{\mathscr {N}}}_T^\mathrm{cyl}\), one can show [16, 43] that:
where \((e_1(x,u),e_2(x,u),u)\) is a positively oriented orthonormal basis of \({\mathbb {R}}^3\). We then obtain:
and with a similar approximation as for the planar part, we end up with:
One should notice that we do not approximate the integration over the normal part (i.e. integrations over \(S_i\) and \(S_j'\)).
For the spherical part, for a point \((x,u) \in {{\mathscr {N}}}_T^\mathrm{sph}\), one can show [16, 43] that:
where \((e_1(x,u),e_2(x,u),u)\) is a positively oriented orthonormal basis of \({\mathbb {R}}^3\)
We compute explicitly the spherical scalar product: we end up with
where x and y are the vertices at stake and \(S_1\) and \(S_2\) are portions of sphere (see Fig. 5, in green).
In the next sections, we will specify the different scalar product with the constant (\(k_n(u,v) = 1\)) or the linear normal kernel (\(k_n(u,v) = \left\langle u,v\right\rangle \)).
4.2 Discrete Scalar Product with Constant Normal Kernel
In this subsection, we express the discrete version of the scalar product eq. (6), with the constant normal kernel,
With such kernel, it is easy to show that the planar scalar product vanishes, as well as the spherical scalar product. Only the cylindrical part and the boundary term remain:
Proposition 3
Let \({{\mathscr {T}}}\) and \({{\mathscr {T}}}'\) be two triangulated meshes. The approximated scalar product between the associated normal cycles with spatial kernel \(k_p\) and constant normal kernel \(k_n(u,v) = 1\) is
where \(A_i = \sum _{k}f_k^i/|f_k^i|\) is the sum of the normalized edges of the border, with \(x_i\) as vertex, and oriented outward from \(x_i\), and \(n_{T_i,f_i}\) is the normal vector of the triangle \(T_i\) such that \(n_{T_i, f_i} \times f_i\) is oriented inward for the triangle T.
Proof
See “Appendix”. \(\square \)
This can be rewritten:
The expression \(\left\langle N(\partial {{\mathscr {T}}}),N(\partial {{\mathscr {T}}}') \right\rangle _{W'}\) is exactly the scalar product of the curves \(\partial {{\mathscr {T}}}\) and \(\partial {{\mathscr {T}}}'\) that has been computed in [43]. Notice that the planar part and the spherical part are not involved in this scalar product (except for the spherical part of the border).
Some remarks: first, we recall that the previous expression does not necessitate a coherent orientation for the mesh. Second, even with a constant kernel \(k_n\) for the normal part, the metric is sensitive to curvature. Indeed, for an edge f, the cylindrical part of the scalar product involves scalar products between normal vectors of the adjacent triangles which are required quantities to compute the discrete mean curvature. Another interesting feature to notice is that the scalar product involves a specific term for the boundary which will enforce the matching of the boundaries of the shapes. The fact that the boundary has a special behaviour for the normal cycle metric is not surprising. Indeed, a normal cycle encodes generalized curvature information of the shape. Hence, the boundary corresponds to a singularity of the curvature and has a specific behaviour in the kernel metric. We will see that this feature is of interest for a matching purpose.
In terms of computational complexity, we see in (10) that the model of normal cycles on surfaces is more sophisticated than varifolds (see Sect. 4.4 for a recall on varifolds), even with a constant normal kernel. The scalar product involves a double loop on the edges of the triangulations, as well as for each edge, the computation of the sum of the normal vector of the adjacent triangles. However, it is the same order of complexity as varifolds for the computation of the scalar product, i.e. \(O(n_e^2)\) where \(n_e\) is the number of edges which is often the same order as the number of triangles.
4.3 Discrete Scalar Product with Linear Normal Kernel
Now, we focus on the linear normal kernel, \(k_n(u,v) = \left\langle u,v\right\rangle \).
Proposition 4
Suppose that \({{\mathscr {T}}}\) and \({{\mathscr {T}}}'\) are two triangulated meshes. The scalar product between the associated normal cycles with spatial kernel \(k_p\) and linear normal kernel \(k_n(u,v) = \left\langle u,v\right\rangle \) is
where
where \(N_{x_k}\) is the number of triangles with vertex \(x_k\), \(m_{x_k}\) is the number of edges with vertex \(x_k\) and \(\varphi _{i,x_k}\) is the angle at vertex \(x_k\) of the triangle \(T_i\).
Proof
See “Appendix”; the second-order spherical terms are also explained. \(\square \)
Now, suppose for sake of simplicity that the two triangulated meshes have no border and no branching edge or vertex. Then, it is easy to see that for every vertex x of the triangulations \(N_x = m_x\), and then, \(G_{{{\mathscr {T}}}}(x)\) is the discrete Gaussian curvature of the triangulation \({{\mathscr {T}}}\) at vertex x. The scalar product is then a classical varifold scalar product, with an additional measure term, located at the vertices, and with intensity equal to the discrete Gaussian curvature.
We remind that we put this linear term to be complete, but that for the moment we do not present any results with such a metric. There is indeed not yet a satisfactory implementation.
4.4 Comparison with Kernel Metrics on Varifolds
This subsection is for comparison purpose. We briefly express the discrete metric on varifolds. For more details, one can see [30].
Rigorously speaking, a 2-varifold in \({\mathbb {R}}^3\) is a Borel finite measure on \({\mathbb {R}}^3 \times G_2({\mathbb {R}}^3)\) where \(G_2({\mathbb {R}}^3)\) is the Grassmanian: the space of all unoriented planes of \({\mathbb {R}}^3\). \(G_2({\mathbb {R}}^3)\) can be made in correspondence with \({\mathbb {R}}^3\) by associating to a plane one of its normal vectors.
Now, considering \((x,T) \in {\mathbb {R}}^3 \times G_2({\mathbb {R}}^3)\), we define the Dirac varifold\(\delta _{(x,T)}\) which is simply the Dirac measure located at (x, T).
We can define a scalar product between two such measures using two scalars kernel \(k_p\) for the spatial part (\({\mathbb {R}}^3\)), and \(k_t\) for the Grassmanian part (\(G_2({\mathbb {R}}^3)\)):
Associating T and P with a unit normal vector u and v, and considering \(k_t(T,P) = \left\langle u,v\right\rangle ^2\) which defines a proper reproducing kernel on \(G_2({\mathbb {R}}^3)\), then we have:
Now if we consider a triangulations \({{\mathscr {T}}}\), we can approximate \({{\mathscr {T}}}\) in the space of varifolds with Dirac varifolds located at the barycentre of the triangles, and with unit normal vectors as a unit normal vector of the triangle, and with an area information of the triangles. We denote \(\mu _{{\mathscr {T}}}\) this approximation in the space of varifolds. \(\mu _{{\mathscr {T}}}= \sum _{i = 1}^N\mathrm {Area}(T_i)\delta _{(b_i,n_{T_i})}\). Then the scalar product between two triangulations writes immediately:
Comparing this expression with the one obtained with the linear normal kernel on normal cycles in prop. 4, one can see that the metric on varifolds contains only planar information and thus is not sensitive to curvature. Moreover, it formalizes the fact the model of normal cycles is more complex, and even that the latter encompass the former.
This metric is the one with which we will compare the results in the experiment.
5 Deformation Model: LDDMM
Previous sections provide a theoretical framework to compute distance between shapes with kernel metrics on normal cycles. This distance can be used for various applications. In this article, we propose an application for a registration purpose: we use this distance as a residual distance between a deformed shape and a target shape, or in other words, we use this distance as a data attachment term for an inexact matching problem.
This data attachment term can be fitted in any kind of registration framework. In the following, we will consider diffeomorphic deformations that are generated through flows of regular time-varying vector fields. This is the large deformation diffeomorphic metric mapping (LDDMM) framework that we will briefly recall in the following.
After stating an existence result for this problem, we detail in 6.1 a practical algorithm to minimize the functional associated with the inexact matching problem [see Eq. (13)] with discrete shapes. The concrete numerical implementation is detailed in the next section. Several examples of registration with normal cycles are presented on synthetic and real data in the following sections.
As explained in [49], in the LDDMM framework, the study of shape variability is carried by the study of geometrical transformations from one shape to another. The group of deformations at stake, \(G_V\), is generated through integration of time-varying vector fields living in a Hilbert space V, with \(V \hookrightarrow {\mathscr {C}}^1_0({\mathbb {R}}^d)\). With this hypothesis, V is a reproducing kernel Hilbert space with kernel \(K_V\) and \(G_V\) is endowed with a nice Riemannian structure. For example, the Riemannian distance between the identity and a deformation \(\varphi \in G_V\) writes:
This distance between the identity and \(\varphi \) can be interpreted as the energy of the deformation \(\varphi \). Thus, the optimal deformation between two shapes C and S will be the deformation \(\varphi \) with least energy and such that \(\varphi (C) = S\). For practical purpose, we cannot assume that any two shapes can be registered with a deformation \(\varphi \in G_V\). That is why we relax this hypothesis and say that the optimal deformation is the one that minimizes the sum of the energy and a discrepancy measure between the deformed shape and the target, \(A(\varphi (C),S)\). This new registration problem, called inexact matching problem, is a trade-off between the regularity of the deformation, quantified by the energy \(E(\varphi )\) and the registration accuracy, quantified by a term \(A(\varphi (C),S)\). The aim of this section is to use kernel metrics on normal cycles for the dissimilarity measure A. Given two shapes C and S
where W is a RKHS such that \(W \hookrightarrow \varOmega _0^{d-1}({\mathbb {R}}^d \times {\mathbb {S}}^{d-1})\). The minimization problem with dual Hilbert norm on normal cycles as data attachment term is then:
where \(\gamma \) is a trade-off parameter and \(\varphi ^v\) is the deformation obtained at time 1 through the flow of \((v_t)_{0\le t \le 1}\).
One should notice that we have defined the action \(\varphi .N(C)\) of diffeomorphism on normal cycles for sets \(C \in \mathcal {U}_{PR}\) in [43]. This includes smooth submanifolds of \({\mathbb {R}}^d\), but also polyhedral meshes. This has been studied with more details in [42]. This general framework will be the one we work with in the following.
5.1 Existence of a Minimizer
We remind that for smooth submanifold C, we have \(\varphi .N(C) = N(\varphi (C))\). For discrete shapes, we refer to [43] for a rigorous definition of such transport.
We now state the theorem of existence of a minimizer for (13) that encompasses both the case of smooth shapes and the one of polyhedral shapes:
Theorem 1
(Existence of a minimizer for (13)) Suppose that C, S are either smooth or discrete shapes and assume that one has the embeddings \(V \hookrightarrow {{\mathcal {C}}}^{3}_0({\mathbb {R}}^d, {\mathbb {R}}^d)\), and \(W \hookrightarrow \varOmega _{1,0}^{d-1}({\mathbb {R}}^d \times S^{d-1})\). Then there exists a minimizer for the problem (13).
The proof of this theorem relies on the weak continuity of \(v \in L^2_V \mapsto \left\| \varphi ^v.N(C)-N(S)\right\| ^2_{W'}\) and is fully proved in [42, 43].
In the following, \(K_V\) will be, depending on the application, a Cauchy kernel with width \(\sigma _V\):
a Gaussian kernel with width \(\sigma _V\):
or a sum of Gaussian kernel with decreasing width. W is generated through the kernels \(k_p\) and \(k_n\) as in Sect. 4. So that we have existence of a minimizer for (13).
5.2 Discrete Framework
Knowing that a minimizer exists is a first step, and we will focus now on the problem of finding such a minimizer.
In the following, we focus on the discrete problem: we consider discrete shapes \(C_d\) and \(S_d\). The geodesic equation followed by \(\varphi ^v_t\) is simpler, and we will explicit the approximations made for the data attachment term in order to have a tractable algorithm for the minimization procedure.
A discrete shape \(C_d\) is defined by a set of N points \((x_i)_{1 \le i \le N}\) in \({\mathbb {R}}^d\) (the vertices), with a connectivity matrix describing the connection between the vertices. This applies for curves in \({\mathbb {R}}^3\) but also for any polyhedral shape in \({\mathbb {R}}^d\). However, we will restrain our problem to curves and surfaces in \({\mathbb {R}}^d\), and we will use the metric on surfaces seen in Sect. 4. The functional to minimize is then:
However, \(\varphi ^v_1.N(C_d)\) is too complex to be implemented numerically. To overcome this difficulty, we approximate the action of \(\varphi ^v\) on \(C_d\). For this purpose, we define \(C_{d,\varphi ^v}\) as the discrete curve or surface with vertices \((\varphi ^v_1(x_i))_{1 \le i \le N}\) with the same connectivity matrix as \(C_d\). This means that we consider that \(\varphi ^v\) induces a displacement of the vertices only, and the displaced vertices are linked with straight lines. From this, we introduce the approximate matching problem, with the functional \({\tilde{J}}\):
As shown in [26], if we denote by \(q_i(t) = \varphi ^v_t(x_i)\) the points trajectories, the energy term in (15) enforces the optimal vector field to be a geodesic path and to write
where the \(p_i(t) \in {\mathbb {R}}^d\) are auxiliary variables and are called momentum vectors. Further, it was shown in [35] (and detailed in an optimal control point of view in [3]) that the problem can be written in Hamiltonian form: if we denote \(H_r\) the reduced Hamiltonian:
\(q_i\) and \(p_i\) must satisfy coupled geodesic equations which write
This Hamiltonian is constant along geodesic path and thus is a function of the initial momenta \(p_0\) and the initial positions \(q_0\). As could be expected, this implies that the optimal velocity vector field \(v_t\) in (16) is of constant norm: \(\left\| v_t\right\| ^2_V = cste = H_r(q_0,p_0)\). Initial positions being fixed, we can consider \(H_r\) and further \(\varphi ^v\) as function of the \(p_0\) only and denote it \(\varphi ^{p_0}\). The Hamiltonian formalism reduces the initial problem of minimization on an infinite dimensional Hilbert space V (15) to a minimization on \(({\mathbb {R}}^d)^N\):
and where q and p follow the coupled geodesic equations (17). The second term depends only on the position of the final vertices: \((q_i(1))_{1 \le i \le N} = \left( \varphi _1^{p_0}(q_i(0))\right) _{1 \le i \le N}\) that we will denote q(1). The data attachment term is then a function of q(1): g(q(1)).
with q and p following (17). As said before, g is a measure of the residual dissimilarity between the deformed shape at time 1 with vertices q(1) and the target shape \(S_d\).
6 Numerical Implementation
6.1 Registration Algorithm
Functional (19) is explicit using the expressions for the scalar products of normal cycles appearing in g(q(1)) and that have been computed in Sect. 4. In order to minimize it depending on the initial momenta, one classically uses a geodesic shooting algorithm [3, 35]. We explain here briefly the heuristic of this algorithm. In order to compute \(\nabla _{p_0}J(p_0)\), we need to compute \(\nabla _{p_0}g(q(1))\). However, g(q(1)) depends on \(p_0\) through the integration of the geodesic equations [Eq. (17)]. Hopefully, we have explicitly access to \(\nabla _{q(1)}g(q(1))\), and starting with this gradient, we obtain \(\nabla _{p_0}g(q(1))\) through backward integration of the linearized geodesic equations which are recalled in [3], and which involve the Hessian of the Hamiltonian. Integrating these equations from time 1 to time 0, we end up with \(\nabla _{p_0}g(q(1))\).

In fact, once we can compute \(\nabla _{p_0}J(p_0)\), one can plug any optimization procedure in order to minimize the functional with respect to \(p_0\). We use a quasi-Newton Broyden–Fletcher–Goldfarb–Shanno algorithm with limited memory (L-BFGS) [33] rather than the gradient descent with fixed step presented in Algorithm 1.
The BFGS algorithm is a quasi-Newton method that computes an approximation of the Hessian, which is updated and improved at each step. With the limited memory implementation of BFGS, there is no storage of a \(N\times N\) (where N is the number of variables) matrix and the memory storage is linear with respect to N. See [33] for more details. This method provides a direction of descent, and the step in this direction is fixed by a Wolfe line search.
For our numerical implementation, the forward integration scheme is done with a Ralston numerical scheme. This is a higher-order discrete ode solver than the classical Euler scheme.
The challenging part of the implementation is the calculation of the gradient, which requires the integration of linearized backward differential equations involving the second-order derivatives of the deformation kernel (as briefly explained above and extensively studied in [3]). In the next section, we will see how to take advantage of PyTorch’s auto-differentiation libraries to automatically evaluate the gradient \(\nabla _{p_0}J(p_0)\), without implementing it, and therefore without implementing the backward step in Algorithm 1.
6.2 PyTorch and KeOps
Our code for surface registration with normal cycles as data attachment term is available at https://proussillon.gitlab.io/en/code/surface-registration-lddmm/projects/.
We provide a Python implementation using the PyTorch library, together with the KeOps library developed by Benjamin Charlier, Jean Feydy, and Joan Glaunès and freely available at https://plmlab.math.cnrs.fr/benjamin.charlier/libkeops.
This allows for a user-friendly implementation which performs automatic differentiation (to compute the gradient of the metrics). Moreover, the PyTorch + KeOps library automatically transfers the calculus on GPU (graphics processing unit), with a smart parallelization. All this is briefly detailed in the following. See [8, 9] for more details.
PyTorch is a Python native language, developed by Facebook for neural networks applications. It handles the computation on GPU, allowing for a pain free parallelization. On top of that, PyTorch performs automatic differentiation. Indeed, with the recent development of neural network, there has been an increasing necessity to compute the gradient of loss functions, obtained through elementary operations, linear or nonlinear, across different layers. Even though each operation is simple, with an explicit differential, it may be hard to compute the whole gradient (i.e. across all the layers). With PyTorch, it is possible to keep track of the sequence of operations and to automatically differentiate it through backward propagation.
Now, if we look closely at our scalar products of the kernel metrics [e.g. Eq. (10)], the typical expressions that we want to evaluate and differentiate are of the form \(\gamma _i = \sum _j c_{ij}\) with \(c_{ij}=k_p(x_i,y_j)\left\langle b_i,c_j\right\rangle \) or \(c_{ij}=k_p(x_i,y_j)\left\langle b_i,c_j\right\rangle ^2\).
The main limitation inherent with PyTorch is that we need to store the matrix \((c_{ij})_{i,j}\), transfer this matrix to the GPU and then perform the computations. However, this matrix is of size \(N^2\) where N is the number of vertices which may be huge. For surfaces with 100,000 vertices, this may exceed the memory capacity of the GPU.
In order to solve this problem, Benjamin Charlier, Jean Feydy and Joan Glaunès developed the KeOps library which is an interface for a CUDA implementation that computes and automatically differentiate such expressions on the fly, without storing the whole matrix on GPU.
The code provided in this article uses with benefits all the functionality allowed by the coupling PyTorch + CUDA in terms of automatic differentiation and GPU implementation thanks to the KeOps Library.
6.3 Computation Time for the Data Attachment Term and Its Gradient
We present here indications on the calculation time of the kernel distance with normal cycles and compare them with those on varifolds. For this purpose, we provide benchmarks of calculation time, for mesh size ranging from \(10^1\) to \(10^6\) points. In Fig. 8 , we present the calculation times for a single evaluation of the distance and its gradient (with respect to the vertices) on the normal cycles and on the varifolds according to the number of points.
In Fig. 9, we present the computational time with respect to the number of vertices for the evaluation of the total loss in the LDDMM framework, i.e. Eq. (19), with varifolds or normal cycles as data attachment term. The time needed here is higher because on top of the evaluation of the previous distance, we also need to integrate the geodesic equation and to do backpropagation to compute the gradient.
Let us now make some comments on these results. First of all, it is important to note that the implementation coupling auto-differentiation on PyTorch and parallelization on GPU via KeOps provides a method that is fast and scalable to surfaces up to a million points (for the distance evaluation, as well as for the gradient evaluation). Second, even if the normal cycle model is more complex, the computation times are comparable with those of varifolds (from Figs. 8, it can be said that there is a factor 3 between the two methods). And the difference in computation time is reduced even further when this distance is integrated into the LDDMM machinery. Indeed, we observe in Fig. 9 that the calculation times are almost identical with varifolds or normal cycles. This means that in this context, the time-consuming part of the calculation comes more from the forward and backward integration of geodesic equations than from the evaluation of the data attachment term and its gradient. This is even if the normal cycle model is more complex.
Note 6
The integration of the geodesic equations is made using a Ralston’s method. It is a Runge–Kutta method of order 2 (an Euler scheme method).
Note 7
These results are obtained with a NVIDIA GeForce GTX 1080. With a standard graphic card on a laptop (e.g. a Quadro M1200), the computation time is approximately 8 times higher.
Time needed to compute the distance between two triangulated meshes, as well as its gradient (with respect to the vertices) for varifolds and normal cycles. On the y-axis: time of computation in seconds, on the x-axis: number of vertices of the meshes. The computation is scalable to surfaces up to millions of points. Note that the calculation time is of the same order of magnitude for normal cycles and varifolds. This benchmark is made with a NVIDIA GeForce GTX 1080
Time needed to compute the total loss of the LDDMM framework [Eq. (19)] as well as its gradient (with respect to the initial momenta) for varifolds and normal cycles as data attachment term. On the y-axis: time of computation in seconds, on the x-axis: number of vertices of the meshes. The computation is scalable to surfaces up to millions of points. Note that the calculation time is of the same order of magnitude for normal cycles and varifolds. This benchmark is made with a NVIDIA GeForce GTX 1080
7 Experiments
Let us now move to the experiments of surface matching using LDDMM and kernel metrics on normal cycles. The aim of this section is to illustrate the properties of a matching with normal cycles, as well as some limitations.
For each type of data, the different synthetic examples aim to illustrate the curvatures properties and a comparison with varifolds [11, 30] are shown when it is relevant. The examples on real data are a first step to show the advantage of this new dissimilarity metric for applicative purpose.
The algorithm is run until convergence with a stopping criterion on the norm of the successive iterations, with a tolerance of \(10^{-6}\). Our implementation with the use of GPU allows to perform matching of surfaces with 10,000 points in a reasonable time, which will be specified for each experimentation.
For all the following matchings, the geometric kernel \(k_p\) is a Gaussian kernel of width \(\sigma _W\) and \(k_n\) is constant kernel as in Sect. 4.2. The kernel \(K_V\) is a sum of 4 Gaussian kernels of decreasing sizes, in order to capture different features of the deformation. The trade-off parameter \(\gamma \) is fixed at 0.01 for all the experiments.
7.1 Synthetic Data: Illustration of the Curvature Properties
7.1.1 Registration of an Ellipsoid to a Duck
Let us start with the simple, yet interesting example of Fig. 10. We want to perform a matching between an ellipsoid (the source shape, in blue) and a duck shape (the target, in orange). The duck shape contains 2000 points and the ellipsoid 10,000.
The registration is performed with normal cycles and varifolds. We chose a Gaussian kernel for the spatial kernel and a sum of 4 Gaussian kernels of decreasing size (\(\sigma _V = 0.2, 0.1, 0.05, 0.025\)) for the deformation kernel \(k_V\). We recall that for normal cycles, we chose a constant normal kernel and for varifolds, a linear kernel on the Grassmanian. One run is performed at size \(\sigma _W = 0.075\) for spatial kernel. For normal cycles, the 1000 iterations were made in 1018 s (1 s/it). For varifolds, the run ended in 890 s (0.9 s/it). These computation times were obtained with a Nvidia GeForce GTX 1080. The registrations can be found in Fig. 11. As expected, the matching with normal cycles is more accurate that the one with varifolds. This appears clearly in the neighbourhood of regions with high curvature as the beak or the eyes. It is interesting to notice that even the coarse mesh of the duck appears in the deformed ellipsoid for normal cycles.
For validation purposes, in order to have a measurement of the closeness between the deformed shape and the target, and compare the different registrations, we computed the Hausdorff distance and a root-mean-square (RMS) Hausdorff distance between two surfaces S and \(S'\), defined as:
To compute these distances, we used the MeshLab software [14]. In practice, these quantities were approximated by upsampling meshes and evaluating all pairwise distances between vertices. Note that for an interpretation purpose, we also renormalized these distances with the typical size of the data (i.e. the diagonal of the box containing the data). The reader can find the distances on the figures for each experiment.
Registration of a blue ellipsoid to an orange duck. The left column represents the matching with normal cycles and the right column the one with varifolds. The registration with normal cycles is more accurate as it can be seen with the beak or the eyes. One can even notice that the coarse mesh of the duck appears in the deformed ellipsoid. Hausdorff distance with normal cycles: \(d = 0.015, d_\mathrm{RMS} = 0.004\). Hausdorff distance with varifolds: \( d = 0.021, d_\mathrm{RMS} = 0.005\). See Eq. (20) for the definition of d and \(d_\mathrm{RMS}\) (Color figure online)
Sensitivity to the size of the kernel \(\sigma _W\), normal cycles, \(\gamma = 0.01\). We show here two views of the final matching of the blue ellipsoid to the orange duck with normal cycles, depending on \(\sigma _W\). \(\sigma _W\) decreases from left to right, respectively, \(\sigma _W = 0.15, 0.075, 0.0375\) (Color figure online)
Sensitivity to the size of the kernel \(\sigma _W\), normal cycles, \(\gamma = 0.01\). We show here two views of the final matching of the blue ellipsoid to the orange duck with varifolds, depending on \(\sigma _W\). \(\sigma _W\) decreases from left to right, respectively, \(\sigma _W = 0.15, 0.075, 0.0375\). The varifolds data term is scaled to have the same order of magnitude as the normal cycles data term (Color figure online)
Registration of an ellipsoid (in blue) to a hippopotamus shape (in orange). The left column represents the matching with normal cycles and the right column the one with varifolds. The registration with normal cycles is satisfactory. The one with varifolds is bad near the flat regions of the target. Hausdorff distance with normal cycles: \(d = 0.014, d_\mathrm{RMS} = 0.0037\). Hausdorff distance with varifolds: \(d = 0.024, d_\mathrm{RMS} = 0.0055\). See Eq. (20) for the definition of d and \(d_\mathrm{RMS}\) (Color figure online)
View 1. Registration of an ellipsoid to a hippopotamus (zoom, with the mesh). The left column shows the matching with normal cycles and the right column the one with varifolds. The last row is the overlay of the target and the final registration. In order to reduce the varifolds norm between the source and the target at small scales, the deformation concentrates small triangles of the source near vertices of big triangles for the target. This is because, with the discrete varifolds setting, the mass is concentrated at the barycentre of the triangles
Beyond the precision of the matching, we want to insist on the stability of the results in relation to the parameters. Unlike varifolds, where precise parameter adjustment is sometimes required, the result of matching for normal cycles is less crucially dependent on the parameters of the spatial kernel \(\sigma _W\), as well as the trade-off parameter \(\gamma \). As an illustration, we can look at Figs. 12 and 13 which shows the result of the final matching on the duck as a function of the size of \(\sigma _W\). It is noteworthy that even at small scale (\(\sigma _W = 0.0375\)), the metric on normal cycles still enforces the matching of mean curvature through the factor
This allows to be less concerned about the parameter setting of \(\sigma _W\). Indeed, if we compare the results for \(\sigma _W = 0.0375\) for normal cycles and varifolds (bottom right in Figs. 12, 13), we see that the matching with normal cycles is very accurate. With varifolds, we cannot retrieve fine details in the eyes and we obtain artifacts in the chest (see the bottom right Fig. 13). Note that in these experiments, we increase the varifolds data term so that it has the same order of magnitude as the data term with normal cycles.
If we increase \(\gamma \), that is the importance of regularization, this would strongly deteriorate the accuracy for varifolds, whereas it remains fully satisfactory for normal cycles.
A way to avoid such behaviour for varifolds is to use a coarse to precise scale strategy, by decreasing progressively \(\sigma _W\). The lower sensitivity of the metric on normal cycles with respect to the parameters allows us to avoid this costly step in time and adjustment.
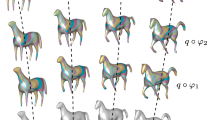
Two views (profile and face) at times \(t = 0\) and \(t = 1\) of the matching of two hippocampi with normal cycles. The target shape is in orange and the source in blue. Each shape has 6600 points. Three runs at different geometric kernel sizes are performed (\(\sigma _W = 25, 10, 5\)), and the kernel of deformation is a sum of Gaussian kernels with \(\sigma _V = 10, 5, 2.5, 1.25\). Each run ended, respectively, at 72, 100 and 100 iterations for a total time of 565 s (2 s/it) (Color figure online)
7.1.2 Registration of an Ellipsoid to a Hippopotamus
Now let us move to an other example (Fig. 14). We want to perform a matching between an ellipsoid (source shape, in blue) and a hippopotamus shape (target, in orange). The hippopotamus contains 20,000 points and the ellipsoid 10,000. Notice that the size of the mesh of the hippopotamus is curvature dependent (coarse near flat regions, precise around region with high curvature). This feature will be of importance to compare the matching results.
The hippopotamus fits in a box of size \(52 \times 26 \times 16\). The registration was performed with normal cycles and varifolds. We chose a Gaussian kernel for the spatial kernel and a sum of 4 Gaussian kernels of decreasing size (\(\sigma _V = 10, 5, 2.5, 1.25\)) for the deformation kernel \(k_V\). We recall that for normal cycles, we chose a constant normal kernel and for varifolds, a linear kernel on the Grassmanian. Three runs were performed, one at size \(\sigma _W = 10\), one at size \(\sigma _W = 5\) and the last one at size \(\sigma _W = 2\). The first runs can be seen as initialization procedures in order to avoid local minima. In this example, these runs are compulsory since the target has fine details (located in the head), but also coarse features, such as the legs.
For normal cycles, each run was stopped after 200 iterations, for a total time of 660 s (1,1 s/it). The same number of iterations was used for varifolds, for a total time of 600 s (1 s/it). The registrations are depicted in Fig. 15. The matching with normal cycles is satisfactory considering the difficulty of the registration. Not all details are retrieved in the head, but this could be achieved with another run at smaller scale.
The result obtained with varifolds may seem surprising at first. If the registration is good near the head of the hippopotamus, it is much worse on the body. On this region, one can observe pinches of the deformed shape, whereas the target is flat. In order to understand this behaviour, Fig. 16 is illuminating. On this figure, one can observe the superimposition of the target mesh and the final matching mesh. The first thing to notice is that for the varifolds (right column), the deformation tends to concentrate triangles at different locations (the pinches). And on the last row, one can observe that these locations can be made in correspondence with vertices of the target that are in the middle of big triangles. To explain this phenomenon, one needs to remember that in the discrete case, the varifold is approximated as Diracs located in the couple (barycentre of the triangles \(\times \) tangent plane of the triangles), with mass equals to the area of the triangle. Thus, one way to reduce the varifold norm is to concentrate the mass of the deformed shape at points far from all the barycentres of the surrounding triangles, i.e. the vertices. This is particularly true at small scales \(\sigma _W\), and this is why we can observe this behaviour for the varifolds norm. However, the runs at small scales are necessary in order to fit the details of the head.
For normal cycles, the metric penalizes the difference of curvatures between the source and the target, and one can observe a nice fitting of the flat region with a coarse mesh (Fig. 16, left column).
7.1.3 Registration of Hippocampi
The second example is a matching of two human hippocampi, of typical size \(10 \times 20 \times 40\). Each shape is around 7000 points. Three runs at different geometric kernel sizes are performed (see Fig. 17). We can see the final deformation matches well the two hippocampus, even the high curved regions of the shape.
7.1.4 Real Data: Retinas
This data set was provided by B. Charlier, N. Charon and M.F. Beg is a set of retina layers from different subjects. Originally, each surface comes with a signal that represents the thickness of the retina layers at each vertex. In [31], a statistical analysis of these functional shapes is made using atlas estimation in the framework of LDDMM and with a varifolds kernel metric. We refer to this article for the procedure of generation of this data set. In the following, we only use the geometrical information of the shapes to illustrate the properties of a matching with normal cycles. The difficulty of this example is to perform a matching that is convincing for the interior of the retina, as well as for the boundary. One should notice that the border has no real physical meaning but is the result of the data acquisition. The hole in the centre of each retina corresponds to optical nerve. Even though these boundaries are not the interesting part for a medical application, they make the registration harder. We will see that the matching with normal cycles will incorporate the boundaries during the registration, resulting in a much smoother deformation.
The retina are surfaces of typical size \(8 \times 8\,\mathrm {mm}\). Each retina is sampled with approximately 5000 points. As for hippocampi, three runs were performed, with \(\sigma _W = 0.8, 0.4, 0.2\), and the deformation kernel \(K_V\) used was a sum of 4 Gaussian kernels, \(\sigma _V = 2.4, 1.2, 0.6, 0.3\). All the details of the matching are in Fig. 18. The retinas have a boundary which will be seen as a region with singularities for the kernel metric on normal cycles. This is not the case for the varifolds metric which makes the matching of the corresponding corners harder. The matching of the boundaries is better with normal cycles and provides a much more regular deformation (see Fig. 18).
In the last example (Fig. 19), the two retinas are the result of an unsatisfactory segmentation . This leads to artifacts in each retina: two triangles for the source retina (in blue, Fig. 19) and only one for the target, in orange. We would like that during the matching, these artificial features are not taken into account. However, these are regions of high curvature, and as we could expect, the kernel metric on normal cycles will make a correspondence between those points. As we can see in the second row of Fig. 19, the two triangles are crushed together, into one triangle, even though the cost of the resulting deformation is high. This example shows how sensitive to noise or artifacts normal cycles are. The data must be smooth and well segmented so that the matching works well.
8 Conclusion and Perspectives
In this paper, we have used the theory of the shapes representation with normal cycles to define a distance between surfaces. Using reproducing kernels, we are able to construct a distance that becomes completely explicit in the case of triangulated surfaces. In addition, this distance still contains curvature information that is inherent in the normal cycle model, even if the selected kernels are simple. We also proposed an implementation in PyTorch, using both auto-differentiation libraries, and optimized GPU calculations, and with a linear memory footprint (with the KeOps library). Gradient calculations are greatly simplified, despite the complexity of the model (both for normal cycles and for the deformation model).
The examples presented show that the use of normal cycles improves matching results (even when the size of the spatial kernel is large compared to the features to be matched), at a cost that is similar compared to varifolds. We can also highlight the fact that normal cycles take naturally into account the boundary of the shapes. This implies a good matching of the boundary for surfaces. This implies also that normal cycles are sensitive to topological changes, as opposed to currents or varifolds. This may be a drawback if we have uncertainty on the data (for example, a poor segmentation that creates artificial holes). However, it also allows the use of coarse meshes on regions of low curvature without affecting the registration (see example of Fig. 16).
An obvious future work is to develop the computation of the metric in the case of discrete surfaces for non-constant \(k_n\), at least for the linear normal kernel. This is of interest since we have already seen that the kernel metric with linear kernel encodes Gaussian curvature information of the surfaces. A normal kernel \(k_n(u,v) = 1 + \left\langle u,v\right\rangle \) would thus contain all the curvatures information. However, the calculus remains intricate and this may lead to another approach: to find interesting compact approximation of the spherical part of a normal cycle. Indeed, in our discretization strategy, replacing the spherical part of the normal cycle by Dirac masses as we do for the spatial part would not be directly possible, as it would not guarantee convergence of the discrete model to a continuous version when the size of the mesh goes to zero. In place of that, we decided not to approximate this part, which leads to heavy computations. Finding efficient approximations of integrations over the spherical part of the normal bundle would be of great interest.
We believe also that kernel metrics on normal cycles can prove useful outside the LDDMM framework, in the spirit of [12, 13, 15, 16], where the authors study the curvature information of a smooth surface that one could retrieve from a surface approximation using normal cycles. The estimation of the mean curvature of a surface from a points cloud approximation has also been done using the first variation of varifolds in [5]. The advantage of our setting is that it provides a Hilbert space \(W'\) where all the representation of shapes lives, and it might be possible to obtain convergence rate of the approximation on \(W'\) and retrieve information on the curvatures convergence. Of course, these are only guess for now, and we need to work further on this direction.
Each column represents the matching of two retinas with kernel metric on normal cycles (left) and varifolds (right). The target shape is in orange and the source shape is in blue. Each shape has 5000 points. For the varifolds metric, the geometric kernel is Gaussian. The kernel on the Grassmanian is chosen linear so that no additional parameter is involved. The same parameters are used for each data attachment term. Three runs at different geometric kernel sizes are performed (\(\sigma _W = 0.8, 0.4, 0.2\)). \(K_V\) is a sum of Gaussian kernels with \(\sigma _V = 2.4, 1.2, 0.6, 0.3\). For normal cycles, the registration algorithm took 1000 s (0.5 s/it). Hausdorff distance with normal cycles: \(d = 0.1997, d_\mathrm{RMS} = 0.0017\). Hausdorff distance with varifolds: \(d = 0.2086, d_\mathrm{RMS} = 0.0036\). See Eq. (20) for the definition of d and \(d_\mathrm{RMS}\) (Color figure online)
The theoretical study of the link between the kernels defined on the normal cycles and the information of curvatures that we retrieve is also an aspect that we would like to study. Going further in this direction, it seems that we can formalize a precise link between normal cycles and varifolds. It is obvious from the expression of prop. 4 that with the projection on the planar space of the discrete scalar product we retrieve the scalar product on varifolds. We would like to investigate this projection independently of the metric.
Matching of two retinas with normal cycles: the target is in orange and the source in blue. Three runs at different geometric kernel sizes are performed (\(\sigma _W = 0.8, 0.4, 0.2\)). \(K_V\) is a sum of Gaussian kernels with \(\sigma _V = 2.4, 1.2, 0.6, 0.3\). The first row shows the initial configuration. The second row shows the matching in the specific zone delimited by the red rectangle. The metric on normal cycles enforces the matching of corresponding high curvature points, which leads to the alignment of the two triangles into the single one of the target (Color figure online)
References
Allard, W.: On the first variation of a varifold. Ann. Math. 95(3), 417–491 (1972)
Almgren, F.: Plateau’s Problem: An Invitation to Varifold Geometry. Mathematical Library, Amsterdam (1966)
Arguillère, S., Trélat, E., Trouvé, A., Younès, L.: Shape deformation analysis from the optimal control viewpoint. J. Math. Pures Appl. 104(1), 139–178 (2015)
Aronszajn, N.: Theory of reproducing kernels. Trans. Am. Math. Soc. 68, 337–404 (1950)
Buet, B., Leonardi, G.P., Masnou, S.: A varifold approach to surface approximation. Arch. Ration. Mech. Anal. 226(2), 639–694 (2017)
Carmeli, C., De Vito, E., Toigo, A., Umanit, V.: Vector valued reproducing kernel Hilbert spaces and universality. arXiv:0807.1659 [math] (2008)
Charlier, B., Charon, N., Trouvé, A.: The fshape framework for the variability analysis of functional shapes. In: Foundations of Computational Mathematics, pp. 1–71 (2015). https://doi.org/10.1007/s10208-015-9288-2
Charlier, B., Feydy, J., Glaunès, J.: Kernel operations on the GPU, with autodiff, without memory overflows. http://www.kernel-operations.io/. Accessed 21 Dec 2018
Charlier, B., Feydy, J., Glaunès, J.: KeOps: Calcul rapide sur GPU dans les espaces à noyaux. In: Proceedings of Journées de Statistique de la SFdS. Paris, France (2018)
Charon, N.: Analysis of geometric and functionnal shapes with extension of currents. Application to registration and atlas estimation. Ph.D. thesis, École Normale Supérieure de Cachan (2013)
Charon, N., Trouvé, A.: The varifold representation of nonoriented shapes for diffeomorphic registration. SIAM J. Imaging Sci. 6(4), 2547–2580 (2013)
Chazal, F., Cohen-Steiner, D., Lieutier, A., Thibert, B.: Stability of curvature measures. CoRR arXiv:0812.1390 (2008)
Chazal, F., Cohen-Steiner, D., Lieutier, A., Thibert, B.: Stability of curvature measures. Comput. Graph. Forum (2009). https://doi.org/10.1111/j.1467-8659.2009.01525.x
Cignoni, P., Callieri, M., Corsini, M., Dellepiane, M., Ganovelli, F., Ranzuglia, G.: MeshLab: an open-source mesh processing tool. In: Scarano, V., Chiara, R.D., Erra, U. (eds.) Eurographics Italian Chapter Conference. The Eurographics Association (2008). https://doi.org/10.2312/LocalChapterEvents/ItalChap/ItalianChapConf2008/129-136
Cohen-Steiner, D., Morvan, J.M.: Restricted Delaunay triangulations and normal cycle. In: SoCG’03 (2003)
Cohen-Steiner, D., Morvan, J.M.: Second fundamental measure of geometric sets and local approximation of curvatures. J. Differ. Geom. 74(3), 363–394 (2006). https://doi.org/10.4310/jdg/1175266231
Csernansky, J., Wang, L., Swank, J., Miller, J., Gado, M., McKeel, D., Miller, M., Morris, J.: Preclinical detection of Alzheimer’s disease: hippocampal shape and volume predict dementia onset in the elderly. NeuroImage 25(3), 783–792 (2005)
Csernansky, J.G., Wang, L., Joshi, S.C., Ratnanather, J.T., Miller, M.I.: Computational anatomy and neuropsychiatric disease: probabilistic assessment of variation and statistical inference of group difference, hemispheric asymmetry, and time-dependent change. NeuroImage 23(Supplement 1), S56–S68 (2004). Mathematics in Brain Imaging
Durrleman, S., Allassonnière, S., Joshi, S.: Sparse adaptive parameterization of variability in image ensembles. Int. J. Comput. Vis. 101(1), 161–183 (2013)
Durrleman, S., Fillard, P., Pennec, X., Trouvé, A., Ayache, N.: Registration, atlas estimation and variability analysis of white matter fiber bundles modeled as currents. NeuroImage 55(3), 1073–1090 (2011)
Durrleman, S., Prastawa, M., Charon, N., Korenberg, J.R., Joshi, S., Gerig, G., Trouvé, A.: Morphometry of anatomical shape complexes with dense deformations and sparse parameters. NeuroImage 101, 35–49 (2014)
Federer, H.: Curvature measures. Trans. Am. Math. Soc. 93, 418–491 (1959)
Federer, H.: Geometric Measure Theory. Springer, Berlin (1969)
Federer, H., Fleming, W.: Normal and integral currents. Ann. Math. 72, 458–520 (1960)
Feydy, J., Charlier, B., Vialard, F.X., Peyré, G.: Optimal transport for diffeomorphic registration. In: MICCAI 2017, Proceedings of MICCAI 2017, Quebec, Canada (2017)
Glaunès, J.: Transport par difféomorphismes de points, de mesures et de courants pour la comparaison de formes et l’anatomie numérique. Ph.D. thesis, Université Paris 13 (2005)
Glaunès, J., Qiu, A., Miller, M., Younes, L.: Large deformation diffeomorphic metric curve mapping. Int. J. Comput. Vis. 80(3), 317–336 (2008). https://doi.org/10.1007/s11263-008-0141-9
Grenander, U., Miller, M.I.: Computational anatomy: an emerging discipline. Q. Appl. Math. LVI(4), 617–694 (1998)
Helm, P.A., Younes, L., Beg, M.F., Ennis, D.B., Leclercq, C., Faris, O.P., McVeigh, E., Kass, D., Miller, M.I., Winslow, R.L.: Evidence of structural remodeling in the dyssynchronous failing heart. Circ. Res. 98(1), 125–132 (2006). https://doi.org/10.1161/01.RES.0000199396.30688.eb
Kaltenmark, I., Charlier, B., Charon, N.: A general framework for curve and surface comparison and registration with oriented varifolds. In: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2017)
Lee, S., Charon, N., Charlier, B., Popuri, K., Lebed, E., Sarunic, M.V., Trouvé, A., Beg, M.F.: Atlas-based shape analysis and classification of retinal optical coherence tomography images using the functional shape (fshape) framework. Med. Image Anal. 35, 570–581 (2017)
Lee, S., Heisler, M.L., Popuri, K., Charon, N., Charlier, B., Trouvé, A., Mackenzie, P.J., Sarunic, M.V., Beg, M.F.: Age and glaucoma-related characteristics in retinal nerve fiber layer and choroid: localized morphometrics and visualization using functional shapes registration. Front. Neurosci. 11, 381 (2017)
Liu, D.C., Nocedal, J.: On the limited memory BFGS method for large scale optimization. Math. Program. 45(1–3), 503–528 (1989). https://doi.org/10.1007/BF01589116
Mansi, T., Voigt, I., Leonardi, B., Pennec, X., Durrleman, S., Sermesant, M., Delingette, H., Taylor, A.M., Boudjemline, Y., Pongiglione, G., Ayache, N.: A statistical model for quantification and prediction of cardiac remodelling: application to tetralogy of fallot. IEEE Trans. Med. Imaging 30(9), 1605–1616 (2011). https://doi.org/10.1109/TMI.2011.2135375
Miller, M.I., Trouvé, A., Younes, L.: Geodesic shooting for computational anatomy. J. Math. Imaging Vis. 24(2), 209–228 (2006)
Morvan, J.M.: Generalized Curvatures. Springer, Berlin (2008)
Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E., DeVito, Z., Lin, Z., Desmaison, A., Antiga, L., Lerer, A.: Automatic differentiation in pytorch. In: NIPS-W (2017)
Pennec, X.: Intrinsic statistics on Riemannian manifolds: basic tools for geometric measurements. J. Math. Imaging Vis. 25(1), 127–154 (2006)
Qiu, A., Younes, L., Miller, M.I., Csernansky, J.G.: Parallel transport in diffeomorphisms distinguishes the time-dependent pattern of hippocampal surface deformation due to healthy aging and the dementia of the Alzheimer’s type. NeuroImage 40(1), 68–76 (2008)
Rataj, J., Zähle, M.: Curvatures and currents for unions of sets with positive reach, II. Ann. Global Anal. Geom. 20(1), 1–21 (2001)
Rekik, I., Li, G., Lin, W., Shen, D.: Multidirectional and topography-based dynamic-scale varifold representations with application to matching developing cortical surfaces. NeuroImage 135, 152–162 (2016)
Roussillon, P.: Modèle de cycles normaux pour l’analyse des dformations. Ph.D. thesis, Université Paris Descartes (2017)
Roussillon, P., Glaunès, J.: Kernel metrics on normal cycles and application to curve matching. SIAM J. Imaging Sci. 9, 1991–2038 (2016)
Roussillon, P., Glaunès, J.: Surface matching using normal cycles. In: GSI’17: Geometric Science Information, 2017, Paris (2017)
Tang, X., Holland, D., Dale, A.M., Younes, L., Miller, M.I.: for the Alzheimer’s disease neuroimaging initiative: shape abnormalities of subcortical and ventricular structures in mild cognitive impairment and Alzheimer’s disease: detecting, quantifying, and predicting. Hum. Brain Mapp. 35(8), 3701–3725 (2014)
Thäle, C.: 50 years sets with positive reach, a survey. Surv. Math. Appl. 3, 125–165 (2008)
Vaillant, M., Glaunès, J.: Surface matching via currents. In: Christensen, G.E., Sonka, M. (eds.) Information Processing in Medical Imaging, no. 3565 in Lecture Notes in Computer Science, pp. 381–392. Springer, Berlin (2005)
Wang, L., Beg, F., Ratnanather, T., Ceritoglu, C., Younes, L., Morris, J.C., Csernansky, J.G., Miller, M.I.: Large deformation diffeomorphism and momentum based hippocampal shape discrimination in dementia of the Alzheimer type. IEEE Trans. Med. Imaging 26(4), 462–470 (2007). https://doi.org/10.1109/TMI.2006.887380
Younès, L.: Shapes and Diffeomorphisms. Springer, Berlin (2010)
Zähle, M.: Integral and current representation of Federer’s curvature measure. Arch. Maths. 23, 557–567 (1986)
Zähle, M.: Curvatures and currents for unions of set with positive reach. Geom. Dedicata 23, 155–171 (1987)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Discrete Scalar Product with the Constant Kernel
1.1 Discrete Surfaces
For discrete surfaces, and with the constant normal kernel, it can be easily seen that the planar part is not involved. The scalar product of normal cycles above vertices (i.e. the spherical scalar product) involves terms as:
If we focus on portion of sphere, one can show that if
is a portion of sphere, then \(\int _{S_1} u \mathrm{d}{\mathscr {H}}^2(u) = \pi \sin \big (\varphi _0/2\big ) \begin{pmatrix} \cos (\varphi _0/2)\\ \sin (\varphi _0/2) \\ 0 \end{pmatrix}\). Note that we retrieve the half sphere with \(\varphi _0 = \pi \) and the total sphere with \(\varphi _0 = 2\pi \). Now, taking into account the orientation, we have to compute for the spherical part:
where s stands for sphere, \({\hbox {h.s}}\) for half sphere and \({\hbox {p.s}}\) for portion of spheres. In fact, one can show that for a given vertex, summing the contributions of the sphere, the half spheres (associated with the edges), and the portion of spheres (associated with the triangles), then the spherical part vanishes for a vertex that is not in the border. Moreover, we have the following equality:
and thus, the spherical part is exactly the scalar product of the curves associated with the border, scalar product that has been computed in [43].
Decomposition of the normal bundle for two triangles with a common edge. In this figure, the two normal bundles of the open triangles appear. Then, we add (only once) the normal bundle of the open edge (the red cylinder and the two green half spheres). Then, we add (only once) the normal bundle of the vertices of the edge (the two green spheres) (Color figure online)
Now let us focus on the cylindrical part. Using expression (8), with \(k_n = 1\), one can see that the scalar product involving a full cylinder is null, and thus, only the half cylinders remains. Consider thus the scalar product between two half cylinders. If we denote \(HCyl_1 = [a,b] \times S_{b-a}^{\perp }\), \(HCyl_2 = [c,d] \times S_{d-c}^{\perp }\) two half cylinders (where \(S_{b-a,\alpha }^{\perp +} =\Big \{ u \in {\mathbb {S}}^2 | \left\langle u,b-a\right\rangle = 0, \left\langle u,\alpha \right\rangle \ge 0 \Big \}\) is a half circle), we compute the scalar product in \(W'\) between these two half cylinders. With the approximations of (8):
In a triangle T, [a, b] corresponds to an edge and \(\alpha \) corresponds to a unitary vector orthogonal to [a, b], in the plane defined by the triangle and oriented in the interior of the triangle. Finally, if we consider two triangulations \({{\mathscr {T}}}\) and \({{\mathscr {T}}}'\), with a decomposition of the unit normal bundle as in Fig. 20, we have

where \(n_{T_i,f_i}\) is the normal vector of the triangle \(T_i\) such that \(n_{T_i, f_i} \times f_i\) is oriented inward for the triangle T.
For the boundary, \(\left\langle N(\partial {{\mathscr {T}}}),N(\partial {{\mathscr {T}}}')\right\rangle _{W'}\), we can show similarly that:
where \(A_k = \sum _{i}f_i^k/|f_i^k|\) is the sum of the normalized edges of the boundary with \(x_k\) as vertex, and oriented outward from \(x_k\).
Discrete Scalar Product with Linear Normal Kernel
We can show that only the planar and the spherical parts are involved in this scalar product. For the planar part, we have already seen that
In this appendix, we want to compute explicitly the spherical scalar product for normal cycles, with the linear normal kernel. The generic expression involved is the following integral:
where \(S_1\) and \(S_2\) are two portions of spheres (that may be the whole sphere, half sphere) with no assumption on the relative position of one sphere compared to the other.
To compute this expression, without loss of generality, we can suppose that \(S_1\) is parametrized as follows:
where \(\varphi _1\) is the aperture angle of the portion of sphere (\(\varphi _1 = 2\pi \) for a whole sphere, and \(\pi \) for a half sphere). Suppose that \(v = \begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix}\), then:
which can be made explicit using the fact that
Integrating first with respect to \(\theta _u\) and then to \(\varphi _u\), we end up with:
The quantity of interest is now:
The main limitation is that we do not have an obvious parameterization of \(S_2\) since there is no assumption on the relative disposition of \(S_1\) and \(S_2\). Suppose now that R is the rotation which brings \(S_2\) to \(S_2'\), where
We have:
This computation is similar to the one of \(\int _{S_1}\left\langle u,v\right\rangle ^2 \mathrm{d}u\) and we obtain:
where \(R = (r_{ij})_{1 \le i,j \le 3}\). The same reasoning for the term \(v_1v_2\) leads to
Finally, if we combine all the terms, we obtain:
with
Note 8
Expression (23) simplifies greatly when one of the involved sphere is a half sphere or a sphere. Indeed, all the terms with a sinus vanish, and it remains: \(\int _{S_1}\int _{S_2}\left\langle u,v\right\rangle ^2\mathrm{d}u\mathrm{d}v = \frac{4}{3}\varphi _1\varphi _2\).
Note 9
Note that this computation is useful to compute the scalar product between portions of sphere in the triangulation. For an implementation, remember that the portion of sphere is not defined by the edges of the triangles, say \(e_1\), \(e_2\), but by the orthogonals: \(-e_2^{\perp }, e_1^\perp \).
Now, if we are given two triangulated meshes, we will express one part of the spherical scalar product: at two vertex x and y, as we have done for the constant normal kernel, we need to compute
If we use the previous expressions of \(\int _{S_1}\int _{S_2}\left\langle u,v\right\rangle ^2 \mathrm{d}u\mathrm{d}v\), ad gathering all the terms \(4/3\varphi _1\varphi _2\), we end up with:
where
and where the second-order spherical terms appear when considering the crossed terms
we do not explicit these second-order terms since we still not have a satisfying implementation of this metric.
Rights and permissions
About this article
Cite this article
Roussillon, P., Glaunès, J.A. Representation of Surfaces with Normal Cycles and Application to Surface Registration. J Math Imaging Vis 61, 1069–1095 (2019). https://doi.org/10.1007/s10851-019-00888-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-019-00888-x