Surface Matching Using Normal Cycles

Abstract

In this article we develop in the case of triangulated meshes the notion of normal cycle as a dissimilarity measure introduced in [13]. Our construction is based on the definition of kernel metrics on the space of normal cycles which take explicit expressions in a discrete setting. We derive the computational setting for discrete surfaces, using the Large Deformation Diffeomorphic Metric Mapping framework as model for deformations. We present experiments on real data and compare with the varifolds approach.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The field of computational anatomy focuses on the analysis of datasets composed of anatomical shapes through the action of deformations on these shapes. The key algorithm in this framework is the estimation of an optimal deformation which matches any two given shapes. This problem is most of the time formulated as the minimization of a functional composed of two terms. The first one is an energy term which enforces the regularity of the deformation. The second one is a data-fidelity term which measures a remaining distance between the deformed shape and the target. This data attachment term is of importance since it drives the registration and relaxes the constraint of exact matching.

In the case of shapes given as curves or surfaces, a framework based on currents have been developed in [8, 14] to provide a satisfying data attachment term, which does not necessitate point correspondences. However, currents are sensitive to orientation, and consequently insensitive to high curvature points of the shapes, which can lead to incorrect matchings of these points, or boundaries of shapes. To overcome this drawback, the varifold representation of shapes was introduced in [4]. Such a representation is orientation-free, and thus overcomes the difficulties experienced with currents. In [13], we developed a new data-attachment term using the theory of normal cycles. The normal cycle of a shape is the current associated with its normal bundle. It is orientation-free and encodes curvature information of the shape. The general framework have been set in [13] as well as the application to three dimensional curves.

In this article, we extend this framework to the case of surfaces. Section 2 focuses on the description of the normal bundle for a triangulation. When this description is done, we will introduce kernel metrics on normal cycles, so that we have an explicit distance between shapes represented as normal cycles (Sect. 3). In Sect. 4 we present some results of surface matching using the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework and kernel metrics on normal cycles. We illustrate the properties of a matching with normal cycles, as well as some limitations. Using parallel computations, we are able to provide examples on real data with a large number of points (around 6000 for each shape).

2 Normal Cycle of a Triangulated Mesh

Normal Cycles. This section requires basics knowledge about currents. The interested reader can see [5, 7] for an approach in the field of computational anatomy. Moreover, we only very briefly remind the mathematical notion of normal cycle in this section, one should refer to [13] for a more extensive presentation.

Normal cycles are defined for sets with positive reach (see [6] for the original definition). For such a set $X\in \mathbb {R}^d$, one can consider its normal bundle $\mathcal{{N}}_X$, which is the set of all (x, n), $x\in X$, with n unit normal vector at point x. Here the notion of normal vector is considered in a generalized sense (see again [6]). For a given point $x \in X$, we denote $\mathrm {Nor}^u(X,x)$ all the unit normal vectors of the set X at this point. In the following, we denote $\varLambda ^{d-1}(\mathbb {R}^d \times \mathbb {R}^d)$ the space of $(d-1)$-vectors in $\mathbb {R}^d \times \mathbb {R}^d$ and $\varOmega ^{d-1}_0(\mathbb {R}^d \times S^{d-1}):= \mathcal{{C}}^0\big (\mathbb {R}^d \times S^{d-1}, \varLambda ^{d-1}(\mathbb {R}^d \times \mathbb {R}^d)^*\big )$ the space of continuous $(d-1)$-differential forms of $\mathbb {R}^d \times S^{d-1}$ vanishing at infinity, endowed with the supremum norm.

Definition 1

(Normal cycle). The normal cycle of a positive reach set $X\subset \mathbb {R}^d$ is the $(d-1)$-current associated with $\mathcal{{N}}_X$ with its canonical orientation (independent of any orientation of X). For any differential form $\omega \in \varOmega _0^{d-1}(\mathbb {R}^d\times S^{d-1})$, one has:

$$\begin{aligned} N(X)(\omega ) := [\mathcal{{N}}_X](\omega ) = \int _{\mathcal{{N}}_X}\omega _{(x,n)}(\tau _{\mathcal{{N}}_X}(x,n))d\mathcal{{H}}^{d-1}(x,n) \end{aligned}$$

(1)

The theory of normal cycles can be extended to the case of finite unions of sets with positive reach, as done in [15], with the use of the following additive property:

$$\begin{aligned} N(C \cup S) := N(C) + N(S) - N(C \cap S) \end{aligned}$$

(2)

This allows to define normal cycles for a very large class of subsets, in particular for unions of triangles, which will be used in our discrete model.

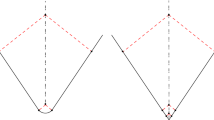
Normal Cycle of a Triangle. Consider a single triangle T, with vertices $x_1,x_2,x_3$ and edges: $f_1 = x_2-x_1$, $f_2 = x_3-x_2$, $f_3 = x_1-x_3$. The normal vectors of the face are: $n_T = \frac{f_1 \times f_2}{|f_1 \times f_2|}$ and $-n_T$. The description of the normal bundle of a triangle is quite straightforward. As illustrated in Fig. 1, it can be decomposed into a planar part, composed of two triangles, a cylindrical part, composed of three “half” cylinders located at the edges, and a spherical part, composed of three portions of sphere located at the vertices:

$$\begin{aligned} \mathcal{{N}}_T^p:= & {} \cup _{x \in T \setminus \partial T} \mathrm {Nor}^u(T,x)=T\times \{-n_T,n_t\},\\ \mathcal{{N}}_T^c:= & {} \cup _{i = 1}^3 [x_i,x_{i+1}] \times S^{\perp +}_{f_i,f_i\times n_T},\\ \mathcal{{N}}_T^s:= & {} \cup _{i = 1}^3 \{x_i\} \times S^+_{f_{i-1},-f_{i+1}}, \end{aligned}$$

where for any non zero vectors $\alpha , \beta \in \mathbb {R}^3$, we denote the semicircle $S^{\perp +}_{\alpha ,\beta }= \big (S^2 \cap \alpha ^\perp \big ) \cap \left\{ u | \left\langle u,\beta \right\rangle \ge 0 \right\}$, and the portion of sphere $S^+_{\alpha ,\beta }:= \left\{ u\in S^2, \left\langle u,\alpha \right\rangle \ge 0, \left\langle u,\beta \right\rangle \ge 0 \right\}$.

Fig. 1.

Illustration of the decomposition of the normal bundle of a triangle into a planar (in purple), a cylindrical (in blue) and a spherical (in yellow) parts. Note that the actual normal bundle lives in $\mathbb {R}^3\times S^2$ (Color figure online)

Normal Cycle of a Triangulated Mesh. Let $\mathcal {T}$ be a triangulated mesh, which we define as a finite union of triangles $\mathcal {T}=\cup _{i=1}^{n_T} T_i$ such that the intersection of any two triangles is either empty or a common edge. The normal cycle of a triangulated mesh is defined using the additive formula (2) as a combination of normal cycles of its faces (triangles), edges (segments) and vertices (points). All these elements further decompose into planar, cylindrical and spherical parts.

3 Kernel Metrics on Normal Cycles with Constant Normal Kernel

Construction of the Kernel Metric. As detailed in [13], we use the framework of Reproducing Kernel Hilbert Spaces (RKHS) to define a metric between normal cycles. The kernel has the form

This defines a RKHS W, and under some regularity conditions on the kernels ([13], Proposition 25), we have $W \hookrightarrow \varOmega _0^2(\mathbb {R}^3 \times S^2)$, and thus, $\varOmega _0^2(\mathbb {R}^3 \times S^2)' \subset W'$. The corresponding metric on $W'$ can be used as a data attachment term for shapes represented as normal cycles. In this work, for simplicity and efficiency reasons, we consider the following normal kernel: $k_n(u,v) = 1$ (constant kernel). Other simple and interesting choices will be $k_n(u,v) = \left\langle u,v\right\rangle$ (linear kernel) or $k_n(u,v) = 1+\left\langle u,v\right\rangle$, but we keep them for future work.

The expression of scalar product between two normal cycles N(C) and N(S), associated with shapes S and C is then:

$$\begin{aligned} \left\langle N(C),N(S)\right\rangle _{W'} = \int _{\mathcal{{N}}_C}\int _{\mathcal{{N}}_S}k_p(x,y) \left\langle \tau _{\mathcal{{N}}_C}(x,u),\tau _{\mathcal{{N}}_S}(y,v)\right\rangle d\mathcal{{H}}^{2}(x,u)d\mathcal{{H}}^{2}(y,v), \end{aligned}$$

(3)

for the constant kernel, where $\tau _{\mathcal{{N}}_C}(x,u) \in \varLambda _2(\mathbb {R}^3 \times \mathbb {R}^3)$ is a 2-vector associated with an orthonormal basis of $T_{(x,u)}\mathcal{{N}}_C$, positively oriented.

Scalar Product Associated with the Kernel Metric for Discrete Surfaces. Let $\mathcal{{T}}= \cup _{i = 1}^n T_i$ and $\mathcal{{T}}' = \cup _{i = 1}^m T'_i$ be two triangulated meshes. As explained in Sect. 2, we decompose the two corresponding normal cycles into combinations of planar, cylindrical and spherical parts which, as was proven in [13], are orthogonal with respect to the kernel metric. Moreover, we approximate integrations over triangles and edges by a single evaluation at the center of these elements. This is equivalent to approximate in the space of currents the cylindrical and planar part by Dirac functionals as explained in [13], Sect. 3.2.2. For integrations over the sphere however, we can get simple analytic formulas for the integrations with our choice of kernel. The new approximations in the space of currents are denoted $\tilde{N}(\mathcal{{T}})$ and $\tilde{N}(\mathcal{{T}}')$. We do not further detail the calculus of the different integrations over the normal bundle and express only the result obtained:

$$\begin{aligned} {\begin{aligned}&\left\langle \tilde{N}(\mathcal{{T}}),\tilde{N}(\mathcal{{T}}')\right\rangle _{W'} \\&= \sum _{\begin{array}{c} f \text { edge of the} \\ \text { border of }\mathcal{{T}} \end{array}}\sum _{\begin{array}{c} g \text { edge of the}\\ \text { border of }\mathcal{{T}}' \end{array}}\frac{\pi ^2}{4}\big (k_p(x^1_f,y^1_g) + k_p(x^2_f,y^2_g) - k_p(x^2_f,y^1_g) - k_p(x^1_f,y^2_g)\big )\left\langle \frac{f}{|f|},\frac{g}{|g|}\right\rangle \\&+\sum _{i = 1}^F \sum _{j = 1}^G 4k_p(c_i,d_j)\left\langle f_i,g_j\right\rangle \left\langle \sum _{\left\{ T | f_i \text { edge of } T \right\} }n_{T,f_i},\sum _{\left\{ T' | g_j \text { edge of } T' \right\} }n_{T',g_j}\right\rangle , \end{aligned}} \end{aligned}$$

(4)

where

• $x_f^1$ and $x_f^2$ are the two vertices of f with $f = x_f^2-x_f^1$.

• $c_i$ (resp. $d_j$) is the middle of the edge $f_i$ (resp. $g_j$).

• $n_{T,f_i}$ is the normal vector of the triangle T such that $n_{T, f_i} \times f_i$ is oriented inward for the triangle T.

Let us make a few remarks here. First, we recall that the previous expression does not necessitate a coherent orientation for the mesh.

Secondly, even with a constant kernel $k_n$ for the normal part, the metric is sensitive to curvature. Indeed, for an edge f, the cylindrical part of the scalar product involves scalar products between normal vectors of the adjacent triangles which are required quantities to compute the discrete mean curvature.

Another interesting feature to notice is that the scalar product involves a specific term for the boundary which will enforce the matching of the boundaries of the shapes. The fact that the boundary has a special behaviour for the normal cycle metric is not surprising. Indeed a normal cycle encodes generalized curvature information of the shape. Hence, the boundary corresponds to a singularity of the curvature and has a specific behaviour in the kernel metric. We will see in Sect. 4 that this feature is of interest for a matching purpose.

4 Results

We used the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework (see for example [1, 2, 12]) in our experiments to model deformations of the ambient space. We emphasize here that this choice of framework is not mandatory, and that other registration models could be used together with our normal cycle data attachment term. We used the discrete formulation of LDDMM via initial momentum parametrization and a geodesic shooting algorithm [1, 12]. For the optimization of the functional we used a quasi Newton Broyden Fletcher Goldfarb Shanno algorithm with limited memory (L-BFGS) [11]. The step in the descent direction is fixed by a Wolfe line search. For the numerical integrations of geodesic and backward equations, a Runge-Kutta (4,5) scheme is used (function ode45 in Matlab). In order to improve the computational cost, the convolution operations involved are done with parallel computing on a graphic card. The CUDA mex files using GPU are included in the MATLAB body program. The algorithm is run until convergence with a stopping criterion on the norm of the successive iterations, with a tolerance of $10^{-6}$.

For all the following matchings, the geometric kernel $k_p$ is a Gaussian kernel of width $\sigma _W$, and $k_n$ is a constant kernel. The kernel $K_V$ is a sum of 4 Gaussian kernels of decreasing sizes, in order to capture different features of the deformation (see [3]). The trade-off parameter $\gamma$ is fixed at 0.1 for all the experiments.

The first example is a matching of two human hippocampi. Each shape has around 7000 vertices. Three runs at different geometric kernel sizes are performed (see Fig. 2). We can see that the final deformation matches well the two hippocampi, even the high curved regions of the shape.

Fig. 2.

Two views (profile and face) at times $t = 0$ and $t = 1$ of the matching of two hippocampi with normal cycles. The target shape is in orange and the source in blue. Each shape has 6600 points. Three runs at different geometric kernel sizes are performed ($\sigma _W = 25, 10, 5$) and the kernel of deformation is a sum of Gaussian kernels with $\sigma _V = 10, 5, 2.5, 1.25$ (the diameter of hippocampus is about 40 mm). Each run ended respectively at 62, 66 and 48 iterations for a total time of 4076 s (23 s per iteration). (Color figure online)

The second data set was provided by B. Charlier, N. Charon and M.F. Beg. It is a set of retina layers from different subjects [10], which has been already used for computational anatomy studies [9]. The retinas are surfaces of typical size 8 $\mathrm {mm}^2$. Each retina is sampled with approximately 5000 points. All the details of the matching are in Fig. 3. The retinas have a boundary which will be seen as a region with singularities for the kernel metric on normal cycles. This is not the case for the varifolds metric which makes the matching of the corresponding corners harder. The matching of the boundaries is better with normal cycles, and provides a much more regular deformation (see Fig. 3).

Fig. 3.

Matching of two retinas with kernel metric on normal cycles (left) and varifolds (right). The target shape is in orange and the source shape is in blue. Each shape has 5000 points. For the varifolds metric, the geometric kernel is Gaussian and the kernel on the Grassmanian is chosen linear. The same parameters are used for each data attachment term. Three runs at different geometric kernel sizes are performed ($\sigma _W = 0.8, 0.4, 0.2$). $K_V$ is a sum of Gaussian kernels with $\sigma _V = 2.4, 1.2, 0.6, 0.3$. For normal cycles, each run ended respectively at 88, 297 and 5 iterations for a total time of 5487 s (14 s/it). For varifolds, it was 55, 1 and 1 iterations for a total time of 2051 s (35 s/it). (Color figure online)

In the last example (Fig. 4), the two retinas are the result of an unsatisfactory segmentation. This leads to artifacts in each retina: two triangles for the source retina (in blue, Fig. 4) and only one for the target, in orange. These are regions of high curvature and as we could expect, the kernel metric on normal cycles will make a correspondence between those points. As we can see in the second row of Fig. 4, the two triangles are crushed together, into one triangle, even though the cost of the resulting deformation is high. This example shows how sensitive to noise or artifacts normal cycles are.

Fig. 4.

Matching of two retinas with normal cycles: the target (in orange) and the source (in blue). Three runs at different geometric kernel sizes are performed ($\sigma _W = 0.8, 0.4, 0.2$). $K_V$ is a sum of Gaussian kernels with $\sigma _V = 2.4, 1.2, 0.6, 0.3$. The first row shows the initial configuration. The second row shows the matching in the specific zone delimited by the red rectangle. The metric on normal cycles enforces the matching of corresponding high curvature points, which leads to the alignment of the two triangles into the single one of the target. Each run ended respectively at 211, 90 and 202 iterations for a total time of 8114 s (16 s/it). (Color figure online)

5 Conclusion

In this article we extended to the case of surfaces the methodology introduced in [13] for curve matching, based on the notion of normal cycle. Compared to the representation of shapes with currents or varifolds, this model encodes the curvature information of the surfaces. We define a scalar product between two triangulations represented as normal cycles using the theory of reproducing kernels. The intrinsic complexity of the model is simplified by using a constant normal kernel for the metric. Even though it may seem rough, we do not get rid of all curvature information of the shape, as it can be seen in Eq. (4) or in the example showed in Figs. 3 and 4. Using parallel computing on GPU, we are able to match two surfaces with a large number of points in a reasonable time, with a descent algorithm that is run until convergence.

The examples of this article show promising first results. For the retinas data set, the weighting of the boundaries and corner points provided by the metric on normal cycles allows a much more precise and regular deformation than with varifolds. As a future work, it will be interesting to study more complex normal kernels $k_n$, as the linear kernel or a combination of a linear kernel and a constant kernel. The exact type of curvatures (mean, Gaussian) that we are able to retrieve with such kernels is not clear yet and should be investigated. We also would like to work on data sets were the refinement of normal cycles is relevant.