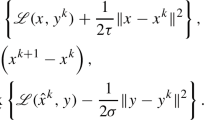An Algorithmic Framework of Generalized Primal–Dual Hybrid Gradient Methods for Saddle Point Problems

Abstract

The primal–dual hybrid gradient method (PDHG) originates from the Arrow–Hurwicz method, and it has been widely used to solve saddle point problems, particularly in image processing areas. With the introduction of a combination parameter, Chambolle and Pock proposed a generalized PDHG scheme with both theoretical and numerical advantages. It has been analyzed that except for the special case where the combination parameter is 1, the PDHG cannot be casted to the proximal point algorithm framework due to the lack of symmetry in the matrix associated with the proximal regularization terms. The PDHG scheme is nonsymmetric also in the sense that one variable is updated twice while the other is only updated once at each iteration. These nonsymmetry features also explain why more theoretical issues remain challenging for generalized PDHG schemes; for example, the worst-case convergence rate of PDHG measured by the iteration complexity in a nonergodic sense is still missing. In this paper, we further consider how to generalize the PDHG and propose an algorithmic framework of generalized PDHG schemes for saddle point problems. This algorithmic framework allows the output of the PDHG subroutine to be further updated by correction steps with constant step sizes. We investigate the restriction onto these step sizes and conduct the convergence analysis for the algorithmic framework. The algorithmic framework turns out to include some existing PDHG schemes as special cases, and it immediately yields a class of new generalized PDHG schemes by choosing different step sizes for the correction steps. In particular, a completely symmetric PDHG scheme with the golden-ratio step sizes is included. Theoretically, an advantage of the algorithmic framework is that the worst-case convergence rate measured by the iteration complexity in both the ergodic and nonergodic senses can be established.

1 Introduction

We consider the saddle point problem

$$\begin{aligned} \min _{x\in \mathcal{X}}\max _{y\in \mathcal{Y}} \; \Phi (x,y):= \theta _1(x) - {y^TAx} - \theta _2(y), \end{aligned}$$

(1.1)

where $A\in \mathfrak {R}^{m\times n}$, $\mathcal{X}\subseteq \mathfrak {R}^{n}$ and $\mathcal{Y}\subseteq \mathfrak {R}^m$ are closed convex sets, $\theta _1: \mathfrak {R}^{n} \rightarrow \mathfrak {R}$ and $\theta _2: \mathfrak {R}^{m} \rightarrow \mathfrak {R}$ are convex but not necessarily smooth functions. The solution set of (1.1) is assumed to be nonempty throughout our discussion. The model (1.1) captures a variety of applications in different areas. For examples, finding a saddle point of the Lagrangian function of the canonical convex minimization model with linear equality or inequality constraints is a special case of (1.1). Moreover, a number of variational image restoration problems with the total variation (TV) regularization (see [25]) can be reformulated as special cases of (1.1), see details in, e.g., [5, 27,28,29].

Since the work [29], the primal–dual hybrid gradient (PDHG) method has attracted much attention and it is still being widely used for many applications, especially in image processing areas. We start the discussion of PDHG with the scheme proposed in [5]:

$$\begin{aligned} \left\{ \begin{array}{rcl} x^{k+1} &{}=&{} \arg \min \left\{ \Phi (x,y^k) + \frac{r}{2} \Vert x-x^k\Vert ^2 \, |\, x\in \mathcal{X}\right\} , \\ \bar{x}^k &{}=&{} x^{k+1} + \tau ( x^{k+1} -x^k), \\ y^{k+1} &{}=&{} \arg \max \left\{ \Phi (\bar{x}^k,y) - \frac{s}{2} \Vert y-y^k\Vert ^2 \, |\, y\in \mathcal{Y}\right\} , \end{array} \right. \nonumber \\ \end{aligned}$$

(1.2)

where $\tau \in [0,1]$ is a combination parameter, and $r>0$ and $s>0$ are proximal parameters of the regularization terms. The scheme (1.2) splits the coupled term $y^TAx$ in (1.1) and treats the functions $\theta _1$ and $\theta _2$ individually; the resulting subproblems are usually easier than the original problem (1.1). In [5], it was shown that the PDHG scheme (1.2) is closely related to the extrapolational gradient methods in [20, 24], the Douglas-Rachford splitting method in [9, 21] and the alternating direction method of multipliers (ADMM) in [12]. In particular, we refer to [10, 26] for the equivalence between a special case of (1.2) and a linearized version of the ADMM. As analyzed in [5], the convergence of (1.2) can be guaranteed under the condition

$$\begin{aligned} rs > \Vert A^TA\Vert . \end{aligned}$$

(1.3)

When $\tau =0$, the scheme (1.2) reduces to the PDHG scheme in [29] which is indeed the Arrow–Hurwicz method in [1]. In addition to the numerical advantages shown in, e.g., [5, 16], the theoretical significance of extending $\tau =0$ to $\tau \in [0,1]$ was demonstrated in [15]. That is, if $\tau =0$, then the scheme (1.2) could be divergent even if r and s are fixed at very large values; thus, the condition (1.3) is not sufficient to ensure the convergence of (1.2). Note that it could be numerically beneficial to tune the parameters r and s as shown in, e.g., [16, 28], and it is still possible to investigate the convergence of the PDHG scheme (1.2) with adaptively adjusted proximal parameters, see, e.g., [3, 10, 13]. Here, to expose our main idea more clearly and to avoid heavy notation, we only focus on the case where both r and s are constant and they satisfy the condition in (1.3) throughout our discussion.

In [16], we showed that the special case of (1.2) with $\tau =1$ is an application of the proximal point algorithm (PPA) in [22], and thus the scheme in [14] can be immediately combined with the PDHG scheme (see Algorithm 4 in [16]). Its numerical efficiency has also been verified therein. This PPA revisit has been further studied in [23], in which a preconditioning version of the PDHG scheme (1.2) was proposed. When $\tau \ne 1$,¹ it is shown in [16] [see also (2.7b)] that the matrix associated with the proximal regularization terms in (1.2) is not symmetric and thus the scheme (1.2) cannot be casted to an application of the PPA. The techniques in [14] are thus not applicable to (1.2) with $\tau \ne 1$. But the convergence can be guaranteed if the output of the PDHG subroutine (1.2) is further corrected by some correction steps (see Algorithms 1 and 2 in [16]). The step sizes of these correction steps, however, must be calculated iteratively and they usually require expensive computation (e.g., multiplications of matrices or matrices and vectors) if high dimensional variables are considered. It is thus natural to ask whether or not we can further correct the output of (1.2) when $\tau \ne 1$ while the step sizes of the correction steps are iteration-independent (more precisely, constants)? Moreover, it is easy to notice that the PDHG scheme (1.2) is not symmetric also in the sense that the variable x is updated twice while y is updated only once at each iteration. So one more question is whether or not we can update y also right after the PDHG subroutine and modify (1.2) as a completely symmetric version? To answer these questions, we propose the following unified algorithmic framework that allows the variables to be updated both, either, or neither, after the PDHG subroutine (1.2):

In (1.4), the output of the PDHG subroutine (1.2) is denoted by $(\tilde{x}^k,\tilde{y}^k)$, $\alpha >0$ and $\beta >0$ are step sizes of the correction steps to further update the variables. This new algorithmic framework is thus a combination of the PDHG subroutine (1.2) with a correction step. We also call $(\tilde{x}^k, \tilde{y}^k)$ generated by (1.4a) a predictor and the new iterate $(x^{k+1},y^{k+1})$ updated by (1.4a) a corrector. Note that compared with the PDHG (1.2), two more constants $\alpha$ and $\beta$ are involved in the algorithmic framework (1.4). But the framework (1.4) with different choices of $\alpha$ and $\beta$ corresponds to various specific PDHG-like algorithms, and as we shall show, it is very easy to theoretically determine these constants and thus a series of PDHG-like algorithms can be specified by the framework (1.4). Therefore, the additional constants in (1.4) do not increase the difficulty of implementing PDHG-like algorithms based on (1.4).

To see the generality of (1.4), when $\alpha =\beta =1$, the algorithmic framework (1.4) reduces to the generalized PDHG (1.2) in [5]; when $\tau =1$ and $\alpha =\beta \in (0,2)$, the improved version of PDHG from the PPA revisit (Algorithm 4 in [16]) is recovered. Moreover, if $\alpha =1$, we obtain a symmetric generalized PDHG [see (4.9)] that updates both the variables twice at each iteration, and in particular, a completely symmetric version with the golden-ratio step sizes [see (4.12)]. Therefore, based on this algorithmic framework, some existing PDHG schemes can be recovered and a class of new generalized PDHG schemes can be easily proposed by choosing different values of $\alpha$, $\beta$ and $\tau$. We shall focus on the case where $\tau \in [0,1]$ and investigate the restriction onto these constants so that the convergence of the algorithmic framework can be ensured. The analysis is conducted in a unified manner. In addition, the mentioned nonsymmetry features of the PDHG scheme (1.2) may also explain the difficulty of proving its worst-case convergence rate measured by the iteration complexity in a nonergodic sense. For the generalized PDHG algorithmic framework (1.4), we shall show that the worst-case convergence rate in both the ergodic and nonergodic senses can be derived when the parameters are appropriately restricted. This is a theoretical advantage of the algorithmic framework (1.4).

Finally, we would like to mention that there is a rich set of literature discussing how to extend the PDHG with more sophisticated analysis to more complicated saddle point models or to more abstract spaces, e.g., [6,7,8]. But in this paper, we concentrate on the canonical saddle point model (1.1) in a finitely dimensional space and the representative PDHG scheme (1.2) to present our idea of algorithmic design clearly.

The rest of this paper is organized as follows. In Sect. 2, we summarize some understandings of the model (1.1) and the algorithmic framework (1.4) from the variational inequality perspective. Then, we prove the convergence of (1.4) in Sect. 3. In Sect. 4, we elaborate on the conditions that can ensure the convergence of (1.4); some specific generalized PDHG schemes are thus yielded based on the algorithmic framework (1.4). Then, we derive the worst-case convergence rate measured by the iteration complexity for (1.4) in Sect. 5. We test the efficiency of these specific generalized PDHG algorithms by an image restoration model in Sect. 6. Finally, we draw some conclusions in Sect. 7.

2 Variational Inequality Understanding

In this section, we provide the variational inequality (VI) reformulation of the model (1.1) and characterize the algorithmic framework (1.4) via a VI. These VI understandings are the basis of our analysis to be conducted.

2.1 Variational Inequality Reformulation of (1.1)

We first show that the saddle point problem (1.1) can be written as a VI problem. More specifically, if $(x^*,y^*)\in \mathcal{X}\times \mathcal{Y}$ is a solution point of the saddle point problem (1.1), then we have

$$\begin{aligned} {\forall y\in \mathcal{Y}, \; \forall x\in \mathcal{X},\ \Phi (x^*,y) \le \Phi (x^*,y^*) \le \Phi (x,y^*).}\nonumber \\ \end{aligned}$$

(2.1)

Obviously, the second inequality in (2.1) is equivalent to

$$\begin{aligned}&x^*\in \mathcal{X},\;\; \theta _1(x)-\theta _1(x^*)+(x-x^*)^T(-A^Ty^*)\ge 0,\\&\quad \forall \, x\in \mathcal{X}; \end{aligned}$$

and the first one in (2.1) can be written as

$$\begin{aligned} y^*\in \mathcal{Y},\;\; \theta _2(y)-\theta _2(y^*)\,+\,(y-y^*)^T( {Ax^*})\ge 0, \;\; \forall \, y\in \mathcal{Y}. \end{aligned}$$

Therefore, finding a solution point $(x^*,y^*)$ of (1.1) is equivalent to solving the VI problem: Find $u^*=(x^*,y^*)$ such that

$$\begin{aligned}&\hbox {VI}(\Omega ,F,\theta ) \qquad u^*\in \Omega , \quad \theta (u)-\theta (u^*) \nonumber \\&\quad +\,(u-u^*)^TF(u^*) \ge 0 , \quad \forall \; u\in \Omega , \end{aligned}$$

(2.2a)

where

$$\begin{aligned} u= & {} \left( \begin{array}{c} x \\ y \end{array}\right) , \theta (u)=\theta _1(x) + \theta _2(y), \quad F(u)=\left( \begin{array}{c} -A^Ty \\ {Ax} \end{array}\right) \nonumber \\&\quad \hbox {and}\quad \Omega =\mathcal{X}\times \mathcal{Y}. \end{aligned}$$

(2.2b)

We denote by $\Omega ^*$ the set of all solution points of VI$(\Omega ,F,\theta )$ (2.2). Notice that $\Omega ^*$ is convex (see Theorem 2.3.5 in [11] or Theorem 2.1 in [17]).

Clearly, for the mapping F given in (2.2b), we have

$$\begin{aligned} (u-v)^T(F(u)-F(v))= 0, \quad \forall \, u, v \in \Omega . \end{aligned}$$

(2.3)

Moreover, under the condition (1.3), the matrix

$$\begin{aligned} \left( \begin{array}{cc} r I_n &{} A^T \\ A &{} sI_m \end{array} \right) \end{aligned}$$

(2.4)

is positive definite. The positive definiteness of this matrix plays a significant role in analyzing the convergence of the PDHG scheme (1.2), see e.g. [5, 10, 16, 28].

2.2 Variational Inequality Characterization of (1.4)

Then, we rewrite the algorithmic framework (1.4) also in the VI form. Note that the PDHG subroutine (1.4a) can be written as

Thus, the optimality conditions of (2.5a) and (2.5c) are

$$\begin{aligned}&\tilde{x}^k\in \mathcal{X}, \quad \theta _1(x) \!-\!\theta _1(\tilde{x}^k) \,+ \, (x\!-\!\tilde{x}^k)^T \bigl ( - A^Ty^k \,+ \,r(\tilde{x}^k -x^k)\bigr )\\&\quad \ge 0, \;\; \forall \; x \in \mathcal{X}, \end{aligned}$$

and

$$\begin{aligned}&\tilde{y}^k\in \mathcal{Y}, \quad \theta _2(y) -\theta _2(\tilde{y}^k) + (y-\tilde{y}^k)^T \bigl ({A\bar{x}^k} + s(\tilde{y}^k -y^k)\bigr )\\&\quad \ge 0, \;\; \forall \; y\in \mathcal{Y}, \end{aligned}$$

respectively. Using (2.5b), we get the following VI containing only $(x^k, y^k)$ and $(\tilde{x}^k, \tilde{y}^k)$:

$$\begin{aligned}&(\tilde{x}^k, \tilde{y}^k) \in \mathcal{X}\times \mathcal{Y}, \quad (\theta _1(x) -\theta _1(\tilde{x}^k)) + ( \theta _2(y) -\theta _2(\tilde{y}^k) ) \nonumber \\&\qquad + \left( \begin{array}{c} x-\tilde{x}^k \\ y-\tilde{y}^k \end{array}\right) ^T \left\{ \left( \begin{array}{c} - A^T\tilde{y}^k\\ {A\tilde{x}^k} \end{array}\right) + \left( \begin{array}{c} r(\tilde{x}^k -x^k) + A^T(\tilde{y}^k -y^k)\\ \tau A(\tilde{x}^k-x^k) + s(\tilde{y}^k - y^k) \end{array}\right) \right\} \nonumber \\&\quad \ge 0, \; \forall (x,y) \in \mathcal{X}\times \mathcal{Y}. \end{aligned}$$

(2.6)

Then, because of the notation in (2.2b), the PDHG subroutine (1.4a) can be written compactly as (2.7). Accordingly, the step (1.4a) can be rewritten as (2.8) and overall the algorithmic framework (1.4) can be explained as the prediction-correction way (2.7)–(2.8).

3 Convergence

In this section, we investigate the convergence of the algorithmic framework (1.4). Recall that (1.4) can be rewritten as the prediction-correction way (2.7)–(2.8). We prove the convergence of (1.4) under the condition

where the matrices Q and M are given in (2.7b) and (2.8b), respectively. Thus, it suffices to check the positive definiteness of two matrices to ensure the convergence of the algorithmic framework (1.4). The condition (3.1) also implies some specific restrictions onto the involved parameters in (1.4) to be discussed in Sect. 4.

Because of the VI reformulation (2.2) of the model (1.1), we are interested in using the VI characterization (2.7) to discern how accurate an iterate generated by the algorithmic framework (1.4) is to a solution point of VI$(\Omega ,F,\theta )$. This analysis is summarized in the following theorem.

Theorem 3.1

Let $u^{k}=(x^k,y^k)$ be given by the algorithmic framework (1.4). Under the condition (3.1), we have

$$\begin{aligned}&\theta (u) - \theta (\tilde{u}^k) + (u- \tilde{u}^k)^T F(\tilde{u}^k) \ge \frac{1}{2} \bigl (\Vert u-u^{k+1}\Vert _H^2 \nonumber \\&\quad -\,\Vert u-u^k\Vert _H^2 \bigr ) + \frac{1}{2}\Vert u^k-\tilde{u}^k\Vert _G^2, \;\; \forall u\in \Omega . \end{aligned}$$

(3.2)

Proof

It follows from (3.1a) that $Q=HM$. Using (2.8a), we know that (2.7a) can be written as

$$\begin{aligned}&\theta (u) - \theta (\tilde{u}^k) + (u- \tilde{u}^k )^T F(\tilde{u}^k) \ge (u- \tilde{u}^k)^T H(u^k\nonumber \\&\quad -\,u^{k+1}), \; \forall u\in \Omega . \end{aligned}$$

(3.3)

For H satisfying (3.1a), we apply the identity

$$\begin{aligned} (a-b)^TH(c-d)= & {} \frac{1}{2} \left\{ \Vert a-d\Vert _H^2 -\Vert a-c\Vert _H^2\right\} \\&+\,\frac{1}{2} \left\{ \Vert c-b\Vert _H^2 -\Vert d-b\Vert _H^2\right\} \end{aligned}$$

to the right-hand side of (3.3) with

$$\begin{aligned} a=u, \quad b=\tilde{u}^k, \quad c=u^k , \quad \hbox {and} \quad d=u^{k+1}, \end{aligned}$$

and obtain

$$\begin{aligned}&(u- \tilde{u}^k)^T H(u^k - u^{k+1}) = \frac{1}{2} \bigl ( \Vert u-u^{k+1}\Vert _H^2\nonumber \\&\quad - \Vert u-u^k\Vert _H^2 \bigr ) + \frac{1}{2}\left( \Vert u^k-\tilde{u}^k\Vert _H^2 - \Vert u^{k+1}-\tilde{u}^k\Vert _H^2\right) .\nonumber \\ \end{aligned}$$

(3.4)

For the last term of the right-hand side of (3.4), we have

$$\begin{aligned}&\Vert u^k-\tilde{u}^k\Vert _H^2 - \Vert u^{k+1}-\tilde{u}^k\Vert _H^2 \nonumber \\&\quad = \Vert u^k-\tilde{u}^k\Vert _H^2 - \Vert (u^k-\tilde{u}^k) -(u^k- u^{k+1})\Vert _H^2 \nonumber \\&\mathop {=}\limits ^{(3.1a)} \Vert u^k-\tilde{u}^k\Vert _H^2 - \Vert (u^k-\tilde{u}^k) - M (u^k-\tilde{u}^k)\Vert _H^2 \nonumber \\&\quad = 2 (u^k-\tilde{u}^k)^TH M (u^k-\tilde{u}^k) \nonumber \\&\qquad - (u^k-\tilde{u}^k)^T M ^THM (u^k-\tilde{u}^k) \nonumber \\&\quad = (u^k-\tilde{u}^k)^T ( Q^T +Q - M^THM)(u^k-\tilde{u}^k) \nonumber \\&\mathop {=}\limits ^{(3.1b)} \Vert u^k-\tilde{u}^k\Vert _G^2. \end{aligned}$$

(3.5)

Substituting (3.4) and (3.5) into (3.3), we obtain the assertion (3.2). $\square$

With the assertion in Theorem 3.1, we can show that the sequence $\{u^k\}$ with $u^{k}$ given by (1.4) is strictly contractive with respect to the solution set $\Omega ^*$. We prove this property in the following theorem.

Theorem 3.2

Let $u^{k}=(x^k,y^k)$ be given by the algorithmic framework (1.4). Under the condition (3.1), we have

$$\begin{aligned} \Vert u^{k+1}-u^*\Vert _H^2 \le \Vert u^k -u^*\Vert _H^2 - \Vert u^k-\tilde{u}^k\Vert _G^2, \quad \forall u^*\in \Omega ^*. \end{aligned}$$

(3.6)

Proof

Setting $u=u^*$ in (3.2), we get

$$\begin{aligned}&\Vert u^k -u^*\Vert _H^2 - \Vert u^{k+1}-u^*\Vert _H^2 \ge \Vert u^k-\tilde{u}^k\Vert _G^2 \nonumber \\&\quad + \,2\{\theta (\tilde{u}^k) -\theta (u^*) + ( \tilde{u}^k -u^*)^T F(\tilde{u}^k)\}. \end{aligned}$$

(3.7)

Then, using (2.3) and the optimality of $u^*$, we have

$$\begin{aligned}&\theta (\tilde{u}^k) -\theta (u^*) + ( \tilde{u}^k -u^*)^T F(\tilde{u}^k) \nonumber \\&\quad = \theta (\tilde{u}^k) -\theta (u^*) + ( \tilde{u}^k -u^*)^T F(u^*) \ge 0 \end{aligned}$$

and thus

$$\begin{aligned} \Vert u^k -u^*\Vert _H^2 - \Vert u^{k+1}-u^*\Vert _H^2 \ge \Vert u^k-\tilde{u}^k\Vert _G^2. \end{aligned}$$

(3.8)

The assertion (3.6) follows directly. $\square$

Theorem 3.2 shows that the sequence $\{u^k\}$ with $u^k$ given by (1.4) is Fèjer monotone and the convergence of $\{u^k\}$ to a $u^*\in {\Omega }^*$ in H-norm is immediately implied, see, e.g., [2].

4 How to Ensure the Condition (3.1)

In Sect. 3, the convergence of the algorithmic framework (1.4) is derived under the condition (3.1). Now, we discuss how to appropriately choose the parameters $\tau$, $\alpha$ and $\beta$ to ensure the condition (3.1). With different choices of these parameters in the algorithmic framework (1.4), a series of PDHG schemes are specified for the saddle point problem (1.1).

4.1 General Study

Recall the definitions of Q and M in (2.7b) and (2.8b), respectively. Let us take a closer look at the matrices H and G defined in (3.1).

First, we have

$$\begin{aligned} H= QM^{-1} = \left( \begin{array}{cc} r I_n &{} A^T \\ \tau A &{} sI_m \end{array} \right) \left( \begin{array}{cc} \frac{1}{\alpha } I_n &{} 0 \\ 0 &{} \frac{1}{\beta } I_m \end{array} \right) = \left( \begin{array}{cc} \frac{r}{\alpha } I_n &{} \frac{1}{\beta } A^T \\ \frac{\tau }{\alpha } A &{} \frac{1}{\beta } s I_m \end{array} \right) . \end{aligned}$$

Thus, we set $\beta = \frac{\alpha }{\tau }$ to ensure that H is symmetric. With this restriction, we have

$$\begin{aligned} H = \left( \begin{array}{cc} \frac{r}{\alpha } I_n &{} \frac{\tau }{\alpha } A^T \\ \frac{\tau }{\alpha } A &{} \frac{\tau }{\alpha } s I_m \end{array} \right) = \frac{1}{\alpha } \left( \begin{array}{cc} {r} I_n &{} \tau A^T \\ \tau A &{} \tau s I_m \end{array} \right) . \end{aligned}$$

Then, it is clear that under the condition (1.3), we can choose any $\tau \in (0,1]$ to ensure the positive definiteness of H. Overall, to ensure the positive definiteness and symmetry of H, we pose the restriction:

$$\begin{aligned} \tau \in (0,1], \qquad \beta = \frac{\alpha }{\tau } \qquad \hbox {and} \qquad \alpha >0. \end{aligned}$$

(4.1)

Second, let us deal with the matrix G in (3.1). Since $HM=Q$, we have

$$\begin{aligned}&Q^T + Q - M^THM =Q^T + Q - M^TQ \nonumber \\&\quad = \left( \begin{array}{cc} 2r I_n &{} (1+\tau ) A^T \\ (1+\tau ) A &{} 2 s I_m \end{array} \right) - \left( \begin{array}{cc} \alpha I_n &{} 0 \\ 0 &{} \frac{\alpha }{\tau }I_m \end{array} \right) \left( \begin{array}{cc} r I_n &{} A^T \\ \tau A &{} sI_m \end{array} \right) \nonumber \\&\quad = \left( \begin{array}{cc} 2r I_n &{} (1+\tau ) A^T \\ (1+\tau ) A &{} 2 s I_m \end{array} \right) - \left( \begin{array}{cc} \alpha r I_n &{} \alpha A^T \\ \alpha A &{} \frac{\alpha }{\tau } sI_m \end{array} \right) \nonumber \\&\quad = \left( \begin{array}{cc} (2-\alpha ) r I_n &{} (1+\tau -\alpha )A^T \\ (1+\tau -\alpha ) A &{}(2- \frac{\alpha }{\tau } ) s I_m \end{array} \right) . \end{aligned}$$

(4.2)

Therefore, we need to ensure

$$\begin{aligned} G= \left( \begin{array}{cc} (2-\alpha ) r I_n &{} (1+\tau -\alpha )A^T \\ (1+\tau -\alpha ) A &{}(2- \frac{\alpha }{\tau } ) s I_m \end{array} \right) \succ 0. \end{aligned}$$

(4.3)

We present a strategy to ensure (4.3) in the following theorem.

Theorem 4.1

For given $\tau \in (0,1]$, under the condition (1.3), the assertion (4.3) holds when

$$\begin{aligned} \tau =1 \qquad \hbox {and}\qquad \alpha \in (0,2), \end{aligned}$$

(4.4)

or

$$\begin{aligned} \tau \in (0,1), \qquad \hbox {and} \qquad 0<\alpha \le (1+\tau ) - \sqrt{1-\tau }. \end{aligned}$$

(4.5)

Proof

First, if $\tau =1$, it follows from (4.2) that

$$\begin{aligned} G= (2-\alpha ) \left( \begin{array}{cc} r I_n &{} A^T \\ A &{} s I_m \end{array} \right) . \end{aligned}$$

Under the condition (1.3), we have $G\succ 0$ for all $\alpha \in (0,2)$.

Now, we consider $\tau \in (0,1)$. According to numerical linear algebra, e.g., Theorem 7.7.7 in [19], for $G \succ 0$, we need to ensure

$$\begin{aligned} (2-\alpha )> & {} 0, \quad \left( 2-\frac{\alpha }{\tau }\right)>0 \quad \hbox {and} \quad (2-\alpha ) \left( 2-\frac{\alpha }{\tau } \right) rs\\> & {} (1+\tau -\alpha )^2 \Vert A^TA\Vert . \end{aligned}$$

Thus, under the condition (1.3), it is enough to guarantee

$$\begin{aligned} (2-\alpha )>0, \qquad \left( 2-\frac{\alpha }{\tau }\right) >0 , \end{aligned}$$

(4.6a)

and

$$\begin{aligned} (2-\alpha ) \left( 2-\frac{\alpha }{\tau }\right) \ge (1+\tau -\alpha )^2. \end{aligned}$$

(4.6b)

By a manipulation, the inequality (4.6b) is equivalent to

$$\begin{aligned} \Bigl (\frac{1}{\tau } \!-\!1\Bigr ) \alpha ^2 \!+\! 2\Bigl ((1\!+\!\tau ) \!-\! \left( 1\!+\!\frac{1}{\tau }\right) \Bigr ) \alpha \!+\! \bigl ( 4 \!-\! (1\!+\!\tau )^2\bigr ) \ge 0, \end{aligned}$$

and thus

$$\begin{aligned} \Bigl (\frac{1-\tau }{\tau } \Bigr )\alpha ^2 + 2\Bigl (\frac{\tau ^2-1}{\tau } \Bigr ) \alpha + (3+\tau )(1-\tau ) \ge 0. \end{aligned}$$

Multiplying by the positive factor $\displaystyle {\frac{\tau }{1-\tau }}$, we get

$$\begin{aligned} \alpha ^2 - 2(1+\tau ) \alpha + \tau (3+\tau ) \ge 0. \end{aligned}$$

Because the smaller root of the equation

$$\begin{aligned} \alpha ^2 - 2(1+\tau ) \alpha + \tau (3+\tau ) =0 \end{aligned}$$

is $(1+ \tau ) - \sqrt{1-\tau }$, the condition (4.6b) is satisfied when (4.5) holds.

In the following, we show that (4.6a) is satisfied when (4.5) holds. It follows from (4.5) directly $\alpha < 2$ for all $\tau \in (0,1)$. In addition, because

$$\begin{aligned} (1-\tau ) -\sqrt{1-\tau } <0, \; \forall \, \tau \in (0,1), \end{aligned}$$

we have

$$\begin{aligned} (1+ \tau ) -\sqrt{1-\tau } < 2\tau , \quad \forall \, \tau \in (0,1). \end{aligned}$$

Consequently, using (4.5), we get

$$\begin{aligned} \frac{\alpha }{\tau } \le \frac{(1+ \tau ) -\sqrt{1-\tau }}{\tau } < 2 , \quad \forall \, \tau \in (0,1). \end{aligned}$$

The proof is complete. $\square$

In the following theorem, we summarize the restriction onto the involved parameters that can ensure the convergence of the algorithmic framework (1.4).

Theorem 4.2

Under the condition (1.3), if the parameters $\tau ,\alpha$ and $\beta$ in (1.4) are chosen such that either

$$\begin{aligned} \tau =1, \qquad \hbox {and} \qquad \alpha =\beta \in (0,2), \end{aligned}$$

(4.7a)

or

$$\begin{aligned} \tau \!\in \! (0,1), \qquad 0\!<\!\alpha \!\le \!1\!+\!\tau \!-\!\sqrt{1-{\tau }} \qquad \hbox {and} \qquad \beta = \frac{\alpha }{\tau },\nonumber \\ \end{aligned}$$

(4.7b)

then the matrices Q and M defined, respectively, in (2.7b) and (2.8b) satisfy the convergence condition (3.1). Thus, the sequence $\{u^k\}$ with $u^k$ given by the algorithmic framework (1.4) converges to a solution point of VI$(\Omega , F, \theta )$.

4.2 Special Cases

In this subsection, we specify the general restriction posed in Theorem 4.2 on the parameters of the algorithmic framework (1.4) and discuss some special cases of this framework.

4.2.1 Case I: ${\varvec{\tau =1}}$

According to (4.7a), we can take $\alpha =\beta \in (0,2)$ and thus the algorithmic framework (1.4) can be written as

This is exactly Algorithm 4 in [16] which can be regarded as an improved version of (1.2) using the technique in [14]. Clearly, choosing $\alpha =\beta =1$ in (4.8) recovers the special case of (1.2) with $\tau =1$

4.2.2 Case II: ${\varvec{\alpha =1}}$

Now let $\alpha =1$ be fixed. In this case, the algorithmic framework (1.4) can be written as

$$\begin{aligned} \left\{ \begin{array}{rcl} x^{k+1} &{}=&{} \arg \min \left\{ \Phi (x,y^k) + \frac{r}{2} \Vert x-x^k\Vert ^2 \, |\, x\in \mathcal{X} \right\} , \\ \bar{x}^k &{}=&{} x^{k+1} + \tau ( x^{k+1} -x^k), \\ \tilde{y}^k &{}=&{} \arg \max \left\{ \Phi ( \bar{x}^k,y) - \frac{s}{2} \Vert y-y^k\Vert ^2 \, |\, y\in \mathcal{Y}\right\} ,\\ y^{k+1} &{} = &{} y^k + \beta (\tilde{y}^k-y^k), \end{array} \right. \end{aligned}$$

(4.9)

which is symmetric in the sense that it updates both the variables x and y twice at each iteration. For this special case, the restriction in Theorem 4.2 can be further specified. We present it in the following theorem.

Theorem 4.3

Under the condition (1.3), if $\alpha =1$; the parameters $\beta$ and $\tau$ satisfy

$$\begin{aligned} \tau \in \Bigl [\frac{\sqrt{5}-1}{2}, 1 \Bigr ], \qquad \hbox {and} \qquad \beta = \frac{1}{\tau }, \end{aligned}$$

(4.10)

then the condition (4.7a) or (4.7b) is satisfied and thus the PDHG scheme (4.9) is convergent.

Proof

If $\alpha =1$ and $\tau =1$, it follows from (4.10) that the condition (4.7a) is satisfied. Now we consider $\alpha =1$ and $\tau \in (0,1)$. In this case, the condition (4.7b) becomes

$$\begin{aligned} \tau \in (0,1) \qquad \hbox {and} \qquad 1 \le 1+ \tau -\sqrt{1-\tau }, \end{aligned}$$

and thus

$$\begin{aligned} \tau \in (0,1) \qquad \hbox {and} \qquad \tau ^2 + \tau - 1 \ge 0 . \end{aligned}$$

The above condition is satisfied for all $\tau \in \bigl [\frac{\sqrt{5}-1}{2}, 1 \bigr )$. The proof is complete. $\square$

Therefore, with the restriction in (4.10), the PDHG scheme (4.9) can be written as

$$\begin{aligned} \left\{ \begin{array}{rcl} x^{k+1} &{}=&{} \arg \min \left\{ \Phi (x,y^k) + \frac{r}{2} \Vert x-x^k\Vert ^2 \, |\, x\in \mathcal{X} \right\} , \\ \bar{x}^k &{}=&{} x^{k+1} + \tau ( x^{k+1} -x^k), \\ \tilde{y}^k &{}=&{} \arg \max \left\{ \Phi (\bar{x}^k,y) - \frac{s}{2} \Vert y-y^k\Vert ^2 \, |\, y\in \mathcal{Y}\right\} ,\\ y^{k+1} &{} = &{} y^k + \frac{1}{\tau } (\tilde{y}^k-y^k), \end{array} \right. \end{aligned}$$

(4.11)

where $\tau \in \Bigl [\frac{\sqrt{5}-1}{2}, 1 \Bigr ]$. Indeed, we can further consider choosing $\tau _0 =\frac{\sqrt{5}-1}{2}$. Then, we have $\frac{1}{\tau _0} = 1 + \tau _0$ and it follows from (4.11) that

$$\begin{aligned}&y^k + \frac{1}{\tau _0} ({\tilde{y}}^{k}-y^k) = y^k + (1+\tau _0) ({\tilde{y}}^{k}-y^k) \\&\quad = {\tilde{y}}^{k} + \tau _0({\tilde{y}}^{k}-y^k). \end{aligned}$$

Thus, the scheme (4.11) can be further specified as

$$\begin{aligned} \left\{ \begin{array}{rcl} x^{k+1} &{}=&{} \arg \min \left\{ \Phi (x,y^k) + \frac{r}{2} \Vert x-x^k\Vert ^2 \, |\, x\in \mathcal{X} \right\} , \\ \bar{x}^k &{}=&{} x^{k+1} + \tau _0 ( x^{k+1} -x^k), \\ \tilde{y}^k &{}=&{} \arg \max \left\{ \Phi ( \bar{x}^k,y) - \frac{s}{2} \Vert y-y^k\Vert ^2 \, |\, y\in \mathcal{Y}\right\} ,\\ y^{k+1} &{} = &{} \tilde{y}^k + \tau _0 (\tilde{y}^k-y^k), \end{array} \right. \end{aligned}$$

(4.12)

where $\tau _0=\frac{\sqrt{5}-1}{2}$. It is a completely symmetric PDHG scheme in the sense that both the variables are updated twice at each iteration and the additional updating steps both use the golden-ratio step sizes.

4.2.3 Case III: ${\varvec{\beta =1}}$

We can also fix $\beta =1$. In this case, the algorithmic framework (1.4) reduces to

For this case, the restriction on the involved parameters in Theorem 4.2 can be further specified as the following theorem.

Theorem 4.4

Under the condition (1.3), if $\beta =1$; the parameters $\alpha$ and $\tau$ satisfy

$$\begin{aligned} \alpha =\tau \in (0,1], \end{aligned}$$

(4.14)

then the convergence condition (4.3) is satisfied.

Proof

First, in this case, the condition (4.1) is satisfied. The matrix G in (4.3) becomes

$$\begin{aligned} G= \left( \begin{array}{cc} (2-\alpha ) r I_n &{} A^T \\ A &{} s I_m \end{array} \right) , \end{aligned}$$

which is positive definite for all $\alpha \in (0,1]$ under the assumption (1.3). $\square$

Therefore, considering the restriction in (4.14), we can specify the scheme (4.13) as

where $\tau \in \bigl (0, 1 \bigr ]$.

5 Convergence Rate

In this section, we establish the worst-case convergence rate measured by the iteration complexity for the algorithmic framework (1.4) in both the ergodic and nonergodic senses.

5.1 Convergence Rate in the Ergodic Sense

We first derive the worst-case convergence rate in the ergodic sense for the algorithmic framework (1.4). For this purpose, we need to define an approximate solution of the problem (1.1).

Let $(x^*, y^*) \in \Omega ^*$ be a saddle point of (1.1). According to the definition (2.1), we have

$$\begin{aligned} \Phi (x,y^*)-\Phi (x^*,y)\ge 0, \; \forall x \in \mathcal{X}, y\in \mathcal{Y}, \end{aligned}$$

which, by using the notation defined in (2.2b), can be specified as

$$\begin{aligned} \theta (u)-\theta (u^*)+(u-u^*)^TF(u^*) \ge 0, \; \forall u \in \Omega . \end{aligned}$$

That is, $\theta (u) - \theta (u^*) + (u-u^*)^TF(u^*)$ can be used to measure the primal–dual gap of the model (1.1) at the point $u \in \Omega$. It is thus reasonable to define an approximate solution of the problem (1.1) in terms of the primal–dual gap, as stated below.

Definition 5.1

For given $\epsilon >0$ and a solution point $u^*$ of the problem (1.1), $u \in \Omega$ is called an $\epsilon$-approximate solution of the problem (1.1) if it satisfies

$$\begin{aligned} 0\le \theta (u) - \theta (u^*) + (u-u^*)^T F(u^*)\le \epsilon . \end{aligned}$$

(5.1)

The following theorem essentially implies that we can find an $\epsilon$-approximate solution of the problem (1.1) based on $O(1/\epsilon )$ iterations generated by the algorithmic framework (1.4).

Theorem 5.2

Let $\{u^{k}=(x^k,y^k)\}$ be the sequence generated by the algorithmic framework (1.4) under the conditions (1.3) and (3.1); and $u^*\in \Omega ^*$ be a saddle point of (1.1). For any integer $t>0$, let $\tilde{u}_t$ be defined as

$$\begin{aligned} \tilde{u}_t = \frac{1}{t+1} \sum _{k=0}^t \tilde{u}^k. \end{aligned}$$

(5.2)

Then we have

$$\begin{aligned}&\tilde{u}_t\in \Omega ,\quad \theta (\tilde{u}_t) -\theta (u^*) + (\tilde{u}_{t}-u^*)^T F(u^*)\nonumber \\&\quad \le \frac{1}{2(t+1)}\Vert u^0-u^*\Vert _H^2. \end{aligned}$$

(5.3)

Proof

First, we know $\tilde{u}^k\in \Omega$ for all $k\ge 0$. Because of the convexity of $\mathcal{X}$ and $\mathcal{Y}$, it follows from (5.2) that $\tilde{u}_t\in \Omega$. Using (2.3) and (3.2), we have

$$\begin{aligned}&\theta (u) - \theta (\tilde{u}^k) + (u- \tilde{u}^k)^TF(u) + \frac{1}{2}\Vert u-u^k\Vert _H^2 \nonumber \\&\quad \ge \frac{1}{2}\Vert u-u^{k+1}\Vert _H^2, \; \forall u\in \Omega . \end{aligned}$$

(5.4)

Summing the inequality (5.4) over $k=0,1,\ldots , t$, we obtain

$$\begin{aligned}&(t+1)\theta (u) - \sum _{k=0}^t \theta (\tilde{u}^k) + \Bigl ((t+1)u - \sum _{k=0}^t \tilde{u}^k\Bigr )^T F(u) \\&\quad +\,\frac{1}{2}\Vert u-u^0\Vert _H^2 \ge 0, \quad \forall u\in \Omega . \end{aligned}$$

Since $\tilde{u}_{t}$ is defined in (5.2), we have

$$\begin{aligned}&\frac{1}{t+1} \sum _{k=0}^t \theta (\tilde{u}^k) -\theta (u) + (\tilde{u}_{t}-u)^T F(u) \nonumber \\&\quad \le \frac{1}{2(t+1)}\Vert u-u^0\Vert _H^2,\quad \forall u\in \Omega . \end{aligned}$$

(5.5)

Further, because of the convexity of $\theta (u)$, we get

$$\begin{aligned} \theta (\tilde{u}_t) \le \frac{1}{t+1}\sum _{k=0}^t \theta (\tilde{u}^k). \end{aligned}$$

Substituting it into (5.5) and setting $u=u^*$, the assertion of this theorem follows directly. $\square$

In the following theorem, we state the worst-case O(1 / t) convergence rate measured by the iteration complexity for the algorithmic framework (1.4) in the ergodic sense. The proof is clear based on Theorem 5.2; thus omitted.

Theorem 5.3

Let $\{u^{k}=(x^k,y^k)\}$ be the sequence generated by the algorithmic framework (1.4) under the conditions (1.3) and (3.1); and $u^*\in \Omega ^*$ be a saddle point of (1.1). For given $\epsilon >0$, based on t iterations of (1.4) with $t= \lceil \frac{\Vert u^0-u^*\Vert _H^2}{2\epsilon }-1\rceil =O(1/\epsilon )$ , the point $\tilde{u}_t$ defined as the average of all these t iterations in (5.2) is an $\epsilon$-approximate solution of the problem (1.1) in sense of (5.1), i.e., it satisfies

$$\begin{aligned} \tilde{u}_t\in \Omega ,\quad 0\le \theta (\tilde{u}_t) - \theta (u^*) + (\tilde{u}_t-u^*)^T F(u^*)\le \epsilon . \end{aligned}$$

Finally, we would like to remark that the condition of $G\succ 0$ in (3.1) can be relaxed to $G\succeq 0$ for deriving the convergence rate result in this subsection.

5.2 Convergence Rate in a Nonergodic Sense

In this subsection, we derive the worst-case $O(1/\sqrt{t})$ convergence rate in a nonergodic sense for the algorithmic framework (1.4). Note that a nonergodic worst-case convergence rate is generally stronger than its ergodic counterparts. We first prove a lemma.

Lemma 5.4

Let $u^{k}=(x^k,y^k)$ be given by the algorithmic framework (1.4). Under the condition (3.1), we have

$$\begin{aligned}&(u^k - \tilde{u}^k)^T M^THM \{ (u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})\}\nonumber \\&\quad \ge \frac{1}{2} \Vert (u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})\Vert _{(Q^T+Q)}^2. \end{aligned}$$

(5.6)

Proof

Setting $u=\tilde{u}^{k+1}$ in (2.8a), we get

$$\begin{aligned}&\theta (\tilde{u}^{k+1}) -\theta (\tilde{u}^k) + (\tilde{u}^{k+1} - \tilde{u}^k)^T F(\tilde{u}^k)\nonumber \\&\quad \ge (\tilde{u}^{k+1} - \tilde{u}^k)^T Q(u^k -\tilde{u}^k). \end{aligned}$$

(5.7)

Note that (2.8a) is also true for $k:=k+1$. Thus, it holds that

$$\begin{aligned}&\theta (u)-\theta (\tilde{u}^{k+1}) + (u -\tilde{u}^{k+1} )^TF(\tilde{u}^{k+1})\\&\quad \ge (u -\tilde{u}^{k+1} )^T Q(u^{k+1} -\tilde{u}^{k+1}), \, \forall u\in \Omega . \end{aligned}$$

Then, setting $u=\tilde{u}^k$ in the above inequality, we obtain

$$\begin{aligned}&\theta (\tilde{u}^k)-\theta (\tilde{u}^{k+1}) + (\tilde{u}^k -\tilde{u}^{k+1} )^T F(\tilde{u}^{k+1})\nonumber \\&\quad \ge (\tilde{u}^k -\tilde{u}^{k+1} )Q(u^{k+1} -\tilde{u}^{k+1} ). \end{aligned}$$

(5.8)

Combining (5.7) and (5.8), and using the monotonicity of F [see (2.3)], we have

$$\begin{aligned} (\tilde{u}^k - \tilde{u}^{k+1})^T Q \{ (u^k-\tilde{u}^k)-(u^{k+1} -\tilde{u}^{k+1})\} \ge 0. \end{aligned}$$

(5.9)

Adding the term

$$\begin{aligned} \{(u^k \!- \!\tilde{u}^k) \!-\!(u^{k+1}-\tilde{u}^{k+1})\}^T Q \{(u^k \!-\! \tilde{u}^k) \!-\!(u^{k+1}-\tilde{u}^{k+1})\} \end{aligned}$$

to both sides of (5.9), and using $v^TQv= \frac{1}{2}v^T(Q^T+Q)v$, we obtain

$$\begin{aligned}&(u^k - u^{k+1})^T Q \{ (u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})\}\\&\quad \ge \frac{1}{2} \Vert (u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})\Vert _{(Q^T+Q)}^2 . \end{aligned}$$

Substituting $(u^k - u^{k+1})= M(u^k-\tilde{u}^k)$ into the left-hand side of the last inequality and using $Q=HM$, we obtain (5.6) and the lemma is proved. $\square$

Now, we establish the worst-case $O(1/\sqrt{t})$ convergence rate in a nonergodic sense for the algorithmic framework (1.4). Similar techniques can be found in [18].

Theorem 5.5

Let $u^{k}=(x^k,y^k)$ be given by the algorithmic framework (1.4). Under the condition (3.1), for any integer $t>0$, we have

$$\begin{aligned} \Vert M(u^t-\tilde{u}^t)\Vert _H^2 \le \frac{1}{(t+1)c_0} \Vert u^0-u^*\Vert _H^2, \end{aligned}$$

(5.10)

where $c_0>0$ is a constant independent of t.

Proof

First, setting $a=M(u^k-\tilde{u}^k)$ and $b=M(u^{k+1}-\tilde{u}^{k+1})$ in the identity

$$\begin{aligned} \Vert a\Vert _H^2 - \Vert b\Vert _H^2 = 2a^TH(a-b) - \Vert a-b\Vert _H^2, \end{aligned}$$

we obtain

$$\begin{aligned}&\Vert M(u^k-\tilde{u}^k)\Vert _H^2 - \Vert M(u^{k+1}-\tilde{u}^{k+1})\Vert _H^2 \\&\quad = 2(u^k-\tilde{u}^k)^TM^THM[(u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})]\\&\qquad - \Vert M[(u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})]\Vert _H^2. \end{aligned}$$

Inserting (5.6) into the first term of the right-hand side of the last equality, we obtain

$$\begin{aligned}&\Vert M(u^k-\tilde{u}^k)\Vert _H^2 - \Vert M(u^{k+1}-\tilde{u}^{k+1})\Vert _H^2 \\&\quad \ge \Vert (u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})\Vert _{(Q^T+Q)}^2\\&\qquad - \Vert M [(u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})]\Vert _H^2 \\&\quad = \Vert (u^k-\tilde{u}^k) - (u^{k+1}-\tilde{u}^{k+1})\Vert _G^2 \ge 0. \end{aligned}$$

The last inequality holds because the matrix $(Q^T+Q)- M^THM =G$ and $G\succeq 0$. We thus have

$$\begin{aligned} \Vert M(u^{k+1}-\tilde{u}^{k+1})\Vert _H \le \Vert M(u^k-\tilde{u}^k)\Vert _H, \quad \forall \, k>0. \end{aligned}$$

(5.11)

Recall that the matrix M is positive definite. Thus, the sequence $\{\Vert M(u^k-\tilde{u}^k)\Vert _H^2 \}$ is monotonically non-increasing. Then, it follows from $G\succ 0$ and Theorem 3.2 there is a constant $c_0>0$ such that

$$\begin{aligned} \Vert u^{k+1}-u^*\Vert _H^2&\le \Vert u^k -u^*\Vert _H^2 - c_0\Vert M(u^k-\tilde{u}^k)\Vert _H^2,\nonumber \\&\quad \forall u^*\in \Omega ^*. \end{aligned}$$

(5.12)

Furthermore, it follows from (5.12) that

$$\begin{aligned} \sum _{k=0}^{\infty } c_0\Vert M(u^k - \tilde{u}^k)\Vert _H^2 \le \Vert u^0 - u^*\Vert _H^2,\quad \forall \, u^*\in \Omega ^*. \end{aligned}$$

(5.13)

Therefore, for any integer $t>0$, we have

$$\begin{aligned} (t+1)\Vert M(u^t -\tilde{u}^t)\Vert _H^2 \le \sum _{k=0}^{t} \Vert M(u^k -\tilde{u}^k)\Vert _H^2. \end{aligned}$$

(5.14)

The assertion (5.10) follows from (5.13) and (5.14) immediately. $\square$

Let $d: = \inf \{ \Vert u^0 - u^*\Vert _H \, |\, u^*\in \Omega ^*\}$. Then, for any given $\epsilon >0$, Theorem 5.5 shows that the algorithmic framework (1.4) needs at most $\lfloor {{d^2}/{(c_0\epsilon )}} \rfloor$ iterations to ensure that $\Vert M(u^k- \tilde{u}^k)\Vert _H^2\le \epsilon$. Hence, if $\Vert M(u^k- \tilde{u}^k)\Vert _H$ is regarded as an measurement of the accuracy of $u^k$ to a solution point, Theorem 5.5 indicates a worst-case $O(1/\sqrt{t})$ convergence rate in a nonergodic sense for the algorithmic framework (1.4). It is worthwhile to mention that the specific sequence $\{u^k\}$ with $u^k$ given by the algorithmic framework (1.4) has the special property of that $u^k$ being a solution point of VI$(\Omega ,F,\theta )$ if $\Vert M(u^k- \tilde{u}^k)\Vert _H^2=0$ (see (2.8a) and due to $Q=HM$). Thus, it is reasonable to use $\Vert M(u^k- \tilde{u}^k)\Vert _H$, or $\Vert M(u^k- \tilde{u}^k)\Vert _H^2$, to measure the accuracy of an iterate $u^k$ to a solution point.

6 Numerical Results

In this section, we report some preliminary numerical results and verify the efficiency of some specific generalized PDHG algorithms stemming from the proposed algorithmic framework (1.4). The proposed algorithms were coded by MATLAB R2015a, and all our experiments were performed on a desktop with Windows 7 system and an Intel(R) Core(TM) i5-4590 CPU processor (3.30 GH) with a 8 GB memory.

We consider the standard total variational (TV) blurry and noisy imaging restoration model

$$\begin{aligned} \min _y \int _D |\nabla y| + \frac{\lambda }{2}\Vert By-z\Vert ^2, \end{aligned}$$

(6.1)

where D is the image domain with its area being |D|, z is the given observed image, $\nabla$ is a discrete gradient operator(see [25]), B is the matrix representation of a space invariant blurring operator, and $\lambda >0$ is a constant balancing the data-fidelity and TV regularization terms. As shown in, e.g. [5, 10, 29], the model (6.1) can be reformulated as the saddle point problem

$$\begin{aligned} \min _{y \in \mathfrak {R}^N} \max _{x \in X} \, y^TAx + \frac{\lambda }{2} \Vert By - z\Vert ^2 \end{aligned}$$

(6.2)

where X is the Cartesian product of some unit balls in $\mathfrak {R}^2$ (see, e.g., [5, 16, 25, 29], for details), and A is the matrix representation of the negative divergence operator.

Clearly, (6.2) is a special case of (1.1) and thus the algorithmic framework (1.4) is applicable. We now illustrate how to solve the resulting subproblems (1.4a) when (1.4) is applied to (6.2); more details are referred to, e.g., [5, 16, 29]. For the x-subproblem, it reduces to

$$\begin{aligned} \tilde{x}^k = \arg \min \left\{ (y^k)^TAx + \frac{r}{2} \Vert x-x^k\Vert ^2 \, |\, x\in X \right\} . \end{aligned}$$

(6.3)

Fig. 1

Original images: cameraman ($256 \times 256$) and pepper ($256 \times 256$)

Table 1 Scenarios to be tested

Fig. 2

Degraded images: first row (cameraman) and second row (pepper). From left to right: scenarios of Gaussian blur, medium motion blur and severe motion blur as specified in Table 1

Hence, the solution is given by

$$\begin{aligned} \tilde{x}^k = P_X \left[ x^k+\frac{1}{r}A^Ty^k\right] , \end{aligned}$$

(6.4)

where $P_X$ denotes the projection operator onto X. As mentioned, X is the Cartesian product of some unit balls in $\mathfrak {R}^2$, thus the projection operator $P_X$ can be computed easily. For the y-subproblem, it is

$$\begin{aligned} \tilde{y}^k= & {} \arg \max \left\{ y^TA\bar{x}^k + \frac{\lambda }{2} \Vert By - z\Vert ^2 \right. \nonumber \\&\left. - \frac{s}{2} \Vert y-y^k\Vert ^2 \, |\, y\in \mathfrak {R}^N\right\} . \end{aligned}$$

(6.5)

Thus, we need to solve the system of equations

$$\begin{aligned} ( \tilde{y}^k-y^k)+\frac{1}{s}\big (\lambda B^T (B\tilde{y}^k-z)+A\bar{x}^k\big )=0, \end{aligned}$$

(6.6)

whose solution can be obtained by the Fast Fourier Transform (FFT) or Discrete Cosine Transform (DCT) (see e.g., [29] for details).

We test the grayscale image cameraman ($256 \times 256$) and pepper($256 \times 256$), as shown in Fig. 1. These images are degraded by convolutions and the zero-mean Gaussian noise with standard deviation $\sigma = 10^{-3}$. The blur operator is generated by the functions fspecial and imfilter in MATLAB Image Processing Toolbox with the types “motion” and “Gaussian”; zero-mean Gaussian noise is added by the script imnoise. The specific scenarios (i.e., the input of the script fspecial) under test are listed in Table 1, and the degraded images are shown in Fig. 2. For the parameter $\lambda$ in (6.2), we take $\lambda =250$ for the “motion” blur cases and $\lambda =1000$ for the “Gaussian” blur case.

Table 2 Three Specific Algorithms Based on (1.4)

Fig. 3

Evolutions of SNRs with respect to iterations for “Gaussian” blur (cameraman)

Fig. 4

Evolutions of SNRs with respect to iterations for “motion” blur. Left: the scenario of medium motion blur; right: the scenario of severe motion blur (cameraman)

As we have mentioned, the quantity $\Vert M(u^k-\tilde{u}^k) \Vert ^2_H$ measures the accuracy of the iterate $u^k$ to a solution point of VI$(\Omega , F, \theta )$. Therefore, we could use

$$\begin{aligned} \frac{\Vert M(u^k-\tilde{u}^k) \Vert ^2_H}{\max \{1,\Vert Mu^k \Vert ^2_H \} } \le Tol \end{aligned}$$

(6.7)

as the stopping criterion, where $Tol>0$ is an assigned accuracy. The quality of a restored image (denoted by $y^k$) is measured by the signal-to-noise (SNR) value in decibel (dB):

$$\begin{aligned} \text {SNR} := 20 \log _{10} \frac{\Vert y^*\Vert }{\Vert y^k-y^*\Vert }, \end{aligned}$$

(6.8)

where $y^*$ represents a clean image.

Among algorithms based on the algorithmic framework (1.4), we choose three representative cases to test with parameters specified in Table 2. Case I is Algorithm (4.8) in Sect. 4.2.1, and as mentioned, it is Algorithm 4 considered in [16] which is also an improved version of (1.2) using the technique in [14]. As reported in [16], usually $\alpha =1.8$ is numerically favorable. So we fix it as 1.8 too in our experiments. Case II is the completely symmetric version (4.12) in Sect. 4.2.2; this case is of our interests because of its theoretical beauty. Case III is the generalized PDHG originally considered in [5] which is also a special case of the algorithmic framework (1.4); it usually works very well as widely shown in imaging processing literature, and thus we use it as a benchmark in our experiments. For the step-size parameters r and s in the subproblems of the algorithmic framework (1.4), throughout we fix $1/r = 0.03$ and $s = \frac{10}{9} \cdot 8/r$. Thus, the condition $rs > \Vert A^TA \Vert$ is guaranteed to be satisfied, since $A^T$, the matrix representation of the discrete gradient operator, has $\Vert A^TA \Vert \le 8$ as proved in [4]. Note that our emphasis is to test the possible improvement in speed by combining the step (1.4a) with the original PDHG step (1.4a). So we just fix the values of r and s and observe the difference in $\alpha$ and $\beta$ in the framework (1.4). We refer to [16] for some empirical study on the step-size parameters r and s. The initial iterates to implement all algorithms are set as $x^0 = 0$ and $y^0$ be the degraded image. In the following, “It.” and “CPU” represent the iteration numbers and computing time in seconds, respectively.

Table 3 Numerical results for cameraman with $Tol = 10^{-6}$

Table 4 Numerical results for cameraman with Severe motion blur and different Tol

Fig. 5

Evolutions of SNRs with respect to iterations for “Gaussian” blur (pepper)

Fig. 6

Evolutions of SNRs with respect to iterations for “motion” blur. Left: the scenario of medium motion blur; right: the scenario of severe motion blur (pepper)

In Figs. 3 and 4, we plot the evolutions of SNR values with respect to iterations for cameraman. Then, in Table 3, we set $Tol=10^{-6}$ in the stopping criterion (6.7) and report the respective “It.” and “CPU” for the Gaussian and medium motion blur cases when some well-approximated “maximal” SNR values (as observed in Figs. 3, 4) are achieved. The reason we set $Tol=10^{-6}$ is that we found it is sufficiently accurate for these cases to achieve high SNR values. In Table 4, we report the results for the severe motion blur case. Since the model is generally more ill-conditioned with severer blur, $Tol=10^{-6}$ is not enough to restore images with acceptable quality. So, in this table, we test the case with Tol is as small as $10^{-8}$ and report all the results when $Tol=10^{-6}, 10^{-7}$ and $10^{-8}$. Figures 5 and 6 and Tables 5 and 6 are the results for the pepper.

The reported experiment results clearly show the efficiency of some specific generalized PDHG algorithms derived from the algorithmic framework (1.4). In particular, the completely symmetric version (4.12) is competitive with the overrelaxed version (4.8) and they both improve the generalized PDHG in (1.2) favorably. These preliminary numerical results verify the possibility of specifying more efficient algorithms based on the algorithmic framework (1.4).

Table 5 Numerical results for pepper with $Tol = 10^{-6}$

Table 6 Numerical results for pepper with severe motion blur and different Tol

7 Conclusions

We propose an algorithmic framework of generalized primal–dual hybrid gradient (PDHG) methods for saddle point problems. We theoretically study its convergence and numerically verify the efficiency of some specific algorithms derived from the algorithmic framework. This algorithmic framework includes some existing PDHG schemes as special cases, and it yields a class of new generalized PDHG schemes. It also possesses some theoretical advantages such as the worst-case convergence rate measured by the iteration complexity in a nonergodic sense. Our analysis provides a unified perspective to the study of some PDHG schemes for saddle point problems. It is interesting to know if our analysis could be extended to some special nonconvex cases with strong application backgrounds in image processing such as some semiconvex variational image restoration models. We leave it as a research topic in the future.