On the Convergence of Primal–Dual Hybrid Gradient Algorithms for Total Variation Image Restoration

Abstract

In this paper we establish the convergence of a general primal–dual method for nonsmooth convex optimization problems whose structure is typical in the imaging framework, as, for example, in the Total Variation image restoration problems. When the steplength parameters are a priori selected sequences, the convergence of the scheme is proved by showing that it can be considered as an ε-subgradient method on the primal formulation of the variational problem. Our scheme includes as special case the method recently proposed by Zhu and Chan for Total Variation image restoration from data degraded by Gaussian noise. Furthermore, the convergence hypotheses enable us to apply the same scheme also to other restoration problems, as the denoising and deblurring of images corrupted by Poisson noise, where the data fidelity function is defined as the generalized Kullback–Leibler divergence or the edge preserving removal of impulse noise. The numerical experience shows that the proposed scheme with a suitable choice of the steplength sequences performs well with respect to state-of-the-art methods, especially for Poisson denoising problems, and it exhibits fast initial and asymptotic convergence.

1 Introduction

Image restoration is an inverse problem that consists in finding an approximation of the original object $\tilde{x}\in R^{n}$ from a set g∈R ^m of detected data. In a discrete framework, we assume that each component of the data g _i is the realization of a random variable whose mean is $(H\tilde{x} + b)_{i}$, where H∈R ^m×n represents the distortion due to the acquisition system and b∈ℝ^m is a nonnegative constant background term. We assume that H is known and, in particular, when H=I we have a denoising problem while, in the other cases, we deal with a deblurring problem.

In the Bayesian framework [17, 27], an approximation of the original object $\tilde{x}$ is obtained by solving a minimization problem where the objective function is the combination of two terms: the first one is a nonnegative functional measuring the data discrepancy, to be chosen according to the noise statistics, while the second one is a regularization term weighted by a positive parameter balancing the two terms. Some physical constraint can be added, such as non negativity and flux conservation. When the goal is preserving sharp discontinuities while removing noise and blur, we can use as regularization term the Total Variation (TV) functional (introduced first in [25]), which, in the discrete framework, is defined as

$$\sum_{k=1}^n \big\|(\nabla x)_k\big\| $$

(1)

where (∇x) _k denotes a discrete approximation of the gradient of x at the pixel k.

For Gaussian noise, the fit-to-data term is given by the following quadratic function

$$\frac{1}{2} \|Hx+b-g\|^2 $$

(2)

and the variational model combining (2) and (1) has been extensively studied; its primal and dual formulations have been deeply investigated in order to design algorithms specifically tailored for image processing applications. The large size of these problems requires schemes with a low computational cost per iteration (typically only a matrix–vector product per iteration) and a fast initial convergence that enables to obtain medium accurate and visually satisfactory results in a short time. In the class of first order methods, requiring only function and gradient evaluations, popular methods for TV minimization include the time-marching method [25], split Bregman [19, 22], Chambolle’s [4, 8, 9], gradient projection [29, 32], Nesterov-type methods [2, 14]. For the most part of these algorithms, Matlab codes are available in the public domain (see [14] for references).

We mention also second-order methods proposed in [11, 18]. These can be quadratically convergent, but they require the solution of a system at each iteration and information about the Hessian matrix.

Another approach is based on the primal–dual formulation of (3) as saddle point problem. In [31], Zhu and Chan propose a first-order method named Primal–Dual Hybrid Gradient (PDHG) method, where at any iteration both primal and dual variables are updated by descent and ascent gradient projection steps respectively. Furthermore, the authors propose to let the steplength parameters varying trough the iterations and to choose them as prefixed sequences. The twofold aim is to avoid the difficulties that arise when working only on the primal or dual formulation and to obtain a very efficient scheme, well suited also for large scale problems.

The convergence of PDHG has been investigated in [16], where the algorithm with variable stepsizes is interpreted as a projected averaged gradient method on the dual formulation, while in [10] the convergence of PDHG with fixed stepsizes is discussed (see also [2]). Numerical experiments [10, 16, 31] show that the method exhibits fast convergence for some special choices of the steplength sequences, but, at the best of our knowledge, a theoretical justification of the convergence of the PDHG scheme with these a priori choices is still missing.

A recent development on the primal–dual methods can be found also in [10] as a special case of a primal–dual algorithm for the minimization of a convex relaxation of the Mumford-Shah functional. This last algorithm generalizes the classical Arrow-Hurwicz algorithm [1] and converges for constant steplength parameters. Furthermore, for uniformly convex objective functions, a convenient strategy to devise adaptive step sizes is theoretically obtained and it seems to be numerically effective.

The aim of this paper is to define a robust convergence framework for primal–dual methods with variable steplength parameters which apply to optimization problems of the form

$$\min_{x\in X}f_0(x)+f_1(Ax) $$

(3)

where f ₀ and f ₁ are convex proper lower semicontinuous functions, over ℝⁿ and ℝ^m respectively, not necessarily differentiable, A∈ℝ^m×n and X represents the domain of the objective function or a subset of it expressing physical features. The key point of our analysis is to consider the primal–dual method as an ε-subgradient method [13, 20, 23] on the primal formulation (3). Then, the two main contributions of this paper are the following:

• we establish the convergence proof of a primal–dual method where the steplength are chosen as a priori sequences; this analysis provides also, as a special case, the convergence proof of the PDHG method [31] with the steplength choices suggested by the authors as the best performing one on the variational problem (2)–(1);

• we design a general algorithm which can be applied to general TV restoration problems such as

  • the denoising or deblurring of images corrupted by Poisson noise, where the data discrepancy is expressed by the generalized Kullback–Leibler (KL) divergence:

    $$f_0(x) = \sum_{k} \biggl \{g_k\ln\frac{g_k}{{(Hx+b)}_k} + {(Hx+b)}_k -g_k\biggr\} $$

    (4)

    with g _k lng _k =0 if g _k =0;

  • the edge preserving removal of impulse noise, where a suitable fit-to-data term is the ℓ ₁ norm

    $$f_0(x) = \|x-g\|_1$$

The paper is organized as follows: in Sect. 2 some basic definitions and results about ε-subgradient and ε-subgradient methods are restated. In Sect. 3 we introduce the primal–dual scheme and the connections with ε-subgradient methods are investigated. In particular, we provide the convergence analysis for primal-explicit and primal-implicit schemes. In Sect. 4 some applications of our results are described. The numerical experiments in Sect. 5 show that the proposed scheme, with a suitable choice of the steplength sequences, can be a very effective tool for TV image restoration also in presence of Poisson and impulse noise.

2 Definitions and Preliminary Results

We denote by ℝⁿ the usual n-dimensional Euclidean space, by 〈x,y〉=x ^T y the inner product of two vectors of ℝⁿ and by ∥⋅∥ the l ₂ norm.

The domain of a function f:ℝⁿ→ ] −∞,+∞] is dom (f)={x∈ℝⁿ:f(x)<+∞}. A function f is said proper if dom (f)≠∅. The diameter of a set X is defined as diam (X)=max _x,z∈X ∥x−z∥.

Let P _Ω (z) denote the orthogonal projection of the point z∈ℝⁿ onto the nonempty, close, convex set Ω⊆ℝⁿ, $P_{\varOmega}(z) = \arg\min_{u\in\varOmega}\frac{1}{2} \|u-z\|^{2}$.

We recall that for a convex function f, the resolvent operator (I+θ∂f)⁻¹ is defined as

$$(I+\theta\partial f)^{-1}(z) = \arg\min f(x) + \frac{1}{2\theta }\|x-z\|^2$$

where ∂f is the subdifferential mapping and θ is a positive parameter.

Definition 1

[24, Sect. 23]

Let f a proper convex function on ℝⁿ.

The ε-subdifferential of f at x∈dom (f), defined for ε∈ℝ, ε≥0, is the set

$$\partial_{\varepsilon} f(x)= \bigl\{w\in\mathbb{R}^n:\ f(z)\geq f(x) +\langle w,z-x\rangle-\varepsilon,\ \forall z\in\mathbb{R}^n\bigr \}$$

For ε=0 the definition of subdifferential is recovered while for ε>0 we have a larger set; furthermore, for ε ₁>ε ₂>0, we have $\partial_{\varepsilon_{1}} f(x)\supseteq \partial_{\varepsilon_{2}} f(x)\supseteq\partial f(x)$. Every element of ∂ _ε f(x) is an ε-subgradient of f at x. In the following we will make use of the linearity property of the ε-subgradient, which, for sake of completeness, is restated below.

Property 1

If $f(x) = \sum_{i=1}^{n} \alpha_{i}f_{i}(x)$, where α _i ≥0, $w_{i}\in\partial_{\varepsilon_{i}}f_{i}(x)$ and $x\in\bigcap_{i=1}^{n}\operatorname{dom}(f_{i})$, then $\sum_{i=1}^{n} \alpha_{i}w_{i}\in\partial_{\varepsilon}f(x)$, where $\varepsilon= \sum_{i=1}^{n} \varepsilon_{i}$.

Proof

By Definition 1, we have

$$f_i(z) -f_i(x) \geq\langle w_i,z-x\rangle-\varepsilon_i, \quad i=1,\ldots,n$$

Then, the claim follows by multiplying the previous inequalities by α _i and summing up for i=1,…,n. □

Definition 2

[24, Sect. 12]

The conjugate of a convex function f is the function f ^∗ defined by

$$f^*(y) = \sup_{x} \langle x,y\rangle- f(x)$$

If f(x) is lower semicontinuous and proper, then f ^∗ is lower semicontinuous and f ^∗∗=f.

Proposition 1

Let f(x) a proper lower semicontinuous convex function. Then, for every x∈dom (f) and y∈dom (f ^∗) we have y∈∂ _ε f(x), with ε=f(x)−(〈y,x〉−f ^∗(y)).

Proof

Let x,z∈ℝⁿ and y∈dom (f ^∗). Then, we can write

Since f(x)=sup _x 〈y,x〉−f ^∗(y), then ε≥0; thus, Definition 1 is fulfilled. □

We remark that ε=0 (that is y∈∂f(x)) if and only if f(x)=〈y,x〉−f ^∗(y). Now we state the following corollary, which is useful for the subsequent analysis; its proof can be carried out by employing similar arguments as in the previous proposition.

Corollary 1

Let f a proper lower semicontinuous convex function and let A be a linear operator. Consider the composition (f∘A)(x)=f(Ax): then, for every x∈dom (f∘A) and y∈dom (f ^∗) we have A ^T y∈∂ _ε (f∘A)(x), with ε=f(Ax)−(〈y,Ax〉−f ^∗(y)).

An important property of the ε-subgradients is their boundedness over compactly contained subsets of int dom (f), as we prove in the following proposition.

Proposition 2

Assume that S is a compactly contained bounded subset of int dom (f). Then, the set ⋃ _x∈S ∂ _ε f(x) is nonempty, closed and bounded.

Proof

Let λ>0 be such that S+B ^λ⊆int dom (f), where B ^λ is the ball of ℝⁿ with radius λ and S+B ^λ={u∈ℝⁿ:∥u−x∥≤λ,x∈S}. By Theorem 6.2 in [15] it follows that $\bigcup_{x\in S}\partial_{\varepsilon}f(x)\subseteq\bigcup_{x\in S+B^{\lambda}}\partial f(x) + B^{\frac{\varepsilon}{\lambda}}$. The last term in the previous inclusion is nonempty, closed and bounded (see [24, Theorem 24.7]); thus the theorem follows. □

Proposition 3

Let $x,\bar{x}\in\operatorname{dom}f$ and g∈∂f(x); then, $g\in\partial_{\varepsilon}f(\bar{x})$ with $\varepsilon= D_{f}(\bar{x},x)$, where $D_{f}(\bar{x},x)=f(\bar{x})-f(x)-\langle g, \bar{x}-x\rangle$ is the Bregman divergence associated with f at x.

Proof

Since g∈∂f(x), for all z we have

where ε≥0 by the hypothesis on g. □

2.1 The ε-Subgradient Projection Method

Consider the constrained minimization problem

$$\min_{x\in X} f(x), $$

(5)

where f is a convex, proper, lower semicontinuous function; the ε-subgradient projection method is defined as follows

$$x^{(k+1)}= P_{X}\bigl(x^{(k)}-\theta_k w^{(k)}\bigr), \quad w^{(k)}\in\partial_{\varepsilon^k}f \bigl(x^{(k)}\bigr) $$

(6)

given the steplength sequence {θ _k } and subgradient residuals {ε ^k} (see for example [13, 20, 23] and reference therein).

The convergence properties of a subgradient method strongly depends on the steplength choice, and different selection strategies can be devised in the literature (see [5, Chap. 6.8] for a recent review). In this paper we focus on the diminishing divergent series stepsize rule, that consists in choosing any sequence of positive steplength θ _k >0 such that

The convergence of the ε-subgradient projection method can be stated as in [20, Theorem 3]. For sake of completeness we report the statement below.

Theorem 1

Let {x ^(k)} be the sequence generated by the method (6) and assume that the set X ^∗ of the solutions of (5) is bounded. Under the Assumptions A1–A2, if w ^(k) is bounded and lim _k ε ^k=0, then {f(x ^(k))} converges to a minimum of f(x) over X and dist (x ^(k),X ^∗)→0.

Remark

When problem (5) has a unique solution x ^∗, the previous theorem assures the convergence of the sequence {x ^(k)} to the minimum point x ^∗.

3 The Primal–Dual Scheme

We consider the minimization of

$$f(x) \equiv f_0(x) + f_1(Ax)$$

where f ₀(x) and f ₁(x) are convex, proper, lower semicontinuous functions, not necessarily differentiable, and such that

$$\operatorname{diam}\bigl(\operatorname{dom}\bigl(f_1^*\bigr)\bigr)=D<+\infty $$

(7)

We consider problems of the form (5) where the constraint set X is a closed convex subset X of dom (f); otherwise, for the unconstrained case, we set X=dom (f). We assume also that the set of the minimum points X ^∗ is bounded.

We remark that, the boundedness of X ^∗ together with (7), ensures that the min–max theorem [24, p. 397] holds. As a consequence of this, the minimization problem (5) is equivalent to the saddle point problem

$$\min_{x\in X}\max_{y} F(x,y)\equiv f_0(x) + \langle y,Ax\rangle-f_1^*(y) $$

(8)

Indeed, by definition, the pair (x ^∗,y ^∗) is a saddle point of (8) when

$$F\bigl(x^*,y\bigr) \leq F\bigl(x^*,y^*\bigr)\leq F\bigl(x,y^*\bigr) \quad \forall x\in X $$

(9)

and (9) holds if and only if A ^T y ^∗∈∂f ₁(x ^∗) and x ^∗∈X ^∗.

3.1 Primal-Explicit Scheme

We consider the following algorithm.

Algorithm 1

Primal-explicit scheme

In order to prove the convergence of Algorithm 1, we make the following assumptions on the parameters τ _k and δ _k :

Lemma 1

Let x ^(k) any sequence in dom (f) and assume that (7) holds. Under the Assumptions A1 and A3, we have that $A^{T}y^{(k+1)}\in\partial_{\varepsilon^{k}}(f_{1}\circ A)(x^{(k)})$ with lim _k→∞ ε ^k=0.

Proof

Corollary 1 guarantees that

$$A^Ty^{(k+1)}\in \partial_{\varepsilon^{k}} (f_1\circ A)\bigl(Ax^{(k)}\bigr)$$

with $\varepsilon^{k} = f_{1}(Ax^{(k)}) + f_{1}^{*}(y^{(k+1)})-\langle y^{(k+1)},Ax^{(k)}\rangle$.

By (10) it follows that

We have

which results in

Since τ _k →+∞ and ε ^k≥0 ∀k, then ε ^k→0. □

We are now ready to state the following convergence result for Algorithm 1, which directly follows from Theorem 1 and Lemma 1.

Theorem 2

We assume X ^∗ bounded. Let {x ^(k)} be the sequence generated by Algorithm  1. Under the Assumptions A1–A4, if {g ^(k)} is bounded, then {f(x ^(k))} converges to a minimum of f(x) over X and dist (x ^(k),X ^∗)→0.

One of the main advantages of Algorithm 1 is its generality, and different algorithms can be defined according to the strategy chosen to compute the approximate subgradient g ^(k).

In particular, when the function f ₀(x) is differentiable, we may set

$$g^{(k)}= \nabla f_0\bigl(x^{(k)}\bigr),$$

so that we have δ _k =0 for all k.

3.2 Primal-Implicit Scheme

We observe that the constrained problem (5) can be formulated also as

$$\min_{x \in\mathbb{R}^n} f_0^X(x) + f_1(Ax)$$

where $f_{0}^{X}(x) = f_{0}(x) + \iota_{X}(x)$ and ι _X (x) is the indicator function of the set X, defined as

$$\iota_X(x) = \left \{ \begin{array}{l@{\quad}l}0 &\mbox{if } x\in X\\+\infty &\mbox{if } x\notin X\end{array} \right .$$

We consider the following implicit version of Algorithm 1.

Algorithm 2

Primal-implicit scheme

Then, the new point x ^(k+1) is defined also as

$$x^{(k+1)}= \arg\min_{x\in X} f_0(x) + \frac{1}{2\theta_k} \big\| x-x^{(k)}+\theta_k A^Ty^{(k+1)}\big\|^2\nonumber $$

and, thus, the updating step (13) implies that

$$\frac{x^{(k)}-x^{(k+1)}}{\theta_k} - A^Ty^{(k+1)}\in\partial f_0^X\bigl(x^{(k+1)}\bigr) $$

(14)

In particular, we have that $x^{(k+1)}\in\operatorname{dom}(f_{0}^{X})$ and

$$x^{(k+1)}= x^{(k)}-\theta_k\bigl(g^{(k)}+A^Ty^{(k+1)}\bigr) $$

(15)

where $g^{(k)}\in\partial f_{0}^{X}(x^{(k+1)})$. From Proposition 3, it follows that

$$g^{(k)}\in\partial_{\delta_k}f_0^X\bigl(x^{(k)}\bigr)$$

with

$$\delta^k = f_0^X\bigl(x^{(k)}\bigr)-f_0^X\bigl(x^{(k+1)}\bigr)-\bigl\langle g^{(k)}, x^{(k)}-x^{(k+1)}\bigr\rangle $$

(16)

Thus, Algorithm 2 can be considered an ε-subgradient method and the convergence analysis previously developed still applies, as we show in the following. However, this semi-implicit version has stronger convergence properties: in particular, we are able to prove the boundedness of the iterates {x ^(k)}.

Lemma 2

Assume that

$$\sum_{k=0}^\infty\frac{\theta_k}{\tau_k}<+\infty \quad\mbox{\textit{and}}\quad \sum_{k=0}^\infty \theta_k^2 <+\infty $$

(17)

Then, the sequence {x ^(k)} generated by Algorithm  2 is bounded.

Proof

Let (x ^∗,y ^∗) a saddle point of (8). From (14) and from the definition of the subgradient, we obtain

where

which gives

(18)

Similarly, from (13) we obtain

(19)

We observe that, if we define

$$F^X(x,y) = f_0^X(x)+\langle x,A^Ty\rangle-f_1^*(y)$$

we have

where the last inequality follows from the saddle point property (9) of the pair (x ^∗,y ^∗).

The last term can be further estimated as in [10, Sect. 3.2], by observing that for any t∈(0,1] we have

$$\biggl \Vert \sqrt{\frac{t}{\theta_k}} \bigl(x^{(k+1)}-x^{(k)}\bigr)+ \sqrt{\frac {\theta_k}{t}} A^T\bigl(y^{(k+1)}-y^*\bigr)\biggr \Vert ^2\geq0$$

which yields

where L=∥A∥. Thus, summing up (19) and (18) yields

(20)

In particular, recalling (7), the inequality (20) results in

$$\frac{\|x^{(k+1)}-x^*\|^2}{2\theta_k} \leq\frac{\|x^{(k)}-x^*\|^2}{2\theta_k} + \frac{D^2}{2\tau_k} +\frac{\theta_k}{2t} L^2D^2$$

By multiplying both sides of the previous inequality by 2θ _k and summing up for k=0,…,N−1 we obtain

$${\big\|x^{(N)}-x^*\big\|^2} \leq{\big\|x^{(0)}-x^*\big\|^2} + {D^2}\sum_{k=0}^{N-1}\frac{\theta_k}{\tau_k}+ \frac{L^2D^2}{t}\sum_{k=0}^{N-1}\theta_k^2$$

Then, the boundedness of {x ^(k)} is ensured by the hypothesis (17). □

Thanks to the previous lemma, the boundedness of the subgradients g ^(k) is assured.

Theorem 3

Assume that f ₀(x) is locally Lipschitz in its domain. If the steplength sequences {θ _k } and {τ _k } satisfy the conditions A1–A3 and (17), then {f(x ^(k))} converges to a minimum of f(x) over X and dist (x ^(k),X ^∗) converges to zero.

Proof

From the previous lemma and by Proposition 2, the sequence of subgradients g ^(k) is bounded, thus, from (15) and A1, we have ∥x ^(k)−x ^(k+1)∥→0 as k→∞. If f ₀(x) is locally Lipschitz continuous, then for every compact subset $K\subset\operatorname{dom}(f_{0}^{X})$, there exists a positive constant M _K such that ∥f ₀(z)−f ₀(x)∥≤M _K ∥z−x∥ for all x,z∈K. Thus, since all the iterates are contained in a suitable compact subset of $\operatorname{dom}(f_{0}^{X})$, we have $|f_{0}^{X}(x^{(k)})-f_{0}^{X}(x^{(k+1)})|\rightarrow0$ as k→∞. As consequence, the sequence {δ ^k} defined in (16) converges to zero as k diverges. Then, we can invoke Theorem 2 to conclude that {f(x ^(k))} converges to a minimum of f(x) over X and, furthermore, lim _k→∞dist (x ^(k),X ^∗)=0. □

Remark

If X ^∗={x ^∗}, Theorems 2 and 3 state the convergence of the sequences {x ^(k)} generated by the Algorithms 1 and 2 to the unique solution x ^∗ of the problem (5).

In the following section we discuss the implementation of Algorithms 1 and 2 for the TV restoration of images.

4 Applications to Total Variation Image Restoration Problems

In this section we consider problem (5) where the objective function is the combination of a convex, proper, lower semicontinuous function measuring the data fidelity with the discrete TV function (1).

In this case we define the function f ₁ on ℝ²ⁿ such that

$$f_1(y) = \beta\sum_{i=1}^n\|y_i\|, \quad y= \begin{pmatrix} y_1\\\vdots\\y_n\end{pmatrix} ,\ y_i\in\mathbb{R}^2,\ i=1,\ldots,n$$

where β>0 is the regularization parameter. We denote by A _i ∈R ^2×n the discrete approximation of the gradient of x at the pixel i and by A∈ℝ^2n×n the following block matrix

Then, we have

$$f_1(Ax) = \beta\sum_{i=1}^n\|A_ix\| $$

(21)

The conjugate of f ₁ is $f_{1}^{*}(y) = \iota_{Y}(y)$, namely the indicator function of the set Y⊂ℝ²ⁿ defined as follows

(22)

As a consequence of this, $\operatorname{dom}(f^{*}_{1})=Y$ satisfies (7) and we can write

$$f_1(Ax) = \max_{y\in Y} \beta\langle y,Ax\rangle $$

We remark that the updating rules (10) and (12) for the variable y reduce to the orthogonal projection onto the set Y, which is defined by the following closed formula

$$y^{(k+1)}_i = \frac{y^{(k)}_i +\beta\tau_kA_ix^{(k)}}{\max\{1,\|y^{(k)}_i +\beta\tau_kA_ix^{(k)}\|\}}, \quad i=1,\ldots,n $$

(23)

4.1 Gaussian Noise

We notice that the PDHG algorithms proposed in [31] are special cases of Algorithm 2 for $f_{0}(x) = \frac{1}{2}\|Hx-g\|^{2}$, X=ℝⁿ. In this case, denoting by ${\mathcal{N}}(A)$ and ${\mathcal{N}}(H)$ the null spaces of A and H, under the usual assumption that

$${\mathcal{N}}(A)\cap{\mathcal{N}}(H)=\{0\}, $$

(24)

the solution of the minimization problem (3) is unique. Thus, Theorem 3 establishes the convergence to this unique solution.

In particular, we stress that the steplength choices indicated by the authors in [31] and employed for the numerical experiments also in [10, 16] guarantee the convergence, according to Theorem 3. Indeed, the proposed steplength choices are

(25)

for denoising problems, while

$$\theta_k = 0.5/\tau_k $$

(26)

for deblurring problems. Both these choices satisfy the hypotheses of Theorem 3, which provides the theoretical foundation to the convergence that, so far, was experimentally observed.

An explicit variant of PDHG can be derived from Algorithm 1, by setting g ^(k)=H ^T(Hx ^(k)+b−g). For denoising problems, in order to define a bounded set X containing the solution x ^∗, we recall the following result.

Lemma 3

Let x ^∗ be the unique minimum point of f(x)≡f ₀(x)+f ₁(Ax), where $f_{0}(x)=\frac{1}{2}\|x-g\|^{2}$ and f ₁(Ax) is the TV function (21). Then we have

$${g}_{\min}\equiv\min_j g_j \leq x^*_i \leq g_{\max} \equiv\max_jg_j$$

Proof

See for example [7]. □

We observe that the previous result can be adapted also for constrained problems of the form min _x≥η f(x). In this case, the lower bound of the solution becomes max{η,g _min}, where the maximum is intended componentwise. In summary, if we define

$$X = \bigl\{x\in\mathbb{R}^n: \max\{\eta, g_{\min}\}\leq x\leq g_{\max}\bigr\}$$

Algorithm 1 with g ^(k)=x ^(k)−g is convergent to the unique solution x ^∗ of min _x≥η f(x), thanks to Theorem 1.

For general deblurring problems, convergence of Algorithm 1 is ensured under the hypothesis that the generated sequence is bounded.

4.2 Poisson Noise

Algorithms 1 and 2 can be applied to the denoising or deblurring of images corrupted by Poisson noise, where the data discrepancy is expressed by the generalized KL divergence (4) and X is a subset of the domain of f ₀(x). It is well known that f ₀(x) is a proper, convex and lower semicontinuous function. Under the hypothesis (24), the solution of the minimization problem (3) on X exists and it is unique. Since f ₀(x) is a differentiable function, an explicit version of Algorithm 1 can be implemented by setting g ^(k)=∇f ₀(x ^(k))=H ^T e−H ^T Z(x ^(k))⁻¹ g, where e is the n-vector with all entries equal to one and Z(x)=diag (Hx+b).

For deblurring problems, in order to state the convergence of Algorithm 1 using Theorem 1, we need to assume that the sequence of the iterates stays bounded.

In case of a denoising problem (H=I), the convergence of Algorithm 1 is ensured by defining X as a suitable bounded set containing the unique solution, as suggested in the following Lemma.

Lemma 4

Let x ^∗ be the unique solution of the problem

$$\min_{x\geq0} f(x)\equiv f_0(x) +f_1(Ax), $$

(27)

where $f_{0}(x)=\sum_{i} g_{i}\log\frac{g_{i}}{x_{i}}+x_{i}-g_{i}$, with g _i logg _i =0 if g _i =0, and f ₁(Ax) is the TV function (21). Then, for all i such that g _i >0 we have

$${g}_{\min}\equiv\min\{g_j: g_j > 0\} \leq x^*_i \leq g_{\max} \equiv \max_jg_j$$

Proof

See [6]. □

Consequently, for denoising problems from data corrupted by Poisson noise, if we define

then, the unique solution x ^∗ of (27) belongs to X and the sequence generated by Algorithm 1 converges to x ^∗.

Furthermore, it is easy to see that the i-th component of (I+θ∂f ₀)⁻¹(p) is given by

$$(I+\theta\partial f_0)^{-1}(p)_i =\frac{1}{2} \Bigl( p_i-\theta +\sqrt{(\theta-p_i)^2+4\theta g_i} \,\Bigr)$$

which can be exploited for the computation of the step (13) in Algorithm 2.

For the deblurring problems, a closed form formula for (13) is not available, thus Algorithm 2 can be difficult to implement in this case.

4.3 Impulse Noise

When the noise affecting the data contains strong outliers (e.g. impulse or salt & pepper noise), a well suited data discrepancy function is the non-smooth L ¹ norm:

$$f_0(x)=\|x-g\|_1=\sum_{k=1}^n|x_i-g_i| $$

(28)

The resolvent operator of f ₀ is given by the pointwise shrinkage operations:

$$(I+\theta\partial f_0)^{-1}(p)_i = \left \{\begin{array}{l@{\quad}l}p_i-\theta & \mbox{if } p_i-g_i>\theta\\[4pt]p_i+\theta & \mbox{if } p_i-g_i<-\theta\\[4pt]g_i & \mbox{if } |p_i-g_i|\leq\theta \end{array} \right . $$

(29)

This closed-form representation of the resolvent operator (I+θ∂f ₀)⁻¹ enables us to apply Algorithm 2 to the minimization of the L ¹-TV model (28)–(21).

4.4 Smoothed Total Variation

In many papers (see, for example, [2, 3, 11, 30]), the discrete TV (21) is replaced by the following smoothed approximation

$$f_1(Ax)=\beta\sum_{i=1}^n\left \Vert \left ( \begin{array}{c}A_i x \\\rho \end{array} \right )\right \Vert $$

(30)

where ρ is a small positive parameter. This variant has been considered also in a general edge-preserving regularization framework as Hypersurface (HS) potential [12]. When the smoothed TV regularization (30) is used, if f ₀(x) is a differentiable function, the minimization of f(x) can be obtained by efficient differentiable optimization methods. In this section we show that Algorithms 1 and 2 can also be applied with minor modifications.

In this case the conjugate is the indicator function of the following set

In particular, setting , with y _i ∈ℝ², Algorithms 1 and 2 can be adapted to the smoothed TV model by modifying the projection at the steps (10) and (12), detailed in (23), as follows:

$$y^{(k+1)}_i = \frac{y^{(k)}_i +\beta\tau_kA_ix^{(k)}}{d_i^{(k)}}, \quad\quad z_i^{(k+1)}= \frac{z_i^{(k)} +\beta\tau_k\rho}{d_i^{(k)}}$$

for i=1,…,n, where

$$d_i^{(k)}=\max \left\{1,\left \Vert \begin{pmatrix}y^{(k)}_i +\beta\tau_kA_ix^{(k)}\\[3pt]z^{(k)}_i +\beta\tau_k\rho \end{pmatrix}\right \Vert \right\}$$

As observed in [6], numerical methods which are not based on the differentiability of (30) can be convenient for the smoothed TV minimization, especially when the smoothing parameter ρ is very small.

5 Numerical Experience

The steplength selection is a crucial issue for the practical performance of many algorithms. In particular, as pointed out in [31], some choices yield a fast initial convergence, but they are less suited to achieve fast asymptotic convergence and vice versa. One of the main strength of the proposed method is that variable steplength parameters are allowed, and this can help to achieve both fast initial and asymptotic convergence. In the case of the quadratic data fidelity function (2), Algorithm 2 with the choices (25)–(26) is equivalent to the PDHG method and its performances has been experimentally evaluated in [10, 16, 31], showing that convenient steplength sequences lead to a very appealing efficiency with respect to the state-of-the-art methods.

This section is devoted to numerically evaluate the effectiveness of Algorithm 1 for TV restoration of images corrupted by Poisson noise. Algorithm 1 and 2 can be used also for other imaging problems. At the end of the section, we show as Algorithm 2 can be applied for solving an image denoising problem with impulse noise.

The numerical experiments described in this section have been performed in MATLAB environment, on a server with a dual Intel Xeon QuadCore E5620 processor at 2.40 GHz, 12 Mb cache and 18 Gb of RAM.

5.1 Poisson Noise

We compare Algorithm 1 with two methods, especially tailored for the TV restoration in presence of data corrupted by Poisson noise. The first one is the PIDSplit+ algorithm [26], based on a very efficient alternating split Bregman technique. The algorithm guarantees that the approximate solution satisfies the constraints and it depends only on a positive parameter γ. The second one is the Alternating Extragradient Method (AEM) [6], that solves the primal–dual formulation of the problem (3) by a successive updating of dual and primal iterates in an alternating, or Gauss-Seidel, way. Algorithm 1 and AEM are very similar, but AEM requires an additional ascent (extragradient) step at any iteration and it employs the same adaptively computed steplength in the three steps. Furthermore, in the denoising experiments, we include in the comparison also the algorithm in [10, Algorithm 1, p. 122], with θ=1, that in the following is denoted by CP. This general primal–dual algorithm requires that the resolvent operators of f ₀ and $f_{1}^{*}$ have a closed-form representation. As observed in Sect. 4.2, the resolvent of the Kullback–Leibler divergence is easy to compute only for the denoising case. The CP method depends on two parameters σ,τ, which should be chosen such that στL ²=1, where β∥A∥≤L.

In the experiments we consider a set of test problems, where the Poisson noise has been simulated by the imnoise function in the Matlab Image Processing Toolbox. The considered test problems are described in the following.

Denoising Test Problems

• LCR phantom: the original image is the phantom described in [21]; it is an array 256×256, consisting in concentric circles of intensities 70, 135 and 200, enclosed by a square frame of intensity 10, all on a background of intensity 5 (LCR-1). We can simulate a different noise level by multiplying the LCR phantom by a factor 10 (LCR-10) and 0.2 (LCR-0.2) and generating the corresponding noisy images. The relative difference in l ₂ norm between the noisy and the original images is 0.095318, 0.030266, 0.21273 respectively.

• Airplane (AIR): the original image is an array 256×256 (downloadable from http://sipi.usc.edu/database/), with values in the range [0,232]; the relative difference in l ₂ norm between the noisy and noise-free images is 0.070668.

• Dental Radiography (DR): the original image [30] is an array 512×512, with values in the range [0,255]; for this test problem, simulating a radiographic image obtained by a lower dose, the relative difference in l ₂ norm between the noisy and the noise-free images is 0.17866.

Deblurring Test Problems

• micro: the original image is the confocal microscopy phantom of size 128×128 described in [28]; its values are in the range [0,70] and the total flux is 2.9461×10⁵; the background term b in (4) is set to zero.

• cameraman: following [26], the simulated data are obtained by convolving the image 256×256 with a Gaussian psf with standard deviation σ=1.3, then adding Poisson noise; the values of the original image are in the range [0,1000]; the background term b in (4) is set to zero.

In the first set of experiments we compare the numerical behavior of Algorithm 1, AEM, PIDSplit+ and CP on the denoising test problems described above. In order to compare the convergence rate from the optimization point of view, we compute the ideal solution x ^∗ of the minimization problem, by running 100000 iterations of AEM. Then, we evaluate the progress toward the ideal solution at each iteration in terms of the l ₂ relative error

$$e^k=\frac{\|x^{(k)}- x^*\|}{\|x^*\|}$$

It is noticed that computing the ideal solution with AEM makes a small bias in favour of AEM itself. However the obtained results are sufficiently convincing to forget this bias.

In Table 1 for any test problem we report the number of iterations it and, in brackets, the computational time in seconds needed to satisfy the inequality

$$e^k\leq\mu, $$

(31)

for different values of the tolerance μ. We report also the l ₂ relative reconstruction error

$$e^{rec}=\frac{\|x^{\mu}- \tilde{x}\|}{\|\tilde{x}\|}$$

where $\tilde{x}$ is the original image and x ^μ is the reconstruction corresponding to the tolerance μ. The symbol ^∗ denotes that 3000 iterations have been performed without satisfying the inequality (31). All methods have been initialized with x ⁽⁰⁾=max{η,g}, where the maximum is intended componentwise and η _i =0 for g _i =0, η _i =g _min otherwise, and the constraint set X is defined as in Sect. 4.2. In Algorithm 1, AEM and CP, the initial guess for the dual variable y ⁽⁰⁾ has been set to zero. For the initial setting of the others variables involved in PIDSplit+ see [26]; the value of γ used for the different runs of PIDSplit+ is detailed in Table 1. The value of γ suggested by the authors in [26] is $\frac{50}{\beta}$. In Table 1 we report also the value of τ used for the different runs of CP. In Table 2 we report the sequences chosen for the steplength parameters in Algorithm 1, which have been optimized for the different test problems.

Table 1 Denoising problems: comparison between Algorithm 1, AEM and PIDSplit+

Table 2 Steplength sequences chosen for Algorithm 1

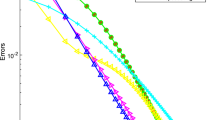
Figure 1 shows the convergence speed of the considered methods for each test problem: we plot, in log-scale, the l ₂ relative error e ^k with respect to the computational time. In Tables 3 and 4 we report some results obtained by running each method for 3000 iterations. In particular, Table 3 shows the l ₂ norm of the relative error and corresponding computational time after 3000 iterations. We report also, for any test-problem, the relative reconstruction error and the value of the objective function f(x ⁽³⁰⁰⁰⁾). In order to show the quality of the restored images, in Fig. 2 we report the superposition of the row 128 of the original image LCR-0.2 and the related noisy image; besides, we show the same row of the reconstruction corresponding to μ=10⁻⁴, obtained by Algorithm 1.

Fig. 1

Denoising problems: convergence speed of Algorithm 1, AEM, PIDSplit+ (with different values of γ) and CP (with τ=10 in all test problems except (a) where τ=5): plot of l ₂ norm of the relative error e ^k with respect to the ideal solution of the minimization problem versus the computational time. All the methods run for 3000 iterations

Fig. 2

Reconstructions at the level μ=10⁻⁴: lineouts of row 128 of the image LCR-0.2. Left panel: superposition of the row 128 of the original image and of the noisy image. Right panel: reconstruction by Algorithm 1 (706 it and time=20.2 seconds)

Table 3 Denoising problems: l ₂ norm of the relative error and computational time after 3000 iterations

Table 4 Deblurring problems: l ₂ norm of the relative error and computational time after 3000 iterations of the considered methods

In Figs. 3 and 4 we report the original, noisy and reconstructed images related to test problems AIR and DR. Since at the tolerance μ=10⁻⁴ all the restored images are visually the same, we report only the one provided by the two fastest algorithms.

Fig. 3

Test problem AIR, β=0.05, μ=10⁻⁴. Upper left panel: original image. Upper right panel: noisy image. Bottom left panel: Algorithm 1 reconstruction. Bottom right panel: PIDSplit+ reconstruction with $\gamma=\frac {5}{\beta}$

Fig. 4

Test problem DR β=0.27, μ=10⁻⁴. Upper left panel: original image. Upper right panel: noisy image. Bottom left panel: Algorithm 1 reconstruction. Bottom right panel: PIDSplit+ reconstruction, $\gamma=\frac {0.5}{\beta}$

The results of this numerical experimentation on denoising problems suggests the following considerations.

• For denoising problems, Algorithm 1 performs well with respect to the other methods; indeed for careful choices of the steplength parameters, the method exhibits a fast initial convergence and this good behavior is preserved also asymptotically; furthermore a single iteration is faster than in the other methods.

• About PIDSplit+, depending on the value of the parameter γ, we can observe either an initial or an asymptotic fast convergence, but we unlikely obtain both the behaviors. Furthermore, any iteration involves the solution of a linear system. Although this operation is performed by fast transforms, the computational complexity of each iteration of PIDSplit+ is greater than in the other methods, where only matrix–vector products and simple projections are performed.

• The choice of the steplength sequences is crucial for the effectiveness of Algorithm 1, as well as the choice of γ for PIDSplit+ and of τ for CP. The numerical experience shows that Algorithm 1 is more sensible to the choice of the sequence {θ _k } rather than {τ _k }; this can be explained by observing that the projection over the domain Y, due to its special structure (22), may overcome the effect of a too large steplength. Furthermore, about the choice of θ _k , if we set $\theta_{k}=\frac{1}{a k+b}$, we observe that b affects the initial rate of convergence while the asymptotic behavior of the method is governed by the value of a.

The second set of experiments concerns the deblurring test problems micro and cameraman. We compare Algorithm 1, AEM and PIDSplit+, considering as ideal solution x ^∗ the image obtained by running 100000 iterations of AEM. We consider the same initial setting used for the denoising test problems, except for the primal variable: since for deblurring the constraints are x≥0, then we set x ⁽⁰⁾=max{0,g}. In Table 4 for each method we report the computational time and the relative error e ³⁰⁰⁰ with respect to the ideal solution after 3000 iterations. We report also the minimum value f(x ⁽³⁰⁰⁰⁾) and the l ₂ norm of relative reconstruction error e ^rec (since all methods produce the same optimal values, we report them only once). In Fig. 5 we compare the convergence rate of the considered methods for each test problem, by plotting in log-scale the l ₂ relative error e ^k with respect to the computational time. In Figs. 6 and 7 we show the restored images obtained after 3000 iterations by Algorithm 1 and PIDSplit+ with the more effective choice of γ.

Fig. 5

Deblurring problems: convergence speed of Algorithm PDHG, AEM, PIDSplit+ (with different value of γ): plot of l ₂ norm of the relative error e ^k with respect to the ideal solution of the minimization problem versus the computational time. All the methods run for 3000 iterations

Fig. 6

Test problem micro, β=0.09, 3000 iterations. Upper left panel: original image. Upper right panel: noisy blurred image. Bottom left panel: Algorithm 1 reconstruction. (time=51.1 seconds). Bottom right panel: PIDSplit+ reconstruction, $\gamma=\frac{50}{\beta}$ (time=85.5 seconds)

Fig. 7

Test problem cameraman, β=0.005, 3000 iterations. Upper left panel: original image. Upper right noisy blurred image. Bottom left panel: Algorithm 1 reconstruction (time=177.7 seconds). Bottom right panel: PIDSplit+ reconstruction, $\gamma=\frac{5}{\beta}$ (time=306.3 seconds)

For deblurring problems, the PIDSplit+ method exhibits a very fast convergence. Indeed, the operator H could be severely ill conditioned, and in this case the implicit step in PIDSplit+ may help to improve the convergence rate. We observe also that for deblurring problems, the complexity of a single iteration of the three methods is similar, since the matrix–vector products involving the matrix H require the same fast transforms employed to compute the implicit step in PIDSplit+.

5.2 Impulse Noise

In this section we apply Algorithm 2 to the L ¹-TV problem described in Sect. 4.3. The 512×512 original image boat (downloadable from http://sipi.usc.edu/database/) has been corrupted by 25% salt&pepper noise (after adding noise, the image was rescaled so that its value are between 0 and 1). The original and the noisy images are shown in Fig. 8, together with the restoration provided by Algorithm 2 after 2000 iterations. For this test problem we set β=0.65 and the sequences for the steplength parameters are τ _k =0.1+0.1k and $\theta_{k}=\frac{1}{0.05k+0.1}$. Table 5 shows the results of a comparison between Algorithm 2 and CP (θ=1,τ=0.02). Since the solution of the minimization problem (28)–(21) is in general not unique, we evaluate the normalized error on the primal objective function $E^{k}=\frac{f(x^{(k)})-f(x^{*})}{f(x^{*})}$, where x ^∗ is computed by running 100000 iterations of CP. In Table 5 we report the number of iterations it and the CPU time in seconds needed to drop the normalized error E ^k below the tolerance μ. Figure 9 shows the convergence speed of Algorithm 2 and CP for the test problem boat: we plot in log-scale the normalized error E ^k with respect to the computational time.

Fig. 8

Image denoising in the case of impulse noise: test problem boat, β=0.65, 2000 iterations. Left panel: original image. Central panel: noisy image. Left panel: Algorithm 2 reconstruction (time=193 seconds)

Fig. 9

Image denoising in the case of impulse noise: test problem boat. Convergence speed of Algorithm 2 and PC (τ=0.02): plot of normalized error E ^k versus the computational time. All the methods run for 2000 iterations

Table 5 Image denoising problems in the case of impulse noise: test problem boat, β=0.65; comparison between Algorithm 2 and CP

6 Conclusions

The main contribution of this paper is the analysis of a class primal–dual algorithms for convex optimization problems, providing the related convergence proof based on the ε-subgradient techniques. The developed analysis applies, as a special case, to the PDHG method [31], but allows further generalizations. Indeed, as immediate consequence, new methods for solving TV denoising and deblurring problems can be derived from the basic scheme. These methods can be applied also to other imaging problems based on convex regularization terms and data discrepancy functions with simple resolvent operator (see [10] for some examples of applications).

The crucial point to obtain fast convergence is the selection of a priori steplength sequences: numerical experiments show that there exists clever choices leading to very appealing performances (at the initial iterations and also asymptotically), comparable to other state-of-the-art methods.

The numerical experimentation highlights also the importance of the parameters choice for the convergence behaviour of all the considered methods.

For image denoising problems, where the relationship between image and object is simpler, the proposed scheme seems very efficient in terms of accuracy and computational complexity, although the choice of convenient steplength sequences is a difficult problem.

Future work will concern the design of an adaptive rule for generating the steplength sequences, following a strategy similar to that suggested in [5] for the subgradient method.