1 Introduction

In the last two decades, the regularity based variational approach has aroused a large impact on the image processing society [1, 17, 46]. Most of the models in this approach take the form of an unconstrained regularized data fitting model, where the desired image is obtained as a regularized minimizer to a certain energy functional which contains both fidelity and regularization terms. For example, the total variation based image restoration model [14, 45], which has become one of the most popular image denoising models due to its edge preserving property, can be described as an unconstrained problem with the total variation as the regularization term.

Often, it is hard, if not impossible, to find a regularized minimizer solution in closed form for the regularized variational model. Therefore, iterative schemes are exploited to obtain the regularized minimizer. In earlier works, iteration schemes have been written in the Euler-Lagrange type, which often result in nonlinear partial differential equations (PDEs), which are normally slow and not applicable for industrial purposes [1, 55]. To accelerate the computation, several real-time working discretizations of Euler-Lagrange type equations have been proposed. In [9], a real-time working discretization of the Euler-Lagrange equation is proposed for the estimation of the optical flow field, which combines two hierarchical strategies. Bidirectional multigrid methods have also been applied to accelerate the speed of a broad class of variational optic flow models [10]. Furthermore, specific algorithms designed for parallel hardwares make real-time computation possible [31].

Recently, the iterative schemes have undergone a lot of optimization, and faster iteration schemes, such as Bregman-type iteration schemes, have been developed [2, 30, 43, 57, 61]. The development of iterative schemes not only has resulted in faster computation but also has made it easier to incorporate nonlinear regularization terms into variational functionals.

Meanwhile, another type of variational approach, which is in its nature a nonparametric data fitting approach and is based on localized least squares method, has recently appeared in the literature of image processing [5, 20, 27, 52, 60]. In this approach, the problem is formulated in the form of a constrained data fitting model. The characteristics of this approach is that it takes the data and its position to define the structure of the approximation model, and therefore, the local characteristics of the data can be taken into account in the approximation. One of the most popular method in this framework is the moving least squares (MLS) model [35]. The MLS model constructs and evaluates a local polynomial fit continuously over the entire domain, resulting in the MLS fit function. The MLS model has shown good performance for interpolation based image processing such as image zooming and superresolution [5, 20, 27, 52, 60]. Normally, the MLS model seeks to find a solution in closed form, which is often the case with methods in the least squares framework.

In this paper, we propose to put the MLS model into the iterative regularity based variational framework. By putting the MLS model in the iterative framework, it becomes possible for the MLS model to adopt several well-known regularization terms that were formerly proposed in other regularized variational problems. To illustrate an example, we show in this paper that the well-known total variation (TV) minimizing regularizer can be successfully adopted in the MLS model in the proposed framework. We want to emphasize the fact that, until now, there exists no method which has successfully adopted the TV regularizer into the MLS model using the conventional least squares framework.

The adoption of the TV regularization term endows the MLS model with better denoising property. Normally, MLS based algorithms are weak against noise, since, in general, least squares methods are weak against outliers. In contrast, TV based methods are strong against outliers, since outliers have large variation values. The TV regularization term eliminates the outliers very fast and helps the regularized MLS to produce a better approximation to the original noise-free image.

Furthermore, the proposed scheme can also provide a better solution than conventional TV schemes. Conventional TV schemes process the observed image towards a piecewise constant image, which exhibits many false jump discontinuities and is visually unpleasant. This phenomenon is called the staircase effect. The staircase effect of the TV denoising is due to the fact that the total variation is not differentiable and the differential equations involved in this problem are at most second order. This makes the solution of the TV denoising to have a first order approximation. By incorporating the constraints used in the MLS problem into the proposed scheme, the solution becomes more constrained achieving a higher order approximation than that of the conventional TV denoising. As a result, smooth regions are well preserved, and the staircase effect is avoided without sacrificing the edge preserving property too much, as is the case with schemes trying to obtain a solution using higher order regularization terms [16, 18, 19, 51, 56].

A main difference between the proposed model and other regularized variational models is that we obtain an energy functional, whose minimization is done with respect to the parameters used in the reconstruction of the image rather than the image itself. In other words, instead of working on the image, we are working on the localized parameters used to reconstruct a local region of the image, which gives us the chance of finer control on the solution image. The proposed framework can benefit from extensions of both the regularized variational framework and the MLS framework. It is possible to generate combinations of both extensions, resulting in numerous denoising schemes with different properties.

2 Previous Works

Several different algorithms are used in the construction of the proposed scheme. In this section, we briefly review the previous works related to the different algorithms used.

The Moving Least Squares (MLS) approximation was introduced first in [34], and the details on the approximation power, stability, and implementational issues related to MLS surfaces are presented in [35]. Since then, the MLS method has been applied to many areas. For example, a diffuse approximation method is proposed in [40] to replace the FEM interpolation for solving partial differential equations. The MLS is generalized in [38], and it is proved that it produces the diffuse derivatives introduced in [40]. In [7], the MLS approximation applied to optimization problems, such as the construction of response formulation and the optimization of sheet forming method. The MLS technique is also related to local M-smoothers [20, 58] in the aspect that it approximates the local data by certain approximation functions. The usage of such approximation in variational/regularization method has been the topic of [39] and [44].

Recently, the MLS method has been proved to be quite useful in interpolation based image processing such as superresolution and image zooming [5, 20, 27, 52, 60]. The work in [27] applies MLS for image denoising by using two different kinds of robust estimators. A paper that uses a KR-based method as an edge-preserving smoother is given in [20]. In [52], a steering kernel regression is proposed which steers the local kernels along the directions of the local edge structure. Bose and Ahuja applied the MLS to noise filtering and approximation of irregularly spaced data in the superresolution problem [5]. Yoon and Lee employed the Gaussian radial basis functions instead of algebraic polynomials for an edge-directed image upsampling method [60]. However, the models show weakness against outliers, which is the main reason that the denoising properties of MLS based models normally are not good.

Meanwhile, the total variation based denoising model was first introduced in [45] in the following form:

$$ \min_{u} \| \nabla u \|_1 + \frac{\mu}{2}\|u-f\|_{2}^2, $$
(1)

where u is the solution image, f is the measured noisy image, and ∇ is the gradient operator. The term ∥∇u∥1 is called the total variation norm, and μ controls the balance between the fidelity term and the total variation term. The minimization of the total variation term smooths out very fast small-scaled variations which results in removal of the noise. Compared to the minimizing of the L 2 norm of the image gradient, the minimizing of the total variation has the property of preserving sharp discontinuities (edges) in images while removing the noise. This is a desirable property for images, since the visual quality of an image greatly depends on the preservation of edges.

However, the minimizing of the TV norm also makes smooth regions flat which makes the image look unnatural. This is known as the staircasing effect [4, 42]. As shown in [12] and [41], the staircasing effect of the total variation based denoising is due to the fact that the total variation is not differentiable and the total variation minimization tries to approximate the image to an approximation of first order. Therefore, to obtain higher order approximation of the solution image, smooth approximations and variants of the total variation functional have been proposed to avoid the staircasing effect [4, 16, 18]. In [14], the infimal convolution of functionals with first and second order derivatives as regularizers is used to obtain a higher order approximation. General modified infimal convolution functionals which combine L 1 norms with linear operators and which can be implemented with fast algorithms are used in [50].

Extra constraint terms have also been proposed to preserve the smooth areas. For example, in [56], they introduce a constraint term for smooth area protection as a penalty function. In [19], a second-order derivative is introduced into the functional to reduce the penalty for slow variation in smooth regions. These approaches try to obtain a higher order approximation by modifying the regularization function or the fidelity function. However, by modifying the regularization function, the nice geometrical properties of the total variation and the fast and strong denoising property may be lost.

Another important topic relating the total variation minimization is the implementation issue. At the early stage, Euler-Lagrange formulations have been used to implement the total variation minimization. However, the Euler-Lagrange formulation contains the non-differentiable term \(\nabla\cdot\frac{\nabla u}{|\nabla u|}\) which can not be computed exactly at ∇u=0. Therefore, splitting methods have been exploited. Using operator splitting methods, the term \(\nabla\cdot\frac{\nabla u}{|\nabla u|}\) can be split into sub-operators of simpler forms which can be implemented easier. Osher proposed the split Bregman algorithm to solve the TV problem using the Bregman iteration [30]. The equivalence of the split Bregman algorithm and the augmented Lagrangian method have been shown in [25, 49, 59]. In [48], it is shown that the alternating split Bregman algorithm can be interpreted also as a Douglas-Rachford splitting algorithm [36] which is known to be a special case of the proximal point algorithm [23]. Meanwhile, Chambolle proposed an algorithm based on a dual formulation which is fast and effective for minimizing the total variation [13]. When the dual part becomes more complicated primal-dual formulations can be used, which update both a primal and a dual variable. Zhu and Chan proposed an efficient primal-dual hybrid gradient algorithm for total variation image restoration [63]. Esser et al. proposed a modified version of the primal-dual hybrid gradient algorithm proposed by Zhu and Chan [26]. Zhang et al. proposed a unified primal-dual algorithm framework for two classes of problems [62]. Currently, one of the most efficient primal-dual splitting schemes is the scheme of Chambolle and Pock which shows a fast convergence for problems where the primal or the dual objective is uniformly convex [15]. As will be explained in Sect. 3, we exploit splitting methods to get an explicit form for the sought solution.

In the next subsections, we give a detailed explanation of the used methods in our formulation.

2.1 Moving Least Squares Based Denoising

The solution of the MLS method has a closed form and is easily computed by solving a linear system. To explain the MLS method, we use the following notations: Suppose that our observed image is a discrete sampling of a function \(f:{\mathcal{D}} \rightarrow{\mathbb{R}}\) at an equally spaced point set in a rectangle \({\mathcal{D}}\subset{\mathbb{R}}^{2}\). We want to find an overall MLS approximation function Lf of the data function f. For this aim, we first construct local approximation functions p:=p x for each point \({\mathbf{x}}\in{\mathcal{D}}\). Then the overall MLS approximation function Lf is obtained by collecting all the function values p x (x) from each local approximation function p x at the points \({\mathbf{x}}\in{\mathcal{D}}\):

$$ Lf({\mathbf{x}}) = p_{{\mathbf{x}}}({\mathbf{x}}), \quad \forall_{{\mathbf{x}}}. $$
(2)

For example, let us derive the local approximation functions from a polynomial space of degree L, denoted by Π L , where the degree of a polynomial space represents the highest degree of a polynomial in the polynomial space. We denote by m the dimension of Π L , i.e., the number of basis in Π L , which is calculated as

$$m:= \dim\varPi_{L}=\frac{(L+2)(L+1)}{2}, $$

and denote by \(\{ p_{\ell}\}_{\ell=1}^{m} \) the basis of Π L . For example, for L=2, \(m=\frac{(2+2)(2+1)}{2}=6\), we get the polynomial space Π 2 with the corresponding basis \(\{ p_{\ell}\}_{l=1}^{6} = \{ 1, x, y, x^{2}, xy, y^{2}\}\). To solve a local polynomial approximation function p around a certain point x, a finite set of data points around x have to be involved into the computation. Let \(\mathcal{N}({\mathbf{x}})\) be a finite set of distinct data points in ℝ2 around x, and N be the number of points in \(\mathcal{N}({\mathbf{x}})\). Usually, N has to be bigger than m so that the problem can be solved. Then, for a point \({\mathbf{x}}\in{\mathcal{D}}\), the polynomial approximation function p is obtained by solving the following quadratic minimization problem:

$$ \mathop{\operatorname{argmin}}_{p\in\varPi_L} \Biggl\{\sum_{n=1}^N \big\| p({\mathbf{x}}_n) - f({\mathbf{x}}_n) \big\|^{2}_2 \theta\bigl(\|{\mathbf{x}}-{\mathbf{x}} _n\|_2\bigr) \Biggr\}, $$
(3)

where θ is a radial and fast decreasing smooth function and N>dimΠ L . The θ function is a weight function which decides how much the data point f(x n ) contributes to the construction of the polynomial approximation p(x n ). If θ(∥x−x n ∥2) is large, f(x n ) contributes much to the construction. This is done by reducing the error of the data f(x n ) and the evaluated value p(x n ) at x n , i.e., by reducing \(\| p({\mathbf{x}}_{n}) - f({\mathbf{x}}_{n}) \|^{2}_{2}\). A typical choice of θ is the Gaussian function

$$ \theta({\mathbf{r}}) = e^{-|{\mathbf{r}}|^2/\sigma} $$
(4)

having a scale parameter σ>0. This is based on the premise that the data points near to x should have a large effect in the construction. The minimizer p differs from pixel to pixel. Since we construct p in Π L of dimension m, we can write p as a linear combination of the basis \(\{ p_{\ell}\}_{l=1}^{6}\):

$$ p:= \sum_{\ell=1}^{m} c_\ell p_\ell. $$
(5)

Therefore, we see that (3) is a least squares problem that can be solved for the coefficients {c ℓ :ℓ=1,…,m} of the polynomial p. The coefficients {c ℓ :ℓ=1,…,m} satisfying (3) are found by calculating the derivative of the function in (3) with respect to {c ℓ :ℓ=1,…,m} and setting them equal to zero:

(6)

When the solution, say p x (x), of the above quadratic minimization problem is obtained for a certain point \({\mathbf{x}}\in{\mathcal{D}}\), then the function value Lf(x) for the point x becomes Lf(x)=p x (x). Thus, the overall MLS approximation function Lf is defined as follows:

$$ Lf({\mathbf{x}}) = p_{{\mathbf{x}}}({\mathbf{x}}), \quad \forall_{{\mathbf{x}}}, $$
(7)

where p x (⋅) denotes the minimizer of (3) for the point x.

Figure 1 is an exemplary illustration showing the concept of constructing the MLS approximation function for a 1-D data profile. The blue and the red dotted lines show the constructed polynomial functions \(p_{{\mathbf{x}}_{i}}\) and \(p_{{\mathbf{x}}_{i+1}}\) for the points x i and x i+1, respectively, using the data in the neighborhoods \(\mathcal{N}({\mathbf{x}}_{i})\) and \(\mathcal {N}({\mathbf{x}}_{i+1})\), respectively. The value \(p_{{\mathbf{x}}_{i}}({\mathbf{x}}_{i})\) denotes the value of \(p_{{\mathbf{x}}_{i}}\) at the point x i , and likewise for \(p_{{\mathbf{x}}_{i+1}}({\mathbf{x}}_{i+1})\). The overall approximation MLS function Lf becomes the collection of all the values p x (x) for all \({\mathbf{x}}\in{\mathcal{D}}\), which are shown as black circle points in Fig. 1.

Fig. 1
figure 1

Exemplary illustration showing the construction of the MLS approximation for a 1-D data profile

Full size image

If f in (3) is a noisy version of the original data, the approximation Lf becomes a smoother one. By obtaining a smoother approximation Lf, denoising is achieved. However, it is well-known that the MLS method has limitations in denoising, because the output of least squares method is highly affected by singular data (or outlier) error, which results in noisy artifacts. The proposed scheme aims to reduce this artifact by introducing the TV norm into the least squares method.

2.2 Split Bregman Method

Even though other splitting methods can be applied to the proposed scheme, as will be explained in Sect. 3, we exploit the split Bregman method for its simplicity. The split Bregman method [30, 61] solves a minimization problem by operator splitting and then applying Bregman iteration to solve the split problem. It solves the problem

$$ \min_u \big\| \varPhi(u) \big\|_1 + E(u) $$

by the operator splitting

$$ \min_{u,d} \| d \|_1 + E(u) \quad\mbox{subject to} \quad\varPhi(u)=d, $$

where E is convex and Φ is convex and differentiable. For image processing applications, u is the solution image, and d is used to obtain the constraint formulation. Applying Bregman iteration with J(u,d)=∥d∥1+E(u) and \(H(u,d)=\frac{1}{2} \| d - \varPhi(u) \|_{2}^{2}\) yields

(8)

where p u and p d are in the set of the sub-gradients of E with respect to u and d, respectively, λ is a parameter that controls the balance, k and k+1 denote the current and the next iteration step, and ∇ u H(u,d)=(∇Φ(u))∗(Φ(u)−d) and ∇ d H(u,d)=d−Φ(u).

It is shown in [30] that (8) is equivalent to the following two subproblems:

(9)

Here, the first subproblem works on the primal variable u, on the image itself, and the second one works on the dual variable b, which can be seen as the noise. The first subproblem can be solved by alternatingly minimizing u and then d,

(10)

The step for u k+1 can be solved as a linear system, while in the step for d k+1, the minimizer can be expressed in closed-form as a shrinkage. For the total variation problem, E(u) and Φ(u) becomes \(E(u)=\|u-f\|_{2}^{2}\) and Φ(u)=∇u, and thus the problem is solved by the following iterative 3 steps:

(11)

Here, the shrinkage operator is defined as follows:

$$\mathrm{shrink}(x,\tau) = \left \{\begin{array}{l@{\quad}l} x - \tau \operatorname{sgn}(x) & \mbox{if $|x| \geq\tau$},\\ 0 & \mbox{if $|x| < \tau$}, \\ \end{array} \right . $$

where \(\operatorname{sgn}(\cdot)\) is the sign operator.

By using the split Bregman method, the total variation problem can be solved faster than using conventional nonlinear partial differential equations. However, in this paper, we do not use the Bregman method for fast computation, but utilize and vary it to introduce the TV norm into the MLS model.

3 Proposed Scheme

In this section, we first propose a new energy functional to be minimized for data approximation. Then, we propose a new computational framework that can solve the minimization problem. Let f be a given reference image defined on a domain Ω, and let \({\bf x}\) be a fixed point in Ω. Then, we construct a local polynomial approximation of degree L:

$$p({\mathbf{r}}) := p_{\bf x}({\mathbf{r}}) :=\sum _{|\alpha|_1\leq L} c_\alpha{\mathbf{r}}^\alpha $$

by minimizing the following energy functional:

$$ \mathop{\operatorname{argmin}}_{p\in\varPi_m} \Biggl\{ \sum_{n=1}^N \big\| \nabla p({\mathbf{x}}_n) \big\|_1 + \frac{\mu}{2} \big\| p({\mathbf{x}}_n) - f({\mathbf{x}}_n)\big\|^{2}_2 \theta ({\mathbf{x}}, {\mathbf{x}}_n) \Biggr\}. $$
(12)

In this construction, we use a nonlocal weight function θ which is defined as

where h 0 is a small positive value, G a is the Gaussian function with standard deviation a, and + ⋅ denotes the shifting operator. Nonlocal similarity measures have been used in nonlocal denoising methods to decide whether a certain pixel should be used in the denoising process or not [6, 8, 21, 22, 24, 28, 29, 33, 44, 53]. In comparison, we use it as a weight function such that the weight function becomes data adaptive and consider the similarity of the local areas between two positions \({\bf x}\) and r. The weight function has a large value if the local areas around \({\bf x}\) and r are similar. In this case, the f(r) value is taken much into account in constructing the local approximation at \({\bf x}\). This is based on the premise that the approximation function value should be similar to the data value if the corresponding neighborhoods are similar. Thus, pixel values which are spatially distant are also incorporated into the approximation process if the corresponding θ value is large.

We construct p at each pixel in the image, and so we are solving the minimization problem in (12) as many times as there are pixels in Ω. Then, the overall approximation function Lf becomes Lf(x):=p(x):=p x (x) for all x∈Ω.

Without the first term, the energy functional in (12) becomes just that used in the conventional MLS model. The incorporation of the TV norm endows the MLS model with several desirable properties that helps to overcome the weaknesses of the MLS model. Again, we want to emphasize the fact that even though the incorporation of the TV term may seem simple, the problem cannot be solved in the conventional moving least squares framework, and therefore, has never been proposed. This is due to the fact that a solution of the problem (12) having a closed form cannot be obtained. This is in contrast with TV approaches, for which quadratic data penalization have been frequently used with the TV norm [3, 32, 55].

The proposed model is also different from the conventional TV approach, in the sense that the solution sought is not the image u, but are the parameters that are used in the reconstruction of the p function which approximates the image from the polynomial space. We call the proposed method the MLS with TV minimizing (MLS-TV) model. We will first explain the properties of the MLS-TV model by explaining its contributions to the conventional MLS and the TV models. Then, we will propose a computational framework which solves the problem in (12). The proposed framework can be applied for denoising schemes with other regularization terms.

3.1 Contribution of the MLS-TV Model to the MLS Model

By incorporating the TV norm, the proposed model gets the following advantageous properties over the conventional MLS model:

  • The denoising property becomes better.

  • The approximation becomes less affected by outliers.

  • The local noisy artifact is eliminated.

These properties are due to the fact that the minimization of the TV norm eliminates small scaled structures very fast from the image.

As the outliers are eliminated very fast by the TV minimization, the local noisy artifact is greatly reduced and the approximation to the noise-free image gets better.

Figure 2 illustrates the fact that the incorporation of the total variation minimizing term reduces the influence of outliers. Figure 2(a) shows a noisy 1-D profile. The noisy profile is generated by adding Gaussian type noise to all positions, and some outlier noise to some positions (indicated by arrows in the figure) of the original profile. Figure 2(b) is the result of applying the conventional MLS to Fig. 2(a) which shows that the large noise results in local noisy artifacts. Figure 2(c) shows the denoised result using the TV model which reveals also the staircasing artifact. Figure 2(d) shows the result of applying the MLS-TV to the noisy 1-D profile. Compared with Fig. 2(b), the local noisy artifact is eliminated with the proposed scheme, while effectively removing the noise.

Fig. 2
figure 2

Comparison of denoising properties on a 1-D profile (a) Noisy (b) MLS denoised (c) TV denoised (d) MLS-TV denoised

Full size image

Experimental results on images verifying the above properties will be given in the experimental section.

3.2 Contribution of the MLS-TV Model to the TV Model

As explained in Sect. 2, the minimization of the total variation norm tries to approximate the image to an approximation of first order. The fidelity term prevents the image from becoming totally flat, but cannot preserve the order of approximation, since there exist no inherent constraints in the u function that prevents the order from decreasing.

In contrast, the p function in the proposed model is constrained to have a pre-defined order due to the constraint to lie in the polynomial space Π m . Therefore, the proposed model has the following advantageous properties over the conventional TV model.

  • An approximation of any pre-defined order can be obtained.

  • The scheme is less sensitive to the parameter deciding the strength of total variation minimization.

Here, one important fact is that a higher order approximation is obtained without varying the total variation minimization term, i.e., we can control the order of the solution without changing the regularization term. For example, if we want to achieve an approximation of degree 2 (which is equal to an approximation of order 3), we just let the solution p in (12) to lie in the polynomial space Π 2. The constraint to lie in a certain polynomial space makes the solution also less sensitive to the parameter μ in (12) which decides the strength of competition between the regularization term and fidelity term in (12). This is due to the fact that the number of basis used in the reconstruction of p has a larger influence than the parameter μ. Furthermore, since the proposed scheme still uses the total variation minimization, it keeps the property of effective removing of outliers.

3.3 Iterative Algorithm to Solve the MLS-TV Model

In this section, we explain the numerics to obtain the minimizer p(r) in (12). Since we construct p in Π L of dimension m, we can write p as a linear combination of the basis {p ℓ ,ℓ=1,…,m}:

$$ p({\bf x}):= \sum_{\ell=1}^{m} c_\ell p_\ell({\bf x}). $$
(13)

Therefore, to find the minimizer p(r) we have to obtain the following coefficients of the polynomial p,

$${\bf c}=\{c_\ell: \ell=1,\ldots, m\}. $$

A first try to obtain the coefficients might be to employ the energy function with variable \({\bf c}\)

$$ {\mathcal{E}}({\bf c}) : = \frac{\mu}{2} \|{\bf p}- {\bf f} \|^2_{\theta,{\bf x}} + \| \nabla{\bf p} \|_1 $$
(14)

and try to find the coefficients by letting the derivative of the function \({\mathcal{E}}({\bf c})\) equal to zero:

$$ \frac {\partial{\mathcal{E}}({\bf c})}{\partial c_\ell} = 0, \quad \ell=1, \dots, m. $$
(15)

Here, \({\bf p}:=\{p({\bf x}_{n}): {\bf x}_{n}\in \mathcal{N}({\bf x}) \}\) and \({\bf f}:=\{f({\bf x}_{n}): {\bf x}_{n} \in \mathcal{N}({\bf x}) \}\) denote the evaluated values of the polynomial \(p({\bf x})\) at \({\bf x}_{i}\) and the vectors of the data points in \(\mathcal{N}({\bf x})\), respectively, and thus \({\bf p}\) depends on \({\bf c}\).

However, due to the L 1 norm, a linear system for the coefficients \({\bf c}=\{c_{\ell}: \ell=1,\ldots, m\}\) cannot be obtained. Therefore, to obtain a linear system for the coefficients, we exploit splitting methods. It will be shown later that using splitting methods we not only get a linear system but also an explicit form for \({\bf c}\). This is in contrast with the total variation minimization problem, where a linear system has to be solved, for example, by Gauss-Seidel iteration. We might employ any splitting method that results in a linear system for \({\bf c}\), but here we use the split Bregman iteration algorithm [30], which was introduced to solve the L 1 regularized optimization problem in Sect. 2.2, due to its simplicity.

By placing the iterative minimization scheme into our problem (12), we get the following iteration steps for each x:

(16)

where \({\mathbf{x}}_{n} \in\mathcal{N}({\mathbf{x}})\), and k and k+1 indicate the current and the next iteration level. The following notations are helpful for further discussion of the suggested method. From now on, any bolded character means a vector or matrix. Moreover, for a given function g and a weight function θ, the weighted norm for a vector \({\mathbf{g}} := \{g({\bf x}_{n}): {\bf x}_{n}\in\mathcal{N}({\bf x}) \}\) is defined by

$$ \|{\bf g}\|^2_{\theta,{\bf x}} = \sum_{n=1}^{N} \big\|g({\bf x}_n) \big\|^{2}_{2} \theta({\bf x}, {\bf x}_n). $$

We are now ready to explain the specific algorithm of the proposed scheme.

• Step 1: Let

$${\bf f}:=\bigl\{f({\bf x}_n): {\bf x}_n\in \mathcal{N}({\bf x}) \bigr\} $$

be the vector of the image brightness values at the data points \({\bf x}_{i}\) in \(\mathcal{N}({\bf x})\) and

$${\bf p}:=\bigl\{p({\bf x}_n): {\bf x}_n\in \mathcal{N}({\bf x}) \bigr\} $$

be the vector of the evaluated values of the polynomial p at the data points \({\bf x}_{n}\) in \(\mathcal{N}({\bf x})\). In other words, \({\bf p}\) is the vector form of the polynomial p. Furthermore, let \(\partial_{x} {\bf p}\) and \(\partial_{y} {\bf p}\) be the vectors of the partial derivatives of \(p({\bf x}_{i})\) with respect to x and y, respectively:

and let

where \(b^{k}_{x}({\bf x}_{n})\) and \(b^{k}_{y}({\bf x}_{n})\) are the x and y components of \(b^{k}({\bf x}_{n})\), respectively, and likewise for \(d^{k}_{x}({\bf x}_{n})\) and \(d^{k}_{y}({\bf x}_{n})\). Then the first step (1) of the proposed model can be written in vector form as

(17)

Since we construct p in Π L of dimension m, we can write p as a linear combination of the basis {p ℓ ,ℓ=1,…,m}:

$$ p({\bf x}):= \sum_{\ell=1}^{m} c_\ell p_\ell({\bf x}). $$
(18)

Therefore, we see that (17) is a least squares problem that can be solved for the following coefficients of the polynomial p,

$${\bf c}=\{c_\ell: \ell=1,\ldots, m\}. $$

To this end, let us employ the energy function with variable \({\bf c}\),

(19)

which is indeed a quadratic polynomial of the variables c ℓ with ℓ=1,…,m. Then, the coefficient vector \({\bf c}\) satisfying (19) can be found by calculating the derivative of the function \({\mathcal{E}}({\bf c})\) and setting this equal to zero:

$$ \frac{\partial{\mathcal{E}}({\bf c})}{ \partial c_\ell} = 0, \quad\ell=1, \dots, m. $$
(20)

In order to find the solution of this linear system, we need to express (20) in a matrix form. For this, we denote by \({\bf E}\), \({\bf E}_{x}\) and \({\bf E}_{y}\) the matrices which (n,ℓ) components are defined as:

(21)

where ∂ x and ∂ y are the partial derivative operators, i.e., \({\partial_{x}}=\frac{\partial}{\partial x} \) and \({\partial_{y}}=\frac {\partial }{\partial y} \). Moreover, recalling that the given weight function θ is non-zero for any \(({\bf x}_{1},{\bf x}_{2}) \in\mathbb{R}^{2}\times\mathbb {R}^{2}\), let \({\bf D}_{\theta}\) indicate the N×N diagonal matrix whose (n,n)-component is defined by

$$ {\bf D}_\theta(n,n) := \theta({\mathbf{x}}_n, { \mathbf{x}}), \quad{\bf x}_n \in\mathcal{N}. $$
(22)

Then, using these notations, a simple calculation reveals that the condition (20) is equivalent to the following linear system:

This leads to the identity

(23)

We see that the solution \({\bf c}\) is expressed explicitly, and therefore there is no need to solve a linear equation, which is in contrast with the TV minimization case. Each column of the matrices \({\bf E}\),\({\bf E}_{x}\) and \({\bf E}_{y}\) are composed of the polynomial basis and their partial derivatives. Therefore, it is easy to see that the matrix \([{\bf E} ; {\bf E}_{x} ; {\bf E}_{y}]\) is a full rank matrix. It is shown in [35], that for the conventional MLS problem we get the system matrix \(\mu{\bf E}^{T}{\bf D}_{\theta}{\bf E}\), and that this matrix is invertible if \({\bf E}\) is a full rank matrix and \({\bf D}_{\theta}\) is diagonal. Although it is not straightforward, following the same procedure, it can be shown that the system matrix \(\mu{\bf E}^{T} {\bf D}_{\theta}{\bf E}+ \lambda{\bf E}^{T}_{x} {\bf D}_{\theta}{\bf E}_{x} + \lambda{\bf E}^{T}_{y} {\bf D}_{\theta}{\bf E}_{y}\) becomes invertible if \([{\bf E} ; {\bf E}_{x} ; {\bf E}_{y}]\) is a full rank matrix. Therefore, the inverse matrix always exists.

We see that (17) can be solved if the vectors \({\bf d}\) and \({\bf b}\), and the initial noisy image \({\bf f}\) are given. We initialized the vectors as \({\bf d}= {\bf0}\) and \({\bf b}={\bf0}\). Finally, after obtaining this coefficient vector \({\bf c}\), our solution p k+1 is obtained by

$$p^{k+1} := \sum_{\ell=1}^mc_\ell p_\ell. $$

• Step 2: After p k+1 has been obtained in step 1, we can update d k+1. To update \(d^{k+1}:=(d^{k+1}_{x}, d^{k+1}_{y})\) in step 2, we explicitly solve the minimization problem using the shrinkage operator used in [57] which is defined in Sect. 2.2, and simply compute

(24)

where \(\operatorname{sgn}(\cdot)\) is the sign operator.

• Step 3: After ∇p k+1 and d k+1 have been computed, the update of b k+1 is done using the same update method as in the Bregman algorithm.

(25)

All the three steps have to be iteratively performed for each pixel x∈Ω, which gets us all the local polynomial functions p(x)=p x (x) for all x∈Ω. Then, finally, the overall MLS approximation function Lf is obtained by

$$ Lf({\mathbf{x}}) = p({\mathbf{x}})= p_{{\mathbf{x}}}({\mathbf{x}}), \quad \forall{{ \mathbf{x}}}\in\varOmega. $$
(26)

3.4 Other Combinations Using the Proposed Computational Framework

Other combinations of the least squares methods and the regularized variational models can be implemented using the computational framework explained in Sect. 3.3. For example, the least squares method with directional kernel [52] and the g-norm regularizer [37] can be put together with the proposed computational framework in the same manner as the MLS-TV model. Furthermore, we can also use other basis than polynomial basis to reconstruct p, for example, exponential basis [47, 54]. This will result in denoising models with other properties.

4 Experimental Results

We compared the denoising results of the proposed scheme with the conventional TV based denoising [45], the conventional MLS based denoising [35], the nonlocal TV (NLTV) based denoising [61], the kernel regression (K-R) based denoising [52], nonlocal mean (NLM) based denoising [11], the nonlocal scale-shape (NL-SS) [28], and the nonlocal method with shape-adaptive patches (NLM-SAP) [22] methods. The TV and the NLTV methods are implemented using the split Bregman method. The NL-SS uses the nonlocal weighted linear diffusion process, while the NLM-SAP uses more general shapes for the patch in NLM instead of the usual square patches.

The easiness in choosing the parameters is also an important factor to measure the goodness of the algorithm. While the proposed scheme is not so sensitive to the parameters, the other schemes are sensitive to the choice of parameters, especially the K-R based method. This is shown in Fig. 5 and also in Table 1, where it can be observed that the PSNR values vary much for different parameters with other algorithms, while for the proposed one the PSNR values are similar.

Table 1 PSNR comparison of the denoised images by 8 different denoising algorithms, where the noise is derived from a Gaussian distribution with standard deviation σ=15.3 (and σ=20.4 for the ‘Cameraman’ image with PSNR=22.2497)
Full size table

Figure 3 compares the denoising results on the ‘Bird’ image with Gaussian noise, where the PSNR is 26.0636 dB, and the noise is generated from a zero mean Gaussian distribution with σ=12.75, where σ is the standard deviation. The local density and the global smoothing parameters [52] used in the K-R method are 0.1 and 0.5, respectively, and the structural sensitivity is 0.1. The width of Gaussian kernel in the NLM is 0.06. The fidelity parameters (μ) for the TV, NLTV, MLS-TV are all set to 15 (with λ=5 in (16)), and the number of data used in the reconstruction of the local polynomial approximation (N in (16)) is 49 for both the MLS and the MLS-TV models. Here, the parameter λ is the Bregman parameter which appears in the Bregman formulation of the model, and has an effect on the convergence speed of the algorithm. The degree of polynomials and the width of Gaussian are 3 and 0.3, respectively, for both the MLS and the MLS-TV.

Fig. 3
figure 3

Comparing the denoised results with the ‘Bird’ image (a) original (b) noisy (σ=12.75, PSNR = 26.0636 dB) (c) denoised with MLS (PSNR = 28.2529 dB) (d) denoised with K-R (PSNR = 28.3158 dB) (e) denoised with TV (PSNR = 29.5978 dB) (f) denoised with NLM (PSNR = 29.7249 dB) (g) denoised with NLTV (PSNR = 28.0798 dB) (h) denoised with MLS-TV (PSNR = 30.5168 dB)

Full size image

As can be seen in the backgrounds of Figs. 3(c) and 3(d), the conventional MLS and the K-R based denoising show local noisy artifacts due to the strong noise which affects the neighborhood of kernel size. In contrast, with the proposed scheme, the noisy artifact is effectively removed due to the TV minimizing term. Compared with the conventional TV based denoising scheme, the proposed scheme produces a higher order approximation to the intensity function, and the staircasing artifact does not appear in smooth regions. The visual quality of the denoised image seems to be better even than those removed by the conventional NLTV and the NLM based denoising schemes.

Figure 4 shows some details of Figs. 3(e) and 3(h) to verify that the approximation using the proposed scheme is of higher order than that of the TV model.

Fig. 4
figure 4

Showing some details of Fig. 3 for the denoised results using the TV and the MLS-TV models (a) TV (b) MLS-TV

Full size image

Figure 5 shows that the proposed scheme is not so sensitive to the parameter deciding the strength of fidelity (μ in (12)) as the TV model is. This is due to the additional constraint in the reconstruction of the p function. The insensitiveness to the parameter makes the scheme stable.

Fig. 5
figure 5

Upper row: MLS-TV (a) μ=15 (b) μ=5 (c) μ=1, Lower row: TV (d) μ=15 (e) μ=5 (f) μ=1

Full size image

Figure 6 compares the denoising results with the ‘Barbara’ image, which contains image structures with large oscillation. We used the following parameters in the denoising of the ‘Barbara’ image. The used in the K-R method are same as used in the ‘Bird’ image. The width of the Gaussian kernel in the NLM is 0.08. The fidelity parameters (μ) for the TV, NLTV, MLS-TV are 10, 20, and 10, respectively, with λ=5. The number of data (N), the degree of polynomials, and the width of Gaussian are 49, 3, 0.3, respectively, for both the MLS and the MLS-TV. Again, the staircase artifact and the noise halo artifact can be observed with the results of the TV and the NLM schemes, respectively, especially in the enlarged figures in Fig. 7. With the proposed scheme, these artifacts are suppressed. The proposed scheme can also preserve the stripes in the ‘Barbara’ image, as the NLM scheme does, as can be seen in Fig. 8.

Fig. 6
figure 6

Comparing the denoised results with the ‘Barbara’ image (a) original (b) noisy (σ=15.3, PSNR = 24.4437 dB) (c) denoised with MLS (PSNR = 29.8410 dB) (d) denoised with K-R (PSNR = 27.2142 dB) (e) denoised with TV (PSNR = 26.2151 dB) (f) denoised with NLM (PSNR = 30.7963 dB) (g) denoised with NLTV (PSNR = 29.0939 dB) (h) denoised with MLS-TV (PSNR = 32.5240 dB)

Full size image
Fig. 7
figure 7

Enlarged versions of the denoised results in Fig. 6. (a) TV (b) NLTV (c) NLM (d) MLS-TV

Full size image
Fig. 8
figure 8

Enlarged versions of the denoised results in Fig. 6. (a) TV (b) NLTV (c) NLM (d) MLS-TV

Full size image

Figure 9 compares the denoising results with the ‘Cameraman’ image, which has a stronger Gaussian noise (σ=20.4, PSNR = 22.2497 dB) than the ‘Bird’ and ‘Barbara’ image. For this, we compare the result with two more nonlocal approach, NLM-SAP and NL-SS. The width of Gaussian in the both methods is 0.08. We used 15 different shapes for the patch in NLM-SAP and Δt=1/14 for the steepest descent in NL-SS. The other parameters are the same as with the ‘Barbara’ image for the other methods. Due to the strong noise, the results with the conventional MLS and the K-R based denoising suffer from significant local noisy artifacts. In removing the strong noise, the staircase artifact of the TV and the NLTV scheme and the noise halo artifact of the NLM scheme and NL-SS scheme, a typical artifact of the NLM scheme which is due to an abrupt lack of redundancy around edges, become apparent. These artifacts can be better observed in the enlarged images in Fig. 10. The NLM-SAP has the largest PSNR value, but artifacts can be seen in the background. In contrast, the MLS-TV scheme has a better visual quality as can be seen in Figs. 9(i) and 10(i).

Fig. 9
figure 9

Comparing the denoised results with the ‘Cameraman’ image (a) noisy (σ=20.4, PSNR = 22.2497 dB) (b) denoised with MLS (PSNR=28.9740 dB) (c) denoised with K-R (PSNR = 24.1324 dB) (d) denoised with TV (PSNR = 27.2562 dB) (e) denoised with NLM (PSNR=27.8477 dB) (f) denoised with NLTV (PSNR=28.5713 dB) (g) denoised with NLM-SAP (PSNR = 29.4391 dB) (h) denoised with NL-SS (PSNR = 28.8289 dB) (i) denoised with MLS-TV (PSNR = 28.8635 dB)

Full size image
Fig. 10
figure 10

Enlarged versions of the denoised results in Fig. 9 (a) noisy (σ=20.4, PSNR = 22.2497 dB) (b) denoised with MLS (PSNR = 28.9740 dB) (c) denoised with K-R (PSNR = 24.1324 dB) (d) denoised with TV (PSNR = 27.2562 dB) (e) denoised with NLM (PSNR=27.8477 dB) (f) denoised with NLTV (PSNR=28.5713 dB) (g) denoised with NLM-SAP (PSNR = 29.4391 dB) (h) denoised with NL-SS (PSNR = 28.8289 dB) (i) denoised with MLS-TV (PSNR = 28.8635 dB)

Full size image

Table 1 further compares the PSNR values of the denoising results on five different 512×512 noisy images, where the noise was generated with a zero mean Gaussian distribution with σ=15.3. For the ‘Cameraman’ image, we also tabled the results from Fig. 9, which has a stronger noise (σ=20.4, PSNR = 22.2497 dB). Especially, the NLTV, TV, and MLS-TV methods are implemented with four different fidelity parameters for each image. The width of the Gaussian kernels used in the NLM, NLM-SAP and NL-SS methods is 0.06, and the other parameters are the same as those used in Fig. 10. We see that the proposed MLS-TV method has a good denoising result compared to the other algorithms, when the noise is not too strong.

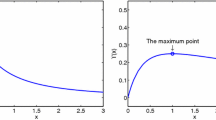
We used a stopping criterion to terminate the iteration of the proposed scheme. The iteration stops if ∥Lf k+1−Lf k∥/∥Lf k∥<10−3, where Lf k denotes the approximated image at the current step, and Lf k+1 denotes that at the next step. To show the convergence property of the proposed scheme, we draw a convergence plot of the proposed scheme in Fig. 11. Figure 11 shows that the value ∥Lf k+1−Lf k∥/∥Lf k∥<10−3 converges.

Fig. 11
figure 11

Change of the ∥Lf k+1−Lf k∥/∥Lf k∥ value according to the number of iterations

Full size image

Figure 12 shows the plot of the PSNR value and the total iteration number versus the fidelity parameter value, where the PSNR values corresponds to the resulted images obtained with the stopping criterion ∥Lf k+1−Lf k∥/∥Lf k∥<10−3 for the TV method and the proposed method. This plot shows the fact that the proposed method is less sensitive to the fidelity parameter than the TV method.

Fig. 12
figure 12

Change of the PSNR and the total iteration according to the fidelity parameter (μ). The small dots corresponds to the proposed method and the large dot to the TV method

Full size image

Figure 13 shows how the denoised result of the proposed method depends on the degree of the approximation and on \(\mathcal{N}({\mathbf{x}})\), the size of the neighborhood. It can be seen that the denoised results are similar for the images of degree 3 and degree 4 approximations, since the difference in the approximation error between the degree 3 and the degree 4 approximations is small.

Fig. 13
figure 13

Showing the denoising results on Fig. 9(a) with the proposed method using a degree 0 (first column), degree 3 (second column), degree 4 (third column) approximation, and a neighborhood of size 5×5 (first row), 7×7 (second row), 9×9 (third row), 11×11 (fourth row). The parameters μ=15, λ=5 have been used for all images

Full size image

All the algorithms are implemented with the Matlab program (version R2011a, 64-bit) using only Matlab commands on an Intel Core2 CPU (2.66 GHz) and 8 GB memory. With this configuration, the running time was about 180 seconds on a 256×256 image with the proposed scheme. The running time is large compared with the TV method which took about 0.8 seconds. The K-R, MLS, NLTV, NLM, NLM-SAP, and the NL-SS methods took 47, 23, 1, 60, 36, 518 seconds, respectively. However, the code corresponding to the proposed scheme was not optimized, and there is the possibility that the running time of the proposed scheme can be significantly reduced after optimization.

5 Conclusion

In this paper, we have proposed a computational framework which can put regularity based variational methods and least squares methods together. As an example, we showed how the total variation minimization can be incorporated into the moving least squares method, which resulted in a denoising scheme that can overcome the drawbacks of both the conventional total variation based and the moving least squares based denoising schemes. The proposed framework can be used to further incorporate several other regularization terms which have been proposed in the variational approaches into the least squares methods. Meanwhile, methods adopted from the least squares framework such as the usage of steering kernels can also be incorporated in the proposed framework. The proposed framework has opened possibilities for numerous schemes which can be derived in the same manner as the proposed MLS-TV scheme.