Variational optic flow on the Sony PlayStation 3

Abstract

While modern variational methods for optic flow computation offer dense flow fields and highly accurate results, their computational complexity has prevented their use in many real-time applications. With cheap modern parallel hardware such as the Cell Processor of the Sony PlayStation 3, new possibilities arise. For a linear and a nonlinear variant of the popular combined local-global method, we present specific algorithms on this architecture that are tailored towards real-time performance. They are based on bidirectional full multigrid methods with a full approximation scheme in the nonlinear setting. Their parallel design on the Cell hardware uses a temporal instead of a spatial decomposition, and processes operations in a vector-based manner. Memory latencies are reduced by a locality-preserving cache management and optimised access patterns. For images of size 316 × 252 pixels, we obtain dense flow fields for up to 210 frames per second.

1 Introduction

For many modern applications in image processing and computer vision, motion estimation is an important building block for algorithms providing highly qualitative results. Since both the structure of the captured scene and the ego-motion of the camera are thereby often unknown, only the projection of this motion onto the camera plane is taken into account. This so-called optic flow is described by a vector field representing the displacement of pixels in a pair of two subsequent frames.

Modern optic flow models often rely on variational approaches that yield dense flow fields. Going back to early techniques such as the ones proposed by Horn and Schunck [26] or Nagel and Enkelmann [32], recent models provide very accurate results, such as the combined local-global (CLG) approach proposed by Bruhn et al. [10], the model by Brox et al. [7] based on warping, the level set approach by Amiaz and Kiryati [1], the over-parameterised variational model by Nir et al. [34], or the TV-L ¹ flow approach by Wedel et al. [39]. However, since they rely on the solution of large systems of equations with several thousands to millions of unknowns, they come along with a huge computational workload, and are thus rarely used in real-time applications. Instead, one often finds local or search-based approaches [13] which are typically very fast, but cannot provide precise results.

With the research on efficient numerical solvers making progress in the recent past, several techniques have been proposed to accelerate the estimation of the variational optic flow significantly. Iterative solvers, such as those based on successive over-relaxation approach [43] and preconditioned conjugate gradient methods [36], have been actively used for many years. An alternative to these methods is found in hierarchical approaches which reduce the computational complexity by one order, and which are thus more and more considered in modern applications. Uni- and bidirectional multigrid schemes [5, 6] are nowadays the fastest solvers available, outperforming the classic schemes even for small problem sizes.

As a consequence, they are often applied when it comes to optic flow estimation from both 2D and 3D data [20, 21, 45]. By the use of these techniques, it is already possible to obtain optic flow fields from frames of 160 × 120 pixels in real-time, using standard PC hardware. Bruhn et al. [9] compared a nonlinear approach to a linear one, and obtained rates of 12.17 and 62.79 frames per second (FPS), respectively.

Unfortunately, this performance is still inadequate for many recent applications, demanding the computation of larger frames in a fraction of this time, to guarantee the overall runtime to be real-time capable as well. A remedy to this problem is promised by customised hardware, or by novel parallel architectures, which supply more computing resources in terms of additional processor cores.

Optic flow systems based on customised hardware seldomly implement variational approaches, but for certain applications, such as robot navigation, their quality is often sufficient. Examples for a fully customised layout for real-time optic flow estimation can be found in the RETIMAC chip by Nesi [33]. Prototyping hardware such as erasable programmable logic devices (EPLD) or later also field programmable gate arrays (FPGA) has been used as well [2, 25, 40]. With the help of such hardware solutions, a simple local approach already allows to compute non-dense flow fields of 640 × 480 pixels with 64 FPS [40].

Recently, both distributed and shared memory architectures have been investigated for the computationally more challenging variational optic flow problem. Examples are the implementation on massively parallel computer clusters by El Kalmoun et al. [15] or adaptations to graphics hardware (GPU) proposed by Zach et al. [44] and Mizukami and Tadamura [31]. From a numerical perspective, the work of Grossauer and Thoman [22] is also very close to this subject, since they describe nonlinear multigrid techniques on the GPU.

Much less in price compared to a PC equipped with modern programmable graphics hardware, the Sony PlayStation 3 video console forms one of the cheapest parallel computers on the market. Thanks to its powerful processor, the Cell Broadband Engine, and potential speedup gains prospected thereby, it has also lately gained popularity for scientific research. After first simple tasks mostly implemented and evaluated for benchmarking purposes, such as matrix multiplications [12], fast Fourier transforms [41], and an evaluation of the heat equation [42], more sophisticated and complex algorithms have recently been proposed as well. Elgersma et al. [16] use the platform for the computation of Stokes’ equation, Benthin et al. [4] suggested a complete ray tracer running on this platform, and Köstler et al. [29] showed how to use this architecture for video compression based on partial differential equations.

Apart from our own preliminary work published on a conference [23], variational optic flow methods have so long not been evaluated on this platform, which is surprising. Such methods are typically consuming a significant amount of computational time in modern algorithms, and are thus often replaced by less accurate, but fast alternatives. That is why we are going to discuss the applicability of such a platform for the optic flow problem in the present paper. We extend our previous work describing a linear algorithm for the CLG model by an even faster variant thereof. Moreover, we present a new parallel algorithm for the nonlinear CLG method that provides flow fields of even higher quality. We evaluate both algorithms with respect to their runtime performance and scaling behaviour. We show that compared to standard PC hardware, it is indeed possible to accelerate the algorithm noticeably, and obtain throughputs of up to 210 FPS for an image sequence of 316 × 252 pixels.

Our paper is structured as follows. In Sect. 2, we first discuss the so-called CLG model that we use for the parallel optic flow estimation, and distinguish between the linear and the nonlinear variant thereof. After commenting on minimisation and discretisation, we proceed with an introduction to the numerical solvers we apply, covered by Sect. 3. In Sect. 4, we then give a brief overview of the hardware characteristics that we exploit. Moreover, we present the special adaptations and optimisations we applied in order to exhaust the full potential of this hardware, and structured these by memory level parallelisation concepts in Sect. 5 and instruction level parallelism in Sect. 6. Finally, we then evaluate our new algorithms on the PlayStation 3 in Sect. 7, and conclude with a short summary in Sect. 8.

2 CLG optic flow

In order to evaluate the applicability of variational optic flow approaches on the PlayStation 3, we decided to create parallel algorithms based on the CLG model proposed by Bruhn et al. [10]. Combining the noise robustness of the local Lucas/Kanade technique [30] with a global smoothness constraint from the Horn/Schunck model [26], this approach forms an ideal basis for our evaluations. From a theoretical point of view, it provides a sound mathematical description of the problem as a continuous optimisation problem and thanks to the global smoothness constraint, it yields dense flow fields as well. However, also from a technical standpoint, this model can be regarded as ideal, because it combines accuracy on the one hand with a moderate computational complexity on the other hand. Many novel approaches, such as the highly accurate optic flow approach by Brox et al. [7], still require to solve huge but sparse linear or nonlinear systems of equations and extend the CLG method by additional concepts, such as better data terms or an improved handling of large displacements by warping strategies. The runtime performance of a parallel implementation of this CLG model can thus be expected to be representative for many other algorithms of this kind, and will allow justified predictions for speedups achievable with other variational optic flow approaches being adapted to the Cell Processor.

2.1 Variational model

Given a rectangular image domain $\Upomega \subset \ensuremath{{\mathbb{R}}}^2,$ let f(x, y, t) be a grey value image sequence with (x, y) ∈ Ω denoting the location and $t \in \ensuremath{{\mathbb{R}}}^+_0$ specifying the time. We then define $f_{\sigma } (x,y,t): = K_{\sigma } * f(x,y,t)$ to be the spatially presmoothed counterpart to f, which is obtained by a convolution with a Gaussian K _σ of standard deviation σ. This preprocessing step yields a first robustification of the model against high frequent perturbations.

The 2D CLG method then computes the optic flow ${\user2{w}}(x,y) := (u(x,y),v(x,y),1)^\top$ as minimiser of the global energy functional [10]:

$$ E(u, v) = E_{\text{D}} (u,v) + \alpha E_{\text{S}}(u,v). $$

(1)

The data term E _D(u,v) penalises deviations from the grey value constancy assumption. This means that it steers the model towards a solution in which objects are assumed not to change their grey value throughout the image sequence. As it turns out, this constraint performs well to estimate the so-called normal flow, i.e. the optic flow component parallel to the image gradient. In any region of the image where the displacement direction does not coincide with the gradient or where the gradient vanishes, the optic flow, however, cannot be accurately estimated only using the data term. This is also known as the aperture problem. As a remedy, the smoothness term E _S(u,v) is employed that propagates neighbourhood information into locations with insufficient data. Due to this filling-in effect, the solution found by the model is a dense optic flow field with smoothed transitions at boundaries. The regularisation parameter α is used to steer the influence of the smoothness term on the model, thus creating a balance between smoothness of the solution and sharp discontinuities at the boundaries of moving objects.

Depending on the choice of the data and smoothness terms, we discriminate in the following between two concrete variants of this model: a linear and a nonlinear version.

2.2 Linear CLG model

The linear CLG model is a simple instance of the variational approach described above. In this method, the data and smoothness terms are given by the quadratic expressions:

$$ E_{\text{LD}}(u,v) := \int_\Upomega({\user2{w}}^\top J_{\rho}(\nabla_{3} f_\sigma) {\user2{w}})\,{\text{d}}x\,{\text{d}}y, $$

(2)

$$ E_{\text{LS}}(u,v) := \int_\Upomega(| \nabla u |^2 + |\nabla v |^2)\,{\text{d}}x\,{\text{d}}y, $$

(3)

where $\nabla = \left({\frac {\partial}{\partial x}},{\frac {\partial}{\partial y}} \right)^\top$ and $\nabla_{3} = \left({\frac{\partial}{\partial x}}, {\frac{\partial}{\partial y}}, {\frac{\partial}{\partial t}} \right)^\top$ denote the spatial and spatiotemporal gradients, respectively. In this context,

$$ J_\rho(\nabla_{3} f_\sigma) := K_{\rho} * ( \nabla_{3} f_\sigma \; \nabla_{3} f_\sigma^\top ) $$

(4)

represents the motion tensor whose channels have been spatially convolved using a Gaussian kernel K _ρ of standard deviation ρ. Note that since we use the linearised grey value constancy assumption [11], the motion tensor equals the structure tensor. As we shall see in Sect. 3, minimising a quadratic energy functional leads to a linear problem.

2.3 Nonlinear CLG model

The linear model from Sect. 2.2 already provides a good flow field quality, but does not pay attention to discontinuities in the flow field. Because of the homogeneous smoothness assumption, edges always appear blurred, and outliers in the data term are not treated in a robust manner.

To enhance these results considerably, Bruhn et al. [10] suggested to apply an isotropic flow-driven regulariser based on a subquadratic penaliser function as smoothness term as well as to robustify the data term using the same non-quadratic penaliser function. By making discontinuities more attractive, it is hence possible to benefit from the filling-in effect of the smoothness term while still obtaining sharp edges at object boundaries, and the penaliser on the data term weights down outliers in the input data. Unlike this original method, which uses the function introduced by Charbonnier et al. [14], we follow the idea from Brox et al. [7] and employ a penaliser function minimising the L ¹ distance:

$$ \psi(s^2) = \sqrt{s^2 + \varepsilon^2}. $$

(5)

This comes down to a regularised total variation (TV) penaliser in the smoothness term [35]. Here, ɛ is a numerical parameter ensuring the strict convexity of the function. For our experiments, we use ɛ_ND = 0.1 for the data term and ɛ_NS = 0.001 for the smoothness term, thereby obtaining ψ_ND and ψ_NS. The effect of these functions can best be observed during the minimisation process which is covered in the next section.

Using the notation from Sect. 2.2, we instantiate (1) by a non-quadratic penalisation of data and smoothness terms E _ND and E _NS, respectively, obtaining

$$ E_{\text{ND}}(u,v) := \int_\Upomega (\psi_{\text{ND}}({\user2{w}}^\top J_{\rho}(\nabla_{3} f_\sigma) {\user2{w}}))\,{\text{d}}x\,{\text{d}}y, $$

(6)

$$ E_{\text{NS}}(u,v) := \int_\Upomega(\psi_{\text{NS}} (| \nabla u |^2 + |\nabla v|^2))\,{\text{d}}x\,{\text{d}}y. $$

(7)

By design, both ψ_ND and ψ_NS depend on the current flow field ${\user2{w}},$ making the model nonlinear. As a consequence, we will need a different technique for solving the resulting equation system than in the linear case, as we will see in Sect. 3.

2.4 Minimisation

2.4.1 Linear setting

The energy functional E(u, v) from (1) can be minimised by solving its Euler–Lagrange equations [19]:

$$ 0 = \Updelta u - {\frac{1}{\alpha}} (J_{\rho,{11}}u + J_{\rho,{12}}v + J_{\rho,{13}}), $$

(8)

$$ 0 = \Updelta v - {\frac{1}{\alpha}}(J_{\rho,{12}} u + J_{\rho,{22}} v + J_{\rho,{23}}), $$

(9)

with reflecting Neumann boundary conditions

$$ 0 = {\user2{n}}^\top \nabla u\quad\hbox{and}\quad 0 = {\user2{n}}^\top \nabla v. $$

(10)

J_ρ,nm denotes the corresponding entry (n, m) of the convolved motion tensor J_ρ(∇₃f_σ), Δ is the Laplacian given by

$$ \Updelta u := \partial_{xx} u + \partial_{yy} u, $$

(11)

and ${\user2{n}}$ describes the normal vector orthogonal to the image boundary in the regarded point.

2.4.2 Nonlinear setting

For the nonlinear model, the Euler–Lagrange equations also include the derivatives of the penalisers for data and smoothness terms:

$$ 0 = \hbox{div}(\psi^{\prime}_{\text{s}} \nabla u) - {\frac{\psi^{\prime}_{\text{d}}}{\alpha}} (J_{\rho,{11}} u + J_{\rho,{12}} v + J_{\rho,{13}}), $$

(12)

$$ 0 = \hbox{div}(\psi^{\prime}_{\text{s}} \nabla v) - {\frac{\psi^{\prime}_{\text{d}}}{\alpha}} (J_{\rho,{12}} u + J_{\rho,{22}} v + J_{\rho,{23}}), $$

(13)

with the abbreviations

$$ \psi^{\prime}_{\text{s}} := \psi^{\prime}_{\text{NS}}(|\nabla u|^2 + |\nabla v|^2), $$

(14)

$$ \psi^{\prime}_{\text{d}} := \psi^{\prime}_{\text{ND}}({\user2{w}}^\top J {\user2{w}}), $$

(15)

and $\psi^{\prime}_{\text{NS}}$, $\psi^{\prime}_{\text{ND}}$ denoting the first derivatives of ψ_NS, ψ_ND with respect to their argument, respectively. Using the notation from (5), one obtains a function of the form

$$ \psi^{\prime} (s^2) ={\frac {1}{2 \sqrt{s^2 + \varepsilon^2}}}, $$

(16)

which is strictly decreasing. This leads to the effect that for outliers in the data term, $\psi^{\prime}_{\text{d}}$ becomes very small, thereby causing the smoothness term to fill in reliable information from the neighbourhood instead. A similar effect can be observed near edges, which occur as ‘outliers’ in the smoothness term. Here, $\psi^{\prime}_{\text{s}}$ becomes minimal, and thus prevents smoothing across these edges.

Like for the linear case, we again obtain reflecting boundary conditions as in (10).

2.5 Discretisation

For (8), (9) and (12), (13) to be solved numerically, they need to be suitably discretised with respect to a grid of size N _x  × N _y using a cell spacing of h _x  × h _y .

Choosing N _x and N _y to coincide with the input frame dimensions, those images as well as the resulting flow field frames are just sampled at the respective grid points (i, j) ∈ [1, N _x ] × [1, N _y ]. Spatial derivatives with respect to this grid are realised by a fourth-order finite difference scheme evaluated in between the two regarded frames, whereas temporal derivatives are in contrast approximated by simple two-point stencils [8]. Products of either of these types can then be used to assemble the discrete motion tensor entries [J _ρ,nm ]_i,j. Likewise, continuous convolutions can just be mapped to their discrete counterparts, therefore sampling the Gaussian kernel at an equally spaced grid and truncating it to a precision of three times the standard deviation.

If we now decompose the four-neighbourhood of pixel (i, j) according to the parts aligned to axis l ∈ {x, y}, we can denote them as ${{\mathcal{N}}}_l(i,j)$ and finally write down the discretised versions of (8) and (9), respectively:

$$ \begin{aligned} 0 &= [J_{\rho,{11}}]_{i,j} u_{i,j} + [J_{\rho,{12}}]_{i,j} v_{i,j} + [J_{\rho,{13}}]_{i,j}\\ &- \alpha \sum_{l\in\{x,y\}}\sum_{(m,n) \in {{\mathcal{N}}}_l (i,j)} {\frac{u_{m,n} - u_{i,j}}{h_l^2}} \end{aligned} $$

(17)

$$ \begin{aligned} 0 &= [J_{\rho,{12}}]_{i,j} u_{i,j} + [J_{\rho,{22}}]_{i,j} v_{i,j} + [J_{\rho,{23}}]_{i,j}\\ &- \alpha \sum_{l\in\{x,y\}}\sum_{(m,n) \in {{\mathcal{N}}}_l (i,j)} {\frac{v_{m,n} - v_{i,j}}{h_l^2}} \end{aligned} $$

(18)

In the nonlinear case, we pursue essentially the same discretisation strategy as before, but insert the discretised variants of the multiplicative penalisation factors from (12) and (13). While $\psi^{\prime}_{\text{d}}$ can immediately be evaluated at the sampled components [J]_i,j and $(u,v)^\top_{i,j}$ , we need to specify a derivative approximation scheme for the argument to the smoothness term weight $\psi^{\prime}_{\text{s}}$. In this context, we use a first-order finite difference scheme and evaluate the function at the grid points, as proposed by Bruhn et al. [10]. With this strategy, we finally obtain the discrete Euler–Lagrange equations as

$$ \begin{aligned} 0 &= [\psi^{\prime}_{\text{d}}]_{i,j} ([J_{\rho,{11}}]_{i,j} u_{i,j} + [J_{\rho,{12}}]_{i,j} v_{i,j} + [J_{\rho,{13}}]_{i,j})\\ &- \alpha \sum_{l\in\{x,y\}}\sum_{(m,n) \in {{\mathcal{N}}}_l (i,j)} {\frac{[\psi^{\prime}_{\text{s}}]_{m,n} + [\psi^{\prime}_{\text{s}}]_{i,j}}{2}}\,{\frac{u_{m,n} - u_{i,j}}{h_l^2}}, \end{aligned} $$

(19)

$$ \begin{aligned} 0 &= [\psi^{\prime}_{\text{d}}]_{i,j} ([J_{\rho,{12}}]_{i,j} u_{i,j} + [J_{\rho,{22}}]_{i,j} v_{i,j} +[J_{\rho,{23}}]_{i,j})\\ &- \alpha \sum_{l\in\{x,y\}}\sum_{(m,n) \in {{\mathcal{N}}}_l (i,j)} {\frac{[\psi^{\prime}_{\text{s}}]_{m,n} + [\psi^{\prime}_{\text{s}}]_{i,j}}{2}} \,{\frac{v_{m,n} - v_{i,j}}{h_l^2}}. \end{aligned} $$

(20)

Note that for a the special case of a quadratic penaliser ψ(s ²) = s ², and thus $\psi^{\prime}_{\text{s}} = \psi^{\prime}_{\text{d}} = 1$, these equations come down to those of the linear case, as seen in (17) and (18).

Equations (19) and (20) can be immediately solved in a numerical way, but since the resulting linear system of equations involves 2N _x N _y unknowns u _i,j and v _i,j, storing the whole matrix is costly. In particular, the restricted RAM dimensioning of the PlayStation 3 does not even allow to process images of reasonable size using a canonical representation.

2.6 Memory representation

Instead, this system matrix turns out to be sparse: The non-trivial entries are just appearing in diagonals describing the relation of u and v in a specific pixel, or the communication of either of these directional flow field components in one pixel with its four-neighbourhood.

Hence, it is sufficient to store only these diagonal entries, and we are in particular aligning them in a grid corresponding to their location of impact within the image domain. This breaks all computations down to simple stencil operations, and also minimises computational overhead, since only non-trivial operations are issued on this dataset. Without loss of generality, we group the values in a Fortran-style column-major order in memory, as we do it for the input frames and the output flow fields.

3 Efficient numerics

For our experiments on the Cell platform, we apply two of the fastest numerical solvers currently available. So-called multigrid strategies, developed in the 1960s and improved in the late 1970s [5, 6, 24], have gained high popularity in the field of visual computing [8, 22, 44]. In particular, Bruhn et al. [8, 11] showed that this solver is even able to accelerate optic flow algorithms to real-time performance on standard PC hardware.

A basic observation motivating the development of these multigrid techniques is the decay behaviour of different error frequencies using traditional solvers. While high frequent errors diminish after a very little number of iterations, low frequent errors remain significantly longer. With respect to a coarser grid, however, these errors reappear with a higher frequency, and can thus be eliminated much faster.

Since one of the regarded problems is of linear type while the other is not, we developed two different solvers, each of which is using the specialities of the respective underlying problems.

3.1 Linear full multigrid scheme

First, we turn to the linear CLG method described in Sect. 2.2. Our solver for the resulting Euler–Lagrange equations depicted in (8) and (9) is the so-called linear full multigrid strategy.

This strategy is based on corrections from coarser grids that are used to improve the immediate solution on a fine grid. The underlying two grid algorithm for the solution of an equation system

$$ A^h x^h = b^h $$

(21)

with linear operator A ^h and right-hand side b ^h on the fine grid h consists of four important stages [6, 8, 38]:

• 1. First, high frequent errors are eliminated applying η₁ presmoothing relaxation steps using a traditional iterative solver.

• 2. The residual system $A^h e^h = b^h - A^h \bar{x}^h, \bar{x}^h$ being the solution from step 1 is then transferred to a coarser grid H. This equation is obtained by a restriction of both the linear operator and the right-hand side, and solved for the error term e ^H. The most efficient way to do so is to use even coarser grids, i.e. to apply the method recursively. To perform transitions between the different grids, prolongation and restriction operators P and R, respectively, need to be defined. In this context, we use an area-based resampling approach as described by Bruhn et al. [8].

• 3. Back on the finer grid, the preliminary solution $\bar{x}^h$ from step 1 is corrected by the (prolongated) error term e ^h obtained in step 2.

• 4. To compensate for high frequent errors introduced during the coarse grid correction, the iterative solver from step 1 is again applied for η₂ post-relaxation steps.

If one recursive call is performed during step 2, this is called a V cycle. The whole run is then abbreviated with the notation V(η₁, η₂).

In our concrete implementation, we apply a Jacobi relaxation during steps 1 and 4. On the finest scale, this solver is given by the equations:

$$ u_{i,j}^{k+1} = {\frac{[J_{\rho,13}]_{i,j} +[J_{\rho,12}]_{i,j} v_{i,j}^k - \alpha \sum\limits_{l \in \{x,y\}} \sum\limits_{(m,n) \in {{\mathcal{N}}}_l(i,j)} {\frac{u^k_{m,n}}{h_l^2}}} {- [J_{\rho,11}]_{i,j} - \alpha \sum\limits_{l \in \{x,y\}} \sum\limits_{(m,n) \in {{\mathcal{N}}}_l (i,j)} {\frac{1}{h_l^2}}}}, $$

(22)

$$ v_{i,j}^{k+1} = {\frac{[J_{\rho,23}]_{i,j} +[J_{\rho,12}]_{i,j} u_{i,j}^k - \alpha \sum\limits_{l \in \{x,y\}} \sum\limits_{(m,n) \in {{\mathcal{N}}}_l(i,j)} {\frac{v^k_{m,n}}{h_l^2}}} {- [J_{\rho,22}]_{i,j} - \alpha \sum\limits_{l \in \{x,y\}} \sum\limits_{(m,n) \in {{\mathcal{N}}}_l (i,j)} {\frac{1}{h_l^2}}}} , $$

(23)

with u ⁰ = v ⁰ = 0. Here, $u_{i,j}^k$ describes the solution u in the grid point (i, j) at time step k, and ${{\mathcal{N}}}_l (i,j)$ denotes the four-neighbourhood around point (i, j). Note that due to being constant over the course of the computations, $[J_{\rho,13}]_{i,j}$ and $[J_{\rho,23}]_{i,j}$ represent the right-hand side of the equation system. By construction of the multigrid correction cycle, their position on the coarser grids is hence taken by the new respective right-hand sides, which are in fact the restricted residuals from the finer stage.

The full multigrid scheme now extends this correction idea by a coarse-to-fine strategy, i.e. the problem is first solved on the coarsest grid, and the solution is then used as an initialisation for the computation on the next finer grid. By construction, this scheme already dampens the global error tremendously, such that for the multigrid recursion steps involved, rather little effort is necessary. The coarser grids can be chosen in such a way that they always contain about half as many sampling points in either dimension than those on the next finer grid. As a consequence, very few relaxations on the respective layers are already sufficient to let the method converge to the desired solution.

3.2 Nonlinear full approximation scheme (FAS)

Secondly, we turn our attention to the nonlinear multigrid solver, the so-called FAS [6], for equations of type

$$ A^h(x^h) = b^h. $$

(24)

The idea behind this approach is different to the linear setting, since there is no longer a single compulsory notion of the nonlinear operator A ^h(x ^h) for the whole run of the solver available, but instead this operator needs to be evaluated against the most current version of the solution: This follows the concept of lagged nonlinearities [18].

Therefore, it is necessary to find a suitable coarse grid representation for the initial problem, instead of regarding its residual equation only, and to project the error compensation back to the fine grid. This works as follows:

• 1. Like in the linear setting, we first apply η₁ iterative relaxation steps using a Jacobi solver with lagged nonlinearities.

• 2. Similar to before, we compute the residual r ^h = b ^h − A ^h(x ^h) and restrict it to the coarse level. In addition, we restrict the preliminary solution $\bar{x}^h$ and use it to evaluate the nonlinear operator $A^H(R\bar{x}^h).$ Using $R\bar{x}^h$ as an initialisation for x ^H, we denote the coarse grid system by

  $$ A^H(x^H) = Rr^h + A^H(R\bar{x}^h). $$

  (25)

  Similar to before, we use area-based resampling to describe the prolongation and restriction operators P and R.

• 3. After recursion, we compute the amount of change applied to each grid location within the new intermediate solution, $\bar{x}^H,$ compared to the initialisation $R\bar{x}^h,$ prolongate this difference, and add it to the previous fine grid solution to compensate for lower frequent errors:

  $$ \bar{x}^h \leftarrow \bar{x}^h + P(\bar{x}^H - R\bar{x}^h) $$

  (26)

• 4. Since the coarse grid correction introduces new high frequent error terms, we finally perform η₂ relaxation steps using the iterative solver from step 1.

Analogous to Sect. 3.1, we use the notation V(η₁, η₂).

Before addressing the hardware-related adaptations and optimisations as well as implementational details, we will first have a look on the special characteristics of the underlying hardware platform. For more details, we refer the reader to [9, 38].

4 The Cell Processor

The Cell Broadband Engine processor is an asymmetric multi-core shared memory unit. It consists of one general purpose core, the PPU, which is supplied with eight stream processor cores, the SPUs, out of which six are available on the PlayStation 3 [3].

Resembling a POWER architecture, the PPU is instruction set compatible to existing platforms implementing this design. In the context of the Cell Processor, it is mainly used to execute the operating system, whereas parallel special-purpose tasks are executed by the SPUs instead. Here, the PPU acts also as an arbiter and resource manager between the single SPU kernels, and regulates the global programme flow and system interaction.

The SPUs in contrast are more focussed towards high performance applications, though they still offer a broad range of functions, such that they can still be seen as general purpose units. To unveil their full potential and to make them interact with the global programme, however, they need to be explicitly addressed using so-called intrinsics [37]. Those instructions extend the C programming language and describe macros to dedicated assembly code structures which cannot be automatically modelled by standard compilers. Meanwhile, the kernel code remains formally designed in a high-level language, such that compiler optimisations can still be applied to a certain degree.

For a higher data throughput for massively parallel computations, the SPUs work on a native pipeline bandwidth of 128 bits. This follows the concept of the single instruction multiple data (SIMD) pattern [17]. Vectors of four single precision floating point values are processed parallel as long as they are all subject to the same operation and aligned to a memory address of a multiple of four. However, this construction does not make loop unrolling strategies obsolete, since pipeline latencies still require a sufficiently high number of independent instructions to be scheduled in an interleaving manner [37].

Sometimes, the power of the intrinsics does not suffice to formulate particular operations in a fully optimised manner. This is for instance the case if bit operations are to be issued on SIMD vector-valued data. However, the programmer can still resort to assembly instructions, such that many optimisation tricks known from traditional hardware can still be applied.

To profit from data locality while still being situated in a complex distributed application setup, the SPUs are equipped with unmanaged caches, each 256 kB of size. As a consequence, those Local Stores are not automatically synchronised with the global memory, but need to be explicitly filled by the application developer by means of direct memory access (DMA) operations. This grants a high amount of freedom and predictability for time critical applications, but comes along with an associated responsibility for any data synchronisation between the RAM on the one hand and the working copies of the SPUs on the other hand. Fortunately, however, the memory flow controllers are designed to work independently from the core, such that DMA operations and arithmetics can be executed independently from each other.

Being issued via the ring-bus chaining the single cores together, such external memory requests finally converge in one single Memory Interface Controller, which provides a peak memory bandwidth of 25.6 GB/s [27]. In practice, it turns out that this component still describes a critical bottleneck for real-time applications that has to be respected during software development. However, each memory flow controller for an SPU can run independently from the actual core, such that latencies on this side do not necessarily affect the overall performance of the algorithm.

Another critical aspect of this novel chip is the lack of a dynamic branch prediction circuit. Despite for simple examples, where compile time evaluations can already yield reasonable results, high misprediction penalties of 18 cycles are likely to be issued [27]. Therefore, branching should be entirely avoided whenever no reliable branch hint can be set at development time, and where alternative solutions are in average faster than the branching variant.

Taking these observations together, several challenges need to be mastered in order to exhaust the full potential of this novel processor and to write extraordinary fast algorithms:

• 1. They must be adapted to the distributed setup, such that all cores are equally charged. Inter-core dependencies for the global problem must hereby be fulfilled using synchronisation messages.

• 2. Their local structure should match the vector processing style of the single cores. Branching should be avoided wherever possible, and loop unrolling strategies furthermore help to exploit both pipelines.

• 3. Memory exchanges need to be issued in time and under use of data locality, where possible. Bursts to the memory flow controller should meanwhile be reduced to a minimum.

In the following sections, we go more into detail about these issues.

5 Memory level parallelisation concepts

5.1 Distribution to the processor cores

A crucial aspect for the successful acceleration of the algorithm using the modern Cell architecture is a good parallelisation strategy. At this point, traditional methods often rely on domain splitting schemes. The image domain is split into regions of about equal size which are henceforth assigned to single cores. These strategies are indeed successful when it comes to iterative solvers [23], but it unfortunately turns out that they are much less suited for our non-data parallel problems computed with multigrid solvers.

Working on a shared memory architecture, boundaries between areas processed by different cores need to be protected by a semaphore system to ensure the integrity of the data. Being frequently synchronised by such system, the cores are tied into a perfectly parallel schedule, thereby performing similar tasks at exactly the same time. While this state is desirable from a theoretical point of view, it is entirely impractical in context of the high data throughput involved. Bursty access to the Memory Interface Controller causes bus contentions, and involved memory delays reduce the overall frame rate significantly.

Another disadvantage of domain splitting approaches is the fluctuating size of the processed grids within a multigrid algorithm. For smaller representations, splits are more costly than processing a whole small area by one single core. Hence, the success or failure of such a strategy strongly depends on a suitable heuristics defining when and where to split and how to distribute the resulting areas to the available cores, which creates an additional computational overhead to the problem. Even more important, several cores are meant to be idle for meaningful periods of time this way, thereby furthermore decreasing the overall performance.

As a remedy, the problem should not be divided spatially, but in a temporal manner. Since a splitting of the algorithm into stages and implementation of a distributed processing pipeline [27] does not match the structure of the solver nicely as well, we decided to shift this splitting to a macroscopic level. A typical application scenario for optic flow computation requires a whole video stream, often gathered from an external camera device, to be transcoded into optic flow information in real-time. It is hence feasible to process whole frames on single cores, where the respective where kernels optimised for single processor performance can run locally and without any interference with other cores. In particular, memory requests are expected to occur offset in time, thus ensuring rather homogeneous traffic amounts on the memory bus. Meanwhile, our method provides at least the same data throughput as any other strategy, by potentially accepting a slightly higher per-frame latency.

In our concrete implementation, we start the SPU kernels only once together with the main programme, which saves initialisation time during the further programme run. The kernels then only pick up incoming frames from the input queue, and place their results into the output queue. In contrast, the PPU does not perform any computations in this respect, but takes care of input and output managements as well as of message passing between the cores.

5.2 Synchronisation

Thanks to our chosen parallelisation strategy, there is no need to enforce a strict synchronisation among the cores. However, since all frames are of equal size, the computation on any core is expected to take about as long as on any other, which allows for an optimisation by avoiding redundancies in the computations.

Both input frames needed to compute one flow frame are to be presmoothed by a convolution with a Gaussian kernel of standard deviation σ (cf. Sect. 2). Since one frame always occurs in context of two flow fields, it only needs to be presmoothed once by one SPU, and the one computing the next flow field can already access this data. Therefore, we establish a linear order of assignments of frame pairs to processor cores, and ensure furthermore that the regarded presmoothed frame is already entirely processed by the predecessing SPU.

5.3 Caching

Because of the missing cache hierarchy and the meagre extent of the Local Stores, an evolved strategy is needed to reduce memory latencies to a minimum. Besides a sufficiently early fetch of relevant data and a back-synchronisation to RAM, data should also be held in cache as long as possible, if this saves external memory requests.

For the present implementation, we split the code into dedicated memory management functions on the one hand and procedures containing the actual algorithm computing the problem on the other hand. The memory-related functions are thereby responsible for the DMA transfers between RAM and the Local Store of the respective SPU, and hide memory latencies by active use of the double buffering technique. Here, not only a current working copy of the global memory is represented in the cache, but also several instances thereof exist simultaneously. While one of those vectors is processed by the algorithm, the others can already be filled with data for the next time step, or can be read out to the main memory if they contain newly computed data from a previous iteration. For stencil-based operations, like they are frequently performed by our algorithm, this concept involves ring buffers of sufficient size, and data can automatically be reused without any additional requests to the RAM.

All such operations are thereby performed on memory lines of fixed size, which coincide with the columns in the rectangular image domain Ω. Though dependent on the actual size of the input frames, this dimensioning has proved to be a good estimate to keep the algorithm as general as possible and thereby to reduce branching to a minimum, while still maintaining memory blocks of reasonable size to hide latencies behind computations. Meanwhile, by processing an image from left to right, a whole neighbourhood can stay cached, which causes each date only to be transferred once per operation.

Note that this property is not universally valid for arbitrary partitions. A size-independent structure of fixed-size tiles for instance, which is desirable for larger image sizes, does in general not offer this opportunity and requires at least data along the inner boundaries to be synchronised multiple times during an operation. This, in turn, would make the algorithms strongly depending on the chosen tile size, and requires in particular a non-canonical ordering of data in the memory.

In order to know which memory line is to be fetched next, our functions are equipped with a prediction logic, which is in particular important during presmoothing convolution steps and on image or partition boundaries. Here, the access pattern is no longer linear and requires hence a more evolved strategy.

Throughout the design of our algorithm, the lifetime of cached variables is a crucial aspect for a high performance. While a sufficient cache validity can be trivially established by construction for many values involved in the process, others need a more detailed examination and planning.

Due to discretisation, our algorithm strongly depends on frequent stencil operations. Sometimes, like for the computation of the nonlinear weight $\psi^{\prime}_{\text{s}}$, several operations of such type are even dependent on each other. This situation, however, bears a severe performance threat. While intermediate results do usually not need to be written back to RAM by processing a whole pipeline of operations upon one pixel and writing back only the final result, the lack of data locality makes a similar approach non-trivial for dependent stencil operations.

One approach to this problem is to expand the single steps to one large stencil operation, and thus to make the final result immediately depend on the input data. This way, however, many redundancies in the computations are implicitly involved.

Instead, we maintain the initial structure of many small stencils, but maintain a spatial offset amongst them to satisfy data dependencies. Thereby, all intermediate values can still be kept entirely cached, only an essential minimum of intermediate data is synchronised with the RAM, and requests to the Memory Interface Controller are reduced to a minimum.

Still, this advantage is bought with a more complicated special case handling at image boundaries, since the different offset operation steps will reach boundary locations to different points in time. Thanks to our memory management functions, however, this drawback is handled in a both elegant and well-performing manner.

6 Instruction level parallelisation concepts

6.1 Convolutions

Most of the setup phase for the equation system is dominated by convolution operations for derivative approximations and presmoothing. Because those are usually of high computational complexity, they deserve further attention with respect to their implementation on the Cell platform.

Thanks to their separability, the problem can be decomposed into axis-aligned components, which are then processed apart from each other. One of those operations is hereby following the major memory direction, while the remaining one is just perpendicularly oriented. In other words, while the first of both operations applies a convolution mask to a coherent memory block, the latter one connects remote memory cells, and renders in return neighbouring cells independent from each other.

Consequently, we designed two different approaches. On the one hand, we use a scalar implementation for the version alongside the memory direction, and perform any of those steps for four columns in parallel to hide pipeline latencies. Since the convolution kernel size is usually unknown, working on misaligned vectors is quite expensive, and branching is costly as well, this solution turned out to perform better than a vector-based version. Reflecting Neumann boundaries are thereby physically established, i.e. after DMA load into a sufficiently large cache representation, data are first extended by the respective boundary pixels, and afterwards fed into the algorithm.

On the other hand, we exploit the full SIMD resources for convolutions in the perpendicular direction, since vectors are internally independent and can thus be treated as atomary elements. By processing the data on a per-column basis, we can reduce the total number of DMA transactions to a minimum, and are furthermore able to hide pipeline latencies. A loop unrolling scheme over four such SIMD vectors of one column provides enough independent operations to be scheduled by the compiler. Reflecting boundary conditions do not need to be considered in a per-value sense at all. The memory management function already keeps track of these special cases and fetches vectors from the respective locations within the image domain, which it declares to be boundary values. Particularly for small convolution kernels, this also causes the first vectors of the image domain itself to be already cached from before, such that this operation in general only generates marginal overhead and is thus way faster than a version based on copying.

6.2 Boundary handling

As soon as a fully data parallel operation alongside the major memory order is performed, the mandatory manual caching of data (cf. Sect. 5.3) has another advantage. To establish SIMD-based processing, loop unrolling, or both, it is often advantageous to have vectors of a certain length and alignment. For typical image sizes, these requirements are seldomly met, such that a dedicated boundary handling on a scalar basis and under application of branching would be necessary. Especially on small problem representations in the multigrid pyramid, however, this fact would significantly reduce the overall performance of the algorithm. Instead, we allow the locally cached variant of all vectors to be not fully consistent in length to their RAM counterparts, but pad them to a sufficient degree.

In our concrete setting, this modification grants a fully SIMD-based processing order on all stages, including the boundary elements. This means, we can process (valid) inner pixels and boundary elements as well as (invalid) padding values without discrimination. For a simplification of the smoothness term notation, we maintain a 1 pixel zero frame around the image domain, which then implicitly treats boundary cases in the correct way. Once invalidated by a SIMD operation across the boundary, these values can easily be re-established, namely by one single scalar write operation. In particular, there is no need to introduce branching, neither for loop unrolling purposes nor for SIMD processing, such that we do not suffer from high branch miss penalties. The additionally processed elements do not also deteriorate the runtime performance, since the operations either come for free, like for the SIMD application, or they are hidden by being scheduled into the processing pipelines instead of using idle instructions (NOP). Thanks to these benefits, we make active use of this technique throughout our implementation.

6.3 Binary optimisations

Since the SPU kernels are only loaded onto their target cores once and they remain online for the rest of the programme run, it is worthwhile to have them optimised for a high throughput rather than for small binary sizes. So, we compiled our programmes with an increased threshold for function inlining, such that DMA management functions can be closer scheduled with arithmetic operations, and latencies are thus more efficiently reused.

7 Experimental results

In the following, we evaluate the runtime performance of our algorithms on the Cell Processor of a PlayStation 3. To this end, we use frames 8 and 9 of the popular Yosemite sequence created by Lynn Quam as well as frames 22 and 23 from the famous Ettlinger Tor sequence by Kollnig et al. [28], to benchmark the runtime performance of our developed algorithms.

One should note at this point that our methods implement the nonlinear and linear CLG variants proposed by Bruhn et al. [10, 11] without restrictions, such that we obtain the same error measures. In the nonlinear case, however, we additionally propose a fair tradeoff between quality and speed, and evaluate our implementations against this modified parameter configuration.

To provide an intuitive measure for the obtained timing results, we denote them in terms of the achieved FPS count. The timing has in all cases been issued over a whole programme run, and thus covers both the preliminary setup of the equation system as well as the solver itself. Meanwhile, we exclude real one-off expenses from the measurements, which are for instance related to an upload of the programme kernels to the computing cores or their first initialisation.

Since presmoothing convolutions are in the first place used to make the system more robust with respect to noise and the amount of presmoothing is hence strictly dependent on the input data, we always present two measurements. One characterises the peak performance without any additional presmoothing applied. The other, in contrast, shows the performance for the same algorithm with additional presmoothing of significant extent, as it is necessary to achieve a good visual quality.

7.1 Scaling over varying SPU counts

In a first experiment, we measure the runtime performance of our algorithm over an varying number of participating SPUs. In the ideal case, one would expect a linear increase in the performance depending on the SPU count, but this theoretical estimate is in practice often significantly deteriorated. Concurrent requests to the Memory Interface Controller and the Element Interconnect Bus cause higher memory latencies, and the SPU kernels will thus be stalled as long as the data dependencies cannot be met.

7.1.1 Linear setting

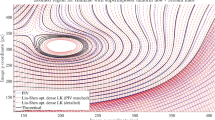
Table 1 and Fig. 1 show the results of this experiment. We obtain 81.4 FPS on frames 8 and 9 of the original Yosemite sequence (with cloud motion in the sky) to obtain the minimal average angular error (AAE) of 7.14°. The visual quality of the flow fields created by our algorithm is hereby depicted in Fig. 2. Here, we use a colour coding representing the direction like depicted in the frame of the flow fields, and the magnitude given by the intensity: The brighter a pixel, the higher is the corresponding flow magnitude. In literature, there exist other visualisation techniques such as arrow plots [26], but their resolution is very low which in turn renders them less suitable to show advantages or disadvantages of an algorithm. For a better understanding of our coding, we refer the reader to the colour circle plot with vector overlay depicted in Fig. 2.

Table 1 SPU scaling on linear full multigrid cycles with presmoothing of σ = 1.3, ρ = 2.3 (ps), and the peak performance without (no), on “Yosemite” 316 × 252

Fig. 1

SPU scaling on linear full multigrid cycles with presmoothing of σ = 1.3,  ρ = 2.3 (ps), and the peak performance without (no), in FPS on “Yosemite” 316 × 252

Fig. 2

Visual quality of the linear (bottom left) and the nonlinear (bottom middle) CLG method, colour-coded. The input images, frames 8 and 9 of the Yosemite sequence, are depicted in the upper row, respectively. The circle (bottom right) depicts the used colour coding and is overlaid with vectors indicating the corresponding direction and magnitude

On the modified Yosemite sequence without clouds provided by Black et al. on http://www.cs.brown.edu/∼black/images.html, our algorithm provides results with an AAE of 2.63°, which is the same value Bruhn et al. describe in [8]. Thereby, we outperform an optimised sequential multigrid code using their suggested pointwise-coupled Gauß-Seidel relaxation step and running on a Pentium 4 3.2 GHz by more than a factor of 6.5 in runtime.

In this context, we choose V(2, 1) cycles, since they let the solver already fairly well converge. We compared this preliminary solution ${\user2{w}}_{\text{p}}$ to the fully converged solution ${\user2{w}}_{\text{c}}$ using the same parameter set. To this extent, we compute the quotient of the L ² norms of the error and the converged solution as a relative convergence error:

$$ e_{\text{rc}} := {\frac{||{\user2{w}}_{\text{p}} - {\user2{w}_{\text{c}}||_2}}{||{\user2{w}}_{\text{c}}||_2}} $$

(27)

For our V(2, 1) cycles, we obtain errors below 1 × 10⁻², which proves that our obtained solution is indeed very close at the best result achievable with the method. Consequently, the AAE is already as low as 7.14°.

If we disregard both the presmoothing of the input frames by standard deviation σ for a moment as well as the local integration scale ρ, but still perform the pure solver step as before, we can measure a peak performance of almost 210 FPS. This means, depending on the characteristics of the sequence and the related presmoothing requirements, even much higher performance rates can be expected.

Observing the increase of the total frame rate, however, we note a damping effect towards a higher SPU number, which is reflected in a sub-linear increase in the performance. This effect is not visible in this extent when we use pointwise-coupled Gauß-Seidel relaxations formulated in a scalar manner [23]. By profiling, we see that there is indeed time lost during the relaxation steps. We conclude that the much shorter runtime of our parallel Jacobi steps, in combination with the almost identical memory bus load per run, finally leads to a contention of the Memory Interface Controller. Since the resulting time gap cannot be hidden by means of double buffering anymore, the SPUs waiting for the next memory line run into a stall, which is immediately reflected in the performance. Nevertheless, this new approach is still significantly faster than our previous sequential notation, and is thus fully justified to be used.

7.1.2 Nonlinear setting

Since our nonlinear method converges much slower than the linear variant, we need to apply significantly more solver steps than before. Again using the relative error measure from (27) as a discriminative criterion, we use two V(2, 1) cycles with two inner iterations per full multigrid stage. With these settings, we again obtain relative errors below 1 × 10⁻², and an AAE of 5.73° on the Yosemite sequence with clouds, depicted in Fig. 2.

As a fair tradeoff between accuracy and speed, we additionally provide benchmarks using only one V(2, 1) cycle with two inner iterations. Though running significantly faster than our high quality solution, we still obtain an AAE of 5.76°, and the relative error is below 2.2 × 10⁻².

Thirdly, as for the linear case, we are interested in a peak performance measure, given no presmoothing needs to be applied at all. In this respect, we again use one nonlinear V(2, 1) cycle with two inner iterations, but do not presmooth the input frames or the motion tensor entries.

Table 2 and Fig. 3 show the measurements from this experiment. Applying optimal smoothness parameters, we obtain a maximum of 25.64 FPS for the highest accuracy solution, and even 41.81 FPS for a visually equal result, which is far beyond real-time. Our measured peak performance of 65.02 FPS thereby additionally promises even higher performance, if the input data require less presmoothing.

Table 2 SPU scaling on nonlinear full multigrid cycles with presmoothing of σ = 1.6, ρ = 1.45 (ps) on two and one V cycle, and the peak performance without presmoothing (no), on “Yosemite” 316 × 252

Fig. 3

SPU scaling on nonlinear full multigrid cycles with presmoothing of σ = 1.6,  ρ = 1.45 (ps) on two and one V cycle, and the peak performance without presmoothing (no), in FPS on “Yosemite” 316 × 252

Furthermore, one can see that due to the higher computational complexity of the underlying model compared to the linear approach, a lower ratio of memory transactions to arithmetic operations is established. Because of fewer bus contentions, this approach scales better towards a larger number of cores.

7.2 Scaling over varying frame sizes

In a second experiment, we compute the scaling of our methods under changes of the input image size. Here, we used frames 22 and 23 from the famous Ettlinger Tor sequence created by Kollnig et al., which can be downloaded from http://i21www.ira.uka.de/image_sequences/, and resampled it from its original size of 512 × 512 pixels to 256², 128², and 64².

It turns out that images of about 512 × 512 pixels are the largest size computable on the Sony PlayStation 3. During experiments with larger frames, both RAM and Local Store requirements exceeded the available capacity of 256 MB and 256 kB, respectively, such that they cannot be computed in our framework without major redesigns. Frames of VGA size (640 × 480) are already too large to entirely fit into the RAM, while vertical dimensions over 600 pixels pose a problem to the cache partitioning.

To counter the frequent swapping processes to the hard disk for large frames without hardware modifications, a different parallelisation strategy can be proposed as a remedy, which comes at the cost of associated performance losses, however. The restrictions on the cache can also be levelled of, namely by a different memory layout, but this change is again immediately connected to a significant runtime loss due to redundant DMA transactions in between RAM and the Local Stores.

Since the amount of presmoothing is depending on the image size, we adapt the standard deviation of our presmoothing steps to the downsampled frames, such that an equal visual impression establishes. Here, we scale σ and ρ linearly with one dimension of the regarded frames, i.e. if we use these for frames of size 512², we apply ${\frac{\sigma}{2}}$ and ${\frac{\rho}{2}}$ to frames of 256² and so on.

7.2.1 Linear setting

Table 3 lists the result of our experiments with the linear model from Sect. 2. Here, we used presmoothing with standard deviations σ = 1.2 and ρ = 2.3 for the 512² original version, which we then scaled in accordance with the frame size. These values have been chosen as ideal with respect to the visual quality of the flow field. The visual quality is hereby shown in Fig. 4.

Table 3 Scaling of our linear method over image sizes with adapted presmoothing based on σ = 1.2, ρ = 2.3 for 512² (ps), and the peak performance without (no), on resampled versions of “Ettlinger Tor”

Fig. 4

Visual quality of the linear (bottom left) and the nonlinear (bottom right) CLG method on a real-world dataset, colour-coded. The input images, frames 22 and 23 of the Ettlinger Tor sequence, are depicted in the upper row, respectively

Frames of size 512² can be computed entirely in real-time, which even outperforms recent implementations on GPUs, like the one proposed by Zach et al. [44], by more than a factor of five.

Observing the development of the runtime over the different frame sizes, one notices a clear preference of larger frames, if no presmoothing is applied, but an almost linear scaling with the number of pixels, if both the input frames and the motion tensor are presmoothed. This characteristic can in the first place be explained by the different ratio of memory transfers and arithmetic operations, compared to the other stages of the algorithm. Convolutions typically require a high data throughput with only a few computations in between, and can additionally not be cached to a degree standard stencil operations can be, which is due to the restricted data locality.

7.2.2 Nonlinear setting

Table 4 shows the results of our benchmarks with the nonlinear model from Sect. 2.3. Even with this approach, which gives much better results than the simpler linear variant, we obtain results in real-time and outperform CPU and GPU implementations of variational optical flow models significantly [11, 44]. Like for the linear case, the visual quality is shown in Fig. 4. Since this sequence does not contain ego-motion of the camera like for Yosemite, one can immediately see the sharp edges of the moving cars, which are more bleeding out using the linear model.

Table 4 Scaling of our nonlinear method over image sizes with adapted presmoothing based on σ = 1.3, ρ = 1.0 for 512² (ps), and the peak performance without (no), on resampled versions of “Ettlinger Tor”

Meanwhile, we observe a similar scaling pattern as in the linear case, though presmoothing does not have as high effects on the runtime. To obtain the respectively best results, the discontinuity-preserving nonlinear method typically requires in total less presmoothing to be applied than the linear one.

8 Summary and conclusion

In this paper, we have proposed two well-performing parallel algorithms for the computation of the CLG optic flow model on the Cell Processor of a Sony PlayStation 3. By a combination of efficient multigrid solvers, adaptations of data structures, an evolved cache strategy, and instruction-level parallel formulations, we are able to exhaust the full potential of the underlying architecture. Though the hardware is only about as expensive as modern CPU-based computers, we still obtain a speedup factor of 6.5, which finally comes down to an absolute number of 210 dense flow fields on image sequences of size 316 × 252 pixels. This way, we could prove that variational optic flow approaches are indeed able to provide a remarkable performance while not forfeiting their characteristic accuracy. In experiments with differently sized images, we showed that the algorithm performs better the larger the image sequence is. In this context, we found the small memory dimensioning of the PlayStation 3 to be one main bottleneck for algorithms of this kind.

Since our algorithm represents a classic optimisation problem, our insights might as well not only be relevant for the concrete application of optic flow, but we rather hope that our work gives direction to a new point of view with respect to variational models and their incorporation into real-time applications. With impressive speedups in prospect, it becomes more and more worthwhile to invest some effort in a suitable adaptation to platforms such as the Cell Processor, and to benefit from the true potential of these architectures.