Introduction

Industrial robots are used for milling large and complex parts owing to their advantages of low cost, wide workspace range, and high flexibility. However, compared with CNC machine tools, the low rigidity of the robot makes chatter more likely, influencing machining accuracy, quality, and efficiency. Extensive research has been conducted on the prediction of chatter and various chatter suppression methods have been summarized. Generally, chatter in robotic milling is composed of both regenerative and mode coupling chatter. However, differing from the typical issues concerning regenerative chatter in conventional CNC machining, mode coupling chatter was identified as the dominant source of vibrations in robotic machining at low cutting speeds and regenerative chatter was the dominant source at high speeds (Pan et al. 2006; Gienke et al. 2019). The stiffness matrix depends on the current configuration in terms of the robot. The damping effect will always increase the stability of the system but is difficult to accurately identify. In addition, the main chatter mechanism of robotic milling is different for different machining cases; thus, chatter analysis cannot yield a confident result using their stability criteria. Except for chatter prediction, detecting the vibration state of milling timely is an efficient method to improve the performance of machining equipment, which reduces the frequency and time of chatter occurrence and contributes to further research on the chatter mechanism. Therefore, it is essential to study chatter identification in robotic milling.

Traditional chatter identification is mainly achieved by observing the processed surface and analysis of the physical signal spectrum. Recently, some scholars have identified chatter through feature extraction and setting thresholds for machined surface images (Lei and Soshi 2017), cutting force signals (Tangjitsitcharoen et al. 2015), vibration signals (Tao et al. 2019; Musselman et al. 2019) and current signals (Aslan and Altintas 2018). The value of the characteristic threshold is important and significantly influences the accuracy of the identification model. By introducing a machine learning-based chatter identification model, with physical vibration signals as the input, the correspondence between the input and output requires establishing. Generally, the chatter identification process is realized by feature extraction and classification. Deep learning such as deep belief networks (DBN) is used to extract feature automatically and classify chatter simultaneously (Fu et al. 2019b). However, the DBN needs more time to complete the model training. In addition, machine learning is more suitable for timely chatter monitoring than deep learning because of its small computation time. Feature selection and extraction of signals in machine learning have a significant impact on model accuracy. In addition, external disturbances, modeling errors, and uncertainties are common when measuring in practical applications (Stojanovic and Prsic 2020; Nannapaneni et al. 2020). These noises and uncertainties affect the performance of feature extraction and classification. Generally, non-Gaussian noise is eliminated by designing appropriate filters. When chatter occurs during machining, the energy is concentrated near the mode frequency of the machining system, and chatter frequency bands will be observed, while the frequency band centers are not fixed. Signal analysis methods based on modal decomposition, such as VMD and empirical mode decomposition (EMD) (Zhao et al. 2020), and empirical wavelet transformation (EWT) are usually used to extract features of the signals with these characteristics. VMD can accurately separate the harmonic components of non-stationary signals, regardless of how close their frequency components are. Compared with VMD, EMD does not have a strong mathematical foundation. In addition, VMD can be used to reduce the impact of non-Gaussian impulsive noise (Dutta et al. 2016). Aneesh et al. (2015) compared the performance of VMD (Dragomiretskiy and Zosso 2013) with EWT in feature extraction. The classification results of SVM show that VMD feature extraction performs better than EWT. VMD, an adaptive signal machining method, is conducive to the extraction of chatter features, effectively dealing with the characteristic that chatter frequency bands shift during machining. Liu et al. (2017) used the chatter of milling on an NC machine as the analysis object, extracted sample features by VMD and Shannon power spectral entropy, and classified and predicted samples using a probabilistic neural network (PNN). However, the parameters that affect the accuracy of the model are selected based on prior knowledge, without further optimization processes. After the data features are extracted, SVM/support vector classification (SVC) is usually used in chatter detection and prediction. Chen et al. (2020) used a multivariate filter method to select the p-leader multifractal features and adopted SVM for chatter classification. The stability lobe diagram of milling was predicted using extended SVC and an artificial neural network (ANN) (Friedrich et al. 2017), and these continuously learning algorithms can be applied to higher-dimensional problems with arbitrary input dimensions. The dominant frequency bands are identified by localizing the frequency bands at which the energy is high in the average fast Fourier transform (FFT) plot to highlight the chatter-related characteristics. Furthermore, the combination of VMD and SVM (Abdoos et al. 2016) facilitated mechanical fault diagnosis. However, the VMD-SVM model is rarely used in chatter detection. The optimization of hyper-parameters can improve model accuracy. Mutation sine and cosine algorithm-particle swarm optimization algorithm (SCA-PSO) (Fu et al. 2019a), chaos sine and cosine algorithm (CSCA) (Fu et al. 2018), quantum chaos fly optimization algorithm (QCFOA) (Xu et al. 2019) and other optimization methods have been used to optimize the hyper-parameters of the VMD-SVM model, where VMD and SVM are optimized respectively.

The VMD-SVM model in the above literature is mainly used in the classification of power quality events, fault diagnosis of variable load-bearing, fault diagnosis for rolling bearings, vibration trend measurement for a hydropower generator, etc. Moreover, there are limited studies on the chatter identification method of robotic milling based on the VMD-SVM model. This study constructs a VMD-SVM model to identify robotic milling chatter. Generally, the hyper-parametric optimization of VMD and SVM is conducted separately, which is insufficient to obtain the optimal performance of the VMD-SVM model. For better performance of the chatter identification model in robot milling based on VMD-SVM, the kMap method is proposed in this paper to jointly optimize the hyper-parameters in the identification model. The remainder of this paper is organized as follows. In section “Dataset construction based on novel chatter classification”, the experiment settings and data augmentation methods for constructing the dataset are presented. An identification model based on VMD-SVM is constructed and the details of the proposed kMap optimization method are described in section "Chatter identification model based on VMD-SVM". In section "Identification accuracy and experiment analysis", the identification models based on raw cutting data and the data containing non-Gaussian noise optimized by different methods are analyzed. The effectiveness of the proposed approach was validated through 12 robot milling experiments. Finally, the conclusions are presented in section "Conclusions".

Dataset construction based on novel chatter classification

The full-discretization method (Tang et al. 2017) was used to obtain the stability lobe diagram in this paper. The ranges of spindle speeds and cutting depths were selected for the cutting experiment according to the case and experience. The vibration data of the experiments were collected to build vibration sample sets under different vibration conditions. Then, the chatter characteristics in robotic milling were analyzed and its identification model was trained.

Experimental platform and parameter setting

The planar milling experiments were conducted on the robotic milling platform with ABB IRB6660, as shown in Fig. 1. The vibration signals of the spindle and the vibration texture of the machined surface in the milling process were recorded. A SANDVIK Φ 25 face milling cutter (600-025A25-10H) with 3 10 mm blade-diameter cutter teeth (600-1045M-ML 1030) was used to cut the Ni–Al bronze workpiece. Vibration signals were collected via an NI data acquisition system and a 3-dimensional acceleration sensor (DYTRAN 3263A2T). Simultaneously, an industrial vision measurement system (Camera: Basler aca2440-20gc, lens: OPT c1614-5m) was used to take pictures of the surface of the workpiece to record the vibration texture of the surface.

Fig. 1
figure 1

Planar milling experiment setup on the robotic milling platform

Full size image

According to the stability lobe diagram (Fig. 2) and actual machining experience, a rotation speed range of 3000–6000 rpm and a cutting depth range of 0.2–2 mm were selected for the cutting experiments. In the milling process, the feed per tooth and cutting width remained constant. The feed per tooth was fz = 0.05 mm/ft and the cutting width was 8 mm. The sampling frequency of the vibration data was 10 kHz. A total of 160 sets of different machining parameters were selected for cutting. Up milling was performed along the positive direction of the Y-axis of the robotic coordinate system. The machining parameters are shown in Table 1, represented visually by four types of differently shaped/colored symbols in the stability lobe diagram. Specifically, the red point and the green ‘ × ’ express the stable and transition machining parameter states, respectively. The black ‘#’ and the blue ‘*’ both denote the chatter state; the black ‘#’ signifies regular chatter and the blue ‘*’ represents irregular chatter. In the stability lobe diagram, above the curve is unstable and below is stable. Stable data are in the stable region and chatter (regular chatter and irregular chatter) data are in the unstable region. In addition, the transition cutting parameter points are around the curve. The accuracy of prediction is not sufficiently high but the cutting data of the four vibrations are similar in size. The practical meanings of these four types used to distinguish different machining vibration states are expounded in section "Classification of vibration states in robotic milling".

Fig. 2
figure 2

Stability lobe diagram

Full size image
Table 1 Milling parameters table
Full size table

Construction of vibration dataset based on the sliding window method

Generally, the original vibration data are collected in three stages: the feeding, cutting, and relieving stages, as shown in Fig. 3. The spectrum features of the three stages are not completely consistent (Fig. 4). To ensure the consistency of the sample characteristics in the sample splicing and sliding window operation, the samples in the feeding and relieving stages were not considered. By intercepting the raw vibration data of each section, the data of the cutting stage can be obtained as samples. Simultaneously, multiple cutting during the experiment will be conducted to collect sufficient vibration samples for analysis under each set of cutting parameters.

Fig. 3
figure 3

Original milling vibration data

Full size image
Fig. 4
figure 4figure 4

FFT spectra of samples with different vibration states at different cutting stages

Full size image

In this study, the machined plane size of the workpiece in the experiments is 70 × 120 mm and the single cutting range is 8 × 70 mm. In the cutting area, it can be seen from Fig. 5 that the features of the vibration signal under the same machining parameters maintain good consistency. Therefore, it is assumed that the robot maintains the same vibration state under the same processing parameters when the cutting area is small. In this way, for the same parameters, vibration data from the cutting stage of multiple data files can be directly collected to represent the vibration state. To facilitate training the identification model in the following chapters, sliding window sampling is conducted for the vibration signals under the same processing parameters to construct standard vibration data sample sets (Fig. 6), according to the following:

$$ S_{ij} = S_{i} [1 + j*s\_len,{\kern 1pt} {\kern 1pt} {\kern 1pt} fs + j*s\_len]{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left(j = 0,1,2,...,INT(\frac{Ni - fs}{{s\_len}})\right) $$
(1)

where Sij is the jth vibration sample obtained from the vibration signal of the ith parameter group. j is the number of sliding windows, and fs is the sampling frequency. fs is uniformly set to 10 k. s_len represents the sliding step size of the window, and INT() is the integer component of the value in parentheses. The process is shown in Fig. 7.

Fig. 5
figure 5

The vibration data in the same machining parameters

Full size image
Fig. 6
figure 6

Standard vibration data sample sets

Full size image
Fig. 7
figure 7

Sliding window sampling process under the same processing parameters

Full size image

Classification of vibration states in robotic milling

Previous studies conducted FFT on vibration signals and analyzed their frequency components to determine whether chatter occurs. In addition to the tool passing frequency and its frequency multiplication, the data of the chatter state contains other obvious frequency components. However, it is found that the frequency distribution in the spectrum diagram of the data in the chatter state is not completely similar in the experimental process. The frequency of some chatter data is regular in the spectrum diagram, while the frequency of others is chaotic. When the time–frequency information of the vibration data is input into the image through a continuous wavelet transform (CWT), it can be found that the frequency components of the data with regular frequency have little change with time, while the frequency components of the data with a disordered frequency vary with time. The vibration data in the chatter state is divided into regular chatter (time-invariant chatter) and irregular chatter (time-varying chatter). All vibration data can be divided into four types: stable, transition, regular chatter, and irregular chatter. FFT is conducted for the vibration signals of the different vibration types with their frequency components being analyzed. The results of the FFT are shown in Fig. 8 and the CWT results are shown in Fig. 9.

Fig. 8
figure 8

Frequency spectra of 4 vibration states based on FFT

Full size image
Fig. 9
figure 9

Time–frequency spectra of 4 vibration states based on CWT

Full size image

According to the wavelet time–frequency spectrum diagram, its frequency component is constant in the stable state and the frequency bands are continuous. In the transition state, most of the frequency components remain unchanged and some frequency bands are discontinuous. In the regular chatter state, there is a small number of time-varying frequency components with discontinuous frequency bands. In the irregular chatter state, most frequency components are time-varying and each frequency band is almost completely discontinuous. Therefore, the time-varying chatter components in robotic milling can be reflected and captured by wavelet analysis.

Obvious differences can be found by observing the vibration patterns of the machined surface (Fig. 10) under four states:

  1. 1.

    Stable state

    There are sometimes normal visible gear marks on the surface but no obvious vibration marks. When directly observed by the naked eye, the surface is very smooth and clean, as shown in Fig. 10a.

  2. 2.

    Transition state

    Compared with the stable state, there is a slight vibration texture on the surface, as shown in Fig. 10b.

  3. 3.

    Regular chatter state

    Compared with the stable state, there is an obvious regular vibration texture on the surface, as shown in Fig. 10c.

  4. 4.

    Irregular chatter state

Fig. 10
figure 10

Vibration texture of workpiece surface under 4 vibration states

Full size image

Compared with the previous states, the surface has obvious irregular vibration textures and the surface quality is the worst, as shown in Fig. 10d.

According to the above standards, vibration textures generated using all the processing parameters are observed. Among them, the stable state and transitional state accounted for 28.75 and 15%, respectively. The percentages of regular chatter and irregular chatter states are 26.875 and 29.375%, respectively.

Chatter identification model based on VMD-SVM

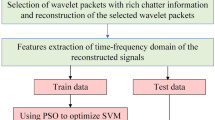
The entire framework of the identification model is shown in Fig. 11. After obtaining the vibration signal datasets, VMD and IE are used in the preprocessing of raw signals. VMD is used to decompose the original signal in the frequency domain. The chaotic characteristics of the vibration signal are further extracted and the dimension of the data is reduced by computing IE. Then, an SVM-based classification model is trained to divide the vibration signals into four types. Finally, the hyper-parameters of the VMD-SVM model are optimized by kMap to improve the accuracy of the identification model.

Fig. 11
figure 11

Chatter identification model framework for robotic milling

Full size image

VMD-SVM model based on IE

In view of higher decomposition accuracy, VMD is used to process signals adaptively, which extracts features of vibration better by considering the characteristic that vibration frequency bands are variable. The solution target of the VMD is shown below:

$$ \begin{gathered} \mathop {\min }\limits_{{\left\{ {u_{k} \left( t \right)} \right\},\left\{ {\omega_{k\left( t \right)} } \right\}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k} {l_{k} } \hfill \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k} {u_{k} } \left( t \right) = f(t) \hfill \\ \end{gathered} $$
(2)

where \(\{ u_{k} (t)\} = \{ u_{1} (t),u_{2} (t), \ldots ,u_{k} (t)\}\) represents the K intrinsic mode function (IMF) components to be preset and estimated. \(\{ \omega_{k} (t)\} = \{ \omega_{1} (t),\omega_{2} (t), \ldots ,\omega_{k} (t)\}\) is the relevant center frequency and f(t) is the raw signal. uk, ωk, and f are simplified to represent \(u_{k} (t),\omega_{k} (t)\), and f(t).

The Lagrangian multiplier method (LMM) is utilized to solve the optimization problem in Eq. (3). The secondary penalty factor α and Lagrangian multiplier λ(t) are introduced to obtain the Lagrangian equation and solution, as follows:

$$ L\left( {\left\{ {u_{k} } \right\},\left\{ {\omega_{k} } \right\},\lambda } \right) = \alpha \sum\limits_{k} {l_{k} } + \left\| {f - \sum\limits_{k} {u_{k} } } \right\|_{2}^{2} + \left\langle {\lambda \left( t \right),f - \sum\limits_{k} {u_{k} } } \right\rangle $$
(3)

Then, the alternate direction method of multipliers (ADMM) is used to solve Eq. (3), and the extreme point is found by alternately updating \(u_{k}^{n + 1} ,\omega_{k}^{n + 1}\), and \(\lambda^{n + 1}\), obtaining k signal sub-sequences (Liu et al. 2017).

The IE of the sub-signals can be obtained as the characteristic variable according to the characteristics that the frequency components of vibration signals become increasingly complex when chatter occurs. The calculation equation for IE is:

$$ E_{i} = - {\mathbf{x}}_{i} \log {\mathbf{x}}_{i} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,...,n $$
(4)

where \(E_{i}\) is the IE of the ith signal subsequence, and \({\varvec{x}}_{i}\) represents the signal subsequence extracted with VMD. The feature vector obtained from IE is taken as the input and the SVM classification model based on the radial basis function (RBF) is used to realize identification of the vibration state in the process of robotic milling (the vibration signal collected in this paper is the signal sequence of sampling points with a sampling frequency of 10 kHz).

kMap identification model optimization method

Generally, the SVM algorithm is used for classification, which involves the hyper-parameters σ and C. The optimization of hyper-parameters is a two-dimensional hyper-parameter optimization problem. With the use of the VMD algorithm, the modal decomposition number K and the second penalty factor α in VMD will also become hyper-parameters of the model. The optimization of hyper-parameters becomes a 4-dimensional hyper-parameter optimization problem. According to the influence of K and α on the reconstruction characteristics of simulation signals, the value of α should be greater than or equal to half of the sampling frequency (Lv et al. 2016). The GS is used to optimize multi-dimensional hyper-parameters but its operation time is long. This paper sets α = 5000 and proposes a GS-based method, the kMap method, to solve the VMD-SVM three-dimensional hyper-parameter optimization problem.

First, the range of hyper-parameters and step length are set:

$$ \left\{ \begin{gathered} C \in [2^{C\_\min } ,2^{C\_\max } ],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} C\_n{\kern 1pt} = INT((C\_\max - C\_\min )/C\_step) \hfill \\ \sigma \in [2^{\sigma \_\min } ,2^{\sigma \_\max } ],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma \_n = INT((\sigma \_\max - \sigma \_\min )/{\kern 1pt} \sigma \_step) \hfill \\ K \in \left\{ {1,2,...,n} \right\} \hfill \\ \end{gathered} \right. $$
(5)

where the value of C and σ are discretized with 2 as the basis number. C_step and σ_step represent the discrete step lengths of the corresponding hyper-parameters. K is the number of modal decompositions, so its value is generally a discrete integer. Within this range, the optimal hyper-parameter combination, (C, σ, K), is determined to ensure that the VMD-SVM model achieves higher training accuracy.

Then, a group value range of hyper-parameters is set with a small degree of dispersion. The influence trend of these 3 hyper-parameters on the model precision is first analyzed using the GS. The accuracy distributions in different parameters obtained by setting C_min = σ_min =  − 5, C_max = σ_max = 5, C_step = σ_step = 0.2, and \(K \in {{\{ 2,3}}...{{10\} }}\), as shown in Fig. 12. Where the surfaces of different colors represent the model training accuracy under combinations of C and σ when K is set as different values.

Fig. 12
figure 12

Training accuracy distribution under different parameter combinations

Full size image

It can be seen from Fig. 12 that the influence of the 3 hyper-parameters on the model precision studied in this paper is not a linear relationship. Especially, when the model precision reaches a higher value range, the influence relationship becomes more complex. Convert Fig. 12 to a plane perspective of C − σ, as shown in Fig. 13. The differently colored regions in the figure correspond to different values of C and σ, representing the value of K that can maintain the highest accuracy of the model in the current region. According to the figure, the optimal value of K is not fixed. However, it is not difficult to find from the figure that these colored areas are divided into continuous blocks in most cases. Therefore, as long as the value of K in each C − σ region can be determined to ensure that the model has the highest accuracy, the 3-dimensional hyper-parameter optimization problem can be transformed into the C − σ two-dimensional optimization problem.

Fig. 13
figure 13

Training accuracy distribution diagram on the C − σ plane

Full size image

The continuous region can be identified by determining the boundaries of different continuous regions. Specifically, a large step size is given and the values of C and are σ updated by GS. The optimal value of K under the current values of C is σ, obtained as follows:

$$ \begin{gathered} k\left( {C,\sigma } \right){\kern 1pt} = \mathop {\arg \max {\kern 1pt} {\kern 1pt} }\limits_{{K \in \{ 1,2,3,...,n\} }} acc(C,\sigma ,K) \hfill \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} k\left( {C,\sigma } \right) = i - 1,({\kern 1pt} {\kern 1pt} \left| {acc_{i} - acc_{i - 1} } \right|{\kern 1pt} {\kern 1pt} \le \varepsilon {\kern 1pt} {\kern 1pt} {\kern 1pt} ) \hfill \\ \end{gathered} $$
(6)

where acc represents the training accuracy of the model. At the same time, the higher the value of K, the higher the computational complexity of the VMD algorithm. Therefore, with the constraint condition set, a smaller value of K is selected as the optimal K when the difference between the model accuracies corresponding to the current K and the previous K is less than the convergence accuracy. The optimal K matrix corresponding to all grid points at the current large step size can be obtained when all values of C and σ are traversed. The specific process is as follows:

  1. 1.

    The value ranges and step sizes of C, σ, K are set.

  2. 2.

    Execute the loop body, update C and σ with GS until the search is completed. Then execute (4).

  3. 3.

    According to Eq. (6), the optimal K of the current C and σ is calculated.

  4. 4.

    Obtain the optimal K distribution diagram for all values of C and σ, referred to as kMap.

The process of obtaining a contour map of K is shown in Fig. 14:

Fig. 14
figure 14

First step: obtain the K-contour map (kMap) under the large step

Full size image

Taking the parameter settings in Fig. 14 as an example. When the optimal matrix K is calculated with C_step = σ_step = 0.5 rather than C_step = σ_step = 0.2, the contour map of the K matrix is drawn in the C − σ plane, as shown in Fig. 15. Different colors represent the K values in different regions corresponding to the highest model accuracy.

Fig. 15
figure 15

Optimal K distribution on the \(C - \sigma\) plane

Full size image

As shown in Fig. 15, each optimal K region is a continuous block; its range is similar to that of when C_step = σ_step = 0.2. Therefore, kMap can be used to further search for the optimal solution with the two-dimensional C − σ grid method under the middle step size, until the target step size is reached.

Bilinear interpolation (BI) is required to interpolate kMap to obtain the same optimal K values as the discrete grid points with a middle step size. The interpolation formula is shown below:

$$ k\left( {C,\sigma } \right) = \left[ {\begin{array}{*{20}c} {\frac{{C_{2} - C}}{{C_{2} - C_{1} }}} & {\frac{{C - C_{1} }}{{C_{2} - C_{1} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {k\left( {C_{1} ,\sigma_{1} } \right)} & {k\left( {C_{1} ,\sigma_{2} } \right)} \\ {k\left( {C_{2} ,\sigma_{1} } \right)} & {k\left( {C_{2} ,\sigma_{2} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{\sigma_{2} - \sigma }}{{\sigma_{2} - \sigma_{1} }}} \\ {\frac{{\sigma - \sigma_{1} }}{{\sigma_{2} - \sigma_{1} }}} \\ \end{array} } \right] $$
(7)

where k(C1, σ1), k(C1, σ2), k(C2, σ1), and k(C2, σ2), are the 4 known points closest to the current interpolation point, as shown in Fig. 16. According to Eq. (7), the kMap corresponding to the middle step size can be obtained. Setting C_step = σ_step = 0.2, the kMap obtained by the BI of the kMap generated by C_step = σ_step = 0.5 is shown in Fig. 17. Its continuous region and boundary are well preserved.

Fig. 16
figure 16

Bilinear Interpolation

Full size image
Fig. 17
figure 17

kMap obtained from BI

Full size image

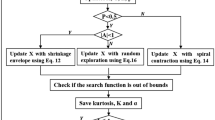
After obtaining kMap with a middle step size, the optimal solution can be further searched according to the GS. The specific process of the algorithm is shown in Fig. 18a. The optimal combination (C, σ, K) generated from the discrete step length can be taken as the value range center. A small value range and search distance are given and the optimal solution can be searched using the GS. If the optimal (C, σ, K) is not updated, the optimal solution can be considered found. The specific process is shown in Fig. 18b.

Fig. 18
figure 18

Flow chart with the middle and small step size

Full size image

For the optimization of the values of the 3 hyper-parameters, the overall algorithm flow based on the kMap method is as follows:

  1. 1.

    Initialize parameters.

  2. 2.

    Search for all K values with the highest accuracy under large step sizes of C, σ and obtain kMap.

  3. 3.

    According to kMap with the large step size, the BI method is used to update and expand kMap. The GS is used to search for the current optimal (C, σ, K) with the middle step size.

  4. 4.

    Taking the optimal hyper-parameter combination generated in (3) as the center point, update the optimal (C, K) by GS with a small step size.

  5. 5.

    Output the optimal (C, K), end.

The overall flow chart is shown in Fig. 19.

Fig. 19
figure 19

Overall flow chart of kMap algorithm

Full size image

To select optimal hyper-parameters, assuming that n C, m σ and g K values are used to identify the model for optimal parameter selection, the time complexity of kMap is O(nmg). The time complexity of kMap is the same as that of the GS algorithm proposed in the following section. However, the number of parameters taken by kMap is far less than that of GS and part of the calculation process is greatly simplified, with the computational burden greatly reduced.

Identification accuracy and experiment analysis

Optimization result and analysis of kMap

As an improved GS algorithm, the operation time of kMap is far less than that of GS. The operation results are shown in Table 2. In the optimizing process of GS, C_min = σ_min =  − 5, C_max = σ_max = 5, C_step = σ_step = 0.02, and \(K \in {{\{ 2,3}}...{{10\} }}\). The obtained optimal model accuracy was 92.59% and the time used was approximately 37 h. The hyper-parameters of the VMD-SVM model are optimized by kMap with the same parameter ranges. The sizes of the large step, middle step, and small step are set as 0.5, 0.2, and 0.02, respectively. The accuracy of the model optimized by kMap was 92.45%. kMap saves large computational expense with a small accuracy cost.

Table 2 The results optimized with GS and kMap
Full size table

The heuristic algorithm (HA) [e.g., PSO (Kennedy and Eberhart 1995) and GA (Holland 1973)] is an effective optimization method. Compare these methods in kMap, with the following optimization settings of PSO, GA, and kMap: optimization ranges of C, σ, K: [− 5, 5], [− 5, 5), [2, 10], evolution time number is 200, and population size is 20. In addition, the maximum velocity of the particle and termination error value are set as 0.02 and 1e-25, respectively, in PSO. The individual length of the gene and the termination error value are 11 × 2 and 1e-25 in GA. The step sizes of kMap are taken as three different sets of values; (0.5, 0.2, 0.02), (0.5, 0.1, 0.02), and (0.4, 0.12, 0.024).

It is assumed that the stochastic disturbance has a non-Gaussian distribution in the case of industrial robotic milling. The measured acceleration data X(t) is written as:

$$ X(t) = X^{\prime}(t){ + }e(t) $$
(8)

where \(X^{\prime}(t)\) and e(t) are the real acceleration data and stochastic noise, respectively. It is assumed that the measurement noise e(t) has a non-Gaussian distribution, with approximately normal distribution classes (Stojanovic and Prsic 2020):

$$ P_{\varepsilon } = \{ p(e):p(e) = (1 - \varepsilon )p_{1} (e) + \varepsilon p_{2} (e)\} $$
(9)

where the probability density p(e) represents a mixture of primary probability density p1(e): N(0, R1) and contaminating probability density p2(e): N(0, R2). The degree ε is in range 0 < ε < 1, while R1 and R2 are covariance matrices of primary and contaminating terms in a non-Gaussian distribution. Non-Gaussian noises with different R1, R2, and ε are added to the cutting data. These datasets containing noise are used to train the identification model, and PSO, GA, and kMap are used to obtain optimal hyper-parameters. The results are shown in Fig. 20.

Fig. 20
figure 20

Identification model accuracies

Full size image

The operation time of kMap is of the same order of magnitude as PSO and GA, i.e., hundreds of seconds. However, the average optimization performance of kMap is slightly better than that of PSO and GA. It is worth noting that kMap inherits the advantages of stable optimization of the GS; this means that in the same optimization range, the optimization result of kMap is almost unchanged when the lengths of the searching steps are changed. It is obvious that non-Gaussian noise affects the accuracy of the identification model so it is important to appropriately design a cutting signal filter.

Chatter identification experiment

The chatter identification model optimized by kMap was used in the experiments of robotic milling. The hardware is a Henrywaltz data acquisition module (Fig. 21). The cutting tools and the material used in the experiment are the same as section "Experimental platform and parameter setting" and are machined by up-milling. Different machining parameters were set for the robotic milling experiments. The experimental machining parameters are listed in Table 3. The results of the software used to monitor vibration states are shown in Fig. 22. The results are presented in the form of four types of vibrations in robotic milling.

Fig. 21
figure 21

Robotic milling vibration monitoring experiment

Full size image
Table 3 Processing parameters of chatter identification experiment
Full size table
Fig. 22
figure 22figure 22

Robotic milling chatter monitoring

Full size image

Take experiments 3, 4, 11, and 12 as examples for analysis. The machined surfaces under the four sets of processing parameters are shown in Fig. 23. In experiment 3, an irregular vibration pattern appears on the machined surface, which is judged as irregular chatter according to experience. In experiment 4, there are slight vibration marks on the processed surface except for the gear mark, which is judged as a transition state according to experience. In experiment 11, the machined surface is smooth and clean, except for the gear mark, and is judged as a stable state according to experience. In experiment 12, the processed surface shows an obvious regular vibration pattern, which is determined as regular chatter according to experience.

Fig. 23
figure 23

Machined surface

Full size image

On average, it takes 1.256 s to identify the vibration state, with the vibration data of 5000 sampling points, and the time for data feature extraction is relatively large. Notably, the identification model can be used for chatter identification when more than 5,000 data are collected in the identification experiment, i.e., after 0.5 s of sampling. The identification results of the 4 groups of experiments are irregular chatter, transition, stable, and regular chatter states. The validity of the model in chatter identification is verified by the same results as those obtained from machining surfaces and experiment results.

Conclusions

To better fit the actual situation of robotic milling and provide the basis for further study of chatter mechanisms, this paper divides the vibration states of industrial robotic milling into four types: stable, transitional, regular chatter, and irregular chatter. The VMD-SVM model is applied for chatter detection of robotic milling for the first time, which is trained using 160 robotic milling experiments. To improve the accuracy of the chatter identification model, a novel optimization method—the kMap algorithm—is proposed in this paper for the optimization of 3-dimensional hyper-parameters of the VMD-SVM model. Finally, validation experiments in 12 parameter sets are used to confirm the effectiveness of the chatter identification model. Through the research of this paper, the efficiency and accurate identification of chatter in robotic milling can be realized. Based on the above research on chatter detection in robotic milling, some conclusions are summarized as follows:

  1. 1.

    The vibration data is identified by classifying the vibration data promptly measured using a VMD-SVM model based on IE where VMD adaptively decomposes the vibration signals and IE quantifies the clutter degree of vibration data. VMD and IE can effectively extract the features of vibration data. The experimental results show that the frequency and time–frequency characteristics of the 4 types of vibration signals proposed in this paper (stable, transitional, regular chatter, and irregular chatter) correspond to the textures on the machined surfaces in robotic milling. The identification accuracy of VMD-SVM model is 92.59% and can effectively identify chatter in robot processing.

  2. 2.

    Compared to the optimization performance of GS, GA, and PSO, the kMap proposed in this paper shows comprehensive advantages in terms of optimization time, accuracy, and stability. The optimization time of kMap was 261 s; this is far less than that of GA (37 h). The average optimization performance of kMap is slightly better than that of PSO and GA. Furthermore, kMap inherits the advantages of stable optimization of GS, i.e., the optimization result of kMap is almost unchanged within the same optimization range. In addition to the application case in this study, the kMap algorithm can be applied to other multidimensional hyper-parameter optimization. To apply kMap to other applications, it is necessary to adjust the optimization range and step size.