A methodology for solving facility layout problem considering barriers: genetic algorithm coupled with A* search

Abstract

This work proposes a new methodology and mathematical formulation to address the facility layout problem. The goal is to minimise the total material handling cost subjected to production-derived constraints. This cost is a function of the distance that the products should cover within the facility. The first idea is to use the ${\text{A}}^{ *}$ algorithm to identify the distances between workstations in a more realistic way. ${\text{A}}^{ *}$ determines the shortest path within the facility that contains obstacles and transportation routes. The second idea is to combine a genetic algorithm and the ${\text{A}}^{ *}$ algorithm with a homogenous methodology to improve the quality of the facility layouts. In an iterative way, the layout solution space is explored using the genetic algorithm. We study the impacts of the appropriate crossover and mutation operators and the values of the parameters used in this algorithm on the cost of the proposed arrangements. These operators and parameter values are fine-tuned using Monte Carlo simulations. The facility arrangements are all compared and discussed based on their material handling cost associated with the Euclidean distance, rectilinear distance, and ${\text{A}}^{ *}$ algorithm. Finally, we present a set of conclusions regarding the suggested methodology and discuss our future research goals.

Introduction

The facility layout problem (FLP) concerns the determination of the most efficient arrangement of equipment in an area. A facility can be a machine tool, workstation, manufacturing cell, machine shop, department, warehouse, and so forth (Palomo-Romero et al. 2017). This problem has broad applications in fields such as layout of hospitals, airports, or manufacturing systems. From the manufacturing perspective, the efficiency of the facility layout is typically measured in terms of the material handling cost (MHC) (Liu and Meller 2007). The MHC is directly linked to the total distance the products and items should travel within the facility according to their manufacturing constraints, i.e., their routings. Various facility arrangements cause different total distances. The resolution of the FLP focuses on minimising the MHC because, according to Ahmadi et al. (2017), approximately 20–50% of the total operating expenses in manufacturing environments are attributed to the MHC.

There are two ways to formulate layout problems: discrete and continuous. The discrete representation of the layout is often linked to the traditional mathematical programming approach. This approach attempts to assign a set of workstations to a set of predetermined and distinct locations. The associated optimisation problem is then addressed as a quadratic assignment problem (Drira et al. 2007). Such discretisation of the space simplifies the solutions space. However, as numerous possible locations are ignored, the chance to obtain an optimal layout is lessened. The continuous formulation allows the workstations to be located anywhere within a planar site. The FLP models deal with workstations that could have all the same footprint or not.

Despite the significant literature in the FLP field, several improvements in the manufacturing context are still possible by (i) modelling the real characteristics of the studied cases in a more efficient way (more complex footprints of workstations, for instance); (ii) exploring new techniques to define the distance among equipment units, considering product routings, obstacles, and transportation routes; and (iii) using the knowledge of human experts for designing a layout, which can be seen for instance in Ahmadi et al. (2017).

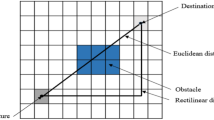
Our main motivation is to explore a more relevant way to define layouts with a satisfactory MHC considering more realistic constraints. This research does not focus on finding the optimal solution; rather, it looks for a cost effective layout. This means that we search for a realistic distance determination among the workstations for products that should cross a workshop. Most of the FLP resolution approaches use the rectilinear or Euclidean distance between workstations (Gonçalves and Resende 2015; Hosseini-Nasab et al. 2017; Xie et al. 2018). These distances are easy to use but have shortcomings. The Euclidean distance can be defined as a straight line between the start and destination machines. It measures the distance between two workstations without considering the obstacles and machines in between (Gomathi et al. 2014). The rectilinear distance is computed by adding the vertical and horizontal distances between centroids of workstations. It is mainly used for problem modelling where the facility space is defined as a grid of surface units. The products are allowed to travel over the borders of these units and cross the obstacles (Friedrich et al. 2018). The obtained solutions based on these distances should be therefore modified afterwards to make them realistic.

To improve the quality of the model, we consider a facility area containing obstacles and transportation routes. The obstacles are the occupied spaces, such as walls and stairs. They cannot contain workstations and products cannot pass through them. The transportation areas refer to permanent transportation paths (i.e., aisles) where no facilities are allowed to be located. However, they can obviously be used for product movements. The facility is modelled as a grid of surface units. The start and destination points for a product in the whole facility area are the centres of these units. Every equipment covers a given number of surface units. The problem to solve is therefore to find out the configuration where the sum of all the product displacements from one item of equipment to the next one is small, smaller than any other suggested configurations. The retained configuration may not be the optimal solution. In this case, we use the ${\text{A}}^{ *}$ algorithm for distance calculations.

To apply such ideas, we need to explore the whole solution space, which is composed of all possible arrangements of workstations within the facility area. This is time consuming and difficult for large scale FLPs. That is the reason why we rely on genetic algorithms (GA), which allow exploring the solution space without any guarantee of studying every possible facility arrangement. However, the application of these algorithms in other areas, including FLP studies (Sadrzadeh 2012; Palomo-Romero et al. 2017; Aiello et al. 2013), shows that very good solutions can be found if and only if suitable algorithm parameters are used. To obtain such a guarantee, we applied the Monte Carlo simulation principles to the entire methodology in order to find out the best set of parameters that provide good arrangements with low MHC.

Our simulations show that the selection of the GA operators and parameters generates two classes of facility arrangements. In the first class, the workstations are densely positioned in the facility area minimising drastically the MHC, while in the second class, the arrangements are porous, and the workstations occupy larger spaces.

The remainder of this paper is organised as follows. Section 2 describes the FLP and reviews the related literature. Section 3 contains the principles of the ${\text{A}}^{ *}$ algorithm and GA. Section 4 provides a detailed description of the developed structure for the proposed approach. The mathematical model of the considered FLP is introduced and the customisation of the ${\text{A}}^{ *}$ algorithm and GA to the FLP resolution is discussed. The identification of the parameter settings of the used GA via the Monte Carlo simulation and the evaluation of the facility arrangement performance is shown in Sect. 5. The whole methodology is applied on an illustrative presented in Sect. 6. Finally, the main conclusions of the paper and suggestions for further studies are presented.

Facility layout problem (FLP): related work

General statements

The facility layout design aims at efficiently positioning n facilities within a given area considering the architecture and structure of the manufacturing facility systems. Finding the most efficient physical layout is regarded as a key to improvement in plant productivity (Tarkesh et al. 2009) and has a significant impact on operational performance measured by lead times, throughput rate, and work in process (El-Baz 2004). This issue has been extensively studied during the past decades. The existing research works on the FLP fall into several categories such as equal- and unequal-sized FLPs, regular and irregular shapes (Azadeh et al. 2016), single- and multi-floor layouts (Park et al. 2011; Ahmadi and Jokar 2016), single- and multi-objective problems (Samarghandi et al. 2010; Jolai et al. 2012), and static and dynamic layout problems (Moslemipour and Lee 2012; Asl and Wong 2015). Kusiak and Heragu (1987), Singh and Sharma (2006), Drira et al. (2007), and Besbes et al. (2018) present an overview of the different schools of thought, trends, and the research niches of the area.

A facility-layout resolution process may involve two phases, the block and detailed layout phases. During the block layout phase, the relative location and size of each department are specified (Armour et al. 1964). Then, the detailed layout phase determines the exact position of workstations, aisle structures, flow paths, and the layout within each department (Meller and Gau 1996).

FLP formulation

It is possible to use a discrete or a continuous representation of an FLP. The discrete representation is the traditional FLP formulation and is the most popular one owing to its simplicity, as seen in Zhou et al. (2017), Ramkumar et al. (2008), Xiaoning and Weina (2011), among other authors. The quadratic assignment problem has been developed to model a discrete FLP. The main assumptions used are (i) unrestricted shop, (ii) equal-sized facilities, (iii) regular shape facilities, and (iv) predetermined locations. The quadratic assignment formulation simplifies the FLP mainly because of the first and fourth assumptions. The first assumption allows unfeasible layouts and the fourth assumption restricts the solution space. The continuous formulation and resolution approaches make it possible to allocate resources anywhere within the facility area (Drira et al. 2007). Table 1 presents a comparison of the main characteristics of the discrete and continuous approaches.

Table 1 Discrete versus continuous FLP formulation

Different FLP resolution approaches

In almost all of the published papers, the layout efficiency is measured in terms of transportation costs and satisfaction of the adjacency requirement. These costs are related to one or more of the following parameters: distance, unit transportation cost, and estimated total flow to be transported from workstation i to workstation j. The workstations may also be defined by some adjacency requirements, which define the needed or desired nearness or remoteness for each pair of machines depending on the shared materials or personnel, or according to security, noise, and vibration reasons (Hosseini-Nasab et al. 2017).

To solve the FLP, various resolution methods have been developed. These approaches can be classified into exact, heuristic, and metaheuristic optimisation approaches. They all look to obtain either good solutions subject to certain constraints or global or local optimum solutions that meet one or more performance objectives. These approaches are applied to illustrative cases randomly generated or to real case studies.

Several research works use exact methods to seek optimal solutions for small-sized FLPs. The mainly used exact methods are the branch and bound, dynamic programming, and cutting plane techniques. Among the research papers that introduce exact algorithms, Solimanpur and Jafari (2008) suggested a branch and bound algorithm to solve a nonlinear mixed-integer programming model. Their objective is to minimise the total distance travelled by materials in a given area. Palubeckis (2012) proposed a branch and bound algorithm to solve the problem of the assignment of n facilities to n locations equally spaced along a straight line in order to minimise the MHC. To solve a dynamic FLP, Dunker et al. (2005) combined a GA to generate a set of candidate layouts with dynamic programming to evaluate the fitness function defined as the costs of material handling and rearrangements. The main weakness of these methods is that they cannot solve large scale FLPs because of the intractable and combinatorial nature of the problem (Ripon et al. 2013). They remain insufficient for realistically sized applications. Hence, heuristic techniques have been introduced to find near-optimal solutions for large size instances with reasonable computation time. These algorithms can be classified into construction, improvement, and hybrid algorithms. The construction algorithms build progressively a layout from scratch by placing a sequence of workstations until a completed layout is obtained. Some of the popular construction algorithms are the computerised relationship layout planning (CORELAP) (Lee and Moore 1967), automated layout design program (ALDEP) (Seehof and Evans 1967), and programming layout analysis and evaluation technique (PLANET) (Deisenroth and Apple 1972). The main drawback of these methods is that the final solution may be unsatisfactory in terms of quality as they generate only one solution. That is the reason why the improvement algorithms start with an initial solution and try then to improve it by swapping the location of facilities. The best-known examples of these methods are the computerised relative allocation of facilities technique (CRAFT) (Armour et al. 1964) and multi-floor plant layout evaluation (MULTIPLE) (Bozer et al. 1994). The hybrid algorithms utilise conjointly the principles of the construction and improvement algorithms. They generate the initial solution and attempt to improve it. BLOCPLAN is a hybrid algorithm (Donaghey and Pire 1990).

Because the FLP is known to be complex, in recent years, metaheuristics approaches have been developed to solve FLPs by GAs (Azadivar and Wang 2000; Shayan and Chittilappilly 2004; Wang et al. 2005; Mazinani et al. 2012; Vitayasak et al. 2016), simulated annealing (Tam 1992; Deb and Bhattacharyya 2003; Mckendall et al. 2006; Sahin and Turkbey 2009; Sahin 2011), tabu search (Chiang and Kouvelis 1996; Liang and Chao 2008; Samarghandi and Eshghi 2010; Bozorgi et al. 2015), ant colony optimisation (Solimanpur et al. 2004; Hani et al. 2007; Komarudin and Wong 2010), and particle swarm optimisation (Samarghandi et al. 2010; Jolai et al. 2012; Asl and Wong 2015; Wang et al. 2014). Interested readers are invited to refer to Kundu and Dan (2012) for an in-depth analysis of the different metaheuristics methods applied in FLPs.

Many hybrid algorithms have been proposed and used in the optimisation of manufacturing and design problems (Pholdee et al. 2017). For example, Moslemipour (2018) proposes a novel hybrid intelligent algorithm by combining the simulated annealing and clonal selection algorithms to solve uncertain dynamic FLPs. A GA combined with a strategy of partial solution deconstruction and reconstruction (PDR) is provided by Paes et al. (2017) to solve the unequal area FLP. Comprehensive comparisons of the efficiency of different optimisation algorithms have been presented by Karagöz and Yildiz (2017). However, Kiani and Yildiz (2016) suggest that it is not enough to present the best and worst results obtained by the used approach, but a comparative study must define whether the algorithms are significantly better than the others or not.

Table 2 provides a synthesis of the related papers in the literature, where the gaps and overlaps are identified with a spotlight on the resolution approaches. Several observations can be made regarding these research works. First, it can be noted that there are two basic types of objectives adopted in the mathematical models for the FLP. Some of them aim to minimise a function related to the travel of parts and operators (MHC, travel distance, etc.) while the others aim to maximise the satisfaction of the proximity requests between two facilities that exchange a large number of parts. Second, it has been noticed that most of the published papers adopted some constraints. Two sets of constraints are introduced: no overlaps are allowed between facilities and the facilities should remain within the site boundaries (Saraswat et al. 2015). However, other sets of constraints such as aisle structure, existing restrictions, and complex geometrical constraints (e.g., fixed barriers, green land, walls, etc.) are rarely considered.

Table 2 Summary of papers related to the FLP

According to the literature, the existing detailed layouts generally use either the rectilinear distance (Ahmadi and Akbari Jokar 2016; Gonçalves and Resende 2015; Heragu and Kusiak 1991; Khalil 1973) or the Euclidean distance (Tompkins and Reed 1976; Van Camp et al. 1991) to evaluate their efficiency. Nevertheless, these methods cannot be applied in the presence of obstacles and barriers. The last column of Table 2 lists the different techniques used to solve the layout problem.

Gaps to fill in FLP resolution

As it can be seen from Table 2, the most frequently used objective function in the FLP is the minimisation of the MHC (71%) followed by the minimisation of the total travelled distance by the material. The table shows that the most commonly used distance determinations are the rectilinear (76%) and Euclidean (6%), which have the shortcomings indicated in Sect. 1. Therefore, the main motivation of this research is to improve the distance computation in order to obtain the most realistic MHC. This was necessary because the facility structure is defined through obstacles and transportation routes. This consideration led to the use of ${\text{A}}^{ *}$. The generation of various candidate layouts was performed by using a GA because we rely on the fact that the FLP does not require a global optimum but a sufficiently good solution, as noticed by Mitchell (1998). This choice was guided by some other facts provided by past research works. In fact, Mazinani et al. (2012) argue that a GA provides better solutions in FLPs than other metaheuristics methods, while other authors have proved the effectiveness of GAs in finding ‘good enough’ solutions to many problems (Palomo-Romero et al. 2017; Aiello et al. 2013; Datta et al. 2011; Hernández Gress et al. 2011). Sadrzadeh (2012) demonstrated that a GA is still an appropriate strategy for addressing problems in many different fields. The genetic-based approaches applied to FLPs make it possible to explore the complex search spaces efficiently while guaranteeing a sound population diversity, i.e., to explore almost every part of the solution space thanks to its crossing and mutation mechanisms. These techniques are encapsulated in a general approach, which is defined hereafter.

Overview of used techniques

Method of calculation of distance between facilities

${\text{A}}^{ *}$ is an optimisation algorithm mainly utilised for determining the shortest paths in a two-dimensional grid, which was developed by Hart et al. (1972). The ${\text{A}}^{ *}$ algorithm aims at finding an efficient, directed path among all possible paths to a destination. Among the different possible paths, it first examines the ones that lead more quickly to the goal and puts aside all the others. All these possibilities are stored, but not removed, as it is not possible to know in advance whether a path is the shortest path or not. If this road reaches a deadlock, this solution becomes inoperable. As described in Zhou et al. (2013), the implementation of the ${\text{A}}^{ *}$ algorithm from source to destination includes the checking of many adjacent nodes, one after another. Using some internal indices, the ${\text{A}}^{ *}$ algorithm is directed towards the destination while detecting the shortest possible path. These indices are (i) the total travel cost from the start node to destination, (ii) the cost of the path from the start node to any intermediate node lastly studied on the path, and finally (iii) the cost of the cheapest path from any intermediate node to the destination. Interested readers may refer to Appendix 3 for a more technical description of the algorithm or to Rafia (2010) and Saleh (2015).

Overview of genetic algorithms (GAs)

The Holland GAs (1975) are robust metaheuristics used to solve difficult optimisation problems (Sadrzadeh 2012). The GA solves problems based on the evolution mechanisms and nature of genes (Mazinani et al. 2012). It operates with a set of problem solutions named population. Each individual of the population is a chromosome and represents a possible solution. The fitness value of an individual (solution) represents its quality according to a given objective function; the higher the fitness value is, the more valuable the solution. Usually, the initial population is randomly generated, although a set of known individuals can be used to launch the evolution process. Then, the GA makes this population evolve iteratively. At each iteration, the evolution process works as follows. A subset of individuals is selected as the parents based on their high fitness value. The next generation is obtained thanks to crossover and mutation. The crossover operator allows the combination of two selected parents to produce a better offspring. The mutation operator is used to introduce a new genetic structure in the population by rearranging the structure of a chromosome. Owing to the randomness nature of both crossover and mutation, some children may violate the constraints that all individuals in a population should respect. Therefore, there would be feasible and infeasible individuals among these newly born children. The infeasible or low performance individuals are excluded from the rest of the process. This iterative evolution process may be applied again to these children if the quality of the solutions is not satisfactory. The iterations are stopped if the gap between the ‘i-th’ and ‘(i + 1)-th’ generations is below a specified threshold. The GAs are sensitive to the parameters (size of population, crossover probability, etc.) and the crossover and mutation operators.

In the following sections, the GA steps are detailed. A GA is implemented in two parts: the initial steps and the iterative steps.

Initial steps of the GA application

• (1) Chromosome encoding and representation. Every individual should be encoded in a relevant way to make it usable for the whole solution determination. The encoding usually takes place after a mathematical modelling phase of the problem.

• (2) Generation of the initial population. A set of initial solution individuals is either generated randomly or defined by the users as a feasible solution via a heuristic, for example. It is also possible to initiate the algorithm by including ‘good’ or ‘already known’ solutions (Grefenstette 1986; Sadrzadeh 2012; Wu et al. 2007). In fact, the GA needs a number of initial solutions to initiate the exploration of the solution space. The randomly generated solutions can be feasible and unfeasible solutions. On the contrary, the ‘solutions found heuristically’ represent a population of known and feasible solutions obtained thanks to ground experience, and they can be used as the initial solutions.

• (3) Initial evaluation of individuals. A fitness function measures the quality of the solutions in the search space.

• (4) Filtering of individuals. The evolutionary algorithms are unconstrained optimisation techniques. First, the individuals are randomly generated without considering constraints. Then, their fitness is evaluated to exclude the worst individuals. Various published papers review the different approaches for handling of constraints (Coello 1999). Among others, Ponsich et al. (2007) identify the following classes: elimination of infeasible individuals, penalisation of their objective function, dominance concepts, preservation of feasibility, repairing of infeasible individuals, and hybrid methods. According to Coello (2002), the majority of studies comparing these constraint-handling techniques are inconclusive. Thus, he suggests to adopt the penalty-based approaches owing to their implementation simplicity and efficiency. The key idea of this technique is to transform a constrained problem into an unconstrained one by introducing the constraints in the objective function via penalty terms, which assign a high penalty to the infeasible solutions that violate at least one constraint.

At the end of this step, if the target performance of the individuals is reached, the algorithm is stopped. Otherwise, a set of iterations will be performed.

Iterations of the GA

The GA seeks to find the best solution over the generations through the following steps that define the process of creating new generations.

• (5) Selection of parents. The purpose is to create a mating pool consisting of individuals of the population to be combined to create the new generation. The mating pool is used by the crossover and mutation operators. Many selection operators exist to select the best chromosomes to be parents for reproduction. Table 9 in Appendix 4 presents the most cited selection operators with their advantages and shortcomings.

• (6) Crossover process. This is the first step for producing new individuals (children) from selected parents. The crossover process is specified thanks to (i) the crossover probability and (ii) the crossover operator.

The crossover probability ($P_{c}$). It is defined to show the proportion of the population of parents that will be chosen for mating via the crossover operator. Generally, the most used rates are between 0.45 and 0.95 (Al-Zuheri et al. 2014). If $P_{c}$ is 100%, then all offspring are obtained by crossover. If it is equal to 0%, the offspring represents an exact copy of the parents.

The crossover operator. The previous research works have defined various crossover operators: linear order crossover, uniform crossover, order crossover, etc. (Sastry et al. 2005; Eiben and Smith 2007; Dalle Mura and Dini 2017). The choice of a crossover operator is strongly linked to the kind of problem and the chromosome encoding. The majority of adopted crossover operators are applied to chromosomes that typically contain a gene sequence where the order is mandatory. In other crossover operators, the gene order is not considered. Among others, the N-point crossover techniques are used (see Appendix 5).

• (7) Mutation process. Mutation helps to maintain diversity in the population by preventing population stagnation at a local optimal solution. The mutation process is specified thanks to (i) the mutation probability and (ii) the mutation operator.

The mutation probability. It defines how often parts of chromosome will be rearranged. If $p_{m}$ is equal to zero for example, there is no mutation. By increasing this probability, more and more chromosomes will be mutated.

The mutation operator. The mutation operator is applied to two children generated by the crossover operation according to the probability $p_{m}$. The two main operators used for mutation are exchange and inversion (see Appendix 6).

• (8) Replacement and evaluation of the children fitness value. The new solutions or chromosomes can be better or worse than their parents are. Therefore, a replacement strategy is applied here to define the new population by keeping the best individuals. Strategies such as replacement, crowding, and elitist can be used for this purpose (Triki et al. 2016). To do so, each child is evaluated using the fitness function (as in step (3)). Thus, to avoid any loss of the best solutions, the elitist strategy retains the best genetic information of the initial population along with the individuals obtained by the crossing and mutation operators to use them for the next generation.

• (9) Stopping criteria. One or more criteria may be used to stop the iterations of the GA, such as maximum number of generations, fitness convergence, or computing time (Wu et al. 2007).

Overview of the proposed approach

The proposed approach of FLP resolution is structured in two phases, as presented in Table 3.

Table 3 Different steps of our proposed approach

Initialisation. The main objective is to minimise the MHC. A set of initial facility arrangements is defined and the distance between workstations is computed. The cost of future facility layouts are compared to the cost of these initial arrangements. The facility area is defined by its global constraints regarding its dimensions and the pre-defined positions of some restricted elements. A restricted element is a limited space within the area that has its own local constraints. A forbidden element is a restricted element, such as walls, stairs, or other barriers, that does not allow any equipment assignment and through which parts cannot pass. A selective element, such as a transportation corridor for materials, parts, and human beings, cannot be assigned to facilities but can be used by product flows. All the workstations are characterised by a rectangular shape whose dimensions are known in advance. The equipment position is defined thanks to the coordinates of the centroid.

Loops of${\mathbf{A}}^{*}$and GA application. The candidate layouts are generated by the GA. This algorithm is specified by its crossover and mutation operators and their parameters. The Monte Carlo simulation is used to determine their influence on the performance of the GA and to select the best set of operators and parameters. Finally, a penalty function is introduced in the GA to handle the violated constraints. The MHC of these layouts is computed.

The following sections define these two phases in detail.

Initialisation: FLP definition

The problem is to position n machines within a generic rectangular facility (see Fig. 1) with a fixed length (L) and width (W). The area is considered as a grid of uniform squares called surface units. An aisle, i.e., a selective element, allows transportation of goods and movement of operators. It is defined by the position of its lower and upper limits, (${\text{y}}_{\text{lower}}$) and (${\text{y}}_{\text{upper}}$). The area contains obstacles, i.e., the forbidden elements (the thick blue line in the figure). Around each forbidden element, an accessibility plan is defined (one unit element at all sides) to prevent the case of having a machine placed side by side with an obstacle. A machine i is defined by its horizontal (${\text{w}}_{\text{i}}$) and vertical (${\text{l}}_{\text{i}}$) dimensions and the coordinates of its centroid (${\text{x}}_{\text{i}} ,{\text{y}}_{\text{i}}$).

Fig. 1

Representation of the layout problem

The following variables and symbols are used to model the FLP:

Parameters

N:

Number of machines

P:

Number of products

L:

Fixed length of shop floor

W:

Fixed width of shop floor

M:

Number of obstacles

${\text{l}}_{\text{i}}$ :

Length of machine i

${\text{w}}_{\text{i}}$ :

Width of machine i

$l_{oi}$ :

Length of obstacle i

$w_{oi}$ :

Width of obstacle i

$x_{oi}$ :

The x coordinates of the geometric centre of obstacle i

$y_{oi}$ :

The y coordinates of the geometric centre of obstacle i

${\text{y}}_{\text{lower}}$ :

Vertical coordinates of the lower side/wall of aisle

${\text{y}}_{\text{upper}}$ :

Vertical dimension of the upper side/wall of aisle

${\text{f}}_{\text{ij}}$ :

Number of trips between two machines

${\text{c}}_{\text{ij}}$ :

Unit cost for transportation over a distance of one unit element from machine i to machine j

Decision variables

${\text{x}}_{\text{i}}$ :

The x coordinates of the geometric centre of facility i

${\text{y}}_{\text{i}}$ :

The y coordinates of the geometric centre of facility i

$Z_{ij}^{x}$ :

$\left\{ {\begin{array}{*{20}l} { = 1{\text{ if facility i is strictly to the right of facility }}j\left( {x_{i} > x_{j} } \right)} \hfill \\ {0{\text{ otherwise}}} \hfill \\ \end{array} } \right.$

$Z_{ij}^{y}$ :

$\left\{ {\begin{array}{*{20}l} {{\text{ = 1 if facility i is strictly above facility j}} (y_{i} > y_{j}}) \hfill \\ {0{\text{ otherwise}}} \hfill \\ \end{array} } \right.$

$Z_{iv}^{x}$ :

$\left\{ {\begin{array}{*{20}l} {\text{ = 1 if obstacle i is strictly to the right of facility v}} \hfill \\ { 0 {\text{ otherwise}}} \hfill \\ \end{array} } \right.$

$Z_{iv}^{y}$ :

$\left\{ {\begin{array}{*{20}l} {\text{ = 1 if obstacle i is strictly above facility v}} \hfill \\ { 0 {\text{ otherwise}}} \hfill \\ \end{array} } \right.$

Fit function

MHC:

$$ {\text{MHC }} = \mathop \sum \limits_{{{\rm{p}} = 1}}^{\text{P}} \mathop \sum \limits_{{{\rm{i}} = 1}}^{\text{N}} \mathop \sum \limits_{{{\rm{j}} = 1}}^{\text{N}}\,{\text{f}}_{{\rm ij}}^{{\rm p}} \ast {\text{c}}_{{\rm ij}} \ast {\text{K}}_{{\rm ij}} $$

(1)

Constraints:

$$ \frac{{{\text{l}}_{\text{i}} }}{2} \le {\text{x}}_{\text{i}} \le {\text{L}} - \frac{{{\text{l}}_{\text{i}} }}{2} \quad \forall {\text{i}} = 1 \ldots {\text{N}} $$

(2)

$$ \frac{{{\text{w}}_{\text{i}} }}{2} \le {\text{y}}_{\text{i}} \le {\text{W}} - \frac{{{\text{w}}_{\text{i}} }}{2} \quad \forall {\text{i}} = 1 \ldots {\text{N}} $$

(3)

$$ \left( {{\text{x}}_{\text{j}} - {\text{x}}_{\text{i}} } \right) > {\text{Z}}_{\text{ij}}^{\text{x}} \left( {\frac{{{\text{l}}_{\text{i}} }}{2} + \frac{{{\text{l}}_{\text{j}} }}{2}} \right)\quad \forall {\text{i}},{\text{j}} = 1 \ldots {\text{N}} \quad {\text{with i}} \ne {\text{j}} $$

(4)

$$ \left( {{\text{x}}_{\text{i}} - {\text{x}}_{\text{j}} } \right) > (1 - {\text{Z}}_{\text{ij}}^{\text{x}} )\left( {\frac{{{\text{l}}_{\text{i}} }}{2} + \frac{{{\text{l}}_{\text{j}} }}{2}} \right) \quad \forall {\text{i}},{\text{j}} = 1 \ldots {\text{N}} \quad {\text{with i}} \ne {\text{j}} $$

(5)

$$ \left( {{\text{y}}_{\text{j}} - {\text{y}}_{\text{i}} } \right) > {\text{Z}}_{\text{ij}}^{\text{y}} \left( {\frac{{{\text{w}}_{\text{i}} }}{2} + \frac{{{\text{w}}_{\text{j}} }}{2}} \right)\quad \forall {\text{i}},{\text{j}} = 1 \ldots ..{\text{N}}\quad {\text{with i}} \ne {\text{j}} $$

(6)

$$ \left( {{\text{y}}_{\text{i}} - {\text{y}}_{\text{j}} } \right) > (1 - {\text{Z}}_{\text{ij}}^{\text{y}} )\left( {\frac{{{\text{w}}_{\text{i}} }}{2} + \frac{{{\text{w}}_{\text{j}} }}{2}} \right) \quad \forall i,j = 1 \ldots N\quad {\text{with i}} \ne {\text{j}} $$

(7)

$$ \left( {{\text{x}}_{\text{v}} - {\text{x}}_{\text{oi}} } \right) > {\text{Z}}_{\text{iv}}^{\text{x}} \left( {\frac{{{\text{l}}_{\text{oi}} }}{2} + \frac{{{\text{l}}_{\text{v}} }}{2}} \right)\quad \forall {\text{i}} = 1 \ldots {\text{M,}}\quad \forall {\text{v}} = 1 \ldots {\text{N}} $$

(8)

$$ \left( {{\text{x}}_{\text{oi}} - {\text{x}}_{\text{v}} } \right) > (1 - {\text{Z}}_{\text{iv}}^{\text{x}} )\left( {\frac{{{\text{l}}_{\text{oi}} }}{2} + \frac{{{\text{l}}_{\text{v}} }}{2}} \right)\quad \forall {\text{i}} = 1 \ldots {\text{M,}}\quad \forall {\text{v}} = 1 \ldots {\text{N}} $$

(9)

$$ \left( {{\text{y}}_{\text{v}} - {\text{y}}_{\text{oi}} } \right) > {\text{Z}}_{\text{iv}}^{\text{y}} \left( {\frac{{{\text{w}}_{\text{oi}} }}{2} + \frac{{{\text{w}}_{\text{v}} }}{2}} \right)\quad \forall {\text{i}} = 1 \ldots {\text{M, }}\quad \forall {\text{v}} = 1 \ldots {\text{N}} $$

(10)

$$ \left( {{\text{y}}_{\text{oi}} - {\text{y}}_{\text{v}} } \right) > (1 - {\text{Z}}_{\text{iv}}^{\text{y}} )\left( {\frac{{{\text{w}}_{\text{oi}} }}{2} + \frac{{{\text{w}}_{\text{v}} }}{2}} \right)\quad \forall {\text{i}} = 1 \ldots..{\text{M, }}\quad \forall {\text{v}} = 1 \ldots ..{\text{N}} $$

(11)

$$ \left( {\left( {{\text{y}}_{\text{i}} + \frac{{{\text{w}}_{\text{i}} }}{2}} \right) - {\text{y}}_{\text{lower}} } \right) \left( {{\text{y}}_{\text{upper}} - \left( {{\text{y}}_{\text{i}} - \frac{{{\text{w}}_{\text{i}} }}{2}} \right)} \right) < 0 \quad \forall {\text{i}} = 1 \ldots ..{\text{N}} $$

(12)

$$ \left( {\left( {{\text{x}}_{\text{i}} + \frac{{{\text{l}}_{\text{i}} }}{2}} \right) - {\text{x}}_{\text{lower}} } \right)\left( {{\text{x}}_{\text{upper}} - \left( {{\text{x}}_{\text{i}} - \frac{{{\text{w}}_{\text{i}} }}{2}} \right)} \right) < 0 \quad \forall {\text{i}} = 1 \ldots {\text{N}}$$

(13)

$$ {\text{Z}}_{\text{ij}}^{\text{x}} \in \left\{ {0,1} \right\}\quad \forall 1 \le {\text{i}},{\text{j}} \le {\text{N}} $$

(14)

$$ {\text{Z}}_{\text{ij}}^{\text{y}} \in \left\{ {0,1} \right\}\quad \forall 1 \le {\text{i}},{\text{j}} \le {\text{N}} $$

(15)

$$ {\text{Z}}_{\text{iv}}^{\text{x}} \in \left\{ {0,1} \right\}\quad \forall 1 \le {\text{i}} \le {\text{N }}\quad \forall 1 \le {\text{v}} \le {\text{M}} $$

(16)

$$ {\text{Z}}_{\text{iv}}^{\text{y}} \in \left\{ {0,1} \right\}\quad \forall 1 \le {\text{i}} \le {\text{N }}\quad \forall 1 \le {\text{v}} \le {\text{M}} $$

(17)

$$ {\text{All other variables }} > = 0 $$

(18)

Equation (1) minimises the cost of the material flow between machines. Constraint sets (2) and (3) ensure that the machines are assigned within the boundaries of the shop floor. Constraint sets (4)–(7) prevent overlapping of machines. Constraints (8)–(11) prevent overlapping between machines and obstacles. Constraints (12) and (13) ensure that no machine would be assigned in the aisle boundaries. Finally, constraints (14)–(18) define the domains for the different variables.

Iterative application of intertwined GA/${\mathbf{A}}^{*}$

The very first step of the GA application is to design a relevant coding for the individuals. We use the equipment centroid to encode the position of each machine by the couple (x,y). Each couple (x,y) is a gene; x and y are the alleles of this gene. There are n machines to place in the facility defined by its limits, the points A, B, C, and D in Fig. 1. It is placed on a 2D orthonormal coordinate plan. The origin of the plan is positioned on the lower left corner of the area, point A in Fig. 1. Each chromosome is composed of 2 × n genes, as shown in Fig. 2. The n alleles { $x_{1} \ldots x_{n}$ } form a vector. This vector represents the position of the machines in the horizontal direction and { $y_{1} \ldots y_{n}$ } defines their position in the vertical direction. The pseudocode of our algorithm is presented below.

Fig. 2

Chromosome associated to the location variables

The other specialisations of the used algorithms are defined hereafter:

Generation of the initial population	The initial-solution individuals are generated randomly
Evaluation of initial individuals	Evaluation of the MHC based on computation of the shortest distances between workstations (using ${\text{A}}^{ *}$), see Eq. (1)
Filtering of individuals	The penalty-based approach.
Selection of parents	Roulette wheel (Michalewicz 1994) and tournament (Goldberg and Deb 1991)
Crossover process
Crossover probability ($P_{c}$)	A normal distribution with $\mu = 0.7$ and $\sigma = \, 0.1$ is used.
Crossover operator	One point crossover (Holland 1975), two point crossover (Starkweather et al. 1991), three point crossover, four point crossover
Mutation process
Mutation probability	A normal distribution with $\mu = 0.18$ and $\sigma = \, 0.06$ is used.
Mutation operator	Exchange and inversion operator
Evaluation of the children fitness value	The elitist strategy
Stopping criteria	130 iterations (the fitness function cannot be further improved)

Tuning of GA parameters by Monte Carlo simulation

The performance of a GA relies on setting the values of the basic parameters, such as crossover probability, mutation probability, population size, and selection strategy. However, the local optimum solutions may survive throughout the algorithm if improper parameters are set. To solve this problem, several methods, such as the full factorial design and Taguchi method, are used to calibrate the parameters that influence the performance of a metaheuristic algorithm (Pourvaziri and Naderi 2014). We use the Monte Carlo simulation principle to identify the effects of the GA parameters on the quality of layout generation. Monte Carlo simulations are powerful tools to investigate randomised trials (Yang and Tian 2012). They produce results that are in good agreement with most of the randomised trials.

The experiments are generated to examine the effects of the population size (N), crossover probability ($P_{c} )$, mutation probability ($P_{m} )$, and behaviour of the operators (selection, crossover, and mutation). The parameters of the applied Monte Carlo simulation are the following (Fig. 3):

Fig. 3

Monte Carlo simulation

• Population size (number of layouts simultaneously considered in the experiment). It is randomly generated between 100 and 250 following a uniform probability distribution. This allows a sufficiently large population for every simulation. There is no preference of size between the limits.

• Crossover probability. We use a normal distribution with a mean of 0.7 and a standard deviation of 0.1. In this way, we guarantee that new individuals will be introduced, which may be better than the old ones (Angelova and Pencheva 2011).

• Mutation probability. It is generated according to a normal distribution with a mean of 0.18 and a standard deviation of 0.06. By choosing this distribution, it is guaranteed that the mutation will affect a few members of a population in any given generation, and small diversions in the genetic structures of the parents will be introduced.

A difference between the roulette wheel and tournament selection methods is revealed. The two simulation results are provided in Appendixs 1 and 2 to study the impact of selection operators on the output of our proposed approach. The crossover and mutation operators also affect the performance of the GA. We choose to make a comparison between {one point, two points, three points, four points} crossover operators and also between the exchange and inversion mutation operators. Therefore, in each iteration, one of these crossover and mutation operators is chosen randomly and applied to the selected parents. Each of these operators has an equal probability of being chosen.

Simulations with these operators and parameters are conducted, giving a total of 100 runs for the Monte Carlo simulation and 130 iterations for the GA.

Experiments

To evaluate the efficiency of the proposed approach, we use an illustrative case inspired by an industrial case we studied in (Besbes et al. 2017). The proposed algorithm has been applied to a layout of eight facilities that must be arranged in a plant floor with 30 * 20 square surface units. An aisle with the same length as the plant configuration layout and two different vertical dimensions ($y_{lower} = 9\, {\text{and}} \,y_{upper} = \, 12$) was considered. The input data corresponding to the obstacles are presented in Table 4.

Table 4 Input data of obstacles

The quantity of material flow between machines is presented in Table 5. This matrix is extracted from Appendix 7. For each couple of facilities, the unit cost to move one product per unit distance from facility i to facility j is fixed equal to 1 monetary unit. The resolution method of the model was programmed and implemented in Matlab and run on an Intel(R)Core™ i5 3360 M CPU@2.8 GHZ processor with 8 GB RAM. The Monte Carlo simulations are used afterwards to make a sensitivity analysis of the used GAs against its various parameters.

Table 5 Quantity of material flow from facility i to facility j

The parameter values for the proposed method and the obtained MHC for each obtained configuration are described in Appendixs 1 and 2.

In the first set of tests, the roulette (wheel selection) operator is used to select parents in order to create better offspring. The second set of tests is done with the tournament operator.

Roulette operator

The best and worst solutions, in terms of the fit function obtained over 100 Monte Carlo simulations by roulette are illustrated in Fig. 5a. This Figure shows the best and worst MHC under different Monte Carlo simulations and the corresponding crossover and mutation probabilities. The best solution (minimum cost) obtained by the roulette operator is 272 and the worst one is equal to 487 (Appendix 1). Figure 12a in Appendix 8 demonstrates the convergence to the best function value of the layout problem. The corresponding layouts are represented in Fig. 6a, b. The machines are not overlapped. Each machine is characterised by its centroid ($x_{i} ,y_{i} )$, a predetermined length $l_{i}$, and width $w_{i}$. The obtained results demonstrate that between each couple of machines there is a distance $d_{ij} \ge$ 1, as shown in Fig. 4b, and there is not a common surface between two machines as illustrated in Fig. 4a.

Fig. 4

Illustrative example of the FLP: machines are overlapped (a) and machines are not overlapped (b)

In the same Fig. (6a, b), we report the shortest paths found by ${\text{A}}^{ *}$, represented by coloured broken lines. The corresponding heat map of distances is illustrated in Fig. 7, in the top maps. These figures show the contrast between the best and the worst solutions obtained by the roulette operator.

Tournament operator

Applying the tournament operator, the cost of the best and worst solutions found by the GA combined with the ${\text{A}}^{ *}$ algorithm over the 100 Monte Carlo simulations are illustrated in Fig. 5b. The best-fit function value of the FLP is equal to 267 and the worst one is equal to 464. Figure 12b in Appendix 8 presents the convergence to the best function value of the layout problem. The configurations associated with the best and the worst solutions are given in Fig. 6c and d. All the machines respect all the constraints. The shortest path values using the ${\text{A}}^{ *}$ algorithm are reported in Appendix 9, and the corresponding heat map of distances is illustrated in Fig. 7.

Fig. 5

Best fitness function value versus experiences of the Monte Carlo simulation: roulette operator (a) and tournament operator (b)

Fig. 6

Monte Carlo simulations and product flow obtained by A* algorithm: best (a) and worst (b) layouts found via roulette, best (c) and worst (d) layouts found via tournament in the Monte Carlo simulations

Fig. 7

Heat map of distances obtained by roulette and tournament

Discussion of the obtained results

Regarding all the experimentations performed, the combination of GA parameters that produces the best results is the following:

• Population size is 194

• Crossover probability is 0.8049

• Mutation probability is 0.1024

• Selection operator is tournament

As shown in Fig. 8, the best MHCs found by the approach with the Monte Carlo simulations, for both the tournament and roulette operators, follow a normal distribution. These variations can be represented by the mean μ and the standard deviation $\sigma$, as reported in the following table.

Fig. 8

Probability associated with normal distribution of the fitness function

Roulette wheel selection method	Tournament selection method
$\mu_{r} = \, 359.61$	$\mu_{t} = \, 374.39$
$\sigma_{r} = 40.1147$	$\sigma_{t} = 36.3092$
$cv_{r} = \frac{{\sigma_{r} }}{{\mu_{r} }} = 11.15\%$	$cv_{t} = \frac{{\sigma_{t} }}{{\mu_{t} }} = 9.70\%$

It might be observed that $\upmu_{\text{r}} <\upmu_{\text{r}}; \, {\text{however}},$$\sigma_{r} > \sigma_{t}$. This means that by focusing only on the mean value, the tournament operator gives in general better solutions than the roulette wheel selection method. However, the density of MHCs is lower than that provided by the roulette operator. By comparing the standard deviations of these two operators, it might be concluded that the tournament gives a distribution less flattened. However, to compare these two distributions appropriately, we use the coefficient of variations. In this case, it can be concluded that these two distributions remain quite similar owing to the very low difference between their coefficients of variations. The final conclusion about the use of these two operators is that the roulette operator tends to suggest more effective configurations with less MHC. However, it is necessary to apply both operators to be sure that the obtained configuration reduces as much as possible the MHC (the best configurations obtained for the roulette and tournament operators are shown in Fig. 6a, c).

These results show the practicability and applicability of the suggested method. Further, they demonstrate that the proposed method is efficient and useful for the placement of a set of rectangular machines with defined area requirements, which have to be located, without overlapping, in a given organisation satisfying a set of constraints. The main advantage of the proposed approach is its ability to explore a large space of solutions, keeping the practicability of the design and considering more realistic distances between the facilities.

Finally, as presented in Table 6, the proposed approach gives a better solution than a GA integrated with Euclidean or rectilinear distances. By using the roulette wheel selection method, the MHC is decreased by 8.93% compared to that with Euclidean distance, and by 33% compared to that with rectilinear distance. As for the tournament selection method, the MHC is decreased by 13.15% compared to that with Euclidean distance and by 36.7% compared to the one with rectilinear distance.

Table 6 Comparison of total cost associated with the Euclidean and rectilinear distances and A* algorithm

Finally, once the best configuration is obtained, the approach determines the best theoretical routes for products from one workstation to another (see in Fig. 6 the configurations with an extract of the routes to obtain a clearer visibility). Hence, it can be presented as a good basis for the development of an advanced support tool to help engineers and designers in determining the most effective layout through a realistic approach. The convergence of the used algorithms is based on genetic parameters, and it is significantly influenced by the population size and the probabilities of crossover and mutation. These solutions are characterised by different values of the fit function. Nevertheless, all of the solutions (the facility arrangements) satisfy all of the constraints and path requirements. Observing the best and worst solutions obtained in both cases, we notice that, in the first one, most equipment units share the same accessibility plan to allow the transportation of materials and operators. In fact, all the facilities are concentrated in a determined location. Consequently, the remaining space in the workshop can be employed for other usages (storage, for example) or new value-added equipment. On the contrary, in the worst solutions, the workstations are distributed and scattered across the plant floor. Each machine has its own accessibility plan. This aspect could be attractive for the decision makers when negative factors (e.g., bad smells and noise) that have not been modelled in the FLP formulation exist within a physical spatial environment, and thus, it is necessary to avoid certain locations for particular facilities. However, if this is not the case, a significant amount of space, which can be exploited for other activities, will be lost.

The best class of configurations may need adjustment by the decision makers if the company needs to include qualitative considerations in the design.

Conclusions and future scope of work

This work proposes a new approach to solve the FLP. The main idea is to arrange facilities in a planar site while taking into account various kinds of geometric facility requirements. Some issues, such as site boundaries, overlap elimination, and aisle and obstacle consideration, were mathematically formulated. The objective is to minimise the MHC.

GAs are adopted in the literature to solve large facility design problems. A GA combined with ${\text{A}}^{ *}$ allows to explore the solution space. The ${\text{A}}^{ *}$ algorithm is used as a new method to determine the shortest path between two facilities. The GA involves chromosome encoding and generation of initial population, fitness function definition, and choice of the selection strategy and the crossover and mutation operators, while defining the handling constraints and stopping criteria.

The proposed algorithm parameters are calibrated using Monte Carlo simulations. The whole approach is applied on an illustrative case and the obtained results show the practicability and applicability of the proposed model. The random variation of the parameters provides one solution for each simulation. Our simulations produce two classes of arrangements. In the first class, the different workstations are concentrated in a determined location. In the second class, the machines are scattered across the workshop. The discussions about the results show that expert knowledge is required to adapt the final solution to the un-modelled usage constraints, i.e., those ones difficult to model through a mathematical model. For future studies, the method should evaluate solutions in terms of flow density on plant aisles in order to make it possible, for example, the identification of potential critical cross points. In addition, some rules can be incorporated to obtain diverse layout configurations, and the most suitable one could be chosen among them. For example, we should avert bypassing and backtracking and eliminate the overlap of all kinds of flows in order to reduce the risk of collisions. The shape of the existing plant floor is another element that can be considered. In fact, a real area can have regular shapes or it could be irregular. In a future research work, the authors aim to integrate these constraints as well as some parameters such as the machines’ types, their supply of parts and delivery of products/components and the potential reworking in the proposed method and to validate its effectiveness through the application to real cases.

Appendices

Appendix 1

See Table 7.

Table 7 Experiment layout and sample experimental data (RWS method)

Appendix 2

See Table 8.

Table 8 Parameter sets of the proposed GAs (tournament selection)

Appendix 3

The A* algorithm seeks a new measure of distance (see Fig. 9). It starts by placing the starting node in the open list called current node. The open list contains the list of nodes to be verified. It consists of nodes that have been visited but not explored yet. After inspecting its entire adjacent squares, the starting node is removed from the open list and placed in another list named closed list. The closed list contains all the nodes that, at one time or another, have been considered as part of the solution path. Before switching to the closed list, a node must first pass through the open list. Before being judged as good, it must first be studied by looking at all surrounding squares of the starting point while ignoring squares with obstacles. These studied nodes are also added to the open list. For each of these squares, the current node is saved as its ‘parent square’. The parent square is required when we want to trace the path. To determine if a node is susceptible to be part of the solution path, it is necessary to quantify its quality. To do this, we calculate the distance between the point studied and the last point that was judged as good. We also calculate the distance between the point studied and the point of destination. The sum of these two distances gives the quality of the studied node. This operation will be carried on until the target node is reached.

Fig. 9

Different shortest paths between two facilities: rectilinear, Euclidean, A* Algorithm

Appendix 4

See Table 9.

Table 9 Advantages and disadvantages of different selection strategies

Roulette wheel selection. A chromosome is selected from the mating pool with a probability proportional to its fitness value. A chromosome with a high fitness value has a higher chance of being selected as a parent. Thus, the main idea is to prefer better solutions to worse ones. Consider a circle divided into n slices, where n is the number of individuals in the population. Each individual is assigned a slice of the roulette wheel, which is proportional to its fitness value. A pointer is chosen on the wheel circumference and the wheel is rotated in a repetitive way. The portion of the wheel that is in front of the fixed point is chosen as the parent.

Tournament selection. N individuals are randomly taken up from the population in a tournament selection. A copy of the best individual (based on fitness values) is kept in the mating pool as a parent. The number of individuals competing in each tournament is referred to as the tournament size.

Appendix 5

N point crossover. Almost all of the N point crossover processes use the same strategy. Hereafter, we define the single point crossover. A split line is randomly determined between 1 and (n − 1) genes (see Fig. 10), where n is the number of genes. Each parent is divided into two blocks of alleles. The portion before the split line is exchanged between the parents to create two new solutions, as illustrated in Fig. 10. This crossover operation is analogue to the binary crossover operation of GAs.

Fig. 10

a Before single point crossover, b after single point crossover

See Fig. 10.

Appendix 6

Several types of mutation exchange and inversion operators are used at this step to permute two or more workstations. The exchange mutation performs a swap of two randomly selected genes. For instance, in Fig. 11, the two genes (x2, y2) and (x4, y4) are swapped. The inversion operator consists in selecting two genes randomly and inverting the position in the chromosome between these two blocks as shown in Fig. 12.

Fig. 11

Exchange operator

Fig. 12

Inversion operator

See Figs. 11, 12.

Appendix 7

Pre-treatment phase In this study, we try to determine the most efficient arrangement of equipment in an area of such company that produce four products {A-E-C-H} and five semi-final products {G-D-B-F-I}. The assembly of G and D gives the product A and the product E comes from the assembly of B, F and I. Data of the products of our problem are provided in Table 10.

Table 10 Data of the products of our problem

Appendix 8

See Fig. 13.

Fig. 13

Best cost versus number of iterations, roulette operator (a) and tournament operator (b)

Appendix 9

SeeTable 11.

Table 11 Obtained distance among equipment units according to the roulette and tournament operators