Introduction

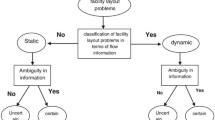
Facility layout problems (FLPs) cope with finding the locations of departments, or facilities in a shop floor in order to minimize the sum of the material handling costs. According to Tompkins et al. (2010), facility design will be one of the most momentous areas in the manufacturing environment in the future. Approximation shows that 20–50 % of the overall operating cost within manufacturing environments are allocated to material handling, and an effective facilities arrangement can reduce it by 10–30 % (Tompkins et al. 2010). According to Fig. 1, two main categories of FLPs that can be considered are: static facility layout problems (SFLPs) and dynamic facility layout problems (DFLPs). In SFLPs, material flows among facilities are stable throughout the time horizon, and this type of formulation is suitable for industries where the material flows among facilities do not change for a long duration. Nevertheless, SFLPs are not appropriate in some industries because companies must be able to respond quickly to changes in product demand. Thus, DFLPs have gained attention since 1986. DFLPs are the extension of SFLPs such that the material flows among facilities can be changed in different periods but are fixed in each period. In DFLPs, the time horizon is split into a number of periods, which could be years, seasons, months, or weeks. The solution for a DFLP is one layout for each period but it is a single layout for an SFLP. Broadly, FLPs can be split into two parts, the first is those with equal areas and the second is those with unequal areas. In the former, each of the facilities or departments has the same area. However, this is not the case in the latter. In accordance with Fig. 1, SFLPs are divided into two categories, the first is equal-area SFLPs (EA SFLPs) and the second is unequal-area SFLPs (UA SFLPs). Similarly, there are two divisions for DFLPs as follows: equal-area DFLPs (EA DFLPs) and unequal-area DFLPs (UA DFLPs). Specifically, there are three main categories for UA DFLPs, which are: (1) UA DFLPs where the areas and shapes of departments or facilities are fixed throughout the time horizon, (2) UA DFLPs where the areas of departments or facilities are fixed in all periods but their shapes are not constant and can change in consecutive periods, and (3) UA DFLPs where both the areas and shapes of departments or facilities are not fixed and can change in consecutive periods. In a factory, application of any change in the areas and shapes of departments or facilities is costly, and the management prefers to reduce the cost in all situations (Yang and Peters 1998). Therefore, this article focuses on UA SFLPs and UA DFLPs where the areas and shapes of departments are constant and cannot change throughout the time horizon.

Fig. 1
figure 1

Types of FLPs

Full size image

Drira et al. (2007) stated that FLPs are complex and NP-hard. Thus, exact approaches could not solve them within a reasonable computational time when the number of departments increases. Their complexity increases when the problems are dynamic. To find good layouts for problems in an efficient manner, it is essential to select a strong meta-heuristic algorithm (Yildiz and Solanki 2012). PSO has few parameters to set and has an effective global search method. Furthermore, in comparison with other meta-heuristic algorithms, the implementation of PSO is easy and simple (Moslemipour et al. 2012). Therefore, this paper utilizes a modified PSO algorithm for solving UA SFLPs and UA DFLPs where the areas and shapes of departments are fixed.

The structure of this paper is as follows: a literature review of UA SFLPs and UA DFLPs is provided in “Literature review” section. The mathematical models developed for UA SFLPs and UA DFLPs are presented in “Mathematical formulation for UA SFLPs and UA DFLPs” section. In “Modified particle swarm optimization (PSO) for solving UA SFLPs and UA DFLPs” section, a modified PSO is proposed for solving them. “Numerical experiments and parameter settings” section is allocated for numerical experiments and parameter settings. In “Results and discussion” section, the results of the proposed algorithm are presented and discussed. Finally, conclusions are provided in “Conclusions” section.

Literature review

FLPs were originally introduced by Koopmans and Beckmann (1957). Two industrial problems with equal-size departments were investigated in order to minimize the material handling costs. Equal-size departments are rarely practical in the industry and real-world competitive market; therefore, Armour and Buffa (1963) formulated the UA SFLPs. Imam and Mir (1989) investigated UA SFLPs and solved two problems with a search algorithm named TOPOPT. Heragu and Kusiak (1991) introduced two models for UA SFLPs which were: single row layout and multi-row layout. A heuristic algorithm was then proposed for solving the problems. Imam and Mir (1993) extended their earlier study and proposed a heuristic method named FLOAT, which created better solutions in contrast to TOPOPT. Mir and Imam (2001) developed a new modified optimization approach (i.e. modified simulated annealing) named HOT for solving UA SFLPs. The results of the HOT approach showed that it created better layouts in comparison with the FLOAT and TOPOPT methods. Xiao et al. (2013) studied UA SFLPs with input/output points and used a two-step heuristic method for solving the problems. SFLPs are not appropriate in some industries because companies must be able to respond quickly to changes in product demand and product price. Thus, researchers have started to focus on DFLPs.

In this respect, EA DFLPs were formulated by Rosenblatt (1986) to minimize the sum of the rearrangement costs and the sum of the material handling costs. He solved the problems using dynamic programming. UA DFLPs were originally formulated by Montreuil and Venkatadri (1991). The length and width of departments could change in consecutive periods but the areas of departments were fixed in all periods. They applied a heuristic algorithm in order to minimize the ‘expected flow traveled’. Lacksonen (1994) investigated UA SFLPs, and UA DFLPs where the shapes and areas of departments could change throughout the entire time horizon. He used a two-stage method for solving the problems, where an improved cutting plane heuristic was used in stage one for solving a quadratic assignment problem and a mixed integer linear programming model was applied in stage two for finding the block diagram arrangements. Subsequently, Lacksonen (1997) proposed a new heuristic method for solving UA DFLPs and showed that this approach created better layouts in comparison with the two-stage method. Yang and Peters (1998) examined UA DFLPs and formulated multiple scenarios where the shapes and areas of departments were fixed. Then, they solved the problems with a heuristic method. Dunker et al. (2005) examined UA DFLPs where the shapes and areas of departments were fixed throughout the time horizon. They joined dynamic programming and genetic algorithm (GA) for solving the problems. Likewise, McKendall and Hakobyan (2010) looked into UA DFLPs where the shapes and areas of departments were fixed and a two-stage algorithm was used to solve the problems. However, they did not report the sum of the rearrangement costs and only the sum of the material handling costs was announced. Multi-objective UA DFLPs with input/output points were formulated by Jolai et al. (2012). They proposed a mathematical model and used a multi-objective PSO to find the solutions. UA DFLPs where the shapes and areas of departments could change throughout the time horizon were formulated by Mazinani et al. (2012). The flexible bay structure (FBS) was used to simplify the problems, and GA was applied to solve them.

It is clear that there is no research on using PSO in the field of UA SFLPs and UA DFLPs where the shapes and areas of departments are fixed. This research aims to solve the problems with a modified PSO under the following constraints: (1) departments have rectangular or square shapes, (2) shape and area of each department are constant for the whole time horizon, (3) departments have free orientation (i.e. the length and width of a department can be exchanged), (4) all departments cannot overlap with each other, (5) there are several periods for material flow when the problem is dynamic, (6) all departments must be arranged in a given area, (7) rectilinear distance is used for calculating the distance between two departments, and (8) objective function minimizes the sum of the material handling costs for static problems, and minimizes the sum of the material handling costs and the sum of the variable and fixed rearrangement costs for dynamic problems.

Mathematical formulation for UA SFLPs and UA DFLPs

Two mixed integer nonlinear programming (MINLP) formulations are proposed for UA SFLPs and UA DFLPs where the shapes and areas of departments are fixed throughout the time horizon, to create a continuous arrangement. The notations are given as follows:

Indexes

\(i, j\) :

Indexes of department

\(t\) :

Index of period

\(n\) :

Number of departments

\(T\) :

Number of periods

Parameters

\(f_{ij}\) :

Frequency of material flow from department \(i\) to department \(j\)

\(W\) :

Length of shop floor

\(H\) :

Width of shop floor

\(w_i\) :

Length of department \(i\)

\(h_i\) :

Width of department \(i\)

\(d_{ij}\) :

Rectilinear distance or city block distance between departments \(i\) and \(j\)

\(A_{it}\) :

Fixed rearrangement cost for department \(i\) in period \(t\)

\(R_{it}\) :

Variable rearrangement cost for department \(i\) in period \(t\)

\(f_{ijt}\) :

Frequency of material flow from department \(i\) to department \(j\) in period \(t\)

\(d_{ijt}\) :

Rectilinear distance or city block distance between departments \(i\) and \(j\) in period \(t\)

\(P_{it}\) :

Rectilinear distance or city block distance to move department \(i\) from period \(t\) to period \(t+1\)

Variables

\((x_i,y_i)\) :

Center-coordinate of department \(i\)

$$\begin{aligned} r_i =\left\{ {{\begin{array}{ll} 1 &{} \quad if \, length \, and \, width \, of department \,i\, exchange \\ &{}\quad in \, comparison \, with \, original \, length \, and \, width \\ &{}\quad of \, department \,i\,(i.e.\, if orientation \, of \\ &{} \quad department\,i\,changes\,in\,comparison\,with \\ &{}\quad original\,orientation\,of\,department\,i) \\ 0 &{}\quad otherwise \\ \end{array} }} \right. \end{aligned}$$
\((x_{it},y_{it})\) :

Center-coordinate of department \(i\) in period \(t\)

$$\begin{aligned}&r_{it} =\left\{ {{\begin{array}{ll} 1 &{}\quad if\,length\,and\,width\,of\,department\, i\, exchange \\ &{}\quad \quad in\,period\,t\,in\,comparison\,with\, \\ &{}\quad original\,length \,and\,width\,of\,department\,i\, \\ &{}\quad (i.e.\,if\,orientation\, of\,department\,i\, \\ &{}\quad changes\,in\,period\,t\,in\,comparison\,with\, \\ &{}\quad original\,orientation\,of\, department \,i) \\ 0 &{}\quad otherwise \\ \end{array} }} \right. \\&u_{it}^x =\left\{ {{\begin{array}{ll} 0 &{}\quad if \,x_{it} =x_{i(t+1)} \\ 1 &{} \quad otherwise \\ \end{array} }} \right. \\&u_{it}^y =\left\{ {{\begin{array}{ll} 0 &{}\quad if \,y_{it} =y_{i(t+1)} \\ 1 &{}\quad otherwise \\ \end{array} }} \right. \\&z_{it} =\left\{ {{\begin{array}{ll} 0 &{}\quad if \,r_{it} =r_{i(t+1)}\, and \,u_{it}^x =u_{it}^y =0 \\ 1 &{}\quad otherwise \\ \end{array} }} \right. \end{aligned}$$
\(xv_{ij}\) :

Violation along \(x\) axis between departments \(i\) and \(j\)

\(yv_{ij}\) :

Violation along \(y\) axis between departments \(i\) and \(j\)

\(v_{ij}\) :

Violation between departments \(i\) and \(j\)

\(xv_{ijt}\) :

Violation along \(x\) axis between departments \(i\) and \(j\) in period \(t\)

\(yv_{ijt}\) :

Violation along \(y\) axis between departments \(i\) and \(j\) in period \(t\)

\(v_{ijt}\) :

Violation between departments \(i\) and \(j\) in period \(t\)

\(v\) :

Total average violation among departments

In the proposed mathematical model, the coordinate of the bottom left of the shop floor is (0, 0). The mathematical model for UA SFLPs where the shapes and areas of departments are fixed is proposed as follows:

$$\begin{aligned}&minimize \mathop \sum \limits _{i=1}^n \mathop \sum \limits _{j=1}^n f_{ij} d_{ij} \nonumber \\&\quad = \mathop \sum \limits _{i=1}^n \mathop \sum \limits _{j=1}^n f_{ij} \left( {\left| {x_i -x_j } \right| +\left| {y_i -y_j } \right| } \right) \quad i\ne j \end{aligned}$$
(1)
$$\begin{aligned}&s.t. \nonumber \\&\frac{w_i }{2}\left( {1-r_i } \right) +\frac{h_i }{2}r_i \le x_i \nonumber \\&\quad \le W-\left( {\frac{w_i }{2}\left( {1-r_i } \right) +\frac{h_i }{2}r_i } \right) \nonumber \\&\qquad i=1, \ldots , n \end{aligned}$$
(2)
$$\begin{aligned}&\frac{h_i }{2}\left( {1-r_i } \right) +\frac{w_i }{2}r_i \le y_i\nonumber \\&\quad \le H-\left( {\frac{h_i }{2}\left( {1-r_i } \right) +\frac{w_i }{2}r_i } \right) \nonumber \\&\qquad i=1, \ldots , n \end{aligned}$$
(3)
$$\begin{aligned}&\left| {x_i -x_j } \right| +\left| {y_i -y_j } \right| \nonumber \\&\quad \ge \left( {\frac{w_i }{2}\left( {1-r_i } \right) +\frac{h_i }{2}r_i +\frac{w_j }{2}\left( {1-r_j } \right) +\frac{h_j }{2}r_j } \right) \nonumber \\&\qquad +\,\left( {\frac{h_i }{2}\left( {1-r_i } \right) +\frac{w_i }{2}r_i +\frac{h_j }{2}\left( {1-r_j } \right) +\frac{w_j }{2}r_j } \right) \nonumber \\&\qquad i,j=1, \ldots , n \, and \, i\ne j\end{aligned}$$
(4)
$$\begin{aligned}&x_i,y_i, x_j,y_j \ge 0 \quad r_i, r_j \in \left\{ {0,1} \right\} \quad i,j=1, \ldots , n \end{aligned}$$
(5)

In this formulation, Eq. (1) shows the objective function of UA SFLP that is rectilinear distance-based and minimizes the sum of the material handling costs among the departments. It is assumed that the cost per unit distance is one. Equations (2) and (3) confirm that departments must be in the shop floor along the \(x\) axis and \(y\) axis, respectively. In other words, each department is restricted in the shop floor based on Eqs. (2) and (3). Equation (4) prevents the overlap between each pair of departments. In other words, Eq. (4) ensures that departments do not overlap.

In this part, the mathematical model is proposed for UA DFLPs when the shapes and areas of departments cannot change throughout the time horizon.

$$\begin{aligned}&minimize \left( \mathop \sum \limits _{t=1}^T \mathop \sum \limits _{i=1}^n \mathop \sum \limits _{j=1}^n f_{ijt} d_{ijt}\right. \nonumber \\&\quad +\,\mathop \sum \limits _{t=1}^T \mathop \sum \limits _{i=1}^n A_{it} z_{it} \left. +\mathop \sum \limits _{t=1}^T \mathop \sum \limits _{i=1}^n R_{it} P_{it} \right) \quad i\ne j\end{aligned}$$
(6)
$$\begin{aligned}&s.t. \nonumber \\&\frac{w_i }{2}\left( {1-r_{it} } \right) +\frac{h_i }{2}r_{it} \le x_{it} \nonumber \\&\quad \le W-\left( {\frac{w_i }{2}\left( {1-r_{it} }\right) +\frac{h_i }{2}r_{it} } \right) \nonumber \\&\qquad i=1, \ldots , n \quad t=1, \ldots , T \end{aligned}$$
(7)
$$\begin{aligned}&\frac{h_i }{2}\left( {1-r_{it} } \right) +\frac{w_i }{2}r_{it} \le y_{it} \nonumber \\&\quad \le H-\left( {\frac{h_i }{2}\left( {1-r_{it}} \right) +\frac{w_i }{2}r_{it} } \right) \nonumber \\&\qquad i=1, \ldots , n \quad t=1, \ldots , T \end{aligned}$$
(8)
$$\begin{aligned}&\left| {x_{it} -x_{jt} } \right| +\left| {y_{it} -y_{jt} } \right| \nonumber \\&\quad \ge \left( {\frac{w_i }{2}\left( {1-r_{it} } \right) +\frac{h_i }{2}r_{it} +\frac{w_j }{2}\left( {1-r_{jt} } \right) +\frac{h_j }{2}r_{jt} } \right) \nonumber \\&\qquad +\,\left( {\frac{h_i }{2}\left( {1-r_{it} } \right) +\frac{w_i }{2}r_{it} +\frac{h_j }{2}\left( {1-r_{jt} } \right) +\frac{w_j }{2}r_{jt} } \right) \nonumber \\&\qquad i,j=1, \ldots , n \, and \, i\ne j \quad t=1, \ldots , T\end{aligned}$$
(9)
$$\begin{aligned}&u_{it}^x +u_{it}^y +\left| {r_{i(t+1)} -r_{it} } \right| \le 3z_{it} \nonumber \\&\qquad i=1, \ldots , n \quad t=1, \ldots , T \end{aligned}$$
(10)
$$\begin{aligned}&x_{it},y_{it}, x_{jt},y_{jt} \ge 0 \quad r_{it}, r_{jt} , u_{it}^x, u_{it}^y, z_{it} \in \left\{ {0,1} \right\} \nonumber \\&\qquad i, j=1, \ldots , n \quad t=1, \ldots , T \end{aligned}$$
(11)

It is obvious, that Eqs. (6), (7), (8) and (9) can be interpreted similarly like Eqs. (1), (2), (3) and (4), respectively. Equation (10) shows whether the position of a department changes or does not change in consecutive periods. In other words, it shows whether the orientation of a department (in comparison with its original orientation) and the center-coordinate of a department are changed or not changed in consecutive periods.

Modified particle swarm optimization (PSO) for solving UA SFLPs and UA DFLPs

PSO is a population-based stochastic optimization approach. It is based on the simulation of social behaviors such as, animal herding, bird flocking, and fish flocking. Basically, PSO is a continuous algorithm that is fundamentally designed to solve continuous problems and it is classified as a meta-heuristic algorithm. Meta-heuristics can solve problems with minimum information. PSO was first designed by Kennedy and Eberhart (1995). In PSO, there are some particles that move through the search space to find the optimal solution. The position of each particle is considered as a solution for the problem. In PSO, the new position of each particle is determined by using its velocity, the best position found by the particle, and the best position for all existing particles. Formulas describing a particle behavior are shown in Eqs. (12) and (13) (Engelbrecht 2007).

$$\begin{aligned} v^{i}\left( {t+1} \right)&= wv^{i}\left( t \right) +c_1 r_1 \left( {x^{i, best }\left( t \right) -x^{i}\left( t \right) } \right) \nonumber \\&\quad +\,c_2 r_2 \left( {x^{ gbest }\left( t \right) -x^{i}\left( t \right) } \right) \end{aligned}$$
(12)
$$\begin{aligned} x^{i}\left( {t+1} \right)&= x^{i}\left( t \right) +v^{i}\left( {t+1} \right) \end{aligned}$$
(13)

where, \(t\) is the index of time, \(i\) is the index of particle, \(x^{i}(t)\) is the position of particle \(i\) at time \(t, v^{i}(t)\) is the velocity of particle \(i\) at time \(t, x^{i, best }(t)\) is the personal best position of particle \(i\) at time \(t\) found until this time, \(x^{ gbest }(t)\) is the global best position at time \(t, w\) is the inertia weight coefficient that must be between 0.4 and 0.9, \(r_1\) and \(r_2\) are uniform random variables between zero and one (i.e. \(r_1\) and \(r_2 \sim U(0,1))\), and \(c_1\) and \(c_2\) are acceleration coefficients of the best personal and global solutions, respectively. \(c_1\) and \(c_2\) should be between 0 and 2.

Steps of normal PSO

  1. 1.

    Create particles and evaluate them.

  2. 2.

    Determine the best personal solution for each particle and the best global solution.

  3. 3.

    Update the velocity and position of each particle by using Eqs. (12) and (13).

  4. 4.

    If the stopping condition is satisfied, then go to step 5; otherwise, go to step 2.

  5. 5.

    End of the algorithm.

Solution representation for UA SFLPs

To represent a solution for UA SFLPs, we have to determine the center-coordinates of departments along the \(x\) and \(y\) axes in the shop floor and the orientations of departments in comparison with the original orientations of departments, that are named \(X, Y\), and \(r\), respectively. PSO prefers to work with variables that are between zero and one. Thus, it is hard for PSO to work with \(X, Y\), and \(r\) variables because each of these variables is not between zero and one. Therefore, \(\hat{x}, \hat{y}\) and \(\hat{r}\) are used instead of \(X, Y\), and \(r\) such that \(\hat{x},\hat{y}\) and \(\hat{r}\) are variables between zero and one. Finally, the proposed method can determine the values of \(X, Y\), and \(r\) by using Eqs. (15), (16), and (14) respectively. In Eqs. (14), (15), and (16), \(x_i, y_i\), and \(r_i\) are members \(i\) of \(X, Y\), and \(r\), respectively.

We can determine the orientations of departments in comparison with their original orientations by using Eq. (14).

$$\begin{aligned} r_i =\left\{ {{\begin{array}{ll} 0 &{}\quad if \,\hat{r}_i <0.5 \\ 1 &{}\quad if \,0.5\le \hat{r}_i \le 1 \\ \end{array} }} \right. \quad i=1, \ldots , n \end{aligned}$$
(14)

According to Eqs. (2) and (3), we can write Eqs. (15) and (16) to find the center-coordinates of departments in a shop floor.

$$\begin{aligned} Xmin _i&= \frac{w_i }{2}\left( {1-r_i } \right) +\frac{h_i }{2}r_i,\nonumber \\ Xmax _i&= W-\left( {\frac{w_i }{2}\left( {1-r_i } \right) +\frac{h_i }{2}r_i } \right) \nonumber \\ \rightarrow x_i&= Xmin _i +\left( { Xmax _i - Xmin _i } \right) \hat{x}_i \quad i=1, \ldots , n\qquad \end{aligned}$$
(15)
$$\begin{aligned} Ymin _i&= \frac{h_i }{2}\left( {1-r_i } \right) +\frac{w_i }{2}r_i,\nonumber \\ Ymax _i&= H-\left( {\frac{h_i }{2}\left( {1-r_i } \right) +\frac{w_i }{2}r_i } \right) \nonumber \\ \rightarrow y_i&= Ymin _i +\left( { Ymax _i - Ymin _i } \right) \hat{y}_i \quad i=1, \ldots , n \end{aligned}$$
(16)

where \(( Xmin _i, Ymin _i)\) and \(( Xmax _i, Ymax _i)\) are the minimum and maximum values of the center-coordinates of department \(i\) respectively. A solution for an 11-department problem is presented in Fig. 2b. Length and width of departments are shown in Fig. 2a for this problem. Length and width of the shop floor are 15. Therefore, the center-coordinates of departments along the \(x\) and \(y\) axes in the shop floor and the orientations of departments are calculated using Eqs. (15), (16), and (14) respectively in Table 1.

Fig. 2
figure 2

a Length and width for 11 departments problem. b Solution representation for 11 departments problem

Full size image
Table 1 Center-coordinates and orientations of departments
Full size table

Solution representation for UA DFLPs

To represent a solution for UA DFLPs, we must determine the center-coordinates of departments along the \(x\) and \(y\) axes in the shop floor and their orientations in comparison with their original orientations in all periods; they can be named \(X, Y\), and \(r\), respectively. It is easy to work with variables that are between zero and one in continuous algorithms. Thus, the proposed method uses \(\hat{x}, \hat{y}\) and \(\hat{r}\) instead of \(X, Y\), and \(r\) such that \(\hat{x}, \hat{y}\) and \(\hat{r}\) are variables between zero and one. \(\hat{x}, \hat{y}, \hat{r}, X, Y\), and \(r\) are matrices with \(T\) rows and \(n\) columns such that the first and last rows show the data of period 1 and period \(T\), respectively. For example, the first member in matrix \(X\) is the center-coordinate of department one along the \(x\) axis in period one and the last member in matrix \(Y\) shows the center-coordinate of department \(n\) along the \(y\) axis in period \(T\). Equations (14), (15), and (16) are applied for each period. It means, Eqs. (18), (19), and (17) are used to find the center-coordinates of departments along the \(x\) and \(y\) axes and the orientations of departments for every period.

$$\begin{aligned}&r_{it} =\left\{ {{\begin{array}{ll} 0 &{}\quad if \ \hat{r}_{it} <0.5 \\ 1 &{}\quad if \ 0.5\le \hat{r}_{it} \le 1 \\ \end{array} }} \right. \nonumber \\&\quad i=1, \ldots , n \quad t=1, \ldots , T \end{aligned}$$
(17)
$$\begin{aligned}&Xmin _{it} =\frac{w_i }{2}\left( {1-r_{it} } \right) +\frac{h_i }{2}r_{it},\nonumber \\&Xmax _{it} =W-\left( {\frac{w_i }{2}\left( {1-r_{it} } \right) +\frac{h_i }{2}r_{it} } \right) \nonumber \\&\rightarrow x_{it} = Xmin _{it} +\left( { Xmax _{it} - Xmin _{it} } \right) \hat{x}_{it}\nonumber \\&\quad i=1,2, \ldots , n \quad t=1,2, \ldots , T \end{aligned}$$
(18)
$$\begin{aligned}&Ymin _{it} =\frac{h_i }{2}\left( {1-r_{it} } \right) +\frac{w_i }{2}r_{it},\nonumber \\&Ymax _{it} =H-\left( {\frac{h_i }{2}\left( {1-r_{it} } \right) +\frac{w_i }{2}r_{it} } \right) \nonumber \\&\rightarrow y_{it} = Ymin _{it} +\left( { Ymax _{it} - Ymin _{it} } \right) \hat{y}_{it}\nonumber \\&\quad i=1, \ldots , n \quad t=1, 2, \ldots , T \end{aligned}$$
(19)

where \(( Xmin _{it}, Ymin _{it})\) and \(( Xmax _{it}, Ymax _{it})\) are the minimum and maximum values of the center-coordinates of department \(i\) in period \(t\), respectively.

In the proposed method, Eq. (20) is used for calculating the cost function of UA SFLPs.

$$\begin{aligned}&minimize \left( \mathop \sum \limits _{i=1}^n \mathop \sum \limits _{j=1}^n f_{ij} \left( {\left| {x_i -x_j } \right| +\left| {y_i -y_j }\right| } \right) (1+\beta v)\right) \nonumber \\&\quad i\ne j \end{aligned}$$
(20)

where \(\beta \) is a coefficient with a value of 120 for UA SFLPs. The authors have run the proposed method on UA SFLPs for 10 times to set the coefficient.

The total average violation among departments (i.e. overlap violation between each pair of departments) for UA SFLPs can be calculated by using Eq. (21) and the violation between department \(i\) and department \(j\) is calculated using Eq. (22). The violations between department \(i\) and department \(j\) along \(x\) axis and \(y\) axis are calculated using Eqs. (23) and (24), respectively.

$$\begin{aligned}&v=\frac{1}{n^{2}-n}\mathop \sum \limits _{i=1}^n \mathop \sum \limits _{j=1}^n v_{ij} \quad i\ne j \end{aligned}$$
(21)
$$\begin{aligned}&v_{ij} =\min \left( {xv_{ij},yv_{ij} } \right) \quad i, j=1, \ldots , n \end{aligned}$$
(22)
$$\begin{aligned}&xv_{ij} {=}\max \left( {1{-}\frac{\left| {x_i {-}x_j } \right| }{\frac{w_i }{2}\left( {1{-}r_i } \right) {+}\frac{h_i }{2}r_i {+}\frac{w_j }{2}\left( {1{-}r_j } \right) {+}\frac{h_j }{2}r_j },0} \right) \nonumber \\&\quad i, j=1, \ldots , n \end{aligned}$$
(23)
$$\begin{aligned}&yv_{ij} {=}\max \left( {1{-}\frac{\left| {y_i {-}y_j } \right| }{\frac{h_i }{2}\left( {1{-}r_i } \right) {+}\frac{w_i }{2}r_i {+}\frac{h_j }{2}\left( {1{-}r_j } \right) {+}\frac{w_j }{2}r_j },0} \right) \nonumber \\&\quad i, j=1, \ldots , n \end{aligned}$$
(24)

For UA DFLPs, the cost function is calculated using Eq. (25)

$$\begin{aligned}&minimize \left( \left( \mathop \sum \limits _{t=1}^T \mathop \sum \limits _{i=1}^n \mathop \sum \limits _{j=1}^n f_{ijt} d_{ijt} \right) (1+\beta v) \right. \nonumber \\&\quad \left. +\mathop \sum \limits _{t=1}^T \mathop \sum \limits _{i=1}^n A_{it} z_{it} +\mathop \sum \limits _{t=1}^T \mathop \sum \limits _{i=1}^n R_{it} P_{it}\right) \quad i\ne j \end{aligned}$$
(25)

where \(\beta \) is a coefficient with a value of 150 for UA DFLPs. The authors have run the proposed method on UA DFLPs for 10 times to set the coefficient.

The total average violation among departments in all periods (i.e. overlap violation between each pair of departments in all periods) for UA DFLPs is calculated by using Eq. (26) and the violation between department \(i\) and department \(j\) is shown in Eq. (27). The violations between department \(i\) and department \(j\) along \(x\) axis and \(y\) axis in period \(t\) are calculated using Eqs. (28) and (29).

$$\begin{aligned}&v=\mathop \sum \limits _{t=1}^T \left( \frac{1}{n^{2}-n}\mathop \sum \limits _{i=1}^n \mathop \sum \limits _{j=1}^n v_{ijt}\right) \quad i\ne j\end{aligned}$$
(26)
$$\begin{aligned}&v_{ijt} {=}\min \left( {xv_{ijt},yv_{ijt} } \right) \quad i, j{=}1, \ldots , n \quad t{=}1, \ldots , T\end{aligned}$$
(27)
$$\begin{aligned}&xv_{ijt}{=}\max \left( {1{-}\frac{\left| {x_{it}{-}x_{jt} } \right| }{\frac{w_i}{2}\left( {1{-}r_{it}}\right) {+}\frac{h_i }{2}r_{it} {+}\frac{w_j }{2}\left( {1{-}r_{jt} } \right) {+}\frac{h_j }{2}r_{jt} },0} \right) \nonumber \\&\quad i, j=1, \ldots , n \quad t=1, \ldots , T\end{aligned}$$
(28)
$$\begin{aligned}&yv_{ijt} {=}\max \left( {1{-}\frac{\left| {y_{it} {-}y_{jt} } \right| }{\frac{h_i }{2}\left( {1{-}r_{it} } \right) {+}\frac{w_i }{2}r_{it} {+}\frac{h_j }{2}\left( {1{-}r_{jt} } \right) {+}\frac{w_j }{2}r_{jt} },0} \right) \nonumber \\&\quad i, j=1, \ldots , n \quad t=1, \ldots , T \end{aligned}$$
(29)

Steps of the proposed modified particle swarm optimization

The flowchart of the proposed modified PSO for solving UA SFLPs and UA DFLPs is presented in Fig. 3. According to Fig. 3, in the first step, particles must be created randomly and then evaluated. The velocity and position of each particle should be updated using Eqs. (12) and (13) in the second step. In the third step, if the number of iterations is \(\le \)100, the proposed method applies the department swapping method; otherwise, it updates the best personal and global solutions. The department swapping method is explained in “Department swapping method” section. In the fourth step, the local search method 1 is applied to the best global solution, and it is described in “Local search method 1” section. In the fifth step, if the number of iterations is less than the maximum iteration minus 20, the proposed algorithm goes to the second step; otherwise, if the problem is dynamic, it uses the period swapping method and then applies the local search method 2 to the best global solution. In this step, if the problem is static, it uses only the local search method 2. In the final step, if the number of iterations is equal to the maximum iteration, the algorithm is stopped; otherwise, it goes to the second step. The period swapping method and local search method 2 are explained in “Period swapping method” and “Local search method 2” sections, respectively.

Fig. 3
figure 3

The flowchart of the proposed modified PSO for UA SFLPs and UA DFLPs

Full size image

Department swapping method

In the proposed algorithm, the department swapping method is applied for each particle when the number of iterations is \(\le \)100. For each particle, the positions of each pair of departments are exchanged and each department exchanges its length and width. After all, the best solution must be selected as a particle. This method is used in each period when the problem is dynamic. The steps of this method are explained for a particle on a pair of department \(i\) and department \(j\)

  1. 1.

    This method saves the current particle as solution 1.

  2. 2.

    In the current particle, the orientation of department \(i\) changes and the result is saved as solution 2.

  3. 3.

    In the current particle, the orientation of department \(j\) changes and the result is saved as solution 3.

  4. 4.

    In the current particle, the orientations of departments \(i\) and \(j\) change and the result is saved as solution 4.

  5. 5.

    In the current particle, the positions of departments \(i\) and \(j\) exchange and the result is saved as solution 5.

  6. 6.

    In the current particle, the positions of departments \(i\) and \(j\) exchange and the orientation of department \(i\) changes, then the result is saved as solution 6.

  7. 7.

    In the current particle, the positions of departments \(i\) and \(j\) exchange and the orientation of department \(j\) changes, then the result is saved as solution 7.

  8. 8.

    In the current particle, the positions of departments \(i\) and \(j\) exchange and the orientations of departments \(i\) and \(j\) change, then the result is saved as solution 8.

  9. 9.

    The best solution is selected as the current particle

Local search method 1

The local search method 1 is used for the best global solution. For each department, eight actions on \(\hat{x}\) and \(\hat{y}\) are tested and in each action, the length and width of a department are exchanged. Then, the best solution must be selected as the best global solution. These actions are explained for department \(i\). In action 1, a random number between 0 and 0.5 is created and \(\hat{x}_i\) is replaced by summing the random number and \(\hat{x}_i\). In other words, department \(i\) moves right along the \(x\) axis. In action 2, a random number between 0 and 0.5 is created and \(\hat{x}_i\) is replaced by subtracting the random number from \(\hat{x}_i\). In other words, department \(i\) moves to the left along the \(x\) axis. In action 3, a random number between 0 and 0.5 is created and then \(\hat{y}_i\) is changed by subtracting the random number from \(\hat{y}_i\). It means, department \(i\) moves downward. In action 4, a random number between 0 and 0.5 is created and then \(\hat{y}_i\) is changed by summing the random number and \(\hat{y}_i\). It means, department \(i\) moves upward. In action 5, two random numbers between 0 and 0.5 are created and then \(\hat{y}_i\) is changed by summing \(\hat{y}_i\) and the first random number and \(\hat{x}_i\) is changed by summing the second random number and \(\hat{x}_i\). It means department \(i\) moves up and then to the right. In actions 6, 7, and 8, department \(i\) moves up and then to the left, down and then to the right, and down and then to the left, respectively. When the problem is dynamic, one period is selected randomly and this method is applied on the selected period. The steps of the local search method 1 are explained for the best global solution as follows:

  1. 1.

    \(n, s, b\), and \(i\) are the number of departments, the counting of solutions, the counting of actions, and the counting of departments, respectively such that \(s, b\), and \(i\) are equal to one at first.

  2. 2.

    The best global solution is saved as a solution where \(s\) is equal to one.

  3. 3.

    For the best global solution, action \(b\) is used on department \(i\) and the result is saved as a solution, then \(s\) is replaced by summing \(s\) and one (i.e. \(s=s+1\)).

  4. 4.

    For the best global solution, action \(b\) is used on department \(i\) and orientation of department \(i\) changes, then the result is saved as a solution. Finally, \(s\) is replaced by summing \(s\) and one and \(i\) is replaced by summing \(i\) and one (i.e. \(s=s+1\) and \(i=i+1\))

  5. 5.

    If \(i\) is \({\le }n\,(i\le n)\) go to step 3; otherwise \(b\) is replaced by summing \(b\) and one and \(i\) is replaced by one (i.e. \(b=b+1\) and \(i=1\))

  6. 6.

    If \(b\) is \(\le \)8 (i.e. \(b\le 8\)) go to step 3; otherwise go to step 7

  7. 7.

    The best solution is selected as the best global solution.

Period swapping method

The period swapping method is common in dynamic problems, and it is applied to the best global solution. When the number of iterations is more than or equal to the maximum iteration minus 20, this method is used for each pair of periods. In this method, the center-coordinates of departments along the \(x\) and \(y\) axes, and the orientation of departments are exchanged for each pair of periods. In other words, for period \(t\) and period \((t+1)\,x_{it}, y_{it}\), and \(r_{it}\) are exchanged with \(x_{i(t+1)}, y_{i(t+1)}\), and \(r_{i(t+1)}\) for all departments respectively. After all, the best solution must be selected as the best global solution.

Local search method 2

The local search method 2 is used for the best global solution when the number of iterations is more than or equal to the maximum iteration minus 20. In this method, a permutation vector of \(\{1, {\ldots }, n\}\) is created randomly, and each number in the vector cell is the department number. For each two sequential departments in the permutation, 20 actions on \(\hat{x}\) and \(\hat{y}\) are tested and in each action the length and width of a department are exchanged. Finally, the best solution must be selected as the best global solution. It is suggested that departments \(i\) and \(j\) are two sequential departments in the permutation vector and these actions are explained for departments \(i\) and \(j\). In action 1, a random number between 0 and 0.5 should be created and then \(\hat{y}_i\) and \(\hat{y}_j\) are replaced by summing the random number and \(\hat{y}_i\) and \(\hat{y}_j\), respectively. In other words, departments \(i\) and \(j\) move up along the \(y\) axis. In action 2, a random number between 0 and 0.5 should be created and then \(\hat{y}_i\) and \(\hat{y}_j\) are replaced by subtracting the random number from \(\hat{y}_i\) and \(\hat{y}_j\), respectively. This means that departments \(i\) and \(j\) move down along the \(y\) axis. Similarly, departments \(i\) and \(j\) move right and left along the \(x\) axis in actions 3 and 4, respectively. In action 5, two random numbers between 0 and 0.5 must be created and then \(\hat{y}_i\) is replaced by summing the first random number and \(\hat{y}_i, \hat{y}_j\) is replaced by summing the first random number and \(\hat{y}_j, \hat{x}_i\) is replaced by summing the second random number and \(\hat{x}_i\), and \(\hat{x}_j\) is replaced by summing the second random number and \(\hat{x}_j\). In other words, departments \(i\) and \(j\) simultaneously move up along the \(y\) axis and then right along the \(x\) axis. In action 6, departments \(i\) and \(j\) simultaneously move up and then left. In action 7, departments \(i\) and \(j\) simultaneously move down and then right. In action 8, departments \(i\) and \(j\) simultaneously move down and then left. In action 9, two random numbers between 0 and 0.5 must be created and then \(\hat{y}_i\) is replaced by summing the first random number and \(\hat{y}_i\) and then \(\hat{x}_j\) is replaced by summing the second random number and \(\hat{x}_j\). In other words, departments \(i\) and \(j\) move up and right, respectively. In action 10, department \(i\) moves right and department \(j\) moves up. In action 11, department \(i\) moves up and department \(j\) moves left. In action 12, department \(i\) moves left and department \(j\) moves up. In action 13, department \(i\) moves up and department \(j\) moves down. In action 14, department \(i\) moves down and department \(j\) moves up. In action 15, department \(i\) moves down and department \(j\) moves left. In action 16, department \(i\) moves left and department \(j\) moves down. In action 17, department \(i\) moves down and department \(j\) moves right. In action 18, department \(i\) moves right and department \(j\) moves down. In action 19, department \(i\) moves right and department \(j\) moves left. In action 20, department \(i\) moves left and department \(j\) moves right. When the problem is dynamic, one period is selected randomly and this method is applied on the selected period. The steps of the local search method 2 are explained on the best global solution as follows:

Table 2 Results of the proposed method for solving static problems
Full size table
Table 3 Results of the proposed method for solving dynamic problems
Full size table
  1. 1.

    It is proposed that the permutation vector be \([1, 2, 3,\) \( {\ldots },n]\)

  2. 2.

    \(n, s, b\), and \(i\) are the number of departments, the counting of solutions, the counting of actions, and the counting of departments respectively such that \(s, b\), and \(i\) are equal to one at first.

  3. 3.

    The best global solution is saved as a solution where \(s\) is equal to one.

  4. 4.

    For the best global solution, action \(b\) is used on department \(i\) and department \(i+1\) and the result is saved as a solution, then \(s\) is replaced by summing \(s\) and one (i.e. \(s=s+1\)).

  5. 5.

    For the best global solution, action \(b\) is used on department \(i\) and department \(i+1\) and orientation of department \(i\) changes, then the result is saved as a solution. Finally, \(s\) is replaced by summing \(s\) and one (i.e. \(s=s+1\))

  6. 6.

    For the best global solution, action \(b\) is used on department \(i\) and department \(i+1\) and orientation of department \(i+1\) changes, then the result is saved as a solution. Finally, \(s\) is replaced by summing \(s\) and one (i.e. \(s=s+1\))

  7. 7.

    For the best global solution, action \(b\) is used on department \(i\) and department \(i+1\) and orientations of department \(i\) and department \(i+1\) change, then the result is saved as a solution. Finally, \(s\) is replaced by summing \(s\) and one and \(i\) is replaced by summing \(i\) and one (i.e. \(s=s+1\) and \(i=i+1\))

  8. 8.

    If \(i\) is \({<}n\,(i<n)\) go to step 4; otherwise \(b\) is replaced by summing \(b\) and one and \(i\) is replaced by one (i.e. \(b=b+1\) and \(i=1\))

  9. 9.

    If \(b\) is \(\le \)20 (i.e. \(b\le 20\)) go to step 4; otherwise go to step 10

  10. 10.

    The best solution is selected as the best global solution.

Numerical experiments and parameter settings

Two types of problems were chosen from the literature to test the proposed method. The first set is problem instances concerning UA SFLPs and the second set is problem instances about UA DFLPs, when the shapes and areas of departments are fixed for the whole time horizon. These problem instances were chosen because there is no other problem instance in the literature that meets our case requirements. The first set comprises three problem instances as follows: 8 departments, 11 departments, and 20 departments which were named SFLP-1, SFLP-2 and SFLP-3, respectively. The problems with 8 departments and 11 departments were taken from Imam and Mir (1989) and the one with 20 departments was taken from Mir and Imam (2001). The second set consists of two problem instances as follows: (1) one with 6 departments and 6 periods that was named P6, and (2) another with 12 departments and 4 periods that was named P12. These two problem instances were taken from Dunker et al. (2005). According to the information of P6, the departments must be arranged in a \(30\times 30\) plant floor. The corner-coordinates of some departments were negative for the initial layout of P6. Therefore, for the initial layout, the center-coordinate of each department is summed with 15 and 10.5 in the \(x\) and \(y\) axes respectively for this problem. With respect to problem P12, the department must be located in a \(50\times 50\) plant floor. Likewise, the corner-coordinates of some departments were negative for the initial layout of P12. Thus, for the initial layout, the center-coordinate of each department is summed with 6 and 14 in the \(x\) and \(y\) axes respectively for this problem. Information about these problem instances is provided in “Summary of UA SFLPs and UA DFLPs (i.e. first set and second set)” and “Center-coordinates of departments in the initial layouts for problems P6 and P12” sections in “Appendix 1”.

Values of parameters were determined by using manual parameter tuning (i.e. trial and error method). The parameter settings for the proposed method are provided in “Appendix 2”. The authors used different numerical experiments to find the suitable values of parameters. The proposed method has five parameters and to set them, the following notations: \(( nPop , maxIt ,w, c_{1}, c_{2})\) were used, where nPop is the number of particles, maxIt is the maximum number of iterations, \(w\) is the inertia weight coefficient, \(c_{1}\) is the acceleration coefficient of the best personal solution, and \(c_{2}\) is the acceleration coefficient of the best global solution. The authors have run SFLP-1 and SFLP-2 20 times with different parametric values and it was concluded that nPop, maxIt, \(w, c_{1}\), and \(c_{2}\) should be 20 or 50, 300 or 400, 0.4 or 0.5, 0.5 or 0.6, and 1.0 or 1.2, respectively. There were \(2^{5}\) situations (i.e. 32 situations) for the parameters, such as (20, 300, 0.4, 0.5, 1.0), (20, 300, 0.5, 0.5, 1.2), (50, 400, 0.4, 0.6, 1.0), and (50, 400, 0.5, 0.6, 1.2) for SFLP-1 and SFLP-2. Subsequently, 20 situations were selected randomly and the proposed method with these parametric values was tested. Finally, the best results for the parameters were presented in “Appendix 2” for problems SFLP-1 and SFLP-2. Similarly, SFLP-3 was run twenty times with different parametric values, and it was concluded that nPop, maxIt, \(w, c_{1}\), and \(c_{2}\) should be 50 or 80, 400 or 450, 0.4 or 0.5, 0.5 or 0.6, and 1.0 or 1.2, respectively. In this case, the authors selected 20 situations randomly for evaluation and the best results for the parameters were reported in “Appendix 2”. The same method was used and it was concluded that nPop, maxIt, \(w, c_{1}\), and \(c_{2}\) should be 50 or 100, 500 or 600, 0.4 or 0.5, 0.5 or 0.6, and 1.0 or 1.2, respectively for problems P6 and P12. The best results for the parameters were presented in “Appendix 2” for P6 and P12. MATLAB R2013a was used to code the proposed algorithm, and it was executed in a computer with the following specifications: an Intel Core i3-2320M CPU of 2.10 GHz, and 4.00 GB of RAM. The proposed method was run ten times for each problem and the results are reported in “Results and discussion” section.

Table 4 Comparison of results of our algorithm with other methods for static problems
Full size table
Table 5 Comparison of results of our algorithm with other methods for dynamic problems
Full size table

Results and discussion

Tables 2 and 3 show the results of the modified PSO method for solving UA SFLPs and UA DFLPs. The problem’s name, best solution, mean solution of 10 replications, worst solution, run time for the best solution, and run time for the worst solution are presented in Table 2 for static problems. With respect to dynamic problems, Table 3 lists the problem’s name, sum of the material handling costs for the best solution, sum of the rearrangement costs for the best solution, total cost for the best solution, sum of the material handling costs for the worst solution, sum of the rearrangement costs for the worst solution, total cost for the worst solution, mean total cost of 10 replications, and run time for the best solution. The problem data, center-coordinates of departments and orientations of departments for the best solution, and the best layout for problems SFLP-1, SFLP-2, SFLP-3, P6, and P12 are shown in Appendixes 3, 4, 5, 6 and 7, respectively.

Equations (30) and (31) were applied to compare the results of the modified PSO with other methods, which are TOPOPT, FLOAT, and HOT for static problems, and heuristic, and combined dynamic programming and GA for dynamic problems.

$$\begin{aligned} dev&= \frac{( MHC _{ com } - MHC _{ MPSO } )}{ MHC _{ com } }\times 100\end{aligned}$$
(30)
$$\begin{aligned} dev&= \frac{( TC _{ com } - TC _{ MPSO } )}{ TC _{ com }}\times 100 \end{aligned}$$
(31)

Specifically, dev is the relative deviation, and \( MHC _{ com }\) and \( MHC _{ MPSO }\) are the sum of the material handling costs using the compared method and our method, respectively. \( TC _{ com }\) is the total cost obtained by the compared method and \( TC _{ MPSO }\) is the total cost generated by the modified PSO.

Tables 4 and 5 show the comparative results for static and dynamic problems, correspondingly. Table 4 consists of the problem’s name, the best material handling cost and its mean value for the modified PSO, TOPOPT, FLOAT, and HOT (i.e. modified simulated annealing) methods. Table 5 lists the problem’s name, the best material handling cost, the best rearrangement cost, and the total cost for the modified PSO, heuristic, and combined dynamic programming and GA methods.

According to Table 4, for the problem SFLP-3, the objective function value of the best solution obtained by the modified PSO is 1206.6489 and it is 1320.72, 1264.94, and 1225.40 using TOPOPT, FLOAT, and HOT, respectively. Furthermore, for the problem SFLP-3, the mean objective function value for 10 replications is 1264.21306 using the proposed algorithm, and it is 1395.64, 1333.81, and 1287.29 using TOPOPT, FLOAT, and HOT, correspondingly. Therefore, our algorithm has improved the best objective function values in comparison with other methods. According to Table 4 and Eq. (30), the improvement obtained by the proposed algorithm is \(+\)8.637, \(+\)4.608 and \(+\)1.53 %, in contrast to TOPOPT, FLOAT, and HOT, respectively.

In Table 5, the total cost of the best solution for the problem P6 is 6763.757 using the proposed algorithm, and it is 6928 and 6906.5 using the heuristic and dynamic programming-GA methods, correspondingly. According to Eq. (31), the modified PSO has improved the problem P6 by \(+\)2.3707 and \(+\)2.06679 % in comparison with the heuristic and dynamic programming-GA methods, respectively. Moreover, the total cost of the best solution obtained by the proposed algorithm is 28,826.67 for the problem P12. However, it is 29,194 and 29,098.5 using the heuristic and dynamic programming-GA methods, correspondingly. Hence, the improvement attained is \(+\)1.258 and \(+\)0.934 %. It can be seen that, in dynamic problems, the total improvement of the proposed algorithm as compared to the other two methods is \(+\)3.6287 and \(+\)3.00079 %, respectively.

The results of the proposed method for UA SFLPs could not be compared with the results of Armour and Buffa (1963), Heragu and Kusiak (1991) and Xiao et al. (2013) because Armour and Buffa (1963) investigated UA SFLPs where the shapes of departments were not fixed during the iteration of their algorithm, Heragu and Kusiak (1991) studied UA SFLPs such that the departments should be arranged in a single row or multi rows, and Xiao et al. (2013) studied UA SFLPs where the departments have input/output points. According to Table 4, the results of SFLP-1 and SFLP-2 were not compared with those of Imam and Mir (1989, 1993); Mir and Imam (2001)) because they designed these problems and did not solve them. With respect to dynamic problems, the authors could not compare their results with those of Montreuil and Venkatadri (1991), Lacksonen (1994), Lacksonen (1997), Mazinani et al. (2012), McKendall and Hakobyan (2010) and Jolai et al. (2012) because Montreuil and Venkatadri (1991), Lacksonen (1994), Lacksonen (1997) and Mazinani et al. (2012) studied UA DFLPs where the shapes or/and areas of departments could change throughout the time horizon, McKendall and Hakobyan (2010) reported only the material handling cost, and Jolai et al. (2012) studied UA DFLPs with input/output points.

In accordance with Tables 4 and 5, the modified PSO has created better layouts in contrast to other methods in the literature. This is because, PSO is classified as a swarm intelligence technique, while other meta-heuristic algorithms, such as GA and simulated annealing are not. In swarm intelligence, there is cooperation among particles. In other words, information and data among particles can be exchanged, and this advantage creates good solutions. Nevertheless, Moslemipour et al. (2012) showed that PSO has a weak local search ability. To address this disadvantage, the authors used local search methods 1 and 2 for both static and dynamic problems. These two methods were applied to improve the local search ability and quality of solutions. The department swapping method was utilized to avoid local optima for both static and dynamic problems, and the period swapping method was used only for dynamic problems to increase the quality of layouts.

Conclusions

A modified PSO was suggested for solving UA SFLPs and UA DFLPs such that the shapes and areas of departments cannot change throughout the whole time horizon. This paper is the first effort which has studied the use of modified PSO to solve UA SFLPs and UA DFLPs in order to minimize the sum of the material handling costs for static problems and minimize the sum of the material handling costs and sum of the rearrangement costs for dynamic problems. It has applied four methods to find better layouts. They are the: (1) department swapping method, (2) local search method 1 for the best global solution, (3) period swapping method, and (4) local search method 2 for the best global solution. Methods 1, 2, and 4 were used for solving static and dynamic problems; however, method 3 was applied only for solving dynamic problems. According to the results, the proposed method has created better layouts in comparison with other algorithms.

For future work, this study can be expanded in many ways. It can be extended to add the input/output points for departments. It is also suggested that other meta-heuristic algorithms can be utilized to solve the same problems. Furthermore, the proposed method will be beneficial for UA SFLPs and UA DFLPs with variable shapes and areas of departments throughout the time horizon.