Multi-objective modified differential evolution algorithm with archive-base mutation for solving multi-objective $p$-xylene oxidation process

Abstract

Maximizing the diversity of the obtained objective vectors and increasing the convergence speed to the true Pareto front are two important issues in the design of multi-objective evolutionary algorithms (MOEAs). To solve complex multi-objective optimization problems (MOPs), a multi-objective modified differential evolution algorithm with archive-base mutation (MOMDE-AM) is proposed. In MOMDE-AM, with the purpose of reducing the loss of population evolution information, a modified mutation strategy with archive is introduced, which could utilize several useful inferior solutions and provide promising direction information toward the true Pareto front. The performance of MOMDE-AM is compared with five other MOEAs on five bi-objective and five tri-objective optimization problems. The simulation and statistical analysis results indicate that the overall performance of MOMDE-AM is better than those of the compared algorithms on these test functions. Finally, MOMDE-AM is used to optimize ten operation conditions of the $p$-xylene oxidation reaction process; the results show that MOMDE-AM is an effective and efficient optimization tool for solving actual MOPs.

Introduction

Purified terephthalic acid (PTA) is one of the most important industrial raw materials because it is the base for the production of audio films, polyester fibers, moulded resins, polyethylene terephthalate bottles, and so on (Kleerebezem and Lettinga 2000). The oxidation of $p$-xylene (PX) to crude terephthalic acid (CTA) is an important step in manufacturing process of PTA. Moreover, The Amoco-MC process is a highly efficient method to produce CTA. In this process, PX is catalyzed by using bromide (Br), manganese (Mn), and cobalt (Co) and is oxidized by air or molecular oxygen in acetic acid (HAc) at 190 to $200~^{\circ }\hbox {C}$ (Cincotti et al. 1997; Chen et al. 2005; Partenheimer 1995; Hong et al. 2010). Additionally, the PX oxidation reaction process involves many burning side reactions (Kenigsberg et al. 1995) wherein the consumption of HAc and PX is very considerable and the quality of CTA is significantly affected by the concentration of 4-carboxybenzaldhyde (4-CBA) (Cincotti et al. 1999; Mu et al. 2003). The operation conditions of the PX oxidation reaction process can significantly impact the quality and production costs of PTA. Therefore, obtaining the optimal operation conditions to reduce the HAc and PX combustion losses and control the concentration of 4-CBA in the suitable level is an urgently issue to be solved.

In the real world, most of optimization problems involve two or more objectives which usually conflict with each other. For these problems, improvement of one objective may lead to deterioration of another. Therefore, it is difficult to obtain a set of the Pareto objective vectors, which are called as Pareto front. Over the past few decades, various multi-objective evolutionary algorithms (MOEAs) (Coello 2006; Schaffer 1985; Fonseca and Fleming 1995, 1998; Zitzler et al. 2000; Zitzler and Thiele 1999; Zitzler et al. 2001; Ray et al. 2001; Coello et al. 2004; Yang et al. 2013; Wang and Zeng 2013; Zhang and Li 2007; Suman et al. 2010; Daneshyari and Yen 2011; Mandli and Modak 2012; Deb et al. 2002a; Triki et al. 2014; Jamali et al. 2014) have been successfully used to solve numerous multi-objective optimization problems (MOPs) and have gained continuing attention from researchers because MOEAs are less susceptible to different characteristics of Pareto front (Coello 2006; Van Veldhuizen and Lamont 1998; Zitzler et al. 2000) and can perform better than traditional multi-objective optimization approaches (Deb 2001; Coello et al. 2002) in most cases.

In the current study, using differential evolution (Storn and Price 1995) (DE) algorithm to solve MOPs is our study focus. Abbass et al. (2001) proposed a Pareto differential evolution (PDE) to solve MOPs and then introduced a self-adaptive Pareto differential evolution algorithm (Abbass 2002) wherein the mutation and crossover control parameters could be automatically adjusted during the evolution process. Their experimental results show that DE is a competitive optimization tool to solve MOPs. Madavan (2002) proposed a Pareto differential evolution approach (PDEA), in which the fast nondominated sorting and crowding distance (Deb et al. 2002a) are used to select individuals for the next generation. Kukkonen and Lampinen (2004) introduced an improved Generalized DE to solve five multi-objective optimization problems, and the obtained results indicate that the proposed algorithm performs better than the compared algorithms. Subsequently, an extension of generalized DE (GDE3) Kukkonen and Lampinen (2004) is proposed to solve a set of different characteristics of multi-objective optimization problems. Santana-Quintero et al. (2010) proposed a hybrid multi-objective optimization algorithm wherein a fast DE algorithm and a local search approach based on rough set theory are used. The experimental results show that the performance of the proposed algorithm is better than those of other compared algorithms on several difficult constrained multi-objective optimization test functions. Ali et al. (2012) proposed a multi-objective differential evolution algorithm wherein opposition-based learning strategy is used to generate the initial population and the concept of random localization is used in mutation strategy; moreover, the proposed algorithm uses a new selection mechanism to check among the parent and trial solutions. Wang et al. (2010) introduced a multi-objective self-adaptive differential evolution algorithm wherein an external elitist archive is used to store the obtained nondominated solutions and a crowding entropy strategy is used to preserve the diversity of the obtained solutions. Wang and Tang (2013) introduced a multi-objective parallel differential evolution with competitive evolution strategies wherein the population is divided into four parts and four mutation strategies are used. Sharma and Rangaiah (2013) proposed an improved multi-objective differential evolution for solving some benchmark test functions and three chemical engineering applications, in which a termination criterion is developed to stop the search and taboo list is used to avoid repeated computations and enhance exploration ability.

It is important to develop an efficient optimization tool which has a good convergence speed as well as good diversity maintenance because balancing convergence and diversity (two conflicting objectives) is a difficult task in multi-objective optimization. Moreover, Pareto dominance is a greedy strategy to select offspring. Therefore, to obtain a better balance between the exploration and exploitation capabilities in multi-objective DE algorithm, a multi-objective modified differential evolution algorithm with archive-base mutation (MOMDE-AM) is proposed. In MOMDE-AM, some inferior solutions may be selected in mutation operation to enhance the exploration ability because they can provide a promising direction to the true Pareto front and increase population diversity. To demonstrate the performance of MOMDE-AM, it is compared with five MOEAs on a set of 10 benchmark MOPs out of which 5 test functions are bi-objective while the remaining 5 problems are tri-objective. Furthermore, MOMDE-AM is used to solve a multi-objective operation conditions optimization of the PX oxidation reaction process, the experimental results show that confliction between the quality and production cost in PTA production can be alleviated by a set of obtained Pareto optimal solutions.

The remainder of this paper is organized in the following way. “Background” section introduces the basic concept of MOPs and the basic DE algorithm. “Multi-objective modified differential evolution algorithm” section presents the proposed MOMDE algorithm. “Performance analysis of MOMDE-AM on ZDT and DTLZ test suites” section reports the experimental results and sensitive analysis of parameters of MOMDE. The industrial application using the proposed algorithm is given in “PX oxidation process optimization using MOMDE-AM” section. Finally, the conclusions are summarized in “Conclusions” section.

Background

Multi-objective optimization problem

Without loss of generality, in this paper, a minimized MOP can be described as follows:

$$\begin{aligned}&{\mathop {\min }\limits _{{{\mathbf {x}}}\in {{\varvec{\varOmega }}}}}\,\, {{\mathbf {F}}}({{\mathbf {x}}})=(f_1 ({{\mathbf {x}}}),\ldots ,f_m ({{\mathbf {x}}}))^{T}\nonumber \\&x_j \in (x_j^{\mathrm{low}} ,x_j^{\mathrm{high}})\,\quad j=1,2,\ldots , D \end{aligned}$$

(1)

where ${{\mathbf {x}}}$ denotes a decision vector in feasible region ${\varvec{\varOmega }} \left( {{\varvec{\varOmega }} \subseteq {{\mathbf {R}}}^{D}} \right)$, $m$ is the number of objective functions and $f_n (n=1,2,\ldots ,m)$ is the $n$th objective to be minimized. $x_j^{\mathrm{low}}$and $x_j^{\mathrm{high}}$are the lower and upper bounds of the $j$th variable, respectively. $D$ denotes the dimensionality of optimization problem.

Contrary to single optimization problem, MOPs do not exist a single global optimal solution. Thus some terminologies and concepts are introduced as follows (Miettinen 1999; Deb 2001):

Definition 1

(Dominance relation) A feasible solution ${{\mathbf {x}}}_1$ is said to dominate another feasible solution ${{\mathbf {x}}}_2$, denotes ${{\mathbf {x}}}_1 \succ {{\mathbf {x}}}_2$, iff $\forall n\in \left\{ {n=1,2,\ldots ,m} \right\} ,f_n ({{\mathbf {x}}}_1 )\le f_n ({{\mathbf {x}}}_2 ),$ and $\exists k\in \left\{ {k=1,2,\ldots ,m} \right\} ,f_k ({{\mathbf {x}}}_1 )<f_k ({{\mathbf {x}}}_2 )$, where $k$ is the number of objective functions.

Definition 2

(Pareto optimal set) a feasible solution ${{\mathbf {x}}}^{{*}}$ is said to be a Pareto optimal solution if there does not exist another feasible solution ${{\mathbf {x}}}$ such that ${{\mathbf {x}}}\succ {{\mathbf {x}}}^{{*}}$. The set of all the Pareto optimal solutions is called the Pareto set (PS), denoted as ${{\mathbf {X}}}^{{*}}$.

Definition 3

(Pareto front) The Pareto front (PF) is defined as $PF=\left\{ {F({{\mathbf {x}}}^{{*}})\left| {{{\mathbf {x}}}^{{*}}\in {{\mathbf {X}}}^{{*}}} \right. } \right\}$, i.e., the image of the PS in the objective space.

Differential evolution algorithm

Differential evolution algorithm, introduced by Storn and Price (1995, (1997) is one of the most powerful evolutionary optimization techniques (Das and Suganthan 2011). The main steps of DE are described as follows (Storn et al. 2005):

• 1) Initialization operation: the mutation control parameter $F$, crossover control parameter CR, population size NP, and maximum number of generations $G_{\max }$ are determined, and the current generation $G=\,0$ is set. The initial individuals ${{\mathbf {x}}}_t^0 ,t=1,2,\ldots ,NP$ is generated randomly in ${\varvec{\varOmega }}$.

• 2) Mutation operation: for each ${{\mathbf {x}}}_t^G$ in the parent population, the mutant individual $\hat{{{{\mathbf {x}}}}}_t^{G+1}$ is generated as follows:

  $$\begin{aligned} \hat{{{{\mathbf {x}}}}}_t^{G+1} ={{\mathbf {x}}}_{r_1 }^G +F\cdot ({{\mathbf {x}}}_{r_2 }^G -{{\mathbf {x}}}_{r_3 }^G ), \end{aligned}$$

  (2)

  where $r_1$, $r_2$, and $r_3$ are randomly chosen within the range [1, NP] and are also different from the index $t$(i.e. $r_1 \ne r_2 \ne r_3 \ne t)$; $F$ is a real constant scaling factor, which controls the amplification of the differential variation $({{\mathbf {x}}}_{r_2 }^G -{{\mathbf {x}}}_{{{\mathbf {r}}}_3 }^G )$.

• 3) Crossover operation: for each ${{\mathbf {x}}}_t^G$, a trial individual $\bar{{{{\mathbf {x}}}}}_t^{G+1}$ is generated as follows:

  $$\begin{aligned}&\bar{{x}}_{tj}^{G+1} \nonumber \\&\quad =\left\{ {\begin{array}{l@{\quad }l} \hat{{x}}_{tj}^{G+1} ,&{}R_j \le CR\hbox { or }j=j_{rand} \\ x_{tj}^G ,&{}\hbox {otherwise} \\ \end{array}} \right. \quad j=1,2,\ldots ,D.,\nonumber \\ \end{aligned}$$

  (3)

  where $R_j$ is a uniform random number in the range [0, 1], and $j_{rand}$ is a randomly chosen integer within the range [1, $D$].

• 4) Selection operation: the offspring $\bar{{x}}_t^{G+1}$ competes one-to-one with its parent $x_t^G$. The evaluation operation is expressed as follows:

  $$\begin{aligned} {{\mathbf {x}}}_t^{G+1} =\left\{ {\begin{array}{l@{\quad }l} \bar{{{{\mathbf {x}}}}}_t^{G+1} ,&{}f(\bar{{{{\mathbf {x}}}}}_t^{G+1} )\le f({{\mathbf {x}}}_t^G ) \\ {{\mathbf {x}}}_t^G ,&{}\hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$

  (4)

• 5) $G=G+\,1.$

• 6) Steps 2 to 5 are repeated as long as the number of generations is smaller than the allowable maximum number $G_{\max }$.

Multi-objective modified differential evolution algorithm

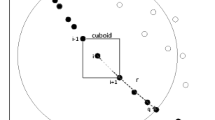
Although the selection operation based on fast nondominated sorting in NSGAII algorithm (Deb et al. 2002a) is very effective, its greediness may lead to lose of some useful inferior individuals during the evolution process. it can be seen from Fig. 1 that dominated solutions may become nondominated solutions after a few generations because these inferior solutions may carry direction information toward the true Pareto front (Zhang and Sanderson 2008). Based on the above observations, we proposed a MOMDE-AM algorithm that can balance between exploration and exploitation capabilities during the search process.

Fig. 1

The evolution of nondominated and dominated solutions during a few generations

Overall implementation of the MOMDE-AM

The proposed algorithm is described as follows:

• 1) Initialization operation

Determine the values of parameters such as mutation control parameter $F$, crossover control parameter CR, the maximum generations $G_{\max }$, and a constant number $Bset = 0.6$. Generate the initial population ${{\mathbf {P}}}_1^0$ and set the current generation $G = 0$. Let ${{\mathbf {P}}}_2^0 ={{\mathbf {P}}}_1^0$.

• 2) Population evolution

For each individual ${{\mathbf {x}}}_t^G ,t=1,2,\ldots ,NP$, the mutation and crossover operations are used to produce the trail vectors

$$\begin{aligned} \hbox {Mutation operation: }\hat{{{{\mathbf {x}}}}}_t^{G+1} ={{\mathbf {x}}}_{r_1 }^G +F\cdot ({{\mathbf {x}}}_\mathrm{archive,t}^G -{{\mathbf {x}}}_{r_2 }^G ). \end{aligned}$$

(5)

where ${{\mathbf {x}}}_\mathrm{archive,t}^G$ is randomly chosen from ${{\mathbf {P}}}_2^G$.

We can see from Eq. (5) that some useful inferior solutions stored in ${{\mathbf {P}}}_2^G$ can participate in the population evolution. Therefore, it can enhance the exploration ability of the proposed algorithm.

Boundary operation: if rand $>$ Bset, then $\hat{{x}}_{tj}^{G+1} = \left\{ {\begin{array}{ll} x_{r_1 j}^G &{}\hat{{x}}_{tj}^{G+1} <x_j^{\mathrm{low}} \\ x_{r_1 j}^G &{}\hat{{x}}_{tj}^{G+1} >x_j^{\mathrm{high}} \\ \end{array}} \right.$, otherwise, infeasible variables are randomly regenerated in feasible region ${\varvec{\varOmega }}$.

Crossover operation:

$$\begin{aligned} \bar{{x}}_{tj}^{G+1}\!=\!\left\{ {\begin{array}{l@{\quad }l} \hat{{x}}_{tj}^{G+1} ,&{}R_j \le CR\hbox { or }j=j_{rand} \\ x_{tj}^G ,&{}\hbox {otherwise} \\ \end{array}} \right. j=1,2,\ldots ,D. \end{aligned}$$

• 3) Selection operation

  • (1) if ${{\mathbf {x}}}_t^G \succ \bar{{{{\mathbf {x}}}}}_t^{G+1}$, ${{\mathbf {x}}}_t^G$ is reserved in the population ${{\mathbf {P}}}_1^G$.

  • (2) if $\bar{{{{\mathbf {x}}}}}_t^{G+1} \succ {{\mathbf {x}}}_t^G$,${{\mathbf {x}}}_t^G$ is replaced by $\bar{{{{\mathbf {x}}}}}_t^{G+1}$ in the population ${{\mathbf {P}}}_1^G$.

  • (3) if ${{\mathbf {x}}}_t^G$ and $\bar{{{{\mathbf {x}}}}}_t^{G+1}$ are nondominated with each other, $\bar{{{{\mathbf {x}}}}}_t^{G+1}$ is added in the population ${{\mathbf {P}}}_1^G$.

• 4) Useful individuals store

NP individuals are randomly chosen from the population ${{\mathbf {P}}}_1^G$, and store them in population ${{\mathbf {P}}}_2^G$.

• 5) Fast nondominated sorting (Deb et al. 2002a) and crowding distance sorting (Deb et al. 2002a) are used to select NP individuals from the population ${{\mathbf {P}}}_1^G$ and store them in population ${{\mathbf {P}}}_1^G$.

• 6) $G=G+1$.

• 7) Repeat steps 2) to 6) as long as the number of generations is equal to the allowable maximum number $G_{\max }$.

Performance analysis of MOMDE-AM on ZDT and DTLZ test suites

To demonstrate the average performance of MOMDE-AM, the proposed algorithm was compared with five MOEAs [i.e., GDE3 citeKL01, NSGAII-DE (Li and Zhang 2009), BB-MOPSO (Zhang et al. 2009), MOEA/D-DE (Li and Zhang 2009), and MODE-RMO (Chen et al. 2014)] on five bi-objective problems (i.e., ZDT1, ZDT2, ZDT3, ZDT4, and ZDT6) (Zitzler et al. 2000) and five problems of DTLZ family (i.e., DTLZ1- DTLZ5) (Deb et al. 2002b). Note that functions DTLZ1- DTLZ5 have three objective functions in the current study. Moreover, the basic descriptions of these MOPs are shown in Table 1. All these compared algorithms were programmed in Matlab (R2012a) and were run on a windows 7 operating system (64 bit). Furthermore, to effectively analyze the experimental results obtained by the compared algorithms, two non-parametric statistical tests with the significance level of 0.05 were utilized in the experiments, namely, Wilcoxon’s rank sum test (Wilcoxon 1945) and Friedman’s test (Friedman 1937). For the Wilcoxon’s rank sum test, the “+”, “-”, and “$\approx$” marks denote that MOMDE-AM performs significantly better than, worse than, and almost the same as the compared algorithms, respectively.

Table 1 ZDT and DTLZ test functions

Performance metric

Zitzler et al. (2000) stated that a multi-objective optimization has two goals, i.e., fast convergence to the true PF and diversity maintenance of the obtained PF, therefore, to validate the quality of the final nondominated solutions for different MOEAs, two performance metric (Deb et al. 2002a; Zitzler et al. 2003; Van Veldhuizen and Lamont 1998) (i.e., the generational distance GD and the inverted generational distance IGD) are used in the current study. GD can be defined as follows:

$$\begin{aligned} GD(PF,PF^{{*}})=\frac{\sqrt{\sum _{v\in PF} {d(v,PF^{{*}})^{2}} }}{\left| {PF} \right| } \end{aligned}$$

(6)

where PF is the set of obtained Pareto objective vectors, $PF^{{*}}$ is Pareto objective vectors in the true PF of multi-objective optimization problem. $d(v,PF^{{*}})$is the Euclidean distance between $v$ and the nearest point in $PF^{{*}}$, $\left| P \right|$ denotes the number of Pareto objective vectors found by evolutionary algorithms in PF. A smaller value of GD indicates a better convergence to the true PF.

IGD is defined as follows:

$$\begin{aligned} IGD(PF,PF^{{*}})=\frac{\sqrt{\sum _{v\in PF^{{*}}} {d(v,PF)} ^{2}}}{\left| {PF^{{*}}} \right| } \end{aligned}$$

(7)

where $\left| {PF^{{*}}} \right|$ is the number of points in $PF^{{*}}$, $d(v,PF)$ is the minimum Euclidean distance between $v$ and the obtained Pareto objective vectors. IGD could measure both the diversity and convergence of obtained PF.

Comparison with five MOEAs on ten MOPs

In this experiment, the experimental results of 10 MOPs using MOMDE-AM are compared with the results of other five MOEAs using performance metrics GD and IGD. For all compared algorithms, the population size NP is set to 100, the maximum generations $G_{\max }$ is set to be the same as in the literatures (Deb et al. 2002a, b), namely, 250 for 5 bi-objective test functions, 300 for DTLZ1 and DTLZ2, 500 for DTLZ3, 200 for DTLZ4 and DTLZ5, and the times of experimental runs are set to be 20. Several control parameter settings of GDE3 and MODE-RMO are suggested in literature (Robič and Filipič 2005), i.e., $F = 0.5$, $CR = 0.3$, some of control parameter settings of NSGAII-DE are maintained as reported in (Li and Zhang 2009), i.e., $F = 1$, $CR = 0.5$. Additionally, based on the studies in Robič and Filipič (2005) and Abbass et al. (2001), MOMDE-AM algorithm uses the following parameter settings: $F = 0.5$, CR is chosen in the range [0.15 to 0.35] and is generated by a normal distribution function (i.e., $N$(0.25,0.03)). The best results are shown in bold in Tables 3, 5, 7, and 8.

The GD metric in terms of the mean and standard deviation values using six compared algorithms and statistical test results obtained by Wilcoxon’s rank sum test are shown in Table 2, it can be seen from Table 2 that the convergence performance of MOMDE-AM is significantly better than GDE3, NSGAII-DE, MODE-RMO, BB-MOPSO, and MOEA/D-DE on 7, 10, 6, 7, and 10 test functions. At the same time, MOMDE-AM performs the best on all bi-objective test functions when compared with GDE3, NSGAII-DE, MODE-RMO, and MOEA/D-DE. However, BB-MOPSO performs better than MOMDE-AM on three functions, i.e., ZDT1, ZDT2, and ZDT3. GDE3 performs better than MOMDE-AM on one test function DTLZ4. However, NSGAII-DE, MOEA/D-DE, and MODE-RMO cannot perform better than MOMDE-AM on any test functions in term of GD metric. Based on the above observations, it is clearly that the obtained Pareto fronts from MOMDE-AM are closer to the true Pareto fronts than those computed by GDE3, NSGAII-DE, MODE-RMO, BB-MOPSO, and MOEA/D-DE on almost all selected MOPs. Furthermore, The Friedman’s test is also employed to evaluate the convergence performances of all compared algorithms; the rankings obtained by Friedman’s test are shown in Table 3. It is clearly that the overall convergence performance of MOMDE-AM is the best among these compared algorithms.

Table 2 Mean and standard deviation of GD

Table 3 Ranking obtained by Friedman’s test on GD

Table 4 Mean and standard deviation of IGD

Table 5 Ranking obtained by Friedman’s test on IGD

The mean and standard deviation values of IGD and the corresponding statistical analysis results are shown in Table 4. The experimental results indicate that MOMDE-AM outperforms GDE3 on all test functions in term of IGD metric. The optimization performances of NSGAII-DE, MODE-RMO, and MOEA/D-DE cannot perform better than that of MOMDE-AM on any test functions. From Table 4, it is clearly that the overall performance of MOMDE-AM is better than those of GDE3, NSGAII-DE, MOEA/D-DE, MODE-RMO, and BB-MOPSO on these test functions. Furthermore, it can be observed from the statistical analysis results shown in Table 5 that the proposed algorithm performs the best among all compared algorithms in term of IGD performance metric.

Based on the above comparisons and analyses, MOMDE-AM significantly performs better than GDE3, MOEA/D-DE, and NSGAII-DE and outperforms MODE-RMO and BB-MOPSO on these test functions in term of GD and IGD. It means that MOMDE-AM can balance between convergence to the Pareto front and population diversity during the search process.

Effect of modified mutation strategy

In this experiment, to demonstrate the effectiveness of the modified mutation strategy in the proposed algorithm, MOMDE-AM is compared with MOMDE-AM without modified mutation strategy (denoted by MOMDE-AM1) on 10 selected test functions. Moreover, some of parameter settings are the same as in “Comparison with five MOEAs on ten MOPs” section. The experimental results are shown in Table 6. For all bi-objective test functions, MOMDE-AM1 outperforms MOMDE-AM in term of GD and IGD metric because the exploitation ability of MOMDE-AM1 is better than that of MOMDE-AM. However, for 5 tri-objective optimization problems, MOMDE-AM1 cannot perform better than MOMDE-AM on any test functions in term of GD and IGD metric. Clearly, the convergence and diversity performances of MOMDE-AM1 decreases with the number of objectives increasing due to its greedy nature. However, the overall performance of MOMDE-AM is better than that of MOMDE-AM1 with the number of objectives increasing because MOMDE-AM can reduce the loss of population evolution information (i.e., population diversity).

Table 6 Comparison of MOMDE-AM and MOMDE-AM without modified mutation strategy

Study of parameter

In this section, to obtain a suitable parameter setting for users, the effect of different parameter setting in MOMDE-AM is analyzed with Bset selected from the set (0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1). For the boundary operation, If infeasible variables are randomly regenerated in the feasible space, it means that MOMDE-AM has good exploration ability. On the other hand, if infeasible variables are randomly chosen from the parent vectors, it helps MOMDE-AM to speed up convergence. To save space, the experimental results are not shown in the paper, but the statistical analysis results are shown in Tables 7 and 8. For GD metric, it can be seen from Table 7 that the local search ability of MOMDE-AM is the best when $Bset =1$ because all infeasible variables are randomly selected from the parents can help to improve the convergence speed. For IGD metric, Table 8 indicates that overall performance (i.e., convergence and diversity) of MOMDE-AM is the best when $Bset = 0.9$ and is the second best when $Bset = 0.6$. Moreover, to provide a visualization of these results, three changing curves of rankings are shown in Fig. 2. In Fig. 2, green and magenta lines denote the changing trends of IGD and GD under different parameter settings, respectively. Blue line denotes changing trend of the sum of GD and IGD rankings. From Fig. 2, it is observed that $Bset = 0.9$ provides the best overall performance (see blue line); however, the conclusions may be unreliable because the experimental results of bi-objective test functions (the simplest problems in MOPs) may significantly affect the final statistical results. To further study the parameter Bset, the experimental results (IGD metric) of 5 bi-objective and 5 tri-objective test functions are analyzed separately. Figure 3 illustrates that the large Bset value can provide better performance on 5 bi-objective test functions while it gives worse performance on 5 tri-objective test functions. The reason is that a low value of Bset can increase the population diversity and is beneficial to solve high-dimensional MOPs. Based on the above analyses, to balance the exploration and exploitation abilities, $Bset = 0.6$ is used in MOMDE-AM.

Fig. 2

The curves of ranking under different Bset values

Fig. 3

The curves of ranking for different number of objectives

Table 7 Ranking obtained by Friedman’s test under different Bset for GD

Table 8 Ranking obtained by Friedman’s test under different Bset for IGD

PX oxidation process optimization using MOMDE-AM

Modeling of the PX oxidation reaction process and HAc and PX combustion loss

Over the past two decades, numerous lumped kinetic model of PX oxidation reaction process (Cao et al. 1994a, b; Sun et al. 2008; Yan et al. 2004) have been presented. In the current study, the lumped kinetic model (Yan et al. 2004), which includes a set of equations, are used. Moreover, considering that the rate constants are difficult to model with reaction factors, therefore, the values of the rate constants are solved by the radical basis functions (RBF) coupled with partial least-squares (PLS). The more detailed descriptions of the lumped kinetic model of PX oxidation reaction process can be found in (Yan et al. 2004).

Generally, the PX oxidation reaction process is accompanied by a large number of side reactions, wherein HAc and PX combustion are two major side reactions (Yan et al. 2005). Although various kinetic models of side reactions (Kenigsberg et al. 1995; Cheng et al. 2006; Cincotti et al. 1997) have been proposed, the consumption of HAc and PX in the industrial PX oxidation reactions is difficult to obtain because the reaction mechanism is very complex. In the current study, the artificial neural network is used to constructed the model of HAc and PX combustion loss under different operation conditions (Yan et al. 2005). The amount of acetic acid combustion loss $m_\mathrm{HAc}^\mathrm{consume}$ (kg/T CTA) and PX combustion loss $m_\mathrm{PX}^\mathrm{consume}$ (kg/T CTA) in reactor can be calculated as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} x_{\mathrm{co}_\mathrm{x }} =f(x_1 ,x_2 ,x_3 ,x_4 ,x_5 ,\tau ) \\ m_\mathrm{HAc}^\mathrm{consume} =\frac{m_\mathrm{gas} \times x_{\mathrm{co}_\mathrm{x }} \times \frac{x_\mathrm{HAc} }{100}\times \frac{60}{1000}}{2\times \frac{m_\mathrm{HAc}^{\mathrm{co}_\mathrm{x }} }{100}\times m_\mathrm{CTA} } \\ \end{array}} \right. \end{aligned}$$

(8)

and

$$\begin{aligned} \left\{ {\begin{array}{l} x_{\mathrm{co}_\mathrm{x }} =f(x_1 ,x_2 ,x_3 ,x_4 ,x_5 ,\tau ) \\ m_\mathrm{PX}^\mathrm{consume} =\frac{m_\mathrm{gas} \times x_{\mathrm{co}_\mathrm{x }} \times \frac{x_\mathrm{PX} }{100}\times \frac{106}{1000}}{8\times \frac{m_\mathrm{PX}^{\mathrm{co}_\mathrm{x }} }{100}\times m_\mathrm{CTA} } \\ \end{array}} \right. \end{aligned}$$

(9)

where $x_{\mathrm{co}_{x}}$ is the carbon dioxide and carbon monoxide contents in the wastegas of the reactor (denoted as D1$-$301 in Fig. 4) and represents the degree of side reactions; $f({\bullet })$ is the content model of the carbon dioxide and carbon monoxide in the wastegas of the reactor developed by artificial neural networks; $x_1 \left( {^{\circ }\hbox {C}} \right)$ is the reaction temperature; $x_2$ (mol/kg acetic acid) is the concentration of PX in acetic acid solvent; $x_3$ (%), $x_4$ (%), and $x_5$ (%) are the weight percentage of cobalt, manganese, and bromine in the feed, respectively; $x_{\mathrm{HAc}}$ and $m_{\mathrm{HAc}}^{\mathrm{co}_\mathrm{x} }$ are 61 and 75 % in the industrial oxidation process; $m_{\mathrm{gas}}$and $m_{\mathrm{CTA}}$ are obtained from industrial production data. $x_{\mathrm{PX}}$ and $m_{PX}^{\mathrm{co}_\mathrm{x} }$ are 39 and 60 % of the industrial oxidation process.

Fig. 4

Flow diagram of the PX oxidation reaction process in Aspen Plus

Modeling of the PX oxidation reaction process by using Aspen Plus

Based on the lumped kinetic model of PX oxidation reaction process, HAc and PX combustion loss models are introduced in “Modeling of the PX oxidation reaction process and HAc and PX combustion loss” section, the industrial PX oxidation reaction model is built by using Aspen Plus 11.1. At the same time, some of property data (Renon and Prausnitz 1968) provided by Aspen Plus are used as part of the PX oxidation reaction model. The flow diagram of PX oxidation reaction process is shown in Fig. 4 (Fan and Yan 2015). MIX-FLOW is the mixed feed of the reactor; FIA2052 is the air feed of the reactor; FIA20602 is the air feed of the first crystallizer; WASTEGAS is the waste gas of the reactor; FIC20577 is the drainage flowrate of the reactor; D1$-$301 is the reactor; D1$-$401, D1$-$402, and D1$-$403 are the crystallizers; E1$-$304, E1$-$305, E1$-$306, and E1$-$307 are the heaters.

Construction of the MOP in the PX oxidation reaction process

During the production process of PTA, the yield and quality of PTA is directly affected by operation conditions of PX oxidation reaction process. For example, with the rise of the concentrations of Co, Br, and Mn in the feed, the consumption of HAc and PX will increase and the content of 4-CBA will decrease. Therefore, reduce HAc and PX combustion loss to achieve greater economic benefits and control the content of 4-CBA at a lower level to ensure the quality of PTA are two conflicting objectives in the PTA production. In this paper, this problem can be regarded as a tri-objective optimization problem and is described as follows:

$$\begin{aligned}&{{\mathbf {F}}}({{\mathbf {x}}})\!=\!\left[ {\min \left\{ {m_\mathrm{HAc}^\mathrm{consume} } \right\} ,\min \left\{ {m_\mathrm{PX}^\mathrm{consume} } \right\} ,\min \left\{ {x_{4-CBA} } \right\} } \right] ^{T}\nonumber \\&\begin{array}{l} s.t.\\ \left\{ {\begin{array}{l} x_{\mathrm{1,}\max } \le x_1 \le x_{\mathrm{1,}\max } \\ x_{2\hbox {,}\min } \le x_2 \le x_{\mathrm{2,}\max } \\ x_{\mathrm{3,}\min } \le x_3 \le x_{\mathrm{3,}\max } \\ x_{\mathrm{4,}\min } \le x_4 \le x_{\mathrm{4,}\max } \\ x_{\mathrm{5,}\min } \le x_5 \le x_{\mathrm{5,}\max } \\ x_{\mathrm{6,}\min } \le x_6 \le x_{\mathrm{6,}\max } \\ x_{\mathrm{7,}\min } \le x_7 \le x_{\mathrm{7,}\max } \\ x_{\mathrm{8,}\min } \le x_8 \le x_{\mathrm{8,}\max } \\ x_{\mathrm{9,}\min } \le x_9 \le x_{\mathrm{9,}\max } \\ x_{\mathrm{10,}\min } \le x_{10} \le x_{\mathrm{10,}\max } \\ l_{\min } \le l\le l_{\max } \\ x_{4-CBA}^{\min } \le x_{4-CBA} \le x_{4-CBA}^{\max } \\ \end{array}} \right. \\ \end{array} \end{aligned}$$

(10)

where $x_1 \left( {^{\circ }\hbox {C}} \right)$ is the reaction temperature; $x_2$ (mol/kg acetic acid) is the concentration of PX in an acetic acid solvent; $x_3$ (%), $x_4$ (%), and $x_5$ (%) are the weight percentages of Co, Mn, and Br in the feed, respectively; $x_6$(T/Hr) is the drainage flowrate of the reactor; $x_7 \left( {^{\circ }\hbox {C}} \right) , x_8 \left( {^{\circ }\hbox {C}} \right) , x_9 \left( {^{\circ }\hbox {C}} \right) ,$ and $x_{10} \left( {^{\circ }\hbox {C}} \right)$ are the first, second, third, and fourth heater temperatures, namely, E1$-$304, E1$-$305, E1$-$306, and E1$-$307, respectively; $l$(%) is the liquid level of the reactor D1$-$301, i.e., the residence time under a given mixed feed; $x_{4-CBA}$(ppm) is the 4-CBA content in CTA. $m_\mathrm{HAc}^\mathrm{consume}$ (kg/T CTA) is the amount of acetic acid combustion loss in a reactor; $m_\mathrm{PX}^\mathrm{consume}$ (kg/T CTA) is the amount of PX combustion loss in a reactor. The lower and upper boundaries of these optimized parameters are shown in Table 9. Furthermore, Note that the lower and upper limits of the concentration of PX in an acetic acid solvent are equal to actual industrial values because it is obtained from long-term optimization. And the content of 4-CBA should be within an appropriate level because it must comply with the actual industrial production.

Table 9 Lower and upper boundaries of optimized parameters

Fig. 5

Framework of the optimization system for the PX oxidation reaction process

Operation conditions optimization of PX oxidation reaction process

In the current study, PX oxidation reaction process model is established by using Aspen Plus 11.1 and the proposed algorithm is programmed in Matlab (R2012a). However, data between Matlab and Aspen Plus cannot be directly exchanged. Fortunately, a MAP interface toolbox based on COM technology that can exchange data between Matlab and Aspen Plus is developed by Geng et al. (Geng et al. 2006). The framework of the optimization system is presented in Fig. 5. Furthermore, The optimization function of PX oxidation reaction process can be seen in Formula 10.

Case study

In this experiment, the proposed algorithm is used to optimize the common state of the PX oxidation reaction process from the PTA industry at 10 a.m. on 16 July 2009. In MOMDE-AM, the population size NP and maximum generations $G_{\max }$ is set to 40 and 100, respectively. The other operation conditions of PX oxidation reaction process, which are used as the parameter settings of the model in Aspen Plus, are shown in the Appendix. Moreover, the content of 4-CBA is within the range [0.225, 0.235]. Three typical Pareto front are shown in Figs. 6, 7, and 8. It can be seen from Fig. 6 that PX combustion losses is proportional to the consumption of HAc. Figure 7 indicates that the content of 4-CBA decreases with increasing HAC combustion loss. Therefore, based on the above observations, it is can beclearly seen that the content of 4-CAB (i.e., PTA quality) and the consumption of PX and HAc (i.e., production cost) are two conflicting objectives. To further investigate the relationship among the mentioned three objectives in Formula 10, the obtained Pareto front is illustrated in Fig. 8. Clearly, it is observed that MOMDE-AM can help decision makers to obtain a tradeoff solution in the decision making process. Table 10 shows that the detailed information of two selected nondominated solutions (i.e., two boundary points S1 and S2 shown in Fig. 8) from the obtained Pareto front. For S1, it denotes that the content of 4-CBA is maximal while the consumption of PX and HAc is minimal. For S2, it means that the quality of PTA is the best, but production cost is the highest among all obtained solutions. It can be observed from Table 10 that MOMDE-AM can reduce PX combustion loss of S1 by 1.04 Kg/T.PTA, HAc combustion loss of S1 by 3.21 Kg/T.PTA, PX combustion loss of S2 by 1.02 Kg/T.PTA, HAc combustion loss of S2 by 3.13 Kg/T.PTA, and that the results of MOMDE-AM are better than the results obtained by Aspen Plus. Note that a single run of Aspen Plus is only able to obtain a single solution. From the above analyses, clearly, MOMDE-AM can obtain the optimal operation conditions for the PX oxidation reaction process when compared with the industrial operation conditions and Aspen Plus, and can provide a wider range of candidate solutions for the decision makers to choose suitable operation conditions based on the production planning.

Fig. 6

Interactions between PX and HAc combustion losses

Fig. 7

Interactions between 4-CBA content and HAc combustion loss

Fig. 8

Interactions among 4-CBA content, and PX and HAc combustion losses

Table 10 Experimental results

Conclusions

In the current study, a multi-objective modified differential evolution algorithm with archive-base mutation (MOMDE-AM) is proposed to solve MOPs. In MOMDE-AM, several inferior solutions are used to balance between the exploration and exploitation capabilities and provide direction information about the true Pareto front. The performance of MOMDE-AM was compared with those of GDE3, NSGAII-DE, MODE-RMO, BB-MOPSO, and MOEA/D-DE on five bi-objective and five tri-objective benchmark test functions. The simulation and statistical analysis results demonstrate that MOMDE-AM outperforms the compared MOEAs in term of GD and IGD performance metric. To reduce manual tuning DE parameters that need to be set by users, some parameters of the proposed algorithm were chosen based on the statistical analysis results obtained by non-parametric statistical tests. At the same time, the performance of MOMDE-AM was compared with that of MOMDE-AM without modified mutation strategy (i.e., MOMDE-AM1). Although the performance of MOMDE-AM is worse than that of MOMDE-AM1 on five bi-objective test functions, MOMDE-AM can perform better than or similar to MOMDE-AM1 on five tri-objective problems. The results indicate that the performance of MOMDE-AM is more robust than MOMDE-AM1 with the number of objectives increasing. Additionally, MOMDE-AM was used to solve an actual MOP which contains three conflicting objective functions. The experimental results show that MOMDE-AM is an effective optimization tool for solving real-world MOPs because it can provide a set of nondominated solutions to help decision makers choose a trade-off solution.

Appendix

See Table 11.

Table 11 Operation conditions of PX oxidation reaction process at 10 a.m. on 16 july 2009